Задание 11. Правописание суффиксов (кроме Н и НН)
Укажите варианты ответов, в которых в обоих словах одного ряда пропущена одна и та же буква.
Задание 1
-
им..нной, берест..ной
-
бахромч..тый, изжелт..-зелёный
-
ветр..ная (девушка), масл..ное (пятно)
-
въедл..вый, насла..вать
-
преодол..вать, вермишел..вый
Задание 2
-
конн..ца, брат..ц
-
ковш..к, горош..на
-
нов..нький, излиш..к
-
сбивч..вый, размораж..вать
-
узорч..тый, издавн..
Задание 3
-
находч..вый, милост..вый
-
заказ..ик, подряд..ик
-
занов…, команд..вать
-
ялт..нский, лягуш..чий
-
фасол..вый, споко..н
Задание 4
-
сызнов.., досыт..
-
выдум..вать, завед..вать
-
никел..вый, достра..вать
-
пупырч..тый, дощ..ной
-
приветл..во, оскуд..вать
Задание 5
-
корч..вка, стаж..р
-
влев.., изредк..
-
скольз..ий, альпинист..кий
-
усва..вающий, сосредоточ..вать
-
ландыш..вый, бахромч..тый
Задание 6
-
застр..вать, милост..вый
-
белорус..кий, скольз..кий
-
гуттаперч..вый, обеззуб..л (к старости)
-
издавн.., засветл..
-
форел..вый, син..ватый
Задание 7
-
размаз..вать, развед..вательный
-
выкорч..вать, застенч..вый
-
кормил..ца, наста..вая
-
эмал..вый, имень..це
-
справ.. (от дома), половинч..тый
Задание 8
-
удоста..вать, зонт..чный
-
(в) плам..ни, юрод..вый
-
забол..вающий, ненавязч..вый
-
досто..н, зелён..нький
-
черешн..вый, труж..ник
Задание 9
-
удушл..вый, удосто..н
-
кормил..ца, наста..вать
-
галч..нок, (вытереть) насух..
-
(смотрит) искос.., пластинч..тый
-
замш..вый, буш..вать
Задание 10
-
син..ватый, обур..ваемый
-
плюш..вый, азот..стые (соединения)
-
сводч..тый (потолок), сначал..
-
абхаз..кий, скольз..кий
-
завед..вать, парч..вое (платье)
Задание 11
-
вынаш..вать, кресл..це
-
забол..вать, больш..ватый
-
обессил..л (противника), ситц..вый
-
ноч..вка, кумач..вый
-
тунгус..кий, дерз..кий
Задание 12
-
выкорч..вать, эмал..вый
-
размаз..вая, разглаж..вая
-
ноч..вка, шапч..нка
-
конн..ца, усва..вать
-
птиц..н, классиц..зм
Задание 13
-
разбуш..вался, обслуж..вание
-
крупитч..тый, (существует) издавн..
-
(наелся) досыт.., (объяснял) доходчив..
-
врем..нной (отрезок), земл..ной (вал)
-
каменщ..к, заботл..вый
Задание 14
-
петуш..к, (наряд) смеш..н
-
реснитч..тый, (повернуть) направ..
-
ветр..ный (день), вод..нистый
-
доверч..вый, прислуш..ваться
-
ветр..ная (мельница), им..нное (оружие)
Задание 15
-
юрод..вый, настойч..вый
-
письм..цо, зайч..нок
-
плос..кий, институт..кий
-
протал..нка, доплач..вая
-
затм..вать, нож..вка
Задание 16
-
плать..це, рул..вой
-
команд..вать, намаз..вая
-
застенч..вый, выкорч..вать
-
карандаш..к, наста..вать
-
половинч..тый, слев..
Задание 17
-
эмал..вый, подмиг..вая
-
удачл..вый, влюбч..вый
-
удоста..вавший, глянц..витый
-
завинч..вать, воробуш..к
-
исслед..вали, занов..
Задание 18
-
канад..кий (клён), ткац..кий (станок)
-
(звон) бубенч..ков, осва..вать (территорию)
-
бич..вать (пороки), обесточ..ли (квартал)
-
предприимч..вый (человек), сосредоточ..вать (внимание)
-
(милый) добряч..к, суш..ные (фрукты)
Задание 19
-
(город) обезлюд..л, подшуч..вать (над приятелем)
-
сторож..вой (пёс), продл..вая (визу)
-
леле..л (мечту), коричн..ватый (оттенок)
-
унаслед..вать (землю), агитир..вавший (за кандидата)
-
клетч..тые (брюки), (протереть) досух..
Задание 20
-
исслед..вать, (свернуть) вправ..
-
молодц..ватый, классиц..зм
-
чайнич..к, завинч..вая
-
фасол..вый, отзывч..вый
-
переливч..тый, издавн..
Задание 11. Правописание суффиксов (кроме Н и НН)
Укажите варианты ответов, в которых в обоих словах одного ряда пропущена одна и та же буква.
Задание 1
Ответ: 245
Задание 2
Ответ: 2345
Задание 3
Ответ: 1235
Задание 4.
Ответ: 14 или 41
Задание 5
Ответ: 14 или 41
Задание 6
Ответ: 35 или 53
Задание 7.
Ответ: 135
Задание 8.
Ответ: 15
Задание 9.
Ответ: 2345
Задание 10.
Ответ: 135
Задание 11.
Ответ: 12 или 21
Задание 12.
Ответ: 14 или 41
Задание 13.
Ответ: 25
Задание 14.
Ответ: 14 или 41
Задание 15.
Ответ: 14 или 41
Задание 16.
Ответ: 45 или 54
Задание 17.
Ответ: 25 или 52
Задание 18.
Ответ: 24 или 42
Задание 19.
Ответ: 245
Задание 20.
Ответ: 15 или 51
Упражнение 1
Свернуть вправо, поглядывать изредка, поворотиться направо, справа от колонны, держаться запросто, наесться досыта, прийти затемно, одеться наскоро, начать сызнова, переписать набело, слева от кабинета, повернуть вправо, издавна знаком, запирать накрепко, соединить воедино, вытереть досуха, заколотить наглухо, проверить снова, отремонтировать заново, заниматься допоздна
Упражнение 2
Подоспеть вовремя, во время экскурсии, действовать наудачу, надеяться на удачу, копать в глубь, вглубь веков, насилу нашел, на силу не надейся, навеки исчезнуть, на веки веков, по началу фильма, обрадоваться поначалу, брызнуть на лицо, оказаться налицо, ввек не сыскать, в век электричества, в половине первого, вполовину меньше, вконец измучился, в конец коридора.
Упражнение 3
Впервые в истории, в первые секунды, на сколько частей, насколько могу судить, со всем коллективом, уехать совсем, разломать надвое, строительный материал на двое ворот, по этому расписанию, поэтому отстал, не за чем спрятаться, незачем спрашивать, не удалось вовсе, налить во все тарелки, сложить вшестеро, группа в шесть человек, подумал, затем написал, за тем поворотом.
На этой странице вы узнаете
- Как мы ежедневно расставляем знаки неравенства в жизни?
- Как быстро определить верное обозначение точки на прямой?
- Как правильно чередовать знаки на числовой прямой?
Решая уравнение, мы стремимся к тому, чтобы обе части были равны. Но существуют такие примеры, где мы заведомо знаем, что два выражения не могут быть равны между собой. Они называются неравенствами.
Метод интервалов
Неравенство — это алгебраическое выражение, в котором одна сторона имеет отличное от другой значение. В неравенствах обычно одна сторона больше другой.
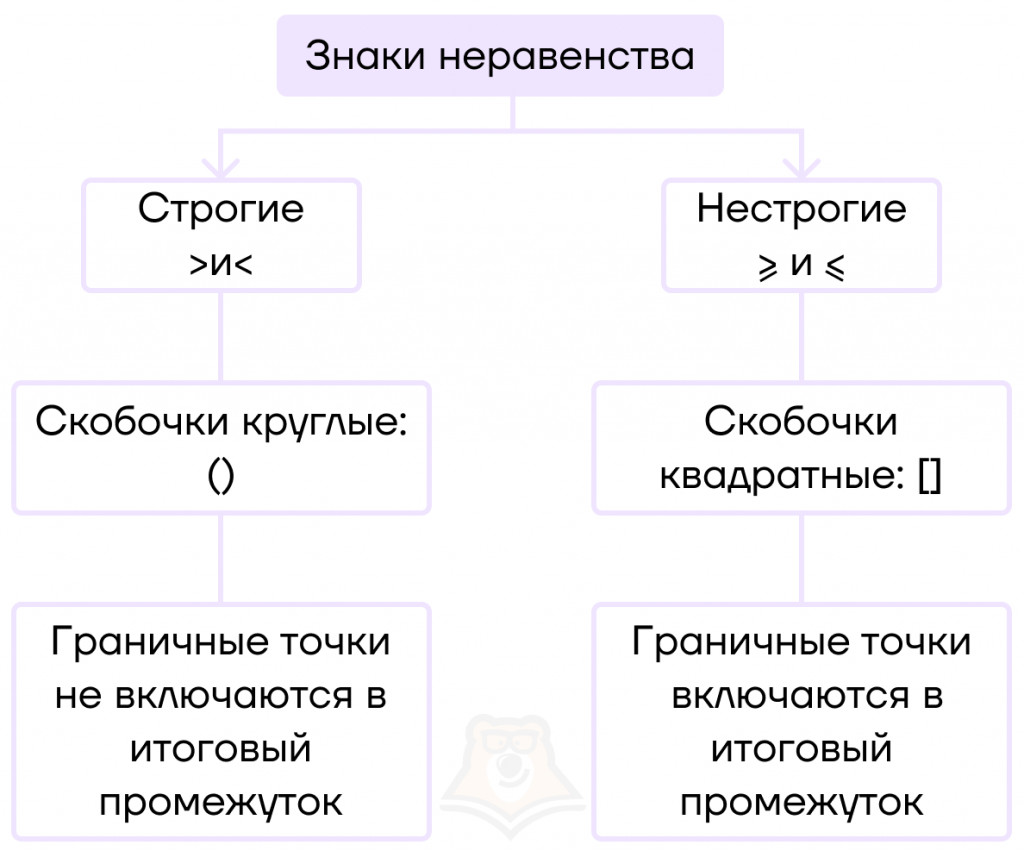
Для записи неравенств используют знаки > , < , ≥ , ≤ .
При этом “>” и “<” — это строгие знаки неравенства, а “≥” и “≤” — нестрогие знаки неравенства.
Их отличие в том, что нестрогие знаки неравенства включают граничные точки в итоговый промежуток, а строгие — нет.
Посмотрим на привычные ситуации с точки зрения строгости знаков неравенства.
Например, возьмем известную игру “Камень, ножницы, бумага”.
Правила игры говорят нам, что камень всегда побеждает ножницы, а бумага побеждает камень. Если перенести это на язык неравенства, то получится:
Теперь зайдем в магазин цифровой техники и попробуем выбрать себе новый мобильный телефон. Задачка непростая, не так ли? Две разные модели могут настолько незначительно отличаться друг от друга своими характеристиками, что будут казаться почти одинаковыми. Тогда мы можем сказать, что они практически равны между собой, то есть неравенство нестрогое. Но один из них всё-таки понравился нам больше.
И каждый наш выбор, каждый шаг – это расстановка знака неравенства в настоящей жизни. Просто по бокам от него не цифры и переменные, а существующие ситуации и вещи.
Рассмотрим пример неравенства (х — 10)(х + 21) > 0.

Его можно решить несколькими способами. Например, вспомним, что положительным будет произведение двух положительных или двух отрицательных множителей, тогда получается совокупность из двух систем.
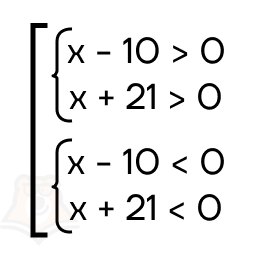
Однако этот способ решения очень трудоемкий и требует много времени. А если множителей будет больше, например, три или четыре, то время на решение в разы увеличивается.
Небольшой секрет тайм-менеджмента: как сократить время при решении неравенств? В таких случаях на помощь приходит метод интервалов.
Метод интервалов — специальный алгоритм решения для сложных неравенств вида f(x) > 0. При этом знак неравенства может быть любым.
Интервал — это промежуток на числовой прямой, ограниченный двумя различными числами.
Алгоритм решения неравенств методом интервалов
1 шаг. Перенести все части неравенства в одну сторону так, чтобы с другой остался только 0.
2 шаг. Найти нули функции, для этого необходимо решить уравнение f(x) = 0.
3 шаг. Начертить числовую прямую и отметить на ней все полученные корни. Таким образом, числовая прямая разобьется на интервалы.
4 шаг. Определить знаки на каждом интервале. Для этого необходимо подставить любое удобное значение в f(x) и определить, какой знак будет иметь функция на данном интервале.
Расставляя полученные корни на прямой, необходимо отмечать их точками. При этом от того, какая отмечена точка (выколотая или закрашенная), будет зависеть ответ.
- Если в неравенстве стоит строгий знак неравенства, то все точки на прямой должны быть выколотыми.
Таким образом, граничные точки не будут включены в итоговый промежуток. Для записи таких точек используют круглые скобочки. Например, в промежуток (2;3) включаются все значения от 2 до 3, но не включаются граничные точки.
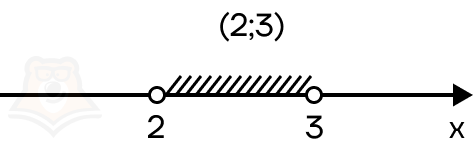
- Если в неравенстве стоит нестрогий знак неравенства, то найденные корни должны быть отмечены закрашенными точками.
Это означает, что мы включаем их в итоговый промежуток. Для записи таких точек используют квадратные скобочки. Например, в промежуток [2;3] включаются все значения от 2 до 3, в том числе и граничные точки.
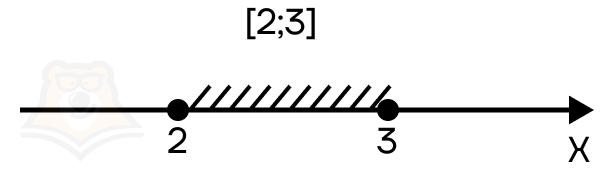
- Если в неравенстве появляются ограничения и некоторые точки нельзя взять в ответ, то такие точки должны быть выколотыми на числовой прямой, при этом знак самого неравенства может быть как строгим, так и нестрогим.
Например, если необходимо решить неравенство с дробью, то нули знаменателя на числовой прямой обязательно должны быть обозначены выколотыми точками.
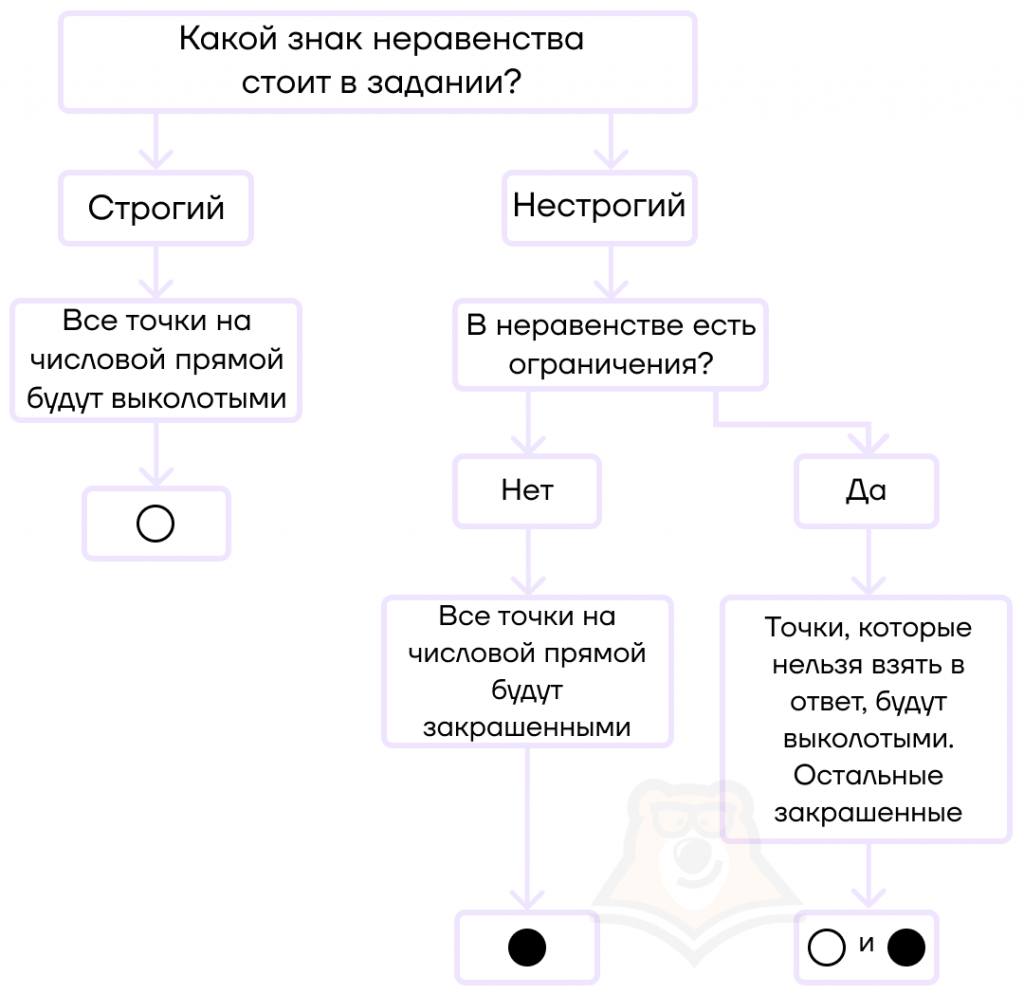
В случае сомнений мы всегда можем проверить себя по простой схеме.
Вывод:
— если знак неравенства строгий, то все точки будут выколотыми;
— если знак неравенства нестрогий, то точки будут закрашенными, кроме тех точек, которые нельзя взять в ответ (например, они не удовлетворяют ОДЗ).
Стоит отметить, что непрерывная функция будет менять знак только в точках, в которых она равна 0. Подробнее узнать про смену знака функции можно в статье «Определение и график функции». Именно поэтому в методе интервалов мы ищем и отмечаем нули функции на прямой — только при переходе через них будет меняться знак функции.
При этом существует способ, с помощью которого можно быстро расставить знаки на прямой. Достаточно определить знак на одном из интервалов, а дальше чередовать знаки при переходе через каждую точку на прямой.
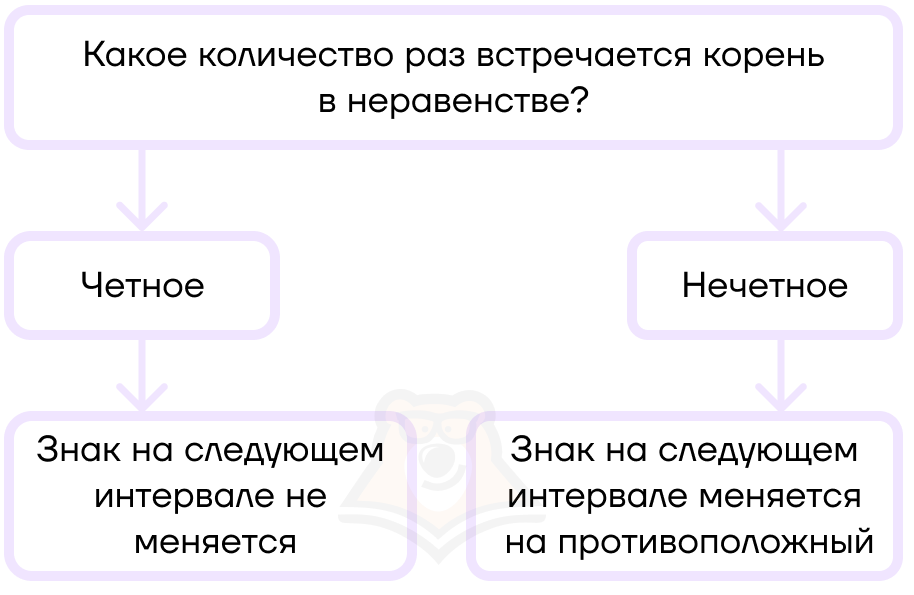
Правила чередования знаков:
- Если корень повторяется нечетное количество раз (то есть его степень нечетная), то знак при переходе на следующий интервал меняется.
- Если корень повторяется четное количество раз (его степень четная), то знак при переходе на следующий интервал не меняется.
Всегда будет нелишним перепроверить знак на каждом интервале, подставив значения в функцию, и убедиться в правильности расстановки знаков на прямой.
Но при расстановке можно пользоваться следующим алгоритмом, что значительно сократит время расстановки знаков.
Методом интервалов можно решить практически любое неравенство в задании 14 из ЕГЭ по профильной математике, также он может понадобиться в заданиях 8, 11 и 17 «профиля» или в задании 17 ЕГЭ по базовой математике.
На ОГЭ данным методом можно воспользоваться при решении неравенств из первой и второй частей — №13 и №20.
Так что осваивайте метод и 2 балла ЕГЭ или 3 балла ОГЭ будут у вас в кармане. Обязательно следуйте алгоритму решения неравенств методом интервалов, тогда вы точно решите неравенство верно.
Практика
Рассмотрим несколько примеров, чтобы на практике разобрать применение метода интервалов для решения неравенств.
Пример 1. Решить неравенство x2 + 8x — 33 > 0.
Шаг 1. Первым шагом необходимо найти нули функции, для этого приравниваем выражение слева к 0: x2 + 8x — 33 = 0.
Шаг 2. Находим корни уравнения, получаем х = 3 и х = -11.
Шаг 3. Расставляем полученные корни на числовой прямой. Поскольку знак неравенства строгий, то точки должны быть выколотыми:

Шаг 4. Дальше необходимо определить знаки на каждом интервале. Для этого подставим х = -12 в x2 + 8x — 33. Получаем:
(-12)2 + 8*(-12) — 33 = 144 — 96 — 33 = 15.
Получается положительное число, следовательно, интервал от минус бесконечности до -11 положительный. Поскольку все корни в неравенстве повторяются нечетное количество раз (по одному разу), то знаки чередуются.
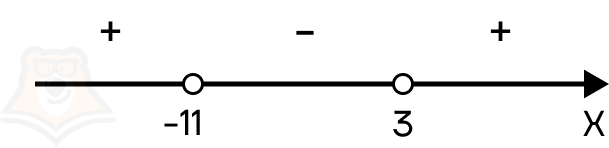
В ответ необходимо записать промежутки с положительным знаком, следовательно, ответом будет х ∈ (-∞; -11) U (3; +∞).
Пример 2. Решить неравенство (frac{2х^2 + 22х — 204}{(х-3)(х+5)} ≤ 0).
1. Находим нули функции.
Нули числителя: 2х2 + 22х — 204 = 0. Решая уравнение, получаем х = 6 и х = -17.
Нули знаменателя: (х — 3)(х + 5) = 0, следовательно, х = 3 и х = -5.
2. Расставляем полученные корни на числовой прямой. Нули числителя будут обозначены закрашенными точками, поскольку знак неравенства нестрогий. А вот нули знаменателя — выколотыми, поскольку знаменатель не может равняться 0, следовательно, и нули знаменателя не должны входить в итоговый промежуток.

3. Определяем знак на крайнем левом промежутке, подставляя х=-20 в дробь:
(frac{2(-20)^2 + 22(-20) — 204}{(-20 -3)(-20 +5)} = frac{2 * 400 — 440 — 204}{(-23) * (-15)} = 156345. )
Следовательно, промежуток положительный.
4. Поскольку каждый корень встречается один раз, то есть нечетное количество раз, то знаки будут чередоваться.

В ответ необходимо включить отрицательные промежутки. Следовательно, ответом будет х ∈ [-17; -5) U (3; 6].
Пример 3. Решить неравенство (frac{1}{х^2} ≥ frac{1}{х+2})
1. Первым делом следует отметить, что знаменатели не могут быть равны 0, следовательно, х2 ≠ 0 и х + 2 ≠ 0, отсюда получаем х ≠ 0 и х ≠ -2.
2. Теперь перенесем все части неравенства влево:
(frac{1}{х^2} — frac{1}{х+2} ≥ 0).
Приведем к общему знаменателю:
(frac{х + 2 — х^2}{х^2 (х + 2)} ≥ 0).
Для решения неравенства будет удобнее, если перед х2 в числителе будет стоять положительный знак, для этого умножим неравенство на -1.
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Получаем:
(frac{х^2 — х — 2}{х^2 (х + 2)} ≤ 0).
Теперь найдем нули функции.
Нули числителя: х2 — х — 2 = 0. Тогда х = -1 и х = 2.
Нули знаменателя: х = 0 и х = -2.
2. Расставим корни на числовой прямой, при этом нули числителя будут обозначены закрашенными точками, а нули знаменателя — выколотыми.

3. Определим знак на крайнем левом промежутке, подставив для этого х = -3 в дробь:
(frac{(-3)^2 — (-3) — 2}{(-3)^2 ((-3) + 2)} = frac{9 + 3 — 2}{9 * (-1)} = frac{10}{-9})
Промежуток отрицательный.
4. Дальше расставляем знаки, чередуя их. При этом следует заметить, что х = 0 — корень, повторяющийся четное количество раз (поскольку у х2 четная степень). Следовательно, при переходе через эту точку знак функции меняться не будет.

В ответ необходимо включить отрицательные промежутки, следовательно: х ∈ (-∞; -2) U [-1; 0) U (0; 2].
Давайте подведем итог. Для чего мы это изучили?
Конечно же, эти знания пригодятся на экзаменах, а также в решении школьных примеров с 8 класса по 11 класс.
Советуем после прочтения этой статьи попрактиковаться в рубрике «Проверь себя», чтобы закрепить полученные знания. После чего можете приступить к решению заданий посложнее, чтобы на экзамене у вас точно получилось решить подобные задания и набрать за них максимум баллов.
Фактчек
- Метод интервалов позволяет упростить решение любого неравенства, а также экономит время, которое ограничено на экзамене.
- Чтобы решить неравенство с помощью метода интервалов необходимо найти нули функции, расставить их на числовой прямой, а после определить знак каждого полученного интервала.
- Нули функции на прямой обозначаются точками, при этом закрашенные точки включают граничные значения в итоговый промежуток, а незакрашенные, напротив, исключают их из промежутка.
- Для определения знака на каждом интервале необходимо подставить любое значение из этого интервала в функцию.
- Для упрощения расстановки знаков можно пользоваться правилами чередования, определив знак только на одном интервале, а дальше менять знаки на каждом следующем. При этом если корень встречается в функции нечетное количество раз, то знак при переходе через эту точку на следующий интервал меняется, а если корень встречается четное количество раз, то знак на следующем интервале не меняется.
Проверь себя
Задание 1.
Какие знаки неравенства существуют?
- Строгие
- Нестрогие
- Строгие и нестрогие
- Больше и меньше
Задание 2.
Какой знак неравенства может встретиться в методе интервалов?
- Только больше или меньше.
- Только “больше или равно” или “меньше или равно”.
- Только “больше” и “больше или равно” или только “меньше” и “меньше или равно”.
- Любой.
Задание 3.
Какое утверждение верное?
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой закрашены.
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой выколоты.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой закрашены, даже если в неравенстве есть ограничения.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой выколоты.
Задание 4.
Какое утверждение верное?
- При переходе на числовой прямой на следующий интервал, знак на интервале всегда будет меняться.
- Если корень встречается в неравенстве четное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Если корень встречается в неравенстве нечетное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Невозможно определить правильное чередование знаков на прямой, не подставляя значение из каждого интервала в функцию.
Задание 5.
Если в неравенстве строгий знак неравенства, то какие скобочки могут встретиться в ответе?
- Круглые
- Квадратные
- И круглые, и квадратные
- Ни один из перечисленных вариантов
Ответы: 1. — 3 2. — 4 3. — 2 4. — 2 5. — 1
Задание №2269.
Правописание приставок, корней и суффиксов. ЕГЭ по русскому
Укажите варианты ответов, в которых в обоих словах одного ряда пропущена одна и та же буква. Запишите номера ответов.
1) перешаг..вающий, кресл..це
2) завистл..вый, взрывч..тые (вещества)
3) глянц..вый, недоум..вать
4) насла..ваться, посе..ть
5) еж..вые (рукавицы), смещ..нный (вправо)
Пояснение:
Приведём верное написание слов:
1) перешагИвающий, креслИце
2) завистлИвый, взрывчАтые (вещества)
3) глянцЕвый, недоумЕвать
4) наслаИваться, посеЯть
5) ежОвые (рукавицы), смещЁнный (вправо)
Показать ответ
Источник: ФИПИ. Открытый банк тестовых заданий
Сообщить об ошибке
Тест с похожими заданиями