Исследовательская работа финансовая математика в задачах егэ

Автор: Канаева Елизавета Алексеевна

Место работы/учебы (аффилиация): ГБОУ СОШ №8 п.г.т. Алексеевка г.о. Кинель, Самарская область, 10 класс

Современная жизнь делает задачи на проценты актуальными, так как сфера практического применения процентных расчетов расширяется. Вопросы инфляции, повышения цен, снижение покупательской способности, платежи, налоги, прибыли, кредиты, вклады, начисление заработной платы, депозитные счета в банках касаются каждого человека в обществе. Семейный бюджет также не может обойтись без умения производить несложные операции с процентами.

Новым типом задач повышенного уровня сложности, впервые введённым в структуру Единого государственного экзамена в 2015 году, является текстовая задача социально-экономической тематики. Задание №15 (с 2022 года, ранее было задание №17) содержит тематику задач на вклады, кредиты, оптимальный выбор. За решение этой задачи согласно спецификациям ЕГЭ предлагается два первичных балла (с 2022 года, ранее начислялось три первичных балла). В данном проекте представлены алгоритмы решения данных задач, выведены универсальные формулы. Но сначала, конечно, мы попробуем разобраться в банковских терминах и схемах, необходимых для решения задач. А именно, в схемах начисления процентов по банковским вкладам.

Актуальность исследовательской работы определяется необходимостью уметь решать экономические задачи при сдаче ЕГЭ, так как жизнь современного человека тесно связана с финансовыми операциями.

Предмет исследования: различные подходы к решению задач о кредитах и вкладах в зависимости от условия задачи.

Объект исследования: простые и сложные проценты, задачи на проценты.

Гипотеза: в современном мире необходимы знания об экономике и в этом может помочь математика.

Цель исследования – исследование методов решения задач с экономическим содержанием.

Задачи исследования:

• изучить теоретический материал по выбранной теме;
• научиться решать задачи с процентами разных видов сложности;
• разобрать основные типы задач с примерами решений;
• создать таблицы для различных видов платежей;
• показать на примерах поиск решения реальной практической задачи (кредит с разными видами платежей – аннуитетные, фиксированные и дифференцированные);

Методы исследования: поиск информации по теме исследования, анализ литературы, сравнение, систематизация, обобщение.

На различных сайтах и в математической литературе я нашла множество решений таких задач, но, либо они содержат много лишней информации, либо они решены непонятным для меня способом. Поэтому я решила сама разобраться и найти оптимальные способы решений задач на банковские проценты.

VI районная научно-исследовательская конференция обучающихся обучающихся общеобразовательных организаций Октябрьского муниципального района

Финансовая математика в задачах ЕГЭ. Решение задач на кредиты

Исследовательская работа по математике

Автор работы: Кутепова Анна, ученица 10 класса        

Руководитель: Моторина  Ольга Робертовна, преподаватель математики «МОУ ОСОШ №1»

с. Октябрьское, 2022 г.

СОДЕРЖАНИЕ

Введение        2

Банковские кредиты и математика        4

Схемы решения экономических задач на кредиты        8

1. Задача на определение величины выплаты/дифференцированные платежи        8
2. Задача на определение ежегодной (ежемесячной) выплаты /аннуитетные платежи        10
3. Определение величины процента ставки кредита /долг, убывающий согласно таблице в условие задачи        12
4. Задача на определение суммы кредита/аннуитетные платежи        14
5. Нахождение количества лет (месяцев) выплаты кредита /дифференцированные платежи        16

Заключение        20

Список информационных источников        22

Введение

В современном, информационно-развитом мире, встречаются люди, которые не умеют правильно распоряжаться своими финансами и контролировать свои доходы и расходы. В этих случаях необходима финансовая грамотность, ведь благодаря данным знаниям мы сможем не только управлять деньгами, правильно инвестировать свои средства, но также будем в безопасности во время сложных жизненных обстоятельств и не потеряем свои доходы. Наша жизнь сегодня настоятельно требует, чтобы каждый человек  имел развитое экономическое мышление и был готов к жизни в условиях рыночных отношений.  Финансовая грамотность необходима при решении экономических задач в ЕГЭ профильного уровня по математике. Данные задания проверяют практические навыки применения математики в повседневной жизни, навыки построения и исследования математических моделей.

Учащиеся при подходе к итоговой аттестации в 9-х и 11-х классах сталкиваются с проблемой решения задач на проценты, а они есть и в ОГЭ и  в ЕГЭ.  На данный момент я являюсь ученицей 10 класса. В следующем году мне предстоит сдать ЕГЭ. Я уже  ознакомлена с заданиями данного экзамена и знаю, что среди них есть  задачи экономической направленности повышенного уровня сложности, которые в курсе старшей общеобразовательной школы не рассматриваются. Для меня стал актуален вопрос о  том,  каким образом подойти к решению таких задач. Кроме того я выбрала эту тему еще и  потому,  что в 7 классе мной был выполнен проект «Сам себе финансист: проценты и скидки».В этой исследовательской работе я хочу углубить и расширить свои знания в области финансовой математики. На выбор темы повлияло и то, что в  будущем я планирую поступить на экономический факультет ВУЗа.

Тема моей работы: Финансовая математика в экономических задачах ЕГЭ. Решение задач на кредиты.

Гипотеза: Не смотря многообразие типов экономических задач профильного экзамена по математике,  их можно классифицировать и  вывести единую схему решения.

Цель работы: Изучить основные типы экономических задач на кредиты ЕГЭ по профильной математике и научиться их решать.

Задачи:

• Изучить теоретические аспекты решения экономических задач;
• Познакомиться с прототипами  экономических задач, представленных в открытом банке заданий  ЕГЭ;
• Создать обучающую презентацию по различным типам задач на кредиты.

Объект исследования: Экономические задачи на кредиты №15 в ЕГЭ.

Предмет исследования: Схемы и алгоритмы решения задач на кредиты.

Методы исследования:

• Изучение и анализ литературы и интернет-источников по данной теме.
• Математическое моделирование
• Классификация
• Анализ

Банковские кредиты и математика

Финансовая математика –  раздел прикладной математики, имеющий дело с математическими задачами, связанными с экономическими расчётами.

В единый государственный экзамен  по математике (ЕГЭ) профильного уровня экономические задачи были включены в 2015 г. Это задания высокого уровня сложности с практическим  содержанием, проверяющее навыки применения математики в повседневной жизни, навыки построения и исследования математических моделей.

Экономические  задачи  предполагают:

1. Умение работать с процентами, частями и долями.
2. Владение понятием «Математическая модель».
3. Умение строить математическую модель задачи.
4. Владение вычислительными навыками.
5. Умение применять математические методы для решения содержательных задач из различных областей науки и практики.
6. Умение интерпретировать полученный результат, учитывать реальные ограничения.

Экономические задачи под номером 15 в ЕГЭ по профильной математике делятся на три основные группы:

1. Задачи на кредиты.
2. Задачи на вклады и ценные бумаги.
3. Задачи на оптимальный выбор.

Данную работу я посвятила разбору примеров задач первого типа.

Банковский кредит – денежная сумма, предоставляемая банком на определённый срок и на определённых условиях; определённая технология удовлетворения заявленной заёмщикомфинансовой потребности.

Потребность в кредите возникает при оплате значительныхпо стоимости объектов потребления без предварительного накопления достаточных ресурсов, необходимости обеспечения своевременных платежей по товарам, приобретенным в рассрочку, оплате эксклюзивных покупок случайного характера, кассовых разрывах при замене старых объектов потребления на новые, покрытии потерь при наступлении рисков, оплате значительных расходов и т. д.

Понимание и структурирование данных условия задачи – важный шаг на пути правильного ее решения. Для упорядочивания данных условия задачи я использовала таблицы, хотя это и не единственный способ решения 15-го задания,  можно использовать и другие методы: последовательности, прикладные методы. Метод решения текстовых задач с помощью таблиц универсальный, знаком каждому школьнику. С помощью таблицможно выработать единый алгоритм решения большинства банковских задач.

В решениях, представленных в работе задач,мною будут использоваться следующие обозначения:

выплатить кредит

Кредитные операции играют основную роль в деятельности банков. Экономические задачи,  конечно,  несколько упрощают реальную ситуацию, в жизни банковские операции по кредитам  значительно  сложнее, тем не менее, именно они дают начальные представления о действиях в мире финансов. При решении экономических задач не обойтись без вычисления процентов, при этом используются «простые» и «сложные проценты». Задачи  простые проценты изучаются в школьном курсе математике и включены в тестовую часть заданий профильного экзамена. Вычислять же «сложные проценты» приходится в тех случаях, когда в задаче идет речь о величине, подверженной поэтапному изменению. При этом каждый раз ее изменениесоставляет определенное число процентов от значения, которое эта величина имела на предыдущем этапе.Существуют разные формулы, по которым происходит вычисление сложных процентов. При выдаче кредитов на срок n проценты могут, например,  начисляться по формуле:  

. Где F – это погашаемая сумма, которую заемщик должен вернуть в банк, а S– начальная сумма, взятая в кредит.

Проанализировав условия задач на кредиты профильного ЕГЭ, я обнаружила, что классифицировать задачи можно разными способами:

1. По типу ежемесячных (ежегодных)  платежей.
2. Разделить на простые (используется одна формула) или сложные (применяются несколько формул, используются системы, неравенства).
3. По неизвестной величине, которую требуется найти в условии (процентной ставке, величине выплаты,  суммы кредита и др.)

По типу платежей  задачи  ЕГЭ  задачами самыми распространенными являются задачи на фиксированный, аннуитетный и дифференцированный платежи.

Фиксированный платеж – это платеж, величина которого четко определена в задаче.

Аннуитетный платеж–  это платеж, которыйустанавливается в равной сумме через равные промежутки времени, то есть  остаётся постоянным на всём периоде кредитования. Ежемесячный платёж, при аннуитетной схеме погашения кредита состоит из двух частей. Первая часть платежа идёт на погашение процентов за пользование кредитом, авторая часть идёт на погашение  суммы долга.  Главная особенность таких платежей  в том, что вначале ежемесячный платеж  практически полностью состоит из  суммы процентов, тогда как основной долг заемщика не уменьшается. Постепенно это соотношение выравнивается: если первое времязаемщик  гасит в основном проценты, то потом основные средства идут в счет погашения задолженности.

Дифференцированный платеж – это способ ежемесячного платежа по кредиту, при котором  размер ежемесячной выплаты по погашению кредита постепенно уменьшается к концу периода кредитования. Ежемесячный платёж, как и при аннуитетной схеме погашения кредита, складывается тоже из двух составляющих. Но в дифференцированной схеме первая часть называется основным платежом, размер которого не изменяется на всём сроке кредитования. Этот  платёж идет на погашение основного долга по кредиту. Вторая часть платежа непостоянная, она уменьшается к концу срока кредитования. Данная часть платежа при дифференцированной схеме идет на погашение процентов по кредиту. При дифференцированной схеме погашения кредита, ежемесячный платеж рассчитывается как сумма основного платежа и проценты, начисляемые на оставшийся размер долга. Естественно, что оставшийся размер долга уменьшается к концу срока кредитования, отсюда и получается уменьшение размера ежемесячной выплаты.

Схемы решения экономических задач на кредиты

В практической части своей работы  я представляюпримеры решений нескольких задач на кредиты. Это задачи на нахождение: процентной ставки, суммы долга, суммы переплаты, ежегодных (ежемесячных, еженедельных т.д.)  выплат, определения срока кредитования.

1. Задача на определение величины выплаты

/дифференцированные платежи

15-го января планируется взять кредит в банке на сумму 2,4 млн. рублей на 24 месяца. Условия его возврата таковы:

– 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

 – 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Какую сумму нужно выплатить банку в первые 12 месяцев?

Решение:

Фраза «15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца» — это означает, что каждый месяц  мы должны выплачивать часть начального долга  + начисленные за этот месяц проценты.

№ мес.	Начальная сумма, млн. руб.	Сумма начисленных процентов, млн. руб.	Выплата, млн. руб.	Конечная сумма, млн. руб.
1
2
3
12
24	…	…	…	0

Первая сумма  =    (т. е. половина взятой заемщиком суммы). Для удобства вычисления суммы вынесем за скобки множитель , тогда получим:

Ответ: 1 866 000 рублей

Примеры задач банка ЕГЭ на определение величины выплаты:

1. В июле планируется взять кредит в банке на сумму 28 млн. рублей на некоторыйсрок (целое число лет). Условия его возврата таковы:

– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;

– с февраля по июнь каждого года необходимо выплатить часть долга;

– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июльпредыдущего года.

Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 9 млн. рублей?

2. В июле планируется взять кредит в банке на сумму 9 млн. рублей на некоторый срок(целое число лет). Условия его возврата таковы:

– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;

– с февраля по июнь каждого года необходимо выплатить часть долга;

– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июльпредыдущего года.

Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платёж составит 1,25 млн. рублей?

1. Задача на определение ежегодной (ежемесячной) выплаты/аннуитетные платежи

В июле планируется взять кредит на сумму 6409000 рублей. Условия его возврата таковы:

— Каждый январь долг возрастает на 12,5% по сравнению с концом предыдущего года.

— С февраля по июнь каждого года необходимо выплатить некоторую часть долга.

Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен двумя равными платежами.

Решение:

№ года	Начальная сумма, руб.	Сумма долга после начисления процентов,  руб.	Выплата, руб.	Конечная сумма, руб.
1 год			x
2 год			x

Ответ: 3817125 руб.

Примеры задач банка ЕГЭна определение ежегодной (ежемесячной) выплаты:

1. В июле планируется взять кредит на сумму 8052000 рублей. Условия его возврата таковы:

– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;

– с февраля по июнь каждого года необходимо выплатить некоторую часть долга.

Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами (то есть за 4 года)?

1. Определение величины процента ставки кредита /долг, убывающий согласно таблице в условие задачи

15-го января планируется взять кредит в банке на шесть месяцев в размере . Условия его возврата таковы:

– 1-го числа каждого месяца долг увеличивается напо сравнению с концом предыдущего месяца, где – целое число;

– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей:

Дата
Долг (млн. руб.)

Найдите наибольшее значение, при котором общая сумма выплат будет меньше 1,2 млн. рублей.

Решение:

	Начальная сумма, млн. руб.	Сумма долга после начисления процентов,млн. руб.	Выплата, млн. руб.	Конечная сумма,млн. руб.
	1

Учитывая, что общая сумма выплат меньше 1,2 млн. руб., составим и решим неравенство:

Ответ: 7%

Примеры задач банка ЕГЭна определение величины процента ставки кредита:

1. 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн. рублей. Условия его возврата таковы:

– 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;

– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; – 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в млн. руб.)	1	0,9	0,8	0,7	0,6	0,5	0

Найдите наименьшее значение r, при котором общая сумма выплат будет больше 1,2 млн. рублей.

1. В июле планируется взять кредит в банке на сумму 4,5 млн. рублей на срок 9 лет. Условия его возврата таковы:

 – каждый январь долг возрастает на r % по сравнению с концом предыдущего года;

– с февраля по июнь каждого года необходимо выплатить часть долга;

– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн. рублей, а наименьший – не менее 0,6 млн рублей.

1. Задача на определение суммы кредита

/аннуитетные платежи

В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

– каждый январь долг увеличивается на 30% по сравнению с концом предыдущего года;

– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.

Сколько рублей планируется взять в банке, если известно, что кредит будет полностью погашен тремя равными платежами (то есть за три года) и общая сумма выплат после полного погашения кредита на 156 060 рублей больше суммы, взятой в кредит?

Решение:

№ года	Начальная сумма, руб.	Сумма долга после начисления процентов, руб.	Выплата, руб.	Конечная сумма, руб.

Определим величину ежегодной выплаты, решив уравнение относительно x:

Известно, что сумма трех выплат на 156060 руб.  больше суммы кредита:

Ответ: 239 400руб.

Примеры задач банка ЕГЭна определение суммы кредита:

1. В июле 2020 года планируется взять кредит в банке на сумму 419 375 рублей. Условия его возврата таковы:

– каждый январь долг увеличивается на 20% по сравнению с концом предыдущего года;

 – с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.

Сколько рублей будет выплачено банку, если известно, что кредит будет полностью погашен четырьмя равными платежами (то есть за четыре года)?

1. В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

– каждый январь долг увеличивается на 10% по сравнению с концом предыдущего года;

– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.

Сколько рублей планируется взять в банке, если известно, что кредит будет полностью погашен тремя равными платежами (то есть за три года) и общая сумма выплат после полного погашения кредита на 40 980 рублей больше суммы, взятой в кредит?

1. Нахождение количества лет (месяцев) выплаты кредита/дифференцированные платежи

В июле планируется взять кредит в банке на сумму 5 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:

– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;

 – с февраля по июнь каждого года необходимо выплатить часть долга;

 – в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 7,5 млн. рублей?

Решение:

«В июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года» — это означает, что каждый год мы должны выплачивать часть начального долга  + начисленные за этот год проценты .

№ года	Начальная сумма, руб.	Сумма долга после начисления процентов, руб.	Выплата, руб.	Конечная сумма, руб.
1
2
n

Сложим все платежи, чтобы определить общую сумму выплат по кредиту:

Сложив все слагаемые  , получим . У оставшихся слагаемых  есть общий множитель  общий множитель ,  тогда имеем:

Выражение в  скобках – арифметическая  прогрессия.Найдём её сумму по формуле:

Подставим полученную сумму в выражение для нахождения общей выплаты:

Вместо буквенных символов подставим известные нам значения величин и найдем n:

Ответ: 4 года

Примеры задач банка ЕГЭна нахождение срокавыплаты кредита:

1. В июле планируется взять кредит в банке на сумму 14 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:

– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;

– с февраля по июнь каждого года необходимо выплатить часть долга; – в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 24,5 млн. рублей?

1. В июле планируется взять кредит в банке на сумму 16 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:

– каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;

– с февраля по июнь каждого года необходимо выплатить часть долга; – в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 38 млн. рублей?

Заключение

Подводя итоги своей работы, целью  которой было познакомиться с типами задач с экономическим содержанием и научиться решать задачи на кредиты, я считаю, что мне удалось достичь этой цели, хотя есть еще к чему стремиться, так как предстоит изучить и задачи других видов.

Проанализировав условия и решения банковских задач,  я пришла к заключению, что в большинстве случаев схему решения можно использовать  таблицу такого вида:

В ходе своего исследования, разбирая примеры задач  и решая задачи самостоятельно,  я заметила, что:

1. Практически все экономические задачи из банка ЕГЭ можно разделить на несколько основных видов
2. Решение экономических задач можно выполнять по одному алгоритму, а именно:

1. Занести данные условия задачи в таблицу.
2. Составить уравнение или неравенство (систему уравнений/неравенств).
3. В ходе решения появится формула, с помощью которой будет найден ответ на вопрос задачи.

Моя гипотеза о том, что, несмотря на сложность  и многообразие типов экономических задач их можно классифицировать и  вывести единую схему решения, подтвердилась. Я убедилась в ее истинности  на примере изучения задач на кредиты.Работу по изучению экономических задач буду продолжать и дальше, так как впереди экзамен по профильной математике и, кроме того, считаю, что решение таких задач позволило мне лучше разобраться в базовых понятиях банковских процессов, что будет полезно  мне в моей будущей профессии.

Думаю, что эта  работа будет полезна ученикам 10 и 11 класса, учителям для подготовки к ЕГЭ профильного уровня по математике. В ходе работы мною была создана презентация с примерами задач на кредиты и их подробными решениями. Эту презентацию можно предложить ребятам для самостоятельной подготовки, кроме решенных примеров она содержит задачи из банка ЕГЭ по математике.

Список информационных источников

1. Лукашин Ю.П. Финансовая математика / Московский международный институт эконометрики, информатики, финансов и права. — М., 2003. https://kpsu.ru/upload/medialibrary/606/606fd86fd3cd2272b6f1f3f1b0e4f96c.pdf
2. https://ru.wikipedia.org
3. https://ege.sdamgia.ru/
4. http://fipi.ru/
5. Курс лекций по финансовой математике  https://lfirmal.com/predmet-finansovaya-matematika/
6. Материалы для подготовки к ЕГЭ по математике https://www.time4math.ru/ege

Финансовая математика (задачи ЕГЭ)

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

В нашем современном обществе огромную роль играет экономика. Она требует от человека глубоких знаний и умений при работе с массивными числовыми потоками информации. Проценты, вклады, кредиты стали неотъемлемой частью нашей жизни. Подтверждением этому служит то, к примеру, что понятие «процент» широко используется как в реальной жизни, так и в различных областях науки.  Без процентов невозможно обойтись ни в финансовом анализе, ни в жизни. Чтобы начислить зарплату работнику необходимо знать процент налоговых отчислений; мы интересуемся размером процентных начислений на сумму вклада, чтобы открыть депозитный счет в банке; чтобы знать приблизительный рост цен в будущем году, мы интересуемся процентом инфляции.

Для того, чтобы развить навыки экономической грамотности, её основы закладываются в школе. Но, особое внимание экономическим задачам уделяется на Едином Государственном Экзамене, где данные задачи представлены в задании №17. Одними из особенностей данных задач является их нестандартность и повышенная сложность решения. Умение эффективно решать задачи на сложные и простые проценты, понимание различия дифференцированных и аннуитетных платежей, а также владение основными теоретическими знаниями в экономике, способствуют правильному решению задач в области экономики на ЕГЭ. Решение многих задач школьного курса, нестандартных задач, практических задач помогает разобраться в новых экономических веяниях жизни.

Исследование данной темы очень важно по нескольким причинам.

Во-первых, я, являюсь учеником старшей школы на физико-математическом профиле, и успешная сдача ЕГЭ для меня приоритетна, что подразумевает под собой умение эффективно решать все типы заданий, в том числе и те, которые связаны с экономикой.

Во-вторых, решение финансовых задач очень полезно, так как вся жизнь современного человека тесно связана с экономическими операциями. Большинство людей в мире совершают банковские операции, вклады, берут кредиты, поэтому рассмотрение данного вопроса поможет не допустить финансовых ошибок в жизни с моей стороны.

Цель проекта: Изучить способы решения экономических задач. Сформировать схемы задач на кредиты и вклады по финансовой математике, показать приемы быстрого счета.

Достижение поставленной цели будет реализовано с помощью решения таких задач как:

Проанализировать научную литературу по данной теме.

Систематизировать все задачи по способам решений.

Разработать наглядные схемы по решению данного вида задач.

Подобрать несколько задач по данным схемам

На основе рассмотренных задач подготовить и создать памятку для учеников по решению данных задач.

Предмет исследования: Способы решения экономических задач ЕГЭ на проценты и вклады.

Объект исследования: Экономические задачи на ЕГЭ.

Целевая аудитория: Ученики 10-11 классов.

Методы:

Теоретический: изучение литературных и Интернет источников, анализ данных, систематизация материала,

Практическая значимость: с помощью составленных схем для учеников старшей школы можно повысить их уровень знания в области задач, связанных с расчётами кредитов, вкладов, подготовку к решению задания № 17, а также увеличить шансы выпускников на хорошую сдачу Единого Государственного Экзамена.

Основная часть

Теоретическая часть

Арифметическая и геометрическая прогрессии

Для того, чтобы начинать разбираться в задании № 17, нужно повторить как арифметическую, так и геометрическую прогрессии, так как они напрямую используются при финансовых расчетах в экономике и применяются в данном задании.

Арифметическая прогрессия

Арифметической называется последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и некоторого фиксированного числа d: , где n принадлежит множеству натуральных чисел;

Фиксированным числом d называется разность арифметическом прогрессии;

Формула n-ого члена арифметической прогрессии: ;

Сумма первых n членов в арифметической прогрессии вычисляется по формуле: ;

В арифметической прогрессии каждый ее член, начиная со второго, является средним арифметическим соседних ему членов: .

Геометрическая прогрессия

Геометрической называется последовательность, каждый член которой, начиная со второго, равен произведению предыдущего члена и некоторого фиксированного числа q:, где n принадлежит множеству натуральных чисел;

Фиксированным числом q называется знаменатель геометрической прогрессии;

Формула n-ого члена геометрической прогрессии: ;

Квадрат каждого члена геометрической прогрессии, начиная со второго, равен произведению соседних: ;

Формула суммы первых n членов геометрической прогрессии можно вычислить по формуле: .

Проценты

В математике, в том числе экономических задачах, мы часто сталкиваемся с понятием «процент». Под этим термином подразумевается сотая часть числа. 1%=0,01 А, где А- некоторое число. В данном задании ученикам встречаются несколько видов задач на проценты. Итак, разберемся с методом решения некоторых из них.

I тип задач — нахождение q% от некоторого числа А.

— Число А умножаем на 0,01*q, и получаем искомое число;

II тип задач — нахождение некоторого числа А по его q%, где q%=B.

— Число B делим на 0,01*q, и получаем искомое число;

III тип задач — сколько процентов составляет число А от числа В.

— Делим число А на число В и умножаем на 100%;

IV тип задач — Вычислить число B, если число A меньше него на q%.

— B = A(1+q/100)

V тип задач — Вычислить число B, если число A больше него на q%.

— B = A(1-q/100)

Разберем несколько типовых задач на проценты.

Найти 15% от 80: 80*0,15=12;

Найти A, если 47%равны 94: 94/0,47=200;

Сколько % составляет 78 от 300:78/300*100%=0,26%

Для того, чтобы рационализировать расчеты, важно помнить, что проценты имеют свойство обратимости. То есть q% от числа А равны p% от числа A. К примеру, 10% от 50 равны 50% от 10 (10% от 50 = 5, 50% от 10 = 5).

Вклады: Простые и сложные проценты

Современная экономическая система определяет два способа начисления доходов на вклады: простые и сложные проценты.

Для начала работы с вкладами и процентами, нужно дать определение вкладам, а также процентам: сложным и простым.

Банковский вкладом (или банковским депозитом) называется сумма денег, переданная лицом кредитному учреждению (банку) с целью получения дохода в виде процентов, образующихся в ходе финансовых операций с вкладом.

Простые проценты — метод начисления доходов на вклад, при котором размер вклада увеличивается на одну и ту же сумму, равную определенному количеству процентов от исходного. За один расчетный период, как правило, принимается один год. Если A — исходное количество денег, q процентов годовых – процентная ставка, то по истечении k лет клиент получит сумму .

Формула для нахождения же простого процента напоминает формулу k-того члена арифметической прогрессии c разностью Разность умножается на k, а не на k-1 по той же причине, что будет показана и для сложных процентов.

Теперь следует обратиться к вкладам и второму методу начисления доходов: сложным процентам.

Сложные проценты — это способ начисления процентов, при котором происходит начисление как на исходную сумму, так и на уже начисленные проценты, то есть на прирост. Более полно понять это определение поможет следующий пример.

Пусть клиент положил на счет сумму A₀на n периодов, ив конце каждого периода на имеющуюся на счете сумму начисляется q%.Тогда через 1 период на счете окажется сумма

В конце второго периода имеющаяся сумма снова увеличится на q%, то есть

Аналогично в конце третьего периода на счете окажется сумма

Несложно заметить, что появляется определённая закономерность. Выведем общую формулу количества денег на счете клиента по истечении nпрошедших периодов:

Формула, которую мы получили, напоминает формулу нахождения n-ного члена геометрической прогрессии, с той лишь разницей, что знаменатель прогрессии в нашем случае в степени n, а не n-1. Это можно объяснить тем, что сумму, лежащую в самом начале, мы обозначили за , а не за .

Обобщая выше сказанное, необходимо отметить тот неоспоримый факт о том, что начисление сложных процентов на сумму вклада более выгодно клиенту, так как в этом случае сумма вклада будет расти в геометрической прогрессии. Банку же, в свою очередь, более выгодно начисление простых процентов на сумму счёта клиента, так как она будет увеличиваться только лишь в арифметической прогрессии. Все это можно проследить на нижеуказанном рисунке (см. приложение 1).

Кредиты: Аннуитетные и дифференцированные платежи

В современном мире в экономике немаловажную роль играют кредиты. Под определением «кредит» подразумевают заем в банке определенной суммы денег с возвращением долга, а также начисленных на него процентов. В зависимости от способа начисления процентов, выплаты по кредитам осуществляются дифференцированными, либо аннуитетными платежами. В каждом из этих случаев начисление процентов всегда происходит на остаток от долга, то есть методом сложных процентов.

Аннуитетный платеж — способ выплаты по кредиту, при котором сумма выплат делится на равные части (столько, сколько планируется платежей), а сумма одной выплаты состоит из остатка по кредиту и процентов, начисленных на остаток долга. При таком способе погашения основной долг, являющийся телом кредита, при первых платежах практически не погашается, а выплачиваются только проценты.

Дифференцированный платеж — способ выплаты по кредиту, при котором сумма долга клиента делится на равные части (столько, сколько планируется платежей для его выплаты), к каждой из которых прибавляются проценты, начисленные на оставшуюся сумму долга. При этом с каждым разом сумма выплаты уменьшается, а в последний раз клиент платит наименьшую сумму.

Более понятно разъяснить суть разницы двух видов платежей поможет следующий рисунок (см. приложение 2).

Дифференцированные платежи более выгодны клиенту, так как переплата в этом случае для намного меньше, чем в случае выбора клиентом аннуитетной схемы. Но при этом стоит учитывать то, что первые платежи могут оказаться слишком большими для клиента. Кроме того, сумму каждого следующего дифференцированного платежа необходимо отслеживать. Все это делает аннуитетную схему выплат более удобной как для клиента, так и более выгодной для банков, а потому и наиболее популярной.

После того, как мы познакомились с определениями кредита, а также двух типов платежей, разберем схемы решения задач на кредиты:

Пусть A — сумма кредита, x — очередная выплата n — количество платёжных периодов, q — процент по кредиту, начисляемый банком. В нашем случае коэффициент показывает то, во сколько раз увеличивается сумма долга после начисления по нему процентов.

Выплата кредита равными платежами (аннуитетные платежи)

Схема погашения кредита:

Преобразуем выражение:

Применим формулу суммы геометрической прогрессии и получим:

=0.

Схема с дифференцированными платежами (равномерное уменьшение суммы долга по кредиту)

Схема погашения для n платёжных периодов:

1-я выплата:

2-я выплата:

…

n-я выплата:

Посчитаем сумму всех выплат:

Теперь применяем формулу суммы для арифметической прогрессии. Тогда общая сумма выплат равна:

В данном случае Z— величина переплаты,

Практическая часть

Примеры решения задач на аннуитетный платёж

Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 2 млн рублей. Найдите наибольший размер первоначального вклада, при котором через четыре года вклад будет меньше 15 млн рублей.

Решение

Пусть S— первоначальная сумма вклада, а по условию q=10%, k=1,1.

Расчёты, для удобства следует проводить в миллионах рублей: по ранее представленной формуле для аннуитетных платежей получаем:

;

;

;

, следовательно, S=7 миллионов рублей.

Ответ:7 миллионов рублей.

31 декабря 2020 года Максим взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплат кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга, то есть увеличивает долг на 12,5%, затем Максим переводит в банк X рублей. Какой должна быть сумма x, чтобы Максим выплатил долг четырьмя равными платежами, то есть за четыре года?

Решение

Данная задача также решается с помощью формулы аннуитетных платежей, так как по условию сказано, что долг выплачивается равными платежами.

Пусть S=6902 тыс. рублей;

Применим формулу геометрической прогрессии:

следовательно,

.

Ответ: 2296350 рублей.

Ольга хочет взять в кредит 100 000 рублей под 10% годовых. Погашение кредита происходит раз в год равными суммами, кроме, может быть, последней, после начисления процентов. На какое минимальное количество лет Ольга может взять кредит, чтобы ежегодные выплаты были не более 24 000 рублей?

Решение

Пусть Оля берет кредит на n лет. Если же последняя выплата по кредиту будет меньше предыдущих, то погасится все тело кредита. Но возьмём, к примеру, что последняя выплата будет всё же равна предыдущим, тогда долг клиента не только погасится полностью, но и станет отрицательным

(на карте останутся некоторые средства). Для удобства будем вести расчёты в тысячах рублей.

.

Тогда следует для такого случая записать неравенство по формуле для расчетов аннуитетного платежа:

Так как в скобках- сумма n членов геометрической прогрессии, то тогда данная сумма равна ;

Тогда: ;

Домножим обе части неравенства на (k-1) и подставим числовые значения:

получаем .

Переведем, округляя до сотых, данную дробь в десятичную и получаем, что ,71.

Теперь, для того, чтобы вычислить значение n, нам необходимо воспользоваться биномом Ньютона, следовательно, и треугольником Паскаля (см. приложение 3).

Выражение есть бином Ньютона и расписывается следующим образом: .

Нам необходимо найти минимальное значение n. Распишем же 1,1 так, чтобы воспользоваться треугольником Паскаля:

Возьмём n=5, тогда ;

Возьмём n=6,тогда .

Следовательно, .

Ответ:6 лет.

Примеры решения задач на дифференцированный платёж

Жанна взяла в банке в кредит 1,8 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 1 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?

Решение

Пусть S— первоначальная сумма долга, при этом, .

Для начала нарисуем схему начисления процентов и выплат. Заметим некоторые закономерности:

S … 0

Начисление 1-ая 2-ая посл.

процентов выплата выплата выплата

Sk …

Как обычно, коэффициент показывает то, во сколько раз увеличивается сумма долга после начисления по нему процентов.

Сумма долга уменьшается равными долями, равномерно. Каждая доля равна

.

Тогда первая выплата *S;

Вторая выплата ;

…

Последняя выплата в году равна .

Посчитаем общую сумму всех выплат в течение первого года:

.

Видим, что в первой скобке находится сумма 12 членов арифметической прогрессии, в которой , . Пусть эта сумма равна .

Видим, что во второй скобке аналогично находится сумма 12 членов арифметической прогрессии, в которой , . Пусть эта сумма равна .

Тогда общая сумма выплат за 1 год:

Ответ:1066500 рублей.

Алексей взял кредит в банке на срок 17 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется q % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 27 % больше, чем сумма, взятая им в кредит. Найдите q.

Решение

Применим формулу для задач с дифференцированными процентами, выведенной в теоретической части.

Пусть на n платежных периодов в кредит взята сумма S, но при этом имеем то, что платежи подобраны таким образом, что сумма долга уменьшается равномерно. Тогда величина переплаты F и полная сумма выплат G за все время выплаты кредита представлены формулами:

; .

Применяя формулу к данной задаче, получаем (величина переплаты)

.

Ответ: q=3.

В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S — целое число. Условия его возврата таковы:

— каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Месяц и год	Июль 2016	Июль 2017	Июль 2018	Июль 2019	Июль 2020
Долг (в млн рублей)	S	0,8S	0,5S	0,1S	0

Решение

В данной задаче .

Составим схему выплат для дифференцированных платежей:

Год 2016 2017 2018 2019 2020

Июль S 0

1-ая 2-ая 3-я 4-ая

процентов выплата Х₁ выплата Х₂ выплата Х₃ выплата Х₄

ЯнварьkS …

Общая сумма X выплат:

.

По условию S— целое число, а . Для удобства произведем расчеты в миллионах рублей.

, значит

Ответ: 29 млн. рублей

Заключение

Цели исследования достигнуты. В данной работе были показаны основные методы решения задач на кредиты, вклады. Тема исследования остается актуальной по причине того, что все рассматриваемые задачи взяты из материалов по подготовке к ЕГЭ по математике «Профиль».

Исследование и рассмотрение задания №17 ЕГЭ показало, что отличное знание теоретического аспекта темы, умение оперировать этими знаниями, позволяют решать задачи повышенной сложности из Единого Государственного Экзамена по теме «Экономические задачи» ученикам старшей школы.

Также, для успешного решения таких задач, необходимо отработать аппарат стандартных вычислений, так как все экономические задачи направлены на серьёзные вычисления. Экономические задачи – это не просто задачи из математики, это часть нашей жизни в современном мире. Умение их решать будет полезно в будущем, как для проверки банковских операций при оформлении кредитов или вкладов, так и в простых жизненных ситуациях, что поможет не совершать мелких и фатальных ошибок.

Составленные схемы по решению задач (см. приложение 4) помогут разобраться и справиться с заданием, посвященным экономике в ЕГЭ, как старшеклассникам, сдающим экзамен в этом году, так и ученикам девятых и десятых классов.

Библиографический список

https://ru.wikipedia.org/wiki/Аннуитет;

https://ru.wikipedia.org/wiki/Дифференцированный_платёж;

https://math-ege.sdamgia.ru/test?theme=293;

https://math-ege.sdamgia.ru/test?theme=292.

Математика: задания высокой и повышенной сложности/ A. Г. Малкова — Изд. 2-е — Ростов н/Д: Феникс, 2019. — 221, с.: ил. — (ЕГЭ. Высший балл).

Приложения

Приложение 1

Приложение 2

Приложение 3

Треугольник Паскаля

Приложение 4

Общие схемы решения задач ЕГЭ задания №17

(аннуитетные и дифференцированные платежи)

A — сумма кредита;

x — очередная выплата;

n — количество платёжных периодов;

q — процент по кредиту, начисляемый банком;

коэффициент показывает то, во сколько раз увеличивается сумма долга после начисления по нему процентов.

Схема выплат кредита равными платежами (аннуитетные платежи)

=0.

Схема с дифференцированными платежами (равномерное уменьшение суммы долга по кредиту)

V— величина переплаты,

Просмотров работы: 1058

Муниципальное автономное общеобразовательное учреждение «Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина»

ИНДИВИДУАЛЬНЫЙ ПРОЕКТ

по теме:

«Экономические задачи ЕГЭ и способы их решения»

Выполнил:

Учащийся 11 класса «А»

Задонский Ярослав Владимирович

Подпись

Научный руководитель:

Сухненко Ирина Александровна

учитель математики

Тамбов, 2018

Содержание:

Введение…………………………………………………………………. С. 3

РАЗДЕЛ ПЕРВЫЙ. Теоретический аспект изучения экономических задач ЕГЭ ………………………………………………………………………. С. 5

Раздел второй. Типы экономических задач на аннуитетный и дифференцированный платежи ………………………………………..

Раздел третий. Особые экономические задачи

Заключение ……………………………………………………………….

Список литературы ………………………………………………………

Введение

В настоящее время общее образование находится на этапе модернизации и обновления системы и содержания в условиях введения новых федеральных государственных стандартов. Приоритетом общества и системы образования является способность вступающих в жизнь людей самостоятельно решать встающие перед ними новые, еще неизвестные задачи. На первый план наряду с общей грамотностью выступает умение выпускников, например, разрабатывать и проверять гипотезы, умение работать в проектном режиме, проявлять инициативу в принятии решений. Это и становится одним из значимых ожидаемых результатов образования и предметом стандартизации.

Русский математик и механик, основоположник Петербургской математической школы, академик Петербургской академии наук П.Л. Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды». С такими задачами в наше время приходится иметь дело представителям самых разных специальностей. Технологи – стараются так организовать производство, чтобы выпускалось как можно больше продукции. Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей. Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными, и т.д.

Актуальность данной темы исследования определяется тем, что начиная с 2015 года, в заданиях ЕГЭ по математике профильного уровня появилась новая практико-ориентированная задача №17, так называемая «банковская» задача. Важным видом учебной деятельности, в процессе которой усваиваются математические знания, умения и навыки, является решение задач и одними из наиболее востребованных типов задач в рамках государственного экзамена являются задачи на проценты, в частности экономические задачи. 

Объектом данного исследования являются экономические задача единого государственного экзамена.

Предметом исследования выступают способы решения экономических задач единого государственного экзамена.

Гипотеза исследования — общего способа решения экономических задач быть не может, не существует единого алгоритма, позволяющего за конечное число шагов решать эти задачи.

Продукт проекта — методические рекомендации по решению банковских задач

В связи с объектом и предметом, цель проекта заключается в нахождении решения экономических задач.

Достижение поставленной цели осуществлялось через постановку и решение следующих исследовательских задач:

— проанализировать учебную и научную литературу по теме исследования, с целью определения базовых понятий и степени изученности проблемы;

— рассмотреть теоретические аспекты изучения экономических задач;

— выделить типы экономических задач;

— рассмотреть особые способы решения экономических задач на аннуитетный и дифференцированный платежи

Все вышесказанное, подчеркивает востребованность и необходимость рассмотрения экономических задач в едином государственном экзамене.

РАЗДЕЛ ПЕРВЫЙ. Теоретический аспект изучения экономических задач

При чтении условий любой задачи можно встретить такие величины как вклады, проценты и кредиты. Потому что именно задачи с процентами с недавних пор добавлены во вторую часть единого государственного экзамена по математике. За решение этой задачи согласно спецификациям ЕГЭ предлагается сразу три первичных балла, т. е. экзаменаторы считают эту задачу одной из самых сложных.

Вместе с тем, для решения любой из указанных задач из ЕГЭ по математике необходимо знать всего лишь две формулы, каждая из которых вполне доступна любому школьному выпускнику.

Вкладываем деньги в банк

Прежде всего, хотелось бы сделать небольшое лирическое отступление, связанное с финансами, банками, кредитами и вкладами, на основании которых мы и получим те формулы, которые будем использовать для решения данной задачи. Итак, давайте немного отвлечемся от экзаменов, от предстоящих школьных проблем, и посмотрим в будущее.

Допустим, вы выросли и собираетесь покупать квартиру. Допустим, вы собираетесь покупать не какую-то плохую квартиру на окраине, а хорошую качественную квартиру за 20 миллионов рублей. При этом также предположим, что вы устроились на более-менее нормальную работу и зарабатываете по 300 тысяч рублей в месяц. В этом случае за год вы сможете отложить примерно три миллиона рублей. Разумеется, зарабатывая по 300 тысяч рублей в месяц, за год у вас получится чуть большая сумма — 3600000 — но эти 600000 пусть будут потрачены на еду, на одежду и на прочие ежедневные бытовые радости. Итого вводные данные таковы: необходимо заработать двадцать миллионов рублей, у нас же в распоряжении имеется лишь три миллиона рублей в год. Возникает естественный вопрос: сколько лет нам необходимо откладывать по три миллиона, чтобы получить эти самые двадцать миллионов. Считается это так:

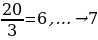
Однако как мы уже отмечали, вы зарабатываете 300 тысяч рублей в месяц, это значит, что вы умные люди и не будете откладывать деньги «под подушку», а отнесете их в банк. И, следовательно, ежегодно на те вклады, которые вы принесете в банк, будут начисляться проценты. Допустим, вы выберете надежный, но при этом более-менее прибыльный банк, и поэтому ваши вклады ежегодно будут расти на 15% годовых. Другими словами можно сказать, что сумма на ваших счетах ежегодно будет увеличиваться в 1,15 раза. Формула:

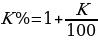
Посчитаем, сколько денег будет на ваших счетах после каждого года:

В первый год, когда вы только начнете откладывать деньги, никакие проценты не накопятся, т. е. в конце года вы отложите три миллиона рублей:

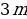
В конце второго года на те три миллиона рублей, которые остались с первого года, уже будут начислены проценты, т.е. нам нужно умножить на 1,15. Однако в течение второго года вы также доложили еще три миллиона рублей. Разумеется, на эти три миллиона еще не были начислены проценты, потому что к концу второго года эти три миллиона только появились на счету:

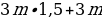
Итак, третий год. В конце третьего года на эту сумму будут начислены проценты, т. е. необходимо всю эту сумму умножить на 1,15. И опять же, в течение всего года вы усердно работали и еще отложили три миллиона рублей:

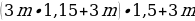
Рассчитаем еще четвертый год. Опять же, вся сумма, которая оказалась у нас к концу третьего года, умножается на 1,15, т.е. на всю сумму будут начислены проценты. В том числе, будут начислены проценты на проценты. И к этой сумме добавляется еще три миллиона, потому что в течение четвертого года вы также работали и также откладывали деньги:

⋅1,15+3m)1,15+3m

А теперь раскроем скобки и посмотрим, какая у нас будет сумма к концу четвертого года откладывания денег:

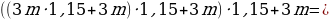
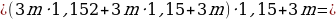
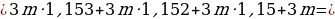
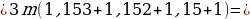
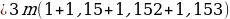
Как видим, в скобках у нас стоят элементы геометрической прогрессии, т. е. у нас стоит сумма элементов геометрической прогрессии.

Если геометрическая прогрессия задана элементом b1, а также знаменателем q, то сумма элементов будет считаться по следующей формуле:

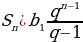
Эту формулу обязательно нужно знать и четко применять.

Обратим внимание: формула n-го элемента звучит следующим образом:

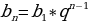
Из-за этой степени многие ученики путаются. В сумме у нас стоит просто n для суммы n-элементов, а сам n-й элемент имеет степень n−1. Другими словами, если мы сейчас попытаемся посчитать сумму геометрической прогрессии, то нужно учитывать следующее:

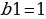
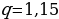
Теперь мы можем посчитать сумму:

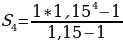
Посчитаем числитель отдельно:

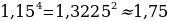
Итого, возвращаясь к сумме геометрической прогрессии, мы получим:

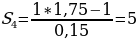
В итоге мы получаем, что за четыре года накоплений наша исходная сумма увеличится не в четыре раза, как если бы мы не клали деньги в банк, а в пять раз, т. е. пятнадцать миллионов. Давайте запишем это отдельно:

4 года → 5 раз

Забегая вперед, отмечу, что если бы мы копили не четыре года, а пять лет, то в итоге наша сумма накоплений увеличилась бы в 6,7 раза:

5 лет → 6,7 раз

Другими словами, к концу пятого года мы бы получили на счету следующую сумму:

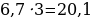
Т. е. к концу пятого года накоплений с учетом процентов по вкладу мы бы уже получили свыше двадцати миллионов рублей. Таким образом, общий счет накоплений за счет банковских процентов снизился бы с почти семи лет до пяти лет, т. е. почти на два года.

Таким образом, даже, несмотря на то, что банк начисляет достаточно низкий процент на наши вклады (15%), уже через пять лет эти самые 15% дают прибавку, существенно превышающую наш ежегодный заработок. При этом основной мультипликационный эффект приходится на последние годы и даже, скорее, на последний год накоплений.

Если мы действительно хотим приумножить свои сбережения, то вкладывать их нужно не в банк, а в реально действующий бизнес, где эти самые проценты, т. е. рентабельность в условиях российской экономики редко опускается ниже 30%, т. е. вдвое больше банковских вкладов.

А вот что действительно полезно во всех этих рассуждениях, так это формула, которая позволяет нам найти итоговую сумму вклада через размер ежегодных платежей, а также через проценты, которые начисляет банк. Так и запишем:

Сам по себе % считается по следующей формуле:

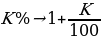
Эту формулу также необходимо знать, как и основную формулу суммы вклада. А, в свою очередь, основная формула способна значительно сократить вычисления в тех задачах с процентами, где требуется посчитать именно вклад.

Почему стоит пользоваться формулами, а не таблицами?

У многих наверняка возникнет вопрос, а к чему вообще все эти сложности, нельзя ли просто расписать каждый год в табличке, как это делают во многих учебниках, посчитать отдельно каждый год, а затем посчитать общую сумму вклада? Конечно, можно вообще забыть про сумму геометрической прогрессии и все считать с помощью классических табличек — так сделано в большинстве сборников для подготовки к ЕГЭ. Однако, во-первых, резко увеличивается объем вычислений, а во-вторых, как следствие, увеличивается вероятность допустить ошибку.

Да и вообще, использовать таблицы вместо этой замечательной формулы — это то же самое, что на стройке копать траншеи руками вместо того, чтобы использовать стоящий рядом и полностью работающий экскаватор.

Ну, или то же самое, что умножить пятерку на десятку не с помощью таблицы умножения, а складывать пятерку с самой собой десять раз подряд. Впрочем, это я уже отвлекся, поэтому еще раз повторю самую главную мысль: если есть какой-то способ упростить и сократить вычисления, то именно этим способом и надо воспользоваться.

Проценты по кредитам

Далее рассмотрим следующий вопрос, а именно — к процентам по кредитам.

Итак, пока вы копите деньги, скрупулезно планируете свой бюджет, думаете о своей будущей квартире, ваш одноклассник, а нынче простой безработный, решил жить сегодняшним днем и просто взял кредит. При этом он еще будет подкалывать и смеяться над вами, мол, у него кредитный телефон и подержанный автомобиль, взятый в кредит, а вы до сих пор ездите на метро и пользуетесь старым кнопочным телефоном. Разумеется, за все эти дешевые вещи вашему бывшему однокласснику придется дорого расплатится. Насколько дорого — вот это именно сейчас мы и посчитаем.

Для начала краткая вводная информация. Допустим, ваш бывший одноклассник взял два миллиона рублей в кредит. При этом согласно договору он должен платить x рублей в месяц. Допустим, что кредит он взял по ставке 20% годовых, что в нынешних условиях выглядит вполне прилично. Кроме того, предположим, что срок кредита составляет всего три месяца. Давайте попробуем связать все эти величины в одну формулу.

Итак, в самом начале, как только ваш бывший одноклассник вышел из банка у него в кармане два миллиона, и это и есть его долг. При этом не год прошел, и не месяц, а это только самое начало:

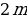
Затем спустя один месяц на сумму задолженности будут начислены проценты. Как мы уже знаем для вычисления процентов достаточно умножить исходную задолженность на коэффициент, который считается по следующей формуле:

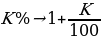
В нашем случае речь идет о ставке 20% годовых, т. е. мы можем записать:

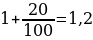
Это коэффициент суммы, которая будет начисляться в год. Однако наш одноклассник не очень умный и он не читал договор, и на деле кредит ему выдали не под 20% в год, а под 20% в месяц. И уже к концу первого месяца на эту сумму будут начислены проценты, и она увеличится в 1,2 раза. Сразу после этого человеку будет необходимо оплатить оговоренную сумму, т. е. x рублей в месяц:

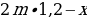
Далее к концу второго месяца уже на эту сумму будут вновь начислены проценты:

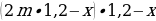
И вновь наш паренек вносит платеж в размере x рублей.

Затем к концу третьего месяца сумма его задолженности еще раз увеличивается на 20%:

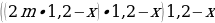
И по условию за три месяца он должен полностью расплатиться, т. е. после внесения последнего третьего платежа его объем задолженности должен быть равен нулю. Мы можем записать такое уравнение:

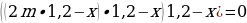
Давайте решать:

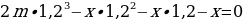
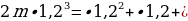
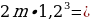
Перед нами вновь геометрическая прогрессия, а точнее, сумма трех элементов геометрической прогрессии. Давайте перепишем ее в порядке возрастания элементов:

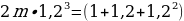
Теперь нам нужно найти сумму трех элементов геометрической прогрессии. Давайте запишем:

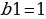
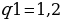
Теперь найдем сумму геометрической прогрессии:

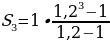
Следует напомнить, что сумма геометрической прогрессии с такими параметрами(b1;q) считается по формуле:

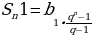
Вот этой формулой мы только что и воспользовались. Подставляем эту формулу в наше выражение:

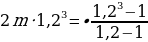
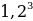
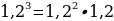
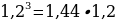
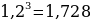
Для дальнейших вычислений нам следует узнать, чему равна  . К сожалению, в этом случае мы уже не можем расписать как в прошлый раз в виде двойного квадрата, но зато можем посчитать так:

Переписываем наше выражение:

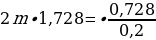
Это классическое линейное выражение. Давайте вернемся к следующей формуле:

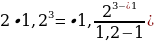
По сути, если обобщить ее, то мы получим формулу, связывающую проценты, кредиты, платежи и сроки. Формула звучит следующим образом:

}

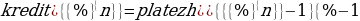
Вот она, самая главная формула, с помощью которой считается не менее 80% всех экономических задач из ЕГЭ по математике во второй части. Знать эту формулу, связывающую кредиты платежи и проценты, также необходимо как и сумму геометрической прогрессии. Именно с помощью этих формул решаются реальные экономические задачи из ЕГЭ по математике

Кредитные инструменты очень полезны и крайне необходимы нашей экономике, но только при условии, что кредит берется на развитие бизнеса. В крайнем случае, можно взять кредит на покупку жилья, т. е. ипотеку либо на неотложное медицинское лечение — все, других причин взять кредит просто не существует.

Помимо ставки вознаграждения по кредиту (проценты по кредиту), клиенту необходимо обратить внимание на такой важный показатель, как метод погашения кредита — аннуитетный и дифференцированный, или еще его называют «равными долями».

Отметим, что в то время как в России существовал только один вид платежа – дифференцированный, на западе практиковался другой – аннуитетный. Оба вида выполняют одну и ту же функцию, помогая гражданам соблюдать свои обязательства по кредиту, говоря простыми словами – выплачивать долги.    

Дифференцированный платеж

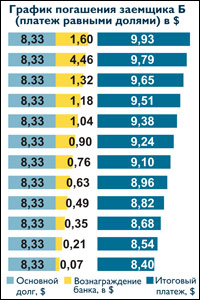
При дифференцированных платежах вся сумма кредита (основного долга) делится на равные части с учетом срока и периодичности погашения платежа по кредиту (ежемесячно, ежедневно, ежеквартально).

В даты платежа по графику клиент выплачивает часть суммы кредита (основного долга) плюс начисленные проценты.
Проценты начисляются на остаток основного долга, соответственно, сумма начисленного вознаграждения по мере погашения кредита уменьшается.

Наиболее распространенной периодичностью погашения является ежемесячный график.

Например, сумма кредита — 100 000 тенге, срок кредита — 1 год, периодичность погашения – ежемесячно (100 000:12 месяцев = 8 333,33 тенге), дополнительно к полученной сумме прибавляется сумма начисленного вознаграждения, которая производится в первый месяц от 100 000 тенге, во второй месяц — от 91 666,66 тенге (100 000 – 8 333,33 = 91 666,66) и т.д.

Недостатком дифференцированного платежа является то, что клиенту необходимо или помнить, или постоянно уточнять, сколько денег ему нужно платить в очередной раз.

При дифференцированном графике в первую половину срока кредита заемщик направляет на погашение кредита гораздо большую сумму из своего дохода, чем во второй ее половине. При таком методе слова «деньги сейчас дороже, чем потом» не работают на клиента, т.к. на деньги, которые заемщик направляет на погашение в первой половине, можно купить гораздо больше, чем через 5, 10 или 20 лет, ведь инфляция велика, и объективных признаков ее снижения в обозримом будущем нет.

Данный вид платежа приемлем для клиентов, у которых нефиксированный доход, который ежемесячно варьируется (больше или меньше). Во-вторых, по кредиту с дифференцированным платежом требования к платежеспособности выше, ведь банк оценивает максимальную сумму кредита, исходя из способности клиента «потянуть» первые платежи по кредиту. Однако учитывая возможность изменения и улучшения условий в будущем (возможное уменьшение % по кредиту, инфляцию, повышение доходов), в последующем выплаты по кредиту становятся все менее обременительными, и к концу срока фактически снижаются.

Плюсы и минусы дифференцированного платежа

Особенности дифференцированного платежа таят в себе как плюсы, так и минусы. Основным плюсом является факт более выгодного способа оплачивать кредит, поскольку данный вид платежа существенно снижает переплаты по кредиту.

Минусом являются большие размеры первоначальных платежей, поэтому дифференцированный платеж называют платежом для обеспеченных людей. Еще одним минусом является отсутствие популярности платежа у банков – большинство банков используют аннуитетную платежную систему, как более выгодную. Несмотря на то, что в России имеется порядка 6-9 банков, где предусмотрена подобная система платежа, среди населения не наблюдается особого ажиотажа – сказывается необходимость выплачивать большие суммы на первоначальном этапе.

Если кредит, к примеру, ипотечный и берется на долгие годы, то имеет смысл перераспределить «тяжесть» платежей таким образом, чтобы основная кредитная нагрузка пришлась на молодые годы, когда человек еще не обременен множеством обязательств, а поиск работы не сопряжен с возрастными ограничениями.

Аннуитетный платеж

Аннуитетный платеж остается неизменным в течение всего срока действия кредитного договора.

Это значит, что каждый месяц клиент платит за кредит одинаковую сумму, которая состоит из начисленных процентов за кредит и части суммы, списывающейся в счет основного долга.

Преимущество аннуитетных платежей заключается в их неизменности. Клиенту известна сумма, которую он должен платить каждый месяц в установленный срок. Больше никаких цифр держать в своей голове ему не надо. Это очень удобно для клиентов, имеющих фиксированный доход.

Таким образом, при выборе графика погашения необходимо выбирать наиболее подходящий для себя метод платежа с учетом текущих ежемесячных расходов, особенно это важно при оформлении кредита на длинные сроки.

К примеру, при оформлении ипотеки на 15-20 лет клиентам, имеющим доход в виде ежемесячной заработной платы, наиболее удобным при планировании семейного бюджета будет аннуитетный вид платежа.

В случае, если вы решите выбрать кредит с дифференцированными платежами, необходимо также учитывать, что максимально возможная сумма кредита может оказаться меньше в отличие от варианта с аннуитетным платежом, так как банк при расчете вашей платежеспособности будет учитывать максимально возможную сумму кредита с учетом первого платежа, который в сравнении с аннуитетом будет больше. 
Исходить нужно исключительно из своих возможностей и не забывать, что независимо от вида выбранного платежа, у вас всегда есть право досрочного погашения кредита.

Пример:

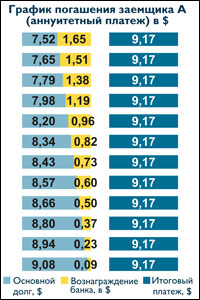
• Клиент А получил кредит 100 долларов сроком на 12 месяцев по ставке 10% (ГЭСВ 10,62 %). Выбрал аннуитетный график платежа по кредиту. 
  Отличительной особенностью данного вида платежа является фиксированный размер платежа на всем сроке кредита, что позволяет клиенту ежемесячно выделять из бюджета равную сумму денежных средств для погашения кредита.

• Клиент Б получил кредит на аналогичных условиях, но выбрал график с дифференцированными платежами (погашение основного долга равными долями). 

Отличительной особенностью данного графика является то, что в течение всего срока кредита размер платежа изменяется от наибольшего к наименьшему.

 Подводя итог, отметим, что выбирая кредитную программу, потенциальные заемщики ориентируются на процентную ставку по кредиту. Но не только ставка влияет на сумму выплачиваемых процентов, а также способ их начисления и метод погашения кредита. Таких методов существует два: аннуитетные платежи и дифференцированные платежи.

На наш взгляд, наиболее выгодная схема погашения ипотечного кредита — дифференцированные платежи. Так, общая сумма выплаченных банку денег, взятых под 12 % годовых и погашенных дифференцированными платежами — намного меньше, чем взятых под 12 % годовых, но погашенных аннуитетными платежами.

Дифференцированные платежи характерны тем, что задолженность по кредиту погашается равномерно начиная с самых первых выплат, а проценты начисляются по фактическому остатку. Таким образом, каждый последующий платеж меньше предыдущего. Досрочное погашение не ограничено ни по времени, ни по сумме и позволяет существенно сэкономить на выплачиваемых процентах.

Аннуитет — начисление равных платежей на весь срок погашения кредита. При этом в первой половине срока погашения задолженность по кредиту практически не гасится — выплачиваются в большей части проценты. Эта особенность делает платежи относительно небольшими, но значительно увеличивает общую сумму начисляемых процентов.

Раздел второй. Типы экономических задач на аннуитетный и дифференцированный платежи

Приведем примеры решения задач формата ЕГЭ на аннуитетный платеж

№ 1. 31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?

Решение. Пусть сумма кредита равна a, ежегодный платеж равен x рублей, а годовые составляют k %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент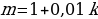 

После первой выплаты сумма долга составит:  . После второй выплаты сумма долга составит: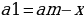

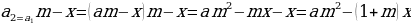
После третьей выплаты сумма оставшегося долга:

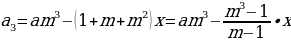
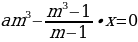
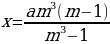
По условию тремя выплатами Сергей должен погасить кредит полностью, поэтому  откуда при  , откуда ,при a = 9 930 000 и k = 10, получаем: m = 1,1

Ответ: 3 993 000 рублей. 

№ 2. В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

— каждый январь долг возрастает на 31% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга, равную 69690821 рубль.

Сколько рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами ( то есть за три года)?

Решение.

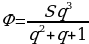
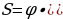
Если искомая сумма составляет S рублей, то при коэффициенте ежегодной процентной ставки q, равной 1,31, фиксированная сумма Ф, которую клиент ежегодно должен возвращать в банк в течение 3 лет, составляет , откуда .

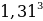
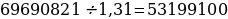
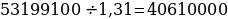
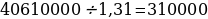
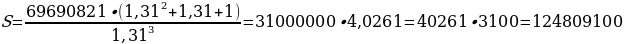
Заметим, что 69690821 кратно . Действительно, ;

 

Ответ: 124 809 100 рублей.

№ 3. 31 декабря 2014 года Алексей взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплат кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк x рублей. Какой должна быть сумма x, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?

Решение.

Пусть сумма кредита равна S, а годовые составляют a%. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент b = 1 + 0,01a. После первой выплаты сумма долга составит S₁ = Sb − x. После второй выплаты сумма долга составит:

.

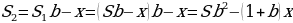
После третьей выплаты сумма оставшегося долга равна:

.

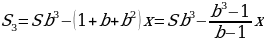
После четвёртой выплаты сумма оставшегося долга равна

.

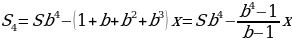
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому

; откуда

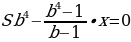
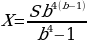
При S = 6 902 000 и a = 12,5, получаем: b = 1,125 и

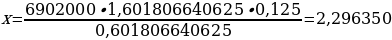
 рублей

Ответ: 2 296 350.

№ 4. 31 декабря 2014 года Тимофей взял в банке 7 007 000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Тимофей переводит в банк платёж. Весь долг Тимофей выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?

Решение.

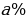
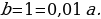
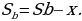
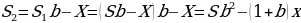
Пусть сумма кредита равна S, а годовые составляют .Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент После первой выплаты сумма долга составит После второй выплаты сумма долга составит

После третей выплаты сумма оставшегося долга равна

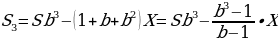
По условию тремя выплатами Тимофей погасил кредит полностью, поэтому

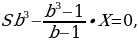
откуда .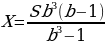

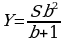
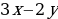
Рассуждая аналогично, находим, что если бы Тимофей гасил долг двумя равными выплатами, то каждый год он должен был бы выплачивать .рублей. Значит, он отдал банку на больше.

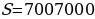
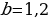
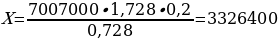
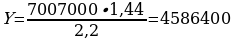
При и a=20, получаем : и (рублей).

(рублей).

Значит,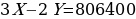

 Ответ: 806400.

№ 5. 31 декабря 2014 года Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк X рублей. Какой должна быть сумма X, чтобы Дмитрий выплатил долг двумя равными платежами (то есть за два года)?

 Решение.

Пусть сумма кредита равна S, а годовые составляют а%. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент b = 1 + 0,01а. После первой выплаты сумма долга составит S₁ = Sb − X. После второй выплаты сумма долга составит 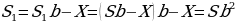–(1+b)X

По условию двумя выплатами Дмитрий должен погасить кредит полностью, поэтому  откуда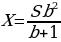 

При S = 4 290 000 и а = 14,5, получаем: b = 1,145 и 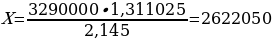 (рублей).

 Ответ: 2 622 050.

Приведем примеры решения задач формата ЕГЭ на дифференцированный платеж

№ 1. Антон взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на одно и то же число процентов (месячную процентную ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Общая сумма выплат превысила сумму кредита на 63%. Найдите месячную процентную ставку.

Решение.

Пусть сумма кредита S у.е., процентная ставка банка x %.

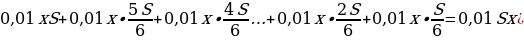
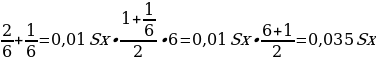
Предложение «Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину» означает: Антон взятую сумму возвращал в банк равными долями. Сумма, образованная применением процентной ставки, составляет: +  (у.е.)

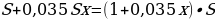
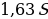
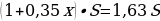
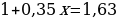
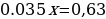
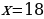
Общая сумма, выплаченная Антоном за 6 месяцев:   (у.е.). А эта сумма по условию задачи равна   у.е. Решим уравнение:

 Ответ: 18.

№2. Жанна взяла в банке в кредит 1,2 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?

Решение.

Пусть B_i — размер долга Жанны на конец месяца i, X_i — платеж Жанны в конце месяца i. Мы знаем, что имеет место соотношение B_i = 1,02B_{i − 1} − X_i. Кроме того, мы знаем, что последовательность (B_i) является арифметической прогрессией. При этом B₀ = 1200 тыс. руб., а B₂₄ = 0, так как в конце срока кредитования долг Жанны должен быть равен нулю. 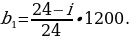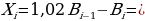Этих двух точек достаточно, чтобы узнать всю последовательность B_i:   Значит,

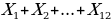
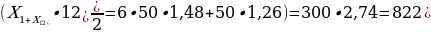
Поскольку X_i линейно зависит от i, последовательность X_i также является арифметической прогрессией. Значит, =  тыс. рублей.

 Ответ: 822 тыс. рублей.

№3 Сергей взял кредит в банке на срок 9 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 12%, а затем уменьшается на сумму, уплаченную Сергеем. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину.

Сколько процентов от суммы кредита составила общая сумма, уплаченная Сергеем банку (сверх кредита)?

Решение.

Предложение «Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину» означает: Сергей взятую сумму, без учета процентов, возвращал равными долями.

Общая сумма, уплаченная Сергеем банку сверх кредита, обусловлена только применением процентной ставки.

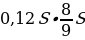
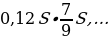
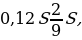
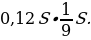
В первом месяце эта часть заплаченной суммы составляла 0,12S, во втором —  , в третьем —   в восьмом —   наконец, в последнем — 

Всего за 9 месяцев:

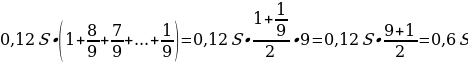
 Искомое процентное отношение есть 60 

 Ответ: 60.

№4. Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит. Найдите r.

Решение.

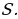
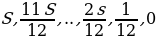
Пусть сумма кредита равна   По условию долг Алексея должен уменьшаться до нуля равномерно:

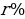
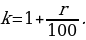
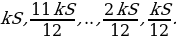
К концу каждого месяца к сумме долга добавляется  . Пусть   Тогда последовательность сумм долга вместе с процентами такова:

Следовательно, выплаты должны быть следующими:

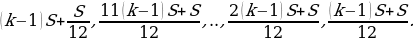
Всего следует выплатить:

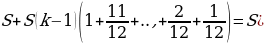
Общая сумма выплат оказалась на 13% больше суммы, взятой в кредит, поэтому:

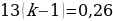
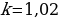
Откуда получаем, что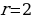 

 Ответ: 2.

№ 5.15-го января планируется взять кредит в банке на девять месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит. Найдите r.

Решение.

По формуле для переплаты П при выплате суммы кредита S дифференцированными платежами имеем: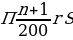

где n = 9 — число месяцев, а r — искомая величина платежной ставки в процентах. По условию, переплата П равна 0,25S, тогда: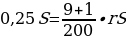

откуда r = 5.

 Приведем другое решение.

Долг уменьшается на 15-е число равномерно: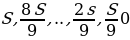 

Первого числа долг возрастает на r%, значит, долг на первое число:

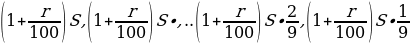
Выплаты:

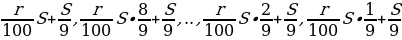
Тогда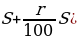

 

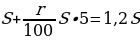
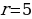
Ответ: 5.

Раздел третий. Особые экономические задачи

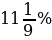
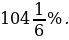
№ 1. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5%, затем 12%, потом   и, наконец, 12,5% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма увеличилась на   Определите срок хранения вклада.

Решение.

Известно:

1. Проценты на вклад начислялись ежемесячно.

2. Каждая последующая процентная надбавка по истечении календарного месяца начислялась с учетом вновь образованной суммы вклада и с учетом предыдущих надбавок.

Если первоначальная сумма вклада при ежемесячной 5%-ной ставке начисления процентов продержалась k месяцев, то вклад ежемесячно увеличивался в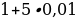   раз, и этот коэффициент будет сохранен до тех пор, пока ставка не изменится.

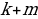
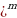
При изменении процентной надбавки с 5% на 12% (ставка 12% продержалась m месяцев) первоначальная сумма вклада за   месяцев увеличится в    раз.

Предположим, что процентная ставка 11 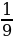  продержалась n месяцев, а процентная ставка 12,5 продержалась t месяцев. Тогда соответствующие коэффициенты повышения составят:

 и  .

Таким образом, коэффициент повышения суммы вклада в целом за весь период хранения вклада в банке составит:

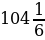
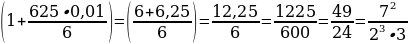
Это — с одной стороны. Но с другой стороны, согласно условию задачи первоначальная сумма вклада за это же время увеличилась на   то есть в  ( раз).

Значит,

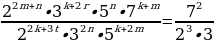
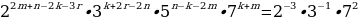
Согласно основной теореме арифметики каждое натуральное число, большее 1, можно представить в виде произведения простых множителей, и это представление единственное с точностью до порядка их следования. В таком случае:

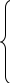
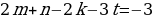
k+2t-2n=-1

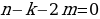
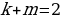
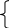
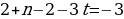
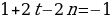
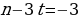
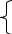
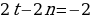
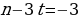
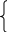
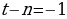
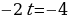
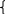
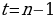
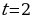
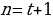
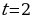
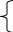
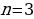
Решим эту систему относительно натуральных k,m,n и t. И з последнего уравнения системы имеем: k=m=1. При этих значениях k и m система примет вид:

 

Итак, 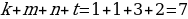  вклад в банке на хранении был 7 месяцев. При найденных значениях k,m,n и t n-k-2m действительно равно нулю.

 Ответ: 7.

№ 2. В июле 2016 года планируется взять кредит в банке на три года в размере S млн рублей, где S — целое число. Условия его возврата таковы:

− каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;

− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

− в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей

Месяц и год	Июль 2016	Июль 2017	Июль 2018	Июль 2019
Долг (в млн рублей)	S	0,7S	0,4S	0

 Найдите наименьшее значение S, при котором каждая из выплат будет больше 5 млн рублей.

Решение.

Долг перед банком (в млн рублей) на июль каждого года должен уменьшаться до нуля следующим образом:

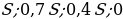
По условию, в январе каждого года долг увеличивается на 25%, значит, долг в январе каждого года равен:

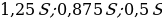
Следовательно, выплаты с февраля по июнь каждого года составляют:

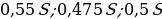
По условию, каждая из выплат должна быть больше 5 млн рублей. Это будет верно, если минимальная из выплат больше 5 млн рублей то есть если0,475S 5 Тогда:

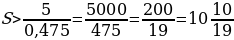
Наименьшее целое решение этого неравенства — число 11. Значит, искомый размер кредита — 11 млн рублей.

 Ответ: 11.

№ 3. В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S — целое число. Условия его возврата таковы:

— каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Месяц и год	Июль 2016	Июль 2017	Июль 2018	Июль 2019	Июль 2020
Долг (в млн рублей)	S	0,8S	0,5S	0,1S	0

Найдите наибольшее значение S, при котором общая сумма выплат будет меньше 50 млн рублей.

Решение.

Долг перед банком (в млн рублей) на июль каждого года должен уменьшаться до нуля следующим образом:

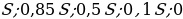
По условию, в январе каждого года долг увеличивается на 15%, значит, долг в январе каждого года равен:

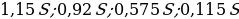
Следовательно, выплаты с февраля по июнь каждого года составляют:

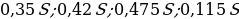
По условию, сумма выплат должна быть меньше 50 млн рублей.

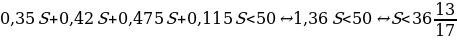
Наибольшее целое решение этого неравенства — число 36. Значит, искомый размер кредита — 36 млн рублей.

 Ответ: 36.

 №4. Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме того, в начале третьего и четвёртого годов вкладчик пополняет вклад на х млн рублей, где х — целое число. Найдите наименьшее значение х, при котором банк за четыре года начислит на вклад больше 6 млн рублей.

Решение.

Составим неравенство согласно условию задачи:

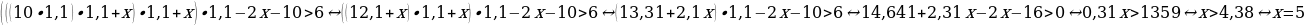
Ответ: 5.

Подводя итог, отметим, что необходимо знать для решения задания №17 на ЕГЭ

1. 1% — это сотая часть чего-либо

2. За 100% принимает ту величину, с которой сравниваем

3. Основные формулы для подсчета процентов

Если величину S увеличить на а%, то получим S(1+0,1а)

Если величину S уменьшить на а%, то получим S(1-0,1а)

Если величину S дважды увеличить на а%, то получим S(1+0,1а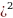

Если величину S уменьшить на а%, то получим S(1-0,01а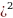

Заключение

В связи с преобразованием России из системы централизованного планирования в экономику рыночной ориентации экономические знания стали необходимыми как в профессиональной сфере, так и в повседневной жизни. Экономические знания позволяют понимать роль и права человека в обществе, готовят учеников к адекватному восприятию общества и производства, помогают им определить для себя сферу деятельности, профессию в будущем.

Эффективному постижению азов экономики поможет решение задач, в содержании которых идет речь о процентах. Понятие «проценты» буквально вошло в нашу жизнь, оно атакует нас в пору утверждения рыночных отношений в экономике, в пору банкротств, инфляций, финансовых кризисов. Сами проценты не дают экономического развития, но их знание помогает в развитии практических способностей, а также умение решать экономические задачи. Обдуманное изучение процентов может способствовать развитию таких навыков как экономичность, расчетливость.

Задачи с экономическим содержанием являются практическими задачами. А их решение, бесспорно, способствует более качественному усвоению содержания курса математики средней школы, позволяет осуществлять перенос полученных знаний и умений в экономику, что в свою очередь, активизирует интерес к задачам прикладного характера и изучению математики в целом. Такие задачи позволяют наиболее полно реализовывать прикладную направленность в обучении и способствуют более качественному усвоению самого учебного материала и формированию умения решать задачи данного типа.

На основе проанализированных задач, мы считаем, что введение такого рода заданий важно в современное время. Данные виды заданий чрезвычайно полезны так как, работая над моделями, сформулированными в условиях, они заставляют задумываться о реальной жизни. О том, что кредиты, отношения с банками, игра на бирже, колебания курсов ценных бумаг, начисление процентов дело сложное и требует больших знаний. К этому нельзя относиться легкомысленно. С чего начинать решать экономические задачи – очень внимательно читать условия задачи и по шагам распределить действия, затем постараться математически выразить их и постараться прийти к ответу.

ЛИТЕРАТУРА

1. Акимов Д.В. Решение задач по экономике: от простых до олимпиадных.М.,2016

2.Бондаренко М. Краткий курс лекций и рекомендаций по решению экономических задач. Чебоксары, 2016.

3. Гришаева Л.С. Основы экономики: задачи с решениями. М., 2016

4.Демонстрационный вариант контрольно-измерительных материалов единого государственного экзамена 2015 года по математике. Профильный уровень. Сайт http://www.ege.edu.ru/Ященко И. В. и др.

5. Колесникова С.И. Экономические задачи ЕГЭ. М., 2016

6. Малыхин В. Финансовая математика. СПб., 2014

7.Подготовка к ЕГЭ по математике в 2016 году. Базовый и профильный уровни. Методические указания / И. В. Ященко, С. А. Шестаков, А. С. Трепалин. – М.: МЦНМО, 2015.

8.Пучков Н.П. Математика в экономике. М., 2015

9.Спецификация контрольно-измерительных материалов для проведения в 2015 году единого государственного экзамена по математике. Профильный уровень. Сайт http://www.ege.edu.ru/

10. Хачатрян С. Методы и модели решения экономических задач. М., 2015

1. ФИНАНСОВАЯ МАТЕМАТИКА В ЗАДАЧАХ ЕГЭ И ПРАКТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ ЧЕЛОВЕКА

2.

Цель: изучить практико-ориентированные задачи,
раскрывающие суть различных видов платежей по
кредитам, выбрать оптимальные способы решения
Задачи:
— Изучить теоретические аспекты решения
«экономических» задач;
— Рассмотреть различные способы решения задач;
-Повысить уровень математической культуры, прививая
навыки самостоятельной исследовательской работы в
математике;
-Выполнить сопоставительно-аналитическую работу с
контрольно–измерительными материалами ЕГЭ, а
также исследовать примеры применения в жизненных
ситуациях.

3.

Гипотеза:
1) Существует много видов «экономических»
задач на проценты и способов их решения, но их
можно проклассифицировать по типам для
облегчения усвоения материала.
2) Одного способа расчета кредита быть не
может, существуют два вида платежей по
кредиту: дифференцированный и аннуитетный.
3) Существует переплата по кредитам. Но при
каких схемах выплаты кредита она меньше?

4. Способы погашения кредита:

■ Дифференцированный
■ Аннуитетный

5.

Схема дифференцированного платежа
При расчете за кредит дифференцированными платежами
расчетная сумма платежа постепенно сокращается. Это
обусловлено тем, что прежде всего клиент вносит тело
кредита, и его сумма остается постоянной на протяжение
всех месяцев. Что касается процентной части, то она
зависит от остатка, который со временем сокращается. Это
значит, что и сумма процентов становится меньше.
Ориентировочную сумму платежа можно рассчитать так:
Платеж = Проценты + Фиксированная часть.
Под фиксированной частью понимают погашение
кредитного тела.
Проценты можно определить так: Проценты = (Ставка *
Остаток) / 100%.

6.

15-го января планируется взять кредит в банке
на сумму 1.5 млн рублей на 24 месяца. Условия
его возврата таковы:
— 1-го числа каждого месяца долг возрастает на
3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца
необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на
одну и ту же величину меньше долга на 15-е
число предыдущего месяца.
Какую сумму нужно вернуть банку:
а) в течение первого года кредитования?
б) в течение всего срока кредитования? Какова
сумма переплаты?

7.

1й способ
Долг перед банком по состоянию на конец второго года должен уменьшаться до
нуля равномерно на сумму равную 62500 рублей (1500000:24=62500). Тогда
последовательность размеров долга будет иметь вид: 1500000; 1437500;
1375000; 1312500; … 62500.
Первого числа каждого месяца долг возрастает на 3%. Тогда последовательность
размеров долга будет иметь вид:
1500000∙1,03; 1437500∙1,03; 1375000∙1,03; 1312500∙1,03; … 62500∙1,03.
Или: 1545000; 1480625; 1416250; 1351875; … 64375.
Найдем размеры выплат:
1 месяц: 1545000 – 1437500 = 107500
2 месяц: 1480625 – 1375000 = 105625
3 месяц: 1416250 – 1312500 = 103750 Замечаем, что выплаты уменьшаются на
одну и ту же величину, равную 1875 р.
Имеем последовательность членов арифметической прогрессии, в которой
первый член равен 107500, а разность равна -1875. Найдем 12-й член этой
прогрессии:
an = a1 +(n-1)*d
a12 = 107500 — 11∙ 1875=86875
Итак, 86875 рублей – это сумма выплат на 12 месяц. An an = a1
Найдем теперь сумму выплат за весь срок кредитования: 2062500 руб.
Переплата по кредиту равна: 2062500 – 1500000 = 562500 руб.
Ответ: а) 1166250 рублей б) 2062500 рублей в) 562500 рублей

8.

2й способ
Пусть S — сумма кредита. Найдем, какую сумму нужно вернуть банку за весь
период кредитования, то есть за 24 месяца. Долг перед банком по состоянию на
конец второго года должен уменьшаться до нуля равномерно. Тогда
последовательность размеров долга будет иметь вид:
24S/24; 23S/24; 22S/24; ….; S/24
Занесем эти данные в таблицу

9.

Найдем теперь размеры выплат:
1 месяц: 24*S*1.03/24 – 23S/24 = S/24*(24∙1.03 – 23).
2 месяц: 23*S*1.03/24 – 22S/24 = S/24* (23∙1.03 – 22).
3 месяц: 22*S*1.03/24 – 21S/24 = S/24* (22∙1.03 – 21).
24 месяц: S*1.03/24 – 0 = S/24*(1∙1.03 – 0).
Найдем сумму всех выплат:
S/24*(24∙1.03+23∙1.03+22∙1.03+…+1∙1.03-23-22-21-…-1) =
S/24* (1.03(24+23+22+…+1) –(23+22+21+…+1)) = S/24* (1.03∙300–
276) =S/24*33=11S/8
Чтобы найти численное значение суммы всех выплат, надо подставить
S=1,5. Получим, что сумма всех выплат равна 2,0625 миллионов
рублей, или 2062500 рублей.

10.

3й способ
Рассмотрим формулу расчета дифференцированного платежа в банке.
Формула расчета дифференцированного платежа выглядит следующим образом:
ДП = ОСЗ: ПП + ОСЗ ∙ ПС, где
ДП — размер дифференцированного платежа
ОСЗ — остаток ссудной задолженности
ПП — количество периодов, оставшихся до погашения кредита
ПС — месячная процентная ставка по кредитному договору, равная 1/12 годовой
процентной ставки
Пример расчета:
В погашение
Остаток после
процентов
платежа
0.00
0.00
100 000.00
17 500.00
16 666.67
833.33
83 333.33
2 месяц
17 361.11
16 666.67
694.44
66 666.67
3
3 месяц
17 222.22
16 666.67
555.56
50 000.00
4
4 месяц
17 083.33
16 666.67
416.67
33 333.33
5
5 месяц
16 944.44
16 666.67
277.78
16 666.67
6
6 месяц
16 805.56
16 666.67
138.89
0.00
100 000.00
2 916.67
№ Год, месяц Всего
В погашение долга
0
0 месяц
-100 000.00
1
1 месяц
2
Всего
заплачено
10 2 916.67

11.

Рассмотрим расчет на примере. Пусть, мы берем на 6 месяцев сумму
100000 рублей под 10% годовых. Тогда график погашения будет выглядеть
следующим образом:
Покажем, как были сделаны расчеты:
1 месяц: 100000:6+100000∙0,00833333=17500.00.
Остаток после платежа: 100000-16 666.67=83 333.33
2 месяц: 83 333.33:5 +83 333.33∙0,00833333=16 666.67+694.44=17361.11
Остаток после платежа: 83 333.33-16 666.67=66 666.67
3 месяц: 66 666.67:4+66 666.67∙0,00833333=16 666.67+555.56=17222.22
Остаток после платежа: 66 666.67-16 666.67=50 000.00
4 месяц: 50 000.00:3+50 000.00∙0,00833333=16 666.67+416.67=17 083.33
Остаток после платежа: 50 000.00-16 666.67=33 333.33
5 месяц: 33 333.33:2+33 333.33∙0,00833333=16 666.67+277.78=16 944.44
Остаток после платежа: 33 333.33-16 666.67=16 666.67
6 месяц: 16 666.67:1+16 666.67∙0,00833333=16 666.67+138.89=16 805.56
Остаток после платежа: 16 666.67-16 666.67=0. Кредит погашен.
Как мы видим из примера, ежемесячная сумма выплаты основного
долга не меняется, а меняется только сумма начисленных процентов на
остаток займа.
Вывод: Переплата составляет 2 916.67рублей

12.

4й способ
Пусть
х — ежемесячные платежи без начисленных %
24х — все выплаты без начисленных %
(24х+23х+ …. +2х+х)0,03=9х-% — за весь период кредитования
24х+9х=33х — все выплаты с начисленными %,
х=1500000/24
х=625000
33*62500=20 625 000

13.

Аннуитетные платежи – вариант ежемесячного платежа по
кредиту, когда размер ежемесячного платежа остаётся
постоянным на всём периоде кредитования. Ежемесячный
платёж при аннуитетной схеме погашения кредита состоит из
двух частей. Первая часть платежа идёт на погашение
процентов за пользование кредитом. Вторая часть идёт на
погашение долга. При аннуитетной схеме выплат по кредиту,
ежемесячный платёж рассчитывается как сумма процентов,
начисленных на текущий период и суммы идущей на
погашения суммы кредита.
31 декабря 2016 года некто взял в банке S рублей в кредит под
a процентов годовых. Схема выплаты кредита следующая:
1 числа каждого следующего года банк начисляет a процентов
на оставшуюся сумму долга. Затем некто переводит в банк
сумму X ежегодного платежа (транш). Весь долг некто должен
выплатить за n лет, то есть за n равных платежей. Необходимо
найти одну из неизвестных величин: S, a, X, или n.

14.

Пример расчёта графика выплат по аннуитетному кредиту
Размер кредита – 100000 р, годовая процентная ставка — 10%,
срок погашения — 6 месяцев.
Для начала рассчитаем ежемесячный платёж:
100000*(0,0083333+0,0083333/(1+0,0083333)6 -1) = 17156,14
Затем рассчитаем по месяцам процентную и кредитную часть аннуитетного платежа.
1 месяц: Проценты: 100000 ∙ 0,1 : 12 = 833,33
Основной долг: 17156,14 – 833, 33 = 16322,81
2 месяц: Остаток кредита: 100000 – 16322,81 = 83677,19
Проценты: 83677,19 ∙ 0,1:12 = 697,31
Основной долг: 17156,14 – 697,31 = 16458,83
3 месяц: Остаток кредита: 83677,19 – 16458,83 = 67218,36
Проценты: 67218,36 ∙0,1:12 = 560,15
Основной долг: 17156,14 – 560,15 = 16595,99
4 месяц: Остаток кредита: 67218,36 – 16595,99 = 50622,38
Проценты: 50622.38 ∙ 0,1:12 = 421.85
Основной долг: 17156,14 – 421,85 = 16734,29
5 месяц: Остаток кредита: 50622,38 – 16734,29 = 33888,09
Проценты: 33888,09 ∙ 0,1:12 = 282,40
Основной долг: 17156,14 – 282,40 = 16873,74
6 месяц: Остаток кредита: 33888.09 – 16873.74 = 17014,35
Проценты: 17014,35 ∙ 0,1:12 = 141,79
Основной долг: 17156,14 – 141,79 = 17014,35

15.

Месяц
Платеж
Проценты
Тело кредита
Остаток
1
17156.14
833.33
16322.81
83677.19
2
17156.14
697.31
16458.83
67218.36
3
17156.14
560.15
16595.99
50622.38
4
17156.14
421.85
16734.29
33888.09
5
17156.14
282.4
16873.74
17014.35
6
17156.14
141.79
17014.35
0
Общая сумма платежей: 102936.84
Общая сумма процентов (переплата): 2936.84
Чтобы узнать размер переплаты по аннуитетному кредиту, необходимо ежемесячный
платёж, умножить на количество периодов и из получившегося числа вычесть
первоначальный размер кредита. В нашем случае переплата будет следующей:
17156,14 ∙ 6 – 100000 = 2936,84

16. Аннуитетные платежи для них применима формула

-платежи клиента с уже
начисленными процентами
а- процентная ставка
В-сумма, взятая в кредит

17.

Если дано:
А1, А2, А3, А 4 – ежемесячные платежи,
а — процентная ставка — арифметический способ
решения.
В — сумма, взятая в кредит, а — процентная ставка линейное уравнение.
А1, А2, А3, А 4 — ежемесячные платежи, В — сумма, взятая
в кредит — квадратное уравнение.

18.

Какая схема выгодней:
Аннуитетная или
Дифференцированная?

19.

Анатолий решил взять кредит в банке 331000 рублей на 3
месяца под 10% в месяц. Существуют две схемы выплаты
кредита.
По первой схеме банк в конце каждого месяца начисляет
проценты на оставшуюся сумму долга (то есть увеличивает долг
на 10%), затем Анатолий переводит в банк фиксированную сумму
и в результате выплачивает весь долг тремя равными платежами
(аннуитетные платежи).
По второй схеме тоже сумма долга в конце каждого месяца
увеличивается на 10%, а затем уменьшается на сумму,
уплаченную Анатолием. Суммы, выплачиваемые в конце каждого
месяца, подбираются так, чтобы в результате сумма долга
каждый месяц уменьшалась равномерно, то есть на одну и ту же
величину (дифференцированные платежи). Какую схему выгоднее
выбрать Анатолию? Сколько рублей будет составлять эта выгода?

20.

Аннуитетная схема
А1, А2, А3, А 4 — ежемесячные платежи,
А — процентная ставка,
В — сумма, взятая в кредит.
В= 331000 руб
а=10%
А1 =А2 =А3 = х – ежемесячная выплата
х/1,1+х/(1,1)2+х/(1,1)3=331000 х= 133100
Весь платеж составит 339300 руб

21.

Дифференцированная схема
х руб – один из 3х равных платежей по основному долгу
3х – вся сумма по основному долгу
Рассчитываем % ставку банка:
(3х+2х+х)*0,1 = 0,6х
3х+0,6х = 3,6х
х=331000/3
3,6х=397200 руб
Сравниваем дифференцированный и аннуитетный
платежи:
339300-397200=2100 (руб)

22.

Спасибо за внимание!

Автор работы: 

Оганесян Сусанна Гагиковна

Руководитель проекта: 

Поликарпова Галина Павловна

Учреждение: 

ГБОУ СОШ лицей №150 Калининского района Санкт-Петербурга

В процессе работы над индивидуальным исследовательским проектом по математике на тему «Экономическая задача в ЕГЭ по математике» автором была поставлена цель, создать методическое пособие к декабрю 2019 года, содержащее много разных типов экономических задач и необходимых теоретических знаний, позволяющих ученикам научиться решать 17 задачу из ЕГЭ по профильной математике, что приведет к успешным результатам сдачи экзамена.

Подробнее о работе:

В ученическом проекте по математике «Экономическая задача в ЕГЭ по математике» автором был изучен принцип работы банков, рассмотрены правила осуществления банковских вкладов и получения кредитов. В работе рассматриваются примеры решения экономических задач на вклады и на кредиты, а также производственно-бытовых задач. В работе предложены экономические задачи для самоподготовки к ЕГЭ.

Учебная исследовательская работа по математике на тему «Экономическая задача в ЕГЭ по математике» будет интересна учащимся 10 и 11 класса, рассматривает теоретическую базу финансовой и математической грамотности. В работе представлен разбор основных типов задач с примерами их решений, автор анализирует ошибки, часто совершаемые учениками при решении экономических задач.

В работе автор приводит информацию, найденную в различных исторических, научных, энциклопедических источниках, и примеры решения текстовой задачи социально-экономической тематики. Это задача на применение математических методов для решения содержательных задач из различных областей науки и практики и интерпретацию результата с учётом реальных ограничений. Автор разрабатывает методические рекомендации, в которых содержится необходимый теоретический материал, примеры решения финансовых задач разных типов, задания для самопроверки, разбор наиболее сложных задач, которые были на ЕГЭ прошлых годов.

Оглавление

Введение
1. Принцип работы банков.
1.1. Вклады.
1.2. Кредиты.
2. Примеры решения экономических задач.
2.1. Задача на вклады.
2.2. Задачи на кредиты.
2.3. Производственно-бытовые задачи.
3. Экономические задачи для самоподготовки.
Заключение
Литература

Введение

Новым типом задач повышенного уровня сложности, впервые введённым в структуру Единого государственного экзамена в 2015 году, является текстовая задача социально-экономической тематики. Это задача на применение математических методов для решения содержательных задач из различных областей науки и практики и интерпретацию результата с учётом реальных ограничений.

Использование подобных задач предполагает проверку следующих умений учащихся:

• переходить от текста задачи к построению соответствующей математической модели степенями с натуральным показателем обращаться с процентами;
• обращаться с целыми числами, то есть уметь использовать при решении задач элементы теории делимости целых чисел;
• производить действия со сложными процентами и долями.

Как показывает анализ содержания подобных задач, сюжеты, описанные в них, являются некоторыми текстовыми упрощениями, моделями реально возникающих в окружающей жизни ситуации. Кроме того, сами сюжеты условно можно разделить на два типа, использующие соответственно дискретные модели (проценты, погашения кредитов и так далее) и непрерывные модели (различные производства, протяжённый во времени объема продукции и так далее).

За правильное выполнение задания выставляются три балла. Пособие поможет обучающимся сдать Единый государственный экзамен по математике на высокий балл, а также послужит учителям для организации имя эффективной подготовки школьников.

Цель проекта: создать методическое пособие к декабрю 2019 года, содержащее много разных типов экономических задач и необходимых теоретических знаний, позволяющих ученикам научиться решать 17 задачу из ЕГЭ по профильной математике, что приведет к успешным результатам.

Задачи проекта:

• Изучить теоретическую базу финансовой и математической грамотности
• Разобрать основные типы задач с примерами решений
• Проанализировать ошибки совершаемые учениками
• Создать продукт

Вопросы проекта:

• Какие темы по математике следует повторить ученикам для успешного решения экономических задач?
• Какие типы экономических задач вызывают наибольшую трудность у учеников?
• Как повысить процент учащихся, которые успешно справляются с решением экономических задач?

Актуальность: решение экономических задач очень полезно, так как жизнь современного человека тесно связана с финансовыми операциями

В соответствии с указом «О национальных целях и стратегических задачах развития Российской Федерации на период до 2024 года» получение качественного образования необходимо ученикам, чтобы быть конкурентоспособными в будущем на рынке труда, а также для обеспечения вхождения России в число 10 ведущих стран мира по качеству среднего образования приближается ЕГЭ, а большинство школьников еще не приступили к решению экономической задачи за решение этого задания на экзамене можно получить 3 первичных балла, что говорит о важности выполнения этого задания несмотря на то, что экономическая задача большинству школьников кажется несложной, в ней ученики чаще всего совершают ошибки.

Продукт проекта: методические рекомендации.

Новым типом задач повышенного уровня сложности, впервые введённым в структуру Единого государственного экзамена в 2015 году, является текстовая задача социально-экономической тематики. Это задача на применение математических методов для решения содержательных задач из различных областей науки и практики и интерпретацию результата с учётом реальных ограничений.

Методические рекомендации будут содержать необходимый теоретический материал, примеры решения финансовых задач разных типов, задания для самопроверки, разбор наиболее сложных задач, которые были на ЕГЭ прошлых годов. Пособие поможет обучающимся сдать Единый государственный экзамен по математике на высокий балл, а также послужит учителям для организации ими эффективной подготовки школьников.

Аналоговый анализ:
Недостатки других методических пособи

• наличие только типовых заданий,
• слабая теоретическая база,
• краткое пояснение к задачам.

Достоинства моего продукта:

• комплексный подход к решению задач,
• решение самых разнообразных заданий,
• грамотно составленная теоретическая база,
• представление подробных решений задач,

Этапы работы над проектом:

Название этапа	Дата	Содержание работы	Отметка о выполнении	Коррективы
Подготовительный	сентябрь 2018 года	Выбор темы, формы представления проекта, типа проекта, формулирование проблемы, цели, задач	Выполнено	Проблема должна быть более точной и лаконичной. Цель проекта следует расширить, сформулировать более глобально
Организационный	Октябрь 2018 года	Составление аннотации и актуальности работы	Выполнено	Указать актуальность проекта как для себя лично, так и более масштабно (например, значение для государства)
Аналитический	ноябрь 2018 года	Поиск статистики	Выполнено	Следует вставить ссылку на статистику
Аналитический	декабрь 2018 года	Аналоговый анализ	Выполнено	Помимо достоинств моего продукта следует также указать недостатки других аналогичных работ
Практический	Январь-сентябрь 2019 года	Работа над исследовательской частью (составление решения разных типов задач)	Частично	В решении задач лучше объяснять значение некоторых математических символов, не часто использующихся на курсе базовой математики
Практический	Август-сентябрь 2019 года	Работа над дизайном методички	Частично	Дизайн должен быть современным, но не слишком броским, чтобы не отвлекать внимание читателей

Принцип работы банков

Итак, 17 задача бывает банковской, то есть на вклады и кредиты, и производственно-бытовой. Второй тип задач интуитивно понятен большинству школьников и требует просто много практики. Для банковских же задач изложим немного теории.

Смоделируем ситуацию. Есть предприимчивый Андрей, который решает открыть банк, имея 100 рублей. Он объявляет, что будет выдавать кредиты под 20 % годовых. Это означает, что если Андрей даст кому-нибудь некую сумму на год, то через год он получит на 20 % больше денег. К Андрею приходит первый клиент, который хочет взять 100 рублей.

Он их получает, и Андрей целый год сидит и ждет, пока пройдет год и он получит уже 120 рублей. Но проблема в том, что прошел целый год, а у Андрея всего 120 рублей, хотя было 100. Разница небольшая. Значит, Андрею нужно действовать по-другому. Тогда он объявляет, что будет принимать вклады и процентная ставка будет составлять 10 % годовых.

Получается, если кто-то вложит в банк некую сумму, то через год получит в 1,1 раз больше денег от банка (на 10 % больше изначальной суммы). К Андрею приходит некий богач и вкладывает в банк 10 000 рублей. Через год банк должен вернуть богачу 11 000. Это достаточно проблематично, так как у Андрея нет 11 000 рублей.

Есть только 10 000 + 120=10120 рублей. С другой стороны целый год деньги богача будут в распоряжении банка, а значит, можно будет выдавать кредиты, увеличивая имеющиеся деньги. Таким образом, при удачном стечении обстоятельств Андрей получит от заемщиков через год сумму, превышающую 11000 рублей. Богач получает деньги от вклада, заемщики возвращают взятые суммы с процентами, а Андрей в плюсе и счастлив.

Вклады

В случае банковского вклада банк выступает в роли заёмщика (получает деньги, обязуясь их вернуть, а вкладчик в роли кредитора (предоставляет деньги).При внесении вкладчиком банка денег отношения между вкладчиком и банком закрепляются договором, в котором банк, принявший поступившую от вкладчика денежную сумму, обязуется возвратить ему сумму вклада и выплатить на неё проценты на условиях и в порядке, предусмотренных договором. Как правило, вкладчик имеет возможность распоряжаться начисленными процентами.

Кредиты

Кредит-это финансовая сделка, в результате которой кредитор (банк или другой финансовое учреждение) предоставляет на определенный срок деньги заемщику. За пользование деньгами заемщик кроме погашения основного долга (называемого в финансовой литературе телом кредита) выплачивает кредитору также проценты.

Разделение повышающих платежей на две части — погашение долга (тела кредита) и погашение процентных денег — принципиально важно, поскольку от этого зависят выплачиваемые налоги. Разберем и сравним две важные схема выплаты кредитов: дифференцированными и аннуитетными платежами. При дифференцированной схеме каждой платёж состоит из двух частей. Первая часть — основной платёж, его размер не изменяется на всём сроке кредитования.

Скажем, если в кредит взяли 1 млн рублей на 5 месяцев, а платежи ежемесячные, то тело кредита делится на пять равных частей по 200000 руб. — это и будет ежемесячный основной платеж. Вторую часть платежа составляют проценты на текущую часть долга. Долг постепенно уменьшается, потому и платежи в счет процентов тоже уменьшаются.

Первый платёж самый большой, последний — самый маленький. На практике платежи обычно ежемесячные, а банки учитывают каждый день кредитования: важно, сколько дней в месяце, високосный год или нет. А в экзаменационных задачах обычно упрощённая схема: за каждый платежный период проценты начисляются один раз.

Иначе говоря, если проценты начисляются ежегодно, то и выплаты по кредиту раз в год. Если проценты начисляются ежемесячно, то и выплаты ежемесячные. При аннуитетных платежах сумма кредита и сумма процентов за всё время пользования кредитом суммируются и делятся на число платежей, все платежи получаются равными.

Примеры решения экономических задач можно посмотреть в полном тексте проекта, прикрепленном внизу этой странице в формате *doc

Задачи для самоподготовки

1)

В июле 2016 года планируется взять кредит в банке на три года в размере S млн рублей, где S — целое число. Условия его возврата таковы:

• каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
• с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
• в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Найдите наименьшее значение S, при котором каждая из выплат будет больше 5 млн рублей.

2) Взяли кредит в банке на сумму 250 000 рублей под r% процентов годовых и выплатили за 2 года платежами 150 000 рублей в первый год и 180 000 рублей — во второй.

Найдите r.

3) В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы:

• в январе каждого года долг увеличивается на 30% по сравнению с предыдущим годом;
• с февраля по июнь нужно выплатить часть долга одним платежом.

Определите, на какую сумму взяли кредита банке, если известно, что кредит был выплачен тремя равными платежами (за 3 года) и общая сумма выплат на 78 030 рублей больше суммы взятого кредита.

4) Георгий взял кредит в банке на сумму 804 000 рублей. Схема выплата кредита такова: в конце каждого года банк увеличивает на 10 процентов оставшуюся сумму долга, а затем Георгий переводит в банк свой очередной платеж. Известно, что Георгий погасил кредит за три года, причем каждый его следующий платеж был ровно вдвое меньше предыдущего. Какую сумму Георгий заплатил в третий раз? Ответ дайте в рублях.

5) 15-го декабря планируется взять кредит в банке на 26 месяцев. Условия возврата таковы:

• 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
• со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
• 15-го числа каждого месяца с 1-го по 25-й долг должен быть на 20 тысяч рублей меньше долга на 15-е число предыдущего месяца;
• к 15-му числу 26-го месяца кредит должен быть полностью погашен.
• Какой долг будет 15-го числа 25-го месяца, если общая сумма выплат после полного погашения кредита составит 1407 тысяч рублей?

6) В июле планируется взять кредит в банке на сумму 9 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы::

• каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
• с февраля по июнь каждого года необходимо выплатить часть долга;
• в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
• Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 1,5 млн рублей?

7) 15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в процентах от кредита)	100%	90%	80%	70%	60%	50%	0%

В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?

8)15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в процентах от кредита)	100%	90%	80%	70%	60%	50%	0%

В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?

9 )Три сестры пришли на рынок и продавали поштучно цыплят. Первая принесла 16 цыплят, вторая — 25, третья — 30 цыпленка. Каждая из них часть товара продала утром, а часть — вечером. Утренняя цена одного цыпленка была у всех сестер одинаковая, и вечерняя цена тоже одинаковая, но более низкая (положительная). К вечеру весь товар был распродан, и дневная выручка (за утро и вечер) у всех сестер оказалась одинаковой: 7 руб 75 коп. Найдите общую утреннюю выручку (в рублях).

10) В банк был положен вклад под 10% годовых. Через год, после начисления процентов, вкладчик снял со счета 2000 рублей, а еще через год снова внес 2000 рублей. Вследствие этих действий через три года со времени открытия вклада вкладчик получил сумму меньше запланированной (если бы не было промежуточных операций со вкладом). На сколько рублей меньше запланированной суммы он получил?

Ответы:

1) 11
2) 20
3) 119700
4) 133100
5) 400 000
6) 16,2
7) 22,5
14
9) 11
10) 220

Заключение

Представленные в данной работе теория и решения задач позволят ученикам успешно справиться с экономической задачей в ЕГЭ, так как не дают им готовые модели, а предлагают методы и средства для самостоятельного составления математических моделей в задачах, что способствует развитию интеллекта школьников. Ведь решение экономических задач нужно не только для сдачи экзамена, а также для повышения финансовой грамотности молодёжи.

Даже достаточно сложные задачи на ЕГЭ можно подать школьникам в доступной и красочной форме. Главное – подавать информацию кратко, структурировано, но с другой стороны стараться охватить как можно более разнообразные типы задач. Именно этот редкий баланс я пыталась соблюдать при разработке своей методички.

Список использованной литературы

1. Софья Колесникова: ЕГЭ. Математика. Экономические задачи
2. ЕГЭ 2019. Математика. Профильный уровень. Типовые тестовые задания. 36 вариантов заданий. Под редакцией И.В.Ященко.
3. С.А. Шестаков: ЕГЭ 2018. Математика. Задачи с экономическим содержанием. Задача 17 (профильный уровень).
4. Прокофьев, Корянов: ЕГЭ. Математика. 10-11 классы. Социально-экономические задачи. Задание 17.
5. Дремов, Дерезин, Кривенко: ЕГЭ. Математика. Задача с экономическим содержанием.

Если страница Вам понравилась, поделитесь в социальных сетях: