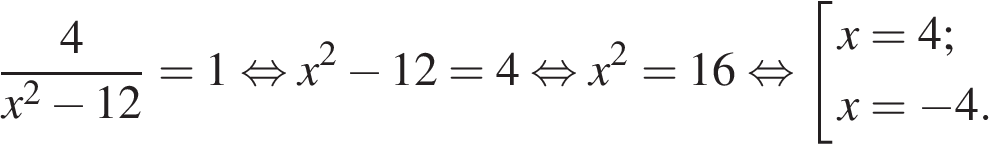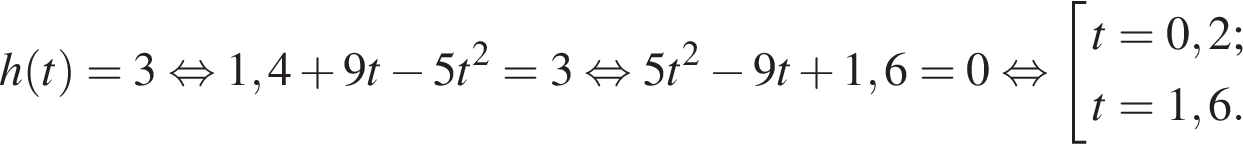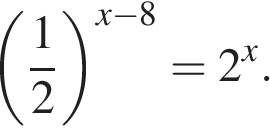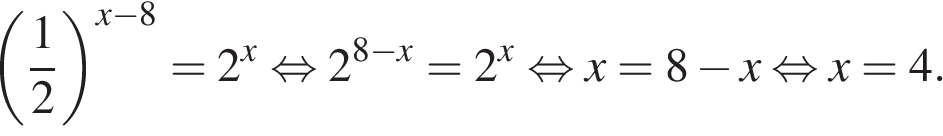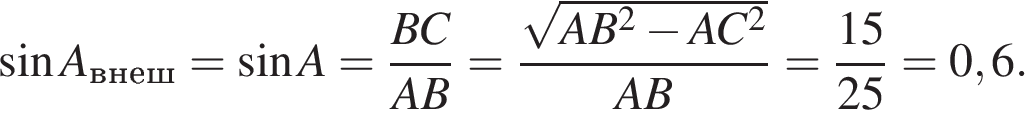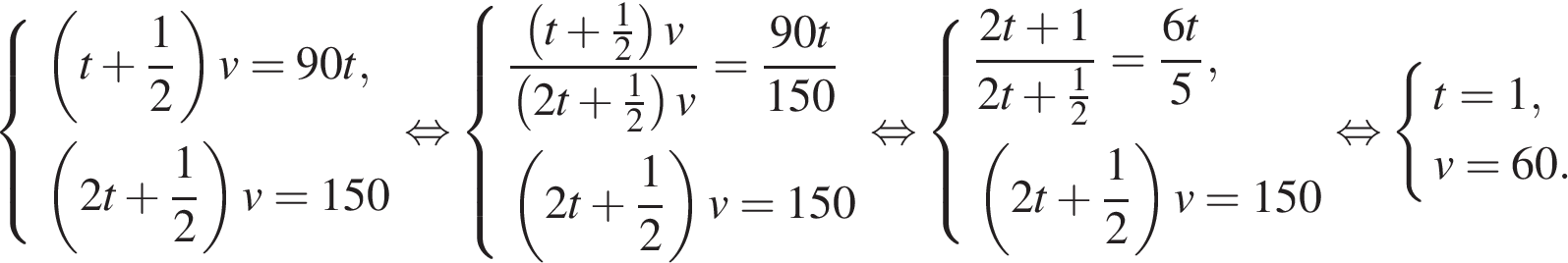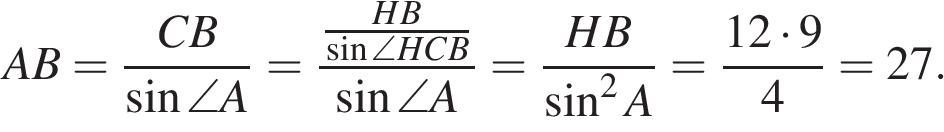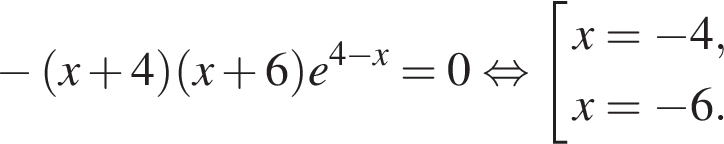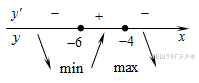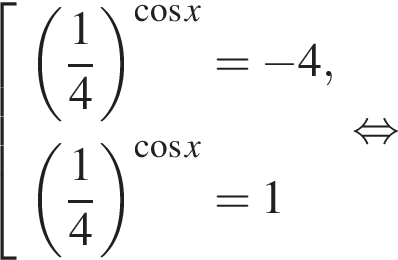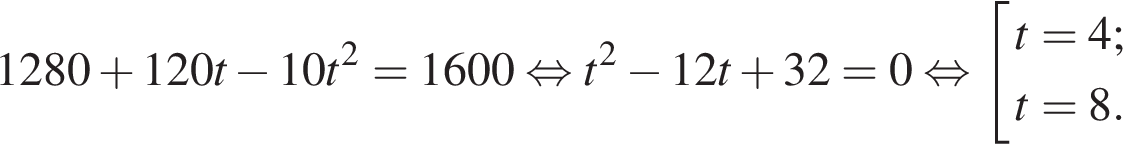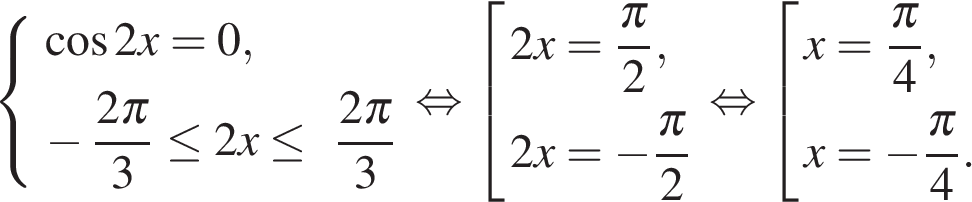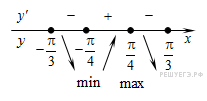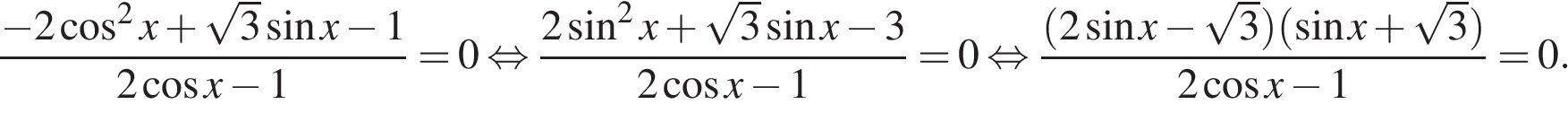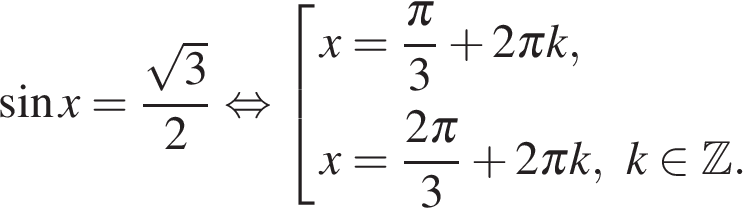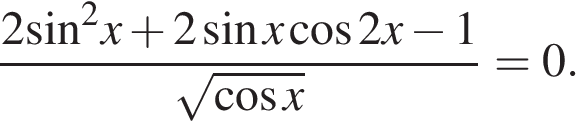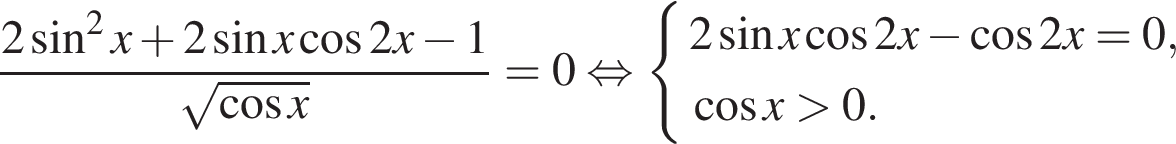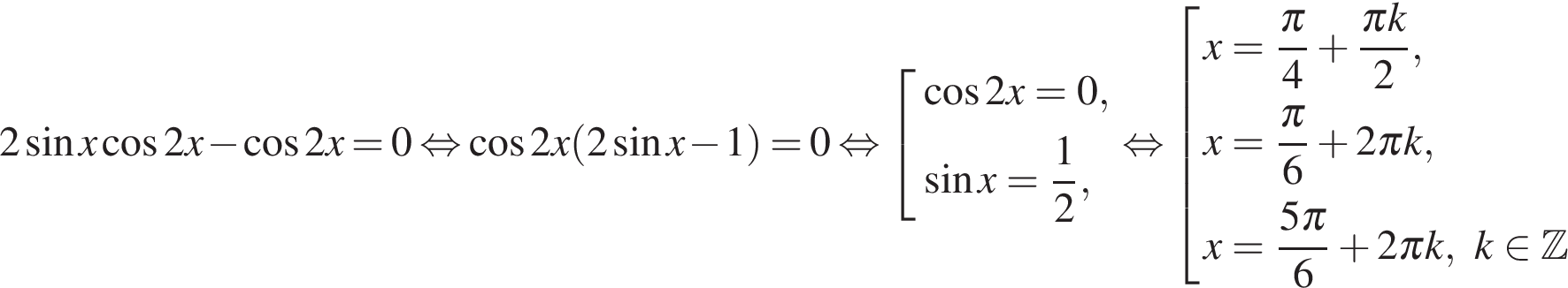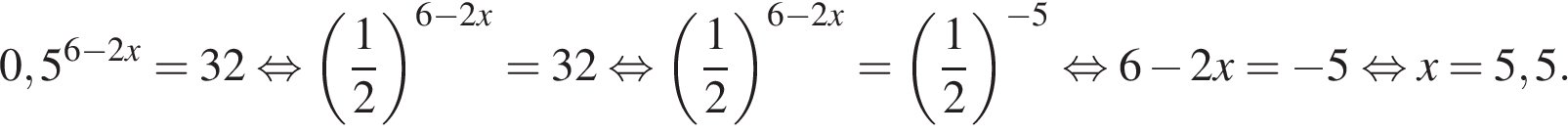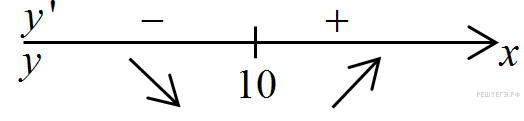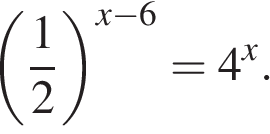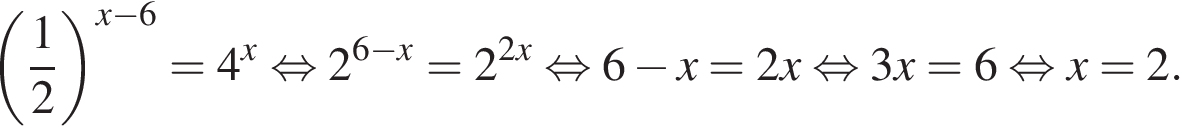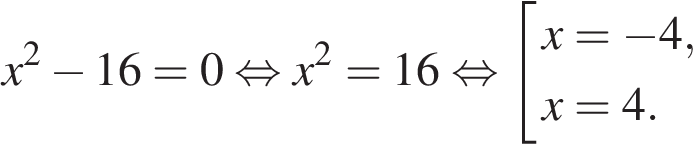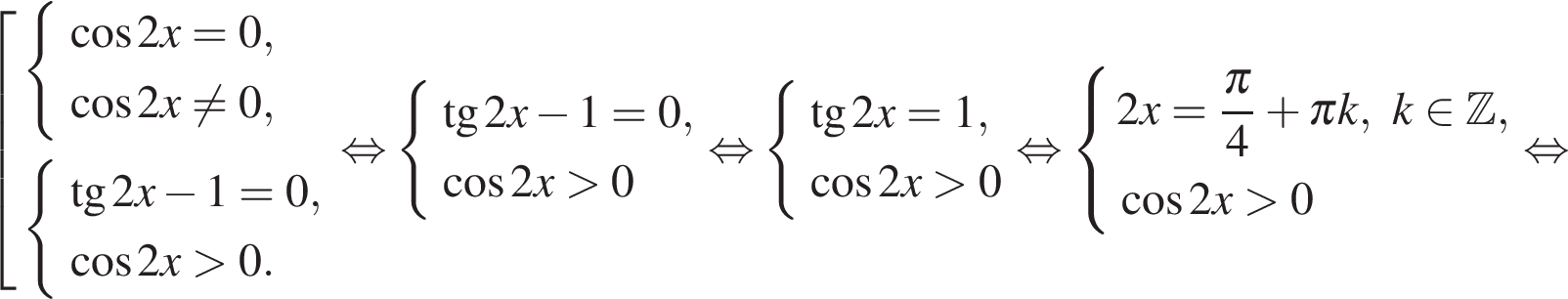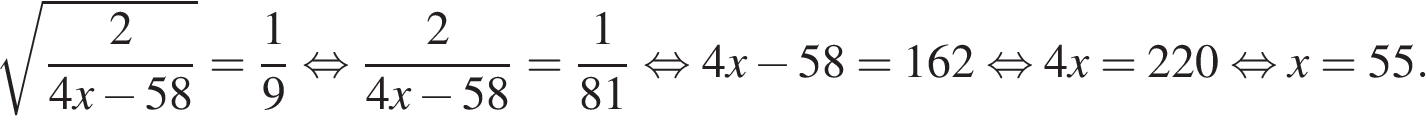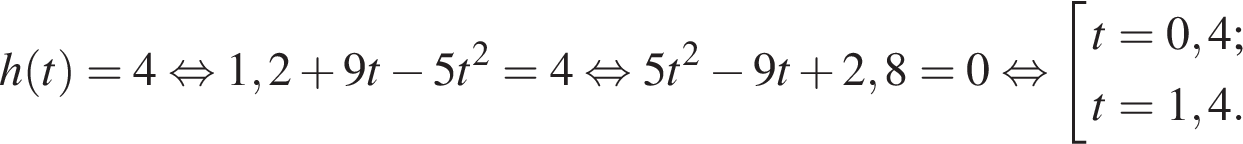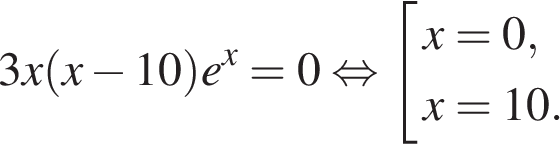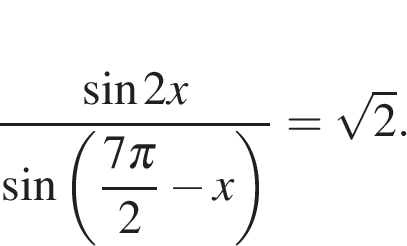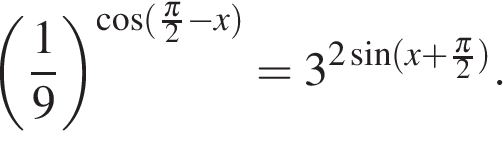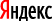Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 1.
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Ананасы стоят 85 руб. за штуку. Какое максимальное число ананасов можно купить на 500 руб., если их цена снизится на 20%?
Ответ:
2
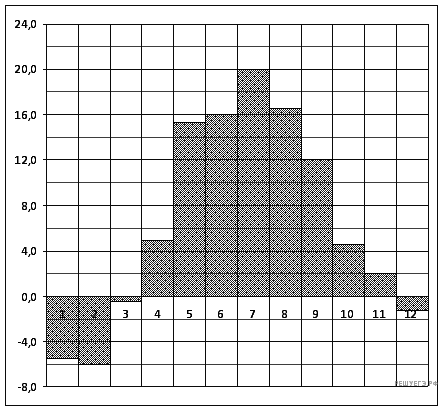
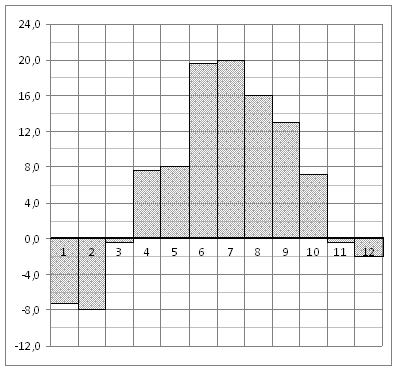
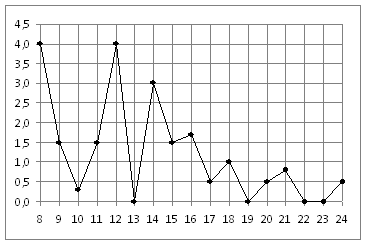
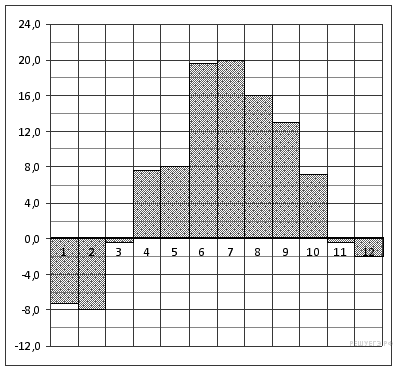
На рисунке жирными точками показано изменение биржевой стоимости акций целлюлозно-бумажного завода в первой половине апреля. Для наглядности жирные точки на рисунке соединены линией. По горизонтали указываются числа месяца, по вертикали — стоимость акции в рублях. 2 апреля бизнесмен приобрёл 250 акций этого завода. 6 апреля он продал 150 акций, а оставшиеся акции продал 11 апреля. Сколько рублей составили убытки бизнесмена в результате этих операций?
Ответ:
3
Фирма планирует закупить 150 м3 древесины у одной из трёх лесопилок. Цены и условия приведены в таблице. Какова стоимость самой выгодной покупки с учётом доставки?
| Перевозчик | Стоимость древесины (руб. за 1 м3) |
Стоимость доставки (руб.) |
Дополнительные условия |
| А | 3600 | 20 000 | При заказе на сумму свыше 550 000 руб. доставка бесплатная |
| B | 3500 | 30 000 | При заказе на сумму свыше 500 000 руб. доставка бесплатная |
| C | 3500 | 25 000 |
Ответ:
4
В равнобедренном треугольнике ABC с основанием AB угол С равен 48°. Найдите угол между стороной AB и высотой АН этого треугольника.
Ответ:
5
У Вити в копилке лежит 12 рублёвых, 6 двухрублёвых, 4 пятирублёвых и 3 десятирублёвых монеты. Витя наугад достаёт из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 70 рублей.
Ответ:
6
Найдите корень уравнения
Ответ:
7
8
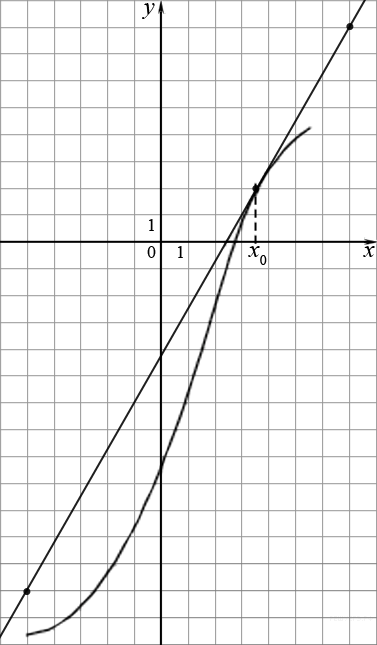
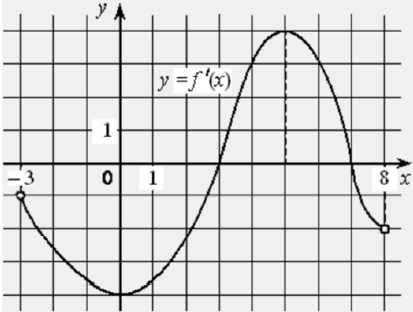
На рисунке изображен график функции y = f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 12 или совпадает с ней.
Ответ:
9
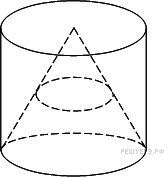
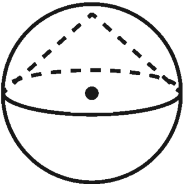
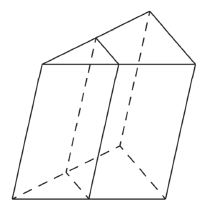
Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.
Ответ:
10
Найдите значение выражения
Ответ:
11
12
В правильной четырёхугольной пирамиде боковое ребро равно 22, а тангенс угла между боковой гранью и плоскостью основания равен Найти сторону основания пирамиды.
Ответ:
13
Два промышленных фильтра, работая одновременно, очищают цистерну воды за 30 минут. Определите, за сколько минут второй фильтр очистит цистерну воды, работая отдельно, если известно, что он сделает это на 25 минут быстрее, чем первый.
Ответ:
14
Найдите наименьшее значение функции на отрезке [−2; 2].
Ответ:
15
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
16
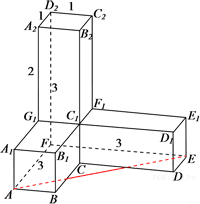
В пирамиде DABC прямые, содержащие ребра DC и AB, перпендикулярны.
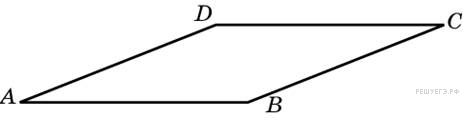
а) Постройте сечение плоскостью, проходящей через точку О — середину ребра DB, и параллельно DC и AB. Докажите, что получившееся сечение является прямоугольником.
б) Найдите угол между диагоналями этого прямоугольника, если DC = 24, AB =10.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
17
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
18
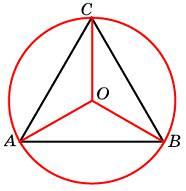
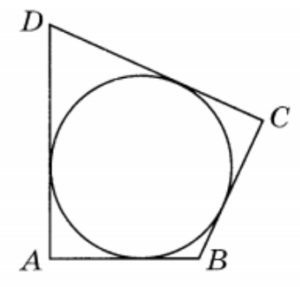
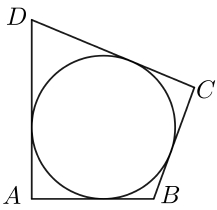
Точка О — центр окружности, вписанной в треугольник ABC. На продолжении отрезка AO за точку О отмечена точка K так, что BK = OK.
а) Докажите, что четырехугольник ABKC вписанный.
б) Найдите длину отрезка AO, если известно, что радиусы вписанной и описанной окружностей треугольника ABC равны 3 и 12 соответственно, а OK = 5.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
19
Фабрика, производящая пищевые полуфабрикаты, выпускает блинчики со следующими видами начинки: ягодная и творожная. В данной ниже таблице приведены себестоимость и отпускная цена, а также производственные возможности фабрики по каждому виду продукта при полной загрузке всех мощностей только данным видом продукта.
| Вид начинки | Себестоимость (за 1 тонну) |
Отпускная цена (за 1 тонну) |
Производственные возможности |
| ягоды | 70 тыс. руб. | 100 тыс. руб. | 90 (тонн в мес.) |
| творог | 100 тыс. руб. | 135 тыс. руб. | 75 (тонн в мес.) |
Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции каждого вида должно быть выпущено не менее 15 тонн. Предполагая, что вся продукция фабрики находит спрос (реализуется без остатка), найдите максимально возможную прибыль, которую может получить фабрика от производства блинчиков за 1 месяц.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
20
Найдите все значения а, при каждом из которых система
имеет единственное решение.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
21
Даны n различных натуральных чисел, составляющих арифметическую прогрессию (n ≥ 3).
а) Может ли сумма всех данных чисел быть равной 16?
б) Каково наибольшее значение n, если сумма всех данных чисел меньше 900?
в) Найдите все возможные значение n, если сумма всех данных чисел равна 235.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
Представлены КИМ по математике в 26 вариантах.
Просмотр содержимого документа
«Вариант 1»
Вариант 1.
1. В школе 1050 учеников, из них 30% — ученики начальной школы. Среди учеников средней и старшей школы 20% изучало французский язык. Сколько учеников в школе изучают французский язык, если в начальной школе французский язык не изучается?
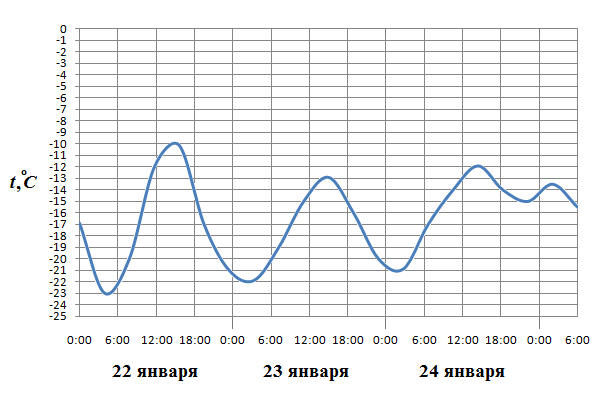
2. На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наименьшую температуру воздуха 23 января. Ответ дайте в градусах Цельсия.
3. 
4. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Сапфир» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Сапфир» выиграет жребий ровно два раза.
5. Найдите корень уравнения .
6. 
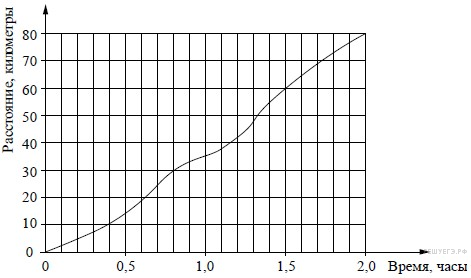
7. На рисунке показан график движения автомобиля по маршруту. На оси абсцисс откладывается время (в часах), на оси ординат — пройденный путь (в километрах). Найдите среднюю скорость движения автомобиля на данном маршруте. Ответ дайте в км/ч.
8. Высота конуса равна 72, а длина образующей — 90. Найдите диаметр основания конуса.
9. Найдите значение выражения при
.
10. При нормальном падении света с длиной волны нм на дифракционную решётку с периодом
нм наблюдают серию дифракционных максимумов. При этом угол
(отсчитываемый от перпендикуляра к решетке), под которым наблюдается максимум, и номер максимума
связаны соотношением
Под каким минимальным углом
(в градусах) можно наблюдать второй максимум на решётке с периодом, не превосходящим 1800 нм.
11. Смешали некоторое количество 11-процентного раствора некоторого вещества с таким же количеством 13-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
12. Найдите наибольшее значение функции на отрезке
13. а) Решите уравнение .
б) Найдите все корни этого уравнения, принадлежащие отрезку .
14. В основании прямой треугольной призмы ABCA1B1C1 лежит равнобедренный прямоугольный треугольник ABC с гипотенузой AB, равной ; высота призмы равна
Найдите расстояние от точки C1 до плоскости BCM, где M — середина ребра A1C1.
15. Решите неравенство:
16. Две окружности, радиусы которых равны 9 и 4, касаются внешним образом. Найдите радиус третьей окружности, которая касается двух данных окружностей и их общей внешней касательной.
17. По вкладу «А» банк в конце каждого года планирует увеличивать на 20% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 10% в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
18. При каких уравнение
имеет ровно три корня?
19. Семь экспертов оценивают кинофильм. Каждый из них выставляет оценку — целое число баллов от 0 до 12 включительно. Известно, что все эксперты выставили различные оценки. По старой системе оценивания рейтинг кинофильма — это среднее арифметическое всех оценок экспертов. По новой системе оценивания рейтинг кинофильма оценивают следующим образом: отбрасываются наименьшая и наибольшая оценки и подсчитывается среднее арифметическое оставшихся оценок.
а) Может ли разность рейтингов, вычисленных по старой и новой системам оценивания, равняться
б) Может ли разность рейтингов, вычисленных по старой и новой системам оценивания, равняться
в) Найдите наибольшее возможное значение разности рейтингов, вычисленных по старой и новой системам оценивания.
Просмотр содержимого документа
«Вариант10»
Вариант № 10
1. На автозаправке клиент отдал кассиру 1000 рублей и залил в бак 28 литров бензина по цене 28 руб. 50 коп. за литр. Сколько рублей сдачи он должен получить у кассира?
Решение.
Цена бензина составляет 28 28,5 = 798 руб. Поэтому причитающаяся сдача 202 рубля.
Ответ: 202
282847
202
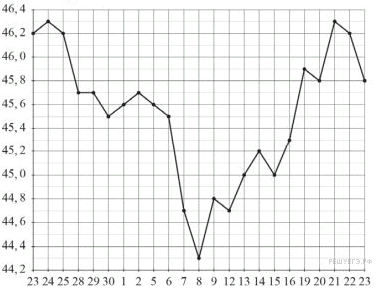
2. На рисунке жирными точками показан курс китайского юаня, установленный Центробанком РФ, во все рабочие дни с 23 сентября по 23 октября 2010 года. По горизонтали указываются числа месяца, по вертикали — цена китайского юаня в рублях. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наименьший курс китайского юаня за указанный период. Ответ дайте в рублях.
Решение.
Из рисунка видно, что наименьший курс китайского юаня был установлен 8 октября и составил 44,3 рубля.
Ответ: 44,3.
Ответ: 44,3
500904
44,3
Источник: МИОО: Тренировочная работа по математике 24.01.2013 вариант 1.
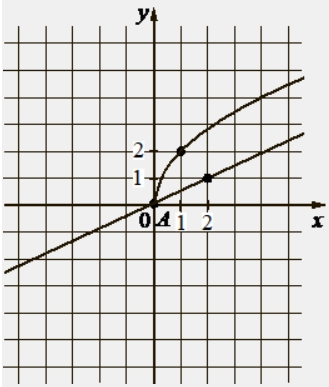
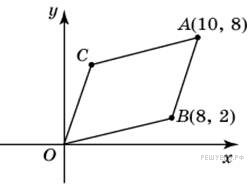
3. 
.
Решение.
Пусть точка P является серединой отрезков OA и BC. Координаты точки P вычисляются следующим образом:
,
,
но с другой стороны,
,
.
Поэтому ,
.
Ответ: 6.
Приведем другое решение.
Поскольку имеем:
Следовательно, ордината точки С равна 6.
Ответ: 6
27680
6
4.
Научная конференция проводится в 4 дня. Всего запланировано 40 докладов — первые два дня по 9 докладов, остальные распределены поровну между третьим и четвертым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение.
За первые два дня будет прочитано 18 докладов, на последние два дня планируется 22 доклада. Поэтому на последний день запланировано 11 докладов. Значит, вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна
Ответ: 0,275.
Ответ: 0,275
286031
0,275
5. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Решение.
Последовательно получаем:
Меньший корень равен −4.
Ответ: −4.
Ответ: -4
99623
-4
6.
Радиус окружности, описанной около правильного треугольника, равен . Найдите сторону этого треугольника.
Решение.
Треугольник ABC правильный, значит, все его углы равны 60°. Тогда имеем:
Ответ: 60.
Ответ: 60
52493
60
7. На рисунке изображён график некоторой функции . Функция
— одна из первообразных функции
. Найдите площадь закрашенной фигуры.
Решение.
Найдем формулу, задающую функцию график которой изображён на рисунке.
Следовательно, график функции получен сдвигом графика функции
на
единиц влево вдоль оси абсцисс. Поэтому искомая площадь фигуры равна площади фигуры, ограниченной графиком функции
и отрезком
оси абсцисс. Имеем:
Ответ: 6.
Ответ: 6
323383
6
8.
Конус вписан в цилиндр. Объем конуса равен 5. Найдите объем цилиндра.
Решение.
Поскольку
а конус и цилиндр имеют общую высоту и основание, имеем:
.
Ответ: 15.
Ответ: 15
245350
15
9. Найдите значение выражения при
.
Решение.
Выполним преобразования:
.
Ответ: 1.
Ответ: 1
67487
1
10. Высота над землeй подброшенного вверх мяча меняется по закону , где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров?
Решение.
Определим моменты времени, когда мяч находился на высоте ровно три метра. Для этого решим уравнение :
Проанализируем полученный результат: поскольку по условию задачи мяч брошен снизу вверх, это означает, что в момент времени (с) мяч находился на высоте 3 метра, двигаясь снизу вверх, а в момент времени
(с) мяч находился на этой высоте, двигаясь сверху вниз. Поэтому он находился на высоте не менее трёх метров 1,6 − 0,2 = 1,4 секунды.
Ответ: 1,4.
Ответ: 1,4
28059
1,4
11. От пристани А к пристани В отправился с постоянной скоростью первый теплоход, а через 8 часов после этого следом за ним со скоростью, на 8 км/ч большей, отправился второй. Расстояние между пристанями равно 209 км. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно. Ответ дайте в км/ч.
Решение.
Пусть км/ч — скорость первого теплохода, тогда скорость второго теплохода по течению равна
км/ч. Первый теплоход находился в пути на 8 часов больше, чем второй, отсюда имеем:
Таким образом, скорость первого теплохода равна 11 км/ч.
Ответ: 11.
Ответ: 11
39507
11
12. Найдите наименьшее значение функции на отрезке [9; 36].
Решение.
Заметим, что и найдем производную этой функции:
Найдем нули производной:
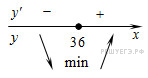
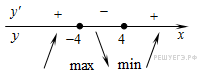
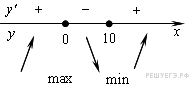
Определим знаки производной функции и изобразим на рисунке поведение функции:
Точка минимума функции принадлежит отрезку [9; 36]. При данном значении аргумента функция принимает минимальное значение:
Ответ: -77.
Ответ: -77
509996
-77
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант Ларина.
13. Решите уравнение:
Решение.
Левая часть уравнения имеет смысл при Поэтому множитель положителен. Рассмотрим два случая.
Первый случай: тогда
Второй случай: тогда
Учитывая условие получаем, что числа не являются решениями данного уравнения.
Ответ:
Источник: МИОО: Диагностическая работа по математике 03.03.2011 вариант 2. (Часть С)
14. В треугольной пирамиде MABC с основанием ABC ребро MA перпендикулярно плоскости основания, стороны основания равны 3, а ребро MB равно 5. На ребре AC находится точка D, на ребре AB точка E, а на ребре AM — точка L. Известно, что AD = 2 и BE = ML = 1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки E, D и L.
Решение.
Сечение — треугольник (см. рис.), найдём его стороны.
Поскольку стороны основания равны, треугольник — равносторонний, следовательно, Поскольку кроме этого треугольник
— равносторонний, поэтому
Треугольник прямоугольный, по теореме Пифагора:
тогда
Треугольник прямоугольный, по теореме Пифагора:
Треугольники и
прямоугольные,
— их общий катет, Следовательно, эти треугольники равны, поэтому равны их гипотенузы:
Следовательно, треугольник — равнобедренный. Проведём в нём высоту
она является медианой, поэтому из треугольника
находим:
Тем самым, реугольник — искомое сечение, найдём его площадь:
Ответ:
Источник: ЕГЭ по математике 19.06.2014. Основная волна, резервный день. Запад. Вариант 1.
15. Решите неравенство:
Решение.
Решим неравенство методом интервалов:
Ответ:
16. Прямая, проведённая через середину N стороны AB квадрата ABCD, пересекает прямые CD и AD в точках M и T соответственно и образует с прямой AB угол, тангенс которого равен 0,5. Найдите площадь треугольника BMT, если сторона квадрата ABCD равна 8.
Решение.
Возможны два случая: точка лежит на продолжении стороны
за точку
или на продолжении стороны
за точку
Пусть
— угол между прямыми
и
Рассмотрим первый случай. Заметим, что Отрезок поэтому Значит, Кроме того, Следовательно,
Во втором случае По-прежнему Следовательно,
Ответ: 12 или 20.
Источник: МИОО: Тренировочная работа по математике 10.02.2011 вариант 2. (Часть С)
17. Транcнациональная компания Amako Inc. решила провести недружественное поглощение компании First Aluminum Company (FAC) путем скупки акций миноритарных акционеров. Известно, что Amako было сделано три предложения владельцам акций FAC, при этом цена покупки одной акции каждый раз повышалась на 1/3. В результате второго предложения Amako сумела увеличить число выкупленных акций на 20% (после второй скупки общее число выкупленных акций увеличилось на 20%), а в результате скупки по третьей цене — еще на 20%. Найдите цену третьего предложения и общее количество скупленных акций FAC, если начальное предложение составляло $27 за одну акцию, а по второй цене Amako скупила 15 тысяч акций.
Решение.
|
Предложения |
Цена одной акции ($) |
Количество выкупленных акций |
|
|
При данном |
Общее количество |
||
|
1 |
27 |
75 000 |
|
|
2 |
36 |
15 000 |
90 000 |
|
3 |
48 |
108 000 |
Ответ: цена третьего предложения составила $48 за одну акцию; всего было выкуплено 108 000 акций.
18. Найдите все значения параметра a, при каждом из которых система имеет ровно два решения.
Решение.
Неравенство (1) задает пару вертикальных углов на координатной плоскости Oxy (см. рисунок). Графиком уравнения (2) является окружность радиуса , центр которой ― точка ― лежит на прямой . Поскольку оба графика симметричны относительно прямой
, система будет иметь ровно два решения тогда и только тогда, когда расстояние PK от центра окружности до прямой
будет равняться радиусу данной окружности. Из треугольника POK находим: , где
― угловой коэффициент прямой . Таким образом, ,
, , откуда
.
Окончательно получаем: , , или
.
Ответ: или
.
19. Семь экспертов оценивают кинофильм. Каждый из них выставляет оценку — целое число баллов от 0 до 12 включительно. Известно, что все эксперты выставили различные оценки. По старой системе оценивания рейтинг кинофильма — это среднее арифметическое всех оценок экспертов. По новой системе оценивания рейтинг кинофильма оценивают следующим образом: отбрасываются наименьшая и наибольшая оценки и подсчитывается среднее арифметическое оставшихся оценок.
а) Может ли разность рейтингов, вычисленных по старой и новой системам оценивания, равняться
б) Может ли разность рейтингов, вычисленных по старой и новой системам оценивания, равняться
в) Найдите наибольшее возможное значение разности рейтингов, вычисленных по старой и новой системам оценивания.
Просмотр содержимого документа
«Вариант11»
Вариант № 11
1. В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 1200 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 4 недели?
Решение.
За 4 недели в офисе расходуется 1200 · 4 = 4800 листов бумаги. Разделим 4800 на 500:
Значит, нужно купить не меньше 10 пачек бумаги.
Ответ: 10.
Ответ: 10
26622
10
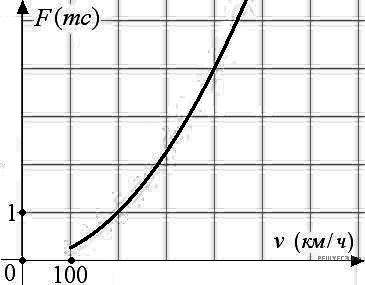
2. 
Решение.
Из графика видно, что при скорости 200 км/час действующая на крылья подъемная сила равна 1 тонне силы.
Ответ: 1.
Ответ: 1
263867
1
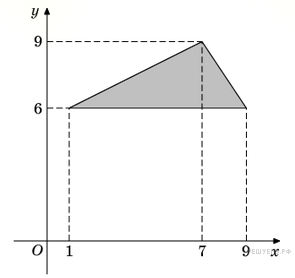
3. 
Решение.
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию. Поэтому
см2.
Ответ: 12.
———-
Дублирует задание 27564.
Ответ: 12
21863
12
4. Родительский комитет закупил 30 пазлов для подарков детям на окончание учебного года, из них 15 с персонажами мультфильмов и 15 с видами природы. Подарки распределяются случайным образом. Найдите вероятность того, что Маше достанется пазл с персонажем мультфильмов.
Решение.
вероятность того, что Маше достанется пазл с персонажем мультфильмов равна
.
Ответ: 0,5.
Ответ: 0,5
1027
0,5
5. Найдите решение уравнения:
Решение.
Перейдем к одному основанию степени:
Ответ: 4.
Ответ: 4
13689
4
6.
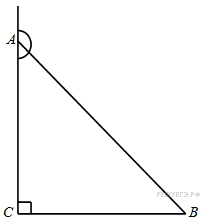
В треугольнике угол
равен 90°,
,
. Найдите синус внешнего угла при вершине
.
Решение.
так как
Ответ: 0,6.
Ответ: 0,6
27380
0,6
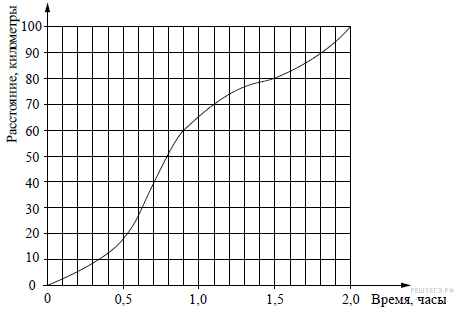
7. На рисунке показан график движения автомобиля по маршруту. На оси абсцисс откладывается время (в часах), на оси ординат — пройденный путь (в километрах). Найдите среднюю скорость движения автомобиля на данном маршруте. Ответ дайте в км/ч.
Решение.
Чтобы найти среднюю скорость, необходимо пройденное расстояние разделить на время прохождения: км/ч
Ответ: 50.
Ответ: 50
512495
50
8. Радиусы трех шаров равны 1, 6 и 8. Найдите радиус шара, объем которого равен сумме их объемов.
Решение.
Объём шара вычисляется по формуле . Поэтому cумма объёмов трёх шаров равна
Следовательно, искомый радиус равен 9.
Ответ: 9.
Ответ: 9
75307
9
9. Найдите , если
при
Решение.
Выполним преобразования:
Ответ: 0.
Ответ: 0
65919
0
10. Если достаточно быстро вращать ведeрко с водой на верeвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведeрка сила давления воды на дно не остаeтся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила еe давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна , где
– масса воды в килограммах,
скорость движения ведeрка в м/с,
– длина верeвки в метрах, g – ускорение свободного падения (считайте
м/с
). С какой наименьшей скоростью надо вращать ведeрко, чтобы вода не выливалась, если длина верeвки равна 40 см? Ответ выразите в м/с.
Решение.
Задача сводится к решению неравенства при заданной длине верёвки
м:
Ответ: 2.
Ответ: 2
27958
2
11. Расстояние между городами и
равно 150 км. Из города
в город
выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе
и повернул обратно. Когда он вернулся в
, автомобиль прибыл в
. Найдите расстояние от
до
. Ответ дайте в километрах.
Решение.
Обозначим км – расстояние от A до C,
км/ч – скорость автомобиля,
ч – время движения мотоциклиста от A до C. Тогда
и
Решим систему полученных уравнений:
Тогда км.
Ответ: 90.
Ответ: 90
99594
90
12. Найдите наименьшее значение функции на отрезке
.
Решение.
Найдем производную заданной функции: Уравнение
не имеет решений, производная положительна при всех значениях переменной, поэтому заданная функция является возрастающей.
Следовательно, наименьшим значением функции на заданном отрезке является
Ответ: −41.
Ответ: -41
70487
-41
13. Решите уравнение
Решение.
Решим уравнение
Из найденный решений условию удовлетворяет только и
Ответ:
14. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра: AB = 6, AD = 8, CC1 = 16. Найдите угол между плоскостями ABC и A1DB.
Решение.
Плоскости и имеют общую прямую
Проведем перпендикуляр
к
По теореме о трех перпендикулярах Значит, линейный угол двугранного угла, образованного плоскостями
и — это угол
Из прямоугольного треугольника
находим:
Из прямоугольного треугольника находим:
Значит, искомый угол равен
Ответ:
15. Решите неравенство:
Решение.
Последовательно получаем:
Ответ:
16. Около равнобедренного треугольника ABC с основанием BC описана окружность. Через точку C провели прямую, параллельную стороне AB. Касательная к окружности, проведённая в точке B, пересекает эту прямую в точке K.
а) Докажите, что треугольник BCK — равнобедренный.
б) Найдите отношение площади треугольника ABC к площади треугольника BCK, если
Решение.
а) Угол KBC равен углу BAC как угол между касательной и хордой. Прямые AB и CK параллельны. Следовательно, ∠ABC = ∠BCK. Получаем, что треугольники ABC и BCK подобны. Следовательно,
Значит, треугольник BCK — равнобедренный.
б) Треугольники ABC и BCK подобны, коэффициент подобия равен Отношение площадей В треугольнике ABC имеем:
Ответ: 2.
Источник: ЕГЭ по математике 05.06.2014. Основная волна. Вариант 901.
17. 31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?
Решение.
Пусть сумма кредита равна a, ежегодный платеж равен x рублей, а годовые составляют k %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент m = 1 + 0,01k. После первой выплаты сумма долга составит: a1 = am − x. После второй выплаты сумма долга составит:
После третьей выплаты сумма оставшегося долга:
По условию тремя выплатами Сергей должен погасить кредит полностью, поэтому откуда При a = 9 930 000 и k = 10, получаем: m = 1,1 и
Ответ: 3 993 000 рублей.
Приведём другое решение.
Пусть — один из трёх разовых платежей. Тогда сумма долга после оплаты в первом году составит: После внесения второго платежа сумма долга станет равной Сумма долга после третьего платежа: Третьим платежом Сергей должен погасить долг, то есть долг станет равным нулю:
Источник: Демонстрационная версия ЕГЭ—2016 по математике. Профильный уровень.
18. Найти все значения a, при каждом из которых система
имеет решения.
Решение.
Рассмотрим второе неравенство системы: Если то неравенство, а значит и система не имеет решений. Если
то решение неравенства — луч Если
то решение неравенства — луч
При первое неравенство системы принимает вид:
Если то решение этой системы — два луча с концами в точках Если
то решение этой системы — полуинтервал с концами в точках
Очевидно, что при , решение системы будет содержать луч, вида , где
меньшее из чисел и , а значит система будет иметь решение.
Чтобы решения были при необходимо и достаточно:
Таким образом, исходная система неравенств имеет решения при
Ответ:
19. Последние члены двух конечных арифметических прогрессий a1 = 5, a2 = 8, …, aN и b1 = 9, b2 = 14, …, bM совпадают, а сумма всех совпадающих (взятых по одному разу) членов этих прогрессий равна 815. Найдите число членов в каждой прогрессии.
Просмотр содержимого документа
«Вариант12»
Вариант № 12
1. В квартире установлен прибор учёта расхода холодной воды (счётчик). Показания счётчика 1 февраля составляли 142 куб. м воды, а 1 марта — 156 куб. м. Сколько нужно заплатить за холодную воду за февраль, если стоимость 1 куб. м холодной воды составляет 22 руб. 50 коп.? Ответ дайте в рублях.
Решение.
Вычислим, сколько кубометров воды было израсходовано за февраль: куб.м. Таким образом, необходимо заплатить:
руб.
Ответ: 315
Ответ: 315
512323
315
Источник: СтатГрад: Тренировочная работа по математике 24.09.2015 вариант МА10107.
2. На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по приведенной диаграмме, сколько месяцев среднемесячная температура не превышала 14 градусов Цельсия.
Решение.
Из диаграммы видно, что 8 месяцев среднесуточная температура не превышала 14 градусов Цельсия.
Ответ: 8.
Ответ: 8
509984
8
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант Ларина.
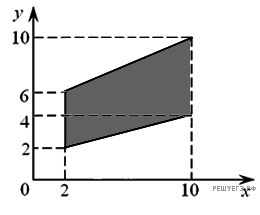
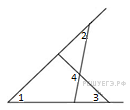
3. 
Решение.
сумма углов в выпуклом четырехугольнике равна 360°.
Ответ: 120.
Ответ: 120
27780
120
4. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0,82. Вероятность того, что окажется меньше 10 пассажиров, равна 0,51. Найдите вероятность того, что число пассажиров будет от 10 до 17.
Решение.
Рассмотрим события A = «в автобусе меньше 10 пассажиров» и В = «в автобусе от 10 до 17 пассажиров». Их сумма — событие A + B = «в автобусе меньше 18 пассажиров». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:
P(A + B) = P(A) + P(B).
Тогда, используя данные задачи, получаем: 0,82 = 0,51 + P(В), откуда P(В) = 0,82 − 0,51 = 0,31.
Ответ: 0,31.
Ответ: 0,31
509916
0,31
Источник: СтатГрад: Тренировочная работа по математике 22.04.2015 вариант МА10410.
5. Найдите корень уравнения .
Решение.
Последовательно получаем:
Ответ: −4.
Ответ: -4
26659
-4
6. 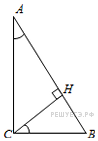
угол
равен 90°,
– высота,
,
. Найдите
.
Решение.
Углы A и HCB равны как углы со взаимно перпендикулярными сторонами, поэтому
Ответ: 27.
Ответ: 27
27431
27
7. Материальная точка движется прямолинейно по закону где х — расстояние от точки отсчёта (в метрах), t — время движения (в секундах). Найдите её скорость (в метрах в секунду) в момент времени t = 6 с.
Решение.
Найдем закон изменения скорости: м/с. При
имеем:
м/с.
Ответ: 72.
Ответ: 72
512493
72
8. 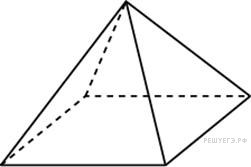
Решение.
Площади подобных тел относятся как квадрат коэффициента подобия. Поэтому, если все ребра увеличены в 2 раза, площадь поверхности увеличится в 4 раза.
Ответ: 4.
Ответ: 4
27172
4
9. Найдите значение выражения 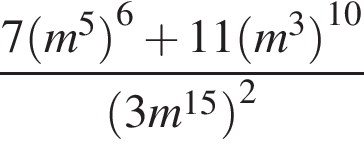
Решение.
Используем свойства степеней:
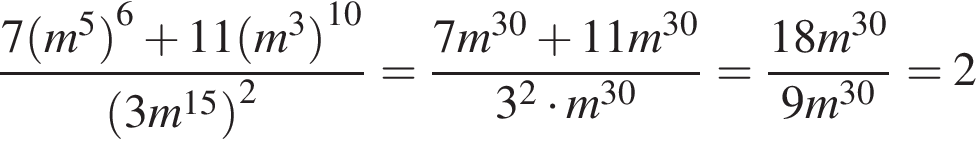
Ответ: 2.
Ответ: 2
26798
2
10. Eмкость высоковольтного конденсатора в телевизоре Ф. Параллельно с конденсатором подключeн резистор с сопротивлением
Ом. Во время работы телевизора напряжение на конденсаторе
кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением
(с), где
— постоянная. Определите (в киловольтах), наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 28 с?
Решение.
Задача сводится к решению неравенства при заданных значениях начального напряжения на конденсаторе
кВ, сопротивления резистора
Ом и ёмкости конденсатора
Ф:
кВ.
Ответ: 6.
Ответ: 6
28463
6
11. Из одной точки кольцевой дороги, длина которой равна 22 км, одновременно в одном направлении выехали два автомобиля. Скорость первого автомобиля равна 113 км/ч, и через 30 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение.
Пусть скорость второго автомобиля равна км/ч. За 1/2 часа первый автомобиль прошел на 22 км больше, чем второй, отсюда имеем
Ответ: 69.
Ответ: 69
509156
69
Источник: СтатГрад: Диагностическая работа по математике 13.02.2015 вариант МА00410.
12. Найдите точку максимума функции .
Решение.
Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка максимума .
Ответ: −4.
Ответ: -4
26728
-4
13. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение.
Сделаем замену
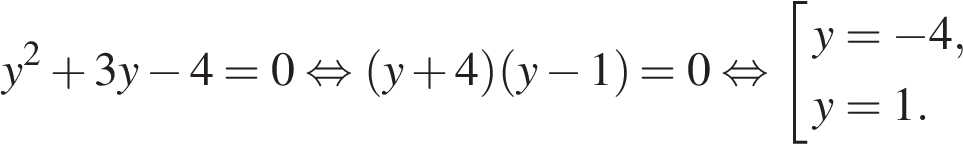
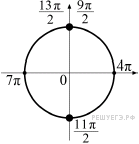
Ответ: а) б)
Источник: МИОО: Тренировочная работа по математике 19.05.2014 вариант МА10701.
14. В треугольной пирамиде MABC с основанием ABC ребро MA перпендикулярно плоскости основания, стороны основания равны 3, а ребро MB равно 5. На ребре AC находится точка D, на ребре AB точка E, а на ребре AM — точка L. Известно, что AD = 2 и BE = ML = 1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки E, D и L.
Решение.
Сечение — треугольник (см. рис.), найдём его стороны.
Поскольку стороны основания равны, треугольник — равносторонний, следовательно, Поскольку кроме этого треугольник
— равносторонний, поэтому
Треугольник прямоугольный, по теореме Пифагора:
тогда
Треугольник прямоугольный, по теореме Пифагора:
Треугольники и
прямоугольные,
— их общий катет, Следовательно, эти треугольники равны, поэтому равны их гипотенузы:
Следовательно, треугольник — равнобедренный. Проведём в нём высоту
она является медианой, поэтому из треугольника
находим:
Тем самым, реугольник — искомое сечение, найдём его площадь:
Ответ:
Источник: ЕГЭ по математике 19.06.2014. Основная волна, резервный день. Запад. Вариант 1.
15. Решите неравенство
Решение.
Заметим, что поскольку равносильны следующие неравенства
С учётом этого имеем
Ответ:
Источник: СтатГрад: Тренировочная работа по математике 03.03.2016 вариант МА10410
16.В остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и
Решение.
а) Углы NAK и NBK, опирающиеся на отрезок KN, равны, значит, точки A, B, N и K лежат на одной окружности, а, следовательно, равны и вписанные углы ABK и ANK этой окружности, опирающиеся на дугу AK, что и требовалось доказать.
б) Прямоугольные треугольники KMB и NMA имеют общий угол KMN, следовательно, они подобны, откуда или но тогда и треугольники KMN и BMA также подобны, причем коэффициент подобия равен откуда Тогда радиус R окружности, описанной около треугольника ABM равен
Ответ:
Источник: Пробный экзамен по математике Санкт-Петербург 2015. Вариант 2.
17. По вкладу «А» банк в конце каждого года планирует увеличивать на 20% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 10% в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Решение.
Пусть на каждый тип вклада была внесена одинаковая сумма S. На вкладе «А» каждый год сумма увеличивается на 20%, то есть умножается на коэффициент 1,2. Поэтому через три года сумма на вкладе «А» будет равна
Аналогично сумма на вкладе «Б» будет равна
где n — некоторое натуральное число.
По условию требуется найти наименьшее натуральное решение неравенства
При n = 26 неравенство
верно, а при n = 25 неравенство
неверно, как и при всех меньших n.
Ответ: 26.
Источник: СтатГрад: Тренировочная работа по математике 20.01.2016 вариант МА10310
18. Найдите все такие значения параметра a, при каждом из которых уравнение не имеет решений.
Решение.
Решение 1. Перепишем данное уравнение в виде и положим где Тогда исходное уравнение принимает вид
Найдем множество значений функции на отрезке [0; 2].
Так как то на промежутке [0; 1) и промежутке (1; 2]. Значит, функция убывает на отрезке [0; 1] и возрастает на отрезке [1; 2]. Поскольку то множество значений функции на отрезке [0; 2] ― отрезок [f (1); f (2)], т. е. отрезок Таким образом, уравнение не имеет решений на отрезке [0; 2] тогда и только тогда, когда выполняются условия или
Решение 2. Положим где и рассмотрим функцию Так как ее производная то на промежутке [0; 1) и промежутке (1; 2]. Значит, на промежутке [0; 2) функция имеет единственный экстремум ― минимум Так как уравнение не имеет решений на отрезке [0; 2] тогда и только тогда, когда выполняются условия или Таким образом, приходим к совокупности
Решение 3. Построить эскиз графика функции на отрезке [0; 2] (см. решение 1) и исследовать взаимное расположения графика этой функции и прямой
Ответ:
Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 2.
19. Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и все их возможные суммы (по 2, по 3 и т.д.) выписывают на доске в порядке неубывания. Если какое-то число n, выписанное на доске, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.
а) Приведите пример задуманных чисел, для которых на доске будет записан набор 3, 6, 9, 12, 15.
б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 5, 6, 8, 9, 11, 12, 13, 14, 17, 18, 19, 21, 23?
в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 8, 9, 10, 17, 18, 19, 20, 27, 28, 29, 30, 37, 38, 39, 47.
Просмотр содержимого документа
«Вариант13»
Вариант № 13
1. В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 800 листов. Какого наименьшего количества пачек бумаги хватит на 9 недель?
Решение.
За 9 недель в офисе расходуется 800 · 9 = 7200 листов бумаги. Разделим 7200 на 500:
Значит, нужно купить не меньше 15 пачек бумаги.
Ответ: 15.
Ответ: 15
508957
15
Источник: СтатГрад: Диагностическая работа по математике 05.03.2015 вариант МА10309.
2. Задание 2 № 27510.
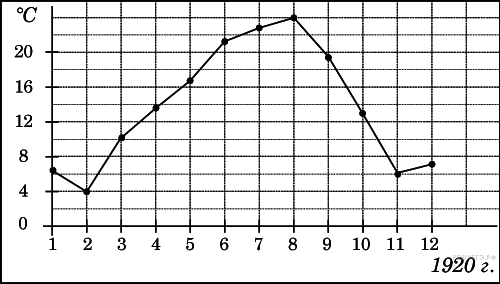
На рисунке жирными точками показана среднемесячная температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку наименьшую среднемесячную температуру в период с мая по декабрь 1920 года. Ответ дайте в градусах Цельсия.
Решение.
Из графика видно, что наименьшая среднемесячная температура в период с пятого по двенадцатый месяц (с мая по декабрь) была в ноябре и составляла 6 °C (см. рисунок).
Ответ: 6.
Ответ: 6
27510
6
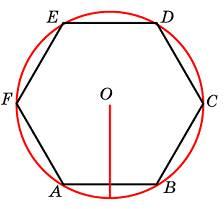
3. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 28?
Решение.
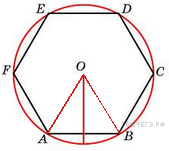
Значит, треугольник AOB — равносторонний. Тогда
Ответ: 28.
Ответ: 28
53073
28
4. В блюде 35 пирожков: 9 с мясом, 12 с яйцом и 14 с рыбой. Катя наугад выбирает один пирожок. Найдите вероятность того, что он окажется с рыбой.
Решение.
Вероятность того, что пирожок окажется с рыбой равна
.
Ответ: 0,4.
Ответ: 0,4
1025
0,4
5. Найдите корень уравнения:
Решение.
Избавимся от знаменателя:
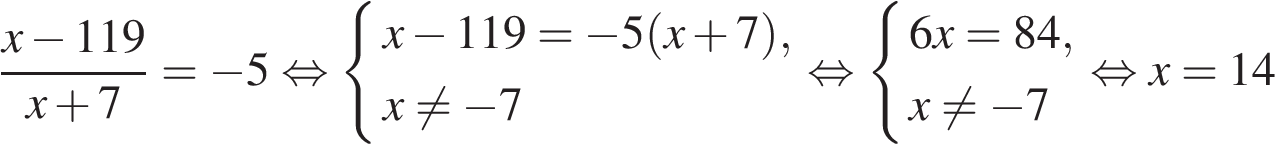
Ответ: 14.
Ответ: 14
26664
14
6. 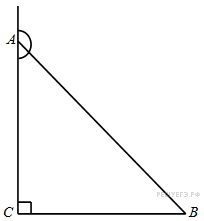
угол
равен 90°, тангенс внешнего угла при вершине
равен -0,1. Найдите
.
Решение.
так как
Ответ: 0,1.
Ответ: 0,1
27400
0,1
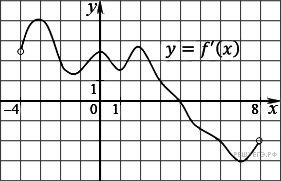
7. 
Решение.
Если производная в некоторой точке равна нулю, а в ее окрестности меняет знак, то это точка экстремума. На отрезке [–2; 6] график производной пересекает ось абсцисс, производная меняет знак с плюса на минус. Следовательно, точка 4 является точкой экстремума.
Ответ: 4.
Ответ: 4
27502
4
8. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, MS = 1. Найдите объем пирамиды.
Решение.
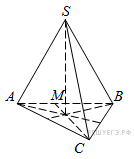
.
Ответ: 1.
Ответ: 1
284355
1
9. Найдите значение выражения .
Решение.
Выполним преобразования:
.
Ответ: 7.
Ответ: 7
77398
7
10. Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур определяется выражением , где t — время в минутах,
К,
К/мин
,
К/мин. Известно, что при температуре нагревателя свыше 1600 К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время после начала работы нужно отключать прибор. Ответ выразите в минутах.
Решение.
Найдем, в какой момент времени после начала работы температура станет равной К. Задача сводится к решению уравнения
при заданных значениях параметров a и b:
Через 4 минуты после включения прибор нагреется до 1600 К, и при дальнейшем нагревании может испортиться. Таким образом, прибор нужно выключить через 4 минуты.
Ответ: 4.
Ответ: 4
41493
4
11. Виноград содержит 90% влаги, а изюм — 5%. Сколько килограммов винограда требуется для получения 36 килограммов изюма?
Решение.
Виноград содержит 10% питательного вещества, а изюм — 95%. 36 кг изюма содержат кг питательного вещества. Таким образом, для получения 36 килограммов изюма требуется
кг винограда.
Ответ: 342.
Ответ: 342
109109
342
12.
Найдите наибольшее значение функции на отрезке
.
Решение.
Найдем производную заданной функции:
Найдем нули производной на заданном отрезке:
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:
Наибольшим значением функции на заданном отрезке будет наибольшее из чисел и
. Найдем их:
,
Заметим, что , поэтому наибольшее значение функции на отрезке равно −33.
Ответ: −33.
Ответ: -33
70787
-33
13. Решите уравнение:
Решение.
Левая часть уравнения имеет смысл при Преобразуем уравнение:
Поскольку получаем:
Учитывая, что получаем,
Ответ:
14. В правильной шестиугольной призме все рёбра равны 1. Найдите расстояние от точки В до плоскости .
Решение.
Прямые и FB перпендикулярны прямой EF. Плоскость , содержащая прямую EF, перпендикулярна плоскости
, значит искомое расстояние равно высоте BH прямоугольного треугольника
, в котором
, , . Поэтому
.
Ответ: .
15. Решите неравенство:
Решение.
Сделаем замену
Учитывая, что получаем или откуда находим множество решений первого неравенства системы:
Ответ:
16. Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Решение.
Задание а). Обозначим центры окружностей O1 и O2 соответственно. Пусть общая касательная, проведённая к окружностям в точке K, пересекает AB в точке M. По свойству касательных, проведённых из одной точки, AM = KM и KM = BM. Треугольник AKB, у которого медиана равна половине стороны, к которой она проведена, — прямоугольный.
Вписанный угол AKD прямой, поэтому он опирается на диаметр AD. Значит, AD ⊥ AB. Аналогично получаем, что BC ⊥ AB. Следовательно, прямые AD и BC параллельны.
Задание б). Пусть, для определенности, первая окружность имеет радиус 4, а радиус второй равен 1.
Треугольники BKC и AKD подобны, Пусть , тогда
У треугольников AKD и AKB общая высота, следовательно, то есть SAKB = 4S. Аналогично, SCKD = 4S. Площадь трапеции ABCD равна 25S.
Вычислим площадь трапеции ABCD. Проведём к AD перпендикуляр O2H, равный высоте трапеции, и найдём его из прямоугольного треугольника O2HO1:
Тогда
Следовательно, 25S = 20, откуда S = 0,8 и SAKB = 4S = 3,2.
Ответ: 3,2.
Источник: Проект демонстрационной версии ЕГЭ—2014 по математике.
17. Производство x тыс. единиц продукции обходится в q = 0,5x2 + x + 7 млн рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет px − q. При каком наименьшем значении p через три года суммарная прибыль составит не менее 75 млн рублей?
Решение.
Прибыль (в млн рублей) за один год выражается величиной
Это выражение является квадратным трёхчленом и достигает своего наибольшего значения при x = p − 1. Прибыль составит не менее 75 млн рублей, если
то есть при p ≥ 9, поскольку цена продукции не может быть отрицательной. Таким образом, наименьшее значение p = 9, искомая наименьшая цена 9 тыс. руб.
Ответ: p = 9.
Источник: СтатГрад: Тренировочная работа по математике 24.09.2015 вариант МА10107.
18. Найдите все значения а, при каждом из которых система
имеет единственное решение.
Решение.
Преобразуем первое уравнение системы:
Эти условия задают «верхнюю» полуокружность с центром в точке (3; 3) радиуса 4. Преобразуем второе уравнение системы:
Эти условия задают «верхнюю» полуокружность с центром в точке (а; а) радиуса 4. Полуокружности, определяемые уравнениями системы, изображены на рисунке 1, обозначив полуокружности через F и Fa, а их центры — О и Оа.
Данная в условии система имеет единственное решение, если полуокружности F и Fa имеют единственную общую точку. Две «верхние» полуокружности одинакового радиуса либо не имеют общих точек, либо имеют ровно одну общую точку, либо совпадают.
При a = 3 полуокружности F и Fa совпадают, т. е. a = 3 не является искомым.
При a 3, точка О расположена выше точки Оа. В этом случае полуокружности F и Fa имеют общую точку, если диаметр BC полуокружности Fa имеет общую точку с полуокружностью F. Крайнее положение диаметра BC, при котором он ещё имеет общую точку полуокружностью F является положение на нижнем рисунке, при этом точка Оа имеет координаты (7; 7)., т. е. a = 7. При a 7 полуокружности F и Fa не имеют общих точек. Таким образом, все значения являются искомыми.
При a Fa может быть получена параллельным переносом полуокружности F на вектор где b = a − 3. Если при параллельном переносе полуокружности F на вектор полученная полуокружность имеет общую точку с F, то это же справедливо и при параллельном переносе полуокружности F на вектор Поэтому искомое множество значений параметра а симметрично относительно точки a = 3, поэтому
Ответ:
Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 1.
19. Целое число S является суммой не менее трех последовательных членов непостоянной арифметической прогрессии, состоящей из целых чисел.
а) Может ли S равняться 8?
б) Может ли S равняться 1?
в) Найдите все значения, которые может принимать S.
Просмотр содержимого документа
«Вариант14»
Вариант № 14
1. В доме, в котором живёт Женя, один подъезд. На каждом этаже по восемь квартир. Женя живёт в квартире 87. На каком этаже живёт Женя?
Решение.
Разделим 87 на 8:
.
Значит, Женя живет на 11 этаже.
Ответ: 11.
Приведём другое решение.
Составим таблицу этажей.
Источник: МИОО: Тренировочная работа по математике 28.01.2014 вариант МА10401.
2. На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в период с января по май 1999 года. Ответ дайте в градусах Цельсия.
Решение.
Из диаграммы видно, что наибольшая среднемесячная температура в период с января по май (т. е. с 1 по 5 месяц) составляла 8 °C (см. рисунок).
Ответ: 8.
Ответ: 8
77251
8
3. 
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Решение.

.
Ответ: 2
244986
2
4.
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Сапфир» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Сапфир» выиграет жребий ровно два раза.
Решение.
Обозначим «1» ту сторону монеты, которая отвечает за выигрыш жребия «Сапфир», другую сторону монеты обозначим «0». Тогда благоприятных комбинаций три: 110, 101, 011, а всего комбинаций 23 = 8: 000, 001, 010, 011, 100, 101, 110, 111. Тем самым, искомая вероятность равна:
Ответ: 0,375.
Ответ: 0,375
321035
0,375
5.
Найдите корень уравнения .
Решение.
Последовательно получаем:
Ответ: −13.
Ответ: -13
3231
-13
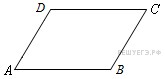
6. 
Решение.
Сумма углов, прилежащих к одной стороне параллелограмма равна 180°, тогда .
Ответ: 120.
Ответ: 120
27805
120
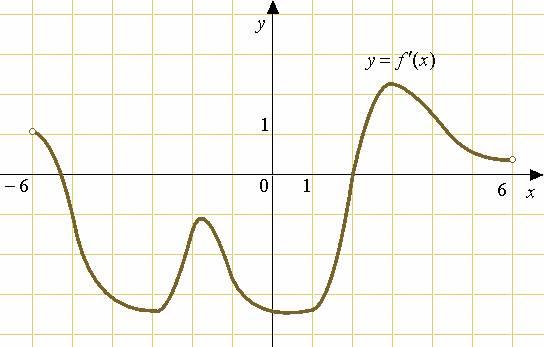
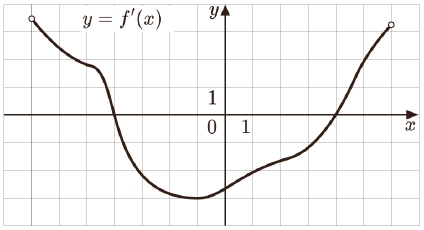
7. На рисунке изображен график производной функции f(x), определенной на интервале (−15; 2). Найдите количество точек максимума функции f(x) на отрезке [−11;0].
Решение.
Точки максимума соответствуют точкам смены знака производной с плюса на минус. На отрезке [−11; 0] функция имеет две точки максимума x = −10 и x = −1.
Ответ: 2.
Ответ: 2
8037
2
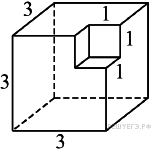
8. 
Решение.
Площадь поверхности заданного многогранника равна площади поверхности куба с ребром 3:
.
Ответ: 54.
Ответ: 54
505146
54
Источник: МИОО: Тренировочная работа по математике 22.04.2014 вариант МА10601.
9. Найдите значение выражения
Решение.
Упростим выражение:
Ответ: 5
Ответ: 5
512352
5
Источник: СтатГрад: Тренировочная работа по математике 18.12.2015 вариант МА10211.
10. При нормальном падении света с длиной волны нм на дифракционную решeтку с периодом d нм наблюдают серию дифракционных максимумов. При этом острый угол
(отсчитываемый от перпендикуляра к решeтке), под которым наблюдается максимум, и номер максимума k связаны соотношением
. Под каким минимальным углом
(в градусах) можно наблюдать третий максимум на решeтке с периодом, не превосходящим 2400 нм?
Решение.
Задача сводится к решению неравенства нм на интервале
при заданных значениях длины волны света
нм и номера максимума
:
.
Ответ: 30.
Ответ: 30
28639
30
11. Теплоход проходит по течению реки до пункта назначения 200 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 15 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 40 часов после отплытия из него. Ответ дайте в км/ч.
Решение.
Пусть км/ч — скорость течения, тогда скорость теплохода по течению равна
км/ч, а скорость теплохода против течения равна
км/ч. На весь путь теплоход затратил 40 – 10 = 30 часов, отсюда имеем:
Таким образом, скорость течения реки равна 5 км/ч.
Ответ: 5.
Ответ: 5
26588
5
12. Найдите точку минимума функции .
Решение.
Найдем производную заданной функции:
.
Найдем нули производной на заданном отрезке:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка минимума .
Ответ: 36.
Ответ: 36
128103
36
13. Решите уравнение
Решение.
Решим уравнение
Из найденный решений условию удовлетворяет только
и
Ответ:
14. В кубе ABCDA1B1C1D1 найдите косинус угла между плоскостями BA1C1 и BA1D1.
Решение.
Пусть точка — центр куба, а
— середина
а
— средняя линия треугольника
, поэтому Треугольник — равносторонний, следовательно, искомый угол равен углу
Примем длины ребер куба за . Найдем стороны треугольника Из треугольника
находим из равностороннего треугольника находим
поскольку — середина диагонали
то Теперь применим к треугольнику теорему косинусов:
Ответ:
15. Решите неравенство:
Решение.
Заметим, что
Поэтому
Ответ:
16. Стороны AB и BC треугольника ABC равны соответственно 13 и 7.25, а его высота BD равна 5. Найдите расстояние между центрами окружностей, вписанных в треугольники ABD и BCD.
Решение.
Пусть точки и
― центры окружностей, вписанных в треугольники
и
соответственно,
и
― радиусы этих окружностей, а точки
и
― точки, в которых окружности касаются отрезка
Из прямоугольных треугольников
и
находим:
Опустим из точки перпендикуляр
на прямую
(см. рис. 1, 2). Искомое расстояние
находим из прямоугольного треугольника
Первый случай (точка лежит между точками
и
см. рис. 1):
Второй случай (точка C лежит между точками и
см. рис. 2):
Ответ: или
17. 31 декабря 2014 года Ярослав взял в банке некоторую сумму в кредит под 12,5% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга ( то есть увеличивает долг на 12,5%), затем Ярослав переводит в банк 2 132 325 рублей. Какую сумму взял Ярослав в банке, если он выплатил долг четырьмя равными платежами (то есть за четыре года)?
Решение.
Заметим сначала, что увеличить число на это тоже самое, что умножить это число на Пусть Ярослав взял в банке
рублей, а его ежегодный платеж равен
(в данном случае ). Тогда из условия следует уравнение: Раскрывая скобки, получаем следующее:
Отсюда
Ответ: 6409000 рублей.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2015 г.
18. Найдите все значения , при каждом из которых неравенство
выполняется при всех
Решение.
Поскольку для всех значений получаем:
Решим полученное неравенство:
Для того, чтобы любое значение удовлетворяло этой системе неравенств, нужно, чтобы каждое из неравенств системы было верным для любого значения
, то есть дискриминанты левых частей этих неравенств должны быть отрицательными:
Ответ:
19. Будем называть четырёхзначное число интересным, если среди четырёх цифр в его десятичной записи нет нулей, а одна из этих цифр равна сумме трёх других из них. Например, интересным является число 6321.
а) Приведите пример двух интересных четырёхзначных чисел, разность между которыми равна пяти.
б) Найдутся ли два интересных четырёхзначных числа, разность между которыми равна 91?
в) Найдите наименьшее нечётное число, для которого не существует кратного ему интересного четырёхзначного числа.
Просмотр содержимого документа
«Вариант15»
Вариант № 15
1.
Оптовая цена учебника 150 рублей. Розничная цена на 15% выше оптовой. Какое наибольшее число таких учебников можно купить по розничной цене на 4550 рублей?
Решение.
С учетом наценки учебник будет стоить 150 + 0,15 150 = 172,5 рубля. Разделим 4550 на 172,5:
.
Значит, можно будет купить 26 учебников.
Ответ: 26.
Ответ: 26
77101
26
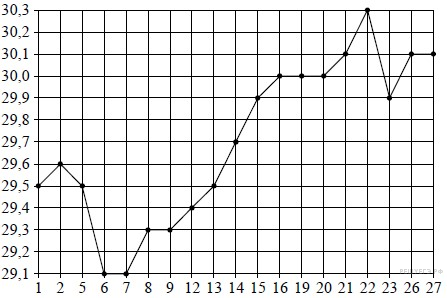
2. На рисунке жирными точками показан курс доллара, установленный Центробанком РФ, во все рабочие дни в октябре 2010 года. По горизонтали указываются числа месяца, по вертикали — цена доллара в рублях. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наибольший курс доллара за указанный период. Ответ дайте в рублях.
Решение.
Из графика видно, что наибольший курс доллара был 22 октября 2010 года и составлял 30,3 рубля
Ответ: 30,3.
Ответ: 30,3
512366
30,3
Источник: СтатГрад: Тренировочная работа по математике 24.09.2015 вариант МА10108.
3. 
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Решение.

Ответ: 1
244984
1
4. За круглый стол на 201 стул в случайном порядке рассаживаются 199 мальчиков и 2 девочки. Найдите вероятность того, что между двумя девочками будет сидеть один мальчик.
Решение.
Пусть первой за стол сядет девочка, тогда есть два места через одно от нее , на каждое из которых претендует 200 человек, из которых только одна девочка. Таким образом, вероятность, что между двумя девочками будет сидеть один мальчик равна
Ответ: 0,01
Другое решение:
Число способов рассадить 201 человек на 201 стул равняется .
Благоприятным для нас исходом будет вариант рассадки, когда на «первом» стуле сидит девочка, и через одно место справа сидит девочка, а на остальных ста девяноста девяти стульях произвольно рассажены мальчики. Количество таких исходов равно Так как «первым» стулом может быть любой из двухсот одного стула (стулья стоят по кругу), то количество благоприятных исходов нужно умножить на 201. Таким образом, вероятность того, что между двумя девочками будет сидеть один мальчик равна
Ответ: 0,01
325909
0,01
5. Найдите корень уравнения
Решение.
Перейдем к одному основанию степени:
Ответ: 5,5.
———-
Дублирует задание 26653.
Ответ: 5,5
509033
5,5
Источник: Пробный экзамен по математике Санкт-Петербург 2015. Вариант 1.
6. 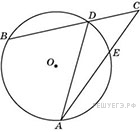
. Градусная величина дуги AB окружности, не содержащей точек D и E, равна
. Найдите угол DAE. Ответ дайте в градусах.
Решение.
Пусть искомый угол равен x. Тогда дуга DE, равна 2x. Угол между секущими CB и CA полуразности дуг AB и DE:
Ответ: 59.
Ответ: 59
52339
59
7. 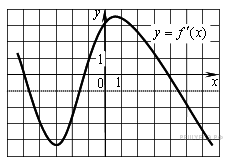
При каком значении x эта функция принимает свое наибольшее значение на отрезке
Решение.
На заданном отрезке производная функции отрицательна, поэтому функция на этом отрезке убывает. Поэтому наибольшее значение функции достигается на левой границе отрезка, т. е. в точке −4.
Ответ: −4.
Ответ: -4
508246
-4
Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 2.
8. 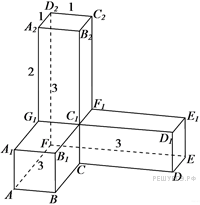
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
Решение.
— диагональ квадрата со стороной 3, значит, треугольник
— прямоугольный и равнобедренный, угол
при основании равен
.
Ответ: 45.
Ответ: 45
281867
45
9.
Найдите значение выражения 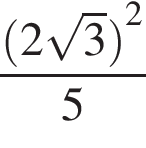
Решение.
Выполним преобразования:
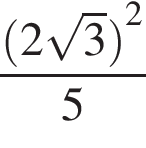
.
Ответ: 2,4.
Ответ: 2,4
61455
2,4
10. Автомобиль, масса которого равна кг, начинает двигаться с ускорением, которое в течение t секунд остаeтся неизменным, и проходит за это время путь
метров. Значение силы (в ньютонах), приложенной в это время к автомобилю, равно
. Определите наибольшее время после начала движения автомобиля, за которое он пройдeт указанный путь, если известно, что сила F, приложенная к автомобилю, не меньше 1200 Н. Ответ выразите в секундах.
Решение.
Найдем, за какое время автомобиль пройдет путь метров, учитывая, что сила
при заданном значении массы автомобиля 1200 H. Задача сводится к решению неравенства
при заданном значении массы автомобиля
кг:
с.
Ответ: 50.
Ответ: 50
42735
50
11.
В сосуд, содержащий 7 литров 14-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Решение.
Концентрация раствора равна
.
Объем вещества в исходном растворе равен литра. При добавлении 7 литров воды общий объем раствора увеличится, а объем растворенного вещества останется прежним. Таким образом, концентрация полученного раствора равна:
.
Ответ: 7.
Ответ: 7
108487
7
12. Найдите наименьшее значение функции на отрезке
.
Решение.
Найдем производную заданной функции:
Найдем нули производной на заданном отрезке:
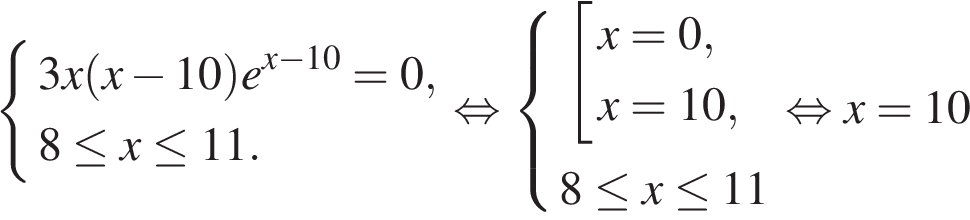
Определим знаки производной функции и изобразим на рисунке поведение функции:
В точке заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
.
Ответ: −24.
Ответ: -24
77478
-24
13. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Решение.
а) Перенесём все члены в левую часть, преобразуем и разложим левую часть на множители:
1 случай. Если то
2 случай. Если то При решений нет. Разделим обе части уравнения на Получаем
Тогда
Отрезку принадлежат корни и
Ответ: а) б) и
Источник: МИОО: Тренировочная работа по математике 24.04.2012 вариант 2. (Часть С)
14. В правильной четырехугольной пирамиде MABCD с вершиной M стороны основания равны 15, а боковые ребра равны 16. Найдите площадь сечения пирамиды плоскостью, проходящей через точку B и середину ребра MD параллельно прямой AC.
Решение.
Пусть точка E — середина ребра MD. Отрезок BE пересекает плоскость MAC в точке P. В треугольнике MBD точка Р является точкой пересечения медиан, следовательно, MP:РО = 2 : 1, где O — центр основания пирамиды. Отрезок FG параллелен AC и проходит через точку P (точка F принадлежит ребру MA, G — ребру MC), откуда
Четырёхугольник BFEG — искомое сечение. Отрезок BE — медиана треугольника MBD, значит,
Поскольку прямая BD перпендикулярна плоскости MAC, диагонали BE и FG четырёхугольника BFEG перпендикулярны, следовательно,
Ответ:
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Центр. Вариант 1.
15. Решите неравенство:
Решение.
Имеем:
Ответ:
16. В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке M , причём AM = 5R и CM = 1,5R.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите расстояние между центрами его вписанной и описанной окружностей, если известно, что R = 4.
Решение.
а) Пусть вписанная окружность касается стороны BC в точке K. Обозначим BK = x. Пусть S — площадь треугольника, p — полупериметр. Тогда
С другой стороны, по формуле Герона
Из уравнения получаем, что R = x. Стороны треугольника ABC равны 6,5R, 6R и 2,5R, следовательно, этот треугольник прямоугольный с прямым углом при вершине B.
б) Пусть I и O — центры соответственно вписанной и описанной окружностей треугольника ABC. Точка O — середина гипотенузы AC = 6,5R = 26, и OM = CO − CM = 13 − 1,5R = 7.
Тогда
Ответ: б)
Источник: СтатГрад: Тренировочная работа по математике 18.12.2015 вариант МА10212.
17. Антон является владельцем двух заводов в разных городах. На заводах производится абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производт t единиц товара.
За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, — 200 рублей.
Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Решение.
Пусть на оплату труда рабочих первого завода выделено x руб., а второго — оставшиеся (900 000 − x) руб. Тогда на первом заводе можно оплатить часов работы, а на втором — часов работы. Количество произведённого за неделю товара равно квадратным корням из этих величин, поэтому для ответа на вопрос задачи требуется найти наибольшее значение функции
на отрезке Найдём производную:
Решая уравнение получаем:
Поскольку производная непрерывной функции f положительна на интервале (0; 400 000), равна нулю в точке 400 000 и отрицательна на интервале (400 000; 900 000), функция f достигает наибольшего на отрезке [0; 900 000] значения в точке 400 000. Найдём его:
Тем самым, наибольшее возможное количество товара, которое могут произвести рабочие за неделю при заданном размере оплаты труда, равно 90 единицам.
Ответ: 90.
Источник: ЕГЭ по математике — 2015. Досрочная волна, резервный день (часть С).
18. Найдите все значения параметра а, при каждом из которых множество значений функции содержит отрезок
Решение.
Запишем функцию в виде
Отрезок содержится в множестве значений данной функции тогда и только тогда, когда уравнения и имеют решения.
Решим первое уравнение. Уравнение имеет решение при любом
Решим второе уравнение. Уравнение имеет решение тогда и только тогда, когда его дискриминант неотрицателен:
откуда
Следовательно,
или
Ответ:
Источник: СтатГрад: Диагностическая работа по математике 21.01.2015 вариант МА10110.
19. Каждое из чисел 2, 3, …, 7 умножают на каждое из чисел 13, 14, …, 21 и перед каждым из полученных произведений произвольным образом ставят знак плюс или минус, после чего все 54 полученных результата складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
Просмотр содержимого документа
«Вариант16»
Вариант № 16
1.
Студент получил свой первый гонорар в размере 900 рублей за выполненный перевод. Он решил на все полученные деньги купить букет лилий для своей учительницы английского языка. Какое наибольшее количество лилий сможет купить студент, если удержанный у него налог на доходы составляет 13% гонорара, лилии стоят 120 рублей за штуку и букет должен состоять из нечетного числа цветов?
Решение.
Налог составит 900 0,13 = 117 рублей. После выплаты налога останется 900 − 117 = 783 рубля. Разделим 783 на 120:
.
Значит, денег хватает на 6 лилий. В букете должно быть нечетное число цветов, поэтому студент купит 5 лилий.
Ответ: 5.
Ответ: 5
83781
5
2. Задание 2 № 18893. На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа за данный период впервые выпало ровно 1,5 миллиметра осадков.
Решение.
Из графика видно, впервые 1,5 мм осадков выпало 9 января (см. рисунок).
Ответ: 9.
Ответ: 9
18893
9
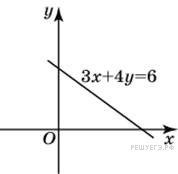
3. 
Решение.
Общий вид уравнения прямой y = kx + b. Тогда выражая y из исходного уравнения, получаем:
Поэтому k = −0,75.
Ответ: −0,75.
Ответ: -0,75
27691
-0,75
4. Чтобы поступить в институт на специальность «Переводчик», абитуриент должен набрать на ЕГЭ не менее 79 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на на специальность «Таможенное дело», нужно набрать не менее 79 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
Вероятность того, что абитуриент Б. получит не менее 79 баллов по математике, равна 0,9, по русскому языку — 0,7, по иностранному языку — 0,8 и по обществознанию — 0,9.
Найдите вероятность того, что Б. сможет поступить на одну из двух упомянутых специальностей.
Решение.
В силу независимости событий, вероятность успешно сдать экзамены на «Переводчика»: 0,9 · 0,7 · 0,8 = 0,504, вероятность успешно сдать экзамены на «Таможенное дело»: 0,9 · 0,7 · 0,9 = 0,567, вероятность успешно сдать экзамены и на «Переводчика», и на «Таможенное дело»: 0,9 · 0,7 · 0,8 · 0,9 = 0,4536. Успешная сдача экзаменов на «Переводчика» и на «Таможенное дело» — события совместные, поэтому вероятность их суммы равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения. Тем самым, поступить на одну из этих специальностей абитуриент может с вероятностью 0,504 + 0,567 − 0,4536 = 0,6174.
Ответ: 0,6174.
Ответ: 0,6174
321893
0,6174
5. Найдите корень уравнения
Решение.
Перейдем к одному основанию степени:
Ответ: 2.
Ответ: 2
509012
2
Источник: СтатГрад: Диагностическая работа по математике 13.02.2015 вариант МА00409.
6. 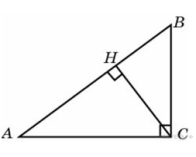
, CH — высота, АВ = 5,
Найдите AH.
Решение.
Заметим, что . Тогда
.
Ответ: 3,2.
Ответ: 3,2
4817
3,2
7.
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Решение.
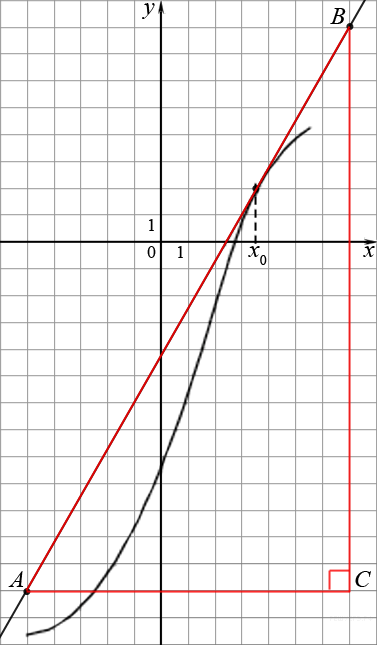
Ответ: 1,75.
Ответ: 1,75
9641
1,75
8.
Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен Найдите образующую конуса.
Решение.
Высота конуса перпендикулярна основанию и равна радиусу сферы. Тогда по теореме Пифагора получаем:
Радиус сферы равен поэтому образующая равна
Ответ:46.
Ответ: 46
501938
46
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Центр. Вариант 101.
9. Найдите значение выражения .
Решение.
Воспользуемся периодичностью синуса:
.
Ответ: 14.
Ответ: 14
26769
14
10. В розетку электросети подключены приборы, общее сопротивление которых составляет Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление
этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями
Ом и
Ом их общее сопротивление даeтся формулой
(Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в омах.
Решение.
Задача сводится к решению неравенства Ом при известном значении сопротивления приборов
Ом:
Ом.
Ответ: 10.
Ответ: 10
27975
10
11.
Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 0,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 25 метрам?
Решение.
Пусть км/ч – скорость второго пешехода, тогда скорость первого −
км/ч. Пусть через
часов расстояние между пешеходами станет равным 0,025 километра. Таким образом,
Следовательно, расстояние станет равным 25 метрам через часа или
минутам.
Ответ: 3.
Ответ: 3
113441
3
12. Найдите точку минимума функции .
Решение.
Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка минимума
Ответ: 4.
Ответ: 4
77420
4
13. Решите уравнение:
Решение.
Преобразуем уравнение:
Откуда получаем, что:
Ответ:
Источник: МИОО: Тренировочная работа по математике 12.04.2011 вариант 2. (Часть С)
14. В конус, радиус основания которого равен 3, вписан шар радиуса 1,5.
а) Изобразите осевое сечение комбинации этих тел.
б) Найдите отношение площади полной поверхности конуса к площади поверхности шара.
Решение.
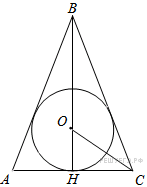
боковые стороны которого являются образующими конуса, а основанием — его диаметр, и вписанная в треугольник окружность, радиус которой равен радиусу шара (см. рис.).
б) Введём обозначения как показано на рисунке. Пусть — центр вписанной окружности, отрезок
— биссектриса угла
и пусть имеем:
Тогда Для площадей поверхностей конуса и шара имеем: Тем самым, искомое отношение равно или 8:3.
Ответ: 8:3.
Источник: РЕШУ ЕГЭ — Предэкзаменационная работа 2014 по математике.
15. Решите неравенство:
Решение.
Пусть тогда неравенство примет вид:
Таким образом,
Ответ:
16. На сторонах AD и BC параллелограмма ABCD взяты соответственно точки M и N , причём M — середина AD, а BN : NC = 1 : 3.
а) Докажите, что прямые AN и AC делят отрезок BM на три равные части.
б) Найдите площадь четырёхугольника, вершины которого находятся в точках С, N и точках пересечения прямой BM c прямыми AN и AC , если площадь параллелограмма ABCD равна 27.
Решение.
а) Обозначим точки пересечения прямой BM c прямыми AN и AC буквами P и R соответственно.
Пусть O – точка пересечения диагоналей параллелограмма. Тогда AO и BM — медианы треугольника ABD, значит,
Из подобия треугольников BPN и MPA находим, что
Значит, Из доказанного следует, что
б) Пусть площадь параллелограмма равна S . Из подобия треугольников MRA и BRC с коэффициентом следует, что высота треугольника BRC, проведённая к стороне BC, составляет
высоты параллелограмма, проведённой к той же стороне. Следовательно, площадь треугольника BRC равна
Аналогично найдём площадь треугольника BNP . Его высота, проведённая к BN , составляет высоты параллелограмма, проведённой к стороне BC , а сама сторона BN в четыре раза меньше стороны параллелограмма BC. Поэтому
Следовательно, площадь четырёхугольника PRCN равна
Ответ: .
17. Известно, что вклад, находящийся в банке с начала года, возрастает к концу года на определенный процент, свой для каждого банка. В начале года Степан положил 60% некоторой суммы денег в первый банк, а оставшуюся часть суммы во второй банк. К концу года сумма этих вкладов стала равна 590 000 руб., а к концу следующего года 701 000 руб. Если бы Степан первоначально положил 60% своей суммы во второй банк, а оставшуюся часть в первый, то по истечении одного года сумма вкладов стала бы равной 610 000 руб. Какова была бы сумма вкладов в этом случае к концу второго года?
Решение.
Пусть сумма денег, которые Степан положил в два разных банка, составляет х руб. Коэффициент повышения суммы, обусловленный годовой процентной ставкой на вклад, составляет в первом банке u, во втором v (это — не процентная ставка).
Тогда к концу первого года хранения (60% процентов в первом банке и 40% во втором банке) вся сумма вклада стала (руб.).
Если бы Степан первоначально положил 60% всей суммы во второй банк, а 40% — в первый банк, то вся сумма была бы равна (руб.).
Решим систему уравнений относительно xu и xv.
Для удобства в расчетах заменим число 590 000 выражением 590t, 610 000 — выражением 610t, t = 1000.
Тогда приведенная система уравнений после некоторых преобразований будет выглядеть так:
Решим ее относительно xu и xv.
Теперь воспользуемся тем, что к концу второго года сумма вкладов (в реале) стала 701 000 руб., т.е. 701t руб.
При
Теперь нетрудно найти и искомую сумму.
(руб.)
Ответ: 749 000.
18. Найдите все значения a, при каждом из которых уравнение имеет хотя бы один корень.
Решение.
Рассмотрим две функции: и Поскольку получаем:
Функция является кусочно-линейной, причём при угловой коэффициент равен либо 3, либо 9, а при
угловой коэффициент равен либо –3, либо –9. Значит, функция возрастает при
и убывает при
поэтому
Исходное уравнение имеет хотя бы один корень тогда и только тогда, когда
Значит, либо
откуда
либо
откуда
Ответ:
19. Найдите все пары натуральных чисел m и n, являющиеся решениями уравнения 2m − 3n = 1.
Просмотр содержимого документа
«Вариант17»
Вариант № 17
1. 1 киловатт-час электроэнергии стоит 1 рубль 60 копеек. Счетчик электроэнергии 1 сентября показывал 79 991 киловатт-час, а 1 октября показывал 80 158 киловатт-часов. Сколько рублей нужно заплатить за электроэнергию за сентябрь?
Решение.
Расход электроэнергии за сентябрь составляет 80 158 − 79 991 = 167 киловатт-часов. Значит, за электроэнергию за сентябрь нужно заплатить 1,6 167 = 267,2 рубля.
Ответ: 267,2.
Ответ: 267,2
78797
267,2
2. На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру во второй половине 1999 года. Ответ дайте в градусах Цельсия.
Решение.
Из диаграммы видно, что наименьшая среднемесячная температура во второй половине года составляла −2 °C (см. рисунок).
Ответ: −2.
Ответ: -2
27516
-2
3. 
Решение.
Площадь трапеции равна произведению полусуммы оснований на высоту. Поэтому
см2.
Ответ: 9.
Ответ: 9
24209
9
4
В классе 16 учащихся, среди них два друга — Олег и Вадим. Класс случайным образом разбивают на 4 равные группы. Найдите вероятность того, что Олег и Вадим окажутся в одной группе.
Решение.
Пусть один из друзей находится в некоторой группе. Вместе с ним в группе окажутся 3 человека из 15 оставшихся одноклассников. Вероятность того, что второй друг окажется среди этих 3 человек, равна 3 : 15 = 0,2.
Ответ: 0,2
321495
0,2
5. Найдите корень уравнения 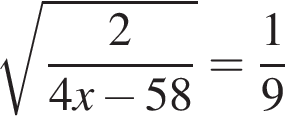
Решение.
Возведем в квадрат:
Ответ: 55.
Ответ: 55
3329
55
6. 
Решение.
Площадь ромба равна половине произведения его диагоналей. Поэтому
.
Ответ: 24.
Ответ: 24
27614
24
7. На рисунке изображен график производной функции , определенной на интервале
. В какой точке отрезка
принимает наибольшее значение.
Решение.
На заданном отрезке производная функции положительна, поэтому функция на этом отрезке возрастает. Поэтому наибольшее значение функции достигается на правой границе отрезка, т. е. в точке 5.
Ответ: 5.
Ответ: 5
6415
5
8. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO = 4, AC = 6. Найдите боковое ребро SC.
Решение.
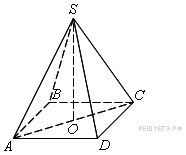
Ответ: 5.
Ответ: 5
284348
5
9. Найдите значение выражения .
Решение.
Выполним преобразования:
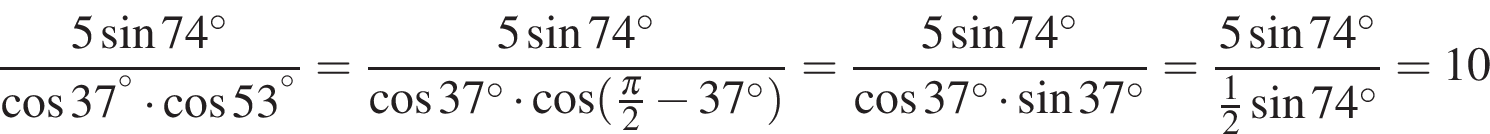
Ответ: 10.
Ответ: 10
77413
10
10. Высота над землeй подброшенного вверх мяча меняется по закону , где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 4 метров?
Решение.
Определим моменты времени, когда мяч находился на высоте ровно четыре метра. Для этого решим уравнение :
Проанализируем полученный результат: поскольку по условию задачи мяч брошен снизу вверх, это означает, что в момент времени (с) мяч находился на высоте 4 метра, двигаясь снизу вверх, а в момент времени
(с) мяч находился на этой высоте, двигаясь сверху вниз. Поэтому он находился на высоте не менее четырёх метров 1,4 − 0,4 = 1 секунду.
Ответ: 1.
Ответ: 1
41337
1
11. Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
Решение.
Пусть км/ч — скорость моторной лодки, тогда скорость лодки по течению равна
км/ч, а скорость лодки против течения равна
км/ч. На путь по течению лодка затратила на 2 часа меньше, отсюда имеем:
Ответ: 16.
Ответ: 16
5687
16
12. Найдите наибольшее значение функции на отрезке
.
Решение.
Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
В точке заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
.
Ответ: 36.
Ответ: 36
77479
36
13. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащее отрезку
Решение.
а) Запишем исходное уравнение в виде:
Значит, 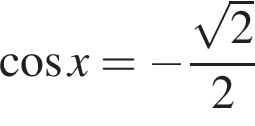
или
Уравнение корней не имеет.
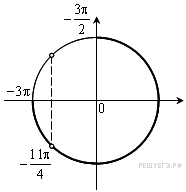
Получим число
Ответ:а) б)
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант 2 (Часть С).
14. Расстояние между боковыми ребрами AA1 и BB1 прямой треугольной призмы ABCA1B1C1 равно 5, а расстояние между боковыми ребрами AA1 и CC1 равно 8. Найдите расстояние от прямой AA1 до плоскости BC1C, если известно, что двугранный угол призмы при ребре AA1 равен 60°.
Решение.
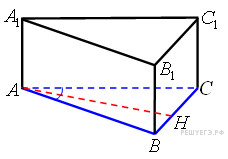
― прямая призма, ее боковые грани ― прямоугольники, следовательно, расстояние между боковыми ребрами
и
равно
а расстояние между боковыми ребрами
и
равно
Кроме того, угол
― линейный угол двугранного угла при ребре
Таким образом,
Пусть отрезок ― высота основания
(см. рисунок). Поскольку и то и, значит, длина отрезка
и есть искомое расстояние от прямой
до параллельной ей плоскости
Рассматривая треугольник находим:
Ответ:
Источник: Добровольное тренировочное тестирование Санкт-Петербург 2013.
15. Решите неравенство
Решение.
Решение будем искать при условиях:
.
Рассмотрим исходное неравенство на множестве тогда откуда то есть .
Рассмотрим исходное неравенство на множестве тогда откуда то есть или
Ответ: .
16. Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L — точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 12.
Решение.
а) Пусть O — центр большей окружности. Линия центров касающихся окружностей проходит через точку касания, поэтому OA — диаметр меньшей окружности.
Точка K лежит на окружности с диаметром OA, значит, ∠AKO = 90°. Отрезок OK — перпендикуляр, опущенный из центра большей окружности на хорду AB. Поэтому K — середина AB. Аналогично, M — середина AC, поэтому KM — средняя линия треугольника ABC. Следовательно, прямые MK и BC параллельны.
б) Отпустим перпендикуляр OH на хорду BC. Тогда H — середина BC. Из прямоугольного треугольника OHB находим, что
Пусть Q — центр меньшей окружности. Тогда прямые QP и OH параллельны. Опустим перпендикуляр QF из центра меньшей окружности на OH. Тогда
а из прямоугольного треугольника APO находим, что
Отрезок KM — средняя линия треугольника ABC, поэтому L средняя AP. Следовательно,
Ответ: б)
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант 2 (Часть С).
17. 31 декабря 2014 года Ярослав взял в банке некоторую сумму в кредит под 12,5% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга ( то есть увеличивает долг на 12,5%), затем Ярослав переводит в банк 2 132 325 рублей. Какую сумму взял Ярослав в банке, если он выплатил долг четырьмя равными платежами (то есть за четыре года)?
Решение.
Заметим сначала, что увеличить число на это тоже самое, что умножить это число на Пусть Ярослав взял в банке
рублей, а его ежегодный платеж равен
(в данном случае ). Тогда из условия следует уравнение: Раскрывая скобки, получаем следующее:
Отсюда
Ответ: 6409000 рублей.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2015 г.
18. Найдите все значения параметра a, при которых уравнение
имеет ровно два решения.
Решение.
Пусть тогда исходное уравнение принимает вид:
(1)
откуда
(2)
Значит, решение исходного уравнения — это решение уравнений или Исследуем сколько решений имеет уравнение в зависимости от и
Запишем уравнение в виде Левая часть этого уравнения — график модуля с вершиной в точке график левой части — график модуля, с вершиной в точке Это уравнение может иметь одно, либо бесконечное множество решений. Уравнение будет иметь одно решение, если одновременно прямая лежит выше прямой
и прямая лежит ниже прямой либо, если одновременно прямая лежит ниже прямой
и прямая лежит выше прямой
Получаем совокупность двух систем уравнений:
(3)
Таким образом, исходное уравнение имеет ровно два решения, если оба уравнения совокупности (2) имеют по одному решению.
Для первого уравнения имеем
Для второго уравнения:
Если уравнения совокупности совпадают, то тогда, даже если каждое из них имеет по одному решению, то эти решения совпадут и исходное уравнение будет иметь не два, а одно решение. Исключим данный случай, найдём при каких значениях параметра уравнения совпадают:
Таким образом, исходное уравнение имеет ровно два решения при значениях параметра
Ответ:
Источник: ЕГЭ по математике 05.06.2014. Основная волна. Восток. Вариант 2.
19. Коля множил некоторое натуральное число на соседнее натуральное число, и получил произведение, равное m. Вова умножил некоторое четное натуральное число на соседнее четное натуральное число и получил произведение, равное n.
а) Может ли модуль разности чисел m и n равняться 6?
б) Может ли модуль разности чисел m и n равняться 13?
в) Какие значения может принимать модуль разности чисел m и n?
Решение 13 задания экзамена по математике
(профильный уровень)
1.
Решите уравнение
2.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
3.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Источник: Досрочная волна ЕГЭ по математике 29.03.2019. Вариант 1
4.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: Задания 13 (С1) ЕГЭ 2016, ЕГЭ по математике 28.03.2016. Досрочная волна, вариант 2 (только часть С)
5.
Решите уравнение
6.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: Типовые тестовые задания по математике под редакцией И.В. Ященко, 2017. Задания С1., Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 8. (Часть C).
7.
а) Решите уравнение .
б) Найдите его корни, принадлежащие отрезку .
8.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: РЕШУ ЕГЭ — Предэкзаменационная работа 2014 по математике.
9.
а) Решите уравнение
б) Укажите корни, принадлежащие отрезку
Источник: Типовые тестовые задания по математике под редакцией И.В. Ященко, 2016.
10.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащего отрезку
Источник: Задания 13 (С1) ЕГЭ 2016, Задания 13 (С1) ЕГЭ 2015
11.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: Задания 13 (С1) ЕГЭ 2017
12.
а) Решите уравнение
б) Укажите корни этого уравнения на интервале
Источник: Задания 13 (С1) ЕГЭ 2016, ЕГЭ по математике — 2016. Досрочная волна, резервный день, вариант А. Ларина (часть С).
13.
а) Решите уравнение:
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: ЕГЭ — 2018. Основная волна, резервный день 25.06.2018. Вариант 992 (C часть)., Задания 13 (С1) ЕГЭ 2018
14.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 1.
15.
а) Решите уравнение .
б) Найдите его корни, принадлежащие отрезку .
Источник: Типовые тестовые задания по математике под редакцией И.В. Ященко, 2018.
МАТЕМАТИКА
Варианты О. А. Иванова
2022—2023 УЧЕБНЫЙ ГОД
Демонстрационная версия ЕГЭ по математике 2023 года с решениями.
2021—2022 УЧЕБНЫЙ ГОД
Демонстрационная версия ЕГЭ по математике 2022 года с решениями.
ЕГЭ по математике 28.03.2022. Досрочная волна. Вариант 1.
ЕГЭ по математике 28.03.2022. Досрочная волна. Вариант 2.
ЕГЭ по математике 28.03.2022. Досрочная волна. Вариант 3.
ЕГЭ по математике 28.03.2022. Досрочная волна. Вариант 4.
ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург, Москва, центр. Вариант 337 (часть С)
ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург, Москва, центр. Вариант 338 (часть С)
ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург. Вариант 319 (часть С)
ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург. Вариант 321 (часть С)
ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург, Москва, центр. Вариант 401 (часть С)
ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург, Москва, центр. Вариант 402 (часть С)
ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург, Москва, центр. Вариант 403 (часть С, сборка из 401 и 402)
ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург, Москва, центр. Вариант 404 (часть С, сборка из 401 и 402)
ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург, Москва, центр. Вариант 405 (часть С, сборка из 401 и 402)
ЕГЭ по математике 02.06.2022. Основная волна. Санкт-Петербург, Москва, центр. Вариант 406 (часть С, сборка из 401 и 402)
ЕГЭ по математике 02.06.2022. Основная волна. Дальний Восток.
ЕГЭ по математике 02.06.2022. Основная волна. Краснодар.
ЕГЭ по математике 02.06.2022. Основная волна. Вариант 991 (часть С).
ЕГЭ по математике 27.06.2022. Резервная волна. Вариант 501 (часть С).
ЕГЭ по математике 27.06.2022. Резервная волна. Вариант 502 (часть С).
ЕГЭ по математике 27.06.2022. Резервная волна. Вариант 992 (часть С).
Все экзаменационные задания № 12 из ЕГЭ–2022.
Все экзаменационные задания № 13 из ЕГЭ–2022.
Все экзаменационные задания № 14 из ЕГЭ–2022.
Все экзаменационные задания № 15 из ЕГЭ–2022.
Все экзаменационные задания № 16 из ЕГЭ–2022.
Все экзаменационные задания № 17 из ЕГЭ–2022.
Все экзаменационные задания № 18 из ЕГЭ–2022.
2020—2021 УЧЕБНЫЙ ГОД
Демонстрационная версия ЕГЭ по математике 2021 года с решениями.
Пробный экзамен Санкт-Петербург, 18.03.2021. Вариант 1.
Пробный экзамен Санкт-Петербург, 18.03.2021. Вариант 2.
2019—2020 УЧЕБНЫЙ ГОД
Демонстрационная версия ЕГЭ по математике 2020 года с решениями.
2018—2019 УЧЕБНЫЙ ГОД
Демонстрационная версия ЕГЭ по математике 2019 года с решениями.
ЕГЭ по математике 29.03.2019. Досрочная волна. Вариант 1.
ЕГЭ по математике 29.03.2019. Досрочная волна. Вариант 2.
ЕГЭ по математике 29.03.2019. Досрочная волна. Вариант 3 (часть С).
ЕГЭ по математике 29.03.2019. Досрочная волна. Вариант 4.
ЕГЭ по математике 10.04.2019. Досрочная волна, резервный день Запад.
ЕГЭ по математике 29.05.2019. Основная волна. Дальний восток. Вариант Имаева-Зубовой.
ЕГЭ по математике 29.05.2019. Основная волна. Центр. Вариант Имаева-Зубовой.
ЕГЭ по математике 29.05.2019. Основная волна. Санкт-Петербург.
ЕГЭ по математике 29.05.2019. Основная волна. Вариант 316 (часть С).
ЕГЭ по математике 29.05.2019. Основная волна. Вариант 324 (часть С).
ЕГЭ по математике 29.05.2019. Основная волна. Вариант 405 (часть С).
ЕГЭ по математике 29.05.2019. Основная волна. Вариант 409 (часть С).
ЕГЭ по математике 29.05.2019. Основная волна. Вариант 991 (часть С).
ЕГЭ по математике 24.06.2019. Основная волна, резервный день. Вариант 992 (часть С).
ЕГЭ по математике 24.06.2019. Основная волна, резервный день. Кавказ. Вариант (часть С).
ЕГЭ по математике 24.06.2019. Основная волна, резервный день. Вариант 503 (часть С).
Все экзаменационные задания ЕГЭ 2019 13 (C1).
Все экзаменационные задания ЕГЭ 2019 14 (C2).
Все экзаменационные задания ЕГЭ 2019 15 (C3).
Все экзаменационные задания ЕГЭ 2019 16 (C4).
Все экзаменационные задания ЕГЭ 2019 17 (C5).
Все экзаменационные задания ЕГЭ 2019 18 (C6).
Все экзаменационные задания ЕГЭ 2019 19 (C7).
Пробный экзамен Санкт-Петербург, 19.03.2019. Вариант 1.
Пробный экзамен Санкт-Петербург, 19.03.2019. Вариант 2.
2017—2018 УЧЕБНЫЙ ГОД
Демонстрационная версия ЕГЭ по математике 2018 года с решениями.
ЕГЭ по математике 30.03.2018. Досрочная волна. Запад.
ЕГЭ по математике 11.04.2018. Досрочная волна, резервный день Запад.
ЕГЭ по математике 01.06.2018. Основная волна. Центр. Вариант 301 (часть С).
ЕГЭ по математике 01.06.2018. Основная волна. Центр. Вариант 302 (часть С).
ЕГЭ по математике 01.06.2018. Основная волна. Центр. Вариант 401 (часть С).
ЕГЭ по математике 01.06.2018. Основная волна. Центр. Вариант 402 (часть С).
ЕГЭ по математике 01.06.2018. Основная волна. Центр. Вариант 991 (часть С).
ЕГЭ по математике 25.06.2018. Основная волна, резервный день. Центр. Вариант 501 (часть С).
ЕГЭ по математике 25.06.2018. Основная волна, резервный день. Центр. Вариант 502 (часть С).
ЕГЭ по математике 25.06.2018. Основная волна, резервный день. Центр. Вариант 751 (часть С).
ЕГЭ по математике 25.06.2018. Основная волна, резервный день. Центр. Вариант 992 (часть С).
Все экзаменационные задания ЕГЭ 2018 13 (C1).
Все экзаменационные задания ЕГЭ 2018 14 (C2).
Все экзаменационные задания ЕГЭ 2018 15 (C3).
Все экзаменационные задания ЕГЭ 2018 16 (C4).
Все экзаменационные задания ЕГЭ 2018 17 (C5).
Все экзаменационные задания ЕГЭ 2018 18 (C6).
Все экзаменационные задания ЕГЭ 2018 19 (C7).
Пробный экзамен Санкт-Петербург, 04.03.2018. Вариант 1.
Пробный экзамен Санкт-Петербург, 04.03.2018. Вариант 2.
2016—2017 УЧЕБНЫЙ ГОД
Демонстрационная версия ЕГЭ по математике 2017 года с решениями.
ЕГЭ по математике 31.03.2017. Досрочная волна. Запад.
ЕГЭ по математике 14.04.2017. Досрочная волна, резервный день. Запад.
ЕГЭ по математике 02.06.2017. Основная волна. Центр. Вариант 301 (часть С).
ЕГЭ по математике 02.06.2017. Основная волна. Центр. Вариант 302 (часть С).
ЕГЭ по математике 02.06.2017. Основная волна. Центр. Вариант 303 (часть С).
ЕГЭ по математике 02.06.2017. Основная волна. Центр. Вариант 401 (часть С).
ЕГЭ по математике 02.06.2017. Основная волна. Центр. Вариант 402 (часть С).
ЕГЭ по математике 02.06.2017. Основная волна. Центр. Вариант 419 (часть С).
ЕГЭ по математике 02.06.2017. Основная волна. Центр. Вариант 431 (часть С).
ЕГЭ по математике 02.06.2017. Основная волна. Центр. Вариант 432 (часть С).
ЕГЭ по математике 02.06.2017. Основная волна. Центр. Вариант 991 (часть С).
ЕГЭ по математике 28.06.2017. Основная волна, резервный день. Центр. Вариант 501 (часть С).
ЕГЭ по математике 28.06.2017. Основная волна, резервный день. Центр. Вариант 502 (часть С).
ЕГЭ по математике 28.06.2017. Основная волна, резервный день. Центр. Вариант 992 (часть С).
ЕГЭ по математике 28.06.2017. Основная волна, резервный день. Восток. Вариант (часть С).
Все экзаменационные задания ЕГЭ 2017 13 (C1).
Все экзаменационные задания ЕГЭ 2017 14 (C2).
Все экзаменационные задания ЕГЭ 2017 15 (C3).
Все экзаменационные задания ЕГЭ 2017 16 (C4).
Все экзаменационные задания ЕГЭ 2017 17 (C5).
Все экзаменационные задания ЕГЭ 2017 18 (C6).
Все экзаменационные задания ЕГЭ 2017 19 (C7).
Пробный экзамен Санкт-Петербург, 11.04.2017. Вариант 1.
Пробный экзамен Санкт-Петербург, 11.04.2017. Вариант 2.
Типовые тестовые задания по математике под редакцией И. В. Ященко, 2017. Задания С1
Типовые тестовые задания по математике под редакцией И. В. Ященко, 2017. Задания С2, С4.
Типовые тестовые задания по математике под редакцией И. В. Ященко, 2017. Задания С3.
Типовые тестовые задания по математике под редакцией И. В. Ященко, 2017. Задания С5.
Типовые тестовые задания по математике под редакцией И. В. Ященко, 2017. Задания С6.
Типовые тестовые задания по математике под редакцией И. В. Ященко, 2017. Задания С7..
2015—2016 УЧЕБНЫЙ ГОД
Демонстрационная версия ЕГЭ по математике 2016 года с решениями.
2014—2015 УЧЕБНЫЙ ГОД
Демонстрационная версия ЕГЭ по математике 2015 года с решениями.
ЕГЭ по математике 26.03.2015. Досрочная волна. Восток.
ЕГЭ по математике 26.03.2015. Досрочная волна. Запад.
ЕГЭ по математике 04.06.2015. Основная волна. Вариант 1.
ЕГЭ по математике 04.06.2015. Основная волна. Вариант 2.
Все экзаменационные задания ЕГЭ 2015 13 (C1).
Все экзаменационные задания ЕГЭ 2015 14 (C2).
Все экзаменационные задания ЕГЭ 2015 15 (C3).
Все экзаменационные задания ЕГЭ 2015 16 (C4).
Все экзаменационные задания ЕГЭ 2015 17 (C5).
Все экзаменационные задания ЕГЭ 2015 18 (C6).
Все экзаменационные задания ЕГЭ 2015 19 (C7).
Пробный экзамен Санкт-Петербург 2015. Вариант 1.
Пробный экзамен Санкт-Петербург 2015. Вариант 2.
Пробный экзамен Санкт-Петербург 2015. Кировский район. Вариант 1.
Пробный экзамен Санкт-Петербург 2015. Кировский район. Вариант 2.
2013—2014 УЧЕБНЫЙ ГОД
Проект демонстрационной версии ЕГЭ по математике 2014 года с решениями.
Демонстрационная версия ЕГЭ по математике 2014 года с решениями.
ЕГЭ по математике 28.04.2014. Досрочная волна. Вариант 1.
ЕГЭ по математике 28.04.2014. Досрочная волна. Вариант 2.
ЕГЭ по математике 08.05.2014. Досрочная волна, резервный день. Запад. Вариант 1 (Часть C).
ЕГЭ по математике 08.05.2014. Досрочная волна, резервный день. Запад. Вариант 2 (Часть C).
ЕГЭ по математике 05.06.2014. Основная волна. Запад. Вариант 1.
ЕГЭ по математике 05.06.2014. Основная волна. Восток. Вариант 1.
ЕГЭ по математике 05.06.2014. Основная волна. Восток. Вариант 2 (Часть C).
ЕГЭ по математике 05.06.2014. Основная волна. Запад. Вариант 301 (Часть C).
ЕГЭ по математике 05.06.2014. Основная волна. Запад. Вариант 302 (Часть C).
ЕГЭ по математике 05.06.2014. Основная волна. Запад. Вариант 901 (Часть C).
ЕГЭ по математике 19.06.2014. Основная волна, резервный день. Запад. Вариант 1 (Часть C).
Все экзаменационные задания ЕГЭ 2014 13 (C1).
Все экзаменационные задания ЕГЭ 2014 14 (C2).
Все экзаменационные задания ЕГЭ 2014 15 (C3).
Все экзаменационные задания ЕГЭ 2014 16 (C4).
Все экзаменационные задания ЕГЭ 2014 18 (C6).
Все экзаменационные задания ЕГЭ 2014 19 (C7).
Пробный экзамен Санкт-Петербург 2014 вариант 1.
Пробный экзамен Санкт-Петербург 2014 вариант 2.
2012—2013 УЧЕБНЫЙ ГОД
Демонстрационная версия ЕГЭ по математике 2013 года с решениями.
ЕГЭ по математике 23.04.2013. Досрочная волна. Запад. Вариант 1.
ЕГЭ по математике 23.04.2013. Досрочная волна. Восток. Вариант 1.
ЕГЭ по математике 03.06.2013. Основная волна. Центр. Вариант 101.
ЕГЭ по математике 03.06.2013. Основная волна. Центр. Вариант 102.
ЕГЭ по математике 03.06.2013. Основная волна. Центр. Вариант 1.
ЕГЭ по математике 03.06.2013. Основная волна. Урал. Вариант 203.
ЕГЭ по математике 03.06.2013. Основная волна. Сибирь. Вариант 302.
ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 402.
ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 701.
ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 702.
ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 501.
ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502.
ЕГЭ по математике 10.07.2013. Вторая волна. Центр. Вариант 601.
ЕГЭ по математике 10.07.2013. Вторая волна. Центр. Вариант 602.
ЕГЭ по математике. Досрочная волна. Вариант 901.
ЕГЭ по математике. Досрочная волна. Вариант 902.
Все экзаменационные задания ЕГЭ 2013 13 (C1).
Все экзаменационные задания ЕГЭ 2013 14 (C2).
Все экзаменационные задания ЕГЭ 2013 15 (C3).
Все экзаменационные задания ЕГЭ 2013 16 (C4).
Все экзаменационные задания ЕГЭ 2013 18 (C6).
Все экзаменационные задания ЕГЭ 2013 19 (C7).
Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2022 из различных источников.
Тренировочные варианты ЕГЭ 2022 по математике (профиль)
| egemath.ru | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| variant 8 | скачать |
| variant 9 | скачать |
| variant 10 | скачать |
| variant 11 | скачать |
| variant 12 | скачать |
| variant 13 | скачать |
| variant 14 | скачать |
| variant 15 | скачать |
| variant 16 | скачать |
| variant 17 | скачать |
| variant 18 | скачать |
| variant 19 | скачать |
| variant 20 | скачать |
| yagubov.ru | |
| вариант 21 | ege2022-yagubov-prof-var21 |
| вариант 22 | ege2022-yagubov-prof-var22 |
| вариант 23 | ege2022-yagubov-prof-var23 |
| вариант 24 | ege2022-yagubov-prof-var24 |
| вариант 25 | ege2022-yagubov-prof-var25 |
| вариант 26 | ege2022-yagubov-prof-var26 |
| вариант 27 | ege2022-yagubov-prof-var27 |
| вариант 28 | ege2022-yagubov-prof-var28 |
| Досрочный Москва 28.03.2022 | скачать |
| egemathschool.ru | |
| вариант 1 | ответ |
| вариант 2 | ответ |
| вариант 3 | ответ |
| вариант 4 | ответ |
| ЕГЭ 100 баллов (с решениями) | |
| Вариант 1 | скачать |
| Вариант 2 | скачать |
| Вариант 3 | скачать |
| Вариант 4 | скачать |
| Вариант 5 | скачать |
| Вариант 6 | скачать |
| Вариант 7 | скачать |
| Вариант 8 | скачать |
| Вариант 9 | скачать |
| Вариант 10 | скачать |
| variant 11 | скачать |
| variant 12 | скачать |
| variant 13 | скачать |
| variant 14 | скачать |
| variant 15 | скачать |
| variant 16 | скачать |
| variant 17 | скачать |
| variant 18 | скачать |
| variant 20 | скачать |
| variant 21 | скачать |
| variant 23 | скачать |
| variant 24 | скачать |
| variant 25 | скачать |
| variant 26 | скачать |
| variant 29 | скачать |
| variant 30 | скачать |
| math100.ru (с ответами) | |
| Вариант 140 | скачать |
| Вариант 141 | скачать |
| Вариант 142 | скачать |
| Вариант 143 | math100-ege22-v143 |
| Вариант 144 | math100-ege22-v144 |
| Вариант 145 | math100-ege22-v145 |
| Вариант 146 | math100-ege22-v146 |
| variant 147 | math100-ege22-v147 |
| variant 148 | math100-ege22-v148 |
| variant 149 | math100-ege22-v149 |
| variant 150 | math100-ege22-v150 |
| variant 151 | math100-ege22-v151 |
| variant 152 | math100-ege22-v152 |
| variant 153 | math100-ege22-v153 |
| variant 154 | math100-ege22-v154 |
| variant 155 | math100-ege22-v155 |
| variant 156 | math100-ege22-v156 |
| variant 157 | math100-ege22-v157 |
| variant 158 | math100-ege22-v158 |
| variant 159 | math100-ege22-v159 |
| variant 160 | math100-ege22-v160 |
| variant 161 | math100-ege22-v161 |
| variant 162 | math100-ege22-v162 |
| variant 163 | math100-ege22-v163 |
| variant 164 | math100-ege22-v164 |
| variant 165 | math100-ege22-v165 |
| variant 166 | math100-ege22-v166 |
| variant 167 | math100-ege22-v167 |
| variant 168 | math100-ege22-v168 |
| variant 169 | math100-ege22-v169 |
| variant 170 | math100-ege22-v170 |
| variant 171 | math100-ege22-v171 |
| variant 172 | math100-ege22-v172 |
| variant 173 | math100-ege22-v173 |
| variant 174 | math100-ege22-v174 |
| alexlarin.net | |
| Вариант 358 |
скачать |
| Вариант 359 | скачать |
| Вариант 360 | скачать |
| Вариант 361 | скачать |
| Вариант 362 | проверить ответы |
| Вариант 363 | проверить ответы |
| Вариант 364 | проверить ответы |
| Вариант 365 | проверить ответы |
| Вариант 366 | проверить ответы |
| Вариант 367 | проверить ответы |
| Вариант 368 | проверить ответы |
| Вариант 369 | проверить ответы |
| Вариант 370 | проверить ответы |
| Вариант 371 | проверить ответы |
| Вариант 372 | проверить ответы |
| Вариант 373 | проверить ответы |
| Вариант 374 | проверить ответы |
| Вариант 375 | проверить ответы |
| Вариант 376 | проверить ответы |
| Вариант 377 | проверить ответы |
| Вариант 378 | проверить ответы |
| Вариант 379 | проверить ответы |
| Вариант 380 | проверить ответы |
| Вариант 381 | проверить ответы |
| Вариант 382 | проверить ответы |
| Вариант 383 | проверить ответы |
| Вариант 384 | проверить ответы |
| Вариант 385 | проверить ответы |
| Вариант 386 | проверить ответы |
| Вариант 387 | проверить ответы |
| Вариант 388 | проверить ответы |
| vk.com/ekaterina_chekmareva (задания 1-12) | |
| Вариант 1 | ответы |
| Вариант 2 | |
| Вариант 3 | |
| Вариант 4 | |
| Вариант 5 | |
| Вариант 6 | |
| Вариант 7 | ответы |
| Вариант 8 | |
| Вариант 9 | |
| Вариант 10 | |
| vk.com/matematicalate | |
| Вариант 1 | matematikaLite-prof-ege22-var1 |
| Вариант 2 | matematikaLite-prof-ege22-var2 |
| Вариант 3 | matematikaLite-prof-ege22-var3 |
| Вариант 4 | matematikaLite-prof-ege22-var4 |
| Вариант 5 | matematikaLite-prof-ege22-var5 |
| Вариант 6 | matematikaLite-prof-ege22-var6 |
| Вариант 7 | matematikaLite-prof-ege22-var7 |
| Вариант 8 | matematikaLite-prof-ege22-var8 |
| vk.com/pro_matem | |
| variant 1 | pro_matem-prof-ege22-var1 |
| variant 2 | pro_matem-prof-ege22-var2 |
| variant 3 | pro_matem-prof-ege22-var3 |
| variant 4 | разбор |
| variant 5 | разбор |
| vk.com/murmurmash | |
| variant 1 | otvet |
| variant 2 | otvet |
| → Купить сборники тренировочных вариантов ЕГЭ 2022 по математике |
Структура варианта КИМ ЕГЭ
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и количеству заданий:
– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;
– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).
Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Связанные страницы:
Средний балл ЕГЭ 2021 по математике
Решение задач с параметром при подготовке к ЕГЭ
Изменения в КИМ ЕГЭ 2022 года по математике
Купить сборники типовых вариантов ЕГЭ по математике
Как решать экономические задачи ЕГЭ по математике профильного уровня?
Решение заданий варианта досрочного периода ЕГЭ 2022 от 28 марта 2022 по математике (профильный уровень). Досрочник КИМ. Досрочная волна 2022. Полный разбор. ГДЗ профиль решебник для 11 класса. Ответы с решением.

Задание 1.
Найдите корень уравнения log2(7 – x) = 5.
Задание 2.
В чемпионате по гимнастике участвуют 4 спортсменки из Аргентины, 7 из Бразилии, 5 из Германии и 4 из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Бразилии.
ИЛИ
В чемпионате по гимнастике участвуют 70 спортсменок: 25 из США, 17 из Мексики, остальные из Канады. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Канады.
Задание 3.
В четырёхугольник ABCD вписана окружность, AB = 8, BC = 5 и CD = 27. Найдите четвёртую сторону четырёхугольника.
ИЛИ
В четырехугольник ABCD, периметр которого равен 56, вписана окружность. Найдите AB, если CD = 13.
Задание 4.
Найдите значение выражения 4^{frac{1}{5}}cdot 16^{frac{9}{10}}
ИЛИ
Найдите значение выражения frac{5^{3,7}cdot 6^{4,7}}{30^{2,7}}
Задание 5.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.
ИЛИ
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 37. Найдите площадь боковой поверхности исходной призмы.
Задание 6.
На рисунке изображён график функции y = f ′(x) − производной функции f(x), определённой на интервале (−3; 8). Найдите точку максимума функции f(x).
ИЛИ
На рисунке изображён график y = f ′(x) – производной функции f(x), определённой на интервале (−7; 6). Найдите точку минимума функции f(x).
Задание 7.
При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу со скоростями u и v (в м/с) соответственно, частота звукового сигнала f (в Гц), регистрируемого приёмником, вычисляется по формуле: , где f0 = 170 Гц – частота исходного сигнала, c – скорость распространения сигнала в среде (в м/с), а u = 2 м/с и v = 17 м/с – скорости приёмника и источника относительно среды. При какой скорости c (в м/с) распространения сигнала в среде частота сигнала в приёмнике f будет равна 180 Гц? Ответ дайте в м/с.
ИЛИ
В розетку электросети подключены приборы, общее сопротивление которых составляет R1 = 90 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление R2 этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R1 Ом и R2 Ом их общее сопротивление дается формулой Rобщ = (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в Омах.
Задание 8.
Имеется два сплава. Первый содержит 50% никеля, второй – 15% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
ИЛИ
Имеется два сплава. Первый сплав содержит 5 % меди, второй – 14 % меди. Масса второго сплава больше массы первого на 5 кг. Из этих двух сплавов получили третий сплав, содержащий 12 % меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Задание 9.
На рисунке изображён график функции f(x) = 5x + 9 и g(x) = ax2 + bx + c, которые пересекаются в точках А и В. Найдите абсциссу точки В.
ИЛИ
На рисунке изображены графики функций видов f(x) = a√x и g(x) = kx, пересекающиеся в точках A и B. Найдите абсциссу точки B.
Задание 10.
Помещение освещается тремя лампами. Вероятность перегорания каждой лампы в течение года равна 0,3. Лампы перегорают независимо друг от друга. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
ИЛИ
Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Задание 11.
Найдите точку минимума функции y = x√x – 5x + 4.
Задание 12.
а) Решите уравнение 4sin x + 4sin(x + π) = frac{5}{2}.
б) Найдите все корни этого уравнения, принадлежащие отрезку [frac{5pi}{2};4pi].
Задание 13.
Вне плоскости правильного треугольника ABC взята точка D так, что cos∠DAB = cos∠DAC = 0, 2.
а) Докажите, что прямые AD и BC перпендикулярны.
б) Найдите расстояние между прямыми AD и BC, если известно, что AB = 2.
Задание 14.
Решите неравенство frac{log_{2}^{}(32x)-1}{log_{2}^{2}x-log_{2}^{}x^{5}}ge -1
Задание 15.
15-го декабря планируется взять кредит размером 600 тыс. рублей в банке на 26 месяцев. Условия возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца с 1-го по 25-й долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца;
– к 15-му числу 26-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 25-го месяца, если общая сумма выплат после полного погашения кредита составит 691 тысяч рублей?
Задание 16.
В треугольник ABC вписана окружность, которая касается AB в точке P. Точка М середина стороны AB.
а) Докажите, что MP=frac{|BC-AC|}{2}.
б) Найдите углы треугольника ABC, если известно, что отрезок MP равен половине радиуса окружности вписанной в треугольник ABC, BC > AC, отрезки MC и MA равны.
Задание 17.
Найдите всe значения параметра a, при каждом их которых система
begin{cases} frac{xy^{2}-2xy-4y+8}{sqrt{4-y}}=0, y=ax. end{cases}
имеет ровно 3 различных решения.
Задание 18.
Каждое из четырех последовательных натуральных чисел поделили на его первую цифру и сложили все полученные числа, а полученную сумму обозначили за S.
а) Может ли S = 41frac{11}{24}?
б) Может ли S = 569frac{29}{72}?
в) Какое наибольшее целое значение может принимать S, если известно, что 4 исходных числа не меньше 400 и не больше 999?
Источники заданий варианта: школа Пифагора, Профиматика, беседы vk.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 12
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
Решу ЕГЭ
Автор 100balnik
ПОДЕЛИТЬСЯ
Новые тренировочные варианты в формате решу ЕГЭ 2022 по математике профильный уровень 11 класс для подготовки к экзамену, каждый вариант составлен по новой демоверсии ФИПИ ЕГЭ 2022 года, к тренировочным заданиям прилагаются правильные ответы и пояснения.
-
Тренировочный вариант №41054170 с ответами
-
Тренировочный вариант №41054171 с ответами
-
Тренировочный вариант №41054172 с ответами
-
Тренировочный вариант №41054173 с ответами
-
Тренировочный вариант №41054174 с ответами
-
Тренировочный вариант №41054175 с ответами
-
Тренировочный вариант №41054176 с ответами
-
Тренировочный вариант №41054177 с ответами
-
Тренировочный вариант №41054178 с ответами
-
Тренировочный вариант №41054179 с ответами
-
Тренировочный вариант №41054180 с ответами
-
Тренировочный вариант №41054181 с ответами
-
Тренировочный вариант №41054182 с ответами
-
Тренировочный вариант №41054183 с ответами
-
Тренировочный вариант №41054184 с ответами
Другие тренировочные варианты ЕГЭ 2022 по математике:
Тренировочные варианты ЕГЭ по математике 11 класс задания с ответами
Пробный вариант ЕГЭ 2022 №211004 по математике 11 класс с ответами
ЕГЭ 2023
Варианты ЕГЭ 2023 базового уровня
ЕГЭбаз 2023 №01-12
ЕГЭбаз 2023 №13-24 в VK по платной подписке
Задачники ЕГЭ 2023 базового уровня
Задание 01. Текстовые задачи (простейшие)
Задание 02. Размеры и единицы измерения
Задание 03. Графики и диаграммы
Задание 04. Преобразование выражений (формулы)
Задание 05. Теория вероятностей
Задание 06. Выбор оптимального варианта
Задание 07. Анализ графиков и таблиц
Задание 08. Анализ утверждений
Задание 09. Площадь
Задание 10. Прикладная планиметрия
Задание 11. Прикладная стереометрия
Задание 12. Планиметрия
Задание 13. Стереометрия
Задание 14. Действия с дробями
Задание 15. Текстовые задачи (проценты)
Задание 16. Вычисления и преобразования
Задание 17. Уравнения
Задание 18. Числа и неравенства
Задание 19. Цифровая запись числа
Задание 20. Текстовая задача
Внимание!
Скачивая материалы с этого сайта, Вы принимаете условия
Пользовательского Соглашения!
Варианты ЕГЭ 2023 профильного уровня
ЕГЭпроф 2023 №01-10
ЕГЭпроф 2023 №11-24 в VK по платной подписке
Задачники ЕГЭ 2023 профильного уровня
Задание 01. Планиметрия
Задание 02. Стереометрия
Задание 03. Теория вероятностей
Задание 04. Теория вероятностей (повыш. сложность)
Задание 05. Простейшие уравнения
Задание 06. Значение выражения
Задание 07. Производная и первообразная
Задание 08. Задачи с прикладным содержанием
Задание 09. Текстовые задачи
Задание 10. Функции
Задание 11. Исследование функций
Задание 12. Уравнения
Задание 13. Стереометрия
Задание 14. Неравенства
Задание 15. Финансовая математика
Задание 16. —-
Задание 17. —-
Задание 18. —-
ОТВЕТЫ к Задачникам ЕГЭ 2023 года
МАТЕРИАЛЫ прошлых лет (ЕГЭ АРХИВ)
Задание 21. Задачи на смекалку
Найденные материалы, документы, бумажные и электронные книги и файлы:
Ниже показаны результаты поиска поисковой системы Яндекс. В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.
Search results:
- Пробный эк за мен по базовой математике Санкт—Петербург…
Пробный экзамен по базовой математике Санкт—Петербург 05.04.2016. Вариант 1.
Если распилить палку по красным линиям, то получится 5 кусков, если по желтым ― 7 кусков, а если по зеленым ― 11 кусков. Сколько кусков получится, если рас пи лить палку по ли ни ям всех трех цветов? 2017-05-12.
mathb-ege.sdamgia.ru
- ЕГЭ–2023: задания, ответы, решения
Пробный экзамен по профильной математике Санкт—Петербург 05.04.2016.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом.
ege.sdamgia.ru
- Канцтовары
Канцтовары: бумага, ручки, карандаши, тетради.
Ранцы, рюкзаки, сумки.
И многое другое.my-shop.ru
- http://решуегэ.рф Пробный экзамен по математике…
Сколько кусков получится, если распилить палку по линиям всех трех цветов? http://решуегэ.рф Пробный экзамен по математике (база) в Санкт‐Петербурге 05.04.2016. Инструкция по выполнению работы. Экзаменационная работа включает в себя 20 заданий.
onlyege.ru
- Пробный эк за мен по базовой математике Санкт—Петербург…
Пробный экзамен по базовой математике Санкт—Петербург 05.04.2016. Вариант 1.
Если распилить палку по красным линиям, то получится 5 кусков, если по желтым ― 7 кусков, а если по зеленым ― 11 кусков. Сколько кусков получится, если рас пи лить палку по ли ни ям всех трех цветов? 2017-05-12.
ege.sdamgia.ru
- Пробный экзамен Санкт—Петербург 05.04.2016. Вариант 1.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
mathb-ege.sdamgia.ru
- Пробный экзамен Санкт—Петербург 05.04.2016. Вариант 2.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
mathb-ege.sdamgia.ru
- http://решуегэ.рф Пробный экзамен по математике…
Сколько кусков получится, если распилить палку по линиям всех трех цветов? http://решуегэ.рф Пробный экзамен по математике (база) в Санкт‐Петербурге 05.04.2016. Инструкция по выполнению работы. Экзаменационная работа включает в себя 20 заданий.
alexlarin.net
- ЕГЭ–2023: задания, ответы, решения
Пробный экзамен по профильной математике Санкт—Петербург 05.04.2016.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом.
ege.sdamgia.ru
- Пробный ЕГЭ по математике базовый в Санкт‐Петербурге 2016
10 тренировочные варианты итогового собеседования 2022 russkiykim.ru. Новые тренировочные варианты ВПР 2022 по математике 4 класс.
Видео уроки. ВАЖНО! Никаких реальных вариантов ЕГЭ ни до экзамена, ни во время его проведения на сайте нет, не было и не будет.
onlyege.ru
- Пробные варианты 1-2 г. С-Петербург Профиль
Пробные варианты 1-2 г. С-Петербург Профильный уровень. Скачать документ в формате pdf. Обсуждение на форуме… Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2 cодержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий высокого уровня сложности с развёрнутым ответом. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
alexlarin.net
- 23348 — Реальный вариант ЕГЭ (профильного уровня)…
Это огромная база вариантов ЕГЭ, ОГЭ(ГИА), олимпиад, вступительных экзаменов и других заданий по математике с такими возможностями, как просмотр ответов, решений и видеоразборов. Реальный вариант ЕГЭ (профильного уровня) № АПРОБАЦИЯ по математике из СПБ от 5 апреля 2016 года.
Yagubov.ru
- Пробный Единый государственный экзамен ЕГЭ по…
Пробный Единый государственный экзамен ЕГЭ по математике профиль в Санкт‐Петербурге 05.04.2016 два варианта с ответами.
vuz-24.ru
- 00008 — Пробный вариант ЕГЭ (профильного уровня) по…
Это огромная база вариантов ЕГЭ, ОГЭ(ГИА), олимпиад, вступительных экзаменов и других заданий по математике с такими возможностями, как просмотр ответов, решений и видеоразборов. Пробный вариант ЕГЭ (профильного уровня) по математике из Питера от 5 апреля 2016 года.
Yagubov.ru
- Пробный экзамен по математике (профиль) в Санкт—Петербурге…
ЕГЭ по математике профильный уровень. математика егэ профильный уровень варианты.
Никаких реальных вариантов ЕГЭ ни до экзамена, ни во время его проведения на сайте нет, не было и не будет.
onlyege.ru
- Пробный ЕГЭ по математике профиль в Санкт‐Петербурге 2016
Видео уроки по биологии Демовариант ЕГЭ 2018.
31 мая, 2017 Математика варианты Комментарии: 0. Пробный ЕГЭ по математике профиль в Санкт‐Петербурге 05.04.2016 два варианта с ответами.
Никаких реальных вариантов ЕГЭ ни до экзамена, ни во время его проведения на сайте нет, не было и не будет.
onlyege.ru
- Пробный экзамен по математике (база) в Санкт‐Петербурге…
ЕГЭ по математике базовый уровень. математика егэ базовый уровень варианты.
Никаких реальных вариантов ЕГЭ ни до экзамена, ни во время его проведения на сайте нет, не было и не будет.
onlyege.ru
- Пробный экзамен по математике (профиль) в Санкт—Петербурге…
б) Могло ли получиться так, что исходно процент учеников, понявших доказательство, выражался целым числом, а после перемены ― нецелым числом? в) Какое наибольшее целое значение может принять процент учеников класса, так и не понявших доказательство этой теоремы? http://решуегэ.рф Пробный экзамен по математике (профиль) в Санкт—Петербурге 05.04.2016.
kvantor.ucoz.ru
- Пробный эк за мен по базовой математике Санкт—Петербург…
Пробный экзамен по базовой математике Санкт—Петербург 05.04.2016. Вариант 1.
Если распилить палку по красным линиям, то получится 5 кусков, если по желтым ― 7 кусков, а если по зеленым ― 11 кусков. Сколько кусков получится, если рас пи лить палку по ли ни ям всех трех цветов? 2017-05-12.
soc-ege.sdamgia.ru
- ЕГЭ 2016. Математика. Пробный экзамен в Санкт‐Петербурге…
Источник: Интернет. — 9 с. Подборка материалов содержит задания пробного экзамена по математике (база) в Санкт‐Петербурге 05.04.2016. Ко всем заданиям прилагаются правильные ответы.
www.studmed.ru
- ЕГЭ 2016. Математика. Пробный экзамен в Санкт‐Петербурге…
Источник: Интернет. — 9 с. Подборка материалов содержит задания пробного экзамена по математике (база) в Санкт‐Петербурге 05.04.2016. Ко всем заданиям прилагаются правильные ответы.
www.studmed.ru
- ЕГЭ–2023, математика: задания, ответы, решения
Тысячи заданий с решениями для подготовки к ЕГЭ–2023 по всем предметам.
Скачать. 1 февраля. Бесплатные курсы подготовки к ЕГЭ и ОГЭ.
Пробный экзамен Санкт—Петербург 2016. Вариант 1 .
math-ege.sdamgia.ru
- ЕГЭ–2023, математика базовый уровень: задания, ответы, решения
ПРОБНЫЕ ЭКЗАМЕНЫ. Пробный экзамен Санкт—Петербург, 11.04.2017. Вариант 1 . Пробный экзамен Санкт—Петербург, 11.04.2017. Вариант 2 . 2015—2016 УЧЕБНЫЙ ГОД. Демонстрационная версия ЕГЭ по базовой математике 2016 года с решениями. ЭКЗАМЕНАЦИОННЫЕ ВАРИАНТЫ.
mathb-ege.sdamgia.ru
- ЕГЭ–2023: задания, ответы, решения
Тысячи заданий с решениями для подготовки к ЕГЭ–2023 по всем предметам.
ЕГЭ по математике 29.05.2019. Основная волна. Санкт—Петербург.
Пробный экзамен Санкт—Петербург, 11.04.2017. Вариант 2. Типовые тестовые задания по математике под редакцией И. В. Ященко, 2017.
Пробный экзамен Санкт—Петербург 2015. Кировский район.
ege.sdamgia.ru
- ПРОБНЫЕ ВАРИАНТЫ , ДОСРОЧНЫЕ | ВКонтакте
Пробный экзамен по математике (профиль ) в Санкт‐Петербурге 5 апреля 2016 год два варианта с ответами. Пробный ЕГЭ Санкт—Петербург профиль.pdf.
vk.com
- Варианты реальных и пробных ЕГЭ прошлых лет — math100.ru
Варианты реальных и пробных ЕГЭ 2020-2021 учебного года. Демо вариант профильного ЕГЭ по математике 2021 года. Варианты пробного ЕГЭ Санкт—Петербург.
Все материалы получены из открытых источников и публикуются после экзамена в ознакомительных целях.
math100.ru
- Задание 15 из пробного варианта 05.04.2016, С-Петербург
04 Задание (2016). 05 Задание (2022).
ЕГЭ-ТРЕНЕР, видеоуроки по математике Ольги Себедаш. ЕГЭ-Студия: подготовка к ЕГЭ и олимпиадам. Математика? Легко!!! Репетитор по математике. Подготовка к ЕГЭ и ДВИ в МГУ. Простая физика — сайт Анны Денисовой. EgeMaximum — сайт Елены Репиной.
ege-ok.ru
- ЕГЭ–2023, математика: задания, ответы, решения
Единицы измерений писать не нужно. Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом.
Источник: Пробный экзамен по профильной математике Санкт—Петербург 05.04.2016. Вариант 1., ЕГЭ — 2017. Основная волна 02.06.2017.
math-ege.sdamgia.ru
- Пробные работы ЕГЭ по математике
Математика, Физика, Информатика, Химия, Русский, Обществознание, Литература, История, Иностранные языки, География, Биология. 11 февраля 2023. 3 варианта ЕГЭ по математике. 9 февраля 2023. Задача №5 базового ЕГЭ по математике.
4ege.ru
- Пробник ЕГЭ ПО МАТЕМАТИКЕ Профильный г. С-Петербург…
№15 пробного ЕГЭ по математике от 04 апреля 2018 года, город Санкт—Петербург, вариант 1. Логарифмическое неравенство. 10 тренировочные варианты итогового собеседования 2022 russkiykim.ru. Новые тренировочные варианты ВПР 2022 по математике 4 класс. Реальные варианты ОГЭ по русскому языку. Решения демоверсии ЕГЭ по информатике 2022 год.
onlyege.ru
- Пробные варианты ЕГЭ (профильного уровня) по математике…
Это огромная база вариантов ЕГЭ, ОГЭ(ГИА), олимпиад, вступительных экзаменов и других заданий по математике с такими возможностями, как просмотр ответов, решений и видеоразборов. Пробные варианты ЕГЭ (профильного уровня) по математике.
Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене! При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой.
Yagubov.ru
- ЕГЭ–2023: задания, ответы, решения
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом.
Источник: Пробный экзамен Санкт—Петербург, 11.04.2017. Вариант 1. Кодификатор ФИПИ/Решу ЕГЭ: 5.1.5 Вписанная и описанная окружность треугольника, 5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника.
ege.sdamgia.ru
- ЕГЭ–2023, математика базовый уровень: задания, ответы, решения
Единицы измерений писать не нужно. Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом.
Источник: Пробный экзамен Санкт—Петербург 2014. Вариант 1., Апробация базового ЕГЭ по математике, 13—17 октября: вариант 166081., Пробный экзамен Саратов 2016.
mathb-ege.sdamgia.ru
На данной странице Вы можете найти лучшие результаты поиска для чтения, скачивания и покупки на интернет сайтах материалов, документов, бумажных и электронных книг и файлов похожих на материал «ЕГЭ 2016, Пробный экзамен по математике в Санкт-Петербурге, 05.04.2016»
Для формирования результатов поиска документов использован сервис Яндекс.XML.
Нашлось 5 млн ответов. Показаны первые 32 результата(ов).
Дата генерации страницы: воскресенье, 26 февраля 2023 г., 14:19:25 GMT