Задания
Версия для печати и копирования в MS Word
Установите соответствие между названиями политических партий и фамилиями их руководящих деятелей весной — летом 1917 г.
ФАМИЛИИ
1) В. И. Ленин
2) П. Н. Милюков
3) А. И. Гучков
4) В. М. Чернов
5) Л. Мартов (Ю. О. Цедербаум)
ПАРТИИ
A) эсеры
Б) меньшевики
B) большевики
Г) кадеты
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Спрятать пояснение
Пояснение.
А) Лидером партии эсеров был В. М. Чернов.
Б) Лидером меньшевиков был Л. Мартов (Ю. О. Цедербаум).
В) В. И. Ленин — лидер партии большевиков.
Г) П. Н. Милюков — лидер партии кадетов.
Лишнее: А. И. Гучков — лидер партии октябристов.
Ответ: 4512.
Задание 1
Решите уравнение $$11^{79}cdot(frac{1}{11})^xcdot(frac{1}{11})^{sqrt{x+11}}=1$$
Ответ: 70
Скрыть
$$79−x−sqrt{x+11}=0$$
$$sqrt{x+11}=79−x$$
ОДЗ: $$x<79$$
Возводим в квадрат
$$x+11=(79−x)^2$$
$$x^2−159x+6230=0$$
$$x=89$$ – не подходит под ОДЗ
$$x=70$$
Задание 2
Найдите вероятность того, что случайно выбранное трехзначное число делится на 34.
Ответ: 0,03
Скрыть
Всего трехзначных чисел $$900$$
Из них на $$34$$ делятся $$102, 136, 170, 204,…,986 (=34cdot3, 34cdot4, 34cdot5,…)$$ – всего их $$27$$ штук $$([900/34]=27)$$
$$P(A)=frac{27}{900}approx0,03$$
Задание 3
Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 4 : 7 : 9. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 338.
Ответ: 117
Скрыть
Пусть $$y$$ – неизвестная сторона
Одно из свойств описанного четырехугольника это суммы противоположных сторон равны друг другу
$$4x+9x=7x+y$$
$$6x=y$$
$$x=frac{y}{6}$$
$$P=4x+7x+9x+y=338$$
$$20x+y=338$$
$$20x+6x=338$$
$$x=13$$
Большая сторона $$9x=117$$
Задание 4
Вычислите $$sin555^{circ}cdotsin1185^{circ}cdottg405^{circ}.$$
Ответ: -0,25
Скрыть
$$sin555°=sin(180°cdot3+15°)=−sin15°$$
$$sin1185°=sin(180°cdot6+105°)=sin105°=sin(90°+15°)=cos15°$$
$$tg405°=tg(360°+45°)=tg45°$$
$$−sin15°cdotcos15°cdottg45°=−0,5sin30°cdot1=−0,25$$
Задание 5
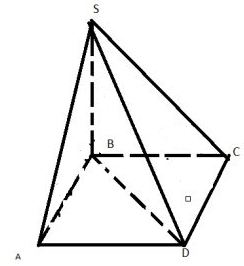
В основании пирамиды лежит прямоугольник. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы $$30^{circ}$$ и $$45^{circ}$$. Найдите диагональ прямоугольника, если высота пирамиды равна 4.
Ответ: 8
Скрыть
$$SB⟂(ABCD)$$
$$BC$$ – проекция $$SC$$ на $$ABCD$$
$$BC⟂DC$$ (т.к прямоугольник)
Значит по теореме о 3-х перпендикулярах $$SC⟂DC$$, значит $$∠BCS$$ – есть линейный угол двугранного угла $$∠SBCD$$
Аналогично с $$∠ABS$$
Пусть $$∠BCS=45$$ и $$∠ABS=30$$
$$△SBC$$ – прямоугольный и р/б значит $$BC=SB=4$$
$$AB=frac{SB}{tg30}=4sqrt{3}$$
$$BD=sqrt{AB^2+BC^2}=8$$
Задание 6
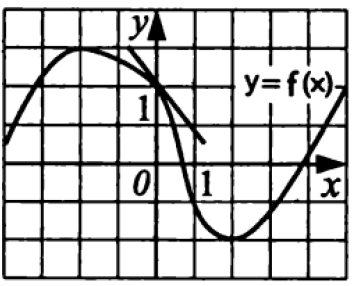
На рисунке изображены участки графика функции $$y=f(x)$$ и касательной к нему в точке с абсциссой $$x=0.$$ Известно, что данная касательная параллельна прямой, проходящей через точки графика с абсциссами $$x=-2$$ и $$x=2$$. Используя это, найдите значение производной $$f'(0)$$.
Ответ: -1,25
Скрыть
Если две прямые параллельные, то их угловые коэффициенты равны.
По геометрическому смыслу производной $$tgα=k$$
$$tgα=tg(180−β)=−tgβ$$
$$tgβ=frac{5}{4}=1,25Rightarrow -1,25$$
Задание 7
Автомобиль, масса которого равна $$m = 1200$$ кг, начинает двигаться с ускорением, которое в течение $$t$$ секунд остается неизменным, и проходит за это время путь $$S = 300$$ метров. Значение силы (в ньютонах), приложенное в это время к автомобилю, можно вычислить по формуле по формуле $$F = frac{2mS}{t^2}$$. Определите наибольшее время после начала движения автомобиля, за которое он пройдет указанный путь, если известно, что сила $$F$$, приложенная к автомобилю, не меньше 1800 Н. Ответ выразите в секундах.
Ответ: 20
Скрыть
$$frac{2cdot1200cdot300}{t^2}geq1800$$
$$t^2leq400$$
$$−20leq tleq 20$$
Наибольшее время $$t=20$$
Задание 8
Готовясь к олимпиаде по математике, школьник за 10 недель прорешал 700 задач. Приобретая опыт, он в каждую последующую неделю, начиная со второй, решал на 10 задач больше, чем в предыдущую. Какое количество задач успеет прорешать школьник за остающиеся до олимпиады 4 недели, если будет увеличивать количество еженедельно решаемых задач прежним образом?
Ответ: 560
Скрыть
Из условия понятно, что задача на арифметическую прогрессию.
$$d=10$$
$$S_{10}=frac{2a_1+10cdot9}{2}cdot10=700$$
$$a_1=25$$
$$S_{14}=frac{2cdot25+10cdot13}{2}cdot14=1260$$
$$S_{14}−S_{10}=560$$
Задание 9
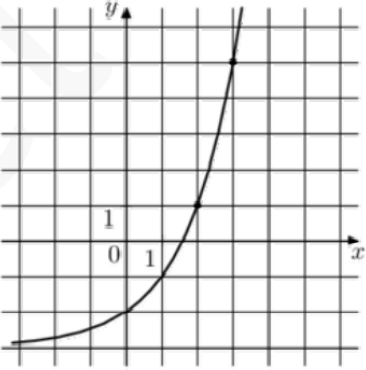
На рисунке изображен график функции $$f(x)=a^{x+b}$$. Найдите $$f(6)$$.
Ответ: 61
Скрыть
Из рисунка видно, какие точки удобнее всего взять
$$1=a^2+b$$
$$5=a^3+b$$
Вычтем одно из другого
$$a^3−a^2=4$$
$$a(a^2−a)=4$$, очевидно, что $$a=2$$
Значит, $$b=3$$
$$f(x)=2^x−3$$
$$f(6)=61$$
Задание 10
Васе нужно забить в дубовую доску гвоздь. Если гвоздь стальной, то он согнется с вероятностью 0,1, а если гвоздь медный, то он согнется с вероятностью 0,3. На столе вперемешку лежат 6 стальных и 4 медных гвоздя. Вася берет первый попавшийся гвоздь со стола и пытается забить его в доску. Найдите вероятность того, что этот гвоздь не согнется.
Ответ: 0,82
Скрыть
События:
$$A_1$$ — достанет стальной гвоздь и он не согнется
$$A_2$$ - достанет медный гвоздь и он не согнется
Они несовместные, значит
$$P(A)=P(A_1+A_2)=P(A_1)+P(A_2)$$
$$P(A_1)=frac{6}{10}cdot0,9=0,54$$
$$P(A_2)=frac{4}{10}cdot0,7=0,28$$
$$P(A)=0,54+0,28=0,82$$
Задание 11
Найдите наибольшее значение функции $$y=frac{3x-pi}{pi}cdotcos x-frac{3}{pi}cdotsin x+21$$ на отрезке $$[0;2pi]$$
Ответ: 26
Скрыть
Найдём критические точки $$y’=0$$
$$frac{3}{π}cdotcos x−frac{3x−π}{π}cdotsin x−frac{3}{π}cos x=0$$
$$−frac{3x−π}{π}cdotsin x=0$$
$$sin x=0x=πn$$
$$x=frac{π}{3}$$
Так как отрезок $$[0;2pi]$$, то подозрительные точки:
$$x=0,frac{π}{3},π,2π$$
Проверяем все.
$$y(2π)=26$$
Задание 12
А) Решите уравнение $$sqrt{3}sin^2 2x-2sin 4x+sqrt{3}cos^2 2x=0$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[-1; 1]$$
Ответ: А)$$frac{pi}{12}+frac{pi n}{2};frac{pi}{6}+frac{pi n}{2},nin Z$$ Б)$$frac{pi}{12};frac{pi}{6}$$
Задание 13
Дана правильная шестиугольная призма $$ABCDEFA_1В_1С_1D_1E_1F_1$$ со стороной основания $$sqrt{3}$$ и боковым ребром $$1$$.
а) Докажите, что плоскости $$АСА_1$$ и $$В_1СЕ_1$$ перпендикулярны.
б) Найдите угол между плоскостями $$В_1СЕ_1$$ и $$АВС$$.
Ответ: $$arctgfrac{2}{3}$$
Задание 14
Решите неравенство: $$(x-1)(2log_3^2 x-5log_3 x+2)<0$$
Ответ: $$(0;1),(sqrt{3};9)$$
Задание 15
Билл несколько лет назад вложил деньги в акции некоего предприятия. Ежегодно он получал прибыль по акциям сначала $$9frac{1}{11}%$$ в год, потом $$37,5%$$ в год и, наконец, $$6frac{2}{3}%$$ в год и сразу же вкладывал деньги в те же акции. Известно, что одинаковые процентные ставки сохранялись равное число лет, в результате стоимость акций увеличилась на $$156%$$. Определите, сколько лет Билл получал прибыль по акциям.
Ответ: 6
Задание 16
Диагонали АС и BD трапеции ABCD пересекаются в точке О, ВС и AD — основания трапеции.
a) Докажите, что $$frac{S_{Delta ABO}}{S_{Delta AOD}}=frac{BC}{AD}$$.
б) Найдите площадь трапеции, если $$AD=4BC, S_{Delta AOB}=2$$.
Ответ: 12,5
Задание 17
Найдите все значения параметра $$a$$, при каждом из которых уравнение:
$$frac{a}{25^x}-a=2-frac{25^{-2x}}{5}$$
имеет ровно 2 корня, хотя бы один из которых не менее 0,5.
Ответ: $$[-2,49;-2)$$
Задание 18
Натуральные числа от $$1$$ до $$n$$ в порядке возрастания записаны в строчку. Под ними записаны те же числа в другом порядке. Можно ли добиться того, что сумма каждого числа и записанного под ним была бы точным квадратом:
а) при $$n = 7$$;
б) при $$n = 12$$;
в) при $$n = 2015$$?
Ответ: А) нет, Б) да, В) да
Задания ЕГЭ по истории. Практика
Решать задания ЕГЭ по истории.
Решать задание 1 ЕГЭ по истории : соответствие между событиями и годами
Решать задание 2 ЕГЭ по истории : исторические события в хронологической последовательности
Решать задание 3 ЕГЭ по истории : соответствие между событиями (процессами, явлениями) и фактами
Решать задание 5 ЕГЭ по истории : соответствие между событиями и участниками этих событий
Решать задание 7 ЕГЭ по истории : соответствие между памятниками культуры и их краткими характеристиками
Решать задания 12, 13 ЕГЭ по истории : работа с историческими источниками
Решать задания 14, 15 ЕГЭ по истории : работа с изображением
Решать задание 17 ЕГЭ по истории : установите причинно-следственные связи
Решать задание 18 ЕГЭ по истории : раскройте смысл понятия
Решать задание 19 ЕГЭ по истории : аргументация
Задание 19 ЕГЭ по истории: аргументация. Практика
1-07-2022, 17:52
- 1-07-2022, 17:52
- ЕГЭ по истории / Задания ЕГЭ по истории. Практика
- adminn
- 2 779
- 0
Подробнее
Задание 18 ЕГЭ по истории: раскройте смысл понятия. Практика
1-07-2022, 17:44
- 1-07-2022, 17:44
- ЕГЭ по истории / Задания ЕГЭ по истории. Практика
- adminn
- 2 844
- 0
Подробнее
Задание 17 ЕГЭ по истории: установите причинно-следственные связи. Практика
1-07-2022, 16:56
- 1-07-2022, 16:56
- ЕГЭ по истории / Задания ЕГЭ по истории. Практика
- adminn
- 2 266
- 0
Подробнее
Задания 14, 15 ЕГЭ по истории: работа с изображением. Практика
1-07-2022, 16:25
- 1-07-2022, 16:25
- ЕГЭ по истории / Задания ЕГЭ по истории. Практика
- adminn
- 4 813
- 0
Подробнее
Задания 12, 13 ЕГЭ по истории: работа с источником. Практика
1-07-2022, 15:54
- 1-07-2022, 15:54
- ЕГЭ по истории / Задания ЕГЭ по истории. Практика
- adminn
- 17 657
- 0
Подробнее
Задание 7 ЕГЭ по истории. Установите соответствие между памятниками культуры и их краткими характеристиками.
23-06-2022, 15:43
- 23-06-2022, 15:43
- ЕГЭ по истории / Задания ЕГЭ по истории. Практика
- adminn
- 14 582
- 0
Подробнее
Задание 5 ЕГЭ по истории. Установите соответствие между событиями и участниками этих событий.
23-06-2022, 12:14
- 23-06-2022, 12:14
- ЕГЭ по истории / Задания ЕГЭ по истории. Практика
- adminn
- 8 222
- 0
Подробнее
Задание 3 ЕГЭ по истории. Установите соответствие между процессами (явлениями, событиями) и фактами.
13-06-2022, 18:09
- 13-06-2022, 18:09
- ЕГЭ по истории / Задания ЕГЭ по истории. Практика
- adminn
- 17 099
- 0
Подробнее
Задание 2 ЕГЭ по истории. Расположите в хронологической последовательности исторические события.
6-06-2022, 10:00
- 6-06-2022, 10:00
- ЕГЭ по истории / Задания ЕГЭ по истории. Практика
- adminn
- 24 297
- 1
Подробнее
Задание 1 ЕГЭ по истории. Установите соответствие между событиями и годами.
6-06-2022, 09:44
- 6-06-2022, 09:44
- ЕГЭ по истории / Задания ЕГЭ по истории. Практика
- adminn
- 10 903
- 0
Подробнее