Время на прочтение
3 мин
Количество просмотров 8.6K
Мы уже анонсировали читателям Хабра набор на магистерскую программу «Разработка программного обеспечения / Software Engineering» на базе Университета ИТМО. Первый этап вступительных испытаний на программу — онлайн тест. И для того, чтобы помочь нашим абитуриентам к нему подготовиться, мы решили опубликовать разбор нескольких математических задач из прошлогоднего варианта.
Задача 1
Решите в натуральных числах уравнение:
.
В ответе укажите максимально возможное значение произведения
и
.
Давайте перенесём единицу в правую часть и применим формулу разности квадратов.
Степень двойки делится только на степени двойки. Поэтому нас интересуют такие
, при которых
и
одновременно являются степенями двойки. При
получаем значения
и
соответственно. Значений больше быть не может, т.к. расстояние между степенями двойки возрастает. Таким образом, получаем
и
. Ответ
.
Задача 2
Чему равен предел последовательности
?
В ответе укажите число. При необходимости оставьте три знака после запятой без округления.
Выделим замечательный предел:
Предел первого множителя вычисляется по формуле замечательного предела:
Предел второго множителя очевиден:
(Если нужно более формальное доказательство, то можно раскрыть скобки и заметить, что при все слагаемые, кроме 1, стремятся к нулю.) Итак, оба предела существуют, следовательно
Задача 3
Упростите сумму:
В ответе укажите число. При необходимости оставьте три знака после запятой без округления.
Представим этот знакопеременный ряд как разность двух положительных последовательностей:
По формуле суммы бесконечной убывающей геометрической последовательности получаем:
Заметим, что , т.е. этот ряд является абсолютно сходящимся. Следовательно, мы можем вычислить его сумму, как разность
и
:
Задача 4
Двадцать пять человек выбирают числа, каждый наугад выбирает число от
до
независимо друг от друга. Далее участники объявляют выбранные номера по очереди (и делают это честно). Первый (если такой человек есть), кто объявляет номер, который уже был объявлен, получает приз.
Какой человек по счету имеет наибольшую вероятность выиграть приз?
Оценим вероятность того, что -ый человек получает приз: он получает приз в том случае, если предыдущие
участников назвали различные числа, а он — одно из предыдущих
чисел. Вероятность назвать одно из прозвучавших
чисел равна
Для участника с номером вероятность назвать число, которое ещё не прозвучало, равна
Тогда искомая вероятность равна:
Осталось вычислить это значения для всех и найти минимум. Это можно сделать небольшим скриптом, табличкой в Excel или через WolframAlpha:
{0, 0.01, 0.0198, 0.029106, 0.0376438, 0.0451725, 0.0514967, 0.0564747, 0.0600245, 0.0621254, 0.0628157, 0.0621875, 0.0603784, 0.0575607, 0.05393, 0.0496926, 0.0450547, 0.0402113, 0.0353386, 0.0305875, 0.0260799, 0.0219071, 0.0181307, 0.0147848, 0.0118793}
Отсюда получаем (максимум достигается на одиннадцатом элементе списка
).
Задача 5
Каждый из девяти единичных квадратов
-квадрата случайным образом окрашен в красный или синий цвет с вероятностью
. Определите вероятность того, что ни один из четырёх квадратов
не является полностью красным.
В ответе укажите число. При необходимости оставьте три знака после запятой без округления.
В квадрате есть 4 различный квадрата
. Назовём их
,
,
и
.
Обозначим этими же буквами события, что в соответствующем квадрате все ячейки окрашены красным. Тогда
Для начала вычислим вероятность обратного события — вероятность того, что один из квадратов является полностью красным . Для того, чтобы её вычислить, воспользуемся формулой включений-исключений:
Искомая вероятность, что ни один из четырёх квадратов не является полностью красным, равна
Задача 6
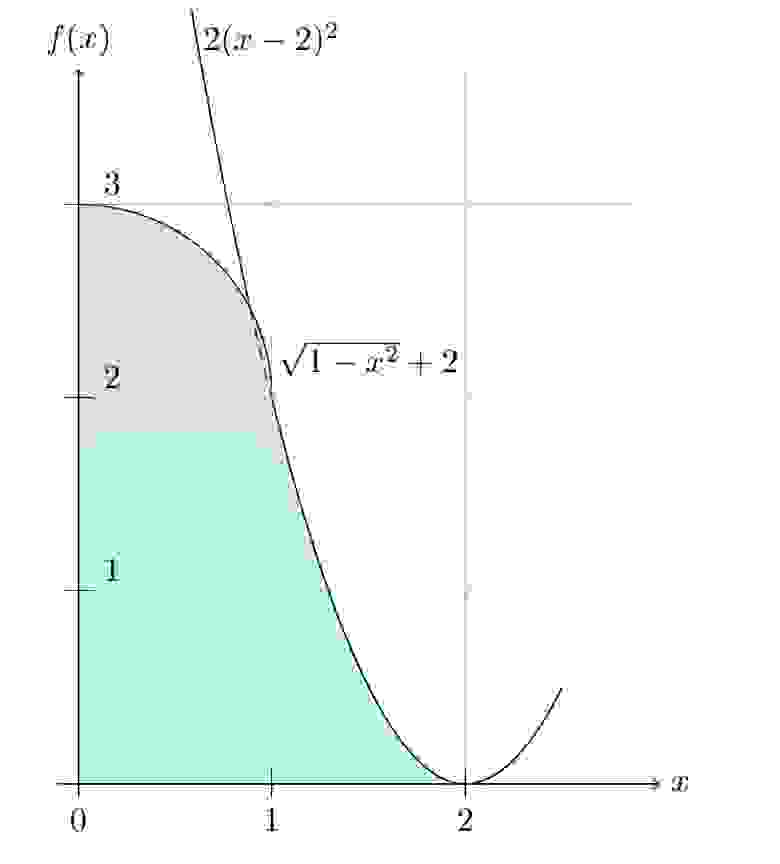
Вычислите объём фигуры вращения, образованной выделенной областью при вращении относительно вертикальной оси.
В ответе укажите число. При необходимости оставьте три знака после запятой без округления.
В нашем случае задача упрощается тем, что верхняя часть фигуры вращения — это половинка шара радиуса 1. Поэтому объём верхней части можно выписать сразу — он равен (объём сферы вычисляется по формуле
).
Осталось разобраться с нижней частью, ограниченной параболой . Объём фигуры вращения можно вычислить, если разбить объём на цилиндры маленькой высоты. Объём цилиндра равен произведению площади основания (
) на высоту. Соответственно, нам нужно получить зависимость радиуса (роль радиуса играет
) от высоты (от
).
На интересует случай , поэтому
. Объём нижней части фигуры можно выразить следующим интегралом:
Итого, в сумме получаем .
Заключение
Надеемся, что этот разбор поможет абитуриентам подготовиться к онлайн- тесту.
В этом году он состоит из 12 задач, на которые мы выделяем 2 часа. Стоит учесть, что помимо математических, в нём есть и задачи на программирование. Весь процесс поступления и подробности о следующих этапах описаны на сайте магистерской программы. Если у вас остались вопросы, кураторы с радостью ответят на них по почте или в телеграм канале.
Вступительный экзамен при поступлении в магистратуру
Информация по времени и месту проведения вступительного экзамена обновляется.
Экзамен проходит следующим образом: поступающий вытягивает билет, который состоит из двух вопросов (перечень доступен по ссылке). Ответ на оба вопроса необходимо тезисно подготовить в письменном виде в течение 25 минут, после чего полный ответ предоставляется комиссии в устном виде. Каждый вопрос оценивается по следующей шкале: «5» — 50 баллов; «4» — 37,5 баллов; «3» — 25 баллов; «2» — 12,5 или 0 баллов. В сумме за два ответа могут быть следующие варианты оценок 100; 87,5; 75; 62,5; 50; 37,5; 25; 12,5.
Результаты экзамена объявляются в течение двух дней и вывешиваются на сайте http://abit.ifmo.ru/master/rating_rank/160401/.
Вопросы из списка затрагивают темы из оптики, электроники и программирования. Рекомендуемый список литературы при подготовке к экзамену:
- Серебрякова В.С., Стригалев В.Е., Пашин В.Ф. Интегральная оптика: учебное пособие. — Санкт-Петербург: Университет ИТМО, 2012. — 87 с.
- Удд Э. Волоконно-оптические датчики. Вводный курс для инженеров и научных работников. Москва: Техносфера, 2008. -520 с.
- С.В. Варжель, Волоконные брэгговские решетки. – СПб: Университет ИТМО, 2015. – 65 с
- Джонс М.Х. Электроника — практический курс. 2-е издание, исправленное. — Москва: Техносфера, 2006. — 512 с.
- Плоткин М.А., Шарков И.А., Дейнека И.Г. Методическое руководство для проведения цикла лабораторных работ по курсу сети связи и системы коммутации: Учебно-методическое пособие. — Санкт-Петербург: Университет ИТМО, 2016. — 90 с. — 90 экз.
- Хэррис Д.М., Хэррис С.Л. Цифровая схемотехника и архитектура компьютера, 2013.
Если у Вас возникли вопросы, их можно задать нашим сотрудникам:
 |
Залесская Юлия https://vk.com/id51172410 ikzalesskaia@itmo.ru |
 |
Смирнов Даниил https://vk.com/smirnov_dany dsmirnov@itmo.ru |
 |
Новикова Виктория https://vk.com/novivial novivial@mail.ru |
Для студентов НИУ ИТМО по предмету Энергоэффективные инженерные системы и технологии СПГОтветы на вопросы к вступительным экзаменам в магистратуру ИТМО Энергоэффективные инженерные системы и технологии СПГОтветы на вопросы к вступительным экзаменам в магистратуру ИТМО Энергоэффективные инженерные системы и технологии СПГ
2022-07-052022-07-05СтудИзба
Ответы: Ответы на вопросы к вступительным экзаменам в магистратуру ИТМО Энергоэффективные инженерные системы и технологии СПГ
Описание
Развернутые ответы на вопросы 10-30 к вступительным экзаменам в магистратуру ИТМО «Энергоэффективные инженерные системы и технологии СПГ».
Характеристики ответов (шпаргалок)
Список файлов
-
Ответы.docx 1,63 Mb
Комментарии
Сопутствующие материалы
Свежие статьи
Популярно сейчас
Зачем заказывать выполнение своего задания, если оно уже было выполнено много много раз? Его можно просто купить или даже скачать бесплатно на СтудИзбе. Найдите нужный учебный материал у нас!
Ответы на популярные вопросы
То есть уже всё готово?
Да! Наши авторы собирают и выкладывают те работы, которые сдаются в Вашем учебном заведении ежегодно и уже проверены преподавателями.
А я могу что-то выложить?
Да! У нас любой человек может выложить любую учебную работу и зарабатывать на её продажах! Но каждый учебный материал публикуется только после тщательной проверки администрацией.
А если в купленном файле ошибка?
Вернём деньги! А если быть более точными, то автору даётся немного времени на исправление, а если не исправит или выйдет время, то вернём деньги в полном объёме!
Отзывы студентов
Добавляйте материалы
и зарабатывайте!
Продажи идут автоматически
652
Средний доход
с одного платного файла
Обучение Подробнее
Занимательные задачки, Математика, Блог компании Образовательные проекты JetBrains
Рекомендация: подборка платных и бесплатных курсов таргетированной рекламе — https://katalog-kursov.ru/
Несколько слов о том, как устроен тест. Абитуриенты получают ссылку на закрытый курс на платформе Stepik.org. Далее у них есть несколько недель на то, чтобы приступить к решению. Тест состоит из 12 задач, на них отводится два часа. Решать задачи можно в произвольном порядке, за каждую из них начисляется один балл. Проходной балл меняется от года к году. В этот раз он был довольно низким — задачи получились сложные. Кураторы программы сделали выводы и постараются к следующему набору подготовить задачи полегче.
Задача 1
Найдите уравнение касательной к кривой
в точке
. Ответ запишите в виде
, где
— целые несократимые числа и
(без пробелов и скобок), например,
.
Когда в задаче спрашивается про касательную к графику функции, то это почти всегда связанно с вычислением производной. В данном случае требуется найти производную для неявно заданной функции. Будем считать, что
— это функция от
. Продифференциируем обе части равенства
по
. Получаем
Это позволяет выразить производную
через
и
.
Теперь можно вычислить значение производной
в точке
. Обозначим это значение
.
Это значение задаёт тангенс угла наклона касательной к кривой в точке
. Осталось вспомнить, что уравнение прямой можно задать в виде
. Зная, что прямая должна проходить через точку
, мы можем вычислить
:
Следовательно,
. Получаем, что уравнение искомой прямой имеет вид:
Приводим его к требуемой форме домножив на 21 и получаем:
Задача 2
На плоскости нарисованы две кривые, заданные многочленами второй степени.
Найдите площадь замкнутой области, которая ограничена этими кривыми. Если такой области нет, то нужно вывести число 0.
Вход
На первой строке три целых числа
,
,
, задающие первую кривую
, на второй строке — три целых числа
,
и
, задающие кривую
. Все числа по модулю не превосходят
.
Выход
Площадь замкнутой области, ограниченная
и
.
Ответ должен быть вычислен с точностью 5 знаков после запятой.
Это задача на программирование, но с некоторой математической составляющей. Чтобы вычислить площадь искомой области, можно вычислить площадь под графиками функций
и
на отрезке между точками пересечения и вычесть одну из другой. Можно поступить проще: сразу рассматривать функцию
и вычислить площадь под графиком этой функции между её корнями. Это немного упростит задачу. Предлагается следующий алгоритм:
- вычисляем коэффициенты
,
- проверяем, что получился квадратный многочлен (
), и что он имеет два различных корня (дискриминант больше нуля), если нет — возвращаем ноль,
- вычисляем корни
и
,
- вычисляем площадь под графиком
между
и
,
- возвращаем модуль этого значения, т.к. при
интеграл будет отрицательным.
Далее идёт реализация этого алгоритма на Питоне
# считываем коэффициенты f(x) и g(x)
a1, b1, c1 = map(int, raw_input().split())
a2, b2, c2 = map(int, raw_input().split())
# вычисляем коэффициенты h(x)
a = a1 - a2
b = b1 - b2
c = c1 - c2
# проверяем наличие корней
d = b * b - 4 * a * c
if a == 0 or d <= 0:
print(0)
exit(0)
# вычисляем корни
r1 = (-b - math.sqrt(d)) / (2.0 * a)
r2 = (-b + math.sqrt(d)) / (2.0 * a)
# первообразная для h(x)
def H(x):
return a*x*x*x/3.0 + b*x*x/2.0 + c*x
# вычисляем определённый интеграл и выводим его модуль в требуемом формате
print("{:.5f}".format(math.fabs(H(r2) - H(r1))))
Задача 3
В пространстве
задано стандартное скалярное произведение,
— подпространство, заданное как линейная оболочка векторов
,
,
. Найти ортогональную проекцию вектора
на подпространство
вектор
и ортогональную составляющую
этого же вектора (
).
В ответ напишите сумму координат вектора
(например, для вектора
сумма координат будет 9).
Ответ укажите с точностью до двух знаков после точки. При необходимости округлите по правилам математики.
Заметим, что вектора
,
и
— ортогональны (это можно проверить вычислив попарные скалярные произведения), но не нормированы. Давайте найдём проекцию
на каждый из трёх векторов.
Таким образом
Осталось выразить
В ответе нужно записать сумму координат
. Можно было бы сначала вычислить
, а потом сложить его координаты, но можно ещё проще: воспользуемся тем, что сумма координат суммы векторов, равна сумме сумм координат каждого из слагаемых.
Для получения ответа, вычислим суммы координат для каждого из векторов отдельно и сложим их с соответствующими коэффициентами:
Задача 4
Обозначим за
— комлексный корень степени
из единицы с минимальным положительным аргументом (аргумент = угол в полярной форме комплексного числа). Например,
.
Найдите минимальное положительное целое
, являющееся решением следующего уравнения.
По определению
можно вывести явную формулу:
(тут мы используем показательную форму записи комплексного числа, это соответствует
). Подставляем это в уравнение и получаем:
Остаётся решить уравнение на показатели. Тут нужно помнить, что
. Поэтому, получаем уравнение
Домножаем на
и делим на
. Получается следующее уравнение в целых числах, где нас интересует решение с минимальным положительным целым
.
Проверив
, находим ответ
при
.
Задача 5
Маленькому мальчику Ване на кружке по системам счисления задали следующую задачу: перевести число
в системе счисления
в систему счисления
. Недолго думая, он позвал на помощь своего лучшего друга Петю, который славился тем, что замечательно умел считать до
на пальцах. После нескольких бессонных ночей ребята общими усилиями справились с задачей.
Однако, на следующем занятии Ване задали похожую задачу, где
, к сожалению, превышало
. Тогда ребята решили обратиться к старшей сестре Пети с просьбой написать универсальную программу, которая решает задачу для любых
,
и
. Ваша цель – выполнить просьбу Вани и Пети.
Входные данные
Во входных данных вашей программе дается три числа: исходное число
, основания систем счисления
и
(
). Число
в десятичной системе счисления не превышает
.
Выходные данные
В выходных данных должно быть число
, записанное в системе счисления
, или
, если входные данные некорректны (число
во входных данных не является корректной записью числа в системе счисления
).
Это задача на перевод числа из одной системы счисления. Если нам дано число
в системе счисления с основанием
, то его значение можно вычислить, как
Это же можно вычислить по схеме Горнера:
Для того, чтоб перевести
в число
в системе счисления по основанию
, нужно повторить эту процедуру в обратном порядке. Тогда цифра
будет вычисляться по формуле
Ниже представлена реализация этой идеи на Питоне.
# считываем входные данные
xstr, b, c = raw_input().split()
s1 = int(b)
s2 = int(c)
# проверяем входные данные и преобразуем в число
x = 0
for c in xstr:
if int(c) >= s1:
print(-1)
exit()
x = x * s1 + int(c)
# переводим в заданную систему счисления
res = ""
if x == 0:
res = "0"
else:
while x > 0:
res = str(x % s2) + res
x = x // s2
print(res)
Задача 6
Про студентов магистерской программы Software Engineering известно, что они дружат друг с другом так, что каждый студент дружит не более чем с 3 другими, и для любых двух студентов верно, что они либо дружат друг с другом, либо есть студент, который дружит с ними обоими.
Какое максимальное число студентов на магистерской программе Software Engineering?
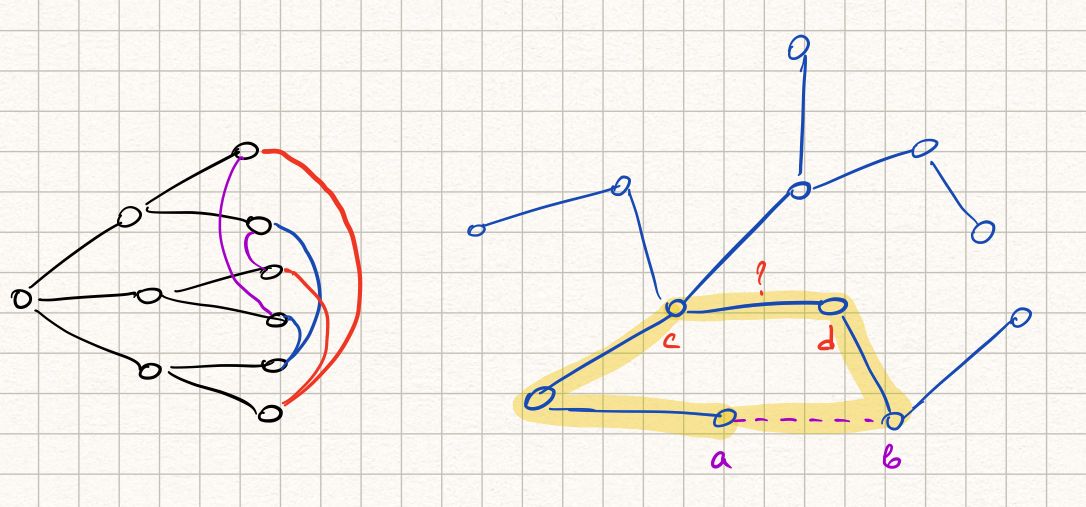
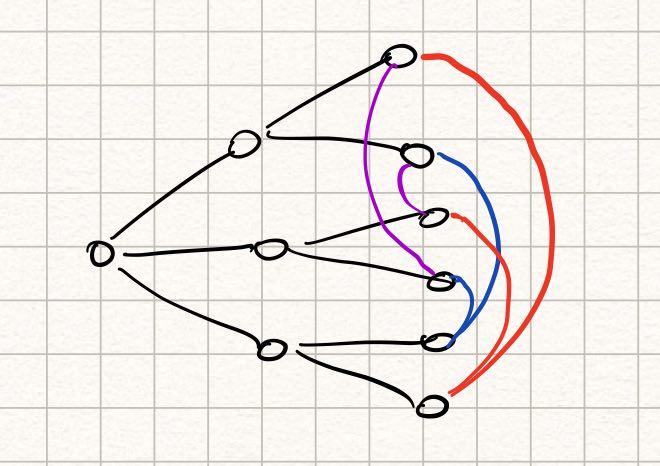
Задача на комбинаторику и теорию графов. Рассмотрим одного студента. Он сам дружит не более, чем с тремя студентами. Каждый его друг имеет не более 2 других друзей. Других студентов по условию быть не может. Получаем, что всего не более
студентов. Осталось проверить, что такую граф существует, но это несложно сделать на листочке.
Левая вершина — рассматриваемый студент, правее три его друга и шесть друзей друзей. Цвета рёбер значения не имеют и нужны только для понятности картинки.
Задача 7
Сколько различных решений имеет следующее уравнение
если известно, что,
,
,
?
Это простая задачка на три цикла — числа небольшие, результат можно быстро посчитать короткой программой.
count = 0
for x1 in range(1,51):
for x2 in range(2,51):
for x3 in range(51):
if x1 + x2 + x3 <= 50:
count = count + 1
print(count)
Но писать программу необязательно, ответ не так сложно вычислить аналитически (на тесте такого требования не было). Для этого заметим, что исходная задача эквивалентна следующей.
Сколько различных решений имеет следующее уравнение
если известно, что?
(Мы вычли
из правой части и добились того, чтобы все переменные начинались с нуля.)
Это уже типовая задача. Нам нужно разбить последовательность
предметов на 4 части. Для этого нужно вставить
перегородки. По формуле для разбиения получаем
Задача 8
Найти длину кривой
, заключённой в первой четверти.
Ответ укажите с точностью до двух знаков после точки. При необходимости округлите по правилам математики.
Это задача на вычисление длины кривой. Длина кривой вычисляется через определённый интеграл
В нашем случае,
,
. Для вычисления
, точки пересечения с осью абсцисс, нужно подставить
: получаем
. Вычислим
:
Вычисляем интеграл:
Задача 9
На вход программе подаётся строка, содержащая слова, разделённые пробелом. Слово – это последовательность латинских символов, окружённая пробелами или границами строк.
Для всех слов, которые встречаются в тексте более одного раза, программа должна вычислить минимальное количество слов между повторениями.
Вход
Строка, содержащая последовательность строчных латинских символов, разделённых пробелами.Выход
Выведите все слова, которые встречаются более одного раза, и минимальное количество слов между их повторениями, в формате
слово: числоВыведите эту информацию в том порядке, в котором слова встречаются в тексте в первый раз.
Это чисто программистская задача на использование массивов, словарей и сортировок. Ниже представлено решение этой задачи на Питоне с комментариями.
# считываем входную строку и разбиваем на слова
words = raw_input().split()
# заводим необходимые словари
idx = {} # хранит номер последнего вхождения слова
dist = {} # хранит минимальное расстояние между повторениями
first = {} # хранит номер первого вхождения
# проходим по словам и вычисляем минимальное расстояние для каждого слова
for i in range(len(words)):
if words[i] in idx:
if dist[words[i]] > i - idx[words[i]] - 1:
dist[words[i]] = i - idx[words[i]] - 1
else:
first[words[i]] = i
dist[words[i]] = 2 * len(words) # замена +бесконечности
idx[words[i]] = i
# массив для хранения слов, которые встречаются более одного раза
good = []
for k in dist:
if dist[k] < len(words):
good.append((k, dist[k], first[k]))
# упорядочиваем массив по номеру первого вхождения
good.sort(key=lambda t: t[2])
# выводим результат
for t in good:
print("{}: {}".format(t[0], t[1]))
Задача 10
В студенческом общежитии ИТМО очень сложно устроена локальная сеть — местный администратор не любит роутеры, потому сетевые кабели протянуты напрямую между некоторыми компьютерами (для этого в некоторые компьютеры пришлось установить дополнительные сетевые карты).
Вам, как новичку в общежитии, хочется выяснить как все устроено. Поэтому вы можете выбрать любые два компьютера и получить ответ на вопрос “проложен ли между ними провод?”. Вам бы хотелось узнать — можно ли в общежитии передать информацию с любого компьютера до любого другого по проводам.
Какое минимальное количество вопросов необходимо задать чтобы гарантированно получить ответ, если всего в общежитии установлено 32 компьютера?
Задача на теорию графов. Тут нужно показать, что какую бы стратегию мы не выбрали, нам придётся перебрать все пары компьютеров, т.е. задать
вопросов. До этого нетрудно догадаться, и для ответа на тест этого достаточно. Тем не менее, давайте постараемся разобраться, почему это так.
Довольно легко придумать следующую простую идею, которая всё объясняет: если мы про какую-то пару компьютеров не спросили, например, не спросим про пару
, то давайте рассмотрим сеть, в которой компьютер
соединён только с компьютером
. Если не спросить про
, то мы не можем быть уверены, что
соединён хоть к каким-то компьютером. Это рассуждение объясняет, почему нужно спросить про все пары компьютеров, и приводит к правильному ответу. Только вот это рассуждение не является корректным. Проблема заключается в том, что мы неявно предполагаем, что наши вопросы не зависят от ответов на предыдущие вопросы. Когда мы предлагаем рассмотреть сеть, в которой компьютер
соединён только с компьютером
, то это уже другая сеть, нежели та, на которой мы не спросили про пару
. На разных сетях вопросы могут быть устроены по-разному. Другими словами, это рассуждение позволяет доказать, что не существует пары компьютеров
, про которую мы не спросим ни для какой конфигурации сети. При этом, если для каждой конфигурации сети существует какая-то пара, про которую мы не спрашиваем, то это не противоречит нашему рассуждению.
Корректное объяснение может выглядеть, например, так. Предположим, что вместо честного ответа на вопросы об устройстве сети, нам отвечают таким образом, чтобы заставить нас задавать как можно больше вопросов (такое доказательство называется рассуждением о противнике (adversary argument)). Как ему это сделать? Можно придерживаться следующей стратегии: отвечать «Да» только в том случае, если ответ «Нет» будет означать, что сеть несвязна. Давайте покажем, что при такой стратегии ответов нам всегда придётся спросить про все пары компьютеров. Рассмотрим граф, в котором вершины соответствуют компьютерам, а рёбра — тем парам, для которых мы получили ответ «Да». Заметим, что при такой стратегии ответов на вопросы получившийся граф будет ациклическим. Действительно, если в какой-то момент в графе появился цикл, то это означает, что мы получили ответ «Да» на вопрос про некоторую пару
, про которую можно было ответить «Нет», ведь
уже связаны другими рёбрами, т.е. ответ «Нет» на вопрос о
не означает несвязность сети. Теперь предположим, что мы убедились в связности сети не спросив про все пары. Это значит, что полученный граф представляет собой дерево содержащее все 32 вершины. Пусть
— пара компьютеров, про которую мы не спросили. Давайте добавим ребро
к дереву. Так как в дереве уже были пути между всеми парами вершин, то новое ребро добавит цикл.
Рассмотрим этот цикл и выберем на нём ребро, про которое мы спрашивали последним. Пусть это ребро
. Спрашивая про пару
мы получили ответ «Да». По нашей стратегии нам отвечают «Да» только, если ответ «Нет» означал бы несвязность графа. Но это противоречит тому, что про пару
мы ничего не спрашивали: можно было бы ответить «Нет» на вопрос о
и всё равно добиться связности графа за счёт ответа «Да» на вопрос об
. Это противоречит предположению о выбранной стратегии ответов на вопросы.
Задача 11
Школьник Ваня приболел, и его мама решила вызвать врача домой. У врача есть статистика по району, где живет Ваня. У
больных детей этого района — грипп, у остальных
— ветрянка. Других болезней в этом районе не зафиксировано.
Один из основных симптомов ветрянки – это сыпь, она появляется в
случаях заболевания ветрянкой. Однако, во время гриппа она тоже возможна и появляется в
случаях.
Осмотрев Ваню, врач обнаружил сыпь. Какова вероятность того, что у Вани ветрянка?
Ответ укажите с точностью до двух знаков после точки. При необходимости округлите по правилам математики.
Это задача на теорию вероятностей и формулу Байеса. Обозначим следующие события:
— у Вани грипп,
— у Вани ветрянка.
Пусть
— это наличие сыпи. Известно, что
Нас просят оценить условную вероятность
. По теореме Байеса:
Вероятность выпадения сыпи можно вычислить по формуле полной вероятности:
В результате получаем:
Заключение
Надеемся, что этот разбор поможет абитуриентам программы подготовиться к онлайн-тесту. Для самостоятельной проверки предлагаем прорешать второй вариант. Все материалы вступительных испытаний опубликованы на сайте программы. Там же вы сможете найти полное описание процесса поступления. Не забывайте, что за успешным прохождением онлайн-теста следует устный этап вступительного испытания.
P.S. Внимательный читатель заметит, что в разборе 11 задач, а в тесте их должно быть 12. Одна из задач оказалась технически сложной, и мы решили её не разбирать, чтобы никого не пугать.
Планируете идти в магистратуру? Стоит уже сейчас начинать выбирать направления и готовиться к вступительным экзаменам. Анастасия ПЕТРОВА рассказывает, какие еще есть способы поступления в магистратуру ИТМО.
Как поступить в магистратуру?
Есть несколько способов. Среди них: ПИГА (перезачет итоговой государственной аттестации), конкурс портфолио, конкурс докладов на Конгрессе молодых ученых, вступительный экзамен, дистанционный экзамен и получение призового места в олимпиаде или конкурсе.
А сложно поступить?
Если вы хорошо учились в бакалавриате и подготовились к экзаменам, то все получится. Для полной уверенности в себе советуем выбирать несколько направлений подготовки и участвовать в олимпиадах и конкурсах. Рейтинги формируются по баллам за вступительные испытания и по среднему баллу приложения к диплому.
ПИГА. Что это такое?
Перезачет итоговой государственной аттестации. Оценка за диплом будет переведена в баллы за вступительный экзамен: «Хорошо» — 75 баллов, «Отлично» — 100 баллов. Если же вы получили «Удовлетворительно», придется сдавать вступительные и проходить по общему конкурсу. Если вы сдавали еще и государственные экзамены, то баллы будут рассчитываться как среднее арифметическое оценок госэкзаменов и оценки за защиту диплома.
КМУ. Как к нему готовиться?
Конгресс молодых ученых проходит ежегодно в Университете ИТМО в апреле. Заявки принимаются с января по март. Суть конгресса в том, чтобы подготовить научную работу и потом представить ее за 15–20 минут. Сначала вам нужно выбрать секцию, в которой хотите выступать, и, конечно же, научного руководителя, который будет координировать вашу деятельность. Победитель КМУ имеет право поступить на некоторые направления подготовки магистров в Университет ИТМО без вступительных испытаний.
Как собирать портфолио?
Еще один вид поступления — оценка за ваше портфолио. В него входят: дипломы за олимпиады для студентов, участие в летних школах, документы о прохождении стажировок, сертификаты, подтверждающие участие в научных мероприятиях, публикации в научных изданиях, изобретения и все то, что отражает ваши успехи в профессиональной деятельности. Если вы уже на 4 курсе, присмотритесь к олимпиадам, сейчас как раз стартуют отборочные этапы.
Игнат Меженцев, магистрант 1 курса,
программа «Технологии разработки компьютерных игр»— О КМУ я узнал от друга. Научный руководитель моей ВКР помог сформулировать тему и выбрать направление. Важно, чтобы в работе была научная составляющая и новизна. Отдельное внимание стоит уделить подготовке выступления, потому что мало написать хороший материал, надо уметь правильно его подать. Я, конечно же, волновался, но все было намного проще, чем предполагал. Я выиграл и это позволило поступить в ИТМО без экзаменов.
Анастасия Двойникова, магистрант 1 курса,
программа «Речевые информационные системы»— Я поступала в магистратуру по конкурсу портфолио. Для этого нужно было подготовить один документ, который включал четыре подраздела: эссе на тему, почему я хочу поступить в Университет ИТМО; еще одно эссе с ответом на вопрос, почему я выбираю конкретное направление; само портфолио и средний балл диплома. За каждый из пунктов можно получить 25 баллов. Чтобы стать победителем, нужно было набрать максимальную сумму баллов, то есть 100. В мое портфолио входили копии научных публикаций и статей, а также документы и сертификаты, подтверждающие участие в конференциях и конкурсах за годы обучения в бакалавриате.
Магистратура в Санкт-Петербургском НИУ ИТМО – третье по популярности место в стране, где студенты получают высшее образование второго уровня. Ежегодно из стен вуза выходят более 2,5 тысяч готовых специалистов. Здесь ведется обучение по 36 направлениям и 78 программам. Подробнее о том, как поступить в магистратуру Университета ИТМО, о стоимости обучения, вступительных испытаниях, количестве бюджетных мест и других интересующих абитуриентов вопросах – далее в статье.
Факультеты и программы
Обучением будущих специалистов в вузе занимаются сразу несколько видов структурных подразделений. Среди них 1 институт, 4 мегафакультета и 1 факультет магистратуры Университета ИТМО. Полный перечень отражен на рисунке.
Особенность обучения в вузе состоит в том, что изначально существующие программы магистратуры Университета ИТМО разделены на 5 типов:
- Научная магистратура. Ориентирована на подготовку специалистов, планирующих поступать в аспирантуру. Вуз предлагает 16 таких программ.
- Индустриальная магистратура. Готовит работников инженерно-конструкторской сферы по 6 специализациям.
- Предпринимательская магистратура. Рассчитана на будущих бизнесменов. Выбрав одну из 15 программ, они обучатся вести успешную деятельность на российском или мировом рынке.
- Магистерская подготовка по перспективным направлениям. Ориентирована на «профессии будущего» и разработку новых образовательных траекторий (пока вуз предлагает 7 таких программ, но их список быстро расширяется).
- Корпоративная магистратура. Основной блок подготовки вуза, состоящий из 34 специализаций. Здесь ведется целевое обучение под определенную отрасль или работающее предприятие. С потенциальными работодателями заключаются договора сотрудничества. Магистранты в этих компаниях стажируются и получают право трудоустройства после окончания ИТМО.
В направлениях подготовки магистратуры Университета ИТМО легко запутаться. Чтобы этого не произошло, на сайте встроен удобный навигатор, с помощью которого можно отфильтровать профили по факультетам, типу, стоимости обучения, наличию бюджетных мест и другим параметрам.

* Чтобы не повторять в тексте одинаковые направления, дальше будут указываться только соответствующие им номера.
Примечательно, что каждая программа в ИТМО разбивается еще на ряд специализаций. Например, в «Биоинженерии и биотехнических системах» (направление биотехнических систем и технологий) их сразу 6:
- «Элементная база для нано- и биофотоники»;
- «Биотехнические системы»;
- «Биоинженерия и биоматериалы»;
- «Современные методы приборостроения»;
- «Органические материалы фотоники»;
- «Молекулярная нано- и биофотоника».
Первые 3 специализации ведутся на русском языке. Вторая тройка рассчитана на англоговорящую аудиторию студентов.
Программы двойных дипломов
Университет ИТМО предоставляет своим студентам возможность одновременно получить сразу два диплома о высшем магистерском образовании. Существует 2 типа таких учебных программ:
- международные;
- совместные.
Основное отличие между ними состоит в том, что в первом случае партнерским вузом выступает иностранное, во втором – отечественное учебное заведение.
Всего ИТМО предлагает 9 международных программ двойного диплома. Среди партнеров вуза престижные учебные заведения Франции, Германии, Финляндии, Нидерландов и других стран.
ИТМО организует международную подготовку магистрантов не только в форме обучения по программам двойного диплома. Существуют зарубежные стажировки, научные школы и другие мероприятия, позволяющие студентам проучиться за границей от 1 недели до 1 года.
Как поступить
ИТМО проводит набор студентов на бюджетные и платные места. Как только абитуриент определился с направлением подготовки, он подает заявление в приемную комиссию вуза и сдает вступительные экзамены. Если результат прохождения испытаний окажется высоким, претендента зачисляют на выбранную программу.
Порядок поступления
Первое, с чего начинается поступление в магистратуру Университета ИТМО, – подача заявления. При условии благоприятной эпидемиологической ситуации в стране сделать это можно по адресу: г. Санкт-Петербург, пр. Кронверкский, д. 49. В противном случае, прием документов осуществляется только в онлайн-режиме (через персональный кабинет абитуриента).
Кроме заявления, для поступления в магистратуру Университета ИТМО потребуется следующий набор документов:
- анкета;
- отсканированный дубликат или фото диплома о в/о;
- паспорт (копии страницы с фотографией и пропиской);
- фото на документы.
Если у абитуриента есть особые права на поступление или индивидуальные достижения, которые могут быть учтены при зачислении, подтверждающие бумаги также стоит прикрепить к заявлению.
Прием документов стартует 10 февраля и длится до 10 августа. После успешного прохождения вступительных испытаний абитуриент должен дать письменное согласие на зачисление.
Экзамены
Порядок проведения вступительных испытаний в магистратуру Университета ИТМО отличается от принятой в большинстве российских вузов схемы. Для основной массы абитуриентов предусмотрена сдача экзамена. Но победители целого ряда научных конкурсов от него освобождаются. Им автоматически проставляются максимальные отметки.
В комплекс значимых для поступления в ИТМО научных мероприятий входят:
- зимняя школа «Тебе решать»;
- конкурс «Световой дизайн»;
- «Науке нужен ты»;
- SCAMT Whorkshop Week (для программ «Химия прикладных материалов», «Молекулярная биология и биотехнология») и др.
Вступительные испытания оцениваются по 100-балльной шкале по следующей схеме:
- 50 баллов – удовлетворительно;
- 75 баллов – хорошо;
- 100 баллов – отлично.
Минимально необходимый проходной балл в магистратуру Университета ИТМО – 50. Этого достаточно, чтобы взяли на платное отделение. Тем, кто нацелился на бюджет, придется набрать больше, чем соперники.
Вступительные испытания проводятся по комплексу профильных дисциплин. Каждый экзаменационный билет состоит из 30 (или большего количества) заданий. На подготовку абитуриенту дается 1 час. Члены приемной комиссии вправе задать до 3 дополнительных вопросов.
Величина достаточных для поступления на бюджет баллов и предметы, включаемые в экзамен, указаны в таблице.
| №* | Дисциплины | Проходной балл |
|---|---|---|
| 1 | Высшая математика, математический анализ и логика, физические основы квантовых вычислений, математическая физика | 62,5 |
| 2 | Математический анализ, логика, высшая математика, математическая физика | 87,5 |
| 3 | Урбанистика, градостроительное проектирование, инженерные сети, архитектура, градостроительство, градостроительная политика | 100 |
| 4 | Операционные системы, компьютерные сети, базы данных, объектно-ориентированное программирование, языки программирования, архитектура ЭВМ | 75 |
| 5 | Компьютерные сети, языки программирования, архитектура ЭВМ, базы данных + практические задания | 75 |
| 6 | Объектно-ориентированное программирование, язык С++, игровая разработка, структура и алгоритмы обработки данных | 75 |
| 7 | Web-мастеринг, базы данных, объектно-ориентированное программирование, компьютерные сети, компьютерная графика, мобильные операционные системы, защита информации, мировые информационные ресурсы | 75 |
| 8 | Информационная безопасность, теория информации, организационно-правовые основы информационной безопасности, моделирование информационных систем, полупроводниковая схемотехника, криптографические средства защиты информации, имитационное моделирование | 100 |
| 9 | Программирование, базы данных, компьютерные сети, архитектура ЭВМ, инфокоммуникационные протоколы, протоколы конвергентных и мобильных сетей | 100 |
| 10 | См. п.8 | 100 |
| 11 | Электротехника, метрология, механика, безопасность жизнедеятельности, материаловедение, электроника, основы автоматизированного управления (АУ), проектирование систем и приборов | 62,5 |
| 12 | Механика, теория АУ, машиностроение, термодинамика и теплоотдача, электротехника и электроника, метрология, сопротивление материалов | 75 |
| 13 | Основы оптики, теория и расчет оптико-электронных приборов, проектирование оптических систем | 75 |
| 14 | Основы оптики, нанокомпозиты и наноматериалы, физика, голография | 62,5 |
| 15 | Наноматериалы в биотехнологии и биоинженерии, нанокомпозиты для фотоники, электроника, конструкционные материалы и биоматериалы | 50 |
| 16 | Лазерные технологии, физическая и геометрическая оптика, математическое моделирование | 75 |
| 17 | Энергетика, основы электротехники, электрические и электронные аппараты, автоматизированное проектирование электротехнических устройств | 75 |
| 18 | Реология, гидродинамика, физическое и математическое моделирование, электротехника, теория механизмов и машин, сопротивление материалов | 87,5 |
| 19 | Системы автоматизированного управления и проектирования, механика, электротехника и электроника, вычислительные машины | 50 |
| 20 | Теория систем автоматизированного управления, проектирование мехатронных и робототехнических устройств, основы робототехники | 50 |
| 21 | Механика, физика, материаловедение, метрология, информтехнологии, инженерная и компьютерная графика, электроника, схемотехника | 75 |
| 22 | Основы холодильной техники, инженерная и компьютерная графика, детали машин и основы конструирования, термодинамика и тепломассообмен | 62,5 |
| 23 | Физика, химия, электротехника, химические технологии, промышленная экология | 75 |
| 24 | Пищевая биотехнология, переработка сырья, основы биотехнологии | 100 |
| 25 | Химия, санитарные нормы, пищевая микробиология, продуктовая технология | 100 |
| 26 | Биохимия, гистология, реология, микробиология | 100 |
| 27 | Экология, безопасность жизнедеятельности, математическое моделирование | 87,5 |
| 28 | Информационная безопасность, робототехника, математическое моделирование, машинное обучение | 75 |
| 29 | Теория вероятности, методы обработки навигационной измерительной информации | 100 |
| 30 | Техническое регулирование, средства измерений, стандартизация, сертификация | 87,5 |
| 31 | Менеджмент, маркетинг, управление качеством, стандартизация, метрология и подтверждение соответствия | 50 |
| 32 | Теория автоматического управления, преобразователи информации и электродвигатели, бизнес-аналитика | 75 |
| 33 | Научные коммуникации, социология академического мира, социология, базы данных, инновации, электронная коммерция | 50 |
| 34 | 100 | |
| 35 | См. п. 3 | 87,5 |
| 36 | Патентование и защита интеллектуальной собственности, эконометрика, инноватика | 100 |
| 37 | Экономическая теория, региональная и мировая экономика | 100 |
| 38 | Введение в цифровые гуманитарные информтехнологии, визуализация данных | 87,5 |
Приведенный в таблице перечень дисциплин не окончателен. Он может незначительно изменяться в зависимости от специализации. Чтобы абитуриенты лучше могли подготовиться к сдаче вступительного экзамена, на сайте университета в карточке каждой образовательной программы выложен актуальный список вопросов к испытаниям.
Для зачисления на бюджет по многим направлениям требуется набрать максимальное количество баллов на экзамене. Хотя есть профили, куда в 2020 году удалось поступить даже с тройками («Инноватика», «Системный анализ», «Техническая физика», «Мехатроника и робототехника», «Лазерная техника»).
Формы обучения
Заочного отделения магистратуры в Университете ИТМО нет. Все обучение проходит в традиционном дневном формате.
Дистанционное обучение в магистратуре Университета ИТМО также не проводится. Хотя вуз обладает целой виртуальной платформой «Электронная информационно-образовательная среда», на ней проходят только онлайн-курсы повышения квалификации.
Бюджетные места
Абсолютно по всем существующим направлениям подготовки вуз проводит набор студентов на бюджет. Количество мест в магистратуре Университета ИТМО примерно одинаковое каждый год. Актуальные контрольные цифры приема отражены в таблице и на диаграмме.
| Направление* | Количество мест |
|---|---|
| 1 | 151 |
| 2 | 16 |
| 3 | 16 |
| 4 | 70 |
| 5 | 64 |
| 6 | 94 |
| 7 | 226 |
| 8 | 138 |
| 9 | 117 |
| 10 | 28 |
| 11 | 62 |
| 12 | 13 |
| 13 | 70 |
| 14 | 88 |
| 15 | 45 |
| 16 | 35 |
| 17 | 25 |
| 18 | 25 |
| 19 | 55 |
| 20 | 80 |
| 21 | 138 |
| 22 | 156 |
| 23 | 119 |
| 24 | 151 |
| 25 | 40 |
| 26 | 27 |
| 27 | 29 |
| 28 | 15 |
| 29 | 13 |
| 30 | 16 |
| 31 | 50 |
| 32 | 80 |
| 33 | 311 |
| 34 | 10 |
| 35 | 43 |
| 36 | 16 |
| 37 | 20 |
| 38 | 25 |
| Всего | 2677 |
Больше всего бюджетных мест магистратуры Университета ИТМО приходится на профиль «Инноватика» (311). На второй позиции – «Программная инженерия» (226). По остальным направлениям подготовки выучиться за счет государства могут от 10 до 156 человек.
Стипендия
Абитуриенты, поступившие на бюджет, получают материальную поддержку (при условии хорошей успеваемости). Стипендия студентам магистратуры Университета ИТМО начисляются на карту банка «Санкт-Петербург». Ее оформляют на 1 курсе сразу после зачисления.
Магистрантам-первокурсникам выплаты могут начислить с первых дней, а не по итогам полугодия как в других вузах. Например, при наличии красного диплома о предыдущем образовании учащийся будет сразу получать 4 100 рублей в месяц. И только через полгода размер материального поощрения начнет определяться семестровыми оценками.
При соблюдении определенных условий, магистрантам могут назначить следующие виды выплат:
- государственная академическая стипендия – 2 000 или 4 100 рублей (отличникам) в месяц;
- повышенная государственная академическая стипендия – от 3 000 до 27 000 рублей в месяц за успехи в учебной, научной, исследовательской, общественной, культурной или спортивной деятельности;
- разовая материальная поддержка студентов, испытывающих временные финансовые сложности – базовый размер 4 000 рублей;
- стипендии Президента и Правительства РФ – назначаются магистрантам-первокурсникам, обучающимся по приоритетным для экономики страны направлениям;
- стипендия фонда В. Потанина – 20 000 рублей в месяц.
Студенты ИТМО постоянно участвуют в конкурсе на президентскую стипендию для обучения за рубежом. Она выделяется из бюджета Минобрнауки РФ и покрывает не только оплату услуг иностранного вуза, но и проживание, транспортные расходы, оформление визы и медицинскую страховку.
Студентам ИТМО полагается ряд льгот в общественном транспорте. Они могут оформить бесконтактную проездную карту, по которой стоимость поездок значительно дешевле стандартных тарифов.
Общежитие
Учебное заведение располагает 6 жилыми корпусами. В 2020 году первокурсникам было выделено всего 55 мест. Общежитие для студентов предоставляется в порядке очередности. Сначала расселяют социально незащищенных учеников, затем иностранцев, третьими идут бакалавры и только потом – магистранты.
Стоимость проживания в общежитии для студентов магистратуры Университета ИТМО зависит от корпуса и комфортности (колеблется от 761 до 3 302 рублей в месяц). Для заселения потребуется медицинская справка (форма 086/у, флюорография и прививочный сертификат).
Стоимость обучения
Расценки на подготовку магистров в вузе полностью зависят от направления. Цены колеблются от 214 до 286 тысяч рублей в год. Стоимость обучения в магистратуре Университета ИТМО в 2020 году отражена в таблице и на графике.
| Направление* | Цена обучения в год, в тыс. руб. |
|---|---|
| 1 | 214 |
| 2 | |
| 3 | 242 |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | 286 |
| 13 | 242 |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | 286 |
| 22 | |
| 23 | 242 |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | 286 |
| 30 | 242 |
| 31 | |
| 32 | |
| 33 | |
| 34 | 214 |
| 35 | 242 |
| 36 | |
| 37 | 214 |
| 38 |
Подготовительные курсы
Подготовительные курсы для поступления в магистратуру Университета ИТМО доступны всем желающим на открытой платформе ITMO.PRE–masters. Они организованы почти по всем направлениям и состоят из нескольких тематических разделов. Подготовительные магистерские курсы разработаны ведущими преподавателями ИТМО. Такие занятия дают возможность лучше познакомиться с предметной областью и повысить шансы на поступление.
Средняя продолжительность курсов – 4 месяца. Периодичность занятий – 2-3 раза в неделю. По итогам обучения слушатели могут получить сертификат.
Редакция Edunews просит своих читателей, уже закончивших этот вуз или пока обучающихся в нем, оставлять отзывы о магистратуре Университета ИТМО. Сделать это можно после статьи в разделе комментариев.
Автор: Киреева Оксана
Перейти на официальный сайт
Помогите рассортировать файлы. К какому предмету относится данный файл?
Ненужные и мусорные файлы можно перемещать в предмет [НА УДАЛЕНИЕ].
Помогите дать файлам осмысленные названия
Примеры:
lab1 => Лабораторная работа №1. Фотоэффект.
Savelev_molekulyarnaya_fizika => Савельев. Молекулярная физика