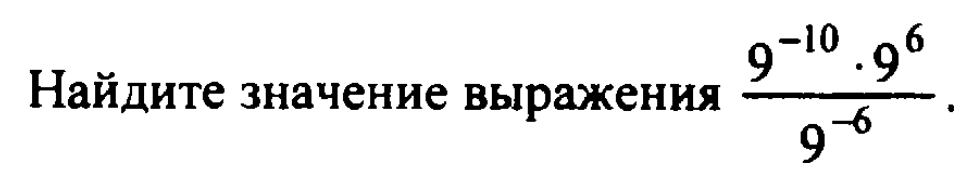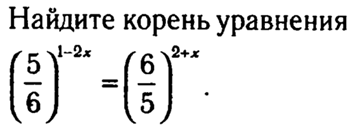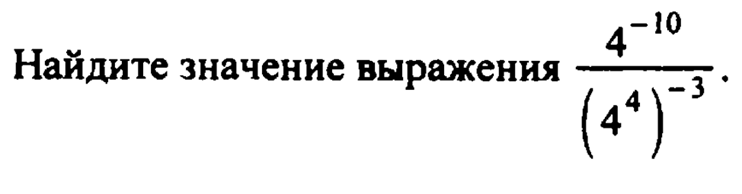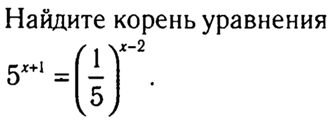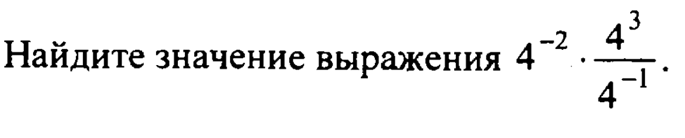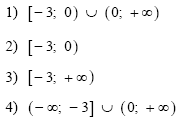Итоговая контрольная по математике 10 класс в форме егэ с ответами

Контрольно-оценочное
средство.

Учитель:

Предмет:
математика

Класс:
10 класс

Тема: Итоговая
контрольная работа по математике за курс 10 класса  в форме ЕГЭ (профиль).

Дата проведения:

Пояснительная
записка

Цели
контроля:

Выявить уровень овладения
учащимися знаний и умений за курс математики 10 класса:

—предметные
знания и умения:

• уметь использовать
приобретенные  знания и умения в практической

деятельности
и повседневной жизни;

• уметь выполнять
вычисления и преобразования;

• уметь решать
уравнения и неравенства;

• уметь выполнять
действия с функциями;

• уметь выполнять
действия с геометрическими фигурами, координатами

и
векторами;

• уметь строить и
исследовать математические модели.

—метапредметные:

   
познавательные: • уметь использовать приобретенные  знания и умения в практической

деятельности
и повседневной жизни;

• уметь выполнять
вычисления и преобразования;

• уметь решать
уравнения и неравенства;

• уметь выполнять
действия с функциями;

• уметь выполнять
действия с геометрическими фигурами, координатами

и
векторами;

• уметь строить и
исследовать математические модели.

    
коммуникативные   отсутствуют

     
регулятивные умение применять алгоритмы при
выполнении заданий.

Краткая
характеристика  КОС :

—
форма контроля: итоговая
 контрольная работа по математике за курс 10 класса  в форме ЕГЭ (профиль)

—
количество вариантов:  3 варианта.

Распределение
заданий по уровню сложности.

Всего
в работе 11 заданий, из которых 7 заданий базового уровня (часть I) и 4
задания повышенного уровня (часть II).

– часть
1 содержит 7 заданий с кратким ответом в виде целого числа или конечной
десятичной дроби;

– часть
2 содержит 3 задания (задания 8–10) с кратким ответом в виде

целого
числа или конечной десятичной дроби и 1 задание (задание 11) с развернутым
ответом (полная запись решения с обоснованием выполненных действий).

Задания
части 1 направлены на проверку освоения базовых умений и практических навыков
применения математических знаний в повседневных ситуациях.

Посредством
заданий части 2 осуществляется проверка освоения математики на профильном
уровне, необходимом для применения математики в профессиональной деятельности.

При
выполнении задания с развернутым ответом части 2 итоговой работы в бланке
ответов № 2 должны быть записаны полное обоснованное решение и ответ.

Задания  репродуктивного
уровня :
№1, №2, №3, №4, №5,  (всего 5 заданий)

Задания
конструктивного
уровня:
№6, №7, №8, №9, №10, №11  (всего 6 заданий)

Репродуктивный
уровень: 45%

Конструктивный
уровень: 55%

Содержание 
контрольно-оценочного материала

Итоговая контрольная работа по математике в 10 классе

Инструкция
по выполнению работы

Экзаменационная
работа состоит из двух частей, включающих в себя 11 заданий. Часть 1 содержит 7
заданий с кратким ответом базового уровня сложности. Часть 2 содержит 3 задания
с кратким ответом повышенного уровня сложности и 1 задания с развёрнутым
ответом повышенного.

На
выполнение экзаменационной работы по математике отводится  90 минут. Ответы к
заданиям 1–10 записываются по приведённому ниже образцу в виде целого числа или
конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а
затем перенесите их в бланк ответов № 1.

Ответ: –0,8 _ .

При выполнении
задания 11 требуется записать полное решение и ответ в бланке ответов № 2.

Все
бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование
гелевой, или капиллярной, или перьевой ручек.

При
выполнении заданий можно пользоваться черновиком. Записи в черновике, а
также в тексте контрольных измерительных материалов не учитываются при
оценивании работы.

Баллы,
полученные Вами за выполненные задания, суммируются.

Постарайтесь
выполнить как можно больше заданий и набрать наибольшее количество баллов.

Желаю
успеха!

1вариант

Ответом
к заданиям 1–10 является целое число или конечная десятичная дробь. Запишите
число в поле ответа в тексте работы, затем перенесите его в БЛАНК ОТВЕТОВ № 1
справа от номера соответствующего задания,

начиная
с первой клеточки. Каждую цифру, знак «минус» и запятую пишите в отдельной
клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений
писать не нужно.

                                                                                                     
Часть 1

1. Аня купила
проездной билет на месяц и сделала за месяц 30 поездок. Сколько рублей она
сэкономила, если проездной билет на месяц стоит 207 рублей, а разовая
поездка — 20 рублей?

2. 

На рисунке показано изменение температуры воздуха на протяжении
трёх суток. По горизонтали указывается дата и время, по вертикали — значение
температуры в градусах Цельсия. Определите по рисунку наибольшую температуру
воздуха 24 января. Ответ дайте в градусах Цельсия.

3. 

Найдите площадь
четырехугольника, вершины которого имеют координаты (1; 7), (4; 6),
(4; 8), (1; 9).

4. 

В сборнике билетов по истории всего 20 билетов, в 18 из них встречается
вопрос по теме «Петр Первый». Найдите вероятность того, что в
случайно выбранном на экзамене билете школьнику достанется вопрос по теме
«Петр Первый».

5. Найдите корень
уравнения 

6. 

Радиус
окружности, вписанной в правильный треугольник, равен  Найдите
сторону этого треугольника.

7. 

Найдите объем
правильной шестиугольной призмы, стороны основания которой равны 1, а боковые
ребра равны 

Не забудьте перенести все ответы в бланк ответов №
1.

Часть
II

8. 

Найдите значение выражения 

9. 

Мотоциклист, движущийся по городу со скоростью  км/ч,
выезжает из него и сразу после выезда начинает разгоняться с постоянным
ускорением  км/ч Расстояние
от мотоциклиста до города, измеряемое в километрах, определяется выражением  Определите
наибольшее время, в течение которого мотоциклист будет находиться в зоне
функционирования сотовой связи, если оператор гарантирует покрытие на
расстоянии не далее чем в 21 км от города. Ответ выразите в минутах.

10. 

Из городов A и B навстречу друг
другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал
в B на 2 часа раньше, чем велосипедист приехал в A,
а встретились они через 1 час 20 минут после выезда. Сколько часов
затратил на путь из B в A велосипедист?

Для
записи решения и ответа  на задание 11 используйте БЛАНК ОТВЕТОВ № 2. Запишите
сначала номер выполняемого задания, а затем полное обоснованное решение и
ответ. Ответ записывайте чётко и разборчиво.

11. а) Решите
уравнение 

б) Укажите корни этого уравнения, принадлежащие отрезку 

Итоговая контрольная работа по математике в 10 классе

Инструкция
по выполнению работы

Экзаменационная
работа состоит из двух частей, включающих в себя 11 заданий. Часть 1 содержит 7
заданий с кратким ответом базового уровня сложности. Часть 2 содержит 3 задания
с кратким ответом повышенного уровня сложности и 1 задания с развёрнутым
ответом повышенного.

На
выполнение экзаменационной работы по математике отводится  90 минут. Ответы к
заданиям 1–10 записываются по приведённому ниже образцу в виде целого числа или
конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а
затем перенесите их в бланк ответов № 1.

Ответ: –0,8 _ .

При
выполнении задания 11 требуется записать полное решение и ответ в бланке
ответов № 2.

Все
бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование
гелевой, или капиллярной, или перьевой ручек.

При
выполнении заданий можно пользоваться черновиком. Записи в черновике, а
также в тексте контрольных измерительных материалов не учитываются при
оценивании работы.

Баллы,
полученные Вами за выполненные задания, суммируются.

Постарайтесь
выполнить как можно больше заданий и набрать наибольшее количество баллов.

Желаю
успеха!

2 вариант

Ответом
к заданиям 1–10 является целое число или конечная десятичная дробь. Запишите
число в поле ответа в тексте работы, затем перенесите его в БЛАНК ОТВЕТОВ № 1
справа от номера соответствующего задания,

начиная
с первой клеточки. Каждую цифру, знак «минус» и запятую пишите в отдельной
клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений
писать не нужно.

                              
                                                                    Часть 1

1. 

Одна таблетка лекарства весит 20 мг и содержит 5% активного
вещества. Ребёнку в возрасте до 6 месяцев врач прописывает 1 мг активного
вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства
следует дать ребёнку в возрасте четырёх месяцев и весом 7 кг в течение суток?

2. 

На диа­грам­ме по­ка­за­но рас­пре­де­ле­ние вы­плав­ки меди в 11
стра­нах мира (в ты­ся­чах тонн) за 2006 год. Среди пред­став­лен­ных стран пер­вое
место по вы­плав­ке меди за­ни­ма­ла Папуа – Новая Гвинея, один­на­дца­тое
место — Индия. Какое место за­ни­ма­ла Португалия?

3. 

Найдите площадь четырехугольника, вершины которого имеют
координаты , , , 

4. 

На конференцию приехали 5 ученых из Швеции, 7 из Италии и 4 из
Чехии. Каждый из них делает на конференции один доклад. Порядок докладов
определяется жеребьёвкой. Найдите вероятность того, что двенадцатым окажется
доклад ученого из Чехии.

5. 

Решите уравнение                              Если
уравнение имеет более одного корня, в ответе запишите больший из корней.

6. 

В
треугольнике ABC AC = BC, AB = 6,  Найдите
высоту AH.

7. 

Около конуса
описана сфера (сфера содержит окружность основания конуса и его вершину). Центр
сферы совпадает с центром основания конуса. Образующая конуса равна  Найдите
радиус сферы.

Не забудьте перенести все ответы в бланк ответов №
1.

Часть
II

8. Найдите
значение выражения                              при 

9.

Высота,
над землёй подброшенного вверх мяча, меняется по закону ,
где  —
высота в метрах,  —
время в секундах, прошедшее с момента броска. Сколько секунд мяч будет
находиться на высоте не менее 8 метров?

10. 

Путешественник переплыл море на яхте со средней скоростью 30 км/ч.
Обратно он летел на спортивном самолете со скоростью 370 км/ч. Найдите среднюю
скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.

Для
записи решения и ответа  на задание 11 используйте БЛАНК ОТВЕТОВ № 2. Запишите
сначала номер выполняемого задания, а затем полное обоснованное решение и
ответ. Ответ записывайте чётко и разборчиво.

11. 
а) Решите
уравнение 

б) Найдите все корни этого
уравнения, принадлежащие промежутку 

Итоговая контрольная работа по математике в 10 классе

Инструкция
по выполнению работы

Экзаменационная
работа состоит из двух частей, включающих в себя 11 заданий. Часть 1 содержит 7
заданий с кратким ответом базового уровня сложности. Часть 2 содержит 3 задания
с кратким ответом повышенного уровня сложности и 1 задания с развёрнутым
ответом повышенного.

На
выполнение экзаменационной работы по математике отводится  90 минут. Ответы к
заданиям 1–10 записываются по приведённому ниже образцу в виде целого числа или
конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а
затем перенесите их в бланк ответов № 1.

Ответ: –0,8 _ .

При
выполнении задания 11 требуется записать полное решение и ответ в бланке
ответов № 2.

Все
бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование
гелевой, или капиллярной, или перьевой ручек.

При
выполнении заданий можно пользоваться черновиком. Записи в черновике, а
также в тексте контрольных измерительных материалов не учитываются при
оценивании работы.

Баллы,
полученные Вами за выполненные задания, суммируются.

Постарайтесь
выполнить как можно больше заданий и набрать наибольшее количество баллов.

Желаю
успеха!

3 вариант

Ответом
к заданиям 1–10 является целое число или конечная десятичная дробь. Запишите
число в поле ответа в тексте работы, затем перенесите его в БЛАНК ОТВЕТОВ № 1
справа от номера соответствующего задания,

начиная
с первой клеточки. Каждую цифру, знак «минус» и запятую пишите в отдельной
клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений
писать не нужно.

                                                                          
                        Часть 1

1. 

Одна таблетка лекарства весит 20 мг и содержит 9% активного
вещества. Ребёнку в возрасте до 6 месяцев врач прописывает 1,35 мг активного
вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства
следует дать ребёнку в возрасте четырёх месяцев и весом 8 кг в течение суток?

2. 

На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­но су­точ­ное ко­ли­че­ство
осадков, вы­па­дав­ших в Ка­за­ни с 3 по 15 фев­ра­ля 1909 года. По го­ри­зон­та­ли
ука­зы­ва­ют­ся числа месяца, по вер­ти­ка­ли — ко­ли­че­ство осадков, вы­пав­ших
в со­от­вет­ству­ю­щий день, в миллиметрах. Для на­гляд­но­сти жир­ные точки на
ри­сун­ке со­еди­не­ны линией. Опре­де­ли­те по рисунку, сколь­ко дней из дан­но­го
пе­ри­о­да вы­па­да­ло более 3 мил­ли­мет­ров осадков.

3. 

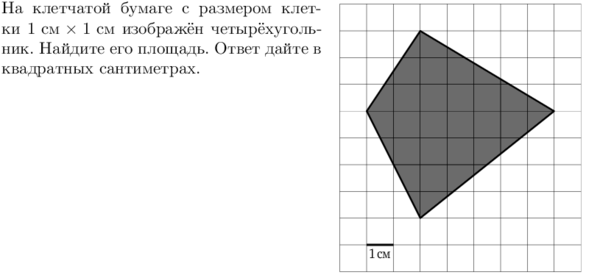
Найдите пло­щадь четырехугольника, изоб­ра­жен­но­го на клет­ча­той
бумаге с раз­ме­ром клетки 1 см  1
см (см. рис.). Ответ дайте в квад­рат­ных сантиметрах.

4. 

Перед началом футбольного матча судья бросает монетку, чтобы
определить, какая из команд начнёт игру с мячом. Команда «Сапфир» играет три
матча с разными командами. Найдите вероятность того, что в этих матчах команда
«Сапфир» начнёт игру с мячом не более одного раза.

5. 

Найдите корень уравнения 

6. 

Боковая сторона
равнобедренного треугольника равна 1, угол при вершине, противолежащей
основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.

7. 

В пра­виль­ной четырёхугольной пи­ра­ми­де вы­со­та равна 2, бо­ко­вое
ребро равно 5. Най­ди­те её объём.

Не забудьте перенести все ответы в бланк ответов №
1.

Часть
II

8. 

Найдите зна­че­ние вы­ра­же­ния                                   
 при       b = 7.

9. 

При температуре  рельс
имеет длину  м.
При возрастании температуры происходит тепловое расширение рельса, и его длина,
выраженная в метрах, меняется по закону,
где  —
коэффициент теплового расширения,  —
температура (в градусах Цельсия). При какой температуре рельс удлинится на
6 мм? Ответ выразите в градусах Цельсия.

10. 

Первый велосипедист выехал из поселка по шоссе со скоростью 15
км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же
направлении выехал второй велосипедист, а еще через час после этого – третий.
Найдите скорость третьего велосипедиста, если сначала он догнал второго, а
через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.

Для
записи решения и ответа  на задание 11 используйте БЛАНК ОТВЕТОВ № 2. Запишите
сначала номер выполняемого задания, а затем полное обоснованное решение и
ответ. Ответ записывайте чётко и разборчиво.

11. 

а) Решите уравнение 

б) Найдите корни этого уравнения,
принадлежащие промежутку 

Поэлементный  анализ  выполнения работы

№ задания	Какие элементы знаний и умений выявляются	Стоимость каждого элемента	Общая стоимость задания
№1	Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни	1 балл	1 балл
№2	Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни	1 балл	1 балл
№3	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	1 балл	1 балл
№4	Уметь строить и исследовать простейшие математические модели	1 балл	1 балл
№5	Уметь решать уравнения и неравенства	1 балл	1 балл
№6	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	1 балл	1 балл
№7	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	1 балл	1 балл
Часть 2
№8	Уметь выполнять вычисления и преобразования	1 балл	1 балл
№9	Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни	1 балл	1 балл
№10	Уметь строить и исследовать простейшие математические модели	1 балл	1 балл
№11	Уметь решать уравнения и неравенства.	1 балл	2 балл
	Итого:	11 баллов	12 баллов

Критерии
оценивания учебных достижений

0 – 2 баллов	3 – 4 баллов	5 – 8 баллов	9 – 12 баллов
«2»	«3»	«4»	«5»

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА  

В ФОРМЕ ЕГЭ В 10 КЛАССЕ

Пояснительная записка

Цель  работы:    

 проверить  уровень  математической  подготовки  учащихся  10 класса  с позиций  Единого  Государственного  экзамена. 

     Содержание  работы:

Итоговая  (годовая)  контрольная  работа  по  алгебре  в 10 классе рассчитана    на  два  астрономических   часа. Контрольная работа  содержит 12 заданий базового уровня, требующих краткого ответа, и два задания повышенного уровня, для которых следует привести полное решение. Задания соответствуют структуре заданий демонстрационной версии ЕГЭ 2015 базового уровня. К каждому заданию требуется дать краткий ответ, представленный в виде целого числа, промежутка и конечной десятичной дроби.

     Оценивание  работы:

 Каждое  задание  первой  части  оценивается  одним  баллом. Во  второй  части  первое  задание – два  балла, второе – три  балла. Вся  работа  оценивается   семнадцатью  баллами.

     ПЕРЕВОД   БАЛЛОВ  В  ОТМЕТКУ:

БАЛЛ	0 — 4	5 — 10	11 — 13	14 – 17
ОТМЕТКА	2	3	4	5

Распределение заданий контрольной работы по основным содержательным блокам

№	Тема
1	Вычисления и преобразования
2	Преобразование выражений, содержащих степень
3	Проценты
4	Корень n-ой степени.
5	Логарифмические уравнения
6	Тригонометрические формулы
7	Задачи с выбором ответа
8	Показательные уравнения
9	Теория вероятностей
10	Задачи практического содержания
11	Текстовая задача
12	Геометрия
13	Система иррациональных уравнений
14	Логарифмическое неравенство

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА   ПО МАТЕМАТИКЕ В ФОРМЕ ЕГЭ В 10 КЛАССЕ
ВАРИАНТ I
1	Найдите значение выражения:
2	Найдите значение выражения:
3	Поступивший в продажу в январе мобильный телефон стоил 2400 рублей. В ноябре он стал стоить 1200 рублей. На сколько процентов снизилась цена на мобильный телефон в период с января по ноябрь?
4	Вычислите:
5	Решить  уравнение:
6	Найдите  сosα, если  sinα= — 0,6 и  <α<.
7	Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.                             ВЕЛИЧИНЫ                  ВОЗМОЖНЫЕ ЗНАЧЕНИЯ  А) площадь почтовой марки                     1) 362  кв. м  Б) площадь письменного стола                 2) 1,2   кв. м  В) площадь Санкт-Петербурга                  3) 1439 кв. км  Г) площадь волейбольной площадки        4) 5,2  кв. см В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения. Ответ:
8	Найдите корень уравнения:
9	В чемпионате по гимнастике участвуют 75 спортсменок: 15 из Чехии, 30 из Словакии, остальные – из Австрии. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Австрии.
10	Выпускники 11 «А» класса покупают букеты цветов для последнего звонка: из 3 роз каждому учителю и из 11 роз классному руководителю и директору. Они собираются подарить букеты 20 учителям (включая директора и классного руководителя), розы покупаются по оптовой цене 35 рублей за штуку. Сколько рублей стоят все розы?
11	От пристани А к пристани В отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним со скоростью на 1 км/ч большей отправился второй. Расстояние между пристанями равно 420 км. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно. Ответ дайте в км/ч.
12	В прямоугольном параллелепипедеABCDA1B1C1D1 известно, что BB1=19, CD=16, BC=. Найдите длину отрезка MK, где M– середина  ребра DC, K – середина ребра  A1D1.
С1	Решить систему уравнений:
С2	Решить неравенство:

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА   ПО МАТЕМАТИКЕ В ФОРМЕ ЕГЭ В 10 КЛАССЕ
ВАРИАНТ II
1	Найдите значение выражения :  1,4 + 3,6 ∙ .
2	Найдите значение выражения :
3	Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 13000 рублей. Какую сумму он получит после вычета налога на доходы? Ответ дайте в рублях.
4	Вычислите:
5	Решить уравнение:
6	Найдите сtgα, еслиcosα= — 0,6 и<α<.
7	Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.                             ВЕЛИЧИНЫ                  ВОЗМОЖНЫЕ ЗНАЧЕНИЯ  А) объём комнаты                      1) 78 200  Б) объём воды в Каспийском море                2) 75    В) объём ящика для овощей            3) 50 л  Г) объём банки сметаны                          4)  0,5 л                                                                                                                                                                           В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения. Ответ:
8	Найдите корень уравнения:
9	В соревнованиях по толканию ядра участвуют 6 спортсменов из Великобрита-нии,  3 спортсмена из Франции, 6 спортсменов из Германии и 10 – из Италии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется  из Франции.
10	Таксист за месяц проехал 10 000 км. Цена бензина 35 рублей  за литр. Средний расход бензина на 100 км составляет 8 литров. Сколько рублей потратил таксист на бензин за этот месяц?
11	На изготовление 99 деталей первый рабочий затрачивает на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей. Известно, что первый рабочий за час делает на 1 деталь больше, чем второй. Сколько деталей в час делает первый рабочий?
12	Длины сторон прямоугольника равны 8  и 6 см. Через точку O пересечения его диагоналей проведена прямая ОK, перпендикулярная его плоскости. Найдите расстояние от точки K до вершин прямоугольника, если ОK=12 см.
С1	Решить систему уравнений:
С2	Решитьнеравенство:

О  Т  В  Е  Т  Ы  

	Вариант  1	Вариант  2
1	1,075	1,85
2	81	16
3	50	11310
4	0	-6
5	76	3,25
6	0,8	-0,75
7	4231	2134
8	3	0,5
9	0,4	0,12
10	2625	28000
11	20	10
12	25	13
С 1	( 0,5;  1,5)	( 5; 1 )
С 2	[log 5 2; log 5 3]	(-∞; 0] U[ log 3 8; 2)

3 новых варианта итоговой контрольной работы по математике 10 класс с ответами профильный уровень для подготовки к ЕГЭ 2022 и для проведения в конце 4 четверти учебного года, официальная дата проведения итоговой контрольной работы в формате ЕГЭ : 14.05.2022 (14 мая 2022 год).

Скачать тренировочный вариант №1

Скачать тренировочный вариант №2

Скачать тренировочный вариант №3

Скачать все ответы для вариантов

Решать онлайн вариант №1 по математике 10 класс:

1вариант_математика10класс_итоговая_контрольная

Решать онлайн вариант №2 по математике 10 класс:

2вариант_математика10класс_итоговая_контрольная

Решать онлайн вариант №3 по математике 10 класс:

3вариант_математика10класс_итоговая_контрольная

Сложные задания и ответы с 1 варианта:

2)В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси.

3)Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

5)Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.

8)Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч.

10)В ящике четыре красных и два синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету?

15)Планируется открыть вклад на 4 года, положив на счет целое число миллионов рублей. В конце каждого года сумма, лежащая на вкладе, увеличивается на 10%, а в начале третьего и четвертого года вклад пополняется на 3 миллиона рублей. Найдите наименьший первоначальный вклад, при котором начисленные проценты за весь срок будут более 5 миллионов рублей.

16)Окружность касается стороны AC остроугольного треугольника ABC и делит каждую из сторон AB и BC на три равные части. а) Докажите, что треугольник ABC равнобедренный. б) Найдите, в каком отношении высота этого треугольника делит сторону BC.

18)На доске написано 30 различных натуральных чисел, десятичная запись каждого из которых оканчивается или на цифру 2, или на цифру 6. Сумма написанных чисел равна 2454. а) Может ли на доске быть поровну чисел, оканчивающихся на 2 и на 6? б) Может ли ровно одно число на доске оканчиваться на 6? в) Какое наименьшее количество чисел, оканчивающихся на 6, может быть записано на доске?

Сложные задания и ответы с 2 варианта:

2)На олимпиаде по русскому языку 250 участников разместили в трёх аудиториях. В первых двух удалось разместить по 120 человек, оставшихся перевели в запасную аудиторию в другом корпусе. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.

3)Найдите хорду, на которую опирается угол 120°, вписанный в окружность радиуса √3.

5)Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.

8)Имеется два сплава. Первый содержит 10% никеля, второй  - 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

10)В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.

15)15-го января планируется взять кредит в банке на сумму 2,4 млн рублей на 24 месяца. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Какую сумму нужно выплатить банку в первые 12 месяцев?

18)На доске написано более 27, но менее 45 целых чисел. Среднее арифметическое этих чисел равно −5, среднее арифметическое всех положительных из них равно 9, а среднее арифметическое всех отрицательных из них равно −18. а) Сколько чисел написано на доске? б) Каких чисел написано больше: положительных или отрицательных? в) Какое наибольшее количество положительных чисел может быть среди них?

Сложные задания и ответы с 3 варианта:

2)На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.

3)Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.

5)Объем первого куба в 8 раз больше объема второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

8)Первый насос наполняет бак за 20 минут, второй — за 30 минут, а третий — за 1 час. За сколько минут наполнят бак три насоса, работая одновременно?

10)Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства  — яйца высшей категории, а из второго хозяйства  — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

15)Необходимо произвести отделку здания, имеющего форму прямоугольного параллелепипеда объемом 432 м3 . Отделка стены здания, примыкающей к внутреннему строению, обходится в 1000 руб. за квадратный метр. Отделка трех фасадных стен обходится в 2000 руб. за квадратный метр. А заливка крыши, форма которой является квадратом, обходится в 7000 руб. за квадратный метр. Найдите размеры здания, отделочные работы которого при данных условиях являются наименьшими по стоимости.

16)Четырёхугольник ABCD вписан в окружность, причем сторона CD — диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке Е, а окружность — в точке F, причем H — середина AE.

18)Красный карандаш стоит 17 рублей, синий — 13 рублей. Нужно купить карандаши, имея всего 495 рублей и соблюдая дополнительное условие: число синих карандашей не должно отличаться от числа красных карандашей больше, чем на пять. а) Можно ли купить при таких условиях 32 карандаша? б) Можно ли купить при таких условиях 35 карандашей? в) Какое наибольшее число карандашей можно купить при таких условиях?

Другие тренировочные варианты ЕГЭ по математике для 11 класса:

• Математика 10 класс полугодовая контрольная работа 2 варианта с ответами

• Тренировочные варианты ЕГЭ 2022 по математике 11 класс задания с ответами

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ В ФОРМЕ ЕГЭ В 10 КЛАССЕ

Пояснительная записка

Контрольная работа содержит 11 заданий базового уровня (4 варианта), которые соответствуют структуре заданий демонстрационной версии ЕГЭ 2015 базового уровня. Время выполнения – 90 минут. К каждому заданию требуется дать краткий ответ, представленный в виде целого числа, промежутка и конечной десятичной дроби.

За выполнение каждого задания ученик получает 1 балл .

Таблица перевода тестовых баллов в школьные отметки.

Тестовый балл	Школьная отметка
0-4	2
5-6	3
7-8	4
10-11	5

Распределение заданий контрольной работы по основным содержательным блокам

№	Тема
1	Вычисления и преобразования
2	Преобразование выражений, содержащих степень
3	Проценты
4	Иррациональные уравнения
5	Корень степени n.
6	Логарифмические уравнения
7	Тригонометрические формулы
8	Задачи практического содержания
9	Логарифмы
10	Показательные уравнения
11	Задачи практического содержания

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ В ФОРМЕ ЕГЭ В 10 КЛАССЕ
ВАРИАНТ I
1
2
3
4
5
6
7
8
9
10
11

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ В ФОРМЕ ЕГЭ В 10 КЛАССЕ
ВАРИАНТ II
1
2
3
4
5
6
7
8
9
10
11

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ В ФОРМЕ ЕГЭ В 10 КЛАССЕ
ВАРИАНТ III
1
2
3
4
5
6
7
8
9
10
11

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ В ФОРМЕ ЕГЭ В 10 КЛАССЕ
ВАРИАНТ IV
1
2
3
4
5
6
7
8
9
10
11

17 мая 2022

В закладки

Обсудить

Жалоба

Работа включает в себя 10 заданий и состоит из двух частей.

Ответом в заданиях первой части (0–9) является целое число или десятичная дробь. В заданиях второй части (12,13.14) требуется записать подробное решение и ответ. При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором.

2 варианта с ответами: k10egem.pdf

Источник: vk.com/ekaterina_chekmareva

ИТОГОВАЯ

контрольная работа

по алгебре и началам анализа

10 класс

в форме ЕГЭ

Работа  рассчитана на два урока.

Оценка «3» выставляется
за любые 5 верно выполненных заданий.

Оценка «4» выставляется
за любые 8 верно выполненных заданий или за любые 6 заданий из части А и 1
задания из частей В или С.

Оценка «5» выставляется
за любые 9 верно выполненных заданий.

Вариант I

А1.       Упростите выражение     

1)
0                           3)   sin2α

2)
1                            4)  cos2α

A2     Решите уравнение

             

           1) , n € Z           3) , n € Z

           2)  , n €Z    4) , n € Z

A3 Решите неравенство

                    

          1) (-∞; — 6)                     3)
(- 1;

         2) [-3; 7]                        4)
[0; +∞)

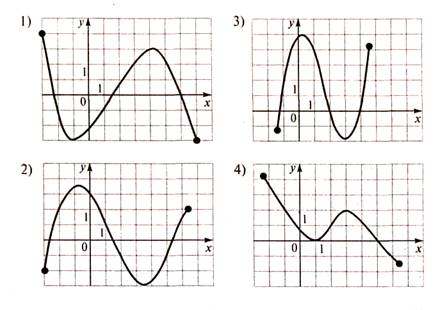
А4   На рисунке изображен график функции, заданной на
промежутке  Укажите множество значений этой
функции.

        1)

        2)

        3)

        4)

А5.  Найдите множество значений функции        

           1) [0; 4]                           3) [3;
∞)

           2) [3; 4]                            4) (3; 4)

А6. Найдите производную функции   

           1)            3) 

           2)             4)

A7. Найдите угловой коэффициент касательной, проведенной к графику
функции      в его точке с абсциссой  

          1)  — 18                               3) – 21

          2) 22                                   4) 17

B1.  Найдите значение выражения 1,5 – 3,4cosx, если sinx=

В2.Найдите значение функции у=f(-x)g(x)-g(-x) в точке x₀, если известно, что функция  y=f(x) – четная, функция y=g(x)-нечетная,  y=f(x₀)=-3, y=g(x₀)=-2

C1. Найдите наибольшее и наименьшее значение заданной функции на заданном
промежутке

    

Вариант II

А1. Упростите выражение      

         1) ;                       3)
;

         2) ;                           4)
.

A2     Решите уравнение

             

A3 Решите неравенство

А4   На одном из рисунков изображен
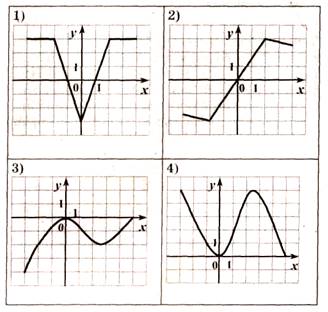
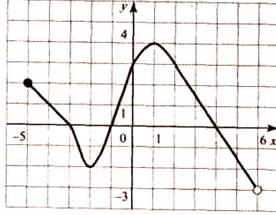
график четной функции. Укажите это рисунок.

А5. Найдите множество значений
функции  

         1) [-2; 2]                        3)
[-5; 5]

         2) [3; 7 ]                         4)
[-1; 1]

А6. Найдите производную функции .

   1) ;    
2) ;    

   3) ;    
4) .

A7. . Найдите угловой коэффициент касательной, проведенной к
графику функции  в его точке с абсциссой .

   1) 16;     2) 17;     3) 0,3;    
4) 0.

B1.  Найдите значение выражения, если sinx=

В2. Функция y=f(x) определена на всей числовой прямой и является периодической
с периодом 5. На промежутке (-1;4] она задается формулой  f(x)=х²-2х-1. Найдите значение выражения 3f(7)-4f(-3).

 C1. Найдите
наибольшее значение функции

f(x)=3(2x-4)⁴-(2x-4)⁵

при

Вариант III

А1. Упростите выражение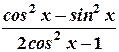      

         1) 1;                               3)
;

         2) ;                           4)
.

А2. Решите уравнение sinx=1

         1) ;             3) ;

         2) ;               4) .

А3. Решите неравенство

         1);                                       3);

         2);                                    4).

А4. На рисунке изображен график
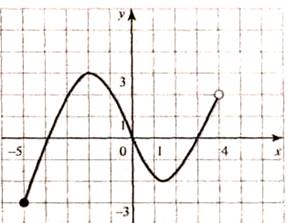
функции, заданной на промежутке  Укажите
множество значений этой функции.

        1)

        2)

        3)

        4)

А5. Найдите множество значений
функции  

         1) [2; 4]                         3)
[-2; 6]

         2) [3; 5]                         4)
[-1; 1]

А6. Найдите производную функции  .

         1) ;            3) ;

         2) ;             4)
.

А7. Найдите угловой коэффициент
касательной, проведенной к графику функции         в
его точке с абсциссой .

         1) 4                                3)
2

         2) 1                                4)
5

В1. Найдите значение выражения, если cosx=

В2. Периодическая четная функция у=f(x) определена для всех действительных чисел. Ее период равен
6. Найдите значения выражения , если f(5)=3.

С1. Найдите наибольшее значение
функции

f(x)=50(0.5x-1)²-(0.5x-1) при

Вариант IV

А1. Упростите выражение      

         1) ;                          3)
;

         2) ;                       4) 4.

А2. Решите уравнение

         1) ;               3) ;

         2) ;            4) .

А3 Решите неравенство

     

         1) ;                                  3);

         2) ;                                     4)
.

А4.  На каком из следующих рисунков
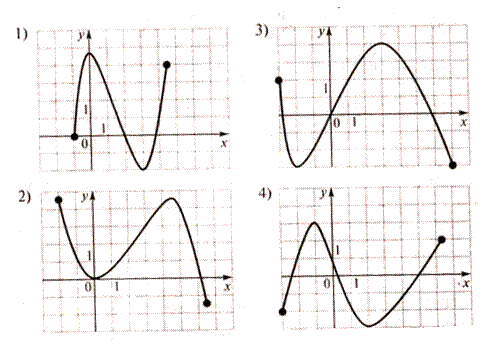
изображен график функции, возрастающей на промежутке

А5. Найдите множество значений
функции  

         1) [-4; 6]                        3)
[0; 2]

         2) [-2; 2]                        4)
[4; 6]

А6. Найдите производную функции  .

         1) ;          3) ;

         2) ;         4) .

А7. Найдите угловой коэффициент
касательной, проведенной к графику функции         в
его точке с абсциссой .

         1) 3                                3)
1

         2) 8                                4)
7

В1. Найдите ,
если cosx=

В2. Функция y=f(x) определена на всей числовой прямой
и является периодической с периодом 5. На промежутке  она
задается формулой f(x)=1+2x—x². Найдите значение выражения 2f(-15)+3f(18).

С1. . Найдите наибольшее значение
функции

f(x)=32(0.5x-3)²-(0.5x-3) при

Вариант V

А1. Упростите выражение     

         1) ;                         3)
;

         2) 2;                               4) .

А2. Решите уравнение  

         1) ;                 3)

         2) ;              4) .

А3. Решите неравенство

     

         1) ;                              
3);

         2) ;                                           
4) .

А4.

А5. Найдите множество значений
функции  

         1) [-1; 3]                        3)
[-4; 4]

         2) [-1; 7]                        4)
(-∞; 3]

А6. Найдите производную функции  .

         1) ;          3) ;

         2) ;        4) .

А7. Найдите угловой коэффициент
касательной, проведенной к графику функции         в
его точке с абсциссой .

         1) 18                              3)
11

         2) 23                              4)
8

В1. Найдите ,
если cosx=

В2. Периодическая четная функция у=f(x) определена для всех действительных чисел. Ее период равен
6. Найдите значения выражения , если f(5)=3.

С1. Найдите наибольшее значение
функции

f(x) =  при

Вариант VI

А1. Упростите выражение    1-sinx ctgx cosx 

         1)0                                 3)
1-sin2x;

         2);                        4)sin²x.

А2. Решите уравнение sin2x=-1

         1) ;            3)

         2) ;            4) .

А3. Решите неравенство

         1) ;                        3);

         2)                       4) .

А4. На каком из следующих рисунков
изображен график функции, убывающей на промежутке [3;7]?

А5. Найдите множество значений
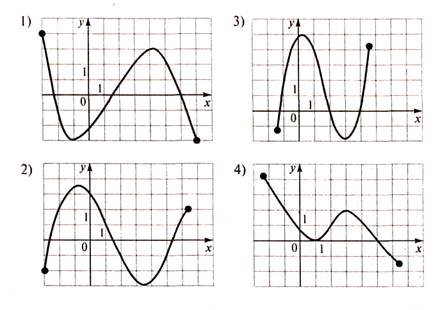
функции  

         1) [-4; 2]                        3)
[2; 6]

         2) [-1; 1]                        4)
[-2; 6]

А6. Найдите производную функции  .

         1) ;          3) ;

         2) ;          4) .

А7. Найдите угловой коэффициент
касательной, проведенной к графику функции         в
его точке с абсциссой .

         1) 7                                3)
0

         2) 1                                4)
5

В1. . Найдите ,
если cosx=

В2. Функция
y=f(x) определена на
всей числовой прямой и является периодической с периодом 5. На промежутке  она задается формулой f(x)=1+2x—x². Найдите значение выражения 2f(-15)+3f(18).

С1. Найдите наибольшее значение
функции

f(x) =  при .

Вариант VII

А1. Упростите выражение      

         1)                           3)

         2)                            4)
1.

А2. Найдите все решения уравнения    

         1)                      3)

         2)                4)

А3. Определите число целых решений
неравенства  

         1) 1;                               3)
3;

         2) 2;                               4)
4.

А4. Функция задана графиком. Укажите
область определения этой функции.

1) [-1; 2]

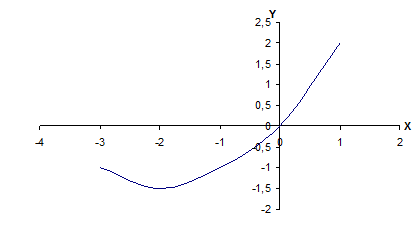
2) [0;  1]

3) [-3; 1]

4) [-3; 0]

А5. Найдите множество значений
функции  

         1) [-2; 2]                        3)
[-5; 5]

         2) [3; 7 ]                         4)
[-1; 1]

А6. Найдите производную функции  .

         1) ;          3) ;

         2) ;          4) .

А7. Найдите угловой коэффициент
касательной, проведенной к графику функции         в
его точке с абсциссой .

         1) 6                                3)
0

         2) 5                                4)
-4

В1. Укажите число корней уравнения   на промежутке  [-; ].

В2. Найдите наибольшее целое значение
функции

С1. Найдите все значения  р,
при которых уравнение   не имеет
корней.

ОТВЕТЫ НА ВАРИАНТЫ ТЕСТОВ

№ Вар. №Зад.	I	II	III	IV	V	VI	VII
А1	3	4	2	2	3	4	1
А2	1	2	1	3	1	2	4
А3	2	2	2	1	2	3	1
А4	3	2	4	1	4	4	3
А5	2	4	2	1	2	4	2
А6	2	3	4	4	1	2	2
А7	3	2	1	4	3	1	3
В1	3	7	4	0	3	3	7
В2	10	12	2	4	3	10	1
С1	(-∞; -5)U(5; ∞)	(-∞; 0)U(1; ∞)	(-∞; -3)U(5; ∞)	(-∞; -3)U(4; ∞)	(-∞; -4)U(9; ∞)	(-∞; -3)U(5; ∞)	(-∞; -5)U(11; ∞)

КИМ по математике

Учебный год: 2020 — 2021

Класс: 10 А, Б( профиль)

Структура работы: экзаменационная работа в формате ЕГЭ, включает материал 5 – 10 классов, состоит из 17 заданий.

Время работы: 3 часа

Дополнительные материалы и оборудование: при выполнении заданий разрешается пользоваться линейкой.

Таблица 1. Структура экзаменационной работы 10 класс 2021 г.

	Часть 1	Часть 2
Число заданий – 17	12	5
Тип заданий и форма ответа	1-12 с кратким ответом в виде целого числа или конечной десятичной дроби	13–17 с кратким ответом в виде целого числа или конечной десятичной дроби 13–17 с развёрнутым ответом (полная запись решения с обоснованием выполненных действий)
Назначение	Проверка освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях	Проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне
Уровень сложности	Базовый	Повышенный (13-16), высокий (17),
Проверяемый учебный материал курсов математики	1. Математика 5–6-х классов 2. Алгебра 7–9-х классов 3. Алгебра и начала анализа 10 класса 4. Планиметрия (7-9 кл.), стереометрия (10 кл.)	1. Алгебра 7–9-х классов 2. Алгебра 10 класса 3. Геометрия: планиметрия (7-9 кл.), стереометрия (10 кл.)

Таблица 2. Распределение заданий экзаменационной работы по содержанию

Содержательные блоки	Число заданий	Максимальный балл
Текстовые задачи: на пропорции, проценты, процентное содержание	2	2
Найти значение выражения: корни n-й степени, степени, логарифмы, тригонометрические выражения	4	4
Уравнения и неравенства	6	10
Функции	1	1
Геометрия	6	8
ИТОГО	17	24

Таблица 3. Распределение баллов по заданиям

№ задания	Кол-во баллов за задание	Примечания
1 — 12	1	1 балл, если дан верный ответ в виде целого числа или конечной десятичной дроби
13	2
14	2
15	2
16	3
17	3

Таблица 4. Система оценивания экзаменационной работы по математике10 класс

всего 21балл

Отметка по 5-ти балльной шкале	«2»	«3»	«4»	«5»
Первичный балл (соответствует количеству верно выполненных заданий	0 — 6	7 — 10	11 — 14	15 — 21

Общие требования к выполнению заданий с развёрнутым ответом: Количество баллов, выставляемых за выполнение заданий 13–17, зависит от полноты решения и правильности ответа. Решение должно быть математически грамотным, полным, в частности все возможные случаи должны быть рассмотрены. Методы решения, формы его записи и формы записи ответа могут быть разными. За решение, в котором обоснованно получен правильный ответ, выставляется максимальное количество баллов. Правильный ответ при отсутствии текста решения оценивается в 0 баллов. При выполнении задания можно использовать без доказательства и ссылок любые математические факты, содержащиеся в учебниках и учебных пособиях, входящих в Федеральный перечень учебников, рекомендованных (допущенных) Министерством образования и науки Российской Федерации.

Экзаменационная работа по алгебре в формате ЕГЭ-2021

Выполнена: ФИО_______________________Класс________

Вариант 1 10 класс

Инструкция по выполнению работы.

Работа состоит из двух частей, включающих в себя 17 заданий.

Первая часть содержит 12 заданий, вторая-5.

При выполнении работы нельзя пользоваться учебником, рабочими тетрадями, другими справочными материалами, калькулятором.

При необходимости можно пользоваться черновиком. Записи в черновике не проверяются, .и оцениваться не будут.

Выполнять задания можно в любом порядке. Главное — правильно решить как можно больше заданий. Советуем Вам для экономии времени пропускать задание, которое не удается решить сразу, и переходить к следующему. Если после выполнения всей работы у Вас останется время, можно будет вернуться к пропущенным заданиям.

Желаем успеха!

Часть 1

Ответом на задания 1-12 должно быть целое число или конечная десятичная дробь. Ответ следует записывать в бланк работы. Единицы измерений писать не нужно.

№ 1.

Ответ:____________________________

№ 2.

Ответ:____________________________

Решите уравнение .

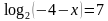
Ответ:____________________________

5

Найдите корень уравнения .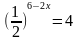

Ответ:____________________________

Ответ:____________________________

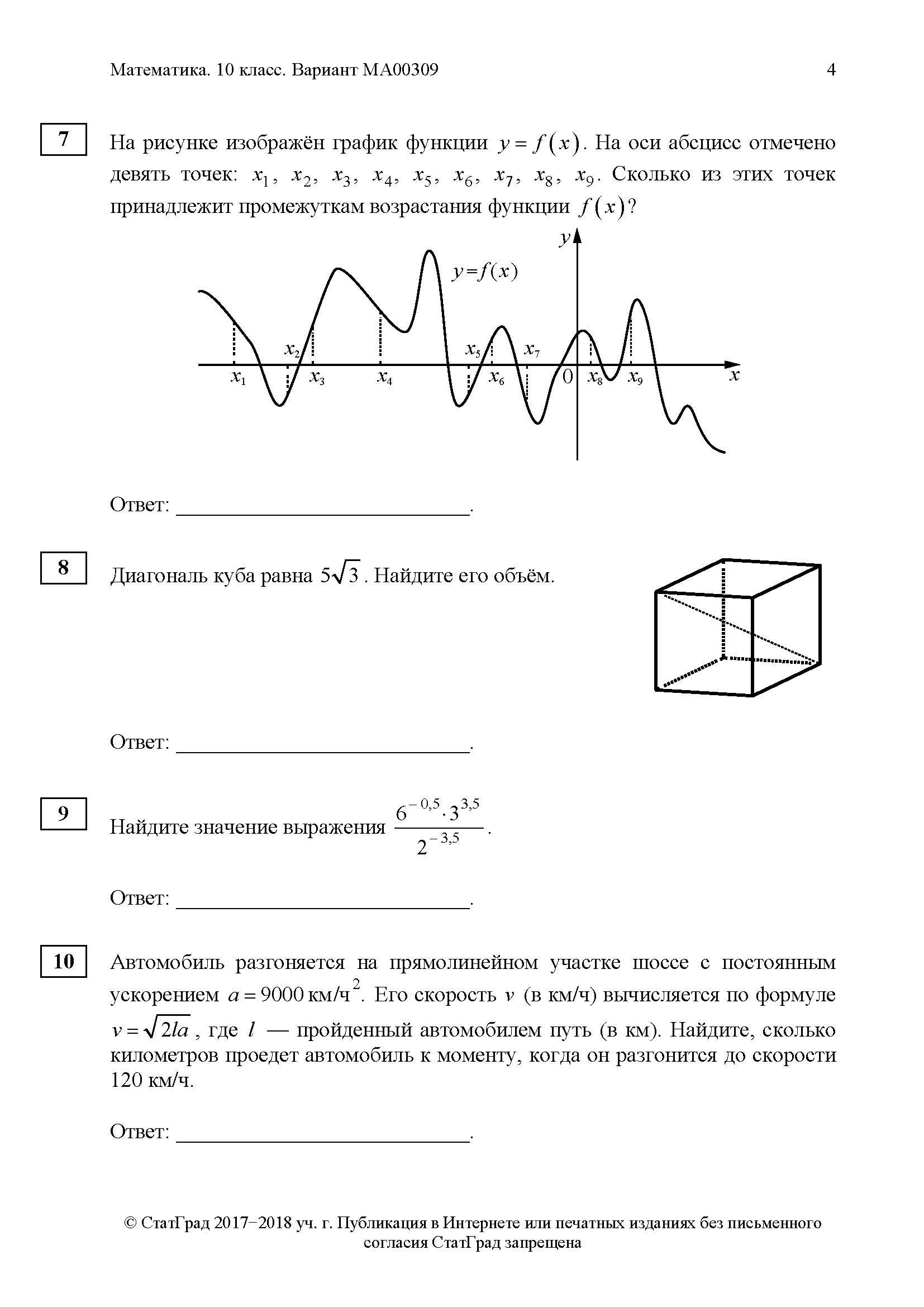
Ответ:____________________________

 Найдите значение выражения  Ответ:____________________________

Ответ:____________________________

Ответ:____________________________

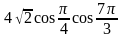
Для записи решений и ответов на задания 13 — 17 используйте чистый лист. Запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ. Ответы записывайте четко и разборчиво.

№13

а) Ре­ши­те урав­не­ние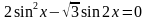  

б) Ука­жи­те корни этого уравнения, при­над­ле­жа­щие от­рез­ку  .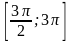

В правильной треугольной призме ABCA₁B₁C₁ сторона основания     а боковое ребро AA₁ = 5.

а) Найдите длину отрезка A₁K, где K — середина ребра BC.

б) Найдите тангенс угла между плоскостями BCA₁ и BB₁C₁.

№15.

Решите неравенство: 

Ольга хочет взять в кредит в сумме 100 000 рублей под 10% годовых. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. На какое минимальное количество лет Ольга может взять кредит, чтобы ежегодные выплаты были не более 24 тысяч рублей?

Экзаменационная работа по алгебре в формате ЕГЭ-2021

Выполнена: ФИО_______________________Класс________

Вариант 2 10 класс

Инструкция по выполнению работы.

Работа состоит из двух частей, включающих в себя 17 заданий.

Первая часть содержит 12 заданий, вторая-5.

При выполнении работы нельзя пользоваться учебником, рабочими тетрадями, другими справочными материалами, калькулятором.

При необходимости можно пользоваться черновиком. Записи в черновике не проверяются, .и оцениваться не будут.

Выполнять задания можно в любом порядке. Главное — правильно решить как можно больше заданий. Советуем Вам для экономии времени пропускать задание, которое не удается решить сразу, и переходить к следующему. Если после выполнения всей работы у Вас останется время, можно будет вернуться к пропущенным заданиям.

Желаем успеха!

Часть 1

Ответом на задания 1-12 должно быть целое число или конечная десятичная дробь. Ответ следует записывать в бланк работы. Единицы измерений писать не нужно.

№1

№2

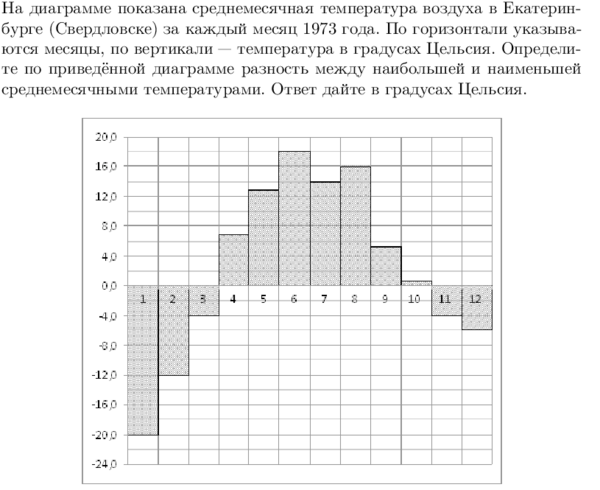
№3

Решите уравнение .

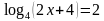
5

Найдите корень уравнения 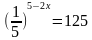. Найдите значение выражения

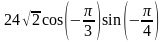
Для записи решений и ответов на задания 13 — 17 используйте чистый лист. Запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ. Ответы записывайте четко и разборчиво.

В правильной треугольной призме ABCA₁B₁C₁ сторона основания    а боковое ребро AA₁ = 8.

а) Докажите, что плоскость BCA₁ перпендикулярна плоскости проходящей через ребро AA₁ и середину ребра B₁C₁.

б) Найдите тангенс угла между плоскостями BCA₁ и BB₁C₁.

№15.

Решите неравенство: 

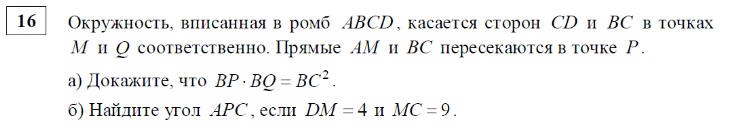
Оля хочет взять в кредит 1 200 000 рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10 % годовых. На какое минимальное количество лет может Оля взять кредит, чтобы ежегодные выплаты были не более 320 000 рублей?

Экзаменационная работа по алгебре в формате ЕГЭ-2021

Выполнена: ФИО_______________________Класс________

Вариант 3 10 класс

Инструкция по выполнению работы.

Работа состоит из двух частей, включающих в себя 17 заданий.

Первая часть содержит 12 заданий, вторая-5.

При выполнении работы нельзя пользоваться учебником, рабочими тетрадями, другими справочными материалами, калькулятором.

При необходимости можно пользоваться черновиком. Записи в черновике не проверяются, .и оцениваться не будут.

Выполнять задания можно в любом порядке. Главное — правильно решить как можно больше заданий. Советуем Вам для экономии времени пропускать задание, которое не удается решить сразу, и переходить к следующему. Если после выполнения всей работы у Вас останется время, можно будет вернуться к пропущенным заданиям.

Желаем успеха!

Часть 1

Ответом на задания 1-12 должно быть целое число или конечная десятичная дробь. Ответ следует записывать в бланк работы. Единицы измерений писать не нужно.

№1

№2

№3

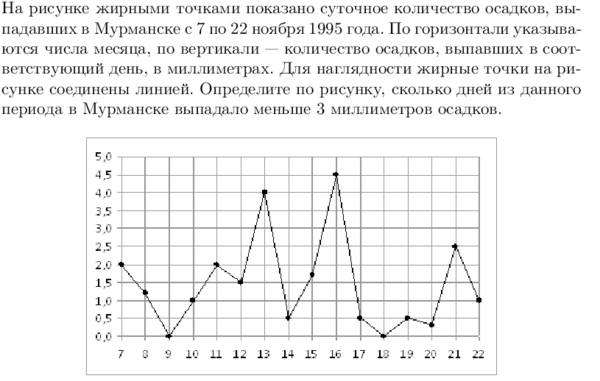
№4. Решите уравнение .

Ответ:____________________________

№5. Найдите корень уравнения .

Ответ:____________________________

№6

Ответ:____________________________

Ответ:____________________________

№8

Ответ:____________________________

№9 . Найдите значение выражения

Ответ:____________________________

№10

Ответ:____________________________

№11

Ответ:____________________________

№12

Ответ:____________________________

Для записи решений и ответов на задания 13 — 17 используйте чистый лист. Запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ. Ответы записывайте четко и разборчиво.

№13

а) Ре­ши­те урав­не­ние cos2x − 3cosx + 2 = 0.

б)Най­ди­те все корни уравнения, при­над­ле­жа­щие от­рез­ку 

№14

Дана правильная треугольная призма АВСА₁В₁С₁, все рёбра которой равны 6. Через точки A, С₁ и середину T ребра А₁В₁ проведена плоскость.

а) Докажите, что сечение призмы указанной плоскостью является прямоугольным треугольником.

б) Найдите угол между плоскостью сечения и плоскостью ABC.

№15

Решите неравенство: 

№16

Окружность проходит через вершины A, B и D параллелограмма ABCD, пересекает сторону BC в точках B и E и пересекает сторону CD в точках K и D.

а) Докажите, что AE = AK.

б) Найдите AD, если CE =12 , DK = 2 и 

№17.

Татьяна хочет взять в кредит 150 000 рублей под 10% годовых. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. На какое минимальное количество лет Ольга может взять кредит, чтобы ежегодные выплаты были не более 35 тысяч рублей?

Экзаменационная работа по алгебре в формате ЕГЭ-2021

Выполнена: ФИО_______________________Класс________

Вариант 4 10 класс

Инструкция по выполнению работы.

Работа состоит из двух частей, включающих в себя 17 заданий.

Первая часть содержит 12 заданий, вторая-5.

При выполнении работы нельзя пользоваться учебником, рабочими тетрадями, другими справочными материалами, калькулятором.

При необходимости можно пользоваться черновиком. Записи в черновике не проверяются, .и оцениваться не будут.

Выполнять задания можно в любом порядке. Главное — правильно решить как можно больше заданий. Советуем Вам для экономии времени пропускать задание, которое не удается решить сразу, и переходить к следующему. Если после выполнения всей работы у Вас останется время, можно будет вернуться к пропущенным заданиям.

Желаем успеха!

Часть 1

Ответом на задания 1-12 должно быть целое число или конечная десятичная дробь. Ответ следует записывать в бланк работы. Единицы измерений писать не нужно.

№1

Ответ:____________________________

№2

Ответ:____________________________

№3

Ответ:____________________________

№4. Решите уравнение .

Ответ:____________________________

№5 Найдите корень уравнения

Ответ:____________________________

№6 Ответ:____________________________

Ответ:____________________________

№8 Ответ:____________________________

№9. Найдите значение выражения .

Ответ:____________________________

№ 10

Ответ:____________________________

№11

Ответ:____________________________

№12

Ответ:____________________________

Для записи решений и ответов на задания 13 — 17 используйте чистый лист. Запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ. Ответы записывайте четко и разборчиво.

№13

а) Ре­ши­те урав­не­ние 

б) Ука­жи­те корни этого уравнения, при­над­ле­жа­щие от­рез­ку 

№14

Дана правильная треугольная призма АВСА₁В₁С₁, все рёбра которой равны 4. Через точки A, С₁ и середину T ребра А₁В₁ проведена плоскость.

а) Докажите, что сечение призмы указанной плоскостью является прямоугольным треугольником.

б) Найдите угол между плоскостью сечения и плоскостью ABC.

№15.

Решите неравенство: 

№16

Окружность проходит через вершины A, B и D параллелограмма ABCD, пересекает сторону BC в точках B и E и пересекает сторону CD в точках K и D.

а) Докажите, что AE = AK.

б) Найдите AD, если CE =10 , DK = 9 и 

№17

Тимофей хочет взять в кредит 1,1 млн рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Тимофей взять кредит, чтобы ежегодные выплаты были не большее 270 тысяч рублей?