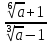Итоговая контрольная работа по геометрии 11 класс атанасян в форме егэ с ответами

Итоговая контрольная работа по геометрии 11 класс

Итоговая контрольная работа по геометрии 11 класс

1.  Образующая конуса равна 10 см, а радиус основания – 6 см. Найдите объем конуса. 
2. Объем шарасм3. Найдите радиус шара.
3. Сторона  основания правильной четырехугольной призмы 5см, а боковое ребро 12см. Вычислите объем призмы.
4. Осевое сечение цилиндра – квадрат со стороной 6 см. Найдите объем цилиндра.
5. Осевое сечение конуса – равносторонний треугольник со стороной 6 см. Найдите объем конуса.
6. Медиана, проведенная к гипотенузе прямоугольного треугольника равна 17 см, а один из катетов – 16 см. Найти радиус окружности, вписанной в треугольник.
7. Диагональ осевого сечения цилиндра равна 12 см и наклонена к плоскости его основания под углом . Найдите площадь боковой поверхности цилиндра.
8. Объем конуса равен 16π см3, а его высота 3см. Найдите площадь боковой поверхности конуса.
9. Основание прямой призмы прямоугольный треугольник с гипотенузой 10см и острым углом 300. Диагональ боковой грани, содержащей катет противолежащий данному углу, равна 13 см. Найдите объем призмы.

1. Образующая конуса равна 13 см, а высота – 12 см. Найдите объем конуса. 
2. Площадь поверхности шара равна 144π см2. Найти объём данного шара.
3. Сторона основания правильной треугольной призмы 6см, а боковое ребро 10см. Вычислите объем призмы.
4. Осевое сечение цилиндра – квадрат со стороной 8 см. Найдите объем цилиндра.
5. Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π.
6. Медиана, проведенная к гипотенузе прямоугольного треугольника равна 13 см, а один из катетов равен 24 см. Найти радиус окружности, вписанной в треугольник.
7. Диагональ осевого сечения цилиндра равнасм и наклонена к плоскости его основания под углом . Найдите площадь боковой поверхности цилиндра.
8. Площадь боковой поверхности конуса равна 20, а его образующая   5 см. Найдите объем конуса.
9. Основание прямой призмы прямоугольный треугольник с катетом 3см и прилежащим углом 600. Диагональ боковой грани,  содержащей  гипотенузу  треугольника, 10см. Найдите объем призмы.

Представлено 10 вариантов

Каждый вариант состоит из трех частей, которые отличаются по сложности и форме содержания заданий.

В І части контрольной работы предложены пять заданий. Записывать следует только ответ. Правильный ответ оценивается одним баллом.

ІІ часть контрольной работы состоит из двух заданий. Решение может иметь краткую запись решения без обоснования. Правильное решение каждого задания этой части оценивается двумя баллами.

ІІІ часть контрольной работы состоит из одного задания. Решение должно иметь развернутую запись. Правильное решение оценивается тремя баллами.

Сумма баллов начисляется за правильно выполненные задания в соответствии с максимально возможным количеством предложенных баллов для каждой части (5; 4; 3 – всего 12 баллов). При переводе в 5-и бальную систему оценивания предлагается следующая шкала перевода баллов в оценку:

11 – 12 баллов − «5»;

8 – 10 баллов − «4»;

4 – 7 баллов – «3»;

1 – 3 балла – «2»;

0 баллов – «1».

Критерии оценивания заданий.

Максимальное количество балл за всю работу – 12.

Критерии оценивания

Отметка	Процент
5	91 – 100
4	66 – 90
3	33 – 65
2	8 – 32

Соответствие количества набранных баллов, оценке по пятибалльной системе оценивания учебных достижений учащихся приведено в таблице:

Количество набранных баллов	Оценка по пятибалльной системе оценивания учебных достижений учащихся
11 – 12	5
8 – 10	4
4 – 7	3
1 – 3	2
0	1

І часть №: 1-5 (1 балл за каждое задание)

Содержание критерия	Баллы
Получен верный ответ	1
Получен неверный ответ	0
Максимальный балл	1

ІІ часть №: 6 — 7 (2 балла за каждое задание)

Содержание критерия	Баллы
Обучающийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ.	2
В решении допущена ошибка, не имеющая принципиального характера и не влияющая на общую правильность хода решения. Задача не доведена до конца при правильном ходе решения.	1
Решение отсутствует или допущены грубые ошибки, которые свидетельствуют о незнании предложенного материала.	0
Максимальный балл	2

ІІІ часть №: 8 (3 балла за задание )

Содержание критерия	Баллы
Обучающийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений с обоснованием, получен верный развёрнутый ответ.	3
В решении допущена ошибка, не имеющая принципиального характера и не влияющая на общую правильность хода решения с обоснованием ИЛИ при вычислении интеграла	2
Допущены ошибки или задача не доведена до конца при правильном ходе решения, или решение представлено кратко ИЛИ при составлении определенного интеграла для нахождения искомой площади ИЛИ при выполнении ряда вычислений, связанных с применением таблицы первообразных функции ИЛИ при вычислении интеграла	1
Решение отсутствует или допущены грубые ошибки, которые свидетельствуют о незнании предложенного материала	0
Максимальный балл	3

Вариант 1

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

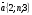
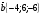
№1. При каком значении n векторы и коллинеарны.

Ответ: ________________________________

№2. Образующая конуса равна10 см, а радиус основания – 6 см.

Найдите объем конуса.

Ответ: ________________________________

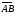
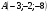
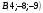
№3. Найдите координаты векторы , если и

.

Ответ: ________________________________

№4. Сторона основания правильной четырехугольной призмы 5см, а

боковое ребро 12см. Вычислите объем призмы.

Ответ: ________________________________

№5. Осевое сечение цилиндра – квадрат со стороной 6 см. Найдите

объем цилиндра

Ответ: ________________________________

ІІ часть (4 балла)

Решение заданий 6– 7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.

№6. Медиана, проведенная к гипотенузе прямоугольного треугольника равна 17 см, а один из катетов – 16 см. Найти радиус окружности, вписанной в треугольник.

№7. В основании прямой призмы лежит ромб с острым углом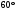 и

стороной 8 см. Найдите меньшую диагональ призмы, если ее боковое

ребро равно 6 см.

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

№8. Диагональ осевого сечения цилиндра равна 12 см и наклонена к

плоскости его основания под углом 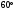. Найдите площадь боковой

поверхности цилиндра.

Вариант 2

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

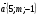
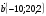
№1. При каком значенииm векторы и коллинеарны?

Ответ: ________________________________

№2. Образующая конуса равна 13 см, а высота – 12 см. Найдите объем

конуса.

Ответ: ________________________________

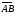
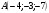
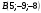
№3. Найдите координаты векторы , если и

.

Ответ: ________________________________

№4. Сторона основания правильной треугольной призмы 6см, а боковое ребро 10см. Вычислите объем призмы.

Ответ: ________________________________

№5. Осевое сечение цилиндра – квадрат со стороной 8см. Найдите

объем цилиндра

Ответ: ________________________________

ІІ часть (4 балла)

Решение заданий 6– 7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.

№6. Медиана, проведенная к гипотенузе прямоугольного треугольника равна 13 см, а один из катетов равен 24 см. Найти радиус окружности, вписанной в треугольник.

№7. В основании прямой призмы лежит ромб с острым углом 60^о и стороной 6см. Найдите меньшую диагональ призмы, если ее боковое ребро равно 8см.

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

№8. Диагональ осевого сечения цилиндра равнасм и наклонена к

плоскости его основания под углом. Найдите площадь боковой

поверхности цилиндра.

Вариант 3

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

№1. Найдите расстояние от точки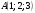 до начала координат.

Ответ: ________________________________

№2. В основании прямой призмы лежит ромб со стороной 6см. Высота

призмы равна 12см. Найдите площадь боковой поверхности призмы.

Ответ: ________________________________

№3. Внутренний угол правильного многоугольника при одной из его вершин равен 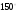. Сколько сторон имеет этот многоугольник?

Ответ: ________________________________

№4. Апофема правильной четырехугольной пирамиды 8 см, а сторона

основания 6 см. Найдите площадь боковой поверхности пирамиды.

Ответ: ________________________________

№5. Образующая конуса равна10 см, а радиус основания – 6 см.

Найдите объем конуса.

Ответ: ________________________________

ІІ часть (4 балла)

Решение заданий 6– 7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.

№6. Одна сторона треугольника равна, а две другие относятся как и образуют угол . Найти периметр треугольника.

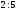
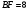
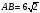
№7. Через вершину В квадрата ABCD проведена прямая BF, перпендикулярная к его плоскости. Найдите расстояние от точки F до прямой АС, если дм, дм.

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

№8. Расстояние от центра основания конуса до середины образующей равно 6 см. Угол между образующей и плоскостью основания равен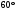. Найдите объем конуса.

Вариант 4

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

№1. Найдите расстояние от точки до начала координат.

Ответ: ________________________________

№2. В основании прямой призмы лежит ромб со стороной 5см. Высота

призмы равна 40см. Найдите площадь боковой поверхности призмы

Ответ: ________________________________

№3. Внутренний угол правильного многоугольника при одной из его

вершин равен . Сколько сторон имеет этот многоугольник?

Ответ: ________________________________

№4. Апофема правильнойтреугольнойпирамиды4 см, а сторона основания8 см. Найдите площадь боковой поверхности пирамиды.

Ответ: ________________________________

№5. Образующая конуса равна 13 см, а высота – 12 см. Найдите объем

конуса.

Ответ: ________________________________

ІІ часть (4 балла)

Решение заданий 6– 7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.

№6. Одна сторона треугольника равна, а две другие относятся как и образуют угол . Найти периметр треугольника.

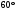
№7. Через вершину А прямоугольника ABCD проведена прямая АК, перпендикулярная к его плоскости. Известно, что см, см, см. Найдите расстояние между прямыми АК и ВC.

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

№8. Расстояние от центра основания конуса до образующей равно 3

см. Угол между образующей и плоскостью основания равен.

Найдите объем конуса.

Вариант 5

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

№1. При каком значении п векторы и будут перпендикулярными?

Ответ: ________________________________

№2. Объем шарасм³. Найдите радиус шара.

Ответ: ________________________________

№3. Дан параллелепипед . Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов

Ответ: ________________________________

№4. Объем треугольной пирамиды равен 24 дм³. Высота пирамиды

дм. Найдите площадь основания данной пирамиды.

Ответ: ________________________________

№5. В основании прямой призмы лежит ромб со стороной 6см. Высота

призмы равна 12см. Найдите площадь боковой поверхности призмы.

Ответ: ________________________________

ІІ часть (4 балла)

Решение заданий 6– 7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.

№6. Трапеция вписана в окружность. Ее основания равны 17 см и 11 см, а один из углов равен . Найти площадь трапеции.

№7. Осевое сечение конуса – прямоугольный треугольник, с катетом 6 см. Найдите объем конуса.

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

№8. Высота правильной четырехугольной пирамиды 4 см. Найдите

площадь боковой поверхности пирамиды, если двугранный угол при

основании равен.

Вариант 6

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

№1. При каком значении k векторы и будут перпендикулярными?

Ответ: ________________________________

№2. Площадь поверхности шара равна см². Найдите радиус шара.

Ответ: ________________________________

№3. Дан параллелепипед . Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов

Ответ: ________________________________

№4. Объем треугольной пирамиды равен 75дм³. Высота пирамиды

 дм. Найдите площадь основания данной пирамиды.

Ответ: ________________________________

№5. В основании прямой призмы лежит ромб со стороной 5см. Высота

призмы равна 40см. Найдите площадь боковой поверхности призмы

Ответ: ________________________________

ІІ часть (4 балла)

Решение заданий 6– 7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.

№6. Трапеция вписана в окружность. Ее основания равны 21 см и 5 см, а один из углов равен . Найти площадь трапеции.

№7. Осевое сечение конуса – равносторонний треугольник со стороной 6см. Найдите объем конуса.

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

№8. Сторона основания правильной четырехугольной пирамиды 10

см, а двугранный угол при основании равен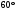. Найдите площадь

полной поверхности.

Вариант 7

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

№1. Длина дуги окружности равна см, а ее градусная мера – .

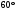
Найдите радиус окружности.

Ответ: ________________________________

№2. Осевое сечение цилиндра – квадрат со стороной 6 см. Найдите

объем цилиндра

Ответ: ________________________________

№3. Найдите радиус окружности,описанной около равнобедренного треугольника,если егооснование 6 см, а угол при вершине .

Ответ: ________________________________

№4. Объем шара см³. Найдите диаметр шара.

Ответ: ________________________________

№5. Внутренний угол правильного многоугольника при одной из его вершин равен 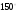. Сколько сторон имеет этот многоугольник?

Ответ: ________________________________

ІІ часть (4 балла)

Решение заданий 6– 7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.

№6. Сторона ромба равна 8см, тупой угол содержит. Найти площадь вписанного в ромб круга.

№7. Площадь боковой поверхности конуса равна см², а его

образующая равна 17см. Найдите объем конуса.

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

№8. В правильной треугольной призме диагональ боковой грани наклонена к плоскости основания под углом α. Определите площадь полной поверхности, если площадь основания равна S.

Вариант 8

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

№1. Длина дуги окружности равнасм, а ее градусная мера равна

. Найдите радиус

Ответ: ________________________________

№2. Осевое сечение цилиндра – квадрат со стороной 8см. Найдите

объем цилиндра

Ответ: ________________________________

№3. В треугольнике одна сторона равнасм, а противолежащий

угол равен . Найдите длину радиуса описанной окружности.

Ответ: ________________________________

№4. Диаметр шара равен 12см. Найдите объем шара.

Ответ: ________________________________

№5. Внутренний угол правильного многоугольника при одной из его

вершин равен . Сколько сторон имеет этот многоугольник?

Ответ: ________________________________

ІІ часть (4 балла)

Решение заданий 6– 7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.

№6. Сторона ромба равна см, тупой угол содержит. Найти площадь вписанного в ромб круга.

№7. Площадь боковой поверхности конуса равна см², а его образующая равна 13см. Найдите объем конуса.

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

№8. В правильной четырехугольной призме диагональ боковой грани наклонена к плоскости основания под углом β. Определите площадь полной поверхности, если площадь основания равна Q.

Вариант 9

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

№1. Какой координатной оси принадлежит середина отрезкаАВ с концами в точках и?

Ответ: ________________________________

№2. Основание прямой призмы− равнобедренный треугольник с

основанием 8см и боковой стороной 5см. Высота призмы равна 10см.

Найдите площадь боковой поверхности призмы.

Ответ: ________________________________

№3. В треугольнике MNKстороны MN=12см, МК=10см, MD– биссектриса, а отрезок KD=5см. Найдите DN.

Ответ: ________________________________

№4. Объем цилиндра . Найдите диаметр цилиндра основания, если высота цилиндра равна 1.

Ответ: ________________________________

№5. Объем треугольной пирамиды равен 24 дм³. Высота пирамиды

дм. Найдите площадь основания данной пирамиды.

Ответ: ________________________________

ІІ часть (4 балла)

Решение заданий 6– 7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.

№6. Найти площадь прямоугольной трапеции, большее основание которой равно 14 см, большая боковая сторона – 12 см, а острый угол равен .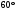

№7. В цилиндре на расстоянии 8 см от его оси и параллельно ей проведено сечение, диагональ которого равна 13 см. Вычислите радиус основания цилиндра, если его высота равна 5 см.

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

№8. В основании пирамиды лежит прямоугольный треугольник с катетом а и противолежащим острым углом α. Боковые ребра пирамиды образуют с плоскостью основания угол φ. Найдите объем пирамиды.

Вариант 10

І часть (5 баллов)

При выполнении заданий 1-5 следует записать только ответ. Верный ответ каждого задания оценивается одним баллом.

№1. Какой координатной оси принадлежит середина отрезка ABс концами в точках и?

Ответ: ________________________________

№2. Основанием прямой призмы является равнобедренный

треугольник с основанием 10 см и боковой стороной 6см. Высота

призмы равна 5см. Найдите площадь боковой поверхности призмы.

Ответ: ________________________________

№3. В треугольнике KMD стороны MD=16 см, МК=20см, MC–

биссектриса, а отрезок CD=4см. Найдите КC.

Ответ: ________________________________

№4. Объем цилиндра . Найдите высоту цилиндра, если диаметр основания равен 1.

Ответ: ________________________________

№5. Объем треугольной пирамиды равен 75дм³. Высота пирамиды

 дм. Найдите площадь основания данной пирамиды.

Ответ: ________________________________

ІІ часть (4 балла)

Решение заданий 6– 7 может иметь краткую запись без обоснования. Правильное решение каждого задания оценивается двумя баллами.

№6. Найти площадь прямоугольной трапеции, меньшее основание

которой равно 7 см, большая боковая сторона – 16 см, а тупой угол

равен .

№7. В цилиндре параллельно его оси проведено сечение, диагональ которого равна 17 см. Высота цилиндра 15 см, а радиус основания 5 см. На каком расстоянии от оси проведено это сечение?

III часть (3 балла)

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения. Правильное решение задания оценивается тремя баллами.

№8. Основанием пирамиды служит прямоугольный треугольник с острым углом β и гипотенузой с. Каждое боковое ребро пирамиды составляет с основанием угол α. Найдите объем пирамиды.

Ответы к вариантам

	№ 1	№ 2	№ 3	№ 4	№ 5	№ 6	№ 7	№ 8
Вариант 1		см3		300 см3	54π см3	6 см	10 см	см2
Вариант 2		см3		см3	128π см3	4 см	10 см	см2
Вариант 3		288 см2	12 сторон	96 см2	см3		10 дм	см3
Вариант 4		800 см2	10 сторон	48 см2	см3		см	см3
Вариант 5		2 см		дм2	288 см2	42 см2	см3	см2
Вариант 6		3 см		дм2	800 см2	104 см2	см	300 см2
Вариант 7	12 см	54π см3	6 см	6 см	12 сторон	4π см2	см
Вариант 8	36 см	128π см3	8 см	см3	10 сторон	9π см2	см
Вариант 9	оси Оz	180 см2	6 см	4	дм2	см2	10 см
Вариант 10	оси Оу	110 см2	5 см	4	дм2	см2	3 см

Годовая контрольная работа по геометрии 11 класс

Вариант 1

В задании 1 – 5 запиши ответ.

1. Найдите длину вектора АВ, если А( -1; 1; -1) и В(-1; 1; 1)

2. При каком значении к векторы а (6; 0; 12) и в (-8; 13; к) перпендикулярны?

3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами

 3 см и 4 см. Высота призмы 10 см. Найдите площадь полной поверхности.

4. Образующая конуса 10 см. Найдите объём конуса, если его высота

8 см

5.Осевое сечение цилиндра есть квадрат, диагональ которого равна 4√2 см. Вычислите объём цилиндра.

Решение заданий 6 – 7 может иметь краткую запись без обоснования.

6.Найдите объём правильной четырёхугольной пирамиды, боковое ребро которой равно 12 см и образует с плоскостью основания угол 600.

7. Образующая конуса составляет с плоскостью основания угол 450, высота конуса равна 3√2 см. Найдите площадь боковой поверхности конуса.

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения

8. В цилиндре на расстоянии 8 см от его оси и параллельно ей проведено сечение, диагональ которого равна 13 см. Вычислите радиус основания цилиндра, если его высота равна 5 см.

Годовая контрольная работа по геометрии 11 класс

Вариант 2

В задании 1 – 5 запиши ответ

1. Найдите координаты середины отрезка АВ, если А( 1; -1; -1) и В(1;- 1; 1)

2. При каком значении т векторы а (6; 0; 12) и в (т; 13; 4) перпендикулярны?

3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетом 5см и гипотенузой 13 см. Высота призмы 8 см. Найдите площадь полной поверхности

4. Образующая конуса 10 см. Найдите объём конуса, если диаметр основания равен 16 см.

5. Осевым сечением цилиндра является квадрат со стороной 8 см. Вычислите площадь боковой поверхности цилиндра.

Решение заданий 6 – 7 может иметь краткую запись без обоснования.

6. Найдите объём правильной четырёхугольной пирамиды, диагональ основания которой равна 4 см, а боковое ребро образует с плоскостью основания угол 450

7. Образующая конуса составляет с плоскостью основания угол 600 и равна 6√3 см. Найдите площадь боковой поверхности конуса

Решение 8 задания должно иметь обоснование. Необходимо записать последовательные логические действия и объяснения

8. В цилиндре параллельно его оси проведено сечение, диагональ которого равна 17 см. Высота цилиндра 15 см, а радиус основания 5см. На каком расстоянии от оси проведено это сечение?

Годовая контрольная работа по геометрии

в 11 классах

учебник авторов: Л. С. Атанасян, В. Ф Бутузов, С. Б. Кадомцев

задания в 2 вариантах.

Каждый вариант состоит из трех частей, которые отличаются по сложности и форме содержания заданий.

В І части контрольной работы предложены пять заданий. Записывать следует только ответ. Правильный ответ оценивается одним баллом.

ІІ часть контрольной работы состоит из двух заданий. Решение может иметь краткую запись решения без обоснования. Правильное решение каждого задания этого блока оценивается двумя баллами.

ІІІ часть контрольной работы состоит из одного задания. Решение должно иметь развернутую запись с обоснованием. Правильное решение оценивается тремя баллами.

Сумма баллов начисляется за правильно выполненные задания в соответствии с максимально возможным количеством предложенных баллов для каждой части (всего 12 баллов). При переводе в 5-и бальную систему оценивания предлагается следующая шкала перевода баллов в оценку:

11 — 12 баллов − «5»;

9 — 10 баллов − «4»;

6 — 8 баллов – «3»;

3 — 5 балла – «2»;

1 – 2 балла – «1».

Контрольные работы по геометрии в 11 классе с ответами по УМК Атанасян и др. (3 уровня сложности по 2 варианта) В учебных целях использованы цитаты из пособия «Поурочные разработки по геометрии. 11 класс / В.А. Яровенко — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 10-11 классы. Учебник для общеобразовательных организаций. М.: Просвещение». Геометрия 11 Контрольные работы + ОТВЕТЫ.

Геометрия 11 класс. Контрольные работы
по учебнику Л.С. Атанасяна и др.

---

Глава V. Метод координат в пространстве (уроки 1-15)

К-1 с ответами «Координаты точки и координаты вектора» (урок 7):

Контрольная работа № 1 + Ответы

К-2 с ответами «Скалярное произведение векторов в пространстве. Движения» (урок 14):

Контрольная работа № 2 + Ответы

Глава VI. Цилиндр, конус и шар (уроки 16-32)

К-3 с ответами «Тела вращения» (урок 29):

Контрольная работа № 3 + Ответы

Глава VII. Объемы тел (уроки 33-54)

К-4 с ответами «Объем призмы, цилиндра и конуса» (урок 46):

Контрольная работа № 4 + Ответы

К-5 с ответами «Объем шара и площадь сферы» (урок 53):

Контрольная работа № 5 + Ответы

Итоговое повторение курса геометрии 10-11 класс (уроки 55-68)

К-6. Самостоятельная работа на повторение.

К-7. Тесты на повторение.

ПОЯСНЕНИЯ

По прохождении каждой темы предусмотрена контрольная работа, состоящая из заданий трех уровней сложности, которые определяются или учителем, или самим учащимся (при этом число экземпляров вариантов должно быть достаточным). Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.

Каждая контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).

Смотрите также:

Геометрия 7 класс. Контрольные работы (Атанасян и др.)

Геометрия 8 класс. Контрольные работы (Атанасян и др.)

Геометрия 9 класс. Контрольные работы (Атанасян и др.)

Геометрия 10 класс. Контрольные работы (Атанасян и др.)

---

Вы смотрели: Геометрия 11 Контрольные работы по геометрии в 11 классе с ответами УМК Атанасян и др. (3 уровня сложности по 2 варианта). В учебных целях использованы цитаты из пособия «Поурочные разработки по геометрии. 11 класс / В.А. Яровенко — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 10-11 классы. Учебник. М.: Просвещение».

Итоговая
контрольная работа по геометрии в 11 классе

1
вариант

(в
заданиях 1-5 запишите ответы, в заданиях  6 и 7 – полное обоснованное решение и
ответ)

1.     В
правильной треугольной пирамиде SABC медианы основания пересекаются в точке К. Объем пирамиды равен 42, SK
=18. Найдите площадь треугольника АВС. (1балл)

2.     Высота
конуса равна 10, диаметр основания равен 48. Найдите образующую. (1 балл)

3.     Площадь
боковой поверхности цилиндра равна 72π, а высота  — 8. Найдите диаметр
основания. (1 балл)

4.      Цилиндр
и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если
объём конуса равен 10. (1 балл)

5.     Сторона
основания правильной треугольной призмы равна 2, а высота  — 4. Вычислите объём призмы
(1 балл)

6.     Площадь
боковой поверхности конуса равна 20, а
его образующая   5 см. Найдите объем конуса.( 2 балла)

7.     Основание
прямой призмы прямоугольный треугольник с катетом 3см и прилежащим углом 60⁰.
Диагональ боковой грани,  содержащей  гипотенузу  треугольника, 10см. Найдите
объем призмы. (2 балла)

2
вариант

1.    
В правильной треугольной пирамиде SABC медианы основания пересекаются в точке К. Объем пирамиды равен 88,
площадь треугольника АВС равна 11. Найдите SK.(1
балл)

2.    
Высота конуса равна 6, образующая -10.
Найдите диаметр основания конуса.(1 балл)

3.    
Площадь боковой поверхности цилиндра равна
96π, диаметр основания  — 8. Найдите высоту цилиндра. (1 балл)

4.    
Сторона основания правильной треугольной
призмы равна 3, а высота  — 5. Вычислите объём призмы
(1 балл)

5.    
Объем конуса равен 16π см³, а
его высота 3см. Найдите площадь боковой поверхности конуса. (2 балла)

6.    
Основание прямой призмы прямоугольный
треугольник с гипотенузой 10см и острым углом 30⁰. Диагональ боковой
грани, содержащей катет противолежащий данному углу, равна 13 см. Найдите объем
призмы.

 (3
балла)

Время
выполнения 1 урок.

Оценка
за работу

«5»
— 7-9 баллов

«4»
— 5-6 баллов

«3»
— 3-4 балла

«2»
— 2 и менее баллов

Варианты для подготовки к ЕГЭ (задания по геометрии)

Вариант № 1

1. Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 800 м и 300 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно огородить забором. Найдите длину этого забора. Ответ дайте в метрах.

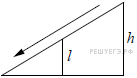
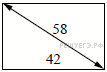
2. Электрику ро­стом 1,8 метра нужно по­ме­нять лампочку, закреплённую на стене дома на вы­со­те 4,2 м. Для этого у него есть лест­ни­ца дли­ной 3 метра. На каком наи­боль­шем рас­сто­я­нии от стены дол­жен быть уста­нов­лен ниж­ний конец лестницы, чтобы с по­след­ней сту­пень­ки элек­трик до­тя­нул­ся до лампочки? Ответ за­пи­ши­те в метрах.

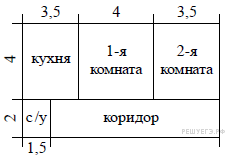
3. Квартира состоит из двух комнат, кухни, коридора и санузла (см. чертёж). Первая комната имеет размеры 4 м × 4 м, вторая — 4 м × 3,5 м, кухня имеет размеры 4 м × 3,5 м, санузел — 2 м × 1,5 м. Найдите площадь всей квартиры (в квадратных метрах).

4. Детская горка укреп­ле­на вер­ти­каль­ным столбом, рас­по­ло­жен­ным по­се­ре­ди­не спуска. Най­ди­те вы­со­ту l этого столба, если вы­со­та h горки равна 2 метрам. Ответ дайте в метрах.

5. Уча­сток земли имеет пря­мо­уголь­ную форму. Сто­ро­ны пря­мо­уголь­ни­ка 25 м и 70 м. Най­ди­те длину за­бо­ра (в метрах), ко­то­рым нужно ого­ро­дить участок, если в за­бо­ре нужно преду­смот­реть во­ро­та ши­ри­ной 4 м.

6.

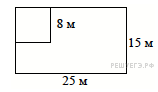
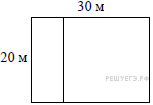
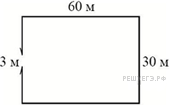
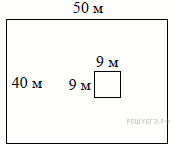
Дачный участок имеет форму прямоугольника со сторонами 25 метров и 15 метров. Хозяин отгородил на участке квадратный вольер со стороной 8 метров (см. рисунок). Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах.

7. Дачный уча­сток имеет форму пря­мо­уголь­ни­ка со сто­ро­на­ми 20 мет­ров и 30 метров. Хо­зя­ин пла­ни­ру­ет об­не­сти его за­бо­ром и раз­де­лить таким же за­бо­ром на две части, одна из ко­то­рых имеет форму квадрата. Най­ди­те общую длину за­бо­ра в метрах.

8. Детская горка укреп­ле­на вер­ти­каль­ным столбом, рас­по­ло­жен­ным по­се­ре­ди­не спуска. Най­ди­те вы­со­ту l этого столба, если вы­со­та h горки равна 2 метрам. Ответ дайте в метрах.

9. Пол в комнате, имеющей форму прямоугольника со сторонами 4 м и 6 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 30 см. Сколько потребуется таких дощечек?

10. Уча­сток земли имеет пря­мо­уголь­ную форму. Сто­ро­ны пря­мо­уголь­ни­ка 30 м и 60 м. Най­ди­те длину за­бо­ра (в метрах), ко­то­рым нужно ого­ро­дить участок, если в за­бо­ре нужно преду­смот­реть во­ро­та ши­ри­ной 3 м.

11. Объем куба равен 8. Най­ди­те площадь его поверхности.

12. Шар впи­сан в цилиндр. Пло­щадь по­верх­но­сти шара равна 48. Най­ди­те пло­щадь пол­ной по­верх­но­сти цилиндра.

13. Плоскость, про­хо­дя­щая через точки A, B и C, рас­се­ка­ет тетраэдр на два мно­го­гран­ни­ка (см. рисунок). Сколь­ко вершин у по­лу­чив­ше­го­ся многогранника с боль­шим числом граней?

14. В прямоугольном параллелепипеде  известно, что , , . Найдите длину диагонали .

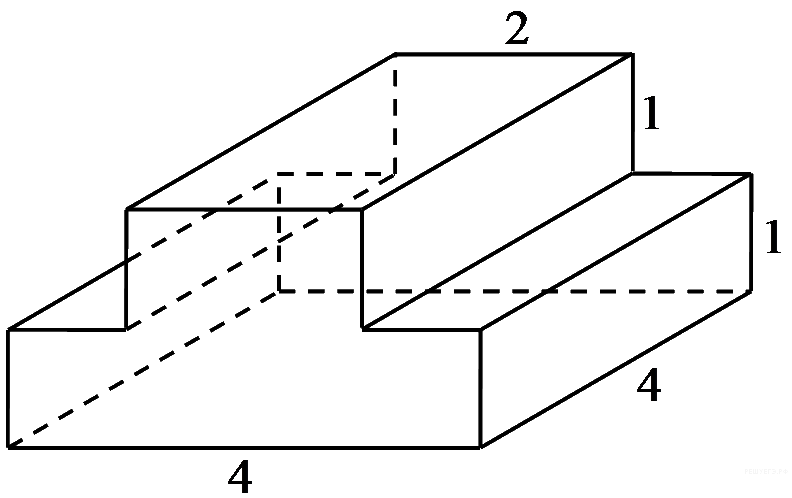
15. Найдите пло­щадь поверхности многогранника, изоб­ра­жен­но­го на ри­сун­ке (все дву­гран­ные углы прямые).

16.В бак цилиндрической формы, площадь основания которого равна 80 квадратным сантиметрам, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 15 см. Ответ дайте в кубических сантиметрах.

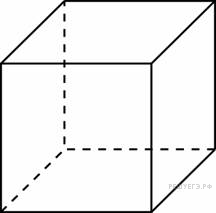
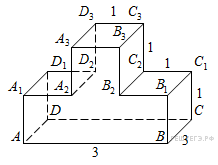
17. Найдите квадрат расстояния между вершинами  и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

18. Даны два шара с ра­ди­у­са­ми 3 и 1. Во сколь­ко раз пло­щадь поверхности пер­во­го шара боль­ше площади по­верх­но­сти второго?

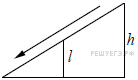
19. Площадь боковой поверхности цилиндра равна , а высота — 1. Найдите диаметр основания.

20. Найдите объем многогранника, изоб­ра­жен­но­го на ри­сун­ке (все дву­гран­ные углы прямые).

Ключ Вариант № 1

№ п/п	Ответ
1	1400
2	1,8
3	66
4	1
5	186
6	311
7	120
8	1
9	800
10	177
11	24
12	72
13	6
14	27
15	60
16	1200
17	11
18	9
19	2
20	93

Вариант № 2

1. Участок земли для строительства дачи имеет форму прямоугольника, стороны которого равны 40 м и 30 м. Одна из больших сторон участка идёт вдоль реки, а три остальные стороны нужно огородить забором. Найдите длину этого забора. Ответ дайте в метрах.

2. Квартира состоит из двух комнат, кухни, коридора и санузла (см. чертёж). Первая комната имеет размеры 3,5 м × 4,5 м, вторая — 3,5 м × 3 м, санузел имеет размеры 1,5 м × 2 м, длина коридора — 9 м. Найдите площадь всей квартиры (в квадратных метрах).

3. Диагональ пря­мо­уголь­но­го те­ле­ви­зи­он­но­го экра­на равна 58 см, а ши­ри­на экра­на — 42 см. Най­ди­те вы­со­ту экрана. Ответ дайте в сантиметрах.

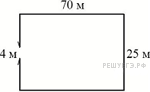
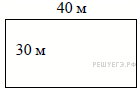
4. Рыболовное хо­зяй­ство строит бас­сейн для раз­ве­де­ния рыбы. Бас­сейн имеет форму пря­мо­уголь­ни­ка со сто­ро­на­ми 4 м и 12 м. В цен­тре бас­сей­на находится тех­ни­че­ская постройка, ко­то­рая имеет форму пря­мо­уголь­ни­ка со сто­ро­на­ми 2 м и 3 м. Най­ди­те площадь остав­шей­ся части бассейна.

5. Уча­сток земли имеет пря­мо­уголь­ную форму. Сто­ро­ны пря­мо­уголь­ни­ка 25 м и 70 м. Най­ди­те длину за­бо­ра (в метрах), ко­то­рым нужно ого­ро­дить участок, если в за­бо­ре нужно преду­смот­реть во­ро­та ши­ри­ной 4 м.

6.

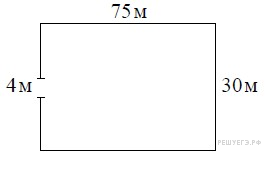
Участок земли имеет пря­мо­уголь­ную форму. Сто­ро­ны пря­мо­уголь­ни­ка равны 30 м и 75 м. Най­ди­те длину за­бо­ра (в метрах), ко­то­рым нужно ого­ро­дить участок, если в за­бо­ре преду­смот­рен про­езд ши­ри­ной 4 м.

7. План мест­но­сти раз­бит на клетки. Каж­дая клет­ка обо­зна­ча­ет квад­рат 1м × 1м . Най­ди­те пло­щадь участка, вы­де­лен­но­го на плане. Ответ дайте в квад­рат­ных метрах.

8. Дачный участок имеет форму прямоугольника, стороны которого равны 40 м и 50 м. Дом, расположенный на участке, имеет на плане форму квадрата со стороной 9 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах.

9. Какой угол (в гра­ду­сах) об­ра­зу­ют ми­нут­ная и ча­со­вая стрел­ки в 16:00?

10. Перила лест­ни­цы дачного дома для надёжности укреп­ле­ны посередине вер­ти­каль­ным столбом. Най­ди­те высоту l этого столба, если наи­мень­шая высота h₁ перил равна 0,7 м, а наи­боль­шая h₂ равна 1,5 м. Ответ дайте в метрах.

11. Высота ко­ну­са равна 15, а диа­метр основания – 16. Най­ди­те образующую конуса.

12. Конус впи­сан в цилиндр. Объем ко­ну­са равен 21. Най­ди­те объем цилиндра.

13.

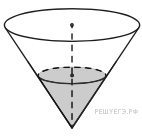
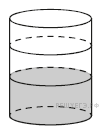
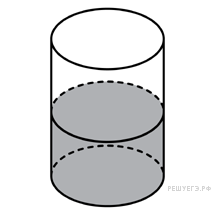
В сосуде, имеющем форму конуса, уровень жидкости достигает  высоты. Объём сосуда 960 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.

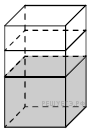
14. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 3 и 4, и боковым ребром, равным 3.

15. Найдите квадрат расстояния между вершинами  и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

16. В бак, име­ю­щий форму пра­виль­ной четырёхугольной приз­мы со сто­ро­ной основания, рав­ной 40 см, на­ли­та жидкость. Чтобы из­ме­рить объём де­та­ли слож­ной формы, её пол­но­стью по­гру­жа­ют в эту жидкость. Най­ди­те объём детали, если после её по­гру­же­ния уро­вень жид­ко­сти в баке под­нял­ся на 2 см. Ответ дайте в ку­би­че­ских сантиметрах.

17. В ци­лин­дри­че­ский сосуд на­ли­ли 5000 см³ воды. Уро­вень воды при этом до­сти­га­ет вы­со­ты 14 см. В жид­кость пол­но­стью по­гру­зи­ли деталь. При этом уро­вень жид­ко­сти в со­су­де под­нял­ся на 7 см. Чему равен объем детали? Ответ вы­ра­зи­те в .

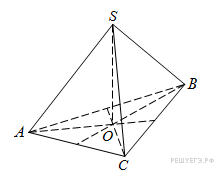
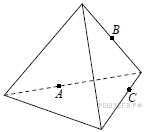
18. В правильной треугольной пирамиде  медианы основания  пересекаются в точке . Площадь треугольника  равна 4; объем пирамиды равен 6. Найдите длину отрезка .

19. Однородный шар диа­мет­ром 3 см имеет массу 162 грамма. Чему равна масса шара, из­го­тов­лен­но­го из того же материала, с диа­мет­ром 2 см? Ответ дайте в граммах.

20.

К правильной шестиугольной призме с ребром основания 1 приклеили правильную шестиугольную пирамиду с ребром основания 1 так, что основания совпали. Сколько граней у получившегося многогранника (невидимые рёбра на рисунке не изображены)?

Ключ

№ п/п	Вариант № 1	Вариант № 2
1	1400	100
2	1,8	55
3	66	40
4	1	42
5	186	186
6	311	206
7	120	12
8	1	1919
9	800	120
10	177	1,1
11	24	17
12	72	63
13	6	120
14	27	42
15	60	11
16	1200	3200
17	11	2500
18	9	4,5
19	2	48
20	93	13