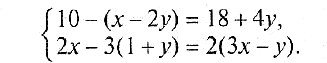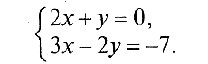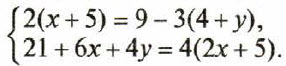Итоговый тест по Алгебре 7 класс
Даны основные примеры итогового теста (не все) 7 класс, Алгебра
Математика 7 класс | Автор: Архиполва НМ | ID: 7821 | Дата: 14.3.2016
Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться
Вопрос №
1
Упростите выражение -4m + 9n — 7m — 2n.
-3m + 11n
-3m + 7n
11m + 7n
-11m + 7n
Вопрос №
2
Решите уравнение 10у – 13,5 = 2у — 37,5.
6,375
3
-3
4
Вопрос №
3
Упростите выражение с7 : c4 • c.
c в 5 степени
c в 6 степени
c в 4 степени
c в 12 степени
Вопрос №
4
Выполните умножение (3a — b)(2b — 4a).
-12a2 – 10ab – 2b2
-12a2 + 10ab – 2b2
6ab – 2b2
6ab – 4b
Вопрос №
5
Найдите значение выражения (-1)3 – (-2)3 + 52 – 72.
83
33
-16
-17
Вопрос №
6
Выразите у через х в выражении -5х + у = -17.
У = 17 + 5х
У = -5х + 17
У = -17 + 5х
У = 17 — 5х
Вопрос №
7
Какое значение принимает сумма х + у, если х = -2,6; y = -4,4?
-1,8
1,8
7
-7
Вопрос №
8
Составьте выражение по условию задачи: «Турист шел со скоростью b км/ч. Какое расстояние он пройдет за 8 часов?».
8 — b
8 + b
8b
8 : b
Вопрос №
9
В одной системе координат заданы графики функций у = 2х – 4 и у = -3. Определите координаты точки их пересечения.
(1,5; -3)
(1,5; 1)
(0,5; -3)
(-0,5; -3)
Вопрос №
10
Через какую точку проходит график функции у = 3х + 5?
(2; -3)
(1; -2)
(2; 11)
(-2; 11)
Итоговый тест по алгебре за 7 класс
Часть 1.
А1. Упростите выражение -4m + 9n — 7m — 2n.
1) -3m + 11n
2) -3m + 7n
3) 11m + 7n
4) -11m + 7n
A2. Решите уравнение 10у – 13,5 = 2у — 37,5.
1) 6,375
2) 3
3) -3
4) 4
A3. Упростите выражение с
7
: c
4
∙ c.
1) c
5
2) c
6
3) c
4
4) c
12
A4. Выполните умножение (3a — b)(2b — 4a).
1) -12a
2
– 10ab – 2b
2
2) -12a
2
+ 10ab – 2b
2
3) 6ab – 2b
2
4) 6ab – 4b
A5. Преобразуйте в многочлен (4х – 5у)
2
.
1) 16х
2
– 20ху + 25у
2
2) 16х
2
— 40ху + 25у
2
3) 4х
2
– 25у
2
4) 16х
2
– 25у
2
A6. Упростите выражение —3а
7
b
2
∙(5a
3
)
2
.
1) 15a
13
b
2
2) -15a
12
b
2
3) 75a
12
b
2
4) -75a
13
b
2
A7. Найдите значение выражения (-1)
3
– (-2)
3
+ 5
2
– 7
2
.
1) 83
2) 33
3) -16
4) -17
А8. Представьте выражение в виде квадрата двучлена 4у
2
— 12у + 9.
1) (4у — 3)
2
2) (2у — 9)
2
3) 2у — 3
2
4) (2у — 3)
2
А9. Выразите у через х в выражении -5х + у = -17.
1) У = 17 + 5х
2) У = -5х + 17
3) У = -17 + 5х
4) У = 17 — 5х
А10. Какое значение принимает сумма х + у, если х = -2,6; y = -4,4?
1) -1,8
2) 1,8
3) 7
А11. Выполните умножение дробей:
Бланк ответов — Алгебра 7 класс
Ключ ответов — Алгебра 7 класс
Пояснительная записка
Работа содержит 16 заданий курса алгебры и геометрии .
Каждый из двух вариантов содержит две части.
Часть 1 — 12 заданий базового уровня
Часть 2 — 4 задачи высокого уровня, где требуется написать развернутое решение.
Критерии оценивания: За каждый верный ответ 1-й части начисляется 1 балл, за каждое верное решение задачи 2-й части – 2 балла. Максимальное количество баллов – 20. Оценка ставится в зависимости от набранных баллов:
|
Баллы |
Оценка |
|
0-6 |
2 |
|
7-10 |
3 |
|
11-15 |
4 |
|
16-20 |
5 |
Вариант № 1
Часть 1
1. Вычислите (32)4 : (35 × 32)
2. Выполните умножение: (с – 5) (c+1)
3. Решением системы уравнений: является пара чисел:
а) (2; 3); б) (- 2; 3); в) (2; — 3); г) (- 2; — 9); д) (- 2; 9).
4. Решите уравнение 3(5 – 2х) – 4 = 4 – 5х
5. Решите систему линейных уравнений:
6. Постройте график функции у=2х+2.
7. Упростите выражение (х – 2)2 + (х – 1)(х +1 )
8. Два угла треугольника равны 300 и 530. Найдите градусную меру третьего угла этого треугольника.
9. В треугольнике АВС А=900,
В=600, АВ=5см. Найдите ВС.
10. Дано: Найдите:
.
C
O
B
11. Выберите верное утверждение:
1. Если при пересечении двух прямых секущей сумма накрест лежащих углов равна 180°,то такие прямые параллельны.
2. Если угол равен 47°, то смежный с ним равен 153°.
3. Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.
4. Через любые две точки проходит бесконечно много прямых.
12. В треугольнике АВС АВ=ВС, ВЕ – медиана треугольника. АВЕ = 400. Найти ∠ АВС.
Часть 2
13.Решите уравнение: х2 + 4х+3=0
14. Расстояние между двумя пунктами по реке равно 80 км. Это расстояние лодка проплывает по течению реки за 4 ч, а против течения – за 5 ч. Найдите собственную скорость лодки и скорость течения реки.
15. Дано: Найти:
m
n
1
2
3
4
A
C
B
16. В треугольнике СКЕ стороны СЕ и КE равны, биссектрисы СМ и КН пересекаются в точке А. Докажите, что треугольники КАМ и САН равны.
Вариант № 2
Часть 1
1. Вычислите 26 * (22)5 : 213
2. Выполните умножение: (а – 3) (а + 4)
3. Решением системы уравнений: является пара чисел:
а) (5; 2); б) ( 5; — 2); в) (- 5; — 2); г) (- 5; — 7); д) (5; — 7).
4. Решите уравнение 6(4 – х) + 4х = 3+х
5. Решите систему уравнений:
6. Постройте график функции у= -2х-2.
7. Упростите выражение: ( х + 3)2 + (х – 1) (х +1)
8. Два угла треугольника равны 400 и 380. Найдите градусную меру третьего угла этого треугольника.
9. В треугольнике АВС А=900,
В=600, ВС=12см. Найдите АВ.
10. Дано: Найдите:
.
C
O
B
A
11. Выберите верное утверждение:
1. Если две прямые параллельны третьей, то они пересекаются.
2. В равнобедренном треугольнике медиана, проведенная к боковой стороне, является высотой и биссектрисой.
3. Если при пересечении двух прямых секущей сумма соответственных углов равна 180°,то такие прямые параллельны.
4. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
12. В треугольнике АВС АВ=ВС, ВК –высота треугольника. АВС = 1300. Найти ∠ КВС.
Часть 2
13.Решите уравнение: х2 – 4х+3=0
14.Теплоход 120 км проходит за 5 ч против течения реки и 180 км за 6 ч по течению. Найдите скорость течения реки и собственную скорость теплохода.
15. Дано: Найти:
A
B
C
b
a
1
2
3
4
16. В равнобедренном треугольнике КЕС с основанием СК медианы СМ и КН пересекаются в точке А. Докажите, что треугольник КАС – также равнобедренный.
Рекомендуется вначале прочитать конспекты уроков по алгебре за 7 класс (учебник Макарычева Ю.Н.) В тесте 20 вопросов, из которых четыре — повышенной сложности (ввод ответа с клавиатуры). Нет ограничения по времени. В случае явно плохих результатов (меньше 15% правильных ответов) тестирование по теме «Алгебра 7: ИТОГОВЫЙ ТЕСТ (Макарычев Ю.Н.)» заканчивается досрочно! Неудовлетворительная оценка выставляется, если правильных ответов меньше 50% ! Автор вопросов теста: Л.И.Мартышова. Вернуться на страницу «Алгебра 7 класс».
1. 1-я часть. Первые 16 вопросов с выбором одного правильного ответа из всех предложенных с проверкой правильного ответа сразу.
Решите уравнение 5у – 3,5 = 2у + 5,5.
2.
Даны прямые a, b, с, d, заданные, соответственно, уравнениями
Укажите пару параллельных прямых.
3.
Упростите выражение –За5b2 * (7а3)2.
–147a11b2
–21а10b2
147а10b2
21а11b2
4.
Выполните умножение (За – b)(2b + 4а).
12a2 – 2ab – 2b2
12a2 + 2ab – 2b2
6ab – 4b
баb – 2b2
5.
Преобразуйте в многочлен (4у – 5х)2.
16y2 – 20ху + 25x2
16y2 – 40xу + 25x2
4y2 – 25x2
16y2 – 25x2
6.
Выясните, на сколько медиана ряда 7, 3, 4, 3, 8, 8, 3, 12, 17, 2 больше его моды.
7.
Упростите выражение 3х(3x2 + 1) – (х – 3)(х + 3) – 9(х3 + 1).
3x – 1
x2 – 3
3x + x2
3x – x2
8.
Решите уравнение 7,5 – 2х = 5x – 6,5.
9.
Даны прямые а, b, с, d, заданные, соответственно, уравнениями
Укажите пару параллельных прямых.
10.
Упростите выражение –8x6y * (2x3)5.
–256x21у
–16x14у
–16x21у
256x21у
11.
Выполните умножение (х – 5у)(3у + 2х).
2x2 – 15y2
2x2 – 7xу – 15y2
2x2 – 13xу – 15y2
7 ху
12.
Преобразуйте в многочлен (5b – 7a)2.
5b2 – 35ab + 7a2
25b2 – 35ab + 49a2
25b2 – 70аb + 49a2
25b2 – 49a2
13.
Выясните, на сколько размах ряда 7, 2, 4, 2, 3, 2, 8, –6, 8, –2 больше его медианы.
14.
Упростите выражение (4 – у)(4 + у) – 2у(2y2 – 1) + 4(y3 – 4).
2y – y2
y2 + 2y
y2 – 2y
2y + y2
15.
Решите систему уравнений

2/7; –29/7
–2/7; 2/7
29/7; –2/7
29/7; –29/7
16.
График линейной функции пересекает ось координат в точках (–3; 0) и (0;6). Задайте эту функцию формулой.
17. 2-я часть. Последние 4 вопроса повышенной сложности. Напечатайте свой ответ в пустое поле. Правильный ответ будет показан в конце теста.
Решите систему уравнений
Ответ: .
Примечание: разделитель между двумя числами — точка с запятой; разделитель целой и дробной части числа — запятая.
18. Решите уравнение 5y2 – 2у = 0.
Ответ: .
Примечание: разделитель между двумя числами — точка с запятой; разделитель целой и дробной части числа — запятая.
19. Найдите два последовательных чётных числа, квадраты которых отличаются на 724.
Ответ: .
Примечание: разделитель между двумя числами — точка с запятой.
20.
Решите систему уравнений

Ответ: .
Примечание: разделитель между двумя числами — точка с запятой; разделитель целой и дробной части числа — запятая.
Представленный материал является итоговой работой учащихся, оканчивающих 8 класс о учебнику «Алгебра 8 кл» для общеобразовательных учреждений (Макарычев Ю.Н. и др.: Просвещение, 2013 г)
Назначение итоговой работы – оценить уровень овладения обучающимися программным материалом, учесть полученные результаты при составлении рабочих программ, дифференцируя уровень заданий по содержательным линиям.
Представленный материал является итоговой работой учащихся, оканчивающих 7 класс о учебнику «Алгебра 8 кл» для общеобразовательных учреждений (Макарычев Ю.Н. и др.: Просвещение, 2013 г)
Назначение итоговой работы – оценить уровень овладения обучающимися программным материалом, учесть полученные результаты при составлении рабочих программ, дифференцируя уровень заданий по содержательным линиям.