Что нужно делать школьнику, чтобы получить 100 баллов?
Чтобы получить 100 баллов, надо любить и понимать математику (быть математиком — по сути, по настроению, по образу жизни). Если школьник рассматривает математику как второстепенный предмет, как предмет, который просто необходимо сдать, например, когда речь идет о поступлении на экономические направления, он не сможет получить 100 баллов ни при каком раскладе. Максимальный балл требует, чтобы человек всем своим «нутром и состоянием своего мозга» был ориентирован на математику. Потому что есть задачи, которые требуют четкого, хорошего логического мышления и владения абсолютно всем материалом. В нужный момент необходимо выудить необходимые знания и применить их для решения задачи. Есть такие задачи, на которые натаскать по принципу «делай вот так» просто нельзя (например, задача № 19). Даже если школьник прекрасно знает математику, 100 баллов получить очень сложно. Это единичные случаи.
По вашему опыту преподавания, какие разделы математики самые сложные и вызывают наибольшие затруднения?
Сегодня для школьника самое сложное — это геометрия. К сожалению, культура геометрии в школе просто отсутствует. И еще, конечно, задачи с параметрами. Старшеклассники их панически боятся. Но ученик, который понимает математику, и с этими задачами справляется. Для их решения требуется именно понимание, а все необходимые для этого знания изложены в курсе школьной математики.
А вообще, в любой теме есть простой материал (азы), который лежит в основе задач из первой части ЕГЭ, и сложный материал, который лежит в основе задач второй части. Думаю, что если есть желание, то каждый в состоянии освоить азы любой темы из школьной программы по математике, а вот более глубокое понимание этих тем и умение решать сложные задачи по силам не всем.
Ни о каком везении разговора быть не может, если школьник хочет получить больше 80 баллов
А какие темы можно назвать самыми простыми?
Обычно школьники легко решают линейные и квадратные уравнения, но только в том случае, если в них нет параметра. Так что по темам «Линейная функция» и «Квадратичная функция» есть простые задачи, а есть сложные. И так по любой теме. Можно сформулировать простую задачу, а можно такую, что никто не решит.
Простыми темами можно считать те, на большинство задач по которым можно школьника натаскать. Простая задача — это гарантированно правильно решенная. А про ЕГЭ (особенно про задачи первой части) так вообще нельзя говорить. Например, школьник знает, как решить задачу, но допускает арифметическую ошибку или невнимательно читает условие (ищет одну величину, а для ответа надо еще что-то с ней сделать). В итоге получается неверный ответ. И задача не решена. И не важно, простая она была или сложная.
Присутствует ли на ЕГЭ по математике фактор везения? Возможно ли получить высокий балл, если знаешь предмет на более скромный результат?
Да, это возможно, но только если речь идет о результате в районе 75 баллов или меньше. Ни о каком везении разговора быть не может, если школьник хочет получить больше 80 баллов. Там нужно решать сложные задачи из второй части, а они требуют четкого обоснования решения, что для большинства является непосильным. Здесь должна быть стабильность.
А можно завалить экзамен, если знаешь предмет очень хорошо?
Элементарно. Арифметические ошибки, невнимательное чтение условия задачи и просто паника. Все это приводит талантливых учеников к более скромным результатам.
Что же делать? Есть «формула успеха», которая поможет подготовиться к ЕГЭ по математике?
Учить математику! Не натаскиваться по вариантам ЕГЭ, а систематически учить темы, разбираться, стараться понять. Тогда до многих задач школьник дойдет сам, своим умом, а это и есть залог успешной подготовки и высоких баллов. Математика — это, в первую очередь, понимание, а потом уже формулы и схемы решения. При подготовке методом натаскивания потолок — это 75 баллов. Одна и та же задача, сформулированная просто «с другого конца», натасканного ребенка деморализует. Он не может узнать знакомую задачу, а разобраться в «новой» сам не в состоянии.
Вот, например, задача № 17. Когда она появилась в вариантах диагностических работ, детям в школе начали давать формулы для ее решения. И школьники заучивали эти формулы, сопротивляясь попыткам учителей объяснить, откуда они взялись. Многие действовали методом «я знаю формулу и по ней буду решать». А на самом экзамене в условие внесли незначительное изменение, и ни одна из выученных формул не подходила. Как получить ту, которая позволит решить задачу, дети не знали. Вроде бы решили все 120 вариантов задания № 17, а на ЕГЭ дали 121-й вариант. В итоге те, кто не разбирался, задачу не решили.
Надо выбросить калькулятор и научиться считать без него
До ЕГЭ по математике осталось 3,5 месяца. Как вы посоветуете выпускникам распределить время, чтобы подготовиться наилучшим образом?
Во-первых, выбросить калькулятор и научиться считать без него. Во-вторых, повторить теорию и выучить формулы (именно сейчас, а не перед экзаменом): то есть подготовить базу, а дальше решать задачи. Можно решать из сборников вариантов ЕГЭ, но, к сожалению, там их не очень много и они часто повторяются.
Каждый ребенок ставит для себя определенную планку в зависимости от того, куда собирается поступать и как знает предмет. Если говорить о заданиях второй части ЕГЭ, то во время подготовки необходимо прежде всего обратить внимание на задачи № 13, № 15 и № 17. Их можно научиться решать. Если решение не вызывает проблем, можно переходить к задачам № 14 и № 16.
Задачи № 18 и № 19 — это, конечно, уже очень высокий уровень, но попробовать можно. Если эти задачи идут хорошо, то я не думаю, что надо тратить оставшееся время на курсы. Лучше решить больше задач самостоятельно. Если же возникают проблемы или неуверенность, что вы все решаете верно, не откладывая обращайтесь за помощью. Эффективная стратегия на этот период — решать, решать и решать!
Как готовиться к заданиям повышенной сложности
| Задание № 10 | Задача легкая. Здесь важно внимательно читать условие. Внимание на единицы измерения! Все величины подставлять в одних единицах измерения. |
| Задание № 11 | Текстовая задача. Не считаю ее сложной. Обратите внимание на вопрос задачи, что именно спрашивают в условии и в каких единицах измерения необходимо записать ответ. Часто школьники пишут скорость не того пешехода или производительность не той трубы. |
| Задания № 13, № 15 | Задания решаемые, но должна быть база по всем темам алгебры. Особенное внимание необходимо обратить на область определения (в особенности это касается логарифма, тангенса и котангенса). Нужно уметь применять те тождественные преобразования, которые помогут решить задачу, а не заведут в тупик, и знать все формулы наизусть. |
| Задания № 14, № 16 | Задачи по геометрии. Самое сложное в них — это умение доказать. Для этого школьник должен владеть всем материалом планиметрии и стереометрии, знать все теоремы и следствия из них, уметь их доказывать. И еще важен чертеж! Он может либо стать эффективным инструментом и подсказать правильный ход решения, либо, если сделан некорректно, помешать решению задачи. |
| Задание № 17 | Несложная задача. Это задание на умение формализовать текстовую задачу, то есть записать условие задачи в виде уравнений или неравенств (этого же требует и решение задачи № 11). На ЕГЭ под этим номером пока стабильно дают задачу на проценты. Теоретически может быть и задача на поиск оптимального решения, но такие варианты пока встречались только в диагностических работах. После формализации условия получается стандартная математическая задача о нахождении экстремума функции или на нахождение наибольшего (наименьшего) значения функции на отрезке (аналогично задаче № 12). Здесь важно не пользоваться готовыми формулами, а разбираться, почему в этой задаче так, а в другой иначе. Только тогда можно научиться переводить условие текстовой задачи на язык математики. |
| Задание № 18 | Для решения этой задачи необходимо отличное владение предметом. Поможет ее решить знание свойств элементарных функций, умение исследовать функции и строить их графики. Все это есть в школьном курсе математики. |
| Задание № 19 | Это задача для тех, кому интересна математика. В ходе решения может возникнуть необходимость обратиться к любому разделу предмета из программы любого класса. Нужно найти в своей голове и грамотно применить эти знания. В одной задаче может сочетаться арифметическая прогрессия со свойствами делимости чисел и нахождением наибольшего значения. Для решения этой задачи нужно понимать, когда достаточно привести пример, а когда необходимо строгое обоснование. |
Обычно базовую математику выбирают ребята, у которых есть план: надо как можно скорее разделаться с бесполезным для поступления предметом и сосредоточиться на своем наборе вступительных. Из этой статьи вы узнаете, как сдать базовую математику максимально быстро и просто.
В этом материале мы сделаем акцент на простых номерах, которые принесут вам балл почти задаром! Они обозначены пометкой «Обязательно делать» — таких заданий 10. Как раз с запасом на ошибки, ведь минимум для сдачи базовой математики — 7 баллов.
Для тех, кто хочет получить выше тройки — это 12 баллов и выше, — мы дали рекомендации по еще 3 задачам. В сумме получается 13 номеров. Решите их все, и твердая четверка у вас в кармане.
Какие задания решать, чтобы сдать базовую математику
Задание 1: обязательно делать
Проверяется ваше умение разделить случаи, когда требуется округлить величину в большую сторону, а когда — в меньшую.

Если вы ходите в магазин с наличными, то сталкиваетесь с подобными задачами каждый день. Разделим 100 рублей на стоимость одной упаковки йогурта. Не забывайте приводить все величины к одной размерности:
100 : 14,6 = 6, 849…
Так сколько баночек йогурта вам продадут? На 7 штук денег не хватает, значит, округлить полученную величину надо до целого в меньшую сторону. Математическое правило округление в этой задаче не поможет.
Ответ: 6.

Если одна пачка рассчитана на 6 рулонов, то на 63 рулона:
63 : 6 = 10,5.
Но полпачки вам не продаст. Включаем логику: возьмем меньше — не хватит еще половины пачки на три последних рулона. Значит, округлить надо в большую сторону, взять клей с небольшим запасом. Математическое правило округления снова игнорируем.
Ответ: 11.
Задание 2: обязательно делать
Это задача на здравый смысл. Нужно соотнести величины с их возможными значениями.

Вряд ли грузовой автомобиль может весить как 3 шоколадки (300 г), а взрослый человек — 8 т.
Давайте вместе подберем значения.
- Взрослый человек обычно весит от 50 до 100 кг — что из этого подходит? Конечно, 65 кг.
- Грузовой автомобиль достаточно большой и тяжелый, скорее всего, он весит несколько тонн. Нам подходит 8 т.
- Книга обычно не такая большая и весит до 1 кг. Из оставшегося подойдет 300 г.
- А пуговка совсем маленькая. Значит, берем самый легкий вес — 5 г.
Ответ:
Главное — внимательно перенести ответы в бланк: 3142.
Задание 3: обязательно делать
Задание на работу с графиком, диаграммой или таблицей. Вооружайтесь карандашом, читайте условие с предельной внимательностью и безжалостно отмечайте нужные по условию значения на изображении в КИМ. Вы и представить не можете, сколько выпускников теряет тут баллы по невнимательности.
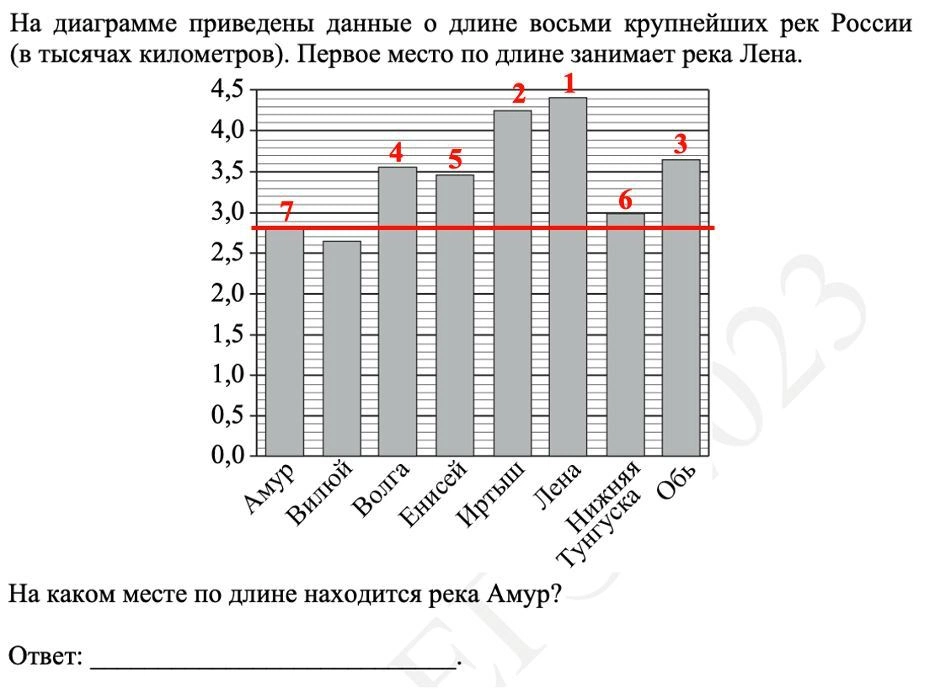
Мы ярко отметили уровень, соответствующий Амуру, в итоге посчитать все более длинные реки стало проще простого. У вас на экзамене будет так же наглядно!
Ответ: 7.
Задание 4: обязательно делать
Задание проверяет навык работы с формулами. Алгоритм решения напоминает решение задачек на уроке по физике:
- Выписываем формулу из условия.
- Определяем, что нужно найти: единственную букву, значение которой не дано.
- Выражаем искомую величину.
- Подставляем значения из условия в формулу.
- Ищем неизвестное.
Самое трудное тут — правильно выразить искомую величину. Для этого повторяем порядок выполнения арифметических операций, свойства умножения, тренируемся перекидывать через равно множители и слагаемые.
И да, в базе эта задача проста настолько, что даже перекидывать ничего не придется. Нужная величина уже будет слева от равно.
Задание 5: обязательно делать
Простая задача на определение вероятности, которая поможет вам точно сдать базовую математику.
Решаем с помощью формулы:
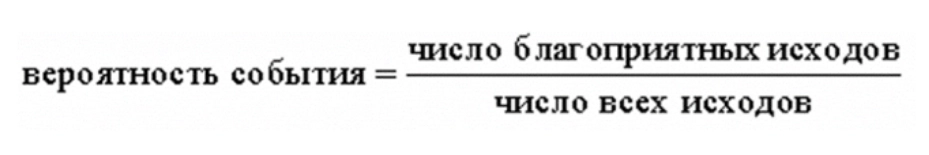

Внимательно читайте вопрос: спрашивают вероятность купить исправную лампочку. Если из ста 3 неисправны, значит, остальные в порядке и подойдет любая из оставшихся 97. Это и есть наши благоприятные исходы из формулы.
97 : 100 = 0,97.
Ответ: 0,97.
Будьте внимательны: иногда в задаче есть указание к округлению. Значит, ответ у вас выйдет некрасивый, в виде бесконечной десятичной дроби, которую вы округлите до нужного разряда.
Еще один подвох: формулировка с предлогом «на». К примеру, «На 100 лампочек 3 неисправны. Найдите вероятность купить неисправную». Подходящие исходы тут даны явно: 3 неисправные лампочки. А вот число всех исходов спрятано, и найти его будет нужно сложением исправных и неисправных лампочек: 100 + 3 = 103.
Задание 6: обязательно делать
Задание проверяет навык чтения информации из таблицы и подбора подходящего по условию варианта.
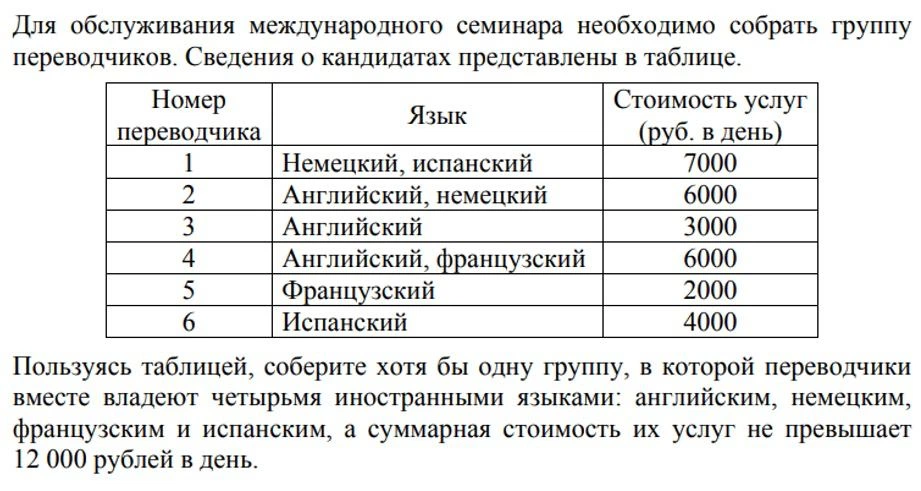
Например, вы нашли вариант позвать первого, третьего и пятого переводчиков. Получите весь набор языков как раз за 12 тысяч. Но обратите внимание, что это решение далеко не единственное.
Ответ: 135.
Задание 7
Мы не выделяем это задание в обязательные, так как для его выполнения понадобится навык анализа поведения функции по графику. Но, как его решать, сейчас коротко расскажем.
Запомним: точка максимума будет на «горке», точка минимума — в «ямке». Функция убывает, если идет вниз слева направо. Возрастает, если идет вверх слева направо.
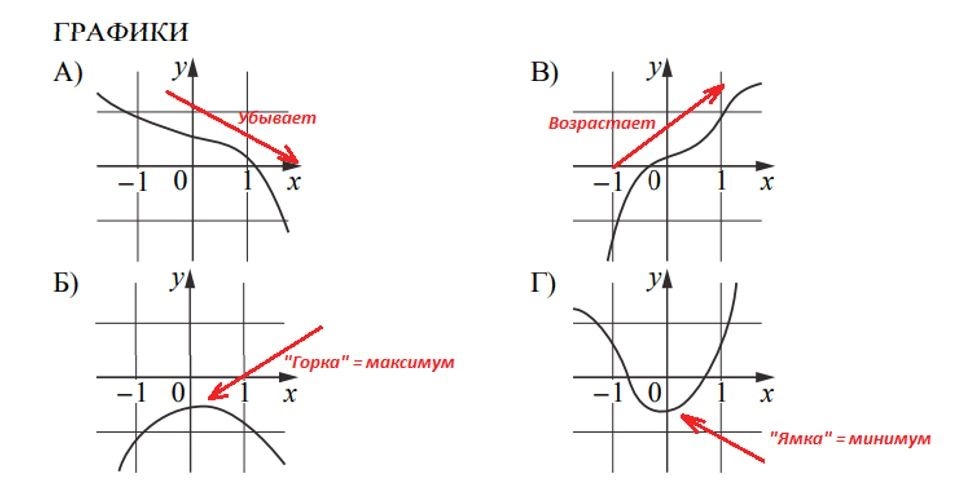
Если не повезет, то придется вспомнить азы теории по производной.
Здесь все дело в касательных. Нужно внимательно к ним присмотреться. Если касательная к графику возрастает, то значение производной будет положительное, если убывает — отрицательное. Производная будет тем больше по величине (модулю), чем быстрее возрастает или убывает касательная.
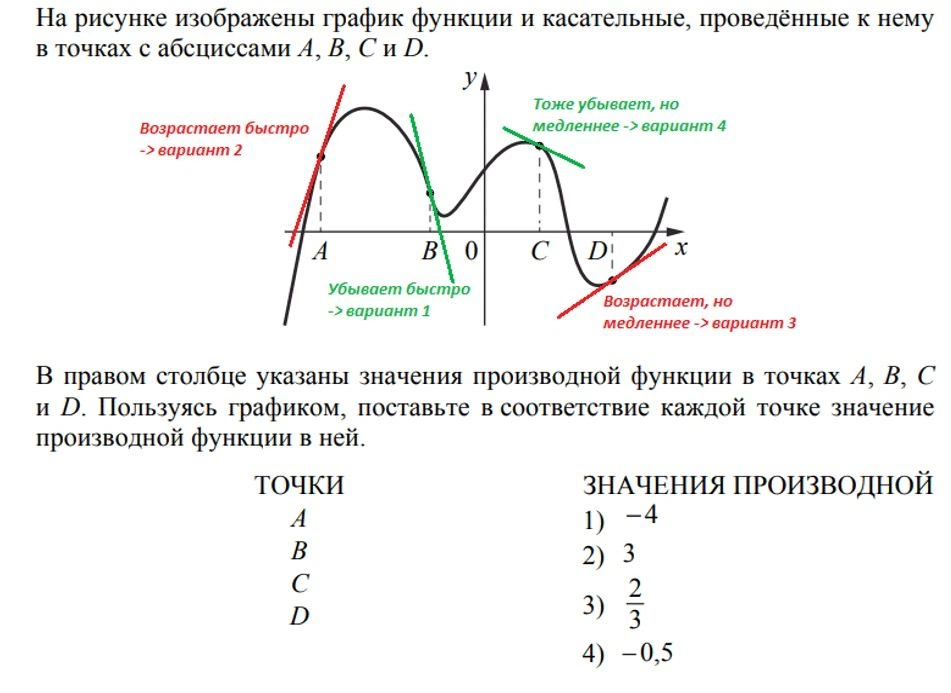
Ответ: 2143.
Задание 8: обязательно делать
Задача проверяет умение делать логичные выводы из утверждения. Иногда попадаются совсем простые задания, к таким даже дополнительно готовиться не надо.

Все, что от вас требуется, — схематично изобразить на черновике ясень, рябину и осину, указать известную разницу в высоте и внимательно сопоставить картинку с утверждениями.
Важно: не додумывайте дополнительные условия, не указанные в тексте задачи. Учитесь читать строго то, что написано.
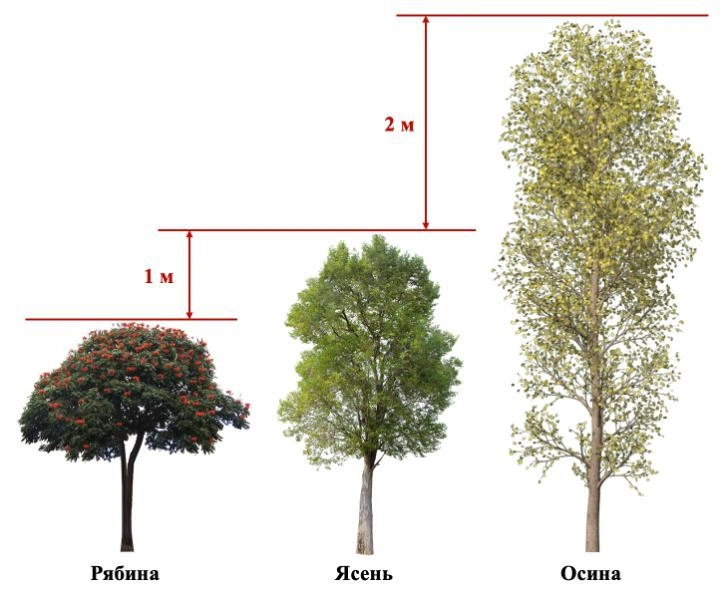
Исходя из рисунка выше получаем, что верны только утверждения 1 и 4.
Ответ: 14.
А бывают случаи, когда с визуализацией задачки придется постараться.

Тут иллюстрация не так очевидна, но нам помогут круги Эйлера. Этот инструмент позволяет наглядно изобразить множество объектов. В данном случае — школьников. Давайте прикинем, как ребята могут распределиться по кружкам.
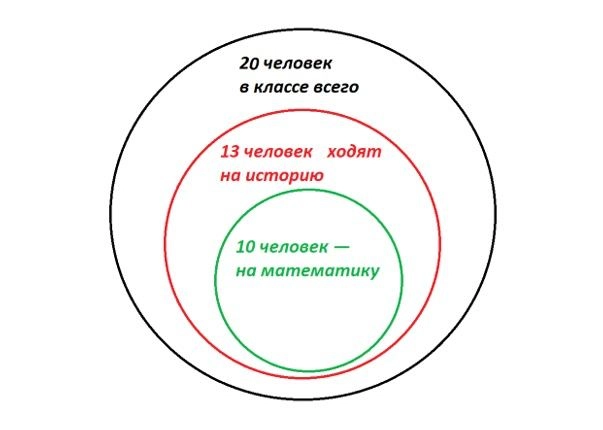
Например, так. Тут из 20 человек на кружки в итоге ходят 13. Причем 10 из них очень активны и выбрали сразу два предмета. Трое ограничились только историей.
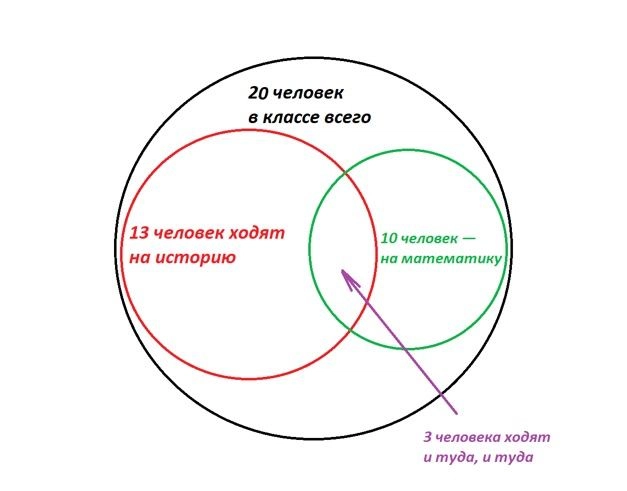
Или вот так. Если ребята задались целью по максимуму не пересекаться на дополнительных занятиях, то… У них не получится, и как минимум трое запишутся сразу на оба факультатива.
Конечно, возможны еще промежуточные варианты, но мы нарисовали два крайних. Теперь попробуем ответить на вопросы.
- Смотрим на первую картинку. Даже если все ребята будут очень стараться посетить оба кружка, они ограничены условиями задачи и максимум на оба попадут 10 человек из 20. Нет.
- Тут надо рассмотреть другую крайность, которую мы изобразили на второй картинке. Как бы ребята ни старались не встречаться на кружках, хотя бы трое попадут на оба сразу. Да.
- Уж точно неверно. На обеих наших картинках есть ребята, которые ходят на историю, но не ходят на математику. Нет.
- Смотрим на первую картинку. Оба кружка могут посещать максимум 10 человек.
Ответ: 24.
Так что для решения иногда мало логики — понадобится еще немного воображения. Потренируйтесь, и ваши шансы получить балл увеличатся.
Задание 14: обязательно делать
Задание проверяет базовые навыки счета, которым учат в 5–6-м классах. Чтобы получить балл и сдать базовую математику, надо:
- уметь выполнять арифметические действия с обыкновенными и десятичными дробями;
- правильно расставлять порядок действий;
- быть предельно внимательными.
Уделите пару вечеров отработке алгоритмов сложения, вычитания, умножения и деления обыкновенных и десятичных дробей, и это задание у вас в кармане.
Задание 15
Составители экзамена проверяют ваш навык работы с процентами и единицами отношения. Такие задачи бывают четырех типов.
Тип 1. Найти часть от числа
Часть может быть выражена в процентах или сразу в виде дроби. Например, придется искать треть от чего-то.
Рассмотрим на примере реальной задачи из экзамена:

Прочувствуйте специфику задачи: нам известно целое — вся зарплата до вычета налога. А работать мы будем с кусочком — 13 процентами. Сколько это в рублях, нам еще предстоит узнать.
Чтобы ответить на вопрос задачи, нужно сделать три шага:
1. Перевести процент в десятичную дробь.
Для этого всегда надо количество процентов поделить на 100.
13 : 100 = 0,13.
2. Найти, сколько это от зарплаты в рублях.
Запоминаем главное правило для этого типа задач: чтобы найти дробь от числа, надо число умножить на эту дробь.
12 500 ∙ 0,13 = 1 625 (руб.) — налог, который удержат с зарплаты Ивана Кузьмича.
3. Ответить на вопрос задачи.
У нас просили зарплату после вычета налога, а не сам налог.
12 500 – 1625 = 10 875 (руб.).
Ответ: 10 875.
Будьте внимательны: многие совершают ошибку именно на последнем шаге!
Тип 2. Найти число по его части

Прочувствуйте разницу с прошлой задачей: тут 124 — и есть 25%, то есть одна и та же величина выражена в процентах и в абсолютных величинах, в данном случае — в учениках. Просят узнать целое — 100%.
1. Переводим процент в десятичную дробь:
25 : 100 = 0,25.
2. Находим, сколько учеников всего.
Правило для этого типа задач: чтобы найти целое, надо часть разделить на дробь.
124 : 0,25 = 496 (уч.) — всего.
Ответ: 496.
Тип 3. Найти, сколько процентов часть составляет от целого

Особенность подобных заданий: не дано процентов, есть только абсолютные величины. В данном случае — стоимость футболки в рублях.
1. Находим, какую долю новая цена составляет от первоначальной.
Запоминаем правило: чтобы найти, какую долю часть составляет от целого, надо часть разделить на целое.
680 : 800 = 0,85.
2. Переводим долю в процент.
В прошлых задачах мы уже дважды выполнили обратное действие. В этот раз сделаем наоборот: умножим полученную дробь на 100.
0,85 ∙ 100 = 85% — столько процентов новая цена составляет от старой.
3. Отвечаем на вопрос задачи.
Нас спросили, на сколько процентов цена снизилась, что стала 85% от первоначальной. Конечно, изначально она была 100%. Итого:
100 – 85 = 15%.
Ответ: 15%.
Тип 4. Задачи на соотношение

Если перефразировать условие, то за первого кандидата проголосовали 3 части избирателей, а за второго — 2 части. Особенность этих частей в том, что они одинаковые по величине.
Если одна будет состоять из 10 человек, то за первого кандидата будет 30, а за второго — 20.
1. Считаем общее количество частей:
3 + 2 = 5.
2. Узнаем, сколько голосов составляет одна такая часть.
Тут речь о процентах проголосовавших. Сколько всего проголосовало? Конечно, 100%! Значит, каждая из пяти частей «весит»
100 : 5 = 20%.
3. Отвечаем на вопрос задачи.
За проигравшего проголосовало меньше частей избирателей. В нашем случае 2.
20 ∙ 2 = 40%.
Ответ: 40%.
Решение этих задач удобнее всего оформить табличкой:

1 часть = 100% : 5 = 20%.
Если рассчитываете решать текстовую задачу, включите здравый смысл. Ответ всегда можно проверить на адекватность благодаря обычной логике.
Задание 16: обязательно делать
Задание на решение выражения. На самом деле оно проверяет знание теории, так как в этом задании вам могут встретиться:
- выражения со степенями,
- иррациональные выражения,
- логарифмические выражения,
- тригонометрические выражения.
Ваша задача, соответственно, — знать:
- свойства степеней

- свойства корней

- свойства логарифмов
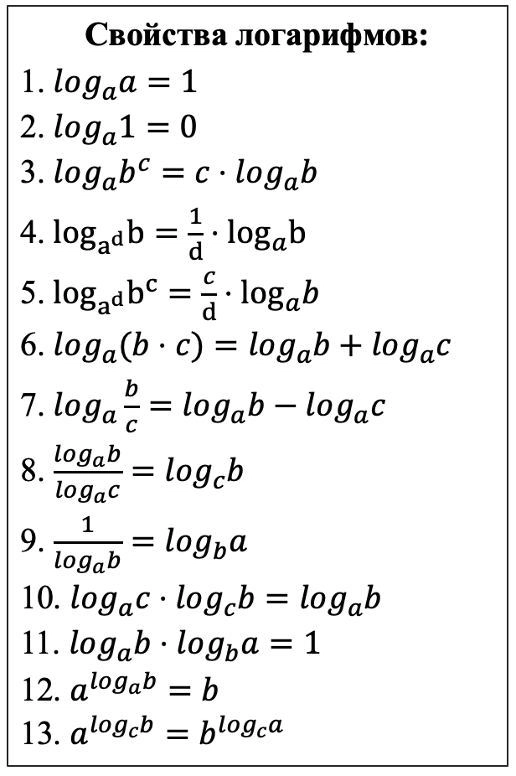
- формулы тригонометрии
Вы можете подробно ознакомиться с ними и научиться выводить в этой статье.
Обратите внимание: нужная теория будет в справочных материалах на экзамене, но это не поможет, если вы не научитесь применять ее для решения заданий. Практика обязательна!
Задание 17: обязательно делать
В номере с уравнениями вам не встретятся тригонометрические. Зато вы точно увидите там:
- линейные уравнения
Раскрываем скобки, если они есть, слагаемые с х переносим в одну сторону от равно, без х — в другую. Приводим подобные и решаем простейшее уравнение.
- квадратные уравнения
Бывают полные и неполные, всего надо повторить три алгоритма решения! А формула дискриминанта еще и в справочных материалах есть.
- иррациональные уравнения
Это те, что с корнем. Чтобы избавиться от корня, возводим обе части уравнения в квадрат и решаем получившееся уравнение. Есть нюансы с областью допустимых значений: подставьте полученные корни в исходное уравнение и проверьте, выполняется ли равенство. Если нет, то подставленное значение решением не будет.
- показательные уравнения
Ваша задача — с помощью формул свойств степеней привести уравнение к виду, когда слева и справа от равно в основании степени будет одно и то же число. После приравниваем показатели и решаем. Вот так:

Ответ: 7.
- логарифмические уравнения
С помощью формул свойств логарифмов приводим уравнение к виду, когда слева и справа от равно будет логарифм с одинаковым основанием. После приравниваем выражения под логарифмом и решаем.

Ответ: 67.
Прелесть уравнений в том, что ответ всегда можно проверить подстановкой вместо x в уравнение. Не забывайте проверять, ведь это возможность убедиться на 100%, что вы не упустите заветный балл.
Задание 19
Если хотите сдать базовую математику и решить номер 19, надо ознакомиться со свойствами целых чисел и признаками делимости. Иногда решение можно найти даже подбором! Попробуйте — времени на базовом ЕГЭ вам точно хватит.
Для начала нужно запомнить все признаки делимости.

А теперь посмотрим на типичное задание 19.

Тут помогут признаки делимости. Отдельного признака для 12 нет, потому нам надо разложить его на множители, признаки делимости для которых есть.
- На 3: сумма всех цифр делится на 3.
- На 4: число, образованное последними двумя цифрами, делится на 4.
Начнем с признака для 4. Пока что наше число заканчивается на 13 и на 4 не делится. Попробуем вычеркнуть последнюю цифру, и число будет заканчиваться на 61. Тоже не подходит. Вычеркнем еще одну: теперь на конце 76… Вот оно! От изначального числа осталось 751576, две цифры уже вычеркнули, осталось убрать одну.
Теперь проверим признак для 3: 7 + 5 + 1 + 5 + 7 + 6 = 31. Какое ближайшее число разделится на 3? Конечно, 30. Если мы вычеркнем единичку, все сойдется.
Ответ: 75576.
Другой вариант задания:

А задание такого типа можно попытаться подобрать, расположений не слишком много. Мы все же постараемся порассуждать, чтобы уменьшить количество возможных вариантов.
Чтобы число делилось на 10, оно должно заканчиваться на 0. Например, это получится, если сложить 7 + □7 + □□6. Уже немного легче. Остальное просто подберем. Под условие задачи подойдет 7 + 27 + 356 = 390.
Ответ: 390.
Какие задания мы не разобрали и почему
Теперь вы знаете, как сдать базовую математику, решив всего семь заданий. Но некоторые номера базового ЕГЭ включают слишком большое разнообразие прототипов, и методы их решения не ограничиваются парой простых алгоритмов.
Например, в эту группу относятся все задания по геометрии: с 9 по 13. Чтобы решать геометрию, мало знать основные фигуры и формулы. Необходим навык, который вырабатывается только практикой. Однако у нас есть статья про окружность — в ней вы найдете много полезной информации.
Задание 18 обычно, хотя и не всегда, содержит неравенство.

Это объемный блок теории, которую тоже необходимо подкреплять практикой. Но, может, вам повезет и попадется задачка на расположение значений на числовой прямой.

Тут достаточно примерно прикинуть значения и аккуратно внести ответы в бланк. Ясно, что 7/3 больше 2, но меньше 3. Корень из 26 равен 5 с копейками, а степень –1 из 3/5 сделает 5/3, или чуть больше 1,5. Подобные задания надо пытаться делать обязательно!
Задание 20. С этим заданием ученики знакомы еще с 9-го класса, так как оно было под номером 21 на ОГЭ. Это текстовая задача:
- на производительность,
- движение (по прямой, воде, окружности),
- сплавы и смеси,
- проценты (пиджаки, рубашки, брюки; бюджет семьи; акции, которые растут и падают),
- прогрессии.
В задании 21 на ОГЭ не было прогрессий, но они были в первой части на ОГЭ, так что ничего нового.
Задание 21. Здесь попадаются разные типы неочевидных задач на логику — чем-то они даже похожи на олимпиадные. Решение каждой нужно рассматривать отдельно и подробно. Если хотите прочитать о том, какие задачи бывают в 21-м номере, пишите в комментариях, и Maximum поделится своими методами решения!
Не знаете, какой вуз выбрать? Воспользуйтесь бесплатной консультацией в нашем центре. Что это такое? Все просто: вы расскажете о себе и о своих интересах. А специалист посоветует, на какие специальности обратить внимание, в какой вуз поступать, какие ЕГЭ сдавать. Так вы сэкономите время на подготовку и сможете выбрать образование, которое точно окажется для вас интересным и полезным!
Прежде всего, давайте я расскажу вам несколько фактов о профильном ЕГЭ по математике:
- Уровень 80+ баллов на математике – это очень серьезно!
Возможно, вы не в курсе, но больше 80 баллов на профильной математике набирает около 7-8% сдающих. То есть 3 человека из 30! Я не раз сталкивалась с ситуацией, когда мой ученик писал экзамен, скажем, на 76 баллов – и это был лучший результат по всей его школе! А всё потому, что…
- В обычной школе на уроках математике (по программе) — не учат решать вторую часть
Да, вот так. Кто бы что ни говорил, но в курсе математики обычной среднестатистической школы практически НЕТ заданий из второй части ЕГЭ. Нет экономических задач на дифференцированный или аннуитентный платеж. Нет задач на делимость чисел. Нет заданий на графическое решение систем уравнений и неравенств с параметрами (а если и есть, то серьезное внимание им не уделяется, т.к. учитель ориентируется на среднего ученика). И поэтому, к большому сожалению, обычный среднестатистический отличник без дополнительной целенаправленной подготовки именно к ЕГЭ получит на экзамене 50-70 баллов.
Конечно, большинство заданий второй части основывается на том, что проходили в школе, но уровень сложности гораздо выше тех задач, что решают в классе. Плюс есть нюансы оформления решений, на которых легко потерять баллы (см пункт 5).
Да, это очень несправедливо. Да, это неправильно, но, увы, на данный момент все обстоит именно так.
4 часа не хватает- Во второй части дают уникальные задачи
- Проверяют ЕГЭ по математике строго
- Задачи не сбалансированы по сложности.
Это ни разу не шутка – если вы решаете на высокий балл, вам в буквальном смысле некогда попить воды! Нужно ведь не только решить, но и переписать на чистовик, плюс что-то перепроверить. А еще драгоценное время будет тратиться, например, на то, чтоб наблюдатель принес вам очередной листочек черновика или бланк ответов, и заполнил циферки на нем. И это тоже потеря времени, особенно когда решаешь все задачи и нужно 6-10 листов для второй части. Например, я сдавала в 2020 году ЕГЭ и знала, как решать 17 из 19 задач сразу, буквально только прочитав их. То есть, я почти не думала над их решением, а просто записывала свои мысли. В итоге я закончила заполнять бланки в последнюю минуту, а условие одной из задач я даже не успела толком прочитать.
Ты не встретишь их ни в одном сборнике. Они абсолютно новые и часто содержат в себе новые подвохи и идеи решений, которые ты не встречал раньше.
Любая неверная строчка — и ты получаешь 0 баллов. Причем даже если это не влияет на ответ и написано в уголке мелким почерком для себя. Вот реальный пример с ЕГЭ 2020:
Если бы не то, что выделено желтым, ученик получил бы 2 балла, но вместо этого получил 0.
А вот тут у ученицы сняли балл за то, что она в пункте б не подписала на круге значения двух точек:

Обращу ваше внимание: решение задачи полное и обоснованное, ответы и в пункте а, и в пункте б – верные, никаких претензий по существу нет. Просто на круге не написано где какая точка расположена – и сразу минус балл.
Таких случаев полно. То есть, надо не просто правильно решить, а также не написать никакой глупости или даже просто неточности, плюс оформить всё как надо по критериям.
То есть может попасть очень жесткая 14-ая задача, которая при правильном решении дает 2 первичных балла, и вполне «лайтовая» 17-ая, которая стоит 3 балла. Это очень частая ситуация!
Что же делать?
Ну, а теперь поговорим, что нам со всей этой «радостью» делать, если мы все равно планируем писать экзамен на 80+.
- Вам нужно уметь решать вторую часть и не более 2 раз ошибиться в первой
Если вы помимо первой части полностью правильно решите 13, 15, 17, 19 (а,б) – вы получите 84 балла. Это хороший, серьезный результат, но перечитайте пункты 4 и 6, и вы поймете, что чтобы УВЕРЕННО набирать 80, надо также уметь решать несложные 18 и 19.
Также неплохо бы быть способным решить 14 и 16-ую, но там есть нюанс — даже если вы хорошо знаете геометрию, это не значит, что вы решите эти задачи. Для решения 14 и 16 надо отлично знать геометрию, в том числе редкие теоремы, а так же прорешать 30-40 задач похожего типа с Решу ЕГЭ. Если вы специально не готовились к этим задачам или решили парочку похожих перед экзаменом, то шансов их решить на ЕГЭ почти нет.
- Нельзя ошибаться
Да, вот так. Если вы собираетесь получать более 80 баллов — у вас нет права на ошибку. Почему? Времени крайне мало, и проверять некогда. На реальном ЕГЭ 2020 я решила досконально проверить 1-13 и 15 задачи. Это было ошибкой, потому что я в итоге потратила на это полчаса, а ошибок не нашла. Как следствие – я не успела более тщательно записать решение 19в и приступить к решению 14ой задачи. В результате мне не хватило одного балла до 100.
Вывод – тренируйтесь сразу решать правильно, без проверок и прочего.
- Нужно понимать математику, алгоритмы не помогут
Если вы не понимаете логики решений и решаете просто перебирая алгоритмы и подбирая формулу под условие – вы не напишите на действительно хорошие баллы. Потому что разных типов задач слишком много, ко всему алгоритмы не заучишь, а различных подвохов и нюансов — еще раз в 5 больше. Единственный способ написать экзамен хорошо – понимать математику. Понимать почему в одном случае делаем так, а в другом эдак.
Вывод – разбирайтесь в логике математики! Тратьте силы на то, чтобы понять, это точно окупится! Для этого:
1. Не учите алгоритмы – вникните, почему они такие какие есть. Разберитесь почему работает метод интервалов, и зачем в неравенствах надо переворачивать знак сравнения при отбрасывании логарифмов с основанием меньше единицы. Поймите, как возникает формула для расчета платежа в 17-ой задаче, а не пользуйтесь уже готовой. И прочее, прочее.
2. Приучайтесь постоянно задавать вопрос: «почему?» Почему решение именно такое? Почему формулы такая? Ну и так далее.
- Нужно не боятся решать задачи, которые кажутся новыми и не стандартными
Вот это очень важный пункт – учитесь не теряться в ситуации абсолютно незнакомой вам задачи. На экзамене вы практически гарантированно попадете в ситуацию «я такое не проходил», потому что, как мы уже говорили, на ЕГЭ часто дают уникальные задачи.
Вывод – сейчас, при подготовке, приучайтесь вгрызаться в каждую задачу, не бегите сразу смотреть решения. Думайте! ДУМАЙТЕ!!! А для этого:
-
Учитесь рассуждать и задавать правильные вопросы.
Например, вы не умеете решать неравенства с модулями и вдруг видите вот такое:
(|3+|x+1||<5)
«Ой, мы это не проходили, я не знаю, как это делать!» Всё? Сдаемся? Теряем баллы?
Ни в коем случае! Вместо этого начинаем задавать вопросы:
— Что передо мной? Неравенство.
— Что оно «хочет»? Чтоб левая часть была меньше пяти.
— А когда левая часть будет меньше пяти? Ну, когда внутри модуля будет число (4); (1,6); (0) или (-4,7), иными словами, любое число от (-5) до (5) (не включительно). Значит, это неравенство будет выполняться, когда одновременно будут выполняться два требования:
(begin{cases}3+|x+1|>-5\3+|x+1|<5end{cases})
То есть мы имеем систему неравенств.
— Когда будет выполнять первое из них?…
И так далее. Вот так это и делается! Теперь, продолжая задавать себе вопросы, дорешайте эту задачу до конца.
-
Даже если вы намертво застряли в задаче — не торопитесь читать решение. Гляньте на него одним глазком, просто для получения подсказки. Поймите одну какую-то идею, до которой вы не догадались, а после продолжите решение сами.
-
Если даже после этого задача не поддалась, то уже прорабатывайте решение плотно и конкретно. Разберитесь в каждой строчке — почему она именно такая? Как она получилась из предыдущей или исходного условия? Есть ли здесь другие пути решения? До какой идеи я не додумался, на что не обратил внимания, чего не понял?
-
- Начинайте готовиться к ЕГЭ НЕ ПОЗЖЕ начала сентября 11 класса
Чтобы уверенно освоить с 13 по 18 нужно решить минимум по 30 задач из каждого номера. 30∙6=180 задач – и это минимум! Плюс еще надо изучить и хорошо понять теорию к этим задачам, а также порешать десяток-другой более простых, подготовительных задач из учебников или сборников.
Да и первую часть тоже никто не отменял, к ней также надо готовится, хотя бы повторять (если вы ее знаете). За пару месяцев освоить такое количество материала просто не реально, даже за полгода – вряд ли.
Кстати, если вы начинаете подготовку в 10-ом классе, лучше не прорешивайте стандартные ЕГЭ-шные задачи, а проходите программу 10 класса в углубленном формате, хорошо вникая в теорию. Помните, что школа не готовит ко второй части, поэтому нужно решать задачи сложнее тех, что проходят в классе. А 16 задачу ЕГЭ можно начать решать еще в 9 классе, используя сборник Гордина (учебник тут не сильно поможет, ибо слишком прост).
Вывод: работы – море, так что не теряйте времени!
Профильная математика — самый популярный предмет по выбору в 2021 году: этот экзамен будут сдавать почти 408 тысяч выпускников. Разбираемся, в чём особенность каждого задания экзамена и как сдать ЕГЭ на максимальный балл.
Кто сдает профиль по математике
Профильную математику сдают те выпускники, которые планируют поступать на технические специальности и некоторые направления в области экономики, менеджмента, социологии и геологии. С полным списком подходящих специальностей можно ознакомиться на сайте любого вуза.
Остальные школьники могут ограничиться экзаменом базового уровня, но в этом году и его сдавать не нужно.
Профиль от базы отличается структурой, заданиями и критериями оценивания. Разберём форму экзамена, который состоит из 19 заданий и двух самостоятельных частей.
Что ждёт в первой части экзамена по профильной математике
В этом блоке заданий с кратким ответом экзаменаторы проверяют знание всей школьной программы по математике. Несмотря на то, что первая часть экзамена гораздо легче второй, правильно решённые 12 заданий принесут выпускнику 62 балла в копилку ЕГЭ.
В заданиях № 1, № 2 и № 5 можно встретить несложную текстовую задачу. Поэтому предлагаем повторить округление с недостатком и избытком, а также алгоритм решения задач на проценты, чтение графиков и диаграмм.
Для решения заданий № 3, № 6 и № 8 нужно хорошо помнить основы геометрии. Темы, которые могут встретиться в этих задачах, касаются координатной плоскости, планиметрии и стереометрии.
Задача № 4 всегда относится к теории вероятностей. Чтобы справиться с заданием на максимальный балл, нужно вспомнить классическое определение вероятности и теорему о вероятностях событий.
Наверное, самое неоднозначное задание первой части экзамена — задача № 7. Все зависит от варианта: условие может быть как очень простым, так и непонятным. Для решения задания необходимо знать геометрический и физический смысл производной, а также уметь выводить первообразную.
Задание № 9 требует от выпускника умения совершать действия со степенями и преобразовывать числовые и буквенные выражения. Эта тема редко вызывает проблемы, но при решении этой задачи нужно быть особенно сконцентрированным, чтобы не пропустить знак или цифру.
В заданиях № 10 и № 11 проверяют навык решения текстовых задачи на движение и задач с прикладным содержанием на неравенства.
В задание № 12 нужно будет найти наибольшее и наименьшее значение функций. Чтобы его выполнить, повторите степенные и иррациональные функции, исследование частных и произведений, а также логарифмические и тригонометрические функции.
Как справиться со второй частью профиля по математике
Задания второй части требуют от выпускника обоснованного и подробного решения. Обычно эти задачи касаются не одного блока тем, а сразу нескольких.
В задании № 13 вам встретится комбинаторное уравнение, которое может включать следующие типы:
- Иррациональные уравнения;
- Рациональные уравнения;
- Тригонометрические уравнения, разложение на множители;
- Логарифмические и показательные уравнения;
- Тригонометрические уравнения;
- Тригонометрические уравнения, исследование ОДЗ;
- Уравнения смешанного типа.
Задание № 14 представляет собой стереометрическую задачу. Чтобы решить её, нужно потренировать каждый тип такой задачи. Обычно они касаются многогранников или круглых тел и проверяют умение находить углы и расстояние между прямыми и плоскостями, от точки до прямой и до плоскости.
В задании № 15 нужно будет решить неравенства. Чтобы написать структурированное решение, повторите, как решаются логарифмические уравнения, смешанные, с модулями и логарифмами, содержащие радикалы.
Задача № 16 всегда относится к планиметрии. Это задание проверяет умение находить элементы окружности в соединении с системой окружностей, треугольниками и четырёхугольниками. Вспомните все свойства многоугольников и окружности для решения этой задачи.
Задание № 17 относится к задачам на оптимальный выбор в финансовой сфере. Выпускнику могут предложить найти процентную ставку по кредиту или определить сумму вклада и платежа. Чтобы решить эту задачу, нужно быстро считать в уме и хорошо помнить алгоритм вычисления процентов.
Задача № 18 на параметр вызывает у школьников больше всего проблем и вопросов, многие даже не приступают к ней на ЕГЭ. Для выполнения этого задания необходимо развитое аналитическое мышление и умение решать все типы уравнений, неравенств и функций.
Олимпиадное задание № 19 требует нестандартного подхода и логического мышления. Справиться с ним поможет знание арифметической и геометрической прогрессии.
Советы, которые помогут сдать ЕГЭ по профильной математике 2021
Повторите теорию. Накануне экзамена структурируйте все знания в голове: повторите определения, табличные значения и формулы. Некоторую информацию вы получите на экзамене в виде раздаточного материала. Это, конечно, поможет в ответственный момент, но лучше повторить все формулы заранее, чтобы на ЕГЭ не тратить время на их преобразование и вывод.
Начните с первой части. Несмотря на то, что задания второй части сложнее и требуют больше времени на решение, начать стоит всё же с первой части. Во-первых, трудные задачи сразу могут поставить вас в тупик, тогда нервное напряжение скажется на результате. Во-вторых, не стоит недооценивать первую часть, ведь за первые 12 заданий можно получить 63 балла из 100!
Обращайте внимание на детали. Большинство выпускников отлично знают формат экзамена и все типовые задачи, но условие задания всё же важно дочитывать до конца. Так в задаче № 7, например, важно определить, какой график вам дан — производной или функции. А ответ текстовой задачи в неверных единицах измерения может стоить драгоценных баллов.
Оставьте время на проверку. В задании № 9 нужно уделить внимание арифметическим знакам, особенно если в варианте попались тригонометрические функции. А в № 13 — выделить верное ограничение. Часто выпускники делают ошибки в обычных расчётах, поэтому перепроверьте числа в задаче на экономику и движение.
Очень важно правильно занести информацию в бланк, ведь ответ другого формата просто не засчитают за верный. Поэтому обратите внимание, в какой графе вы оставили отрицательный знак и верно ли перевели обычную дробь в десятичную.
Не пугайтесь второй части. Не бойтесь приступить к заданиям второй части. Начните с того, в чём разбираетесь лучше всего. Обычно задания № 13 и № 15 не вызывают трудностей. Если ваш конёк — геометрия, начните с № 14 или № 16. Если вы мастер в алгебре, решайте задачи на параметр и свойства чисел — № 18, 19.
Находите время на отдых. Даже в период активной подготовки к экзаменам нужно находить время на отдых. Иначе вы рискуете забыть базовые правила в самый ответственный момент. Составьте комфортное расписание подготовки и даже в преддверии ЕГЭ не забывайте про сон — очень важно давать мозгу время осмыслить и уложить информацию.