Самостоятельная подготовка к ЕГЭ по математике
Анна Малкова
Вы решили готовиться к ЕГЭ по математике самостоятельно?
Вы ждете ответа на вопрос – насколько это реально?
Ответ на этот вопрос – да.
Подготовиться к ЕГЭ по математике самостоятельно абсолютно реально. И к базовому, и к профильному.
Тысячи школьников, у которых не было возможности заниматься с репетиторами, уже подготовились к ЕГЭ по математике самостоятельно, сдали на отлично и стали студентами. И сейчас вы узнаете, как они это сделали.
Конечно же, к базовому ЕГЭ готовиться проще. Смотрите видеокурс Анны Малковой по самым сложным задачам Базового ЕГЭ по математике. Это бесплатно! Просто зарегистрируйтесь – и получите ссылку для просмотра!
А мы поговорим о профильном ЕГЭ. Да, он сложнее, чем базовый. Профильный ЕГЭ по математике дает возможность поступить в вуз на технические и экономические специальности, где математика профильная. А базовая математика – экзамен для гуманитариев, для того чтобы, не перегружаясь математикой, получить по ней хорошую оценку в аттестате.
Так как же подготовиться самостоятельно к профильному ЕГЭ по математике?
Этот экзамен включает в себя 19 заданий, среди которых 12 – более простые, и оценивается в них только ответ. А вторая часть – 7 сложных задач. В них оценивается не только ответ, но и грамотное, обоснованное, правильное решение. И на решение всех задач дается всего 3 часа 55 минут.
Чего точно не надо делать при самостоятельной подготовке к ЕГЭ по математике?
— Не надо начинать с решения вариантов ЕГЭ. Скорее всего, это принесет только разочарование. Можно попробовать решить один вариант, чтобы узнать свой начальный уровень. Записать, сколько задач получилось. И готовиться! А потом сравнить результат.
— Не надо надеяться, что за месяц до ЕГЭ вы купите ответы в Интернете. Последний «глобальный слив» ЕГЭ произошел в 2013 году. Тогда в Сети за 2 дня до экзамена появилось множество вариантов ЕГЭ по математике. Но тем, кто не готовился, и это не помогло. С тех пор «слив» не повторялся, и следят теперь за всеми утечками очень строго. Что касается ответов – каждый год доверчивые люди платят мошенникам немалые деньги и получают вместо ответов бессмысленный набор чисел. Но количество доверчивых людей не уменьшается, и денег им не жалко.
— Не надо начинать с чтения учебников по математике для 5, 6… 11 класса. Во-первых, сколько времени у вас уйдет на это занятие? А во-вторых, эти учебники были написаны до появления ЕГЭ, и многих тем там просто нет.
Выбирайте для подготовки книгу, которая написана репетитором-практиком, готовящим к ЕГЭ, содержит все темы ЕГЭ, написана легким и понятным языком. Ведь самостоятельная подготовка не означает, что вы лишаете себя книг, интернета, любой помощи! Мы рекомендуем вам книгу Анны Малковой «Математика. Авторский курс подготовки к ЕГЭ», издательство «Феникс». Книга включает всю теорию и все задачи и заменит вам десяток учебников.
Хорошо, вы прочитали книгу. Что делать дальше? Ведь нужны задачи для тренировки? Мы приводим Топ-5 сайтов для самостоятельной подготовки к ЕГЭ по математике. Создатели этих сайтов – настоящие профессионалы, репетиторы и учителя с опытом работы более 20 лет. Эти люди не только знают о ЕГЭ всё, но и на основании анализа пробных ЕГЭ делающие прогноз о том, какие же в этом году будут задачи.
Сайт Анны Малковой
В разделе «Материалы ЕГЭ» полный курс математики. Просто, понятно, без «воды». Для многих старшеклассников эти материалы оказались спасением на контрольной! А для самых целеустремленных – возможностью поступить в вуз.
Другие полезные сайты:
Отличная возможность бесплатно подготовиться к ЕГЭ – здесь.
На этом сайте вы сразу получите бесплатно видеокурс по теории вероятностей, полный набор шпаргалок, вариант пробного ЕГЭ с авторскими задачами, ответами и видеоразбором. Вы получите возможность участвовать в ЕГЭ-Турнирах и пробных ЕГЭ. Не только школьники, но и учителя активно пользуются такой помощью!
Сайт www.reshuege.ru – дистанционная обучающая система для подготовки к ЕГЭ по математике «РЕШУ ЕГЭ». Автор — Дмитрий Гущин. Тысячи заданий ЕГЭ с решениями и ответами по всем предметам.
www.alexlarin.net – сайт Александра Ларина, на котором постоянно публикуются варианты пробных и реальных ЕГЭ. Тренировочные варианты ЕГЭ с разбором на форуме.
http://mathus.ru/ –сайт Игоря Яковлева. Информация обо всех московских олимпиадах по математике и физике, которые дают льготы при поступлении в вузы. Материалы по математике и физике для подготовки к ЕГЭ, дополнительным вступительным экзаменам и олимпиадам. Полные сборники задач по части 2 ЕГЭ по математике с ответами.
Обратите внимание, в каком порядке изучать темы ЕГЭ по математике. В книге Малковой «Математика. Авторский курс подготовки к ЕГЭ» они даны именно в таком порядке. От простого – к сложному! Начинаем с текстовых задач. Это задачи на проценты, движение и работу, сплавы и смеси – в общем, все типы задач, где условие дается в виде текста. Выигрышная тема – Теория вероятностей. Есть отличные курсы по теории вероятностей на Ютьюбе. Дальше – геометрия и стереометрия (часть 1). Дальше – понятие функции. Корни, степени, логарифмы, графики функций. Тригонометрия и тригонометрические уравнения. И наконец – производная и первообразная, темы, больше относящиеся к курсу математического анализа.
И это была только часть 1. Дальше – часть 2. Сложные задачи. Важный лайфхак: уравнения, неравенства и задачи с экономическим содержанием – минимальный набор, который, вместе с частью 1, даст вам заветные 72-75 баллов, а их хватит для поступления на бюджет в хороший вуз.
Как готовиться к части 2 ЕГЭ по математике? Если задачи первой части можно освоить самостоятельно, то в задачах второй части ЕГЭ без репетитора не обойтись. Хорошая новость – этому репетитору совсем не обязательно сидеть рядом с вами. И совсем не обязательно платить ему огромные деньги. Попробуйте дистанционный вариант! Например, Годовой Онлайн-курс по математике, где стоимость часа занятий – всего 140 рублей. Это совсем немного. Выпускники курса занимались онлайн, самостоятельно. Их домашние задания проверяли лучшие репетиторы Москвы. А в результате ребята поступили в лучшие вузы России на «бюджет».
Что еще важно при самостоятельной подготовке к ЕГЭ по математике?
Обязательно прохождение пробных ЕГЭ, хотя бы раз в месяц. И не только в школе! Ищите, кто в вашем городе проводит пробные ЕГЭ. Участвуйте в пробных онлайн.
Когда вы готовитесь к ЕГЭ по математике самостоятельно, вы сами себе репетитор. А на что еще обращает репетитор, кроме правильности решения задач? На время, конечно! Ведь если вы правильно решили одну задачу за 5 часов, то на экзамене вряд ли что-то успеете сделать.
Если вы хотите сдать ЕГЭ по математике на 80-100 баллов, вам важно подумать о том, как распределить время на экзамене. Как это сделать?
— Отлично, если вы решаете всю часть 1 (первые 12 задач) за 30 минут. Достигается это только тренировкой! Все перечисленные выше сайты – вам в помощь.
— Дальше вам надо решить «необходимый минимум» – задачи 13 (уравнение), 15 (неравенство) и 17 (экономическую). И если вы готовитесь на 80-100 баллов, вам на эти задачи – еще час-полтора. Иначе не успеете сделать сложные.
Кстати, задача 17 (экономическая) чаще всего решается «по шаблону». Зато в ней есть другая сложность. Может оказаться, что в ней много вычислений. Поэтому важно уметь считать быстро, правильно и без калькулятора.
— И теперь у вас осталось немало времени, но и четыре самых сложных задачи остались! Это задача 14 (стереометрия), задача 16 (геометрия), задача 18 (параметры) и задача 19 (нестандартная).
Посмотрите внимательно на эти задачи. Выберите из них ту, которая вам знакома. Например, вы такие решали на Годовом Онлайн-курсе.
И приступайте! Важный момент: не надо хвататься за много задач сразу! Решаем одну за другой, сразу проверяем оформляем решение и записываем ответ. И когда все готово – переходим к следующей, которая вам кажется проще.
Потренировавшись решать пробные ЕГЭ, вы без труда и волнений справитесь с настоящим экзаменом. Но повторим еще раз: решение вариантов – это заключительный этап вашей тренировки!
А кому же точно не подходит самостоятельная подготовка к ЕГЭ по математике?
— Тем, кто не хочет учиться. Потому что самое главное – ваше желание.
— Тем, кому нужна строгая «училка с указкой».
— Тем, кто хочет, чтобы все сделали за него. Таким ребятам может быть очень трудно во взрослой жизни – ведь там «нянек» не будет.
Желаем вам успеха в самостоятельной подготовке к ЕГЭ по математике! И не отказывайтесь от помощи. Умейте ее получать – от вашей школьной учительницы или из полезных ресурсов в интернете.
Хотите узнать больше о самостоятельной подготовке к ЕГЭ по математике?
Подпишитесь на нашу рассылку здесь.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Самостоятельная подготовка к ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.03.2023
Подготовка к ЕГЭ по математике
Из каких частей состоит ЕГЭ по математике в 2023 году
Математика — один из двух обязательных предметов на ЕГЭ. Но, в отличие от русского языка, эта дисциплина предлагает 2 уровня сложности: профильный и базовый. Какий именно вариант выбрать, зависит от вашей цели. Если вуз, в который вы хотите поступить, требует профильного уровня, нужно сдавать его. Обычно это касается технических специальностей.
Для получения аттестата выпускникам школ хватит и базового. Но финальное решение за вами. Если вы хотите сдать профильный вариант, просто чтобы проверить свои знания и уровень подготовки, — дерзайте!
Структура базового уровня ЕГЭ по математике
Базовый уровень проверяет основные знания школьника по математике. Такой экзамен не делится на части: в него входит только 21 задание с кратким ответом. Ответом может быть целое число, десятичная дробь или ряд цифр. По уровням сложности задания экзамена тоже не делятся — все задачи в нем базового уровня. Чтобы выполнить такую работу, ученику дают 180 минут.
Структура профильного уровня ЕГЭ по математике
Варианты профильного уровня проверяют основные и углубленные знания школьника. В 2023 году ЕГЭ состоит из 2 частей:
-
1-я часть: 11 задач с кратким ответом;
-
2-я часть: 7 задач с развернутым ответом.
В первой части ответом может быть целое число, десятичная дробь или ряд цифр. Во второй части — полное обоснованное решение и ответ. Чтобы выполнить задания экзамена, школьнику дают 235 минут.
Задачи ЕГЭ по математике профильного варианта делятся на категории по уровням сложности. В таблице ниже можно увидеть, как именно.
| Базовый | 6 |
| Повышенный | 10 |
| Высокий | 2 |
| Всего | 18 |
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Демоурок по подготовке к экзаменам
Составим ваш личный путь к высоким баллам — учтем сроки, уровень знаний и цель.
Как сдать ЕГЭ по математике: разбор сложных задач
Экзамен по математике не зря считают одним из самых трудных. Даже в заданиях базового варианта можно легко ошибиться по невнимательности. Что уж говорить о действительно сложных задачах с полным решением, где много «подводных камней»? Чтобы вы знали, как подготовиться к ЕГЭ по профильной математике, мы разобрали несколько из них.
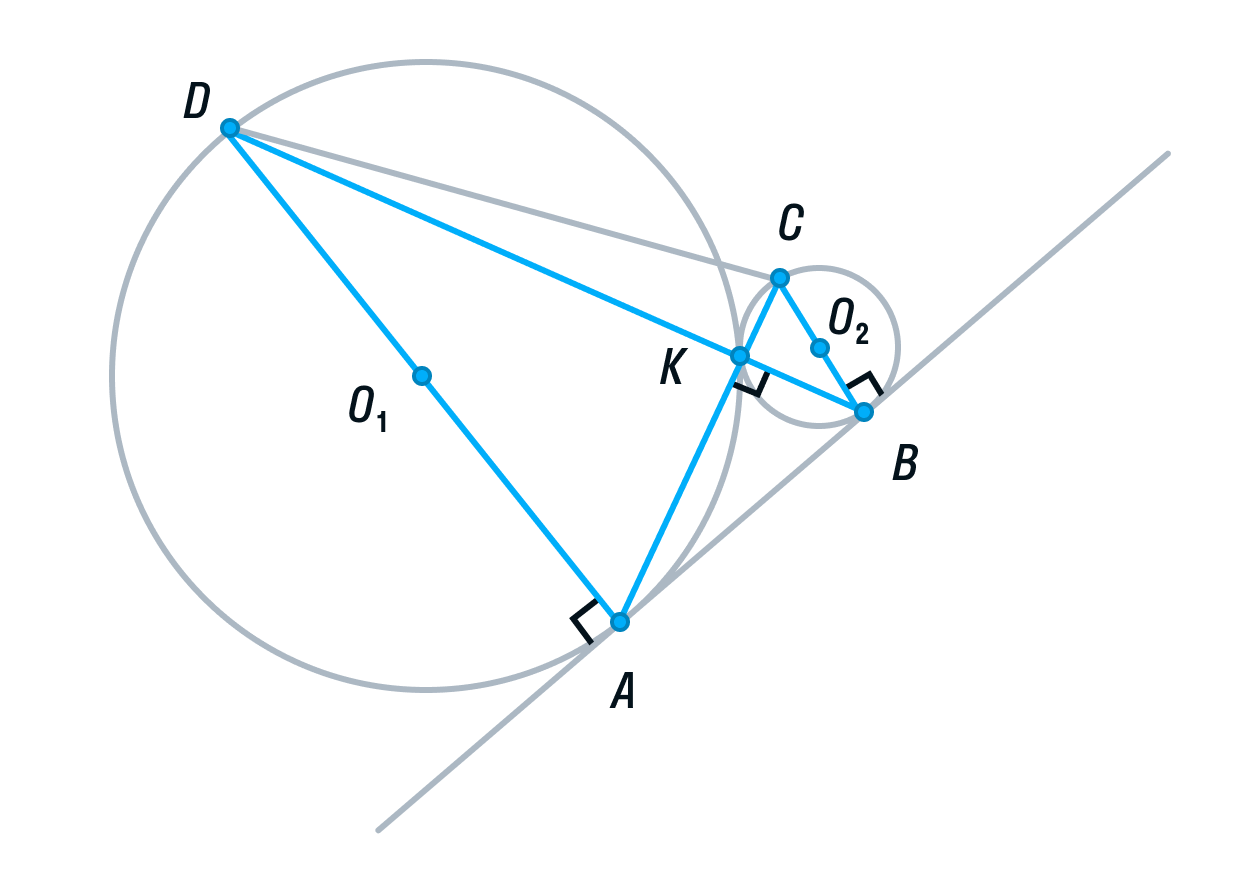
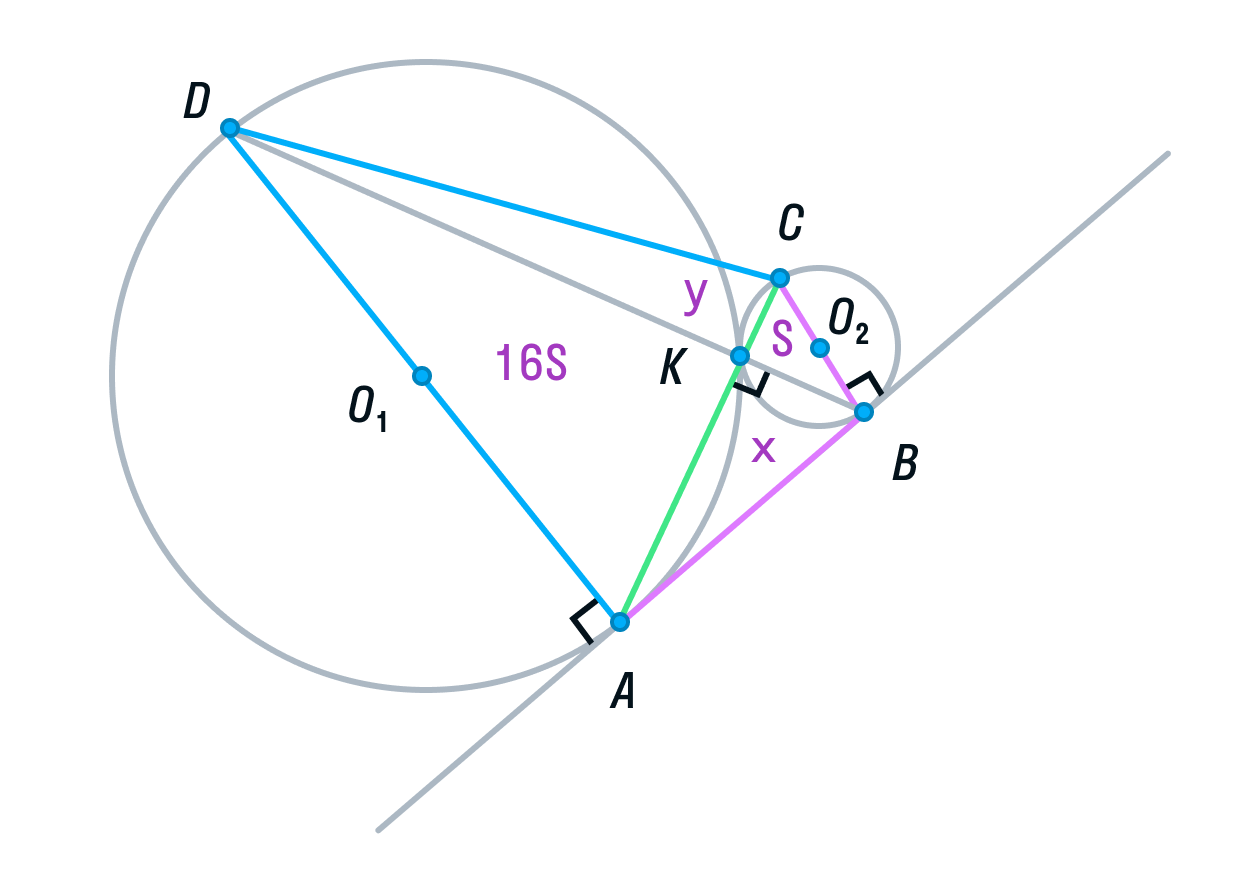
Задание 16
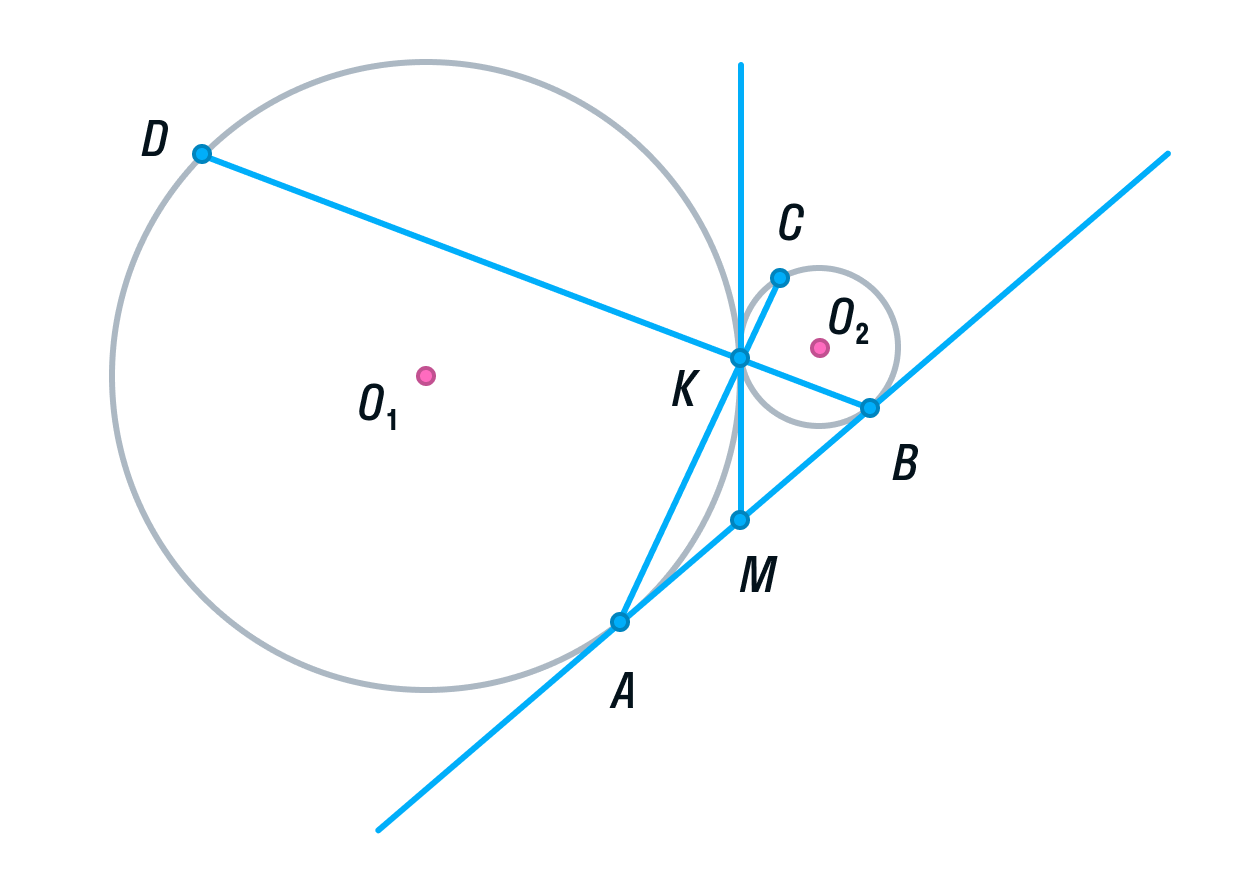
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Совет
Для этого задания советуем повторить темы:
-
Касательные к окружности и их свойства.
-
Свойства вписанных углов.
-
Взаимное расположение окружностей.
-
Свойства прямоугольного треугольника.
-
Признаки и свойства параллельных прямых.
-
Подобные треугольники, площади подобных фигур.
-
Свойство площадей (в частности: отношение площадей треугольников с одинаковой стороной).
-
Трапеция, её свойства. Площадь трапеции.
-
Теорема Пифагора.
Проследите, чтобы они были в вашем плане подготовки к профилю ЕГЭ по математике.
Решение
а) Выполним построение.
-
Окружности с центрами О1 и О2 соответственно касаются друг друга в одной точке К.
-
Прямая АВ касается обеих окружностей в точках А и В соответственно.
-
Прямые АК и ВК пересекают окружности в точках С и D соответственно
-
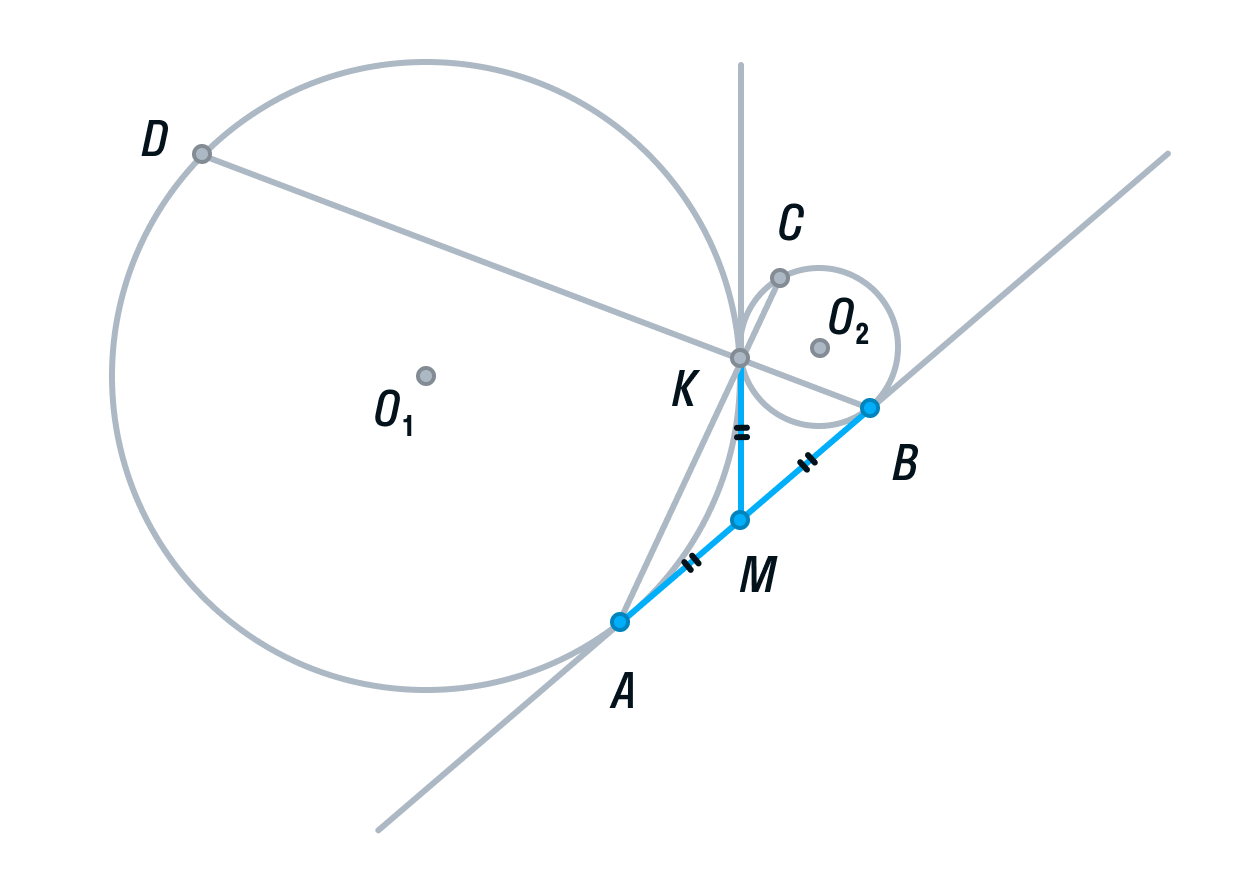
Пусть общая касательная окружностей в точке К, пересекает прямую АВ в точке М.
Тогда по свойству касательных, проведенных из одной точки, AM = KM и KM = BM.
-
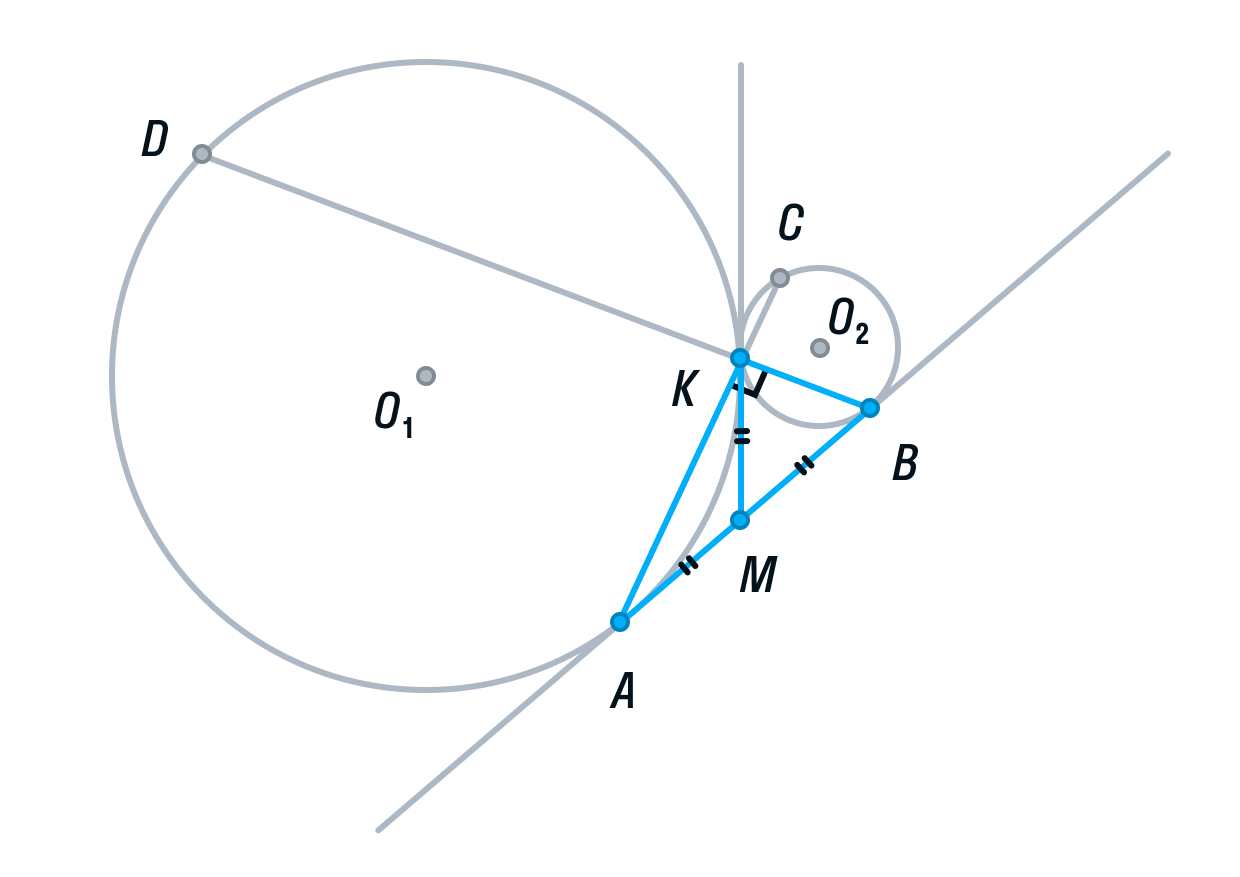
Рассмотрим треугольник АВК. Его медиана АМ равна половине стороны, которую она разбивает. Следовательно, делаем вывод, что треугольник АВК прямоугольный, а угол К = 90°.
-
Вписанный угол AKD является смежным углом АКВ, а значит, он тоже 90° как прямой. Следовательно, угол AKD опирается на диаметр AD. Значит, AD ⊥ AB, так как радиус, а в данном случае диаметр, перпендикулярен касательной в точке касания.
-
Аналогично рассмотрев угол ВКС, получим, что BC⊥ AB.
-
Прямые AD и ВС перпендикулярны третьей прямой АВ, следовательно, прямые AD и BC параллельны. Ч. т. д.
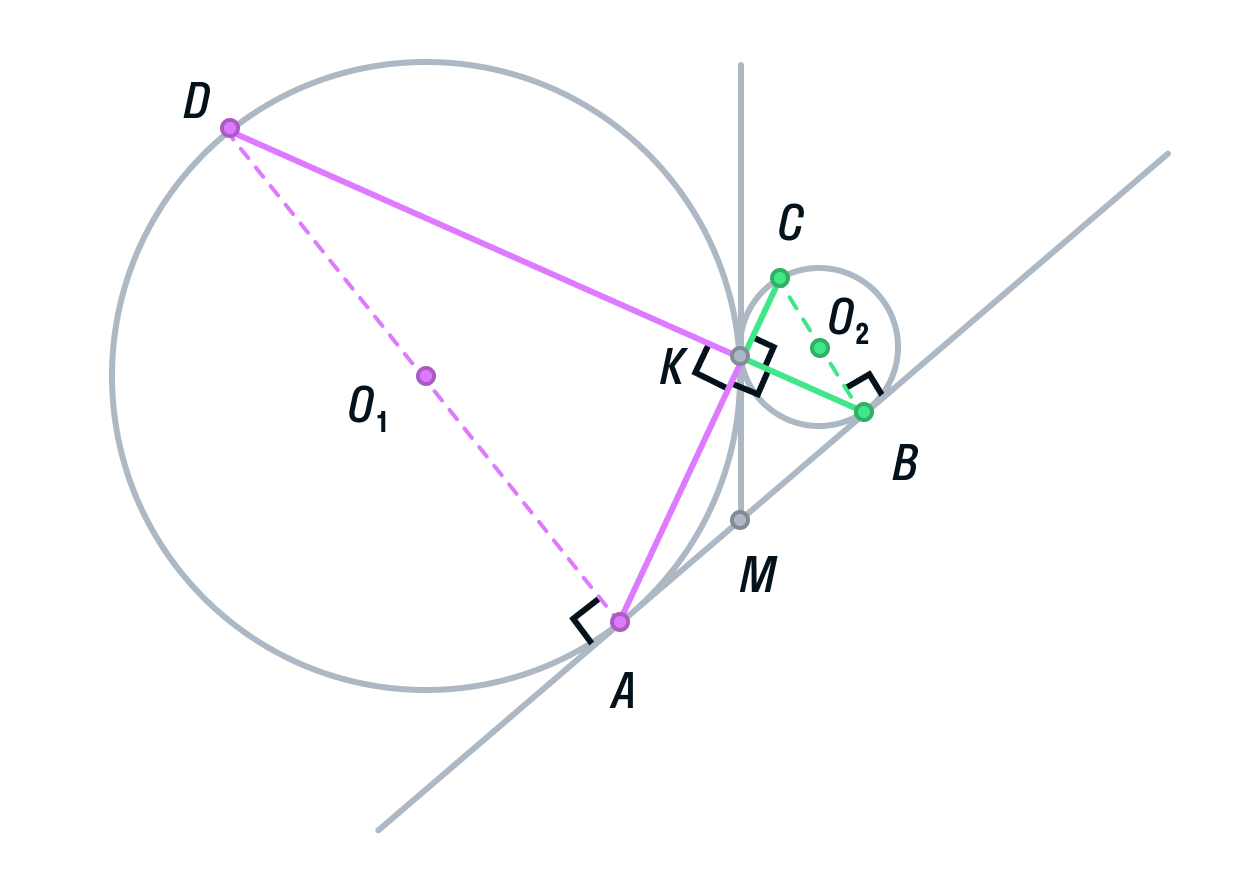
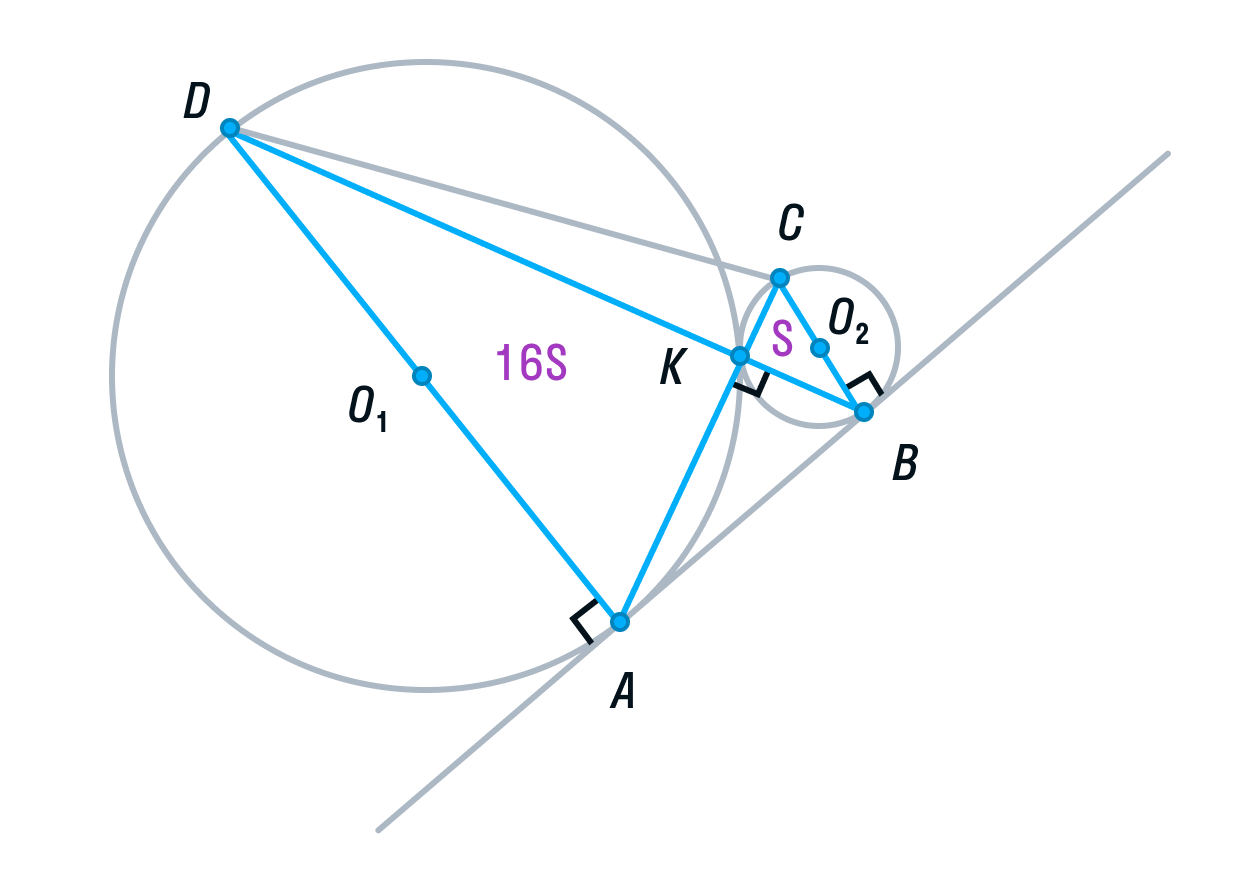
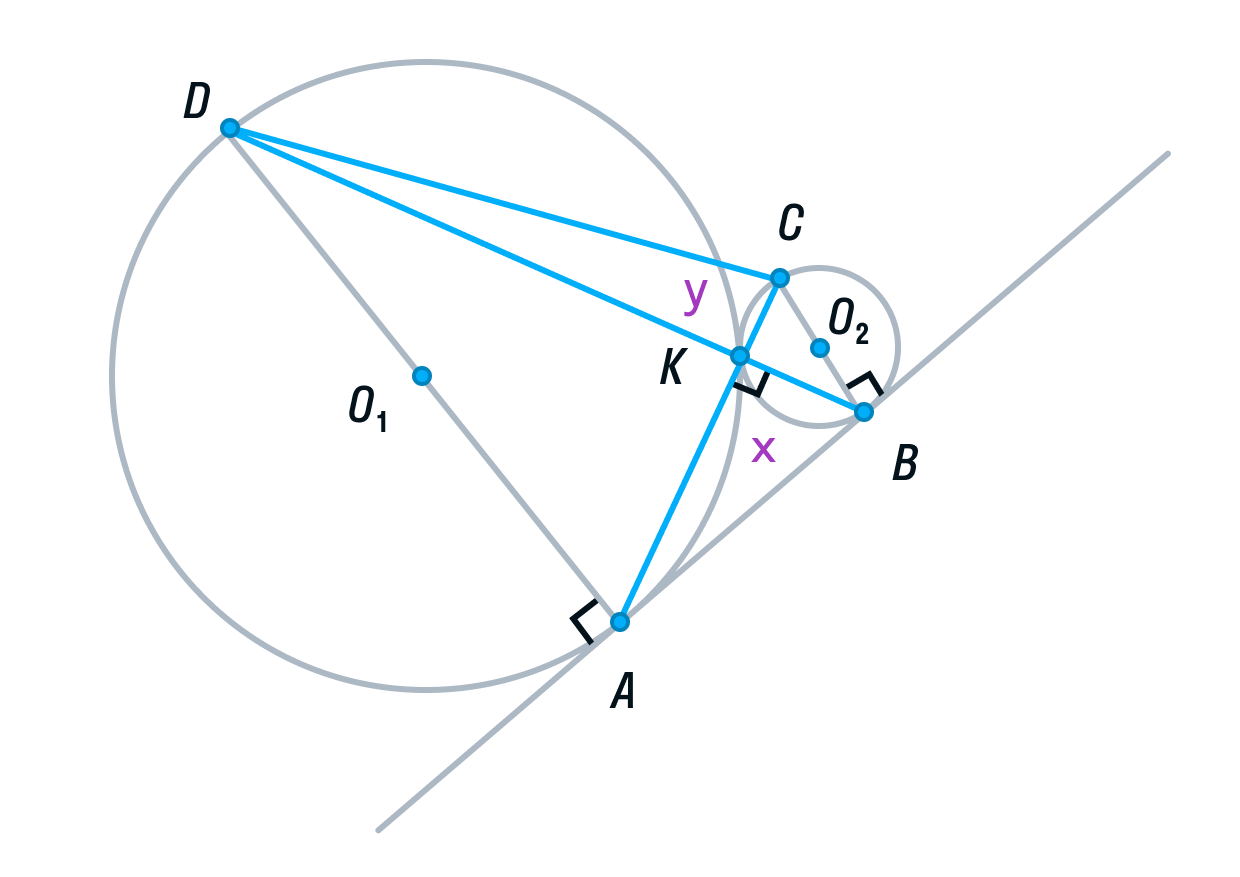
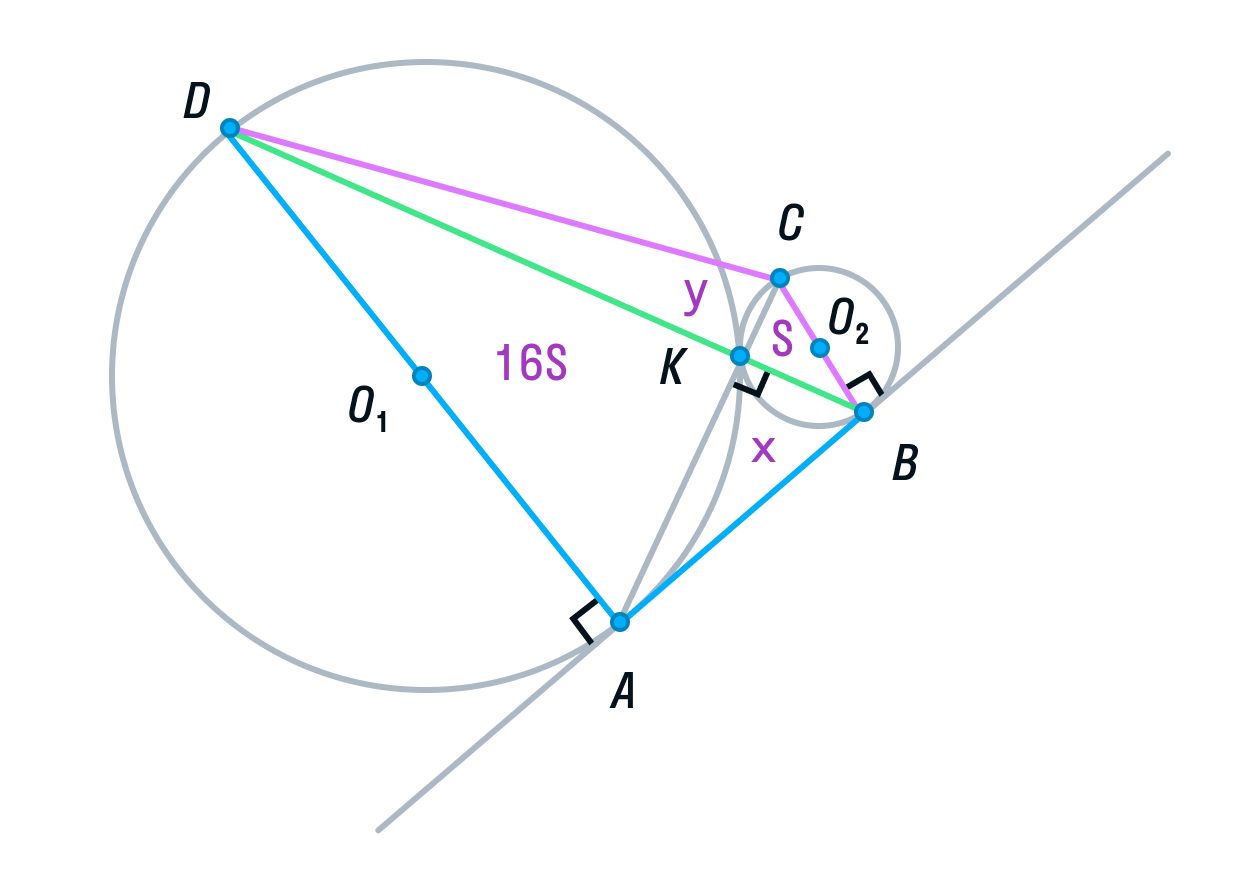
б) Пусть радиус первой окружности равен 4, а радиус второй окружности равен 1. Тогда АD = 8, ВС = 2.
-
Рассмотрим треугольники ADK и СВК. Они подобны, т. к. имеют два равных угла (К – вертикальный, С и А — накрест лежащие). Из подобия треугольников следует, что их площади относятся как коэффициент подобия в квадрате:
-
Обозначим площадь треугольника СВК за S, тогда площадь треугольника ADK будет равна 16S.
-
Пусть площади треугольников АВК и CDK будут равны х и у соответственно.
-
Вспомним свойство, связывающее высоты треугольников с общим основанием и получим следующие равенства: DB — общая сторона треугольников ADB и СDB, следовательно:
(равно 4 из подобия треугольников ADK и СВК, см. выше),
-
Аналогично, AC — общая сторона треугольников ADС и ABC, следовательно,
(равно 4 из подобия треугольников ADK и СВК, см. выше),
-
Решим полученную систему уравнений:
-
Из первого уравнения
подставим во второе и найдем y.
следовательно,
подставим во второе и найдем y.
-
Площадь ABCD равна 16S + 4S + 4S + S = 25S.
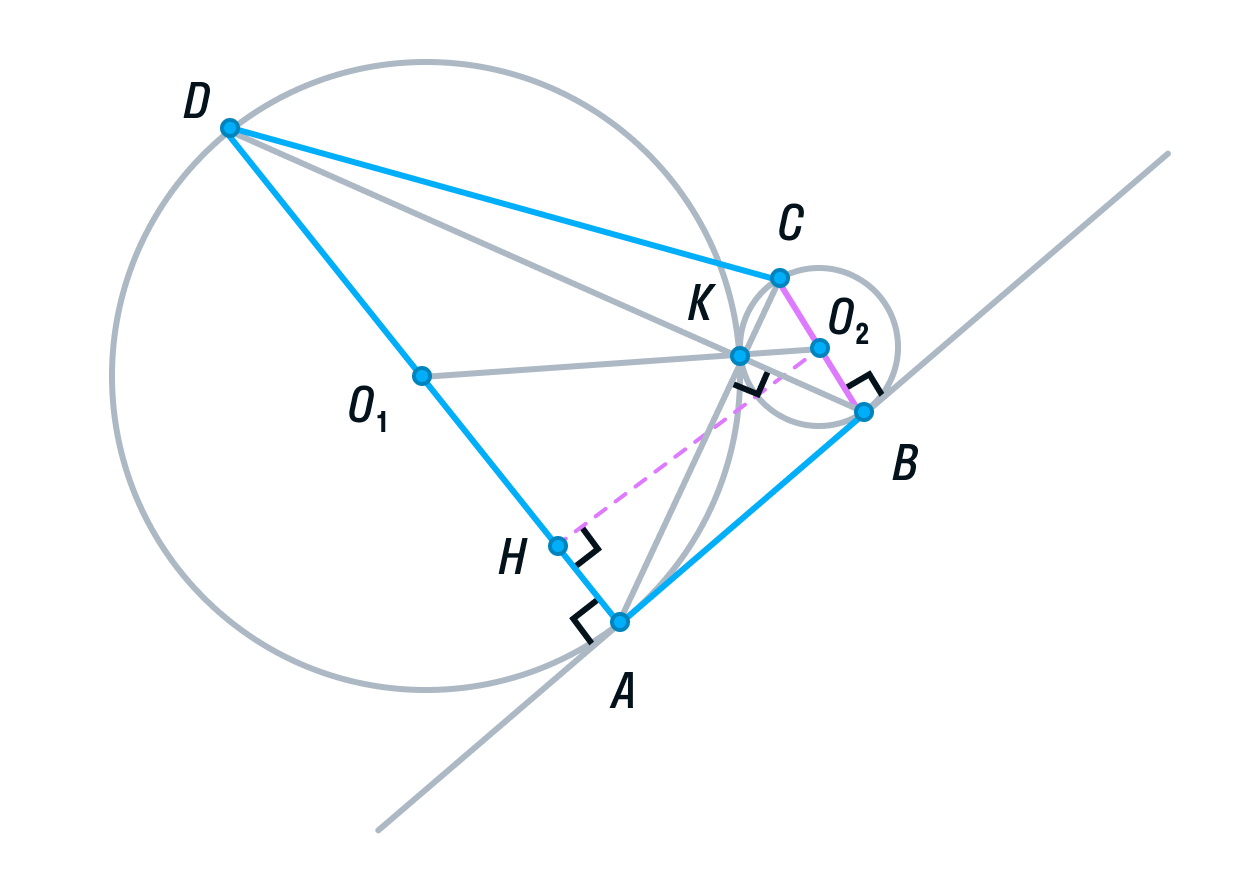
-
Заметим, что ABCD — прямоугольная трапеция (AD||BC, AB — перпендикулярна основаниям). Для вычисления ее площади нужно полусумму оснований умножить на высоту.
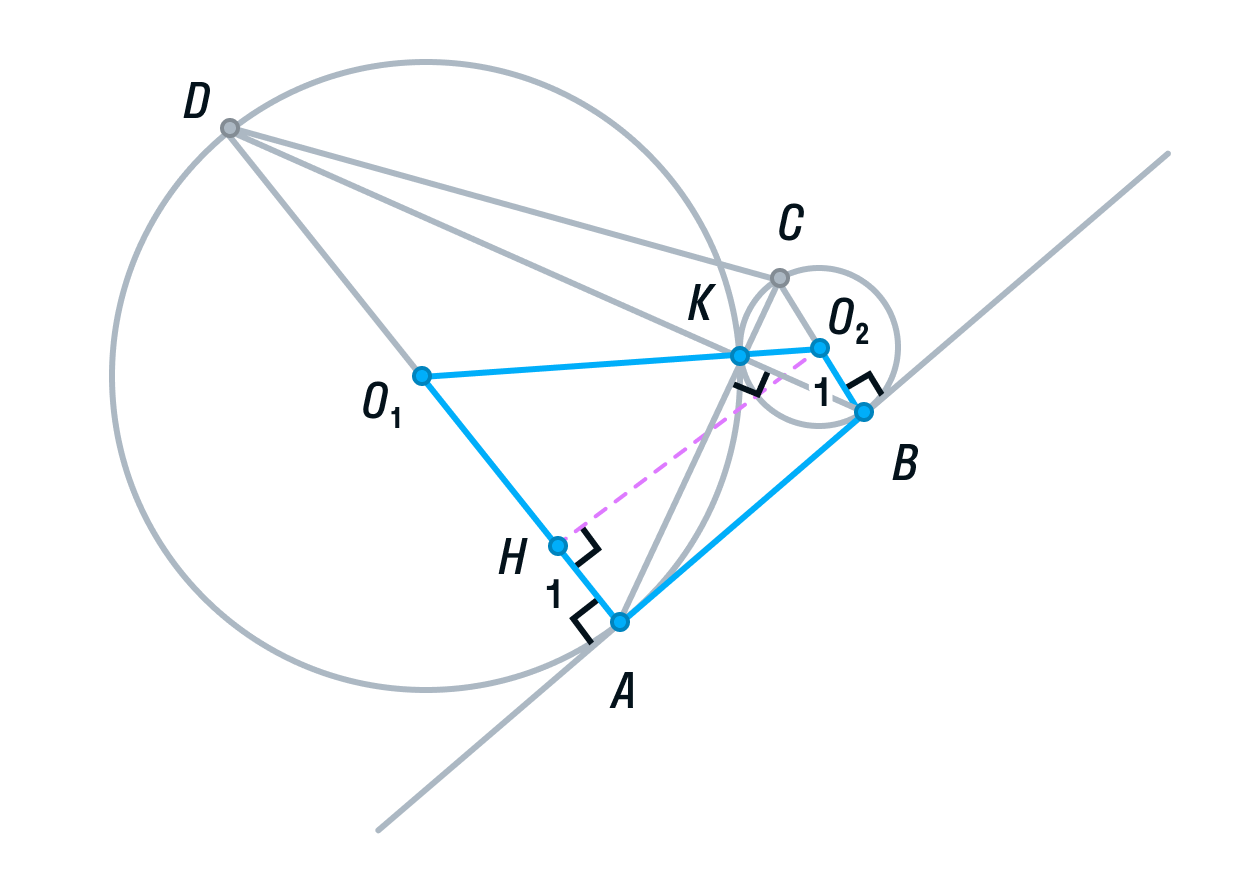
-
Для того, чтобы найти высоту, рассмотрим меньшую трапецию AO1O2B.
Ее основания равны 1 и 4, так как О2В и О1А — радиусы. O1O2 = 5, так как О2К и О1К — радиусы. О2H — высота трапеции AO1O2B.
-
По теореме Пифагора найдём О2H:
-
Вычислим площадь трапеции ABCD:
-
С другой стороны мы нашли
Отсюда S = 0,8.
-
Площадь треугольника АКВ = 4S, следовательно,
Ответ: 3,2.
Задание 18
В школах № 1 и № 2 учащиеся писали тест. В каждой школе тест писали по крайней мере 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?
б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?
в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Совет
Чтобы справиться с этой задачей, нужно повторить темы:
-
Понятие натурального и целого числа.
-
Среднее арифметическое.
-
Делимость чисел.
-
Процент. Нахождение процента от числа, уменьшение числа на заданный процент.
-
Составление и решение линейных уравнений.
Добавьте их в ваш план подготовки к ЕГЭ по математике, если собираетесь сдавать профиль.
Решение:
а)
-
Допустим, что в школе № 1 писали тест 2 учащихся, один из них набрал 1 балл, а второй набрал Х баллов и перешёл в другую школу. Тогда средний балл в школе был равен (1 + Х) : 2 = 10, а стал равен 1, т. е. уменьшился в 10 раз.
-
Решим уравнение и получим Х = 19 — натуральное число. Следовательно, наше предположение верно.
-
Или мы можем предположить другой вариант: что один учащийся набрал 2 балла. Тогда средний балл изначально равняется 20, а после ухода второго станет 2, т. е. изменится в 10 раз.
-
Решим уравнение (2 + Х) : 2 = 20, отсюда Х = 38 — натуральное число, что тоже удовлетворяет условию задачи.
Ответ: средний балл в школе № 1 мог уменьшиться в 10 раз.
б)
-
Пусть в школе № 2 писали тест m учащихся, n — сумма баллов m учащихся, средний балл равнялся B, а перешедший в неё учащийся набрал u баллов.
-
Умножим обе части полученного уравнения на 10, получим:
-
По условию B = 7, тогда получим, что 10u кратно 10, а
не делится на 10, так как ни один из множителей не делится на 10. Это противоречие.
Ответ: Первоначальный средний балл в школе № 2 не мог равняться 7.
в)
-
Пусть в школе № 1 средний балл равнялся A, общее количество баллов — p, количество писавших работу — (9 – m).
(из пункта б).
Следовательно,
-
Попробуем найти средний балл в школе № 2 методом подбора. Пусть:
В = 1, тогда:
кратно 10, а
не делится на 10.
В = 2, тогда:
пусть u = 1, тогда m = 4:
— не является целым числом.
u = 2 не может быть, т. к. m ≥ 1
В = 3, тогда:
кратно 10, а
не делится на 10.
В = 4, тогда:
Чтобы m было натуральным числом u должно быть четным, u = 2, тогда m = 4, что невозможно (доказали при В = 2).
u = 4, тогда m меньше 0, что невозможно т. к. m ≥ 1.
В = 5, тогда:
пусть u = 1, тогда m = 7, что невозможно (доказали в пункте б);
пусть u = 2, тогда m = 5:
— не является целым числом;
пусть u = 3, тогда m = 3:
-
Этот случай реализуется, например, в школе № 2 при m = 3, B = 5. Предположим, что каждый ученик набрал по 5 баллов. Тогда в школе № 1 писали 9 – m = 9 – 3 = 6 учащихся, 3 из них набрали по 1 баллу, а 3 – по 3 балла, тогда средний балл:
-
Переход из школы № 1 в школу № 2 совершил ученик с 3 баллами, тогда
средний балл в школе № 1 стал равен:что на 10% меньше от первоначального значения.
-
Тогда средний балл в школе № 2 стал равен:
что на 10% меньше от первоначального значения.
Ответ: наименьшее значение первоначального среднего балла в школе № 2 равно 5.
Ответ: а) да; б) нет; в) 5.
Как выставляют баллы за ЕГЭ по математике
С базовым уровнем сложности все просто: за каждый правильный ответ вашего варианта вы получаете по 1 первичному баллу. То же самое касается и первой части профиля: задания 1–11 тоже оценивают в 1 балл.
Как вы помните, во 2-й части профильного варианта нужны и решение, и ответ. Здесь задания оценивают по нескольким критериям. Они сложнее, но и баллов за них можно получить больше. Давайте же разберемся, как выставляют баллы во второй части профиля. Это поможет вам подготовиться к заданиям ЕГЭ по математике как самостоятельно, так и с учителем.
| Задание № 12 | Баллы |
|---|---|
| В обоих пунктах есть обоснованные ответы | 2 |
| Есть обоснованный ответ только в пункте а или есть неверный ответ из-за ошибки в вычислениях, но шаги в решениях обоих пунктов верные |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 13 | Баллы |
|---|---|
| Верно доказан пункт а, в пункте б есть обоснованный ответ | 3 |
| Есть только обоснованный ответ в пункте б или верно доказан пункт а, в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ |
2 |
| Есть только верное доказательство пункта а, или в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ, или есть обоснованный ответ в пункте в, который получен с помощью пункта а, но сам пункт а не выполнен |
1 |
| Все остальные случаи. | 0 |
| Максимальный балл | 3 |
| Задание № 14 | Баллы |
|---|---|
| Есть обоснованный ответ | 2 |
| Ответ обоснован, но он отличается от верного исключением точек –12 и/или 0 или шаги решения верные, но из-за ошибки в вычислениях получен неверный ответ |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 15 | Баллы |
|---|---|
| Есть обоснованный ответ | 2 |
| Ученик верно построил математическую модель | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 16 | Баллы |
|---|---|
| Верно доказан пункт а, в пункте б есть обоснованный ответ | 3 |
| Есть только обоснованный ответ в пункте б иЛИ Верно доказан пункт а, в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ |
2 |
| Есть только верное доказательство пункта а, или в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ, или есть обоснованный ответ в пункте в, который получен с помощью пункта а, но сам пункт а не выполнен |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 3 |
| Задание № 17 | Баллы |
|---|---|
| Есть обоснованный ответ | 4 |
| Рассуждения и значения параметра верные, но в ответе есть 1–2 неверных значения или решение недостаточно обосновано | 3 |
| Есть верное рассуждение и хотя бы одно правильное значение | 2 |
| Задача сведена к исследованию взаимного расположения 3 окружностей или двух квадратных уравнений с параметром | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 4 |
| Задание № 18 | Баллы |
|---|---|
| Есть обоснованный ответ в пунктах а, б, в | 4 |
| Есть обоснованный ответ в пункте в и есть обоснованный ответ в пунктах а или б | 3 |
| Есть обоснованный ответ в пунктах а и б или есть обоснованный ответ в пункте в. |
2 |
| Есть обоснованный ответ в пунктах а или б | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 4 |
Узнать больше о структуре экзамена, вариантах и критериях, по которым оценивают работы, можно на официальном сайте ФИПИ, в разделе «Демоверсии, спецификации, кодификаторы». Там же вы найдете методические указания для подготовки.
Сколько баллов нужно набрать, чтобы получить 3, 4 и 5
Теперь, когда мы разобрали критерии, можно посчитать, сколько баллов нужно набрать на конкретную оценку. В этом нам помогут таблицы ниже. Заодно разберемся, как первичные баллы переводятся в тестовые — финальные.
| Шкала перевода баллов в базовой математике | |
|---|---|
| Первичные баллы | Оценка |
| <7 | 2 |
| 7–11 | 3 |
| 12–16 | 4 |
| 17–21 | 5 |
| Максимальный балл | 4 |
Обратите внимание: с 2008 года официально баллы ЕГЭ не переводят в привычные нам оценки по пятибальной системе. Но если вам хочется это сделать, можно примерно оценить работу по таблице ниже.
| Шкала перевода баллов в профильной математике (неофициальная) | ||
|---|---|---|
| Первичные баллы | Тестовые баллы | Оценка |
| <5 | <27 | 2 |
| 5–8 | 27–49 | 3 |
| 8–20 | 50–67 | 4 |
| 21–31 | 68–100 | 5 |
6 советов от эксперта, как готовиться к ЕГЭ по математике
Мы занимаемся подготовкой учеников к экзамену каждый год и понимаем, насколько это важно и волнительно. Вам предстоит ответственная работа, от которой многое зависит. Чтобы облегчить ее, мы собрали несколько советов, которые помогут вам как можно лучше подготовиться к ЕГЭ по математике:
-
Осознанно выберите уровень сложности и поставьте цель в баллах.
-
Составьте план подготовки к ЕГЭ по математике: больше времени уделяйте темам, которые у вас «западают». Чтобы выявить их, ученики Skysmart проходят тест на бесплатном уроке.
-
Узнайте все о ЕГЭ: сколько времени длится экзамен, из каких частей состоит, по каким темам будут задания, сколько вариантов, какие дадут справочные материалы и т. д.
-
Составьте сбалансированное расписание для подготовки и следите, чтобы в нем было достаточно времени для отдыха.
-
Много практикуйтесь: решайте варианты из Открытого банка заданий ЕГЭ и сдавайте тестовые экзамены.
-
Систематически консультируйтесь и занимайтесь с наставником, который часто имеет дело с подготовкой к ЕГЭ — преподавателем в школе или репетитором.
Все пункты в этом списке важны для тех, кто хочет набрать 80–100 баллов, но последний — особенно. Преподаватель расскажет о том, что представляет из себя ЕГЭ, и тогда на реальном экзамене не будет неприятных сюрпризов.
На курсах подготовки к ЕГЭ по математике в Skysmart учителя помогают школьникам разобраться в КИМах и прорешать каждый тип задач. Ученики заранее знакомятся с частыми ошибками, что помогает избегать их в работе и сохранять баллы. А еще мы учим готовиться морально, чтобы не допустить ошибок из-за паники и невнимательности. Начните подготовку к ЕГЭ по математике с нуля вместе со Skysmart: первый урок — бесплатно!
Обычно базовую математику выбирают ребята, у которых есть план: надо как можно скорее разделаться с бесполезным для поступления предметом и сосредоточиться на своем наборе вступительных. Из этой статьи вы узнаете, как сдать базовую математику максимально быстро и просто.
В этом материале мы сделаем акцент на простых номерах, которые принесут вам балл почти задаром! Они обозначены пометкой «Обязательно делать» — таких заданий 10. Как раз с запасом на ошибки, ведь минимум для сдачи базовой математики — 7 баллов.
Для тех, кто хочет получить выше тройки — это 12 баллов и выше, — мы дали рекомендации по еще 3 задачам. В сумме получается 13 номеров. Решите их все, и твердая четверка у вас в кармане.
Какие задания решать, чтобы сдать базовую математику
Задание 1: обязательно делать
Проверяется ваше умение разделить случаи, когда требуется округлить величину в большую сторону, а когда — в меньшую.

Если вы ходите в магазин с наличными, то сталкиваетесь с подобными задачами каждый день. Разделим 100 рублей на стоимость одной упаковки йогурта. Не забывайте приводить все величины к одной размерности:
100 : 14,6 = 6, 849…
Так сколько баночек йогурта вам продадут? На 7 штук денег не хватает, значит, округлить полученную величину надо до целого в меньшую сторону. Математическое правило округление в этой задаче не поможет.
Ответ: 6.

Если одна пачка рассчитана на 6 рулонов, то на 63 рулона:
63 : 6 = 10,5.
Но полпачки вам не продаст. Включаем логику: возьмем меньше — не хватит еще половины пачки на три последних рулона. Значит, округлить надо в большую сторону, взять клей с небольшим запасом. Математическое правило округления снова игнорируем.
Ответ: 11.
Задание 2: обязательно делать
Это задача на здравый смысл. Нужно соотнести величины с их возможными значениями.

Вряд ли грузовой автомобиль может весить как 3 шоколадки (300 г), а взрослый человек — 8 т.
Давайте вместе подберем значения.
- Взрослый человек обычно весит от 50 до 100 кг — что из этого подходит? Конечно, 65 кг.
- Грузовой автомобиль достаточно большой и тяжелый, скорее всего, он весит несколько тонн. Нам подходит 8 т.
- Книга обычно не такая большая и весит до 1 кг. Из оставшегося подойдет 300 г.
- А пуговка совсем маленькая. Значит, берем самый легкий вес — 5 г.
Ответ:
Главное — внимательно перенести ответы в бланк: 3142.
Задание 3: обязательно делать
Задание на работу с графиком, диаграммой или таблицей. Вооружайтесь карандашом, читайте условие с предельной внимательностью и безжалостно отмечайте нужные по условию значения на изображении в КИМ. Вы и представить не можете, сколько выпускников теряет тут баллы по невнимательности.
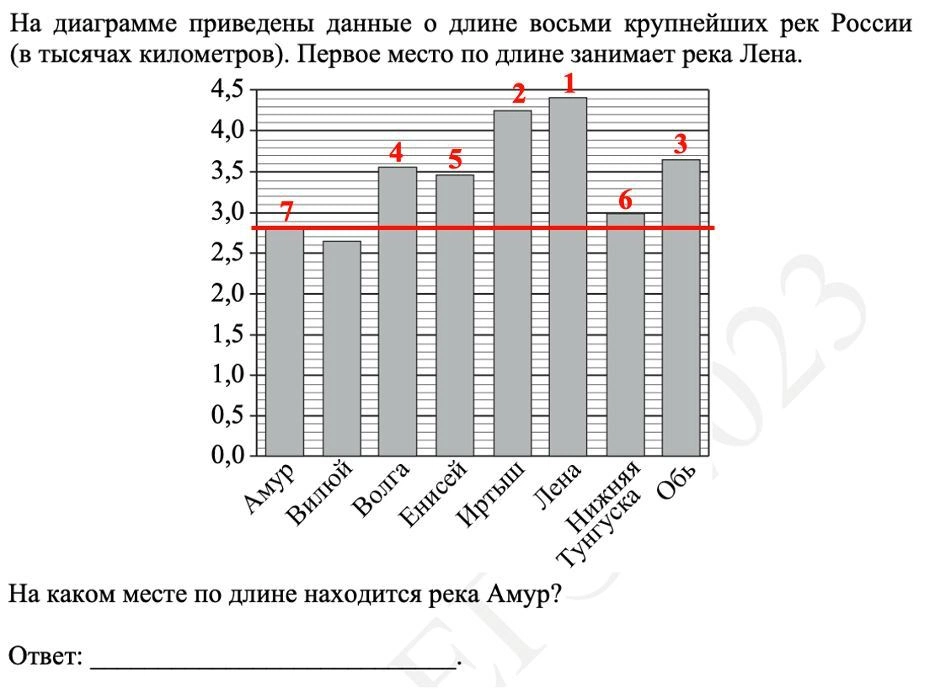
Мы ярко отметили уровень, соответствующий Амуру, в итоге посчитать все более длинные реки стало проще простого. У вас на экзамене будет так же наглядно!
Ответ: 7.
Задание 4: обязательно делать
Задание проверяет навык работы с формулами. Алгоритм решения напоминает решение задачек на уроке по физике:
- Выписываем формулу из условия.
- Определяем, что нужно найти: единственную букву, значение которой не дано.
- Выражаем искомую величину.
- Подставляем значения из условия в формулу.
- Ищем неизвестное.
Самое трудное тут — правильно выразить искомую величину. Для этого повторяем порядок выполнения арифметических операций, свойства умножения, тренируемся перекидывать через равно множители и слагаемые.
И да, в базе эта задача проста настолько, что даже перекидывать ничего не придется. Нужная величина уже будет слева от равно.
Задание 5: обязательно делать
Простая задача на определение вероятности, которая поможет вам точно сдать базовую математику.
Решаем с помощью формулы:
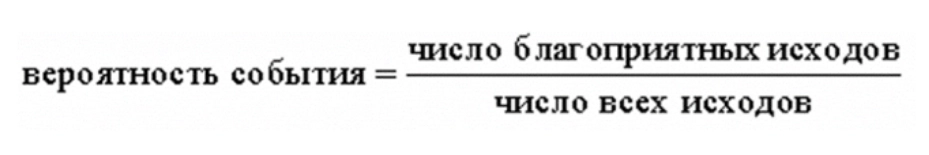

Внимательно читайте вопрос: спрашивают вероятность купить исправную лампочку. Если из ста 3 неисправны, значит, остальные в порядке и подойдет любая из оставшихся 97. Это и есть наши благоприятные исходы из формулы.
97 : 100 = 0,97.
Ответ: 0,97.
Будьте внимательны: иногда в задаче есть указание к округлению. Значит, ответ у вас выйдет некрасивый, в виде бесконечной десятичной дроби, которую вы округлите до нужного разряда.
Еще один подвох: формулировка с предлогом «на». К примеру, «На 100 лампочек 3 неисправны. Найдите вероятность купить неисправную». Подходящие исходы тут даны явно: 3 неисправные лампочки. А вот число всех исходов спрятано, и найти его будет нужно сложением исправных и неисправных лампочек: 100 + 3 = 103.
Задание 6: обязательно делать
Задание проверяет навык чтения информации из таблицы и подбора подходящего по условию варианта.
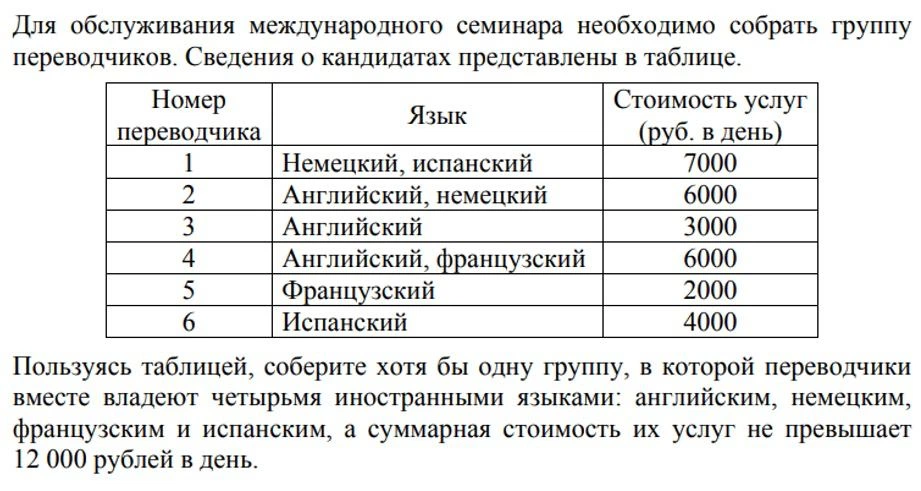
Например, вы нашли вариант позвать первого, третьего и пятого переводчиков. Получите весь набор языков как раз за 12 тысяч. Но обратите внимание, что это решение далеко не единственное.
Ответ: 135.
Задание 7
Мы не выделяем это задание в обязательные, так как для его выполнения понадобится навык анализа поведения функции по графику. Но, как его решать, сейчас коротко расскажем.
Запомним: точка максимума будет на «горке», точка минимума — в «ямке». Функция убывает, если идет вниз слева направо. Возрастает, если идет вверх слева направо.
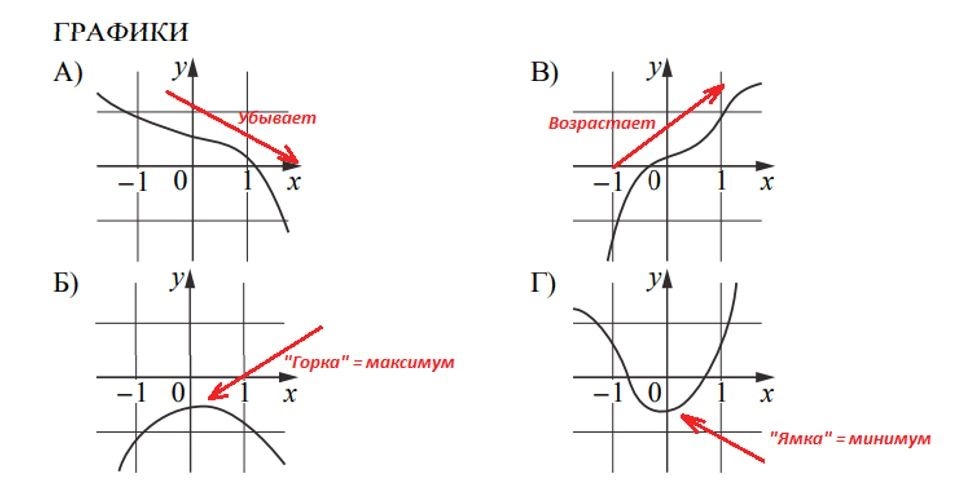
Если не повезет, то придется вспомнить азы теории по производной.
Здесь все дело в касательных. Нужно внимательно к ним присмотреться. Если касательная к графику возрастает, то значение производной будет положительное, если убывает — отрицательное. Производная будет тем больше по величине (модулю), чем быстрее возрастает или убывает касательная.
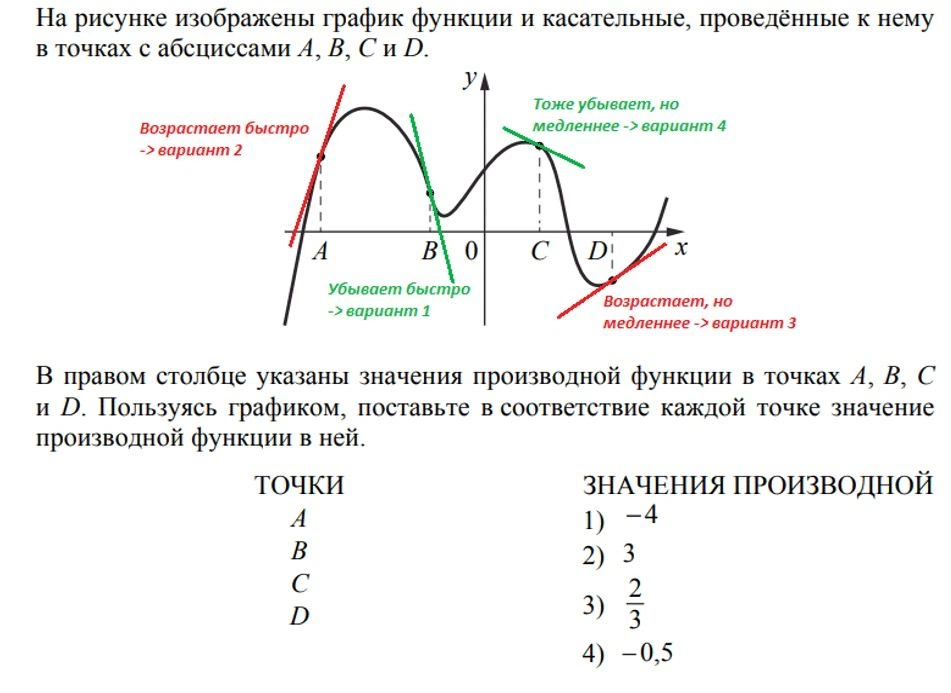
Ответ: 2143.
Задание 8: обязательно делать
Задача проверяет умение делать логичные выводы из утверждения. Иногда попадаются совсем простые задания, к таким даже дополнительно готовиться не надо.

Все, что от вас требуется, — схематично изобразить на черновике ясень, рябину и осину, указать известную разницу в высоте и внимательно сопоставить картинку с утверждениями.
Важно: не додумывайте дополнительные условия, не указанные в тексте задачи. Учитесь читать строго то, что написано.
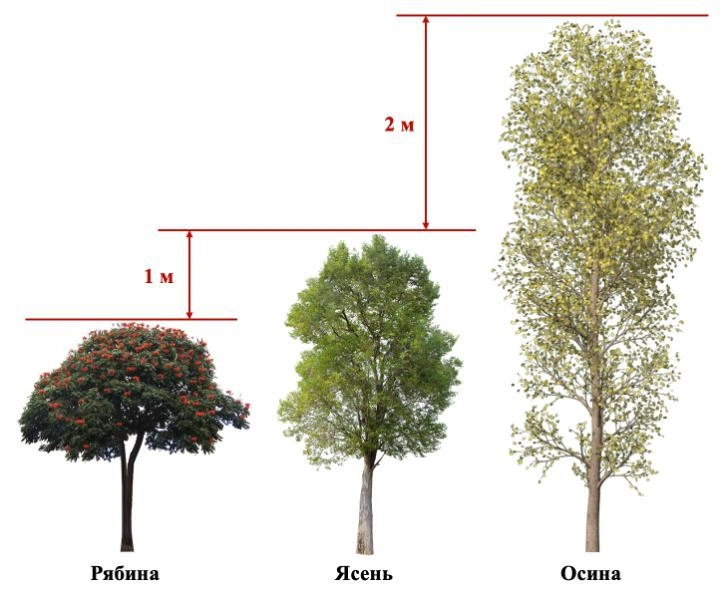
Исходя из рисунка выше получаем, что верны только утверждения 1 и 4.
Ответ: 14.
А бывают случаи, когда с визуализацией задачки придется постараться.

Тут иллюстрация не так очевидна, но нам помогут круги Эйлера. Этот инструмент позволяет наглядно изобразить множество объектов. В данном случае — школьников. Давайте прикинем, как ребята могут распределиться по кружкам.
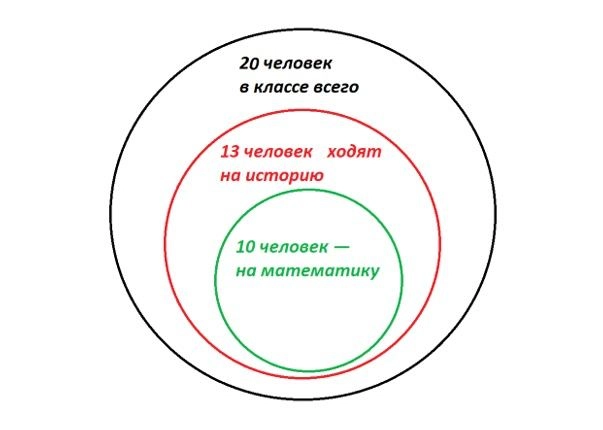
Например, так. Тут из 20 человек на кружки в итоге ходят 13. Причем 10 из них очень активны и выбрали сразу два предмета. Трое ограничились только историей.
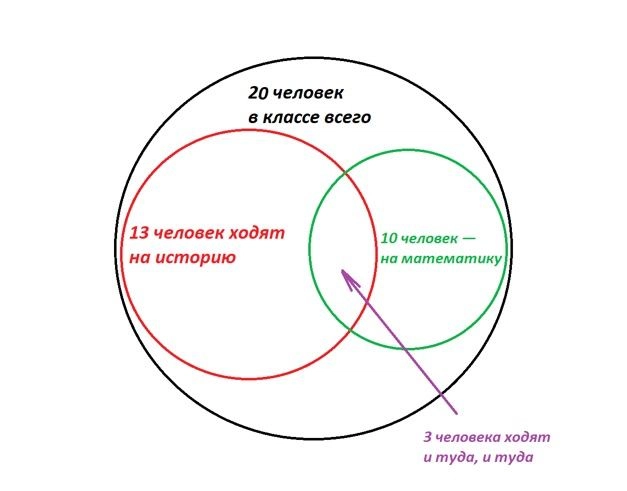
Или вот так. Если ребята задались целью по максимуму не пересекаться на дополнительных занятиях, то… У них не получится, и как минимум трое запишутся сразу на оба факультатива.
Конечно, возможны еще промежуточные варианты, но мы нарисовали два крайних. Теперь попробуем ответить на вопросы.
- Смотрим на первую картинку. Даже если все ребята будут очень стараться посетить оба кружка, они ограничены условиями задачи и максимум на оба попадут 10 человек из 20. Нет.
- Тут надо рассмотреть другую крайность, которую мы изобразили на второй картинке. Как бы ребята ни старались не встречаться на кружках, хотя бы трое попадут на оба сразу. Да.
- Уж точно неверно. На обеих наших картинках есть ребята, которые ходят на историю, но не ходят на математику. Нет.
- Смотрим на первую картинку. Оба кружка могут посещать максимум 10 человек.
Ответ: 24.
Так что для решения иногда мало логики — понадобится еще немного воображения. Потренируйтесь, и ваши шансы получить балл увеличатся.
Задание 14: обязательно делать
Задание проверяет базовые навыки счета, которым учат в 5–6-м классах. Чтобы получить балл и сдать базовую математику, надо:
- уметь выполнять арифметические действия с обыкновенными и десятичными дробями;
- правильно расставлять порядок действий;
- быть предельно внимательными.
Уделите пару вечеров отработке алгоритмов сложения, вычитания, умножения и деления обыкновенных и десятичных дробей, и это задание у вас в кармане.
Задание 15
Составители экзамена проверяют ваш навык работы с процентами и единицами отношения. Такие задачи бывают четырех типов.
Тип 1. Найти часть от числа
Часть может быть выражена в процентах или сразу в виде дроби. Например, придется искать треть от чего-то.
Рассмотрим на примере реальной задачи из экзамена:

Прочувствуйте специфику задачи: нам известно целое — вся зарплата до вычета налога. А работать мы будем с кусочком — 13 процентами. Сколько это в рублях, нам еще предстоит узнать.
Чтобы ответить на вопрос задачи, нужно сделать три шага:
1. Перевести процент в десятичную дробь.
Для этого всегда надо количество процентов поделить на 100.
13 : 100 = 0,13.
2. Найти, сколько это от зарплаты в рублях.
Запоминаем главное правило для этого типа задач: чтобы найти дробь от числа, надо число умножить на эту дробь.
12 500 ∙ 0,13 = 1 625 (руб.) — налог, который удержат с зарплаты Ивана Кузьмича.
3. Ответить на вопрос задачи.
У нас просили зарплату после вычета налога, а не сам налог.
12 500 – 1625 = 10 875 (руб.).
Ответ: 10 875.
Будьте внимательны: многие совершают ошибку именно на последнем шаге!
Тип 2. Найти число по его части

Прочувствуйте разницу с прошлой задачей: тут 124 — и есть 25%, то есть одна и та же величина выражена в процентах и в абсолютных величинах, в данном случае — в учениках. Просят узнать целое — 100%.
1. Переводим процент в десятичную дробь:
25 : 100 = 0,25.
2. Находим, сколько учеников всего.
Правило для этого типа задач: чтобы найти целое, надо часть разделить на дробь.
124 : 0,25 = 496 (уч.) — всего.
Ответ: 496.
Тип 3. Найти, сколько процентов часть составляет от целого

Особенность подобных заданий: не дано процентов, есть только абсолютные величины. В данном случае — стоимость футболки в рублях.
1. Находим, какую долю новая цена составляет от первоначальной.
Запоминаем правило: чтобы найти, какую долю часть составляет от целого, надо часть разделить на целое.
680 : 800 = 0,85.
2. Переводим долю в процент.
В прошлых задачах мы уже дважды выполнили обратное действие. В этот раз сделаем наоборот: умножим полученную дробь на 100.
0,85 ∙ 100 = 85% — столько процентов новая цена составляет от старой.
3. Отвечаем на вопрос задачи.
Нас спросили, на сколько процентов цена снизилась, что стала 85% от первоначальной. Конечно, изначально она была 100%. Итого:
100 – 85 = 15%.
Ответ: 15%.
Тип 4. Задачи на соотношение

Если перефразировать условие, то за первого кандидата проголосовали 3 части избирателей, а за второго — 2 части. Особенность этих частей в том, что они одинаковые по величине.
Если одна будет состоять из 10 человек, то за первого кандидата будет 30, а за второго — 20.
1. Считаем общее количество частей:
3 + 2 = 5.
2. Узнаем, сколько голосов составляет одна такая часть.
Тут речь о процентах проголосовавших. Сколько всего проголосовало? Конечно, 100%! Значит, каждая из пяти частей «весит»
100 : 5 = 20%.
3. Отвечаем на вопрос задачи.
За проигравшего проголосовало меньше частей избирателей. В нашем случае 2.
20 ∙ 2 = 40%.
Ответ: 40%.
Решение этих задач удобнее всего оформить табличкой:

1 часть = 100% : 5 = 20%.
Если рассчитываете решать текстовую задачу, включите здравый смысл. Ответ всегда можно проверить на адекватность благодаря обычной логике.
Задание 16: обязательно делать
Задание на решение выражения. На самом деле оно проверяет знание теории, так как в этом задании вам могут встретиться:
- выражения со степенями,
- иррациональные выражения,
- логарифмические выражения,
- тригонометрические выражения.
Ваша задача, соответственно, — знать:
- свойства степеней

- свойства корней

- свойства логарифмов
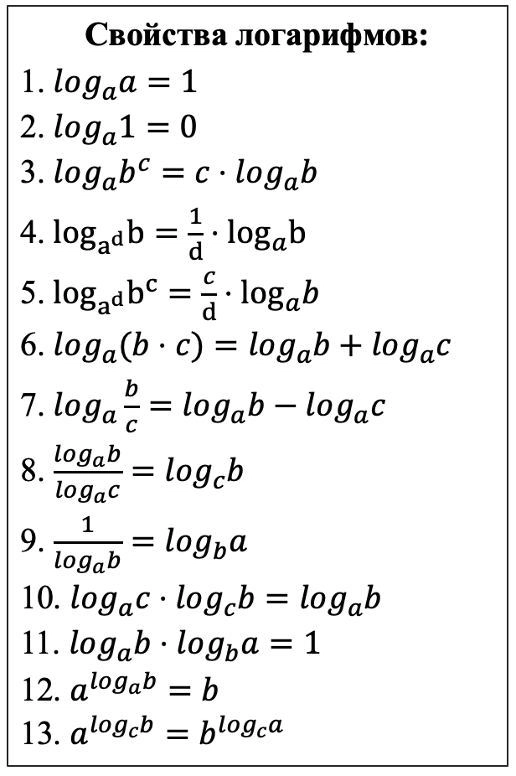
- формулы тригонометрии
Вы можете подробно ознакомиться с ними и научиться выводить в этой статье.
Обратите внимание: нужная теория будет в справочных материалах на экзамене, но это не поможет, если вы не научитесь применять ее для решения заданий. Практика обязательна!
Задание 17: обязательно делать
В номере с уравнениями вам не встретятся тригонометрические. Зато вы точно увидите там:
- линейные уравнения
Раскрываем скобки, если они есть, слагаемые с х переносим в одну сторону от равно, без х — в другую. Приводим подобные и решаем простейшее уравнение.
- квадратные уравнения
Бывают полные и неполные, всего надо повторить три алгоритма решения! А формула дискриминанта еще и в справочных материалах есть.
- иррациональные уравнения
Это те, что с корнем. Чтобы избавиться от корня, возводим обе части уравнения в квадрат и решаем получившееся уравнение. Есть нюансы с областью допустимых значений: подставьте полученные корни в исходное уравнение и проверьте, выполняется ли равенство. Если нет, то подставленное значение решением не будет.
- показательные уравнения
Ваша задача — с помощью формул свойств степеней привести уравнение к виду, когда слева и справа от равно в основании степени будет одно и то же число. После приравниваем показатели и решаем. Вот так:

Ответ: 7.
- логарифмические уравнения
С помощью формул свойств логарифмов приводим уравнение к виду, когда слева и справа от равно будет логарифм с одинаковым основанием. После приравниваем выражения под логарифмом и решаем.

Ответ: 67.
Прелесть уравнений в том, что ответ всегда можно проверить подстановкой вместо x в уравнение. Не забывайте проверять, ведь это возможность убедиться на 100%, что вы не упустите заветный балл.
Задание 19
Если хотите сдать базовую математику и решить номер 19, надо ознакомиться со свойствами целых чисел и признаками делимости. Иногда решение можно найти даже подбором! Попробуйте — времени на базовом ЕГЭ вам точно хватит.
Для начала нужно запомнить все признаки делимости.

А теперь посмотрим на типичное задание 19.

Тут помогут признаки делимости. Отдельного признака для 12 нет, потому нам надо разложить его на множители, признаки делимости для которых есть.
- На 3: сумма всех цифр делится на 3.
- На 4: число, образованное последними двумя цифрами, делится на 4.
Начнем с признака для 4. Пока что наше число заканчивается на 13 и на 4 не делится. Попробуем вычеркнуть последнюю цифру, и число будет заканчиваться на 61. Тоже не подходит. Вычеркнем еще одну: теперь на конце 76… Вот оно! От изначального числа осталось 751576, две цифры уже вычеркнули, осталось убрать одну.
Теперь проверим признак для 3: 7 + 5 + 1 + 5 + 7 + 6 = 31. Какое ближайшее число разделится на 3? Конечно, 30. Если мы вычеркнем единичку, все сойдется.
Ответ: 75576.
Другой вариант задания:

А задание такого типа можно попытаться подобрать, расположений не слишком много. Мы все же постараемся порассуждать, чтобы уменьшить количество возможных вариантов.
Чтобы число делилось на 10, оно должно заканчиваться на 0. Например, это получится, если сложить 7 + □7 + □□6. Уже немного легче. Остальное просто подберем. Под условие задачи подойдет 7 + 27 + 356 = 390.
Ответ: 390.
Какие задания мы не разобрали и почему
Теперь вы знаете, как сдать базовую математику, решив всего семь заданий. Но некоторые номера базового ЕГЭ включают слишком большое разнообразие прототипов, и методы их решения не ограничиваются парой простых алгоритмов.
Например, в эту группу относятся все задания по геометрии: с 9 по 13. Чтобы решать геометрию, мало знать основные фигуры и формулы. Необходим навык, который вырабатывается только практикой. Однако у нас есть статья про окружность — в ней вы найдете много полезной информации.
Задание 18 обычно, хотя и не всегда, содержит неравенство.

Это объемный блок теории, которую тоже необходимо подкреплять практикой. Но, может, вам повезет и попадется задачка на расположение значений на числовой прямой.

Тут достаточно примерно прикинуть значения и аккуратно внести ответы в бланк. Ясно, что 7/3 больше 2, но меньше 3. Корень из 26 равен 5 с копейками, а степень –1 из 3/5 сделает 5/3, или чуть больше 1,5. Подобные задания надо пытаться делать обязательно!
Задание 20. С этим заданием ученики знакомы еще с 9-го класса, так как оно было под номером 21 на ОГЭ. Это текстовая задача:
- на производительность,
- движение (по прямой, воде, окружности),
- сплавы и смеси,
- проценты (пиджаки, рубашки, брюки; бюджет семьи; акции, которые растут и падают),
- прогрессии.
В задании 21 на ОГЭ не было прогрессий, но они были в первой части на ОГЭ, так что ничего нового.
Задание 21. Здесь попадаются разные типы неочевидных задач на логику — чем-то они даже похожи на олимпиадные. Решение каждой нужно рассматривать отдельно и подробно. Если хотите прочитать о том, какие задачи бывают в 21-м номере, пишите в комментариях, и Maximum поделится своими методами решения!
Не знаете, какой вуз выбрать? Воспользуйтесь бесплатной консультацией в нашем центре. Что это такое? Все просто: вы расскажете о себе и о своих интересах. А специалист посоветует, на какие специальности обратить внимание, в какой вуз поступать, какие ЕГЭ сдавать. Так вы сэкономите время на подготовку и сможете выбрать образование, которое точно окажется для вас интересным и полезным!
Тогда самое время познакомиться с пятью наиболее эффективными принципами подготовки к ЕГЭ от репетитора-профессионала, основателя онлайн-школы математики «ЕГЭ. Математика. Профиль» Шеиной Ксении Игоревны.
Важность результатов ЕГЭ для современных школьников трудно переоценить. Поступление в ВУЗ, карьера, да и вся будущая жизнь ученика, так или иначе зависит от баллов, полученных на экзамене. Профильный ЕГЭ по математике — настоящий пропуск в целый мир профессий, профессий востребованных, хорошо оплачиваемых, интересных. Естественно, что выпускники и их родители ожидают от школьных уроков качественной подготовки к ЕГЭ. Но мало кто задумывается, что ЕГЭ проверяет знания за весь курс средней школы, а учитель скован рамками программы 11-го класса, в которой в лучшем случае встречается третья часть всех проверяемых ЕГЭ тем.
Сильная ограниченность во времени, слабый начальный уровень ребят и отсутствие эффективной методики подготовки — серьезные препятствия в работе школьного учителя. Поэтому многие преподаватели даже не берутся за работу над сложными заданиями.
Между тем, даже за последние два года обучения в школе можно качественно улучшить уровень учеников, если грамотно и естественно вписать процесс подготовки в обычную программу занятий. Каждому учителю под силу заложить прочный фундамент знаний, дать четкие алгоритмы работы со сложными заданиями, научить учеников искать собственные ошибки и создать условия для оттачивания навыков на практике.
Предлагаю вам 5 принципов своей работы, которые помогут научить даже самый слабый класс решению сложных задач.
Принцип 1. «Заложите крепкий фундамент»
Бесконечно жаль тратить время и так очень коротких занятий на отработку простейших, элементарных навыков, но именно они — залог будущего успеха ваших учеников! Парадокс состоит в том, что чем больше времени мы потратим на освоение базового набора знаний, тем больше мы его впоследствии сэкономим при решении более сложных заданий. Например, я всегда очень долго и кропотливо учу ребят решать элементарные тригонометрические уравнения, доводя их навыки до автоматизма. Но как только этот с материал станет понятнее, чем дважды два, мы с фантастической скоростью разбираем методы решения более сложных задач. И здесь открывается настоящий простор для экономии времени, как за счет скорости работы с простейшими заданиями, которые всегда встречаются «внутри» сложных, так и за счет возможности разбирать исключительно методы, оставляя их техническую реализацию на дом.
У данного принципа есть и еще одна положительная черта: ребята не только набивают руку, но и приобретают уверенность в себе, своих знаниях и силах, перестают считать себя гуманитариями и начинают действительно понимать предмет.
Принцип 2. «Создайте четкий алгоритм»
Я не раз готовила к ЕГЭ выпускников, не знающих таблицу умножения, не умеющих складывать дроби и не знающих ничего толкового о действиях с отрицательными числами, но ни разу в жизни мне не попадались дети, не умеющие решать квадратные уравнения. И дело тут не в том, что это самый простой раздел математики, а в четкой последовательности действий и большом количестве практики. Когда у ученика есть инструкция по работе с тем или иным заданием, шаги которой он понимает, то успех неизбежен!
Для ребят с техническим складом ума соблюдение определенного алгоритма столь же естественно как дыхание. А более творческим натурам они помогут собраться с мыслями, не потерять нить решения и контролировать свои действия на каждом шаге.
Чем ниже уровень ваших учеников, тем проще и конкретнее должна быть описана последовательность действий. Например, один и тот же алгоритм нахождения наибольшего значения функции для учащихся с разным уровнем подготовки можно записать как в две строчки, так и на страницу текста. И в обоих случаях это будет оправдано, ведь первым не нужны излишние подробности, они и та хорошо ориентируются в вопросе, а вторым, наоборот, без пояснений и «разжёвывания» не обойтись.
Принцип 3 «Много практики»
Вопрос с закреплением новых знаний на практике стоит в школе очень остро. Сложные задачи с развернутыми решением, как правило, требуют много времени. Если класс не профильный, то качественно проработать большой объем материала «от и до» за занятие практически нереально. На мой взгляд, неплохой выход из этой ситуации состоит в том, что мы математически грамотно и аккуратно расписываем образец выполнения одного прототипа задания, а затем, уже более бегло, прогоняем метод на 5-10 аналогичных примерах.
Такой подход, кроме экономии времени, позволяет ученикам сконцентрировать все внимание на методе решения и особенностях данного задания, не отвлекаясь на уже знакомые и отработанные действия. Количество заданий, прорешенных за урок, существенно увеличивается. После такой интенсивной работы ученики «привыкают» к данному типу задач, страх перед ними, как перед чем-то новым и неизвестным пропадает.
Принцип 4 «Эффективные методы»
Качество подготовки к экзаменам во многом зависит от методики преподавателя. Я всегда руководствуясь принципом Парето о том, всего 20% знаний дают 80% результата. Поэтому первостепенной задачей является классификация заданий, выбор наиболее распространенных типов и отбор наиболее эффективных методов их решений.
К сожалению, многие полезные приемы, существенно облегчающие процесс решения и экономящие уйму времени, не входят в школьную программу. Например, метод рационализации, который серьезно упрощает работу со сложными логарифмическими, показательным и другими типами неравенств, изучается только в сильных физмат школах. А между тем он намного легче и проще стандартных преобразований. Его применение не только экономит время, но и сокращает количество случайных ошибок по невнимательности. При этом научиться применять его под силу «троечнику» всего за 1-2 урока. А значит вероятность справиться со сложными задачами профиля у ваших учеников увеличивается в разы.
Принцип 5 «Работа над ошибками»
Чтобы качественно подготовиться к ЕГЭ, да и просто освоить математику, нужно научить ребят искать собственные ошибки. Как правило, ученики страдают от невнимательности, часто ошибаются в одних и тех же трудных местах, например, отбрасывая логарифмы с основаниями меньшими единицы забывают поменять знак неравенства или, извлекая корень из числа в квадрате, теряют модуль.
В наших силах «подстелить соломку». Акцентируя внимание ребят на потенциально проблемном месте в ходе решения, раз за разом напоминая, что именно «здесь» стоит быть предельно аккуратным, мы способны существенно снизить частоту таких досадных ошибок. Более того, получая «подозрительные» ответы, знающие свои «слабые» места ученики намного чаще находят ошибки в решении.
Внимание! Мы расскажем о методе рационализации на бесплатном вебинаре «Применение метода рационализации при решении сложных задач ЕГЭ» — регистрируйтесь по ссылке:
ЗАРЕГИСТРИРОВАТЬСЯ НА ВЕБИНАР
Об авторе: Шеина Ксения Игоревна, преподаватель кафедры фундаментальной математики НИУ ВШЭ Нижний Новгород, научный сотрудник лаборатории Топологических методов в динамике. Контакты: группа Онлайн-школы, персональная страница К. Шеиной.
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.