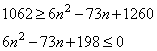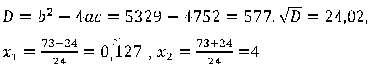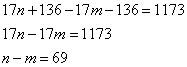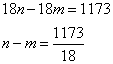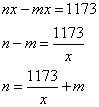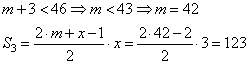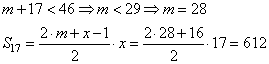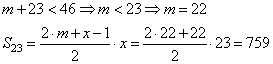Как подготовиться к 19 заданию егэ математика профиль

ЕГЭ по математике — профильный уровень, задача №18

Анна Малкова

Задача 18 на профильном ЕГЭ по математике. Когда-то ее называли С6, позже она была в вариантах под номером 19. Самая страшная и загадочная. Самая нестандартная. Ни на что не похожая.

Конечно, не совсем… Она похожа на задачи олимпиад по математике. Но в школьных учебниках нет даже намека на эту задачу!

Уравнения в целых числах с несколькими неизвестными. Действия в неопределенной ситуации. Метод «Оценка плюс пример» (а многие о нем даже не слышали). И конечно, культура математических рассуждений. В школе такому не учат! И немногие репетиторы умеют решать задачу 18 профильного ЕГЭ по математике.

Зато она оценивается в целых 4 первичных балла, которые пересчитываются в 9-10 тестовых!

Есть хорошая новость. Можно научиться решать эту загадочную задачу! Более того – это нужно сделать, если вы хотите сдать ЕГЭ по математике на достойные баллы. Или если вы участвуете в олимпиадах по математике.

Многим выпускникам ЕГЭ-Студии эта задача дала необходимые для поступления баллы.

Откроем секрет. Оказывается, что один-два из четырех баллов за задачу 18 профильного ЕГЭ по математике буквально лежат у вас под ногами, и вам надо только нагнуться, чтобы взять их! Как это может быть? Смотрите видео! Учитесь строить оценки и находить нужные примеры. Без этого решить эту странную задачу невозможно. Вы узнаете также, как правильно оформлять решение задачи 18 на профильном ЕГЭ по математике.

Вот задача 18 из варианта ЕГЭ по математике. Рассказывает Анна Малкова:

На доске написано 30 различных натуральных чисел, десятичная запись каждого из которых оканчивается или на цифру 2, или на цифру 6. Сумма написанных чисел равна 2454.

а) Может ли на доске быть поровну чисел, оканчивающихся на 2 и на 6.
б) Может ли ровно одно число на доске оканчивается на 6?
в) Какое наименьшее количество чисел, оканчивающихся на 6, может быть записано на доске?

Ну как, сможете решить хотя бы первый пункт задачи 18 на профильном ЕГЭ по математике? Стоит попробовать!

Чтобы научиться решать задачу 18 профильного ЕГЭ по математике, читайте книгу Анны Малковой «Математика. Авторский курс подготовки к ЕГЭ» и смотрите видеокурс Анны Малковой по задачам на числа и их свойства (№18 ЕГЭ).

Удачи на ЕГЭ по математике!

Решение 18 задания ЕГЭ по математике (профиль)

Разбор задания 18 ЕГЭ по математике

Задача 18 считается одной из самых сложных в профильном ЕГЭ 2023 г. по математике, однако набрать 1–2 первичных балла в ней вовсе не так уж сложно.

Согласно спецификации задание 18 имеет дело с построением математических моделей. 

Традиционно задача 18 содержит в себе три подзадачи — пункты а), б) и в).

В пункте а) обычно предлагается решить несложную задачу на построение примера. За какой-либо правильный пример (а их может быть и несколько!) эксперт поставит 1 первичный балл. Особых обоснований в этом пункте не требуется, нужно лишь показать, что приведённый пример действительно удовлетворяет условию задачи.

Пункт б) существенно отличается от пункта а). В нём, как правило, требуется строго доказать, что требуемый пример построить нельзя. Стоит этот пункт тоже 1 балл.

Пункт в), оцениваемый в 2 первичных балла, уже немного сложнее. В нём требуется построение примера, обладающего в некотором смысле «экстремальными» характеристиками (например, задача на максимум или минимум выражения, принимающего дискретные значения), а также доказательство того, что именно этот пример, а не какой-то другой обладает данными характеристиками.

Рассмотрим методы решения 18 задачи:

На доске написано несколько различных натуральных чисел, каждое из которых делится на 3 и оканчивается на 7.

а) Может ли сумма этих чисел быть равна 231?

б) Может ли сумма этих чисел быть равна 1590?

в) Какое наибольшее количество чисел может быть на доске, если их сумма равна 1056?

Решение.

а) Да, может. Числа 27, 57 и 147 дают в сумме 231.

б) Предположим, что это возможно. Каждое число оканчивается на 7, а их сумма на 0. Такое возможно, если количество чисел кратно 10. Значит, таких чисел в любом случае не меньше 10.

Число, делящееся на 3, оканчивается на 7 только, если оно имеет вид 3n, где n – натуральное число, оканчивающееся на 9. Найдём сумму 10 наименьших чисел, оканчивающихся на 7:

27 + 57 + 87 + … = 3·(9 + 19 + … + 99) = 3·540 = 1620 > 1590.

Противоречие. Следовательно, требуемое невозможно.

в) Чтобы узнать последнюю цифру в сумме из n чисел, оканчивающихся на 7, нужно определить последнюю цифру в числе 7n. Последняя цифра равна 6, если n = 8, 18, … и т.д.

Найдём сумму 8 наименьших чисел, оканчивающихся на 7:

27 + 57 + 87 + …+ 237 = 3·(9 + 19 + … + 79) = 3·88·4 = 1056.

Это и будет примером в данной задаче.

Таким образом, наибольшее количество чисел на доске равно 8.

Ответ
: а) да; б) нет; в) 8.

Нетрудно убедиться в том, что в пункте а) здесь возможны и другие примеры. Так, числа

27, 87 и 117 тоже делятся на 3 и дают в сумме 231.

В пункте в) рассуждения, приводящие к тому, что количество чисел обязано оканчиваться на 8, т.е. n = 8, 18, … и т.д., называются оценкой. Однако одной лишь оценки достаточно только для получения 1 балла, ведь в реальности пример, реализующий эту оценку, может и не существовать. В данной задаче построение (единственного!) примера, реализующего эту оценку, т.е. 27, 57, …, 237, даёт ещё 1 балл в пункте в).

Если же в пункте в), подобно пункту а), ограничиться только построением примера, пусть и правильного, то без оценки это, скорее всего, приведёт к выставлению 0 баллов за пункт в).

Таким образом, типичные критерии по проверке задания 18 выглядят так:

Содержание критерия	Баллы
Верно получены все перечисленные (см. критерий на 1 балл) результаты	4
Верно получены три из перечисленных (см. критерий на 1 балл) результатов	3
Верно получены два из перечисленных (см. критерий на 1 балл) результатов	2
Верно получен один из следующих результатов: – обоснованное решение пункта а; – обоснованное решение пункта б; – искомая оценка в пункте в; – пример в пункте в, обеспечивающий точность предыдущей оценки	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	4

Итак, в большинстве случаев для решения задания 19 нужно запомнить следующую структуру этой задачи:

— а) Да + пример;

— б) Нет + доказательство;

— в) Оценка + пример.

Отметим, что наиболее типичной ошибкой в этом задании является приведение только ответов, как в случае заданий с кратким ответом, не подкреплённых никакими рассуждениями. Т.е. просто за ответы а) да; б) нет; в) 8 в рассмотренной задаче никаких баллов Вы не получите.

Что требуется для успешного решения задания 18 ЕГЭ?

Если времени до ЕГЭ достаточно, то рекомендуется изучить внимательно темы, представленные в части 5 книги «Математика. ЕГЭ. Алгебра: задания с развёрнутым ответом». Издательство «Легион».

Если времени мало, то рекомендуем

• 
  Повторить основные признаки делимости (на 2, 3, 4, 5, 9, 10, 11);
• 
  Изучить некоторые приёмы доказательств невозможности (от противного, принцип Дирихле, чётность–нечётность);
• 
  Повторить основные формулы, связанные с арифметической прогрессией и средним арифметическим.

Разберём пример:

9 марта 2018

В закладки

Обсудить

Жалоба

Теория чисел

Задача 19 профильного ЕГЭ.

В данном материале приведено подробное описание тем, которые используются при решении задачи 19 ЕГЭ. Сюда входят и теория чисел, и прогрессии (арифметическая и геометрическая), и деление с остатков, и признаки делимости чисел. По каждой из этих тем приведены методы решения и разбор примеров.

Автор: Колесник Марина Анатольевна.

19pro.docx

---

Элементы теории чисел

---

19 задание в профильном уровне ЕГЭ по математике направлено на выявление у учеников способности оперировать числами, а именно их свойствами. Это задание наиболее сложное и требует нестандартного подхода и хорошего знания свойств чисел. Перейдем к рассмотрению типового задания.

---

Разбор типовых вариантов заданий №19 ЕГЭ по математике профильного уровня

---

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно –3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно –8.

а) Сколько чисел написано на доске?

б) Каких чисел написано больше: положительных или отрицательных?

в) Какое наибольшее количество положительных чисел может быть среди них?

[/su_note]

Алгоритм решения:

1. Вводим переменные k, l, m.
2. Находим сумму набора чисел.
3. Отвечаем на пункт а).
4. Определяем, каких чисел больше (пункт б)).
5. Определяем, сколько положительных чисел.

Решение:

1. Пусть среди записанных на доске чисел положительных k. Отрицательных чисел l и нулевых m.

2. Сумма выписанных чисел равна их количеству в данной записи на доске, умноженному на среднее арифметическое. Определяем сумму:

4k −8l + 0⋅m = − 3(k + l +m)

3. Заметим, что слева в приведенном только что равенстве каждое из слагаемых делится на 4, потому сумма количества каждого типа чисел k + l + m тоже делится на 4. По условию общее число записанных чисел удовлетворяет неравенству:

40 < k + l + m < 48

Тогда k + l + m = 44, потому что 44 единственное между 40 и 48 натуральное число, которое делится на 4.

Значит, написано на доске всего 44 числа.

4. Определяем, чисел какого вида больше: положительных или отрицательных. Для этого приведем равенство 4k −8l = − 3(k + l +m) к более упрощенному виду: 5l = 7k + 3m.

5. m≥ 0. Отсюда вытекает: 5l ≥ 7k, l > k. Получается, что отрицательных чисел записано больше положительных. Подставляем вместо k + l + m число 44 в равенство

4k −8l = − 3(k + l + m).

Имеем

4k − 8l = −132, k = 2l − 33 

k + l ≤ 44, тогда получается: 3l − 33 ≤ 44; 3l ≤ 77; l ≤ 25; k = 2l − 33 ≤17. Отсюда приходим к выводу, что положительных чисел не более 17.

Если же положительных чисел всего 17, то на доске 17 раз записано число 4, 25 раз – число −8 и 2 раза записано число 0. Такой набор отвечает всем требованиям задачи.

Ответ: а) 44; б) отрицательных; в) 17.

---

Второй вариант 1 (из Ященко, №1)

[su_note note_color=”#defae6″]

На доске написано 35 различных натуральных чисел, каждое из которых либо чётное, либо его десятичная запись оканчивается на цифру 3. Сумма написанных чисел равна 1062.

а) Может ли на доске быть ровно 27 чётных чисел?

б) Могут ли ровно два числа на доске оканчиваться на 3?

в) Какое наименьшее количество чисел, оканчивающихся на 3, может быть на доске?

[/su_note]

Алгоритм решения:

1. Приведем пример набора чисел, который удовлетворяет условию (Это подтверждает возможность набора чисел).
2. Проверяем вероятность второго условия.
3. Ищем ответ на третий вопрос, введя переменную n.
4. Записываем ответы.

Решение:

1. Такой примерный перечень чисел на доске соответствует заданным условиям:

3,13,23,33,43,53,63,73,2,4,6,…,50,52,56

Это дает положительный ответ на вопрос а.

2. Пусть на доске написано ровно два числа, у которых последняя цифра 3. Тогда там записано 33 чётных числа. Их сумма:

Это противоречит тому, что сумма написанных чисел равна 1062, то есть, утвердительного ответа на вопрос б нет.

3. Полагаем, что на доске записано n чисел, которые оканчиваются на 3, и (35 – n)из выписанных чётные. Тогда сумма чисел, которые оканчиваются на 3, равна

а сумма чётных:

2+4+…+2(35 – n)=(35 – n)(36 – n)= n²-71 n+1260.

Тогда из условия:

Решаем получившееся неравенство:

Получается, что . Отсюда, зная, что n — натуральное, получаем .

3. Наименьшее число чисел, оканчивающихся на 3, может быть только 5. И добавлено 30 чётных чисел, тогда сумма всех чисел нечётна. Значит, чисел, которые оканчиваются на 3, больше. чем пять, поскольку сумма по условию равна четному числу. Попробуем взять 6 чисел, с последней цифрой 3.

Приведём пример, когда 6 чисел, оканчиваются на три, и 29 чётных чисел. Сумма их равна 1062. Получается такой список:

3, 13, 23, 33, 43, 53, 2, 4, …, 54, 56, 82.

Ответ: а) да; б) нет; в) 6.

---

Третий вариант (из Ященко, №4)

[su_note note_color=”#defae6″]

Маша и Наташа делали фотографии несколько дней подряд. В первый день Маша сделала m фотографий, а Наташа — n фотографий. В каждый следующий день каждая из девочек делала на одну фотографию больше, чем в предыдущий день. Известно, что Наташа за всё время сделала суммарно на 1173 фотографии больше, чем Маша, и что фотографировали они больше одного дня.

а) Могли ли они фотографировать в течение 17 дней?

б) Могли ли они фотографировать в течение 18 дней?

в)  Какое наибольшее суммарное число фотографий могла сделать Наташа за все дни фотографирования, если известно, что в последний день Маша сделала меньше 45 фотографий?

[/su_note]

Алгоритм решения:

1. Ответим на вопрос а).
2. Найдем ответ на вопрос б).
3. Найдем суммарное количество фотографий, сделанных Наташей.
4. Запишем ответ.

Решение:

1. Если Маша сделала m фотографий в 1-й день, то за 17 дней она сфотографировала снимков.

Наташа, за 1-й день сделала n фотографий, тогда за оставшиеся 17 дней она сделала

 кадров.

Найдем такие m и n, чтобы выполнялось равенство:

Возьмем, к примеру, n=70 и m=1. Это ответ на вопрос а).

2. Если фотографировали девочки всего 18 дней, получается:

1173 на 18 не разделится, следовательно, выбрать такие n и m нельзя. Это ответ на вопрос б.

3. Поищем ответ на последний вопрос. Допускаем, что девочки делали фотографии x дней. Тогда Маша сделала бы в последний день снимков

То есть . А согласно условию

число x является делителем 1173. Тогда возможны только варианты: x = 23, 17 или 3.

Вычисляем наибольшее число фотографий, которые могла сделать Маша. Получаем:

Для числа x=3:

При x=17:

А при x=23:

Самое большое количество снимков, которые сделала Наташа:

759+1173=1932.

Ответ: а) да; б) нет; в) 1932.

Даниил Романович | Просмотров: 10.6k

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ПО
ТЕОРИИ ЧИСЕЛ

(ЗАДАНИЕ 19 ИЗ ЕГЭ ПО МАТЕМАТИКЕ, ПРОФИЛЬНЫЙ
УРОВЕНЬ)

Аннотация

Статья посвящена проблеме подготовки учащихся к решению задач по теории
чисел, которые входят в комплект заданий профильного уровня ЕГЭ по математике в
качестве задания под номером 19. Указанные задачи вызывают затруднение даже у
хорошо подготовленных участников, некоторые школьники даже не предпринимают
попыток решения этого задания. В статье перечислены необходимые методы и приемы
решения, а также даны рекомендации по подготовке учащихся к решению задания 19
ЕГЭ.

Ключевые
слова: математика, ЕГЭ, теория чисел.

Важной частью обучения математике сегодня является подготовка к Единому
государственному экзамену (ЕГЭ), особенно в старших классах. Желающие
продолжить обучение по техническим или математическим специальностям выбирают
профильный уровень ЕГЭ по математике, который отличается от базового более
высокой сложностью и разнообразием заданием.

Проведенный анализ результатов ЕГЭ по математике показывает, что у
обучающихся среди заданий по алгебре наибольшую сложность вызывают задачи 18 и
19, требующие развернутого ответа, т.е. уравнения и неравенства с параметром и
задача на исследование простейших математических моделей.

Мы считаем, что эти задачи необходимо рассматривать дополнительно,
обращая внимания на особенности решения. В частности, на некоторых сайтах
указывают, что задача 19 является олимпиадной [10; 11], а иногда даются
рекомендации не тратить время на ее решение [4]. Однако это задание включает в
себя элементы теории чисел и не выходит за пределы школьной программы [8, с.
161]. Как нам кажется, при определенных условиях можно повысить эффективность
подготовки учащихся с целью успешного решения последней задачи профильного
уровня ЕГЭ.

Элементы теории чисел представляют значимость именно для
математического образования, так как позволяют сформировать понятие числа как
основы числовых систем. Кроме того, изучение теории чисел положительно
воздействует на развитие логического мышления, формируют математическую
культуру учащихся, учит их работать с абстрактными понятиями [1, с. 99].

По мнению, И.Л. Мирошниченко и Е.Н. Селезневой необходимо регулярно
разбирать с учащимися задачи на теорию чисел, начиная с 5-6 класса. При этом
содержание задач должно соответствовать изучаемым темам. Например, авторы
приводят примеры задач, которые можно использовать в процессе изучения таких
тем, как «Признаки делимости», «Среднее арифметическое», «Арифметический
квадратный корень», «Квадратный трехчлен» и т.д. [3, с. 55].

Но не всегда один учитель ведет весь курс математики у одного класса,
часто происходят замены учителя, либо школьник меняет образовательное
учреждение. К тому же такой подход требует от учителя серьезных затрат времени
на поиск или составление задачи, подходящей по своему содержанию. Также не
следует исключать вероятности изменения структуры ЕГЭ, в результате чего задача
на теорию чисел будет исключена из комплекта заданий. Поэтому целенаправленную
подготовку учащихся начинают ближе к экзамену, обычно в старших классах.

В своей статье А.Е. Семенова указывает, что для решения задачи 19 ЕГЭ участники
экзамена должны знать признаки делимости, понятие наименьшего общего кратного,
а также свойства чисел [6, с. 994].

На наш взгляд, помимо указанных понятий, следует повторить и закрепить
с учащимися алгоритм нахождения наименьшего общего кратного и наибольшего
общего делителя, порядок вычисления арифметической и геометрической прогрессии.
При повторении следует основной упор сделать на решение задач, как заданных
явно («Последовательность n натуральных чисел представляет собой
арифметическую прогрессию. Может ли их сумма быть равна 10?»), так и в виде
сюжетной задаче: («12 одинаковых монет нужно разместить вдоль стенок квадратной
коробки так, чтобы возле каждой стенки находилось равное количество монет. Каким
образом можно выполнить?»).

В пособии А.Э. Сергеева и И.В. Соколовой выделены следующие группы
типовых задач, составленных по мотивам задания 19: прогрессии, уравнения в
целых числах, обыкновенные дроби, простые числа и свойства делителей [7].

Рассмотрим, какие знания, методы и приемы будут полезны при решении
задания 19 ЕГЭ:

– алгоритм Евклида для нахождения НОД;

– свойство делимости чисел: произведение чисел делится на простое
число, если один из множителей делится на это число;

– свойство делимости чисел: если число а не делится ни на одно простое
число меньше , то оно простое;

– метод математической индукции;

– методы решения линейного диофантова уравнения: поиск частного решения
и переход к общему; выразить одно неизвестное через другое; геометрический;

– перебор вариантов,

– метод
разложения числа на множители,

– метод остатков. [2; 5; 7].

Учитывая, что задание 19 можно отнести к нестандартным задачам, т.е. не
имеющим единого алгоритма решения, то мы считаем необходимым придерживаться
принципов регулярности, систематичности и последовательности при подготовке к
ее решению. Учащиеся должны хорошо ориентироваться в методах решения, знать
основные приемы, упрощающие решение, быть знакомы с типовыми задачами. Поэтому сначала
необходимо рассмотреть простые примеры, позволяющие отработать практическое
применение названых методов и приемов.

Например, изучение метода нахождения НОД с помощью алгоритма Евклида,
может включать в себя задачи различных уровней сложности:

1. Использование алгоритма на конкретном примере, т.е. нахождение НОД
любых двух натуральных чисел (числа могут называть сами учащиеся, либо учитель
выбирает трехзначные и четырехзначные числа).

2. Использование алгоритма для буквенных (нахождение НОД 2n+17 и n+7) или
числовых выражений (нахождение НОД 2¹⁰⁰-1 и 2¹²⁰-1).

3. Решение задач из сборника по подготовке к ЕГЭ (На какое число и при
каких натуральных значениях n сократима дробь  ?).

Наиболее оптимальным вариантом подготовки учащихся, на наш взгляд,
является разработка элективного курса, направленного на знакомство учащихся с
теорией чисел. Курс может быть представлен также и в дистанционном формате,
например, на основе системы MOODLE, возможности использования которой в
обучении школьников математике описывается в работе одного из авторов данной статьи
[9]. Преимущество решения задач по теории чисел во внеурочной деятельности
состоит в том, чтобы научить решать тех школьников, которые стремятся получить
максимальный балл профильного уровня ЕГЭ.

Подводя итоги, можно сделать вывод, что сложность задания 19
профильного уровня ЕГЭ по математике вполне преодолима, если участник будет
заниматься дополнительной подготовкой, изучая элементы теории чисел.

Литература

1. Гапонова Ю.С. Роль и место элементарной теории чисел в математическом
образовании школьников // Концепция «общества знаний» в современной науке: сб.
ст. Межд. науч.-практ. конф. – Уфа: Аэтерна, 2018. – С. 98-103.

2. Иванова В.И. Линейное диофантово уравнение и 4 способы его решения
// Первое сентября. Открытый урок [Электронный ресурсы]. – Режим доступа: https://urok.1sept.ru/articles/501260.

3. Мирошниченко И.Л., Селезнева Е.Н. Элементы теории чисел в школьном
курсе математики // Вестник педагогического опыта. – 2019. – №44. – С. 51-55.

4. Ненко И. Как подготовиться к ЕГЭ по математике //
Нижний Новгород онлайн [Электронный
ресурсы]. – Режим доступа: https://www.nn.ru/news/articles/uchitelya_rasskazali_na_chem_v_ege_po_matematike_zavalivaetsya_kazhdyy_vtoroy/69093625/.

5. Свиридова А.В. Способы решений уравнений в целых числах
// Старт в науке [Электронный
ресурсы]. – Режим доступа: https://school-science.ru/4/7/828

6. Семенова А.Е.  Элементы теории чисел в школьном курсе математики //
Аллея науки. – 2019. – Т. 3. – №5. – С. 993-995.

7. Сергеев А. Э., Соколова И. В. Теория чисел в задаче №19
профильного ЕГЭ по математике: учеб. пособие. – Краснодар : КубГАУ, 2019. – 108
с.

8. Соколова И.В., Сергеев А.Э. Методические рекомендации к
решению задачи № 19 профильного
ЕГЭ по математике // Современные проблемы науки и образования. – 2018. – № 6. –
С. 161.

9. Солощенко М.Ю., Петров И.Л. Использование системы MOODLE в
обучении школьников математике // Проектирование и реализация математического образования в школе и
вузе. Сборник научных трудов. – Стерлитамак, 2015. С. 63-66.

10. Структура ЕГЭ по математике 2019-2020 // Geniusmath [Электронный ресурсы]. – Режим доступа: http://courses.geniusmath.ru/blogs/read/struktura-iege-po-matiematikie-2019-2020/.

11. Шутова О. Профильный ЕГЭ по математике: что нужно
знать к 2021 году? // MaximumBlog [Электронный ресурсы]. – Режим доступа: https://blog.maximumtest.ru/post/profilnyj-ege-po-matematike-chto-nuzhno-znat.html.

Рекомендации по подготовке к выполнению задания №19 ЕГЭ профильного уровня

Что можно ожидать в качестве задания 19 на экзамене?

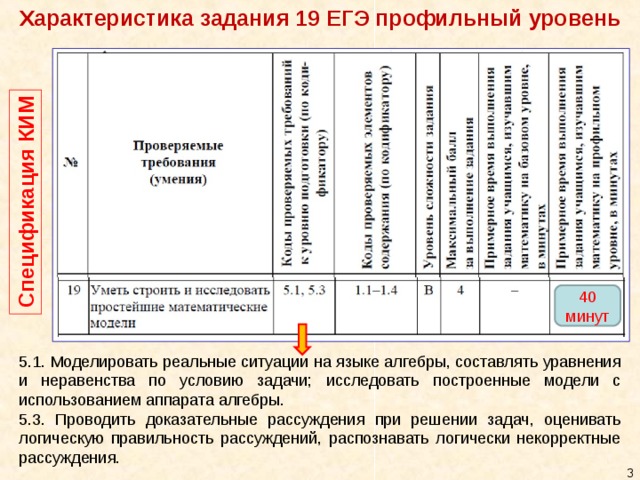
Характеристика задания 19 ЕГЭ профильный уровень

Спецификация КИМ

40

минут

5.1. Моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры.

5.3. Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать логически некорректные рассуждения.

Общность всех формулировок заданий №19

С 2010 года вариант ЕГЭ по математике содержит четырехбалльное задание С6 (сейчас №19) олимпиадного характера. Большую долю среди задач, уже использованных в вариантах экзамена, составляют задачи на последовательности (чисел, ходов, наборов чисел и т.д.)

Характерной особенностью подобных задач является исследование элементов заданной последовательности следующего вида:

а) на наличие элемента, обладающего заданным свойством;

б) подсчет количества элементов, обладающих заданным свойством;

в) оценка (наибольшего или наименьшего значения) либо количества элементов, обладающих заданным свойством, либо некоторой числовой характеристики заданных элементов;

г) приведение примера, подтверждающего полученную оценку ( подразумевается, но в условии не формулируется! ).

Критерии проверки задания №19

Содержание критерия

Баллы

Верно получены все перечисленные (см. критерий на 1 балл) результаты

Верно получены три из перечисленных (см. критерий на 1 балл) результатов

4

3

Верно получены два из перечисленных (см. критерий на 1 балл) результатов

2

Верно получен один из следующих результатов:

– пример в п. а ;

– обоснованное решение п. б ;

– искомая оценка в п. в ;

– пример в п. в , обеспечивающий точность предыдущей оценки

1

Решение не соответствует ни одному из критериев, перечисленных выше

0

Основные олимпиадные идеи, используемые при решении подобных задач

• Идея «чет-нечет» . Используется, когда рассматриваемая величина (например, сумма или произведение) имеет определённую чётность, что позволяет доказать невозможность ситуации, в которых она имеет другую чётность.
• Уравнения в целых числах. Используемые в решении формулы (например, общего члена прогрессии, суммы n первых членов прогрессии, характеристическое свойство) в силу целочисленности входящих в них переменных приводят к необходимости исследования уравнения в целых числах.
• Свойства делимости целых чисел (признаки делимости, деление без остатка, деление с остатком, анализ остатков).
• Идея «усиления неравенства» , используемая при замене в неравенстве какой-нибудь переменной на ее возможное наибольшее или наименьшее значение.
• Метод «перебора» значений целочисленной переменной из ограниченного набора.

Классификация заданий 19 ЕГЭ, в которых присутствуют последовательности

1. Задачи на арифметическую прогрессию.

2. Задачи на геометрическую прогрессию.

3. Задачи на произвольные последовательности чисел, заданные формулой n — го члена или каким-либо ограничением, накладываемым на их элементы.

4. Задачи на последовательности наборов чисел.

5. Задачи на последовательности ходов.

Как правило, во всех подобных задачах оговаривается целочисленность элементов членов последовательностей, элементов в наборах чисел или элементов, получаемых на каждом шаге в последовательности ходов.

Пример из демоверсии ЕГЭ 2018 (профильный уровень)

19

Задачи на арифметическую прогрессию

Набор основных формул для арифметической прогрессии.

Задачи на арифметическую прогрессию

№ 1. ( ЕГЭ , 2013 ). Дано n различных натуральных чисел (не менее трех), составляющих арифметическую прогрессию.

а) Может ли сумма всех данных чисел быть равной 18?

б) Каково наибольшее значение n , если сумма всех данных чисел меньше 800?

в) Найдите все возможные значения n , если сумма всех данных чисел равна 111.

Задачи на арифметическую прогрессию

№ 1. ( ЕГЭ , 2013 ). Дано n различных натуральных чисел (не менее трех), составляющих арифметическую прогрессию.

а) Может ли сумма всех данных чисел быть равной 18?

б) Каково наибольшее значение n , если сумма всех данных чисел меньше 800?

в) Найдите все возможные значения n , если сумма всех данных чисел равна 111.

Ответ : а) да, например, 5, 6, 7; б) 39; в) 3; 6.

Задачи на арифметическую прогрессию

№ 2. ( МИОО , 2014 ). Несколько различных натуральных чисел, в десятичной записи которых отсутствуют цифры 1 и 9, составляют арифметическую прогрессию.

а) Может ли сумма всех членов такой прогрессии быть равной 298?

б) Может ли в прогрессии быть 35 членов?

в) Показать, что если разность этой прогрессии не меньше 4, но не больше 8, то количество членов не превосходит 18.

г) Привести пример, когда разность арифметической прогрессии не меньше 4, но не больше 8, а количество членов равно 18.

Задачи на арифметическую прогрессию

№ 2. ( МИОО , 2014 ). Несколько различных натуральных чисел, в десятичной записи которых отсутствуют цифры 1 и 9, составляют арифметическую прогрессию.

а) Может ли сумма всех членов такой прогрессии быть равной 298?

б) Может ли в прогрессии быть 35 членов?

в) Показать, что если разность этой прогрессии не меньше 4, но не больше 8, то количество членов не превосходит 18.

г) Привести пример, когда разность арифметической прогрессии не меньше 4, но не больше 8, а количество членов равно 18.

Задачи на геометрическую прогрессию

Полезные факты .

Задачи на геометрическую прогрессию

№ 3. ( МИОО, 2011 ). Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 1344 и из них образуют геометрическую прогрессию:

а) три числа;

б) четыре числа;

в) пять чисел?

Основная теорема арифметики . Для каждого натурального числа, большего единицы, существует единственное разложение на простые множители.

Каноническое разложение целого числа

где – попарно различные простые числа, а – натуральные числа.

Задачи на геометрическую прогрессию

№ 3. ( МИОО, 2011 ). Можно ли привести пример пяти различных натуральных чисел, произведение которых равно 1344 и из них образуют геометрическую прогрессию:

а) три числа; б) четыре числа; в) пять чисел?

Ответ : а) да; б) да; в) нет.

Задачи на геометрическую прогрессию

№ 4. (МИОО, 2011). Все члены геометрической прогрессии – различные натуральные числа, заключенные между числами 210 и 350.

а) Может ли такая прогрессия состоять из четырех членов?

б) Может ли такая прогрессия состоять из пяти членов?

Любой вариант ответов без обоснования:

Ответ Оценка

а) да; б) нет. 0

а) нет; б) да. 0

а) нет; б) нет. 0

а) да; б) да. 0

Задачи на геометрическую прогрессию

№ 4. (МИОО, 2011). Все члены геометрической прогрессии – различные натуральные числа, заключенные между числами 210 и 350.

а) Может ли такая прогрессия состоять из четырех членов?

б) Может ли такая прогрессия состоять из пяти членов?

Ответ : а) да; б) нет.

Задачи на последовательности

Иногда последовательность чисел задается возвратным уравнением Рассмотрим один частный случай, используемый в подобных задачах.

Задачи на последовательности

№ 5. Конечная возрастающая последовательность

состоит из различных натуральных чисел, причем при всех натуральных выполнено равенство

а) Приведите пример такой последовательности при

б) Может ли в такой последовательности при некотором

выполняться равенство

в) Какое наименьшее значение может принимать если

Задачи на последовательности

№ 5.

№ 5.

Идея «усиления неравенства»

Ответ : а) например, 1, 65, 113, 149, 176; б) нет; в) 2.

Задачи на последовательности

ЕГЭ 2016

№ 6 .

Идея «чет-нечет»

Решение . а) 1, 4, 21, –16, 41, –36, 61, –56, 81,

– 78, 103, –100, 125, –122, 147, –144, 169, –166, 191, –188, 213, –210, 235.

б) Нет. Поскольку сумма двух соседних членов есть нечетное число, они имеют

разную четность. Следовательно, все члены с нечетными индексами нечетны, а с четными четны. Поэтому 1000-й член не может равняться 235.

в) Рассмотрим три последовательных члена последовательности

Поскольку

Последовательность состоит из нечетного числа членов.

Задачи на последовательности

Значит, последовательность состоит из не менее 23 членов. Пример пункта а) удовлетворяет этой оценке.

Ответ : б) нет; в) 23.

0 баллов

Процент решаемости этого задания

Баллы

Проценты

4

3

1,65

1,03

2

2,67

1

10,53

Задачи на последовательности

ЕГЭ 2016

№ 7.

№ 7 .

Задача на последовательность ходов

ЕГЭ 2016

№ 8 .

б) После первого хода получим 3, 5 или 5, 5. После каждого следующего хода каждое число увеличивается, по крайней мере на 2. За 100 шагов меньшее из чисел будет не менее

3 + 2 · 99 = 201.

в) Первоначально разность равна 1. Далее 504 хода ее увеличиваем на 1 и 503 хода уменьшаем на 1. Получим наименьшее значение, равное 2.

Ответ :

б) нет; в) 2.

Наборы чисел

№ 9

ЕГЭ

2017

Задача на среднее арифметическое

1 9

№ 1 0

ЕГЭ

2017

Идея «усиления неравенства»

Подготовительные задания 19

Ответы к подготовительным заданиям 19

Зачетные задания 19

Зачетные задания 19

Зачетные задания 19

Зачетные задания 19

Зачетные задания 19

Зачетные задания 19

Ответы к зачетным заданиям 19

ЕГЭ по математике профиль