2023-02-01
3 587
Профильная математика на ЕГЭ для большинства школьников остается одним из самых сложных предметов. Однако в действительности всё не так страшно. Многие задания являются типовыми и, чтобы успешно их выполнить, необходимо набить руку. В статье рассказываем — как подготовиться, чтобы получить высокие баллы на экзамене.
Чем профиль отличается от базы
Экзамены отличаются по структуре и содержанию заданий. Профиль нужен для поступления в вуз — поскольку в нём есть задания более сложного уровня, чем в базе. Базовый экзамен необходим для того, чтобы получить аттестат и закончить школу.
Профильная математика на ЕГЭ разделена на две части и включает в себя следующие темы:
- алгебра;
- геометрия;
- уравнения и неравенства;
- статистика и теория вероятности;
- производные и анализ функций;
- начало мат. анализа;
- экономика.
Что важно учесть при подготовке
Основные темы выделяются в каждом экзаменационном предмете — их необходимо выучить, чтобы выполнить задания. В профильной математике нужно обязательно знать следующие темы.
Тригонометрия и формулы. Необходимо запомнить уравнения с синусами и косинусами и научиться правильно их использовать. Однако, справочные материалы на экзамене содержат некоторые из них, поэтому можете не переживать, если вдруг что-то забудете.
Квадратные уравнения. Это база средней школы, однако они могут встречаться как в отдельных заданиях, так и в составе сложных задач. Важно уметь решать их основными способами — дискриминант и теорема Виета. Последняя поможет на экзамене выполнить задание быстрее.
Уравнения могут встречаться в заданиях с математическими моделями и геометрией — 9 и 15, а также в задаче с параметром №17.
Треугольники. Это основа геометрии, но пригодится и для выполнения задач из стереометрии и планиметрии. Многие теоремы базируется на треугольниках. Выпускнику стоит опираться на прямоугольные треугольники — поскольку большинство заданий связано именно с ними.
Проценты. Многие школьники не любят эту тему, однако она необходима для успешной сдачи экзамена. Такие задачи могут попасться в номерах 9 и 15 и принести выпускнику 3 балла.
Как построен экзамен
Профиль включает в себя 18 номеров — одиннадцать с кратким вариантом ответа и семь с подробным. Длительность экзамена 3 часа 55 минут, или 235 минут. Суммарно школьник может набрать 31 первичный балл, который затем переводят в стобалльную систему.
Экзамен содержит три раздела:
- алгебра и начало анализа — 8 заданий, 13 баллов;
- геометрия — 4 задания, 8 баллов;
- реальная математика — 6 заданий, 10 баллов.
Как повысить шансы на успешную сдачу профиля
К сожалению, без усердной подготовки не получится сдать экзамен на хорошие баллы. Но это не повод расстраиваться. Мы подготовили несколько советов, которые помогут подготовиться и успешно сдать профильную математику:
- Решайте демоверсии и варианты прошлых лет — это позволит изучить содержание экзамена и примерно оценить, с чем предстоит столкнуться.
- Изучите кодификатор — это поможет разобраться в темах предмета и выявить проблемные зоны, на которые нужно обратить внимание при подготовке.
- Начните подготовку заранее — математику нужно не только заучить, но и понять, как вывести ту или иную формулу или доказать теорему. Если в знаниях большие пробелы, а для подготовки остался только год — советуем выбрать базовую математику или уделять больше времени на подготовку к профилю.
- Посмотрите, какой проходной балл на желаемую специальность был в прошлом году — это позволит примерно понять, сколько баллов необходимо набрать. Возможно, не придётся разбираться со всеми сложными заданиями и хватит того, в чём выпускник уверен.
- Важно внимательно читать задания и перепроверять ответы — спешка может привести к ошибкам. Это же касается и заполнения бланков.
- Не стоит пытаться прорешать все задания на ФИПИ — лучше сделать упор на те, которые получаются хорошо, чтобы быть уверенными в них. Советуем каждый день решать несколько простых заданий из базы и профиля — это поможет набить руку и будет своеобразной математической разминкой.
- Используйте проверенные источники для подготовки — их список можно посмотреть на сайте ФИПИ.
А лучше доверьте подготовку специалистам. Репетиторы Тетрики помогут разобраться в кодификаторе и сложных заданиях, а также подготовят индивидуальный план занятий для каждого выпускника. Запишитесь на бесплатный пробный урок.
Влюбляем в обучение на уроках в онлайн-школе Тетрика
Оставьте заявку и получите бесплатный вводный урок
Выпускники 11-го класса со способностями в области точных наук желающие связать дальнейшую профессию с математическими вычислениями или техническими специальностями, выбирают в качестве дисциплин по выбору физику, информатику или математику в профильном уровне. Задачи направлены на оценку аналитического мышления, знания терминов и формул. Каждый школьник стремится получить на экзамен максимальный балл, поэтому заранее изучает советы, как сдать ЕГЭ по профильной математике.
Из чего состоит экзамен по профильной математике
Экзаменационные задания делятся на два блока:
Тестовые вопросы с одним ответом
Правильное решение приносит по 1 первичному баллу. Темы:
- Планиметрия;
- Стереометрия;
- Теория вероятности;
- Простейшие уравнения;
- Вероятность возникновения сложных событий;
- Вычисления и преобразования;
- Производные;
- Прикладное содержание;
- Графики функций;
- Текстовые задачи;
- Значения функций.
Задания с развернутым ответом
Правильные вычисления приносят по 2 балла. Темы:
- Уравнения;
- Стереометрия;
- Неравенства;
- Планиметрия;
- Финансовая математика;
- Параметры;
- Числа и их функции.
Структура кимов меняется ежегодно. Актуальные изменения включают исключение:
- Чтения диаграмм;
- Квадратной решетки;
- Системы уравнений;
- Сложной планиметрии.
В профильный уровень включены 18 вопросов – 11 в первом блоке и 7 во втором. Общее количество начисляемых первичных баллов – 31. Перевод в 100-балльную систему осуществляется по таблице.
Экзамен проводится в специализированном пункте проведения ГИА под строгим контролем организаторов и наблюдающих. Школьники заходят в аудитории по паспортам. Каждый класс оборудован системами аудио- и видео фиксации для исключения возможных нарушений. Перед началом аттестации преподаватели проводят инструктаж по заполнению бланков. Внесение информационных данных не входит в общую длительность экзамена.
С собой ученик приносит:
- Основную и запасную ручку;
- Документ, удостоверяющий личность;
- Бутылку воды без этикетки;
- Лекарства при наличии заболевания;
- Перекус в бумажной упаковке при необходимости;
- Линейку.
Справочники и таблицы, необходимые для решения математических задач выдаются в классе и входят в единый комплект с кимами и экзаменационными бланками.
Когда и с чего начать подготовку
Школьники, отличающиеся высокой успеваемостью по алгебре и геометрии достаточно легко справляются с заданиями базового уровня. Решение профильных вопросов требует специализированной подготовки.
Начать тренировки рекомендуется за 1,5 года до экзамена. Этого времени достаточно для повторения пройденных тем и закрепления нового материала.
Ученики выбирают один из трех популярных способов подготовки:
Самостоятельно в домашних условиях
Выпускник подбирает учебный материал по информации в интернете или совету школьного учителя. Рекомендуется выбрать качественный:
- Учебник;
- Методические рекомендации;
- Решебники;
- Сборники с пробными вариантами;
- Видеолекции от профессиональных преподавателей;
- Профильные вебинары с объяснением сложных тем.
Для успешных тренировок необходимы:
- Целеустремленность;
- Высокий уровень мотивации;
- Собранность;
- Активность;
- Педантичность;
- Внимательность;
- Навык саморедактирования и самопроверки.
Для оценки эффективности занятий стоит выполнять демо-версии экзамена и отлеживать динамику повышения количества правильных ответов.
Самостоятельные занятия не лучший способ для подготовки в короткие сроки. Без контроля учителя сложно выявить пробелы в знаниях и разобраться с трудными темами.
С репетиторами
Профессиональные педагоги организуют индивидуальные занятия с учениками в офлайн или онлайн формате. Плюсы:
- Постоянный контроль;
- Участие в повышении мотивации;
- Индивидуализированный подход;
- Детальный разбор теоретического и практического материала.
Недостатки:
- Сложность подбора педагога, отличающегося высоким уровнем квалификации, нацеленностью на результат ученика и коммуникационным талантом.
Занятия с учителем один на один подходят спокойным и собранным детям, с отсутствием необходимости включения соревновательного момента в образовательный процесс.
На курсах по подготовке к ЕГЭ
Профильные занятия ведут преподаватели, знакомые со структурой экзамена и критериями оценки. Многие из них входят в число педагогических комиссий, занимающихся проверкой работ выпускников.
Курсовая подготовка организуется на базе:
- Колледжа;
- Университета;
- Центра дополнительного образования;
- Частной учебной организации.
Преимущества:
- Целенаправленное изучение теории и практики с упором на задания, входящие в кимы;
- Очный или дистанционный формат;
- Обучение в группе.
Недостатки:
- Необходимость соблюдения установленного графика.
Посещение курсов считается оптимальным способом эффективной подготовки. Учащиеся вместе с родителями могут выбрать удобный график занятий с учетом времени до даты проведения экзамена – 12 месяцев, полгода, 3 месяца или экспресс-обучение за месяц до ГИА.
В короткие сроки ученики повторяют наиболее сложный материал, разбирают структуру заданий и часто встречающиеся ошибки, отрабатывают алгоритмы решений.
Советы по подготовке к ЕГЭ по профильной математике
Повторить теорию
Перечень теоретического материала для повторения и устранения пробелов в знаниях:
- Координаты;
- Векторы;
- Математические модели;
- Уравнения;
- Неравенства;
- Функции;
- Математические вычисления в повседневной жизни
Не пропускать первую часть
Простые тестовые задания кажутся легкими, но в них часто встречаются ошибки из-за невнимательности и торопливости учеников. При условии правильного выполнения только этих вопросов школьники получат 64 балла, что выступает проходным значением для поступления на большинство профильным специальностей на бюджет.
Внимательно читать задания
При сдаче профильной математики важно точно прочитывать предложенные варианты. Аккуратность переписывания примеров на черновик помогает избежать ошибки из-за описок и невнимательности.
Потренироваться считать в уме
Арифметические ошибки относятся к числу обидных промахов в получении первичных и тестовых баллов. Счет с калькулятором не помогает в решении заданий. Рекомендуется тренировать выполнение действий письменно во время всего периода подготовки. Эффективные методы развития устного счета:
- Опора на десятку;
- Разбивка слагаемых на разряды;
- Упрощенное умножение.
Развитию навыка считать в уме в игровом формате помогают настольные игры («Уно», «Монополия», «Умножариум») и мобильные приложения («Математические хитрости», «Quick Brain», «1 001 задача для счёта в уме»).
Проверять решения и ответы
Во второй части преподаватели оценивают не только наличие правильного ответа, но и алгоритм и логичность последовательности действий. Стоит внимательно проверять арифметические вычисления и точность заполнения бланков.
Не отказываться от решения заданий во второй части
За решения с развернутым ответом начисляется по 2 первичных балла. Это существенные значения для получения оценки «Отлично». В короткие сроки наиболее реально подготовиться к решению трех заданий из данного блока:
- Экономической задачи;
- Работы с уравнениями;
- Выполнению неравенства.
Для решения геометрических задач требуются:
- Знания теорем и аксиом;
- Формулы;
- Навык пространственного мышления.
Максимально сложными считаются вопросы с параметрами. При ограниченном времени на подготовку на них рекомендуется просто не тратить силы и старания.
Составить расписание подготовки
Оптимальным считаются регулярные занятия длительностью 40 – 45 минут. Общее время на тренировки в день – 2 часа. Повторение пройденного материала организуется 2 – 3 раза в неделю. После изучения теории обязательна тренировка практических навыков. Для профилактики психологического переутомления и эмоционального выгорания не стоит забывать про отдых, прогулки с друзьями и хобби.
План занятий составляется с учетом тем. Задания одной области отрабатываются в течение 3 – 6 месяцев с подключением нового материала.
Рекомендуемый порядок:
- Преобразования;
- Уравнения;
- Текстовые задачи;
- Неравенства;
- Геометрия;
- Параметры.
Как избежать типичных ошибок
- Грамотно, аккуратно и четко записывать решения;
- Не пользовать калькулятором при выполнении домашних заданий и демоверсий;
- Заранее продумать тайминг и последовательность вычислений;
- Повторить теоремы и формулы;
- Тренировать счет в уме.
Сдать профильную математику сложно, но качественная регулярная подготовка помогает получить оценку «отлично» и пройти конкурсный отбор на поступление в вуз.
Подготовка к ЕГЭ по математике
Из каких частей состоит ЕГЭ по математике в 2023 году
Математика — один из двух обязательных предметов на ЕГЭ. Но, в отличие от русского языка, эта дисциплина предлагает 2 уровня сложности: профильный и базовый. Какий именно вариант выбрать, зависит от вашей цели. Если вуз, в который вы хотите поступить, требует профильного уровня, нужно сдавать его. Обычно это касается технических специальностей.
Для получения аттестата выпускникам школ хватит и базового. Но финальное решение за вами. Если вы хотите сдать профильный вариант, просто чтобы проверить свои знания и уровень подготовки, — дерзайте!
Структура базового уровня ЕГЭ по математике
Базовый уровень проверяет основные знания школьника по математике. Такой экзамен не делится на части: в него входит только 21 задание с кратким ответом. Ответом может быть целое число, десятичная дробь или ряд цифр. По уровням сложности задания экзамена тоже не делятся — все задачи в нем базового уровня. Чтобы выполнить такую работу, ученику дают 180 минут.
Структура профильного уровня ЕГЭ по математике
Варианты профильного уровня проверяют основные и углубленные знания школьника. В 2023 году ЕГЭ состоит из 2 частей:
-
1-я часть: 11 задач с кратким ответом;
-
2-я часть: 7 задач с развернутым ответом.
В первой части ответом может быть целое число, десятичная дробь или ряд цифр. Во второй части — полное обоснованное решение и ответ. Чтобы выполнить задания экзамена, школьнику дают 235 минут.
Задачи ЕГЭ по математике профильного варианта делятся на категории по уровням сложности. В таблице ниже можно увидеть, как именно.
| Базовый | 6 |
| Повышенный | 10 |
| Высокий | 2 |
| Всего | 18 |
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Демоурок по подготовке к экзаменам
Составим ваш личный путь к высоким баллам — учтем сроки, уровень знаний и цель.
Как сдать ЕГЭ по математике: разбор сложных задач
Экзамен по математике не зря считают одним из самых трудных. Даже в заданиях базового варианта можно легко ошибиться по невнимательности. Что уж говорить о действительно сложных задачах с полным решением, где много «подводных камней»? Чтобы вы знали, как подготовиться к ЕГЭ по профильной математике, мы разобрали несколько из них.
Задание 16
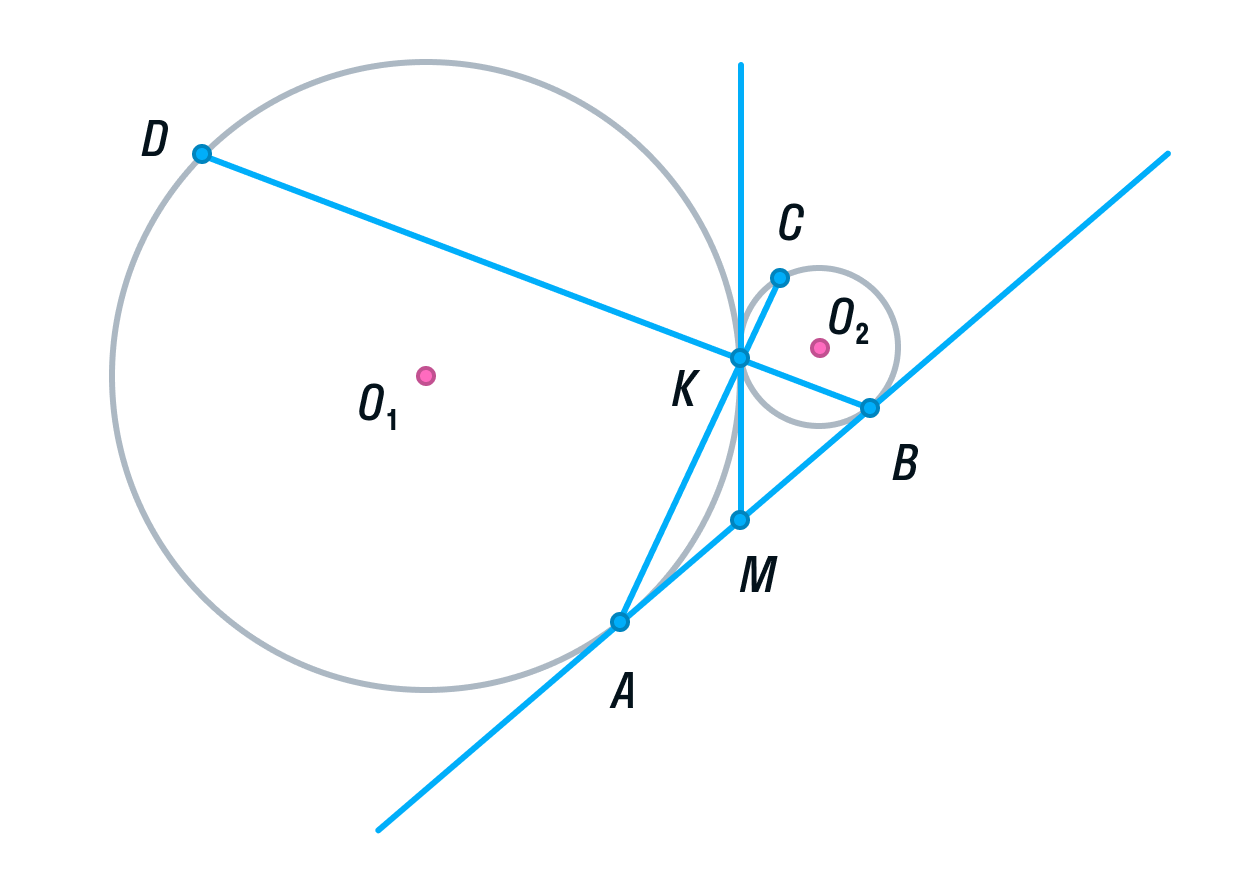
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Совет
Для этого задания советуем повторить темы:
-
Касательные к окружности и их свойства.
-
Свойства вписанных углов.
-
Взаимное расположение окружностей.
-
Свойства прямоугольного треугольника.
-
Признаки и свойства параллельных прямых.
-
Подобные треугольники, площади подобных фигур.
-
Свойство площадей (в частности: отношение площадей треугольников с одинаковой стороной).
-
Трапеция, её свойства. Площадь трапеции.
-
Теорема Пифагора.
Проследите, чтобы они были в вашем плане подготовки к профилю ЕГЭ по математике.
Решение
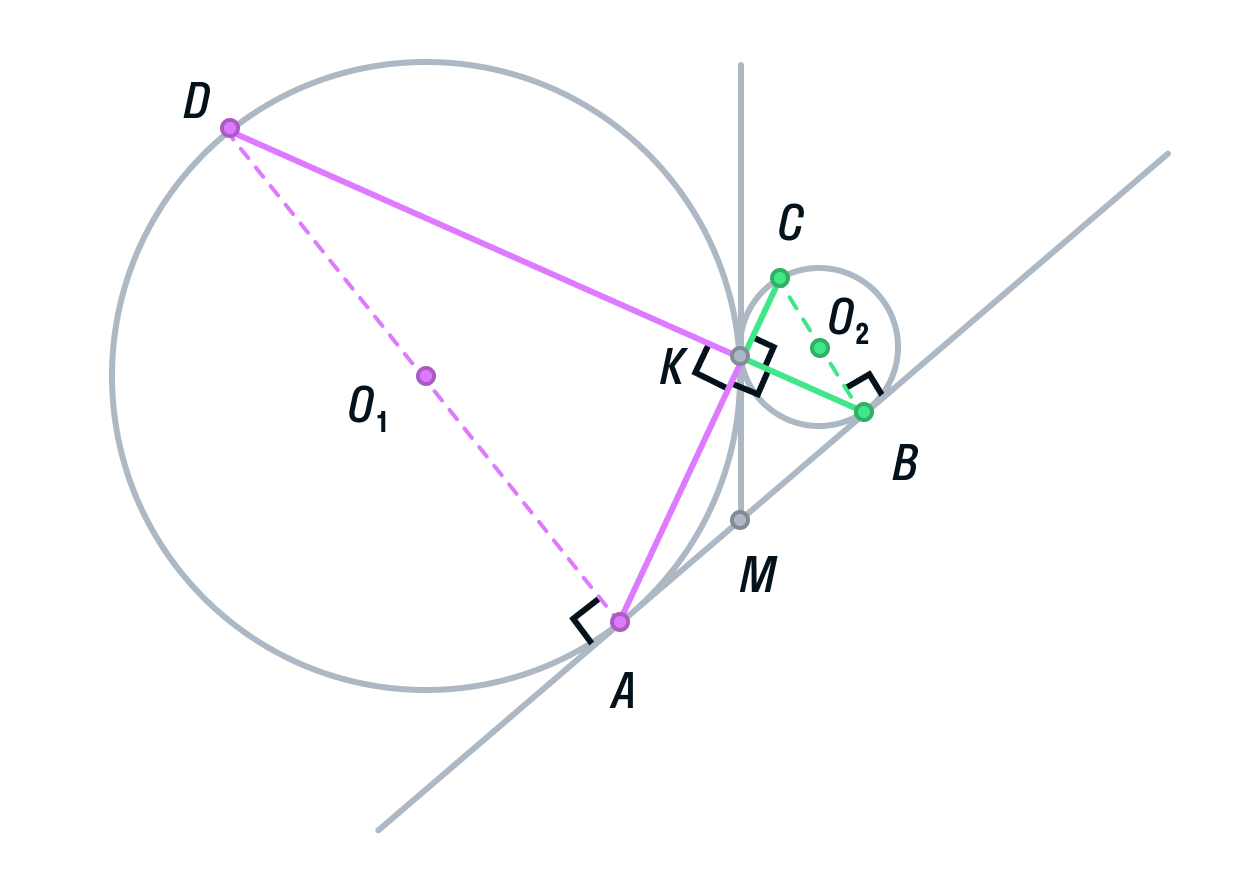
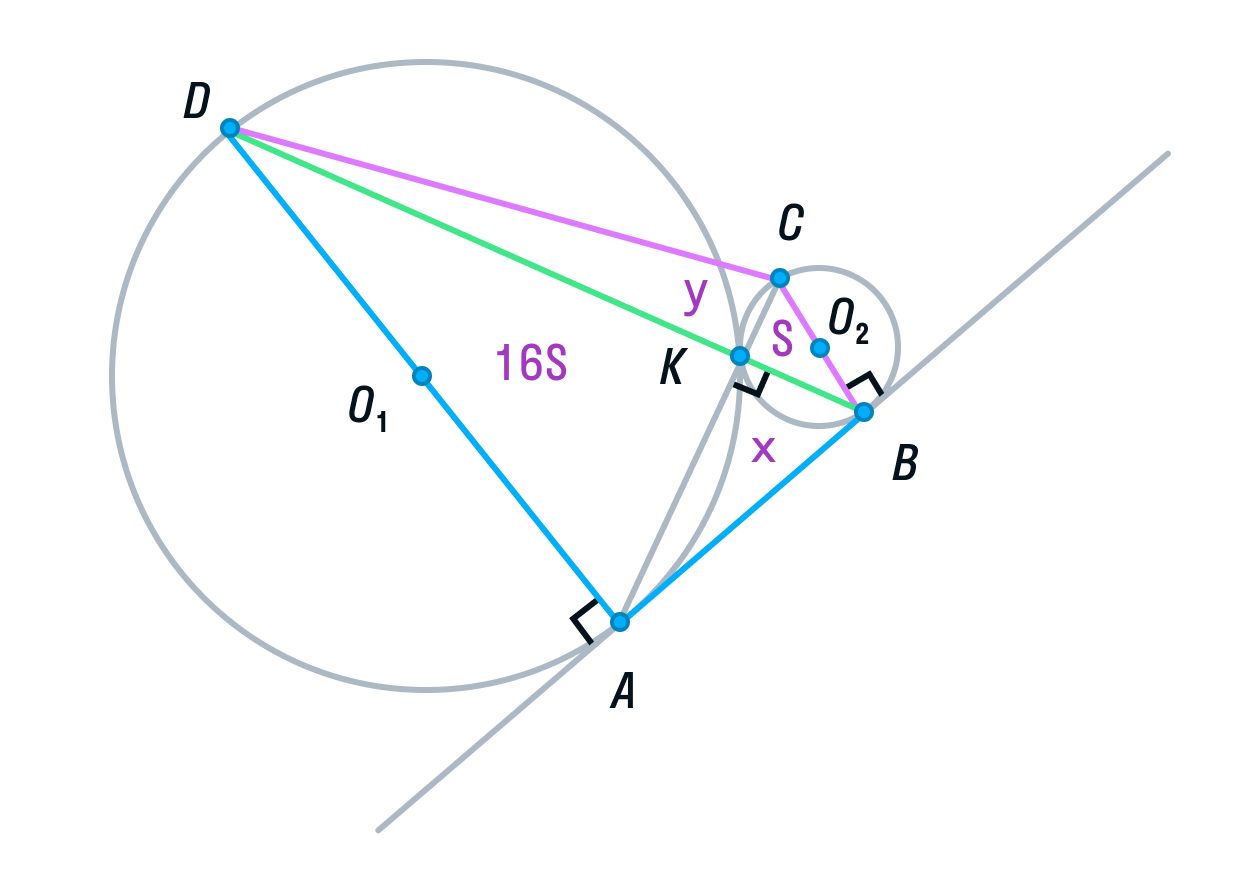
а) Выполним построение.
-
Окружности с центрами О1 и О2 соответственно касаются друг друга в одной точке К.
-
Прямая АВ касается обеих окружностей в точках А и В соответственно.
-
Прямые АК и ВК пересекают окружности в точках С и D соответственно
-
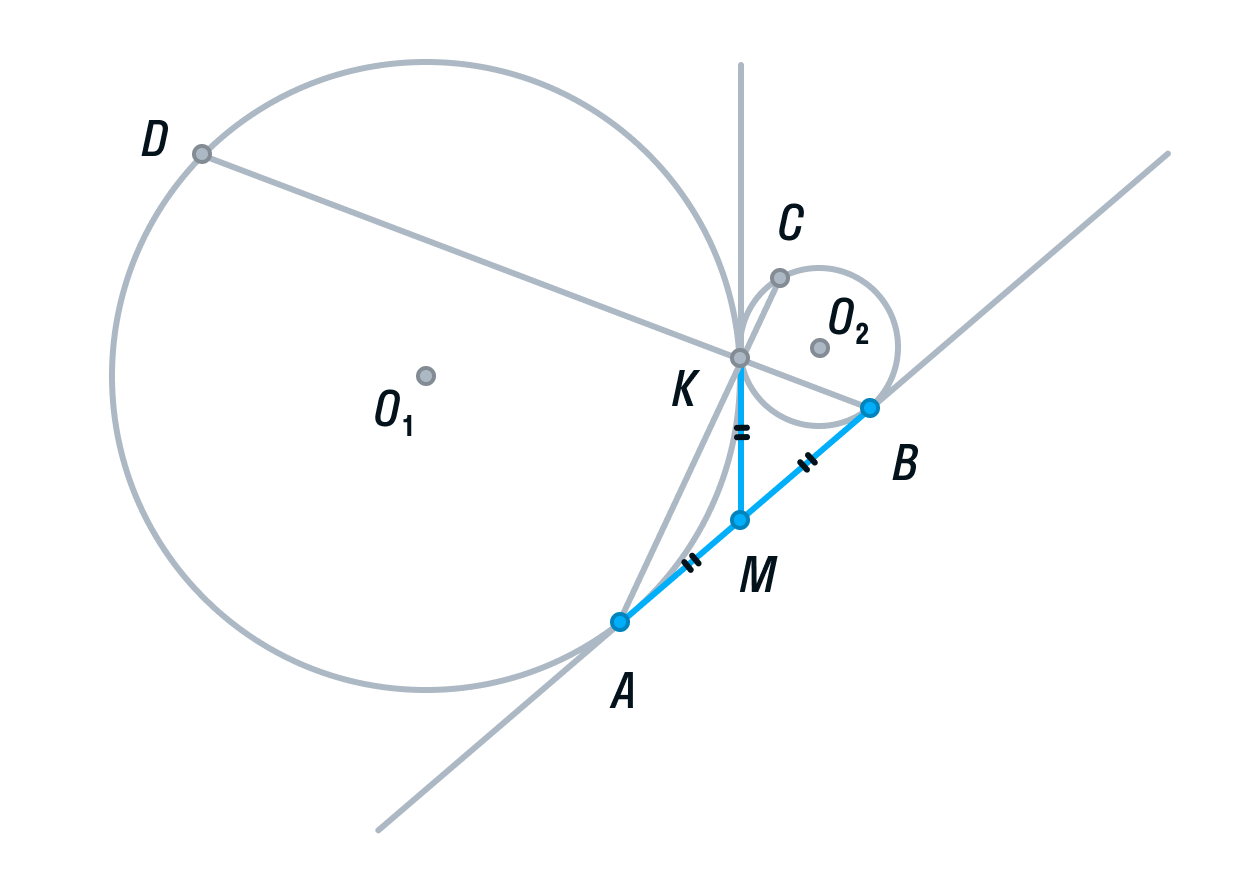
Пусть общая касательная окружностей в точке К, пересекает прямую АВ в точке М.
Тогда по свойству касательных, проведенных из одной точки, AM = KM и KM = BM.
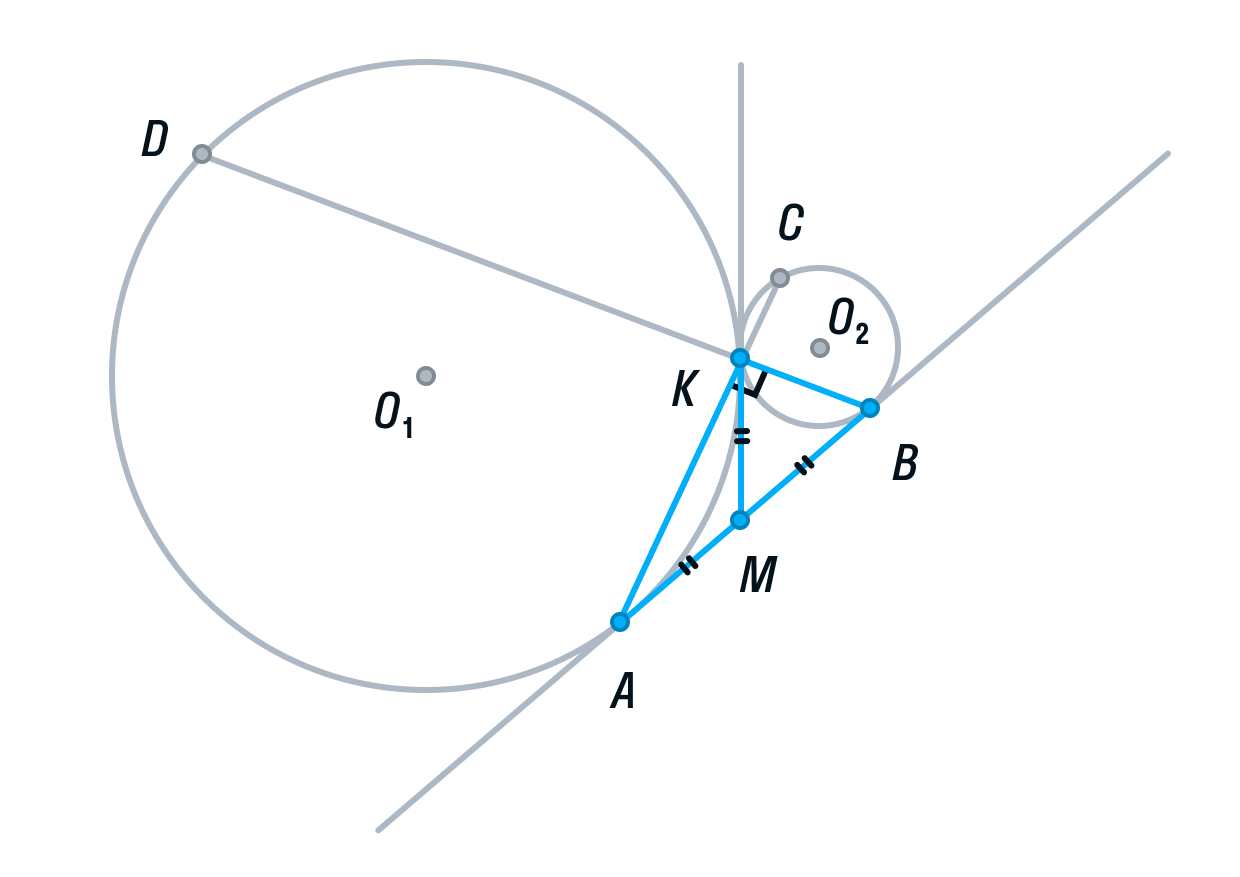
-
Рассмотрим треугольник АВК. Его медиана АМ равна половине стороны, которую она разбивает. Следовательно, делаем вывод, что треугольник АВК прямоугольный, а угол К = 90°.
-
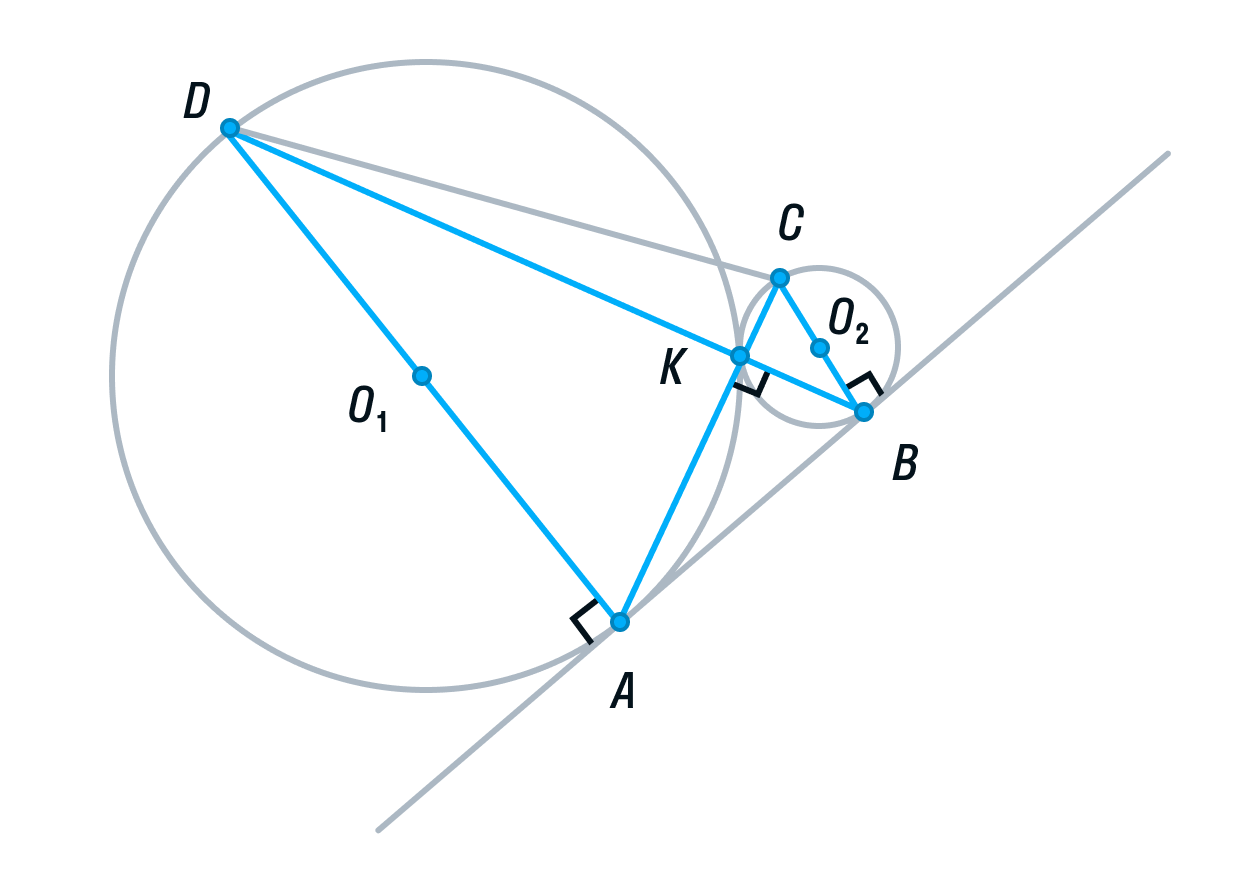
Вписанный угол AKD является смежным углом АКВ, а значит, он тоже 90° как прямой. Следовательно, угол AKD опирается на диаметр AD. Значит, AD ⊥ AB, так как радиус, а в данном случае диаметр, перпендикулярен касательной в точке касания.
-
Аналогично рассмотрев угол ВКС, получим, что BC⊥ AB.
-
Прямые AD и ВС перпендикулярны третьей прямой АВ, следовательно, прямые AD и BC параллельны. Ч. т. д.
б) Пусть радиус первой окружности равен 4, а радиус второй окружности равен 1. Тогда АD = 8, ВС = 2.
-
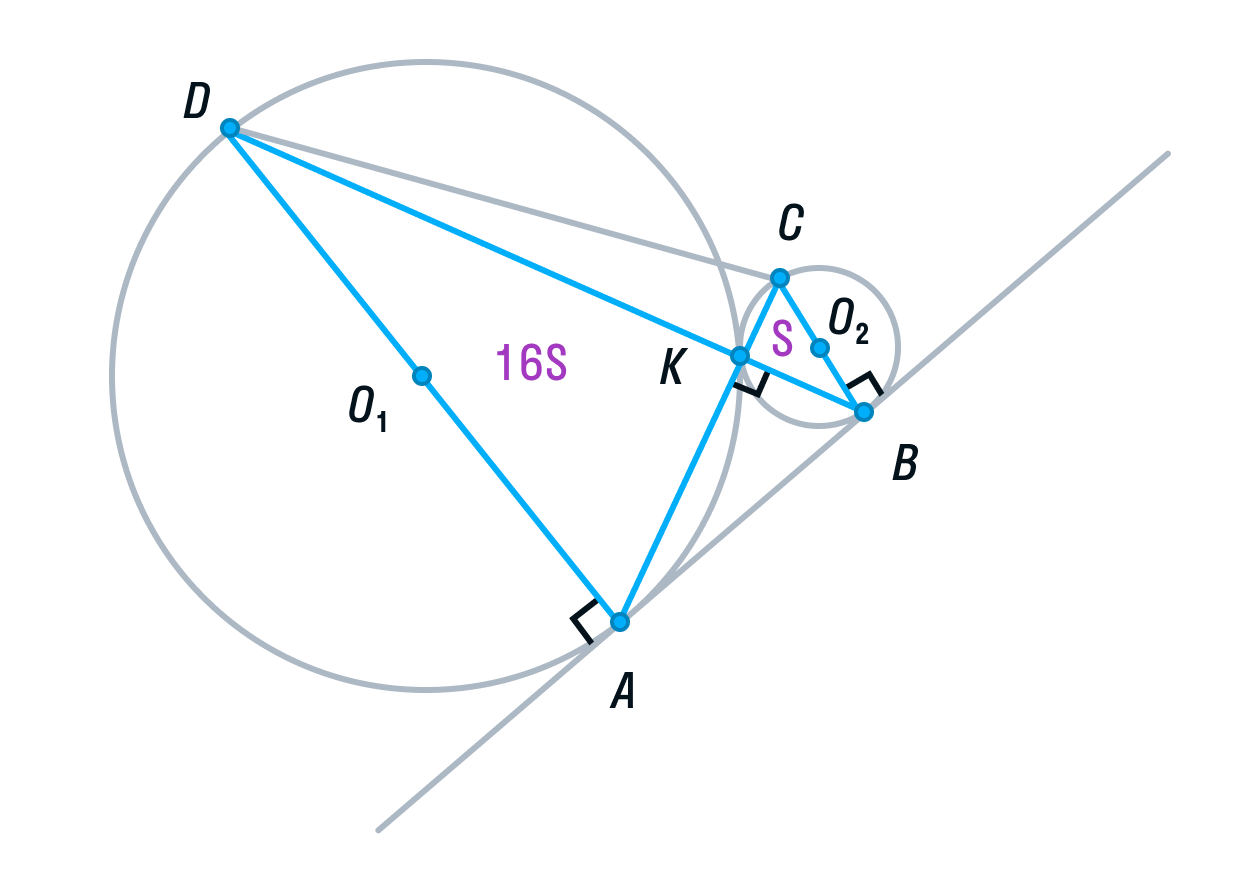
Рассмотрим треугольники ADK и СВК. Они подобны, т. к. имеют два равных угла (К – вертикальный, С и А — накрест лежащие). Из подобия треугольников следует, что их площади относятся как коэффициент подобия в квадрате:
-
Обозначим площадь треугольника СВК за S, тогда площадь треугольника ADK будет равна 16S.
-
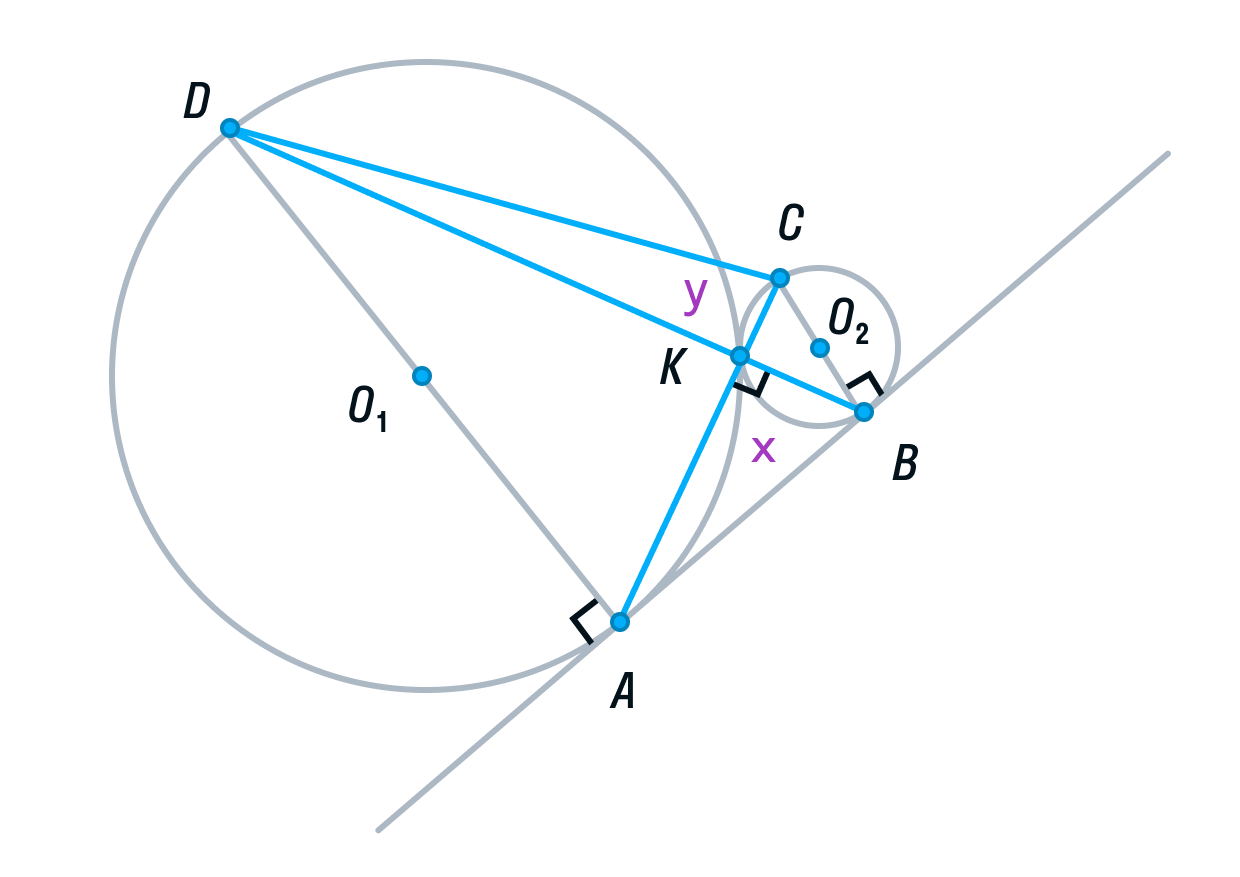
Пусть площади треугольников АВК и CDK будут равны х и у соответственно.
-
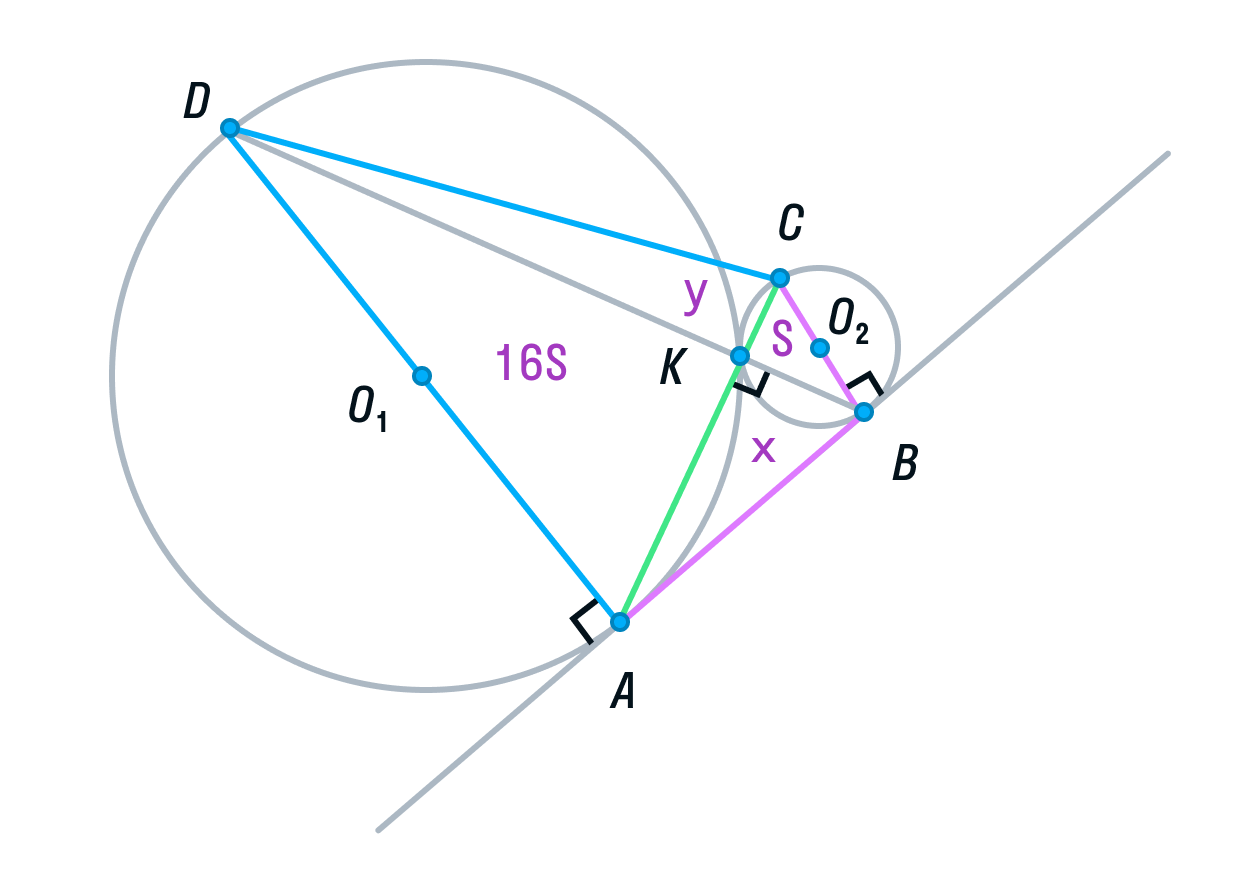
Вспомним свойство, связывающее высоты треугольников с общим основанием и получим следующие равенства: DB — общая сторона треугольников ADB и СDB, следовательно:
(равно 4 из подобия треугольников ADK и СВК, см. выше),
-
Аналогично, AC — общая сторона треугольников ADС и ABC, следовательно,
(равно 4 из подобия треугольников ADK и СВК, см. выше),
-
Решим полученную систему уравнений:
-
Из первого уравнения
подставим во второе и найдем y.
следовательно,
подставим во второе и найдем y.
-
Площадь ABCD равна 16S + 4S + 4S + S = 25S.
-
Заметим, что ABCD — прямоугольная трапеция (AD||BC, AB — перпендикулярна основаниям). Для вычисления ее площади нужно полусумму оснований умножить на высоту.
-
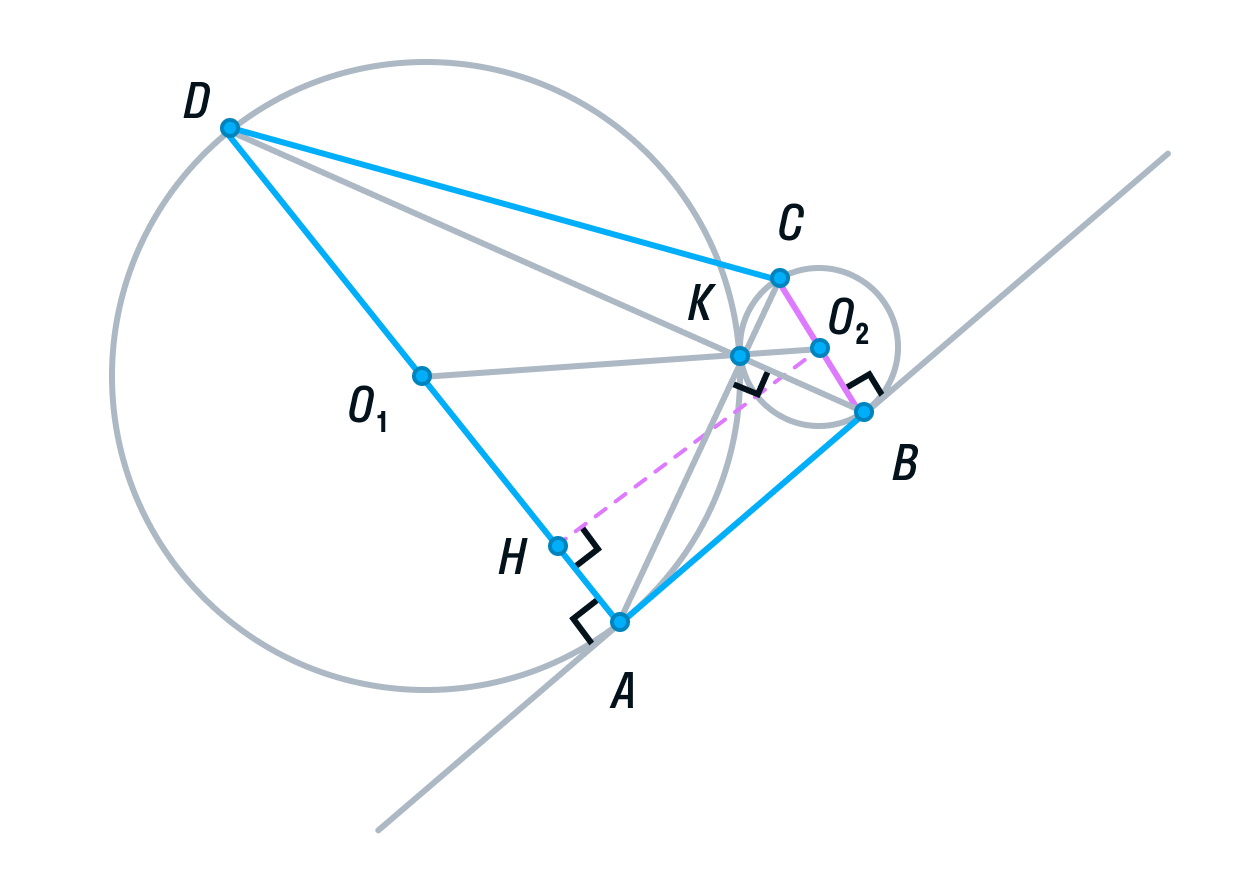
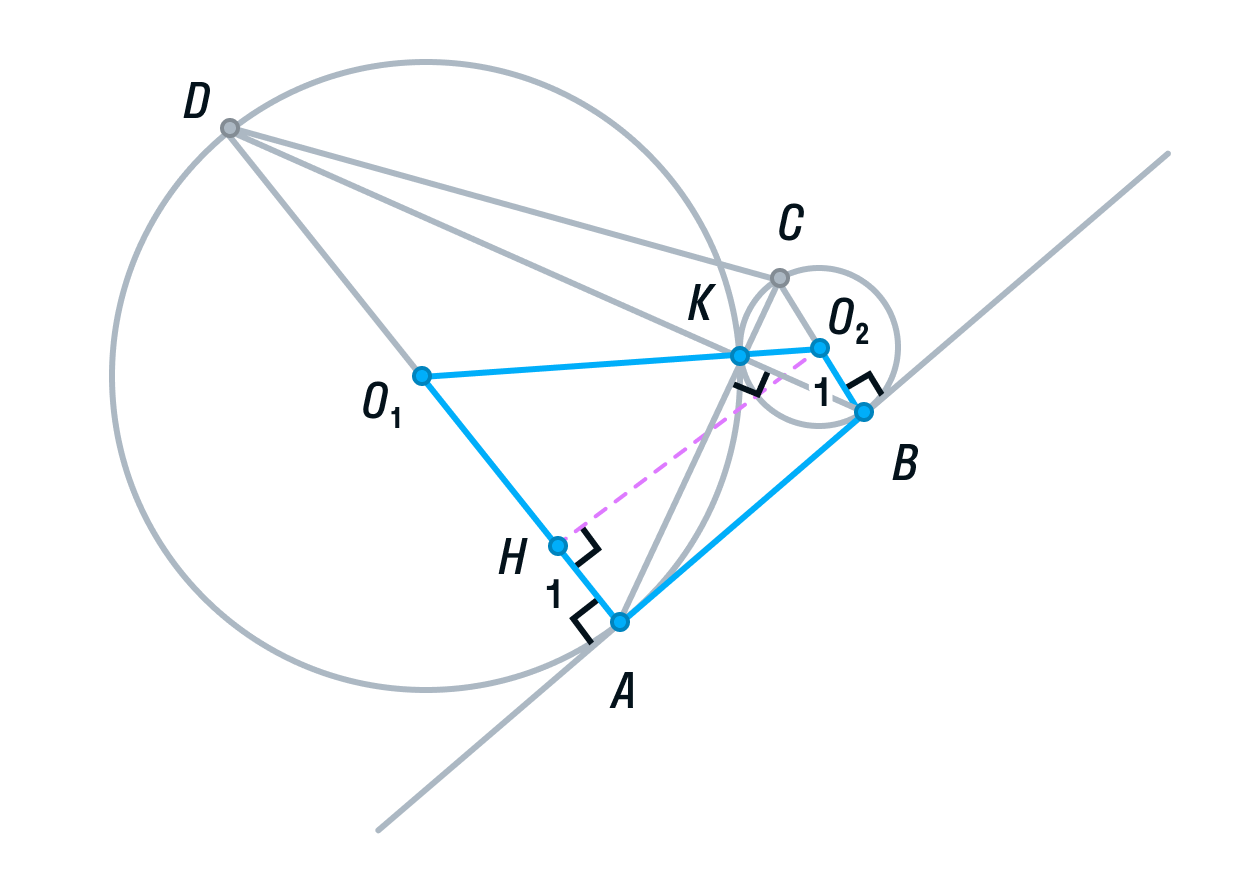
Для того, чтобы найти высоту, рассмотрим меньшую трапецию AO1O2B.
Ее основания равны 1 и 4, так как О2В и О1А — радиусы. O1O2 = 5, так как О2К и О1К — радиусы. О2H — высота трапеции AO1O2B.
-
По теореме Пифагора найдём О2H:
-
Вычислим площадь трапеции ABCD:
-
С другой стороны мы нашли
Отсюда S = 0,8.
-
Площадь треугольника АКВ = 4S, следовательно,
Ответ: 3,2.
Задание 18
В школах № 1 и № 2 учащиеся писали тест. В каждой школе тест писали по крайней мере 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?
б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?
в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Совет
Чтобы справиться с этой задачей, нужно повторить темы:
-
Понятие натурального и целого числа.
-
Среднее арифметическое.
-
Делимость чисел.
-
Процент. Нахождение процента от числа, уменьшение числа на заданный процент.
-
Составление и решение линейных уравнений.
Добавьте их в ваш план подготовки к ЕГЭ по математике, если собираетесь сдавать профиль.
Решение:
а)
-
Допустим, что в школе № 1 писали тест 2 учащихся, один из них набрал 1 балл, а второй набрал Х баллов и перешёл в другую школу. Тогда средний балл в школе был равен (1 + Х) : 2 = 10, а стал равен 1, т. е. уменьшился в 10 раз.
-
Решим уравнение и получим Х = 19 — натуральное число. Следовательно, наше предположение верно.
-
Или мы можем предположить другой вариант: что один учащийся набрал 2 балла. Тогда средний балл изначально равняется 20, а после ухода второго станет 2, т. е. изменится в 10 раз.
-
Решим уравнение (2 + Х) : 2 = 20, отсюда Х = 38 — натуральное число, что тоже удовлетворяет условию задачи.
Ответ: средний балл в школе № 1 мог уменьшиться в 10 раз.
б)
-
Пусть в школе № 2 писали тест m учащихся, n — сумма баллов m учащихся, средний балл равнялся B, а перешедший в неё учащийся набрал u баллов.
-
Умножим обе части полученного уравнения на 10, получим:
-
По условию B = 7, тогда получим, что 10u кратно 10, а
не делится на 10, так как ни один из множителей не делится на 10. Это противоречие.
Ответ: Первоначальный средний балл в школе № 2 не мог равняться 7.
в)
-
Пусть в школе № 1 средний балл равнялся A, общее количество баллов — p, количество писавших работу — (9 – m).
(из пункта б).
Следовательно,
-
Попробуем найти средний балл в школе № 2 методом подбора. Пусть:
В = 1, тогда:
кратно 10, а
не делится на 10.
В = 2, тогда:
пусть u = 1, тогда m = 4:
— не является целым числом.
u = 2 не может быть, т. к. m ≥ 1
В = 3, тогда:
кратно 10, а
не делится на 10.
В = 4, тогда:
Чтобы m было натуральным числом u должно быть четным, u = 2, тогда m = 4, что невозможно (доказали при В = 2).
u = 4, тогда m меньше 0, что невозможно т. к. m ≥ 1.
В = 5, тогда:
пусть u = 1, тогда m = 7, что невозможно (доказали в пункте б);
пусть u = 2, тогда m = 5:
— не является целым числом;
пусть u = 3, тогда m = 3:
-
Этот случай реализуется, например, в школе № 2 при m = 3, B = 5. Предположим, что каждый ученик набрал по 5 баллов. Тогда в школе № 1 писали 9 – m = 9 – 3 = 6 учащихся, 3 из них набрали по 1 баллу, а 3 – по 3 балла, тогда средний балл:
-
Переход из школы № 1 в школу № 2 совершил ученик с 3 баллами, тогда
средний балл в школе № 1 стал равен:что на 10% меньше от первоначального значения.
-
Тогда средний балл в школе № 2 стал равен:
что на 10% меньше от первоначального значения.
Ответ: наименьшее значение первоначального среднего балла в школе № 2 равно 5.
Ответ: а) да; б) нет; в) 5.
Как выставляют баллы за ЕГЭ по математике
С базовым уровнем сложности все просто: за каждый правильный ответ вашего варианта вы получаете по 1 первичному баллу. То же самое касается и первой части профиля: задания 1–11 тоже оценивают в 1 балл.
Как вы помните, во 2-й части профильного варианта нужны и решение, и ответ. Здесь задания оценивают по нескольким критериям. Они сложнее, но и баллов за них можно получить больше. Давайте же разберемся, как выставляют баллы во второй части профиля. Это поможет вам подготовиться к заданиям ЕГЭ по математике как самостоятельно, так и с учителем.
| Задание № 12 | Баллы |
|---|---|
| В обоих пунктах есть обоснованные ответы | 2 |
| Есть обоснованный ответ только в пункте а или есть неверный ответ из-за ошибки в вычислениях, но шаги в решениях обоих пунктов верные |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 13 | Баллы |
|---|---|
| Верно доказан пункт а, в пункте б есть обоснованный ответ | 3 |
| Есть только обоснованный ответ в пункте б или верно доказан пункт а, в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ |
2 |
| Есть только верное доказательство пункта а, или в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ, или есть обоснованный ответ в пункте в, который получен с помощью пункта а, но сам пункт а не выполнен |
1 |
| Все остальные случаи. | 0 |
| Максимальный балл | 3 |
| Задание № 14 | Баллы |
|---|---|
| Есть обоснованный ответ | 2 |
| Ответ обоснован, но он отличается от верного исключением точек –12 и/или 0 или шаги решения верные, но из-за ошибки в вычислениях получен неверный ответ |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 15 | Баллы |
|---|---|
| Есть обоснованный ответ | 2 |
| Ученик верно построил математическую модель | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 16 | Баллы |
|---|---|
| Верно доказан пункт а, в пункте б есть обоснованный ответ | 3 |
| Есть только обоснованный ответ в пункте б иЛИ Верно доказан пункт а, в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ |
2 |
| Есть только верное доказательство пункта а, или в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ, или есть обоснованный ответ в пункте в, который получен с помощью пункта а, но сам пункт а не выполнен |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 3 |
| Задание № 17 | Баллы |
|---|---|
| Есть обоснованный ответ | 4 |
| Рассуждения и значения параметра верные, но в ответе есть 1–2 неверных значения или решение недостаточно обосновано | 3 |
| Есть верное рассуждение и хотя бы одно правильное значение | 2 |
| Задача сведена к исследованию взаимного расположения 3 окружностей или двух квадратных уравнений с параметром | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 4 |
| Задание № 18 | Баллы |
|---|---|
| Есть обоснованный ответ в пунктах а, б, в | 4 |
| Есть обоснованный ответ в пункте в и есть обоснованный ответ в пунктах а или б | 3 |
| Есть обоснованный ответ в пунктах а и б или есть обоснованный ответ в пункте в. |
2 |
| Есть обоснованный ответ в пунктах а или б | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 4 |
Узнать больше о структуре экзамена, вариантах и критериях, по которым оценивают работы, можно на официальном сайте ФИПИ, в разделе «Демоверсии, спецификации, кодификаторы». Там же вы найдете методические указания для подготовки.
Сколько баллов нужно набрать, чтобы получить 3, 4 и 5
Теперь, когда мы разобрали критерии, можно посчитать, сколько баллов нужно набрать на конкретную оценку. В этом нам помогут таблицы ниже. Заодно разберемся, как первичные баллы переводятся в тестовые — финальные.
| Шкала перевода баллов в базовой математике | |
|---|---|
| Первичные баллы | Оценка |
| <7 | 2 |
| 7–11 | 3 |
| 12–16 | 4 |
| 17–21 | 5 |
| Максимальный балл | 4 |
Обратите внимание: с 2008 года официально баллы ЕГЭ не переводят в привычные нам оценки по пятибальной системе. Но если вам хочется это сделать, можно примерно оценить работу по таблице ниже.
| Шкала перевода баллов в профильной математике (неофициальная) | ||
|---|---|---|
| Первичные баллы | Тестовые баллы | Оценка |
| <5 | <27 | 2 |
| 5–8 | 27–49 | 3 |
| 8–20 | 50–67 | 4 |
| 21–31 | 68–100 | 5 |
6 советов от эксперта, как готовиться к ЕГЭ по математике
Мы занимаемся подготовкой учеников к экзамену каждый год и понимаем, насколько это важно и волнительно. Вам предстоит ответственная работа, от которой многое зависит. Чтобы облегчить ее, мы собрали несколько советов, которые помогут вам как можно лучше подготовиться к ЕГЭ по математике:
-
Осознанно выберите уровень сложности и поставьте цель в баллах.
-
Составьте план подготовки к ЕГЭ по математике: больше времени уделяйте темам, которые у вас «западают». Чтобы выявить их, ученики Skysmart проходят тест на бесплатном уроке.
-
Узнайте все о ЕГЭ: сколько времени длится экзамен, из каких частей состоит, по каким темам будут задания, сколько вариантов, какие дадут справочные материалы и т. д.
-
Составьте сбалансированное расписание для подготовки и следите, чтобы в нем было достаточно времени для отдыха.
-
Много практикуйтесь: решайте варианты из Открытого банка заданий ЕГЭ и сдавайте тестовые экзамены.
-
Систематически консультируйтесь и занимайтесь с наставником, который часто имеет дело с подготовкой к ЕГЭ — преподавателем в школе или репетитором.
Все пункты в этом списке важны для тех, кто хочет набрать 80–100 баллов, но последний — особенно. Преподаватель расскажет о том, что представляет из себя ЕГЭ, и тогда на реальном экзамене не будет неприятных сюрпризов.
На курсах подготовки к ЕГЭ по математике в Skysmart учителя помогают школьникам разобраться в КИМах и прорешать каждый тип задач. Ученики заранее знакомятся с частыми ошибками, что помогает избегать их в работе и сохранять баллы. А еще мы учим готовиться морально, чтобы не допустить ошибок из-за паники и невнимательности. Начните подготовку к ЕГЭ по математике с нуля вместе со Skysmart: первый урок — бесплатно!