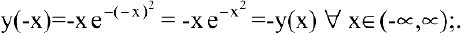Добавил:
Uman
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
471
Добавлен:
04.03.2014
Размер:
2.41 Mб
Скачать
КОНСПЕКТ ЛЕКЦИЙ МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Е. Б. Боронина
Эта книга написана для студентов технических вузов, желающих подготовиться к экзамену по математическому анализу. Содер жание данной книги полностью соответствует программе по курсу «Математический анализ», экзамен по которому предусмотрены в большинстве высших учебных заведений России. Программа по могает быстро и без лишних трудностей найти необходимый ответ на поставленный вопрос. Вопросы составлены автором на основе личного опыта с учетом требований преподавателей.

ЛЕКЦИЯ № 1. Математический анализ функций одной переменной
1. Множества
Понятие множества относится к числу первоначальных поня тий, которые не определяются через другие, более простые. Вместо слова «множество» иногда говорят «совокупность некото рых предметов, объединенных по какому нибудь признаку».
Объекты, из которых состоит множество, называют его эле+ ментами или точками. Множества часто обозначают большими, а их элементы — малыми буквами. Если x — элемент множества X, то пишут x X (точка x принадлежит множеству X). Если x не является элементом множества X, то пишут x X (x не принад лежит X). Если множество X состоит из элементов x1, x2, x3, …, xn записывают X={x1, x2, x3, …, xn}.
Пусть X и Y — два множества. Если X и Y состоят из одних и тех же элементов, то пишут X = Y. Если в Х нет элементов, не принад лежащих Y, то пишут, что x X . Если X не содержится в Y, то пи шут x X . В математике часто используется пустое множество. Оно не содержит ни одного элемента и обозначается символом O. Пустое множество является подмножеством любого множества.
Множество (−∞;+ ∞) называется числовой прямой, а любое чис ло — точкой этой прямой. Пусть a — произвольная точка числовой прямой и δ — положительное число. Интервал (a − δ ; a + δ ) на зывается δ+окрестностью точки a.
Проколотой δ+окрестностью точки a называется ее δ+окрест+ ность, из которой удалена сама точка a.
Точка a называется внутренней точкой множества X, если су ществует δ окрестность точки a, в которой содержатся только точки множества X.
Точка a называется граничной точкой множества X, если в лю бой δ окрестности точки a содержатся точки, принадлежащие и не принадлежащие множеству X.
3

Говорят, что множество X ограничено сверху (снизу), если су ществует такое число c, что для любого x X выполнено нера венство x < c (x > c). Число c в этом случае называется верхней (ниж+ ней) гранью множества X. Множество, ограниченное и сверху и снизу, называется ограниченным. Наименьшая (наибольшая) из верхних (нижних) граней ограниченного сверху (снизу) множест ва называется точной верхней (нижней) гранью этого множества.
2. Теорема о вложенных отрезках
Определение. Пусть дана последовательность таких отрезков [a1, b1], [a2, b2], …, [an, bn], …, что каждый последующий содержит ся в предыдущем: [a1, b1] [a2, b2] … [an, bn] …, т. е. для всех n
|
an |
< |
an+1 < bn+1 |
< |
bn |
(1) |
и пусть lim (bn − an ) . Такая последовательность называется по
n → ∞
следовательностью вложенных отрезков.
Теорема о вложенных отрезках. Для любой последовательности вложенных отрезков существует единственная точка, принадле жащая всем отрезкам этой последовательности.
Доказательство. Из неравенства (1) следует, что левые концы отрезков образуют неубывающую последовательность
|
a1 ≤ a2 ≤ a3 ≤ … ≤ an ≤ an+1 ≤ … , |
(2) |
а правые концы образуют невозрастающую последовательность
|
b1 ≥ b2 ≥ b3 ≥ … ≥ bn ≥ bn+1 ≥ … , |
(3) |
при этом последовательность (2) ограничена сверху, а последова тельность (3) ограничена снизу, так как an < b1, а bn > a1 для любо го n. Следовательно, на основании признака сходимости монотон ной последовательности эти последовательности имеют пределы
|
Пусть |
lim a |
= c‘ , а |
lim b = c» . |
Тогда из условия lim |
(b |
− a )= |
|
|
n→∞ n |
n→∞ n |
n → ∞ |
n |
n |
|||
|
= lim b |
− lim a = c» |
– c‘ = 0 |
|||||
|
n→∞ |
n |
n→∞ |
n |
4

следует, что c‘ ‘ = c‘ , т. е. последовательности {an} и {bn} имеют об щий предел. Обозначая этот предел буквой C, получаем, что для любого n справедливы неравенства an < c < bn, т. е. точка c при надлежит всем отрезкам последовательности (1).
Докажем теперь, что такая точка только одна. Допустим, что су ществует еще одна точка c1(c1 ≠ c), принадлежащая всем отрезкам последовательности (1). Тогда для любого n должно выполняться не
|
равенство b |
– a > | c – c | и, следовательно, |
lim (bn − an ) ≥ |
c1 − c |
, |
||||
|
n |
n |
1 |
n → ∞ |
что противоречит условию теоремы. Таким образом, теорема до казана полностью.
Замечание. Теорема неверна, если вместо отрезков рассматри вать интервалы. Например, для последовательности вложенных
|
интервалов |
|
|
(0, 1) (0, 1/2) (0, 1/4) … (0, 1/2n) |
(4) |
не существует точки, принадлежащей всем интервалам. В самом деле, какую бы точку C на интервале (0,1) ни взять, всегда найдет
|
ся такой номер N, что при n > N будет |
1 |
< c и, следовательно, |
|||
|
n |
|||||
|
2 |
|||||
|
точка C не будет принадлежать интервалам последовательности (4), |
|||||
|
1 |
|||||
|
начиная с интервала 0, |
. |
||||
|
2N +1 |
|||||
3. Числовые последовательности
Определение 1. Если каждому числу n из натурального ряда чи сел 1, 2, 3, …, n поставлено в соответствие вещественное число xn,
|
то множество вещественных чисел |
|
|
x1, x2, x3, …, xn |
(1) |
называют числовой последовательностью или просто последова тельностью.
Числа x1, x2, x3, …, xn называются элементами (или членами) по следовательности (1), символ xn — общим элементом последова тельности, а число n — его номером. Сокращенно последователь ность (1) обозначается символом {xn}.
5

Последовательность задана, если указан способ получения любого ее элемента. Например, формула xn = 1 + (–1)n задает по следовательность:
0, 2, 0, 2, …
Определение 2. Последовательность {xn} называется ограничен+ ной сверху (снизу), если существует такое число M (число m), что любой элемент xn этой последовательности удовлетворяет нера
венству xn < M (xn > m).
Определение 3. Последовательность {xn} называется ограничен+ ной, если она ограничена и сверху и снизу, т. е. существуют числа m и M такие, что любой элемент xn этой последовательности удов летворяет неравенству m < xn < M.
Определение 4. Последовательность {xn} называется неограни+ ченной, если для любого положительного числа A существует элемент xn этой последовательности, удовлетворяющий неравенст
ву | xn | > A(т. е. xn > A, либо xn < –A).
Примеры
1.Последовательность 1, 2, 3, …, n ограничена снизу, но нео граничена сверху.
2.Последовательность –1, –2, –3, …, –n ограничена сверху, но неограничена снизу.
3.Последовательность 1, 1 , 1 , …, 1 ограничена, так как любой
2 3 n
элемент xn этой последовательности удовлетворяет неравенствам: 0 < xn < 1 (m = 0, M = 1).
4.Последовательность –1, 2, –3, 4, …б (–1)nn неограниченная.
Всамом деле, каково бы ни было число A среди элементов xn этой последовательности, найдутся элементы, для которых будет вы
полняться неравенство.
Определение 5. Последовательность {xn} называется бесконеч+ но большой, если она становится и остается, начиная с некоторо го номера N, по абсолютной величине больше любого наперед за данного сколь угодно большого положительного числа A.
Символическая запись определения бесконечно большой по следовательности:
( A > 0)( N )( n> N ): |xn |> A.
6

Определение 6. Последовательность {xn} называется бесконеч+ но малой, если она становится и остается, начиная с некоторого номера N, по абсолютной величине меньше любого наперед за данного сколь угодно малого положительного числа ε.
Символическая запись определения бесконечно малой после довательности:
( ε > 0)( N )( n> N ) : |xn |< ε .
|
Теорема. Если {xn} — бесконечно большая последовательность |
||
|
1 |
||
|
и все ее члены отличны от нуля, то последовательность |
бес |
|
xn
конечно малая, и, наоборот, если {xn} — бесконечно малая после
|
1 |
|||||||||||
|
довательность и x |
≠ 0, то последовательность |
— бесконечно |
|||||||||
|
n |
xn |
||||||||||
|
большая. |
|||||||||||
|
Доказательство. Пусть {xn} — бесконечно большая последова |
|||||||||||
|
тельность, т. е. |
|||||||||||
|
( ε = |
1 |
> 0) ( N )( n> N ) : |xn |> |
1 |
||||||||
|
A |
A |
||||||||||
|
или |
|||||||||||
|
( ε |
1 |
> 0), ( N )( n> N ) : |
1 |
||||||||
|
= |
|xn |< A |
||||||||||
|
A |
1
т.е. бесконечно малая.
xn
Доказательство второй части проводится аналогично.
4. Сходящиеся и расходящиеся последовательности. Критерий Коши
Определение 1. Число a называется пределом последователь+ ности {xn}, если для любого ε > 0 существует такой номер N, что при n > N выполняется неравенство
7

С помощью логических символов это определение можно за писать в виде:
( ε > 0) ( N )( n> N) : |xn − a|< ε .
Последовательность, имеющая предел, называется сходящейся. Если последовательность {xn} сходится и имеет своим преде
лом число a, то символически это записывается так:
|
lim xn = a или xn → a при n → ∞. |
(2) |
|
n → ∞ |
Последовательность, не являющаяся сходящейся, называется
расходящейся.
Определение 2. Говорят, что последовательность {xn} удовле творяет условию Коши, если для любого ε > 0 существует такой номер N, что для всех номеров n и m, удовлетворяющих условию n > N и m > N, справедливо неравенство:
Условие (3) можно сформулировать и таким образом: для лю бого ε > 0 существует такой номер N, что для всех номеров n > N и всех целых неотрицательных p
Для того, чтобы убедиться в равносильности условий (3) и (4), достаточно положить p = n – m, если n > m и p = m – n, , если n < m.
Последовательности, которые удовлетворяют условию Коши, называют также фундаментальными.
|
Определение 3. Последовательность {xn}, k = 1, 2, …— подпо+ |
||||
|
следовательность последовательности {x }, если ( k )( N ): yk = xN , |
||||
|
n |
||||
|
причем (nk |
< nk |
2 |
) (k1k2 ) . Последовательность {y |
} обозначает |
|
1 |
k |
ся в этом случае так же {xn}.
8

Теорема (Больцано—Вейерштрасса). Из любой ограниченной последовательности можно выделить сходящуюся подпоследова тельность.
Теорема (критерий Коши). Для того, чтобы последовательность сходилась, необходимо и достаточно, чтобы она удовлетворяла условию Коши.
Доказательство. Докажем необходимое условие. Пусть после
довательность {x } сходится и lim xn = a . Зададим ε > 0 , тогда
n n → ∞
|
согласно определению предела последовательности существует |
|||||||||
|
такой номер N, что |xn − a| < |
ε |
при n |
> |
N. |
|||||
|
2 |
|||||||||
|
Пусть теперь n > N и m > N, тогда |
|||||||||
|
|xn − xm |= | (xn − a)+ (a − xm )| ≤ | xn − a |+ |
|||||||||
|
+ |xm − a |< |
ε |
+ |
ε |
= ε , |
|||||
|
2 |
|||||||||
|
2 |
|||||||||
|
т. е. выполняется условие Коши. |
|||||||||
|
Докажем достаточное условие. Пусть последовательность {xn} |
|||||||||
|
удовлетворяет условию Коши, т. е. для любого ε > 0 существует |
такой номер N, что для всех номеров n и m, удовлетворяющих условию n > N и m > N, справедливо неравенство |xn − xm |< ε . Возьмем ε = 0 , тогда существует такое N1, что | xn – xm | < 1 при
n > N1 и m > N1.
В частности, если n > N1 a m = N1, то | xn – xN1 | < 1, т. е. xN1 − 1 < xn xN1 + 1 при n > N1. Это и значит, что последователь
ность {xn} при n = N1, N1+1,… ограничена. А это значит, что по
|
теореме Больцано Вейерштрасса существует ее сходящаяся под |
|||||||
|
последовательность { xn }. |
|||||||
|
k |
|||||||
|
Пусть lim xn |
= a . Покажем что и |
lim xn |
= a . |
||||
|
n → ∞ |
k |
n → ∞ |
k |
||||
|
Зададим некоторое ε > 0 . Тогда, во первых, по определению |
|||||||
|
последовательности существует такое K, что |
|||||||
|
| xn |
− a | < |
ε |
(5) |
||||
|
k |
2 |
для всех k > K.
9
Причем согласно определению последовательности неравен ство (5) выполняется для всех nk > nK.
Во вторых, так как последовательность {xn} удовлетворяет
условию Коши, то существует такое N, что |xn − xm | < ε для всех
2
n > N и всех m > N.
Положим Nε = max{N, nk} и зафиксируем некоторое nk >Nε . Тогда для любого nk >Nε получим:
|xn − a |= | (xn − xnk )+ (xnk − a)| ≤ | xn − xnk | + | xnk − a | <
|< ε + ε = ε
2 2
а это и доказывает, что lim xn = a.
n→∞
Теорема доказана.
5. Определение и признак сходимости монотонной последовательности
Определение 1. Последовательность {xn} называется возрастаю+ щей, если xn < xn+1 для всех n; неубывающей — если xn < xn+1 для всех n; убывающей — если xn > xn+1 для всех n; невозрастающей —
если xn > xn+1 для всех n.
Все такие последовательности объединяются одним общим названием: монотонные последовательности. Возрастающие и убы вающие последовательности называются строго монотонными.
|
Примеры |
|||||||||
|
1. Последовательность 1, |
1 |
, |
1 |
, …, |
1 |
убывающая и ограниченная. |
|||
|
n |
|||||||||
|
2 |
3 |
||||||||
|
2. Последовательность 1, |
1,1 |
, |
2,1 |
, 3, …, |
1 |
невозрастающая и огра |
|||
|
3,1 |
n |
||||||||
|
2,1 |
ниченная.
3.Последовательность 1, 2, 3, …, n возрастающая и неограни ченная.
4.Последовательность 1, 1, 2, 2, 3, 3, …, n, n неубывающая
инеограниченная.
10
Курс лекций для студентов 1 курса по математическому анализу любых форм обучения. Я собрала теорию и примеры с решениями к каждой теме, чтобы вы смогли подготовиться к экзамену или освежить память перед контрольной работой!
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Введение в математический анализ
Математический анализ — совокупность разделов математики, посвящённых исследованию функций и их обобщений методами дифференциального и интегрального исчислений. При столь общей трактовке к анализу следует отнести и функциональный анализ вместе с теорией интеграла Лебега, комплексный анализ (ТФКП), изучающий функции, заданные на комплексной плоскости, нестандартный анализ, изучающий бесконечно малые и бесконечно большие числа, а также вариационное исчисление.
Функция. Предел функции
Математический анализ — раздел математики, в котором изучаются функции. В экономическом анализе часто исследуют, например, зависимости спроса и предложения от цены (функции спроса и предложения), зависимость издержек производства от объема продукции (функцию издержек) и др. Зависимость переменной у от переменной х называется функцией, если каждому элементу 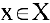
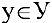
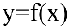
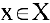
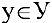
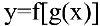
В школьном курсе изучались следующие функции: постоянная 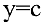
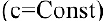
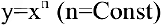
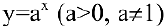
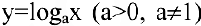
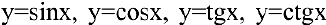
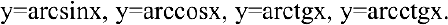
Возможно эта страница вам будет полезна:
Одним из основных понятий математического анализа является предел. Примерами применения понятия предела могут служить окружность как предел вписанных и описанных многоугольников при бесконечном увеличении числа сторон или касательная как предельное положение секущей при сближении точек пересечения. Говорят, что функция 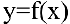
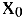
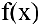
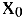
Используя логические символы: 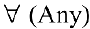
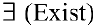
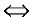

Внимание! Определение предела не требует существования функции в самой предельной точке 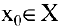
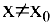
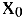
Если функция 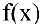
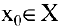
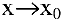
то функция 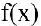
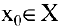
Следовательно, в случае непрерывных функций очень просто находятся пределы в любой точке области определения: для этого достаточно вычислить значение функции в данной точке.
Утверждение 1. Любая элементарная функция непрерывна в области определения.
Утверждение 2. Под знаком непрерывной функции можно переходить к пределу:
Пример №1
Вычислить предел
Решение:
Данная функция элементарная, т.к. получена из основных элементарных функций (постоянной и степенной) с помощью конечного числа арифметических действий. Поскольку 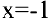
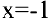
Заметим, что не всякий производственный процесс непрерывен во времени. Аргумент функции может изменяться лишь в отдельные моменты. Так, приняв за область определения функции множество натуральных чисел 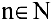
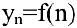
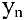
Число А называется пределом числовой последовательности 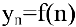
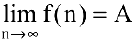
(Символ 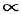
С понятием предела числовой последовательности тесно связано понятие предела функции на бесконечности, которое на языке логических символов имеет вид:
Замечание. Переменная 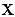
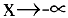
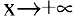
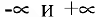
В общем случае если при стремлении 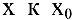
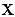
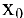
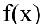
И наоборот, если при стремлении 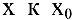
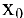
(При 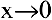
Если односторонние пределы различны или хотя бы один из них не существует, то не существует и предел функции в данной точке. Следовательно,
В следующем параграфе мы познакомимся с основными правилами вычисления пределов при х—»хо(ос).
Основные теоремы о пределах
Внимание! Если предел существует, то он единственный.
Теорема 1. Предел постоянной равен самой постоянной: 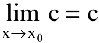
Теорема 2. Пусть 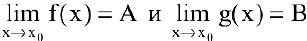
1) предел суммы конечного числа функций равен сумме пределов этих функций:
2) предел произведения конечного числа функций равен произведению пределов этих функций:
в частности, постоянный множитель можно выносить за знак предела:
3) предел частного двух функций равен частному пределов этих функций при условии, что предел делителя не равен нулю:
Возможно эта страница вам будет полезна:
Пример №2
Вычислить предел 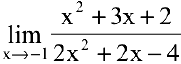
Решение:
Воспользовавшись теоремами о пределах частного, суммы и произведения, получим
Пример №3
Вычислить предел последовательности
Решение:
Теорему о пределе суммы конечного числа функций здесь применить нельзя. Заметим, что 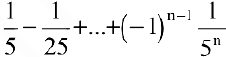
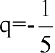
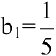
Тогда по теоремам о пределах функций имеем:
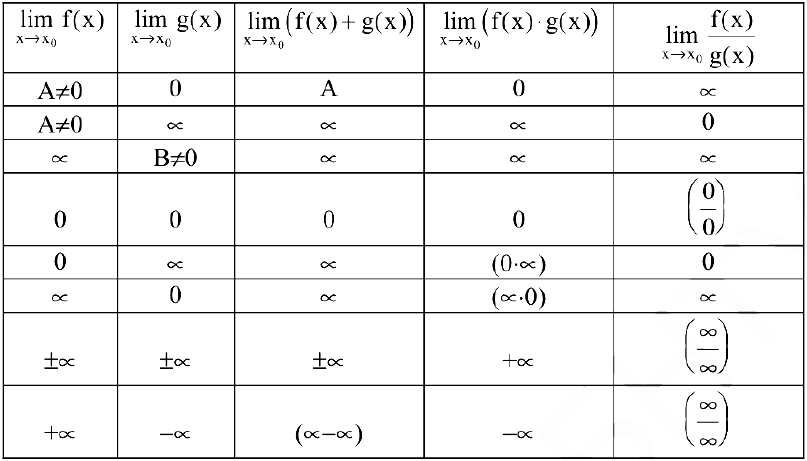
Рассмотрим соотношения пределов суммы, произведения, частного, распространенные на случай бесконечного предела функции.
Если вычисление пределов приводит к неопределенным выражениям вида 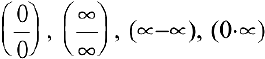
Раскрытие неопределенностей
Раскрытие неопределенностей вида 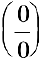
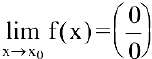
1. Если 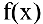
Пример №4
Вычислить предел
Решение:
Числитель и знаменатель дроби 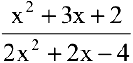
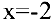
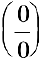
2. Если 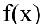
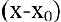
Пример №5
Вычислить предел 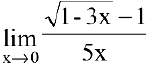
Решение:
Имеем неопределенность вида 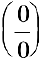
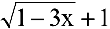
3. В остальных случаях для раскрытия неопределенности вида 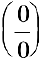
Раскрытие неопределенностей вида 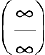
Если 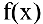
Пример №6
Вычислить предел 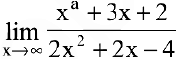
Решение:
Числитель и знаменатель дроби конечного предела не имеют. Имеем неопределенность вида 
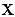
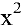
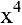
Вывод. Предел рациональной дроби на бесконечности равен отношению коэффициентов при старших степенях, если эти степени совпадают, нулю — если показатель степени числителя меньше показателя степени знаменателя и бесконечности в противном случае.
Замечание. Для раскрытия неопределенностей вида 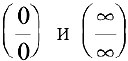
Раскрытие неопределенностей вида 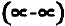
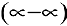
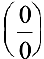

Пример №7
Вычислить предел 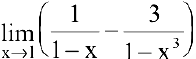
Решение:
Имеем неопределенность вида 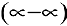
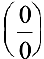
Пример №8
Вычислить предел последовательности
Решение:
Для раскрытия неопределенности вида 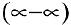
Получили неопределенность вида 
Раскрытие неопределенностей вида 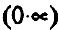
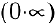
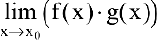
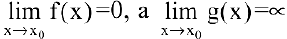
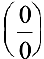

Замечание. При вычислении пределов показательно-степенных функций 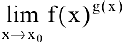
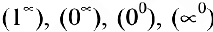
Замечательные пределы
Первый замечательный предел. Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице:
Следовательно,
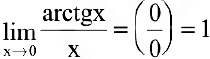
Возможно эта страница вам будет полезна:
Пример №9
Найти
Решение:
Применим первый замечательный предел:
Второй замечательный предел. Числом е называется предел функции 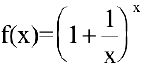
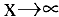
(Для запоминания: 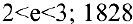
Задача о непрерывном начислении процентов. Первоначальный вклад в банк составил 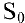
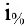
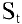
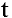
Решение:
Размер вклада будет увеличиваться ежегодно в 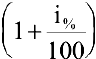
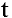
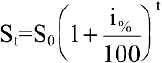
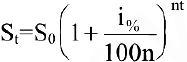
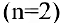
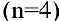
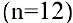
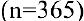
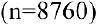
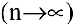
а за 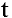
Пример №10
Найти 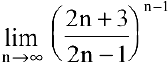
Решение:
Т.к. 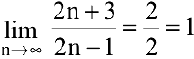
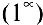
Пример №11
Найти 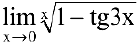
Решение:
Преобразуя выражение и используя непрерывность показательно-степенной функции, получим:
Бесконечно малые и бесконечно большие функции
Математическая интерпретация явления часто заключается в том, что практически очень малые величины принимаются за бесконечно малые. Так, рассматривая годовое производство, мы можем отдельный день представить себе как бесконечно малую частицу годового периода и получать при этом практически верные результаты.
Функция 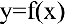
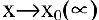
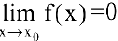
Функция 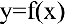
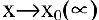
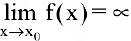
Между бесконечно малыми и бесконечно большими функциями существует связь: если 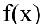
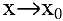
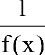
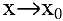
Теорема 1. Алгебраическая сумма и произведение конечного числа бесконечно малых функций при 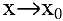
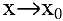
Теорема 2. Произведение бесконечно малой при 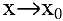
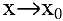
Возможно эта страница вам будет полезна:
Пример №12
Найти 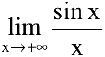
Решение:
Т.к. 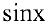
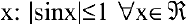

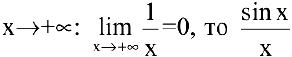
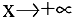
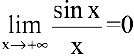
Если 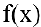
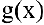
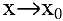
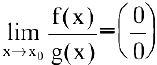
Если 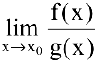
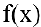
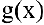
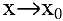
Если 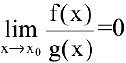
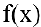
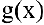
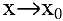
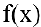
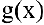
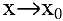
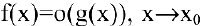
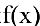
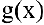
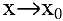
Если 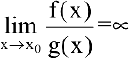
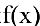
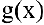
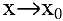
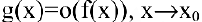
Если 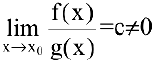
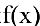
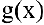
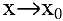
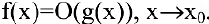
Особенно важен частный случай, когда 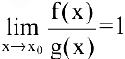
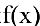
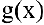
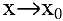
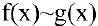
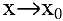
Пример №13
Показать, что 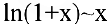
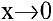
Решение:
Функции 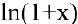
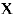
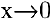
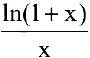
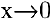
что и требовалось доказать.
Переход к пределу под символом логарифма возможен, т.к. логарифмическая функция непрерывна.
Утверждение. Если 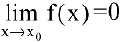
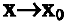
Данная цепочка эквивалентностей используется при нахождении пределов.
Теорема 3. Предел отношения двух бесконечно малых функций не изменится, если эти бесконечно малые заменить им эквивалентными.
Пример №14
Вычислить предел 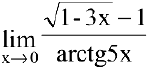
Решение:
Для нахождения предела используем свойства эквивалентности бесконечно малых функций:
Пример №15
Вычислить предел 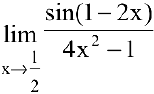
Решение:
Используя теорему об эквивалентных бесконечно малых, получаем:
Точки разрыва и их классификация
Непрерывность или разрыв функции может зависеть от конкретных условий, в которых рассматривается задача. Рассмотрим, например, численность населения земного шара как функцию времени. Она увеличивается на 1 в момент рождения каждого человека и уменьшается на 1 в момент смерти. Но рождения и смерти следуют друг за другом через бесконечно малые интервалы времени и изменение численности населения планеты на 1 настолько мало его меняет, что практически функцию можно рассматривать непрерывной. Но стоит перейти от численности населения земного шара к численности населения одной квартиры, как рождение или смерть отдельного ее жителя будут так заметно менять ее численность, что функцию нельзя будет рассматривать как непрерывную.
Если хотя бы одно из условий определения непрерывности функции в точке (см. п. 3.1) не выполнено, то в данной точке функция терпит разрыв. Различают три вида точек разрыва непрерывной функции.
1. Точка 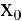
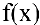
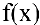
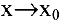
Чтобы устранить разрыв в точке 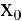
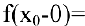
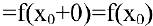
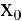
2. Точка Хо называется точкой разрыва первого рода функции 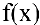
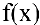
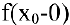
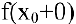
При этом величина 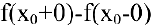
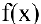
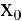
3. Если хотя бы один из односторонних пределов 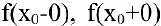
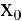
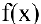
Пример №16
Исследовать функции на непрерывность. В случае устранимого разрыва доопределить функцию до непрерывной.
Решение:
1. Данная функция элементарная, т.к. получена с помощью конечного числа арифметических действий над основными элементарными функциями: экспоненциальной, постоянной и степенной. Следовательно, она непрерывна в области определения 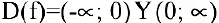
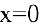
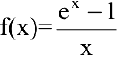
тo 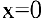
Если положить 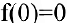
будет непрерывной для всех х.
2. Функция 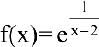
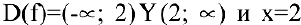
Так как один из односторонних пределов равен бесконечности, то 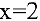
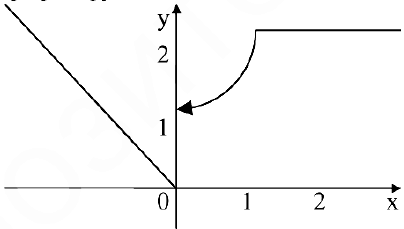
Пример №17
Исследовать функцию на непрерывность. Построить схематично график функции.
Решение:
Область определения этой функции — вся числовая прямая: 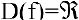
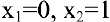
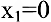
Так как 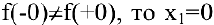
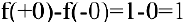
Исследуем точку 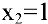
Поскольку 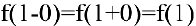
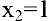
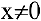
Построим график функции.
Дифференциальное исчисление
Производная функции, ее геометрический и физический смыслы
При изучении различных экономических процессов, описываемых функциями, существенную роль играют скорость роста процесса, ускорение роста, оптимальный режим и другие характеристики, которые исследуются с помощью производной.
Рассмотрим геометрическую задачу о проведении касательной к плоской кривой. Пусть на плоскости 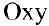
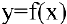
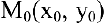
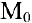
Касательной называется прямая, к которой стремится секущая при стремлении второй точки секущей к первой. Дадим аргументу 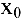
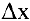
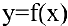
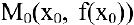
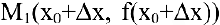
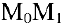
Тогда угловой коэффициент касательной
Это и есть производная функции 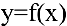
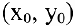
Производная функции имеет несколько обозначений:
Следовательно, уравнение касательной к кривой 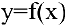
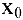
Нахождение мгновенной скорости прямолинейно движущейся точки. Пусть точка М движется прямолинейно и 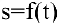
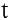
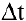
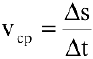
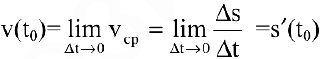
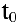
Если 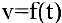
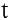
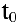
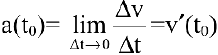
Вывод. Производная есть предел отношения приращения функции к бесконечно малому приращению аргумента.
Важно отметить, что запись 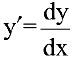
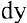
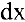
Дифференциалом функции одной переменной называется произведение ее производной на приращение аргумента: 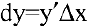
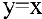
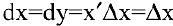
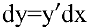
Нахождение для заданной функции ее производной называется дифференцированием данной функции. А учение о производной и ее приложениях является предметом дифференциального исчисления. Фундамент дифференциального исчисления составляют основные правила и формулы дифференцирования функций. Используя их, можно найти производную и дифференциал любой элементарной функции.
Основные правила дифференцирования
Внимание! Для существования производной в некоторой точке необходимо, чтобы функция была непрерывна в этой точке. Однако не всякая непрерывная в точке функция имеет в ней производную.
Теорема 1. Производная постоянной равна нулю: 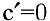
Теорема 2. Пусть 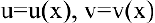
1) производная суммы конечного числа дифференцируемых функций равна сумме производных этих функций:
2) производная произведения конечного числа дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные:
в частности, постоянный множитель можно выносить за знак производной:
3) производная частного двух дифференцируемых функций может быть найдена по формуле:
Теорема 3. Производная сложной функции равна ее производной по промежуточному аргументу, умноженной на производную промежуточного аргумента.
Действительно, пусть задана сложная функция 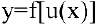
Теорема 4. Производная обратной функции есть величина, обратная производной прямой функции.
Так, если 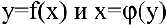
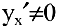
Таблица производных
Приведем основные формулы дифференцирования функций. Пусть 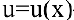
Выведем производные некоторых функций.
1. Если 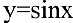
Используя формулу разности синусов
получим
Так как любую тригонометрическую функцию можно вывести через синус, то нетрудно найти производные остальных тригонометрических функций.
2. Пусть 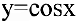
3. Для функции 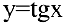
4. Представим 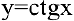
5. Вычислим производную 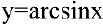
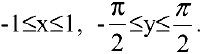
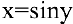
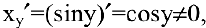
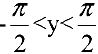
и при 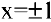
6. Производную 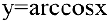
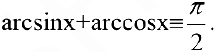
Предельный анализ в экономике
Задача о производительности труда. Пусть функция 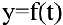
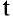
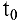
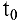
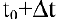
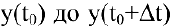
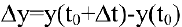
Средней производительностью труда называется отношение количества произведенной продукции к затраченному времени, т.е.
Производительность труда в момент времени 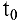
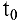
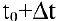
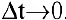
Возможно эта страница вам будет полезна:
Пример №18
Объем продукции хлебобулочных изделий, произведенных бригадой пекарей в течение смены, может быть описан функцией
где 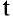
Решение:
Производительность труда выражается производной
В заданный момент времени соответственно имеем:
Задача о предельных издержках производства. Издержки производства у будем рассматривать как функцию количества выпускаемой продукции 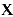
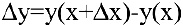
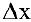
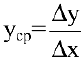
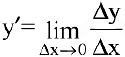
Аналогичным образом могут быть определены предельная выручка, предельный доход, предельная полезность и другие предельные величины.
Таким образом, производная выступает как скорость изменения некоторого экономического процесса во времени или относительно исследуемого фактора.
Для исследования экономических процессов часто используется понятие эластичности функции. Эластичностью функции 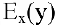
Эластичность дает приближенный процентный прирост функции при изменении независимой переменой на 1%. Например, эластичность спроса у относительно цены х показывает приближенно, на сколько процентов изменится спрос при изменении цены на 1%. Если эластичность спроса по абсолютной величине больше единицы 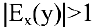
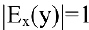
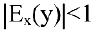
Пример №19
Опытным путем установлены функции спроса 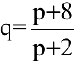
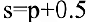
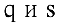
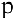
1) равновесную цену, при которой спрос и предложение совпадают;
2) эластичность спроса и предложения для этой цены;
3) изменение дохода при увеличении цены на 5% от равновесной.
Решение:
1) равновесная цепа определяется из условия 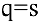
откуда 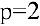
2) найдем эластичности спроса и предложения:
Для равновесной цены 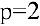
T.к. полученные значения эластичности по абсолютной величине меньше 1, то спрос и предложение данного товара при рыночной цене неэластичны относительно цены. Это означает, что изменение цены не приведет к резкому изменению спроса и предложения. А именно, при увеличении цены на 1% спрос уменьшится на 0.3%, предложение увеличится на 0.8%.
3) при увеличении цены на 5% относительно равновесной спрос уменьшится па (5-0.3)%= 1.5%, и, следовательно, доход возрастет па 3.5%.
Пример №20
Зависимость между издержками производства у и объемом выпускаемой продукции 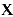
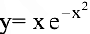
1) определить средние и предельные издержки при объеме продукции 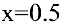
2) найти эластичность издержек при выпуске продукции, равном 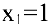
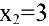
Решение:
1) функция средних издержек (на единицу продукции) выражается отношением
При 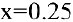
Функция предельных издержек выражается производной
При 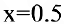
что вдвое меньше средних издержек.
2) эластичность издержек у относительно объема выпускаемой продукции х рассчитывается по формуле:
При 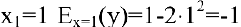
При 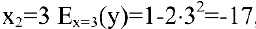
Уравнение нормали к плоской кривой
Нормалью называется прямая, проходящая через точку касания перпендикулярно касательной. Если касательная в точке 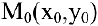
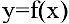
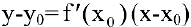
Таким образом, при 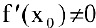
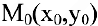
Если же 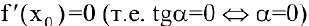
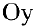
Задача. Показать, что для гиперболы 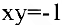
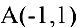
Решение:
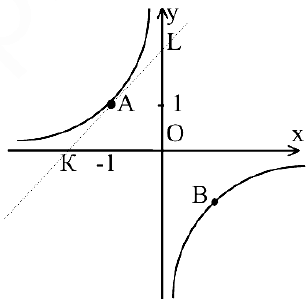
В общем курсе аналитической геометрии давалось каноническое уравнение гиперболы. «Школьная» гипербола 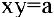
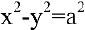
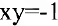
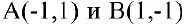
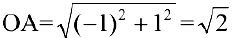
Составим уравнение касательной к гиперболе 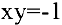
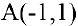
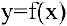
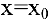
В нашем случае
Искомое уравнение касательной имеет вид:
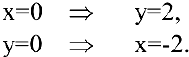
Найдем точки пересечения касательной с осями координат:
Тогда треугольник, образованный координатными осями и касательной, будет иметь вершины 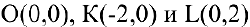
2=2. Задача решена.
Производные высших порядков
До сих пор мы рассматривали производную 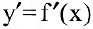
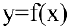
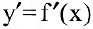
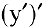
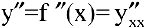
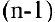
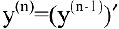
Ранее было установлено, что если точка движется прямолинейно по закону 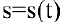
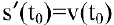
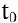
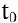
В этом состоит механический смысл второй производной.
Задача. Известно, что траекторией брошенного камня является парабола. Найти его скорость и ускорение.
Решение:
Запишем уравнение траектории брошенного камня 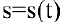
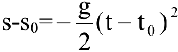
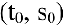
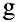
Тогда 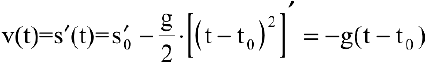
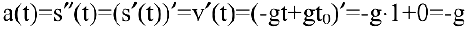
Производная неявной функции
Выше было рассмотрено дифференцирование явных функций, заданных формулой 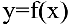
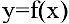
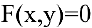
Внимание! Не всякое уравнение 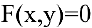
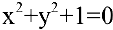
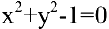
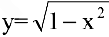
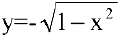
Часто разрешить уравнение 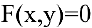
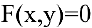
Для нахождения производной функции 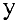
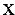
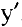
Пример №21
Покажите, что функция 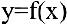
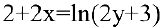
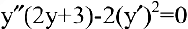
Решение:
Найдем первую производную данной функции. Для этого продифференцируем обе части уравнения 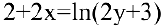
Найдем вторую производную:
Подставим найденные выражения в дифференциальное уравнение:
Правило Лопиталя
С помощью производной можно находить многие пределы. Следующее утверждение позволит свести предел отношения двух функций с случае неопределенностей вида 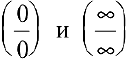
Правило Лопиталя. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если этот предел существует:
Внимание! В правой части формул берется отношение производных, а не производная отношения.
Пример №22
Вычислить предел
Решение:
Имеем неопределенность вида 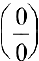
Замечание Правило Лопиталя можно применять повторно, если вновь приходим к соотношению неопределенностей вида 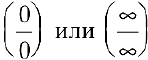
Пример №23
Вычислить предел
Решение:
Числитель и знаменатель дроби непрерывны, дифференцируемы и стремятся к бесконечности. Следовательно, можно применить правило Лопиталя (в данном примере мы воспользовались им дважды):
Замечание. Другие неопределенности раскрываются по правилу Лопиталя, если их предварительно свести к основному виду 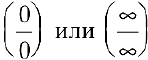
Пример №24
Найти 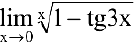
Решение:
Преобразуя выражение и используя непрерывность показательной функции, получим:
Оптимизация
В этом параграфе оптимизацию будем понимать как процесс нахождения экстремума (максимума или минимума) экономических функций, т.е. выбор наилучшего варианта из множества возможных. Говорят, что в точке 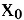
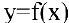
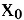
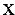
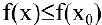
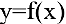
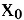
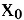
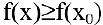
Внимание! Не следует путать понятие локального экстремума функции с ее наибольшим или наименьшим значением (так называемым глобальным максимумом или минимумом). На одном промежутке функция может иметь несколько экстремумов, причем минимум может оказаться больше максимума подобно тому, как впадина в горах может иметь большую отметку над уровнем моря, чем невысокая вершина. А наибольшее и наименьшее значение непрерывной на отрезке функции может достигаться как в точках экстремума, так и на концах отрезка.
Геометрически в точке экстремума касательная к графику функции либо горизонтальна, либо не существует.
Следовательно, непрерывная функция может иметь экстремум лишь в тех точках, где производная функции равна пулю или не существует (необходимое условие экстремума). Точки, в которых выполнено необходимое условие экстремума, называются критическими. (Иногда точки, в которых производная обращается в нуль, называют стационарными.)
Замечание. Критическая точка не обязательно является точкой экстремума. Это лишь точка возможного экстремума функции.
Достаточное условие экстремума. Если в критической точке вторая производная положительна, то это точка минимума, а если отрицательна — точка максимума.
Для запоминания этой теоремы предлагаем мнемоническое правило: если плюс — котелок наполняется, если минус — опустошается.
Пример №25
Пусть в краткосрочном плане производственная функция зависит только от численности персонала и имеет вид
где у — выпуск продукции, а n — число работающих. Определить численность персонала, при которой выпуск у достигает максимального значения.
Решение:
Выпуск продукции 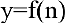
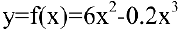
Решая квадратное уравнение, легко находим 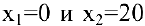
При 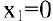
следовательно, в данной точке имеется минимум. Это естественно, т.к. нет выпуска продукции, если нет рабочих. Для второй точки
Поэтому в точке 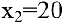
Исследование функции на монотонность
С помощью производной можно найти промежутки возрастания и убывания функции. Функция 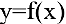
Возрастающие и убывающие функции называются монотонными.
Достаточное условие монотонности. Если производная дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка X, то она возрастает (убывает) на этом промежутке:
Таким образом, если при переходе через критическую точку производная дифференцируемой функции меняет знак с плюса на минус, то это точка (локального) максимума, а если с минуса на плюс — точка (локального) минимума (достаточное условие экстремума):
Если изменение знака производной не происходит, то экстремума нет.
Пример №26
Исследовать функцию 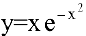
Решение:
Область определения функции 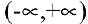
Эти точки разбивают область определения функции на интервалы монотонности. Результаты исследования удобно представить в таблице.
Итак, функция убывает на интервалах 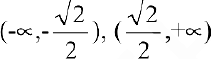
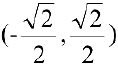
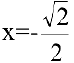
а 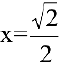
Выпуклость и вогнутость графика функции. Точки перегиба
График дифференцируемой функции 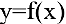
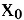
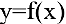
Достаточное условие направления выпуклости. Если вторая производная дважды дифференцируемой функции отрицательна [положительна) внутри некоторого промежутка, то функция выпукла (вогнута) на этом промежутке:
Следовательно, если вторая производная дважды дифференцируемой функции при переходе через некоторую точку меняет знак, то это точка перегиба (достаточное условие перегиба):
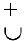
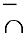
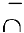
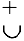
Отсюда вытекает необходимое условие перегиба: вторая производная дважды дифференцируемой функции в точке перегиба равна нулю или не существует.
Замечание. Если критическая точка дифференцируемой функции не является точкой экстремума, то это точка перегиба.
Пример №27
Исследовать функцию 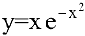
Решение:
Область определения функции 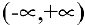
Эти точки разбивают область определения функции на интервалы, в которых сохраняется направление выпуклости или вогнутости. Результаты удобно представить в таблице.
Кривая, изображающая график функции, выпукла на интервалах 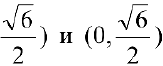
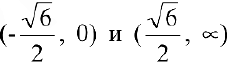
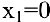
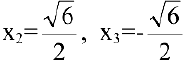
Асимптоты графика функции
При исследовании поведения функции на бесконечности или вблизи точек разрыва часто оказывается, что расстояние между точками графика функции и точками некоторой прямой стремится к нулю при неограниченном удалении точек графика от начала координат. Прямая, к которой стремится кривая в бесконечно удаленной точке, называется асимптотой графика. Различают вертикальные и наклонные асимптоты. Прямая 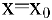
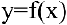
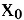
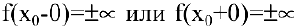
Внимание! Непрерывные на множестве действительных чисел функции вертикальных асимптот на имеют.
Для того чтобы график функции 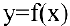
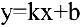
Частным случаем наклонной асимптоты 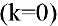
Пример №28
Найти асимптоты графика функции 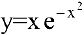
Решение:
Функция 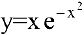
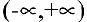
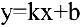
Получаем горизонтальную асимптоту 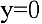
Кстати теория из учебников по математическому анализу тут.
Общее исследование функции и построение графика
С помощью производной функции можно провести ее полное исследование и построить график этой функции. При этом рекомендуется использовать следующую схему.
- Найти область определения функции
- Исследовать функцию на четность
; нечетность
; периодичность
.
- Исследовать функцию на непрерывность, найти точки разрыва.
- Найти асимптоты графика функции.
- Исследовать функцию на монотонность, найти точки экстремума.
- Найти интервалы выпуклости и вогнутости, точки перегиба функции.
- Используя результаты проведенного исследования, построить график функции (можно вычислить координаты точек пересечения с осями координат).
Пример №29
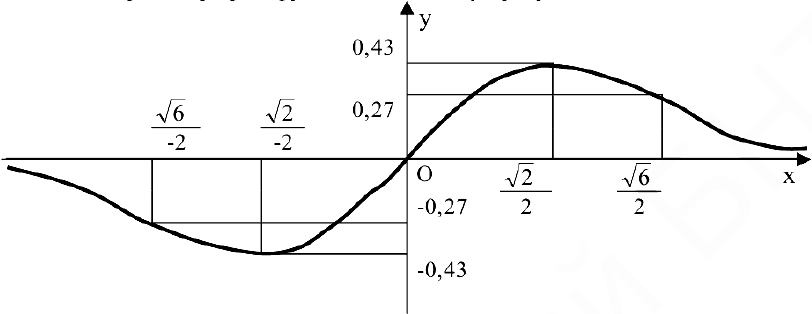
Провести полное исследование функции 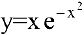
Решение:
- Область определения функции — вся числовая прямая:
.
- Функция непериодическая. Она нечетная, т.к. область определения симметрична относительно начала координат и
:
Следовательно, график функции симметричен относительно начала координат и достаточно исследовать функцию для 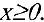
3. Функция непрерывна в области определения как композиция основных элементарных функций. Поскольку 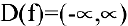
4. Строим график функции, используя результаты исследования.
Как быстро подготовиться к экзамену или зачёту?
Итак, вы оказались в ситуации нормального студента, когда до часа «икс» остаётся 1-2 дня, а подготовка по предмету оставляет желать лучшего. Что делать? Сегодня я сыграю роль антикризисного менеджера Уинстона Вульфа, и поскольку времени у нас мало, то мы сразу приступаем.
Вопрос первый: идти ли на зачёт / экзамен в «аховой» ситуации? Конечно. Даже если вы побывали на единственном занятии по предмету, остаётся небольшой шанс сдать его «на шару». Или может быть, вас «простят». На первом курсе, на первый раз.
Второе: не паникуем, и настраиваемся на спокойную методичную работу. И сутки и половина суток – вполне достаточное время на обнадёживающую подготовку. Главное, методика. Она простая, чёткая и подходит для большинства предметов, как «технических», так и гуманитарных.
Существуют различные формы зачётов и экзаменов, среди которых можно выделить следующие:
Письменная контрольная работа в аудитории
Такая форма отчётности распространена у студентов-заочников, которым предлагается билет с несколькими практическими заданиями (обычно 4-6 штук). Тут всё просто. Берём листок бумаги и пишем задачи, которые ожидаются, например, на экзамене по высшей математике:
1) Решить задачу по аналитической геометрии;
2) Выполнить действия с матрицами;
3) Решить систему линейных уравнений по формулам Крамера;
4) Вычислить предел;
5) Найти производную;
6) Исследовать функцию и построить её график.
Пункт №6 сразу получает низший приоритет – это слишком длинное задание, в котором нужно знать и уметь много чего. Пункт №1 из той же оперы: различных задач по АнГему много, и освоить всю программу (если у вас было 2,5 занятия) – нереально.
Итак, всё длинное, сложное, «ресурсоёмкое» помещаем в конец очереди.
Это вообще фундаментальное правило.
Теперь приступаем к изучению тех тем, которые осваиваются быстрее всего. Это Пункты №№3, 2, 5, и чуть больше времени уйдёт на Пункт №4. Но здесь есть ещё такой момент: некоторые задания могут оказаться трудными ЛИЧНО ДЛЯ ВАС. Так, например, некоторым проще даются пределы, а некоторым производные. В этом случае следует понизить приоритет «проблемной» темы. Попросту говоря,
если начинается какой-то «затык», то спокойно пропускаем задачу и переходим к следующей
В условиях ограниченного времени это непреложное тактическое правило!
Если осталось время, смотрим на задания №1 и 6, но, повторюсь, качественно их освоить нереально. Помочь здесь может время (которого нет) или предэкзаменационные занятия, где преподаватель разбирал какие-то конкретные геометрические задачи. В этом случае есть смысл уделить время именно этому типу задач.
Кто хочет быстро подготовиться по озвученным темам может воспользоваться вышеприведёнными ссылками, ну а мы продолжаем:
«Классический» экзамен с билетами
Билет такого экзамена, как правило, включает в себя первое второе и компот два теоретических вопроса и практическое задание.
Как у вас дела с практикой по предмету? Если плохо, то это плохо; в различных статьях я неоднократно подчёркивал, что практические задания – это мощная «линия обороны», которая может здОрово выручить, если вы отчаянно «плаваете» в теории. Впрочем, тут уже нет времени что-либо изменить, и поэтому мы начинаем предварительный просмотр теоретических вопросов, пусть их будет 50 штук. Но просматривать мы их будем не просто так – берём лист бумаги, расчерчиваем его на три колонки и пишем заголовки: «лёгкие вопросы», «средние», «плохие». Сделайте это прямо сейчас! Есть? Отлично!
Каждый вопрос изучается по следующей схеме:
Сначала выделяем центральное понятие, читаем его определение и сами себе отвечаем на вопрос: что это такое? Или кто. Пусть это будет, например, кошка. Ваша задача состоит в том, чтобы ПОНЯТЬ: кто такая кошка? И ни в коем случае не нужно пытаться что-то запомнить – здесь важно ОСОЗНАТЬ существенные признаки, которые однозначно определяют именно кошку. Ну вот, кстати, первое предложение из указанной по ссылке Вики-статьи мне сразу не нравится (на момент просмотра мной этой статьи):
«Кошка, или домашняя кошка (лат. Félis silvéstris cátus) – домашнее животное…» – во-первых, кошки бывают не только домашними, и, во-вторых, не все домашние животные – кошки.
Прежде всего, здесь следует сказать:
Кошка – это млекопитающее семейства кошачьих отряда хищных (отвечаем на вопрос КТО это такая?) и только потом говорим о том, что, как правило, это животное-«компаньон» человека.
Далее пробуем осознанно воспроизвести определение вслух. Ничего страшного, если получится неточно и «своими словами». Даже если на экзамене вы только и вспомните, что «Кошка – это животное, у которого есть усы и хвост», то преподаватель начнёт «вытягивать» из вас определение наводящими вопросами: к какому классу, семейству, отряду относится это животное.
Кстати, классу млекопитающих, семейству кошачьих и отряду хищных, скорее всего, посвящены 3 других теоретических вопроса. Вот почему очень важно просмотреть ВСЕ вопросы и разобраться в их ключевых понятиях. А ещё потому, что незнание ключевых понятий курса просто «выбешивает» преподавателей, и во многих случаях это автоматический «неуд».
После того, как мы разобрались с понятием Кошки, бегло просматриваем основные кошачьи особенности, классификации, теоремы и другие важные вещи.
Следует отметить, что в точных науках это сделать сложнее – по той причине, что здесь меньше «пространства для манёвра», а стало быть, определения, теоремы придётся ОСОЗНАВАТЬ точнее 
На всё про всё тратим около 5 минут и записываем название вопроса в наш контрольный листок, например, в колонку «Лёгкие вопросы», после чего переходим к изучению следующего вопроса.
Уже через несколько часов вы будете что-то знать по каждому вопросу экзамена!
И это ценно ещё тем, что на экзамене, скорее всего, зададут дополнительные устные вопросы, чтобы посмотреть, насколько хорошо вы ориентируетесь в теме.
И ещё раз подчёркиваю – никакой «зубрёжки»! А в точных науках это вообще величайший грех, и у студента, который хотя бы пытается что-то сообразить, сформулировать, вывести – гораздо больше шансов, чем у того, кто идеально, но бездумно вызубрил все лекции.
Итак, пусть в результате предварительного анализа у нас получилось 10 лёгких, 25 обычных и 15 сложных вопросов.
На следующем этапе
начинаем прорабатывать эти вопросы детальнее. Но опять же не просто так: для каждого вопроса, а ещё лучше билета с 2 вопросами составляем на отдельном листке конспект-«крокодил», в который записываем и снова осознаём основные определения и пункты того или иного вопроса. Причём, если вам что-то не понятно по «гуманитарной части», то это лучше пропустить – это лучше, чем бездумно «ляпнуть» об экзистенциализме кошачьего бытия, после чего вас «уложат на лопатки» (помним, что непонимание – грех!). Но вот в точных науках непонятные вещи в конспект включаем – есть шанс, что разберётесь в них (хотя бы частично) прямо на экзамене.
С каких билетов начать? Конечно с лёгких, которые содержат лёгкие и «средние» вопросы. Если времени совсем в обрез, то готовим «легчайшие» билеты, тут уж сколько успеете. С «плохими» билетами возиться вообще нет смысла, их бегло и в общих чертах просмОтрите перед экзаменом
Особая ценность такой подготовки состоит в том, что она выполняется собственноручно. Не нужно недооценивать механическую память – многое запомнится! И быстро вспомнится, если вам удастся хотя бы на пару минут заглянуть в заготовленный «крокодил».
Кстати, по этой причине крайне не рекомендую делать шпаргалки в Вёрде, что-то записывать на диктофон или использовать другие достижения прогресса. Только собственная голова, собственные руки и собственные ноги – чтобы смочь уйти на них с экзамена =)
Ещё одна популярная форма зачёта или экзамена – это
Тест
Для подготовки к тестированию можно использовать ту же самую схему, но тут следует учесть особенности вашего теста: будут ли там практические задания, насколько детально требуется знание тех или иных вопросов. Не знаю, как сейчас, но раньше в различных «егэ» было много вопросов наподобие «Любил ли Онегин Татьяну?». Ну что ж поделать, коль скоро так, то придётся прочитать о том, с какой ноги любил вставать Пушкин. Как говорится, тест не выбирают – тест сдают 
Возможно, у вас возник вопрос: откуда я всё это взял, и почему к экзаменам нужно готовиться именно так? Данная методика была найдена опытным путём, и успешно применялось мной в далёкие студенческие годы, и чтобы не быть голословным, вот некоторые, особо запомнившиеся результаты:
1) Курс педагогической психологии, слушал «в пол-уха» весь семестр. Двадцать вопросов к зачёту удалось «поднять» за день, примерно за 12 часов, с короткими перерывами. И я не только не сдал на следующий день зачёт, но и ответил на все дополнительные вопросы. Удивился, кстати, как хорошо всё запомнилось.
2) Экзамен по математической логике, около 30 билетов. Так получилось, что пропустил почти все лекции, но хорошо, что с практикой всё хорошо. Тут пришлось тяжелее, готовился 2,5 дня, но преподаватель, естественно, «вынул душу» по полной. Спасло как раз то, что ориентировался в основных понятиях и теоремах всех теоретических вопросов и смог решить дополнительную практическую задачу. Заслуженная «тройка» – как же я был ей рад! Особенно после того, как несколько отвечавших передо мной однокурсниц ушли с «неудом».
Эта «линия обороны по всем вопросам » не раз выручала меня и на других экзаменах, не случайно я уделил ей значительную часть данной статьи.
Ну а тесты для меня были ерундой – по той причине, что важнейшим пунктом подготовки был предварительный поиск правильных ответов 
Надеюсь, изложенные советы не утратили актуальность и сегодня, но возможно у вас есть какой-то свой опыт и какие-то свои интересные фишки для эффективной подготовки к зачётам и экзаменам – пишите в комментариях!
Вторая часть «антикризисного курса» посвящена тому, как правильно сдавать экзамен, то есть, тактике непосредственного «боя»
Автор: Александр Емелин
Знание – сила >>> (к списку статей блога)
Загрузить PDF
Загрузить PDF
Когда изучаешь математику, очень важна практика, именно поэтому учителя часто дают на дом так много сложных заданий! Многие при изучении математики стараются просто запомнить формулы и уравнения, как это делают, например, с историческими фактами и датами. Хотя знание формул и важно, лучше все же научиться ими пользоваться. Не затягивайте изучение материала до последнего, регулярно делайте домашние задания и, когда возникают затруднения, советуйтесь с учителем. Не занимайтесь зубрежкой, выполняйте все вовремя и не забудьте выспаться и нормально поесть перед экзаменом.
-
1
Просматривайте свой конспект. После уроков 15–20 минут посвящайте изучению записей, которые вы делали в классе. С приближением экзамена более внимательно перечитайте соответствующие разделы конспекта. Обращайте особое внимание на приведенные учителем примеры, поскольку в них поясняется, как использовать ту или иную формулу. Если вы не вели собственных записей, попросите конспект у одноклассника.[1]
-
2
Решайте задачи, похожие на те, которые встречались в домашних заданиях. Предположим, вам задали задачи с нечетными номерами, поскольку ответы на задачи с четными номерами приведены в конце учебника. Решите и задачи с четными номерами, а затем сверьтесь с правильными ответами, чтобы проверить, насколько вы усвоили пройденный материал.[2]
- Поинтересуйтесь у учителя, нет ли подходящих учебников в интернете. Иногда такие учебники имеют дополнительные задачи и более подробные объяснения.
-
3
Учитесь в группе. Каждый воспринимает ту или иную идею по-своему. То, что вам дается с трудом, может легко даваться однокласснику. Если же с затруднениями столкнулась вся группа, попросите о помощи учителя.[3]
- Можно собираться 1–2 раза в неделю, обсуждать учебу по телефону или через интернет.
-
4
Попросите кого-нибудь ставить вам задачи. Если вы изучаете математику в группе, то можно придумывать друг для друга практические задачи. Попросите кого-нибудь из родственников или вашей группы составить вам компанию в решении задач. Если у учебника есть собственный веб-сайт, проверьте, нет ли там примерных экзаменационных заданий.[4]
- При решении задач ограничивайте себя по времени, чтобы создать условия, напоминающие реальный экзамен.
-
5
Поощряйте себя за старательную учебу. После нескольких часов интенсивного труда можно немного отдохнуть! Придумайте, как вознаградить себя за упорную учебу, чтобы поддержать высокую мотивацию.[5]
- Например, можно съесть вкусный батончик, покататься на велосипеде, поиграть 20 минут в какую-нибудь игру или заняться чем-то еще, что позволит вам расслабиться и отдохнуть.
-
6
Перед экзаменом как следует выспитесь и поешьте. Постарайтесь снизить уровень стресса перед экзаменом. Накануне экзамена хорошенько выспитесь. После этого плотно позавтракайте, а если экзамен назначен на вторую половину дня, то как следует пообедайте.[6]
- Перекусите перед экзаменом легкой здоровой пищей, например миндалем. Это обеспечит ваш мозг дополнительной энергией.
Реклама
-
1
Не пропускайте учебу. Для хорошей успеваемости необходимо регулярно посещать занятия.
-
2
Будьте внимательны. Нужно не только не пропускать занятия, но и быть внимательным и не отвлекаться на уроках. Следите за тем, как учитель разбирает примеры на доске, — поскольку в математике работают с уравнениями и формулами, то, как вы усвоите материал, часто больше зависит от визуальной составляющей, чем в других предметах.[7]
- Ведите хороший конспект. Записывайте все рассматриваемые в классе примеры и задачи. Когда вы позже будете просматривать конспект, то сможете вспомнить, о чем шла речь на уроке, и лучше усвоите материал.
-
3
Если у вас возникли какие-либо вопросы перед экзаменом, задайте их учителю. Возможно, он не сообщит вам точно, что именно будет на экзамене, но он сможет дать полезные советы и рекомендации. Кроме того, вопросы насчет непонятого материала покажут учителю, что вы стараетесь получить хорошую оценку.[8]
- Каждый вечер после занятий просматривайте свои записи. Подчеркивайте неясные моменты, чтобы затем задать учителю соответствующие вопросы.
-
4
Читайте учебники. Не забывайте не только рассматривать примеры и выполнять задания, но и читать учебный материал. В учебниках часто приводятся доказательства и вывод формул, что позволяет лучше и полнее понимать соответствующую тему. Кроме того, предварительное чтение помогает подготовиться к занятию и лучше усвоить материал.[9]
- Будьте активны на занятиях, поднимайте руку и отвечайте на задаваемые вопросы — это позволит лучше усвоить материал и получить более высокую оценку.
Реклама
-
1
Начните готовиться как можно раньше. Приступите к подготовке к экзамену сразу же, как только начнется соответствующий курс. Каждый вечер после занятий просматривайте свои записи. Зубрежка в ночь перед экзаменом не приведет ни к чему хорошему.[10]
- Постепенное изучение материала позволит вам лучше усвоить его. Кроме того, вы сможете вовремя выявить свои слабые места и при необходимости получить дополнительную помощь.
-
2
Выполняйте домашние задания. Как правило, учитель задает на дом наиболее показательные и полезные примеры. Экзаменационные задачи часто напоминают домашние задания, поэтому, если вы будете их регулярно выполнять, это поможет вам подготовиться к экзамену.[11]
- Если в конце учебника приведены ответы, не подглядывайте раньше времени, а используйте их лишь для того, чтобы проверить правильность своего решения. Смотрите в ответы лишь после того, как решите задачи!
- Подробно записывайте решение и сохраняйте выполненные домашние задания. Используйте их затем при подготовке к экзамену. Ни в коем случае не переписывайте выполненное домашнее задание у кого-то другого.
-
3
Разбирайтесь, как работает та или иная формула. Полезнее понимать, как выводится формула, чем просто запомнить ее. Да, сначала формулу нужно запомнить, но потом необходимо понять, как она работает, решая практические задачи — так вы наверняка сдадите экзамен на отлично![12]
- Например, можно просто запомнить, что сумма внутренних углов треугольника равна 180 градусам. Однако, если вы действительно разберетесь в данном вопросе, то сможете решать и другие задачи, например находить неизвестный угол шестиугольника.
Реклама
Советы
- Время экзамена ограничено, поэтому начните с решения простых задач и лишь затем приступайте к более сложным.
- Если вы боитесь, что можете забыть ту или иную формулу, в начале экзамена запишите наиболее важные формулы на чистом листе бумаги.
- Не тратьте время на исправление ошибок. Для экономии времени просто перечеркните то место, которое нет надобности читать учителю.[13]
Хотя, конечно, каждый привык исправлять ошибки по-своему. - Выполните сначала те задания, за которые дают наибольшее количество баллов.
- Прежде всего старайтесь сохранить спокойствие — не нервничайте и не переживайте. Всегда проверяйте, правильно ли вы решили задачи.
- Не нагружайте себя учебой за день до экзамена, так как это вызовет дополнительный стресс. Просто просмотрите важные формулы и вопросы.
- Математика может казаться тяжелой наукой, но если вы будете внимательны на уроках и проявите упорство, то наверняка достигнете успеха. Наберитесь терпения и не старайтесь выучить все сразу же.
- Ежедневно практикуйтесь в решении задач.
- Не паникуйте перед экзаменом. Чтобы успокоиться, сделайте несколько глубоких вдохов и выдохов и скажите себе: “Я успешно сдам экзамен и получу высокую оценку”. Старайтесь мыслить позитивно во время экзамена.
Реклама
Об этой статье
Эту страницу просматривали 38 829 раз.



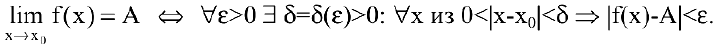
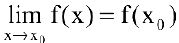
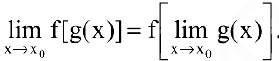
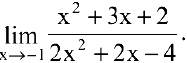
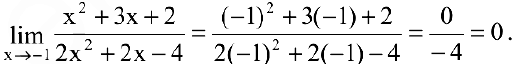
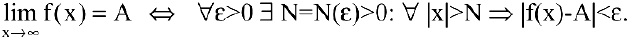
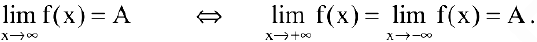
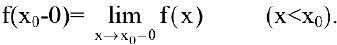
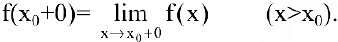
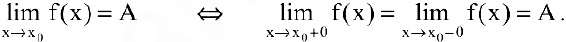
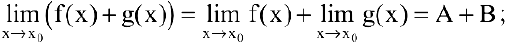
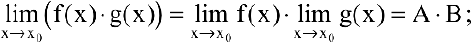
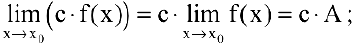
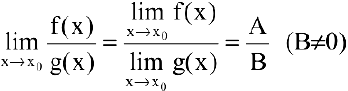
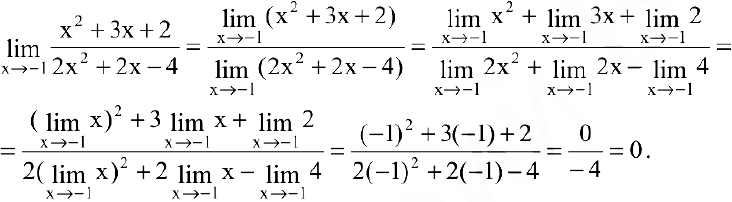
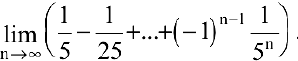
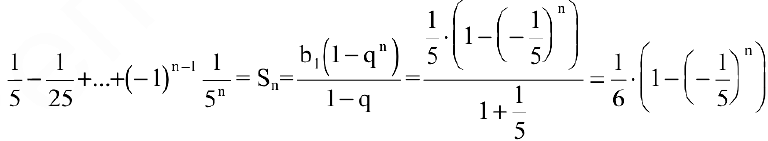
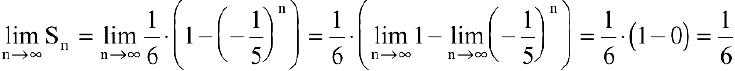
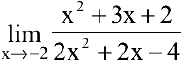
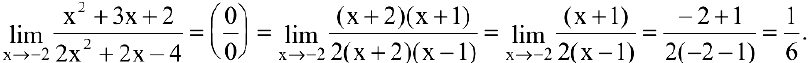
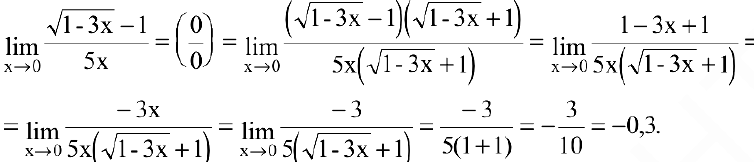
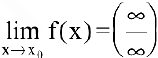
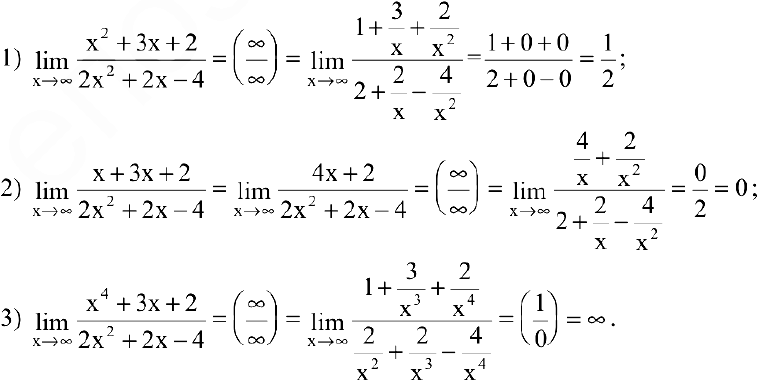
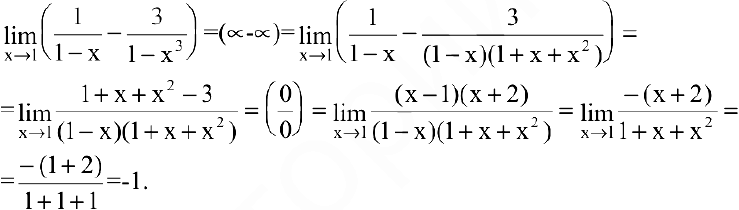
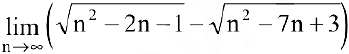
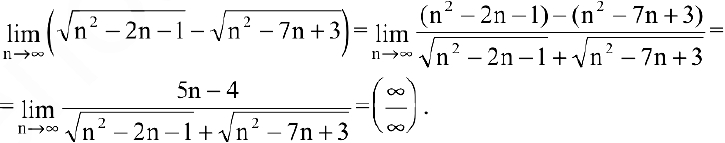
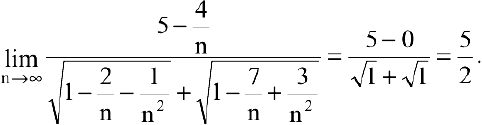
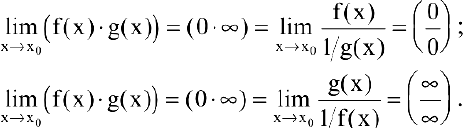
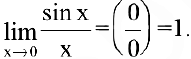
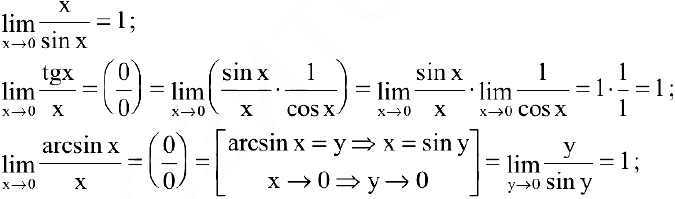
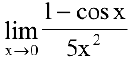
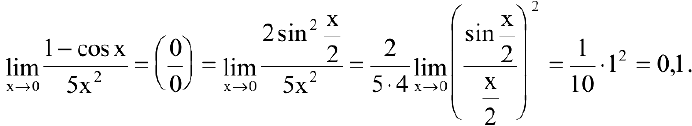
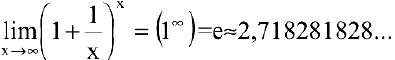
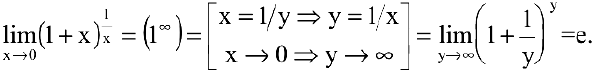
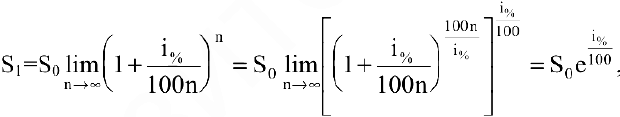
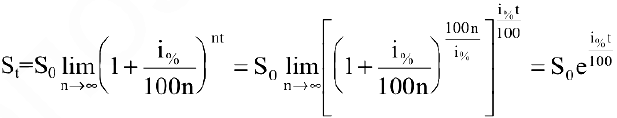
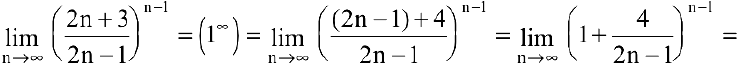
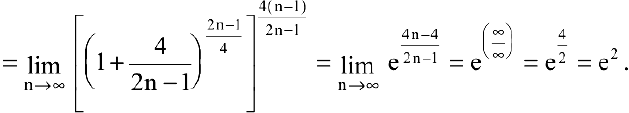
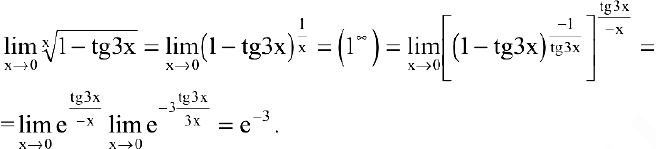
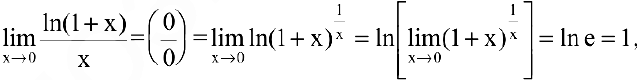
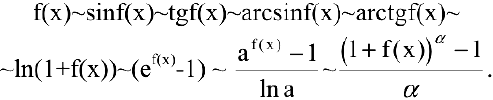
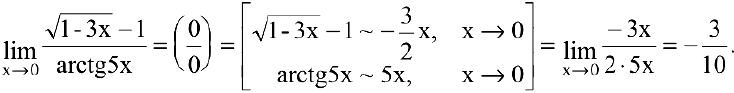
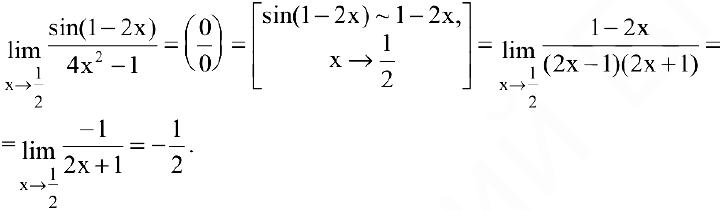
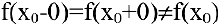
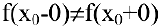
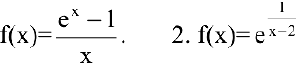
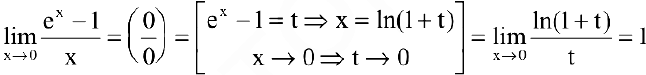
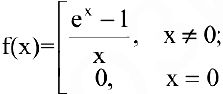
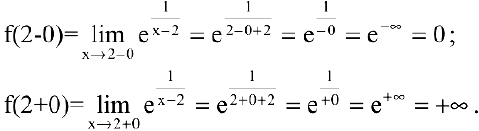
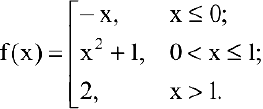
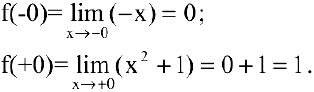
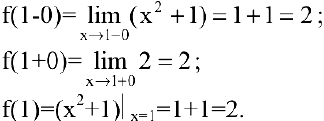
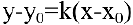
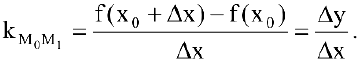
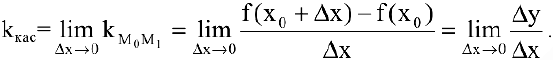
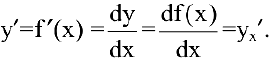
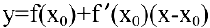
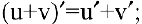
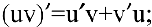
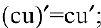
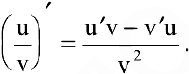
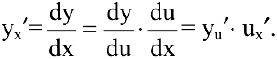
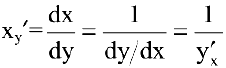

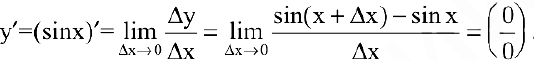
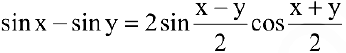
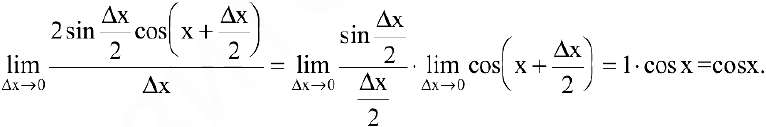
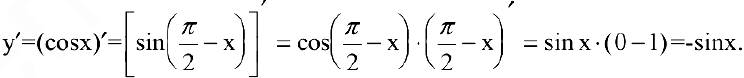
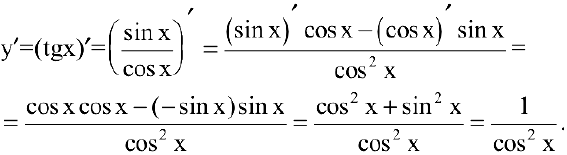
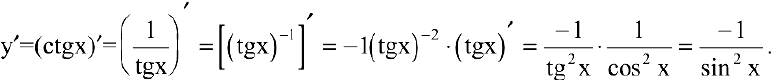
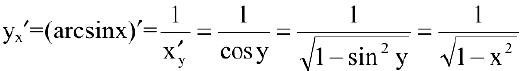
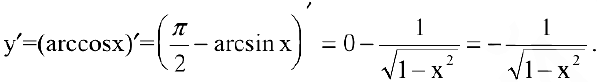
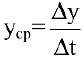
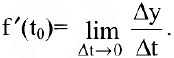
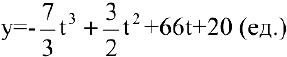
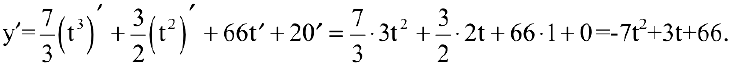
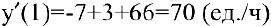
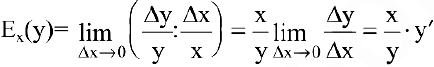
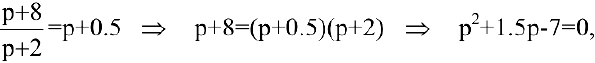
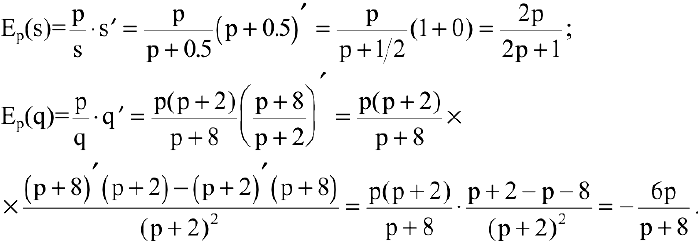
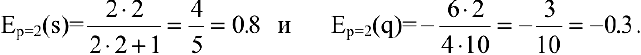
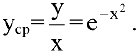
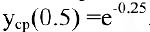
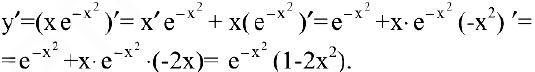
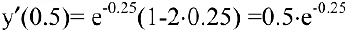
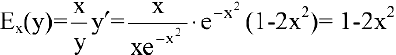
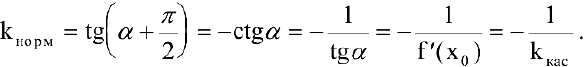
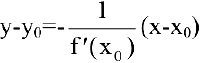
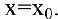
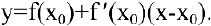
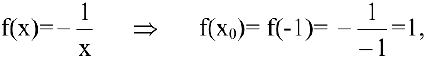
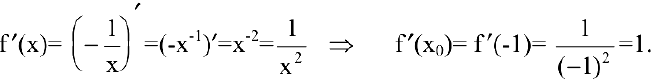

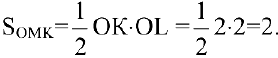
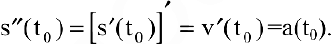
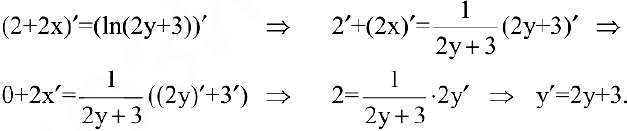
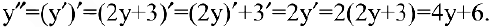
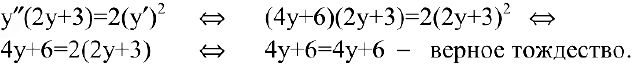
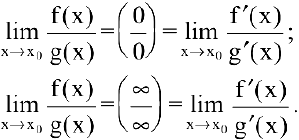
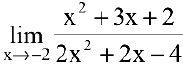
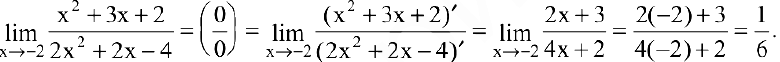
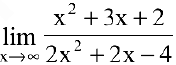
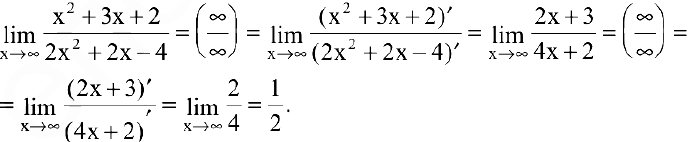
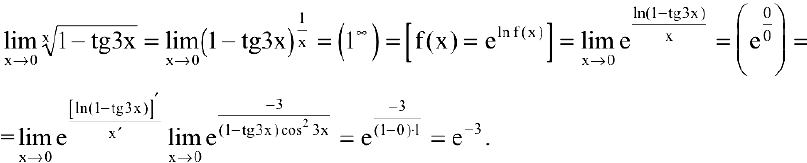
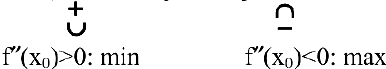
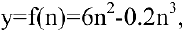
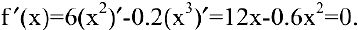
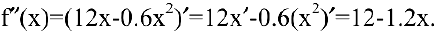
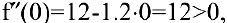
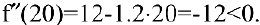
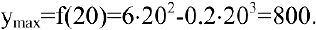
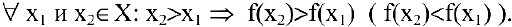
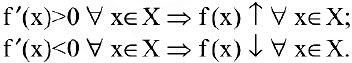
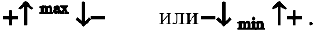
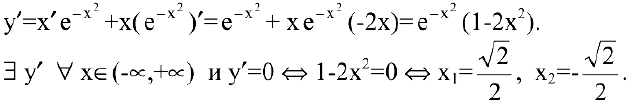

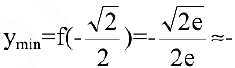
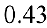
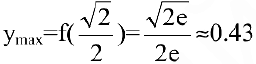
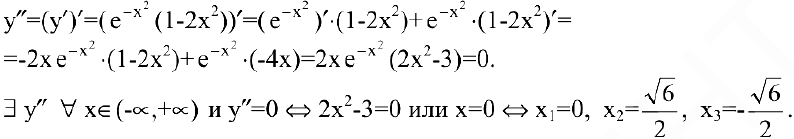

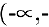
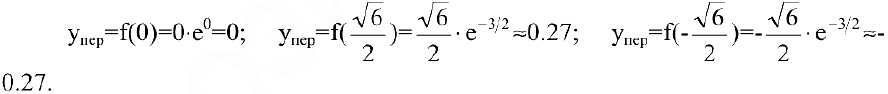
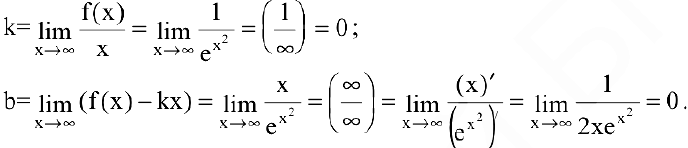
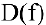
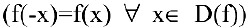 ; нечетность
; нечетность 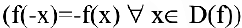 ; периодичность
; периодичность 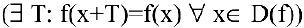 .
.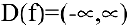 .
.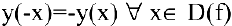 :
: