Как подготовиться к устному экзамену по геометрии 7 класс

Источники

2. Доказать, что против большей стороны в треугольнике лежит больший угол.

3. Задача на тему «Периметр треугольника». Основание равнобедренного треугольника равно 8 см. Медиана,

проведенная к боковой стороне, разбивает треугольник на два треугольника так, что периметр одного

треугольника на 2 см больше периметра другого. Найти боковую сторону данного треугольника.

Билет №20.

1. Объясните, как построить биссектрису данного угла.

2. Доказать, что высота равнобедренного треугольника, проведенная к основанию, является медианой и

биссектрисой.

3. Задача на тему «Свойства прямоугольных треугольников». В прямоугольном треугольнике ABC с

прямым углом С внешний угол при вершине А равен 120, АС + АВ = 18 см. Найти AC и AB.

Билет №21.

1. Объясните, как найти середину отрезка.

2. Доказать, что если при пересечении двух прямых секущей, сумма односторонних углов равна 180, то прямые

параллельны.

3. Задача на тему «Признаки равенства треугольников».

В треугольниках ABC и MKE отрезки СО и EH медианы, BC=KE, угол В равен углу К и угол С равен углу E.

Доказать, что треугольник АСО равен треугольнику MEH.

Билет №22.

1. Определение окружности, центра, радиуса, хорды и диаметра.

2. Свойства прямоугольных треугольников.

3. Задача на тему «Признаки параллельности двух прямых».

Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них равен

42°

Билет №23.

1. Определение параллельных прямых, параллельные отрезки.

2. Доказать, что в треугольнике против большего угла лежит большая сторона.

3. Задача на тему «Свойства равнобедренного треугольника».

Найдите углы при основании MP равнобедренного треугольника МОР, если MK – его биссектриса и OKM

= 96°.

Билет №24.

1. Виды треугольников.

2.Доказать, что если при пересечении двух прямых секущей соответственные углы равны, то прямые

параллельны.

3. Задача на тему «Неравенство треугольника».

В равнобедренном треугольнике одна сторона равна 25см, а другая равна 10 см. Какая из них является

основанием?

Билет №25.

1. Какой треугольник называется прямоугольным. Стороны прямоугольного треугольника.

2. Теорема о сумме углов треугольника.

3. Задача на тему «Вертикальные углы».

Прямые АВ и CD пересекаются в точке О. Угол АОС равен 58

0

. Найдите угол ВОD.

Билет. 1

1. (п.1) К основным геометрическим фигурам на плоскости относятся точка и прямая линия.

Точка — это самая малая геометрическая фигура, которая является основой всех прочих построений

(фигур).

Прямую линию, или прямую, можно представить себе как бесчисленное множество точек, которые

расположены на одной линии, не имеющей ни начала, ни конца. На листе бумаги мы видим только

часть прямой линии, так как она бесконечна. Прямая изображается так:

Часть прямой линии, ограниченная с двух сторон точками, называется отрезком.

Отрезок изображается так: Длина отрезка — положительное число, показывающее,

сколько раз единичный отрезок и его части

укладываются в данном отрезке. Длину отрезка АВ также называют расстоянием между точками А и В.

Свойства:

1) Длины равных отрезков равны;

2) Длина суммы отрезков равны сумме их длин.

Обычно прямые обозначаются малыми латинскими буквами a, b, c, d, а точки – большими A, B, C…

Через любые 2 точки можно провести прямую и притом только одну.

Любые 2 прямые на плоскости либо имеют одну общую точку (пересекаются), либо не имеют

общих точек (параллельны).

2. (п.20) Если три стороны одного треугольника соответственно равны трем сторонам другого

треугольника, то такие треугольники равны.

Дано: ∆АВС и ∆А

1

В

1

С

1

, у них АВ=А

1

В

1

, АС=А

1

С

1

,

ВС=В

1

С

1

. Доказать, что ∆АВС = ∆А

1

В

1

С

1

Доказательство: Приложим ∆АВС к ∆А

1

В

1

С

1

так,

чтобы сторона АВ совпала со стороной А

1

В

1

, а

точки С и С

1

оказались по разные стороны от АВ.

По условию АС=А

1

С

1

, ВС=В

1

С

1

→ ∆А

1

С

1

С и ∆В

1

С

1

С – равнобедренные, а значит ∠1 = ∠2, ∠3 = ∠4 (углы при основании), поэтому весь ∠А

1

СВ

1

= ∠А

1

С

1

В

1

.

Итак, мы получили, что АС=А

1

С

1

, ВС=В

1

С

1

, ∠С = ∠С

1

, следовательно ∆АВС = ∆А

1

В

1

С

1

(по I признаку).

Ч.т.д. 3. Найдите величины смежных углов, если один в 5 раз больше другого.

Решение: Обозначим один из углов х, другой значит будет 5х, т.к. он в 5 раз больше.

Сумма смежных углов всегда 180

0

, получаем уравнение х + 5х = 180

0

, откуда 6х = 180

0

, х = 30

0

. Значит

один из смежных углов 30

0

, другой 30*5 = 150

0

.

Билет. 2

1. (п. 14) Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной

прямой, соединенных отрезками. Точки называются вершинами треугольника, а отрезки – его

сторонами. Виды треугольников:

2. (п.25) Если при пересечении двух прямых секущей соответственные углы равны, то прямые

параллельны.

Дано: прямые а и b, с – секущая, соответственные углы ∠1 = ∠2.

Доказать, что а||b

Доказательство: ∠1 = ∠2 (по условию), ∠2 = ∠3 (вертикальные), следовательно ∠1 = ∠3, а это накрест лежащие углы, поэтому а||b.

Ч.т.д.

3. Отрезки АС и ВМ пересекаются в точке О и делятся ею пополам. Докажите, что ∆АВС = ∆СМА.

Дано: АО = ОС и ВО = ОМ.

Доказать, что ∆АВС = ∆СМА

Доказательство: Пусть отрезки АС и ВМ пересекаются в точке О. Тогда ∆АОВ = ∆СОМ по I признаку (АО = ОС и

ВО = ОМ по условию, а ∠АОВ = ∠СОМ как вертикальные). Следовательно, ∠ВАО = ∠МСО и сторона АВ = МС (в

равных треугольниках против равных углов лежат равные стороны).

Тогда ∆АВС = ∆СМА тоже по I признаку (∠ВАО = ∠МСО, АВ = МС, АС – общая сторона). Ч.т.д.

Билет. 3

1. (п.17)

Медиана – это отрезок, идущий из вершины

треугольника к середине противоположной

стороны. (Нельзя говорить идущий в

противоположную сторону…)

А

1

А

Биссектриса – это отрезок, идущий из вершины

треугольника к противоположной стороне и

делящий угол треугольника пополам.

А

1

30

0

А 30

0

Высота – это перпендикуляр, идущий из вершины

треугольника к противоположной стороне.

(Перпендикуляр – это отрезок, падающий под углом в 90

0

к прямой).

Высота – это единственная линия в треугольнике, которая при

построении может оказаться снаружи треугольника.

В любом треугольнике все 3 медианы пересекаются в одной точке, все 3 биссектрисы

пересекаются в одной точке и все 3 высоты пересекаются в одной точке.

2. (п.25) Если при пересечении двух прямых секущей накрест лежащие углы равны, то

прямые параллельны.

Дано: прямые а и b, АВ – секущая, накрест лежащие углы ∠1 = ∠2.

Доказать, что а||b

Доказательство: (метод от противного). Предположим, что прямые а и b не параллельны, а значит они пересекаются в

некоторой точке М. Рассмотрим ∆АВМ: ∠1 будет внешним углом для этого треугольника, а ∠2 – внутренним. Из

теоремы о внешнем угле треугольника следует, что ∠1 больше ∠2, а это противоречит условию (∠1 = ∠2), значит, прямые

а и b не могут пересекаться, поэтому они параллельны. Ч.т.д.

3. На окружности с центром О отмечены точки А и В так, что ∠АОВ – прямой. Отрезок ВС – диаметр окружности. Докажите, что хорды АВ и АС равны.

Доказательство: Рассмотрим ∆ВОА и ∆СОА, у них сторона ОА – общая, СО = ОВ (как радиусы одной окружности), ∠СОА = ∠ВОА = 90

0

.

Следовательно, ∆ВОА = ∆СОА по I признаку. А раз треугольники равны, то

их соответственные стороны тоже равны, т.е. АВ = АС. Ч.т.д.

Билет. 4

1. (п. 37) Пусть ВА — перпендикуляр, опущенный из точки В на прямую а, и С –

любая точка на прямой а, отличная от точки А (основание перпендикуляра).

Отрезок ВС называется наклонной, проведенной из точки В к прямой а. Точка С

называется основанием наклонной, а отрезок АС — проекцией наклонной.

Расстоянием от точки В до прямой а называется длина перпендикуляра из этой

точки к данной прямой, т.е. длина отрезка ВА.

Перпендикуляр, проведённый из какой—нибудь точки к прямой, меньше всякой наклонной,

проведённой из той же точки к этой прямой. Поэтому расстояние от точки В до прямой а является

наименьшим из расстояний от точки В до любой из точек прямой а.

2. (п.25) Если при пересечении двух прямых секущей сумма односторонних углов равна 180

0

,

то прямые параллельны.

Дано: прямые а и b, с – секущая, односторонние углы ∠1 + ∠4 = 180

0

.

Доказать, что а||b

Доказательство: ∠1 + ∠4 = 180

0

(по условию), ∠3 + ∠4 = 180

0

(смежные), следовательно ∠1 = ∠3, а это накрест лежащие углы, поэтому а||b. Ч.т.д.

3. Два внешних угла треугольника равны (∠1 = ∠2). Периметр равен 74см, а одна из сторон АС = 16см. Найдите две другие стороны треугольника.

Решение: По условию ∠1 = ∠2, следовательно ∠А = ∠С (как смежные с равными углами), а значит ∆АВС – равнобедренный, т.е. АВ = ВС = х. Периметр – это сумма всех сторон, составим уравнение:

х + х + 16 = 74см

2х = 74 – 16

2х = 58

х = 29см = АВ = ВС. Рассмотрим другой случай:

Билет. 5

1. (п. 24) Две прямые называются параллельными, если они лежат в одной

плоскости и не пересекаются. Обозначение: m || n.

Все точки одной параллельной прямой находятся на одинаковом расстоянии от

другой параллельной прямой.

Все прямые, параллельные одной прямой, параллельны между собой.

Принято считать, что угол между параллельными прямыми равен нулю. Все

перпендикуляры к одной и той же прямой параллельны между собой.

Два отрезка называются параллельными, если они лежат на параллельных

прямых.

2. (п.15) Если 2 стороны и угол между ними одного треугольника соответственно равны 2

сторонам и углу между ними другого треугольника, то такие треугольники равны.

Дано: ∆АВС и ∆А

1

В

1

С

1

, у них АВ=А

1

В

1

, АС=А

1

С

1

, ∠А = ∠А

1

. Доказать, что ∆АВС = ∆А

1

В

1

С

1

Доказательство: Наложим ∆АВС на ∆А

1

В

1

С

1

так, чтобы вершина А совпала с вершиной

А

1

. Так как по условию ∠А = ∠А

1

, то луч АВ наложится на луч А

1

В

1

, а луч АС на луч А

1

С

1

.

Еще по условию АВ=А

1

В

1

, значит точка В совпадет с точкой В

1

, АС=А

1

С

1

, значит точка С

совпадет с точкой С

1

. Все три точки у треугольников совпали, значит они равны. Ч.т.д.

3. В равнобедренном ∆АВС с основанием ВС проведена медиана АМ. Найдите её длину, если

периметр ∆АВС = 32см, а периметр ∆АВМ равен 24см.

Решение: Р

АВС

= АВ+ВС+АС

32 = 2АВ+2ВМ (т.к. АВ=АС и ВМ=МС)

32 = 2(АВ + ВМ)

16 = АВ + ВМ.

Р

АВМ

= АВ+ВМ+АМ, 24 = 16 + АМ, следовательно АМ = 24 – 16 = 8см.

Ответ: АМ = 8см.

Билет. 6

1. (п. 3—4) Луч (полупрямая) – часть прямой, имеющая начало и не имеющая конца.

Угол – это геометрическая фигура, которая состоит из двух лучей исходящих из

одной вершины.

Вершина угла — это точка, в которой два луча берут

начало. Стороны угла — это лучи, которые образуют угол.

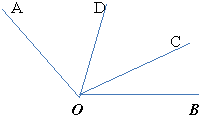
Например, вершина угла — точка O. Стороны угла — OA и OB. Для обозначения угла в тексте используется символ: ∠AOB.

Способы обозначения углов:

2. Тремя заглавными латинскими буквами, которыми

обозначены вершина и две точки, расположенные на

сторонах угла. Угол: ∠AOD.

Называть угол можно с любого края, но НЕ с

вершины. Угол с рисунка выше имеет два названия:

Вершина угла должна всегда находиться в середине

Единица измерения углов — градусы. Углы измеряют с помощью специального прибора – транспортира. Для обозначения градусов в тексте используется символ: °, например ∠В = 50°

Виды углов

2. (п. 18) В равнобедренном треугольнике углы при основании равны.

Дано: ∆АВС, АВ = АС.

Доказать, что ∠В = ∠С.

Доказательство: В ∆АВС из вершины А проведем биссектрису АД. Треугольники ABD и ACD равны по первому признаку равенства треугольников (АВ =

АС по условию, AD – общая сторона, ∠1 = ∠2, так как AD — биссектриса). Из равенства этих треугольников следует, что ∠В = ∠С. Ч.т.д.

3. Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210

0

.

Найдите все углы. Решение:

Билет. 7

1. (п. 25) Прямая с называется секущей к прямым а и b, если она пересекает их в двух точках.

При пересечении двух параллельных прямых секущей, образуются восемь углов, которые попарно

называются:

1) соответственные углы (они попарно равны: ∠1 = ∠5; ∠2 = ∠6; ∠3 = ∠7; ∠4 = ∠8);

2) накрест лежащие углы (4 и 5; 3 и 6); они тоже попарно равны;

3) односторонние углы (3 и 5; 4 и 6); их сумма равна 180

(∠3 + ∠5 = 180; ∠4 + ∠6 = 180).

2. (п.19) Если сторона и 2 прилежащих к ней угла одного треугольника соответственно равны

стороне и 2 прилежащим к ней углам другого треугольника, то такие треугольники равны.

Дано: ∆АВС и ∆А

1

В

1

С

1

, у них АВ=А

1

В

1

, ∠А = ∠А

1

, ∠В = ∠В

1

Доказать, что ∆АВС = ∆А

1

В

1

С

1

Доказательство: Наложим ∆АВС на ∆А

1

В

1

С

1

так, чтобы сторона АВ совпала со стороной А

1

В

1

(по

условию они равны, значит совпадут). Так как по условию ∠А = ∠А

1

и ∠В = ∠В

1

, то сторона АС наложится

на луч А

1

С

1

, а сторона ВС на луч В

1

С

1

. Вершина С окажется лежащей как на луче А

1

С

1

, так и на луче

В

1

С

1

, а значит совпадет с

вершиной С

1

. Все три точки у треугольников совпали, значит они равны. Ч.т.д.

3. АМ – биссектриса ∆АВС. Через точку М проведена прямая, параллельная АС и пересекающая

сторону АВ в точке Е. Докажите, что ∆АМЕ равнобедренный.

Доказательство: АС || ЕМ, значит ∠1 = ∠3 (как соответственные углы), ∠2 = ∠4 (как накрест лежащие углы), ∠1 = ∠2 (т.к. АМ – биссектриса).

Следовательно, ∠1 = ∠4, а это углы при основании в ∆АМЕ, значит этот треугольник равнобедренный и АЕ = ЕМ. Ч.т.д.

Билет. 8

1. Постройте треугольник по 2 сторонам и углу между ними. Смотри презентацию, слайд 10.

2. (п. 30) Сумма углов в треугольнике 180

0

.

Дано: ∆АВС.

Доказать, что ∠А+∠В+∠С = 180

0

.

Доказательство: Проведем через вершину В прямую а, параллельную стороне АС

Очевидно, что сумма углов 4, 2 и 5 равна развернутому углу с вершиной В, т. е.

∠4 + ∠2 + ∠5 = 180° (*).

Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых а и АС

секущей АВ, а углы 3 и 5 – накрест лежащими углами при пересечении тех же параллельных прямых

секущей ВС.

Поэтому ∠4 = ∠1 = ∠А, ∠5 = ∠3 = ∠С. Отсюда, учитывая равенство (*), получаем: ∠l + ∠2 + ∠3 = 180°,

или ∠A + ∠B + ∠C = 180°. Ч.т.д.

3. На биссектрисе угла А взята точка Е, а на сторонах этого угла точки В и С так, что ∠АЕС = ∠АЕВ. Докажите, что ВЕ = СЕ.

Доказательство: Рассмотрим ∆АСЕ и ∆АВЕ.

У них: ∠ВАЕ=∠САЕ, т.к. АЕ – биссектриса угла А, ∠АЕС = ∠АЕВ (по условию). Сторона АЕ – общая.

Значит ∆АСЕ = ∆АВЕ по II признаку. Тогда ВЕ = СЕ. Ч.т.д.

Билет. 9

1. (п. 21) Окружность – геометрическое место точек плоскости, равноудаленных от одной ее точки

(центра). Равные отрезки, соединяющие центр с любой точкой окружности, называются радиусами.

Любые 2 точки окружности делят её на 2 части. Каждая из этих частей называется дугой окружности.

Круг – часть плоскости, лежащая внутри окружности.

Прямая, проходящая через две точки окружности, называется секущей, а ее отрезок, лежащий внутри

окружности, — хордой. Хорда – это отрезок, соединяющий 2 точки окружности. Хорда, проходящая

через центр окружности, точку О, называется диаметром. Диаметр равен двум радиусам. Для

изображения окружности на чертеже пользуются циркулем.

2. (п. 33) Каждая сторона треугольника меньше суммы двух других сторон.

Дано: ∆АВС.

Доказать, что АВ < АС + СВ.

Доказательство: Строим отрезок СМ = ВС на продолжении стороны АС. В равнобедренном ВСМ ∠1 = ∠2 (по свойству углов в равнобедренном треугольнике). ∠1 < ∠АВМ, значит и ∠2 < ∠АВМ.

Рассмотрим треугольник АВМ. Так как в треугольнике против большего угла лежит большая

сторона, то АВ < АМ, АВ < АС + СМ, АВ < АС + ВС.

(т.к. СМ = ВС). Ч.т.д.

3. Отрезки АВ и СD пересекаются в их общей середине. Докажите, что прямые АС и ВD параллельны.

Доказательство:

О

Билет. 10

1. (п. 27—28) Аксиома – это такая истина, которую не надо доказывать. В каждой науке есть свои

аксиомы, на основе которых строят все дальнейшие суждения и доказательства.

Аксиома параллельных прямых: Через данную точку, не лежащую на данной прямой, проходит

только одна прямая, параллельная данной.

Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.

1) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Доказательство: Пусть прямая a || b и прямая с пересекает прямую а в точке М.

Докажем, что тогда прямая с пересекает и прямую b. Если бы прямая с не

пересекала прямую b, то через точку М проходили бы 2 прямые (а и с)

параллельные прямой b. Но это противоречит аксиоме параллельных прямых,

значит прямая с пересекает прямую b.

2) Если две различные прямые параллельны третьей прямой, то они параллельны.

2. (п. 34) Свойства прямоугольных треугольников:

1

0

. Сумма двух острых углов в прямоугольном треугольнике равна 90

0

.

Доказательство: В самом деле, сумма углов треугольника равна 180

0

, а т.к. прямой угол = 90

0

, то

сумма двух других углов в треугольнике = 90

0

.

2

0

. Катет прямоугольного треугольника, лежащий против угла в 30

0

, равен половине

гипотенузы.

Доказательство: Пусть в прямоугольном ∆АСВ ∠В = 30°. Тогда другой его острый угол будет равен 60°.

Докажем, что катет АС равен половине гипотенузы АВ.

Продолжим катет АС за вершину прямого угла С и отложим отрезок СМ,

равный отрезку АС. Точку М соединим с точкой В. Полученный

треугольник ВСМ равен треугольнику АСВ. Мы видим, что каждый угол

треугольника АВМ равен 60°, следовательно, этот треугольник –

равносторонний. Катет АС равен половине AM, а так как AM равняется

АВ, то катет АС будет равен половине гипотенузы АВ. Ч.т.д.

3

0

. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий

против этого катета, равен 30

0

.

3. Доказать, что середины сторон равнобедренного треугольника являются вершинами другого

равнобедренного треугольника.

Доказательство:

Билет. 11

1. (п. 31) Прямоугольный треугольник – это треугольник, у которого один угол

прямой, т.е. равен 90

0

. Сторона, лежащая напротив прямого угла, называется

гипотенузой, а две другие стороны — катетами. Гипотенуза всегда большего любого из

катетов, т.к. лежит напротив большего угла в треугольнике.

2. (п.29) Если две параллельные прямые пересечены секущей, то соответственные углы равны.

Дано: а||b, с – секущая,

Доказать, что соответственные углы ∠1 = ∠2.

Доказательство: т.к. а||b, то ∠1 = ∠3 (накрест лежащие), а ∠3 = ∠2 (вертикальные), следовательно ∠1 = ∠2. Ч.т.д.

3. Найти смежные углы, если один из них на 45

0

больше другого.

Решение: Обозначим ∠2 = х, тогда ∠1 = х + 45

0

.

По свойству смежных углов ∠1 + ∠2 = 180

0

.

Составим уравнение х + х + 45

0

= 180

0

; 2х = 135

0

; х = 135

0

: 2 = 67,5

0

.

Значит ∠2 = 67,5

0

, тогда ∠1 = 67,5

0

+ 45

0

= 112,5

0

.

Ответ: ∠1 = 112,5

0

; ∠2 = 67,5

0

.

Билет. 12

1. (п. 11) Смежные углы – это два угла, у которых одна сторона общая,

а две другие являются продолжениями одна другой.

Свойство: Сумма смежных углов равна 180

0

.

На рисунке ∠1 и ∠2 вместе образуют развернутый угол, а он равен 180

0

, следовательно, ∠1 + ∠2 = 180

0

.

2. (п.35) Если гипотенуза и катет одного прямоугольного треугольника соответственно равны

гипотенузе и катету другого, то такие треугольники равны.

Дано: ∆АВС и ∆А

1

В

1

С

1

– прямоугольные, АВ = А

1

В

1

и СВ =

С

1

В

1

, углы С и С

1

– прямые.

Доказать, что ∆АВС = ∆А

1

В

1

С

1

Доказательство: т.к. ∠С = ∠С

1

= 90

0

, то ∆АВС можно наложить на

∆А

1

В

1

С

1

так, что вершина С совместится с С

1

, а стороны СА и СВ

наложатся на лучи С

1

А

1

и С

1

В

1

. По условию СВ = С

1

В

1

, значит,

вершина В совместится с В

1

. Но тогда и вершина А совместится с А

1.

Ч.т.д.

3. Докажите, что если биссектриса треугольника совпадает с его высотой, то треугольник

равнобедренный.

Дано: В ∆АВС биссектриса ВД – это высота.

Доказать, что ∆АВС равнобедренный.

Доказательство: ∆АВД = ∆СВД по второму признаку

(∠1 =∠2, т.к. ВД – биссек., ∠3 =∠4=90

0

, т.к. ВД – высота, а сторона ВД – общая).

Значит АВ = ВС, т.е. ΔABC – равнобедренный. Ч.т.д.

Билет. 13

1. (п. 11) Вертикальные углы – это два угла, у которых

продолжениями сторон другого.

Теорема: Вертикальные углы равны.

Доказательство: ∠1 + ∠2 = 180

0

(смежные),

2. (п.35) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно

равны гипотенузе и острому углу другого, то такие треугольники равны.

Дано: ∆АВС и ∆А

1

В

1

С

1

– прямоугольные, АВ = А

1

В

1

, ∠С = ∠С

1

= 90

0

, ∠В = ∠В

1

. Доказать, что ∆АВС = ∆А

1

В

1

С

1

Доказательство: т.к. ∠С = ∠С

1

= 90

0

и ∠В = ∠В

1

, следовательно, ∠А = ∠А

1

(по теореме о сумме углов в треугольнике), а значит ∆АВС равен ∆А

1

В

1

С

1

по

второму признаку равенства треугольников (у них равны гипотенуза и два прилежащих к ней угла)

.

Ч.т.д.

3. Отрезки АВ и СЕ пересекаются в их общей середине О. На отрезках АС и ВЕ отмечены точки К и

М так, что АК = ВМ. Доказать, что ОК = ОМ.

Доказательство: Соединим точки А, С, В, Е. Получили четырёхугольник, диагонали которого

делятся точкой пересечения пополам. А, значит, этот четырёхугольник – параллелограмм. ЕС и

АВ – диагонали параллелограмма АСВЕ. ∠ОАС = ∠ОВЕ (как накрест лежащие при параллельных

прямых АС и ВЕ и секущей АВ). Получили, что ∆АОК = ∆ВОМ по первому признаку равенства

треугольников (АО = ОВ, АК = МВ, ∠ОАС = ∠ОВЕ). В равных треугольниках оставшиеся

стороны равны, т.е. ОК = ОМ. Ч.т.д.

Билет. 14

1. Отложить на данном луче от его начала отрезок, равный данному. Смотри презентацию, слайд 2.

2. (п.18) В равнобедренном треугольнике биссектриса, проведенная к основанию, является

медианой и высотой.

Дано: ∆АВС, АВ = ВС, ВО – биссектриса.

Доказать, что ВО – медиана и высота.

Доказательство: Рассмотрим ∆ABO и ∆CBO. У них:

AB = BC (по условию), BO – общая сторона, ∠AВO = ∠СВО (т.к. BO – биссектриса). Значит эти треугольники

равны по 1 признаку. Следовательно, AO = OС, а значит BO – медиана.

Далее, ∠AOC – развернутый угол = 180°. Но т.к. ∆ABO = ∆CBO, то ∠AOB = ∠COB = 180°/2 = 90

0

, значит BO – высота. Ч.т.д.

3. Один из углов прямоугольного треугольника равен 60

0

, а сумма гипотенузы и меньшего из катетов

равна 26,4см. Найдите гипотенузу треугольника.

Решение: Пусть в данном треугольнике ∠В = 90

0

, ∠A = 60

0

.

Тогда ∠С = 180

0

– 90

0

– 60

0

= 30

0

. Меньший из катетов лежит напротив угла в 30

0

и, значит, равен половине гипотенузы (по 2 свойству). Обозначим

гипотенузу АС = х, тогда катет АВ = ½*х. Составляем уравнение: х +

1

2

х = 26,4 (по условию). Отсюда

3

2

х = 26,4 или х = 17,6. Ответ:

гипотенуза АС = 17,6см.

Билет. 15

1. (п.29) Во всякой теореме есть 2 части: условие и заключение. Условие теоремы – это то, что дано, а

заключение – то, что требуется доказать.

Например, рассмотрим теорему: Если 3 стороны первого треугольника соответственно равны 3

сторонам второго треугольника, то такие треугольники равны. В ней условием будет утверждение: 3

стороны первого треугольника соответственно равны 3 сторонам второго треугольника (это дано), а

заключение: треугольники равны (это требуется доказать).

Теоремой, обратной данной, называется такая теорема, в которой условие и заключение меняются

местами.

Например, для данной выше теоремы обратной теоремой будет: Если треугольники равны, то у них

все стороны соответственно равны.

Или для теоремы: Если при пересечении двух прямых секущей соответственные углы равны, то

прямые параллельны. Обратная теорема будет звучать так: Если две параллельные прямые

пересечены секущей, то соответственные углы равны.

2. (п.28) Если две прямые параллельны третьей прямой, то они параллельны.

Доказательство: Действительно, пусть а || с и b || с.

Докажем, что тогда а || b.

Допустим, что прямые а и b не параллельны, т.е. пересекаются в

какой—то точке М. Тогда получим, что через точку М проходят 2

прямые (а и b) параллельные прямой с, а это противоречит аксиоме

параллельных прямых. Поэтому наше предположение было неверным,

а значит, прямые а и b параллельны.

3. Разность двух односторонних углов при пересечении двух параллельных прямых

секущей равна 50

0

. Найти эти углы.

Решение: Т.к. а || b, ∠1 + ∠2 = 180

0

. Пусть ∠1 = х, тогда ∠2 = х – 50.

Составляем уравнение: х + х – 50 = 180. 2х = 230, х = 115,

т.е. ∠1 = 115

0

, ∠2 = 55

0

.

Билет. 16

1. Как построить треугольник по стороне и двум прилежащим к ней углам. Смотри презентацию,

слайд 9.

2. (п.30) Внешним углом треугольника называется угол, смежный с каким—нибудь углом этого

треугольника.

Свойство: Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Дано: ∆АВС, ∠4 – внешний.

Доказать, что ∠4 = ∠1 + ∠3.

Доказательство: ∠1 + ∠3 + ∠2 = 180

0

(по теореме о сумме углов ∆).

∠4 + ∠2 = 180

0

(смежные)

Следовательно, ∠4 = ∠1 + ∠3. Ч.т.д.

3. Через середину отрезка проведена прямая. Доказать, что концы отрезка равноудалены от этой прямой. Дано: О – середина АВ, l – прямая, проходящая через О.

Доказать, что АА

1

= ВВ

1

.

Доказательство: АА

1

 l и ВВ

1

 l. Рассмотрим прямоугольные треугольники АОА

1

и ВОВ

1

. Они равны по гипотенузе и острому углу (АО = ОВ по условию, ∠1 =∠2,

как вертикальные).

Следовательно, АА

1

= ВВ

1

. Ч.т.д.

Билет. 17

1. (п.24, 37) Две прямые называются параллельными, если они лежат в одной плоскости и не

пересекаются. Обозначение: а ǀǀ b.

Два отрезка называются параллельными, если они лежат на параллельных прямых.

Расстоянием от точки до прямой называется длина перпендикуляра, проведенного из этой точки к

прямой.

Расстоянием между параллельными прямыми называется расстояние от произвольной точки одной из

параллельных прямых до другой прямой.

2. (п.32) В треугольнике против большего угла лежит большая сторона.

Дано: ∆АВС, ∠С > ∠В.

Доказать, что АВ > АС.

Доказательство: Предположим, что это не так.

Тогда либо АВ = АС, либо АВ < АС. В первом случае получаем, что ∆АВС

– равнобедренный, а значит углы при основании равны, т.е. ∠С=∠В, а это противоречит условию, что ∠С > ∠В. Во втором случае

получаем, что ∠С < ∠В (т.к. против большей стороны лежит больший угол). Это тоже противоречит условию. Значит, наше

предположение неверно, и, следовательно, АВ > АС. Ч.т.д.

3. В ∆АВС ∠А = 40

0

, а ∠ВСЕ смежный с ∠АСВ равен 80

0

. Доказать, что биссектриса ∠ВСЕ параллельна прямой АВ.

Дано: ∠А = 40

0

, а ∠ВСЕ = 80

0

, СК – биссектриса ∠ВСЕ.

Доказать, СК ǀǀ АВ.

Доказательство: ∠ВСК = ∠КСЕ = ½ ∠ВСЕ = 80

0

/2 = 40

0

.

Получили, что ∠ВАС = ∠КСЕ = 40

0

, а это соответственные углы при прямых АВ, СК и секущей АС. Раз они равны, то СК ǀǀ АВ. Ч.т.д.

Билет. 18

1. (п.35) Признаки равенства прямоугольных треугольников:

1) по двум катетам: Если два катета одного

прямоугольного треугольника соответственно равны двум

катетам другого прямоугольного треугольника, то такие

треугольники равны.

2) по катету и гипотенузе: Если катет и гипотенуза одного

прямоугольного треугольника соответственно равны

катету и гипотенузе другого прямоугольного треугольника,

то такие треугольники равны.

3) по гипотенузе и острому углу: Если гипотенуза и

острый угол одного прямоугольного треугольника

соответственно равны гипотенузе и острому углу другого

прямоугольного треугольника, то такие треугольники

равны.

4) по катету и острому углу: Если катет и острый угол

одного прямоугольного треугольника соответственно равны

катету и острому углу другого прямоугольного

треугольника, то такие треугольники равны.

2. (п. 11) Вертикальные углы – это два угла, у которых стороны одного угла являются

продолжениями сторон другого.

Теорема: Вертикальные углы равны.

Доказательство: ∠1 + ∠2 = 180

0

(смежные),

3. В равнобедренном ∆АВС с основанием АС = 37см, внешний угол при вершине В равен 60

0

. Найти

расстояние от вершины С до прямой АВ.

Дано: ∆АВС – равнобед., внешний ∠НВС = 60

0

, АС = 37см, СН  АВ (т.к. это расстояние).

Найти: длину СН.

Решение: По свойству внешнего угла ∠НВС = ∠А + ∠С = 60

0

. А т.к. ∆АВС – равнобед., то ∠А = ∠С = 60

0

/2 = 30

0

(углы при основании). В прямоугольном

треугольнике АНС, ∠А = 30

0

, значит катет лежащий

напротив него равен половине гипотенузы, т.е. СН 

1

2

АС  37 : 2 18,5см. Ответ: СН = 18,5см.

Билет. 19

1. Как построить треугольник по трем сторонам. Смотри презентацию, слайд 8. Задача имеет

решение только когда выполняется неравенство треугольника, т.е. сумма двух любых сторон должна

быть больше третьей стороны.

2. (п.32) В треугольнике против большей стороны лежит больший угол.

Дано: ∆АВС, АВ > АС.

Доказать, что ∠С > ∠В

Доказательство: Отложим на стороне АВ отрезок AD= АС. Так как AD < АВ, то точка D лежит между точками А и В.

Следовательно, ∠1 является частью ∠С и, значит, ∠C > ∠1. Угол 2 – внешний угол ∆BDC, поэтому ∠2 > ∠В. ∠1 = ∠2 как углы

при основании равнобедренного треугольника ADC. Таким образом, ∠С > ∠1, ∠1 = ∠2, ∠2 > ∠B. Отсюда следует, что ∠С > ∠В. Ч.т.д.

3. Основание равнобедренного треугольника равно 8см. Медиана, проведенная к боковой стороне,

разбивает треугольник на два треугольника так, что периметр одного треугольника на 2см больше

периметра другого. Найти боковую сторону данного треугольника.

Решение:

Билет. 20

1. Как построить биссектрису данного угла. Смотри презентацию, слайд 4.

2. (п.18) В равнобедренном треугольнике высота, проведенная к основанию, является

медианой и биссектрисой.

Дано: ∆АВС, АВ = ВС, ВО  АС (высота).

Доказать, что ВО – медиана и биссектриса.

Доказательство: Рассмотрим ∆ABO и ∆CBO. У них:

AB = BC (по условию), ∠A = ∠С = х (углы при основании в равноб. ∆), ∠AВО = ∠СВО = 90

0

– х (по теореме о сумме углов в ∆).

Значит эти треугольники равны по 2 признаку.

Следовательно, AO = OС, а значит BO – медиана.

Далее, ∠AВО = ∠СВО = 90

0

– х, значит BO – биссектриса. Ч.т.д.

3. В прямоугольном треугольнике АВС с прямым углом С внешний угол при вершине А равен 120

0

,

АС + АВ = 18см. Найти АС и АВ.

Решение: В ∆АВС: ∠А = 180

0

– 120

0

= 60

0

(смежные).

∠В = 180

0

– 90

0

– 60

0

= 30

0

(по теореме о сумме углов в ∆). Следовательно, катет лежащий напротив ∠В равен половине гипотенузы, т.е.

АС 

1

2

АВ или АВ = 2АС.

По условию АС + АВ = 18см, значит АС + 2АС = 18см. Отсюда 3АС = 18см, АС =

6см. Тогда АВ = 2АС = 2*6 = 12см. Ответ: АС = 6см, ВС = 12см.

Билет. 21

1. Как построить середину отрезка. Смотри презентацию, слайд 7.

2. (п.25) Если при пересечении двух прямых секущей сумма односторонних углов равна 180

0

,

то прямые параллельны.

Дано: прямые а и b, с – секущая, односторонние углы ∠1 + ∠4 = 180

0

.

Доказать, что а||b

Доказательство: ∠1 + ∠4 = 180

0

(по условию), ∠3 + ∠4 = 180

0

(смежные), следовательно ∠1 = ∠3, а это накрест лежащие углы, поэтому а||b. Ч.т.д.

3. В треугольниках АВС и МКЕ отрезки СО и ЕН медианы, ВС = КЕ, ∠В = ∠К и ∠С = ∠Е. Доказать, что ∆АСО = ∆МЕН.

Доказательство: По условию: ВС = КЕ, ∠В = ∠К и ∠С = ∠Е, значит, ∆АВС = ∆МКЕ (по 2 признаку).

Следовательно у этих треугольников равны соответственные стороны и углы, т.е. АВ = МК, а значит и АО =

МН, ∠А = ∠М и АС = МЕ. Тогда ∆АСО = ∆МЕН (по 1 признаку).

Билет. 22

1. (п. 21) Окружность – геометрическое место точек плоскости, равноудаленных от одной ее точки

(центра). Равные отрезки, соединяющие центр с любой точкой окружности, называются радиусами.

Любые 2 точки окружности делят её на 2 части. Каждая из этих частей называется дугой окружности.

Круг – часть плоскости, лежащая внутри окружности.

Прямая, проходящая через две точки окружности, называется секущей, а ее отрезок, лежащий внутри

окружности, — хордой. Хорда – это отрезок, соединяющий 2 точки окружности. Хорда, проходящая

через центр окружности, точку О, называется диаметром. Диаметр равен двум радиусам. Для

изображения окружности на чертеже пользуются циркулем.

2. (п. 34) Свойства прямоугольных треугольников:

1

0

. Сумма двух острых углов в прямоугольном треугольнике равна 90

0

.

Доказательство: В самом деле, сумма углов треугольника равна 180

0

, а т.к. прямой угол = 90

0

, то

сумма двух других углов в треугольнике = 90

0

.

2

0

. Катет прямоугольного треугольника, лежащий против угла в 30

0

, равен половине

гипотенузы.

Доказательство: Пусть в прямоугольном ∆АСВ ∠В = 30°. Тогда другой его острый угол будет равен 60°.

Докажем, что катет АС равен половине гипотенузы АВ.

Продолжим катет АС за вершину прямого угла С и отложим отрезок СМ,

равный отрезку АС. Точку М соединим с точкой В. Полученный

треугольник ВСМ равен треугольнику АСВ. Мы видим, что каждый угол

треугольника АВМ равен 60°, следовательно, этот треугольник –

равносторонний. Катет АС равен половине AM, а так как AM равняется

АВ, то катет АС будет равен половине гипотенузы АВ. Ч.т.д.

3

0

. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий

против этого катета, равен 30

0

.

3. Найти все углы, образованные при пересечении двух параллельных прямых секущей, если один из

них равен 42

0

.

Решение: Пусть а ǀǀ b, с – секущая, ∠1 = 42

0

. Тогда ∠3 = ∠1 = 42

0

(вертикальные),

∠5 = ∠3 = 42

0

(накрест лежащие), ∠7 = ∠5 = 42

0

(вертикальные), ∠8 и ∠7 смежные,

значит ∠8 = 180

0

– ∠7 = 180

0

– 42

0

= 138

0

, ∠6 = ∠8 = 138

0

(вертикальные),

∠2 = ∠6 = 138

0

(соответственные), ∠4 = ∠2 = 138

0

(вертикальные).

Билет. 23

1. (п. 24) Две прямые называются параллельными, если они лежат в одной

плоскости и не пересекаются. Обозначение: m || n.

Все точки одной параллельной прямой находятся на одинаковом расстоянии от

другой параллельной прямой.

Все прямые, параллельные одной прямой, параллельны между собой.

Принято считать, что угол между параллельными прямыми равен нулю. Все

перпендикуляры к одной и той же прямой параллельны между собой.

Два отрезка называются параллельными, если они лежат на параллельных прямых.

2. (п.32) В треугольнике против большего угла лежит большая сторона.

Дано: ∆АВС, ∠С > ∠В.

Доказать, что АВ > АС.

Доказательство: Предположим, что это не так.

Тогда либо АВ = АС, либо АВ < АС. В первом случае получаем, что ∆АВС

– равнобедренный, а значит углы при основании равны, т.е. ∠С=∠В, а это противоречит условию, что ∠С > ∠В. Во втором случае

получаем, что ∠С < ∠В (т.к. против большей стороны лежит больший угол). Это тоже противоречит условию. Значит, наше

предположение неверно, и, следовательно, АВ > АС. Ч.т.д.

3. Найдите углы при основании МР равнобедренного ∆МОР, если МК – его биссектриса и ∠ОКМ = 96

0

. Решение: ∠РКМ = 180

0

– 96

0

= 84

0

(смежный с ∠ОКМ).

Пусть ∠КРМ = х, тогда ∠КМР = 0,5х, т.к. МК – биссектриса и ∠М = ∠Р (углы при основании в равноб. ∆). По теореме о сумме углов в ∆МКР:

х + 0,5х + 84

0

= 180

0

. Отсюда, 1,5х = 96

0

, х = 64

0

.

Ответ: углы при основании равны 64

0

.

Билет. 24

1. (п. 14) Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной

прямой, соединенных отрезками. Точки называются вершинами треугольника, а отрезки – его

сторонами. Виды треугольников:

2. (п.25) Если при пересечении двух прямых секущей соответственные углы равны, то прямые

параллельны.

Дано: прямые а и b, с – секущая, соответственные углы ∠1 = ∠2.

Доказать, что а||b

Доказательство: ∠1 = ∠2 (по условию), ∠2 = ∠3 (вертикальные), следовательно ∠1 = ∠3, а это накрест лежащие углы, поэтому а||b.

Ч.т.д.

3. В равнобедренном треугольнике одна сторона равна 25см, а другая 10см. Какая из них является

основанием?

Решение: В треугольнике каждая сторона должна быть меньше суммы двух других. Тогда, если

основание равно 10 см, то каждая сторона удовлетворяет такому условию. Но если основание равно 25

см, то 25 см > 10 см + 10 см — это не верно. Значит, есть только одно правильное решение.

Ответ: основание равно 10 см.

Билет. 25

1. (п. 31) Прямоугольный треугольник – это треугольник, у которого один угол прямой,

т.е. равен 90

0

.

Сторона, лежащая напротив прямого угла, называется гипотенузой, а две другие стороны —

катетами. Гипотенуза всегда большего любого из катетов, т.к. лежит напротив большего

угла в треугольнике.

2. (п. 30) Сумма углов в треугольнике 180

0

.

Дано: ∆АВС.

Доказать, что ∠А+∠В+∠С = 180

0

.

Доказательство: Проведем через вершину В прямую а, параллельную стороне АС

Очевидно, что сумма углов 4, 2 и 5 равна развернутому углу с вершиной В, т. е.

∠4 + ∠2 + ∠5 = 180° (*).

Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых а и АС секущей

АВ, а углы 3 и 5 – накрест лежащими углами при пересечении тех же параллельных прямых секущей

ВС. Поэтому ∠4 = ∠1 = ∠А, ∠5 = ∠3 = ∠С. Отсюда, учитывая равенство (*), получаем:

∠l + ∠2 + ∠3 = 180°, или ∠A + ∠B + ∠C = 180°. Ч.т.д.

3. Прямые АВ и СД пересекаются в точке О, ∠AОС = 58

0

. Найдите ∠ВОД.

Решение: ∠ВОД = ∠AОС = 58

0

, т.к. они вертикальные.