Как проходит устный экзамен по геометрии 7 класс

ПРОМЕЖУТОЧНАЯ АТТЕСТАЦИЯ

Класс

Предмет

Уровень обучения

7

Геометрия

Базовый

Общая характеристика

Форма промежуточной аттестации

Общее количество билетов

Количество заданий базового уровня

Количество заданий повышенного уровня

Устный экзамен

16

16

0

Критерии оценивания

Отметка «5» ставится, если ученик ответил на все теоретические
вопросы и решил задачу.

Отметка «4» ставится, если сформулирована (доказана теорема
при необходимости) теорема, решена задача, но ученик не полностью ответил на
теоретические вопросы.

Отметка «3» ставится, если дано определение геометрического
понятия, рисунок или сформулирована теорема, но не решена задача, то есть при
условии верного ответа на 1 и 2 вопросы.

Отметка «2» ставится, если ученик не ответил на теоретические вопросы
и не решил задачу.

При ответе, обучающемуся
могут быть заданы дополнительные вопросы членами экзаменационной комиссии, но
они не должны выходить за рамки содержания билета, выбранного обучающимися.

Описание

Проверяемый результат

Уровень

Умение читать и делать чертежи, необходимые для
решения.

БУ

Умение выделять необходимую информацию при чтении
чертежа.

БУ

Умение определять необходимость дополнительных
построений при решении задач и выполнять их.

БУ

Умение различать взаимное расположение фигур.

БУ

Умение правильно воспроизвести формулировку
теоремы, проиллюстрировав ее выполнением чертежа по условию теоремы.

БУ

Умение привести доказательство теоремы,
проиллюстрировав ее выполнением чертежа по условию теоремы.

БУ

Умение строить
смежные и вертикальные углы, перпендикулярные и параллельные прямые.

БУ

Умение определять вид
треугольника, различать признаки равенства треугольников.

БУ

Умение строить
медианы, биссектрисы и высоты треугольника.

БУ

Умение строить углы,
с помощью циркуля и линейки.

БУ

Умение строить
окружность, различать диаметр, хорду, радиус.

БУ

ВОПРОСЫ К ИТОГОВОМУ
ЗАЧЕТУ ПО ГЕОМЕТРИИ В 7 КЛАССЕ

(ко всем вопросам должны
быть чертежи и объяснения)

1.     
Смежные и вертикальные углы. Определения
и свойства.

2.     
Теорема о смежных и
вертикальных углах (с доказательством).

3.     
Перпендикулярные прямые.
Определение и свойства.

4.     
Треугольник и его основные
элементы.

5.     
Признаки равенства
треугольников.

6.     
Первый признак равенства
треугольников (с доказательством).

7.     
Второй признак равенства
треугольников (с доказательством).

8.     
Третий признак равенства
треугольников (с доказательством).

9.     
Треугольник, равнобедренный
треугольник, равносторонний треугольник, равные треугольники.

10.  Медианы, биссектрисы и высоты треугольника.
Определения и свойства.

11.  Свойства равнобедренного треугольника.

12.  Свойства равностороннего треугольника.

13.  Окружность, диаметр, хорда, радиус, дуга.
Определения.

14.  Параллельные прямые, признаки параллельности
прямых.

15.  Аксиома параллельных прямых и ее следствия.

16.  Сумма углов треугольника, виды треугольников
(каждый вид нарисовать, объяснить)

17.  Соотношения между сторонами и углами треугольника и
следствия.

18.  Неравенство треугольника.

19.  Прямоугольные треугольники. Свойства прямоугольных
треугольников.

20.  Признаки равенства прямоугольных треугольников.

21.  Как с помощью циркуля и линейки построить угол,
равный данному?

22.  Как с помощью циркуля и линейки построить
биссектрису угла?

23.  Как с помощью циркуля и линейки построить середину
отрезка?

24.  Как с помощью циркуля и линейки построить
перпендикулярные прямые?

25.  Расстояние от точки до прямой. Расстояние между
двумя параллельными прямыми.

БИЛЕТЫ К ИТОГОВОМУ
ЗАЧЕТУ ПО ГЕОМЕТРИИ В 7 КЛАССЕ

БИЛЕТ № 1

1.      Смежные и вертикальные углы. Определения и
свойства.

2.      Аксиома параллельных прямых и ее следствия.

3.      ЗАДАЧА

БИЛЕТ № 2

1.      Перпендикулярные прямые. Определение и свойства.

2.      Треугольник и его основные элементы.

3.      ЗАДАЧА

БИЛЕТ№ 3

1.      Признаки равенства треугольников.

2.      Соотношения между сторонами и углами треугольника и
следствия, неравенство треугольника.

3.      ЗАДАЧА

БИЛЕТ № 4

1.      Медианы, биссектрисы и высоты треугольника.
Определения и свойства.

2.      Как с помощью циркуля и линейки построить угол,
равный данному?

3.      ЗАДАЧА

БИЛЕТ № 5

1.      Свойства равнобедренного треугольника.

2.      Как с помощью циркуля и линейки построить
биссектрису угла?

3.      ЗАДАЧА

БИЛЕТ № 6

1.      Окружность, диаметр, хорда, радиус, дуга.
Определения.

2.      Прямоугольные треугольники. Свойства прямоугольных
треугольников.

3.      ЗАДАЧА

БИЛЕТ № 7

1.      Параллельные прямые, признаки параллельности
прямых.

2.      Как с помощью циркуля и линейки построить середину
отрезка?

3.      ЗАДАЧА

БИЛЕТ № 8

1.      Признаки равенства прямоугольных треугольников.

2.      Как с помощью циркуля и линейки построить
перпендикулярные прямые?

3.      ЗАДАЧА

БИЛЕТ № 9

1.      Теорема о смежных и вертикальных углах (с
доказательством).

2.      Аксиома параллельных прямых и ее следствия.

3.      ЗАДАЧА

БИЛЕТ № 10

1.      Перпендикулярные прямые. Определение и свойства.

2.      Сумма углов треугольника, виды треугольников
(каждый вид нарисовать, объяснить)

3.      ЗАДАЧА

БИЛЕТ№ 11

1.     
Первый признак равенства
треугольников (с доказательством).

2.     
Соотношения между сторонами и
углами треугольника и следствия, неравенство треугольника.

3.     
ЗАДАЧА

БИЛЕТ № 12

1.     
Второй признак равенства треугольников
(с доказательством).

2.     
Как с помощью циркуля и
линейки построить угол, равный данному?

3.     
ЗАДАЧА

БИЛЕТ № 13

1.     
Третий признак равенства
треугольников (с доказательством).

2.      Как с помощью циркуля и линейки построить
биссектрису угла?

3.      ЗАДАЧА

БИЛЕТ № 14

1.      Окружность, диаметр, хорда, радиус, дуга.
Определения.

2.      Треугольник, равнобедренный треугольник,
равносторонний треугольник, равные треугольники.

3.      ЗАДАЧА

БИЛЕТ № 15

1.     
Свойства равностороннего
треугольника.

2.      Как с помощью циркуля и линейки построить середину
отрезка?

3.      ЗАДАЧА

БИЛЕТ № 16

1.     
Расстояние от точки до прямой.
Расстояние между двумя параллельными прямыми.

4.      Как с помощью циркуля и линейки построить
перпендикулярные прямые?

5.      ЗАДАЧА

ЗАДАЧИ К ИТОГОВОМУ
ЗАЧЕТУ ПО ГЕОМЕТРИИ В 7 КЛАССЕ

1.      Одна сторона тупоугольного равнобедренного
треугольника на 8 см больше другой. Периметр треугольника 38 см. Найдите
стороны треугольника.

2.      Один из углов, образовавшихся при пересечении двух
прямых, равен 1620 . Найдите остальные углы.

3.      Один из смежных углов в пять раз меньше другого.
Найдите эти углы.

4.      Найдите периметр треугольника, если два его угла
равны, а две стороны имеют длины 20 см и 10 см.

5.      На высоте АН равнобедренного треугольника АВС с
прямым углом А взята точка О. Докажите, что треугольники АОВ и АОС равны.

6.      Отрезки АВ и СD – диаметры некоторой окружности.
Докажите, что прямые АС и ВD параллельны.

7.      В равнобедренном треугольнике угол при основании на
270 меньше угла, противолежащего основанию. Найдите углы
треугольника.

8.      Отрезки АВ, ВС, СД последовательно отложены на
одной прямой, АС = ВD = 18 см, ВС = 7 см. Найдите АD.

9.      Одна сторона тупоугольного равнобедренного
треугольника на 8 см больше другой. Периметр треугольника 38 см. Найдите
стороны треугольника.

10.        
Один из углов, образовавшихся
при пересечении двух прямых, равен 1620 . Найдите остальные
углы.

11.        
Один из смежных углов в пять
раз меньше другого. Найдите эти углы.

12.        
Найдите периметр треугольника,
если два его угла равны, а две стороны имеют длины 20 см и 10 см.

13.        
На высоте АН равнобедренного
треугольника АВС с прямым углом А взята точка О. Докажите, что треугольники АОВ
и АОС равны.

14.        
Отрезки АВ и СD – диаметры
некоторой окружности. Докажите, что прямые АС и ВD параллельны.

15.        
В равнобедренном треугольнике
угол при основании на 270 меньше угла, противолежащего
основанию. Найдите углы треугольника.

16.        
Отрезки АВ, ВС, СД
последовательно отложены на одной прямой, АС = ВD = 18 см, ВС = 7 см. Найдите
АD.

Источник

Билеты по геометрии

для промежуточной аттестации

обучающихся 7 класса

по УМК Л.С. Атанасян и др.

Составила: Южалина Лариса Николаевна,

учитель первой категории

2020 – 2021 уч.год

Пояснительная записка

Спецификация годовой промежуточной аттестации по геометрии (устно) в 7 классе

  1. Назначение КИМ:

  • оценить уровень общеобразовательной подготовки по геометрии учащихся 7 классов;

-итоговый контроль. Итоговый контроль проводится по экзаменационным билетам.

  1. Документы, определяющие содержание КИМ. Содержание и уровень требований устного экзамена определяются следующими документами:

  • Авторской программы: Бурмистрова Т.А. Геометрия 7 — 9 классы. Программы общеобразовательных учреждений. М., «Просвещение», 2009. рекомендованной Минобразования РФ к использованию в образовательном процессе; Бурмистрова

Т.А. Геометрия 7 — 9 классы. Программы общеобразовательных учреждений. М.,

«Просвещение», 2012.

  • Учебник «Геометрия 7-9 класс» автор Атанасян Л.Н. издательство «Просвещение» 2017 год

  1. Подходы к отбору содержания, разработке структуры КИМ

Структура КИМ отвечает цели построения системы дифференцированного обучения математике в современной школе.

Целью устного экзамена является проверка уровня предметной компетентности учащихся за курс 7 класса по геометрии в рамках проведения переводной аттестации.

Отличие геометрии от всех других общеобразовательных предметов состоит в том,

что ее содержание практически не меняется в течение многих веков и основные цели ее изучения остаются неизменными:

  1. Развитие пространственных представлений, что в требованиях, предъявляемых к знаниям и умениям учащихся стандартом, формулируется как умение:

-читать и делать чертежи, необходимые для решения;

-выделять необходимую конфигурацию при чтении чертежа;

-определять необходимость дополнительных построений при решении задач и выполнять их;

-различать взаимное расположение геометрических фигур.

  1. Формирование и развитие логического мышления, что в требованиях, предъявляемых к знаниям и умениям учащихся стандартом, формулируется как владение методами доказательств, применяемыми при обосновании геометрических утверждений (теорем, следствий и т. д.), а также при проведении аргументации и доказательных рассуждений в ходе решения задач.

4. Характеристика структуры и содержания КИМ

Количество билетов: 15

Билет содержит в себе 2 вопроса

-Первый вопрос – теоретический (освещает весь курс геометрии 7 класса);

-Второй вопрос – решение задачи по определенной теме.

Задания в экзаменационных билетах соответствуют темам, изучаемым в 7 классе, а именно:

1.Начальные геометрические сведения 2.Треугольники

  1. Параллельные прямые

  1. Соотношения между сторонами и углами треугольника.

  1. Распределение заданий КИМ по содержанию, проверяемым умениям и способам деятельности.

Включенные в работу задания проверяют следующие виды познавательной деятельности:

-умение пользоваться языком геометрии для описания предметов окружающего мира;

-умение распознавать геометрические фигуры, различать их взаимное расположение;

-умение изображать геометрические фигуры;

-умение выполнять чертежи по условию задач; осуществлять преобразования фигур;

-умение решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения;

-умение проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;

-умение математически грамотно и ясно записать решение, приводя при этом необходимые пояснения и обоснования.

  1. Распределение заданий КИМ по уровню сложности

Общее число билетов промежуточной аттестации – 15. В каждом билете

представлены вопросы различных уровней сложности: базового, повышенного.

Первый вопрос билета – теоретический (освещает весь курс геометрии 7 класса) – базовый уровень сложности;

второй вопрос билета – решение задачи по определенной теме – повышенный уровень сложности.

  1. Продолжительность выполнения работы.

Учащиеся (4 человека) производят выбор билета и готовятся к ответу в течение 20 минут.

Каждому ученику дается на подготовку не менее 20 минут.

  1. Система оценивания выполнения отдельных заданий и работы в целом

Оценка складывается из следующих компонентов:

  • Оценивание устных ответов:

Оценка «5» ставится за полный, развёрнутый ответ, умение применять знания и излагать их логично.

Оценка «4» ставится за ответ, который в основном соответствует требованиям программы обучения, но при наличии некоторой неполноты знаний или мелких ошибок.

Оценка «3»ставится за ответ, который в основном соответствует требованиям программы обучения, но имеются недостатки и ошибки.

Оценка «2» ставится за существенные недостатки и ошибки, а результат ответа соответствует частично требованиям программы

Оценка «1» ставится при отказе ученика ответить по теме при неуважительной причине или при полном незнании основных положений темы.

  • Оценка за решение задачи билета

Задача считается выполненной верно, если обучающийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ.

Итоговой оценкой является средний показатель между этими компонентами.

Кодификатор элементов содержания

для проведения устного экзамена по геометрии 7 класс

Кодификатор элементов содержания для проведения аттестационной работы по геометрии является одним из документов, определяющих структуру и содержание контрольных измерительных материалов (КИМ). Кодификатор является систематизированным перечнем требований к уровню подготовки учащихся и проверяемых элементов содержания, в котором каждому объекту соответствует определенный код.

Код раздела

Код контролируемого

элемента

Элементы содержания, проверяемые заданиями аттестационной работы

1

Начальные геометрические сведения

1.1

Прямая и отрезок

1.1.1

Точки, прямые, отрезки

1.1.2

Провешивание прямой на местности

1.1.3

Практические задания

1.2

Луч и угол

1.2.1

Луч

1.2.2

Угол

1.2.3

Практические задания

1.3.

Сравнение отрезков и углов

1.3.1

Равенство геометрических фигур

1.3.2

Сравнение отрезков и углов

1.3.3

Задачи

1.4

Измерение отрезков

1.4.1

Длина отрезка

1.4.2

Единицы измерения. Измерительные инструменты

1.4.3

Практические задания. Задачи.

1.5

Измерение углов

1.5.1

Градусная мера угла

1.5.2

Измерение углов на местности

1.5.3

Практические задания. Задачи.

1.6

Перпендикулярные прямые

1.6.1

Смежные и вертикальные угла

1.6.2

Перпендикулярные прямые

1.6.3

Построение прямых углов на местности

1.6.4

Практические задания. Задачи.

2.

Треугольники

2.1.

Первый признак равенства треугольников

2.1.1

Треугольник

2.1.2

Первый признак равенства треугольников

2.1.3

Практические задания.

2.2

Медианы, биссектрисы и высоты треугольника

2.2.1

Перпендикуляр к прямой

2.2.2

Медианы, биссектрисы и высоты треугольника

2.2.3

Свойства равнобедренного треугольника

2.2.4

Практические задания. Задачи

2.3

Второй и третий признаки равенства треугольников

2.3.1

Второй признак равенства треугольников

2.3.2

Третий признак равенства треугольников

2.3.3.

Задачи

2.4

Задачи на построение

2.4.1

Окружность

2.4.2

Построения циркулем и линейкой

2.4.3

Примеры задач на построение

3

Параллельные прямые

3.1

Признаки параллельности двух прямых

3.1.1

Определение параллельных прямых

3.1.2

Признаки параллельности двух прямых

3.1.3

Практические способы построения параллельных прямых

3.1.4

Задачи

3.2

Аксиома параллельных прямых

3.2.1

Об аксиомах геометрии

3.2.2

Аксиома параллельных прямых

3.2.3

Теоремы об углах, образованных двумя параллельными

прямыми и секущей

3.2.4

Углы с соответственно параллельными или

перпендикулярными сторонами

3.2.5

Задачи

4

Соотношения между сторонами и углами треугольника

4.1

Сумма углов треугольника

4.1.1

Теорема о сумме углов треугольника

4.1.2

Остроугольный, прямоугольный и тупоугольный

треугольник

4.1.3

Задачи

4.2

Соотношения между сторонами и углами треугольника

4.2.1

Теорема о соотношениях между сторонами и углами

треугольника

4.2.2

Неравенство треугольника

4.2.3

Задачи

4.3

Прямоугольные треугольники

4.3.1

Некоторые свойства прямоугольных треугольников

4.3.2

Признаки равенства прямоугольных треугольников

4.3.3

Уголковый отражатель

4.3.4

Задачи

4.4

Построение треугольника по трем элементам

4.4.1

Расстояние от точки до прямой. Расстояние между

параллельными прямыми

4.4.2

Построение треугольника по трём элементам

4.4.3

Задачи

Экзаменационные билеты по математике. 7 класс.

Билет №1.

1.Признаки равенства треугольников.

2. Найдите величины смежных углов, если один из них в 5 раз больше другого.

Билет №2.

1.Виды треугольников. Сумма углов треугольника. Соотношения между сторонами и углами треугольника.

2. Отрезки AC и BM пересекаются в точке Ои точкой пересечения делятся пополам. Доказать, что треугольник AОВ равен треугольнику CОM.

Б илет №3.

1. Линии в треугольнике (медиана, биссектриса, высота).

2. Дано: m || n, 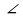3 = 35°. Вычислите градусные меры углов 1 и 2 (рис. 49).

Билет №4.

1. Признаки параллельности прямых.

2. В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине В равен 112°. Найдите величину угла АВС.

Билет №5.

1. Свойства параллельных прямых.

2. Сумма вертикальных углов АОВ и СОD, образованных при пресечении прямы АD и ВС, равна 84°. Найдите 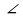ВOD.

Билет №6.

1. Равнобедренный треугольник и его свойства.

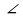
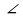
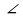
2. В ∆ АВС А= 54°, В = 62°. Найти С.

Билет №7.

1. Измерение углов. Измерение отрезков.

2. Точка М делит отрезок АВ на две части, одна из которой в 4 раза меньше другой. Найдите длину большей части, если длина отрезка АВ равна 50 см.

Билет №8.

1. Прямоугольный треугольник и его свойства.

2. На биссектрисе угла А взята точка E, а на сторонах этого угла точки В и С такие, что угол AEC равен углу AEB. Доказать, что BE равно CE.

Билет №9.

1. Определение окружности, центра, радиуса, хорды и диаметра.

2. Отрезки AB и CM пересекаются в их общей середине. Доказать, что прямые AC и BM параллельны.

Билет №10.

1. Смежные и вертикальные углы.

2. В равнобедренном треугольнике АBC с основанием АС, ОВ– медиана.

Докажите, что ΔАВО=ΔСВО.

Билет №11.

1.Угол. Виды углов. Градусная мера углов.

2. С какими из предложенных измерений сторон могут существовать треугольники?

А)12 см, 6 см, 8 см Б)7 см, 3 см, 5 см В) 6 см, 8 см, 2 см Г) 12 см, 3 см, 8 см

Билет №12.

1. Высота, медиана, биссектриса треугольника.

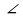
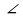
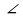
2. В равнобедренном ∆ АВС (АС — основание), В = 60°. Найти: А и С.

Билет №13.

1. Треугольник. Виды треугольников. Свойства треугольников.

2. Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 110°. Найти эти углы.

Билет №14.

1. Равенство треугольников. Три признака равенства треугольников

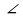
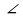
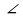
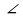
2. Луч ОВ делит АОС на два угла. АОС = 100°, а АОВ в 4 раза меньше ВОС.

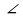
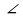
Найдите АОВ и ВОС.

Билет №15.

1. Простейшие геометрические фигуры: точка, прямая, отрезок, луч, угол. Понятие равенства геометрических фигур.

2. Один из смежных углов равен 130°. Найдите другой угол.

Ответы к билетам (вопрос №2)

№ билета

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

Ответ

300

1500

—

350

1450

680

1380

640

10

40

—

—

—

АБ

600

550

200

800

500
Источник

Муниципальное общеобразовательное бюджетное учреждение

«Якутская городская национальная гимназия им. А.Г. и Н.К. Чиряевых»

ГО «город Якутск»

Методическое пособие для проведения устного экзамена по геометрии

Автор: Габышевой Ольги Ксенофонтовны

                 2021 г.

Предисловие

Данное методическое пособие предназначено для учителей математики как общеобразовательных школ, так и в школах с углубленным изучением математики при работе с любым учебником.

О проведении экзамена по геометрии в 7-11 классах

Цель: проверка уровня предметной компетентности учащихся за курс 7-11 класса по геометрии в рамках проведения переводной аттестации.

Отличие геометрии от всех других общеобразовательных предметов состоит в том, что ее содержание практически не меняется в течение многих веков и основные цели ее изучения остаются неизменными:

1. Развитие пространственных представлении, что в требованиях, предъявляемых к знаниям и умениям учащихся стандартом, формулируется как умение:

  • читать и делать чертежи, необходимые для решения;
  •  выделять необходимую конфигурацию при чтении чертежа;
  • определять необходимость дополнительных построений при решении задач и выполнять их;
  •  различать взаимное расположение геометрических фигур.

2. Формирование и развитие логического мышления, что в требованиях, предъявляемых к знаниям и умениям учащихся стандартом, формулируется как владение методами
доказательств, применяемыми при обосновании геометрических утверждений (теорем, лемм, следствий и т. д.), а также при проведении аргументации и доказательных рассуждений в ходе решения задач.

Билеты по геометрии составлены на основе Требований к результатам освоения основной общеобразовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте общего образования.

В билетах представлен материал, изучаемый в курсе геометрии 7-11класса. Практические задания составлены аналогично заданиям ГИА по математике. Устная форма проведения экзамена выбрана не случайно, именно она позволяет более правильно и глубоко оценить предметные знания и все виды умений (практические, теоретические, интеллектуальные, организационно – коммуникативные), которыми должен владеть учащийся, охватить все изучаемые темы.

Структура экзаменационного билета.

Билеты содержат два вопроса по различным темам курса геометрии 7-11 класса (один теоретический и один практический).

Теоретическая часть. В первом вопросе обучающиеся должны, как правило, дать определение фигуры, сформулировать её свойство или признак, указанный в теореме, и доказать эту теорему.

При ответе на первый вопрос обучающиеся должны:

  • дать определение фигуры, включающее в себя как вербальное определение, так и графическое – чертёж;
  • правильно воспроизвести формулировку теоремы, проиллюстрировав её выполнением чертежа по условию теоремы;
  • привести доказательство теоремы, при этом доказательство считается выполненным верно, если обучающийся правильно привел схему доказательства, обосновал все логические шаги, выполнил чертежи, которые правильно отражают, кроме условия, ещё и ход доказательства.

Практическая часть. Второй  вопрос билета – задача. Цель включения этих заданий – проверка овладения обучающимися основными практическими умениями, полученными в ходе изучения курса.

Целью является проверка уровня сформированности логического мышления или логической интуиции. При выполнении второй части работы обучающиеся должны продемонстрировать умение геометрически грамотно записывать условие (что дано) и заключение (что требуется найти или доказать) задачи, её решение, сопровождая само решение необходимой аргументацией и доказательными рассуждениями. Кроме того, обучающиеся должны показывать умение геометрически грамотно выполнять чертежи.

Ответы на два практических задания билета позволяют судить об уровне сформированности предметной компетентности обучающегося.

Время подготовки учащегося. Система оценивания ответа.

Примерное время, отводимое на подготовку обучающегося к ответу, ‒ 20-25 минут. Оценивание ответа осуществляется по традиционной пятибалльной шкале. В одних случаях устный опрос производится по вопросам теории, а решения задач предъявляются комиссии без комментариев в письменной форме, в других случаях у доски рассматривается подробное решение задач со ссылками на все используемые факты, а теория оценивается по представленным записям. Поэтому и даны общие рекомендации по оцениванию ответов обучающихся.

Отметка «5» ставится, если обучающийся ответил на теоретический вопрос и решил  задачу.

Отметка «4» ставится, если обучающийся ответил на теоретический вопрос не достаточно хорошо и  решил задачу.

Отметка «3» ставится, если обучающийся ответил на теоретический вопрос и ли решил задачу

Во всех остальных случаях ставится отметка «2».

Билеты устного экзамена по геометрии

7 класс

Билет № 1

1. Первый признак равенства треугольников.

2. Отрезок АК – биссектриса треугольника САЕ. Через точку К проведена прямая, параллельная стороне СА и пересекающая сторону АЕ в точке N. Найдите углы треугольника AKN, если угол .

Билет № 2

1. Второй признак равенства треугольника.

2. В прямоугольном треугольнике АВС (уголС=90°) биссектрисы CD  и AE пересекаются в точке О. Угол АОС равен 105°. Найдите острые углы треугольника АВС.

Билет № 3

  1. Смежные углы (определение). Теорема о сумме смежных углов.

  2. В треугольнике АВС угол А равен 90°, а угол С на 40° больше угла В. Найдите углы В и С.

Билет № 4

1. Параллельные прямые (определение). Признаки параллельности двух прямых (доказательство одного из них).

2. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 42 см. Найдите гипотенузу.

Билет № 5

 1. Теорема о соотношении между сторонами и углами треугольника

 2. Один из углов прямоугольного треугольника равен 60°, а разность                                        гипотенузы и меньшего катета равна 15 см. Найдите гипотенузу.

Билет № 6

          1.Вертикальные углы (определение).  Свойства вертикальных углов.

          2. В треугольнике АВС угол а угол . Высота ВВ1 равна 2 см.

 Найдите АВ.

Билет № 7

1.Третий признак равенства треугольника

2. В треугольнике АВС угол С равен 90°, а угол В равен 35°,CD – высота. Найдите углы треугольника ACD.

Билет № 8

          1. Неравенство треугольника.

2.  В треугольнике АВС угол С равен 90°,  – высота,                             . Найдите угол САВ.

Билет № 9

1. Свойства равнобедренного треугольника (доказательство одного из них).

2. Периметр равнобедренного треугольника равен 50 см, а один из его сторон на 13 см меньше другой. Найдите стороны треугольника.

Билет № 10

1. Внешний угол треугольника (определение). Теорема о внешнем угле  треугольника.

2. В треугольнике АВС угол А равен 50°, а угол В в 12 раз меньше угла С. Найдите углы В и С.

Билет № 11

1. Теорема о свойстве катета, лежащего против угла в 30º.

2. Отрезок AD – биссектриса треугольника АВС. Через точку Dпроведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найти углы треугольника ADF, если угол ВАС равен 72°.

Билет № 12

1. Треугольник (определение). Теорема о сумме углов треугольника.

2. В равнобедренном треугольнике с периметром 48 см боковая сторона относится к основанию как 5:2. Найдите стороны треугольника.

Билет № 13

1. Признаки равенства прямоугольных треугольников

2. Один из углов, образовавшихся при пересечении двух прямых, на 70° больше другого. Найдите эти углы.

Билеты устного экзамена по геометрии

 8 класс

Билет №1

1. Параллелограмм. Определение, свойства, признаки.

2. В прямоугольном треугольнике гипотенуза равна 24 см, угол А равен 35о. Найдите второй острый угол. Выразите катеты через гипотенузу и угол А.

Билет№2

1. Трапеция. Определение, виды, средняя линия.

2. Прямые АВ и АС касаются окружности с центром О в точках В и С. Найдите ВС, если угол ОАВ равен 30о, АВ=5см.

Билет №3

1. Прямоугольник. Определение, свойства, признак.

2. Прямые МА и МВ касаются окружности с центром О в точках А и В. Точка С симметрична точке О относительно точки В. Докажите, что угол АМС равен трем углам ВМС.

Билет№4

1. Ромб. Определение, свойства, признак.

2. Длина тени дерева равна 10,2 м, а длина тени человека, рост которого 1,7 м, равна 2,5 м. Найдите высоту дерева.

Билет№5

1. Квадрат. Определение, свойства, признак.

2. Зная , что , найдите косинус и тангенс данного угла.

Билет№6

1. Теорема Пифагора.

2. Через точку А проведены касательные АВ (В — точка касания) и секущая, которая пересекает окружность в точках С и Д. Найдите СД, если АВ = 4см и  АС = 2см.

Билет№7

1. Средняя линия треугольника.

2. Стороны параллелограмма равны 10 см и 3 см. Биссектрисы двух углов, прилежащих к большей стороне, делят противоположную сторону на три отрезка. Найдите эти отрезки.

Билет№8

1. Свойство медиан треугольника.

2. Меньшая сторона параллелограмма равна 29 см. Перпендикуляр, проведенный из точки пересечения диагоналей к большой стороне, делит ее на отрезки, равные 33 см и 12 см. Найдите площадь параллелограмма.

Билет№9

1. Синус, косинус, тангенс в прямоугольном треугольнике.

2. В трапеции АВСД с большим основанием АД диагональ АС перпендикулярна к боковой стороне СД, угол ВАС равен углу САД. Найдите АД, если периметр трапеции равен 20 см, а угол Д равен 60о.

Билет№10

1. Касательная к окружности.

2. Найдите острый угол, образованный двумя секущими, проведенными из точки, лежащей вне окружности, если дуги, заключенные между секущими, равны 140о и 52о.

Билет№11

1. Центральные и вписанные углы.

2. Основание равнобедренного треугольника относится к боковой стороне как 4:3, а высота, проведенная к основанию, равна 30 см. Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.

Билет№12

1. Вписанная окружность.

2. Диагонали прямоугольной трапеции АВСД с прямым углом А взаимно перпендикулярны. Основание АВ равно 6 см, а боковая сторона АД равна 4см. Найдите ДС, ДВ и СВ.

Билет№13

1. Описанная окружность.

2. Диагональ АС квадрата АВСД равна 18,4 см. Прямая, проходящая через точку А и перпендикулярная к прямой АС, пересекает прямые ВС и СД соответственно в точках М и N. Найдите MN.

Билеты устного экзамена по геометрии

9 класс

Билет № 1

1. Первый признак равенства треугольников.

2. Найдите координаты точки  А(х; у), если она симметрична точке В(–20; 11) относительно точки М (0; –5).

Билет № 2

1. Второй признак равенства треугольников.

2. В прямоугольном треугольнике АВС угол  В равен 30°. Вершина прямого угла С соединена отрезком с точкой М, принадлежащей гипотенузе. Угол АМС равен 60°. Докажите, что СМ является медианой треугольника.

Билет № 3

1. Третий признак равенства треугольников.

2. Постройте фигуру, в которую перейдет квадрат АВСD при повороте вокруг точки D по часовой стрелке на угол 45°.

Билет № 4

1. Теорема о сумме внутренних углов треугольника.

2. В треугольнике АВС углы А и С равны. На стороне АС взяты точки D и Е такие, что АD = СЕ. Докажите, что треугольник DВЕ — равнобедренный.

Билет № 5

1. Теорема о сумме углов выпуклого n-угольника.  

2.  В прямоугольных треугольниках АВС и А1В1С1 из вершин прямых углов С и С1 проведены высоты СН и С1Н1; СН = С1Н1, АН = А1Н1. Докажите, что треугольники АВС и А1В1С1 равны.

Билет № 6

1. Теорема о средней линии треугольника.

2. Точки М и М1 симметричны относительно точки А. Точки М1 и М2 симметричны относительно точки В. Докажите, что отрезок ММ2 = 2АВ.

Билет № 7

1. Теорема о средней линии трапеции.

2. Окружность разделена тремя точками на части, которые относятся между собой как 2:3:5. Через точки деления проведены хорды. Определите вид получившегося треугольника.

Билет № 8

1. Теорема Фалеса.

2. В параллелограмме АВСD биссектриса угла А пересекает продолжение ВС в точке Е. Найдите периметр параллелограмма, если ВЕ = 16 см, СЕ = 5 см.

Билет № 9

1. Теорема Пифагора.

2. На отрезке АВ взята произвольная точка С. Через точки А и В проведены по одну сторону от данного отрезка параллельные лучи. На них соответственно взяты точки D и Е таким образом, что АD = АС и ВЕ = ВС. Найдите угол DСЕ.

Билет № 10

1. Теорема синусов.

2. Хорда окружности пересекает ее диаметр под углом 30° и делится им на части, равные 12 см и 6 см. Найдите расстояние от середины хорды до диаметра.

Билет № 11

1. Теорема косинусов.

2.  Даны точки М(–2; 6), К(1; 2) и L(4; –2). Определите, принадлежат ли данные точки одной прямой.

Билеты устного экзамена по геометрии

10 класс

Билет №1.

  1. Сформулируйте аксиомы стереометрии и их следствия. Сделайте чертежи и пояснения.
  2. Сторона основания правильной треугольной призмы равна 6 см, а диагональ боковой грани 
    10 см. Найдите площадь боковой и полной поверхности призмы.

Билет №2.

  1. Сформулируйте определение параллельности прямой и плоскости. Сформулируйте признак параллельности прямой и плоскости. Сделайте чертежи и пояснения.
  2. В правильной треугольной пирамиде апофема образует с плоскостью основания угол 30º. Сторона основания равна 12 см. Найдите площадь поверхности пирамиды.

Билет №3.

  1. Сформулируйте определение скрещивающихся прямых. Сформулируйте признак скрещивающихся прямых. Сделайте чертежи и пояснения.
  2. Боковое ребро правильной треугольной призмы равно 9 см, а диагональ боковой грани равна 15 см. Найдите площадь боковой и полной поверхности призмы

Билет №4.

  1. Опишите взаимное расположение прямых в пространстве. Как определяется угол между двумя прямыми в пространстве? Сделайте пояснения и чертежи.
  2. В правильной четырехугольной пирамиде апофема образует с плоскостью основания угол 60º. Высота пирамиды равна 6 см. Найдите площадь боковой поверхности пирамиды.

Билет №5.

  1. Перпендикулярность прямой и плоскости. Сформулируйте признак перпендикулярности прямой и плоскости. Сделайте чертежи и пояснения.
  2. Высота правильной четырехугольной пирамиды равна 6 см и образует с боковой гранью угол 30º. Найдите площадь боковой поверхности пирамиды.

Билет №6.

  1. Сформулируйте лемму о параллельных прямых, перпендикулярных третьей. Сделайте чертежи и пояснения.
  2. Через вершину прямого угла К треугольника DKF проведена прямая КМ, перпендикулярная к плоскости этого треугольника. Известно, что КМ = 15 см, 
    FK = DK = 10 см. Найдите расстояние от точки М до прямой DF.

Билет №7.

  1. Сформулируйте лемму о параллельных прямых, пересекающих плоскость. Сделайте пояснения и чертежи.
  2. В правильной треугольной пирамиде боковое ребро образует с плоскостью основания угол 60º. Сторона основания пирамиды равна 8 см. Найдите площадь боковой поверхности пирамиды.

Билет №8.

  1. Сформулируйте определение параллельных плоскостей. Сформулируйте признак параллельности двух плоскостей.
  2. Дан куб ABCDA1B1C1D1. Точки К, М и Т – середины ребер СС1, В1С1 и С1D1соответственно. Найдите АС1, если периметр сечения куба плоскостью КМТ равенhello_html_23d1b532.gifсм.

Билет №9.

  1. Тетраэдр и его элементы. Сделайте чертеж и пояснения..
  2. В правильной треугольной пирамиде сторона основания равна высоте и равна 12 см. Найдите площадь поверхности пирамиды.

Билет №10.

  1. Параллелепипед и его элементы. Сделайте чертеж и пояснения.
  2. Дан куб ABCDA1B1C1D1. Диагональ АС1 равна hello_html_7a22eef.gif.Найдите периметр сечения куба плоскостью РТН, где точки Р, Т и Н – середины ребер ВС, ВВ1 и АВ соответственно.

Билет №11.

  1. Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости.
  2. Основание прямой призмы – прямоугольный треугольник с катетами 15 см и 20 см. Большая боковая грань и основание призмы равновелики. Найдите площадь полной и боковой поверхности призмы.

Билет №12.

  1. Признак перпендикулярности прямой и плоскости.
  2. Через вершину угла Е прямоугольного треугольника НРЕ с гипотенузой НЕ проведена прямая МЕ, перпендикулярная к плоскости этого треугольника. Найдите расстояние от точки М до плоскости ЕРН, если ЕР = 5 см, а расстояние от точки М до прямой РН равно 10.

Билет №13.

  1. Угол между прямой и плоскостью. Приведите примеры величины угла между прямой и плоскостью. Сделайте чертежи и пояснения.
  2. Через вершину прямого угла С равнобедренного треугольника DСЕ проведена прямая СК, перпендикулярная к плоскости этого треугольника. Найдите расстояние от точки К до прямой DЕ, если СК = 35 см, CD = hello_html_ma04135b.gif см.

Билет №14.

  1. Признак перпендикулярности двух плоскостей.
  2. Основание прямой призмы – прямоугольный треугольник с гипотенузой 25 см и катетом 20 см. Меньшая боковая грань и основание призмы равновелики. Найдите площадь боковой и полной поверхности призмы.

Билет №15.

  1. Призма и его элементы. Сделайте чертеж и пояснения..
  2. Высота правильной четырехугольной пирамиды равна 16 см, а боковое ребро пирамиды равно 20 см. Найдите площадь боковой поверхности пирамиды.

Билеты устного экзамена по геометрии

11 класс

Билет № 1

1. Перпендикуляр и наклонная. Расстояние от точки до плоскости. Теорема о трех перпендикулярах.

2. Каждый из четырех равных шаров радиуса 6 касается двух других шаров и касается некоторой плоскости. Найдите радиус пятого шара, который касается той же плоскости и каждого из данных четырех шаров.

Билет № 2

1. Цилиндр. Боковая и полная поверхности цилиндра. Объем цилиндра.

2. В прямоугольном параллелепипеде АВСDА1В1С1D1 сечение BDD1B1 – квадрат и образует с сечением ACC1A1 угол 60°. Диагональ параллелепипеда равна  . Найдите объем параллелепипеда.

Билет № 3

1. Параллелепипед. Виды параллелепипеда. Формулы для вычисления объема прямоугольного параллелепипеда и объема наклонного параллелепипеда. Площадь полной поверхности.

2. Ребро правильного тетраэдра равно 1. Первый шар вписан в этот тетраэдр. Второй шар касается вписанного шара и трех граней тетраэдра. Найдите объем второго шара.

Билет № 4

1. Призма. Виды призм. Формулы для вычисления объема прямой призмы и объема наклонной призмы.

2. Высота правильной треугольной пирамиды равна  см, а боковая грань наклонена к плоскости основания под углом 60°. Найдите площадь боковой поверхности пирамиды.

Билет № 5

1. Пирамида. Виды пирамид. Формула для вычисления объема пирамиды.

2. Найдите угол развертки конуса, осевое сечение которого правильный треугольник.

Билет № 6

1. Цилиндр и его элементы. Объем цилиндра. Формула для вычисления объема цилиндра.

2. Основания наклонной призмы АВСА1В1С1 – правильные треугольники ABC и A1B1C1. Боковое ребро призмы вдвое больше ребра ее основания, а основанием высоты призмы, опущенной из вершины А1 на плоскость АВС, является точка В. Найдите косинус угла между скрещивающимися прямыми АВ и СС1.

Билет № 7

1. Конус и его элементы. Объем конуса. Формула для вычисления объема конуса.

2. Дана правильная треугольная призма АВСА1В1С1. Вершина А1 удалена от прямой ВС на расстояние 5 и от плоскости ВСС1 на расстояние 3. Найдите площадь полной поверхности призмы.

2. Найдите отношение ребра правильного тетраэдра к радиусу шара, описанного около этого тетраэдра.

Билет № 8

1. Векторы в пространстве. Задание вектора. Модуль вектора. Равенство векторов. Определение суммы двух векторов в пространстве.

2. Найдите отношение ребра правильного тетраэдра к радиусу шара, вписанного в этот тетраэдр.

Билет № 9

1. Усеченный конус и его элементы. Площадь боковой поверхности усеченного конуса.

2. Через образующую АВ цилиндра проведены осевое сечение ABCD и сечение ABFH, образующее с плоскостью АВС угол в 30°. Радиус цилиндра равен 5. Найдите расстояние между прямыми AF и CD.

Билет № 10

1. Правильный тетраэдр. Объем правильного тетраэдра.

2. Точка М, равноудаленная от вершин А1, В1, С правильной треугольной призмы АВСА1В1С1, лежит в плоскости АВС. Высота призмы равна ребру ее основания и равна . Найдите объем пирамиды МА1В1С.

Билет № 11

1 . Усеченный конус и его элементы. Объем усеченного конуса.

2. Дан прямоугольный параллелепипед АВСDА1В1С1D1, АВ = 1, AD = 2, AA1 = 3. Точка М лежит на диагонали параллелепипеда и не совпадает ни с одной вершиной параллелепипеда. Докажите, что сумма расстояний от точки М до всех граней параллелепипеда не зависит от ее расположения на диагонали. Найдите эту сумму.

Билет № 12

1. Усеченная пирамида. Виды усеченных пирамид. Формула для вычисления объема усеченной пирамиды.

2. Точки А и В лежат в различных гранях двугранного угла, равного 60°, на расстояниях а и b от ребра t двугранного угла соответственно (а < b). Расстояние между ортогональными проекциями этих точек на ребро t равно d. Найдите АВ.

Источник

Составными частями современной деятельности учителя и учащихся по освоению программного материала являются ориентировочная, исполнительная и контролирующая. В контролирующей части устанавливается обратная связь в системе учитель-ученик, позволяющая регулярно получать информацию, используемую для определения качества усвоения учащимися учебного материала, своевременного диагностирования и корректирования их знаний и умений. Иначе говоря, в ходе контроля выявляются и оцениваются знания и умения учащихся, что дает возможность получать и накапливать сведения, необходимые для успешного управления их обучением, воспитанием и развитием.

Один из распространенных типов контроля – внешний контроль учителя за деятельностью учащихся. Этот тип контроля приучает учащихся добросовестно и систематически выполнять учебную работу, развивает стремление сделать ее лучше.

С введением формы итоговой аттестации в виде ГИА для предмета «математика» возникла необходимость более глубокого изучения геометрии, т.к. часть заданий контрольно-измерительных материалов предлагает знание этого предмета.

Для более качественного изучения геометрии мы проводим зачеты в конце каждой четверти и мини-экзамен в конце года. Задания по геометрии, предлагаемые для учащихся седьмого класса в рамках экзамена-собеседования:

   

Задачи на построение

4-1. Построить угол равный данному.

4-2. Построить биссектрису данного угла.

4-3. Построить середину данного отрезка.

4-4. Построить прямую перпендикулярную данной.

4-5. Построить треугольник по трем сторонам.

4-6. Построить треугольник по углу и двум сторонам.

4-7. Построить треугольник по стороне и двум углам, прилежащим к ней.

4-8. Построить прямоугольный треугольник по двум катетам.

4-9. Построить прямоугольный треугольник по катету и прилежащему острому углу.

4-10. Построить прямоугольный треугольник по гипотенузе и острому углу.

4-11. Построить треугольник по стороне и двум углам, прилежащим к ней.

4-12. Построить прямоугольный треугольник по двум катетам.

4-13. Построить биссектрису данного угла.

4-14. Построить середину данного отрезка.

Билет № 1

1.Теорема о смежных углах.

2.Определение медианы, биссектрисы, высоты треугольника.

Билет № 2

1.Теорема о вертикальных углах.

2.Определение треугольника.

Билет № 3

1.Первый признак равенства треугольников.

2.Определение перпендикулярных прямых.

Билет № 4

1.Признак параллельности прямых (на выбор).

2.Определение параллельных прямых.

Билет № 5

1.Второй признак равенства треугольников.

2.Определение окружности.

Билет № 6

1.Свойства равнобедренного треугольника (на выбор).

2.Определение расстояния от точки до прямой.

Билет № 7

1.Теорема о сумме углов треугольника.

2.Расстояние между параллельными прямыми.

Билет № 8

1.Третий признак равенства треугольников.

2.Определение угла.

Билет № 9

1.Свойства прямоугольного треугольника.

2.Определение отрезка.

Билет № 10

1.Свойство равнобедренного треугольника об углах при основании.

2.Определение луча.

С введением такой оценки знаний учащиеся стали ответственнее подходить к выполнению домашних заданий, тщательнее разбирать задачи и вникать в их суть. В результате повысилась качественная успеваемость по геометрии и процент выполнения заданий из модуля «Геометрия».

Источник

БИЛЕТ №1.

1. Точки, прямые, отрезки.

2. Признаки равенства прямоугольных треугольников (без доказательства).

3.Точка К — середина отрезка МN, точка Е — середина отрезка КN, ЕN = 5 см. Найдите отрезки МК, МЕ и МN.

БИЛЕТ №2.

1. Луч и угол.

2. Свойства прямоугольных треугольников (без доказательства).

3. Точка К принадлежит отрезку СВ, длина которого равна 28 см. Найдите отрезки СК и КВ, если отрезок СК на 4 см меньше отрезка КВ.

БИЛЕТ №3.

1. Измерение отрезков. Сравнение отрезков.

2. Теорема о неравенстве треугольника (доказательство).

3. Точка К принадлежит отрезку СВ, длина которого равна 28 см. Найдите отрезки СК и КВ, если отрезок СК в 6 раз больше отрезка КВ.

БИЛЕТ №4.

1. Измерение углов. Сравнение углов.

2. Теорема о соотношениях между сторонами и углами треугольника (доказательство).

3. Точка К принадлежит отрезку СВ, длина которого равна 28 см. Найдите отрезки СК и КВ, если СК:КВ = 3:4 .

БИЛЕТ №5.

1. Смежные и вертикальные углы.

2. Теорема о сумме углов треугольника (доказательство).

3. Луч ВD делит угол АВС на два угла. Найдите угол АВС, если угол АВD= 54°, угол СВD = 72°.

БИЛЕТ №6.

1. Перпендикулярные прямые.

2. Аксиома параллельных прямых, следствия.

3. Луч ВD делит угол АВС на два угла. Найдите угол СВD, если угол АВС = 158°, угол АВD = 93°.

БИЛЕТ №7.

1. Треугольник.

2. Аксиомы геометрии.

3. Угол CEF равен 152°, луч ЕМ проходит между его сторонами, угол СЕМ на 18° больше угла FEM. Найдите углы СЕМ и FEM.

БИЛЕТ №8.

1. Перпендикуляр к прямой.

2. Теоремы об углах, образованных двумя параллельными прямыми и секущей (без доказательства).

3. Луч АК принадлежит углу BAD. Найдите углы ВАК и DAK, если угол ВАК в 7 раз меньше угла DAK и угол BAD = 72°.

БИЛЕТ №9.

1. Медианы, биссектрисы и высоты треугольника.

2. Признаки параллельности прямых (без доказательства).

3. Найдите смежные углы, если один из них на 70° больше другого.

2 ) один из них в 8 раз меньше

другого;

3) их градусные меры относятся как 3 : 2 .

БИЛЕТ №10.

1. Равнобедренный треугольник. Равносторонний треугольник.

2. Объясните, как построить прямую, проходящую через данную точку, лежащую на данной прямой, и перпендикулярную к этой прямой.

3. Найдите смежные углы, если один из них в 8 раз меньше другого.

БИЛЕТ №11.

1. Окружность.

2. Объясните, как построить середину данного отрезка.

3. Найдите смежные углы, если их градусные меры относятся как 3 : 2 .

БИЛЕТ №12.

1. Параллельные прямые.

2. Объясните, как построить биссектрису данного угла.

3. Найдите углы, образованные при пересечении двух прямых, если сумма двух из них равна 106°.

БИЛЕТ №13.

1. Углы, образованные при пересечении двух прямых секущей.

2. Объясните, как отложить от данного луча угол, равный данному.

3. Одна из сторон треугольника в 5 раз меньше второй и на 25 см меньше третьей. Найдите стороны треугольника, если его периметр равен 74 см.

БИЛЕТ №14.

1. Внешний угол треугольника.

2. Объясните, как отложить на данном луче от его начала отрезок, равный данному.

3. Периметр треугольника равен 48 см, а его стороны относятся как 7 : 9 : 8 . Найдите стороны треугольника.

БИЛЕТ №15.

1. Виды треугольников (классификация по углам).

2. Признак равенства треугольников: по трём сторонам (доказательство).

3. С помощью линейки и транспортира постройте треугольник, две стороны которого равны 3 см и 4 см, а угол между ними — 90°. Укажите вид этого треугольника.

БИЛЕТ №16.

1. Следствия из теоремы о соотношениях между сторонами и углами треугольника.

2. Признак равенства треугольников: по стороне и прилежащим к ней углам (доказательство).

3. С помощью линейки и транспортира постройте треугольник, одна сторона которого равна 6 см, а углы, прилежащие к этой стороне, — 90° и 45°.

БИЛЕТ №17.

1. Следствие из теоремы о неравенстве треугольника.

2. Теорема о биссектрисе равнобедренного треугольника (доказательство).

3. Периметр равнобедренного треугольника равен 39 см, а основание — 15 см. Найдите боковые стороны треугольника.

БИЛЕТ №18.

1. Расстояние от точки до прямой.

2. Докажите, что углы при основании равнобедренного треугольника равны.

3. Найдите стороны равнобедренного треугольника, периметр которого равен 54 см, а основание в 4 раза меньше боковой стороны.

БИЛЕТ №19.

1.Докажите, что все точки каждой из двух параллельных прямых равноудалены от другой прямой.

2. Теорема о перпендикуляре, проведённом из данной точки к данной прямой (доказательство).

3. Разность односторонних углов, образованных при пересечении двух параллельных прямых секущей, равна 50°. Найдите эти углы.

БИЛЕТ №20.

1. Построение треугольника по трём элементам (любая задача на выбор).

2. Признак равенства треугольников: по двум сторонам и углу между ними (доказательство).

3. Один из углов треугольника в 3 раза меньше второго угла и на 35° меньше третьего. Найдите углы треугольника.

Источник

Систему зачетов в зависимости от склонностей
учителя, стиля его работы, особенностей класса и
т.д. можно строить по-разному.

С помощью зачетов проверяют овладение
различными порциями учебного материала. В
соответствии с этим их можно разделить на
тематические и текущие. Тематические зачеты
проводятся в конце изучения темы и направлены на
проверку усвоения ее материала в целом. Текущие
зачеты проводятся систематически в ходе
изучения темы по небольшим, законченным по
смыслу порциям учебного материала.

Оба вида зачетов можно проводить в открытой или
закрытой форме. В первом случае учащиеся
предварительно знакомятся со списком задач
обязательного уровня. Во втором случае этот
список в явном виде учащимся не предъявляется.
Однако, это не означает, что учащимся совсем
неизвестно, какие типы задач относятся к
обязательным. В ходе изучения материала учитель
акцентирует внимание учеников на задачах
обязательного уровня, подчеркивая, что подобные
им необходимо будет решить на зачете.

Итак, можно выделить, например, следующие
четыре вида зачетов:

  • открытый тематический зачет,
  • закрытый тематический зачет,
  • открытый текущий зачет,
  • закрытый текущий зачет.

Требования к проведению зачетов:

  • зачет не должен содержать большой объем
    информации
  • зачет должен быть дифференцированным
  • с вопросами и задачами учащиеся должны быть
    предварительно ознакомлены
  • на зачете должна быть возможность улучшения
    оценки
  • четкая организация зачета.

Приведу пример открытого тематического зачета
по геометрии в 7 классе.

(учебник под ред. Л.С.Атанасяна).

Цель проведения зачета:


  1. Обобщение и систематизация знаний учащихся
    по изученной теме;
  2. Проверка умений и навыков решения задач по
    изученной теме.


Зачет №1 (глава первая)

Вопросы к зачету по теме “Треугольники”:

  1. Определение треугольника, элементы
    треугольника, периметр.
  2. Первый признак равенства треугольников.
  3. Второй признак равенства треугольников.
  4. Третий признак равенства треугольников.
  5. Определение биссектрисы угла треугольника.
  6. Определение высоты треугольника.
  7. Определение медианы треугольника.
  8. Определение равнобедренного треугольника.
  9. Свойства равнобедренного треугольника.
  10. Какие треугольники называются равными.

В проведении зачета на уроке мне помогают
консультанты. Обычно, это

3-4 человека, имеющие по предмету оценку “5”.
Консультанты сдают такой зачет заранее.

Класс распределяется на группы по числу
консультантов. Консультанты объ-

являются на зачете. Каждый консультант
опрашивает учащихся своей группы и заполняет
следующую карточку:

Консультант

Алферов А.

 1 2 3 4 5 6 7 8 9 10
1.Бубнов А. + + + — + + — + + + 4
2.Андреева О. — + — + — + + + + + 3
3.Киреев С. — — — + + + + + + + 3
4.Власова Т. + + + + + + + + + + 5
5.Никитин М. + — + + + + + + + + 4

Каждому ученику выставляется оценка за
вопросы:

  • “5”- 10 вопросов
  • “4”- 9-8 вопросов
  • “3”- 7-6 вопросов
  • “2”- менее 6 вопросов.

Ученик, сдавший теорию, приступает к решению
задач.

Предлагаются следующие виды задач:

1.На “3”:

Отрезки АС и ВД пересекаются и точкой
пересечения делятся пополам.

Докажите, что треугольник АВС равен
треугольнику СДА.

2.На “4”:

В равнобедренном треугольнике основание в два
раза меньше боковой

стороны, а периметр равен 50 см. Найдите стороны
треугольника.

3. На “5”:

Докажите, что в равных треугольниках медианы,
проведенные к равным

сторонам, равны.

Зачет №2

Зачет по теме “Параллельные прямые” (глава
третья)

Вопросы к зачету:

  1. Определение параллельных прямых
  2. Что такое секущая?
  3. Назовите углы, образованные при пересечении
    двух прямых и секущей.
  4. Признаки параллельности двух прямых.
  5. Условие и заключение теоремы; определение
    теоремы, обратной данной.
  6. Теоремы, обратные признакам параллельности
    прямых.
  7. Что такое аксиома ?
  8. Аксиома параллельных прямых.

Примерные типы задач к зачету №2:

1.На оценку “3”:

При пересечении двух параллельных прямых
третьей прямой сумма двух

накрест лежащих углов равна 130 градусов.
Найдите остальные углы.

2.На оценку “4”:

Разность двух односторонних углов при
пересечении двух параллельных

прямых секущей равна 50 градусам. Найдите эти
углы.

3.На оценку “5”:

Две параллельные прямые пересечены секущей.
Докажите, что биссектрисы накрест лежащих углов
параллельны.

Зачет №3 (глава 4)

Зачет по теме “Соотношения между углами и
сторонами треугольника”

Вопросы к зачету:

  1. Теорема о сумме углов треугольника.
  2. Виды треугольников (по типу углов).
  3. Определение прямоугольного треугольника;
    стороны прямо угольного треугольника.
  4. Теорема о соотношениях между сторонами и углами
    треугольника.
  5. Следствия из теоремы.
  6. Неравенство треугольника.
  7. Свойства прямоугольных треугольников.
  8. Признаки равенства прямоугольных
    треугольников.

 Примерные типы задач к зачету №3:

1.На оценку “3”:

а)Найдите угол А треугольника АВС, если угол В
равен 78 градусам, а

угол С на 23 градуса больше угла В.

б) Найдите угол при основании равнобедренного
треугольника, если

угол при вершине 84 градуса.

2.На оценку “4”:

а) В равнобедренном треугольнике СДЕ с
основанием СЕ проведена высота

СК .Найдите угол ЕСК, если угол Д равен 54
градуса.

б) Постройте треугольник по катету и
противолежащему углу.

3.На оценку “5”:

а) Высота, проведенная к основанию
равнобедренного треугольника, равна

7,6 см , а боковая сторона треугольника равна 15,2
см. Найдите углы это-

го треугольника.

б) Периметр равнобедренного треугольника равен
25 см, а разность двух

сторон равна 4 см. Один из его углов — острый.
Найдите стороны

треугольника.

Зачет считается сданным, если ученик сдал
теоретическую часть и решил задачу.

Учитель может выставить за зачет две или одну
оценку. При спорных ситу-

ациях (например, задача решена верно, а теория
на оценку “3”) учитель может задать
дополнительный вопрос, либо выставить среднее
арифметическое.

Консультанты могут оказывать помощь в решении
задач только слабым учащимся, либо решают
дополнительную задачу. Решение задач на “3” и
“4” могут проверить консультанты, задачи на “5”
проверяет учитель.

Т.о., помощь консультантов значительно экономит
время и позволяет проводить небольшие по объему
зачеты во время урока.

Источник

Теоретический
блок №1 (07.05) [7 вопросов]

«Угол.
Виды углов. Их свойства. Единицы измерения углов»

1.     
Угол
—

2.     
Виды
углов:

3.     
Свойство
смежных углов «»

4.     
Свойство
вертикальных  углов «»

5.     
Свойство
внешнего угла «»

6.     
Свойство
углов треугольника «»

7.     
Единицы
измерения углов «»

Теоретический
блок №2 (12.05) [9 вопросов]

«Равнобедренный и равносторонний
треугольники. Определения, свойства, признаки равенства»

8.     
Равнобедренный
треугольник –

9.     
Равносторонний
треугольник –

10. 
Биссектриса
треугольника –

11. 
Медиана
треугольника –

12. 
Высота
треугольника –

13. 
Признак
равнобедренного треугольника «»

14. 
Свойства
равнобедренного треугольника:

15. 
Свойства
равностороннего треугольника:

16. 
Признаки
равенства треугольников:

Теоретический
блок №3 (14.05) [5 вопросов]

«Прямоугольные треугольники. Определения,
свойства и признаки равенства»

17. 
Прямоугольный
треугольник –

18. 
Гипотенуза
–

19. 
Катет
–

20. 
Свойства
прямоугольного треугольника:

21. 
Признаки
равенства прямоугольных треугольников:

Теоретический
блок №4 (19.05) [5 вопросов]

«Параллельные прямые. Определение, признаки
параллельности прямых. Виды углов при параллельных прямых и секущей, их
свойства»

22. 
Параллельные
прямые –

23. 
Признаки
параллельности прямых:

24. 
Виды
углов при пересечении двух параллельных прямых секущей:

25. 
Свойства
углов при пересечении двух параллельных прямых секущей:

26. 
Расстояние
между двумя параллельными прямыми –

Теоретический
блок №5 (21.05) [9 вопросов]

«Окружность»

27. 
Окружность
–

28. 
Круг
–

29. 
Радиус
–

30. 
Диаметр
–

31. 
Хорда
–

32. 
Дуга
–

33. 
Формула
диаметра

34. 
Формула
длины окружности

35. 
Формула
площади круга

36. 

Источник

Понравилась статья? Поделить с друзьями:
  • Как проходит устный экзамен по английскому огэ
  • Как проходит процесс получения прав в гаи после сдачи экзаменов
  • Как проходит устный экзамен вуз
  • Как проходит процесс получения водительских прав после сдачи экзамена
  • Как проходит устный экзамен в школе