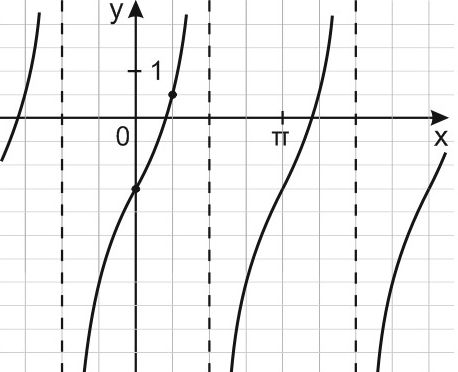
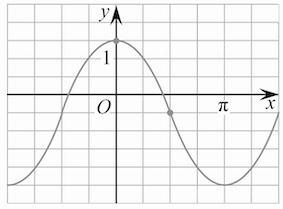
Как решать 10 задание егэ математика профиль с косинусом - Помощь в подготовке к экзаменам и поступлению

В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №10 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.

Как формулируется задание 10 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.

Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.

Вот необходимая теория для решения задания №10 ЕГЭ.

Что такое функция

Чтение графика функции

Четные и нечетные функции

Периодическая функция

Обратная функция

5 типов элементарных функций и их графики

Преобразование графиков функций

Построение графиков функций

Да, теоретического материала здесь много. Но он необходим — и для решения задания 10 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.

Рекомендации:

Запоминай, как выглядят графики основных элементарных функций. Замечай особенности графиков, чтобы не перепутать параболу с синусоидой : -)

Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?

Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.

Задание 10 в формате ЕГЭ-2021

Линейная функция

Необходимая теория

1. На рисунке изображён график функции . Найдите значение , при котором

Решение:

Найдем, чему равны k и b. График функции проходит через точки (3; 4) и (-1; -3). Подставив по очереди координаты этих точек в уравнение прямой y = kx + b, получим систему:

$left{ begin{array}{c}3k+b=4 \-k+b=-3 end{array}right..$

Вычтем из первого уравнения второе:

$left{ begin{array}{c}4k=7 \-k+b=-3 end{array};right. left{ begin{array}{c}k=frac{7}{4} \b=-frac{5}{4} end{array}right. .$

Уравнение прямой имеет вид:

$displaystyle y=frac{7}{4}x-frac{5}{4}.$

Найдем, при каком значение функции равно -13,5.

$displaystyle frac{7}{4}x-frac{5}{4}=-13,5;$

7x=-49;

x=-7.

Ответ: -7.

2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Запишем формулы функций.

Одна из них проходит через точку (0; 1) и ее угловой коэффициент равен -1. Это линейная функция y=-x+1.

Другая проходит через точки (-1; -1) и (-2; 4). Подставим по очереди координаты этих точек в формулу линейной функции y=kx+b.

$left{ begin{array}{c}-k+b=-1 \-2k+b=4 end{array}right. .$

Вычтем из первого уравнения второе.

k=-5; тогда b=-6.

Прямая задается формулой:

Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:

$left{ begin{array}{c}y=-x+1 \y=-5x-6 end{array} ;right. begin{array}{c}-x+1=-5x-6 ; \x=-frac{7}{4}=-1,75. end{array}$

Ответ: -1,75.

3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Прямая, расположенная на рисунке ниже, задается формулой y=x+1, так как ее угловой коэффициент равен 1 и она проходит через точку (-3; -2).

Для прямой, расположенной выше, угловой коэффициент равен $displaystyle frac{3}{2}=1,5.$

Эта прямая проходит через точку (-2; 4), поэтому: b=7, эта прямая задается формулой

Для точки пересечения прямых:

x=-12.

Ответ: -12.

Квадратичная функция. Необходимая теория

4. На рисунке изображен график функции Найдите b.

Решение:

На рисунке — квадратичная парабола $y={left(x-aright)}^2,$ полученная из графика функции y=x^2 сдвигом на 1 вправо, то есть a=1.

Получим: $fleft(xright)={left(x-1right)}^2=x^2-2x+1;$

b=-2.

Ответ: -2.

5. На рисунке изображен график функции $y={left(x-cright)}^2$ . Найдите с.

Решение:

На рисунке изображена парабола, ветви которой направлены вверх, значит, коэффициент при x^2 положительный. График сдвинут относительно графика функции y=x^2 на 1 единицу вправо вдоль оси Ох. Формула функции имеет вид $y={left(x-1right)}^2$ .

Значит, с = 1.

Ответ: 1

6. На рисунке изображён график функции Найдите

Решение:

График функции проходит через точки с координатами (1; 1) и (-2; -2). Подставляя координаты этих точек в формулу функции, получим:

$left{ begin{array}{c}2+b+c=1 \2cdot 4-2b+c=-2 end{array}right. .$

$left{ begin{array}{c}b+c=-1 \-2b+c=-10 end{array};right.$ отсюда b=3, c=-4.

Формула функции имеет вид:

Ответ: 31.

7. На рисунке изображены графики функций и которые пересекаются в точках А и В. Найдите абсциссу точки В.

Решение:

Найдем a, b и c в формуле функции . График этой функции пересекает ось ординат в точке (0; -3), поэтому c=-3.

График функции g(x) проходит через точки (-1; -3) и (2; 3). Подставим по очереди координаты этих точек в формулу функции:

$left{ begin{array}{c}a-b-3=-3 \4a+2b-3=3 end{array};right.$ отсюда a=b=1;

Найдем абсциссу точки B. Для точек A и B:

x=-2 (это абсцисса точки A) или x=6 (это абсцисса точки B).

Ответ: 6.

Степенные функции. Необходимая теория

8. На рисунке изображены графики функций $displaystyle fleft(xright)=frac{k}{x}$ и , которые пересекаются в точках А и В. Найдите абсциссу точки В.

Решение:

График функции $displaystyle y=frac{k}{x}$ проходит через точку (2; 1); значит, $displaystyle frac{k}{2}=1;$

$displaystyle k=2, ; fleft(xright)=frac{2}{x}.$

График функции проходит через точки (2; 1) и (1; -4), a=5 — угловой коэффициент прямой; (находим как тангенс угла наклона прямой и положительному направлению оси X); тогда b=-9.

Для точек A и B имеем:

$displaystyle frac{2}{x}=5x-9;$

Отсюда x=2 (абсцисса точки A) или x=-0,2 (абсцисса точки B).

Ответ: -0,2.

9. На рисунке изображён график функции . Найдите f (6,76).

Решение:

Функция задана формулой:

Ее график проходит через точку (4; 5); значит, k=2,5;

Тогда

Ответ: 6,5.

10. На рисунке изображен график функции . Найдите .

Решение:

График функции на рисунке симметричен графику функции относительно оси Y. Он проходит через точку (-1; 1). Значит, формула изображенной на рисунке функции: , а = — 1. Тогда = 5.

Ответ: 5.

Показательная функция. Необходимая теория

11. На рисунке изображён график функции $fleft(xright)=a^{x+b}.$ Найдите

Решение:

График функции проходит через точки (-3; 1) и (1; 4). Подставив по очереди координаты этих точек в формулу функции $fleft(xright)=a^{x+b},$ получим:

$left{ begin{array}{c}a^{-3+b}=1 \a^{1+b}=4 end{array}.right.$

Поделим второе уравнение на первое:

$a^{1+b+3-b}=4; ; a^4=4;; a=sqrt{2}.$

Подставим во второе уравнение:

$displaystyle {sqrt{2}}^{1+b}=4;; 2^{frac{1+b}{2}}=2^2;; 1+b=4;; b=3.$

$displaystyle fleft(xright)={left(sqrt{2}right)}^{x+3};; fleft(-7right)={left(sqrt{2}right)}^{-7+3}={left(sqrt{2}right)}^{-4}=frac{1}{4}=0,25.$

Ответ: 0,25.

12. На рисунке изображен график функции . Найдите

Решение:

График функции проходит через точку Это значит, что

a=2, формула функции имеет вид: .

Ответ: 2.

Логарифмическая функция. Необходимая теория

13. На рисунке изображён график функции $fleft(xright)={{log}_a left(x+bright)}.$ Найдите

Решение:

График функции $y={{log}_a left(x+bright) }$ проходит через точки (-3; 1) и (-1; 2). Подставим по очереди эти точки в формулу функции.

$left{ begin{array}{c}{{log}_a left(-3+bright)=1 } \{{log}_a left(-1+bright) }=2 end{array}.right.$

Отсюда: $left{ begin{array}{c}b-3=a \b-1=a^2 end{array}.right.$

Вычтем из второго уравнения первое:

a=2 или a=-1 — не подходит, так как (как основание логарифма).

Тогда $fleft(xright)={{log}_2 left(x+5right) };$

$fleft(11right)={{log}_2 16=4.}$

Ответ: 4.

14. На рисунке изображен график функции $fleft(xright)=a{{log}_5 x }-c$ .

Найдите f(0,2).

Решение:

График логарифмической функции на рисунке проходит через точки и . Подставив по очереди координаты этих точек в формулу функции, получим систему уравнений:

$left{ begin{array}{c}a{{log}_5 1 }-c=-2 \a{{log}_5 5 }-c=3 end{array};right.$

$left{ begin{array}{c}-c=-2 \a-c=3 end{array};right.$

$left{ begin{array}{c}c=2 \a=5 end{array}.right.$

Формула функции: $fleft(xright)=5{{log}_5 x }-2.$

Найдем $displaystyle fleft(0,2right)=fleft(frac{1}{5}right)$ :

$displaystyle 5cdot {{log}_5 frac{1}{5} }-2=-5-2=-7.$

Ответ: -7.

Тригонометрические функции. Необходимая теория

15. На рисунке изображён график функции Найдите

Решение:

График функции сдвинут на 1,5 вверх; Значит, b=1,5. Амплитуда a=2 (наибольшее отклонение от среднего значения).

Это график функции Он получен из графика функции растяжением в 2 раза по вертикали и сдвигом вверх на 1,5 .

Ответ: b=1,5.

16. На рисунке изображён график функции

Найдите .

Решение:

На рисунке — график функции Так как b=-1,5.

График функции проходит через точку A $displaystyle (frac{pi}{4}; ; frac{1}{2}).$ Подставим и координаты точки А в формулу функции.

$displaystyle a tg frac{pi}{4}-1,5=frac{1}{2}.$

Так как $displaystyle tg frac{pi}{4}=1,$ получим: a = 2.

Ответ: 2.

17. На рисунке изображен график периодической функции у = f(x). Найдите значение выражения

Решение:

Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если то

Пользуясь периодичностью функции , период которой T = 4, получим:

Ответ: 5.

Друзья, мы надеемся, что на уроках математики в школе вы решаете такие задачи. Для углубленного изучения темы «Функции и графики» (задание 10 ЕГЭ по математике), а также задач с параметрами и других тем ЕГЭ — рекомендуем Онлайн-курс для подготовки к ЕГЭ на 100 баллов.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 10 ЕГЭ по математике. Графики функций» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

В ЕГЭ 2022 года добавили новую задачу на графики функций. Для решения этой задачи нужно сначала определить формулу функции, а затем вычислить ответ на вопрос задачи. И если вычисление ответа по известной формуле обычно не составляет труда, то вот определение самой формулы часто ставит школьников в тупик. Поэтому мы разберем три разных подхода к этому вопросу.

Замечание. Про то как определяется формула у прямой и параболы я написала в этой и этой статьях. Поэтому здесь в примерах я буду использовать другие функции – дробные, иррациональные, показательные и логарифмические, но все три описанных здесь способа работают и для линейных, и для квадратичных функций в том числе.

1 способ – находим формулу по точкам

Этот способ подходит вообще для любой девятой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений.

Давайте разберем алгоритм на примере конкретной 9-ой задачи ЕГЭ:

Алгоритм:

1. Находим 2 точки с целыми координатами. Обычно они выделены жирно, но если это не так, то не проблема найти их самому.
Пример:

2. Подставляем эти координаты в «полуфабрикат» функции. Вместо (f(x))– координату игрек, вместо (x) – икс. Получается система.

3. Решаем эту систему и получаем готовую формулу.

4. Готово, функция найдена, можно переходить ко второму этапу – вычислению (f(-8)). Если вы вдруг не знаете, что это значит – в конце статьи я рассматриваю этот момент более подробно.

Давайте посмотрим метод еще раз на примере с логарифмической функцией.
Пример:

2 способ – преобразование графиков функций

Этот способ сильно быстрее первого, но требует больше знаний. Для использования преобразований функций нужно знать, как выглядят функции без изменения и как преобразования их меняют. Наиболее удобно использовать этот способ для иррациональной функции ((y=sqrt{x}) ) и функции обратной пропорциональности ((y=frac{1}{x})).

Вот как выглядит применение этого способа:

Для использования этого способа надо знать, как выглядят изначальные функции:

И понимать, как меняются функции от преобразований:

Часто даже по «полуфабрикату» функции понятно, какие преобразования сделали с функцией:

Пример:

3 способ – гибридный

Идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти. С другой стороны, независимо от оснований любая показательная функция должна проходить через точку ((0;1)), а любая логарифмическая — через точку ((1;0)).

По смещению этих точек легко понять, как именно двигали функцию, но только если ее не растягивали, а лишь перемещали вверх-вниз, влево-вправо (как обычно и бывает в задачах на ЕГЭ).

Основание же лучше находить уже следующим действием, используя подстановку координат точки в «полуфабрикат» функции.

Как отвечать на вопросы в задаче, когда уже определили функцию

— Если просят найти (f)(любое число), то нужно это число подставить в готовую функцию вместо икса.
Пример:

— Если просят найти «при каком значении x значение функции равно *любому числу*», то надо решить уравнение, в одной части которого будет функция, а в другой — то самое число. Аналогично надо поступить, если просят «найти корень уравнения (f(x)=) *любое число*».
Пример:

— Если просят найти абсциссу точки пересечения – надо приравнять 2 функции и решить получившееся уравнение. Корень уравнения и будет искомой абсциссой. Аналогично надо делать в задачах, где даны две точки пересечения (A)(*любое число*;*другое число*) и (B(x_0;y_0)) и просят найти (x_0).
Пример:

— Если просят найти ординату точки пересечения – надо приравнять 2 функции, найти иксы и подставить подходящий икс в любую функцию. Точно также решаем если просят найти (y_0) точки пересечения двух функций.
Пример:

— Иногда просят найти просто какой-либо из коэффициентов функции. Тогда надо просто восстановить функцию и записать в ответ то, о чем спросили:
Пример:

Источник

Поиск

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 364 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Боковая сторона равнобедренного треугольника равна 7, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.

В равнобедренном треугольнике ABC с основанием AB боковая сторона равна Найдите длину высоты AH.

Найдите значение выражения если

Боковая сторона равнобедренного треугольника равна 5, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.

Найдите если

Найдите значение выражения

Источник: Пробный экзамен по математике Санкт-Петербург 2014. Вариант 1., ЕГЭ по математике 29.06.2021. Резервная волна. Центр. Вариант 402

Основания равнобедренной трапеции равны 43 и 7. Высота трапеции равна 27. Найдите тангенс острого угла трапеции.

Найдите значение выражения

В треугольнике ABC угол C равен 90°, BC  =  4, Найдите АВ.

В треугольнике ABC угол C равен 90°, ВС  =  9. Найдите АС.

Найдите если

В треугольнике ABC угол C равен 90°, АС  =  4, Найдите АВ.

В треугольнике ABC угол C равен 90°, АС  =  8, Найдите BC.

В треугольнике ABC угол C равен 90°, BC  =  4, Найдите АВ.

В треугольнике ABC угол C равен 90°, ВС  =  4. Найдите АС.

Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен Найдите боковую сторону.

Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.

В треугольнике ABC угол C равен 90°, АС  =  20, Найдите BC.

Основания равнобедренной трапеции равны 27 и 33. Косинус острого угла трапеции равен Найдите боковую сторону.

Боковая сторона равнобедренного треугольника равна 27, угол при вершине, противолежащей основанию, равен Найдите диаметр описанной окружности этого треугольника.

Всего: 364 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ Профиль №10. Тригонометрические функции

ЕГЭ Профиль №10. Тригонометрические функцииadmin2023-01-16T21:35:50+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №10. Тригонометрические функции

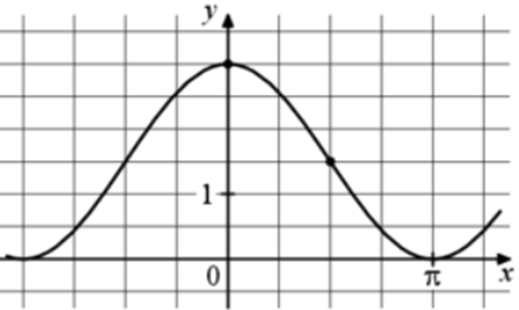
Задача 1. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите a. Ответ ОТВЕТ: 2.
Решение График функции (fleft( x right) = acos x + b) проходит через точки (left( {0;frac{3}{2}} right)) и (left( {frac{pi }{2}; — frac{1}{2}} right)). Следовательно: (left{ {begin{array}{{20}{c}}{frac{3}{2} = acos 0 + b}\{ — frac{1}{2} = acos frac{pi }{2} + b}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{{20}{c}}{frac{3}{2} = a cdot 1 + b}\{ — frac{1}{2} = a cdot 0 + b}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{a + b = frac{3}{2}}\{b = — frac{1}{2}}end{array}} right.,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Ответ: 2.
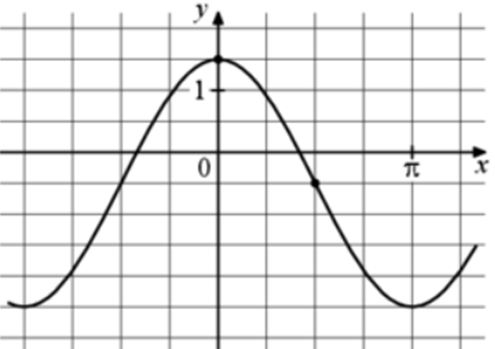
Задача 2. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите a. Ответ ОТВЕТ: 1,5.
Решение График функции (fleft( x right) = acos x + b) проходит через точки (left( {0;3} right)) и (left( {frac{pi }{2};frac{3}{2}} right)). Следовательно: (left{ {begin{array}{{20}{c}}{3 = acos 0 + b}\{frac{3}{2} = acos frac{pi }{2} + b}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{{20}{c}}{3 = a cdot 1 + b}\{frac{3}{2} = a cdot 0 + b}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{a + b = 3}\{b = frac{3}{2},,,,,}end{array}} right.,,,,,,,,, Leftrightarrow ,,,,,,,,a = frac{3}{2}.) Ответ: 1,5.
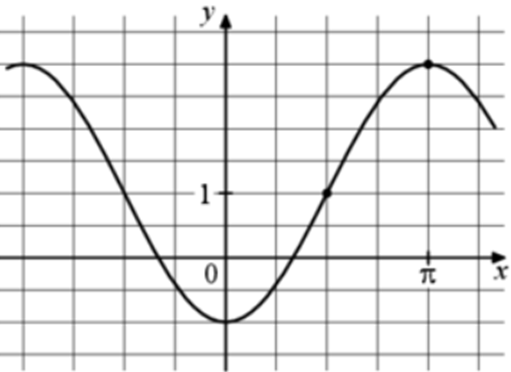
Задача 3. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите a. Ответ ОТВЕТ: — 2.
Решение График функции (fleft( x right) = acos x + b) проходит через точки (left( {0; — 1} right)) и (left( {frac{pi }{2};1} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 1 = acos 0 + b}\{ 1 = acos frac{pi }{2} + b}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{{20}{c}}{ — 1 = a cdot 1 + b}\{1 = a cdot 0 + b}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{a + b = — 1}\{b = 1,,,,,,,,,}end{array}} right.,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Ответ: – 2.
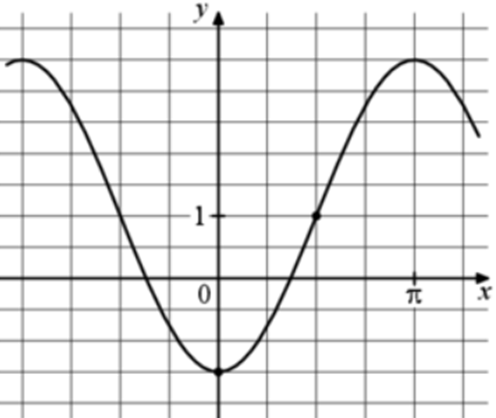
Задача 4. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите a. Ответ ОТВЕТ: — 2,5.
Решение График функции (fleft( x right) = acos x + b) проходит через точки (left( {0; — frac{3}{2}} right)) и (left( {frac{pi }{2};1} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — frac{3}{2} = acos 0 + b}\{1 = acos frac{pi }{2} + b}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{{20}{c}}{ — frac{3}{2} = a + b}\{1 = a cdot 0 + b}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{a + b = — frac{3}{2}}\{b = 1,,,,,,,,,}end{array}} right.,,,,,,,,, Leftrightarrow ,,,,,,,,a = — frac{5}{2}.) Ответ: – 2,5.
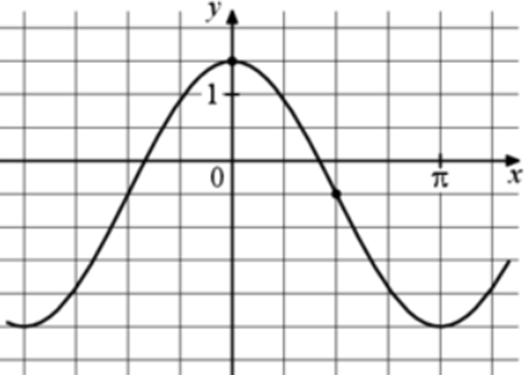
Задача 5. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите b. Ответ ОТВЕТ: — 0,5.
Решение График функции (fleft( x right) = acos x + b) проходит через точку (left( {frac{pi }{2}; — frac{1}{2}} right)). Следовательно: ( — frac{1}{2} = acos frac{pi }{2} + b,,,,,,,, Leftrightarrow ,,,,,,,,, — frac{1}{2} = a cdot 0 + b,,,,,,,, Leftrightarrow ,,,,,,,,,b = — frac{1}{2}.) Ответ: – 0,5.
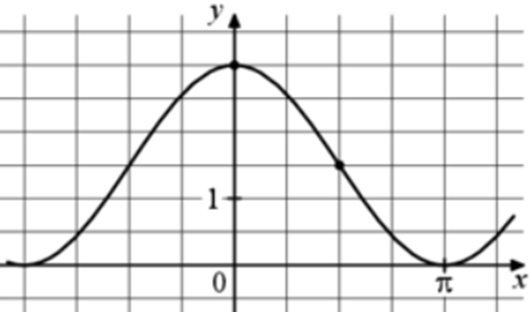
Задача 6. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите b. Ответ ОТВЕТ: 1,5.
Решение График функции (fleft( x right) = acos x + b) проходит через точку (left( {frac{pi }{2};frac{3}{2}} right)). Следовательно: (frac{3}{2} = acos frac{pi }{2} + b,,,,,,,, Leftrightarrow ,,,,,,,,,frac{3}{2} = a cdot 0 + b,,,,,,,, Leftrightarrow ,,,,,,,,,b = frac{3}{2}.) Ответ: 1,5.
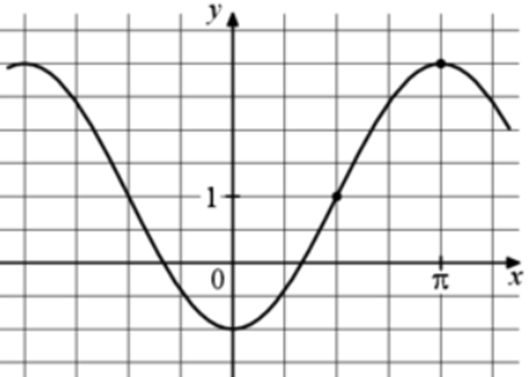
Задача 7. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите b. Ответ ОТВЕТ: 1.
Решение График функции (fleft( x right) = acos x + b) проходит через точку (left( {frac{pi }{2};1} right)). Следовательно: (1 = acos frac{pi }{2} + b,,,,,,,, Leftrightarrow ,,,,,,,,,1 = a cdot 0 + b,,,,,,,, Leftrightarrow ,,,,,,,,,b = 1.) Ответ: 1.
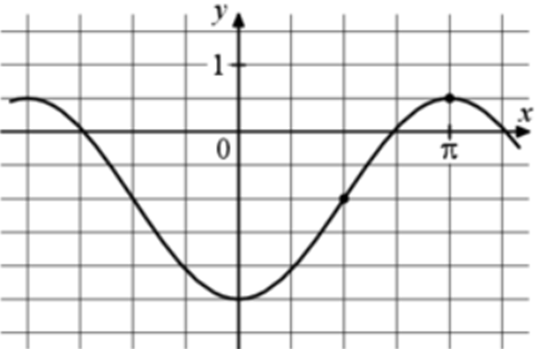
Задача 8. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите b. Ответ ОТВЕТ: — 1.
Решение График функции (fleft( x right) = acos x + b) проходит через точку (left( {frac{pi }{2}; — 1} right)). Следовательно: ( — 1 = acos frac{pi }{2} + b,,,,,,,, Leftrightarrow ,,,,,,,,, — 1 = a cdot 0 + b,,,,,,,, Leftrightarrow ,,,,,,,,,b = — 1.) Ответ: – 1.
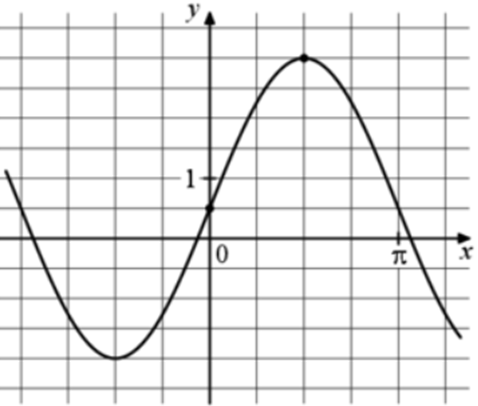
Задача 9. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите a. Ответ ОТВЕТ: 2,5.
Решение График функции (fleft( x right) = asin x + b) проходит через точки (left( {0;frac{1}{2}} right)) и (left( {frac{pi }{2};3} right)). Следовательно: (left{ {begin{array}{{20}{c}}{frac{1}{2} = asin 0 + b}\{3 = asin frac{pi }{2} + b}end{array},,,,,,,,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{{20}{c}}{frac{1}{2} = a cdot 0 + b}\{3 = a cdot 1 + b}end{array},,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{b = frac{1}{2},,,,,,,}\{a + b = 3}end{array}} right.} right.} right.,,,,,,,,, Leftrightarrow ,,,,,,,,a = frac{5}{2}.) Ответ: 2,5.
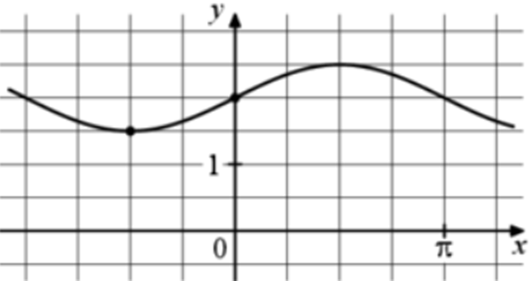
Задача 10. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите a. Ответ ОТВЕТ: 0,5.
Решение График функции (fleft( x right) = asin x + b) проходит через точки (left( {0;2} right)) и (left( {frac{pi }{2};frac{5}{2}} right)). Следовательно: (left{ {begin{array}{{20}{c}}{2 = asin 0 + b}\{frac{5}{2} = asin frac{pi }{2} + b}end{array},,,,,,,,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{{20}{c}}{2 = a cdot 0 + b}\{frac{5}{2} = a + b,,,,}end{array},,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{b = 2,,,,,,,}\{a + b = frac{5}{2}}end{array}} right.} right.} right.,,,,,,,,, Leftrightarrow ,,,,,,,,a = frac{1}{2}.) Ответ: 0,5.
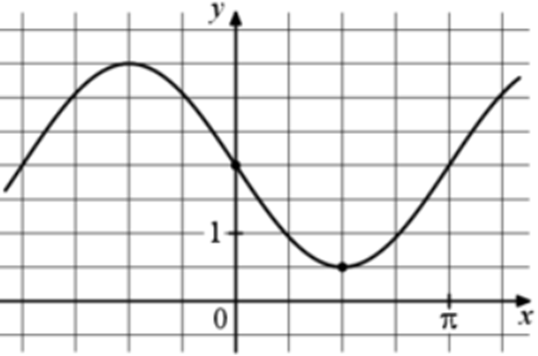
Задача 11. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите a. Ответ ОТВЕТ: — 1,5.
Решение График функции (fleft( x right) = asin x + b) проходит через точки (left( {0;2} right)) и (left( {frac{pi }{2};frac{1}{2}} right)). Следовательно: (left{ {begin{array}{{20}{c}}{2 = asin 0 + b}\{frac{1}{2} = asin frac{pi }{2} + b}end{array},,,,,,,,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{{20}{c}}{2 = a cdot 0 + b}\{frac{1}{2} = a + b,,,,,}end{array},,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{b = 2,,,,,,,}\{a + b = frac{1}{2}}end{array}} right.} right.} right.,,,,,,,,, Leftrightarrow ,,,,,,,,a = — frac{3}{2}.) Ответ: – 1,5.
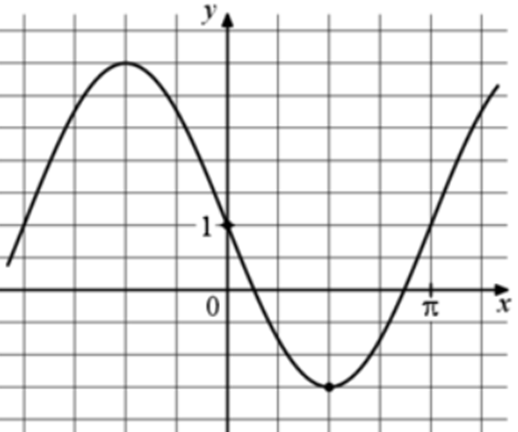
Задача 12. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите a. Ответ ОТВЕТ: — 2,5.
Решение График функции (fleft( x right) = asin x + b) проходит через точки (left( {0;1} right)) и (left( {frac{pi }{2}; — frac{3}{2}} right)). Следовательно: (left{ {begin{array}{{20}{c}}{1 = asin 0 + b}\{ — frac{3}{2} = asin frac{pi }{2} + b}end{array},,,,,,,,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{{20}{c}}{1 = a cdot 0 + b}\{ — frac{3}{2} = a cdot 1 + b,,,,,}end{array},,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{b = 1,,,,,,,}\{a + b = — frac{3}{2}}end{array}} right.} right.} right.,,,,,,,,, Leftrightarrow ,,,,,,,,a = — frac{5}{2}.) Ответ: – 2,5.

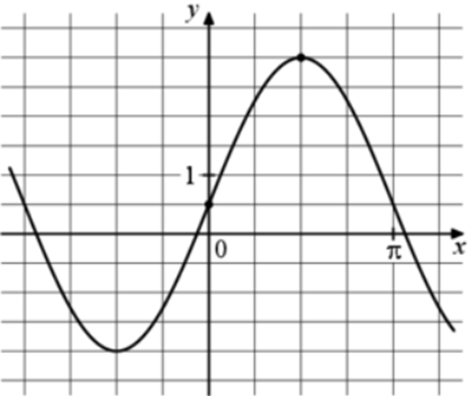
Задача 13. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите b. Ответ ОТВЕТ: 0,5.
Решение График функции (fleft( x right) = asin x + b) проходит через точку (left( {0;frac{1}{2}} right)). Следовательно: (frac{1}{2} = asin 0 + b,,,,,,,, Leftrightarrow ,,,,,,,,,,frac{1}{2} = a cdot 0 + b,,,,,,,, Leftrightarrow ,,,,,,,,b = frac{1}{2}.) Ответ: 0,5.
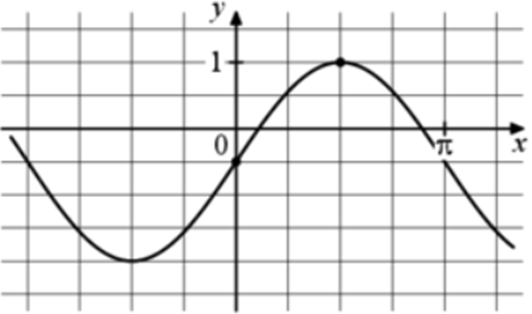
Задача 14. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите b. Ответ ОТВЕТ: — 0,5.
Решение График функции (fleft( x right) = asin x + b) проходит через точку (left( {0; — frac{1}{2}} right)). Следовательно: ( — frac{1}{2} = asin 0 + b,,,,,,,, Leftrightarrow ,,,,,,,,,, — frac{1}{2} = a cdot 0 + b,,,,,,,, Leftrightarrow ,,,,,,,,b = — frac{1}{2}.) Ответ: – 0,5.
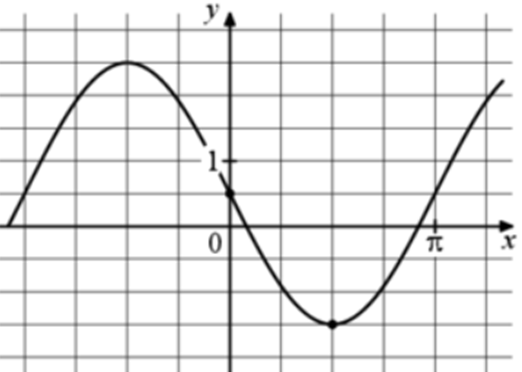
Задача 15. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите b. Ответ ОТВЕТ: 0,5.
Решение График функции (fleft( x right) = asin x + b) проходит через точку (left( {0;frac{1}{2}} right)). Следовательно: (frac{1}{2} = asin 0 + b,,,,,,,, Leftrightarrow ,,,,,,,,,,frac{1}{2} = a cdot 0 + b,,,,,,,, Leftrightarrow ,,,,,,,,b = frac{1}{2}.) Ответ: 0,5.
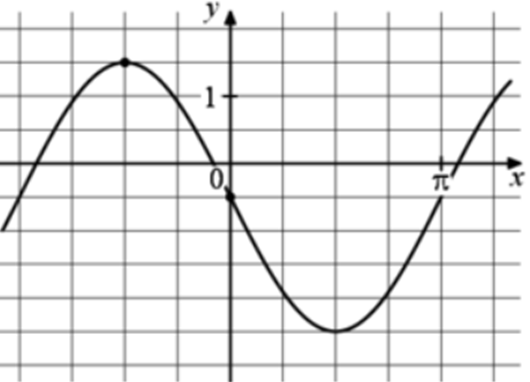
Задача 16. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите b. Ответ ОТВЕТ: — 0,5.
Решение График функции (fleft( x right) = asin x + b) проходит через точку (left( {0; — frac{1}{2}} right)). Следовательно: ( — frac{1}{2} = asin 0 + b,,,,,,,, Leftrightarrow ,,,,,,,,,, — frac{1}{2} = a cdot 0 + b,,,,,,,, Leftrightarrow ,,,,,,,,b = — frac{1}{2}.) Ответ: – 0,5.
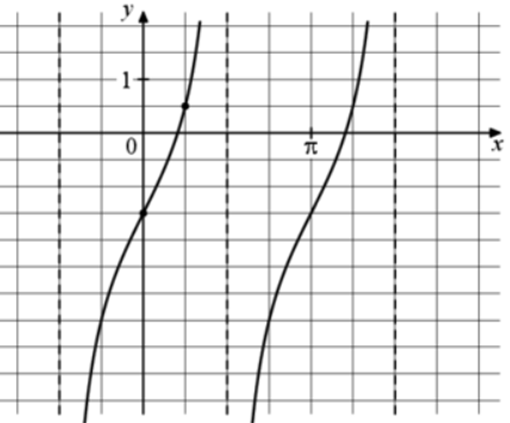
Задача 17. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите a. Ответ ОТВЕТ: 2.
Решение График функции (fleft( x right) = a,tgx + b) проходит через точки (left( {0; — frac{3}{2}} right)) и (left( {frac{pi }{4};frac{1}{2}} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — frac{3}{2} = a,tg,0 + b}\{frac{1}{2} = a,tgfrac{pi }{4} + b}end{array},,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{{20}{c}}{ — frac{3}{2} = a cdot 0 + b}\{frac{1}{2} = a cdot 1 + b}end{array},,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{b = — frac{3}{2}}\{a + b = frac{1}{2}}end{array},,,,,,,,, Leftrightarrow ,,,,,,,a = 2.} right.} right.} right.) Ответ: 2.
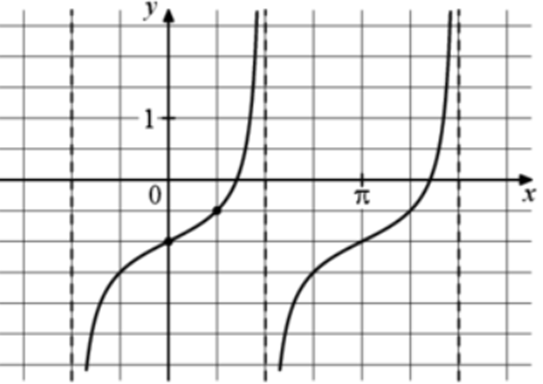
Задача 18. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите a. Ответ ОТВЕТ: 0,5.
Решение График функции (fleft( x right) = a,tgx + b) проходит через точки (left( {0; — 1} right)) и (left( {frac{pi }{4}; — frac{1}{2}} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 1 = a,tg0 + b}\{ — frac{1}{2} = a,tgfrac{pi }{4} + b}end{array},,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{{20}{c}}{ — 1 = a cdot 0 + b}\{ — frac{1}{2} = a cdot 1 + b}end{array},,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{b = — 1}\{a + b = — frac{1}{2}}end{array},,,,,,,,, Leftrightarrow ,,,,,,,a = frac{1}{2}.} right.} right.} right.) Ответ: 0,5.
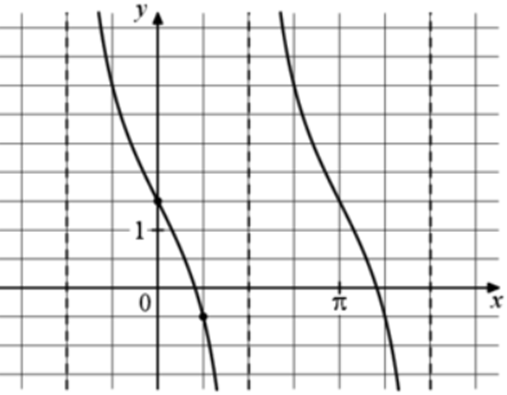
Задача 19. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите a. Ответ ОТВЕТ: — 2.
Решение График функции (fleft( x right) = a,tgx + b) проходит через точки (left( {0;frac{3}{2}} right)) и (left( {frac{pi }{4}; — frac{1}{2}} right)). Следовательно: (left{ {begin{array}{{20}{c}}{frac{3}{2} = a,tg0 + b}\{ — frac{1}{2} = a,tgfrac{pi }{4} + b}end{array},,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{{20}{c}}{frac{3}{2} = a cdot 0 + b}\{ — frac{1}{2} = a cdot 1 + b}end{array},,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{b = frac{3}{2},,,,,,,,,,}\{a + b = — frac{1}{2}}end{array},,,,,,,,, Leftrightarrow ,,,,,,,a = — 2.} right.} right.} right.) Ответ: – 2.
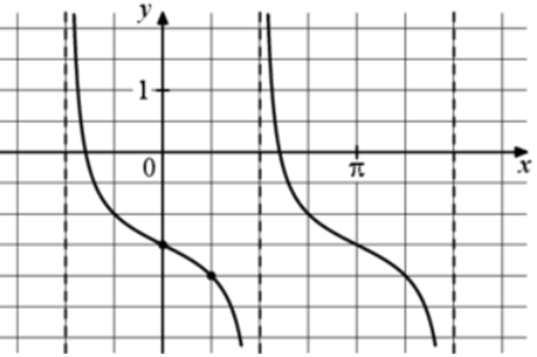
Задача 20. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите a. Ответ ОТВЕТ: — 0,5.
Решение График функции (fleft( x right) = a,tgx + b) проходит через точки (left( {0; — frac{3}{2}} right)) и (left( {frac{pi }{4}; — 2} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — frac{3}{2} = a,tg0 + b}\{ — 2 = a,tgfrac{pi }{4} + b}end{array},,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{{20}{c}}{ — frac{3}{2} = a cdot 0 + b}\{ — 2 = a cdot 1 + b}end{array},,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{b = — frac{3}{2},,,,,,,,,,}\{a + b = — 2}end{array},,,,,,,,, Leftrightarrow ,,,,,,,a = — frac{1}{2}.} right.} right.} right.) Ответ: – 0,5.
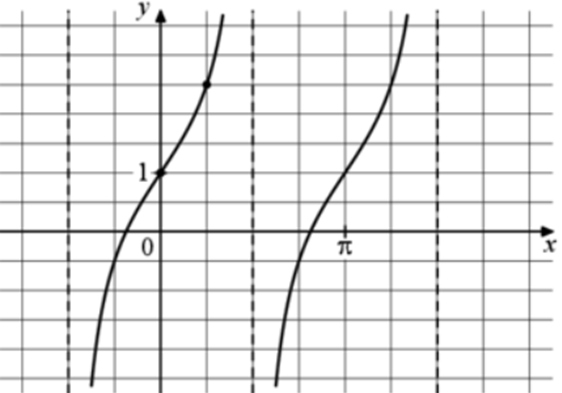
Задача 21. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите b. Ответ ОТВЕТ: 1.
Решение График функции (fleft( x right) = atgx + b) проходит через точку (left( {0;1} right)). Следовательно: (1 = a cdot tg0 + b,,,,,,,, Leftrightarrow ,,,,,,,,,1 = a cdot 0 + b,,,,,,,,, Leftrightarrow ,,,,,,,,,,b = 1.) Ответ: 1.
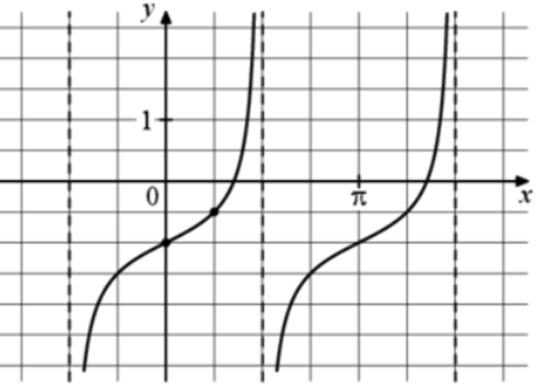
Задача 22. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите b. Ответ ОТВЕТ: — 1.
Решение График функции (fleft( x right) = a,tgx + b) проходит через точку (left( {0; — 1} right)). Следовательно: ( — 1 = a cdot tg0 + b,,,,,,,, Leftrightarrow ,,,,,,,,, — 1 = a cdot 0 + b,,,,,,,,, Leftrightarrow ,,,,,,,,,,b = — 1.) Ответ: – 1.
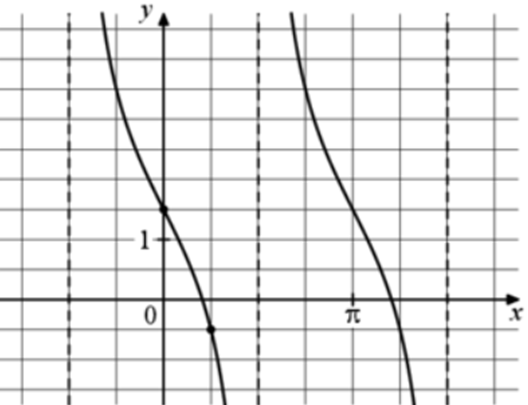
Задача 23. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите b. Ответ ОТВЕТ: 1,5.
Решение График функции (fleft( x right) = a,tgx + b) проходит через точку (left( {0;frac{3}{2}} right)). Следовательно: (frac{3}{2} = a cdot tg0 + b,,,,,,,, Leftrightarrow ,,,,,,,,,frac{3}{2} = a cdot 0 + b,,,,,,,,, Leftrightarrow ,,,,,,,,,,b = frac{3}{2}.) Ответ: 1,5.
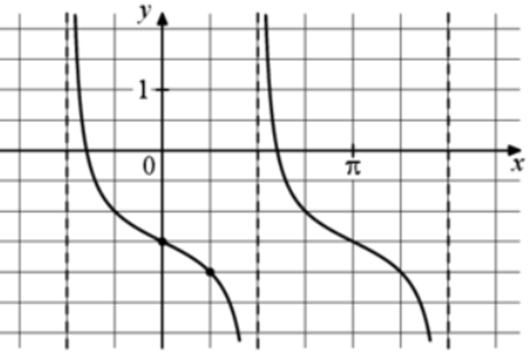
Задача 24. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите b. Ответ ОТВЕТ: — 1,5.
Решение График функции (fleft( x right) = a,tgx + b) проходит через точку (left( {0; — frac{3}{2}} right)). Следовательно: ( — frac{3}{2} = a cdot tg0 + b,,,,,,,, Leftrightarrow ,,,,,,,,, — frac{3}{2} = a cdot 0 + b,,,,,,,,, Leftrightarrow ,,,,,,,,,,b = — frac{3}{2}.) Ответ: – 1,5.