На уроке рассмотрен разбор 19, 20, 21 задания ЕГЭ по информатике: дается подробное объяснение и решение задания
Содержание:
- Объяснение заданий 19, 20 и 21 ЕГЭ по информатике
- Теория игр. Поиск выигрышной стратегии
- Решение 19, 20, 21 заданий ЕГЭ по информатике
- Игра с двумя кучами камней или табличка
- Задания для тренировки 19, 20, 21 заданий ЕГЭ (взяты из КИМ и сборников прошлых лет)
- Игра с одной кучей камней
- Игра с набором слов
Объяснение заданий 19, 20 и 21 ЕГЭ по информатике
19-е задание: «Анализ алгоритма логической игры»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 6 минут.
Проверяемые элементы содержания: Умение анализировать алгоритм логической игры
20-е задание: «Поиск выигрышной стратегии»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 6 минут.
Проверяемые элементы содержания: Умение найти выигрышную стратегию игры
21-е задание: «Дерево игры для выигрышной стратегии»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 10 минут.
Проверяемые элементы содержания: Умение построить дерево игры по заданному алгоритму и найти выигрышную стратегию
До ЕГЭ 2021 года — эти задания были объединены в задание № 26 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Для пункта 2 или 3 в представленной стратегии рассмотрены не все возможные ходы проигрывающего игрока, которые он может сделать при игре выигрывающего игрока по выигрышной стратегии.
Для пункта 3 представлено дерево игры, содержащее лишние ветви, не относящиеся к выигрышной стратегии.
Дерево, являющееся частью ответа на пункт 3, представлено с использованием ссылок на
фрагменты, являющиеся решениями других пунктов задания.
В задании спрашивается, в частности, кто выиграет, а в ответе не указан в явном виде выигрывающий игрок. На все вопросы, поставленные в задании, должны быть даны чёткие ответы. Ответ на вопрос о выигрышной стратегии в стиле «Может выиграть первый игрок, но если он неправильно пойдёт, то выиграет второй» является ошибочным, поскольку выигрышная стратегия одного игрока не оставляет возможности победы другому игроку»
ФГБНУ «Федеральный институт педагогических измерений»
* Некоторые изображения и примеры страницы взяты из материалов презентации К. Полякова
Теория игр. Поиск выигрышной стратегии
Для решения 19 задания необходимо вспомнить следующие темы и понятия:
- для того чтобы найти выигрышную стратегию в несложных играх, достаточно использовать метод перебора всех возможных вариантов ходов игроков;
- для решения задач 19 задания чаще всего для этого применяется метод построения деревьев;
- если от каждого узла дерева отходят две ветви, т.е. возможные варианты хода, то такое дерево называется двоичным (если из каждой позиции есть три варианта продолжения, дерево будет троичным).
- все позиции в простых играх делятся на выигрышные и проигрышные;
- выигрышная позиция – это такая позиция, в которой игрок, делающий первый ход, обязательно выиграет при любых действиях соперника, если не допустит ошибки; при этом говорят, что у данного игрока есть выигрышная стратегия – алгоритм выбора очередного хода, позволяющий ему выиграть;
- если игрок, делающий первый ход, находится в проигрышной позиции, то он обязательно проиграет, если ошибку не сделает его оппонент; в этом случае говорят, что у данного игрока нет выигрышной стратегии; таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для оппонента;
- выигрышные и проигрышные позиции характеризуются так:
- позиция, из которой все возможные ходы ведут в выигрышные позиции – проигрышная;
- позиция, из которой хотя бы один из последующих возможных ходов ведет в проигрышную позицию — выигрышная, при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для оппонента) позицию.
- для того чтобы определить, какой из игроков выиграет при стратегически правильной игре, необходимо ответить на вопросы:
- Может ли какой-либо из игроков выиграть, независимо от ходов других игроков?
- Что должен сделать игрок с выигрышной стратегией первым ходом, чтобы он смог выиграть, независимо от действий ходов игроков?
Выигрышная стратегия
Выигрышные и проигрышные позиции
Кто выиграет при стратегически правильной игре?
Рассмотрим пример:
Игра: в кучке лежит 5 спичек; играют два игрока, которые по очереди убирают спички из кучки; условие: за один ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке 1 спичку
Решение:
- Будем использовать метод построения дерева. Первый играющий может убрать одну спичку (в этом случае их останется 4) или сразу 2 (останется 3), эти два варианта отобразим при помощи дерева:
- если первый игрок оставил 4 спички, второй может своим ходом оставить 3 или 2; а если после первого хода осталось 3 спички, второй игрок может выиграть, взяв две спички и оставив одну:
- если осталось 3 или 2 спички, то 1-ый игрок (в обеих ситуациях) выиграет своим ходом:
- если первый игрок своим первым ходом взял две спички, то второй сразу выигрывает; если же он взял одну спичку, то своим вторым ходом он может выиграть, независимо от хода второго игрока;
- итак, убрав всего одну спичку первым ходом, 1-ый игрок всегда может выиграть на следующем ходу;
- тогда как второй игрок не может выиграть, независимо от действий первого: потому что, если первый игрок сначала убрал одну спичку, второй всегда проиграет.
проанализируем стратегию игры:
Ответ: при правильной игре (стратегии игры) выиграет первый игрок; для этого ему достаточно своим первым ходом убрать одну спичку.
Решение 19, 20, 21 заданий ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Игра с двумя кучами камней или табличка
19_8:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 59. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 59 или больше камней.
В начальный момент в первой куче было 5 камней, во второй куче – S камней; 1 ≤ S ≤ 53.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Задание 20 ЕГЭ.
Найдите минимальное значение S, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Задание 21 ЕГЭ.
Найдите два значения S, при которых одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Найденные значения запишите в ответе в порядке возрастания.
✍ Решение:
- Нарисуем таблицу, в первом столбце которой будем откладывать количество камней в первой куче, а в первой строке — количество камней во второй куче. Получим матрицу. Поскольку в первой куче количество начинается с 5, то это и будет первым значением в таблице. Во второй куче начнем с наибольшего возможного числа — 53. Таблица пригодится для решения заданий 20 и 21:
- Для начала найдем все выигрышные позиции для первой строки таблицы, т.е. для первого хода. Обозначим их плюсами (
+): - Для того, чтобы получить наименьшее значение
S, в качестве первого хода Пети необходимо увеличивать в два раза вторую кучу. Т.е. для решения задания необходимо найти такое наименьшееS, при котором Петя походил неверно, и попал своим ходом в выигрышную позицию для своего соперника, т.е. в ячейку с плюсом:
Выигрышные позиции для первой строки ищем по принципу увеличения количества камней S в 2 два раза: 5 + S*2 >=59. Получим S>=27
S = 14 1 ход Петя: 14*2 = (5,28) 2 ход Ваня: 28*2 = (5,56), Сумма = 61, Выигрыш!
Ответ: 14
✎ Задание 20:
- Проанализируем таблицу, и для каждой строки найдем выигрышные позиции с одного хода. Т.е. которые позволят игроку, оказавшемуся «на них», выиграть за один ход (получить суммарно 59 и более камней):
- Найдем проигрышные позиции: те, которые ведут только в выигрышные позиции для соперника (ведут только в плюсы)
- В задании требуется найти минимальное
S, котором выиграет Петя, но выиграет он НЕ первым своим ходом, а вторым. То есть в нашем случае необходимо найтиS, которое может перевести соперника в проигрышную позицию. То есть в минус. Для первой строки (так как первым будет ходить Петя) таких значений два: - Наименьшее S = 24
При заполнении таблицы выигрышными позициями можно проследить закономерность «узора», а заполнять позиции по аналогии.
Проигрышные позиции: (6,26) (8,25) (10,24) (12,23) (14,22)
- Для решения этого задания найдем выигрышные позиции со второго хода, т.е. которые могут перевести соперника в проигрышную позицию (с минусом):
- Чтобы выиграл Ваня, но выиграл не первым ходом, а вторым, необходимо, чтобы Петя находился в такой позиции, которая ведет его только на выигрышные позиции со второго хода:

Ответ: 23 25
>19_9:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя.
За один ход игрок может убрать из одной из куч один камень или уменьшить количество камней в куче в два раза (если количество камней в куче нечётно, остаётся на 1 камень больше, чем убирается).
Например, пусть в одной куче 6, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из позиции (6, 9) можно получить любую из четырёх позиций: (5, 9), (3, 9), (6, 8), (6, 5).
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не более 20. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 20 или меньше камней. В начальный момент в первой куче было 10 камней, во второй куче – S камней, S > 10.
Найдите значение S, при котором Ваня выигрывает своим первым ходом при любой игре Пети?
Задание 20 ЕГЭ.
Найдите минимальное и максимальное значение S, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Задание 21 ЕГЭ.
Найдите значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
✍ Решение (Excel):
✎ Задание 19:
- В столбце
Аотложим значения — количество камней в первой куче. Начнем с ячейкиА2, в которую внесем начальное количество камней, т.е. 10. Автозаполнением продлим значения вниз до 0: - В строке 1 таблицы (начиная с ячейки
B1) отложим значения для второй кучи. Поскольку в задании говорится, что победа будет достигнута при S<=20, и достигнуть этого значения более сильной командой можно уменьшив кол-во камней во второй куче в два раза, начиная с числа 40: 40/20. То есть возьмем значение больше 40, примерно 45. Используем автозаполнение до значения 11: - Из двух команд, которые могут выполнять игроки, выберем наиболее сильную, т.е. благодаря которой можно быстрее достичь выигрышного диапазона и попасть в значения S<=20. Это команда уменьшения количества камней в два раза, т.е.
/2. - Для каждой из ячеек полученной таблицы рассчитаем значение, полученное в результате уменьшения в два раза той кучи камней, в которой большее количество камней (так как это даст меньший результат). Например, для ячейки
С5, в которой игрок имеет в первой куче 7 камней, а во второй куче 44 камня, мы бы выполнили действие 44/2+7. Т.е. уменьшили вдвое вторую кучу, т.к. в ней больше камней. Еще необходимо обращать внимание на четность и нечетность значений (в Excel это функцияЕНЕЧЁТ— возвращает ИСТИНУ, если значение нечетно). - Чтобы автоматизировать процесс необходимо использовать формулу, в которой найдем максимальное значение из двух вариантов:
Минимальное из (ЕСЛИ(ЕНЕЧЁТ(1-я куча)то(1-я куча+1)/2+2-я куча,иначе1-я куча/2+2-я куча);ЕСЛИ(ЕНЕЧЁТ(2-я куча)то(2-я куча+1)/2+1-я куча,иначе2-я куча/2+1-я куча)).
B2:= МИН(ЕСЛИ(ЕНЕЧЁТ($A2);($A2+1)/2+B$1;$A2/2+B$1);ЕСЛИ(ЕНЕЧЁТ(B$1);(B$1+1)/2+$A2;B$1/2+$A2))
$ будем использовать для фиксации столбца А и строки 1 при копировании формулы.
Ответ: 21
✎ Задание 20:
- Продолжаем работать с той же таблицей, что и в задании 19. Выделим все проигрышные позиции (из которых можно походить только в выигрышные позиции для соперника, т.е. в выделенные ячейки):
- Петя может выиграть свои вторым ходом, если он не может выиграть первым ходом, но может выполнить ход в позицию, проигрышную для соперника (в ячейку, выделенную красным). Такие позиции назовем выигрышные позиции со второго хода. Найдем минимальное и максимальное значение
Sпри таком первом ходе Пети:
При S=44 Пете необходимо уменьшить 2-ю кучу вдвое (44/2 = 22), чтобы оказаться в проигрышной позиции для соперника.
Ответ: 22 44
✎ Задание 21:
- Выделим все такие выигрышные позиции со второго хода:
- Далее придерживаемся следующей логики: Ваня сможет выиграть свои первым или вторым ходом, но при этом не гарантированно первым ходом, если у Пети будет возможность выполнить ходы только в позиции выигрышные со второго хода. Найдем такое S:
При S = 24 Петя сможет уменьшить кучи на один камень, и тогда оказывается в выделенной зеленой области — выигрышные позиции со второго хода для Вани, либо уменьшить количество камней вдвое, и тогда Ваня оказывается в выигрышной позиции с первого хода (розовая область).
Ответ: 24
19_7: с экзамена ЕГЭ 2020г. (со слов учащегося):
Два игрока, Петя и Ваня, играют в следующую игру. На табличке написаны два значения. Оба игрока в свой ход могут заменить одно из значений на сумму обеих (по своему выбору). Первый ход делает Петя. Игра считается законченной когда сумма обеих значений равняется не меньше 56. То есть выигрывает игрок, получивший 56 или более в сумме. Начальное значение (10, S).
Найдите максимальное S при котором Петя не может выиграть первым ходом.
Задание 20 ЕГЭ.
У кого из игроков есть выигрышная стратегия при начальном значении (9, 15).
Задание 21 ЕГЭ.
У кого из игроков есть выигрышная стратегия при начальном значении (3,7)? Опишите эту стратегию и изобразите дерево всех возможных партий
при этой стратегии
.
Типовые задания для тренировки
✍ Решение:
- Задание 19.
Максимальное S при котором Петя НЕ может выиграть своим первым ходом S = 22. Петя проиграет, если в сумме получится 55 и меньше. Первое значение = 10, необходимо найти второе значение, при этом максимальное. Схематично отобразим варианты ходов:
(10,22) - ход Пети - (10+22, 22) - итог суммы обеих значений таблички: 32 + 22 = 54 (<56)
Для того, чтобы сделать сумму большей, Петя заменит первое значение на сумму, так как оно меньше второго значения (10<22)
В начальной позиции (9, 15) выигрышная стратегия есть у Вани. Для себя отобразим схематично выигрышную партию Вани:
Зеленым цветом выделены выигрышные ходы.
В начальной позиции (3, 7) выигрышная стратегия есть у Вани. Изобразим дерево всех возможных партий при этой стратегии (раз говорится «при этой стратегии» имеем в виду, выигрышную стратегию Вани):

Дерево для выигрышной стратегии Вани: для Вани отображены только ходы по стратегии, для Пети — все возможные ходы. Зеленым цветом — выигрышный ход, красная обводка — ход по стратегии.
Решение подобного задания в Excel смотрите на видео:
📹 Видео
📹 Видеорешение на RuTube здесь
19_6:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) два камня или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 44.
Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, что в кучах всего будет 44 или больше камней.
В начальный момент в первой куче было 5 камней, во второй куче – S камней; 1 ≤ S ≤ 38.
Задание 19 ЕГЭ.
При каких S: 1а) Петя выигрывает первым ходом; 1б) Ваня выигрывает первым ходом?
Задание 20 ЕГЭ.
Назовите одно любое значение S, при котором Петя может выиграть своим вторым ходом.
Задание 21 ЕГЭ.
Назовите значение S, при котором Ваня выигрывает своим первым или вторым ходом.
✍ Решение:
- Нарисуем таблицу, в первом столбце которой будем откладывать количество камней в первой куче, а в первой строке — количество камней во второй куче. Получим матрицу. Поскольку в первой куче количество начинается с 5, то это и будет первым значением в таблице. Во второй куче начнем с наибольшего возможного числа — 38:
- Далее будем рассуждать так: Петя может выиграть первым ходом, выполнив команду *2 (увеличить количество камней в куче в два раза), если вместо S (кол-во камней во второй куче), мы будем изменять значение, начиная от 20, до последнего возможного по условию значения 38:
Задание 19 а):
5 + 20*2 = 45 (>44) * 5 - кол-во камней в первой куче, оно не меняется по условию
+ означает выигрышную позицию с первого хода:Ответ 1 а):
S = [20;38] (На ЕГЭ пояснить ходы, например: (5; 20) -> (Ход Пети)-> (5;40); 40 + 5 = 45)
Задание 19 б):
+). Отметим такие позиции, учитывая, что это первый ход Пети, и кол-во камней в первой куче должно быть 5. Найденные позиции будут проигрышными позициями (-):S = 19 (На ЕГЭ пояснить ходы, например: (5; 19) -> (Ходы Пети): (5;21),(5;28);(7;19);(7;28). Везде следующим ходом выиграет Ваня, см. предыдущ. пункт)
Задание 20:
2+):
S = 16, 17 или 18 (На ЕГЭ пояснить ходы, ссылаясь на объяснения в предыдущих пунктах)
Задание 21:
+), либо в позицию выигрышную со второго хода или n-го хода (2+). Это позиция при S = 14:
Ответ 3: S = 14 (На ЕГЭ пояснить ходы, ссылаясь на объяснения в предыдущих пунктах)
📹 YouTube здесь
Видеорешение на RuTube здесь
Задания для тренировки 19, 20, 21 заданий ЕГЭ (взяты из КИМ и сборников прошлых лет)
Игра с одной кучей камней
19_3: Демоверсия ЕГЭ 2018 информатика:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 29 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Задание 19 ЕГЭ
а) Укажите такие значения числа S, при которых Петя может выиграть в один ход.
б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
Задание 20 ЕГЭ
Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причем:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Для указанных значений S опишите выигрышную стратегию Пети.
Задание 21 ЕГЭ
Укажите значение S, при котором:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На ребрах дерева указывайте, кто делает ход; в узлах — количество камней в позиции
Дерево не должно содержать партий, невозможных при реализации выигрывающим игроком своей выигрышной стратегии. Например, полное дерево игры не является верным ответом на это задание.
✍ Решение:
-
Задание 19.
- а) Петя может выиграть, если S = 15, … 28
15, ..., 28 - выигрышные позиции с первого хода
S = 14 Петя: 14 + 1 = 15 выигрышная позиция (см. п. а). Выигрывает Ваня Петя: 14 * 2 = 28 выигрышная позиция (см. п. а). Выигрывает Ваня 14 - проигрышная позиция
Задание 20.
S = 7 Петя: 7 * 2 = 14 проигрышная позиция (см. п. 1 б). Выигрывает Петя S = 13 Петя: 13 + 1 = 14 проигрышная позиция (см. п. 1 б). Выигрывает Петя 7, 13 - выигрышные позиции со второго хода
Задание 21.
S = 12 Петя: 12 + 1 = 13 Ваня: 13 + 1 = 14 проигрышная позиция (см. п. 1 б). Выигрывает Ваня вторым ходом!
В таблице изображено дерево возможных партий (и только их) при описанной стратегии Вани. Заключительные позиции (в них выигрывает Ваня) подчеркнуты. На рисунке это же дерево изображено в графическом виде.
Дерево всех партий, возможных при стратегии Вани:
* красный круг означает выигрыш
19_4: Досрочный егэ по информатике 2018, вариант 1. Задание 19:
Два игрока, Паша и Вася, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Паша. За один ход игрок может добавить в кучу один или четыре камня или увеличить количество камней в куче в пять раз. Игра завершается в тот момент, когда количество камней в куче становится не менее 69.
Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 69 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 68.
а) Укажите все такие значения числа S, при которых Паша может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S.
б)Укажите такое значение S, при котором Паша не может выиграть за один ход, но при любом ходе Паши Вася может выиграть своим первым ходом. Опишите выигрышную стратегию Васи.
Задание 20 ЕГЭ.
Укажите 2 таких значения S, при которых у Паши есть выигрышная стратегия, причём Паша не может выиграть за один ход и может выиграть своим вторым ходом независимо от того, как будет ходить Вася. Для каждого указанного значения S опишите выигрышную стратегию Паши.
Задание 21 ЕГЭ.
Укажите хотя бы одно значение S, при котором у Васи есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Паши, и у Васи нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите выигрышную стратегию Васи. Постройте дерево всех партий, возможных при этой выигрышной стратегии Васи (в виде рисунка или таблицы).
Типовые задания для тренировки
✍ Решение:
-
19.
а) S ≥ 14. При количестве камней в куче от 14 и выше Паше необходимо увеличить их количество в пять раз, тем самым получив 70 или более камней.
S ≥ 14 выигрышные позиции
б) S = 13. Паша своим первым ходом может сделать 14, 17 или 65 камней, после этого Вася увеличивает количество в пять раз, получая 70, 85 или 325 камней в куче.
S = 13 Паша 1 ход: 13 + 1 = 14 Паша 1 ход: 13 + 4 = 17 Паша 1 ход: 13 * 5 = 65 Ваня 1 ход: [14, 17, 65] * 5 = S ≥ 14 Ваня выигрывает 13 - проигрышная позиция
20. S = 9, 12. Для данных случаев Паше необходимо прибавить 4 камня к куче из 9 камней, либо 1 камень к куче из 12, и получить кучу из 13 камней.
После чего игра сводится к стратегии, описанной в пункте 1б.
S = 13 Паша 1 ход: 9 + 4 = 13 Паша выигрывает Паша 1 ход: 12 + 1 = 13 Паша выигрывает 9, 12 - выигрышные позиции со второго хода
21. S = 8. Своим первым ходом Паша может сделать количество камней в куче 9, 12 или 40. Если Паша увеличивает кол-во в пять раз, тогда Вася выигрывает своим первым ходом, увеличивая количество камней в пять раз.
Для случая 9 и 12 камней Вася использует стратегию, указанную в п.2.
S = 8 Паша 1 ход: 8 + 1 = 9 Ваня Выигрывает (см. п.2) Паша 1 ход: 8 + 4 = 12 Ваня Выигрывает (см. п.2) Паша 1 ход: 8 * 5 = 40

Аналитическое решение 19 задания смотрите на видео:
📹 YouTube здесь
Видеорешение на RuTube здесь
19_1:
Два игрока, Паша и Валя, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Паша. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Например, имея кучу из 7 камней, за один ход можно получить кучу из 14 или 8 камней. У каждого игрока, чтобы сделать ход, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 28. Если при этом в куче осталось не более 44 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. Например, если в куче было 23 камня, и Паша удвоит количество камней в куче, то игра закончится и победителем будет Валя. В начальный момент в куче было S камней, 1≤ S ≤ 27.
Задание 19 ЕГЭ
а) При каких значениях числа S Паша может выиграть в один ход? Укажите все такие значения и соответствующие ходы Паши.
б) У кого из игроков есть выигрышная стратегия при S = 26, 25, 24? Опишите выигрышные стратегии для этих случаев.
Задание 20 ЕГЭ
У кого из игроков есть выигрышная стратегия при S = 13, 12? Опишите соответствующие выигрышные стратегии.
Задание 21 ЕГЭ
У кого из игроков есть выигрышная стратегия при S = 11? Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На ребрах дерева указывайте, кто делает ход; в узлах — количество камней в позиции.
✍ Решение:
а) Паша имеет выигрышную стратегию и может выиграть за один ход, если S = 27: тогда ему достаточно добавить один камень, чтобы игра закончилась при 28 камнях в куче; или если S = 14, 15, 16, 17, 18, 19, 20, 21, 22 (44/2 = 22 и 28/2 = 14, т.е. от 14 до 22): тогда необходимо удвоить кучу.
S=27 Паша: 27 + 1 = 28 - Выигрыш! 27 - выигрышная позиция
б) При S = 26 выигрышная стратегия есть у Вали. Паша делает ход первым, у него есть возможность либо удвоить количество камней в куче, и тогда количество превысит 44, — выигрывает Валя; либо увеличить количество на один камень, станет 27 камней: следующая Валя, — она может положить один камень и выиграть.
S=26 Паша: 26 * 2 = 52 Валя выигрывает! или: Паша: 26 + 1 = 27 Валя: 27 + 1 = 28 - Выигрыш! 26 - проигрышная позиция
При S = 25 выигрышная стратегия есть у Паши. Удваивать количество камней нет смысла, т.к. количество превысит 44, значит, Паша добавит один камень, их станет 26, следующая Валя, — она может либо добавить камень (станет 27 камней, следующим ходом выиграет Паша) либо удвоить — и сразу проиграть, т.к. станет более 44 камней.
S=25 Паша: 25 + 1 = 26 Валя: 26 ... проигрышная позиция (см. выше) Паша выигрывает! 25 - выигрышная позиция
При S = 24 выигрышная стратегия есть у Вали. Паша делает ход первым: удваивать кучу нет смысла, т.к. в ней станет более 44, значит, Паша добавит один камень, их станет 25; следующая — Валя: она может только добавить один камень (станет 26 камней, следующим ходом Паша оказывается в проигрышной позиции, см. пункт при S = 26).
S=24 Паша: 24 + 1 = 25 Валя: 25 ... выигрышная позиция (см. выше) Валя выигрывает! 24 - проигрышная позиция
Задание 20 ЕГЭ:
При S = 13 или S = 12 выигрышная стратегия есть у Паши. Паша удваивает количество и в куче остается 26 или 24 камня. Это проигрышная позиция для того, кто ходит (см. п. 1 б), а следующий ход за Валей.
Задание 21 ЕГЭ:
При S = 11 выигрышная стратегия есть у Вали. Паша делает первый ход: в куче остается либо 22, либо 12 камней. Обе эти позиции выигрышные для того, кто ходит. При S = 12 последовательность игры описана в пункте 2, а при S = 22 — в пункте 1а.
Дерево возможных партий:
* Для Вали отображены только ходы по стратегии
** красный круг означает выигрыш
*** фиолетовый круг — конец игры (проигрыш)
Подробное объяснение 19 задания ЕГЭ смотрите на видео (аналитическое решение):
📹 YouTube здесь
Видеорешение на RuTube здесь
Игра с двумя кучами камней или табличка
19_5:
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 73.
Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, что в кучах всего будет 73 камня или больше.
Задание 1.
Для каждой из начальных позиций (6, 33), (8, 32) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Задание 2.
Для каждой из начальных позиций (6, 32), (7, 32), (8, 31) укажите, кто из игроков имеет выигрышную стратегию.
Задание 3.
Для начальной позиции (7, 31) укажите, кто из игроков имеет выигрышную стратегию. Постройте дерево всех партий, возможных при указанной вами выигрышной стратегии. Представьте дерево в виде рисунка или таблицы.
✍ Решение:
- Задание 1. В начальных позициях (6, 33), (8, 32) выигрышная стратегия есть у Вани.
- Задание 2. В начальных позициях (6, 32), (7, 32) и (8, 31) выигрышная стратегия есть у Пети.
- Задание 3. В начальной позиции (7, 31) выигрышная стратегия есть у Вани.

Видео решения 19 задания с двумя кучами (аналитическое решение):
📹 YouTube здесь
Видеорешение на RuTube здесь
Игра с набором слов
19_2: 2017 год (один из вариантов со слов выпускника):
Петя и Ваня играют в игру: есть набор слов, необходимо последовательно называть буквы этих слов. Побеждает тот игрок, который называет последнюю букву любого слова из набора. Петя ходит первым.
Например, есть набор слов {Волк, Информатика, Страшно}; для заданного набора слов Петя своим первым ходом может назвать букву В, И или С. Если Петя выберет букву В, то победит Ваня (следующие ходы: Петя — В, Ваня — О, Петя — Л, Ваня — К).
Задание 1
А) Даны 2 слова (набора букв) {ИКЛМНИКЛМНХ, НМЛКИНМЛКИ}. Определить выигрышную стратегию.
Б) Даны 2 слова {ТРИТРИТРИ…ТРИ, РИТАРИТАРИТАРИТА…РИТА}. В первом слове 99 букв, во втором 164. Определить выигрышную стратегию.
Задание 2
Необходимо поменять две буквы местами из набора пункта 1А в слове с наименьшей длинной так, чтобы выигрышная стратегия была у другого игрока. Объяснить выигрышную стратегию.
Задание 3
Дан набор слов {Ворона, Волк, Волна, Производная, Прохор, Просо}. У кого из игроков есть выигрышная стратегия? Обосновать ответ и написать дерево всех возможных партий для выигрышной стратегии.
✍ Решение:
- Если поменять местами во втором слове (НМЛКИНМЛКИ) буквы Н и И, то получится следующий набор слов:
{ИКЛМНИКЛМНХ, ИМЛКННМЛКИ}Для данного набора выигрышная стратегия есть у Вани. Петя в любом случае должен будет выбрать букву И, а Ваня следующим ходом может перевести игру в проигрышную позицию для Пети, т.е. перейти на второе слово, назвав букву М. Такая стратегия приведет Ваню к выигрышу, так как последнюю букву слова — И — запишет именно он.
- Выигрышная стратегия есть у Вани, так как при любом выборе Пети, Ваня может перевести игру в проигрышную позицию для Пети, т.е. «перейти» на слово с четным количеством букв. Такая стратегия позволит Ване написать последнюю букву и тем самым выиграть игру.
А) Для выигрыша Пете достаточно выбрать первую букву слова с нечетным количеством букв, тогда последний ход делает Петя. При исходном наборе слов выигрышная стратегия есть у Пети. Она заключается в том, что своим первым ходом он должен выбрать букву И (слово ИКЛМНИКЛМНХ из 11 букв). Ване придется выбрать букву К. Таким образом, они последовательно будут называть буквы первого слова, пока Петя не выберет последнюю букву Х. На этом игра закончится выигрышем Пети. При данной стратегии возможна только одна партия. Заключением партии будет написано слово ИКЛМНИКЛМНХ.
Б) При исходном наборе слов выигрышная стратегия есть у Пети. Она заключается в том, чтобы выбрать слово с нечетным количеством букв, т.к. при такой стратегии последнюю букву в любом случае записывает Петя. Т.о., Петя должен выбрать букву Т, т.к. в первом слове 99 букв.
Дерево возможных партий:
* Для Вани отображены только ходы по стратегии
** Красный круг означает выигрыш
Подробней с решением задания про слова ознакомьтесь в видеоуроке (аналитическое решение):
📹 YouTube здесь
Видеорешение на RuTube здесь
На уроке рассмотрен разбор 19, 20, 21 задания ЕГЭ по информатике: дается подробное объяснение и решение задания.
Читать текстовую версию — https://labs-org.ru/ege-19/
Объяснение заданий 19, 20 и 21 ЕГЭ по информатике
19-е задание: «Анализ алгоритма логической игры»
Уровень сложности — повышенный,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 6 минут.
Проверяемые элементы содержания: Умение анализировать алгоритм логической игры
20-е задание: «Поиск выигрышной стратегии»
Уровень сложности — повышенный,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 6 минут.
Проверяемые элементы содержания: Умение найти выигрышную стратегию игры
21-е задание: «Дерево игры для выигрышной стратегии»
Уровень сложности — повышенный,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 10 минут.
Проверяемые элементы содержания: Умение построить дерево игры по заданному алгоритму и найти выигрышную стратегию
Привет! Сегодня порешаем задачи из 19 задания ЕГЭ по информатике 2021.
Девятнадцатое задание связано с теорией игр.
Давайте приступим к практике решения.
Задача (Разминочная)
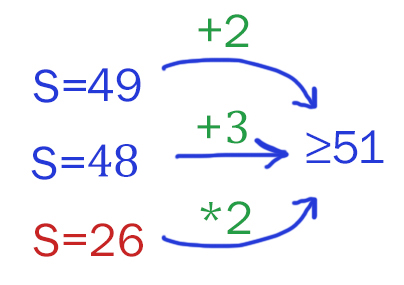
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу 2 камня или добавить в кучу 3 камня или увеличить количество камней в куче в два раза. Например, имея кучу из 8 камней, за один ход можно получить кучу из 10, 11, 16 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 51. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 51 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 50.
При каких минимальных значениях числа S Петя может выиграть первым ходом ?
Решение:
Распишем при каких значениях S первый игрок может выиграть сразу за один ход.
В ответ мы выберем значение 26, потому что оно самое маленькое.
Ответ: 26
Продолжаем набирать обороты в 19 задании из ЕГЭ по информатике 2021.
Задача (Стандартная, 1 куча)
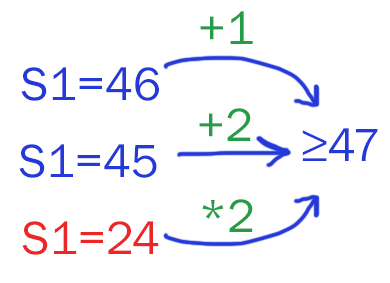
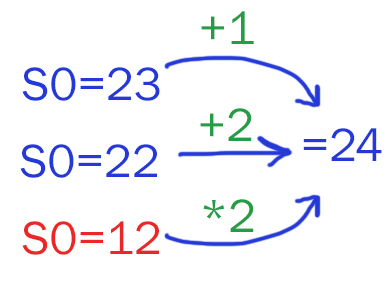
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или два камня или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 17 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 47. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 47 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 46.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Решение:
Известно, что Ваня точно должен выиграть, после Петиного хода. S1 — количество каменей после первого хода.
Чтобы найти минимальное значение S, при котором будет выполняться ситуация, описанная в задаче, мы возьмём минимальное значение камней в куче после первого Петиного хода, когда Ваня будет точно выигрывать.
Т.е. первым ходом Петя должен получить 24 камня в куче. Как он это может сделать ?
Видим, что, если в куче было изначально 12 камней, то возможная ситуация, которая описана в задаче. Значит, ответ будет 12.
Ответ: 12
Задание 19 из ЕГЭ по информатике 2021 в тренировочных задачах выглядит громоздким, но решается, как правило, при должной тренировке, не так сложно.
Задача (Стандартная, 2 кучи, Демонстрационный вариант ЕГЭ по информатике 2021)
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 5 камней; такую позицию в игре будем обозначать (10, 5). Тогда за один ход можно получить любую из четырёх позиций: (11, 5), (20, 5), (10, 6), (10, 10). Для того чтобы делать ходы,
у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 77. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 77 или больше камней.
В начальный момент в первой куче было семь камней, во второй куче –
S камней; 1 ≤ S ≤ 69.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Решение:
Обозначим первую кучу за a, вторую кучу за b.
Распишем все комбинации для суммы двух куч для каждого хода:
1. a + 1 + b (Добавляем камень к первой куче)
2. a + b + 1 (Добавляем камень ко второй куче)
3. 2*a + b (Удваиваем первую кучу)
4. a + 2*b (Удваиваем вторую кучу)
Ⅰ ход Пети.
S0 — первоначальное количество камней во второй куче.
a=7, b=S0.
Находим a и b после хода Пети.
1. a=8, b=S0
2. a=7, b=S0+1
3. a=14, b=S0
4. a=7, b=2*S0
ⅠⅠ ход Вани.
Разберём все варианты.
1. a=8, b=S0
Снова подставляем a и b в блок 1.
8+1 + S0 => S0+9 +
8 + S0+1 => S0+9 +
2*8 + S0 => S0+16 +
8 + 2*S0 => 2*S0+8 +
2. a=7, b=S0+1
Подставляем a и b в блок 1.
7+1 + S0+1 => S0+9 +
7 + S0+1+1 => S0+9 +
2*7 + S0+1 => S0+15 +
7 + 2*(S0+1) => 2*S0+9 +
3. a=14, b=S0
Подставляем a и b в блок 1.
14+1 + S0 => S0+15 +
14 + S0+1 => S0+15 +
2*14 + S0 => S0+28 +
14 + 2*S0 => 2*S0+14 +
4. a=7, b=2*S0
Подставляем a и b в блок 1.
7 + 1 + 2*S0 => 2*S0+8 +
7 + 2*S0+1 => 2*S0+8 +
2*7 + 2*S0 => 2*S0+14 +
7 + 2*2*S0 => 4*S0+7 +
Теперь возле выражений, у которых коэффициент после переменной S0 равен единице, поставим синим цветом плюсик.
Возле выражений, у которых коэффициент после переменной S0 равен двойке, поставим оранжевым цветом плюсик.
Возле выражений, у которых коэффициент после переменной S0 равен четвёрки, поставим бордовым цветом плюсик.
Выберем из тех выражений, где стоят синие плюсы, то выражение, где к S0 прибавляется наибольшее число. Это выражение S0 + 28.
Найдём при каком наименьшем S0 это выражение будет больше или равно 77.
S0 + 28 ≥ 77
S0 ≥ 77 — 28 = 49
S0 = 49
Аналогично для других цветов.
2*S0 + 14 ≥ 77
S0 ≥ (77 — 14) / 2 = 32
(округляем в большую сторону)
S0 = 32
И для последнего выражения.
4*S0 + 7 ≥ 77
S0 ≥ (77 — 7) / 4 = 18
(округляем в большую сторону)
S0 = 18
Берём меньшее число среди всех трёх значений. Получается число 18.
Ответ: 18
21-11-2020 в 20:36:16
Поддержать сайт:
Похожая статья:

ЕГЭ по информатике — Задание 2 (Мощнейший метод)
Сегодня разберём, как решать второе задание из ЕГЭ по информатике 202…
Категория: ЕГЭ Подкатегория: Информатика
Дата: 03-05-2020 в 11:26:53
11
Комментарии:
Кто-нибудь помогите решить такой тип 19 задания…
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может убрать из одной из куч один камень или уменьшить количество камней в куче в два раза (если количество камней в куче нечётно, остаётся на 1 камень меньше, чем убирается). Например, пусть в одной куче 6, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из позиции (6, 9) можно получить любую из четырёх позиций: (5, 9), (3, 9), (6, 8), (6, 4).
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не более 20. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 20 или меньше камней.
В начальный момент в первой куче было 10 камней, во второй куче — S камней, S > 10.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при разли
Влад 23-11-2020 в 22:44:35
Влад, добавил данную задачку в очередь для разбора на ютуб канале.
Калужский Александр 24-11-2020 в 03:57:44
Спасибо вам Александр)
Влад 24-11-2020 в 09:40:30
Подскажите, почему в решении «Задача (Стандартная, 2 кучи, Демонстрационный вариант ЕГЭ по информатике 2021)» а=7 ?
Никита 19-12-2020 в 20:12:57
В начальный момент в первой куче было 7 камней.
Калужский Александр 19-12-2020 в 20:16:17
Спасибо большое!!!!!!!! Изучаю информатику у вас и понимаю!! Лучше чем любой репетитор! Спасибо вам!
Никита 19-12-2020 в 20:45:18
=)
Калужский Александр 19-12-2020 в 21:29:32
Здравствуйте можно разобрать эту задачу?
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может убрать из одной из куч один камень или уменьшить количество камней в куче в два раза (если количество камней в куче нечётно, остаётся на 1 камень меньше, чем убирается). Например, пусть в одной куче 6, а в другой 9 камней; такую позицию мы будем обозначать (6, 9). За один ход из позиции (6, 9) можно получить любую из четырёх позиций: (5, 9), (3, 9), (6, 8), (6, 4).
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не более 20. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 20 или меньше камней.
В начальный момент в первой куче было 10 камней, во второй куче — S камней, S > 10.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной иг
Денис 26-12-2020 в 20:22:55
Денис! Здравствуйте! Добавил данную задачу в очередь для разбора на ютуб канале: https://www.youtube.com/channel/UCGBaXVk4CKyCOuoj49IxK5w
Калужский Александр 26-12-2020 в 22:16:32
Здравствуйте! А почему был удален ролик про удаление камней?
Влад 31-12-2020 в 14:18:31
Тоже обратил на это внимание. Почему?
Егор 31-12-2020 в 14:23:19
Здравствуйте! Там была небольшая ошибка, вместо -1 писал +1. Скоро залью исправленный! ))
Калужский Александр 31-12-2020 в 15:37:43
Два игрока Сергей и Анатолий, играют в следующую игру. Перед игроками лежит две кучи камней. игроки ходят по очереди, первый ход делает Сергей. за один ход игрок может из каждый кучи убрать по три камня или убрать целиком одну кучу, а другую разделить на две равные (если это позволяет количество камней)
Игра завершается после того хода, когда хотя бы одна куча становится пустой или когда невозможно сделать очередной ход по правилам. побеждает тот кто сделал последний ход. В начальный момент времени в одной куче лежит N камней, а в другой K камней.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации которая ему может встретиться при различной игре противника.
Известно, что после неудачного первого хода Сергея Анатолий выиграл первым своим ходом. При каком наибольшем значении К это возможно, если N= 32?
Екатерина 27-01-2021 в 23:02:14
ЕГЭ информатика 19-21 задание разбор, теория, как решать.
Теория игр, выигрышная стратегия, 19.(Б) — 1 балл, 20.(П) — 1 балл, 21.(В) — 1 балл
Е19-21.31 когда количество камней в куче становится не менее 129
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается …
Читать далее
Е19-21.31 Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 211.
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока …
Читать далее
Е19-21.30 когда количество камней в куче становится не менее 29
Игра завершается в тот момент, когда количество камней в куче становится не менее 29. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. …
Читать далее
Е19-21.29 когда суммарное количество камней в кучах становится не менее 44
когда суммарное количество камней в кучах становится не менее 44 Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) два камня или увеличить количество камней в куче в …
Читать далее
Е19-21.28 Игра завершается в тот момент, когда количество камней в куче становится не менее 84.
Игра завершается в тот момент, когда количество камней в куче становится не менее 84. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или четыре камня или увеличить количество камней в куче в …
Читать далее
Е19-21.27 добавить в кучу один камень, два камня, увеличить количество камней
добавить в кучу один камень, два камня, увеличить количество камней. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может а) добавить в кучу один камень; б) добавить в кучу два камня; г) увеличить количество камней в куче …
Читать далее
Е19-21.26 добавить в кучу один камень, два камня, три камня; увеличить количество камней
добавить в кучу один камень, два камня, три камня; увеличить количество камней в куче в два раза. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может а) добавить в кучу один камень; б) добавить в кучу два …
Читать далее
Е19-21.25 добавить в кучу два камня, добавить в кучу три камня или увеличить
добавить в кучу два камня, добавить в кучу три камня или увеличить. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу два камня, добавить в кучу три камня или увеличить количество камней в куче …
Читать далее
Е19-21.24 добавить в кучу три камня или увеличить количество камней в куче в два раза
добавить в кучу три камня или увеличить количество камней в куче в два раза. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу три камня или увеличить количество камней в куче в два раза. …
Читать далее
Е19-21.23 когда количество камней в куче становится не менее 25
Игра завершается в тот момент, когда количество камней в куче становится не менее 25. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу два камня или увеличить количество камней в куче в два раза. …
Читать далее
Разбор заданий 19,20,21 ЕГЭ по информатике в Excel.
Задание 19.
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10камней, а в другой 5 камней; такую позицию в игре будем обозначать (10,5). Тогда за один ход можно получить любую из четырёх позиций: (11,5), (20,5), (10,6), (10,10). Для того чтобы делать ход, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 77. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 77 или больше камней.
В начальный момент впервой куче было семь камней, вовторой куче – S камней: 1S69
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Решение.
Поскольку у нас 2 кучикамней, будем использовать 2 ячейки. В ячейку A4 введём 7 (количество камней в первой куче) и поскольку количество камней во второй куче неизвестно, введём в ячейкуB4 Excelпроизвольное число, например 10. Распишем ходы Пети.
Для того чтобы Ваня гарантировано выиграл первым ходом, последний ход его должен быть самым сильным. Для этого количество камней из кучи с максимальным количеством камней умножаем на 2 и прибавляем количество камней из другой кучи. В ячейку E4 вводим формулу
=МАКС(C4:D4)*2 + МИН(C4:D4). Копируем эту формулу в ячейки E5:E7.
т.к. по условию задачи Ваня должен выиграть своим первым ходом, то суммарное количество камней в двух кучах должно быть 77. При этом количество камней во второй куче должно быть минимальным. Будем подбирать количество камней во второй куче, пока не найдем минимальное, при котором суммарное количество камней количество камней у Вани не станет 77.
И
Для наглядности выполним условное форматирование. Выделим ячейки E4:E7. Выбираем Условное форматирование – Правила выделения ячеек – другие правила – значения 77 – форма – заливка – зеленая – ОК — ОК
такое количество камней во второй куче будет равно 18.
Задание 20. Для игры, описанной в предыдущем задании, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
— Петя не может выиграть за один ход;
— Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Ответ:
Решение.
Введём в ячейку A10количество камней в первой куче — 7, в ячейку B10 – количество камней во второй куче, т.к. количество камней во второй куче неизвестно, введём 10 (число произвольное). Скопируем таблицу, полученную в первом задании, в ячейку C9.
Так как Петя должен сделать свои 4 хода, а затем Ваня свои ходы, скопируем таблицу из первого задания ещё три раза. Распишем все первые ходы Пети. Ходы Вани и второй ход Пети при этом рассчитываются автоматически.
При S=10 Петя выигрывает своим вторым ходом только при одном ходе Вани (7,40), а нам надо, чтобы Петя после своего первого хода при любом ходе Вани выигрывал своим вторым ходом, т.е. нам нужно найти такое S, при котором все вторые ходы Пети в одном из прямоугольников были 77. Кроме того, нам надо будет следить за последним ходом Вани, т.к. может случиться так,что Петя выигрывает своим вторым ходом, но до этого побеждает Ваня. Для этого создадим дополнительный столбец, в который будем записывать сумму камней в двух кучах у Вани и следить, чтобы это значение было 77. В ячейку H10вводим формулу =E10 + F10и копируем её в ячейки H11:H25. Для наглядности выполним условное форматирование.
Меняя значение Sво второй куче, находим решение задачи. Первое значение S=31 ивторое значение S=34
Ответ: 3134
Задание 21.
Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия:
— у Вани естьвыигрышная стратегия,позволяющая ему выиграть первым иливторым ходом при
любой игре Пети;
— у Вани нет стратегии,которая позволит ему гарантированно выиграть первым ходом.
Решение.
Скопируем таблицу из второго задания в ячейку K3 и снова поменяем местами Петя, Ваня, Петя. В ячейку I4 введём количество камней в первой куче, в ячейку J4 – число, например, 10 (количество камней во второй куче). Тогда при первом ходе Пети K4 =I4+1, L4=J4.
Выделим данный фрагмент таблицы жирным. Так как Петя не должен выиграть своим первым ходом, скопируем полученную таблицу ещё 3 раза. Введём формулы в ячейкиK20=I4, L20=J4+1, K36=I4*2, L36=J4, K52=I4, L52=J4*2. Также надо проверить, не выиграет ли Ваня своим первым ходом. Для этого в ячейку M5 введём формулу =M4+N4. Скопируем эту формулу в ячейкиM9, M13,M17, M21, M25, M29, M33, M37, M41, M45, M49. Снова будем проверять, используя условное форматирование. Меняя значение вячейке J4, находим такое минимальное S, при которому Вани естьвыигрышная стратегия,позволяющая ему выиграть первым иливторым ходом прилюбой игре Пети;у Вани нет стратегии,которая позволит ему гарантированно выиграть первым ходом.
Задача (Стандартная)
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх — в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монеты с собой; это также относится к начальной и конечной клетке маршрута Робота.
Откройте файл. Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю. В ответ запишите два числа друг за другом без разделительных знаков — сначала максимальную сумму, затем минимальную.
Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
|
1 |
8 |
8 |
4 |
|
10 |
1 |
1 |
3 |
|
1 |
3 |
12 |
2 |
|
2 |
3 |
5 |
6 |
Для указанных входных данных ответом должна быть пара чисел 35 и 15.
Решение:
Открываем файл к данной задачке.
В начале найдём максимальную сумму.
Выделяем область всех ячеек, где написаны числа, вырезаем её и вставляем на столбец правее. Это нужно для того, чтобы при составлении формулы решения не было ошибок.
Обозначим мысленно ту область, где мы будем составлять наше решение, пропустив одну или две строчки снизу. По размеру область будет такая же.
В каждой ячейке этой области будет лежать максимальная cумма, которую может собрать Робот, дойдя до этой клетки. Т.к. Робот идёт в верхнюю правую клетку, то, соответственно, в ячейке K12 будет находится нужный нам ответ.
Наш Робот идёт из левой нижней клетки. Поэтому формулу, решающую эту задачу, составим сначала для ячейки B21.
Кликаем на ячейку B21 и пишем формулу:
=МАКС(A21;B22)+B10
Примечание: Чтобы в ячейке начать писать формулу, нужно поставить знак «=».
В любую ячейку нашей области можно попасть либо слева, либо снизу (Т.к. составляем формулу для любой ячейки, то не играет роли, что в данная ячейка угловая). Поэтому для ячейки B21 мы берём предыдущий результат — либо из левой ячейки, либо из правой ячейки, в зависимости от того, где собранная сумма больше.
Эту роль исполняет функция МАКС(). Она помогает выбрать откуда нужно идти, чтобы сумма всегда была максимальна.
Плюс, мы должны добавить сумму для данной ячейки к максимальной сумме предыдущей клетки. Поэтому в формулу дописываем ячейку B10
После того, как составили формулу для одной ячейки B21, можно распространить формулу на всю область.
Подносим мышку к правому нижнему углу. Как только появился чёрный крестик, кликаем левую кнопку мыши, и тянем вверх на 10 строчек вверх.
После того, как столбец готов, выделяем этот столбец, и аналогично, распространяем его на всё пространство.
В итоге получается такая картина:
Видим, что в ячейке K12 значение 1298. Это значение нам и нужно.
Аналогичным образом ищется минимальное значение, только в формуле вместо функции МАКС будет использоваться функция МИН.
Минимальное значение получилось 589.
Ответ: 1298589
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

В задание №19_20_21
Тема: Теория игр. Поиск выигрышной стратегии.
Проверяется умение анализировать алгоритм логической игры. Умение найти выигрышную стратегию игры. Умение построить дерево игры по заданному алгоритму и найти выигрышную стратегию.
-
Одна куча — варианты решений -
Две кучи — варианты решений -
Три кучи — варианты решений
Немного теории:
☆ Все позиции в простых играх делятся на выигрышные и проигрышные
- выигрышная позиция – это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если не сделает ошибку; при этом говорят, что у него есть выигрышная стратегия – алгоритм выбора очередного хода, позволяющий ему выиграть
- если игрок начинает играть в проигрышной позиции, он обязательно проиграет, если ошибку не сделает его соперник; в этом случае говорят, что у него нет выигрышной стратегии; таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для соперника
- выигрышные и проигрышные позиции можно охарактеризовать так:
- позиция, из которой все возможные ходы ведут в выигрышные позиции – проигрышная;
- позиция, из которой хотя бы один из возможных ходов ведет в проигрышную позицию — выигрышная, при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для соперника) позицию.
Одна куча:
Задание 19
Два игрока, Петя и Вася, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может:
- Добавить в кучу один камень или
- Добавить в кучу три камня или
- Увеличить количество камней в куче в четыре раза.
Например, имея кучу из 20 камней, за одни ход можно получить кучу из 21, 23 или 80 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 78. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 78 или больше камней. В начальный момент в куче было S камней: 1 ≤ S ≤ 77.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретится при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Известно, что Вася выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Решение:

Ответ: 5
Задание 20
Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
- Петя не может выиграть за один ход;
- Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Теперь попробуем определить значение S, при которых у Пети будет выигрышная стратегия, причём Петя не сможет выиграть первым ходом, но сможет выиграть своим вторым ходом, независимо от того, как будет ходить Ваня.

Ответ: 16 18
Задание 21
Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия:
- У Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
- У Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
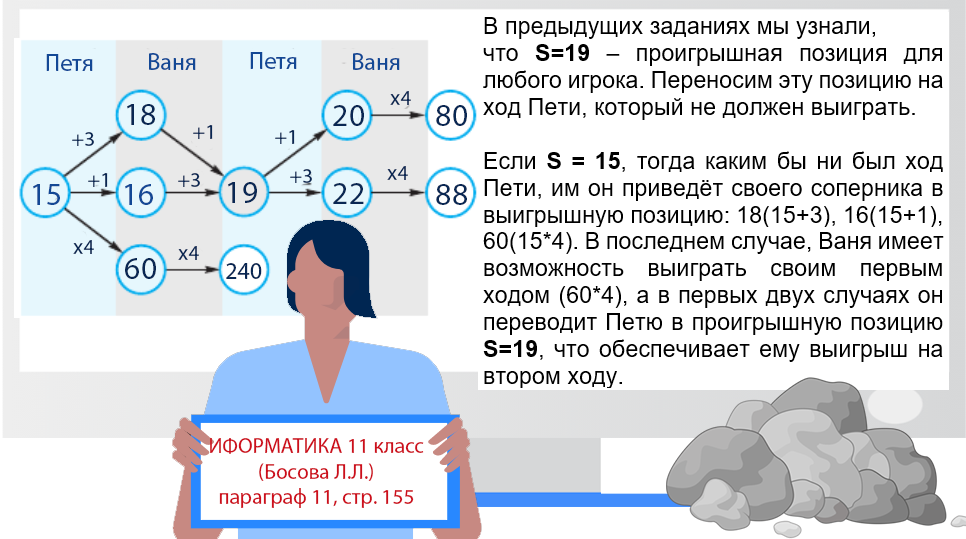
Ответ: 15
Задание 19 (самостоятельно)
Два игрока, Петя и Вася, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может:
- Добавить в кучу один камень или
- Добавить в кучу два камня или
- Увеличить количество камней в куче в четыре раза.
Например, имея кучу из 20 камней, за одни ход можно получить кучу из 21, 22 или 79 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 85. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 85 или больше камней. В начальный момент в куче было S камней: 1 ≤ S ≤ 84.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретится при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Задание 20 (самостоятельно)
Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
- Петя не может выиграть за один ход;
- Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Задание 21 (самостоятельно)
Для игры, описанной в задании 19, найдите максимальное значение S, при котором одновременно выполняются два условия:
- У Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
- У Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Задание 19_20_22(DEMO) пишем программу Phyton
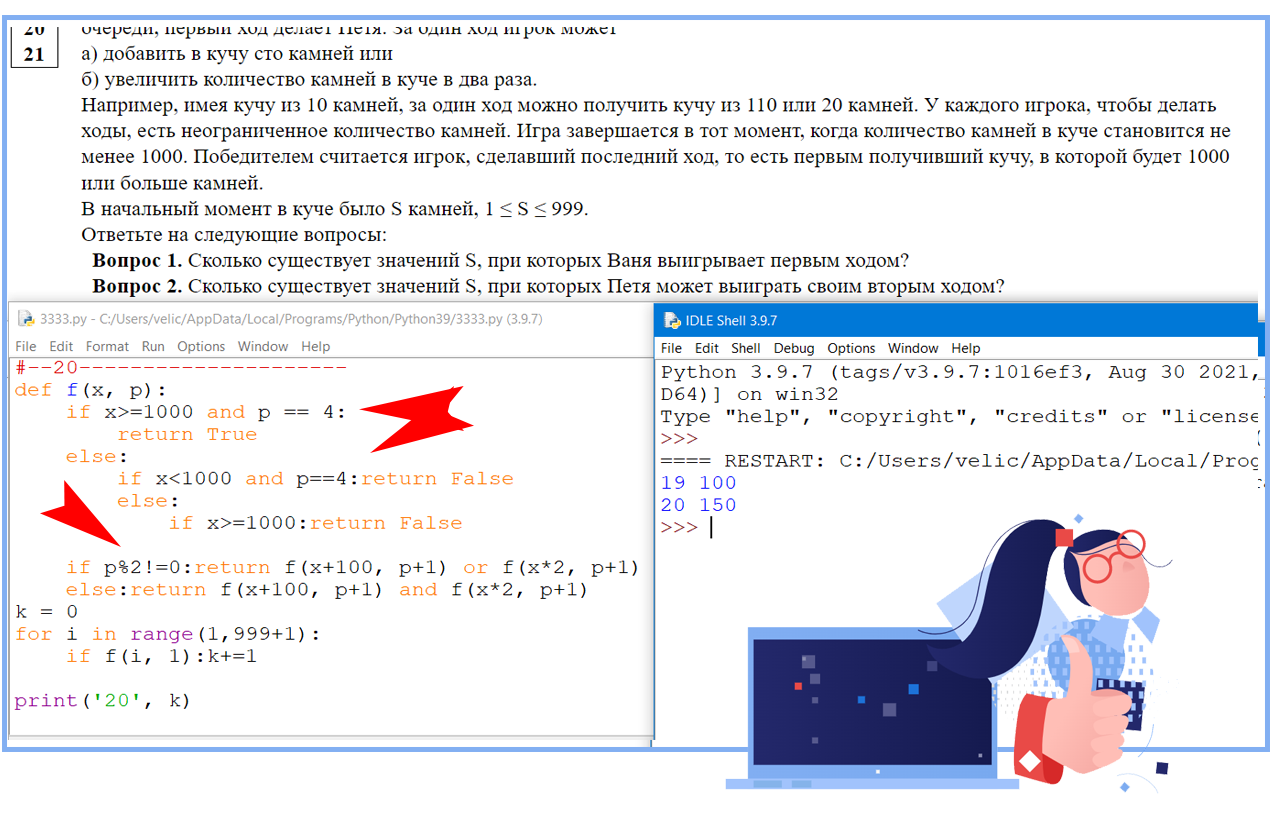
P-01 (демо-2022). Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит
куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 29 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 28.
Задание 19.
Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.
Задание 20.
Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Задание 21
Найдите значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
n = 29
def gameResult(s):
if s>=n:return 0
nYes = [gameResult(s+1), gameResult(s*2)]
nNo = [i for i in nYes if i<=0]
if nNo:res = -max(nNo) + 1
else:res = -max(nYes)
return res
# основная программа
results = [(s,gameResult(s)) for s in range(1,n)]
print( '19:', [s for s, r in results if r == -1] )
print( '20:', [s for s, r in results if r == 2] )
print( '21:', [s for s, r in results if r == -2] )

Задание 19_20_22 (Поляков) пишем программу Phyton

Две кучи — варианты решений
Задание 19 (разбираем задание)
Два игрока, Петя и Вася, играют в следующую игру. Перед игроками лежит две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может:
- Добавить в одну из куч (по своему выбору) один камень или
- Добавить в одну из куч (по своему выбору) удвоенное число камне из другой кучи.
Например, пусть в одной куче 8 камней, а в другой куче 5 камней. Тогда за один ход можем получить четыре позиции: (9, 5); (18, 5); (8, 6); (8, 21).
Для того что бы играть, у игроков есть неограниченное количество камне.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 77. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 77 или больше камней.
В начальный момент в первой куче было 9 камней, во второй S камней: 1 ≤ S ≤ 67.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретится при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Известно, что Вася выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
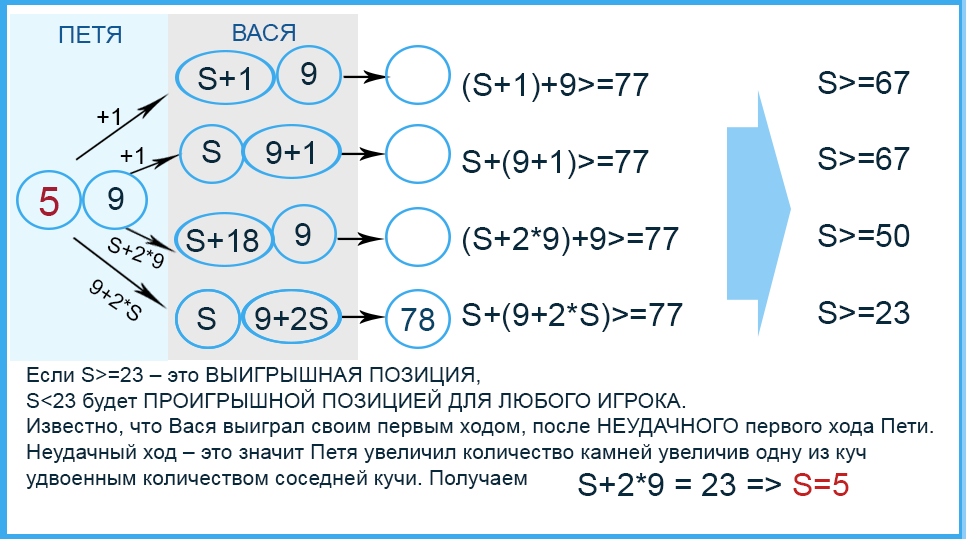
Можно решить с помощью рассуждений:
- Если S = 67, то добавив в любую кучу один камень (67+1+9=77), или добавить удвоенную соседнюю кучу в любую из куч (9+(67+2*9)=94 или ((9+2*67)+67=210), Петя становится победителем.
- Если S = 66, добавив удвоенную соседнюю кучу в любую из куч (9+(66+2*9)=93 или ((9+2*66)+66=207), Петя становится победителем.
- Если S = 65, добавив удвоенную соседнюю кучу в любую из куч (9+(65+2*9)=92 или ((9+2*65)+65=204), Петя становится победителем.
- Обратим внимание, если удваиваем 9 камней и добавляем во вторую кучу, уменьшение ровно на 1, поэтому ускорим процесс 92-77=15, 65 -15 =50, идем дальше
- Если S = 50, добавив удвоенную соседнюю кучу в любую из куч (9+(50+2*9)=77 или ((9+2*50)+50=159), Петя становится победителем.
- У нас остается только один вариант, ускорим процес, усли удваиваем вторую кучу, уменьшение ровно на три, поэтому ускорим процесс 159-77=82, 82/3=27,333, 50-27=23
- Если S = 23, добавив удвоенную соседнюю кучу в эту из куч ((9+2*23)+23=78), Петя становится победителем. СТОП!!!
Получили – S>=23 – это ВЫИГРЫШНАЯ ПОЗИЦИЯ,
S<23 будет ПРОИГРЫШНОЙ ПОЗИЦИЕЙ ДЛЯ ЛЮБОГО ИГРОКА.
Известно, что Вася выиграл своим первым ходом, после НЕУДАЧНОГО первого хода Пети.
Неудачный ход – это значит Петя увеличил количество камне увеличив одну из куч удвоенным количеством соседней кучи. Получаем S+2*9 = 23 => S=5
Можно проверить программой:
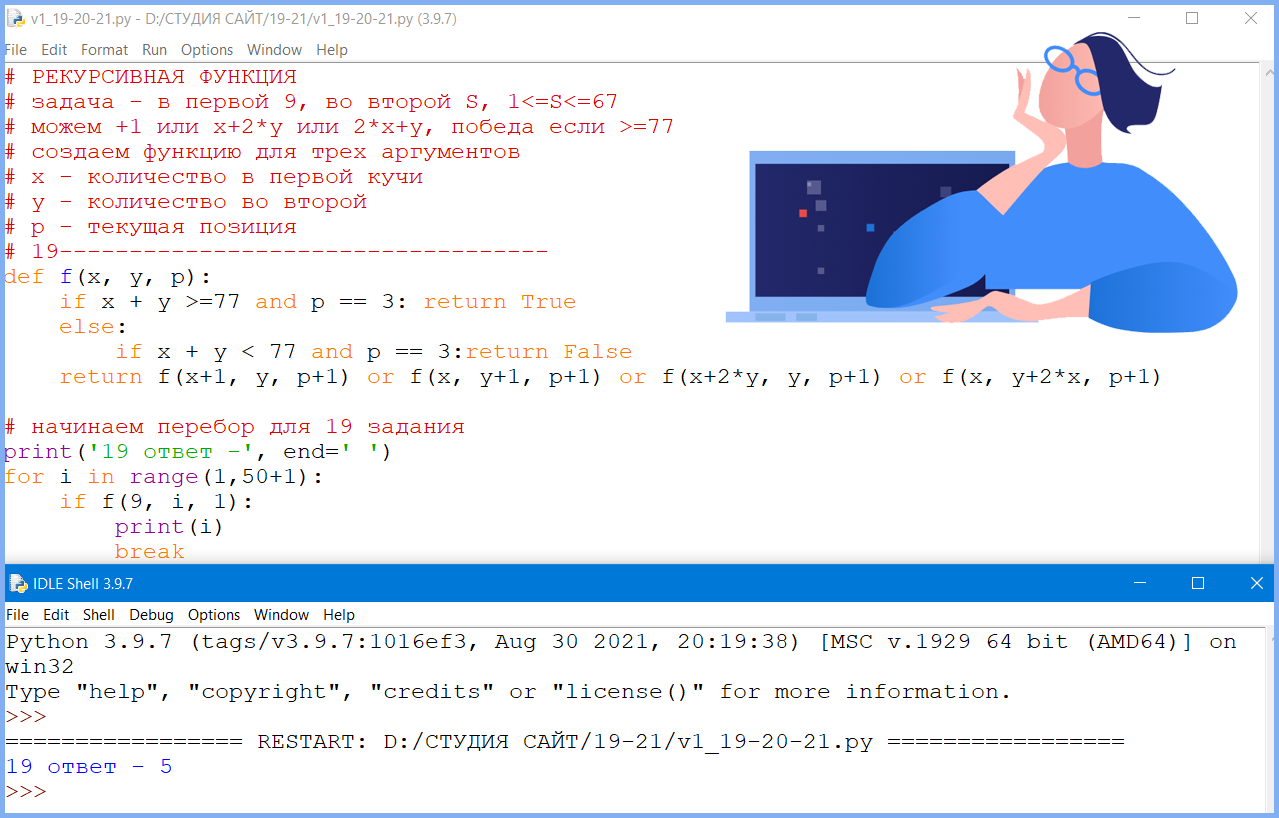
# 19-----------------------------------
def f(x, y, p):
if x + y >=77 and p == 3: return True
else:
if x + y < 77 and p == 3:return False
return f(x+1, y, p+1) or f(x, y+1, p+1) or f(x+2*y, y, p+1) or f(x, y+2*x, p+1)
# начинаем перебор для 19 задания
print('19 ответ -', end=' ')
for i in range(1,50+1):
if f(9, i, 1):
print(i)
break
Ответ: 5
Задание 20 (разбираем задание)
Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:
- Петя не может выиграть за один ход;
- Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
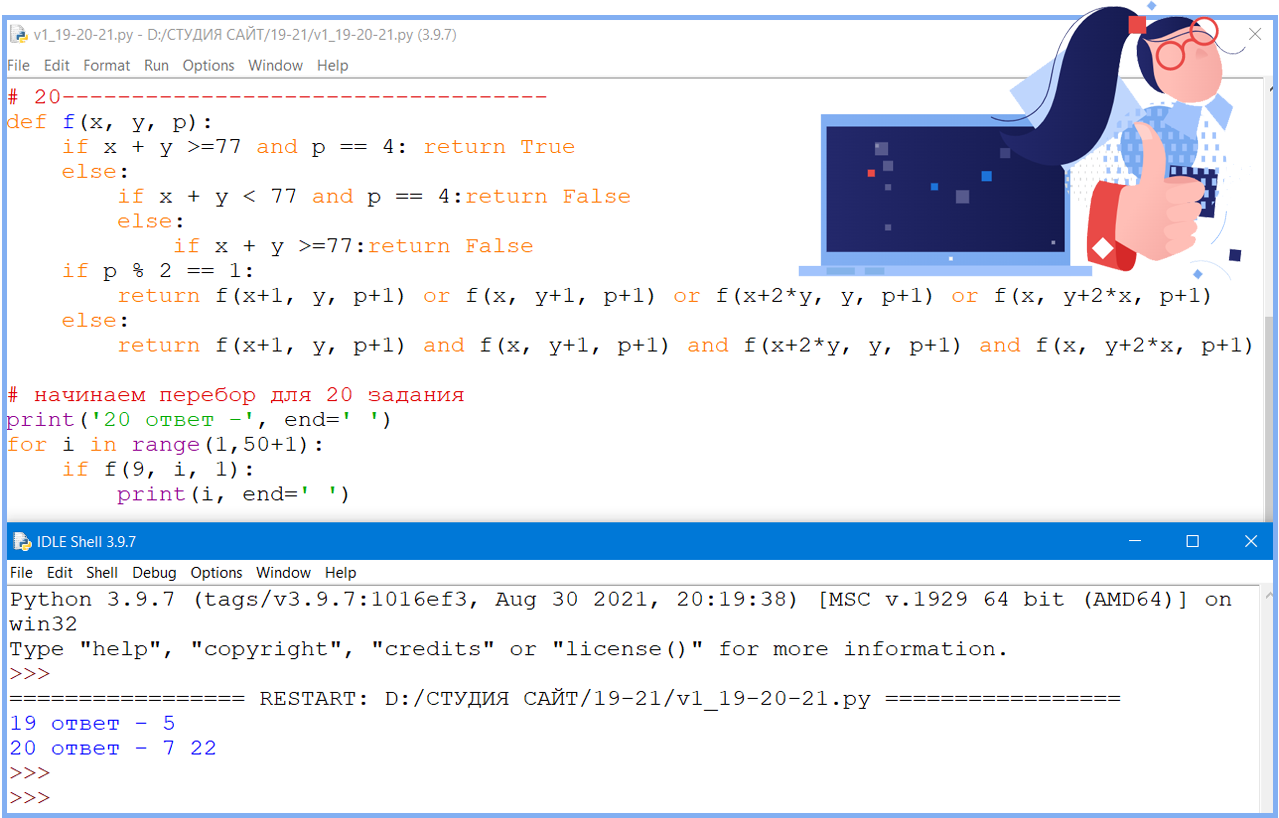
Ответ: 7 22
Задание 21 (разбираем задание)
Найдите значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
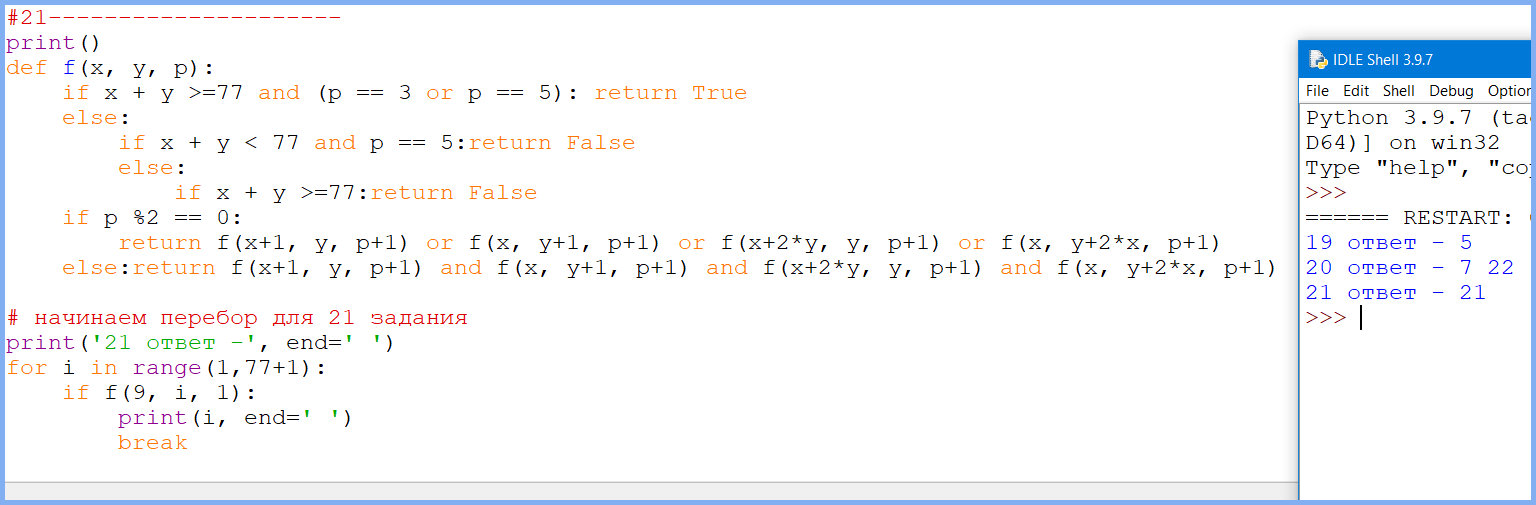
Ответ: 21
Три кучи — варианты решений
Задание 19_20_21 (разбираем задание)
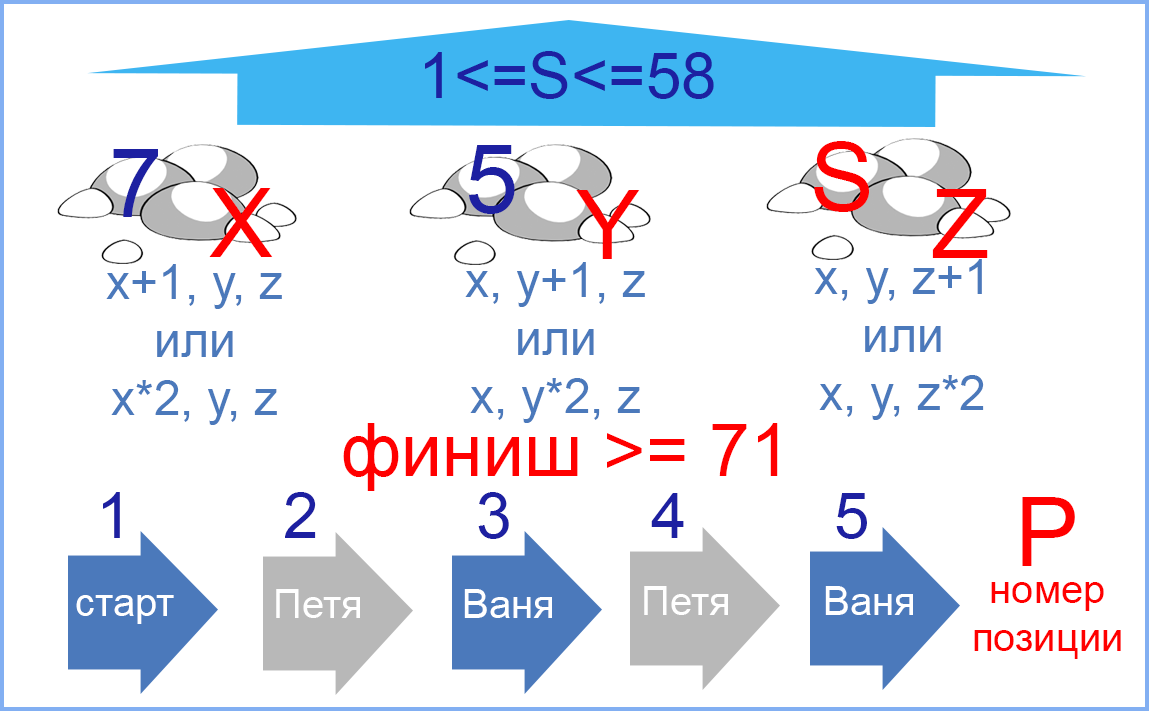
(№ 4725) (И. Осипов) Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат три кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) три камня или увеличить количество камней в куче в два раза. Например, пусть в первой куче 10 камней, во второй 7, а в третьей 4 камня; такую позицию в игре будем обозначать (10, 7, 4). Тогда за один ход можно получить любую из шести позиций: (13, 7, 4), (20, 7, 4), (10, 10, 4), (10, 14, 4), (10, 7, 7), (10, 7, 8). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 71. Победителем считается игрок, сделавший последний ход, т. е. первым получивший такую позицию, что в кучах всего будет 71 или больше камней. В начальный момент в первой куче было семь камней, во второй куче пять камней, в третьей куче – S камней; 1 ≤ S ≤ 58.
Ответьте на следующие вопросы:
Вопрос 1.При некотором значении S Ваня одержал победу свои первым ходом после неудачного хода Пети. Укажите минимальное значение S, при котором это возможно.
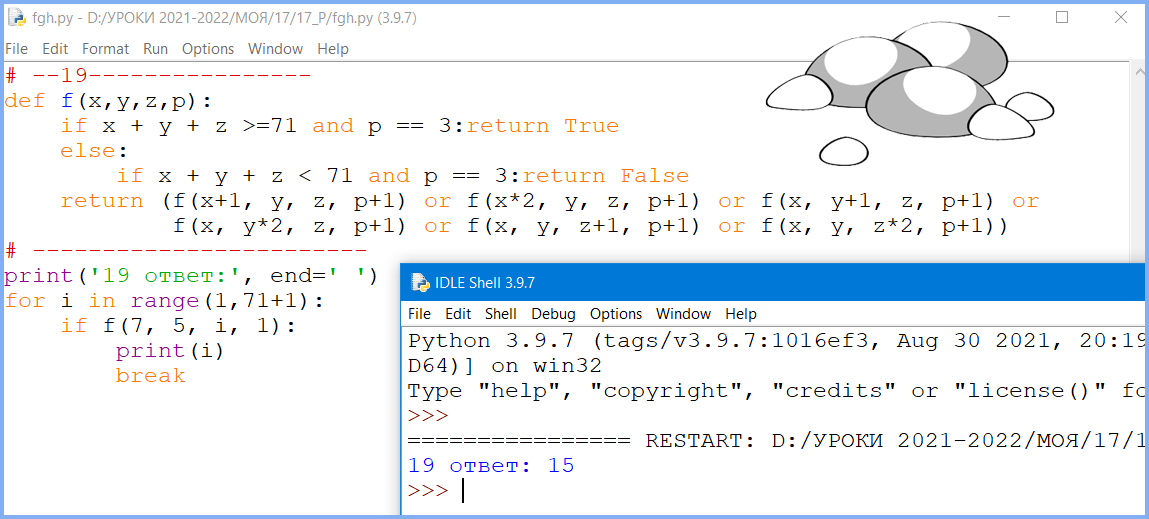
Вопрос 2. Найдите минимальное и максимальное значения S, при которых Петя выигрывает вторым ходом при любом ходе Вани.
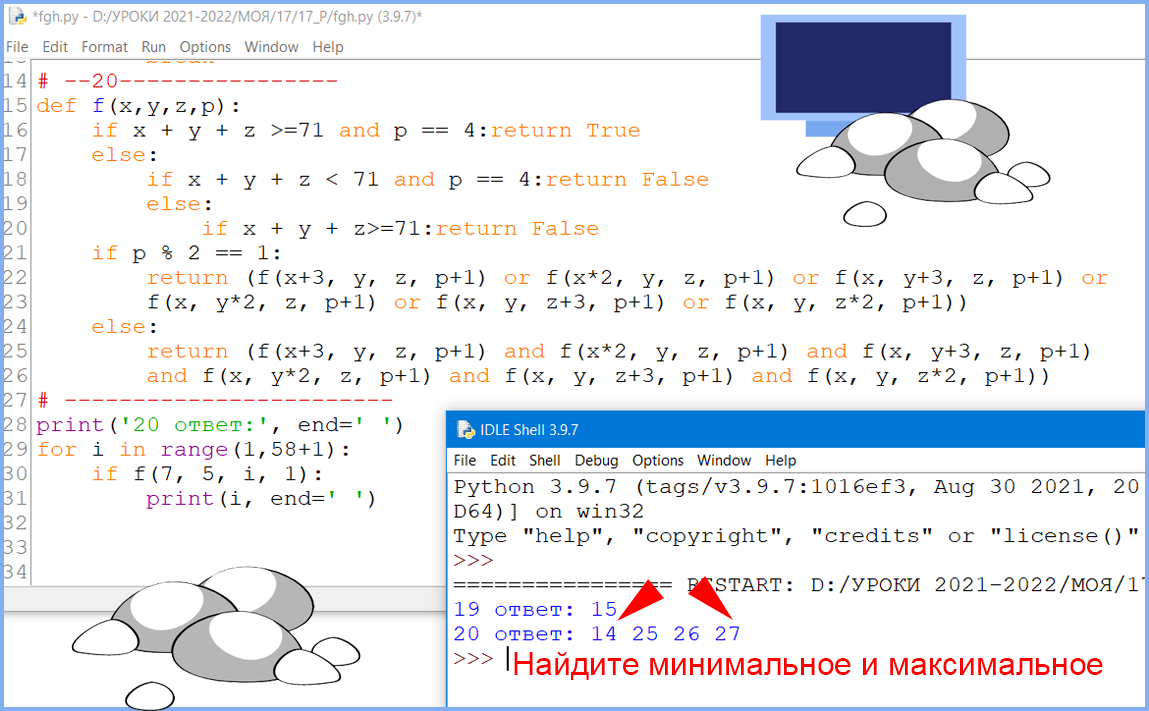
Вопрос 3. Найдите значение S, при котором одновременно выполняются два условия: а) у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети; б) у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
# --19----------------
def f(x,y,z,p):
if x + y + z >=71 and p == 3:return True
else:
if x + y + z < 71 and p == 3:return False
return (f(x+3, y, z, p+1) or f(x*2, y, z, p+1) or f(x, y+3, z, p+1) or
f(x, y*2, z, p+1) or f(x, y, z+3, p+1) or f(x, y, z*2, p+1))
# ------------------------
print('19 ответ:', end=' ')
for i in range(1,58+1):
if f(7, 5, i, 1):
print(i)
break
Ответ: 15
# --20----------------
def f(x,y,z,p):
if x + y + z >=71 and p == 4:return True
else:
if x + y + z < 71 and p == 4:return False
else:
if x + y + z>=71:return False
if p % 2 == 1:
return (f(x+3, y, z, p+1) or f(x*2, y, z, p+1) or f(x, y+3, z, p+1) or
f(x, y*2, z, p+1) or f(x, y, z+3, p+1) or f(x, y, z*2, p+1))
else:
return (f(x+3, y, z, p+1) and f(x*2, y, z, p+1) and f(x, y+3, z, p+1)
and f(x, y*2, z, p+1) and f(x, y, z+3, p+1) and f(x, y, z*2, p+1))
# ------------------------
print('20 ответ:', end=' ')
for i in range(1,58+1):
if f(7, 5, i, 1):
print(i, end=' ')
Ответ: 14 27
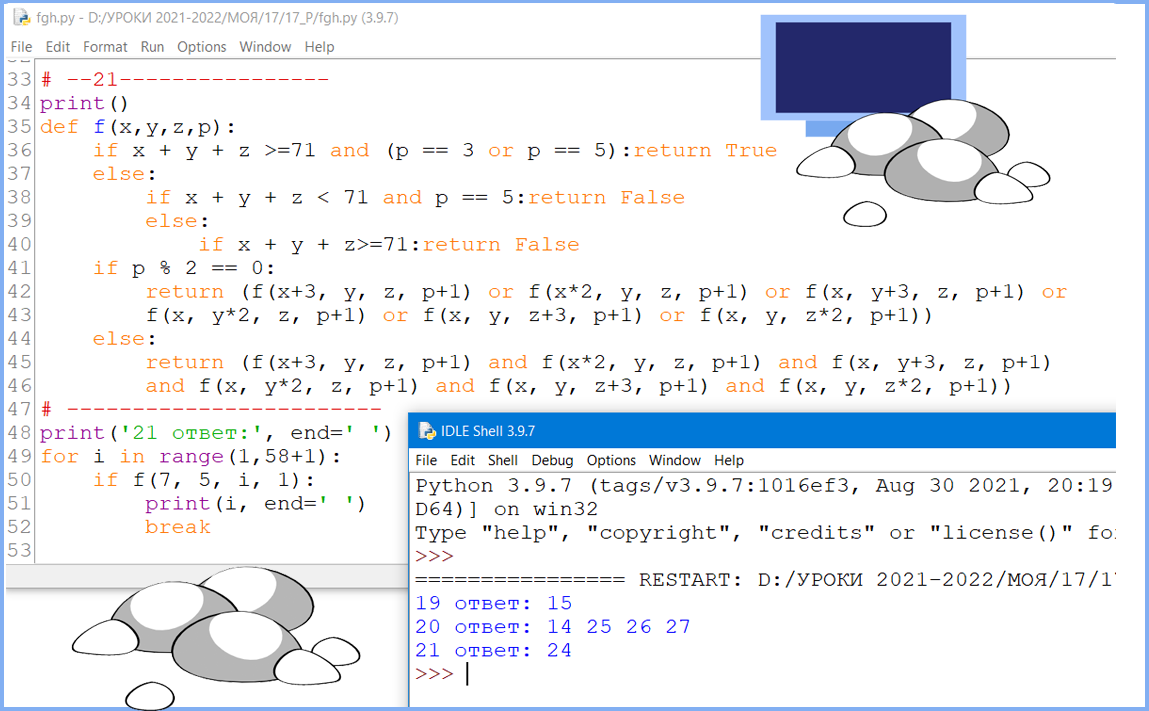
# --21----------------
print()
def f(x,y,z,p):
if x + y + z >=71 and (p == 3 or p == 5):return True
else:
if x + y + z < 71 and p == 5:return False
else:
if x + y + z>=71:return False
if p % 2 == 0:
return (f(x+3, y, z, p+1) or f(x*2, y, z, p+1) or f(x, y+3, z, p+1) or
f(x, y*2, z, p+1) or f(x, y, z+3, p+1) or f(x, y, z*2, p+1))
else:
return (f(x+3, y, z, p+1) and f(x*2, y, z, p+1) and f(x, y+3, z, p+1)
and f(x, y*2, z, p+1) and f(x, y, z+3, p+1) and f(x, y, z*2, p+1))
# ------------------------
print('21 ответ:', end=' ')
for i in range(1,58+1):
if f(7, 5, i, 1):
print(i, end=' ')
break
Ответ: 24