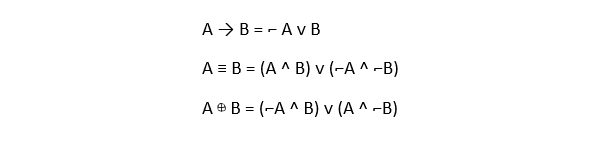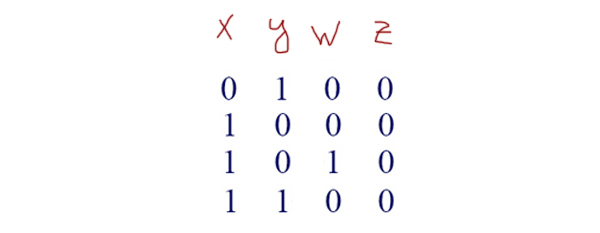На уроке рассматривается разбор 2 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи
Содержание:
- Объяснение задания 2 ЕГЭ по информатике
- Таблицы истинности и порядок выполнения логических операций
- Решение заданий 2 ЕГЭ по информатике
- Задания для тренировки
2-е задание: «Таблицы истинности»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 3 минуты.
Проверяемые элементы содержания: Умение строить таблицы истинности и логические схемы
Типичные ошибки и рекомендации по их предотвращению:
«Игнорирование прямо указанного в условии задания требования, что заполненная таблица истинности не должна содержать одинаковых строк. Это приводит к внешне правдоподобному, но на самом деле неверному решению»
ФГБНУ «Федеральный институт педагогических измерений»
Таблицы истинности и порядок выполнения логических операций
Для логических операций приняты следующие обозначения:
| операция | пояснение | в программировании |
|---|---|---|
| ¬ A, A | не A (отрицание, инверсия) | not(A) |
| A ∧ B, A ⋅ B | A и B (логическое умножение, конъюнкция) | A and B |
| A ∨ B, A + B | A или B (логическое сложение, дизъюнкция) | A or B |
| A → B | импликация (следование) | A <= B |
| A ↔ B, A ≡ B, A ∼ B | эквиваленция (эквивалентность, равносильность) | A==B (python) A=B(pascal) |
| A ⊕ B | строгая дизъюнкция | A != B (python) A <> B (pascal) |
Егифка ©:
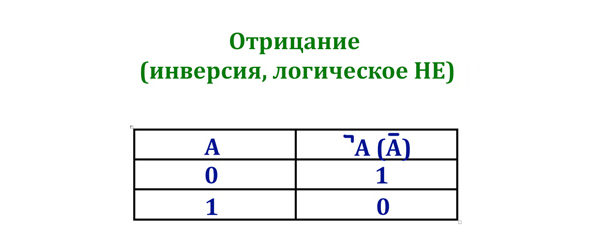
Отрицание (НЕ):
Таблица истинности операции НЕ
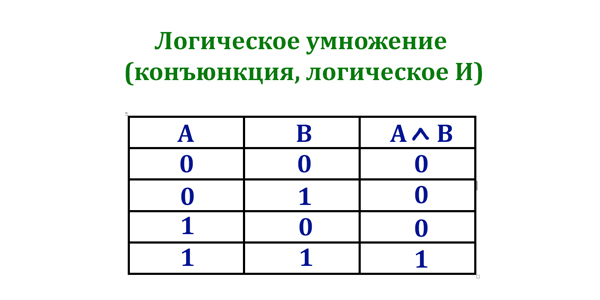
Конъюнкция (И):
Таблица истинности операции И (конъюнкция)
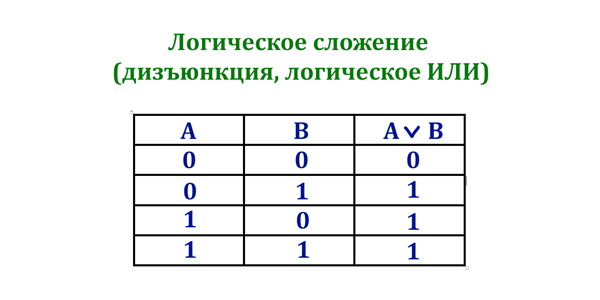
Дизъюнкция (ИЛИ):
Таблица истинности операции ИЛИ (дизъюнкция)
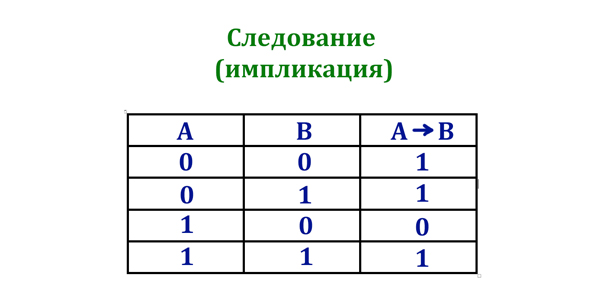
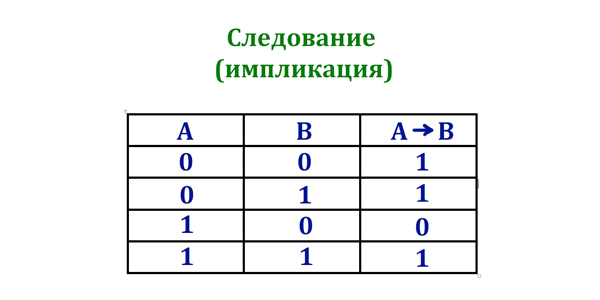
Импликация (если…, то…):
Таблица истинности операции Импликация (если…, то…)
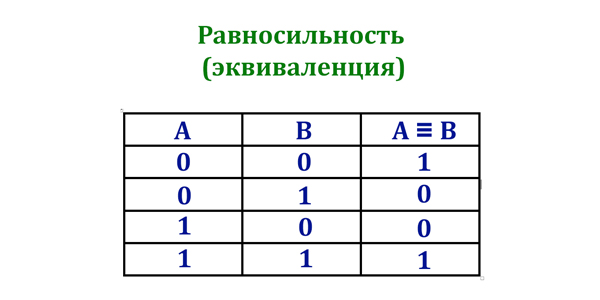
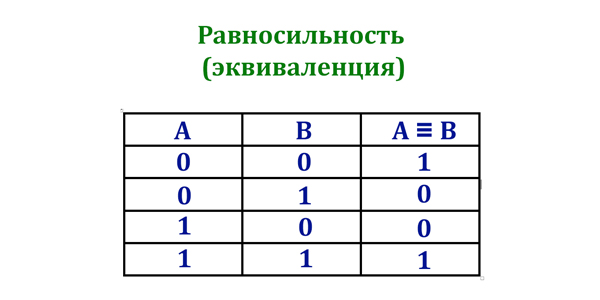
Эквивалентность (тогда и только тогда, …):
Таблица истинности операции Эквивалентность (тогда и только тогда, …)
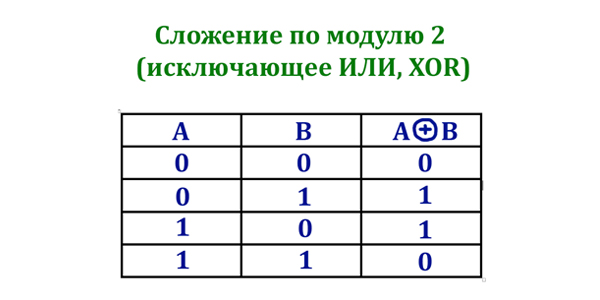
Сложение по модулю 2 (XOR):
| A | B | A ⊕ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Порядок выполнения операций:
- если нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», импликация, равносильность
Еще о логических операциях:
- логическое произведение X∙Y∙Z∙… равно 1, т.е. выражение является истинным, только тогда, когда все сомножители равны 1 (а в остальных случаях равно 0)
- логическая сумма X+Y+Z+… равна 0, т.е. выражение является ложным только тогда, когда все слагаемые равны 0 (а в остальных случаях равна 1)
О преобразованиях логических операций читайте здесь.
Егифка ©:
Решение заданий 2 ЕГЭ по информатике
Задание 2_11: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
✎ Способ 1. Электронные таблицы Excel + Логические размышления:
- Отобразим перебор всех значений использующихся в выражении переменных (всю таблицу истинности). Поскольку в выражении используются 4 переменных, то строк таблицы будет 24=16:
- Далее обе скобки исходного выражения необходимо записать в виде логического выражения, каждую — в отдельном столбце. Также в отдельном столбце добавьте формулу итоговой функции F:

xwzy
-
✎ Способ 2. Программирование:
- В результате будут выведены значения для
F=0:
Язык python:
print('x y z w') for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: F = (not(x) or y or z) and (x or not(z) or not(w)) if not(F): print(x, y, z, w)
x y z w 0 0 1 1 0 1 1 1 1 0 0 0 1 0 0 1
xwzy
Язык pascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not x or y or z) and (x or not z or not w)) then writeln(x:7, y:7, z:7,w:7); end.
F=0:x y z w False False True True False True True True True False False False True False False True
false = 0, True = 1Ответ:
xwzy
-
✎ Способ 3. Логические размышления:
- Внешняя операция выражения — конъюнкция (∧). Во всех указанных строках таблицы истинности функция принимает значение 0 (ложь). Конъюнкция ложна аж в трех случаях, поэтому проверить на ложь очень затруднительно. Тогда как конъюнкция истинна (= 1) только в одном случае: когда все операнды истинны. Т.е. в нашем случае:
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w) = 1 когда: 1. (¬x ∨ y ∨ z) = 1 И 2. (x ∨ ¬z ∨ ¬w) = 1
| x | y | z | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | z | w | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | w | z | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
Результат: xwzy
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_12: Разбор 2 задания ЕГЭ:
Миша заполнял таблицу истинности функции:
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w)
но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:
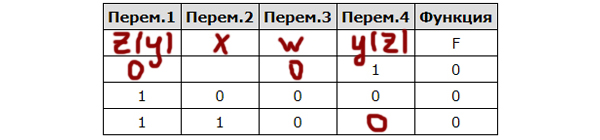
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 0 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.
Подобные задания для тренировки
✍ Решение:
✎ Способ 1. Логические размышления (бескомпьютерный вариант):
- Решим задание методом построения полной таблицы истинности.
- Посчитаем общее количество строк в таблице истинности и построим ее:
4 переменных -> 24 = 16 строк
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w) 1. Избавимся от импликации: ¬(¬z ∧ ¬(x ≡ y)) ∨ ¬(y ∨ w) 2. Внесем знак отрицания в скобки (закон Де Моргана): (z ∨ (x ≡ y)) ∨ (¬y ∧ ¬w) = 0 1 часть = 0 2 часть = 0 * Исходное выражение должно быть = 0. Дизъюнкция = 0, когда оба операнда равны 0.
(z ∨ (x ≡ y)) = 0 когда z = 0 и x ≡ y = 0 ¬y ∧ ¬w = 0 когда: 1. ¬y = 0 ¬w = 0 2. ¬y = 1 ¬w = 0 3. ¬y = 0 ¬w = 1
| x | y | w | z | F |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| y | w | x | z | F |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
Результат: ywxz
✎ Способ 2. Программирование:
- В результате будут выведены значения для F=0:
Язык PascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not z and (x xor y)) <= not(y or w)) then writeln(x:7, y:7, z:7,w:7); end.
x y z w False True False False False True False True True False False True
false = 0, True = 1Сопоставив их с исходной таблицей, получим результат: ywxz
Язык Python:
print ('x y z w') for x in 0,1: for y in 0,1: for z in 0,1: for w in 0,1: F=(not z and not(x==y))<=(not(y or w)) if not F: print (x,y,z,w)
F=0:x y z w 0 1 0 0 0 1 0 1 1 0 0 1
Сопоставив их с исходной таблицей, получим результат:
Результат: ywxz
🎦 Доступно видео решения этого задания (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
🎦 Видео (решение 2 ЕГЭ в Excel):
📹 здесь
📹 Видеорешение на RuTube здесь
📹 Видеорешение на RuTube здесь (Программирование)
Задание 2_10: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
¬a ∧ b ∧ (c ∨ ¬d)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
🎦 (Бескомьютерный вариант) Предлагаем подробный разбор посмотреть на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_3: Решение задания 2. Демоверсия ЕГЭ 2018 информатика:
Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таб. ист-ти функции F, содержащий все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Подобные задания для тренировки
✍ Решение:
-
✎ Логические размышления (бескомпьютерный вариант):
- Внешним действием (последним выполняемым) в исходном выражении является дизъюнкция:
¬x ∨ y ∨ (¬z ∧ w)
| x1 | x2 | F |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
¬x = 1 или 0, y = 1 или 0, ¬z ∧ w = 1 или 0).¬x = 0, иными словами x = 1. Значит первый столбец соответствует переменной x. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
y = 0. Значит четвертый столбец соответствует переменной y. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | y | F |
| 1 | 1 | 1 | 0 | 0 |
¬z ∧ w должно равняться 0, чтобы функция была ложной. Конъюнкция истинна только тогда, когда оба операнда истинны (=1); в нашем случае функция должна быть ложной, но пойдем от обратного. Если ¬z = 1, т.е. z = 0, а w = 1, то это неверно для нашего случая. Значит всё должно быть наоборот: z = 1, а w = 0. Таким образом столбец второй соответствует z, а столбец третий — w. | x | z | w | y | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
Результат: xzwy
✎ Способ 2. Программирование:
Язык pascalABC.NET:
begin writeln('x ','y ','z ','w '); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not(not x or y or(not z and w)) then writeln(x:7,y:7,z:7,w:7); end.
🎦 (бескомпьютерный вариант) Подробное решение данного 2 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_13: Разбор досрочного егэ по информатике 2019
Логическая функция F задаётся выражением
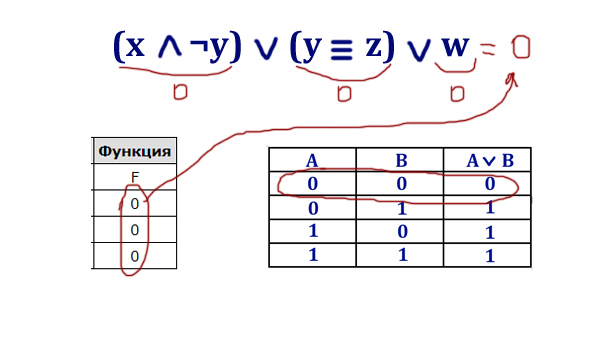
(x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
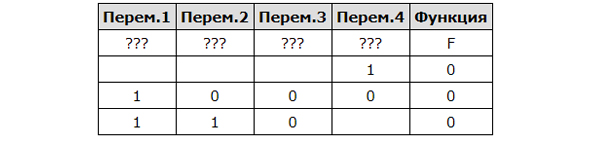
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 |
✍ Решение:
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задания для тренировки
Задание 2_2: Задание 2 ЕГЭ по информатике:
Каждое из логических выражений F и G содержит 5 переменных. В табл. истинности для F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1.
Сколько строк таблицы истинности для F ∨ G содержит 1 в столбце значений?
Подобные задания для тренировки
✍ Решение:
- Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из 32 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет 25=32, т.е. 32 строки.
- Из этих 32 строк и для F и для G мы знаем наверняка только о 5 строках: 4 из них истинны (=1), а одна ложна (=0).
- Вопрос стоит о количестве строк = 1 для таб. истинности F ∨ G. Данная операция — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0
- В исходных таблицах для F и G мы знаем о существовании только одного 0, т.е. в остальных строках может быть 1. Т.о., и для F и для G в 31 строке могут быть единицы (32-1=31), а лишь в одной — ноль.
- Тогда для F ∨ G только в одном случае будет 0, когда и F = 0 и G = 0:
- Соответственно, истинными будут все остальные строки:
| № | F | G | F ∨ G |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 |
| … | … | … | 1 |
| 32 | … | … | 1 |
32 - 1 = 31
Результат: 31
Подробное объяснение данного задания смотрите на видео:
📹 здесь
Задание 2_6: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы.
Каково максимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 27 = 128 строк.
- В четырех из них результат равен единице, значит в остальных — 0.
- A ∨ B истинно в том случае, когда либо A = 1 либо B = 1, или и A и B = 1.
- Поскольку А = 1 только в 4 случаях, то чтобы получить максимальное количество единиц в результирующей таблице истинности (для A ∨ B), расположим все единицы т.и. для выражения A так, чтобы они были в строках, где B = 0, и наоборот, все строки, где B = 1, поставим в строки, где A = 0:
- Итого получаем 8 строк.
- Если бы в задании требовалось найти минимальное количество единиц, то мы бы совместили строки со значением = 1, и получили бы значение 4.
| A | B |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 0 |
| … | … |
Результат: 8
Задание 2_7: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 6 единиц.
Каково максимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 28 = 256 строк.
- В шести из них результат равен единице, значит в остальных — 0.
- A ∧ B ложно в том случае, когда:
A ∧ B = 0 если: 1. A = 0, B = 1 2. B = 0, A = 1 3. A = 0 и B = 0
- Во всех случаях там где А=1 может стоять B=0, и тогда результат F = 0. Поскольку нам необходимо найти максимально возможное число нулей, то как раз для всех шести А=1 сопоставим B=0, и наоборот, для всех шести возможных B=1 сопоставим A=0
- Поскольку строк всего 256, то вполне возможно, что все 256 из них возвратят в результате 0
| A | B | F |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| … | … | … |
Результат: 256
Задание 2_4: 2 задание:
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
✍ Решение:
- В первом внешняя операция (выполняется последней) — конъюнкция. Начнем рассмотрение с нее. Соответственно, проверяем по второй строке таб. ист-ти, там где F = 1, так как в таком случае все аргументы должны быть истинными (см. таб. истинности для конъюнкции).
- Если мы подставим в нее все аргументы выражения, то функция действительно возвращает истину. Т.е. пункт первый подходит:
- Но проверим на всякий случай остальные.
- Второй пункт проверяем по первой и третьей строке, так как основная операция — дизъюнкция — ложна только в том случае, если все аргументы ложны (см. таб. истинности для дизъюнкции). Проверяя по первой строке, сразу видим, что x1 в ней равен 1. В таком случаем функция будет = 1. Т.е. этот пункт не подходит:
- Третий пункт проверяем по второй строке, так как основная операция — конъюнкция — возвратит истину только тогда, когда все операнды равны 1. Видим, что x1 = 0, соответственно функция будет тоже равна 0. Т.е. выражение нам не подходит:
- Четвертый пункт проверяем по первой и третьей строкам. В первой — x1 = 1, т.е. функция должна быть равна 1. Т.е. пункт тоже не подходит:
- Таким образом, ответ равен 1.
Результат: 1
Решение 2 задания ГВЭ по информатике смотрите на видео:
📹 здесь
Задание 2_8: Решение 2 задания ЕГЭ по информатике:
Дано логическое выражение, зависящее от 5 логических переменных:
(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)
Сколько существует различных наборов значений переменных, при которых выражение истинно?
1) 0
2) 30
3) 31
4) 32
Подобные задания для тренировки
✍ Решение:
- Поскольку выражение включает 5 переменных, то таб. ист-ти состоит из 25 = 32 строк.
- Внешней операцией (последней) является конъюнкция (логическое умножение), а внутри скобок — дизъюнкция (логическое сложение).
- Обозначим первую скобку за А, а вторую скобку за B. Получим A ∧ B.
- Найдем сколько нулей существует для таб. истинности:
A B F 1. 0 0 0 2. 0 1 0 3. 1 0 0
Теперь рассмотрим каждый случай отдельно:
¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5 = 0
и
x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 = 0.
32 - 2 = 30, что соответствует номеру 2
Результат: 2
Подробное решение задания смотрите в видеоуроке:
📹 здесь
Задание 2_5: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | F |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 |
Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x3 не совпадает с F.
Подобные задания для тренировки
✍ Решение:
- Полная таблица истинности будет иметь 26 = 64 строк (т.к. 6 переменных).
- 4 из них нам известны: в них x3 два раза не совпадает с F.
- Неизвестных строк:
64 - 4 = 60
60 + 2 = 62
Результат: 62
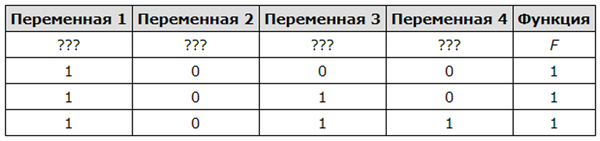
Задание 2_9: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 0 | 0 | 0 | |||||
| 0 | 0 | 1 | |||||
| 1 | 1 | 1 |
Каким выражением может быть F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7
✍ Решение:
- Рассмотрим отдельно каждый пункт и найдем последнюю операцию, которая должна быть выполнена (внешнюю).
1 пункт:
(((x1 ∧ (x2 → x3) ∧ ¬x4) ∧ x5) ∧ x6) ∧ ¬x7
2 пункт:
(((x1 ∨ (¬x2 → x3) ∨ ¬x4) ∨ ¬x5) ∨ x6) ∨ ¬x7
3 пункт:
(((¬x1 ∧ (x2 → ¬x3) ∧ x4) ∧ ¬x5) ∧ x6) ∧ x7
Результат: 4
В видеоуроке рассмотрено подробное решение 2 задания:
📹 здесь
Задание 2_1: Задание 2 ЕГЭ по информатике:
Логическая функция F задается выражением
(y → x) ∧ (y → z) ∧ z.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| ??? | ??? | ??? | F | |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 0 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 |
| 8 | 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
- Сначала необходимо рассмотреть логическую операцию, которую мы будем выполнять в последнюю очередь — это логическое И (конъюнкция) или ∧. То есть внешнюю операцию:
(y → x) ∧ (y → z) ∧ z
(y → x) ∧ (y → z) ∧ z = 1 если: 1. (y → x) = 1 2. (y → z) = 1 3. z = 1
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| 3 | 0 | 1 | 0 | 1 |
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| _ | ??? | z | ??? | F |
| № | Перем. 1 | z | Перем. 3 | F |
|---|---|---|---|---|
| 4 | 0 | 1 | 1 | 1 |
Результат: yzx
Детальный разбор данного задания 2 ЕГЭ по информатике предлагаем посмотреть в видео:
📹 здесь
Здравствуйте, дорогие друзья! Сегодня разберём, как решать второе задание из ЕГЭ по информатике 2020.
Во втором задании ЕГЭ по информатике у нас обычно есть логическая функция, которая зависит от логических переменных. Логические переменные могут принимать только два значения: 0 (Ложь) или 1 (Истина).
С логическими переменными можно производить логические операции. При решении второго задания из ЕГЭ по информатике необходимо твёрдо знать каждую логическую операцию, и давайте рассмотрим их.
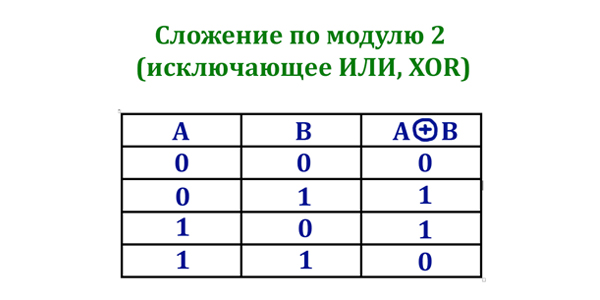
- () — операции в скобках
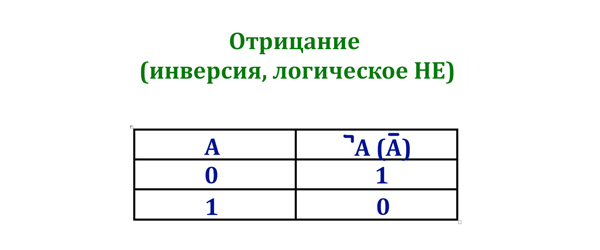
- ¬ — логическое отрицание
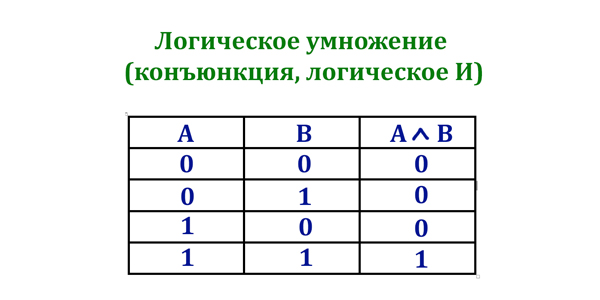
- ∧ — логическое умножение
- ∨ — логическое сложение
- ⟶ — следование
- ≡ — равнозначность
Так же на ЕГЭ по информатике будет полезно знать логические формулы :
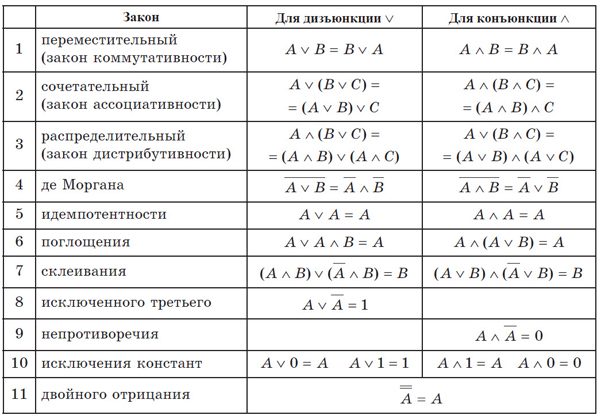
Передём к решению задач из ЕГЭ по информатике
Задача 1 (лёгкая)
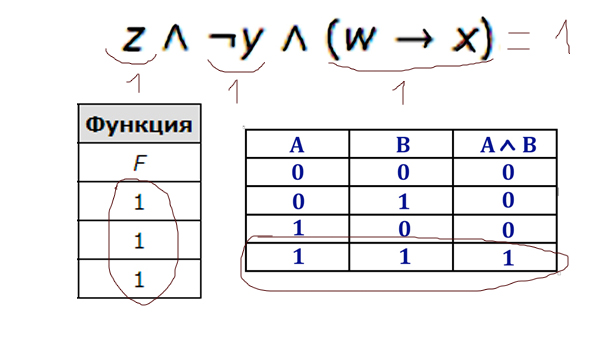
Логическая функция F задаётся выражением z ∧ ¬y ∧ (w → x).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
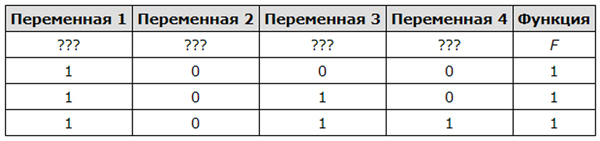
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
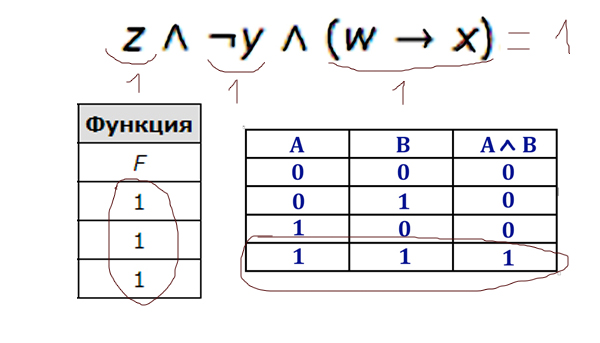
Решение:
Видим, что у функции основным действием является логическое умножение. По таблице видно, что функция имеет значение только 1 . Логическое умножение даёт 1 (единицу) тогда, когда каждое выражение равно 1 (единице). Значит каждое выражение в нашей функции должно равняться единице.
Отсюда видно, что переменная z должна всегда быть равна 1 (единице). Это первый столбец. Отрицание y тоже должно быть 1 (единицей), тогда просто y всегда будет 0 (нулём). Это второй столбец.
Осталось определить положение w и x. Здесь делаем предположение, что в третьем столбце стоит w, а в 4-ом x. Проверяем построчно и видим, что во второй строчке при таком расположении из 1 следует 0, что в итоге приводит выражение (w → x) в 0, а у нас это выражение всегда должно быть 1 (единицей). Значит, мы предположение сделали неверное, и получается x — это третий столбец, а w — четвёртый.
Ответ: zyxw
Задача 2 (средний уровень)
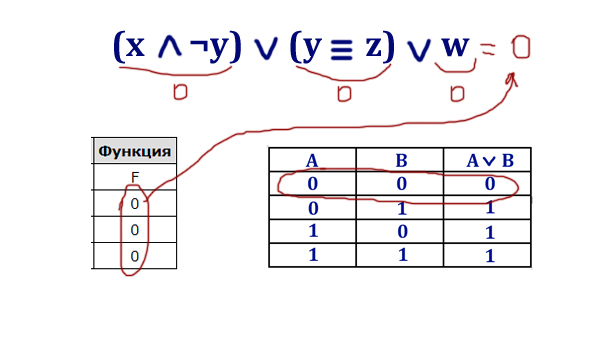
Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ w.
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение:
Определяем главную логическую операцию («главную скрипку»), которая соединяет разные выражения. Видим, что это логическое сложение.
Во всех строчках таблицы функция принимает значение 0 (ноль). Значит, и каждое выражение должно принимать значение 0 (ноль).
Самым слабым звеном является переменная w, потому что она стоит одна. Переменная w должна равняться всегда 0(нулю) — этому условию может удовлетворить только третий столбец. Значит w стоит на третьем месте.
Следующим слабым звеном является равносильность. Она должна «выдавать» 0 (ноль). Равносильность «выдаёт» 0 (ноль), когда переменные разные!
Проанализируем первый и второй столбец. В третьей строчке, и там, и там, стоит 1 (единица). Значит, первый и второй столбец не могут быть одновременно y и z (или z и y).
Рассмотрим второй и четвёртый столбец. Вторая строчка содержит одинаковое значение 0 (ноль), и там, и там. Значит, второй и четвёртый столбец не могут быть одновременно y и z (или z и y).
Таким образом, y и z (или z и y) будут столбцы первый и четвёртый! И теперь можно расставить недостающие значения в этих столбцах. Расставляем, чтобы были разные значения, а второй столбец получается x.
Осталось разобраться с z и y. Обратимся к первому выражению (x ∧ ¬y) и посмотрим на третью строчку. Если в четвёртом столбце будет стоять y, то отрицание на y превратит ноль(ноль) в 1(единицу) в четвёртой строчке. Тогда окажется, что у x — 1 и ¬y — 1, и выражение (x ∧ ¬y) тоже получится 1(единицей). А у нас каждое выражение должно равняться 0(нулю). Получается y будет стоять в первом столбце, а z в четвёртом.
Тогда ответ будет равен yxwz.
Ответ: yxwz
Мощнейший метод для решения второго задания из ЕГЭ по информатике
Задача 3 (хороший уровень)
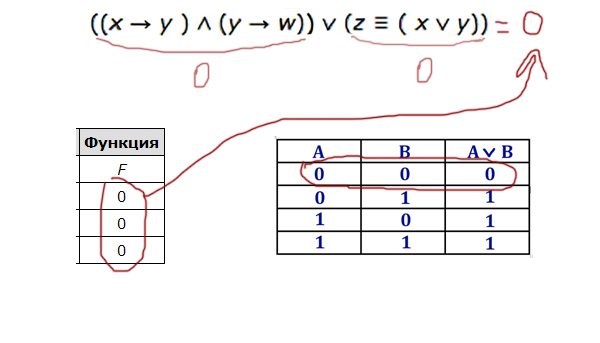
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение:
«Главной скрипкой» в нашей функции является логическое сложение, потому что соединяет два выражения ((x → y ) ∧ (y → w)) и (z ≡ ( x ∨ y)).
Тогда каждое выражение должно равняться 0(нулю).
Теперь кульминация мощнейшего метода. У нас всего 4 переменных. Выпишем все комбинации для 4-х переменных. Таблица будет точно такая же, как мы писали в первом задании (её очень легко составить). Всего получается 16 комбинаций (16 = 24).
Теперь отметим зелёным плюсом те строчки, которые обращают выражение ((x → y ) ∧ (y → w)) в 0(ноль). Следующий шаг: Отметим галочкой те строчки, которые обращают в ноль второе выражение (z ≡ ( x ∨ y)) (Мы должны искать среди тех, которые уже отмечены плюсом).
При небольшой тренировке анализ подобных выражений занимает сущие секунды!
У нас получается 4 строчки, которые удовлетворяют нашей функции:
Отсюда видно, что переменная z может быть равна только 0(нулю)! Значит, она занимает третий столбец, потому что в остальных столбцах есть хотя бы одна 1(единица).
Переменная w имеет только одну 1(единицу). Значит, её ставим во второй столбец, потому что в первом и четвёртом уже по 2 единицы минимум, а третий уже занят z.
Теперь находим строчку c 1(единицей) в переменной w (Таблица данная в условии задачи) Кто в этой строчке будет иметь единицу (кроме w) — будет x! Это четвёртый столбец! Значит, x — это четвёртый столбец. Переменной y — достаётся первый столбец
Ответ: ywzx.
На этом всё! Сегодня рассмотрели теорию и основные методы для эффективного решения второго задания из ЕГЭ по информатике!
Пока!
В спецификации написано, что эту задачу нужно решать без компьютера. Тем более её решить совсем не сложно с помощью «Мощнейшего метода».
Да ужметод. На простых заданиях разбирать можно
Примеры заданий ЕГЭ по информатике с решением на Паскале. На странице использованы условия задач из демо вариантов и задачника с сайта Полякова Константина Юрьевича (kpolyakov.spb.ru)
Содержание
- Задание 5
- Задание 6
- Задание 14
- Задание 15
- Задание 16
- Задание 17
- Задание 22
- Задание 24
- Задание 25
Задание 5
Демо-2022
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. К этой записи дописываются справа ещё два разряда по следующему
правилу:
а) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью результирующегочисла R.
Укажите такое наименьшее число N, для которого результат работы данного алгоритма больше числа 77. В ответе это число запишите в десятичной системе счисления.
Решение:
var n, i, b, s, k: integer; r: real; st: string; begin for n := 1 to 100 do begin k := n; //перебор исходного числа N s := 0; //сумма цифр двоичного кода r := 0; //результирующее десятичное число R st := ''; //очищаем строку двоичного кода для нового числа while k >= 1 do //цикл перевода в двоичный код исходного числа begin s := s + (k mod 2); //вычисление суммы цифр двоичного кода st := st + (k mod 2);//формирование строки двоичного кода из остатков деления на 2 k := k div 2;// деление на 2 end; st := ReverseString(st) + s mod 2; //переворачиваем код и дописываем остаток s := s + s mod 2;//вычисление суммы нового кода st := st + s mod 2;//формирование строки двоичного кода с добавлением остатка for i := 1 to Length(st) do //преобразование двоичного кода в десятичное число if st[i] = '1' then r := r + power(2, Length(st) - i); if r > 77 then begin println(n, r);break; end;//вывод найденных чисел end; end.
Задание 6
Демо-2022 Определите, при каком наибольшем введённом значении переменной s программа выведет число 64.
Решение: Используем исходный код. Добавим в него цикл перебора значений S и вывода при выполнении условия. Последнее значение и будет ответом.
var s, n, i: integer; begin for i := 1 to 510 do begin s := i; s := s div 10; n := 1; while s < 51 do begin s := s + 5; n := n * 2 end; if n = 64 then writeln(i); end; end.
Задание 14
Демо-2022 Значение арифметического выражения: 3*438+2*423+420+3*45+2*44+1 – записали в системе счисления с основанием 16. Сколько значащих нулей содержится в этой записи?
Решение:
var k,x:biginteger; begin k:=0; x:=3*4bi**38+2*4bi**23+4bi**20+3*4bi**5+2*4bi**4+1; while x>0 do begin if x mod 16=0 then k:=k+1; x:=x div 16; end; print(k) end.
Демо-2021 Значение арифметического выражения: 497 + 721 – 7 – записали в системе счисления с основанием 7. Сколько цифр 6 содержится в этой записи?
Решение:
var s, i,k6,x:integer; osn,n:biginteger; begin osn:=7; k6:=0; n:=power(osn,14)+power(osn,21)-7; while n>0 do begin if n mod 7 = 6 then k6:=k6+1; n:=n div 7; end; print(k6); end.
Демо-2020 Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 70 идущих подряд цифр 8? В ответе запишите полученную строку.
НАЧАЛО
_ПОКА нашлось (2222) ИЛИ нашлось (8888)
__ЕСЛИ нашлось (2222)
___ТО заменить (2222, 88)
___ИНАЧЕ заменить (8888, 22)
__КОНЕЦ ЕСЛИ
_КОНЕЦ ПОКА
КОНЕЦ
Решение:
begin var s: string := '8' * 70; while (s.contains('2222')) or (s.contains('8888')) do begin if (s.contains('2222')) then s := s.replace('2222', '88') else s := s.replace('8888', '22'); end; writeln(s); end.
Задание 15
Демо-2021 Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула ¬ДЕЛ(x, А) → (ДЕЛ(x, 6) → ¬ДЕЛ(x, 9)) тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Решение:
// Делители var a,x, flag: integer; begin for a := 1 to 100 do begin flag := 0; for x := 1 to 1000 do if not(x mod a = 0) <= ((x mod 6 = 0) <= not (x mod 9 = 0)) = false then begin flag := 1; break; end; if flag = 0 then print(a); end; end.
К.Поляков №161 Определите наименьшее натуральное число A, такое что выражение
(X & 29 ≠ 0) → ((X & 17 = 0) → (X & A ≠ 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?
Посмотреть решение
var A, x, flag: integer; begin for A := 0 to 31 do begin flag := 0; for x := 0 to 31 do if (((x and 29) = 0) or ((x and 17) <> 0) or ((x and A) <> 0))=false then flag := 1; if flag = 0 then begin writeln(A); break; end; end; end.
Задание 16
Демо-2022 Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1 при n = 1;
F(n) = n + F(n − 1), если n – чётно,
F(n) = 2 × F(n − 2), если n > 1 и при этом n – нечётно.
Чему равно значение функции F(26)?
Решение:
var i, n: integer; f: array[1..100] of integer; begin print('Введите значение n'); readln(n); f[1] := 1; for i := 2 to n do if i mod 2 = 0 then f[i] := i + f[i - 1] else f[i] := 2 * f[i - 2]; print(f[n]); end.
К.Поляков №46Алгоритм вычисления функции F(n) задан следующими соотношениями:
F(n) = n при n ≤ 3;
F(n) = 2 · n · n + F(n – 1) при чётных n > 3;
F(n) = n · n · n + n + F(n – 1) при нечётных n > 3;
Определите количество натуральных значений n, при которых F(n) меньше, чем 107.
Посмотреть решение
var i: integer; f: array[1..1000] of integer; begin i:=3; f[1] := 1; f[2] := 2; f[3] := 3; while f[i]< 10**7 do begin i:=i+1; if i mod 2 = 0 then f[i] := 2*i*i + f[i - 1] else f[i] := i*i*i+i +f[i - 1]; end; print(i-1);// не учитываем последнее число end.
Задание 17
Демо-2022
В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите и запишите в ответе сначала количество пар элементов последовательности, в которых хотя бы одно число делится на 3, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.Файл с данными: 17.txt
Решение:
var a,b,k,maxsum: integer; begin Assign( input, '17.txt' ); maxsum:=-20000; k:=0; readln(a); while not eof do begin readln(b); if (a mod 3 = 0) or (b mod 3 = 0) then begin k := k + 1; if a + b > maxsum then maxsum := a + b; end; a := b; end; Println( k, maxsum) end.
Задание 22
Демо-2022
Ниже на языке программирования записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа: L и M. Укажите наибольшее число x, при вводе которого алгоритм печатает сначала 4,а потом 5.

Решение:
var x, i, L, M, Q: integer; begin for i := 9 to 50 do begin x := i; Q := 9; L := 0; while x >= Q do begin L := L + 1; x := x - Q; end; M := x; if M < L then begin M := L; L := x; end; if (L = 4) and (M = 5) then print(i); end; end.
Задание 24
Демо-2022
Текстовый файл состоит из символов P, Q, R и S. Определите максимальное количество идущих подряд символов в прилагаемом файле, среди которых нет идущих подряд символов P. Для выполнения этого задания следует написать программу.Файл с данными: 24.txt
Решение:
var i, maxlen, curlen: longint; {описание переменных} s: string; f: text;{текстовый файл} begin assign(f, '24.txt'); {исходный текстовые файл с данными} reset(f); readln(f, s);{открываем файл для чтения данных} maxlen := 1; curlen := 1; for i := 2 to Length(s) do if not ((s[i] = 'P') and (s[i-1] = 'P')) then begin curLen := curLen + 1; if curLen > maxLen then maxLen := curLen; end else curLen := 1; writeln(maxLen); close(f); { закрываем файл} end.
Задание 25
Демо-2022
Пусть M – сумма минимального и максимального натуральных делителей целого числа, не считая единицы и самого числа. Если таких делителей и у числа нет, то значение M считается равным нулю. Напишите программу, которая перебирает целые числа, большие 700 000, в порядке возрастания и ищет среди них такие, для которых значение M оканчивается на 8. Выведите первые пять найденных чисел и соответствующие им значения M.
Формат вывода: для каждого из пяти таких найденных чисел в отдельной строке сначала выводится само число, затем – значение М.
Строки выводятся в порядке возрастания найденных чисел.
Решение:
var d1, chislo: integer; begin for chislo := 700001 to 700100 do for d1 := 2 to chislo - 1 do if chislo mod d1 = 0 then begin if (d1 + chislo div d1) mod 10 = 8 then println(chislo, d1 + chislo div d1); break; end; end.
Канал видеоролика: Видеоуроки по информатике
Смотреть видео:
#информатика #егэинформатика #икт #экзамены #егэ_2020 #мгту #школьникам #помощь_студентам #подготовкакэкзаменам
Свежая информация для ЕГЭ и ОГЭ по Информатике (листай):
С этим видео ученики смотрят следующие ролики:

14 задание ЕГЭ информатика | Теория и практика ЕГЭ | Решаем с помощью Pascal и Python | 2022
Видеоуроки по информатике

ЕГЭ по информатике — Задание 1 (Системы счисления. Теория)
Code Enjoy
ЕГЭ по информатике 2023 — Задание 19-21 (Теория игр на Python)
Code Enjoy

Cтрим #12. ЕГЭ по информатике 2020, 11 класс. Решаем задание 18
ЕГЭ по информатике
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
12.11.2021
Автор материалов — Лада Борисовна Есакова.
В компьютере вся информация представлена в двоичной системе счисления, в которой используется две цифры – 0 и 1. Собственно, и цифр как таковых у компьютера нет, а есть электрический сигнал, проходящий по электронным схемам и соединительным проводникам (шинам) компьютера, который может принимать значения “высокий уровень электрического напряжения” (принимаемый нами за 1) и “низкий уровень электрического напряжения” (принимаемый за 0). Для различных действий над этими нулями и единичками нам необходимы специальные операции, которые работают с двоичными переменными. Такие операции называются логическими операциями.
Логические операции и их аргументы принимают только два значения: 1 (“истина”) и 0 (“ложь”).
Таблица истинности выражения определяет его значения при всех возможных комбинациях исходных данных.
Количество строк в таблице истинности выражения от N переменных равно 2N.
Основные логические операции:
1). Логическое умножение (конъюнкция, логическое И). Обозначается: AND, &, /.
Таблица истинности:
|
A |
B |
А&В |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
0 |
2). Логическое сложение (дизъюнкция, логическое ИЛИ). Обозначается: OR, |, /.
Таблица истинности:
|
A |
B |
A / B |
|
1 |
1 |
1 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
0 |
0 |
0 |
3). Логическое отрицание (инверсия, логическое НЕ). Обозначается: NOT, ¬, .
Таблица истинности:
4). Логическое следование (импликация). Обозначается: →.
Таблица истинности:
|
A |
B |
A → B |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
1 |
|
0 |
0 |
1 |
5). Логическое равенство (эквивалентность). Обозначается: ↔, ~.
Таблица истинности:
|
A |
B |
A ~ B |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
1 |
Порядок (приоритет) выполнения логических операций:
Если в выражении нет скобок, то операции выполняются в следующем порядке:
— Логическое отрицание (инверсия, логическое НЕ);
— Логическое умножение (конъюнкция, логическое И);
— Логическое сложение (дизъюнкция, логическое ИЛИ);
— Логическое следование (импликация);
— Логическое равенство (эквивалентность).
Выбор выражения по таблице истинности
Пример 1.
Дан фрагмент таблицы истинности выражения F:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
F |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
Каким выражением может быть F?
1) (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6)
2) (x1 ∧ x3) ∨ (x3 ∧ x5) ∨ (x5 ∧ x1)
3) (x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2)
4) (x1 ∧ x4) ∨ (x2 ∧ x5) ∨ (x3 ∧ x6)
Решение:
Все представленные варианты ответа — дизъюнкции трёх конъюнкций. Все значения F в таблице равны нулю. Дизъюнкция равна нулю, когда все слагаемые равны нулю.
Рассмотри поочерёдно все четыре выражения.
1) В первой строке таблицы x1=1 и x2=1, значит x1∧x2=1. Выражение не подходит.
2) Во второй строке таблицы x1=1 и x3=1, значит x1∧x3=1. Выражение не подходит.
3) Подставим в третье выражение поочередно значения всех строк таблицы:
Первая строка
(x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2) = (1 ∧ 0) ∨ (0 ∧ 0) ∨ (0 ∧ 1) = 0 ∨ 0 ∨ 0 = 0
Вторая строка
(x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2) = (0 ∧ 0) ∨ (0 ∧ 1) ∨ (1 ∧ 0) = 0 ∨ 0 ∨ 0 = 0
Третья строка
(x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2) = (0 ∧ 1) ∨ (1 ∧ 0) ∨ (0 ∧ 0) = 0 ∨ 0 ∨ 0 = 0
Выражение подходит.
4) В третьей строке таблицы x1=1 и x4=1, значит x1∧x4=1. Выражение не подходит.
Ответ:3
Пример 2.
Для таблицы истинности функции F известны значения только некоторых ячеек:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
F |
|
1 |
0 |
1 |
|||||
|
0 |
0 |
1 |
|||||
|
0 |
1 |
0 |
Каким выражением может быть F?
1) x1 ∧ x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ x5 ∧ x6 ∧ x7
4) x1 ∨ x2 ∨ ¬ x3 ∨ x4 ∨ x5 ∨ ¬x6 ∨ x7
Решение:
Рассмотри поочерёдно все четыре выражения.
1) Выражение является конъюнкцией переменных и их отрицаний. Конъюнкция равна единице, когда все операнды равны единице. В первой строке x6 = 0, а значит и все выражение F равно нулю, что не соответствует таблице истинности.
2) Выражение является дизъюнкцией переменных и их отрицаний. Дизъюнкция равна единице, когда хотя бы один операнд равен единице. Подставим во второе выражение поочередно значения всех строк таблицы:
Первая строка
x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7 = x1 ∨ ¬x2 ∨ x3 ∨ 0 ∨ ¬x5 ∨ 0 ∨ ¬x7 может принимать значение 1, если хотя бы один из операндов равен 1.
Вторая строка
x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7 = x1 ∨ ¬x2 ∨ x3 ∨ 1 ∨ ¬x5 ∨ x6 ∨ 1 = 1
Третья строка
x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7 = 0 ∨ ¬x2 ∨ x3 ∨ 0 ∨ ¬x5 ∨ x6 ∨ ¬x7 может принимать значение 0, если все остальные операнды равны 0.
3) Выражение является конъюнкцией переменных и их отрицаний. Конъюнкция равна единице, когда все операнды равны единице. Во второй строке x4 = 0, а значит и все выражение F равно нулю, что не соответствует таблице истинности.
4) Выражение является дизъюнкцией переменных и их отрицаний. Дизъюнкция равна единице, когда хотя бы один операнд равен единице. В третьей строке x4 = 1, значит и все выражение F равно 1, что не соответствует таблице истинности.
Ответ:2
Пример 3.
Логическая функция F задаётся выражением (¬z) ∧ x ∨ x ∧ y. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
|
Перем. 1 |
Перем. 2 |
Перем. 3 |
Функция |
|
??? |
??? |
??? |
F |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая 1-му столбцу; затем – буква, соответствующая 2-му столбцу; затем – буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение:
Выражение (¬z) ∧ x ∨ x ∧ y является дизъюнкцией двух конъюнкций:
((¬z) ∧ x) ∨ (x ∧ y) . В обеих конъюнкциях присутствует x. Т. е. при x = 0 все выражение равно 0. Это выполняется только при Перем.3 = x.
Выражение равно 1, если x =1 и выполняется хотя бы одно из условий: y = 1 или z = 0. Из четвертой строки следует, что Перем.1 = z, а Перем.2 = y.
Ответ: zyx
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задача №2. Построение таблиц истинности логических выражений. Выбор выражения, соответствующего условию.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.03.2023
Примерное время на чтение статьи: 2 минут
Задача № 2 из ЕГЭ по информатике относится к разделу «Логика и алгоритмы» школьного курса «Информатика» и ориентирована на проверку умения строить таблицы истинности и логические схемы.
Данная задача не предполагает какого-то программного решения, однако, ее можно решить и программированием.
В последние версии PascalABC.NET разработчиками добавлен модуль School (англ. школа), который содержит реализацию алгоритмов, часто встречающихся в школьных задачах.
Рассмотрим конструкции языка, используемые при построении логических высказываний.
- Расширение
a.Imp(b)возвращает результат операции импликацииa → b, допускается записьa<=b; - Функция
TrueTable((a, …, e) -> f(a, …, e))возвращает матрицу типаboolean, содержащую таблицу истинности для заданной функции n-аргументов (где n не больше 5); - Процедура
TrueTablePrint(a)выводит таблицу истинности, полученную посредством функцииTrueTable; - Процедура
TrueTablePrint(a, f)выводит таблицу истинности, полученную посредством функцииTrueTable. Параметрfпозволяет фильтровать выводимые строки: приf = 0выводятся только строки, в которых значение функции равно False, приf = 1– только строки, в которых оно равно True
Пример. Построим таблицу истинности для логического выражения
##
uses school;
var tt := TrueTable((a, b, c) → a and b or c);
TrueTablePrint(tt);Результат работы программы:
a b c F
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
Использование параметра f со значением 0 или 1 процедуры TrueTablePrint позволит отфильтровать выводимые строки, пропустив на печать те из них, в которых значений функции совпадает со значением f.
Рассмотрим решение задачи из ЕГЭ-2019 (досрочная волна)
Пример. Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w. Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
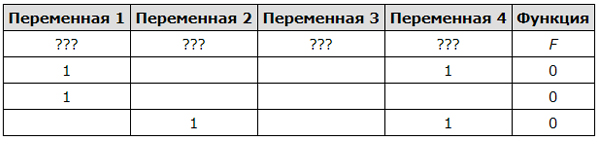
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
| ??? | ??? | ??? | ??? | F |
| 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 |
В ответе напишите буквы x, y, z, w; в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 1 | Функция |
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Поскольку пока не известно, в каком столбце заголовка стоит какая переменная, дадим им произвольные имена по порядку, например a, b, c, d. После чего подставим их в функцию F и отобразим только строки, соответствующие значению F=0:
##
uses school;
var tt := TrueTable((a, b, c, d) → (a and not b) or (b = c) or not d);
TrueTablePrint(tt, 0);Результат работы программы:
a b c d F
0 0 1 1 0
0 1 0 1 0
1 1 0 1 0
Сопоставляя выходную таблицу и до конца не заполненную по заданию, заключаем, что d=w, b=y, c=z, a=x.
Ответ: xwzy
Здравствуйте, дорогие друзья! Сегодня разберём, как решать второе задание из ЕГЭ по информатике 2020.
Во втором задании ЕГЭ по информатике у нас обычно есть логическая функция, которая зависит от логических переменных. Логические переменные могут принимать только два значения: 0 (Ложь) или 1 (Истина).
С логическими переменными можно производить логические операции. При решении второго задания из ЕГЭ по информатике необходимо твёрдо знать каждую логическую операцию, и давайте рассмотрим их.
- () — операции в скобках
- ¬ — логическое отрицание
- ∧ — логическое умножение
- ∨ — логическое сложение
- ⟶ — следование
- ≡ — равнозначность
Ещё соотношения:
Передём к решению задач из ЕГЭ по информатике
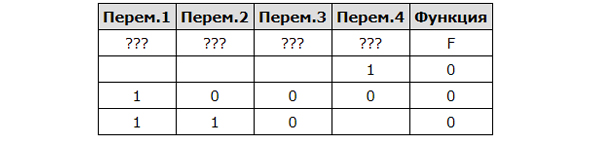
Логическая функция F задаётся выражением z ∧ ¬y ∧ (w → x). Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно. Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Видим, что у функции основным действием является логическое умножение. По таблице видно, что функция имеет значение только 1 . Логическое умножение даёт 1 (единицу) тогда, когда каждое выражение равно 1 (единице). Значит каждое выражение в нашей функции должно равняться единице.
Отсюда видно, что переменная z должна всегда быть равна 1 (единице). Это первый столбец. Отрицание y тоже должно быть 1 (единицей), тогда просто y всегда будет 0 (нулём). Это второй столбец.
Осталось определить положение w и x. Здесь делаем предположение, что в третьем столбце стоит w, а в 4-ом x. Проверяем построчно и видим, что во второй строчке при таком расположении из 1 следует 0, что в итоге приводит выражение (w → x) в 0, а у нас это выражение всегда должно быть 1 (единицей). Значит, мы предположение сделали неверное, и получается x — это третий столбец, а w — четвёртый.
Задача 2 (средний уровень)
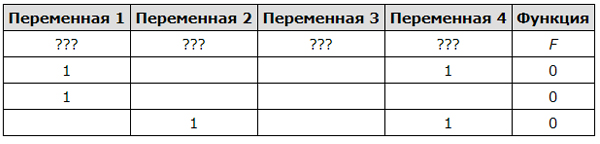
Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ w.
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Определяем главную логическую операцию («главную скрипку»), которая соединяет разные выражения. Видим, что это логическое сложение.
Во всех строчках таблицы функция принимает значение 0 (ноль). Значит, и каждое выражение должно принимать значение 0 (ноль).
Самым слабым звеном является переменная w, потому что она стоит одна. Переменная w должна равняться всегда 0(нулю) — этому условию может удовлетворить только третий столбец. Значит w стоит на третьем месте.
Следующим слабым звеном является равносильность. Она должна «выдавать» 0 (ноль). Равносильность «выдаёт» 0 (ноль), когда переменные разные!
Проанализируем первый и второй столбец. В третьей строчке, и там, и там, стоит 1 (единица). Значит, первый и второй столбец не могут быть одновременно y и z (или z и y).
Рассмотрим второй и четвёртый столбец. Вторая строчка содержит одинаковое значение 0 (ноль), и там, и там. Значит, второй и четвёртый столбец не могут быть одновременно y и z (или z и y).
Таким образом, y и z (или z и y) будут столбцы первый и четвёртый! И теперь можно расставить недостающие значения в этих столбцах. Расставляем, чтобы были разные значения, а второй столбец получается x.
Осталось разобраться с z и y. Обратимся к первому выражению (x ∧ ¬y) и посмотрим на третью строчку. Если в четвёртом столбце будет стоять y, то отрицание на y превратит ноль(ноль) в 1(единицу) в четвёртой строчке. Тогда окажется, что у x — 1 и ¬y — 1, и выражение (x ∧ ¬y) тоже получится 1(единицей). А у нас каждое выражение должно равняться 0(нулю). Получается y будет стоять в первом столбце, а z в четвёртом.
Тогда ответ будет равен yxwz.
Ответ: yxwz
Мощнейший метод для решения второго задания из ЕГЭ по информатике
Задача 3 (хороший уровень)
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F. Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
«Главной скрипкой» в нашей функции является логическое сложение, потому что соединяет два выражения ((x → y ) ∧ (y → w)) и (z ≡ ( x ∨ y)).
Тогда каждое выражение должно равняться 0(нулю).
Теперь кульминация мощнейшего метода. У нас всего 4 переменных. Выпишем все комбинации для 4-х переменных. Таблица будет точно такая же, как мы писали в первом задании (её очень легко составить). Всего получается 16 комбинаций (16 = 2 4 ).
Теперь отметим зелёным плюсом те строчки, которые обращают выражение ((x → y ) ∧ (y → w)) в 0(ноль). Следующий шаг: Отметим галочкой те строчки, которые обращают в ноль второе выражение (z ≡ ( x ∨ y)) (Мы должны искать среди тех, которые уже отмечены плюсом).
При небольшой тренировке анализ подобных выражений занимает сущие секунды!
У нас получается 4 строчки, которые удовлетворяют нашей функции:
Отсюда видно, что переменная z может быть равна только 0(нулю)! Значит, она занимает третий столбец, потому что в остальных столбцах есть хотя бы одна 1(единица).
Переменная w имеет только одну 1(единицу). Значит, её ставим во второй столбец, потому что в первом и четвёртом уже по 2 единицы минимум, а третий уже занят z.
Теперь находим строчку c 1(единицей) в переменной w (Таблица данная в условии задачи) Кто в этой строчке будет иметь единицу (кроме w) — будет x! Это четвёртый столбец! Значит, x — это четвёртый столбец. Переменной y — достаётся первый столбец
Ответ: ywzx.
На этом всё! Сегодня рассмотрели теорию и основные методы для эффективного решения второго задания из ЕГЭ по информатике!
Строки с пропущенными значениями 2 задание егэ информатика как решать
Тип 2 № 14688
Логическая функция F задаётся выражением (x ∨ y) → (z ≡ x).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.
| Переменная 1 | Переменная 2 | Переменная 3 | Функция |
|---|---|---|---|
| . | . | . | F |
| 0 | 0 | 0 | |
| 0 | 0 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 2 | Функция |
|---|---|---|
| . | . | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Данная импликация принимает значение 0 тогда и только тогда, когда
Пусть x = 0, тогда y = z = 1. В первой строке нет двух единиц, значит, x = 1, и эта переменная находится в первом столбце. Тогда первая строка имеет вид 1 0 0.
Вторая строка должна отличаться от первой, поэтому она имеет вид 1 0 1. Рассмотрим два варианта:
Первый вариант не удовлетворяет системе (*), а второй удовлетворяет.
Приведем другое решение.
Составим таблицу истинности для выражения (x ∨ y) → (z ≡ x) и выпишем те наборы переменных, при которых данное выражение равно 0. В наборах переменные запишем в порядке х, y, z. Получим следующие наборы:
Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности.
Первая строка таблицы может соответствовать только набору (1, 0, 0), следовательно, первый столбец таблицы соответствует переменной x, и в первом столбце первой строки стоит 1.
Второй столбец таблицы может соответствовать только переменной z, поскольку переменная y принимает нулевое значение только в одном наборе. Тогда третий столбец соответствует переменной y.
Тип 2 № 15097
Логическая функция F задаётся выражением (x ≡ z ) ∨ (x → (y ∧ z)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.
. . . F
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Данная импликация принимает значение 0 тогда и только тогда, когда
Пусть . Исходя из системы (*), , тогда . В первой строке нет единицы, значит, переменная x находится в третьем столбце. Тогда первая строка имеет вид 0 0 1.
Вторая строка должна отличаться от первой, поэтому она имеет вид 1 0 1. Рассмотрим два варианта:
Второй вариант не удовлетворяет системе (*), а первый удовлетворяет.
Приведем другое решение.
Составим таблицу истинности для выражения (x ≡ z ) ∨ (x → (y ∧ z)) и выпишем те наборы переменных, при которых данное выражение равно 0. В наборах переменные запишем в порядке х, y, z. Получим следующие наборы:
Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности.
Первая строка таблицы может соответствовать только набору (1, 0, 0), следовательно, третий столбец — это переменная x. Вторая строка соответствует набору (1, 1, 0), в котором единичное значение принимает также переменная y, следовательно, первый столбец — это переменная у, тогда второй столбец — это переменная z.
Тип 2 № 15124
Логическая функция F задаётся выражением (x ≡ y ) ∨ ((y ∨ z) → x).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.
. . . F
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Данная импликация принимает значение 0 тогда и только тогда, когда
Пусть . Исходя из системы (*), , тогда . В первой строке нет нуля, значит, переменная x находится в первом столбце. Тогда первая строка имеет вид 0 1 1.
Вторая строка должна отличаться от первой, поэтому она имеет вид 0 0 1. Рассмотрим два варианта:
Первый вариант не удовлетворяет системе (*), а второй удовлетворяет.
Приведем другое решение.
Составим таблицу истинности для выражения (x ≡ y ) ∨ ((y ∨ z) → x) и выпишем те наборы переменных, при которых данное выражение равно 0. В наборах переменные запишем в порядке х, y, z. Получим следующие наборы: (0, 1, 0), (0, 1, 1).
Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности.
В обоих наборах переменная x принимает значение 0, значит, ей может соответствовать только первый столбец таблицы. Переменная z принимает значение 1 только в одном наборе, значит, ей может соответствовать только второй столбец таблицы, тогда третий столбец соответствует переменной у.
Тип 2 № 15618
Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w. На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z. Все строки в представленном фрагменте разные.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 |
|---|---|---|---|
| . | . | . | . |
| 0 | |||
| 1 | 0 | 0 | |
| 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (без разделителей).
Рассмотрим данное выражение. Преобразуем логическое выражение (x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w и получим систему, при которой оно ложно:
Cразу видно, что первый столбец это w, поскольку w всегда должна равняться единице. Также, ясно, что x это переменная 4, так как . Из первого выражения x ∧ ¬y и последней строчке таблицы видно, что переменная 3 это y, а вторая переменная это z.
Рассмотрим, как будет выглядеть полная таблица истинности. Переменная w всегда должна принимать значение 1, поэтому в первом столбце во всех строках будет стоять единица. Исходя из условия можно заключить, что во втором столбце в последней строке будет стоять единица, и в первых двух строках третьего столбца тоже будут стоять единицы. В первой четвёртого столбца должна стоять единица, поскольку строки в таблице истинности должны быть разными.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 |
|---|---|---|---|
| . | . | . | . |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Вариант wyzx не подходит, поскольку в первой строке функция F окажется истинной.
Приведем другое решение.
Составим таблицу истинности функции F и выпишем наборы переменных, при которых функция ложна. Для удобства обозначим эти наборы буквами:
А: (х=0, y=0, z=1, w=1)
Б: (х=0, y=1, z=0, w=1)
В: (х=1, y=1, z=0, w=1)
Заметим, что переменная w всегда должна быть равна 1, поэтому ей соответствует первый столбец заданной таблицы.
Заметим, что вторая и третья строки заданной таблицы, содержащие по два нуля, соответствуют наборам переменных А или Б, тогда первая строка соответствует набору В. Значит, в первой строке z=0, а все остальные переменные равны 1, и переменной z соответствует второй столбец заданной таблицы.
Тогда вторая строка заданной таблицы, в которой переменная z также равна 0, соответствует набору Б, в котором х=0, а остальные переменные равны 1, поэтому переменной х соответствует четвертый столбец таблицы.
Строки с пропущенными значениями 2 задание егэ информатика как решать
Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | Функция |
| . | . | . | . | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
Логическая функция F задается выражением
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | Функция |
| . | . | . | . | F |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
Миша заполнял таблицу истинности функции
(¬x ∧ ¬y) ∨ (y ≡ z) ∨ w,
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:
| ? | ? | ? | ? | (¬x∧¬y)∨(y≡z)∨w |
|---|---|---|---|---|
| 0 | 1 | 0 | ||
| 1 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 0 |
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
Логическая функция F задается выражением
¬(z ∨ (y ∧ ¬x))
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Функция |
|---|---|---|---|
| . | . | . | F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Видеоразбор
Логическая функция F задается выражением
(x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z. Все строки в представленном фрагменте разные.