Операции со степенями
[su_box title=”Описание задания” style=”soft” box_color=”#c1e8cc” title_color=”#0c0a0a”]
Во задании №2 ЕГЭ по математике необходимо продемонстрировать знания работы со степенными выражениями.
Тематика заданий: операции со степенями
Бал: 1 из 20
Сложность задания: ♦◊◊
Примерное время выполнения: 3 мин.
[/su_box]
Теория к заданию №2
Правила обращения со степенями можно представить следующим образом:
Кроме этого, следует напомнить об операциях с дробями:
Теперь можно перейти к разбору типовых вариантов! 🙂
Разбор типовых вариантов заданий №2 ЕГЭ по математике базового уровня
Во всех заданиях, аналогично первому заданию, нам необходимо найти значение выражения.
Вариант 2МБ1
Алгоритм выполнения:
- Представить число с отрицательным показателем в виде правильной дроби.
- Выполнить первое умножение.
- Представить степени чисел в виде простых чисел, заменив степени их умножением.
- Выполнить умножение.
- Выполнить сложение.
Решение:
Чтобы представить отрицательную степень числа в виде обыкновенной дроби, необходимо 1 разделить на это число, но уже в положительной степени.
То есть: 10-1 = 1/101 = 1/10
Выполним первое умножение, то есть умножение целого числа на правильную дробь. Для этого числитель дроби умножим на целое число, а знаменатель оставим без изменения.
9 · 1/10 = (9 · 1)/10 = 9/10
Первая степень числа всегда есть само число.
101 = 10
Вторая степень числа – это число умноженное само на себя.
102 = 10 · 10 = 100
Вычислим значение выражения, учитывая, что
получим:
Ответ: 560,9
Вариант 2МБ2
Алгоритм выполнения:
- Представить первую степень числа в виде целого числа.
- Представить отрицательные степени чисел в виде правильных дробей.
- Выполнить умножение целых чисел.
- Выполнить умножение целых чисел на правильные дроби.
- Выполнить сложение.
Решение:
Первая степень числа всегда есть само число. (101 = 10)
Чтобы представить отрицательную степень числа в виде обыкновенной дроби, необходимо 1 разделить на это число, но уже в положительной степени.
То есть:
10-1 = 1/101 = 1/10
10-2 = 1/102 = 1/(10 · 10) = 1/100
Выполним умножение целых чисел.
3 · 101 = 3 · 10 = 30
Выполним умножение целых чисел на правильные дроби.
4 · 10-2 = 4 · 1/100 = (4 ·1)/100 = 4/100
2 · 10-1 = 2 · 1/10 = (2 · 1)/10 = 2/10
Вычислим значение выражения, учитывая, что
получим:
Ответ: 30,24
Вариант 2МБ3
Алгоритм выполнения:
- Представить степени чисел в виде умножения и вычислить значение степеней чисел.
- Выполнить умножение.
- Выполнить сложение.
Решение:
Представим степени чисел в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
24 = 2 · 2 · 2 · 2 = 16
23 = 2 · 2 · 2 = 8
Выполним умножение:
4 · 24 = 4 · 16 = 64
3 · 23 = 3 · 8 = 24
Вычислим значение выражения:
Ответ: 88
Вариант 2МБ4
Алгоритм выполнения:
- Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
- Вынести общий множитель за скобку.
- Выполнить действие в скобках.
- Представить степень числа в виде умножения и вычислить значение степени числа.
- Выполнить умножение.
Решение:
Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
44 = 4 · 43
Вынесем общий множитель за скобку
3 · 43 + 2 · 44 = 43 · (3 + 2 · 4)
Выполним действие в скобках.
(3 + 2 · 4) = (3 + 
Представим степень числа в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
43 = 4 · 4 · 4 = 64
Вычислим значение выражения, учитывая, что
получим:
Ответ: 704
Вариант 2МБ5
Алгоритм выполнения:
- Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
- Вынести общий множитель за скобку.
- Выполнить действие в скобках.
- Представить степень числа в виде умножения и вычислить значение степени числа.
- Выполнить умножение.
Решение:
Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
53 = 5 · 52
Вынесем общий множитель за скобку
2 · 53 + 3 · 52 = 52 · (2 · 5 + 3)
Выполним действие в скобках.
(2 · 5 + 3) = (10 + 3) = 13
Представим степень числа в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
52 = 5 · 5 = 25
Вычислим значение выражения, учитывая, что
, а
получим:
Выполняем умножение в столбик, имеем:
Ответ: 325
Вариант 2МБ6
Решение:
В данном задании удобней привести значения к более привычному виду, а именно записать числа в числителе и знаменателе в стандартном виде:
После этого можно выполнить деление 24 на 6, в результате получим 4.
Десять в четвертой степени при делении на десять в третьей степени даст десять в первой, или просто десять, поэтому мы получим:
4 • 10 = 40
Ответ: 40
Вариант 2МБ6
Решение:
В данном случае мы должны заметить, что число 6 в знаменателе раскладывается на множители 2 и 3 в степени 5:
После этого можно выполнить сокращения степеней у двойки: 6-5=1, у тройки: 8-5=3.
Теперь возводим 3 в куб и умножаем на 2, получая 54.
Ответ: 54
Вариант 2МБ6
Алгоритм выполнения
- Применяем к числителю св-во степеней (ах)у=аху. Получаем 3–6.
- Применяем к дроби св-во степеней ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
(3–3)2 /3–8 = 3–6 /3–8= 3–6–(–8)) = 3–6+8 = 32 = 9
Ответ: 9
Вариант 2МБ7
Алгоритм выполнения
- Используем для степени в числителе (149) св-во (аb)х=ax·bx. 14 разложим на произведение 2 и 7. Получим произведение степеней с основаниями 2 и 7.
- Преобразуем выражение в 2 дроби, каждая из которых будет содержать степени с одинаковыми основаниями.
- Применяем к дробям св-во степеней ax/ay=ax–y.
- Находим полученное произведение.
Решение:
149 / 27·78 = (2·7)9 / 27·78 = 29·79 / 27 78 = 29–7·79–8 = 22·71 = 4·7 = 28
Ответ: 28
Вариант 2МБ8
Алгоритм выполнения
- Выносим за скобки общий множитель 52=25.
- Выполняем в скобках умножение чисел 2 и 5. Получаем 10.
- Выполняем в скобках сложение 10 и 3. Получаем 13.
- Выполняем умножение общего множителя 25 и 13.
Решение:
2·53+3·52 = 52·(2·5+3) = 25·(10+3) = 25·13 = 325
Ответ: 325
Вариант 2МБ9
Алгоритм выполнения
- Возводим в квадрат (–1). Получим 1, поскольку происходит возведение в четную степень.
- Возводим (–1) в 5-ю степень. Получим –1, т.к. происходит возведение в нечетную степень.
- Выполняем действия умножения.
- Получаем разность двух чисел. Находим ее.
Решение:
6·(–1)2+4·(–1)5 = 6·1+4·(–1) = 6+(–4) = 6–4 = 2
Ответ: 2
Вариант 2МБ10
Алгоритм выполнения
- Преобразуем множители 103 и 102 в целые числа.
- Находим произведения путем переноса десят.запятой вправо на соответствующее число знаков.
- Находим результирующую сумму.
Решение:
9,4·103+2,2·102 = 9,4·1000+2,2·100 = 9400+220 = 9620
Ответ: 9620
Вариант 2МБ11
Алгоритм выполнения
- Преобразуем 102 в целое число и выполняем умножение в числителе путем переноса деся.запятой.
- Преобразуем 10–2 в десят.дробь и выполняем умножение в знаменателе путем переноса десят.запятой влево.
- Домножаем числитель и знаменатель на 100, чтобы избавиться от десят.запятой в знаменателе.
- Находим результат путем деления числителя дроби на ее знаменатель.
Решение:
1,6·102 / 4·10–2 = 1,6·100 / 4·0,01 = 160/ 0,04 = 160·100 / 0,04·100 = 16000 / 4 = 4000
Ответ: 40000
Вариант 2МБ12
Алгоритм выполнения
- Применяем к дроби св-ва степеней ax·ay=ax+y и ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
3–10·35 / 3–7 = 3–10+5 /3–7 = 3–5 / 3–7 = 3–5–(–7)) = 3–5+7 = 32 = 9
Ответ: 9
Вариант 2МБ13
Алгоритм выполнения
- Представляем выражение в знаменателе как степень с основанием 8. Далее применяем св-во степеней (ах)у=аху, получаем 812.
- Применяем к дроби св-во степеней ax/ay=ax–y.
Решение:
813 /646 =813 / (82)6 =813 /812 = 813–12 = 81 = 8
Ответ: 8
Вариант 2МБ14
Алгоритм выполнения
- Преобразуем степени в числителе дроби и в делителе (число 92) так, чтобы получились степени с основанием 3.
- Используем св-во степеней (ах)у=аху для преобразованных степеней.
- Используем св-во степеней ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
274 /36 : 92 =(33)4 / 36 : (32)2 = 312/36 : 34 = 312–6–4 = 32 = 9
Ответ: 9
Вариант 2МБ15
Алгоритм выполнения
- Возводим каждый из множителей в соответствующую степень. Получим соответственно: 0,01, 1000, 4.
- Перемножаем 0,01 и 1000 путем переноса десят.запятой вправо на 3 знака. Получим 10.
- Умножаем 10 на 4.
Решение:
(0,1)2·103·22 = 0,01·1000·4 = 10·4 = 40
Ответ: 40
Даниил Романович | Просмотров: 18.6k
- ЕГЭ по математике база
Практика по заданию №2 ЕГЭ по математике базового уровня — простейшие текстовые задачи.
Для выполнения задания №2 необходимо уметь выполнять вычисления и преобразования
Практика
Коды проверяемых элементов содержания (по кодификатору) — 1.4.3–1.4.5
Уровень сложности задания — базовый
Максимальный балл за выполнение задания — 1
Примерное время выполнения задания выпускником, изучавшим математику на базовом уровне (в мин.) — 7
Примеры заданий:
1. В летнем лагере 229 детей и 28 воспитателей. В одном автобусе можно перевозить не более 48 пассажиров. Какое наименьшее количество таких автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?
2. Теплоход рассчитан на 750 пассажиров и 25 членов команды. Каждая спасательная шлюпка может вместить 70 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды?
3. В летнем лагере 150 детей и 21 воспитатель. В одном автобусе можно перевозить не более 20 пассажиров. Какое наименьшее количество таких автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?
4. Система навигации самолёта информирует пассажира о том, что пол1т проходит на высоте 21 000 футов. Выразите высоту полёта в метрах. Считайте, что 1 фут равен 30,5 см.
5. Файл размером 1,5 Гбайта скачался за 12 минут (скорость загрузки считайте постоянной). За сколько минут скачается файл размером 2,5 Гбайта, если скорость загрузки останется прежней?
Связанные страницы:
В статье представлен полный разбор демонстрационной версии ЕГЭ 2022 по математике на базовом уровне. Надеемся, что данный разбор поможет подготовиться к решению базовых заданий, так как в демоварианте есть лишь ответы, но нет решений.
Разумеется, приступая к работе, внимательно читаем инструкцию, а в процессе решения используем справочный материал КИМа.
Задание 1
Сдавая экзамен, нужно решить одно задание на выбор, но мы будем рассматривать все варианты. Чтобы найти значение первого выражения, сначала выполним действия в скобках. 6,7 – 3,2 = 3,5 и умножим 3,5 на 2,4, получим 8,4. Не забываем, что ответ нужно записать, отводя на каждый символ по клеточке, то есть на запятую тоже отводим клеточку. Ответ:
Второй пример содержит обыкновенные дроби, решаем аналогично первому, сначала сложим дроби в скобках, общий знаменатель 66, это наименьшее общее кратное для чисел 33 и 22, получаем
8х2+13х3/66=55/66=5/6 , и теперь заменим деление умножением на взаимно обратное число («перевернем дробь-делитель»), 5/6 х 18/5 =3
Задание 2
Чтобы решить первую задачу, разделим 100 на 14,6, получаем приблизительно 6,8 (дальше делить не нужно, лишь потратим драгоценное время), поскольку можно купить целое число баночек, ответ: 6.
Для решения второй задачи вычислим, сколько денег потрачено на 1,6 кг моркови. Умножим 40 на 1,6, получим 64. Сдача со 100 рублей составит 36 рублей. Ответ: 36
Наконец, третья задача. Разделим 63 на 6, получаем 10,5. Полпачки клея не купишь, значит, придется покупать 11 пачек. Ответ: 11
Не забудьте, нужно решить один вариант, решайте тот, в котором больше всего уверены!
Задание 3
Первый вариант. Рост ребенка может составить 110 см, значит, А 4, толщина листа бумаги 0,2 мм, Б 3, автобус проедет 32 км, соответственно, В 1, и остается Г 2, что вполне отвечает здравому смыслу (9-10 этажный дом, считая по 3 м на этаж).
Ответ 4312
Во втором варианте А 3, Б 1, В 4 и Г 2.
Ответ 3142
Нужно уметь сравнивать различные единицы длины, массы и т.д., так как в реальном варианте может встретиться скорость, время и другие единицы измерения.
Задание 4
Первый вариант. Находим Амур и смотрим, сколько рек имеют длину больше, чем Амур. Это Волга, Енисей, Иртыш, Лена, Нижняя Тунгуска и Обь. Итого 6 рек. Амур на седьмом месте.
Ответ: 7
Во втором варианте просто выберем самый дешевый смартфон. Он стоит 6559 рублей.
Ответ: 6559
Третий вариант. Находим 19 февраля (выделено синим), находим максимальную температуру (красная точка).
Теперь нужно посмотреть, какой температуре она соответствует. Посередине между минус 4 и минус 2 градусами может быть только минус 3. Ответ: — 3
Задание 5
Две клеточки заполнены озером почти полностью, еще две примерно наполовину, и примерно на четверть еще одна. Значит, примерно 3 кв. километра, чуть больше или меньше, неважно.
Ответ: 3
Перед нами трапеция, площадь равна произведению полусуммы оснований на высоту. Основания 5 и 3, высота 3, площадь 5+3/2 х 3=12
(Или просто считаем клеточки и их половинки)
Ответ: 12
Задание 6
Первый вариант. Найдем 13 процентов от 20 000. 20 000 : 100 =200, 200*13 = 2 600. Теперь вычтем налог из начисленного заработка, 20 000 – 2 600 = 17 400.
Ответ: 17400
Второй вариант. Так как 25 составляет одну треть всех выпускников, всего выпускников 25*3 = 75. Из них не сдавали физику 75-25=50.
Ответ: 50
Третий вариант. Составим уравнение. Пусть 5х гектар занимают зерновые, а 3х гектар овощные, тогда 5х+3х=24, 8х=24, х=24:8, получаем х=3. Зерновые занимают 5*3=15, а овощные 3*3=9.
Ответ: 9
Задание 7
Вариант 1. Представим 14 как 2*7. 29 х 79/ 27 х 78 сократим, получим 22*7=4*7=28.
Ответ: 28
Вариант 2. Сначала воспользуемся основным тригонометрическим тождеством sin2a+cos2a=1 0,64+ cos2a=1, cos2a=1-0,64, cos2a=0,36, таким образом cos a= 0,6 или -0,6, чтобы выяснить знак, построим единичную окружность, кстати, в КИМе указан именно такой угол.
Видим, что косинус данного угла отрицателен.
Ответ: -0,6
Вариант 3. Используем формулу сокращенного умножения
справа налево, получим (2 )2 – 1=4*13 – 1=51.
Ответ: 51
Вариант 4.
Смотрим в КИМе формулы, нам поможет подчеркнутая
используя ее справа налево, получаем:
log3(1,8*5)=log39 = 2, так как 32=9, логарифм числа по данному основанию равен показателю степени, в которую нужно возвести основание, чтобы получить данное число.
Ответ: 2
Задание 8
Просто подставляем значения и вычисляем.
Вариант 1. Р=72*5=49*5=245.
Ответ: 245
Вариант 2. g= ³√5*25*27 было бы нерационально и громоздко просто умножить выражение под корнем, поступим так: ³√5*5*5*3*3*3= ³√5³ *³√3³ =5*3=15
Ответ: 15
Задание 9
Вариант 1. 3х-3=34 основания равны, значит, равны и показатели, х-3=4, х=7
Ответ: 7
Вариант 2. 26=64, значит, log2(x-3)=log264, x-3=64, x=67
Ответ: 67
Вариант 3. Решаем квадратное уравнение, D=1-4*(-6)=25, х1,2 = 1+5/2, х1=3, х2= — 2, меньший -2
Ответ: -2
Задание 10
Вариант 1. Забор будет иметь две стороны по 30, две по 25 снаружи участка, и внутри разделяющий забор составит, как видно из чертежа, 25. Итого 60+50+25=135 метров.
Ответ: 135
Вариант 2. Окружность составляет 360 градусов, на одно деление циферблата приходится 360:12=30 градусов. На 4 деления 30*4=120 градусов.
Ответ: 120
Задание 11
Несложные задании на вероятность.
Вариант 1. Всего 35 участников, из них россиян 7. Делим 7 на 35, получаем 0,2.
Ответ: 0,2
Вариант 2. Из условия следует, что в среднем исправны 97 лампочек из 100. Далее делим число исправных в среднем лампочек на число всех лампочек, 97:100=0,97.
Ответ: 0,97
Заметим, что если бы спрашивали вероятность того, что лампочка будет неисправной, нужно было бы разделить 3 на 100.
Задание 12
У данного варианта множество ответов, найдем один. Например, попробуем набрать нужные языки, а потом проверим стоимость. Нужный набор языков составят номера 2, 5 и 6. Услуги составят 6000+2000+4000=12000, что отвечает условию.
Ответ: 256
Другие ответы попробуйте подобрать сами.
Вариант 2
Проверим каждый чемодан, но сначала отбросим слишком тяжелые, это номера 2, 4, 6. Сумма трех измерений первого чемодана 65+40+25=130, подходит. Третий чемодан 92+80+36=208 не подходит, пятый 83+65+48=196 подходит.
Ответ: 15 или 51
Вариант 3
Считаем услуги каждого поставщика. Поставщик А: 70*2600=182 000 плюс за доставку 10000, получаем 192 000.
Поставщик Б: 70*2800=196 000, доставка будет бесплатной, но это все равно дороже, чем у А.
Поставщик В: 70*2700=189 000 плюс доставка 8000, итого 197 000. Самый дешевый поставщик обойдется в 192 000.
Ответ: 192 000
Задание 13
Вариант 1. Объем цилиндра равен произведению площади основания (круга) на высоту. Объем воды при переливании не изменится, а так как площадь круга равна числу пи, умноженному на радиус в квадрате, уровень уменьшится во столько же раз, во сколько площадь второго основания больше первого. А она больше в 42=16 раз. 80:16=5.
Ответ: 5
Вариант 2. Грани — это участки плоскостей. У кубика было 6 граней и 8 вершин, вместо каждой теперь грань, значит, 6+8 =14.
Ответ: 14
Задание 14
Для базового уровня задание довольно сложное, воспользуемся справочным материалом КИМа.
Если функция в точке возрастает, тангенс положительный, если убывает — отрицательный. Чем график круче, тем тангенс больше (по модулю). Тогда А соответствует значение под номером 2, В – 1, С – 4 и Д – 3.
Ответ: 2143
Вариант 2 гораздо легче. Разметим график для наглядности.
А: Участок от 0 до 1 минуты — температура не более 30, верно, соответствует 4.
Б: от 1 до 3 минут — соответствует 1, 2 и 3 явно не подходят, температура не падала и не была от 40 до 80.
В: от 3 до 6 минут — вот здесь рост от 40 до 80, значит, выбираем 3.
С: от 8 до 10 минут температура понижается, значит, 2.
Ответ: 4132
Максимум — на графике «холмик», минимум — «впадина», возрастает — при движении слева направо график вверх, убывает — вниз. Проще начать с номеров, подобрав к ним графики. 1 соответствует графику Б:
2 — графику Г
3 — графику В, а 4 графику А (на В при движении слева направо взбираемся в гору, а на А спускаемся)
Ответ: 4132
Задание 15
Почему-то номер 15 представлен всего одним вариантом. Ну, тем лучше. Так как треугольник равнобедренный (АВ=ВС), его медиана одновременно будет и высотой, то есть ВМ перпендикулярна основанию АС. Медиана делит сторону пополам, тогда АМ=10:2=5. Получился прямоугольный треугольник, по теореме Пифагора АМ2+ВМ2=АВ2, 25+ВМ2=169, ВМ2=144, ВМ=12.
Ответ: 12
Задание 16
Зато здесь целых три варианта.
Вариант 1.
Сечение — прямоугольник, нужно найти его стороны. Одна из сторон равна высоте цилиндра, то есть образующей, 18, найдем вторую сторону.
Посмотрим на цилиндр сверху.
Ищем АВ, радиус АО=13, ОС=12, угол АСО прямой. Тогда АС находим по теореме Пифагора как корень квадратный из АО2-СО2, получаем корень из 169-144=25, корень из 25 будет равен 5, АВ = 2*5=10, тогда искомая площадь 18*10=180.
Ответ: 180
Вариант 2. Объем пирамиды равен одной трети от произведения площади основания на высоту пирамиды. Так как пирамида правильная, в основании квадрат со стороной 4, площадь 16. Найдем высоту.
Высота ОС2=АС2-АО2, АС2=17, ищем АО, АО равен половине АД, АД находим по теореме Пифагора как корень из 42+42=корень из 32, АО равен половине корня из 32. Корень не берется, но это не страшно.
АД= √32, АО=√32/2 , АО2 =32/4 =8
Находим ОС2=(√17 )2 –8=17-8=9, ОС=3,объем (16*3):3=16.
Ответ: 16
Вариант 3. Площадь поверхности шара
пропорциональна квадрату радиуса, поэтому если радиус большего шара в три раза больше радиуса маленького (9:3=3), то площадь будет больше в 32=9 раз.
Ответ: 9
Задание 17
Вариант 1. Сначала разберемся с числами. Логарифм десяти по основанию 2 равен степени, в которую нужно возвести 2, чтобы получить 10. Точно его не посчитать, но 23=8, значит, логарифм немножко больше 3. Подходит точка С, итак, С1.
Дробь 7/3 примерно равна 2,3. Подходит точка В, то есть В2.
Корень из 26 чуть больше 5, точка Д. Д3
И точка А соответствует числу 4. Проверим, будет 5/3, это примерно 1,6.
Ответ: 4213
Вариант 2. Проще всего не пытаться подбирать интервалы под неравенства, а просто аккуратно решить каждое неравенство.
А) 2х>=4
2x>=22
x>=2 соответствует интервалу 4. А4
Б)0,5х >=4
(1/2)х>=22
2— х >= 22
— х >=2
х <= -2 соответствует интервалу 3. Б3
В)0,5х<=4
решение «наоборот» чем в варианте Б, то есть х >= -2, интервал 2. В2
Ну и Г1.
Ответ 4321
Задание 18
Придется порассуждать логически.
Вариант 1.
Утверждение 1 — нет, не обязательно.
Утверждение 2 — да, верно, ведь всего получается 23 участника кружков при числе учащихся 20 человек.
Утверждение 3 — нет, неверно,
Утверждение 4 — да, верно, ведь на математику ходят всего 10 человек.
Ответ: 24
Вариант 2.
1 — верно, все деревья разные по высоте.
2 — нет, ясень ниже осины.
3 — нет, ясень выше рябины на 1 метр, дерево ниже ясеня может быть выше рябины.
4 — да, рябина ниже ясеня, все, что ниже рябины, автоматически ниже ясеня.
Ответ: 14
Задание 19
Задание придется решать подбором, чтобы не тратить драгоценное время экзамена, лучше оставьте его на конец работы.
Вариант 1.
Сначала выпишем трехзначные числа, сумма цифр которых равна 20, исключая варианты, где две цифры делятся на 3, а третья нет, так как сумма квадратов таких цифр не будет кратна 3. Затем проверим оставшиеся варианты. Получаем, например, числа776, 578, 884, 875, 974. Проверим каждое число на соответствие условию задачи. Так, проверим число 776. Сумма квадратов цифр данного числа составит 49+49+36=134 не подходит, число 875, 64+49+25=138, 138:3=46, 138 на 9 нацело не делится. Подходит.
Ответ: 875 (или другое число, их будет несколько, достаточно найти одно).
Вариант 2.
Для того, чтобы число делилось на 10, оно должно заканчиваться на 0. А чтобы оно не делилось на 20, надо, чтобы оно, разделенное на 10, было нечетным. Вначале можно подобрать карточки так, чтобы в конце числа был 0. Например, первое слагаемое 6, второе заканчивается на 7, третье тоже. Далее подберем числа так, чтобы результат, у которого убрали последний ноль, был нечетным. Получаем 6+27+357=390. На 10 делится, на 20 нет.
Ответ: 390 (найдите еще два ответа)
Вариант 3.
Чтобы число делилось на 12, оно должно делиться на 3 и на 4. Далее пригодится признак делимости на 4, согласно которому число делится на 4, если оно заканчивается двумя цифрами, образующими число, делящееся на 4. Так что отбросим последние цифры 1 и 3, остается 751576. Чтобы число делилось на 3, нужно, чтобы сумма его цифр делилась на 3. Проверим число, и если условие не выполнится, будем убирать мешающие цифры. В нашем случае придется удалить цифру 1.
Ответ: 75576
Задание 20
Вариант 1
Первый автомобиль проехал 350 км, следовательно, второй 120 км, так как все расстояние составляет 470 км. Скорость второго известна, 60 км/ч, а поскольку проехал он 120 км, время его движения составило 2 часа: 120 : 60=2. Значит, первый автомобиль находился в пути 5 часов – второй выехал через 3 часа после первого, и еще через 2 часа (как мы посчитали) они встретились. Итак, первый автомобиль за 5 часов проехал 350 км, скорость равна 350:5=70.
Ответ: 70
Вариант 2.
Пусть акции подорожали на Х процентов (процент – одна сотая) и до подорожания стоили А рублей. Значит, подорожавшие акции стоят А+Х*А, а подешевевшие стоят соответственно (А+Х*А) – Х(А+Х*А). Упростим второе выражение: А+ХА-ХА-Х2А=А-Х2А. Используем условие, что подешевевшие акции стали на 4 процента дешевле. Значит, они стоят 0,96 от первоначальной стоимости (1-0,04=0,96)
А-Х2А=0,96А сократим на А
1-Х2=0,96 получили квадратное уравнение
Х2=0,04, Х=0,2 (отрицательный корень отбросим, акции подешевели-подорожали на положительное число процентов)
Итак, 0,2 или 0,20 соответствует 20%.
Ответ: 20
Уважаемый посетитель!
Если у вас есть вопрос, предложение или жалоба, пожалуйста, заполните короткую форму и изложите суть обращения в текстовом поле ниже. Мы обязательно с ним ознакомимся и в 30-дневный срок ответим на указанный вами адрес электронной почты
Статус Абитуриент Студент Родитель Соискатель Сотрудник Другое
Филиал Абакан Актобе Алагир Алматы Алушта Анапа Ангарск Архангельск Армавир Асбест Астана Астрахань Атырау Баку Балхаш Барановичи Барнаул Белая Калитва Белгород Бельцы Берлин Бишкек Благовещенск Бобров Бобруйск Борисов Боровичи Бронницы Брянск Бузулук Чехов Челябинск Череповец Черкесск Дамаск Дербент Димитровград Дмитров Долгопрудный Домодедово Дубай Дубна Душанбе Екатеринбург Электросталь Елец Элиста Ереван Евпатория Гана Гомель Гродно Грозный Хабаровск Ханты-Мансийск Хива Худжанд Иркутск Истра Иваново Ижевск Калининград Карабулак Караганда Каракол Кашира Казань Кемерово Киев Кинешма Киров Кизляр Королев Кострома Красноармейск Краснодар Красногорск Красноярск Краснознаменск Курган Курск Кызыл Липецк Лобня Магадан Махачкала Майкоп Минеральные Воды Минск Могилев Москва Моздок Мозырь Мурманск Набережные Челны Нальчик Наро-Фоминск Нижневартовск Нижний Новгород Нижний Тагил Ногинск Норильск Новокузнецк Новосибирск Новоуральск Ноябрьск Обнинск Одинцово Омск Орехово-Зуево Орел Оренбург Ош Озёры Павлодар Пенза Пермь Петропавловск Подольск Полоцк Псков Пушкино Пятигорск Радужный Ростов-на-Дону Рязань Рыбинск Ржев Сальск Самара Самарканд Санкт-Петербург Саратов Сергиев Посад Серпухов Севастополь Северодвинск Щербинка Шымкент Слоним Смоленск Солигорск Солнечногорск Ставрополь Сургут Светлогорск Сыктывкар Сызрань Тамбов Ташкент Тбилиси Терек Тихорецк Тобольск Тольятти Томск Троицк Тула Тверь Тюмень Уфа Ухта Улан-Удэ Ульяновск Ургенч Усть-Каменогорск Вёшенская Видное Владимир Владивосток Волгодонск Волгоград Волжск Воркута Воронеж Якутск Ярославль Юдино Жлобин Жуковский Златоуст Зубова Поляна Звенигород
Тип обращения Вопрос Предложение Благодарность Жалоба
Тема обращения Поступление Трудоустройство Обучение Оплата Кадровый резерв Внеучебная деятельность Работа автоматических сервисов университета Другое
* Все поля обязательны для заполнения
Я даю согласие на обработку персональных данных, согласен на получение информационных рассылок от Университета «Синергия» и соглашаюсь c политикой конфиденциальности
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
2
Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.
3
Для ремонта квартиры требуется 63 рулона обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 6 рулонов?
4
Для покраски 1 м2 потолка требуется 240 г краски. Краска продается в банках по 2,5 кг. Сколько банок краски нужно купить для покраски потолка площадью 50 м2?
5
Одного рулона обоев хватает для оклейки полосы от пола до потолка шириной 1,6 м. Сколько рулонов обоев нужно купить для оклейки прямоугольной комнаты размерами 2,3 м на 4,1 м?
Пройти тестирование по этим заданиям
ЕГЭ База по математике . Задание №2
Итоговый экзамен по математике сдают все. Те, кто поступает на гуманитарные специальности (филология, юриспруденция, международные отношения) выбирают базовый уровень — вопросы в нем легче, а оценки «3» достаточно для получения аттестата. Профильный уровень сдают будущие экономисты, инженеры и программисты — на этих специальностях без знания математики не обойтись, ее обязательно изучают на первых курсах. Но это непростой предмет. Даже в профильных математических классах не всегда дают достаточно знаний. Если ваша цель — поступление в топовый вуз на техническую специальность, без курсов подготовки к ЕГЭ не обойтись. Это касается не только профильного уровня, но и ЕГЭ по математике базового. «Задание 2, как решать?» — часто спрашивают школьники, сдающие этот экзамен. В этой статье мы проведем разбор задания 2 из ЕГЭ по математике профильного и базового уровня.
Теория
В задании 2 ЕГЭ по профильной математике теория достаточно простая. Это номер базового уровня сложности, он приносит 1 балл. Выпускникам дается график (иногда — диаграмма), нужно проанализировать его в соответствии с условием. Определение аргумента функции, поиск максимального и минимального значения — навыки, которые нужны для этого задания ЕГЭ. 2 часть математики профильного уровня тоже содержит номера с графиками, поэтому эта теория пригодится и там. То, что нужно знать для решения задания 2 ЕГЭ по математике профильного уровня:
функция и ее график;
- оси абсцисс и ординат;
- промежутки возрастания и убывания функции;
- области определения и значения функции;
- максимум и минимум функции;
- наибольшее и наименьшее значения на промежутке;
- диаграммы;
- цена деления на графике.
Перечисленные понятия нужны для сдачи любого уровня ЕГЭ. Но задание 2 по базовой математике проверяет другие навыки. В нем выпускник должен произвести вычисления со степенями. Этот номер тоже считается легким, однако для его выполнения нужно знать куда больше теории. Формулы для ЕГЭ по базовой математике, к заданию 2:
- определение степени — an = a • a • a … • a, где n — натуральное число. a называют основанием степени, n — показателем.
- a0 = 1.
- a1 = a.
- a-n = 1 / an.
- anm=man.
- an • am = an+m.
- an • bn = (a • b)n.
- an / am = an-m.
- an / bn = (a / b)n.
Разбор задания 2
Решение задания 2 по математике ЕГЭ мы начнем с профильного уровня.
Задача. Замеры температуры проводились в течение 3 дней. Какой была минимальная температура 18 апреля?
Решение. Подобное задание 2 на ЕГЭ по математике профильного уровня кажется очень простым, однако в нем легко ошибиться. Обратим внимание на два момента: «18 апреля» и «минимальная». Для начала отсекаем колонки, относящиеся к 19 и 20 апреля — про них ничего не спрашивают. После этого ищем самую низкую точку и находим ее ординату.
Ответ: 6.
Задача. В помещении стоит кондиционер с датчиком температуры. Когда она достигает определенного максимального значения, кондиционер включается. Когда комната остужается до необходимой температуры, кондиционер автоматически выключается. На графике показана зависимость температуры от времени. Укажите, сколько минут кондиционер был выключен.
Решение. В этом номере важно умение логически рассуждать. Когда кондиционер отключен, температура увеличивается. На графике это показывается ростом функции вверх. Чтобы определить, сколько минут кондиционер был выключен, нужно найти область возрастания функции. Это промежуток между числами 6 и 9 на оси абсцисс. Теперь мы ищем время: 9 — 6 = 3.
Ответ: 3.
За выполнение такого простого номера можно получить 1 балл на экзамене по математике. Разбор задания 2 ЕГЭ мы продолжим базовым уровнем. Здесь встречаются несколько типов вопросов: степенные выражения с одинаковыми и разными основаниями, поиск частного, произведения и суммы. Чтобы посмотреть все существующие виды заданий, зайдите на «Решу ЕГЭ» по базовой математике. Задание 2 там представлено более чем 40 вариантами. А в рамках этой статьи мы разберем несколько примеров задания 2 из ЕГЭ по математике базового уровня.
 Найти значение выражения
Найти значение выражения
Задача. 4 • 72 + 6 • 72.
Решение. У слагаемых есть общий множитель, который мы можем вынести за скобку. После этого считаем выражение в скобке, потом возводим число в степень и перемножаем: (4 + 6) • 72 = 10 • 72 = 10 • 49 = 490.
Ответ: 490.
Найти значение выражения (разные основания)
Задача. 80,76 • 640,12.
Решение. Нужно привести степени к одинаковому основанию, представив 64 как 82. После этого их можно перемножить: 80,76 • 640,12 = 80,76 • (8)2*0,12 = 80,76+0,24 = 81 = 8.
Ответ: 8.
Найти значение выражения (одинаковые основания)
Задача. 26 • 2-2 / 22.
Решение. В данном примере расчеты можно провести сразу же. Умножение степеней с одинаковым основанием заменяем на сложение показателей, деление — на их вычитание: 26 + (-2) — 2 = 26 — 4 = 22 = 4.
Ответ: 4.
 Найти частное от деления
Найти частное от деления
Задача. 1,6 • 102 : 4 • 10-2.
Решение. У степеней одинаковое основание, поэтому мы можем поделить их, найдя разность показателей. После этого мы делим числа без степеней и выполняем умножение: 1,6 : 4 • 102 — (-2) = 1,6 : 4 • 104 = 1,6 : 4 • 10000 = 0,4 • 10000 = 4000.
Ответ: 4000.
Найти произведение
Задача. 4 • 105 • 2,3 • 10-7.
Решение: Степени имеют одинаковые основания, поэтому мы можем умножить их, сложив показатели. После этого результат умножаем на остальные числа: 4 • 2,3 • 105 + (-7) = 4 • 2,3 • 10-2 = 4 • 2,3 • 0,01 = 9,2 • 0,01 = 0,092.
Ответ: 0,092.
Найти сумму
Задача. 9,4 • 102 + 2,1 • 103.
Решение. Мы возводим числа в степень, затем выполняем умножение и сложение: 9,4 • 100 + 2,1 • 1000 = 940 + 2100 = 3040.
Ответ: 3040.
Теперь вы знаете чуть больше теории для ЕГЭ по математике. Задание 2 из профильного уровня достаточно легкое (хотя без практики тут тоже не обойтись), а вот в базе придется рассуждать и выполнять вычисления. Но и его можно выполнить без труда, если должным образом подготовиться к ЕГЭ. Однако, лучший результат всегда дают занятия с опытными преподавателями, знающими специфику экзамена. Если нанимать репетитора для вас дорого, обратите внимание на курсы. Там разбирают не только задание 2 ЕГЭ по математике, но и многие другие номера, в том числе вторую часть. Грамотная подготовка — ключ к хорошим баллам, а значит, и месту на бюджете.



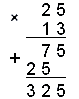
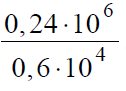
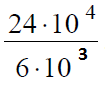
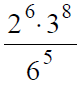
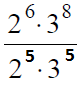
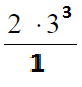












































 функция и ее график;
функция и ее график; Найти значение выражения
Найти значение выражения Найти частное от деления
Найти частное от деления