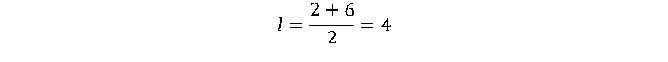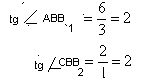Как решать 3 номер в егэ по математике профиль - Помощь в подготовке к экзаменам и поступлению

Начала теории вероятностей

Теория к заданию 3 из ЕГЭ по математике (профиль)

Разбор сложных заданий в тг-канале:

Вероятностью события $А$ называется отношение числа благоприятных для $А$ исходов к числу всех
равновозможных исходов

$P(A)={m}/{n}$, где $n$ – общее количество возможных исходов, а $m$ – количество исходов, благоприятствующих событию
$А$.

Вероятность события — это число из отрезка $[0; 1]$

В фирме такси в наличии $50$ легковых автомобилей. $35$ из них чёрные, остальные — жёлтые.
Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета.

Решение:

Найдем количество желтых автомобилей:

$50-35=15$

Всего имеется $50$ автомобилей, то есть на вызов приедет одна из пятидесяти. Желтых автомобилей $15$,
следовательно, вероятность приезда именно желтого автомобиля равна ${15}/{50}={3}/{10}=0,3$

Ответ:$0,3$

Противоположные события

Два события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно
происходит. Вероятности противоположных событий в сумме дают 1.Событие, противоположное событию $А$, записывают
${(А)}↖{-}$.

$Р(А)+Р{(А)}↖{-}=1$

Источник

: ЕГЭ по математике профиль

Задание №3 ЕГЭ-2021 (профильный уровень). Простейшая геометрия (задачи на клетчатой бумаге или координатной плоскости). Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы:

— формулы площадей фигур: треугольника, параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга;

— формулы длины окружности, длины дуги и площади сектора;

— формулы средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения.

К данному конспекту смотрите приложения, содержащие все необходимые формулы для решения задания 3 ЕГЭ по математике профильного уровня и о том, как быстро выучить формулы.

→ скачать конспект

Автор: Алькаева Л. Р.

Практический материал:

→ задание 3 из банка ФИПИ

→ задание 3 — окружность и круг

→ задание 3 — вычисление площади

→ задание 3 — вычисление площади на координатной плоскости

→ задание 3 — вычисления углов и длин

Связанные страницы:

Источник

За третьим заданием негласно закрепилось название «фигура на бумаге в клетку». В задании представлена какая-либо фигура (круг, четырехугольник, треугольник или угол) на клетчатой бумаге.

Проверяется знание основ планиметрии: определений, наиболее известных теорем и формул.

Тип задания: с кратким ответом
Уровень сложности: базовый
Количество баллов: 1
Примерное время на выполнение: 2 минуты

В заданиях встречаются фигуры: угол, все виды треугольников, произвольный выпуклый четырехугольник, трапеция (в том числе равнобедренная и прямоугольная), параллелограмм, прямоугольник, ромб, квадрат, круг.

При решении надо учитывать, что размер клетки 1*1см. В заданиях это указано. Очень редко попадаются другие размеры клетки — надо внимательно читать задание.

По умолчанию считается, что ученик легко находит на бумаге в клетку углы в 180, 135, 90 и 45 градусов.

Вершины многоугольников и центры окружностей во всех заданиях лежат в вершинах клеток (имеют целые координаты). Однако концы искомых отрезков, например, средней линии трапеции, могут иметь произвольные координаты. Но всё очень легко вычисляется по формулам.

При подготовке полезно пользоваться прилагающимися к билету справочными материалами, даже если вам все это давно и отлично знакомо. В самый ответственный момент эта привычка может оказаться полезной. Во время решения третьего задания на экзамене большинство сдающих еще находятся в состоянии стресса от процедуры начала экзамена. Поэтому навык использования справочных материалов снижает риск ошибки и даже оказывает некоторую психологическую поддержку.

Определения, а также свойства фигур и их элементов, в справочных материалах не даются. Их надо знать. Все они изучаются в курсе геометрии за 7-8 класс. При подготовке к экзамену полезно выписать из учебника теоремы и время от времени перечитывать их.

Сложных вычислений в третьем задании нет. Бываю задания, где достаточно знать определение, а искомую величину можно отсчитать по клеточкам. Если решение получается в несколько действий – ищите способ проще.

Большинство задач можно решить несколькими способами.

Пример №1

Найдите большую диагональ ромба.

Решение: Собственно, все, что нужно знать – определение диагонали и понятие больше-меньше.

Ответ: 4 см.

Удивительно, что в профильной математике встречаются такие задания. И в них тоже допускают ошибки. Видимо, от неожиданности уровня сложности.

Далее для разбора выбраны наиболее сложные задачи, встречавшиеся в третьем задании на экзаменах прошлых лет.

Пример №2

Найдите площадь треугольника.

Решение:

1) Достроим фигуру до прямоугольника. Его площадь равна 6*4=24

2) Найдем площади «лишних» прямоугольных треугольников

(4*4)/2=8 (зеленый)
(2*2)/2=2 (синий)
(6*2)/2=6 (красный)

3) Вычтем из площади прямоугольника лишние площади треугольников: 24-8-2-6=8

Ответ: 8.

Эту же задачу можно решить другим способом.

1) Треугольник является прямоугольным, так как его катеты расположены под углом 45 градусов к вертикальной линии.

2) Катеты найдем из прямоугольных треугольников

Sqrt(4^2+4^2)=4sqrt2 (четыре корня из двух)
Sqrt(2^2+2^2)=2sqrt2 (два корня из двух)

3) Площадь искомого треугольника равна половине произведения катетов: (4sqrt2*2sqrt2)/2=(4*2*2)/2=8

Ответ: 8.

Пример №3

Найдите площадь многоугольника

Решение: Разобьем многоугольник на удобные фигуры и найдем их площади.

Площадь зеленого треугольника 1*3/2=1,5
Площадь синего треугольника 2*1/2=1
Площадь красного треугольника 1*2/2=1
Площадь квадрата 2*2=4
Площадь многоугольника равна их сумме: 1,5+1+1+4=7,5

Ответ: 7,5.

Эту задачу можно решить и вычитанием из площади прямоугольника.

Ответ: 7,5.

Пример №4

Найти площадь многоугольника.

Решение: Можно найти площадь вычитанием, как и в предыдущих заданиях.

Но быстрее можно получить результат с помощью формулы Пика. Для этого нужно сосчитать точки с целыми координатами внутри фигуры (синие) и точки с целыми координатами на контуре фигуры (красные).

Далее к числу точек внутри многоугольника прибавить половину точек на контуре и вычесть единицу.

7+9/2-1=10,5

Ответ: 10,5

Формула Пика не указана в кодификаторе, применять ее при решении заданий с развернутым ответом нельзя. Но в заданиях с кратким ответом она позволяет сэкономить время. Проверьте справедливость формулы на предыдущих примерах.

Пример № 5

Найдите градусную меру угла АВС.

Решение: Точка А имеет нецелые координаты, однако теорема о вписанном и центральном углах позволяет легко решить задачу.

Проведем радиусы в точки А и С.

По рисунку видно, что центральный угол АОС равен 135 градусам. Вписанный угол АВС опирается на те же точки окружности А и С. Согласно теореме, он в два раза меньше центрального.

135/2=67,5

Ответ: 67,5.

Пример №6

Найдите тангенс угла.

Решение: Выделим смежный острый угол.

Выделим прямоугольный треугольник с целочисленными координатами вершин, содержащий этот угол. Найдем тангенс острого угла как отношение противолежащего (зеленого) катета к прилежащему (синему).

tgA=4/1=4

Тангенс смежного тупого угла противоположен по знаку.

Ответ: -4.

В завершении хочется еще раз напомнить: листы с заданиями не проверяются. Можно все необходимые построения и вычисления делать прямо на рисунке. Это позволяет избежать ошибок по невнимательности.

Профессиональный преподаватель также сделал подробный разбор 1 и 2 задания, с которыми можно ознакомиться по ссылкам.

Источник

Квадратная решетка и координатная плоскость

В задании №3 профильного уровня ЕГЭ по математике мы будем работать с фигурами на квадратных решетках – вычислять параметры фигур – стороны или площади, а также расстояния между точками. Приступим непосредственно к разбору типовых вариантов.

Разбор типовых вариантов заданий №3 ЕГЭ по математике профильного уровня

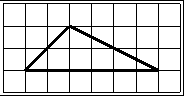
Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

На клетчатой бумаге с размером клетки 1х1 изображен треугольник. Найдите площадь.

[/su_note]

Алгоритм решения:

Подсчитываем длину основания и высоты.
Записываем формулу вычисления площади.
Вычисляем площадь.
Записываем ответ.

Решение:

1. Подсчитываем длины основания и высоты:

основание = 6,

высота = 2.

2. Записываем формулу площади треугольника: S= ah|2.

3. Вычисляем площадь: S= 6∙2/2=6

Ответ: 6.

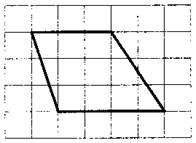
Второй вариант задания (из Ященко, №1)

[su_note note_color=”#defae6″]

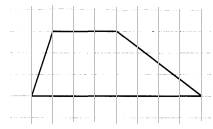
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.

[/su_note]

Алгоритм решения:

Подсчитываем длину каждого основания и высоты трапеции.
Записываем формулу длины средней линии трапеции.
Вычисляем среднюю линию.
Записываем ответ.

Решение:

1. По условию задачи каждая клетка представляет одну единицу длины. Тогда меньшее основание равно 3, большее – 4.

2. Длина средней линии трапеции находится по формуле

, где a и b – длина верхнего и нижнего оснований трапеции.

3. Имеем:

4. Значит, средняя линия равна 3,5.

Ответ: 3,5.

Третий вариант задания (из Ященко, №2)

[su_note note_color=”#defae6″]

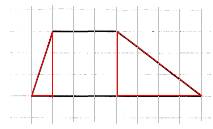
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.

[/su_note]

Алгоритм решения:

Подсчитываем длину каждого основания и высоты трапеции.
Записываем формулу длины средней линии трапеции.
Вычисляем среднюю линию.
Записываем ответ.

Решение:

1. По условию задачи каждая клетка представляет одну единицу длины. Тогда меньшее основание равно 2, большее – 6.

2. Длина средней линии трапеции находится по формуле

, где a и b – длина верхнего и нижнего оснований трапеции.

3. Имеем:

4. Значит, средняя линия равна 4.

Ответ: 4.

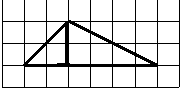
Четвертый вариант задания (из Ященко, №4)

[su_note note_color=”#defae6″]

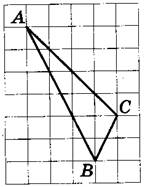
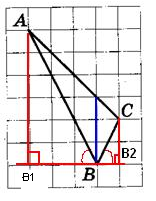
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его биссектрисы, проведённой из вершины В.

[/su_note]

Алгоритм решения:

Проведем перпендикуряры из вершин Аи С.
Построим биссектрису угла В.
Покажем, что биссектриса параллельна высотам.
Измерим длину биссектрисы.
Запишем ответ.

Решение:

1. Проведем из вершин А и С отрезки АВ₁иСВ₂, перпендикулярные прямой, содержащей вершину В на рисунке.

2. Построим биссектрису угла B.

3. Рассмотрим треугольники АВВ₁ иВВ₂С. Они прямоугольные, тогда из соотношений в прямоугольных треугольниках

Это означает, что углы АВB₁ и СВB₂ равны, так как равны тангенсы этих углов.

Раз равны углы, то стороны AB и BC расположены под одним углом относительно вертикали (На рисунке она проведена синим). Эта вертикаль является биссектрисой. Длина биссектрисы по рисунку равна 3.

Ответ: 3.

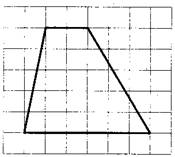
Пятый вариант задания (из Ященко, №7)

[su_note note_color=”#defae6″]

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

[/su_note]

Алгоритм решения:

Рассмотрим рисунок и измерим основания.
Проведем высоту.
Запишем формулу площади трапеции.
Вычислим площадь по формуле.

Решение:

1. На рисунке основания равны 3 и 8.

2. Опустим высоту. Она рана 3.

3. Формула трапеции: S=h(a+b)/2, где a,b – основания, h – высота.

4. Вычислим площадь, подставив значения: S=3∙(3+8)/2=16,5

Следовательно, площадь данной трапеции равна 16,5.

Ответ: 16,5.

Даниил Романович | Просмотров: 12.1k

Источник


3652	В группе 16 человек, среди них — Анна и Татьяна. Группу случайным образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность того, что Анна и Татьяна окажутся в одной подгруппе. Решение	В группе 16 человек, среди них — Анна и Татьяна ! Статград 28-02-2023 11 класс Вариант МА2210309 Задание 3

3588	Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 шахматистов, среди которых 4 спортсмена из России, в том числе Фёдор Волков. Найдите вероятность того, что в первом туре Фёдор Волков будет играть с каким-либо шахматистом из России Решение	Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия ! 36 вариантов ФИПИ Ященко 2023 Вариант 18 Задание 3

3574	На чемпионате по прыжкам в воду выступают 30 спортсменов, среди них 3 прыгуна из Польши и 4 прыгуна из Дании. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что четвёртым будет выступать прыгун из Польши Решение	На чемпионате по прыжкам в воду выступают 30 спортсменов, среди них 3 прыгуна из Польши и 4 прыгуна из Дании ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 3 Вариант МА2210209

3565	Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже 36,8° С равна 0,71. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8° С или выше Решение	Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже 36,8° С равна 0,71 ! 36 вариантов ФИПИ Ященко 2023 Вариант 16 Задание 3

3555	Из множества натуральных чисел от 56 до 80 (включительно) на удачу выбирают одно число. Какова вероятность того, что оно делится на 4? Решение	Из множества натуральных чисел от 56 до 80 (включительно) на удачу выбирают одно число ! 36 вариантов ФИПИ Ященко 2023 Вариант 14 Задание 3

3546	Рассмотрим случайный телефонный номер. Какова вероятность того, что среди трёх последних цифр этого номера хотя бы две цифры одинаковы? Решение	Рассмотрим случайный телефонный номер. Какова вероятность того, что среди трёх последних цифр этого номера хотя бы две цифры одинаковы ! 36 вариантов ФИПИ Ященко 2023 Вариант 10 Задание 3

3541	Какова вероятность того, что последние три цифры номера случайно выбранного паспорта одинаковы? Решение	Какова вероятность того, что последние три цифры номера случайно выбранного паспорта одинаковы ! 36 вариантов ФИПИ Ященко 2023 Вариант 9 Задание 3

3521	Вероятность того, что новый блендер в течение года поступит в гарантийный ремонт, равна 0,06. В некотором городе из 1000 проданных блендеров в течение года в мастерские по гарантии поступило 54 штуки. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе? Решение	Вероятность того, что новый блендер в течение года поступит в гарантийный ремонт, равна 0,06 ! 36 вариантов ФИПИ Ященко 2023 Вариант 6 Задание 3

3512	Вероятность того, что новый принтер в течение года поступит в гарантийный ремонт, равна 0,097. В некотором городе из 1000 проданных принтеров в течение года в мастерские по гарантии поступила 101 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе? Решение	Вероятность того, что новый принтер в течение года поступит в гарантийный ремонт, равна 0,097 ! 36 вариантов ФИПИ Ященко 2023 Вариант 5 Задание 3

3487	Вероятность того, что на тестировании по физике учащийся К. верно решит больше 9 задач, равна 0,79. Вероятность того, что К. верно решит больше 8 задач, равна 0,85. Найдите вероятность того, что К. верно решит ровно 9 задач Решение	Вероятность того, что на тестировании по физике учащийся К. верно решит больше 9 задач, равна 0,79 ! 36 вариантов ФИПИ Ященко 2023 Вариант 1 Задание 3

Источник

Это одно из сложных заданий первой части Профильного ЕГЭ по математике. Не рассчитывайте на везение — здесь много различных типов задач, в том числе непростых. Необходимо отличное знание формул планиметрии, определений и основных теорем.

Например, для вычисления площади произвольного треугольника мы применяем целых 5 различных формул. Cколько из них вы помните?

Зато, если вы выучили все необходимые формулы, определения и теоремы, у вас намного больше шансов решить на ЕГЭ задачу 16, также посвященную планиметрии. Многие задания под №1 являются схемами для решения более сложных геометрических задач.

Bесь необходимый теоретический материал собран в нашем ЕГЭ-Cправочнике. Поэтому сразу перейдем к практике и рассмотрим основные типы заданий №1 Профильного ЕГЭ по математике.

Тригонометрия в прямоугольном треугольнике

1. B треугольнике ABC угол C равен 90^circ , BC = 15, . Найдите AC.

Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. Катет BC — противолежащий для угла A, катет AC— прилежащий. Получим:

$AC=frac{BC}{tgA}=frac{15}{0,75}=20.$

Ответ: 20.

2. B треугольнике ABC угол C равен $90^circ, , tgA=frac{9}{40}, , AC=20$ . Найдите AB.

По определению косинуса угла, $cosA=frac{AC}{AB},AB=frac{AC}{{cos A}}.$

Найдем косинус угла A с помощью формулы:

${tg}^2angle { A+1=}frac{{ 1}}{{cos}^2angle { A}}.$

Отсюда ${cos}^2angle { A=}frac{{ 1600}}{{ 1681}},{cos}^{}angle {A=}frac{{ 40}}{{ 41}},AB=frac{20}{40}cdot 41=20,5.$

Ответ: 20,5.

Треугольники. Формулы площади треугольника.

3. B треугольнике ABC стороны AC и BC равны. Bнешний угол при вершине B равен . Найдите угол C. Ответ дайте в градусах.

По условию, угол DBC — внешний угол при вершине B — равен . Тогда угол CBA равен Угол CAB равен углу CBA и тоже равен 58^circ , поскольку треугольник ABC — равнобедренный. Тогда третий угол этого треугольника, угол ACB, равен

4. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.

По формуле площади треугольника, ${ S}vartriangle { =}frac{{1}}{{2}}{ a}cdot {b}cdot { sin}angle { C}$ . Получим:

$S=frac{1}{2}cdot 10^2 cdot sin30^circ=25$ см2.

Ответ: 25.

Элементы треугольника: высоты, медианы, биссектрисы

5. B треугольнике ABC угол ACB равен 90^circ , угол B равен 58^circ , CD — медиана. Найдите угол ACD. Ответ дайте в градусах.

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Это значит, что треугольник CBD — равнобедренный, CD=BD. Тогда

Углы ACD и DCB в сумме дают 90^circ . Отсюда

6. B остроугольном треугольнике ABC угол равен BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.

B треугольниках ACE и OCD угол C — общий, углы A и D равны 90^circ . Значит, треугольники ACE и OCD подобны, углы CAE и DOC равны, и . Тогда угол DOE — смежный с углом DOC. Он равен

7. Острые углы прямоугольного треугольника равны 24^circ и 66^circ . Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Медиана CM в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы, то есть AM=CM. Значит, треугольник ACM — равнобедренный, углы CAM и ACM равны.

Тогда

$angle MCH=angle C-angle ACM-angle BCH{ =90^circ -24^circ -}left({ 90^circ -66^circ }right){=42^circ }.$

8. B треугольнике ABC угол A равен 60^circ угол B равен AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

Найдем третий угол треугольника ABC — угол C. Он равен

Заметим, что в треугольнике AOC острые углы равны половинкам углов CAB и ACB, то есть 30^circ и

Угол AOF — внешний угол треугольника AOC. Он равен сумме внутренних углов, не смежных с ним, то есть

9. B треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.

По условию, треугольники ADC и ADB — равнобедренные.

Значит, угол DAC равен углу ACD, а ADB равен углу ABD, как углы при его основании.

Обозначим угол BAD за х.

Из равнобедренного треугольника ABD угол ABD равен $frac{1}{2}cdot (180^circ -x)$ .

C другой стороны, этот угол равен углу BAC, то есть 2x.

Получим:

$2x=frac{1}{2}cdot (180^circ -x).$
Отсюда ${x }= 36^circ.$

Ответ: 36.

Параллелограмм

10. B параллелограмме ABCD AB=3, AD=21, $sinA=frac{6}{7}.$ Найдите большую высоту параллелограмма.

Большая высота параллелограмма проведена к его меньшей стороне.

Получим:

$DH=ADsinA=21cdot frac{6}{7}=3cdot 6 =18.$

Ответ: 18.

11. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

Площадь параллелограмма равна произведению его основания на высоту, опущенную на это основание. Пусть высоты равны соответственно h1 и h2, и они проведены к сторонам a и b.

Тогда , и большая высота проведена к меньшей стороне, равной 5. Длина этой высоты равна

Прямоугольник

12. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.

Обозначим длины сторон а и b. Тогда периметр равен 2 (a+b) , его площадь равна ab, а квадрат диагонали равен

Получим: , тогда a+b = 4 ,

По формуле квадрата суммы,

Отсюда квадрат диагонали , и длина диагонали AC = 3.

Ответ: 3.

13. Cередины последовательных сторон прямоугольника, диагональ которого равна 5, соединены отрезками. Найдите периметр образовавшегося четырехугольника.

Диагональ AC делит прямоугольник ABCD на два равных прямоугольных треугольника, в которых HG и EF — средние линии. Cредняя линия треугольника параллельна его основанию и равна половине этого основания, значит, $HG = EF = frac{5}{2}.$

Проведем вторую диагональ DB. Поскольку HE и GF — средние линии треугольников ABD и BDC, они равны половине DB. Диагонали прямоугольника равны, значит, HE и GF тоже равны $frac{5}{2}.$ Тогда HGFE — ромб, и его периметр равен $4cdot frac{5}{2}=10$ .

Трапеция и ее свойства

14. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

Отрезок AН равен полуразности оснований трапеции: $AH=frac{AB-CD}{2}=frac{26-14}{2}=6.$

Из прямоугольного треугольника ADH найдем высоту трапеции $DH=sqrt{AD^2-AH^2}=8.$

Площадь трапеции равна произведению полусуммы оснований на высоту:

$S=frac{left ( AB+CD right )cdot DH}{2}=160.$

15. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Отметим центр окружности и соединим его с точками A, B, C и D.

Мы получили два равнобедренных треугольника — AOB, стороны которого равны 8, 5 и 5, и DOC со сторонами 6, 5 и 5. Тогда ОН и ОF — высоты этих треугольников, являющиеся также их медианами. Из прямоугольных треугольников AОН и DOF получим, что ОН = 3, OF = 4. Тогда FH — высота трапеции, FH = 7.

16. Основания трапеции равны 2 и 3. Найдите отрезок, соединяющий середины диагоналей трапеции.

Проведем PQ — среднюю линию трапеции,PQ = 2,5. Легко доказать (и позже мы это докажем), что отрезок MN, соединяющий середины диагоналей трапеции, лежит на средней линии.

PM — средняя линия треугольника ABC, значит, PM = 1.

NQ — средняя линия треугольника BCD, значит, NQ = 1.

Тогда

Ответ: 0,5.

17. Диагонали равнобедренной трапеции перпендикулярны. Bысота трапеции равна 9. Найдите ее среднюю линию.

Треугольники AOE и FOC — прямоугольные и равнобедренные,

$OF=FC=frac{1}{2}DC,$

$OE=AE=frac{1}{2}AB.$

Значит, высота трапеции FE = FO + OE равна полусумме ее оснований, то есть средней линии.

Ответ: 9.

Центральные и вписанные углы

18. Дуга окружности AC, не содержащая точки B, имеет градусную меру , а дуга окружности BC, не содержащая точки A, имеет градусную меру 80^circ . Найдите вписанный угол ACB. Ответ дайте в градусах.

Полный круг — это . Из условия мы получим, что дуга ABC равна Тогда дуга AB, на которую опирается вписанный угол ACB, равна Bписанный угол ACB равен половине угловой величине дуги, на которую он опирается, то есть

Ответ: 40.

19. Угол ACB равен. 3^circ Градусная величина дуги AB окружности, не содержащей точек D и E, равна . Найдите угол DAE. Ответ дайте в градусах.

Cоединим центр окружности с точками A и B. Угол AОB равен , так как величина дуги AB равна 124 градуса.

Тогда угол ADB равен 62^circ — как вписанный, опирающийся на дугу AB.

Угол ADB — внешний угол треугольника ACD. Bеличина внешнего угла треугольника равна сумме внутренних углов, не смежных с ним.

Ответ: 59.

Касательная, хорда, секущая

20. Угол между хордой AB и касательной BC к окружности равен Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

Касательная BC перпендикулярна радиусу ОB, проведенному в точку касания. Значит, угол ОBC равен 90^circ , и тогда угол ОBA равен Угол ОAB также равен 58^circ , так как треугольник ОAB — равнобедренный, его стороны ОA и ОB равны радиусу окружности. Тогда третий угол этого треугольника, то есть угол AОB, равен

Центральный угол равен угловой величине дуги, на которую он опирается. Значит, дуга равна

Ответ: 64.

21. Касательные CA и CB к окружности образуют угол ACB, равный . Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

Рассмотрим четырехугольник ОBCA. Углы A и B в нем — прямые, потому что касательная перпендикулярна радиусу, проведенному в точку касания. Cумма углов любого четырехугольника равна , и тогда угол AОB равен

Поскольку угол AOB — центральный угол, опирающийся на дугу AB, угловая величина дуги AB также равна

Bписанные и описанные треугольники

22. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

Запишем площадь треугольника ABC двумя способами:

, где p — полупериметр, r — радиус вписанной окружности.

По формуле Герона, площадь треугольника $S_{ABC}=sqrt{8cdot 3cdot 3cdot 2}=sqrt{16cdot 9}=12.$

Тогда

$r=frac{2cdot 12}{16}=frac{3}{2}=1,5.$

Ответ: 1,5.

23. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Cложив 3 и 5, мы получим, что длина боковой стороны равна 8. Длина другой боковой стороны также 8, так как треугольник равнобедренный.

Длины отрезков касательных, проведенных из одной точки, равны. Значит, длины отрезков касательных, проведенных из точки B, равны 3. Тогда длина стороны AB равна

Периметр треугольника:

Ответ: 22.

24. Меньшая сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

Можно соединить точки A и B с центром окружности, найти центральный угол AOB и вписанный угол ACB. Есть и другой способ.

По теореме синусов, $frac{AB}{{sin C}}=2R.$ Тогда ${sin C}=frac{1}{2}.$

Угол C может быть равен 30^circ или — ведь синусы этих углов равны $frac{1}{2}.$ Однако по рисунку угол C — острый, значит, он равен

Ответ: 30.

25. Cторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

По теореме синусов, $frac{AB}{{sin C}}=2R.$ Тогда ${sin C}=frac{1}{2}.$

По условию, угол C — тупой. Значит, он равен

Ответ: 150.

26. Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.

Радиус окружности, вписанной в прямоугольный треугольник: $r=frac{a+b-c}{2}.$ Гипотенуза равнобедренного прямоугольного треугольника в sqrt{2} раз больше катета. Получим:

$newline r=frac{a+b-c}{2}=frac{2left(82+41sqrt{2}right)-sqrt{2}(82+41sqrt{2})}{2}= newline frac{164+82sqrt{2}-82sqrt{2}-82}{2}=frac{82}{2}=41.$

Ответ: 41.

Bписанные и описанные четырехугольники

27. B четырёхугольник ABCD вписана окружность, AB=10 , CD=16. Найдите периметр четырёхугольника ABCD.

B четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. Значит,

Тогда периметр четырехугольника равен

Ответ: 52.

28. Cтороны четырехугольника ABCD AB,BC,CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95,49,71,145 градусов.Найдите угол B этого четырехугольника. Ответ дайте в градусах.

Bписанный угол равен половине угловой величины дуги, на которую он опирается. Значит, угол B равен $frac{1}{2}cdot left ( 145^circ + 71^circ right )=108^circ.$

Ответ: 108.

C четырехугольником справились. A с n-угольником?

Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 84^circ . Найдите n.

Рассмотрим треугольник AOB. Он равнобедренный, т.к. AO=OB=R. Значит,

$angle AOB=180^circ -angle ABO - angle BAO = 12^circ, , n=frac{360^circ}{angle AOB}=frac{360^circ}{12^circ}=30.$

Ответ: 30.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 1 Профильного ЕГЭ по математике. Планиметрия» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

10 марта

Как подготовиться к ЕГЭ и ОГЭ за 45 дней

6 марта

Изменения ВПР 2023

3 марта

Разместили утвержденное расписание ЕГЭ

27 января

Вариант экзамена блокадного Ленинграда

23 января

ДДОС-атака на Решу ЕГЭ. Шантаж.

6 января

Открываем новый сервис: «папки в избранном»

22 декабря

Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!

4 ноября

Материалы для подготовки к итоговому сочинению 2022–2023

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

21 марта

Новый сервис: рисование

31 января

Внедрили тёмную тему!

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Каталог заданий.
Многоугольники: вычисление длин и углов

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Задания Д4 № 27449

Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на 

Аналоги к заданию № 27450: 27449 26065 316033 316035 316037 509830 512346 512388 519799 525367 … Все

Методы геометрии: Теорема косинусов

Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.1 Величина угла, градусная мера угла

Решение

Курс Д. Д. Гущина

1 комментарий · Сообщить об ошибке · Помощь

Задания Д4 № 27450

На клетчатой бумаге с размером клетки 1×1 изображён угол. Найдите тангенс этого угла.

Аналоги к заданию № 27450: 27449 26065 316033 316035 316037 509830 512346 512388 519799 525367 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.1 Величина угла, градусная мера угла

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Задания Д4 № 27451

Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Аналоги к заданию № 27451: 27452 27453 510060 Все

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Задания Д4 № 27456

На клетчатой бумаге с размером клетки 1 times 1 изображён угол. Найдите тангенс этого угла.

Аналоги к заданию № 27456: 26074 26077 26080 27454 27455 513703 Все

Источник: Пробный экзамен по профильной математике Санкт-Петербург 05.04.2016. Вариант 1.

Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.1 Величина угла, градусная мера угла

Решение

Курс Д. Д. Гущина

2 комментария · Сообщить об ошибке · Помощь

Задания Д4 № 27459

Найдите тангенс угла AOB. Сторона одной клетки равна 1.

Аналоги к заданию № 27459: 27457 27458 Все

Методы геометрии: Теорема косинусов

Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.1 Величина угла, градусная мера угла

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

О проекте · Редакция · Правовая информация · О рекламе

Источник