Как решать 6 задание егэ математика профиль формулы

Есть в Профильном ЕГЭ по математике, и даже в первой его части, такие задачи, для решения которых нужно знать ВСЁ. То есть всю школьную программу алгебры, с 5 класса до 11. Или почти всю.

Например, задание №6 Профильного ЕГЭ по математике – вычисления и преобразования. Вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки. Например, вычисление и преобразование иррациональных выражений, тригонометрических, логарифмических. Задачи на определение модуля и понятие функции. В общем, типов задач здесь множество, по всему курсу алгебры.

И помните, что в ответе в заданиях первой части Профильного ЕГЭ по математике у вас должны получаться целые числа или конечные десятичные дроби.

Дробно-рациональные выражения. Формулы сокращенного умножения

Темы для повторения: Формулы сокращенного умножения, Приемы быстрого счета

Если вам встретится такое задание на ЕГЭ – значит, повезло!

1. Найдите значение выражения frac{2,88cdot 44,5}{0,288cdot 4,45}.

Не спешите перемножать десятичные дроби. Посмотрите на задачу внимательно.

frac{2,88cdot 44,5}{0,288cdot 4,45}=frac{2,88cdot 44,5}{2,88cdot 0,445}=frac{44,5}{0,445}=100.

Первый множитель в знаменателе умножили на 10, а второй поделили на 10, просто передвинув запятую.

Ответ: 100.

2. Найдите значение выражения 7frac{9}{13}:frac{5}{13}.

7frac{9}{13}:frac{5}{13}=frac{100}{13}cdot frac{13}{5}=20.

Ответ: 20.

Корни и степени. Иррациональные выражения

Темы для повторения: Арифметический квадратный корень.

Арифметический квадратный корень из числа a — это такое неотрицательное число, квадрат которого равен a.

left ( sqrt{a} right )^{2}=a;;sqrt{a}geq 0;;ageq 0 .

3. Вычислите sqrt{12+4sqrt{5}}cdot sqrt{12-4sqrt{5}} .

sqrt{12+4sqrt{5}}cdot sqrt{12-4sqrt{5}}=sqrt{left ( 12+4sqrt{5} right )left ( 12-4sqrt{5} right )}=

=sqrt{144-80}=sqrt{64}=8.

Применили одну из формул сокращенного умножения.

Ответ: 8.

4. Вычислите:
left ( sqrt{28}-sqrt{12} right )cdot sqrt{10+sqrt{84}}.

Упростим множители:

sqrt{28}-sqrt{12}=sqrt{4cdot 7}-sqrt{3cdot 4}=2left ( sqrt{7}-sqrt{3} right );

sqrt{84}=sqrt{3cdot 7cdot 4}=2sqrt{3cdot 7};

left ( sqrt{28}-sqrt{12} right )cdot sqrt{10+sqrt{84}}=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{10+2sqrt{3cdot 7}}=

=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{left ( sqrt{7} right )^{2}+2sqrt{3}cdot sqrt{7}+left ( sqrt{3} right )^{2}}=

=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{left ( sqrt{7}+sqrt{3}right )^{2}}=2left ( sqrt{7}-sqrt{3} right )left ( sqrt{7}+sqrt{3} right )=

=2cdot left ( 7-3 right )=8.

Ответ: 8.

Действия со степенями

Темы для повторения:
Вспомним правила действий со степенями.

a^{m}cdot a^{n}=a^{m+n}.

frac{a^{m}}{a^{n}}=a^{m-n}.

left ( a^{m} right )^{n}=left ( a^{n} right )^{m}=a^{mn}.

a^{n}b^{n}=left ( ab right )^{n}.

frac{a^{n}}{b^{n}}=left ( frac{a}{b} right )^{n}.

5. Найдите значение выражения: frac{a^{8,9}}{a^{4,9}} при a=4.

frac{a^{8,9}}{a^{4,9}}=a^{8,9-4,9}=a^{4}=4^{4}=256.

Применили формулу частного степеней frac{a^{m}}{a^{n}}=a^{m-n}.

Ответ: 256.

6. Вычислите left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{sqrt[12]{2}} right )^{2}.

left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{sqrt[12]{2}} right )^{2}=left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{2^{frac{1}{12}}} right )^{2}=left ( 2^{frac{1}{3}+frac{1}{4}-frac{1}{12}} right )^{2}=left ( 2^{frac{4}{12}+frac{3}{12}-frac{1}{12}} right )^{2}=

=left (2^{frac{1}{2}} right )^{2}=2.

Ответ: 2.

7. Вычислите frac{5left ( m^{6} right )^{5}+13left ( m^{10} right )^{3}}{left ( 2m^{15} right )^{2}}, если m=3,7.

Спокойно, не пугаемся. И конечно, не спешим подставлять значение m=3,7. Сначала упростим выражение.

frac{5left ( m^{6} right )^{5}+13left ( m^{10} right )^{3}}{left ( 2m^{15} right )^{2}}=frac{5m^{30}+13m^{30}}{4m^{30}}=frac{18m^{30}}{4m^{30}}=4,5.

Ответ: 4,5.

8. Вычислите 0,75^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 12^{frac{7}{8}}.

0,75^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 12^{frac{7}{8}}=left ( frac{3}{4} right )^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot left ( 3cdot 4 right )^{frac{7}{8}}=frac{3^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 3^{frac{7}{8}}cdot 4^{frac{7}{8}}}{4^{frac{1}{8}}}=3cdot 4=12.

Применили формулу для произведения степеней: a^{m}cdot a^{n}=a^{m+n}.

Ответ: 12.

9. Вычислите frac{sqrt[28]{3}cdot 3cdot sqrt[21]{3}}{sqrt[12]{3}}.

frac{sqrt[28]{3}cdot 3cdot sqrt[21]{3}}{sqrt[12]{3}}=frac{3^{frac{1}{28}}cdot 3cdot 3^{frac{1}{21}}}{3^{frac{1}{12}}}=3^{frac{1}{28}+1+frac{1}{21}-frac{1}{12}}=3^{frac{3}{84}+1+frac{4}{84}-frac{7}{84}}=3.

Записали корни в виде степеней (это удобно!) и применили формулу произведения степеней.

Ответ: 3.

Логарифмические выражения

Темы для повторения:
Логарифмы

Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.

log _{a}b=cLeftrightarrow a^{c}=b.

При этом b> 0, a > 0, aneq 1.

Основные логарифмические формулы:

Основное логарифмическое тождество: boldsymbol{log _{a}a^{c}=c, ; a^{log _{a}b}=b}.

Логарифм произведения равен сумме логарифмов: boldsymbol{log _{a}left ( bc right )=log _{a}b+log _{a}c}.

Логарифм частного равен разности логарифмов: boldsymbol{log _{a}left ( frac{b}{c} right )=log _{a}b-log _{a}c}.

Формула для логарифма степени: boldsymbol{log _{a}b^{m}=mlog_{a}b}.

Формула перехода к новому основанию: boldsymbol{log _{a}b=frac{1}{log _{b}a},; log _{a}b=frac{log _{c}b}{log _{c}a}}.

10. Вычислите: log _{5}7cdot log _{7}25.

log _{5}7cdot log _{7}25=log _{5}7cdot log _{7}5^{2}=2log _{5}7cdot log _{7}5=2.

Снова формула перехода к другому основанию.

log _{a}b=frac{1}{log _{b}a}, поэтому
log _{a}bcdot log _{b};a=1.

11. Найдите log _{a}frac{a^{6}}{b^{4}}, если log _{a}b=-2.

log _{a}frac{a^{6}}{b^{4}}=log _{a}a^{6}-log _{a}b^{6}=6-4log _{a}b=6-4cdot left ( -2 right )=6+8=14.

12. Найдите значение выражения frac{log _{2}80}{3+log _{2}10}.

frac{log _{2}80}{3+log _{2}10}=frac{log _{2}left (8cdot 10 right )}{3+log _{2}10}=frac{log _{2}8+log _{2}10}{3+log _{2}10}=frac{3+log _{2}10}{3+log _{2}10}=1.

13. Найдите значение выражения frac{log _{9}sqrt[10]{8}}{log _{9}8}.

frac{log _{9}sqrt[10]{8}}{log _{9}8}=frac{log _{9}8^{frac{1}{10}}}{log _{9}8}=frac{1}{10}=0,1.

14. Найдите значение выражения left ( 1-log _{3}18 right )left ( log _{6}54 -1right ).

left ( 1-log _{3}18 right )left ( log _{6}54 -1right )=-left ( log _{3}18-log _{3}3 right )cdot left ( log _{6}54-log _{6}6 right )=-log _{3}6cdot log _{6}9=-2log _{3}6cdot log _{6}3=-2.

Тригонометрия. Формулы тригонометрии и формулы приведения

Темы для повторения:
Тригонометрический круг.
Формулы тригонометрии.
Формулы приведения.

15. Вычислите: 44sqrt{3}tgleft ( -480^{circ} right ).

44sqrt{3}tgleft ( -480^{circ} right )=44sqrt{3}cdot frac{sin left ( -480^{circ} right )}{cos left ( -480^{circ} right )}=-44sqrt{3}cdot frac{sin 480^{circ}}{cos 480^{circ}}=-44sqrt{3}cdot frac{sin 120^{circ}}{cos 120^{circ}}=-44sqrt{3}cdot frac{sqrt{3}}{2}:left ( -frac{1}{2} right )=132.

16. Найдите 3cos alpha, если sin alpha =-frac{2sqrt{2}}{3} и alpha in left ( frac{3pi }{2};;2pi right ).

cos ^{2}alpha =1-sin ^{2}alpha =1-left ( -frac{2sqrt{2}}{3} right )^{2}=1-frac{8}{9}=frac{1}{9}.

Т.к. alpha in left ( frac{3pi }{2};;2pi right ), то cos alpha =frac{1}{3}.
3cos alpha =3cdot frac{1}{3}=1.

17. Найдите tgalpha, если sin alpha =-frac{1}{sqrt{5}} и alpha in left ( 1,5pi ;;2pi right ).

cos ^{2}alpha =1-sin ^{2}alpha =1-left ( -frac{1}{sqrt{5}} right )^{2}=1-frac{1}{5}=frac{4}{5}.

Т.к. alpha in left ( 1,5pi ;;2pi right ), то
cos alpha =frac{2}{sqrt{5}}.

tgalpha =frac{sin alpha }{cos alpha }=-frac{1}{sqrt{5}}:frac{2}{sqrt{5}}=-2.

18. Найдите значение выражения: frac{13sin 152^{circ}}{cos 76^{circ}cdot cos 14^{circ}}.

frac{13sin 152^{circ}}{cos 76^{circ}cdot cos 14^{circ}}=frac{13cdot 2sin 76^{circ}cdot cos 76^{circ}}{cos 76^{circ}cdot cos 14^{circ}}=frac{26sin 76^{circ}}{cos 14^{circ}}=frac{26sin left ( 90^{circ}-14^{circ} right )}{cos 14^{circ}}=

=frac{26cos 14^{circ}}{cos 14^{circ}}=26.

Применили формулу приведения.

19. Упростите выражение: frac{3cos(pi - beta)+sin(frac{pi}{2}+beta)}{cos(beta+3pi)}.

frac{3cos left ( pi -beta right )+sin left ( frac{pi }{2}+beta right )}{cos left ( beta +3pi right )}=frac{-3cos beta +cos beta }{-cos beta }=frac{-2cos beta }{-cos beta }=2.

Применили формулу приведения.

20. Найдите 2cos 2alpha, если sin alpha =-0,7..

2cos 2alpha =2left ( 1-2sin ^{2}alpha right )=2-4sin ^{2}alpha =2-4cdot left ( -0,7 right )^{2}=0,04.

21. Вычислите frac{1-cos 2alpha +sin 2alpha }{1+cos 2alpha +sin 2alpha }, если tgalpha =0,3.

frac{1-cos 2alpha +sin 2alpha }{1+cos 2alpha +sin 2alpha }=frac{1-cos ^{2}alpha +sin ^{2}alpha +2sin alpha cos alpha }{1+cos ^{2}alpha -sin ^{2}alpha +2sin alpha cos alpha }=

=frac{2sin ^{2}alpha +2sin alpha cos alpha }{2cos ^{2}alpha +2sin alpha cos alpha }=frac{sin alpha left ( sin alpha +cos alpha right )}{cos alpha left ( cos alpha +sin alpha right )}=frac{sin alpha }{cos alpha }=tgalpha =0,3.

Алгебраические выражения, корни, степени и логарифмы. И еще тригонометрия. Это всё, что может встретиться в задании 6 Профильного ЕГЭ по математике?

Оказывается, и это не всё! Еще нужно знать, что такое модуль. И как найти sqrt{a^{2}}.

Другие типы заданий

Темы для повторения:
Модуль числа.
Что такое функция.

22. Найдите значение выражения
sqrt{left ( a-2 right )^{2}}+sqrt{left ( a-4 right )^{2}} при 2leq aleq 4.

Запомним: sqrt{a^{2}}=left | a right |.

sqrt{left ( a-2 right )^{2}}+sqrt{left ( a-4 right )^{2}}=left | a-2 right |+left | a-4 right |.

Если 2leq aleq 4, то a-2geq 0 и left | a-2 right |=a-2.

При этом a-4leq 0 и left | a-4 right |=4-a.

При 2leq aleq 4 получаем: left | a-2 right |+left | a-4 right |=a-2+4-a=2.

Ответ: 2.

23. Найдите значение выражения

x+sqrt{x^{2}-24x+144} при xleq 12.

При xleq 12 получим:

x+sqrt{x^{2}-24x+144}=x+sqrt{left ( x-12 right )^{2}}=x+left | x-12 right |=x+12-x=12.

Ответ: 12.

24. Найдите frac{gleft ( 5-x right )}{gleft ( 5+x right )}, если gleft ( x right )=sqrt[9]{xleft ( 10-x right )}, при left | x right |neq 5.

Что такое gleft ( x right )? Это функция, каждому числу ставящая в соответствие число sqrt[9]{xleft ( 10-x right )}. Например, gleft ( 0 right )=0;

gleft ( 1 right )=sqrt[9]{1cdot left ( 10-1 right )}=sqrt[9]{9}.

Тогда:

gleft ( 5-x right )=sqrt[9]{left ( 5-x right )left ( 10-5+x right )}=sqrt[9]{left ( 5-x right )left ( 5+x right )};

gleft ( 5+x right )=sqrt[9]{left ( 5+x right )left ( 10-5-x right )}=sqrt[9]{left ( 5+x right )left ( 5-x right )}.

Заметим, что gleft ( 5-x right )=gleft ( 5+x right ).

Значит, при left | x right |neq 5.
frac{gleft ( 5-x right )}{gleft ( 5+x right )}=1.

25. Найдите frac{pleft ( b right )}{pleft ( frac{1}{b} right )}, если pleft ( b right )=left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right ), при bneq 0.

pleft ( b right )=left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right ) — функция, каждому числу b ставящая в соответствии число
left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right ).

Тогда при bneq 0.

pleft ( frac{1}{b} right )=left ( frac{1}{b}-9b right )left ( -frac{9}{b} +bright )=left ( b-frac{9}{b} right )left (-9b +frac{1}{b} right )=pleft ( b right ), и значение выражения frac{pleft ( b right )}{pleft ( frac{1}{b} right )} равно 1.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 6 ЕГЭ по математике. Вычисления и преобразования» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник
ЕГЭ по математике профиль

Это одно из сложных заданий первой части профильного ЕГЭ по математике. Здесь очень много различных типов задач, в том числе непростых. Необходимо отличное знание формул планиметрии, определений и основных теорем.

→ подборка заданий № 6 из открытого банка ФИПИ

→ формулы для вычисления площадей многоугольников

→ тригонометрия в прямоугольном треугольнике

Автор: Алькаева Лариса Рахимовна

Основные типы заданий № 6 профильного ЕГЭ по математике.

Задание 6. Планиметрия

Треугольник равнобедренный

Треугольник прямоугольный

Треугольник произвольный

Параллелограмм, ромб

Окружность вписанная и описанная

Окружность (углы, касательная, хорда)

Если вы выучили все необходимые формулы, определения и теоремы, у вас намного больше шансов решить на ЕГЭ задачу 16 (часть 2), также посвященную планиметрии. Многие задания № 6 являются схемами для решения более сложных геометрических задач.

Связанные страницы:

Источник

центральный и вписанный углы

1. Выполняем рисунок. 2. Угол, который нужно найти является центральным. Он опирается на ту же дугу, что и угол АВС. 3. Вспомнить правило: “центральный угол в два раза больше вписанного, который опирается на ту же дугу”. 4. Вписанный угол АВС, согласно условию, равен 32 0 . Тогда центральный угол BOC равен 32 0 ∙ 2 = 64 0 Ответ: 64 0 .
Площадь треугольника ABC равна 152. DE — средняя линия. Найдите площадь треугольника CDE.

Задание 6. Планиметрия

За правильное выполненное задание получишь 1 балл.

На решение отводится примерно 3 минуты.

Чтобы решить 6 задание по математике профильного уровня необходимо знать:

Задачи из раздела «Планиметрия» в ЕГЭ подразделяются на несколько видов:

  1. решение прямоугольного треугольника;
  2. решение равнобедренного треугольника;
  3. треугольники общего вида;
  4. параллелограммы;
  5. трапеция;
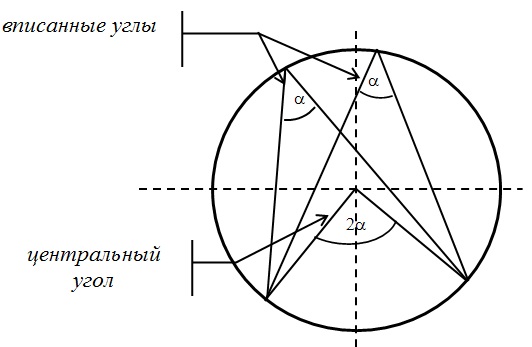
  6. центральные и вписанные углы;
  7. касательная, хорда, секущая;
  8. вписанные окружности;
  9. описанные окружности.
Для того чтобы правильно решать подобные задания необходимо:
  • понимать способы нахождения длин и углов многоугольника;
  • знать формулы вычисления площадей многоугольника.

Задачи для тренировки

Периметр прямоугольника равен 20. Найдите его площадь, если большая сторона на 4 больше меньшей стороны.

6 задание егэ математика профиль как решать

Катеты равнобедренного прямоугольного треугольника равны `54+27sqrt(2)` (см. рис. 167). Найдите радиус окружности, вписанной в этот треугольник.
Катеты равнобедренного прямоугольного треугольника равны `54+27sqrt(2)
Катеты равнобедренного прямоугольного треугольника равны `46+23sqrt(2)` (см. рис. 162). Найдите радиус окружности, вписанной в этот треугольник.
Катеты равнобедренного прямоугольного треугольника равны `46+23sqrt(2)
Боковые стороны равнобедренного треугольника равны 15, основание равно 18 (см. рис. 158). Найдите радиус вписанной окружности.
Боковые стороны равнобедренного треугольника равны 15, основание равно
Боковые стороны равнобедренного треугольника равны 10, основание равно 12 (см. рис. 154). Найдите радиус вписанной окружности.
Боковые стороны равнобедренного треугольника равны 10
Основания равнобедренной трапеции равны 3 и 15, а ее площадь равна 72 (см. рис. 150). Найдите периметр трапеции.
Основания равнобедренной трапеции равны 3 и 15, а ее площадь равна 72
Основания равнобедренной трапеции равны 26 и 8, а ее периметр равен 64 (см. рис. 146). Найдите площадь трапеции.
Основания равнобедренной трапеции равны 26 и 8, а ее периметр равен 64

Источник

  • Главная


  • Теория ЕГЭ


  • Математика — теория ЕГЭ



  • Задание 6 ЕГЭ 2021 по математике, теория

08.10.2018

Необходимая теория для успешного освоения и решения заданий №6 по математике профильного уровня на ЕГЭ в 2021 году.

Представлена вся теория и алгоритм решения различных заданий такого типа.

  • Тренировочные кимы ЕГЭ по математике
  • Практика — примеры для решения каждого типа заданий

Обсудить решение конкретных заданий вы можете в комментариях ниже.

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Сохранить ссылку:

Комментарии (0)
Добавить комментарий

Добавить комментарий

Комментарии без регистрации. Несодержательные сообщения удаляются.

Имя (обязательное)

E-Mail

Подписаться на уведомления о новых комментариях

Отправить

Источник

За это задание ты можешь получить 1 балл. На решение дается около 5 минут. Уровень сложности: повышенный.
Средний процент выполнения: 74.8%
Ответом к заданию 6 по математике (профильной) может быть целое число или конечная десятичная дробь.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

Найдите значение выражения $log_5 27 ⋅ log_3 25$.

Решение

$ log_5 3^3· log_3 5^2 = 3 log_5 3 · 2 log_3 5 $

Воспользуемся свойством: $log _b (a)= 1/{log _a (b)}$

$6 · log_5 3 · {1}/{log_5 3} = 6$.

Ответ: 6

Задача 2

Найдите значение выражения $ {14} / {sin^2 25°+ cos^2 205°}$.

Решение

Учитывая, что $cos(180° + 25) = — cos 25$,

$cos^2 (180° + 25) = (- cos 25°)⋅(- cos 25°)=cos^2 25°$

получим ${14}/{sin^2 25° + cos^2 (180° + 25°)} = {14}/{sin^2 25° + cos^2 25°} = 14$.

Ответ: 14

Задача 3

Найдите значение выражения $ {5} / {cos^2 33°+ cos^2 123°}$.

Решение

Учитывая, что $cos(90°+α)=-sinα$, получим:

$cos^2 (123°)=cos^2 (90°+33°)=(-sin 33°)⋅(-sin 33°)=sin^2 33°$, таким образом

$ {5} / {cos^2 33°+ cos^2 (90°+33°)}= {5} / {cos^2 33°+ sin^2 33°}= 5$.

Ответ: 5

Задача 4

Найдите значение выражения ${18(sin^2 16°- cos^2 16°)} / {cos 32°}$.

Решение

Применив формулу двойного аргумента $cos 2α = cos^2 α — sin^2 α$, получим

$cos 32°=cos^2 16° — sin^2 16°$

${18(sin^2 16° — cos^2 16°)}/{cos^2 16° — sin^2 16°} = {18(sin^2 16° — cos^2 16°)}/{-( sin^2 16°-cos^2 16° )}=-18$.

Ответ: -18

Задача 5

Найдите значение выражения $(1-log_3 18)(1-log_6 18)$.

Решение

$(log__3 3 — log_3 18)(log_6 6 — log_6 18) = log_3 {1}/{6} · log_6 {1}/{3} = log_3 6^(-1) · log_6 3^(-1) = log_3 6 · log_6 3 = log_3 6 · 1/(log_3 6) = 1$.

Ответ: 1

Задача 6

Найдите значение выражения $ {log_{3} 36} / {2+log_{3} 4}$.

Решение

$ {log_{3} (9⋅4)} / {2+log_{3}4} ={log_{3} 9+log_3 4} / {2+log_{3}4} ={2+log_3 4} / {2+log_{3}4} =1$.

Ответ: 1

Задача 7

Найдите значение выражения $ log_2 (log_5 625)$.

Решение

$log_2(log_5 5^4) = log_2 4 = 2$.

Ответ: 2

Задача 8

Найдите значение выражения ${7^{log_5 50}} / {7^{log_{5}2 }}$.

Решение

${7^{log_5(2·25)}}/{7^{log_5 2}} = {7^{log_5 2+log_5 25}}/{7^{log_5 2}} = 7^{log_ 5 2+log_5 5^2 -log_ 5 2} = 7^2 = 49$.

Ответ: 49

Задача 9

Найдите значение выражения ${log_7 23} / {log_{49}23} $.

Решение

${log_7 23} / {log_{7^2}23} ={log_7 23} / {{1} / {2}log_{7 }23}=2$.

Ответ: 2

Задача 10

Найдите значение выражения ${15 cos 19°} / {cos341°}$.

Решение

Применив формулу приведения $cos(360° -α) = cosα$, получим ${15cos19°}/{cos(360° — 19°)} = {15cos19°}/{cos19°} = 15$.

Ответ: 15

Задача 11

Найдите значение выражения ${3 cos 39°} / {sin51°}$.

Решение

Применив формулу приведения $sin(90° -α) = cosα$, получим ${3cos39°}/{sin(90° — 39°)} = {3 cos 39°}/{cos 39°} = 3$.

Ответ: 3

Задача 12

Найдите значение выражения ${15√ {x}-3} / {√ {x}}+{3√ {x}} / {x}+2x-8$ при $x=3$.

Решение

${15√x}/{√x} — {3}/{√x} + {3√x}/{(√x)^2} + 2x — 8 = 15 — {3}/{√x} + {3}/{√x} + 2x — 8 = 7 + 2x$.

При $x = 3$ получим $7 + 2·3 = 13$.

Ответ: 13

Задача 13

Найдите значение выражения ${f(x+3)} / {f(x-3)}$, если $f(x)=5^x$.

Решение

$f(x)=5^x$

${f(x+3)}/{f(x-3)}={5^{x+3}}/{5^{x-3}}=5^6=15 625$

Ответ: 15625

Задача 14

Найдите значение выражения $(√ {23} — √ {15})(√ {23}+√ {15})$.

Решение

$(√{23} — √{15})(√{23} + √{15}) = (√{23})^2 — (√{15})^2 = 23 — 15 = 8$.

Ответ: 8

Задача 15

Найдите значение выражения ${6^{3√2+2}·6^{2√2}}/{6^{5√2-1}}$.

Решение

${6^{3√2+2}·6^{2√2}}/{6^{5√2-1}}=6^{3√2+2+2√2-(5√2-1)} = 6^{5√2+2-5√2+1} = 6^3 = 216$.

Ответ: 216

Задача 16

Найдите значение выражения $8^{3√ {5}-1}⋅ 8^{1-√ {5} }: 8^{2√ {5}-1}$.

Решение

$8^{(3√5-1)+(1-√5)-(2√5-1)} = 8^1 = 8$.

Ответ: 8

Задача 17

Найдите значение выражения $6x⋅(2x^9)^4:{(4x^{12})}^3$ при $x=5$.

Решение

$6x·(2x^9)^4 : (4^3 · (x^{12})^3) = 6x · (2^4 · x^{36}) : ((2^2)^3 · x^{36}) = {6x · 2^4 · x^{36}}/{2^6·x^{36}} = {6x}/{4} = 1.5x$.
При $х=5$, $1.5·х=1.5·5=7.5$

Ответ: 7.5

Задача 18

Найдите значение выражения $x⋅5^{2x+1}⋅ 25^{-x}$ при $x=3$.

Решение

$x⋅5^{2x+1}⋅ (5^2)^{-x}=x⋅5^{2x+1-2x}=x⋅5$. При $x=3$ получим $3⋅5=15$.

Ответ: 15

Задача 19

Найдите значение выражения ${3sin β +15cos β -8} / {sinβ +5cosβ +2}$, если $tg β = — 5$.

Решение

$tgβ={sinβ}/{cosβ}=-5$
$ sinβ=-5cosβ$
$ (3sinβ+15cosβ−8)/(sinβ+5cosβ+2)=(3⋅(-5cosβ)+15cosβ-8)/(-5cosβ+5cosβ+2)=(-15cosβ+15cosβ-8)/2=-8/2=-4$

Ответ: -4

Рекомендуемые курсы подготовки

Источник
  • Взрослым: Skillbox, Хекслет, Eduson, XYZ, GB, Яндекс, Otus, SkillFactory.
  • 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
  • До 7 класса: Алгоритмика, Кодланд, Реботика.
  • Английский: Инглекс, Puzzle, Novakid.
  • Оценивание (первичные баллы) — 1
  • Время на выполнение (мин) — 3
  • Сложность — базовая

Теория по заданию 6

1.1. Числа, корни и степени

1.1.1. Целые числа

1.1.2. Степень с натуральным показателем

1.1.3. Дроби, проценты, рациональные числа

1.1.4. Степень с целым показателем

1.1.5. Корень степени n > 1 и его свойства

1.1.6. Степень с рациональным показателем и её свойства

1.1.7. Свойства степени с действительным показателем

1.2. Основы тригонометрии

1.2.1. Синус, косинус, тангенс, котангенс произвольного угла

1.2.2. Радианная мера угла

1.2.3. Синус, косинус, тангенс и котангенс числа

1.2.4. Основные тригонометрические тождества

1.2.5. Формулы приведения

1.2.6. Синус, косинус и тангенс суммы и разности двух углов

1.2.7. Синус и косинус двойного угла

1.3. Логарифмы

1.3.1. Логарифм числа

1.3.2. Логарифм произведения, частного, степени

1.3.3. Десятичный и натуральный логарифмы, число е

1.4. Преобразования выражений

1.4.1. Преобразования выражений, включающих арифметические операции

1.4.2. Преобразования выражений, включающих операцию возведения в степень

1.4.3. Преобразования выражений, включающих корни натуральной степени

1.4.4. Преобразования тригонометрических выражений

1.4.5. Преобразование выражений, включающих операцию логарифмирования

1.4.6. Модуль (абсолютная величина) числа

  • Взрослым: Skillbox, Хекслет, Eduson, XYZ, GB, Яндекс, Otus, SkillFactory.
  • 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
  • До 7 класса: Алгоритмика, Кодланд, Реботика.
  • Английский: Инглекс, Puzzle, Novakid.
Источник

Понравилась статья? Поделить с друзьями:
  • Как решать 5 задание егэ химия 2022 теория
  • Как решать 4 задание егэ математика профиль теория
  • Как решать 4 задание егэ информатика деревом
  • Как решать 34 задачу по химии егэ 2022
  • Как решать 3 номер егэ биология