Доброго времени суток каждому жителю Хабрвилля! Давненько я не писал статей! Пора это исправить!
В сегодняшней статье поговорим о насущной для многих выпускников школ теме — ЕГЭ. Да-да-да! Я знаю, что Хабр — это сообщество разработчиков, а не начинающих айтишников, но сейчас ребятам как никогда нужна поддержка именно сообщества. Ребят опять посадили на дистант. Пока не ясно на какой период, но уже сейчас можно сказать, что ЕГЭ по информатике будет на компьютерах и его можно зарешать при помощи языка Python.
Вот я и подумал, чтобы не получилось как в песне, стоит этим заняться. Я расскажу про все задачи первой части и их решения на примере демо варианта ЕГЭ за октябрь.
Всех желающих — приглашаю ниже!
Быстрый перевод из системы в систему
В Python есть интересные функции bin(), oct() и hex(). Работают данные функции очень просто:
bin(156) #Выводит '0b10011100'
oct(156) #Выводит '0o234'
hex(156) #Выводит '0x9c'Как вы видите, выводится строка, где 0b — означает, что число далее в двоичной системе счисления, 0o — в восьмеричной, а 0x — в шестнадцатеричной. Но это стандартные системы, а есть и необычные…
Давайте посмотрим и на них:
n = int(input()) #Вводим целое число
b = '' #Формируем пустую строку
while n > 0: #Пока число не ноль
b = str(n % 2) + b #Остатот от деления нужной системы (в нашем сл записываем слева
n = n // 2 #Целочисленное деление
print(b) #ВыводДанная программа будет работать при переводе из десятичной системы счисления в любую до 9, так как у нас нет букв. Давайте добавим буквы:
n = int(input()) #Вводим целое число
b = '' #Формируем пустую строку
while n > 0: #Пока число не ноль
if (n % 21) > 9: #Если остаток от деления больше 9...
if n % 21 == 10: #... и равен 10...
b = 'A' + b #... запишем слева A
elif n % 21 == 11:#... и равен 11...
b = 'B' + b#... запишем слева B
'''
И так далее, пока не дойдём до системы счисления -1 (я переводил в 21-ную систему и шёл до 20)
'''
elif n % 21 == 11:
b = 'B' + b
elif n % 21 == 12:
b = 'C' + b
elif n % 21 == 13:
b = 'D' + b
elif n % 21 == 14:
b = 'E' + b
elif n % 21 == 15:
b = 'F' + b
elif n % 21 == 16:
b = 'G' + b
elif n % 21 == 17:
b = 'H' + b
elif n % 21 == 18:
b = 'I' + b
elif n % 21 == 19:
b = 'J' + b
elif n % 21 == 20:
b = 'K' + b
else: #Иначе (остаток меньше 10)
b = str(n % 21) + b #Остатот от деления записываем слева
n = n // 21 #Целочисленное деление
print(b) #ВыводСпособ объёмен, но понятен. Теперь давайте используем тот же функцию перевода из любой системы счисления в любую:
def convert_base(num, to_base=10, from_base=10):
# Перевод в десятичную систему
if isinstance(num, str): # Если число - строка, то ...
n = int(num, from_base) # ... переводим его в нужную систему счисления
else: # Если же ввели число, то ...
n = int(num) # ... просто воспринять его как число
# Перевод десятичной в 'to_base' систему
alphabet = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ" # Берём алфавит
if n < to_base: # Если число меньше системы счисления в которую переводить...
return alphabet[n] # ... вернуть значения номера в алфавите (остаток от деления)
else: # Иначе...
return convert_base(n // to_base, to_base) + alphabet[n % to_base] # ... рекурсивно обратиться к функии нахождения остаткаВызвав функцию вывода print(convert_base(156, 16, 10)) мы переведём 156 из 10 в 16 систему счисления, а введя print(convert_base('23', 21, 4)) переведёт 23 из 4-ичной в 21-ичную систему (ответ: B).
Задача 2
Все задания беру из первого октябрьского варианта (он же вариант № 9325894) с сайта Решу.ЕГЭ.
Решение данной задачи совсем простое: банальный перебор.
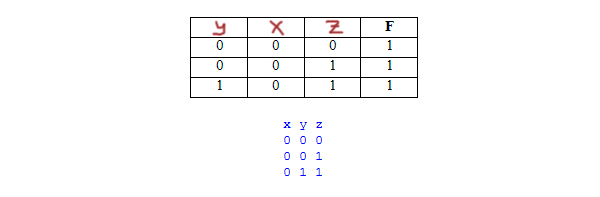
print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы
for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1'
for x in range(2):
for z in range(2):
for w in range(2):
F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию
print(x, y, z, F) #Выводим результатРезультат:
Нам вывелась вся таблица истинности (1 = True, 0 = False). Но это не очень удобно. Обратите внимание, что в задании, функция равно 0, так и давайте подправим код:
print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы
for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1'
for x in range(2):
for z in range(2):
for w in range(2):
F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию
if not F:
print(x, y, z, F) #Выводим результатРезультат:
Далее — простой анализ.
Задача 5
Данная задача легко решается простой последовательностью действий в интерпретационном режиме:
Задача 6
Перепечатали и получили ответ:
s = 0
k = 1
while s < 66:
k += 3
s += k
print(k)Задача 12
В очередной раз, просто заменим слова на код:
a = '9' * 1000
while '999' in a or '888' in a:
if '888' in a:
a = a.replace('888', '9', 1)
else:
a = a.replace('999', '8', 1)
print(a)Задача 14
Компьютер железный, он всё посчитает:
a = 4 ** 2020 + 2 ** 2017 - 15
k = 0
while a > 0:
if a % 2 == 1:
k += 1
a = a // 2
print(k)Задача 16
Опять же, просто дублируем программу в python:
def F(n):
if n > 0:
F(n // 4)
print(n)
F (n - 1)
print(F(5))Результат:
Задача 17
Задача с файлом. Самое сложное — достать данные из файла. Но где наша не пропадала?!
with open("17.txt", "r") as f: #Открыли файл 17.txt для чтения
text = f.read() #В переменную text запихнули строку целиком
a = text.split("n") #Разбили строку энтерами (n - знак перехода на новую строку)
k = 0 #Стандартно обнуляем количество
m = -20001 #Так как у нас сумма 2-ух чисел и минимальное равно -10000, то минимум по условию равен -20000, поэтому...
for i in range(len(a)): #Обходим все элементы массива
if (int(a[i - 1]) % 3 == 0) or (int(a[i]) % 3 == 0): #Условное условие
k += 1 #Счётчик
if int(a[i - 1]) + int(a[i]) > m: #Нахождение минимума
m = int(a[i - 1]) + int(a[i])
print(k, m) #ВыводНемного пояснений. Функция with() открывает файл считывает данные при помощи функции read() и закрывает файл. В остальном — задача стандартна.
Задача 19, 20 и 21
Все три задачи — задачи на рекурсию. Задачи идентичны, а вопросы разные. Итак, первая задача:
Пишем рекурсивную функцию и цикл перебора S:
def f(x, y, p): #Рекурсивная функция
if x + y >= 69 or p > 3: #Условия завершения игры
return p == 3
return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
for s in range (1, 58 + 1): #Перебор S
if f(10, s, 1): #Начали с 10 камней
print(s)
breakНемного пояснений. В рекурсивной функции существует 3 переменные x — число камней в первой куче, y — число камней во второй куче, p — позиция. Позиция рассчитывается по таблице:
|
Игра |
Петя |
Ваня |
Петя |
Ваня |
Петя |
|
|
p |
1 |
2 |
3 |
4 |
5 |
6 |
Далее — всё по условию задачи.
Вторая задача на теорию игр:
Все отличия в рамке. Ну и код, соответственно, не сильно отличается:
def f(x, y, p): #Рекурсивная функция
if x + y >= 69 or p > 4: #Условия завершения игры
return p == 4
if p % 2 != 0:
return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
else:
return f(x + 1, y, p + 1) and f(x, y + 1, p + 1) and
f(x * 2, y, p + 1) and f(x, y * 3, p + 1) #Варианты действий
for s in range (1, 58 + 1): #Перебор S
if f(10, s, 1): #Начали с 10 камней
print(s)Отличия:
-
Выиграл Петя, соответственно, позиция 4
-
Так как Петя не может выиграть за один ход — он выигрывает за 2 хода (and, а не or на нечётных позициях (играх Пети))
-
Убрали break, так как нам нужны все S, а не единственный
Последняя вариация задачи:
Сразу код:
def f(x, y, p): #Рекурсивная функция
if x + y >= 69 or p > 5: #Условия завершения игры
return p == 3 or p == 5
if p % 2 == 0:
return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
else:
return f(x + 1, y, p + 1) and f(x, y + 1, p + 1) and
f(x * 2, y, p + 1) and f(x, y * 3, p + 1) #Варианты действий
for s in range (1, 58 + 1): #Перебор S
if f(10, s, 1): #Начали с 10 камней
print(s)Ну и всего лишь 2 отличия:
-
Позиции 3 или 5, а не 4, так как выиграл Ваня
-
На второй ход выигрывает Ваня и нам нужно or и and поменять. Я заменил только кратность 2.
Задача 22
Ctrl+C, Ctrl+V — наше всё! 
for i in range(1, 100000):
x = i
L = 0
M = 0
while x > 0 :
L = L+1
if (x % 2) != 0:
M = M + x % 8
x = x // 8
if L == 3 and M == 6:
print(i)Задача 23
Итак, код:
def f(x, y):
if x > y: #Перегнали цель
return 0
if x == y: #Догнали цель
return 1
if x < y: #Догоняем цель тремя методами
return f(x + 1, y) + f(x + 2, y) + f(x * 2, y)
print(f(3, 10) * f(10, 12)) #Прошло через 10, значит догнали 10 и от де догоняем 12Так как в условии задачи мы увеличиваем число, но будем числа «догонять». Три метода описаны, ну а пройти через 10 — значит дойти до него и идти от него.
Собственно, это и есть вся первая часть ЕГЭ по информатике решённая на Python.
Ссылка на репозиторий со всеми программами:
Надеюсь, что смог помочь в своей статье выпускникам и готовящимся 
Остался один вопрос — нужен ли разбор второй части ЕГЭ по информатике на Python? Оставлю этот вопрос на ваше голосование.
Всем удачи!
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Делаю разбор второй части?
Проголосовали 105 пользователей.
Воздержались 15 пользователей.
Продолжаем наш видеокурс по подготовке к ЕГЭ по информатике 2022. Сегодня разоблачим второе задание!
Кто незнаком с основными логическими операциями, можете посмотреть прошлогоднюю статью по заданию 2 из ЕГЭ по информатике.
В этой статье будут раскрыты методики решения 2 задания через язык программирования Питон.
Будем перебирать для каждой логической переменной все возможные варианты в программе. А логическая переменная всего два значения может принимать: 1 или 0 (истину или ложь). Таким образом, если к примеру у нас 4 переменные, мы получим 24=16 различных комбинаций.
Кто знаком с мощнейшим методом для 2 задания из ЕГЭ по информатике, о котором я рассказывал в прошлогодней статье, тот поймёт, что мы будем применять тот же самый мощнейший метод, но автоматизированный с помощью питона.
Нам нужно будет запрограммировать логическую функцию на языке Питон. Вот таблица, которая поможет это сделать.
| Логическая операция | Представление в Питоне |
| Отрицание ¬ | not() |
| Логическое умножение ∧ | and |
| Логическое сложение ∨ | or |
| Следование A ⟶ B | not(A) or B |
| Равносильность ≡ | == |
Перейдём к практике решения задач задания 2 с помощью языка программирования Python.
Задача (Классическая)
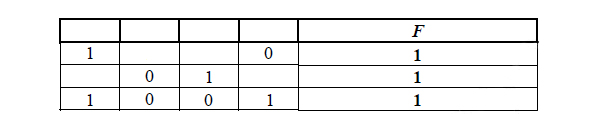
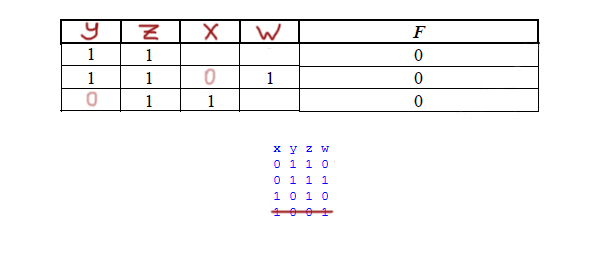
Миша заполнял таблицу истинности логической функции F
(w → z) ∧ ((y → x) ≡ (z → y)),
но успел заполнить лишь фрагмент из трёх различных её строк, даже
не указав, какому столбцу таблицы соответствует каждая из переменных
w, x, y, z.
Определите, какому столбцу таблицы соответствует каждая из переменных
w, x, y, z.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут
соответствующие им столбцы (сначала буква, соответствующая первому
столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы
в ответе пишите подряд, никаких разделителей между буквами ставить
не нужно.
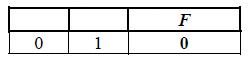
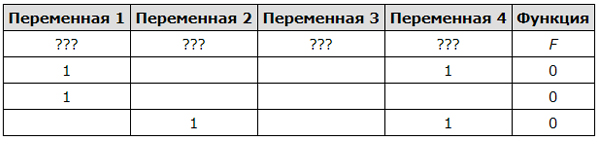
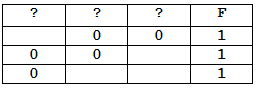
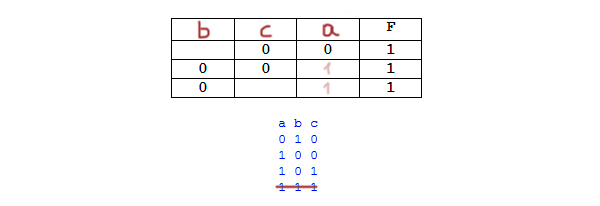
Пример. Функция F задана выражением ¬x / y, зависящим от двух
переменных, а фрагмент таблицы имеет следующий вид.
В этом случае первому столбцу соответствует переменная y, а второму
столбцу – переменная x. В ответе следует написать: yx.
Решение:
Решать задачу будем с помощью шаблона на языке Python (Питон).
print('x y z w') for x in range(0, 2): for y in range(0, 2): for w in range(0, 2): for z in range(0, 2): if (not(w) or z) and ((not(y) or x) == (not(z) or y)): print(x, y, z, w)
В задаче у нас 4 переменные, значит, формируем 4 вложенных цикла. В каждом цикле перебираем все возможные значения для конкретной переменной. Мы перебираем значения 0 и 1.
Функция должна выдавать всегда 1 (единицу, истину). Внутри всех циклов прописываем условие, которое срабатывает как раз на истину. В этом условии прописываем нашу функцию. Если наша функция будет выдавать истину, то мы распечатаем значения переменных, при которых это произошло. Если функция будет выдавать ложь, значит, ничего распечатано не будет.
Четыре вложенных цикла проверяют все возможные варианты (24 = 16 вариантов), и мы получим таблицу истинности, почти такую же, как нам и дали в условии задачи.
Так же вверху печатаем названия переменных, чтобы знать, какие значения каким переменным принадлежат.
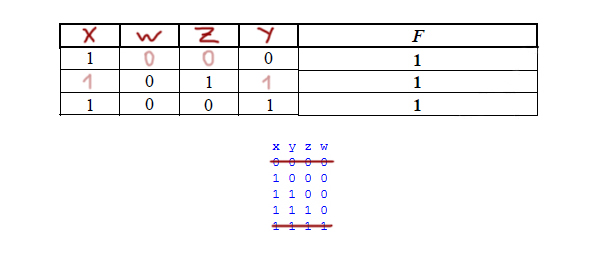
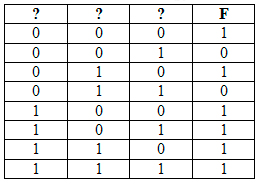
Запустим программу, и на экране распечатается табличка:
В получившийся табличке может быть больше строчек, чем в условии. Так же при поиске переменных нельзя опираться на порядок, в котором идут нули и единицы в нашей табличке. А можно опираться лишь на количество нулей и единиц в строчках или столбцах.
Можно вычеркнуть первую строчку и последнюю, потому что в таблице, которую дали в условии, в каждой строчке есть хотя бы один ноль и хотя бы одна единица.
Сразу видно, что первый столбец принадлежит переменной x, только там могут быть все единицы.
Второй столбец принадлежит переменной w, только там могут быть все нули.
У нас остались две пустые клеточки в самой таблице. Нам нужно где-то поставить единицу, а где-то ноль, потому что у нас остались столбцы с двумя единицами и одним нулём, а так же с двумя нулями и одной единицей. Если мы в третий столбец поставим единицу, а в четвёртый ноль, то первая строчка и вторая будут совпадать.
А в условии сказано, что строки не должны повторяться. Поэтому нужно ноль и единицу расставить наоборот.
Получается, что в третий столбец идёт z, а в четвёртый y
Ответ: xwzy
Посмотрим, как решать задачи второго задания из ЕГЭ по информатике, когда функция выдаёт нули в таблице истинности.
Задача (Классическая, закрепление)
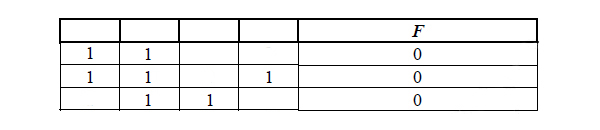
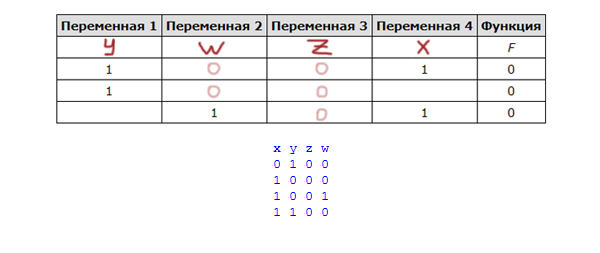
Миша заполнял таблицу истинности функции (x ≡ ¬y) → ((x ∧ w) ≡ z), но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
Определите, какому столбцу таблицы соответствует каждая из переменных
w, x, y, z.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут
соответствующие им столбцы (сначала буква, соответствующая первому
столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы
в ответе пишите подряд, никаких разделителей между буквами ставить
не нужно.
Пример. Функция F задана выражением ¬x / y, зависящим от двух
переменных, а фрагмент таблицы имеет следующий вид.
В этом случае первому столбцу соответствует переменная y, а второму
столбцу – переменная x. В ответе следует написать: yx.
Решение:
Воспользуемся программой на языке Python.
print('x y z w') for x in range(0, 2): for y in range(0, 2): for w in range(0, 2): for z in range(0, 2): if not( not(( x == (not(y)) )) or ((x and w) == z) ): print(x, y, z, w)
От прошлой программы эта программа отличается только функцией!
В таблице видим, что функция должна выдавать ноль. Поэтому в условии мы функцию «оборачиваем» в not().
После == операцию not() мы заключили в скобки, чтобы не было синтаксической ошибки.
Получаем следующую таблицу истинности:
Разгадаем, где какая переменная находится.
Последнюю строку из нашей таблицы можно вычеркнуть, потому что, если мы вычеркнем другую строку, то не получится столбца, где все три единицы, а он должен быть.
Получается, что второй столбец достаётся переменной z.
В первом столбце должно быть две единицы. На эту роль подходит переменная y.
В нашей таблице нет строчки, где все единицы, значит, во второй строчке в пустом окошке выставляем ноль. И в этой строчке нулём обладает переменная x. Следовательно, в третьем столбце будет находится x.
А в последний столбец идёт переменная w по остаточному принципу.
Ответ: yzxw
А как Питон справится с более сложной функцией из примерного варианта ЕГЭ по информатике?
Задача (Сложная функция)
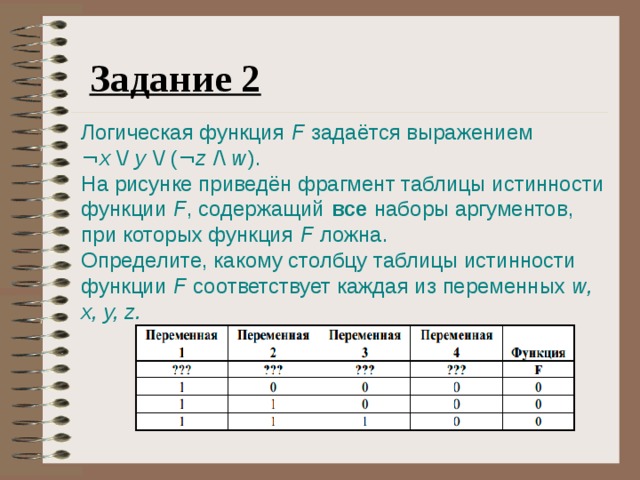
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
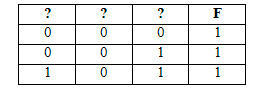
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Источник задачи сайт решу ЕГЭ: https://inf-ege.sdamgia.ru/
Решение:
Запрограммируем функцию на языке Python.
print('x y z w') for x in range(0, 2): for y in range(0, 2): for w in range(0, 2): for z in range(0, 2): if not( ((not(x) or y) and (not(y) or w)) or (z == (x or y)) ): print(x, y, z, w)
Запустим программу и расставим переменные по своим местам.
Переменная z может быть только в третьем столбце.
Во второй столбец идёт переменная w, только этот столбец может иметь одну единицу.
Посмотрим на строчку, где у w стоит единица. В этой же строчке и у x единица. Значит, x идёт в последний столбец, а y в первый столбец.
Ответ: ywzx
Тот же шаблон работает, когда у нас во втором задании три переменные.
Задача (Три переменные)
(№ 1608) Логическая функция F задаётся выражением (¬x ∧ z) ∨ (¬x ∧ ¬y ∧ ¬z)
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
Источник задачи сайт К. Ю. Полякова: https://kpolyakov.spb.ru/
Решение:
Для трёх переменных шаблон на Питоне отлично работает.
print('x y z') for x in range(0, 2): for y in range(0, 2): for z in range(0, 2): if (not(x) and z) or (not(x) and not(y) and not(z)): print(x, y, z)
Здесь и так понятно, куда какая переменная идёт.
Ответ: yxz
Посмотрим, как решать задачи из второго задания ЕГЭ по информатике, когда в таблице истинности разные значения у функции F.
Задача (Разные значения функции)
Логическая функция F задаётся выражением (¬a ∨ b ∨ ¬c) ∧ (b ∨ ¬c). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
В ответе напишите буквы a, b, c в том порядке, в котором идут соответствующие им столбцы (без разделителей).
Источник задачи сайт К. Ю. Полякова: https://kpolyakov.spb.ru/
Решение:
Когда такая ситуация, что функция имеет различные значения в таблице, мы можем проверить, какие значения переменных дают единицу у всей функции. А потом проверить, какие значения выдают ноль у всей функции, если это потребуется.
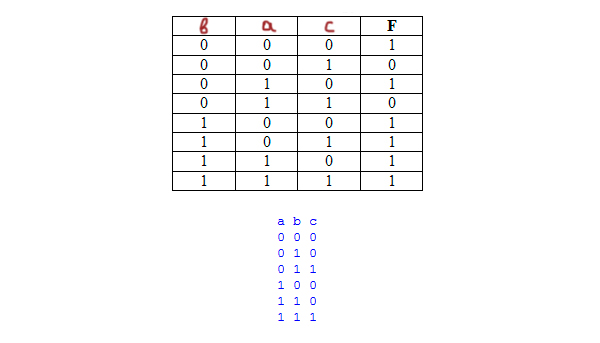
print('a b c') for a in range(0, 2): for b in range(0, 2): for c in range(0, 2): if (not(a) or b or not(c)) and (b or not(c)): print(a, b, c)
В таблице 6 строчек, в которых главная функция превращается в единицу. Далее эти строчки и будем рассматривать. У нас тоже получилось 6 строчек.
Переменная a имеет три единицы. Это второй столбец, потому что там три единицы.
Переменная b имеет четыре единицы, значит, она расположена в первом столбце.
Переменной c достаётся последний столбец.
Ответ: bac
Ещё одна интересная задача для подготовки к ЕГЭ по информатике 2022.
Задача(С подвохом)
Логическая функция F задаётся выражением a ≡ b ∨ b → c.
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
Источник задачи группа Евгения Джобса: https://vk.com/inform_web
Решение:
Подвох заключается в том, что если мы переведём бездумно функцию на язык Питон, то получится a==b or not(b) or c. Но у нас существуют приоритеты для логических операций, которые описаны в прошлогодней статье по подготовке к ЕГЭ по информатике.
В начале должно обрабатываться или, которое было изначально. Затем должно обработаться следование, а потом равносильность. А если мы переведём формулу бездумно, порядок будет не правильный.
Операцию b ∨ b можно представить, как просто b. Ведь, если b принимает значение 0, тогда будет 0 ∨ 0 = 0. Если значение будет 1, то 1 ∨ 1 = 1. Поэтому формулу можно переписать следующим образом:
a ≡ b → c
a == (not(b) or c)
В предыдущих задачах нам не приходилось думать над приоритетами, потому что везде были расставлены скобки. И в основном они уже расставлены в задачах второго задания из ЕГЭ по информатике.
Дальше решаем как обычно.
print('a b c') for a in range(0, 2): for b in range(0, 2): for c in range(0, 2): if a == (not(b) or c): print(a, b, c)
Последнюю строчку можно вычеркнуть из нашей таблицы, т.к. у нас в каждой строчке есть хотя бы один ноль.
Последний столбец занимает переменная a, т.к. только в последний столбец может влезть две единицы.
В строчке, где у a ноль, так же ноль и у переменной c. Значит, во второй столбец идёт переменная c. Если мы ноль поставим в первой строчке в первом столбце, то получится первый столбец из всех нулей. А такого у нас в таблице истинности нет.
Тогда переменная b в первом столбце.
Ответ: bca
слишком много лишних скобок ни к чему. Код очень грязный
А есть какой-нибудь простой код, который смог бы помочь с таким заданием: «Сколькими способами можно поставить в соответствие переменные w, x, y, z столбцам таблицы истинности функции F, опираясь на информацию из данного фрагмента?», или же в данном случае нужно самому подбирать комбинации?
Доброго времени суток, есть вопрос про операции в последней задаче. Вот там написано что b ∨ b можно представить как b. А если будет b ∧ b, то это можно будет представить как b? И можете объяснить почему?
Как в циклах идут переменные, это не важно. Это просто перебор всех возможных вариантов.
Володя, b ∧ b = b, эти формулы приведены в материале, на который я даю ссылку в начале статьи.
На уроке рассматривается разбор 2 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи
Содержание:
- Объяснение задания 2 ЕГЭ по информатике
- Таблицы истинности и порядок выполнения логических операций
- Решение заданий 2 ЕГЭ по информатике
- Задания для тренировки
2-е задание: «Таблицы истинности»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 3 минуты.
Проверяемые элементы содержания: Умение строить таблицы истинности и логические схемы
Типичные ошибки и рекомендации по их предотвращению:
«Игнорирование прямо указанного в условии задания требования, что заполненная таблица истинности не должна содержать одинаковых строк. Это приводит к внешне правдоподобному, но на самом деле неверному решению»
ФГБНУ «Федеральный институт педагогических измерений»
Таблицы истинности и порядок выполнения логических операций
Для логических операций приняты следующие обозначения:
| операция | пояснение | в программировании |
|---|---|---|
| ¬ A, A | не A (отрицание, инверсия) | not(A) |
| A ∧ B, A ⋅ B | A и B (логическое умножение, конъюнкция) | A and B |
| A ∨ B, A + B | A или B (логическое сложение, дизъюнкция) | A or B |
| A → B | импликация (следование) | A <= B |
| A ↔ B, A ≡ B, A ∼ B | эквиваленция (эквивалентность, равносильность) | A==B (python) A=B(pascal) |
| A ⊕ B | строгая дизъюнкция | A != B (python) A <> B (pascal) |
Егифка ©:
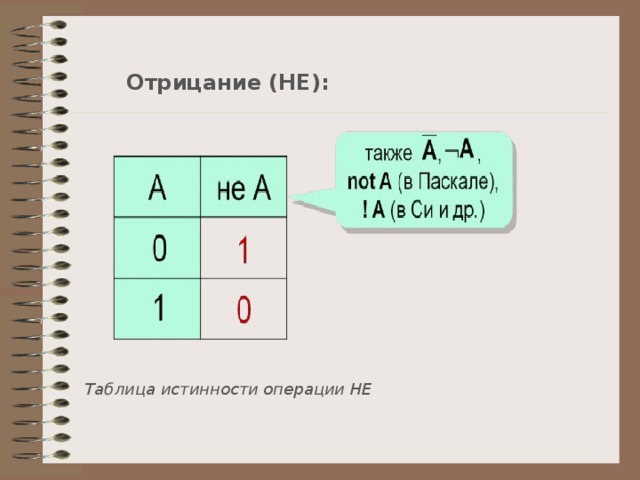
Отрицание (НЕ):
Таблица истинности операции НЕ
Конъюнкция (И):
Таблица истинности операции И (конъюнкция)
Дизъюнкция (ИЛИ):
Таблица истинности операции ИЛИ (дизъюнкция)
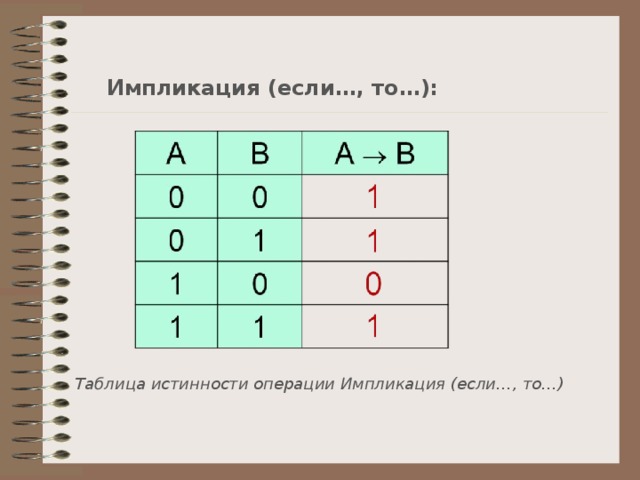
Импликация (если…, то…):
Таблица истинности операции Импликация (если…, то…)
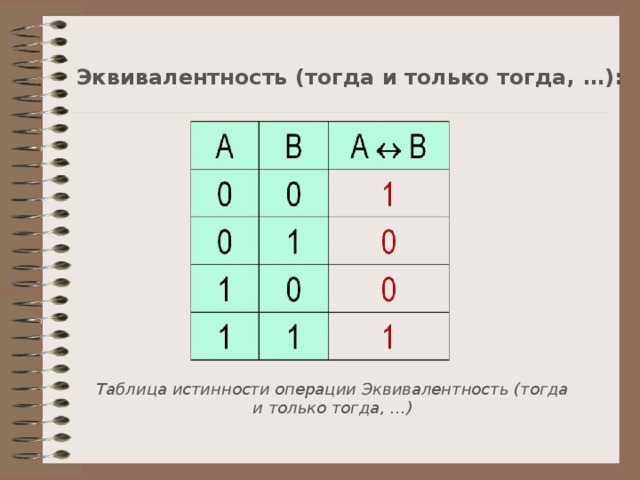
Эквивалентность (тогда и только тогда, …):
Таблица истинности операции Эквивалентность (тогда и только тогда, …)
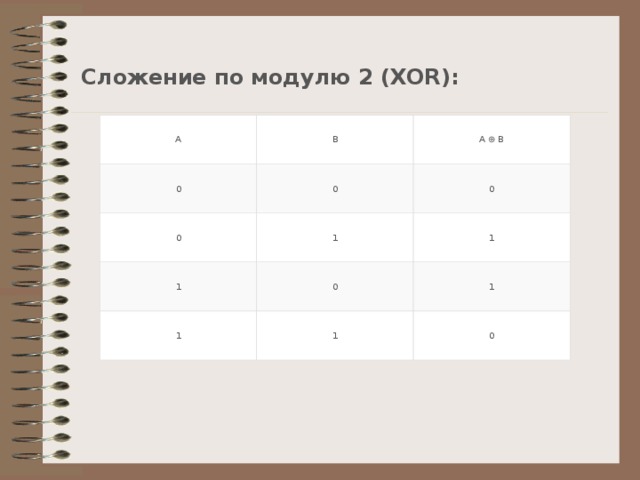
Сложение по модулю 2 (XOR):
| A | B | A ⊕ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Порядок выполнения операций:
- если нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», импликация, равносильность
Еще о логических операциях:
- логическое произведение X∙Y∙Z∙… равно 1, т.е. выражение является истинным, только тогда, когда все сомножители равны 1 (а в остальных случаях равно 0)
- логическая сумма X+Y+Z+… равна 0, т.е. выражение является ложным только тогда, когда все слагаемые равны 0 (а в остальных случаях равна 1)
О преобразованиях логических операций читайте здесь.
Егифка ©:
Решение заданий 2 ЕГЭ по информатике
Задание 2_11: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
✎ Способ 1. Электронные таблицы Excel + Логические размышления:
- Отобразим перебор всех значений использующихся в выражении переменных (всю таблицу истинности). Поскольку в выражении используются 4 переменных, то строк таблицы будет 24=16:
- Далее обе скобки исходного выражения необходимо записать в виде логического выражения, каждую — в отдельном столбце. Также в отдельном столбце добавьте формулу итоговой функции F:

xwzy
-
✎ Способ 2. Программирование:
- В результате будут выведены значения для
F=0:
Язык python:
print('x y z w') for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: F = (not(x) or y or z) and (x or not(z) or not(w)) if not(F): print(x, y, z, w)
x y z w 0 0 1 1 0 1 1 1 1 0 0 0 1 0 0 1
xwzy
Язык pascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not x or y or z) and (x or not z or not w)) then writeln(x:7, y:7, z:7,w:7); end.
F=0:x y z w False False True True False True True True True False False False True False False True
false = 0, True = 1Ответ:
xwzy
-
✎ Способ 3. Логические размышления:
- Внешняя операция выражения — конъюнкция (∧). Во всех указанных строках таблицы истинности функция принимает значение 0 (ложь). Конъюнкция ложна аж в трех случаях, поэтому проверить на ложь очень затруднительно. Тогда как конъюнкция истинна (= 1) только в одном случае: когда все операнды истинны. Т.е. в нашем случае:
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w) = 1 когда: 1. (¬x ∨ y ∨ z) = 1 И 2. (x ∨ ¬z ∨ ¬w) = 1
| x | y | z | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | z | w | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | w | z | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
Результат: xwzy
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_12: Разбор 2 задания ЕГЭ:
Миша заполнял таблицу истинности функции:
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w)
но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 0 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.
Подобные задания для тренировки
✍ Решение:
✎ Способ 1. Логические размышления (бескомпьютерный вариант):
- Решим задание методом построения полной таблицы истинности.
- Посчитаем общее количество строк в таблице истинности и построим ее:
4 переменных -> 24 = 16 строк
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w) 1. Избавимся от импликации: ¬(¬z ∧ ¬(x ≡ y)) ∨ ¬(y ∨ w) 2. Внесем знак отрицания в скобки (закон Де Моргана): (z ∨ (x ≡ y)) ∨ (¬y ∧ ¬w) = 0 1 часть = 0 2 часть = 0 * Исходное выражение должно быть = 0. Дизъюнкция = 0, когда оба операнда равны 0.
(z ∨ (x ≡ y)) = 0 когда z = 0 и x ≡ y = 0 ¬y ∧ ¬w = 0 когда: 1. ¬y = 0 ¬w = 0 2. ¬y = 1 ¬w = 0 3. ¬y = 0 ¬w = 1
| x | y | w | z | F |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| y | w | x | z | F |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
Результат: ywxz
✎ Способ 2. Программирование:
- В результате будут выведены значения для F=0:
Язык PascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not z and (x xor y)) <= not(y or w)) then writeln(x:7, y:7, z:7,w:7); end.
x y z w False True False False False True False True True False False True
false = 0, True = 1Сопоставив их с исходной таблицей, получим результат: ywxz
Язык Python:
print ('x y z w') for x in 0,1: for y in 0,1: for z in 0,1: for w in 0,1: F=(not z and not(x==y))<=(not(y or w)) if not F: print (x,y,z,w)
F=0:x y z w 0 1 0 0 0 1 0 1 1 0 0 1
Сопоставив их с исходной таблицей, получим результат:
Результат: ywxz
🎦 Доступно видео решения этого задания (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
🎦 Видео (решение 2 ЕГЭ в Excel):
📹 здесь
📹 Видеорешение на RuTube здесь
📹 Видеорешение на RuTube здесь (Программирование)
Задание 2_10: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
¬a ∧ b ∧ (c ∨ ¬d)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
🎦 (Бескомьютерный вариант) Предлагаем подробный разбор посмотреть на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_3: Решение задания 2. Демоверсия ЕГЭ 2018 информатика:
Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таб. ист-ти функции F, содержащий все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Подобные задания для тренировки
✍ Решение:
-
✎ Логические размышления (бескомпьютерный вариант):
- Внешним действием (последним выполняемым) в исходном выражении является дизъюнкция:
¬x ∨ y ∨ (¬z ∧ w)
| x1 | x2 | F |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
¬x = 1 или 0, y = 1 или 0, ¬z ∧ w = 1 или 0).¬x = 0, иными словами x = 1. Значит первый столбец соответствует переменной x. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
y = 0. Значит четвертый столбец соответствует переменной y. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | y | F |
| 1 | 1 | 1 | 0 | 0 |
¬z ∧ w должно равняться 0, чтобы функция была ложной. Конъюнкция истинна только тогда, когда оба операнда истинны (=1); в нашем случае функция должна быть ложной, но пойдем от обратного. Если ¬z = 1, т.е. z = 0, а w = 1, то это неверно для нашего случая. Значит всё должно быть наоборот: z = 1, а w = 0. Таким образом столбец второй соответствует z, а столбец третий — w. | x | z | w | y | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
Результат: xzwy
✎ Способ 2. Программирование:
Язык pascalABC.NET:
begin writeln('x ','y ','z ','w '); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not(not x or y or(not z and w)) then writeln(x:7,y:7,z:7,w:7); end.
🎦 (бескомпьютерный вариант) Подробное решение данного 2 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_13: Разбор досрочного егэ по информатике 2019
Логическая функция F задаётся выражением
(x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 |
✍ Решение:
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задания для тренировки
Задание 2_2: Задание 2 ЕГЭ по информатике:
Каждое из логических выражений F и G содержит 5 переменных. В табл. истинности для F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1.
Сколько строк таблицы истинности для F ∨ G содержит 1 в столбце значений?
Подобные задания для тренировки
✍ Решение:
- Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из 32 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет 25=32, т.е. 32 строки.
- Из этих 32 строк и для F и для G мы знаем наверняка только о 5 строках: 4 из них истинны (=1), а одна ложна (=0).
- Вопрос стоит о количестве строк = 1 для таб. истинности F ∨ G. Данная операция — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0
- В исходных таблицах для F и G мы знаем о существовании только одного 0, т.е. в остальных строках может быть 1. Т.о., и для F и для G в 31 строке могут быть единицы (32-1=31), а лишь в одной — ноль.
- Тогда для F ∨ G только в одном случае будет 0, когда и F = 0 и G = 0:
- Соответственно, истинными будут все остальные строки:
| № | F | G | F ∨ G |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 |
| … | … | … | 1 |
| 32 | … | … | 1 |
32 - 1 = 31
Результат: 31
Подробное объяснение данного задания смотрите на видео:
📹 здесь
Задание 2_6: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы.
Каково максимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 27 = 128 строк.
- В четырех из них результат равен единице, значит в остальных — 0.
- A ∨ B истинно в том случае, когда либо A = 1 либо B = 1, или и A и B = 1.
- Поскольку А = 1 только в 4 случаях, то чтобы получить максимальное количество единиц в результирующей таблице истинности (для A ∨ B), расположим все единицы т.и. для выражения A так, чтобы они были в строках, где B = 0, и наоборот, все строки, где B = 1, поставим в строки, где A = 0:
- Итого получаем 8 строк.
- Если бы в задании требовалось найти минимальное количество единиц, то мы бы совместили строки со значением = 1, и получили бы значение 4.
| A | B |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 0 |
| … | … |
Результат: 8
Задание 2_7: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 6 единиц.
Каково максимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 28 = 256 строк.
- В шести из них результат равен единице, значит в остальных — 0.
- A ∧ B ложно в том случае, когда:
A ∧ B = 0 если: 1. A = 0, B = 1 2. B = 0, A = 1 3. A = 0 и B = 0
- Во всех случаях там где А=1 может стоять B=0, и тогда результат F = 0. Поскольку нам необходимо найти максимально возможное число нулей, то как раз для всех шести А=1 сопоставим B=0, и наоборот, для всех шести возможных B=1 сопоставим A=0
- Поскольку строк всего 256, то вполне возможно, что все 256 из них возвратят в результате 0
| A | B | F |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| … | … | … |
Результат: 256
Задание 2_4: 2 задание:
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
✍ Решение:
- В первом внешняя операция (выполняется последней) — конъюнкция. Начнем рассмотрение с нее. Соответственно, проверяем по второй строке таб. ист-ти, там где F = 1, так как в таком случае все аргументы должны быть истинными (см. таб. истинности для конъюнкции).
- Если мы подставим в нее все аргументы выражения, то функция действительно возвращает истину. Т.е. пункт первый подходит:
- Но проверим на всякий случай остальные.
- Второй пункт проверяем по первой и третьей строке, так как основная операция — дизъюнкция — ложна только в том случае, если все аргументы ложны (см. таб. истинности для дизъюнкции). Проверяя по первой строке, сразу видим, что x1 в ней равен 1. В таком случаем функция будет = 1. Т.е. этот пункт не подходит:
- Третий пункт проверяем по второй строке, так как основная операция — конъюнкция — возвратит истину только тогда, когда все операнды равны 1. Видим, что x1 = 0, соответственно функция будет тоже равна 0. Т.е. выражение нам не подходит:
- Четвертый пункт проверяем по первой и третьей строкам. В первой — x1 = 1, т.е. функция должна быть равна 1. Т.е. пункт тоже не подходит:
- Таким образом, ответ равен 1.
Результат: 1
Решение 2 задания ГВЭ по информатике смотрите на видео:
📹 здесь
Задание 2_8: Решение 2 задания ЕГЭ по информатике:
Дано логическое выражение, зависящее от 5 логических переменных:
(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)
Сколько существует различных наборов значений переменных, при которых выражение истинно?
1) 0
2) 30
3) 31
4) 32
Подобные задания для тренировки
✍ Решение:
- Поскольку выражение включает 5 переменных, то таб. ист-ти состоит из 25 = 32 строк.
- Внешней операцией (последней) является конъюнкция (логическое умножение), а внутри скобок — дизъюнкция (логическое сложение).
- Обозначим первую скобку за А, а вторую скобку за B. Получим A ∧ B.
- Найдем сколько нулей существует для таб. истинности:
A B F 1. 0 0 0 2. 0 1 0 3. 1 0 0
Теперь рассмотрим каждый случай отдельно:
¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5 = 0
и
x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 = 0.
32 - 2 = 30, что соответствует номеру 2
Результат: 2
Подробное решение задания смотрите в видеоуроке:
📹 здесь
Задание 2_5: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | F |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 |
Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x3 не совпадает с F.
Подобные задания для тренировки
✍ Решение:
- Полная таблица истинности будет иметь 26 = 64 строк (т.к. 6 переменных).
- 4 из них нам известны: в них x3 два раза не совпадает с F.
- Неизвестных строк:
64 - 4 = 60
60 + 2 = 62
Результат: 62
Задание 2_9: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 0 | 0 | 0 | |||||
| 0 | 0 | 1 | |||||
| 1 | 1 | 1 |
Каким выражением может быть F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7
✍ Решение:
- Рассмотрим отдельно каждый пункт и найдем последнюю операцию, которая должна быть выполнена (внешнюю).
1 пункт:
(((x1 ∧ (x2 → x3) ∧ ¬x4) ∧ x5) ∧ x6) ∧ ¬x7
2 пункт:
(((x1 ∨ (¬x2 → x3) ∨ ¬x4) ∨ ¬x5) ∨ x6) ∨ ¬x7
3 пункт:
(((¬x1 ∧ (x2 → ¬x3) ∧ x4) ∧ ¬x5) ∧ x6) ∧ x7
Результат: 4
В видеоуроке рассмотрено подробное решение 2 задания:
📹 здесь
Задание 2_1: Задание 2 ЕГЭ по информатике:
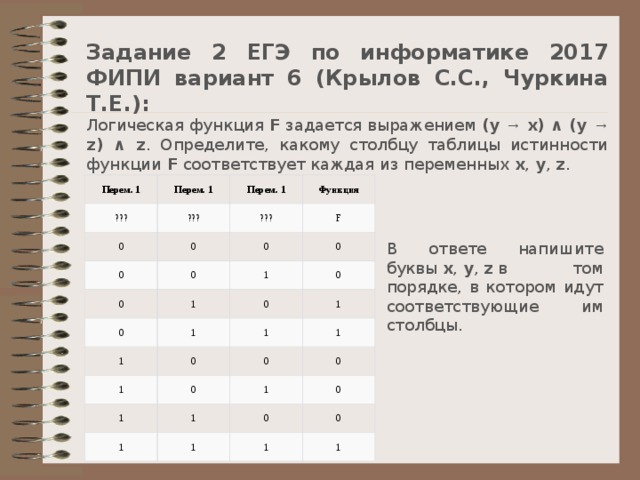
Логическая функция F задается выражением
(y → x) ∧ (y → z) ∧ z.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| ??? | ??? | ??? | F | |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 0 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 |
| 8 | 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
- Сначала необходимо рассмотреть логическую операцию, которую мы будем выполнять в последнюю очередь — это логическое И (конъюнкция) или ∧. То есть внешнюю операцию:
(y → x) ∧ (y → z) ∧ z
(y → x) ∧ (y → z) ∧ z = 1 если: 1. (y → x) = 1 2. (y → z) = 1 3. z = 1
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| 3 | 0 | 1 | 0 | 1 |
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| _ | ??? | z | ??? | F |
| № | Перем. 1 | z | Перем. 3 | F |
|---|---|---|---|---|
| 4 | 0 | 1 | 1 | 1 |
Результат: yzx
Детальный разбор данного задания 2 ЕГЭ по информатике предлагаем посмотреть в видео:
📹 здесь
Еще один способ решения данного задания – написание программы.
На примере первой задачи посмотрим несколько способов решения.
Задание 1
У исполнителя Утроитель две команды, которым присвоены номера:
1. прибавь 1
2. умножь на 3
Сколько есть программ, которые число 1 преобразуют в число 20?
В решении электронными таблицами мы получили формулы для расчетов:
Если число n НЕ делится на 3, количество программ для него
kn = kn-1
Если же число делится на 3, то
kn = kn-1 + kn / 3
их мы и будем использовать в данном задании.
1 способ решения. Заполнение списка.
Необходимые навыки:
- работа со списками
- условный оператор
- цикл for
# +1 *3 1->20
a = [0] * 21 # создаем список из такого количества
# элементов, чтобы нам хватило индексов от 0 до 20
a[1] = 1 # заполняем элемент с индексом стартового числа
for i in range(2, 20 + 1): # перебираем остальные числа от 2 до 20
if i % 3 == 0: # если кратно 3, добавляем предыдущее и / 3
a[i] = a[i – 1] + a[ i // 3]
else: # если не кратно 3, добавляем только предыдущее
a[i] = a[i – 1]
print(a[20]) # выводим на экран значение конечного числа
Данное решение является самым частным и не всегда получится им хорошо решить. Потребуются дополнительные условия когда могут получаться отрицательные индексы.
2 вариант решения без инверсии команд
# +1 *3 1->20 a = [0] * 100 # создаем список из такого количества # элементов, чтобы нам хватило индексов от 0 до 20 * 3 (я взял сильно с запасом) a[20] = 1 # заполняем элемент с индексом стартового числа for i in range(19, 0, -1): # перебираем остальные числа от 2 до 20 a[i] = a[i + 1] + a[i * 3] print(a[1]) # выводим на экран значение конечного числа
При таком решении не требуется условный оператор, но размер списка надо предусмотреть в 3 раза больше.
3 вариант решения. Рекурсивная функция
# +1 *3 1->20 def f(n): if n > 20: # перепрыгнули 20 return 0 if n == 20: # попали в 20 return 1 return f(n + 1) + f(n * 3) # число до 20
print(f(1))
Задача 2. Все варианты решения
Исполнитель Июнь15 преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя Июнь15 – это последовательность команд. Сколько существует программ, для которых при исходном числе 2 результатом является число 40 и при этом траектория вычислений содержит число 20 и не содержит число 8?
Разобьем решение со списком на два этапа
# +1 *2 2->40 v20 x8 a = [0] * 100
a[20] = 1 # заполняем элемент с индексом стартового числа a[40] = 1 for i in range(19, 2 - 1, -1): if i != 8: a[i] = a[i + 1] + a[i * 2] for i in range(39, 20 - 1, -1): a[i] = a[i + 1] + a[i * 2] print(a[2] * a[20]) # выводим на экран значение конечного числа
Усовершенствуем рекурсивный алгоритм: добавим в функцию еще один параметр. Теперь их два: из какого числа считаем и в какое.
# +1 *2 2->40 v20 x8 def f(n, finish): if n == finish: return 1 if n > finish or n == 8: return 0 return f(n + 1, finish) + f(n * 2, finish) print(f(2, 20) * f(20, 40))
Решение задания программированием наиболее кратко получается с использованием рекурсивной функции. В целом, написание кода занимает время примерно равное решению в электронных таблицах, за исключением случаев когда дан большой диапазон чисел.
Следует рассматривать такой вариант решения как средство для проверки ручного решения.
Применение языка программирования Python в решении задач компьютерного
ЕГЭ по информатике
Автор:
Кусточкин Александр Валерьевич
учитель
информатики, МБОУ «Поспелихинская СОШ №1»
2021
г.
Оглавление
Введение
1. Основы
языка программирования Python
2. Обзор
задач компьютерного ЕГЭ по информатике и их решение на языке Python
3. Сравнение
эффективности программ, написанных на языках Pascal,
C и Python
Заключение
Введение
Единый
государственный экзамен по информатике необходим тем, кто планирует поступать в
российские вузы на специальности, связанные с IT-технологиями. Этот экзамен
нужен тем, кто хочет стать программистом, разработчиком, специалистом по
информационным технологиям.
Единый
государственный экзамен по информатике будет проходить на компьютерах уже с
2021 года. Новая модель реализована в виде компьютерной системы тестирования, а
ее апробация прошла в нашем городе осенью 2019. Смысл новой модели состоит в
том, что все задания выпускники будут выполнять при помощи компьютеров и с
применением различных языков программирования и программного обеспечения.
В
настоящее время все большую популярность приобретает язык Python.
Одна из причин популярности Python – более простое и компактное оформление,
чем в других языках. Это самый популярный язык общего назначения: он
используется для машинного обучения, аналитике, разработке игр и в науке о
данных. В данной работе будет применение языка Pythonв
решении задач компьютерного ЕГЭ по информатике.
Объект
работы – процесс решения задач компьютерного ЕГЭ
по информатике.
Предмет
работы – средства решения задач компьютерного
ЕГЭ по информатике.
Цель
работы – провести обзор возможностей языка
программирования Pythonв
решении задач компьютерного ЕГЭ по информатике.
Задачи:
— рассмотреть
основы языка программирования Python;
— выделить
типы задач компьютерного ЕГЭ по информатике и, по возможности, решить их
средствами языка программирования Python;
— сравнить
эффективность программ, написанных на языках Pascal,
C
и Python.
1. Основы
языка программирования Python
Сценарии
исходного кода Python состоят из так называемых логических строк, каждая из которых в свою очередь
состоит из физических
строк. Для обозначения комментариев используется символ #.
Комментарии и пустые строки интерпретатор игнорирует.
Физические строки
разделяются самим символом конца строки. Для выделения блоков кода используются
исключительно отступы. Логические строки с одинаковым размером отступа
формируют блок, и заканчивается блок в том случае, когда появляется логическая
строка с отступом меньшего размера. Именно поэтому первая строка в сценарии
Python не должна иметь отступа.
Других радикальных
отличий от других языков программирования в синтаксисе Python нет. Также
используются стандартные правила для заданий идентификаторов переменных,
методов и классов – имя должно начинаться с подчеркивания или латинского символа
любого регистра и не может содержать символов @, $, %. Также не может
использоваться в качестве идентификатора только один символ подчеркивания.
Типы данных, используемых
в Python, совпадают с другими языками – целые и вещественные типы данных;
дополнительно поддерживается комплексный тип данных – с вещественной и мнимой
частью. Python поддерживает строки, которые могут быть заключены в одинарные,
двойные или тройные кавычки, при этом строки являются immutable-объектами, т.е.
не могут изменять свое значение после создания.
Есть в Python и
логический тип данных bool c двумя вариантами значения – True и False. Для
повышения читаемости кода рекомендуется использовать для логических переменных
тип bool.
В Python определены три
типа коллекций для хранения наборов данных:
—
кортеж (tuple);
—
список (list);
—
словарь (dictionary).
Кортеж представляет собой
неизменяемую упорядоченную последовательность данных. В нем могут содержаться
элементы различных типов, например другие кортежи. Кортеж определяется в круглых
скобках, а его элементы разделяются запятыми. Специальная встроенная функция
tuple() позволяет создавать кортежи из представленной последовательности
данных.
Список – это изменяемая
упорядоченная последовательность элементов. Элементы списка также разделяются
запятыми, но задаются уже в квадратных скобках. Для создания списков
предлагается функция list().
Словарь является
хеш-таблицей, сохраняющей элемент вместе с его идентификатором-ключом.
Последующий доступ к элементам выполняется тоже по ключу, поэтому единица
хранения в словаре – это пара объект-ключ и связанный с ним объект-значение.
Словарь – это изменяемая, но не упорядоченная коллекция, так что порядок
элементов в словаре может меняться со временем. Задается словарь в фигурных
скобках, ключ отделяется от значения двоеточием, а сами пары ключ/значение
разделяются запятыми. Для создания словарей доступна функция dict().
В
листинге 1 приведены примеры различных коллекций, доступных в Python.
Листинг 1. Виды коллекций, доступные в Python
|
(‘w’,‘o’,‘r’,‘l’,‘d’) (2.62,) [“test”,’me’] [ { 5:‘a’, |
Многие возможности Pythonреализованы в виде
отдельных функций; кроме того, модули расширения чаще всего делаются тоже в
виде библиотеки функций. Функции также применяются и в классах, где они по
традиции называются методами.
Синтаксис
определения функций в Python крайне простой; с учетом изложенных выше
требований (листинг 2).
Листинг 2. Виды коллекций, доступные в Python
|
def выражение выражение … |
Как
видно, необходимо использовать служебное слово def, двоеточие и отступы.
Вызвать функцию также очень просто:
Есть
только несколько моментов, специфичных для Python, которые стоит учитывать.
Параметры могут передаваться как просто по порядку перечисления, так и по
именам, в этом случае не нужно указывать при вызове те параметры, для которых
есть значения по умолчанию, а передавать только обязательные или менять порядок
параметров при вызове функции (листинг 3).
Листинг 3. Виды коллекций, доступные в Python
|
#функция, def return print print |
Функция в Python
обязательно возвращает значение – это делается либо явно с помощью оператора
return, за которым следует возвращаемое значение, либо, в случае отсутствия
оператора return, возвращается константа None, когда достигается конец функции.
Как видно из примеров объявлений функций, в Python нет необходимости указывать,
возвращается что-либо из функции или нет, однако если в функции имеется один
оператор return, возвращающей значение, то и другие операторы return в этой
функции должны возвращать значения, а если такого значения нет, то необходимо
явно прописывать return None.
Если функция очень
простая и состоит из одной строки, то ее можно определить прямо на месте
использования, в Python подобная конструкция называется лямбда-функцией
(lambda). lambda-функция – это анонимная функция (без собственного имени),
телом которой является оператор return, возвращающий значение некоторого
выражения. Такой подход может оказаться удобным в некоторых ситуациях, однако
стоит заметить, что повторное использование подобных функций невозможно.
Еще стоит описать
отношение Python к использованию рекурсии. По умолчанию глубина рекурсии
ограничена 1000 уровней, и когда этот уровень будет пройден, возникнет
исключительная ситуация, и работа программы будет остановлена. Однако при
необходимости величину этого предела можно изменить.
2. Обзор
задач компьютерного ЕГЭ по информатике и их решение на языке Python
В
проекте компьютерного ЕГЭ по информатике предлагаются десять типов заданий на
следующие темы.
1.
Вычисления
2.
Решение уравнений численными методами
3.
Перебор целых чисел. (Разбиение числа на
цифры)
4.
Перебор чисел. Проверка делимости
5.
Перебор целых чисел. Количество делителей
6.
Символьные строки. Цепочки символов
7.
Функции двух аргументов. Таблицы значений
8.
Электронные таблицы. Встроенные функции
(не решается средства Python)
9.
Рекурсия. Рекурсивные функции
10.
Исследование моделей. Оптимизация
1.
Пример задания на вычисление
С помощью программы Калькулятор или электронных
таблиц вычислите значение выражения. В ответе запишите только целую часть
результата. Можно также написать программу.
ПрограмманаязыкеPython
from math
import sqrt, cos, pi
print( sqrt(1
+ cos(3.53*pi)*10)*310 )
Ответ:
431.
Для
решения данного задания, нужно знать правила записи математических функций на
языке Python. В связи с невозможностью записи некоторых стандартных
математических функций с клавиатуры персонального компьютера в языке Python
существуют так называемые встроенные функции, с помощью которых пользователь
записывает арифметические выражения.
Основные
математические функции языка Python представлены в таблице 1. Прежде чем
использовать математические функции, необходимо в начале программы написать
инструкцию import math, однако тогда перед упоминанием каждой функции необходимо
будет добавлять имя модуля — math, например, y=math.sin(x). Другой способ,
который позволит избежать многократного вызова модуля math, — сделать следующую
запись в начале программы: from math import *.
Таблица
1. Общие математические функции модуля Math
|
Запись на Python |
Действие |
|
math.sin (x) |
Возвращает значение функции Sin от числа х |
|
math.cos (x) |
Возвращает значение функции Cos от числа х |
|
math.tan (x) или math.sin (x) / math.cos (x) |
Возвращает значение функции Tg от числа х |
|
math.cos |
Возвращает значение функции Ctg от числа х |
|
math.abs (x) |
Возвращает абсолютную величину числа х |
|
math.exp (x) |
Возвращает результат возведения числа е в степень X |
|
math.Log lp (x) |
Возвращает натуральный логарифм от х+1 |
|
math.sqrt (x) |
Возвращает результат извлечения квадратного корня |
|
math.log (x) |
Возвращает логарифм числа х по основанию 10 |
|
math.cos |
Возвращает результат возведения функции Cos х в квадрат |
|
math.acos (x) |
Возвращает значение функции арккосинус от числа х |
|
math.asin (x) |
Возвращает значение функции арксинус от числа х |
|
math.atan (x) |
Возвращает значение функции арктангенс от числа х |
|
Pi |
Возвращает 3.141592653589793 |
|
math.degrees(x) |
Преобразует радианы в градусы |
|
math.radians(x) |
Преобразует градусы в радианы |
|
math.floor(x) |
Возвращает значение, округленное до ближайшего |
|
math.ccil(x) |
Возвращает значение, округленное до ближайшего |
|
math.factorial(x) |
Возвращает факториал числа. 3 != 1 *2*3 |
В таблице2 представлены
некоторые встроенные функции для работы с числами, не требующие подключения
модуля math.
Таблица
2. Функции для работы с числами
|
Запись на Python |
Описание |
|
round(x) |
Возвращает результат округления числа х до ближайшего меньшего целого |
|
pow(x,y) другой вариант х**у |
Возвращает результат возведения числа х в степень у |
|
mах(список чисел через |
Возвращает большее значение из списка чисел |
|
min(список чисел через |
Возвращает меньшее значение из списка чисел |
|
sum(список K чисел через запятую) |
Возвращает сумму значений элементов последовательности |
|
float(число) |
Преобразует объект (например, строковое значение, целое |
2. Пример задания на решение уравнения численным
методом
Известно, что уравнение на отрезке [0; 1,5] имеет единственный корень.
Найдите его приблизительное значение с точностью не менее 0,00001 и запишите
в ответе найденное значение ровно с пятью значащими цифрами после запятой.
Программа
на языке Python:
from math
import cos, exp # подключить функции cos, exp
def
f(x): # это функция f(x)
return
0.01*exp(x) — cos(3*x)
a, b =
0, 1.5 # границыотрезка
while b-a
> 1e-6: # пока ширина отрезка >= 10^(-6)
c = (a +
b) / 2 # середина отрезка
if
f(a)*f(c) <= 0: # сдвигаем правую или левую границу
b =
c
else: a =
c
# вывод с 5
знаками в дробной части
print(
«{:.5f}».format((a + b) / 2) )
Ответ:
0.51800
3. Пример
задания на перебор целых чисел. Разбиение числа на цифры
Назовём натуральное четырёхзначное число N
(1000 £N£
9999) счастливым, если суммы двух его первых и двух последних цифр
различаются не более, чем на 3. Найдите количество таких чисел.
Программа на языке Python
count = 0
for n in
range(1000, 10000):
d0 = n %
10; n //= 10
d1 = n %
10; n //= 10
d2 = n %
10
d3 = n //
10
if
abs(d3+d2-d1-d0) <= 3:
count
+= 1
print(count)
Поскольку
заданный отрезок [1000; 9999] содержит всего 9000 чисел, можно решать задачу
простым перебором. Для этого сначала нужно разбить число на цифры с помощью
операций деления нацело и остатка от деления; цифры помещаем в переменные d0,
d1, d2, d3. Затем проверяем «счастливость» числа: число счастливое при
выполнении условияв этом случае увеличиваем счётчик найденных счастливых чисел.
Ответ:
4071.
4. Пример
задания на перебор целых чисел. Проверка делимости
Рассматривается
множество целых чисел, принадлежащих отрезку [1033;
7737], которые делятся на 5 и не делятся на 11, 17, 19 и 23. Найдите
количество таких чисел и максимальное из них. В ответе запишите два числа
через пробел: сначала количество, затем максимальное число.
Программа на языке Python
count = 0
maxGood = 0
for n in
range(1033, 7737+1):
if (n % 5
== 0) and (n % 11 != 0) and
(n %
17 != 0) and (n % 19 != 0) and (n % 23 != 0):
maxGood
= n
count += 1
print(count,
maxGood)
Поскольку
заданный отрезок [1033; 7737] содержит не так много чисел, можно решать задачу
простым перебором. Условие будем понимать так: интересующие нас числа делятся
на 5 и не делятся ни на одно из чисел 11, 17, 19 и 23. Нам выгоднее перебирать
числа в порядке возрастания, тогда последнее найдённое число – это и есть искомое
максимальное подходящее число (если требуется найти наименьшее подходящее
число, удобнее перебирать числа в порядке убывания)
Ответ:
1040 7730
Напишите программу, которая ищет среди целых
чисел, принадлежащих числовому отрезку [194455;
194500], числа, имеющие ровно 4 различных делителя. Выведите эти четыре
делителя для каждого найденного числа в порядке возрастания.
ПрограмманаязыкеPython
for n in
range(194455, 194500+1):
divs = []
for d in
range(1,n+1):
if n %
d == 0:
divs.append(d)
if
len(divs) == 4:
print(
*divs )
При
написании программы на языке Python можно поступить так
for для
всех чисел n в интервале:
divs =
массив всех делителей n
if
len(divs) == 4:
вывести
массив делителей
5. Пример
задания на работу с простыми числами
Напишите программу, которая ищет среди целых
чисел, принадлежащих числовому отрезку [3532000;
3532160], простые числа. Выведите все найденные простые числа в порядке
возрастания, слева от каждого числа выведите его номер по порядку.
ПрограмманаязыкеPython
from
math import sqrt
count
= 0
for
n in range(3532000, 3532160+1):
prime = True
for d in range(2, round(sqrt(n))):
if n % d == 0:
prime = False
break
ifprime:
count
+= 1
print(
count, n )
6. Пример
задания на работу с символьными строками
В текстовом файле k7.txt
находится цепочка из символов латинского алфавита A, B, C, D, E. Найдите
количество цепочек длины 3, удовлетворяющих следующим условиям:
·
1-й символ – один из символов B, C или D;
·
2-й символ – один из символов B, D, E, который не
совпадает с первым;
·
3-й символ – один из символов B, C, E, который не
совпадает со вторым.
Программанаязыке
Python
s =
open(‘k7.txt’).read()
count = 0
for i in
range(len(s)-2):
if s[i]
in ‘BCD’ and s[i+1] in ‘BDE’
and
s[i+2] in ‘BCE’ and s[i]!=s[i+1]
and
s[i+1]!=s[i+2]:
count
+= 1
print(count)
Решение:
1)
Считываем из файла и перебираем символы.
2)
Перебираем все тройки символов. Примем,
что переменная i будет хранить номер первого элемента в тройке, то есть, будем
рассматривать тройки (s[i], s[i+1], s[i+2]).
3)
Организуем цикл который перебирает
значения i от 1 до len(s)-2
for i in
range(len(s)-2):
…
4) Проверяем
символы в каждой тройке на соответствие условию. Проверка принадлежности
символов набору аналогична заданию 1. Дополнительно необходимо указать условия
неравенства символов, указанных в условии задачи. Если условия выполняются, то
к переменной количества прибавляется единица.
7. Пример задания на
вычисление значения функции от двух переменных
С помощью редактора
электронных таблиц создайте таблицу вещественных значений выражения для следующих вещественных
значений x и y:
x = 5,5; 6,0; …; 8,5; y
= 10,0; 10,3; …; 13,0.
Вычислите сумму
получившихся значений и запишите её целую часть в ответе.
Для выполнения этого
заданий также можно написать программу.
Решение:
1)
Чтобы написать программу, нужно
использовать вложенный цикл: в одном цикле будем перебирать значения x,
а во втором (вложенном) – значения y; учитывая, что цикл с переменной (for
… in …)
работает только с целыми последовательностями чисел, придётся использовать
циклы с условием:
s =
0 # это неправильная программа
x =
5.5 # это неправильная программа
while x
<= 8.5: # это неправильная программа
y = 10
while y
<= 13:
#
print(x, y) # отладочная печать, см. обсуждение ниже
s +=
2*x**3/(y+1)
y +=
0.3
x += 0.5
print( s )
сумма значений функции накапливается в
переменной s
2)
однако эта программа выводит неверный
ответ.
3)
Дело в том, что вещественные числа,
которые нельзя представить в виде суммы целых (в том числе и отрицательных)
степеней числа 2, в двоичной системе счисления представляют собой бесконечную
дробь и поэтому не могут быть точно записаны в памяти двоичного компьютера; при
выполнении вычислений с такими числами ошибка накапливается, и к последнему
шагу (это можно проверить с помощью отладочной печати) значение y равно
не 12,7, а чуть больше:
12.700000000000006
из-за
этого следующее значение, равное 13,000000000000006, уже больше, чем 13, и не
удовлетворяет условию работы цикла; таким образом, на каждом шаге цикла по x
мы теряем одно значение y, и соответствующее значение функции не
включается в сумму.
4)
с переменной x подобных проблем
нет, так как шаг изменения x равен 0,5 = 2–1
5)
исправить ситуацию можно так: организовать
перебор только целых значений, используя вспомогательные целочисленные
переменные x10 = x×
10 и y10
= y×
10:
s
= 0
for
x10 in range(55, 86, 5):
for y10 in range(100, 131, 3):
s
+= 2*(x10/10)**3/(y10/10+1)
print(s)
8. Пример задания на
вычисление значения рекурсивной функции
Определите
наименьшее значение n, при котором сумма чисел, которые будут выведены при
вызове F(n), будет больше 500000. Запишите в ответе сначала найденное значение
n, а затем через пробел – соответствующую сумму выведенных чисел.
def F( n ):
print(2*n)
if n > 1:
print(n-5)
F(n-1)
F(n-2)
Решение:
Первое,
что может прийти в голову – вызывать приведённую процедуру при разных значениях
параметра и увеличивать это значение до тех пор, пока сумма выведенных чисел не
превысит заданное значение 500000; это тупиковый подход, поскольку чисел очень
много и сложение займет очень много времени при низкой вероятности правильного
ответа
Можно
попробовать изменить программу так, чтобы сумма выводимых чисел считалась
автоматически: добавим в программу глобальную переменную s
и будем увеличивать её при выводе каждого числа на значение этого числа; при
этом для ускорения (значительного!) работы программы сразу закомментируем вывод
чисел на экран:
def
F( n ):
global s # если не объявить s глобальной – ошибка!
#
print(2*n)
s += 2*n
if n >
1:
#
print(n-5)
s += n — 5
F(n-1)
F(n-2)
Дальше
можно написать такую программу и запускать её при различных значениях
переменной n:
n
= 15
s
= 0
F(n)
print(
n, s )
Увеличивая
каждый раз значение n
на 1, мы в конце концов найдём первое (минимальное) значение n,
при котором сумма чисел, которые будут выведены при вызове F(n),
будет больше 500000 – это F(24) = 531864
Ответ:
24 531864.
9. Пример задания на
оптимизацию
На покупку мебели выделено 500 тыс. рублей.
Стоимость одного комплекта составляет 18 тыс. рублей. Запишите наборы
вариантов покупки максимального количества комплектов мебели, при условии,
что производитель М продает мебель упаковками по 6 комплектов в упаковке, а
производитель N – по 4 комплекта в упаковке.
Запишите в ответ пары чисел: количество упаковок
производителя М далее через пробел количество упаковок производителя N.
Каждую пару записывайте с новой строки. Пары должны быть отсортированы по
возрастанию значений в первом столбце.
Решение:
В
простейшем варианте можно просто вывести на экран все варианты сочетаний a
и b с соответствующими значениями K,
в конце программы вывести макcимальное
значение K; затем вручную найти все строки, где значение K
равно максимальному.
S0
= 500000 # доступная сумма
cost1
= 18000 # стоимость одного комплекта
packM
= 6 # количество комплектов в упаковке M
packN
= 4 # количество комплектов в упаковке N
# максимальное значение a
aMax = int(S0 /
(packM*cost1))
#
поиск максимального K по всем вариантам
maxK = 0
for a in
range(aMax+1):
Sb = S0 —
a*packM*cost1 # сумманазакупкуу N
b =
int(Sb / (packN*cost1))
K =
packM*a + packN*b # общее количество
print(a, b,
K)
if K >
maxK:
maxK = K
# новыймаксимум
print(maxK,
maxK*cost1)
3. Сравнение
эффективности программ, написанных на языках Pascal, C и Python
Сравним
программы, написанные на языках Pascal,
C
и Python
по таким критериям, как время работы и используемая память. Для примера возьмем
линейные программы, программы с циклами и программы с рекурсивными функциями.
Задача
1:дано натуральное число.
Выведите его последнюю цифру.
|
Pascal |
C |
Python |
|
var a: integer; begin readln(a); writeln(a end. |
#include main() { int x; } |
x=int(input()) print(x%10) |
|
Время Используемая |
Время работы: Используемая |
Время Используемая 360448 бит |
Как видно из таблицы, при реализации линейных
алгоритмов программа на Pythonпроигрывает во времени реализации и используемой
памяти программам на Pascalи C.
Задача2:подсчитайте количество натуральных
делителей числа x (включая
1 и само число;x2
109).
|
Pascal |
C |
Python |
|
var x, i, k: longint; begin readln(x); k:=0; for i:=1 to x do begin if (x mod i =0) then inc(k); end; writeln(k); end. |
#include #include main() { int x, i, k; scanf(«%i», k=0; for (i=1; i<=x; i++) if (x % i ==0) { k=k+1; } } printf(«%i», } |
x=int(input()) k=0 for i in range(1,x+1): if x%i==0: k+=1 print(k) |
|
Время Используемая |
Время работы: Используемая |
Время Используемая 376832 бит |
Из-за того, что значение xможет быть достаточно большим, все написанные программы не проходят все
тесты. Последние два теста не выполняются из-за того, что превышено
максимальное время работы (рис. 1).
Рис. 1. Результаты
прохождения тестов
Поэтому простым перебором данную задачу решать
нельзя. Повысим эффективность программы, идея состоит в
том, чтобы для определения количества делителей числа N
перебирать только числа до ;
если число q целое, его нужно
добавить в список делителей, а все остальные делители – парные, то есть если a
– делитель N, то b
= N
/ a
– тоже делитель N.
Таким
образом, циклом пробегаемся от 1 до (корня X)-1, и проверяем на делимость, если
делится, то увеличиваем счетчик. После цикла удваиваем наш счетчик, так как
любое число если имеет делитель до корня этого числа, то он имеет ещё один
делитель после корня этого числа. Проверяем отдельным if-ом случай для корня X,
если делится нацело, то увеличиваем на один и выводим наш счетчик, иначе просто
выводим счетчик.
|
Pascal |
C |
Python |
|
var x, i, k: longint; begin readln(x); k:=0; for i:=1 to x do begin if (x mod i =0) then inc(k); end; writeln(k); end. |
#include #include main() { int x, i, k,q; double fp,ip; scanf(«%i», k=0; if (x%2==0) { q=trunc(sqrt(x)); } else { q=trunc(sqrt(x))-1; } for (i=1; i<=q; i++) if (x % i ==0) { k=k+1; } } k=k*2; fp = modf(sqrt(x) , if(fp==0) { k=k+1; } printf(«%i», } |
import math x=int(input()) if(x%2==0): q=math.trunc(math.sqrt(x)) else: q=math.trunc(math.sqrt(x))—1 k=0 for i inrange(1,q+1): if(x%i==0): k=k+1 k=k*2 if(math.sqrt(x)%1==0): k=k+1 print(k) |
|
Время Используемая |
Время работы: Используемая |
Время Используемая 380928 бит |
Заключение
Девяносто
процентов задач компьютерного ЕГЭ по информатике решается с помощью программирования.
В
процессе выполнения работы были решены следующие задачи:
— рассмотрены
основы языка программирования Python;
— выделены
типы задач компьютерного ЕГЭ по информатике. Задачи решены средствами языка
программирования Python;
— проанализирована
эффективность программ, написанных на языках Pascal,
C
и Python.
Список литературы
1.
Сайт К. Ю. Полякова. Методические материалы и
программное обеспечение [Электронный ресурс]. Режим доступа:http://kpolyakov.spb.ru
2.
Прохоренок Н. А. Python 3. Самое
необходимое [Текст]. – Спб.: БХВ-Петербург, 2019. – 608 с.
3.
Основы Python [Электронный ресурс]. Режим доступа:
4.
Применение и основы Python [Электронный ресурс]. Режим доступа:
5.
Дистанционная подготовка к информатике [Электронный ресурс]. Режим доступа
https://informatics.mccme.ru
137) Логическая функция F задаётся выражением (x → y) → (¬x ∧ z). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| ? | ? | ? | F |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы, никаких разделителей между буквами ставить не нужно.
Разбор 2 задания ЕГЭ по информатике
2-е задание: «Таблицы истинности»
Уровень сложности — базовый,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 3 минуты.
Проверяемые элементы содержания: Умение строить таблицы истинности и логические схемы
«Игнорирование прямо указанного в условии задания требования, что заполненная таблица истинности не должна содержать одинаковых строк. Это приводит к внешне правдоподобному, но на самом деле неверному решению»
Таблицы истинности и порядок выполнения логических операций
| операция | пояснение | в программировании |
|---|---|---|
| ¬ A, A | не A (отрицание, инверсия) | not(A) |
| A ∧ B, A ⋅ B | A и B (логическое умножение, конъюнкция) | A and B |
| A ∨ B, A + B | A или B (логическое сложение, дизъюнкция) | A or B |
| A → B | импликация (следование) | A |
| A ↔ B, A ≡ B, A ∼ B | эквиваленция (эквивалентность, равносильность) | A==B (python) A=B(pascal) |
| A ⊕ B | строгая дизъюнкция | A != B (python) |
Таблица истинности операции НЕ
Таблица истинности операции И (конъюнкция)
Таблица истинности операции ИЛИ (дизъюнкция)
Таблица истинности операции Импликация (если…, то…)
Таблица истинности операции Эквивалентность (тогда и только тогда, …)
| A | B | A ⊕ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- если нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», импликация, равносильность
- логическое произведение X∙Y∙Z∙… равно 1, т.е. выражение является истинным, только тогда, когда все сомножители равны 1 (а в остальных случаях равно 0)
- логическая сумма X+Y+Z+… равна 0, т.е. выражение является ложным только тогда, когда все слагаемые равны 0 (а в остальных случаях равна 1)
О преобразованиях логических операций читайте здесь.
Решение заданий 2 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Логическая функция F задается выражением
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| . | . | . | . | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
-
Отобразим перебор всех значений использующихся в выражении переменных (всю таблицу истинности). Поскольку в выражении используются 4 переменных, то строк таблицы будет 2 4 =16:
- ✎ Способ 2. Программирование:
Язык python:
print(‘x y z w’) for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: F = (not(x) or y or z) and (x or not(z) or not(w)) if not(F): print(x, y, z, w)
Язык pascalAbc.net:
begin writeln(‘x’:7, ‘y’:7, ‘z’:7,’w’:7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not x or y or z) and (x or not z or not w)) then writeln(x:7, y:7, z:7,w:7); end.
Ответ:
- ✎ Способ 3. Логические размышления:
- Внешняя операция выражения — конъюнкция (∧). Во всех указанных строках таблицы истинности функция принимает значение 0 (ложь). Конъюнкция ложна аж в трех случаях, поэтому проверить на ложь очень затруднительно. Тогда как конъюнкция истинна (= 1) только в одном случае: когда все операнды истинны. Т.е. в нашем случае:
- Общая идея дальнейшего решения такова: поскольку внешняя операция — конъюнкция, и результат ее истинен, когда оба сомножителя в скобках будут истинны (=1), то нам необходимо сначала составить все наборы таблицы истинности для обоих сомножителей в скобках. Затем, так как конъюнкция подразумевает пересечение, необходимо сопоставить обе таблицы истинности и выбрать для каждого подходящего набора первого сомножителя подходящий (подходящие) набор (наборы) второго сомножителя. НО! так как у нас в задании известны только наборы для F = 0, то мы сопоставлять будем наборы, которые возвращают ложь. Теперь подробно.
- Разобьём исходное выражение на две части и составим таблицу истинности отдельно для двух частей.
- Для сомножителя (¬x ∨ y ∨ z):
x y z результат 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1 - Получили ложь в одном наборе, так как дизъюнкция (∨) ложна только тогда, когда ложны все операнды.
- Для сомножителя (x ∨ ¬z ∨ ¬w):
x z w результат 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 1 - Соответственно, опять получили ложь в одном наборе, когда ложны все операнды.
- Учтем, что нам нужно выбрать и «пересечь» (так как внешняя операция ∧) из всех наборов только те, которые возвращают ложь (так как по заданию известны только строки, где F = 0):
Результат: xwzy
🎦 Видео решения 169 задания К.Полякова (бескомпьютерный вариант):
📹 Видеорешение на RuTube здесь
Миша заполнял таблицу истинности функции:
но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| . | . | . | . | F |
| 1 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 0 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.
- Решим задание методом построения полной таблицы истинности.
- Посчитаем общее количество строк в таблице истинности и построим ее:
Результат: ywxz
✎ Способ 2. Программирование:
begin writeln(‘x’:7, ‘y’:7, ‘z’:7,’w’:7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not z and (x xor y)) <= not(y or w)) then writeln(x:7, y:7, z:7,w:7); end.
Сопоставив их с исходной таблицей, получим результат: ywxz
print (‘x y z w’) for x in 0,1: for y in 0,1: for z in 0,1: for w in 0,1: F=(not z and not(x==y))<=(not(y or w)) if not F: print (x,y,z,w)
Результат: ywxz
🎦 Доступно видео решения этого задания (бескомпьютерный вариант):
📹 Видеорешение на RuTube здесь
🎦 Видео (решение 2 ЕГЭ в Excel):
📹 Видеорешение на RuTube здесь
📹 Видеорешение на RuTube здесь (Программирование)
Логическая функция F задается выражением
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| . | . | . | . | F |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
Результат: cbad
🎦 (Бескомьютерный вариант) Предлагаем подробный разбор посмотреть на видео:
📹 Видеорешение на RuTube здесь
Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таб. ист-ти функции F, содержащий все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| . | . | . | . | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
✍ Решение:
-
✎ Логические размышления (бескомпьютерный вариант):
Результат: xzwy
✎ Способ 2. Программирование:
Язык pascalABC.NET:
begin writeln(‘x ‘,’y ‘,’z ‘,’w ‘); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not(not x or y or(not z and w)) then writeln(x:7,y:7,z:7,w:7); end.
🎦 (бескомпьютерный вариант) Подробное решение данного 2 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 Видеорешение на RuTube здесь
Логическая функция F задаётся выражением
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| . | . | . | . | F |
| 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 |
Результат: xwzy
🎦 Видеорешение (бескомпьютерный вариант):
📹 Видеорешение на RuTube здесь
Задания для тренировки
Каждое из логических выражений F и G содержит 5 переменных. В табл. истинности для F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1.
Сколько строк таблицы истинности для F ∨ G содержит 1 в столбце значений?
✍ Решение:
- Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из 32 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет 2 5 =32, т.е. 32 строки.
- Из этих 32 строк и для F и для G мы знаем наверняка только о 5 строках: 4 из них истинны (=1), а одна ложна (=0).
- Вопрос стоит о количестве строк = 1 для таб. истинности F ∨ G. Данная операция — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0
- В исходных таблицах для F и G мы знаем о существовании только одного 0, т.е. в остальных строках может быть 1. Т.о., и для F и для G в 31 строке могут быть единицы (32-1=31), а лишь в одной — ноль.
- Тогда для F ∨ G только в одном случае будет 0, когда и F = 0 и G = 0:
№ F G F ∨ G 1 0 0 0 2 0 1 1 … … … 1 32 … … 1 - Соответственно, истинными будут все остальные строки:
Результат: 31
Подробное объяснение данного задания смотрите на видео:
Каждое логическое выражение A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы.
Каково максимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 2 7 = 128 строк.
- В четырех из них результат равен единице, значит в остальных — 0.
- A ∨ B истинно в том случае, когда либо A = 1 либо B = 1, или и A и B = 1.
- Поскольку А = 1 только в 4 случаях, то чтобы получить максимальное количество единиц в результирующей таблице истинности (для A ∨ B), расположим все единицы т.и. для выражения A так, чтобы они были в строках, где B = 0, и наоборот, все строки, где B = 1, поставим в строки, где A = 0:
A B 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 0 0 … … - Итого получаем 8 строк.
- Если бы в задании требовалось найти минимальное количество единиц, то мы бы совместили строки со значением = 1, и получили бы значение 4.
Результат: 8
Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 6 единиц.
Каково максимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 2 8 = 256 строк.
- В шести из них результат равен единице, значит в остальных — 0.
- A ∧ B ложно в том случае, когда:
- Во всех случаях там где А=1 может стоять B=0, и тогда результат F = 0. Поскольку нам необходимо найти максимально возможное число нулей, то как раз для всех шести А=1 сопоставим B=0, и наоборот, для всех шести возможных B=1 сопоставим A=0
A B F 1 0 0 1 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0 0 … … … - Поскольку строк всего 256, то вполне возможно, что все 256 из них возвратят в результате 0
Результат: 256
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
✍ Решение:
- В первом внешняя операция (выполняется последней) — конъюнкция. Начнем рассмотрение с нее. Соответственно, проверяем по второй строке таб. ист-ти, там где F = 1, так как в таком случае все аргументы должны быть истинными (см. таб. истинности для конъюнкции).
- Если мы подставим в нее все аргументы выражения, то функция действительно возвращает истину. Т.е. пункт первый подходит:
Результат: 1
Решение 2 задания ГВЭ по информатике смотрите на видео:
Дано логическое выражение, зависящее от 5 логических переменных:
(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)
Сколько существует различных наборов значений переменных, при которых выражение истинно?
✍ Решение:
- Поскольку выражение включает 5 переменных, то таб. ист-ти состоит из 2 5 = 32 строк.
- Внешней операцией (последней) является конъюнкция (логическое умножение), а внутри скобок — дизъюнкция (логическое сложение).
- Обозначим первую скобку за А, а вторую скобку за B. Получим A ∧ B.
- Найдем сколько нулей существует для таб. истинности:
Теперь рассмотрим каждый случай отдельно:
¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5 = 0
и
x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 = 0.
Результат: 2
Подробное решение задания смотрите в видеоуроке:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | F |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 |
Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x3 не совпадает с F.
✍ Решение:
- Полная таблица истинности будет иметь 2 6 = 64 строк (т.к. 6 переменных).
- 4 из них нам известны: в них x3 два раза не совпадает с F.
- Неизвестных строк:
- В неизвестных x3 может не совпадать с F, кроме того, в двух известных x3 не совпадает с F. Соответственно максимально возможное число строк с несовпадающими x3 и F, будет:
Результат: 62
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 0 | 0 | 0 | |||||
| 0 | 0 | 1 | |||||
| 1 | 1 | 1 |
Каким выражением может быть F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7
✍ Решение:
- Рассмотрим отдельно каждый пункт и найдем последнюю операцию, которая должна быть выполнена (внешнюю).
2 пункт:
3 пункт:
Результат: 4
В видеоуроке рассмотрено подробное решение 2 задания:
Логическая функция F задается выражением
(y → x) ∧ (y → z) ∧ z.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| . | . | . | F | |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 0 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 |
| 8 | 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
- Сначала необходимо рассмотреть логическую операцию, которую мы будем выполнять в последнюю очередь — это логическое И (конъюнкция) или ∧. То есть внешнюю операцию:
- Конъюнкцию легче рассматривать по тем строкам таб. ист-ти, в которых F = 1, т.е. №3, №4, и №8
- Поскольку для конъюнкции функция истинна только тогда, когда все переменные истинны, то необходимо чтобы отдельно каждая скобка была истинна ((y → x) = 1 и (y → z)=1) и переменная z тоже была истинной (=1)
- Поскольку с выражениями в скобках сложней работать, определим сначала какому столбцу соответствует z. Для этого выберем строку (№3), где F = 1, а в остальных ячейках только одна единица, остальные — нули.
№ Перем. 1 Перем. 2 Перем. 3 F 3 0 1 0 1 - Таким образом, делаем вывод, что z находится во втором столбце (отсчет ведем слева):
№ Перем. 1 Перем. 2 Перем. 3 F _ . z . F - Дальше нам необходимо рассмотреть две скобки, в которых находится операция импликации: (y → x) и (y → z). Обе эти скобки должны возвращать истину (=1). В таб. истинности для импликации, функция возвращает в результате 1 тогда, когда:
- вторая переменная (заключение) равна 1 (первая при этом может быть любой),
- вторая переменная (заключение) равна 0, а первая обязательно должна быть равна тоже 0.
- Рассмотрим скобку (y → x) и строку 4 таблицы:
№ Перем. 1 z Перем. 3 F 4 0 1 1 1 - Для этой строки только y может быть равен 0, т.к. если x = 0, тогда y=1, и скобка в результате возвратит ложь (1 → 0 = 0). Соответственно, y находится в первом столбце. А x значит должен стоять в третьем:
Результат: yzx
Детальный разбор данного задания 2 ЕГЭ по информатике предлагаем посмотреть в видео:
Теория и практика решения задания 2 ЕГЭ по информатике
Данная разработка предназначена для подготовки к ЕГЭ по информатике. В работе предлагаются теретические сведения и примеры задач к заданию 2.
Просмотр содержимого документа
«Теория и практика решения задания 2 ЕГЭ по информатике»
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа №101»
Теория и практика решения задания 2
ЕГЭ по информатике
Угулава Наталия Владимировна
Саратов, 2018
Типы задания 2
- Задания на отрезки
- Задания на множества
- Задания на поразрядную конъюнкцию
- Задания на условие делимости
Разбор 2 задания ЕГЭ 2018 по информатике и ИКТ из демоверсии.
Это задание базового уровня сложности.
Примерное время выполнения задания 3 минуты.
— умение строить таблицы истинности и логические схемы
— умение строить таблицы истинности и логические схемы
— умение строить таблицы истинности и логические схемы
Проверяемые элементы содержания:
— умение строить таблицы истинности и логические схемы.
Элементы содержания, проверяемые на ЕГЭ:
— высказывания, — логические операции, — кванторы, — истинность высказывания.
ТАБЛИЦЫ ИСТИННОСТИ И ПОРЯДОК
ВЫПОЛНЕНИЯ ЛОГИЧЕСКИХ ОПЕРАЦИЙ
Для логических операций приняты следующие обозначения :
не A (отрицание, инверсия)
A и B (логическое умножение, конъюнкция)
A или B (логическое сложение, дизъюнкция)
эквиваленция (эквивалентность, равносильность)
сложение по модулю 2 (XOR)
Отрицание (НЕ):
Таблица истинности операции НЕ
Конъюнкция (И):
Таблица истинности операции И (конъюнкция)
Дизъюнкция (ИЛИ):
Таблица истинности операции ИЛИ (дизъюнкция)
Импликация (если … , то … ):
Таблица истинности операции Импликация (если … , то … )
Логическая функция F задаётся выражением ¬ x / y / ( ¬ z / w ). На рисунке приведён фрагмент таблицы истинности функции F , содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
Эквивалентность (тогда и только тогда, … ):
Таблица истинности операции Эквивалентность (тогда и только тогда, … )
Сложение по модулю 2 (XOR):
Порядок выполнения операций:
- если в выражении нет скобок, сначала выполняются все операции « НЕ » , затем – « И » , затем – « ИЛИ » , импликация, равносильность
Решение заданий 2 ЕГЭ по информатике
Задание 2 ЕГЭ по информатике 2017 ФИПИ вариант 6 (Крылов С.С., Чуркина Т.Е.):
Логическая функция F задается выражением (y → x) ∧ (y → z) ∧ z . Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x , y , z .
В ответе напишите буквы x , y , z в том порядке, в котором идут соответствующие им столбцы.
- За основу необходимо взять логическую операцию, которую мы будем выполнять в последнюю очередь — это логическое И (конъюнкция) или ∧
- Конъюнкцию легче рассматривать по тем строкам таблицы, там где функция F = 1
- Поскольку для конъюнкции функция истинна только тогда, когда все переменные истинны, то необходимо чтобы отдельно каждая скобка была истинна ((y → x) = 1 и (y → z)=1) и переменная z тоже была истинной (1)
- Поскольку со скобками сложней работать, определим сначала какому столбцу соответствует z . Для этого выберем строку, где F=1 и в остальных ячейках только одна единица, а остальные нули:
- Таким образом, из этой строки делаем вывод, что z находится во втором столбце (отсчет ведем слева):
- Рассмотрим скобку (y→x) и строку таблицы:
- Для этой строки только y может быть 0 , т.к. если x = 0 , тогда y=1 , и скобка в результате возвратит ложь ( 1→0 = 0 ). Соответственно, y находится в первом столбце. А x значит в третьем:
- Для этой строки только y может быть 0 , т.к. если x = 0 , тогда y=1 , и скобка в результате возвратит ложь ( 1→0 = 0 ). Соответственно, y находится в первом столбце. А x значит в третьем:
Результат: yzx
Задание 2 ЕГЭ по информатике 2017 ФИПИ вариант 11 (Крылов С.С., Чуркина Т.Е.): Каждое из логических выражений F и G содержит 5 переменных. В таблицах истинности выражений F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1 . Сколько строк таблицы истинности для выражения F ∨ G содержит 1 в столбце значений?
- Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из 32 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет 25=32 , т.е. 32 строки.
- Из этих 32 строк для каждого выражения (и F и G) мы знаем наверняка только о 5 строках: в 4 из них 1, а в одной — 0.
- В исходных таблицах для каждого выражения F и G мы знаем о существовании только одного 0, т.е. в остальных строках может быть 1. Т.о. для каждого выражения и F и G в 31 строке могут быть единицы ( 32-1=31 ), а лишь в одной — ноль.
- Тогда для выражения F∨ G только в одном случае будет 0, когда и F=0 и G = 0:
- Вопрос стоит о количестве строк = 1 для таблицы истинности выражения F∨ G . Данной выражение — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0
Результат: 31
Решение задачи на отрезки
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
¬ x / y / (¬ z / w )
Дизъюнкция (логическое сложение) истинна тогда и только тогда, когда истинно хотя бы одно высказывание.
Следовательно, для того чтобы вся функция была ложна, переменной х должен соответствовать тот столбец, в котором стоит значение 1 (так как, ¬ x превращает 1 в 0) , а переменной y столбец со значениями 0 .
Таким образом: — переменной x соответствует столбец с переменной 1 , — переменной y соответствует столбец с переменной 4 .
Решение задачи на отрезки
Конъюнкция (логическое умножение) истинна тогда и только тогда, когда истинны все высказывания (ложна — если ложно хотя бы одно высказывание). Конъюнкция ¬ z / w в нашем выражении будет истинна только если z=0, w=1.
Посмотрим на вторую строчку таблицы, где переменная 2 равна 1, а переменная 3 равна 0.
Решение задачи
Так как ¬ z / w должна равняться 0, то z = 1 и w = 0 (в противном случае произведение будет равно 1)
Таким образом: — переменной z соответствует столбец с переменной 2 (2 столбец), — переменной w соответствует столбец с переменной 3 (3 столбец).
Решение варианта ИН2010401 на Python
Рассмотрим решение некоторых задач из варианта ИН2010401 (Статград 2021 № 4).
Задача 2
Логическая функция F задаётся выражением ¬((?∨?)→(?∧?))∧(?→?) . Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F . Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w .
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
| . | . | . | . | F |
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | ||
| 1 | 1 | 1 |
В ответе напишите буквы x, y, z, w ; в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y , зависящее от двух переменных x и y , и фрагмент таблицы истинности:
| Переменная 1 | Переменная 1 | Функция |
| . | . | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y , а второму столбцу соответствует переменная x . В ответе нужно написать: yx .
Решение. Поскольку пока не известно, в каком столбце заголовка стоит какая переменная, дадим им произвольные имена по порядку, например a, b, c, d . После чего подставим их в функцию F и отобразим только строки, соответствующие значению F=1 . Рассмотрим два варианта решения:
Результат работы программы:
Ответ: zxy
Задача 5
Алгоритм получает на вход натуральное число ?>1 и строит по нему новое число ? следующим образом:
- Строится двоичная запись числа ?.
- Подсчитывается количество нулей и единиц в полученной записи. Если их количество одинаково, в конец записи добавляется её последняя цифра. В противном случае в конец записи добавляется та цифра, которая встречается реже.
- Шаг 2 повторяется ещё два раза.
- Результат переводится в десятичную систему счисления.
Пример. Дано число ?=19. Алгоритм работает следующим образом:
- Двоичная запись числа N: 10011.
- В полученной записи нулей меньше, чем единиц, в конец записи добавляется 0. Новая запись: 100110.
- В текущей записи нулей и единиц поровну, в конец записывается последняя цифра, это 0. Получается 1001100. В этой записи единиц меньше, в конец добавляется 1: 10011001.
- Результат работы алгоритма ?=153.
При каком наименьшем исходном числе ?>99 в результате работы алгоритма получится число, кратное 4?
Ответ: 103
Задание 6
Определите, при каком наименьшем введённом значении переменной ? программа выведет число 11. Для Вашего удобства программа представлена на двух языках программирования.
Ответ: 191
Задание 7
В информационной системе хранятся изображения размером 1024×768 пикселей. Методы сжатия изображений не используются. Каждое изображение дополняется служебной информацией, которая занимает 1280 Кбайт. Для хранения 2048 изображений потребовалось 4 Гбайт. Сколько цветов использовано в палитре каждого изображения?
Ответ: 256
Задача 8
Вероника составляет 3-буквенные коды из букв В,Е,Р,О,Н,И,К,А, причём буква В должна входить в код ровно один раз. Все полученные коды Вероника записала в алфавитном порядке и пронумеровала. Начало списка выглядит так:
- ААВ
- АВА
- АВЕ
- …
На каком месте будет записан первый код, не содержащий ни одной буквы А?
Ответ: 23
Задание 11
Каждый объект, зарегистрированный в информационной системе, получает уникальный код из 14 символов, каждый из которых может быть одной из 26 заглавных латинских букв или одной из 10 цифр. Для представления кода используют посимвольное кодирование, все символы кодируют одинаковым минимально возможным количеством битов, а для кода в целом выделяется минимально возможное целое количество байтов. Кроме того, для каждого объекта в системе выделено 79 байт для хранения содержательной информации. Сколько байтов потребуется для хранения данных (код и содержательная информация) о 30 объектах? В ответе запишите только целое число – количество байтов.
Ответ: 2700
Задание 14
Значение выражения 729 7 +3 16 –18 записали в системе счисления с основанием 9. Сколько раз в этой записи встречается цифра 0?
Ответ: 14
Задание 15
Для какого наименьшего натурального числа ? формула ДЕЛ(?,45)∧(ДЕЛ(750,?)→(¬ДЕЛ(. )→¬ДЕЛ(120,?))) тождественно истинна, то есть принимает значение 1 при любом натуральном ??
Ответ: 90
Задача 16
Обозначим через . (. ) остаток от деления натурального числа ? на натуральное число ?. Алгоритм вычисления значения функции ?(?), где ? – целое неотрицательное число, задан следующими соотношениями:
- ?(0)=0;
- ?(?)=?(?/3), если ?>0 и при этом . (?,3)=0;
- ?(?)=. (?,3)+?(?–. (?,3)), если . (?,3)>0.
Назовите минимальное значение ?, для которого ?(?)=11.
Ответ: 485
Задача 17
Назовём натуральное число подходящим, если у него ровно 3 различных простых делителя. Например, число 180 подходящее (его простые делители – 2, 3 и 5), а число 12 – нет (у него только два различных простых делителя). Определите количество подходящих чисел, принадлежащих отрезку [10001;50000], а также наименьшее из таких чисел. В ответе запишите два целых числа: сначала количество, затем наименьшее число.
Ответ: 15652 10002
Задача 22
Ниже записана программа, которая вводит натуральное число ?, выполняет преобразования, а затем выводит два числа. Укажите наименьшее возможное значение ?, при вводе которого программа выведет числа 3 и 10.
Ответ: 874
Задача 23
Исполнитель преобразует число на экране. У исполнителя есть три команды, которым присвоены номера:
- Прибавить 1
- Умножить на 2
- Умножить на 3
Первая команда увеличивает число на экране на 1, вторая умножает его на 2, третья – умножает на 3. Программа для исполнителя – это последовательность команд.
Сколько существует программ, которые преобразуют исходное число 2 в число 36, и при этом траектория вычислений содержит число 12 и не содержит числа 30?
Ответ: 60
Задача 24
Текстовый файл содержит строки различной длины. Общий объём файла не превышает 1 Мбайт. Строки содержат только заглавные буквы латинского алфавита (. …?).
Необходимо найти строку, содержащую наименьшее количество букв ? (если таких строк несколько, надо взять ту, которая находится в файле раньше), и определить, какая буква встречается в этой строке чаще всего. Если таких букв несколько, надо взять ту, которая позже стоит в алфавите.
Пример. Исходный файл:
В этом примере в первой строке две буквы G, во второй и третьей – по одной. Берём вторую строку, т. к. она находится в файле раньше. В этой строке чаще других встречаются буквы A и B (по два раза), выбираем букву B, т. к. она позже стоит в алфавите. В ответе для этого примера надо записать B.
Ответ: T
Задача 25
Найдите все натуральные числа, принадлежащие отрезку [35000000;40000000], у которых ровно пять различных нечётных делителей (количество чётных делителей может быть любым). В ответе перечислите найденные числа в порядке возрастания.
Идея. Нас интересуют числа, являющиеся четвертой степенью простого числа, возможно умноженные на некоторую степень двойки.
Ответ: 35819648; 38950081; 39037448; 39337984
Задача 26
В текстовом файле записан набор натуральных чисел, не превышающих 10 9 . Гарантируется, что все числа различны. Необходимо определить, сколько в наборе таких пар чётных чисел, что их среднее арифметическое тоже присутствует в файле, и чему равно наибольшее из средних арифметических таких пар.
Входные данные Первая строка входного файла содержит целое число ? – общее количество чисел в наборе. Каждая из следующих ? строк содержит одно число.
Пример входного файла
В данном случае есть две подходящие пары: 8 и 14 (среднее арифметическое 11), 14 и 2 (среднее арифметическое 8). В ответе надо записать числа 2 и 11. В ответе запишите два целых числа: сначала количество пар, затем наибольшее среднее арифметическое.
Ответ: 15; 976339247
Задача 27
В текстовом файле записан набор натуральных чисел, не превышающих 10 8 . Гарантируется, что все числа различны. Из набора нужно выбрать три числа, сумма которых делится на 3. Какую наибольшую сумму можно при этом получить?
Входные данные Первая строка входного файла содержит целое число ? – общее количество чисел в наборе. Каждая из следующих ? строк содержит одно число.
В данном случае есть две подходящие тройки: 5,14,11 (сумма 30) и 8,14,11 (сумма 33). В ответе надо записать число 33.
Вам даны два входных файла (? и ?), каждый из которых имеет описанную выше структуру. В ответе укажите два числа: сначала значение искомой суммы для файла ?, затем для файла ?.
Теперь ЕГЭ по информатике выпускники сдают в компьютерной форме, а это значит, что и в процессе подготовки их ждет немало изменений.
Как связаны программирование и подготовка к ЕГЭ по информатике
Некоторые задания из ЕГЭ по информатике 2022 (номера 8, 11, 19, 20, 21, 24, 25 и 27) требуют знаний одного из языков программирования и минимальных навыков работы с ним. В первых из перечисленных заданий проверяется умение выпускников понимать и анализировать текст программы, в 25 задаче нужно самостоятельно написать фрагмент программы, в 27 — законченную программу.
В формулировках заданий перечислены следующие языки программирования: Basic, Pascal, C/C++, Алгоритмический язык, Python, Естественный язык. Выбор языка программирования не влияет на оценку, несмотря на то, что на каком-то из них программа может получиться длиннее, а на другом короче. Эксперты в области подготовки к ЕГЭ по информатике говорят, что за все время их деятельности на экзамене еще ни разу не попалось задание, которое нельзя было бы выполнить, например, с использованием Basic.
Как решать задачи на программирование при подготовке
Прежде чем приступать к решению задач, нужно разобраться с теоретической частью. Для того, чтобы успешно выполнять задания и получить высокие баллы, вам необходимо разбираться в:
- синтаксисе используемого языка программирования,
- алгоритмических конструкциях,
- работе со строками и символами,
- работе с массивами,
- базовых алгоритмах программ,
- составных типах данных.
Приступая к практической части подготовки, в первую очередь решите демонстрационную версию экзамена (можно даже на специальной онлайн-платформе, где КИМ будет выглядеть ровно так, как компьютерная версия самого ЕГЭ) и посмотрите, какие задания вам даются легко, какие вызывают небольшие трудности, а с какими вы совсем не можете справиться. Такое распределение задач по категориям поможет вам лучше организовать подготовку, расставить приоритеты и повысить эффективность практики.
После этого обязательно изучите критерии и постарайтесь понять, что именно от вас хотят увидеть проверяющие, на что нужно обратить внимание при выполнении заданий и какие условия нужно соблюдать.
И только после этого начинайте практиковаться. Лучше делать это каждый день, а также привлечь к подготовке человека, который в этом хорошо разбирается — репетитора или куратора онлайн-школы. Он поможет вам прояснить непонятные моменты и научит находить ошибки.
Какой язык программирования выбрать для сдачи ЕГЭ по информатике в 2022 году
В большинстве школ языкам программирования уделяется не так много времени, а где-то о них и не упоминают, поэтому ученикам приходится брать на себя целых две сложных и важных задачи:
- выбрать язык(и) программирования для ЕГЭ по информатике,
- научиться с ними работать.
Сейчас посмотрим, какие языки программирования выпускники выбирают чаще всего и какие из них лучше для подготовки к ЕГЭ по информатике 2022.
- Pascal
Даже если в вашей школе информатика преподавалась “для галочки”, об этом языке вы уж точно слышали. Несмотря на то, что Паскаль является устаревшим языком программирования и не используется разработчиками в крупных компаниях, для ЕГЭ он вполне подойдет.
С использованием Паскаля можно решить все базовые задания на программирование, хотя выполнение более сложных задач, скорее всего, получится не совсем удобным и весьма громоздким.
- C++
Этот язык пользуется наибольшей популярностью среди выпускников, несмотря на то, что написание программ на нем — не самое быстрое. Если у вас медленный темп работы, то в целях экономии времени на ЕГЭ по информатике 2022 лучше выбрать другой язык программирования, тем более, что в большинстве заданий проверяются ответы, а не написание программ.
- Python
Питон совсем недавно вошел в список разрешенных языков программирования для ЕГЭ по информатике, поэтому для многих (в том числе проверяющих) он покажется непривычным. Однако этот язык почти идеально подходит под формат экзамена: он быстрый, на нем можно решить 18 заданий из 27, он имеет простой синтаксис.
- Другие варианты
Вы можете выбрать другой язык программирования, например, C или Basic, которые также рекомендуют многие преподаватели. Однако здесь могут возникнуть две сложности: это усложнит подготовку, так как в большинстве методических материалов по подготовке используются первые три языка из нашего списка, а также может случиться такое, что эксперт, проверяющий работу, не будет знать выбранный вами язык (это, конечно, не ваша проблема, но неприятные ситуации могут возникнуть).
Итог
При выборе языка программирования для ЕГЭ по информатике 2022 мы советуем руководствоваться именно легкостью, распространенностью языка и быстротой использования. Самое важное — чтобы он помог вам решить задания из КИМа, а все остальное уже второстепенно.