Мотивация
Если вы откроете список всех задач по Планиметрии №16, которые встречались на ЕГЭ по Профилю за всё время его существования, вы удивитесь тому, как сильно она усложнилась, и на сегодняшний день на этой позиции стоит достаточно содержательная геометрическая задача с действительно порой навороченными конструкциями, которые вводят в ступор, начинающих её решать школьников. Всё это еще приправлено тем, что из года в год, на фоне эволюции этой задачи, или из-за этого, процент учеников школ решающих геометрию в ЕГЭ весьма низкий:
Хуже решается только задача по Стереометрии №13. Отсюда комом накатывается мнение, что «№16 решать дано не всем», «лучше меньше баллов, зато точно решу №12», «я нарисовал треугольник, а что делать не вижу дальше» и куча других деструктивных мыслей, которые точно не помогают вам в подготовке к ЕГЭ. По факту, из моего личного опыта, задачи по Геометрии что в ЕГЭ, что в ОГЭ, очень плохо решаются в силу отсутствия какого-то четкого алгоритма действий(как это есть в параметрах, уравнениях и неравенствах, финансовой математике), которые бы точно приводили к конкретным результатам — делай раз, делай два…
Всё правда, нам нужен не просто набор теории и формул с фактами, этого недостаточно. Нам нужна практика, опыт решения задач и стараться чувствовать эту логику при решении задач. И тут я не открою странных лайфхаков, секретных методик, будистких тайн и введьминых приколов. Будем честны, нужно время, конкретная структура и понятный набор ресурсов.
В рамках этой статьи я вложу весь свой преподавательский опыт и свои знания, как человека, который не перестаёт учиться и осваивать новые знания, чтобы помочь вам забрать на экзамене баллы за одну из самых сложных задач.
Начинаем с азов
Давайте представим, что ваша задача поднять с нуля ваши знания по геометрии на приемлемый для ЕГЭ и выше уровень. Нам не обойтись без основ и фундамента, с которым вы встречались со времен 7 класса. Что делаем? Берем учебник Атанасяна, и тут у многих расширятся зрачки и волна ужаса пройдет ледяной лавиной от бровей до мизинцев. На самом деле прошу не пугаться, нам нужен какой-то подробный школьный учебник, в котором будет изложена вся структурированная теория, необходимая и та, что мы можем применять для решения задач. Если у вас есть альтернативный — без проблем, используйте его.
Схема работы следующая: открываем со второй главы и для каждого параграфа нас будут интересовать все доказанные теоремы, а вернее не просто сухой факт, а то откуда он берется и как его доказать. Сначала пробуем сами как-то к этому придти, если не получается, то смотрим на то, какое доказательство приводит автор.
Важно! Мы не сидим тупо перед книжкой, развивая геморрой, мы берем ручку и листочек, и сидим выписываем, конспектируем и пробуем доказывать все указанные теоремы. А после просматриваем задачи в конце, решать все не нужно, только те, которые вам покажутся реально сложными и с наскока не понятными как решать.
Что нам это даст? Мы учимся воспринимать конструкции, понимать логику построения доказательства в геометрии того или иного утверждения, а также мы сами того не подозревая запоминаем всю нужную информацию, которую мы будем применять позже для решения задач №16 на ЕГЭ!
Подумайте сами, математика — это про структуру, логику, и сколько вам нужно времени чтобы зазубрить строчку предложения? 5 ? 10 минут? А на сколько вас хватит держать это всё в голове? Вы забудете при первой же возможности. Нам нужна логика доказательства этого факта, благодаря которой наш мозг будет обучаться новому подходу в мышлении и все что связанно с геометрическими фактами вы запомните намного лучше, если будете реально пытаться доказать простейшие факты из учебника. А также на самом экзамене, уровень стресса которого пробивает все возможные значения, вы будете 100% уверены, что используемый вами факт при решении задачи не вымысел возбужденного воображения.
Сколько нужно на это времени? Если идти со скоростью две главы в день, то около недели.
Как закрепить полученный результат на практике?
Теперь, друг, ты — мощь и сила! Но без практики нам не обойтись поэтому все полученные навыки начинаем применять для решения конкретных задач. Тут нам поможет книга Гордина «Планиметрия».
Схема работы с ней следующая: можете кратко просмотреть задачи данные в качестве разобранных в начале каждой главы, попробовать решить самостоятельно и потом сравнить с данным решением. Далее, переходим на отработку задач первого уровня, тут прям всё решать нет большого смысла, хоть и страшно полезно, но в режиме ограниченного времени сразу смотрим на задачи второго уровня и пытаемся прорешать максимальное количество в каждом разделе. После того как разобрались со вторым уровнем стараемся решить задачи из третьего, но тут уже можно прыгать с задачи на задачу, так как местами именно в третий уровень уже включены задачи чуть сложнее ЕГЭ. И ещё: главы про симметрии, вектора, координаты и повороты можете пропускать, если чувствуете нехватку сил, времени и вдохновения.
Кабанеем
Если со всем предыдущими пунктами справились — Glückwünsch! Поздравляю! У нас как раз есть время чтобы порешать сложные задачи и разобрать другие методы для планиметрии Прасолова. Это поможет вам разобраться с самыми разнообразными методами, которые могут повстречаться вам при решении геометрических задач. Плюс, будет реально посмотреть эту книгу и книгу Ткачука при подготовке уже к ДВИ МГУ, но это совсем другая история))
Уровень: Убийца планиметрии
На этом мы выходим на финальный этап и раз наша цель именно ЕГЭ, то дальше делаем следующее:
Открываем все задачи ЕГЭ с 2014 года и планомерно их прорешиваем. Такая процедура даст нам понимание того, что такое реальные ЕГЭшные задачи, а не Статград, от которого порой хочется сбежать. Плюс нарабатывается навык решения задачи за ограниченное время и правильное оформление всего что вы нарешали.
На этом всё?
На этом этапе я всегда даю себе время на подумать, потому что хочется что-то ещё добавить и впихнуть максимальное количество пользы. Но в данном случае, я в одной статье уместил годы опыта и сотни учеников. Схема рабочая, пользуйтесь.
Всегда рад отзывам и комментариям!
С Пламенной любовью,
Никита Салливан из Умскул.
7 декабря 2017
В закладки
Обсудить
Жалоба
Основные методы решения задач по геометрии на ЕГЭ
Задания №14 и №16 повышенного уровня сложности с развёрнутым ответом.
Презентация: mr-geo.pdf
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.
а) докажите, что биссектриса угла С делит отрезок МN пополам
б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Источник: ЕГЭ по математике 19.06.2014. Основная волна, резервная волна. Запад. Вариант 1
2
Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°.
а) Докажите, что ∠CBE = ∠COE.
б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE = 24.
3
Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 12.
4
На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M — середина стороны AB.
а) Докажите, что
б) Найдите расстояние от точки M до центров квадратов, если AC = 10, BC = 32 и ∠ACB = 30°.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
5
На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.
а) Докажите, что точки A, B, K и E лежат на одной окружности.
б) Найдите радиус этой окружности, если AB = 12, CH = 5.
Пройти тестирование по этим заданиям
Как подготовиться к решению заданий ЕГЭ № 16 по планиметрии | 1С:Репетитор
Задача № 16 по планиметрии, которую включает вариант КИМ ЕГЭ по математике профильного уровня, – объективно одна из самых трудных, если не самая сложная для абитуриентов. Дело в том, что в обычной (не профильной или специализированной) школе планиметрию изучают только в 7–9-х классах, на эту дисциплину отводится два урока в неделю, что совершенно недостаточно для того, чтобы хорошо изучить свойства фигур планиметрии и научиться применять их при решении задач. Кроме того, каждая задача по геометрии уникальна по своему содержанию, поэтому для решения таких задач практически неприменим алгоритмический подход, который является весьма успешным при решении задач по алгебре, в результате многие школьники даже не пытаются решать геометрические задачи. Все это приводит к тому, что и сравнительно несложная задача по планиметрии становится непосильной для выпускников школ.
Ситуацию можно исправить, но потребуется немало сил и времени и, конечно, хорошая методика подготовки. Наша методика основана на концепции известного отечественного методолога и методиста, специалиста по преподаванию геометрии И.Ф. Шарыгина. Суть концепции, которую сам автор называл «геометрией фигуры», заключается в том, что в учебных материалах последовательно разбираются свойства геометрических фигур и их элементов (замечательных линий и точек), начиная от прямоугольного треугольника и заканчивая комбинациями многоугольников и окружностей, причем внимание акцентируется именно на решении задач.
Конечно, для решения геометрических задач большое значение имеет хорошее знание теории, поэтому в наших материалах много кратких видеолекций, суммирующих необходимые теоретические знания . Обучая теории, мы сразу же разбираем опорные задачи, в которых она применяется, осваиваем специальные приемы решения задач – например метод проекций, метод площадей, метод вспомогательной окружности и т. д.
После изучения теории нужно браться за самостоятельное решение задач. При этом можно выбрать приемлемую траекторию продвижения по системе задач. Для менее подготовленных школьников мы рекомендуем решать задачи «по фигурам», то есть в следующем порядке.
Сначала – прямоугольный треугольник, медиана в прямоугольном треугольнике, биссектриса в прямоугольном треугольнике, высота в прямоугольном треугольнике . Затем переходим к равнобедренному и произвольному треугольникам, параллелограмму, трапеции и т. д.
Для более сильных школьников предлагается другой путь – систематизация и обобщение свойств геометрических фигур и их элементов.
Прямоугольный треугольник, произвольный треугольник (теорема синусов, теорема косинусов, площади), медиана в прямоугольном треугольнике, медиана в равнобедренном и произвольном треугольнике и т. д.
Описанный подход позволяет нашим ученикам актуализировать свои школьные знания, обобщить и углубить их, систематически сочетая изучение теории с практикой ее применения. Большую помощь в решении задач оказывают пошаговые тренажеры: в геометрической задаче, ход решения которой может быть неочевиден с самого начала, тренажер позволяет сориентироваться в шагах решения, проверить промежуточные вычисления на каждом шаге и обосновать сами шаги нужной теоремой или свойством.
После такой подготовки задачи по планиметрии варианта КИМ ЕГЭ покажутся и не такими уж сложными. Посмотрим, например, как можно «раскусить» следующую довольно непростую, но в то же время изящную задачу, предлагавшуюся на экзамене в 2016–2017 годах.
Пример задачи № 16 по планиметрии:
Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC =∠OBC +∠OCB.
Чертеж 1
- Докажите, что точка I лежит на окружности, описанной около треугольника BOC.
- Найдите угол OIH, если ∠ABC =55°.
Ответ: 175°.
Решение:
- Посмотрим на чертеж. Если нам предлагают доказать, что четыре точки лежат на одной окружности, то согласно теореме об угле, вписанном в окружность, и следствиям из нее, нужно либо поискать на чертеже 1 равные углы, опирающиеся на один и тот же отрезок (хорду) и расположенные по одну сторону от него, либо углы, сумма которых равна 180° и которые также опираются на один и тот же отрезок, но расположены по разные стороны от него. В нашем случае подходит первый вариант.
- Итак, во-первых, по теореме об угле, вписанном в окружность, ∠BAC =∠OBC +∠OCB=12∠BOC,
но ∠OBC +∠OCB+∠BOC=180°,
то есть ∠BOC+12∠BOC=180°⇔∠BOC=120°⇒∠BAC=60°
- Во-вторых, находим угол между двумя биссектрисами. В нашем случае ∠BIC=90°+12∠BAC=120°.
Этот факт мы доказываем в своем курсе, чтобы на экзамене вы могли без труда им воспользоваться. - Прежде всего найдем все углы треугольника ABC: ∠BAC =60°, ∠ABC =55°, ∠ACB =65°.
- Затем подумаем вот о чем: а не лежит ли точка H на окружности, описанной около треугольника BOC? И это действительно так: обсуждая в нашем курсе свойства высот треугольника, мы обращаем внимание учащихся на тот факт, что угол между высотами – в данном случае ∠BHC =180°-∠BAC=120°, то есть наша догадка верна.
- Теперь осталось правильно расположить точки B, H, I,O, C на окружности (чертеж 2) и вычислить угол OIH. Например, так:
∠OIH=180°-∠HCO,
∠HBO=∠HCB-∠OCB,
∠HCB=90°-∠ABC=35°,
∠OCB=30° ⇒ ∠HBO= ∠HCB — ∠OCB =5° ⇒ ∠OIH=175° — Вот и ответ.
Итого, ∠BOC=∠BIC=120°, следовательно точка I лежит на окружности, описанной около треугольника BOC.
Оценить свои стартовые знания по планиметрии вы можете с помощью заданий с кратким ответом: №3 и №6 . Если возникнут затруднения, воспользуйтесь подсказками: они помогут справиться с решением. Если же эти задачи вы решаете легко, то приступайте к более сложным (и более увлекательным) задачам по планиметрии.
Регулярно тренируйтесь в решении задач
Чтобы начать заниматься на портале «1С:Репетитор», достаточно зарегистрироваться.
Вы можете:
- Начать заниматься бесплатно.
- Получить доступ ко всей теории и тренажерам задачи №16. Это стоит всего 990 рублей.
- Купить доступ к этой задаче в составе экспресс-курса «Геометрия» и научиться решать задачи №14 и №16 на максимальный балл.
Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Включают теорию в форме текстов, слайдов и видео, задачи с решениями, интерактивные тренажеры, модели, и тесты.
Остались вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.
Здесь ключевые фразы, чтобы поисковые роботы лучше находили наши советы:
Как решать задание 16 на экзамене ЕГЭ, задачи по планиметрии, решение задач, по планиметрии, методы решения задач, теория по теме «Планиметрия, часть С», пробники ЕГЭ, а основе экзаменов прошлых лет просмотреть, подготовка к ЕГЭ 2018, учимся решать задачи по планиметрии, Планиметрические задачи профильного ЕГЭ, Решение задач по планиметрии, тесты по планиметрии, примеры и решения заданий по теме планиметрии, задачи сопровождаются подробными пояснениями и чертежами, задачи на нахождение углов и радиусов, треугольник, трапеция, параллелограмм, квадрат, ромб, прямоугольник, примеры решения задач ЕГЭ по геометрии, Видеокурс по решению задач по планиметрии, какого радиуса должна быть окружность, тесты для подготовки и самоподготовки к ЕГЭ, КИМ ЕГЭ 2017, подготовка к ЕГЭ, профиль математика, математика профильного уровня, задачи ЕГЭ 2017 по стереометрии, подготовка к ЕГЭ, выпускникам 11 класса, в 2018 году, поступающим в технический вуз, материал для подготовки к ЕГЭ.
- Угол между двумя прямыми
Задача 1, Задача 2.
- Угол между прямой и плоскостью
Задача1. Задача 2.
- Угол между двумя плоскостями
Задача 1. Задача 2.
- Расстояние от точки до прямой
Задача 1. Задача 2.
- Расстояние от точки до плоскости
Задача 1. Задача 2.
- Расстояние между скрещивающимися прямыми
Задача 1. Задача 2.
1.Определение: Две пересекающиеся прямые образуют смежные и вертикальные углы.
Углом между двумя прямыми называется меньший из них.
Угол между перпендикулярными прямыми равен 90°. Угол между параллельными прямыми равен 0°.
С 1
D 1
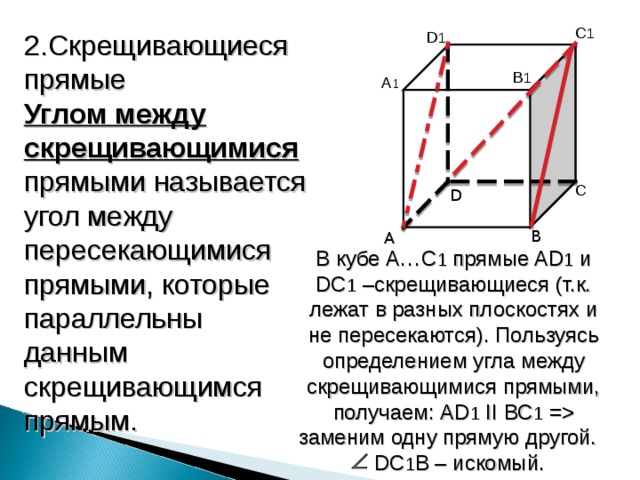
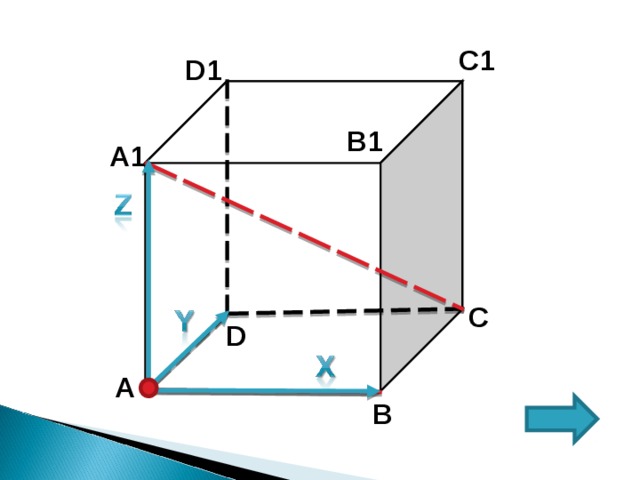
2.Скрещивающиеся прямые
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, которые параллельны данным скрещивающимся прямым.
B 1
А 1
С
D
В
А
В кубе A…C 1 прямые AD 1 и DC 1 –скрещивающиеся (т.к. лежат в разных плоскостях и не пересекаются). Пользуясь определением угла между скрещивающимися прямыми, получаем: AD 1 II BC 1 = заменим одну прямую другой. DC 1 B – искомый.
.
Для решения задач C 2 первого типа, практически всегда приходиться применять формулы и теоремы.
- Теорема косинусов: Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
- При решении векторным способом : скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
a²=b² + c²- 2∙b∙c∙cos α
Ключевая задач а
В единичном кубе А… D 1 найдите угол между прямыми АВ1 и ВС1 .
D 1
C 1
B 1
А1
Рисунок
С
РЕШЕНИЕ
D
А
В
6
С1
D 1
B 1
А1
С
D
А
В
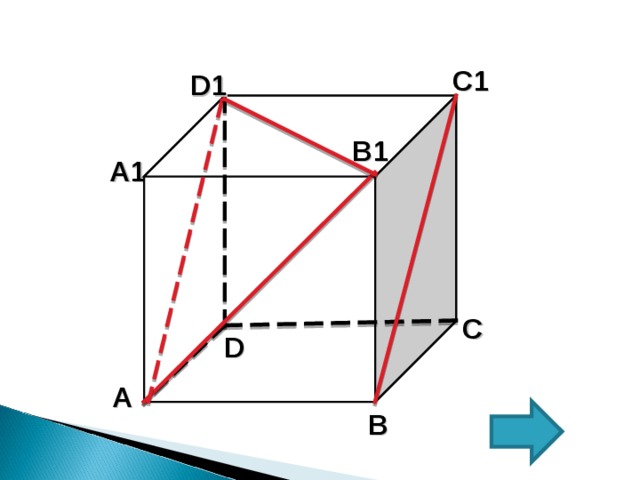
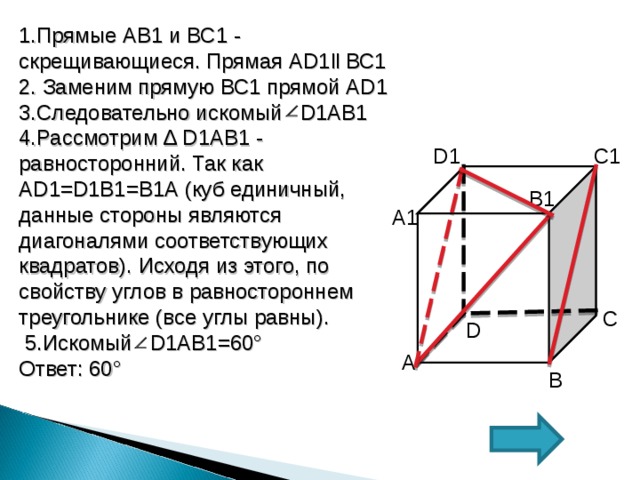
1.Прямые АВ1 и ВС1 — скрещивающиеся. Прямая А D 1 ll ВС1
2. Заменим прямую ВС1 прямой А D 1
3.Следовательно искомый D 1АВ1
4.Рассмотрим ∆ D 1АВ1 — равносторонний. Так как А D 1= D 1В1=В1А (куб единичный, данные стороны являются диагоналями соответствующих квадратов). Исходя из этого, по свойству углов в равностороннем треугольнике (все углы равны).
5.Искомый D 1АВ1=60°
Ответ: 60°
C 1
D 1
B 1
А1
С
D
А
В
8
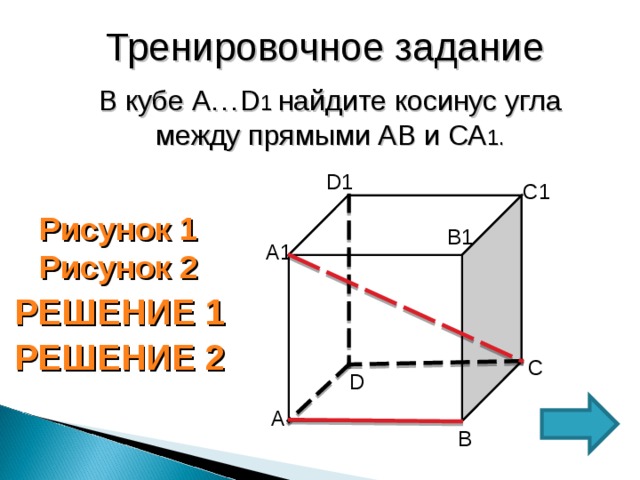
Тренировочное задание
В кубе А… D 1 найдите косинус угла между прямыми АВ и СА 1.
D 1
C 1
Рисунок 1
Рисунок 2
B 1
А1
РЕШЕНИЕ 1
РЕШЕНИЕ 2
С
D
А
В
D 1
C 1
B 1
А1
С
D
А
В
C 1
D 1
B 1
А1
С
D
А
В
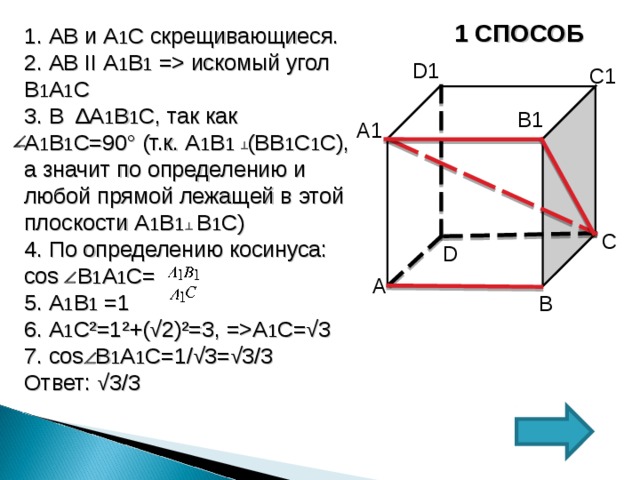
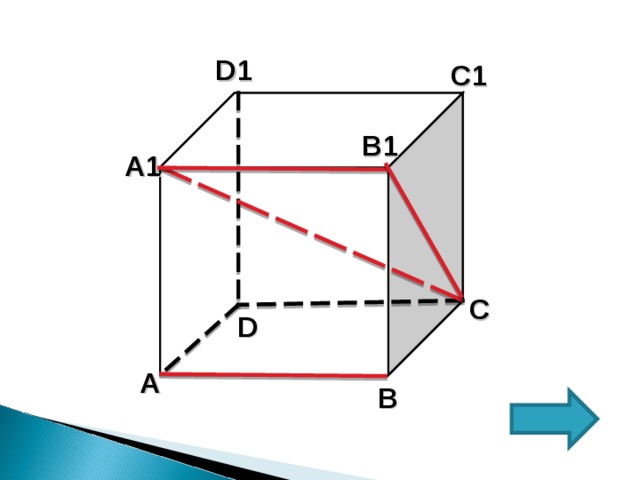
1 СПОСОБ
1. АВ и А 1 С скрещивающиеся.
2. АВ II А 1 В 1 = искомый угол В 1 А 1 С
3. В ∆А 1 В 1 С, так как
А 1 В 1 С=90° (т.к. А 1 В 1 (ВВ 1 С 1 С), а значит по определению и любой прямой лежащей в этой плоскости А 1 В 1 В 1 С)
4. По определению косинуса:
cos В 1 А 1 С=
5. А 1 В 1 =1
6. А 1 С²=1²+(√2)²=3, =А 1 С=√3
7. с os В 1 А 1 С=1/√3=√3/3
Ответ: √3/3
D 1
C 1
B 1
А1
С
D
А
В
12
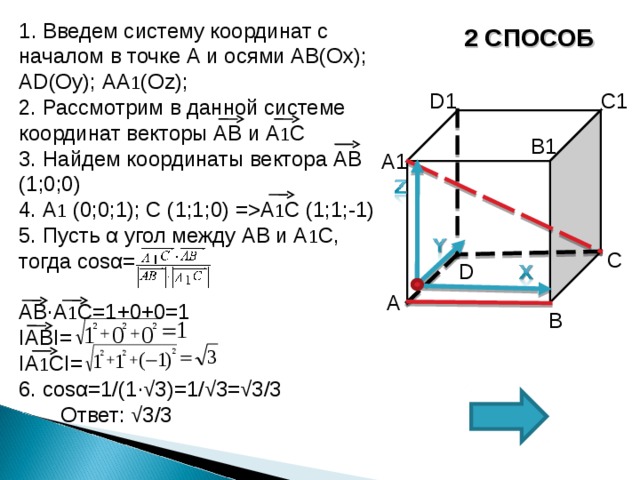
1 . Введем систему координат с началом в точке А и осями АВ(Ох); А D (Оу); АА 1 (О z );
2. Рассмотрим в данной системе координат векторы АВ и А 1 С
3. Найдем координаты вектора АВ (1;0;0)
4. А 1 (0;0;1); С (1;1;0) =А 1 С (1;1;-1)
5. Пусть α угол между АВ и А 1 С,
тогда cos α =
АВ∙А 1 С=1+0+0=1
I АВ I =
I А 1 С I =
6. с os α =1/(1∙√3)=1/√3=√3/3
Ответ: √3/3
2 СПОСОБ
C 1
D 1
B 1
А1
С
D
А
В
1 . Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость.
2. Угол между взаимно перпендикулярными прямой и плоскостью равен 90 .
3. Если прямая параллельна плоскости (или лежит в ней), то угол между ними считается равным 0 .
В
а
С
α י
А
α
а ∩ α =А
ВС α
ВАС – искомый угол
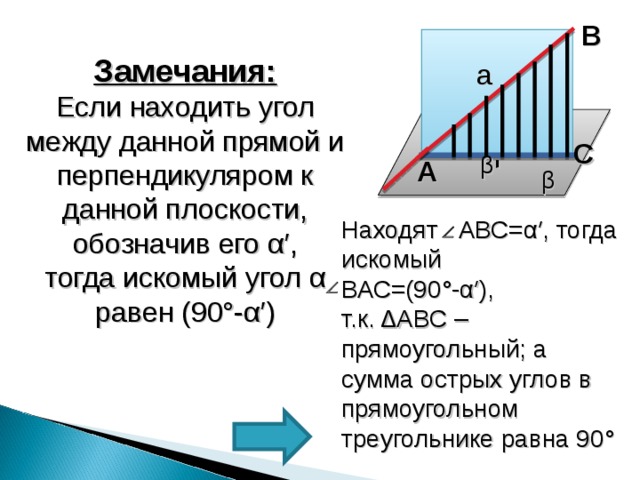
Замечания:
Если находить угол между данной прямой и перпендикуляром к данной плоскости, обозначив его α′ ,
тогда искомый угол α равен (90°- α′ )
В
а
С
β י
А
β
Находят АВС= α′ , тогда искомый ВАС=(90°- α′ ),
т.к. ∆АВС – прямоугольный; а сумма острых углов в прямоугольном треугольнике равна 90°
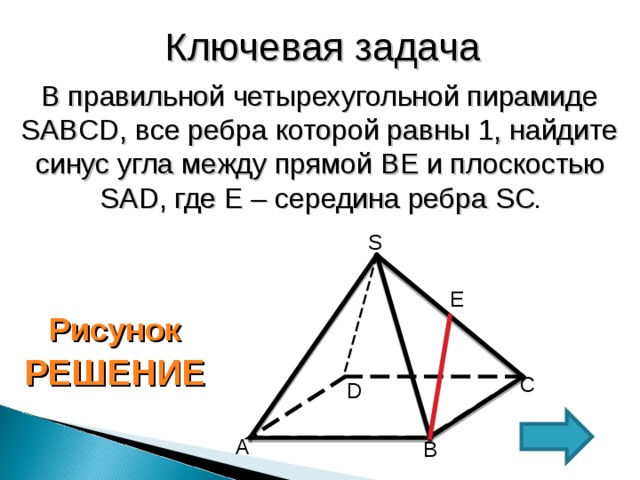
Ключевая задача
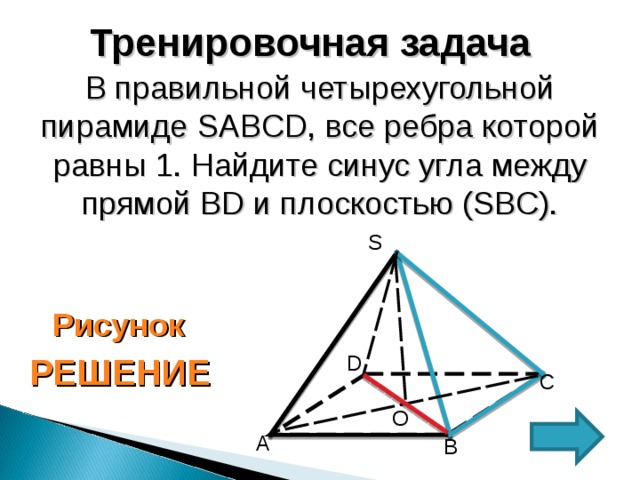
В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите синус угла между прямой BE и плоскостью SAD , где Е – середина ребра SC .
S
E
Рисунок
РЕШЕНИЕ
C
D
А
B
S
F
E
S
C
D
А
B
E
F
К
S 1
C
B
H
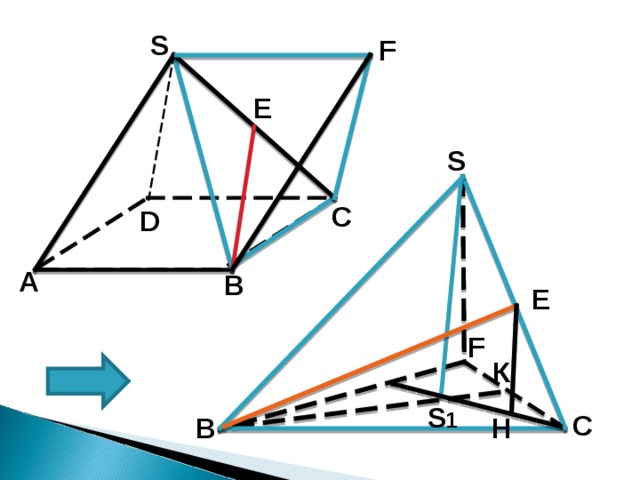
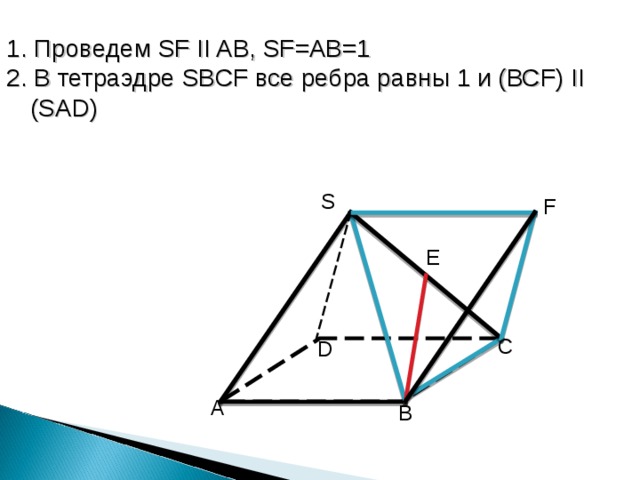
1. Проведем SF II AB , SF = AB =1
2. В тетраэдре SB С F все ребра равны 1 и (ВС F) II (SAD)
S
F
E
C
D
А
B
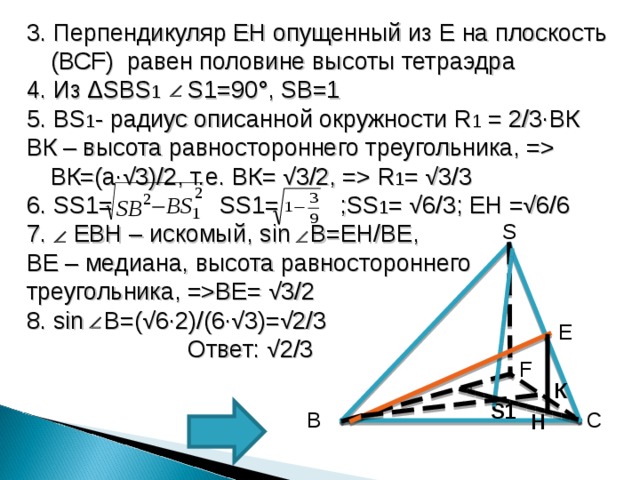
3. Перпендикуляр EH опущенный из Е на плоскость (ВС F) равен половине высоты тетраэдра
4. Из ∆ SBS 1 S 1=90°, SB =1
5. BS 1 — радиус описанной окружности R 1 = 2/3∙ B К
B К – высота равностороннего треугольника, = B К=(а∙√3)/2, т.е. B К= √3/2, = R 1 = √3/3
6. SS1= SS1= ; SS 1 = √6/3 ; EH =√6/6
7. EBH – искомый, sin B=EH/BE ,
BE – медиана, высота равностороннего
треугольника, = BE = √3/2
8. sin B =(√6∙2)/(6∙√3)=√2/3
Ответ: √2/3
S
E
F
К
S1
B
C
H
Тренировочная задача
В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1. Найдите синус угла между прямой BD и плоскостью (SBC).
S
Рисунок
D
РЕШЕНИЕ
C
O
А
B
S
H
D
C
O
А
B
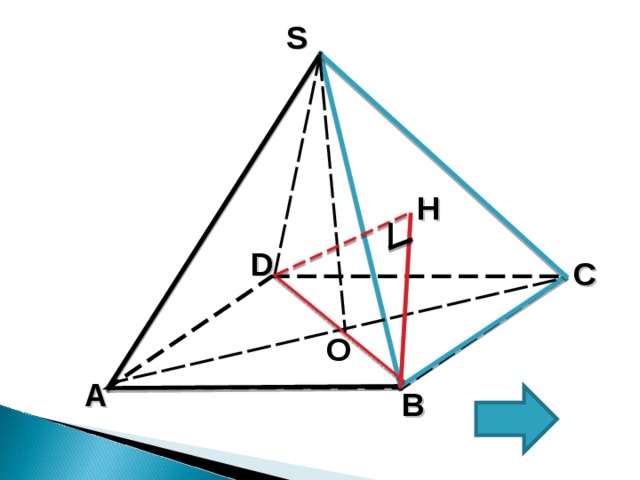
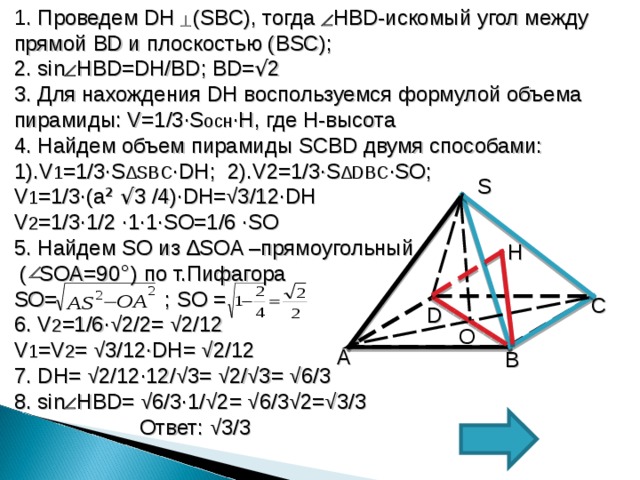
1 . Проведем DH (SBC) , тогда HBD -искомый угол между прямой BD и плоскостью ( BSC) ;
2. sin HBD=DH/BD ; BD= √ 2
3. Для нахождения DH воспользуемся формулой объема пирамиды: V=1/3∙S осн ∙ H , где H -высота
4. Найдем объем пирамиды SCBD двумя способами:
1). V 1 =1/3∙S ∆ SBC ∙DH ; 2). V2=1/3∙S ∆ DBC ∙SO ;
V 1 =1/3∙ ( a ² √ 3 /4 ) ∙DH= √ 3/12∙DH
V 2 =1/3∙1/2 ∙ 1 ∙1∙SO=1/6 ∙SO
5. Найдем SO из ∆ SOA –прямоугольный
( SOA=90 ° ) по т.Пифагора
SO= ; SO =
6. V 2 =1/6∙ √ 2/2= √ 2/12
V 1 =V 2 = √ 3/12∙DH= √ 2/12
7. DH= √ 2/12∙12/ √ 3= √ 2/ √ 3= √ 6/3
8. sin HBD= √ 6/3∙1/ √ 2= √ 6/3 √ 2= √ 3/3
Ответ: √ 3/3
S
H
C
D
O
А
B
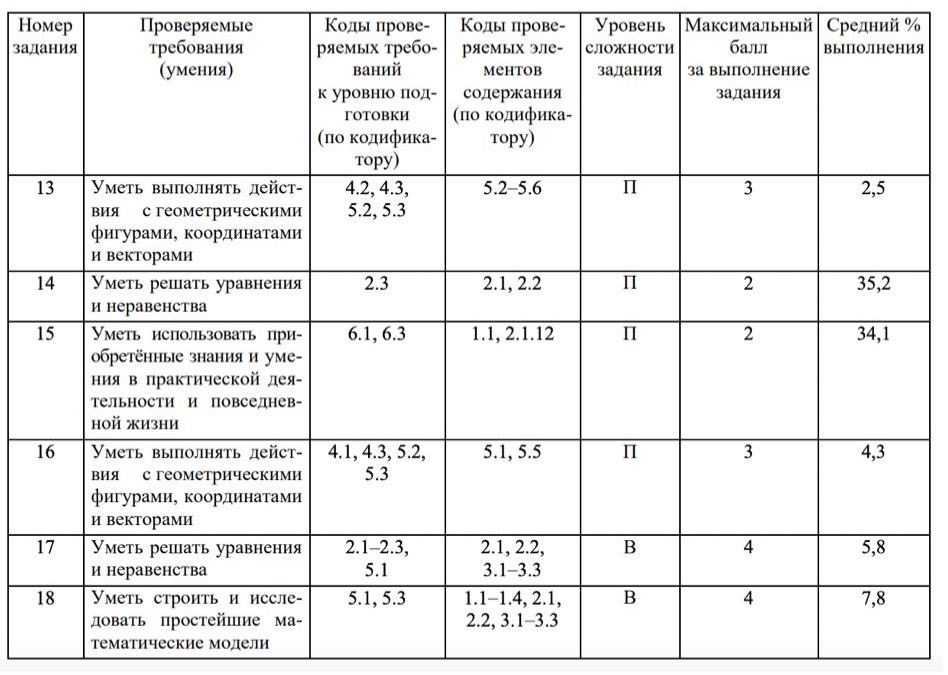
Двугранный угол , образованный полуплоскостями измеряется величиной его линейного угла,
получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру.
Величина двугранного угла принадлежит промежутку (0°; 180°).
Величина угла между пересекающимися плоскостями принадлежит промежутку (0°; 90°].
Угол между двумя параллельными плоскостями равен 0° .
Ключевая задача
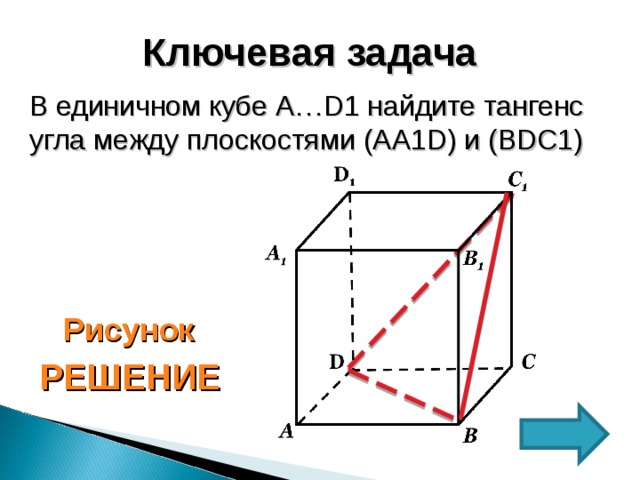
В единичном кубе А…D1 найдите тангенс угла между плоскостями (АА1D) и (BDC1)
Рисунок
РЕШЕНИЕ
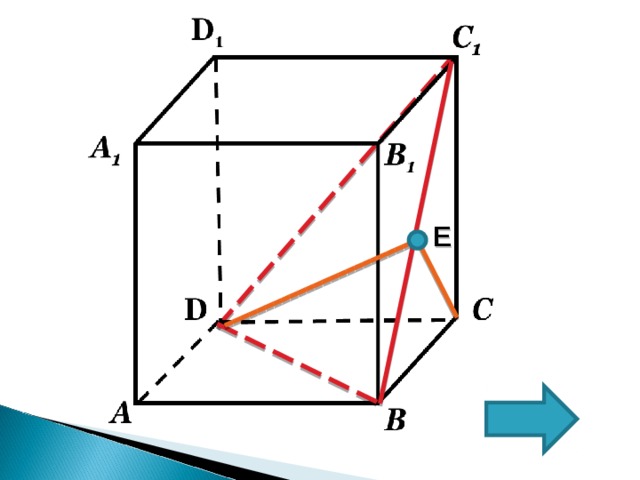
E
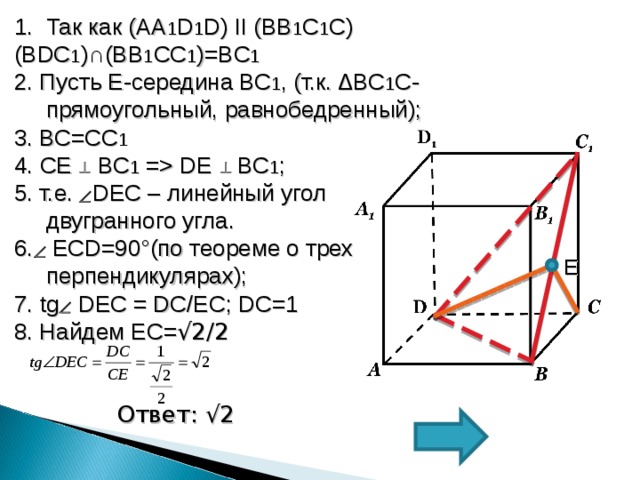
- Так как (АА 1 D 1 D) II ( BB 1 C 1 С)
( BDC 1 )∩(BB 1 CC 1 )=BC 1
2. Пусть Е-середина ВС 1 , (т.к. ∆ BC 1 C- прямоугольный, равнобедренный);
3. ВС=С C 1
4. CE BC 1 = DE BC 1 ;
5. т.е. DEC – линейный угол двугранного угла.
6. ECD=90°( по теореме о трех перпендикулярах);
7. tg DEC = DC/EC ; DC=1
8. Найдем EC = √2/2
Ответ: √2
E
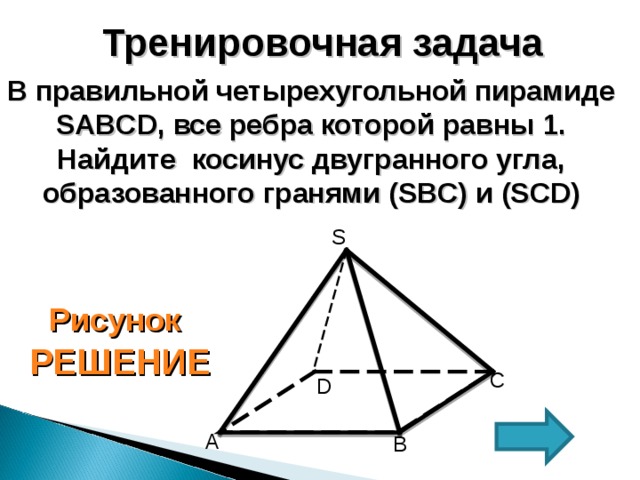
Тренировочная задача
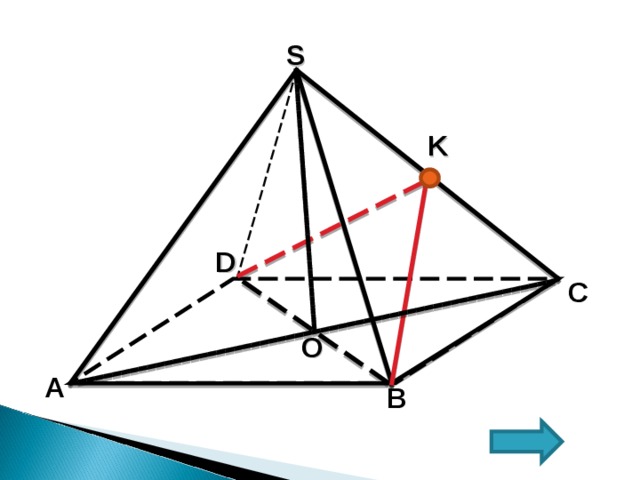
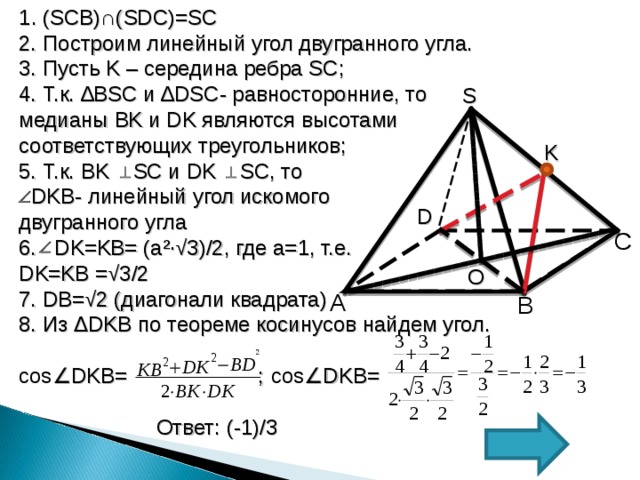
В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1. Найдите косинус двугранного угла, образованного гранями ( SBC) и (SCD)
S
Рисунок
РЕШЕНИЕ
C
D
А
B
S
K
D
С
O
А
B
1 . (SCB)∩(SDC)=SC
2. Построим линейный угол двугранного угла.
3. Пусть K – середина ребра SC ;
4. Т.к. ∆BSC и ∆ DSC — равносторонние, то медианы BK и DK являются высотами соответствующих треугольников;
5. Т.к. BK SC и DK SC , то
DKB- линейный угол искомого
двугранного угла
6. DK=KB= (a²∙√3)/2 , где а=1, т.е.
DK=KB =√3/2
7. DB=√2 (диагонали квадрата)
8. Из ∆ DKB по теореме косинусов найдем угол.
cos ∠ DKB= ; cos ∠ DKB=
Ответ: (-1)/3
S
K
D
C
O
А
B
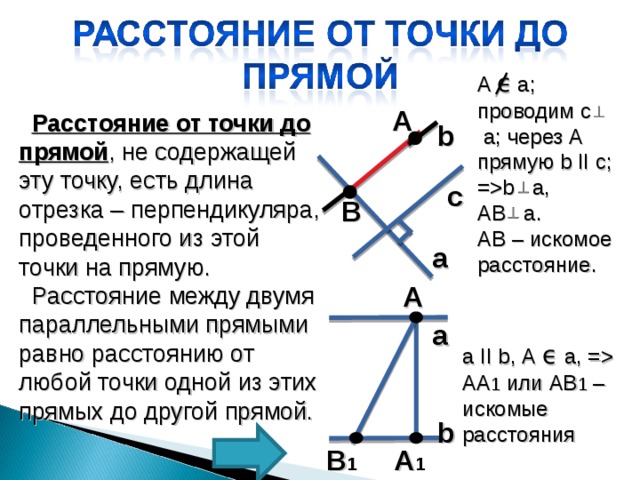
A ϵ а; проводим с
а; через А прямую b II с; = b a ,
AB а .
AB – искомое расстояние.
A
Расстояние от точки до прямой , не содержащей эту точку, есть длина отрезка – перпендикуляра, проведенного из этой точки на прямую.
Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой.
b
с
B
a
A
a
a II b, А ϵ а, = АА 1 или АВ 1 – искомые расстояния
b
A 1
B 1
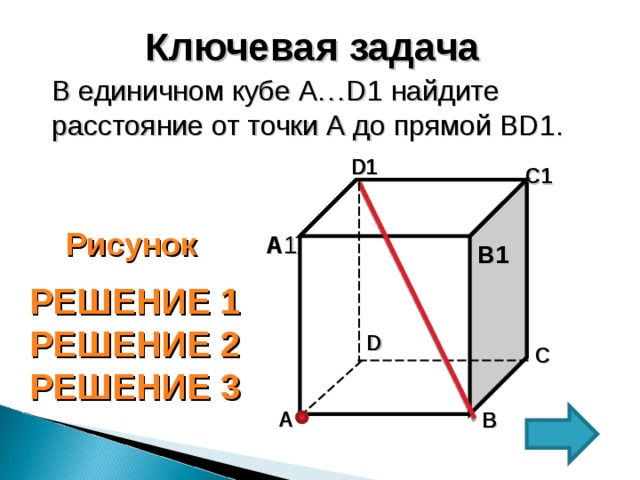
Ключевая задача
В единичном кубе А…D 1 найдите расстояние от точки А до прямой BD 1 .
D
D 1
C 1
Рисунок
A 1
B 1
РЕШЕНИЕ 1
РЕШЕНИЕ 2
РЕШЕНИЕ 3
D
C
A
B
B
D 1
С1
A 1
B 1
H
D
C
A
B
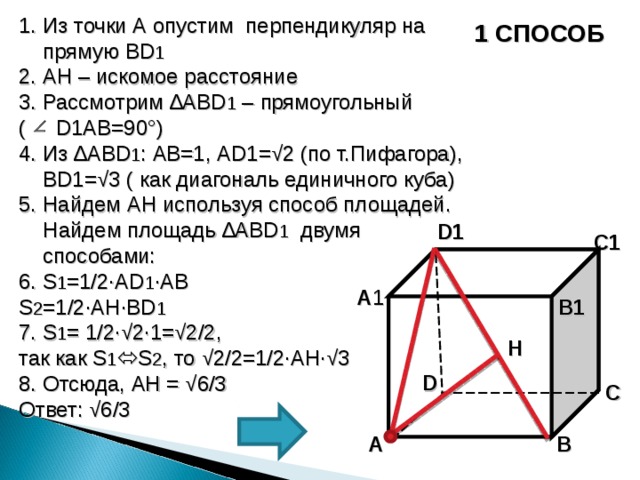
1. Из точки А опустим перпендикуляр на прямую BD 1
2. AH – искомое расстояние
3. Рассмотрим ∆ ABD 1 – прямоугольный
( D1AB =90°)
4. Из ∆ ABD 1 : AB =1, AD1 =√2 (по т.Пифагора), BD1 =√3 ( как диагональ единичного куба)
5. Найдем AH используя способ площадей. Найдем площадь ∆ ABD 1 двумя способами:
6. S 1 =1/2∙AD 1 ∙AB
S 2 =1/2∙AH∙BD 1
7. S 1 = 1/2∙√2∙1=√2/2 ,
так как S 1 S 2 , то √2/2=1/2∙AH∙√3
8. Отсюда, AH = √ 6/3
Ответ: √6/3
1 СПОСОБ
D 1
C 1
A 1
B 1
H
D
C
A
B
30
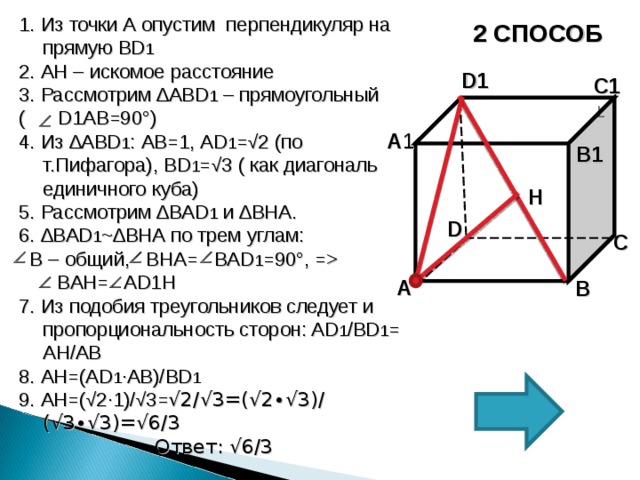
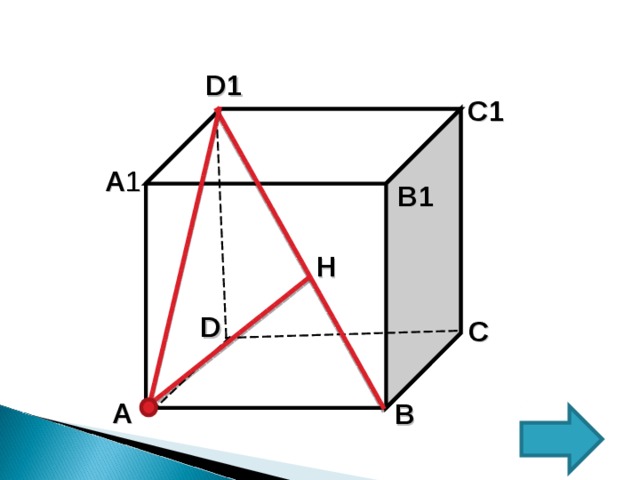
1. Из точки А опустим перпендикуляр на прямую BD 1
2. AH – искомое расстояние
3. Рассмотрим ∆ ABD 1 – прямоугольный
( D1AB =90°)
4. Из ∆ ABD 1 : AB =1, AD 1 =√2 (по т.Пифагора), BD 1 =√3 ( как диагональ единичного куба)
5. Рассмотрим ∆ BAD 1 и ∆ BHA .
6. ∆ BAD 1 ~ ∆ BHA по трем углам:
B – общий, BHA= BAD 1 =90°, =
BAH= AD1H
7. Из подобия треугольников следует и пропорциональность сторон: AD 1 /BD 1 = AH/AB
8 . AH =( AD 1 ∙AB )/ BD 1
9. А H = ( √ 2∙1)/√3= √2/√3=(√2∙√3)/(√3∙√3)=√6/3
Ответ: √6/3
2 СПОСОБ
D 1
C 1
A 1
B 1
H
D
C
H
A
B
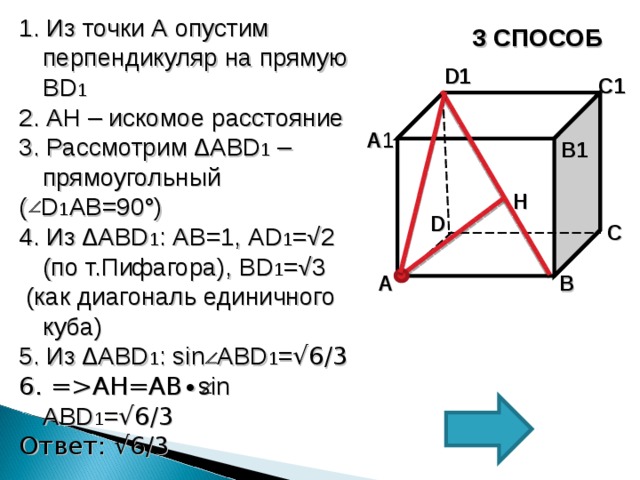
1. Из точки А опустим перпендикуляр на прямую BD 1
2. AH – искомое расстояние
3. Рассмотрим ∆ ABD 1 – прямоугольный
( D 1 AB =90°)
4. Из ∆ ABD 1 : AB =1, AD 1 =√2 (по т.Пифагора), BD 1 =√3
(как диагональ единичного куба)
5. Из ∆ ABD 1 : sin ABD 1 = √6/3
6 . = AH=AB∙ sin ABD 1 = √6/3
Ответ: √6/3
3 СПОСОБ
D 1
C 1
A 1
B 1
H
D
C
A
B
Тренировочное задание
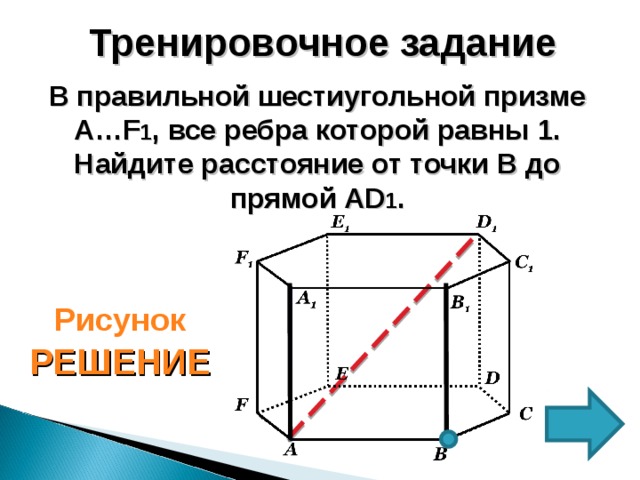
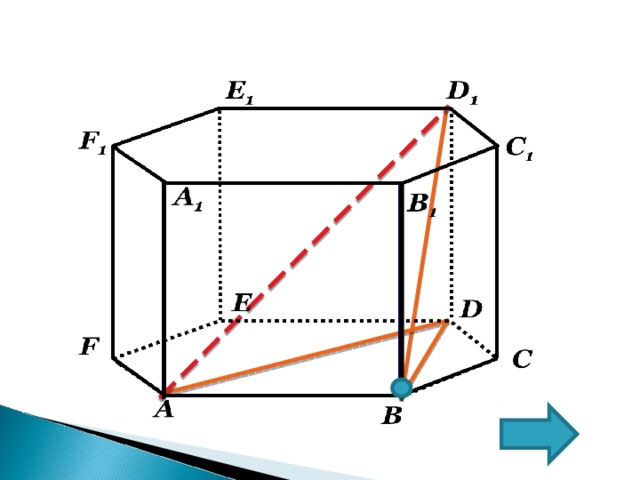
В правильной шестиугольной призме A…F 1 , все ребра которой равны 1. Найдите расстояние от точки B до прямой AD 1 .
Рисунок
РЕШЕНИЕ
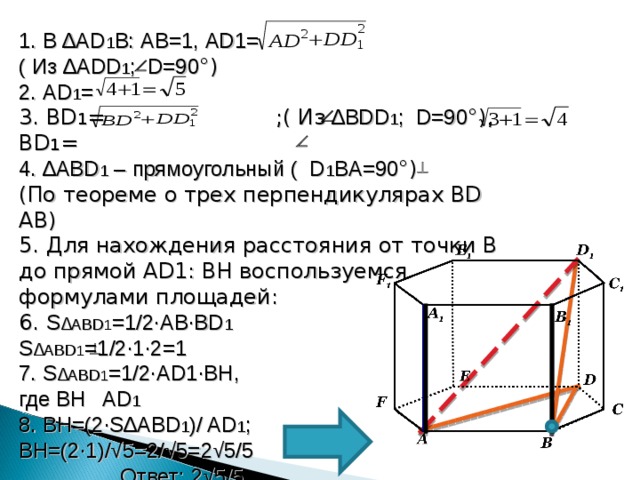
1. В ∆ AD 1 B : AB=1 , AD1=
( Из ∆ ADD 1 ; D=90 °)
2. AD 1 =
3. BD 1 = ;( Из ∆ BDD 1 ; D=90 °) , BD 1 =
4. ∆ ABD 1 – прямоугольный ( D 1 BA=90 °)
( По теореме о трех перпендикулярах BD AB)
5. Для нахождения расстояния от точки В до прямой AD1 : BH воспользуемся формулами площадей:
6. S ∆ ABD 1 =1/2∙AB∙BD 1
S ∆ ABD 1 =1/2∙1∙2=1
7. S ∆ ABD 1 =1/2∙AD1∙BH ,
где BH AD 1
8. BH=(2∙S ∆ ABD 1 )/ AD 1 ;
BH=(2∙1)/√5=2/√5=2√5/5
Ответ: 2√5/5
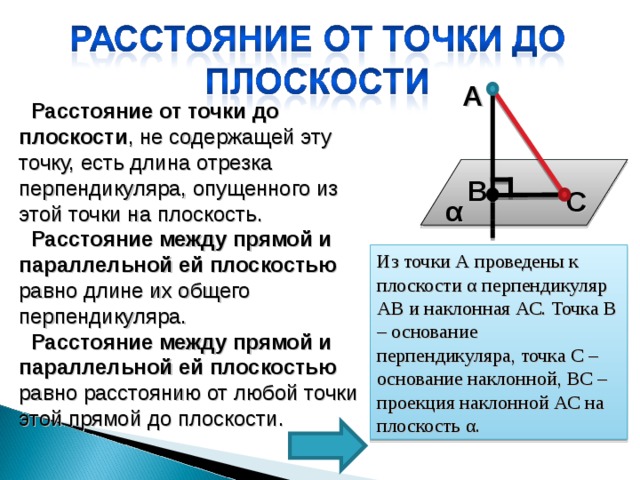
A
Расстояние от точки до плоскости , не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость.
Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.
Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.
B
C
α
Из точки А проведены к плоскости α перпендикуляр АВ и наклонная АС. Точка В – основание перпендикуляра, точка С – основание наклонной, ВС – проекция наклонной АС на плоскость α .
А
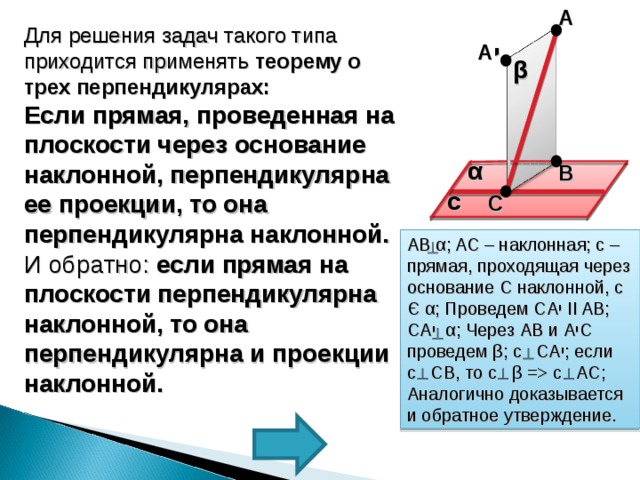
Для решения задач такого типа приходится применять теорему о трех перпендикулярах:
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
A י
β
α
B
c
C
AB α ; AC – наклонная; с – прямая, проходящая через основание С наклонной, с Є α ; Проведем С A י II AB ; С A י α ; Через AB и A י С проведем β ; с СА י ; если
с СВ, то с β = с АС;
Аналогично доказывается и обратное утверждение.
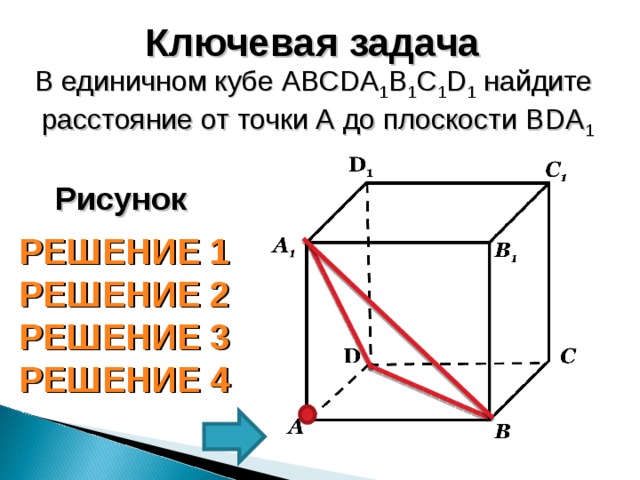
Ключевая задача
В единичном кубе АВС D А 1 В 1 С 1 D 1 найдите
расстояние от точки А до плоскости В D А 1
Рисунок
РЕШЕНИЕ 1
РЕШЕНИЕ 2
РЕШЕНИЕ 3
РЕШЕНИЕ 4
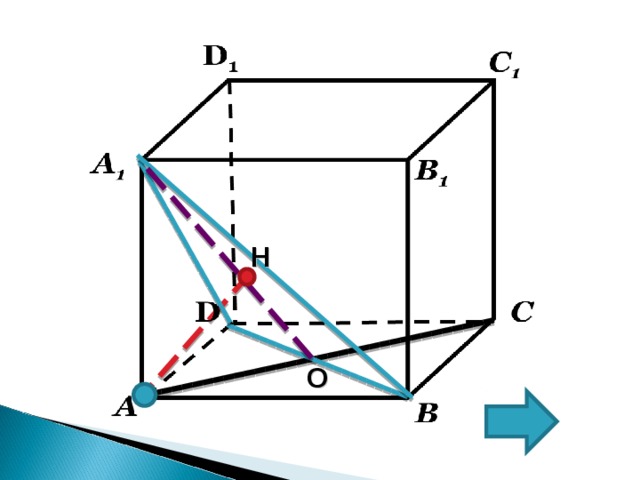
H
O
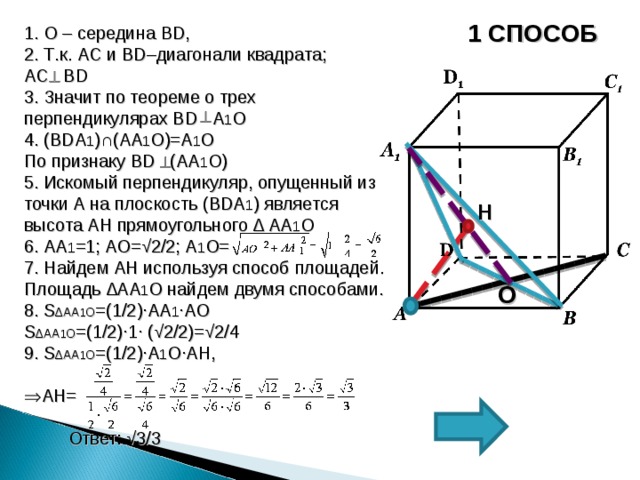
1 СПОСОБ
1. О – середина BD ,
2. Т . к. AC и BD –диагонали квадрата;
AC BD
3. Значит по теореме о трех перпендикулярах BD A 1 О
4. ( BDA 1 ) ∩ (АА 1 О)=А 1 О
По признаку BD (А A 1 О)
5. Искомый перпендикуляр, опущенный из точки А на плоскость ( BDA 1 ) является высота AH прямоугольного ∆ А A 1 О
6. АА 1 =1; АО=√2/2; А 1 О=
7. Найдем А H используя способ площадей.
Площадь ∆АА 1 О найдем двумя способами.
8. S ∆АА 1 О =(1/2)∙ АА 1 ∙ А O
S ∆АА 1 О =(1/2)∙1∙ ( √ 2/2)=√2/4
9. S ∆АА 1 О =(1/2)∙ А 1 О ∙ А H ,
- А H=
Ответ: √3/3
H
О
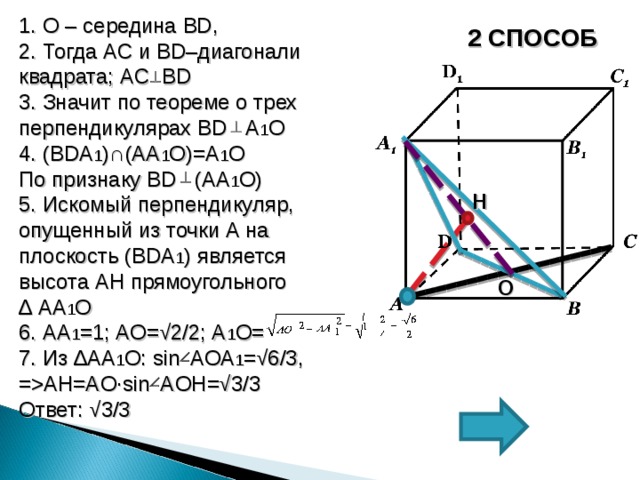
1. О – середина BD ,
2. Тогда AC и BD –диагонали квадрата; AC BD
3. Значит по теореме о трех перпендикулярах BD A 1 О
4. ( BDA 1 ) ∩ (АА 1 О)=А 1 О
По признаку BD (А A 1 О)
5. Искомый перпендикуляр, опущенный из точки А на плоскость ( BDA 1 ) является высота AH прямоугольного
∆ А A 1 О
6. АА 1 =1; АО=√2/2; А 1 О=
7. Из ∆ A А 1 О: sin A ОА 1 =√6/3 ,
= AH=A О ∙sin A О H=√ 3 /3
Ответ: √ 3 /3
2 СПОСОБ
H
О
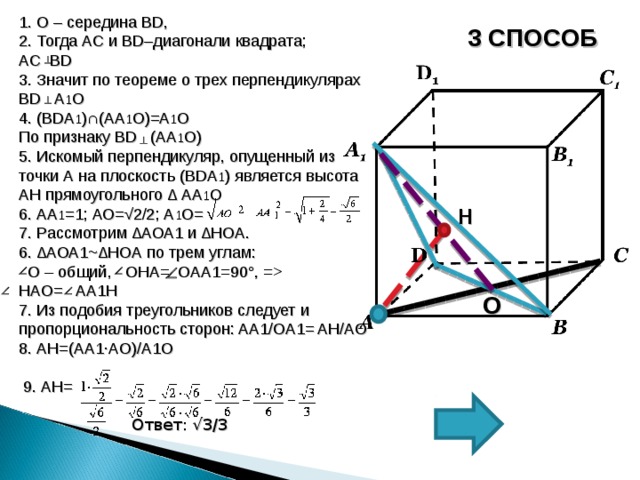
1. О – середина BD ,
2. Тогда AC и BD –диагонали квадрата;
AC BD
3. Значит по теореме о трех перпендикулярах BD A 1 О
4. ( BDA 1 ) ∩ (АА 1 О)=А 1 О
По признаку BD (А A 1 О)
5. Искомый перпендикуляр, опущенный из точки А на плоскость ( BDA 1 ) является высота AH прямоугольного ∆ А A 1 О
6. АА 1 =1; АО=√2/2; А 1 О=
7. Рассмотрим ∆АОА 1 и ∆ H О A .
6. ∆АОА 1~ ∆ H О A по трем углам:
О – общий, О HA= О A А 1=90°, = HA О = A А 1H
7. Из подобия треугольников следует и пропорциональность сторон: A А 1/ ОА 1= AH/A О
8 . AH =( A А 1∙A О)/А 1 О
9. А H =
Ответ: √3/3
3 СПОСОБ
H
О
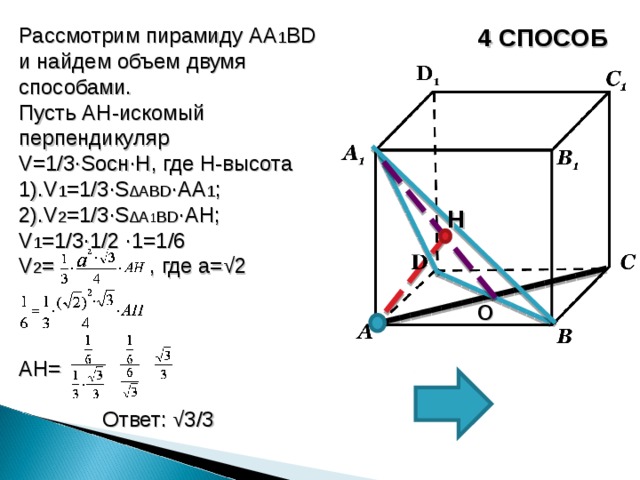
Рассмотрим пирамиду AA 1 BD и найдем объем двумя способами.
Пусть AH -искомый перпендикуляр
V=1/3∙S осн∙ H , где H -высота
1). V 1 =1/3∙S ∆А BD ∙AA 1 ; 2). V 2 =1/3∙S ∆ A 1 BD ∙AH ;
V 1 =1/3∙1/2 ∙ 1 =1/6
V 2 = , где а=√2
AH =
Ответ: √3/3
4 СПОСОБ
H
О
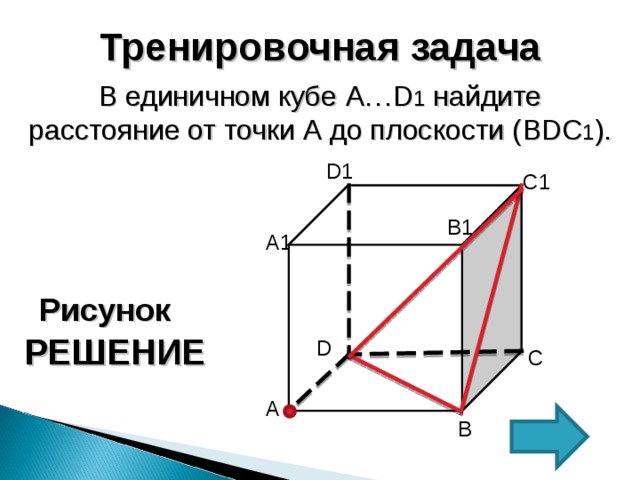
Тренировочная задача
В единичном кубе A … D 1 найдите расстояние от точки А до плоскости ( BDC 1 ).
D1
C1
B1
А 1
Рисунок
РЕШЕНИЕ
D
С
А
В
D1
C1
B1
А 1
D
С
K
А
В
H
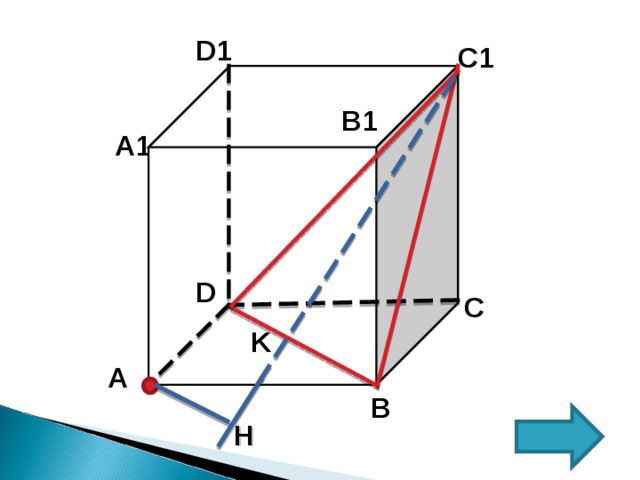
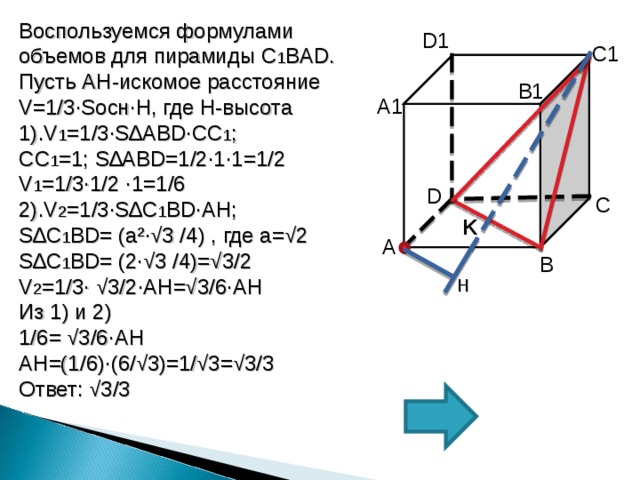
Воспользуемся формулами объемов для пирамиды C 1 BAD .
Пусть AH -искомое расстояние
V=1/3∙S осн∙ H , где H -высота
1). V 1 =1/3∙S ∆А BD∙ СС 1 ;
СС 1 =1; S ∆А BD =1/2∙1∙1=1/2
V 1 =1/3∙1/2 ∙ 1 =1/6
2). V 2 =1/3∙S ∆С 1 BD∙AH ;
S ∆С 1 BD = ( a² ∙√ 3 /4 ) , где а=√2
S ∆С 1 BD = (2∙√ 3 /4 )=√3/2
V 2 =1/3∙ √3/2 ∙AH =√3/6 ∙AH
Из 1) и 2)
1/6= √3/6 ∙AH
AH =(1/6)∙(6/√3)=1/√3=√3/3
Ответ: √3/3
D1
C1
B1
А 1
D
С
K
А
В
H
β
А
а
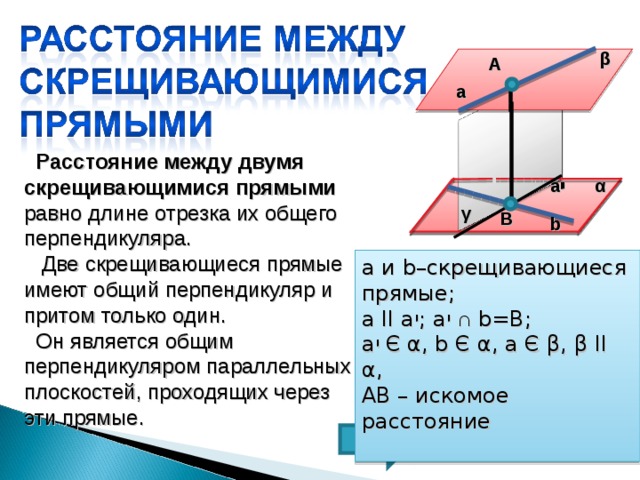
Расстояние между двумя скрещивающимися прямыми равно длине отрезка их общего перпендикуляра.
Две скрещивающиеся прямые имеют общий перпендикуляр и притом только один.
Он является общим перпендикуляром параллельных плоскостей, проходящих через эти прямые.
а י
α
γ
В
b
а и b –скрещивающиеся прямые;
а II а י ; а י ∩ b=B ;
a י Є α , b Є α , a Є β , β II α ,
АВ – искомое расстояние
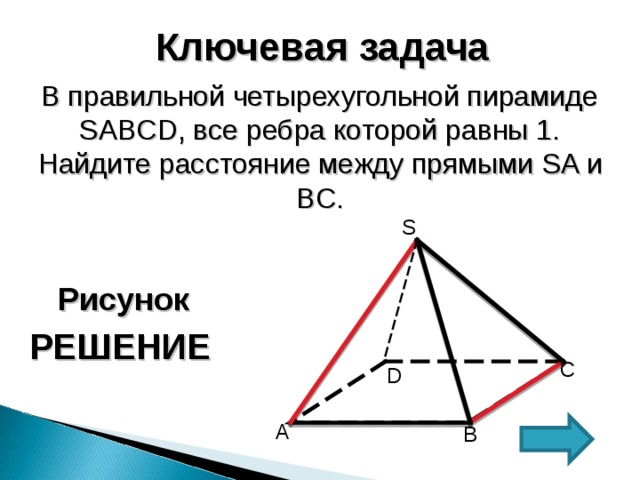
Ключевая задача
В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1. Найдите расстояние между прямыми SA и BC .
S
Рисунок
РЕШЕНИЕ
C
D
А
B
S
H
D
C
E
F
O
А
B
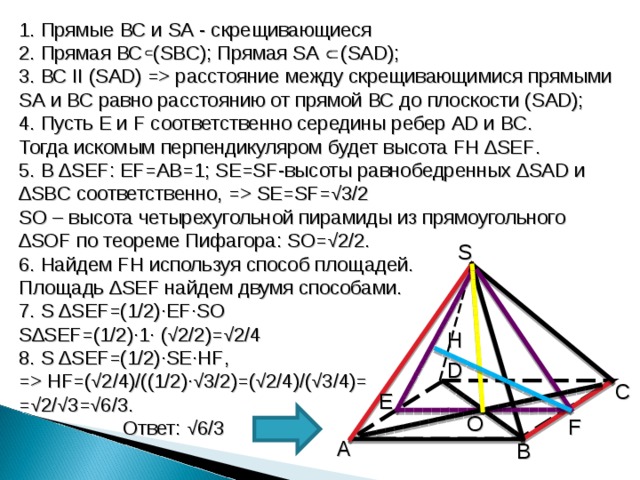
1. Прямые ВС и SA — скрещивающиеся
2. Прямая ВС ( SBC ); Прямая SA ( SAD );
3. ВС II ( SAD ) = расстояние между скрещивающимися прямыми SA и ВС равно расстоянию от прямой ВС до плоскости ( SAD );
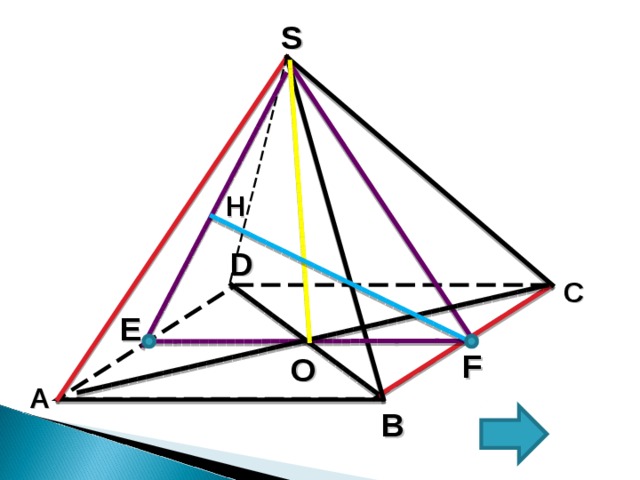
4. Пусть E и F соответственно середины ребер AD и BC .
Тогда искомым перпендикуляром будет высота FH ∆ SEF .
5. В ∆ SEF : EF =АВ=1; SE=SF -высоты равнобедренных ∆ SAD и ∆ SBC соответственно, = SE=SF =√3/2
SO – высота четырехугольной пирамиды из прямоугольного ∆ SOF по теореме Пифагора: SO =√2/2.
6. Найдем FH используя способ площадей.
Площадь ∆ SEF найдем двумя способами.
7. S ∆ SEF=(1/2)∙EF∙SO
S ∆ SEF=(1/2)∙1∙ ( √ 2/2)=√2/4
8. S ∆ SEF=(1/2)∙SE∙HF ,
= HF=(√2/4)/((1/2)∙√3/2)=(√2/4)/(√3/4)=
= √2/√3=√6/3 .
Ответ: √6/3
S
H
D
C
E
O
F
А
B
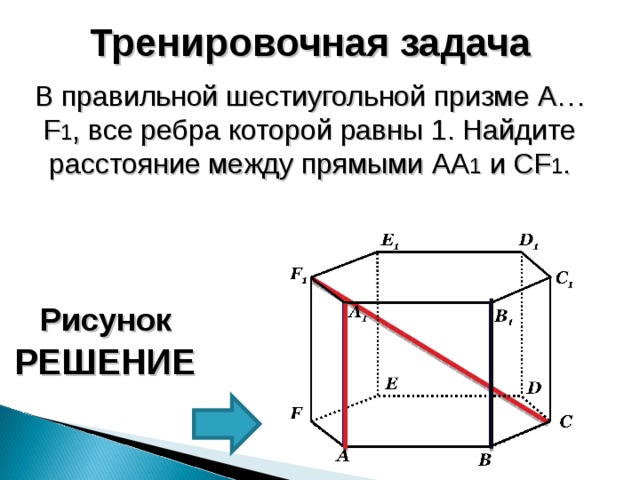
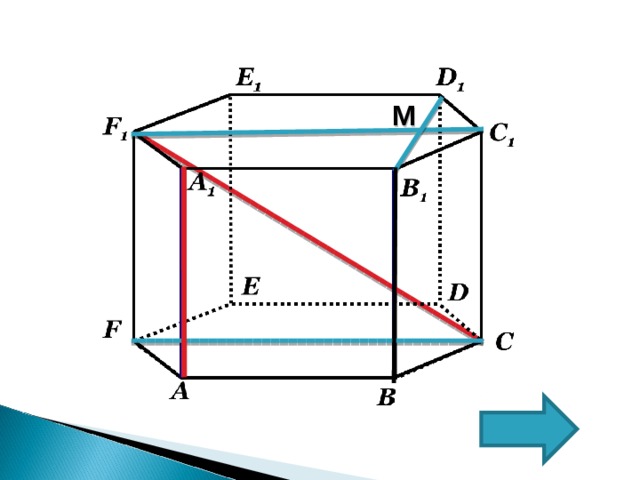
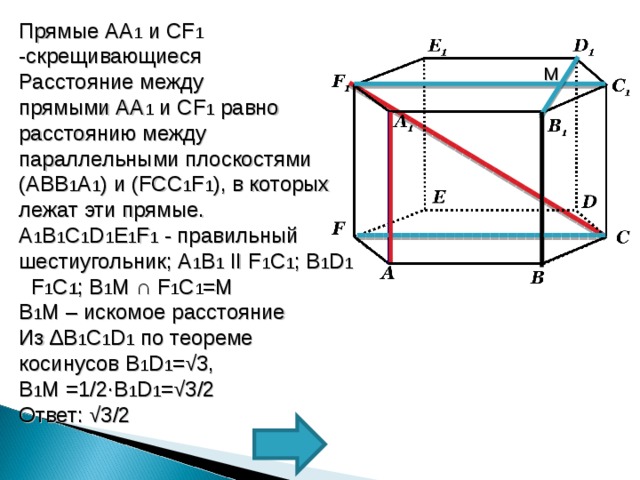
Тренировочная задача
В правильной шестиугольной призме A…F 1 , все ребра которой равны 1. Найдите расстояние между прямыми AA 1 и CF 1 .
Рисунок
РЕШЕНИЕ
M
Прямые АА 1 и СF 1 -скрещивающиеся
Расстояние между
прямыми АА 1 и СF 1 равно
расстоянию между
параллельными плоскостями (АВВ 1 А 1 ) и (FCC 1 F 1 ), в которых
лежат эти прямые.
A 1 B 1 C 1 D 1 E 1 F 1 — правильный шестиугольник; A 1 B 1 II F 1 C 1 ; B 1 D 1 F 1 C 1 ; B 1 M ∩ F 1 C 1 =M
B 1 M – искомое расстояние
Из ∆ B 1 C 1 D 1 по теореме косинусов B 1 D 1 =√3,
B 1 M =1/2∙B 1 D 1 =√3/2
Ответ: √3/2
M
Геометрические задачи ЕГЭ с решениями
Суббота, 3 сентября, 2016
В данной статье разобраны решения геометрических задач, встречающихся в вариантах профильного ЕГЭ по математике. Всего таких задач 5: 3 из первой части и 2 из второй. По крайней мере, такой расклад был на момент написания статьи. Представленные материалы будут полезны тем, кто только начал подготовку к предстоящему экзамену. Здесь вы найдёте геометрические задачи ЕГЭ с решениями, снабжёнными подробными и понятными комментариями от профессионального репетитора по математике. Представлен также видеоразбор решений каждого задания.
Задачи представлены под номерами, под которыми они числятся в вариантах профильного ЕГЭ по математике.
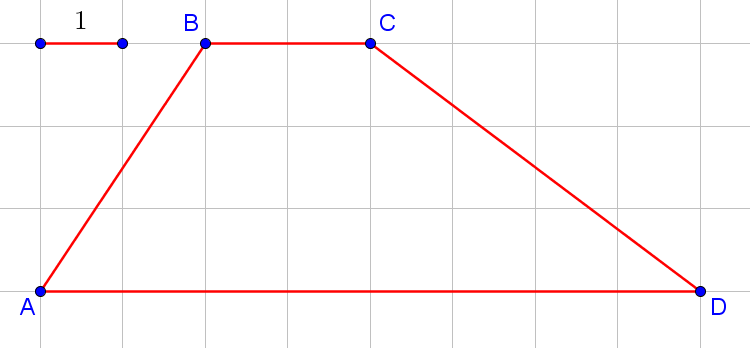
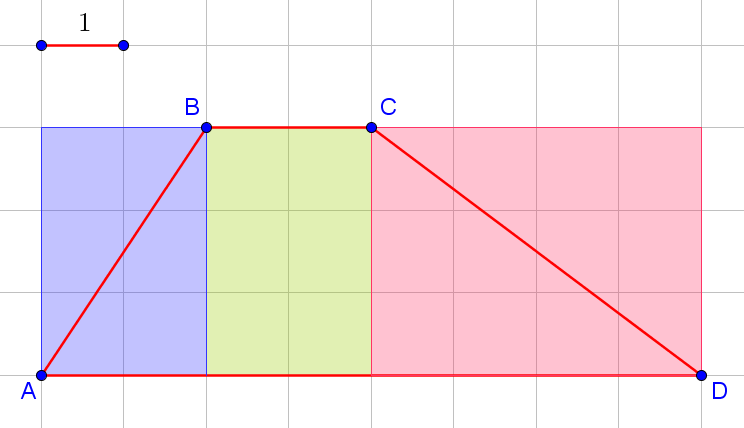
Задача 3. На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Даже если вы забыли формулу площадь трапеции на экзамене, не спешите отчаиваться. Вы всегда может решить задачу проще, чем вас научили в школе. В данном случае можно просто посчитать площадь по клеточкам:
Искомая площадь равна половине площади синего прямоугольника, плюс площади зелёного прямоугольника, плюс половина площади красного прямоугольника. Итого, получаем .
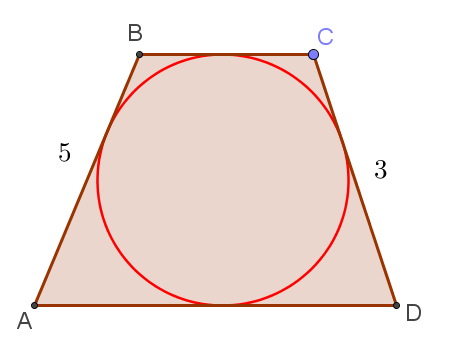
Задача 6. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
По-хорошему, рисунок здесь не нужен. Поскольку в трапецию вписана окружность, то суммы противоположных сторон равны. Следовательно, сумма оснований равна 8, а полусумма и, соответственно, средняя линия трапеции равны 4.
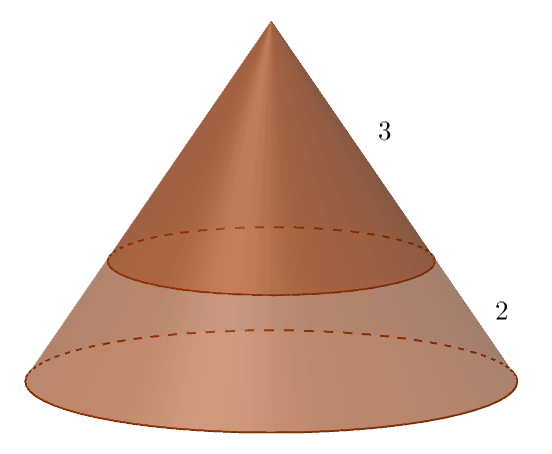
Все линейные размеры малого конуса в раз отличаются от линейных размеров большого конуса. Следовательно, квадратичные размеры (площадь поверхности) малого конуса в
раз отличаются от квадратичных размеров большого конуса. То есть искомая площадь полной поверхности отсечённого конуса равна
.
а) Докажите, что прямая, проходящая через точку O и центр описанной около треугольника ABC окружности, перпендикулярна плоскости ABC.
б) Найдите радиус описанной сферы, если AB = 6, а AD = 4.
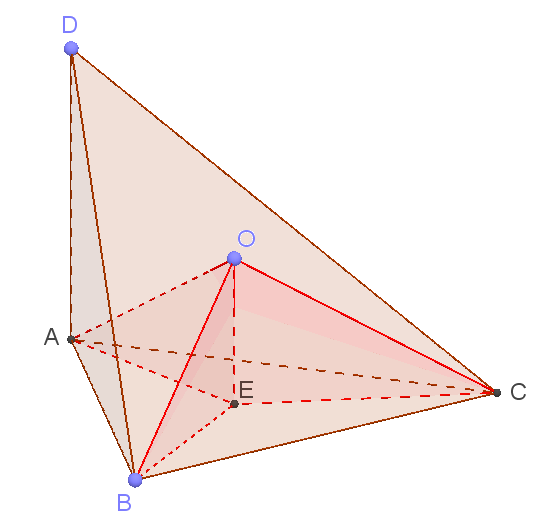
а) Из точки O опустим перпендикуляр OE на плоскость ABC:
Точка O равноудалена от точек A, B и C, так как O — центр описанной около пирамиды окружности. Тогда выделенные красным цветом прямоугольные треугольники AOE, BOE и COE равны по гипотенузе и катету.
Тогда AE = BE = CE. То есть точка E, лежащая в плоскости треугольника ABC, равноудалена от его вершин. Следовательно, она является центром описанной около него окружности. Что и требовалось доказать.
При доказательстве мы использовали так называемый метод решения с конца. Построили требуемый перпендикуляр и доказали, что данные условия задачи удовлетворены.
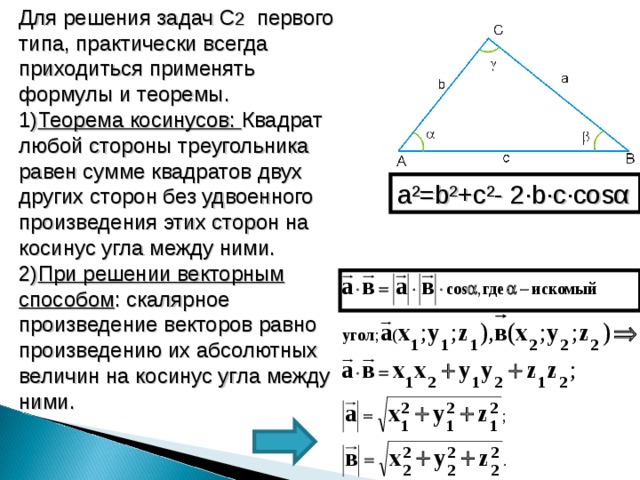
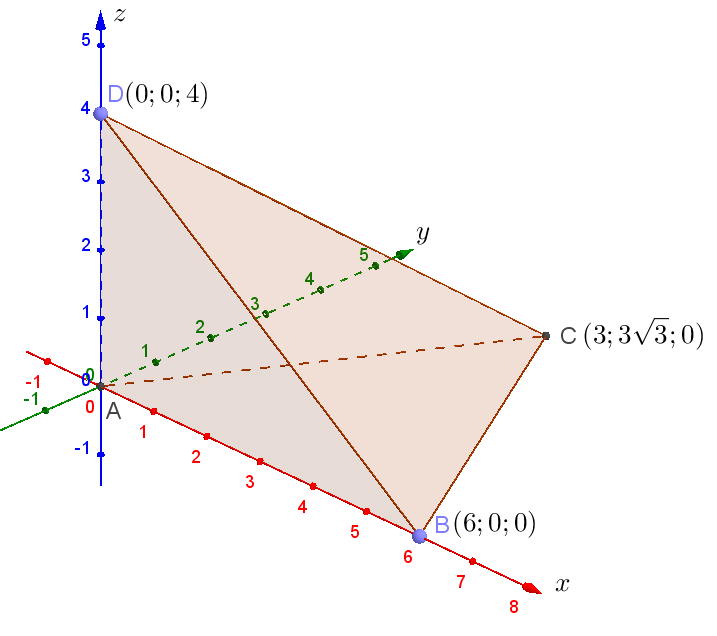
б) Введем систему координат, как показано на рисунке, и определим координаты вершин пирамиды в этой системе:
Пусть центр описанной около этой пирамиды сферы имеет координаты . Пусть радиус сферы равен
. Тогда уравнение сферы во введённой системе координат имеет вид:
Этой сфере принадлежат все вершины данной пирамиды. Следовательно, имеет место следующая система:
Сравнивая первые два уравнения, получаем , откуда
. Аналогично, сравнивая первое и третье уравнения, получаем
, откуда
.
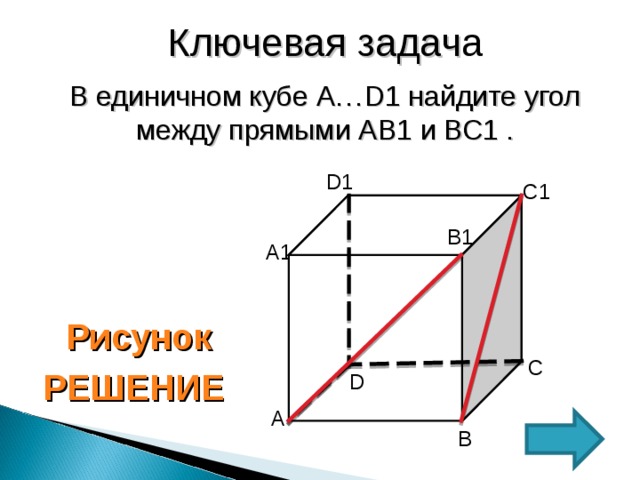
Теперь подставляем полученные значения в первое и последнее уравнение. В результате приходим к системе:
Вычитаем почленно из первого уравнения второе и получаем:
Тогда из первого уравнения получаем, что , откуда
. Отрицательное значение не берём, так как радиус не может быть отрицателен.
Обратите внимание, что попутно мы также получили координаты центра описанной сферы .
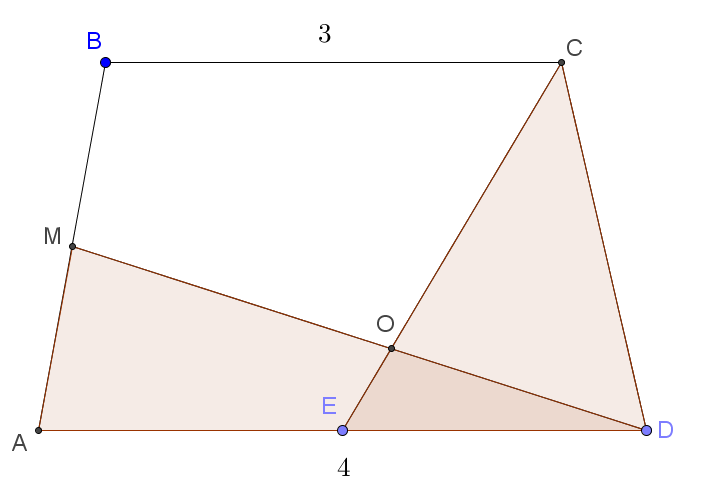
a) Докажите, что площади четырёхугольника AMOE и треугольника COD равны.
б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC = 3, AD = 4.
Изобразим чертёж к задаче:
а) Высота треугольника AMD из вершины M вдвое меньше высоты треугольника ECD из вершины C. При этом основание AD вдвое больше основания ED. Значит площади этих треугольников равны. А поскольку EOD — общая часть этих этих треугольников, то площади четырёхугольника AMOE и треугольника COD равны.
б) Обозначим высоту трапеции за . Тогда её площадь равна
кв. ед., а площадь треугольника AMD равна
кв. ед. Цель состоит в том, чтобы найти площадь треугольника EOD.
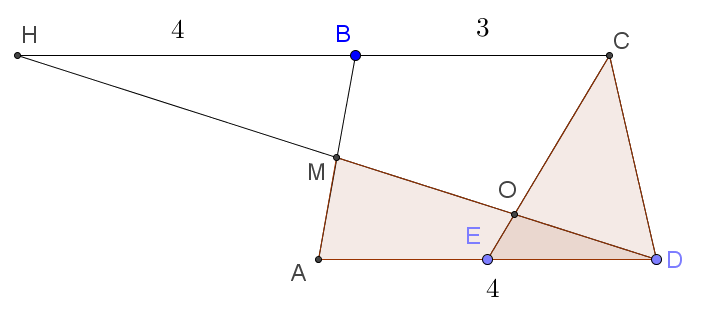
Выполним дополнительное построение: продолжим отрезок MD до пересечения с прямой BC в точке H. Тогда рисунок будет выглядеть следующим образом:
Треугольник HMB равен треугольнику AMD по стороне и двум прилежащим к ней углам. Следовательно, HB равно 4. Треугольник HCO подобен треугольнику ODE по двум углам. При этом коэффициент подобия равен .
Следовательно, высота треугольника OEA, проведенная к основанию ED, равна . Тогда площадь четырёхугольника AMOE равна
кв. ед. Тогда искомое отношение равно
.
Материал подготовлен репетитором по математике и физике в Москве, Сергеем Валерьевичем
Смотрите также:
- Задачи на доказательство геометрических фактов из ГИА;
- Разбор заданий первой части профильного ЕГЭ по математике;
- Разбор задачи 14 профильного ЕГЭ по математике.







![Двугранный угол , образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру. Величина двугранного угла принадлежит промежутку (0°; 180°). Величина угла между пересекающимися плоскостями принадлежит промежутку (0°; 90°]. Угол между двумя параллельными плоскостями равен 0° .](https://fsd.intolimp.org/html/2017/09/18/i_59bfd35d14a4c/img_phpRVR3Z4_S2_22.jpg)
![Rendered by QuickLaTeX.com [ begin{cases} X^2+Y^2+Z^2 = R^2 \ (X-6)^2+Y^2+Z^2 = R^2 \ X^2+Y^2+(Z-4)^2 = R^2 \ (X-3)^2+(Y-3sqrt{3})^2+Z^2 = R^2 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-cc1799655065b3d0f89be57c057d31e3_l3.png)
![Rendered by QuickLaTeX.com [ begin{cases} Y^2 = R^2-13 \ (Y-3sqrt{3})^2 = R^2-4 end{cases} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-8644bbd0eebf2ed67aab0bbdcc379a40_l3.png)