Как решать гиперболу егэ 9 задание

09
Янв 2022

Категория: 10 Графики функций

2022-01-09
2022-09-11

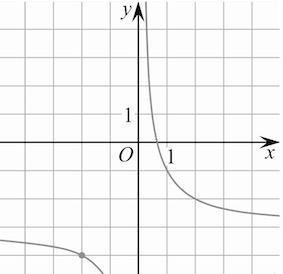
Задача 1. На рисунке изображён график функции $f(x)=frac{k}{x}+a.$ Найдите

Решение: + показать

Задача 2. На рисунке изображён график функции вида $f(x)=frac{a}{x+b}+c,$ где числа и — целые. Найдите значение , при котором

Решение: + показать

Задача 3. На рисунке изображён график функции вида $f(x)=frac{a}{x+b}+c,$ где – целые числа. Найдите $f(frac{8}{3}).$

Решение: + показать

Задача 4. На рисунке изображён график функции $f(x)=frac{kx+a}{x+b}.$ Найдите

Решение: + показать

Задача 5. На рисунке изображены графики функций $f(x)=frac{k}{x}$ и и которые пересекаются в точках и . Найдите ординату точки

Решение: + показать

Вы можете пройти тест “Гиперболы”

Автор: egeMax |

Нет комментариев

Источник

Каталог заданий.
Гиперболы

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 10 № 508951

На рисунке изображён график функции $f левая круглая скобка x правая круглая скобка =dfrackx плюс a.$ Найдите

Аналоги к заданию № 508951: 508971 508952 508953 508954 508955 508956 508957 508958 508959 508960 … Все

Источник: А. Ларин: Тренировочный вариант № 110.

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график

Решение

Сообщить об ошибке · Помощь

Тип 10 № 508961

На рисунке изображён график функции $f левая круглая скобка x правая круглая скобка =dfrackx плюс a.$ Найдите, при каком значении x значение функции равно 0,8.

Аналоги к заданию № 508961: 508983 508962 508963 508964 508965 508966 508967 508968 508969 508970 … Все

Решение

Сообщить об ошибке · Помощь

Тип 10 № 564197

На рисунке изображён график функции вида где числа a, b и c  — целые. Найдите

Аналоги к заданию № 564197: 564198 564199 564200 564201 564202 564203 564204 564205 564206 564207 … Все

Решение

Сообщить об ошибке · Помощь

Тип 10 № 564198

На рисунке изображён график функции вида где числа a, b и c  — целые. Найдите

Аналоги к заданию № 564197: 564198 564199 564200 564201 564202 564203 564204 564205 564206 564207 … Все

Решение

Сообщить об ошибке · Помощь

Тип 10 № 564199

На рисунке изображён график функции вида где числа a, b и c  — целые. Найдите

Аналоги к заданию № 564197: 564198 564199 564200 564201 564202 564203 564204 564205 564206 564207 … Все

Решение

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

Задание
№9 «Графики функции»

ЕГЭ
математика профиль

1) Гиперболы

2) Кусочно-линейная функция

3)Параболы

4) Синусоиды

1) Гиперболы

1. На рисунке изображён график функции вида где числа a, b и c — целые.
Найдите

Решение.

1. На рисунке
изображён график функции вида где
числа a, b и c — целые. Найдите

Решение.

График функции имеет горизонтальную асимптоту значит,

График функции имеет вертикальную асимптоту значит,

По графику тогда

Таким образом, Найдём

Асимпто́та, или аси́мптота^[1] (от др.-греч. ἀσύμπτωτος — несовпадающая, не касающаяся кривой с бесконечной ветвью) — прямая, обладающая тем свойством, что расстояние от
точки кривой до этой прямой стремится к нулю при удалении точки вдоль
ветви в бесконечность^[2]. Термин впервые появился у Аполлония
Пергского, хотя
асимптоты гиперболы исследовал ещё Архимед^[3].

2. На рисунке изображён график функции вида где числа a, b и c — целые.
Найдите

2. На рисунке
изображён график функции вида где
числа a, b и c — целые. Найдите

Решение.

График функции имеет горизонтальную асимптоту значит,

График функции имеет вертикальную асимптоту значит,

По графику тогда

Таким образом, Найдём

Ответ: −0,75.

3. На рисунке изображён график функции вида где числа a, b и c — целые.
Найдите

3. На рисунке
изображён график функции вида где
числа a, b и c — целые. Найдите

Решение.

График функции имеет горизонтальную асимптоту значит,

График функции имеет вертикальную асимптоту значит,

По графику тогда

Таким образом, Найдём

Ответ: 2,875.

2) Кусочно-линейная функция

1. На рисунке
изображён график функции вида где
числа a, b, c и d — целые.
Найдите корень уравнения

1. На рисунке
изображён график функции вида где числа a, b, c и d —
целые. Найдите корень уравнения

Решение.

В любом из
случаев раскрытия модуля получаем линейную функцию  где угловой коэффициент  или  а
свободный член  или  Очевидно, что  значит, большему значению
углового коэффициента соответствует  а
меньшему —  Аналогично большему
значению свободного члена соответствует  а
меньшему —

По рисунку определяем, что Значит,

Решим уравнение

Ответ: 1.

На
рисунке изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения

2. На рисунке
изображён график функции вида где числа a, b, c и d — целые.
Найдите корень уравнения

Решение.

Заметим, что в точке излома, т.е.
при Значит, корнем уравнения является число 2.

3. На рисунке изображён график функции вида где числа a, b, c и d — целые.
Найдите корень уравнения

4. На рисунке изображён график функции вида где числа a, b, c и d — целые.
Найдите корень уравнения

4. На рисунке
изображён график функции вида где числа a, b, c и d — целые.
Найдите корень уравнения

Решение.

Заметим, что в точке излома, т.е.
при Значит, корнем уравнения является число 3.

3)Параболы

На рисунке изображён график функции вида где числа a, b и c —
целые. Найдите значение .

Решение.1 способ

По рисунку определяем, что значит,

Тогда

Решение.2 способ

Выбрать три точки . Например (0;-1),
(6,8), (2;4). Подставив координаты первой точки, мы найдем с=-1. Далее
подставив две другие координаты и с, решаем систему уравнений и находим а и в.

4) Синусоиды

На рисунке
изображён график функции вида где числа a, b, c и d — целые.
Найдите

Решение.

По графику тогда и

По графику тогда, если то

— не
имеет целочисленных решений,

если то

Значит, и

Найдём наименьший положительный период функции

Наименьший положительный период функции равен а по графику наименьший
положительный период равен 2, тогда

Таким образом, Найдём

Ответ: −2.

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ Профиль №10. Гипербола

ЕГЭ Профиль №10. Гиперболаadmin2023-01-13T14:34:23+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №10. Гипербола

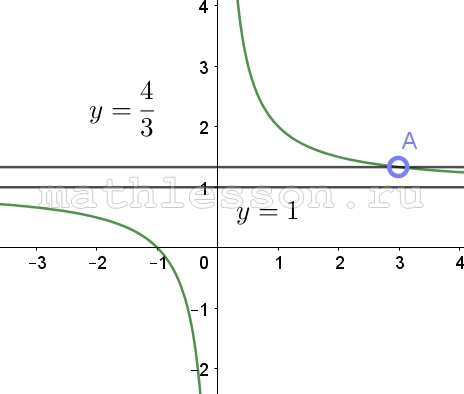
Задача 1. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите (fleft( { — 12} right).) Ответ ОТВЕТ: 0,75.
Решение 1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1;4} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{4 = frac{k}{1} + a}\{2 = frac{k}{3} + a}end{array}} right.) Вычтем из первого уравнения второе: (2 = k — frac{k}{3},,,,,,,, Leftrightarrow ,,,,,,,k = 3.) Тогда: (4 = 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{3}{x} + 1) и (fleft( { — 12} right) = frac{3}{{ — 12}} + 1 = 0,75.) Ответ: 0,75. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = 1). Следовательно, (a = 1). График проходит через точку (left( {1;4} right)), поэтому: (4 = frac{k}{1} + 1,,,,,,,, Leftrightarrow ,,,,,,,k = 3.) Таким образом, (fleft( x right) = frac{3}{x} + 1) и (fleft( { — 12} right) = frac{3}{{ — 12}} + 1 = 0,75.) Ответ: 0,75.
Задача 2. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите (fleft( {50} right).) Ответ ОТВЕТ: — 2,96.
Решение 1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1; — 1} right)) и (left( {2; — 2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = frac{k}{1} + a}\{ — 2 = frac{k}{2} + a}end{array}} right.) Вычтем из первого уравнения второе: (1 = k — frac{k}{2},,,,,,,, Leftrightarrow ,,,,,,,k = 2.) Тогда: ( — 1 = 2 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 3.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{2}{x} — 3) и (fleft( {50} right) = frac{2}{{50}} — 3 = — 2,96.) Ответ: – 2,96. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = — 3). Следовательно, (a = — 3). График проходит через точку (left( {1; — 1} right)), поэтому: ( — 1 = frac{k}{1} — 3,,,,,,,, Leftrightarrow ,,,,,,,k = 2.) Таким образом, (fleft( x right) = frac{2}{x} — 3) и (fleft( {50} right) = frac{2}{{50}} — 3 = — 2,96.) Ответ: – 2,96.
Задача 3. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите (fleft( {7,5} right).) Ответ ОТВЕТ: 1,6.
Решение 1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1; — 1} right)) и (left( {3;1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = frac{k}{1} + a}\{1 = frac{k}{3} + a}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = k — frac{k}{3},,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Тогда: ( — 1 = — 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Следовательно, уравнение гиперболы: (fleft( x right) = — frac{3}{x} + 2) и (fleft( {7,5} right) = — frac{3}{{7,5}} + 2 = 1,6.) Ответ: 1,6. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = 2). Следовательно, (a = 2). График проходит через точку (left( {1; — 1} right)), поэтому: ( — 1 = frac{k}{1} + 2,,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Таким образом, (fleft( x right) = — frac{3}{x} + 2) и (fleft( {7,5} right) = — frac{3}{{7,5}} + 2 = 1,6.) Ответ: 1,6.
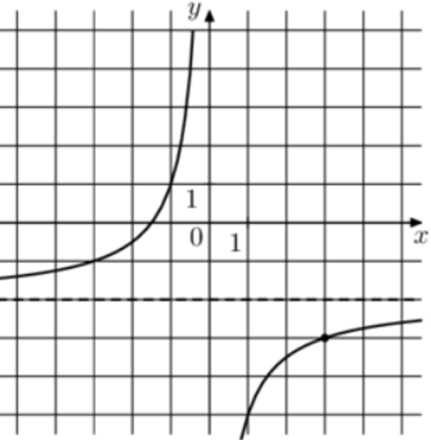
Задача 4. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите (fleft( {0,25} right).) Ответ ОТВЕТ: — 14.
Решение 1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1; — 5} right)) и (left( {3; — 3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 5 = frac{k}{1} + a}\{ — 3 = frac{k}{3} + a}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = k — frac{k}{3},,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Тогда: ( — 5 = — 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Следовательно, уравнение гиперболы: (fleft( x right) = — frac{3}{x} — 2) и (fleft( {0,25} right) = — frac{3}{{0,25}} — 2 = — 14.) Ответ: – 14. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = — 2). Следовательно, (a = — 2). График проходит через точку (left( {1; — 5} right)), поэтому: ( — 5 = frac{k}{1} — 2,,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Таким образом, (fleft( x right) = — frac{3}{x} — 2) и (fleft( {0,25} right) = — frac{3}{{0,25}} — 2 = — 14.) Ответ: – 14.
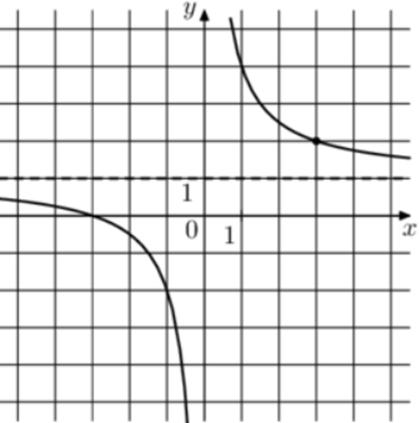
Задача 5. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите, при каком значении x значение функции равно 0,8. Ответ ОТВЕТ: — 15.
Решение 1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1;4} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{4 = frac{k}{1} + a}\{2 = frac{k}{3} + a}end{array}} right.) Вычтем из первого уравнения второе: (2 = k — frac{k}{3},,,,,,,, Leftrightarrow ,,,,,,,k = 3.) Тогда: (4 = 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{3}{x} + 1) и (frac{3}{x} + 1 = 0,8,,,,,,, Leftrightarrow ,,,,,,,,frac{3}{x} = — frac{1}{5},,,,,,,,, Leftrightarrow ,,,,,,,,,x = — 15.) Ответ: – 15. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = 1). Следовательно, (a = 1). График проходит через точку (left( {1;4} right)), поэтому: (4 = frac{k}{1} + 1,,,,,,,, Leftrightarrow ,,,,,,,k = 3.) Таким образом, (fleft( x right) = frac{3}{x} + 1) и (frac{3}{x} + 1 = 0,8,,,,,,,, Leftrightarrow ,,,,,,,,frac{3}{x} = — frac{1}{5},,,,,,,,, Leftrightarrow ,,,,,,,,,,x = — 15.) Ответ: – 15.
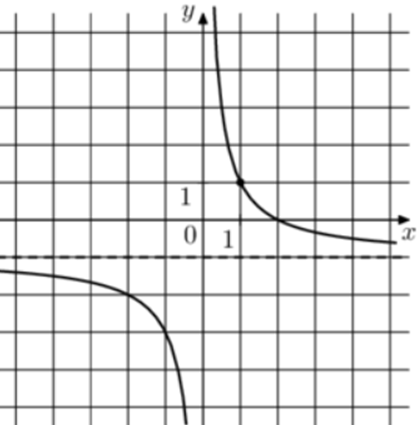
Задача 6. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите, при каком значении x значение функции равно 19. Ответ ОТВЕТ: 0,1.
Решение 1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1;1} right)) и (left( {2;0} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = frac{k}{1} + a}\{0 = frac{k}{2} + a}end{array}} right.) Вычтем из первого уравнения второе: (1 = k — frac{k}{2},,,,,,,, Leftrightarrow ,,,,,,,k = 2.) Тогда: (1 = 2 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 1.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{2}{x} — 1) и (frac{2}{x} — 1 = 19,,,,,,,, Leftrightarrow ,,,,,,,,,frac{2}{x} = 20,,,,,,,,, Leftrightarrow ,,,,,,,,,x = 0,1.) Ответ: 0,1. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = — 1). Следовательно, (a = — 1). График проходит через точку (left( {1;1} right)), поэтому: (1 = frac{k}{1} — 1,,,,,,,, Leftrightarrow ,,,,,,,k = 2.) Таким образом, (fleft( x right) = frac{2}{x} — 1) и (frac{2}{x} — 1 = 19,,,,,,, Leftrightarrow ,,,,,,,,,frac{2}{x} = 20,,,,,,,, Leftrightarrow ,,,,,,,,x = 0,1.) Ответ: 0,1.
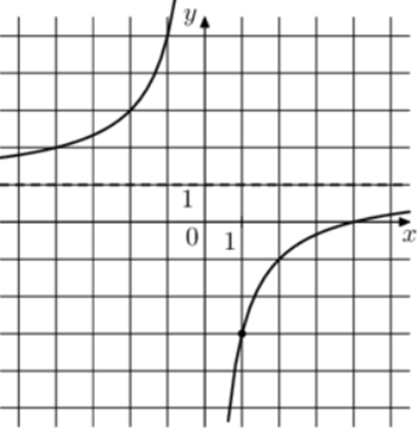
Задача 7. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите, при каком значении x значение функции равно 0,75. Ответ ОТВЕТ: 16.
Решение 1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1; — 3} right)) и (left( {2; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 3 = frac{k}{1} + a}\{ — 1 = frac{k}{2} + a}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = k — frac{k}{2},,,,,,,, Leftrightarrow ,,,,,,,k = — 4.) Тогда: ( — 3 = — 4 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Следовательно, уравнение гиперболы: (fleft( x right) = — frac{4}{x} + 1) и ( — frac{4}{x} + 1 = 0,75,,,,,,, Leftrightarrow ,,,,,,, — frac{4}{x} = — frac{1}{4},,,,,,,, Leftrightarrow ,,,,,,,,x = 16.) Ответ: 16. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = 1). Следовательно, (a = 1). График проходит через точку (left( {1; — 3} right)), поэтому: ( — 3 = frac{k}{1} + 1,,,,,,,, Leftrightarrow ,,,,,,,k = — 4.) Таким образом, (fleft( x right) = — frac{4}{x} + 1) и ( — frac{4}{x} + 1 = 0,75,,,,,,, Leftrightarrow ,,,,,, — frac{4}{x} = — frac{1}{4},,,,,,, Leftrightarrow ,,,,,,x = 16.) Ответ: 16.
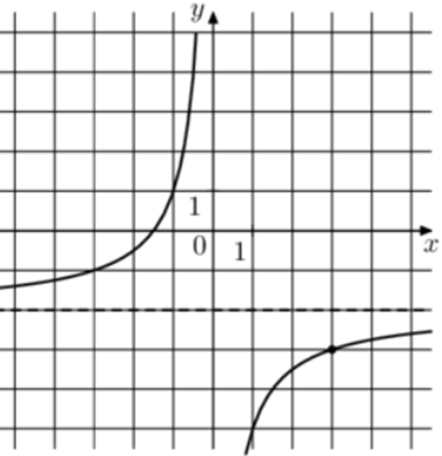
Задача 8. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите, при каком значении x значение функции равно ( — 9,5.) Ответ ОТВЕТ: 0,4.
Решение 1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1; — 5} right)) и (left( {3; — 3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 5 = frac{k}{1} + a}\{ — 3 = frac{k}{3} + a}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = k — frac{k}{3},,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Тогда: ( — 5 = — 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Следовательно, уравнение гиперболы: (fleft( x right) = — frac{3}{x} — 2) и ( — frac{3}{x} — 2 = — 9,5,,,,,,,, Leftrightarrow ,,,,,,,, — frac{3}{x} = — frac{{15}}{2},,,,,,,, Leftrightarrow ,,,,,,,,x = 0,4.) Ответ: 0,4. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = — 2). Следовательно, (a = — 2). График проходит через точку (left( {1; — 5} right)), поэтому: ( — 5 = frac{k}{1} — 2,,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Таким образом, (fleft( x right) = — frac{3}{x} — 2) и ( — frac{3}{x} — 2 = — 9,5,,,,,,, Leftrightarrow ,,,,,,, — frac{3}{x} = — frac{{15}}{2},,,,,, Leftrightarrow ,,,,,,x = 0,4.) Ответ: 0,4.
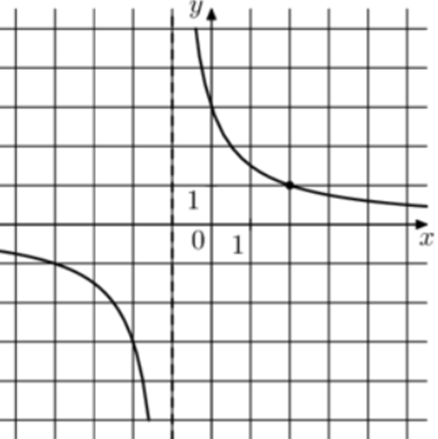
Задача 9. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите (fleft( {19} right).) Ответ ОТВЕТ: 0,15.
Решение 1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( {0;3} right)) и (left( {2;1} right)). (left{ {begin{array}{{20}{c}}{3 = frac{k}{{0 + a}}}\{1 = frac{k}{{2 + a}}}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{{20}{c}}{k = 3a,,,,,}\{k = 2 + a}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,3a = 2 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1,,,,k = 3.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{3}{{x + 1}}) и (fleft( {19} right) = frac{3}{{19 + 1}} = 0,15.) Ответ: 0,15. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = — 1). Следовательно, (a = 1). График проходит через точку (left( {0;3} right)), поэтому: (3 = frac{k}{{0 + 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 3.) Таким образом, (fleft( x right) = frac{3}{{x + 1}}) и (fleft( {19} right) = frac{3}{{19 + 1}} = 0,15). Ответ: 0,15.
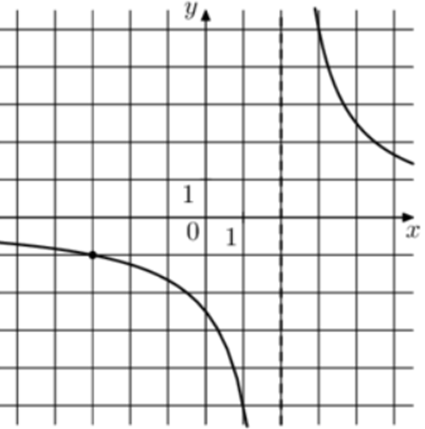
Задача 10. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите (fleft( { — 4frac{2}{3}} right).) Ответ ОТВЕТ: — 0,75.
Решение 1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( { — 3; — 1} right)) и (left( {1; — 5} right)). (left{ {begin{array}{{20}{c}}{ — 1 = frac{k}{{ — 3 + a}}}\{ — 5 = frac{k}{{1 + a}}}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{{20}{c}}{k = 3 — a,,,,,}\{k = — 5 — 5a}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,3 — a = — 5 — 5a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2,,,,k = 5.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{5}{{x — 2}}) и (fleft( { — 4frac{2}{3}} right) = frac{5}{{ — 4frac{2}{3} — 2}} = frac{5}{{ — frac{{20}}{3}}} = — 0,75.) Ответ: – 0,75. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = 2). Следовательно, (a = — 2). График проходит через точку (left( { — 3; — 1} right)), поэтому: ( — 1 = frac{k}{{ — 2 — 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 3.) Таким образом, (fleft( x right) = frac{3}{{x — 2}}) и (fleft( { — 4frac{2}{3}} right) = frac{3}{{ — 4frac{2}{3} — 2}} = frac{5}{{ — frac{{20}}{3}}} = — 0,75.) Ответ: – 0,75.
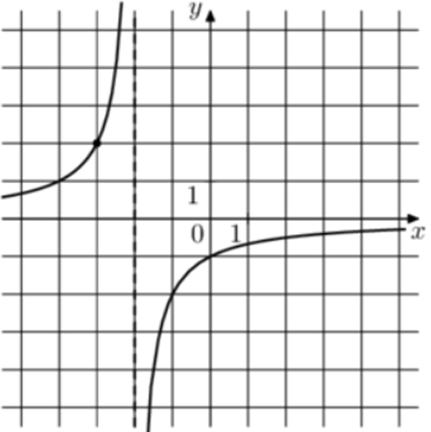
Задача 11. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите (fleft( {18} right).) Ответ ОТВЕТ: — 0,1.
Решение 1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( { — 1; — 2} right)) и (left( { — 3;2} right)). (left{ {begin{array}{{20}{c}}{ — 2 = frac{k}{{ — 1 + a}}}\{2 = frac{k}{{ — 3 + a}}}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{{20}{c}}{k = 2 — 2a,,,,,}\{k = 2a — 6,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,2a — 6 = 2 — 2a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2,,,,k = — 2.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (fleft( {18} right) = frac{{ — 2}}{{18 + 2}} = — 0,1.) Ответ: – 0,1. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = — 2). Следовательно, (a = 2). График проходит через точку (left( { — 1; — 2} right)), поэтому: ( — 2 = frac{k}{{ — 1 + 2}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 2.) Таким образом, (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (fleft( {18} right) = frac{{ — 2}}{{18 + 2}} = — 0,1.) Ответ: – 0,1.
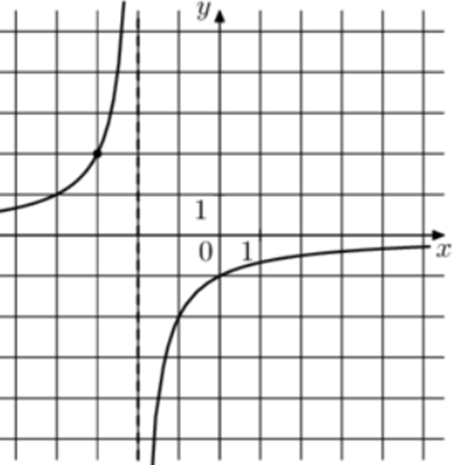
Задача 12. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите (fleft( {6frac{1}{3}} right).) Ответ ОТВЕТ: — 0,24.
Решение 1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( { — 1; — 2} right)) и (left( { — 3;2} right)). (left{ {begin{array}{{20}{c}}{ — 2 = frac{k}{{ — 1 + a}}}\{2 = frac{k}{{ — 3 + a}}}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{{20}{c}}{k = 2 — 2a,,,,,}\{k = 2a — 6,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,2a — 6 = 2 — 2a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2,,,,k = — 2.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (fleft( {6frac{1}{3}} right) = frac{{ — 2}}{{6frac{1}{3} + 2}} = frac{{ — 2}}{{frac{{25}}{3}}} = — 0,24.) Ответ: – 0,24. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = — 2). Следовательно, (a = 2). График проходит через точку (left( { — 1; — 2} right)), поэтому: ( — 2 = frac{k}{{ — 1 + 2}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 2.) Таким образом, (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (fleft( {6frac{1}{3}} right) = frac{{ — 2}}{{6frac{1}{3} + 2}} = frac{{ — 2}}{{frac{{25}}{3}}} = — 0,24.) Ответ: – 0,24.
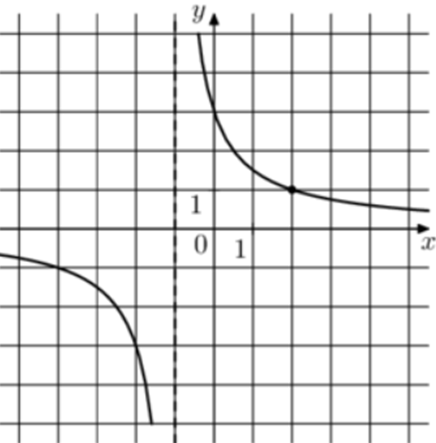
Задача 13. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите значение x, при котором (fleft( x right) = 0,2.) Ответ ОТВЕТ: 14.
Решение 1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( {0;3} right)) и (left( {2;1} right)). (left{ {begin{array}{{20}{c}}{3 = frac{k}{a},,,,,,}\{1 = frac{k}{{2 + a}}}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{{20}{c}}{k = 3a,,,,,,,,,,,}\{k = 2 + a,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,3a = 2 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1,,,,k = 3.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{3}{{x + 1}}) и (frac{3}{{x + 1}} = 0,2,,,,,,,, Leftrightarrow ,,,,,,,x + 1 = 15,,,,,,, Leftrightarrow ,,,,,,,x = 14.) Ответ: 14. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = — 1). Следовательно, (a = 1). График проходит через точку (left( {0;3} right)), поэтому: (3 = frac{k}{{0 + 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 3.) Таким образом, (fleft( x right) = frac{3}{{x + 1}}) и (frac{3}{{x + 1}} = 0,2,,,,,,,, Leftrightarrow ,,,,,,,x + 1 = 15,,,,,,, Leftrightarrow ,,,,,,,x = 14.) Ответ: 14.
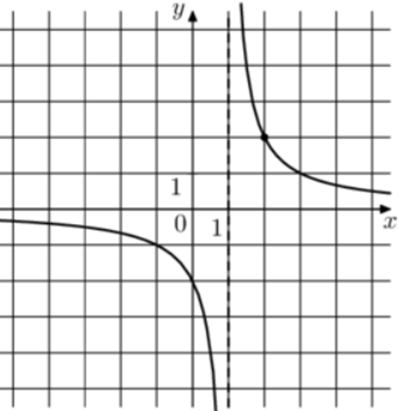
Задача 14. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите значение x, при котором (fleft( x right) = — 0,08.) Ответ ОТВЕТ: — 24.
Решение 1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( {2;2} right)) и (left( {3;1} right)). (left{ {begin{array}{{20}{c}}{2 = frac{k}{{2 + a}},,,,,,}\{1 = frac{k}{{3 + a}},,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{{20}{c}}{k = 4 + 2a,,,,,,,,,,,}\{k = 3 + a,,,,,,,,,,,,,,}end{array}} right., Leftrightarrow ,,,,,,,4 + ,2a = 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 1,,,,k = 2.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{2}{{x — 1}}) и (frac{2}{{x — 1}} = — 0,08,,,,,,,, Leftrightarrow ,,,,,,,x — 1 = — 25,,,,,,, Leftrightarrow ,,,,,,,x = — 24.) Ответ: – 24. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = 1). Следовательно, (a = — 1). График проходит через точку (left( {2;2} right)), поэтому: (2 = frac{k}{{2 — 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 2.) Таким образом, (fleft( x right) = frac{2}{{x — 1}}) и (frac{2}{{x — 1}} = — 0,08,,,,,,,, Leftrightarrow ,,,,,,,x — 1 = — 25,,,,,,, Leftrightarrow ,,,,,,,x = — 24.) Ответ: – 24.
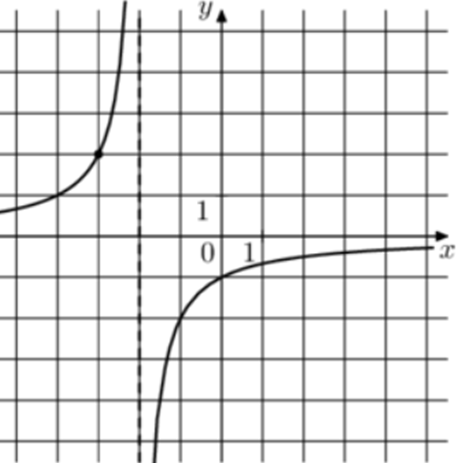
Задача 15. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите значение x, при котором (fleft( x right) = — 0,04.) Ответ ОТВЕТ: 48.
Решение 1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( { — 1; — 2} right)) и (left( { — 3;2} right)). (left{ {begin{array}{{20}{c}}{ — 2 = frac{k}{{ — 1 + a}},,,,,,}\{2 = frac{k}{{ — 3 + a}},,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{{20}{c}}{k = 2 — 2a}\{k = 2a — 6}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,2a — 6 = 2 — 2a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2,,,,k = — 2.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (frac{{ — 2}}{{x + 2}} = — 0,04,,,,,,,, Leftrightarrow ,,,,,,,x + 2 = 50,,,,,,, Leftrightarrow ,,,,,,,x = 48.) Ответ: 48. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = — 2). Следовательно, (a = 2). График проходит через точку (left( { — 1; — 2} right)), поэтому: ( — 2 = frac{k}{{ — 1 + 2}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 2.) Таким образом, (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (frac{{ — 2}}{{x + 2}} = — 0,04,,,,,,,, Leftrightarrow ,,,,,,,x + 2 = 50,,,,,,, Leftrightarrow ,,,,,,,x = 48.) Ответ: 48.
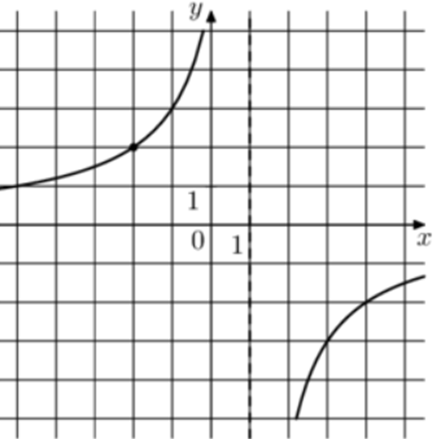
Задача 16. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите значение x, при котором (fleft( x right) = 0,2.) Ответ ОТВЕТ: — 29.
Решение 1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( {3; — 3} right)) и (left( { — 1;3} right)). (left{ {begin{array}{{20}{c}}{ — 3 = frac{k}{{3 + a}},,,,,,}\{3 = frac{k}{{ — 1 + a}},,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{{20}{c}}{k = — 9 — 3a,,,,,,,,,,,}\{k = 3a — 3,,,,,,,,,,,,,,}end{array}} right., Leftrightarrow ,,,,,,,3a — 3 = — 9 — 3a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 1,,,,k = — 6.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{{ — 6}}{{x — 1}}) и (frac{{ — 6}}{{x — 1}} = 0,2,,,,,,,, Leftrightarrow ,,,,,,,x — 1 = — 30,,,,,,, Leftrightarrow ,,,,,,,x = — 29.) Ответ: – 29. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = 1). Следовательно, (a = — 1). График проходит через точку (left( {3; — 3} right)), поэтому: ( — 3 = frac{k}{{3 — 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 6.) Таким образом, (fleft( x right) = frac{{ — 6}}{{x — 1}}) и (frac{{ — 6}}{{x — 1}} = 0,2,,,,,,,, Leftrightarrow ,,,,,,,x — 1 = — 30,,,,,,, Leftrightarrow ,,,,,,,x = — 29.) Ответ: – 29.

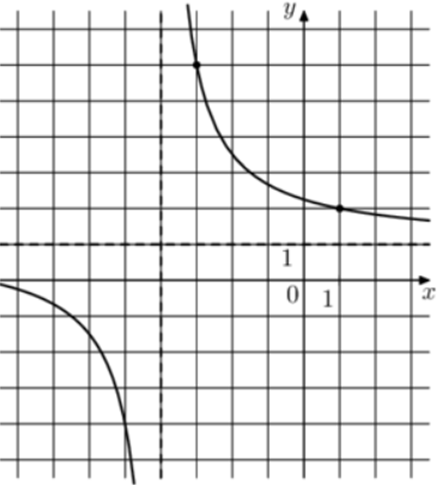
Задача 17. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите k. Ответ ОТВЕТ: 1.
Решение Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = 1), то (k = 1). Ответ: 1.
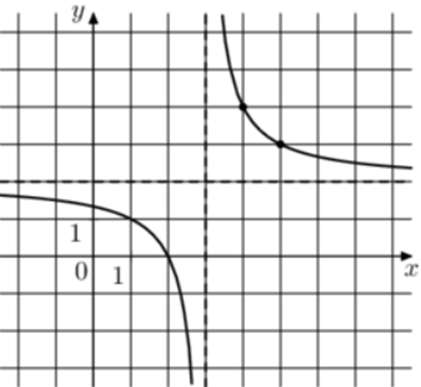
Задача 18. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите k. Ответ ОТВЕТ: 2.
Решение Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = 2), то (k = 2). Ответ: 2.
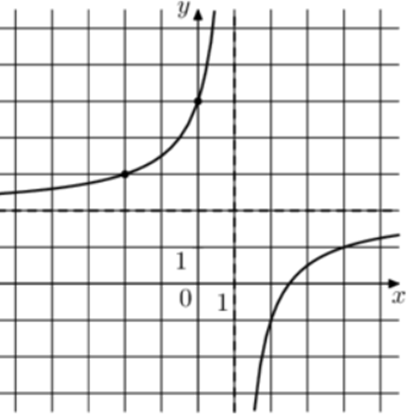
Задача 19. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите k. Ответ ОТВЕТ: 2.
Решение Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = 2), то (k = 2). Ответ: 2.
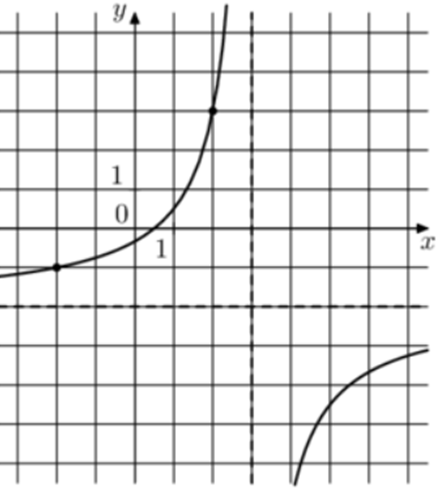
Задача 20. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите k. Ответ ОТВЕТ: — 2.
Решение Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = -2), то (k = -2). Ответ: -2.
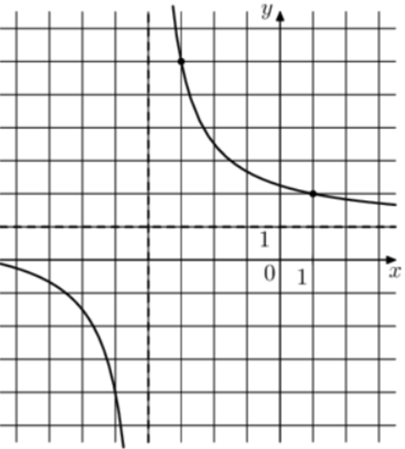
Задача 21. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите a. Ответ ОТВЕТ: 9.
Решение Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = 1), то (k = 1). Так как график функции имеет вертикальную асимптоту (x = — 4), то (b = 4). Следовательно: (fleft( x right) = 1 + frac{{a — 4}}{{x + 4}}.) Воспользуемся тем, что график функции проходит через точку (left( { — 3;6} right)). Тогда: (6 = 1 + frac{{a — 4}}{{ — 3 + 4}},,,,,,,, Leftrightarrow ,,,,,,,,frac{{a — 4}}{1} = 5,,,,,,,,, Leftrightarrow ,,,,,,,,a = 9.,,,) Ответ: 9.
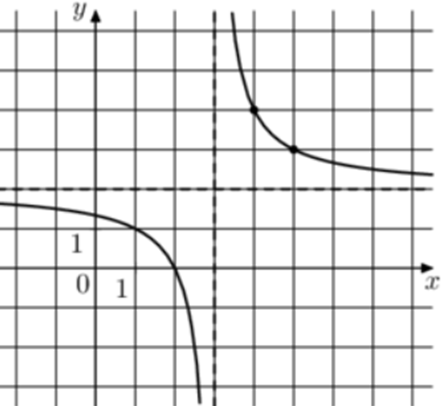
Задача 22. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите a. Ответ ОТВЕТ: — 4.
Решение Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = 2), то (k = 2). Так как график функции имеет вертикальную асимптоту (x = 3), то (b = — 3). Следовательно: (fleft( x right) = 2 + frac{{a + 6}}{{x — 3}}.) Воспользуемся тем, что график функции проходит через точку (left( {5;3} right)). Тогда: (3 = 2 + frac{{a + 6}}{{5 — 3}},,,,,,,, Leftrightarrow ,,,,,,,,frac{{a + 6}}{2} = 1,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 4.,,,) Ответ: – 4.
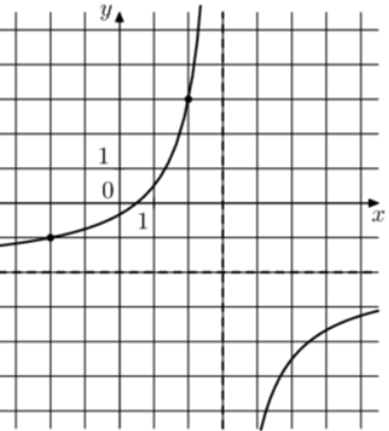
Задача 23. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите a. Ответ ОТВЕТ: 1.
Решение Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = — 2), то (k = — 2). Так как график функции имеет вертикальную асимптоту (x = 3), то (b = — 3). Следовательно: (fleft( x right) = — 2 + frac{{a — 6}}{{x — 3}}.) Воспользуемся тем, что график функции проходит через точку (left( {2;3} right)). Тогда: (3 = — 2 + frac{{a — 6}}{{2 — 3}},,,,,,,, Leftrightarrow ,,,,,,,,frac{{a — 6}}{{ — 1}} = 5,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.,,,) Ответ: 1.
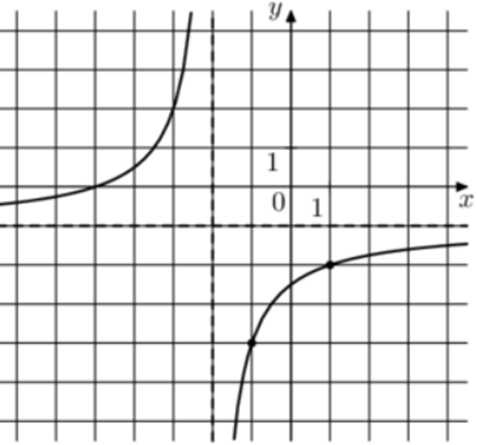
Задача 24. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите a. Ответ ОТВЕТ: — 5.
Решение Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = — 1), то (k = — 1). Так как график функции имеет вертикальную асимптоту (x = — 2), то (b = 2). Следовательно: (fleft( x right) = — 1 + frac{{a + 2}}{{x + 2}}.) Воспользуемся тем, что график функции проходит через точку (left( { — 1; — 4} right)). Тогда: ( — 4 = — 1 + frac{{a + 2}}{{ — 1 + 2}},,,,,,,, Leftrightarrow ,,,,,,,,a + 2 = — 3,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 5.,,,) Ответ: – 5.
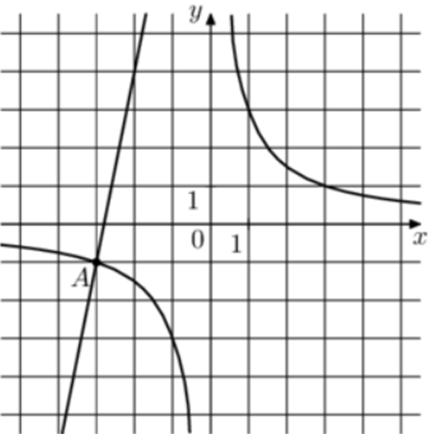
Задача 25. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите абсциссу точки B. Ответ ОТВЕТ: 0,2.
Решение График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( {1;3} right)). Следовательно: (3 = frac{k}{1},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 3.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = frac{3}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( { — 3; — 1} right)) и (left( { — 2;4} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 1 = — 3a + b}\{4 = — 2a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 5 = — a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = 5.) Тогда: ( — 1 = — 3 cdot 5 + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = 14.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = 5x + 14.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{{20}{c}}{y = 5x + 14}\{y = frac{3}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,5x + 14 = frac{3}{x},,,,,,,,, Leftrightarrow ,,,,,,,5{x^2} + 14x — 3 = 0,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 0,2,,,,{x_2} = — 3.) Значение (x = — 3) является абсциссой точки А. Следовательно, абсцисса точки В равна 0,2. Ответ: 0,2.
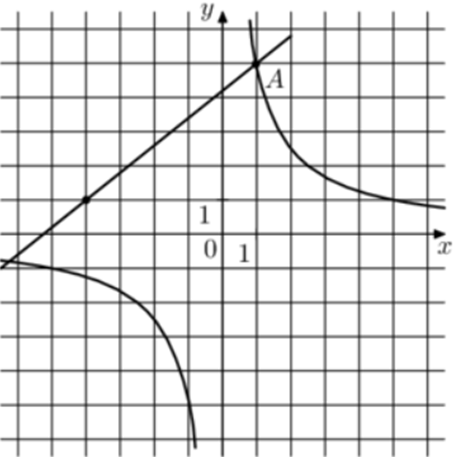
Задача 26. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите абсциссу точки B. Ответ ОТВЕТ: — 6,25.
Решение График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( {1;5} right)). Следовательно: (5 = frac{k}{1},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 5.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = frac{5}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( { — 4;1} right)) и (left( {1;5} right)). Следовательно: (left{ {begin{array}{{20}{c}}{1 = — 4a + b}\{5 = a + b,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 4 = — 5a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = frac{4}{5}.) Тогда: (1 = — 4 cdot frac{4}{5} + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = frac{{21}}{5}.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = frac{4}{5}x + frac{{21}}{5}.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{{20}{c}}{y = frac{4}{5}x + frac{{21}}{5}}\{y = frac{5}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,frac{4}{5}x + frac{{21}}{5} = frac{5}{x},,,,,,,,, Leftrightarrow ,,,,,,,4{x^2} + 21x — 25 = 0,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = — 6,25.) Значение (x = 1) является абсциссой точки А. Следовательно, абсцисса точки В равна – 6,25. Ответ: – 6,25.
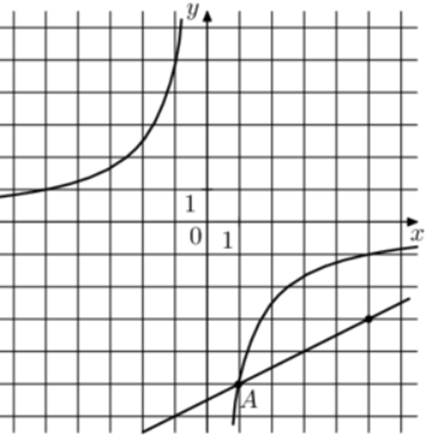
Задача 27. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите абсциссу точки B. Ответ ОТВЕТ: 10.
Решение График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( {1; — 5} right)). Следовательно: ( — 5 = frac{k}{1},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 5.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = — frac{5}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( {1; — 5} right)) и (left( {5; — 3} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 5 = a + b,,,}\{ — 3 = 5a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = — 4a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = frac{1}{2}.) Тогда: ( — 5 = frac{1}{2} + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = — frac{{11}}{2}.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = frac{1}{2}x — frac{{11}}{2}.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{{20}{c}}{y = frac{1}{2}x — frac{{11}}{2}}\{y = — frac{5}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,frac{1}{2}x — frac{{11}}{2} = — frac{5}{x},,,,,,,,, Leftrightarrow ,,,,,,,{x^2} — 11x + 10 = 0,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = 10.) Значение (x = 1) является абсциссой точки А. Следовательно, абсцисса точки В равна 10. Ответ: 10.
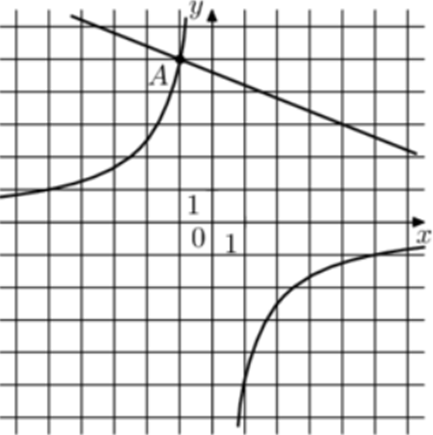
Задача 28. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите абсциссу точки B. Ответ ОТВЕТ: 12,5.
Решение График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( { — 1;5} right)). Следовательно: (5 = frac{k}{{ — 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 5.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = — frac{5}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( { — 1;5} right)) и (left( {4;3} right)). Следовательно: (left{ {begin{array}{{20}{c}}{5 = — a + b}\{3 = 4a + b}end{array}} right.) Вычтем из первого уравнения второе: (2 = — 5a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = — frac{2}{5}.) Тогда: (5 = frac{2}{5} + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = frac{{23}}{5}.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = — frac{2}{5}x + frac{{23}}{5}.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{{20}{c}}{y = — frac{2}{5}x + frac{{23}}{5}}\{y = — frac{5}{x},,,,,,,,,,,,,,,,}end{array}} right.,,,,,, Leftrightarrow ,,,,,,, — frac{2}{5}x + frac{{23}}{5} = — frac{5}{x},,,,,,, Leftrightarrow ,,,,,,2{x^2} — 23x — 25 = 0,,,,,, Leftrightarrow ,,,,,,{x_1} = — 1,,,,{x_2} = 12,5.) Значение (x = — 1) является абсциссой точки А. Следовательно, абсцисса точки В равна 12,5. Ответ: 12,5.
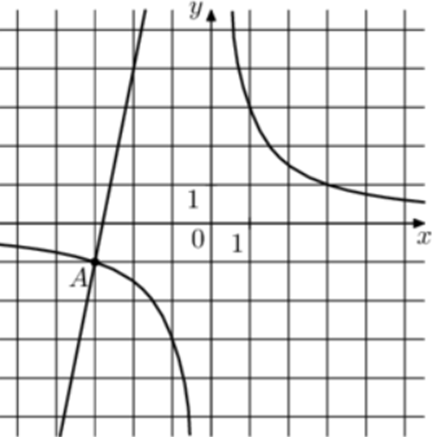
Задача 29. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите ординату точки B. Ответ ОТВЕТ: 15.
Решение График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( { — 3; — 1} right)). Следовательно: ( — 1 = frac{k}{{ — 3}},,,,,, Leftrightarrow ,,,,,,,k = 3.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = frac{3}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( { — 3; — 1} right)) и (left( { — 2;4} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 1 = — 3a + b}\{4 = — 2a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 5 = — a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = 5.) Тогда: ( — 1 = — 15 + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = 14.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = 5x + 14.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{{20}{c}}{y = 5x + 14}\{y = frac{3}{x},,,,,,,,,,,,,}end{array}} right.,,,,,, Leftrightarrow ,,,,,,5x + 14 = frac{3}{x},,,,,, Leftrightarrow ,,,,,5{x^2} + 14x — 3 = 0,,,,,, Leftrightarrow ) ( Leftrightarrow ,,,,,{x_1} = — 3,,,,{x_2} = frac{1}{5},,,,{y_1} = — 1,,,,,{y_2} = 15.) Следовательно, (Aleft( { — 3; — 1} right)) и (Bleft( {frac{1}{5};15} right)). Таким образом, ордината точки В равна 15. Ответ: 15.
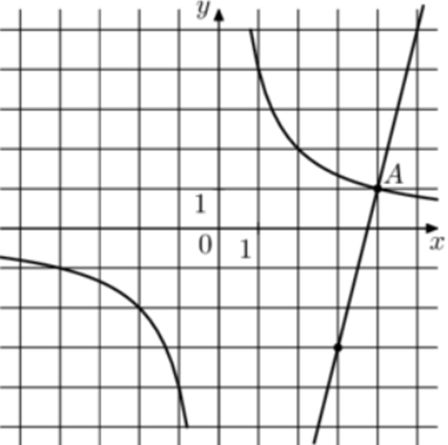
Задача 30. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите ординату точки B. Ответ ОТВЕТ: — 16.
Решение График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( {4;1} right)). Следовательно: (1 = frac{k}{4},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 4.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = frac{4}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( {4;1} right)) и (left( {3; — 3} right)). Следовательно: (left{ {begin{array}{{20}{c}}{1 = 4a + b,,}\{ — 3 = 3a + b}end{array}} right.) Вычтем из первого уравнения второе: (4 = a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = 4.) Тогда: (1 = 16 + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = — 15.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = 4x — 15.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{{20}{c}}{y = 4x — 15}\{y = frac{4}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,4x — 15 = frac{4}{x},,,,,,,,, Leftrightarrow ,,,,,,,4{x^2} — 15x — 4 = 0,,,,,,, Leftrightarrow )( Leftrightarrow ,,,,,{x_1} = 4,,,,{x_2} = — frac{1}{4},,,,{y_1} = 1,,,,,{y_2} = — 16.) Следовательно, (Aleft( {4;1} right)) и (Bleft( { — frac{1}{4}; — 16} right)). Таким образом, ордината точки В равна – 16. Ответ: – 16.
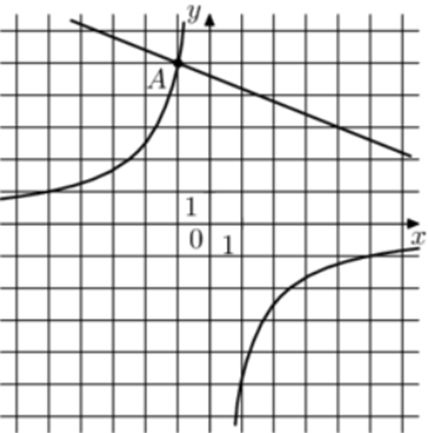
Задача 31. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите ординату точки B. Ответ ОТВЕТ: — 0,4.
Решение График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( { — 1;5} right)). Следовательно: (5 = frac{k}{{ — 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 5.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = — frac{5}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( { — 1;5} right)) и (left( {4;3} right)). Следовательно: (left{ {begin{array}{{20}{c}}{5 = — a + b,,}\{3 = 4a + b,,}end{array}} right.) Вычтем из первого уравнения второе: (2 = — 5a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = — frac{2}{5}.) Тогда: (5 = frac{2}{5} + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = frac{{23}}{5}.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = — frac{2}{5}x + frac{{23}}{5}.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{{20}{c}}{y = — frac{2}{5}x + frac{{23}}{5}}\{y = — frac{5}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,, — frac{2}{5}x + frac{{23}}{5} = — frac{5}{x},,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} — 23x — 25 = 0,,,,,,, Leftrightarrow ,,,,,,,,,,,) ( Leftrightarrow ,,,,,,{x_1} = — 1,,,,{x_2} = frac{{25}}{2},,,,,,,,,,{y_1} = 5,,,,{y_2} = — 0,4.) Следовательно, (Aleft( { — 1;5} right)) и (Bleft( {frac{{25}}{2}; — 0,4} right)). Таким образом, ордината точки В равна – 0,4. Ответ: – 0,4.
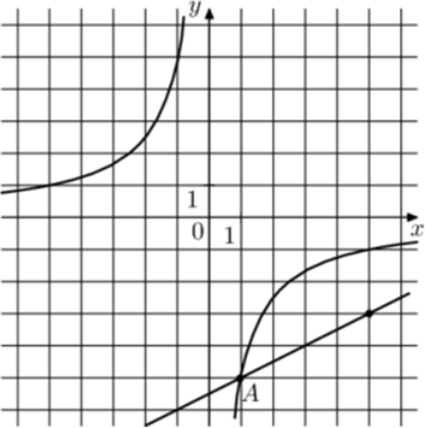
Задача 32. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите ординату точки B. Ответ ОТВЕТ: — 0,5.
Решение График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( {1; — 5} right)). Следовательно: ( — 5 = frac{k}{1},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 5.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = — frac{5}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( {1; — 5} right)) и (left( {5; — 3} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 5 = a + b,,,}\{ — 3 = 5a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = — 4a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = frac{1}{2}.) Тогда: ( — 5 = frac{1}{2} + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = — frac{{11}}{2}.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = frac{1}{2}x — frac{{11}}{2}.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{{20}{c}}{y = frac{1}{2}x — frac{{11}}{2}}\{y = — frac{5}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,frac{1}{2}x — frac{{11}}{2} = — frac{5}{x},,,,,,,,, Leftrightarrow ,,,,,,,{x^2} — 11x + 10 = 0,,,,,,, Leftrightarrow ,,,,,,,,) ( Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = 10,,,,,,,,,,,{y_1} = — 5,,,,{y_2} = — 0,5.) Следовательно, (Aleft( {1; — 5} right)) и (Bleft( {10; — 0,5} right)). Таким образом, ордината точки В равна – 0,5. Ответ: – 0,5.

Источник

Cайты учителей
Все блоги
Все файлы
Все тесты

1
Войти
Зарегистрироваться / Создать сайт

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Была в сети 31.01.2022 15:49

Бабошкина Любовь Юрьевна

Учитель математики

66 лет

1 724
23 226

09.11.2021 20:48

В презентации разбирается один из способов решения задания №9 ЕГЭ (гиперболы)

Просмотр содержимого документа

«Графики функции. Задание №9 ЕГЭ-2022»

Графики функций

Щёлкать мышкой не надо. Презентация с голосовым сопровождением и будет перелистываться сама

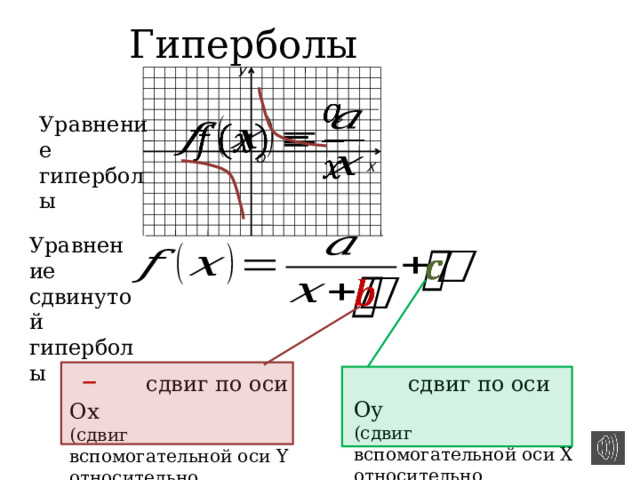
Гиперболы

Уравнение гиперболы

Уравнение

сдвинутой

гиперболы

– сдвиг по оси Ох

(сдвиг вспомогательной оси Y относительно основной)

сдвиг по оси Оу

(сдвиг вспомогательной оси Х относительно основной)

y 1

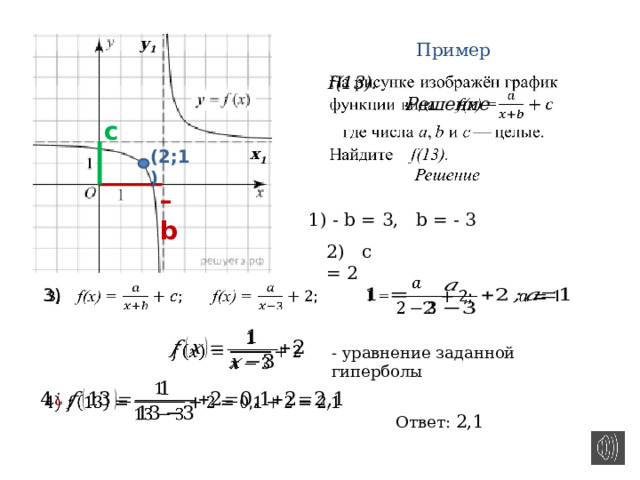
Пример

f(13).

Решение

x 1

(2;1)

– b

1) — b = 3, b = — 3

2) c = 2

— уравнение заданной гиперболы

Ответ: 2,1

ОГЭ

(C3) Функции и их свойства. Графики функций

Гиперболы

Задание 3407

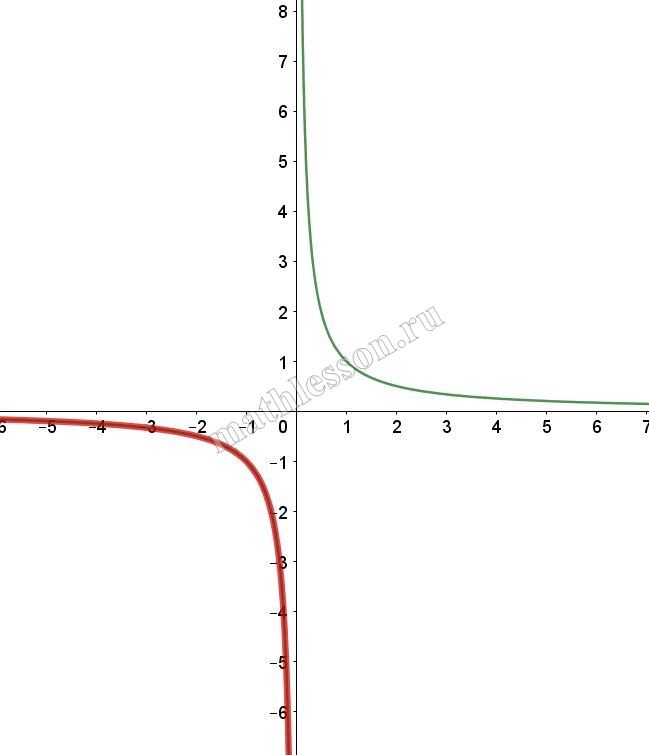
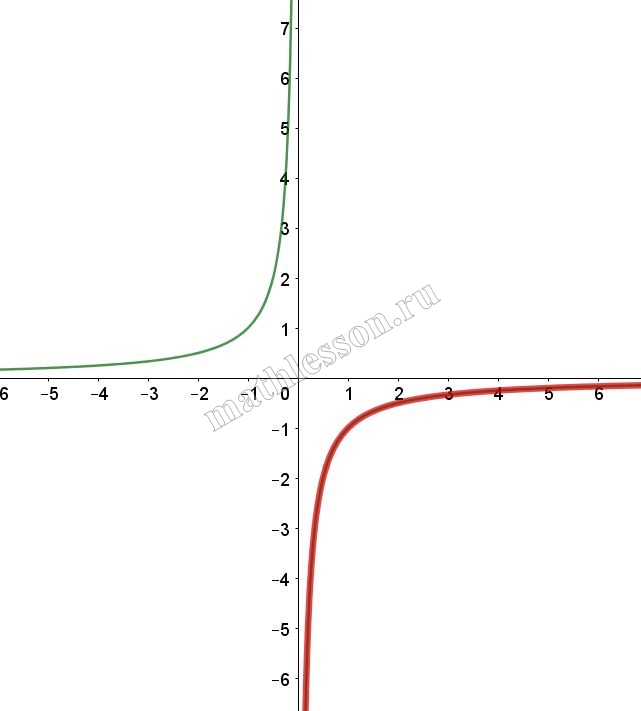
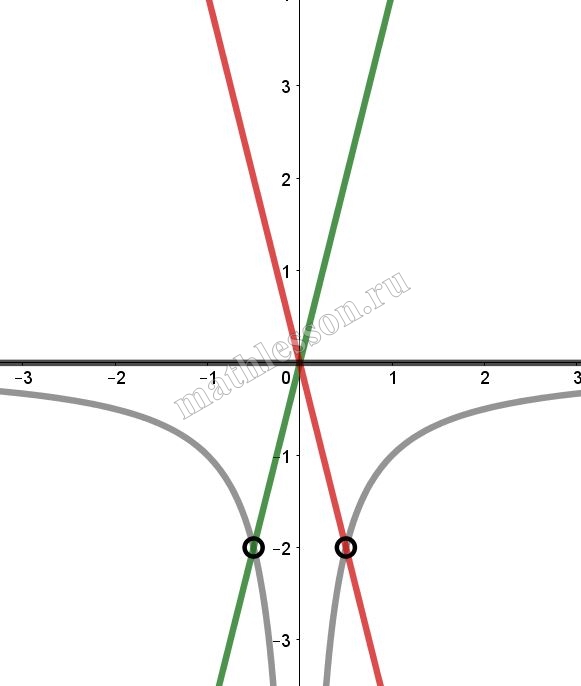
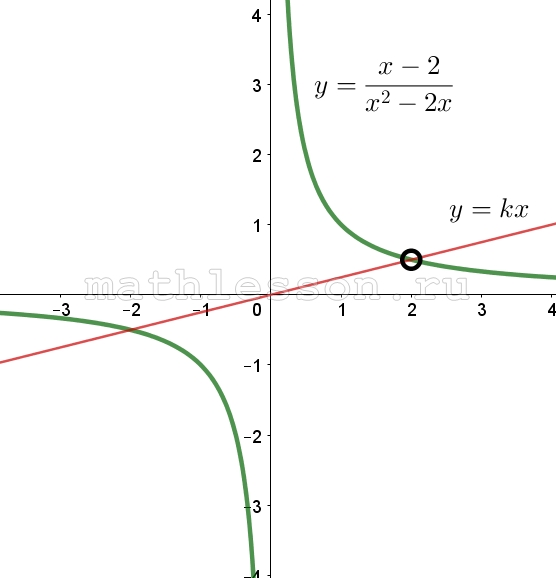
Постройте график функции $$y=frac{x+2}{x^{2}+2x}$$ и определите, при каких значениях k прямая $$y=kx$$ имеет с графиком ровно одну общую точку.

Ответ: $$frac{1}{4}$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 3843

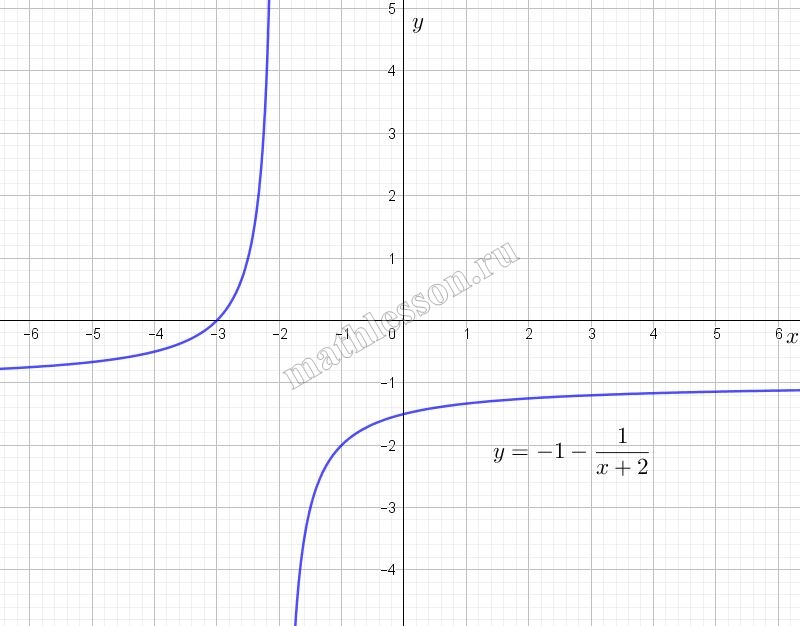
Постройте график функции $$y=1-frac{2x+4}{x^{2}+2x}$$ и определите, при каких значениях а прямая $$y=а$$ не имеет с графиком ни одной общей точки.

Ответ: $${1;2}$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$y=1-frac{2x+4}{x^{2}+2x}=1-frac{2(x+2)}{x(x+2)}=1-frac{2}{x}$$

$$xneq0$$; $$xneq2$$ $$Rightarrow$$ $$(-2;2)$$ не входит

Тогда $$y=2$$; $$y=1$$ не имеют общих точек с $$y=1-frac{2x+4}{x^{2}+2x}$$

Задание 4534

Постройте график функции $$y=2+frac{x+2}{x^{2}+2x}$$ и определите, при каких значениях m прямая y = m не имеет с графиком ни одной общей точки.

Ответ: $$m=1,5$$; $$m=2$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$y=2+frac{x+2}{x^{2}+2x}=2+frac{x+2}{x(x+2)}=2+frac{1}{x}$$; $$x^{2}neq2xneq0$$; $$xneq0$$; $$xneq-2$$.

$$m=1,5$$; $$m=2$$

Задание 5271

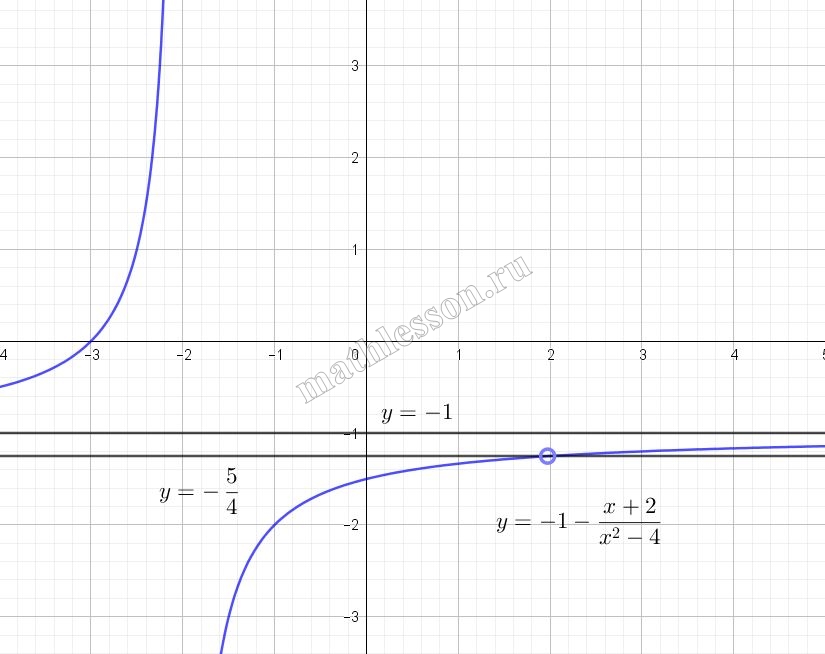
Постройте график функции $$y=-1-frac{x-2}{x^{2}-4}$$ и определите, при каких значениях $$a$$ прямая $$y=a$$ не имеет с графиком ни одной общей точки.

Ответ: $$-frac{5}{4} ; -1$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

ОДЗ: $$x^{2}-4 neq 0 Leftrightarrow$$$$xneqpm 2$$. Преобразуем правую часть функции: $$-1-frac{x-2}{x^{2}-4}=$$$$-1-frac{x-2}{(x-2)(x+2)}=$$$$-1-frac{1}{x+2}$$

То есть график функции $$y_{1}=-1-frac{1}{x+2}$$ и график искомой функции совпадают, если к $$y_{1}$$ применить ОДЗ для искомой. График функции $$y_{1}$$ — гипербола, смещенная на 1 единицу вних и на две влево относительно графика эталонной обратной пропорциональности $$y=frac{1}{x}$$. Начертим график функции $$y_{1}$$:

Учтем, что $$xneqpm 2$$. В случае $$xneq -2$$ можно отдельно не рассматривать, так как это условие уже выполняется для графика функции $$y_{1}$$. Для $$xneq 2$$: подставим значение $$x=2$$ в функции $$y_{1}$$: $$y_{1}(2)=-1-frac{1}{2+2}=-frac{5}{4}$$. То есть точку, с координатами $$(2;-frac{5}{4})$$ необходимо отметить пустой на графике функции $$y_{1}$$ и тогда мы получим график искомой функции:

Прямая $$y=a$$ — прямая паралленая оси Ох, чтобы она не имела с графиком искомой функции точек пересечения она должны использоваться следующие значения $$a=-1;-frac{5}{4}$$:

Задание 5481

Постройте график функции $$y=frac{2,5|x|-1}{|x|-2,5x^{2}}$$. Определите, при каких значениях k прямая y = kx не имеет с графиком общих точек.

Ответ:

Задание 5482

Постройте график функции $$y=3-frac{x+5}{x^{2}+5x}$$ и определите, при каких значениях m прямая y = m не имеет с графиком ни одной общей точки.

Ответ:

Задание 5483

Постройте график функции $$y=frac{1-2x}{2x^{2}-x}$$, и определите, при каких значениях k прямая y=kx имеет с график ровно одну общую точку

Ответ:

Задание 6070

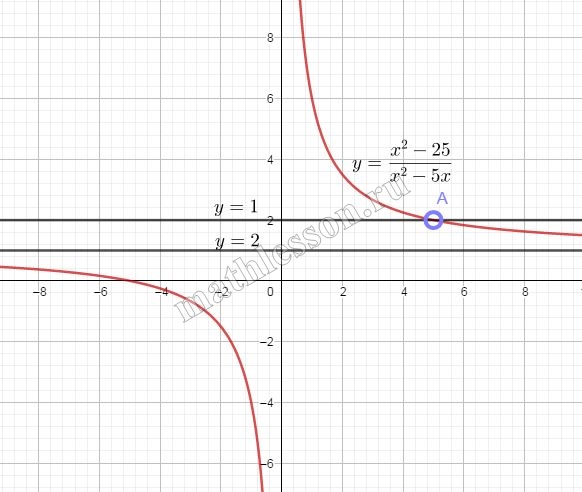
Постройте график функции $$y=frac{x^{2}-25}{x^{2}-5x}$$ и определите, при каких значениях a прямая $$y=a$$ не имеет с графиком ни одной общей точки.

Ответ: a=1 и a=2

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$y=frac{x^{2}-25}{x^{2}-5x}$$

ОДЗ: $$x^{2}-5xneq 0 Leftrightarrow x(x-5)=0Leftrightarrow$$$$ xneq 0; xneq 5Rightarrow xin (-infty; 0)cup(5 ;+infty ).$$

Упростим выражение: $$frac{x^{2}-25}{x^{2}-5x}=frac{(x-5)*(x+5)}{x(x-5)}=frac{x+5}{x}=1+frac{5}{x}$$ Т.е. график $$y=1+frac{5}{x}$$ такой же, как $$y=frac{x^{2}-25}{x^{2}-5x}$$ при условии ОДЗ:

Прямая $$y=a$$ — это прямая, параллельная оси Ох. Она не будет иметь пересечения с графиком исходной функции при a=2 и a=1.

Задание 6449

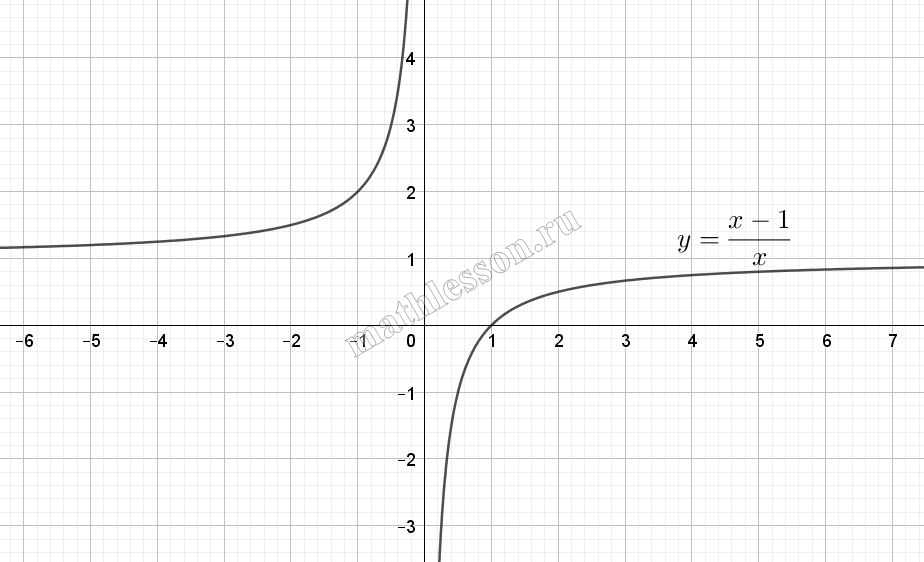
Постройте график функции $$y=|frac{x-1}{x}|$$ и определите, при каких значениях а прямая y=ах имеет с графиком ровно две общие точки.

Ответ: 0,25

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Преобразуем правую часть функции: $$y=left | frac{x-1}{x} right |=left | 1-frac{1}{x} right |$$. То есть у нас дан график функции $$y=frac{1}{x}$$, смещенный на 1 вверх по оси Оу и отображенный относительно оси Оу.

Кроме того, наличие модуля отобрадает ту часть графика, которая находится под осью Ох (показана на рисунке), симметрично относительно Ох:

Итоговый график функции будет выглядить, как:

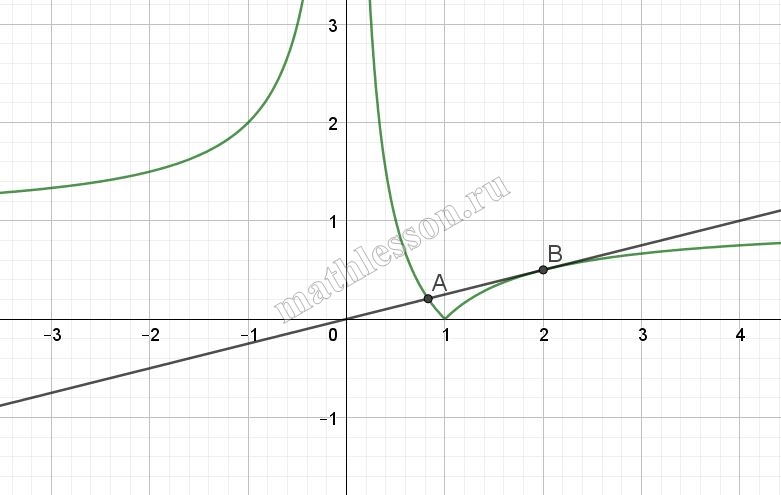
Необходимо найти такое значение а, при котором будет ровно два решения. В таком случае график прямой должен касаться графика исходной функции (точка B):

Так как касается в той части графика, где функции (с учетом раскрытия модуля) выглядит как $$y=1-frac{1}{x}$$. Так как там касается, то должна быть одна точка пересечения с данным графиком: $$ax=1-frac{1}{x}Leftrightarrow$$$$frac{ax^{2}-x+1}{x}=0$$ При этом $$D=1-4a=0Leftrightarrow$$$$a=frac{1}{4}=0,25$$

Задание 6740

Постройте график функции $$y=frac{2|x|-1}{|x|-2x^{2}}$$ и определите, при каких значениях k прямая y=kx не имеет с графиком ни одной общей точки.

Ответ: $$-4;0;4$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

ОДЗ: $$left | x right |-2x^{2}neq 0Leftrightarrow$$ $$left | x right |-2left | x right |^{2} neq 0Leftrightarrow$$ $$left | x right |(1-2left | x right |)neq 0Leftrightarrow$$ $$left{begin{matrix}xneq 0\ xneq 0,5\ xneq -0,5end{matrix}right.$$.

При $$x>0$$: $$y=frac{2x-1}{x(1-2x)}=-frac{1}{x}$$ (выдерена красным)

При $$x<0$$: $$y=frac{-2x-1}{-x-2x^{2}}=frac{1}{x}$$(выделена красным)

Итоговый график с учетом ОДЗ:

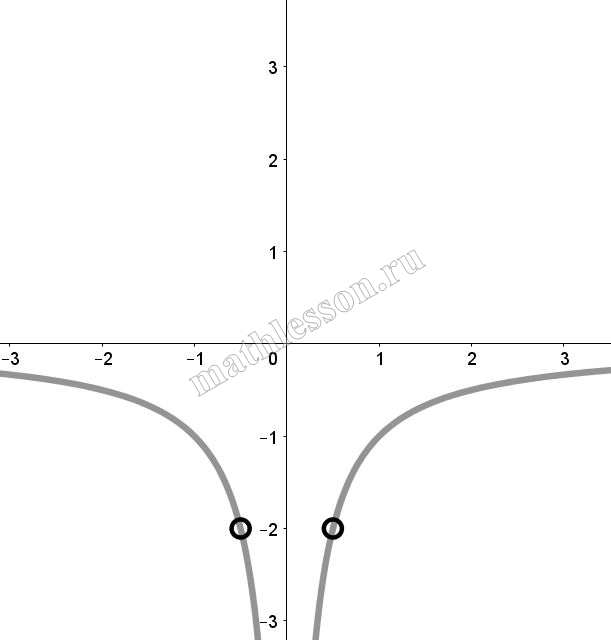
Найдем k: $$y=kx$$ проходит через (-0,5 ; -2): $$-2=-0,5*kRightarrow k=4$$(зеленая) и через (0,5; -2): $$-2=0,5kRightarrow k=-4$$(красная). При k=0 (черная) тоже не имеет пересечений

Задание 6787

Постройте график функции $$y=frac{x-2}{x^{2}-2x}$$ и определите, при каких значениях k прямая $$y=kx$$ имеет с графиком ровно одну общую точку.

Ответ: 0,25

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Найдем ограничения по x: $$x^{2}-2xneq 0Leftrightarrow$$ $$xneq 0 xneq 2(1)$$. Тогда $$y=frac{x-2}{x(x-2)}=frac{1}{x}$$ с учетом (1) аналогичен искомой функции

Построим график функции:

$$y=kx$$ имеет 1 общую точку если проходит через (2;0,5): $$0,5=2kRightarrow$$ $$k=frac{1}{4}$$

Задание 6906

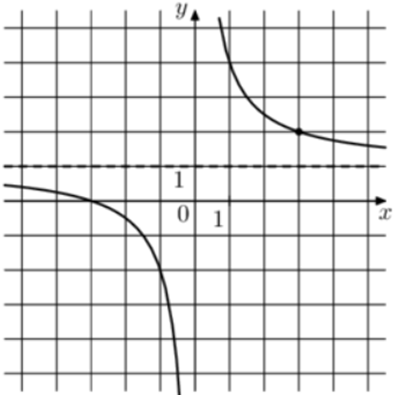
Постройте график функции $$y=1+frac{x-3}{x^{2}-3x}$$ и определите, при каких значениях а прямая y=а не имеет с графиком ни одной общей точки.

Ответ: $$1; frac{4}{3}$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$y=1+frac{x-3}{x^{2}-3x}$$$$Leftrightarrow$$ $$y=1+frac{x-3}{x(x-3)}$$$$Leftrightarrow$$ $$left{begin{matrix}y=1+frac{1}{x}\x-3neq 0end{matrix}right.$$

Начертим график данной функции:

Найдем оординату точки А: $$y(3)=1+frac{1}{3}=frac{4}{3}$$

Т.к. $$y=a$$ – прямая, параллельная Ox, то не будет иметь общих точек при $$a=frac{4}{3}$$ (проходит через А) и $$a=1$$ (проходит через горизонтальную асимптоту)

Задание 7135

Постройте график функции $$y=-1-frac{x-1}{x^{2}-x}$$ и определите, при каких значениях а прямая y=а не имеет с графиком ни одной общей точки

Ответ: -2 ; -1

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Упростим формулу: $$y_{1}=-1-frac{x-1}{x(x-1)}=-1-frac{1}{x}$$ . Следовательно , график функции $$y_{1}$$ совпадает с $$y$$ при учете , что $$xneq 1$$.

Не имеет при $$a=-2$$ и при $$a=-1$$.

Задание 7906

Постройте график функции $$y=frac{x-3}{(sqrt{x^{2}-9})^{2}}+4$$ . Найдите все значения k , при которых прямая $$y=kx$$ имеет с графиком функции ровно две общие точки.

Ответ: $$(frac{-14+2sqrt{13}}{9};0);(0;frac{25}{6})$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 9026

Постройте график функции $$y=frac{|x|-1}{|x|-x^{2}}$$ и определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.

Ответ: -1;0;1

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Источник

Решение
Видеорешение

Чтобы найти точку, в которой (displaystyle f(x)) равно (displaystyle 2{small,})

найдем неизвестные коэффициенты (displaystyle k) и (displaystyle b) в уравнении гиперболы,
решим уравнение (displaystyle f(x)=2{small.})

Найдем (displaystyle k) и (displaystyle b{small.})

Для этого составим и решим систему уравнений относительно (displaystyle k) и (displaystyle b{small.})

Заметим, что гипербола (displaystyle y=frac{k}{x+b}) проходит через точки (displaystyle (-2;, -4)) и (displaystyle (2;, 1){small.})

Значит,

если в уравнение гиперболы (displaystyle y=frac{k}{x+b}) подставить (displaystyle color{blue}{x=-2}) и (displaystyle color{blue}{y=-4},) то получится первое верное равенство (первое уравнение на (displaystyle k) и (displaystyle b)),
если в уравнение гиперболы (displaystyle y=frac{k}{x+b}) подставить (displaystyle color{green}{x=2}) и (displaystyle color{green}{y=1},) то получится второе верное равенство (второе уравнение на (displaystyle k) и (displaystyle b)).

Получаем систему уравнений:

(displaystyleleft{begin{aligned}color{blue}{-4}&=frac{k}{color{blue}{-2}+b}{small,}\color{green}{1}&=frac{k}{color{green}{2}+b}{small.}end{aligned}right.)

Решение данной системы уравнений (displaystyle k=3{,}2) и (displaystyle b=1{,}2{small.})

Тогда уравнение гиперболы имеет вид:

(displaystyle f(x)=frac{3{,}2}{x+1{,}2}{small.})

Найдём те значения (displaystyle x{small,}) при которых значение (displaystyle f(x)) равно (displaystyle 2{small.})

Все такие (displaystyle x) удовлетворяют уравнению

(displaystyle 2=frac{3{,}2}{x+1{,}2}{small.})

Решим его.

Для (displaystyle x{ small ,}) не равных (displaystyle -1{,}2{ small ,}) можно домножить обе части уравнения на (displaystyle x+1{,}2{small.})

Тогда:

(displaystyle 2cdot(x+1{,}2)=3{,}2{small,})

(displaystyle x=frac{3{,}2}{2}-1{,}2{small,})

(displaystyle x=0{,}4{small.})

Полученное значение (displaystyle x) отлично от (displaystyle -1{,}2{ small .})

Значит, (displaystyle f(0{,}4)=2{small.})

Ответ: (displaystyle f(0{,}4)=2{small.})

Источник

ЕГЭ Профиль №10. Гипербола

ЕГЭ Профиль №10. Гипербола

Просмотр содержимого документа

«Графики функции. Задание №9 ЕГЭ-2022»

Рекомендуем курсы ПК и ППК для учителей

Похожие файлы

ОГЭ

Гиперболы

Задание 3407

Задание 3843

Задание 4534

Задание 5271

Задание 5481

Задание 5482

Задание 5483

Задание 6070

Задание 6449

Задание 6740

Задание 6787

Задание 6906

Задание 7135

Задание 7906

Задание 9026

ЕГЭ Профиль №10. Гипербола

ЕГЭ Профиль №10. Гипербола

Просмотр содержимого документа «Графики функции. Задание №9 ЕГЭ-2022»

Рекомендуем курсы ПК и ППК для учителей

Похожие файлы

ОГЭ

Гиперболы

Задание 3407

Задание 3843

Задание 4534

Задание 5271

Задание 5481

Задание 5482

Задание 5483

Задание 6070

Задание 6449

Задание 6740

Задание 6787

Задание 6906

Задание 7135

Задание 7906

Задание 9026

Просмотр содержимого документа

«Графики функции. Задание №9 ЕГЭ-2022»