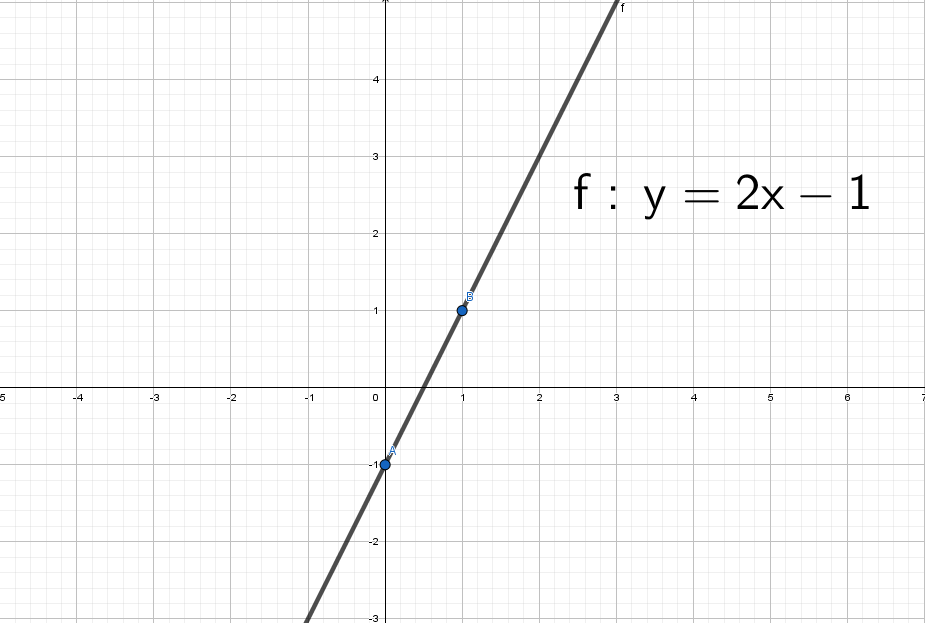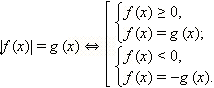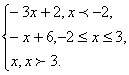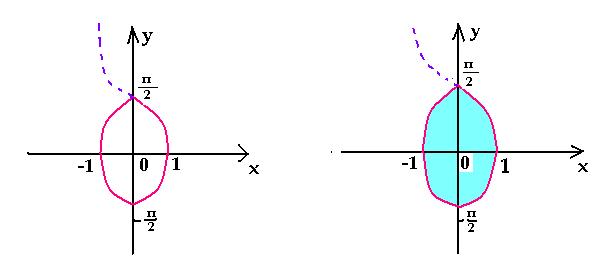Пошаговое построение графиков.
«Навешивание» модулей на прямые, параболы, гиперболы.
Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.
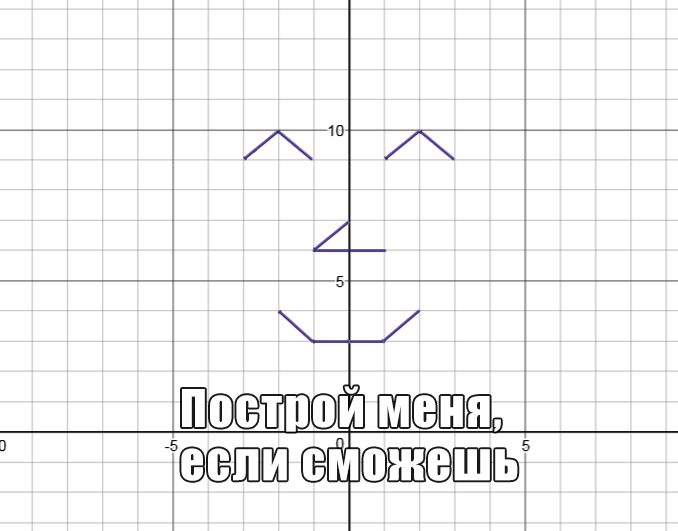
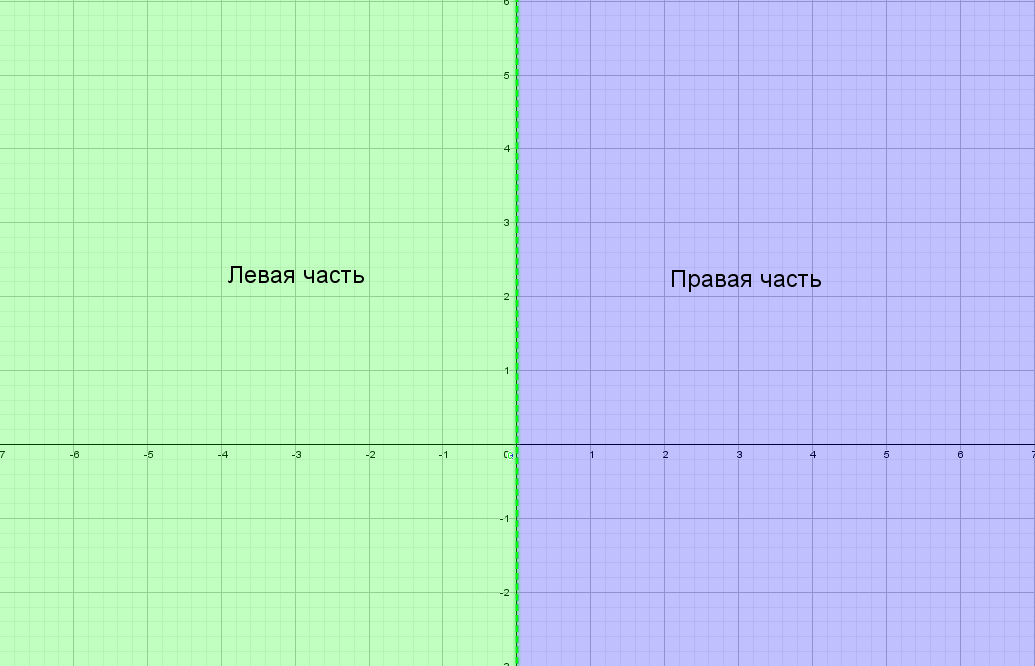
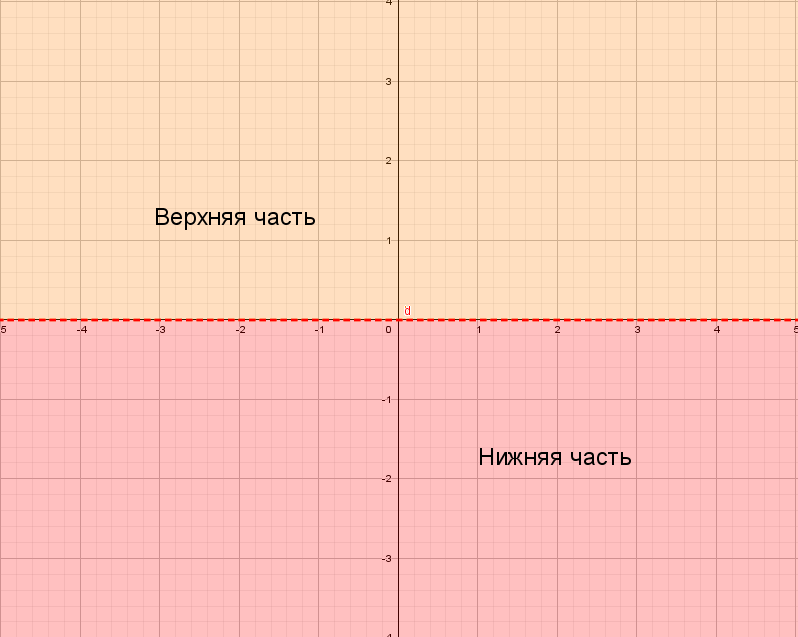
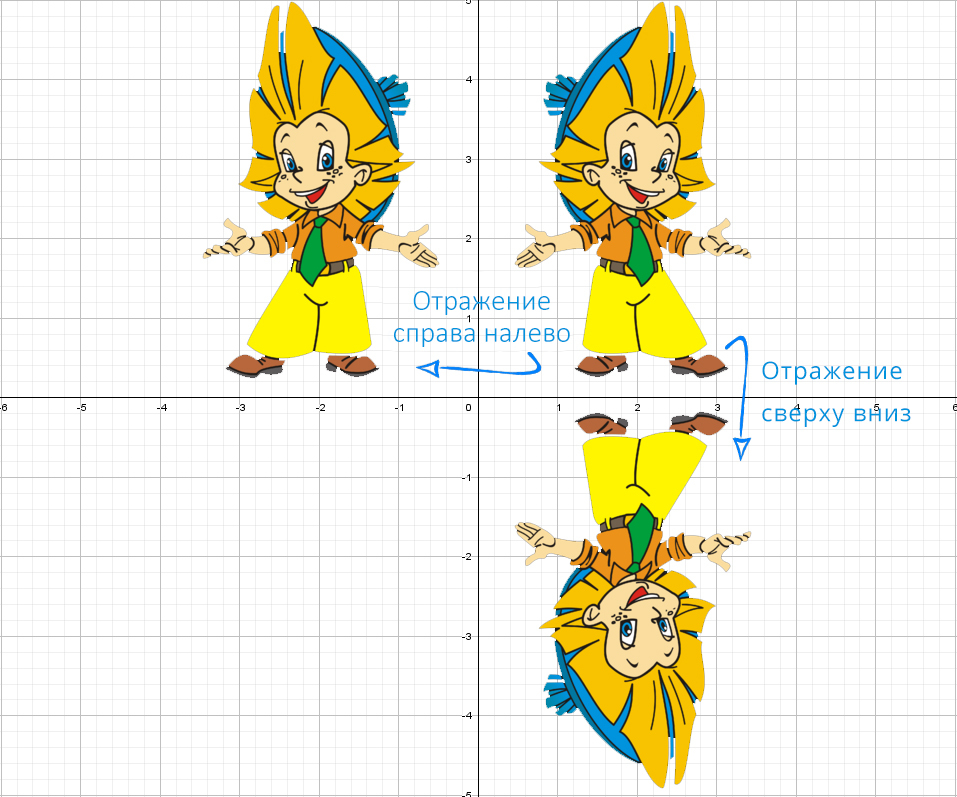
Для понимания друг друга введу немного «обзываний» системы координат:
Для начала построим график прямой y = 2x − 1.
Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую.
Возьмем значение X = 0 и Х = 1 и подставим в выражение y = 2x − 1, тогда соответственно Y = − 1 и Y = 1
Через данные две точки А = (0; −1) и B = (1; 1) проводим единственную прямую:
А если теперь добавить модуль y = |2x − 1|.
Модуль — это всегда положительное значение, получается, что «y» должен быть всегда положительным.
Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю (как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).
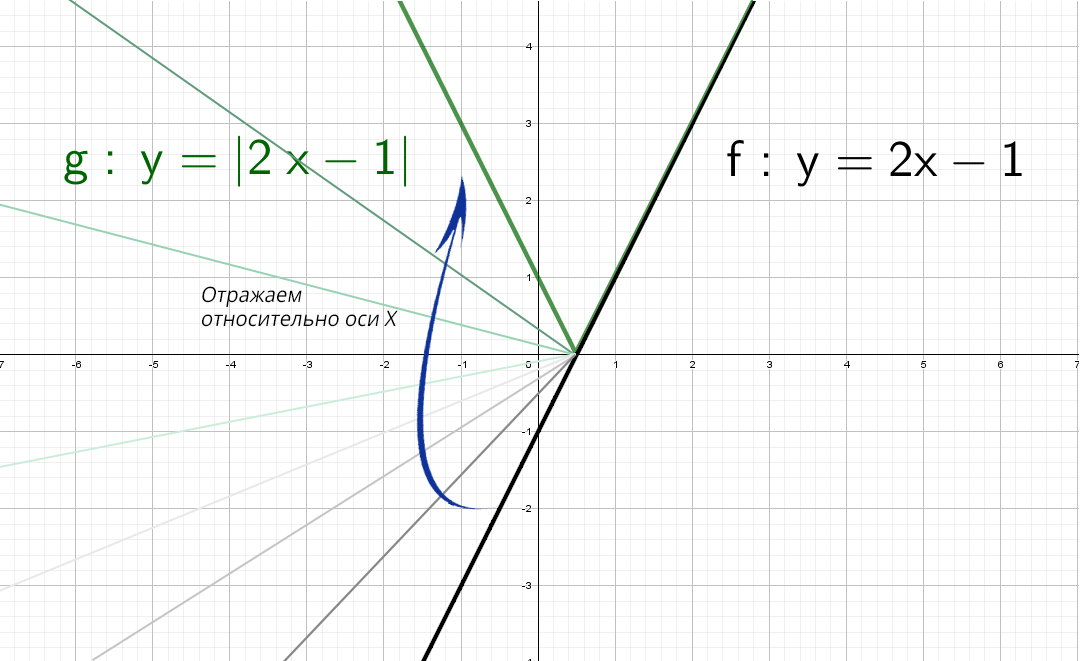
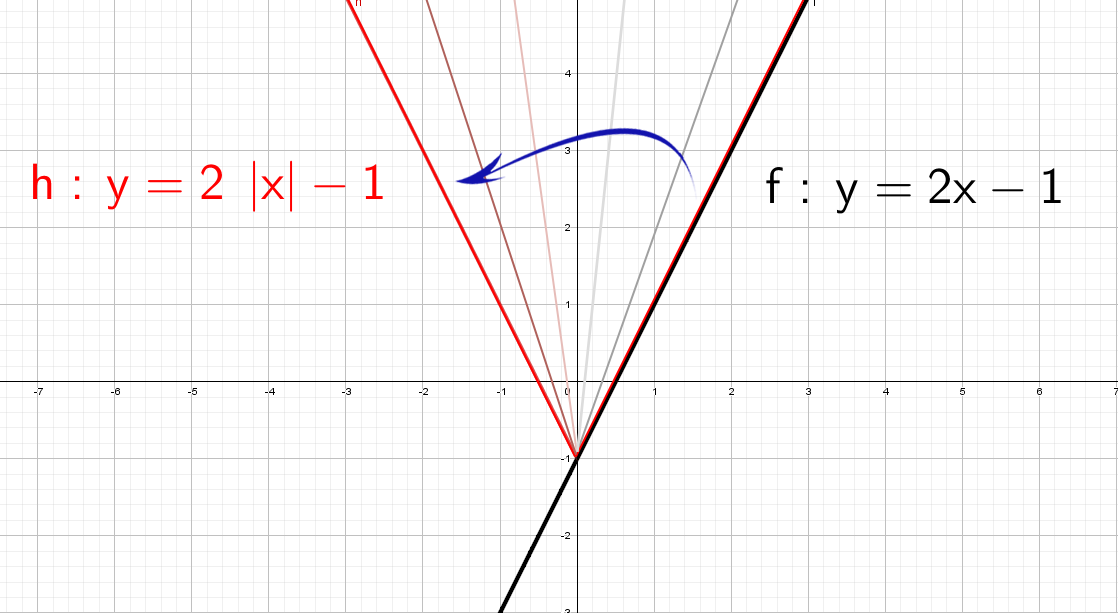
Красота! А как же будет выглядеть график, если надеть модуль только на «х»: y = 2|x| − 1?
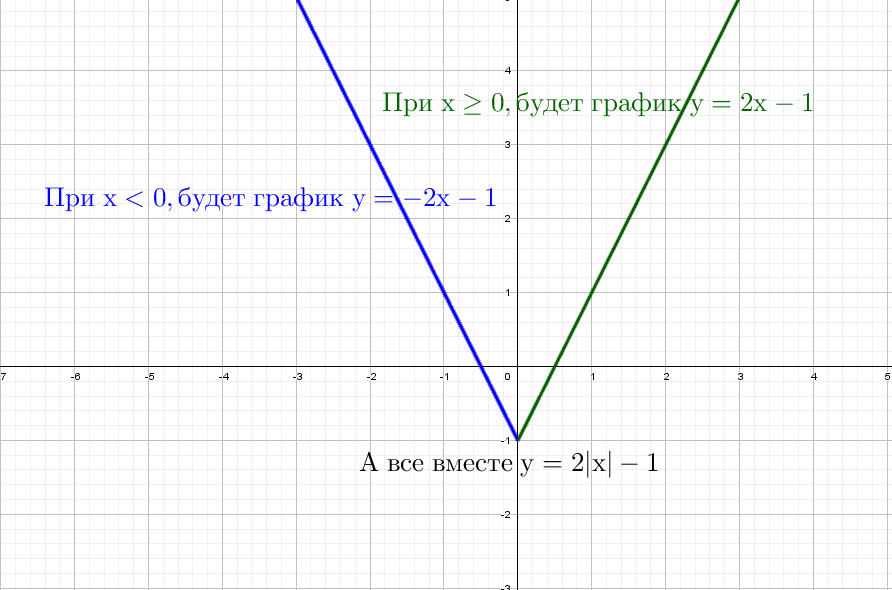
Одна строчка рассуждений и рисуем:
Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.
Здесь отражаем относительно оси «y». Такая же галочка, только теперь через другую ось.
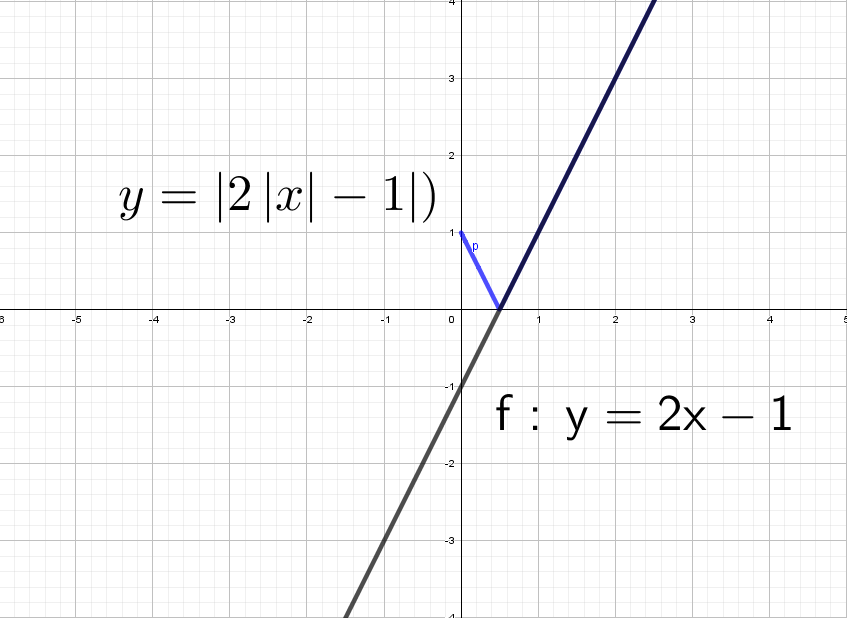
Смертельный номер: y = |2|x| − 1|.
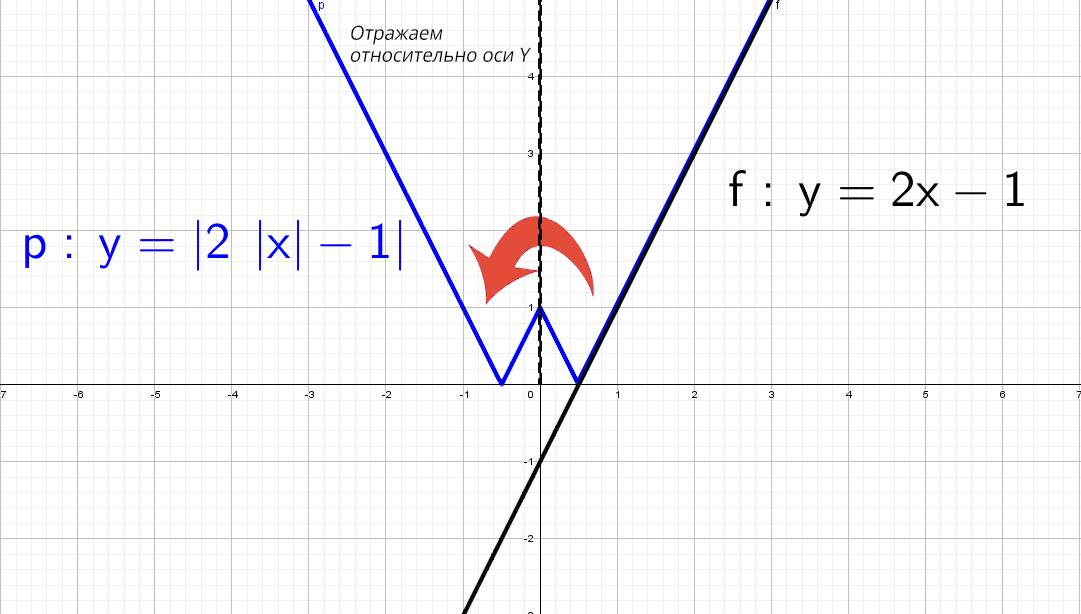
Черную прямую y = 2x − 1 отражаем относительно оси Х, получим y = |2x − 1|. Но мы выяснили, что модуль на х влияет только на левую часть.
В правой части: y = |2x − 1| и y = |2|x| − 1| идентичны!
А после этого отражаем относительно оси «y» то, что мы получили справа налево:
Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках, значит делаем по аналогии.
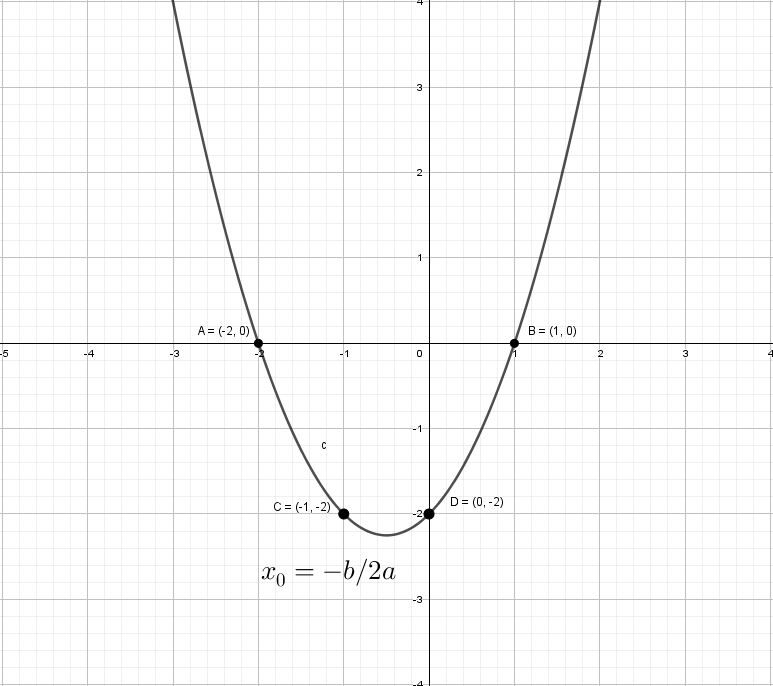
Разберем по винтикам параболу y = x² + x − 2. Точки пересечения с осью «x» получим с помощью дискриминанта: x₁ = 1 и x₂ = -2.
Можно найти вершину у параболы и взять пару точек для точного построения.
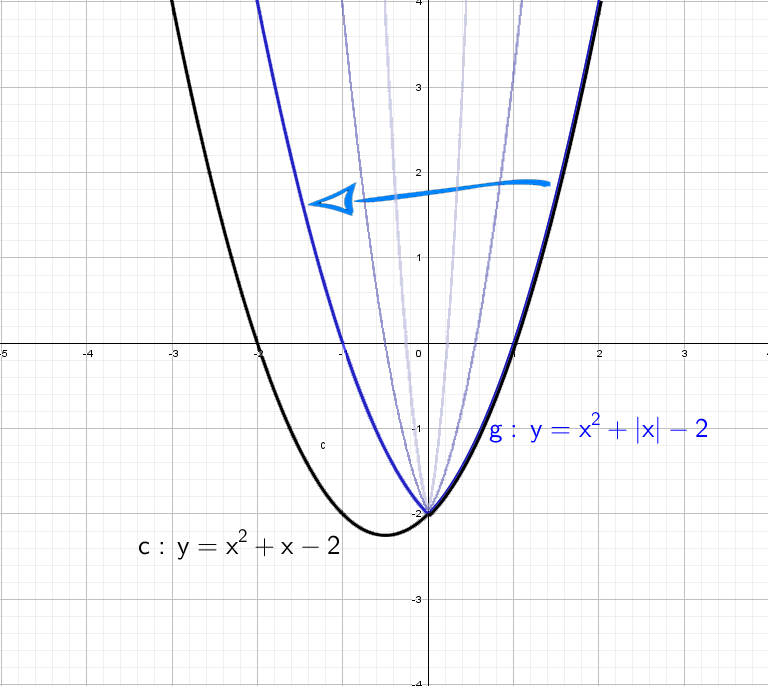
А как будет выглядеть график: y = |x²| + x − 2? Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.
При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:
А дальше что мелочиться: рассмотри сразу остальные графики с модулем!
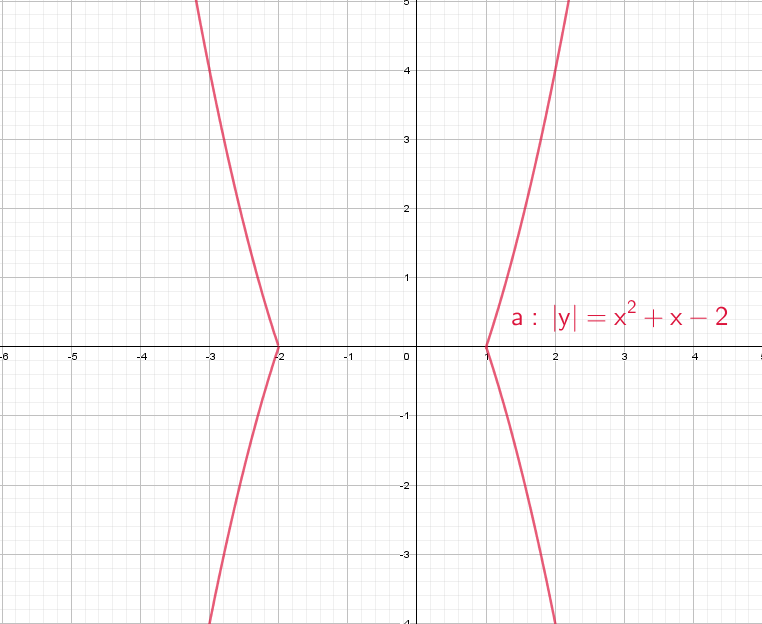
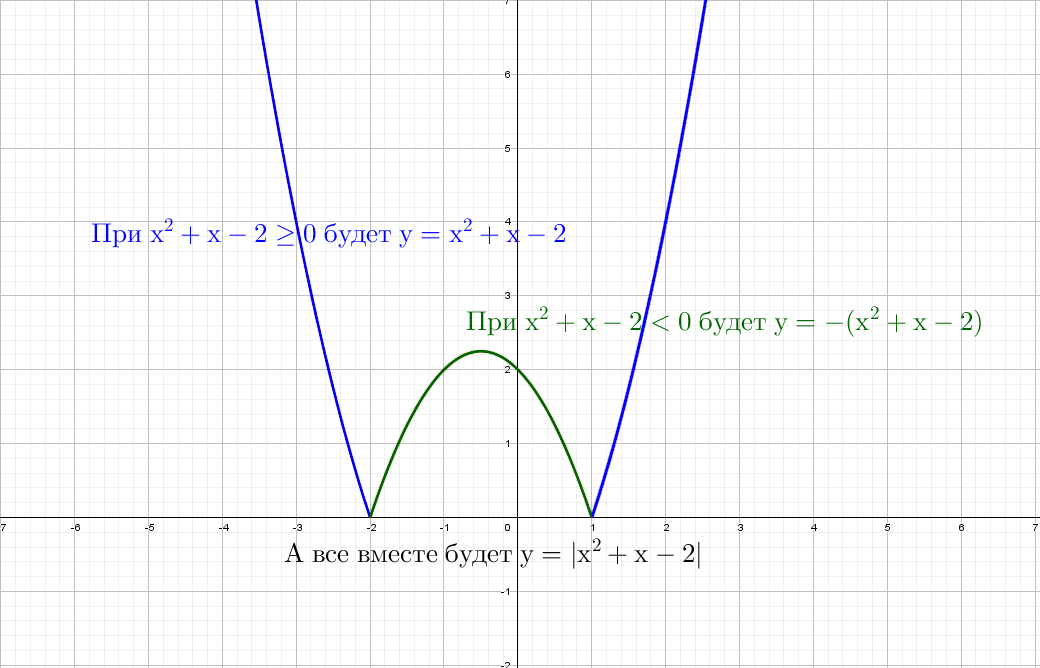
Следующий смертельный номер: |y| = x² + x − 2, подумай хорошенько, а еще лучше попробуй нарисовать сам.
При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!
Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.
А теперь сразу комбо:
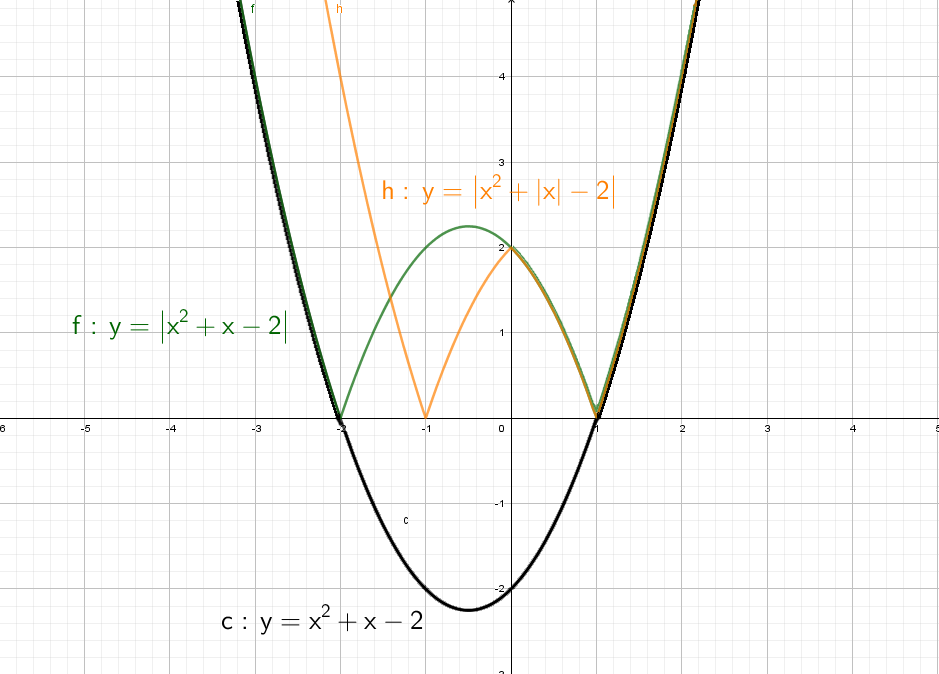
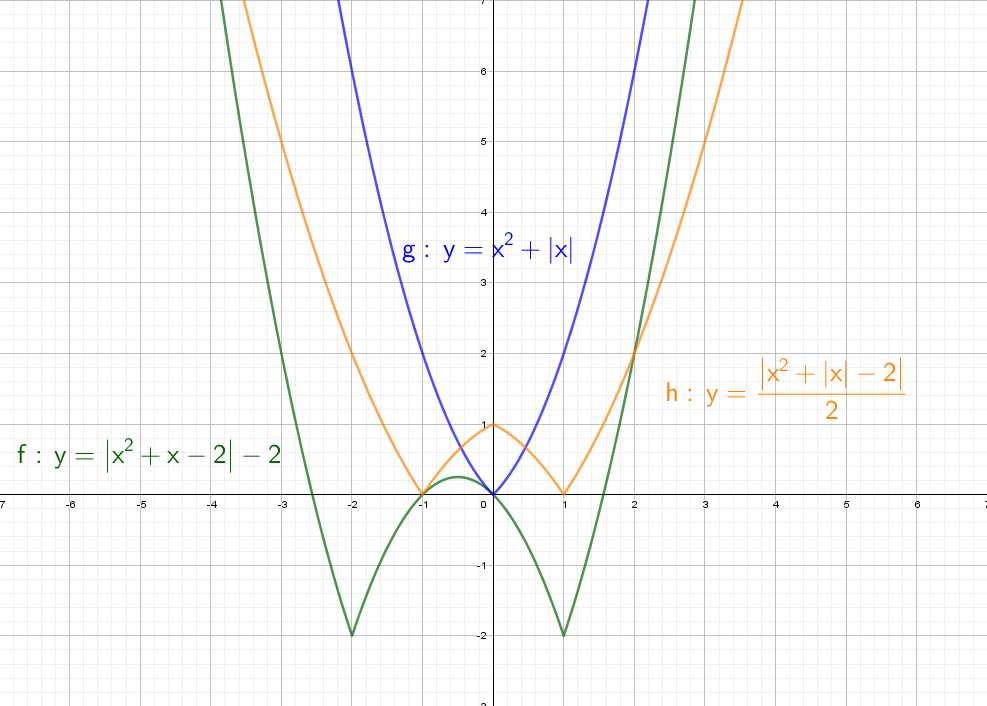
Cиний: похож на y = x² + |x| − 2, только поднят вверх. Строим график в правой части, а затем отражаем через ось Y влево.
Оранжевый: строим в правой части и отражаем относительно оси Х. Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет «шире», расходится в бока он быстрее остальных.
Зеленый: Так же начинаем с правой части и отражаем относительно оси оси Y. Получается график y = |x² + x − 2|, но еще есть −2, поэтому опустим график на 2 вниз. Теперь параболы как бы отражается относительно Y = − 2.
Легкий и средний уровень позади, и настала пора выжать концентрацию на максимум, потому что дальше тебя ждут гиперболы, которые частенько встречаются во второй части ЕГЭ и ОГЭ.
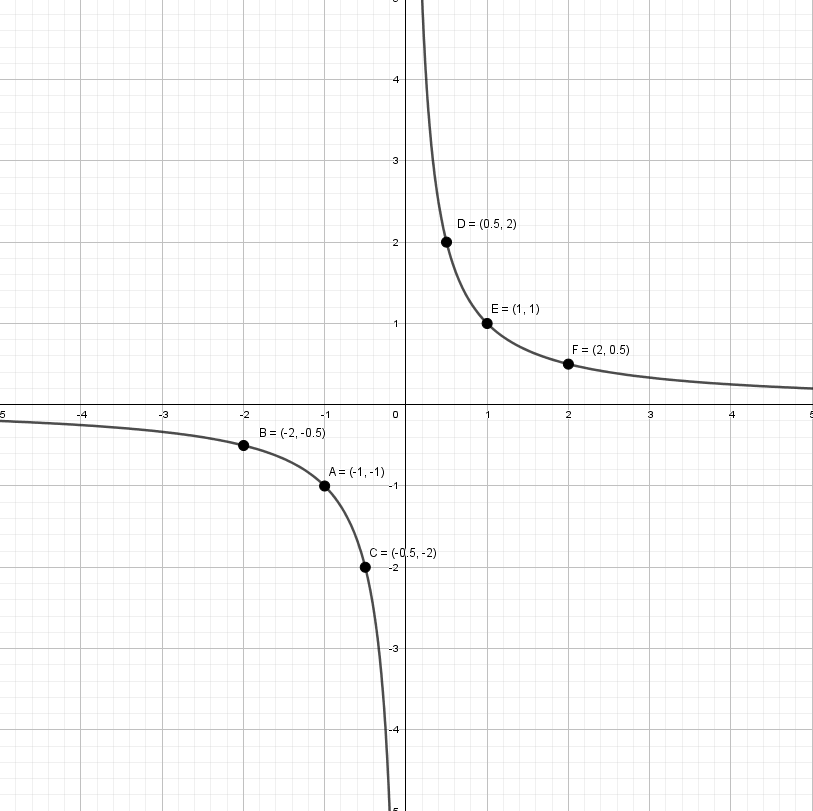
y = 1/x — простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:
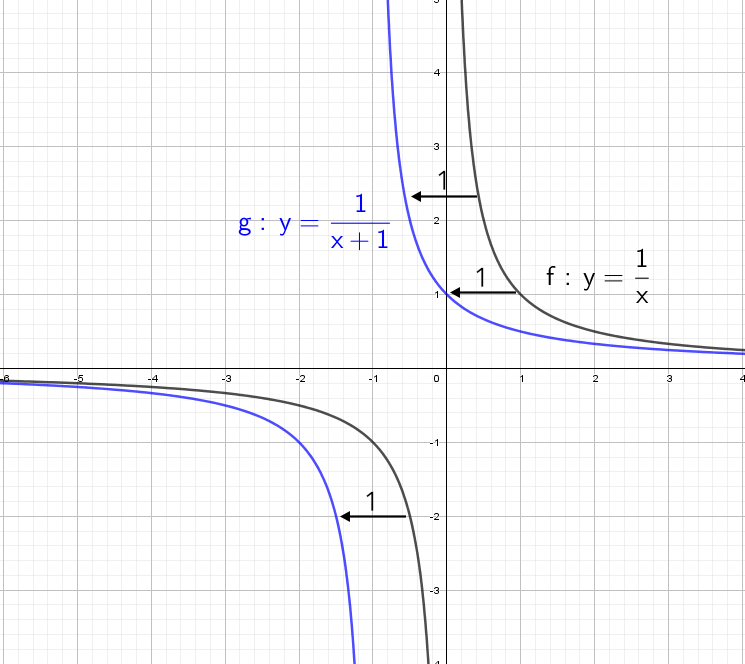
А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:
А что будет, если мы добавим в знаменателе «−1»? График сдвинется вправо на единицу.
А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!
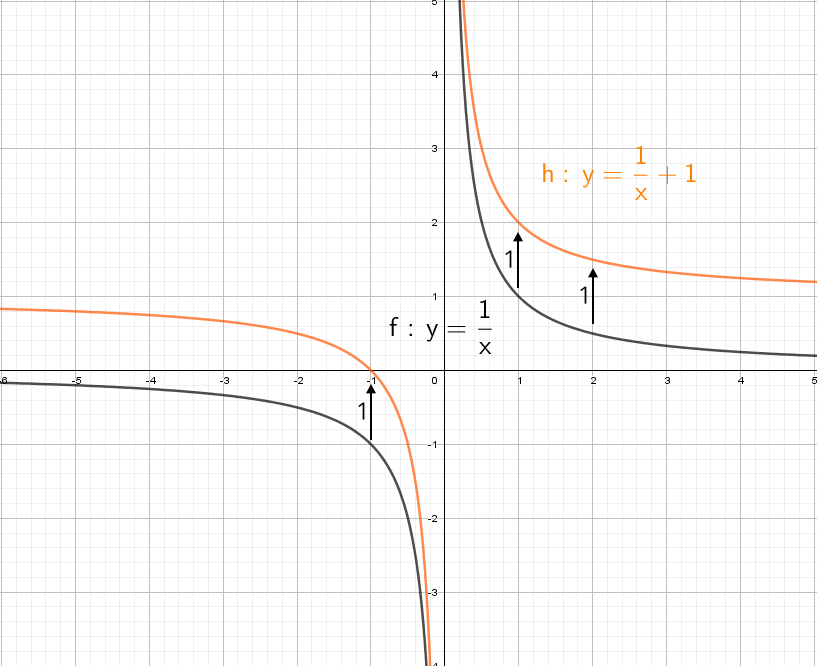
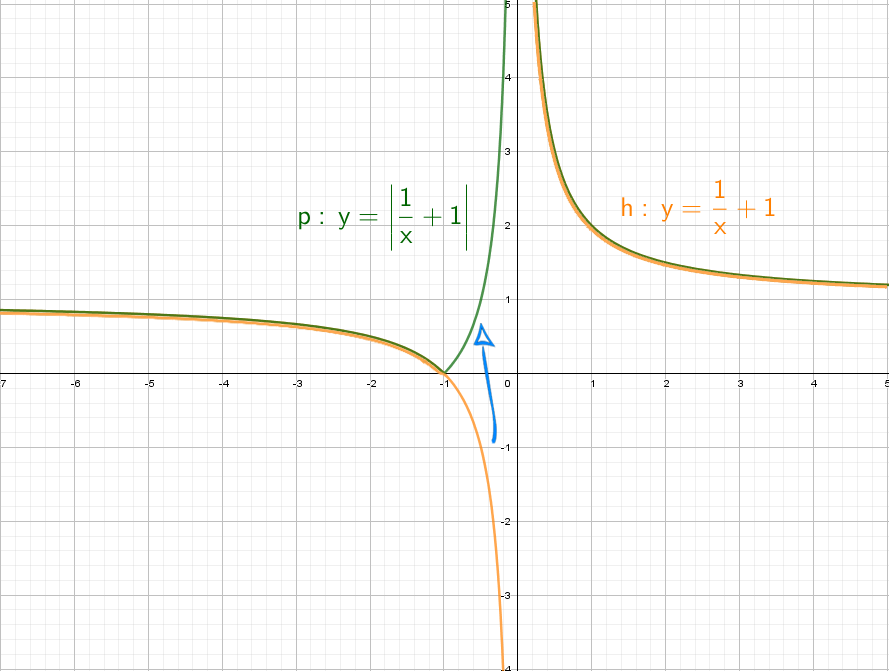
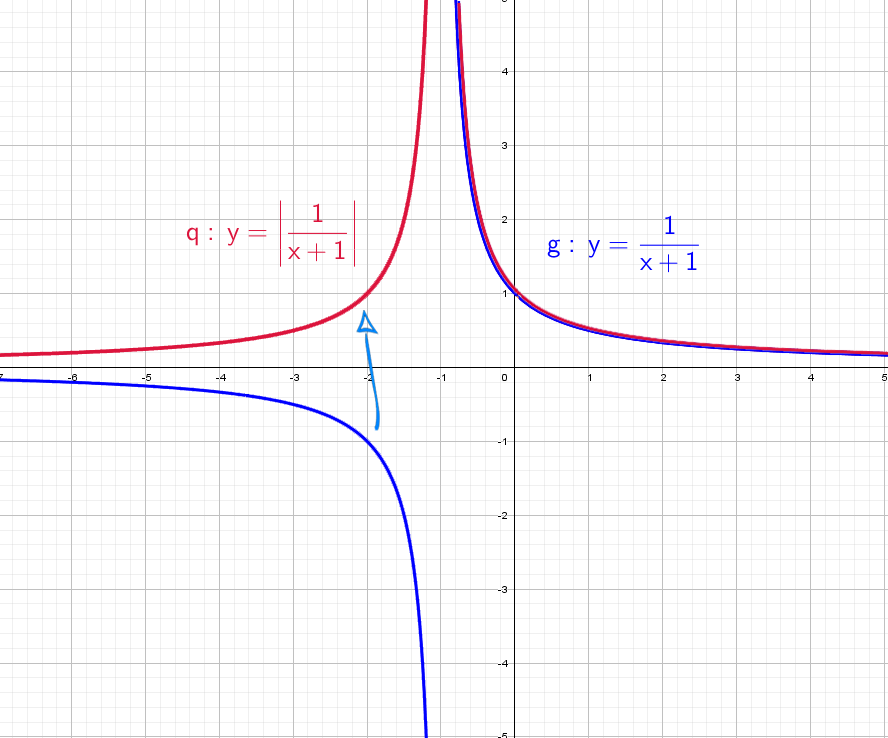
Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.
Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.
Можно придумывать массу вариантов, но общий принцип остается для любого графика. Принципы повторим в выводах в конце статьи.
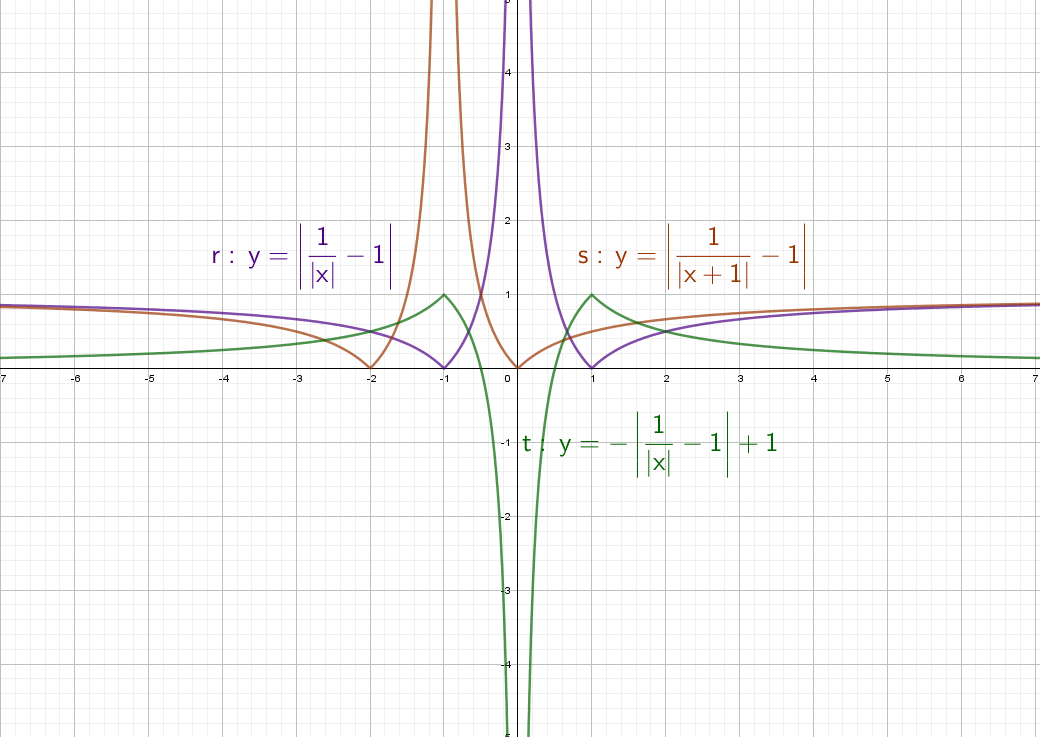
Фиолетовый: Вычитаем из дроби −1 и сдвигаем график вниз на единицу. Ставим модуль − отражаем все, что снизу вверх.
Оранжевый: Ставим +1 в знаменателе и график смещается влево на единицу. Вычитаем из дроби −1 и сдвигаем график вниз на единицу. А после этого ставим модуль − отражаем все, что снизу вверх.
Зеленый: Сначала получим фиолетовый график. После этого ставим «−» и отражаем график по горизонтали. Сгибаем лист по оси Х и переводим его вниз. Остается добавить +1, это значит, что его нужно поднять вверх на единицу.
Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определению:
И построить график, разбив его на кусочно-заданные функции.
Например для прямой:
Для параболы с одним модулем будет два кусочно-заданных графика:
C двумя модулями кусочно-заданных графиков будет четыре:
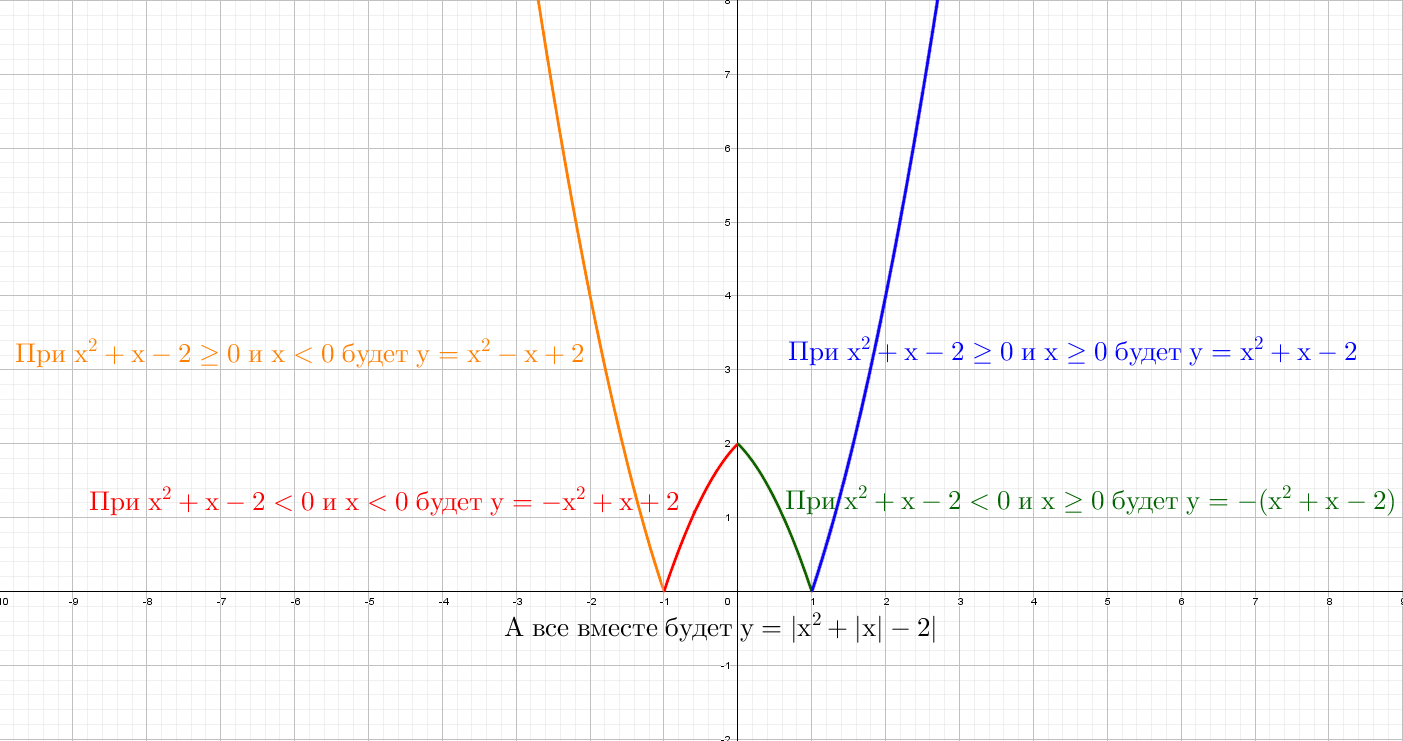
Выводы:
- Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
- Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
- Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль.
- Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:
- Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
- Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
- Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.
- Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.
Будь в курсе новых статеек, видео и легкого математического юмора.
Знак модуля, пожалуй, одно из самых интересных явлений в математике. В связи с этим у многих школьников возникает вопрос, как строить графики функций, содержащих модуль. Давайте подробно разберем этот вопрос.
1. Построение графиков функций, содержащих модуль
Пример 1.
Построить график функции y = x2 – 8|x| + 12.
Решение.
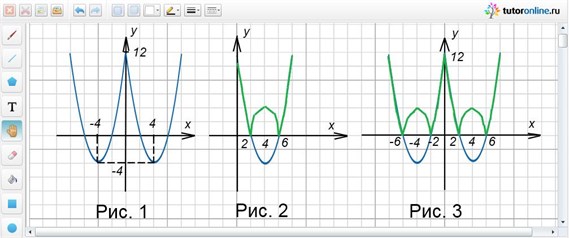
Определим четность функции. Значение для y(-x) совпадает со значением для y(x), поэтому данная функция четная. Тогда ее график симметричен относительно оси Oy. Строим график функции y = x2 – 8x + 12 для x ≥ 0 и симметрично отображаем график относительно Oy для отрицательных x (рис. 1).
Пример 2.
Следующий график вида y = |x2 – 8x + 12|.
– Какова область значений предложенной функции? (y ≥ 0).
– Как расположен график? (Над осью абсцисс или касаясь ее).
Это значит, что график функции получают следующим образом: строят график функции y = x2 – 8x + 12, оставляют часть графика, которая лежит над осью Ox, без изменений, а часть графика, которая лежит под осью абсцисс, симметрично отображают относительно оси Ox (рис. 2).
Пример 3.
Для построения графика функции y = |x2 – 8|x| + 12| проводят комбинацию преобразований:
y = x2 – 8x + 12 → y = x2 – 8|x| + 12 → y = |x2 – 8|x| + 12|.
Ответ: рисунок 3.
Рассмотренные преобразования справедливы для всех видов функций. Составим таблицу:
|
Функция |
Преобразование |
|
f(|x|) |
1) Для x ≥ 0, y = f(x) 2) Для x < 0 – преобразование симметрии относительно Oy графика y = f(x), для x ≥ 0 симметричные части графика из правой полуплоскости в левую |
|
|f(x)| |
1) Для f(x) ≥ 0, |f(x)| = f(x) 2) Для f(x) < 0, |f(x)| = -f(x) Симметричное отображение части графика из нижней полуплоскости в верхнюю относительно Ox |
|
|f(|x|)| |
f(x) → f(|x|) → |f(|x|)|. |
2. Построение графиков функций, содержащих в формуле «вложенные модули»
Мы уже познакомились с примерами квадратичной функции, содержащей модуль, а так же с общими правилами построения графиков функций вида y = f(|x|), y = |f(x)| и y = |f(|x|)|. Эти преобразования помогут нам при рассмотрении следующего примера.
СЛОЖНА-А-А 🙀 Ты же знаешь, что если не разобраться в теме сейчас, то потом придется исправлять оценки. Беги на бесплатное онлайн-занятие с репетитором (подробности тут + 🎁).
Пример 4.
Рассмотрим функцию вида y = |2 – |1 – |x|||. Выражение, задающее функцию, содержит «вложенные модули».
Решение.
Воспользуемся методом геометрических преобразований.
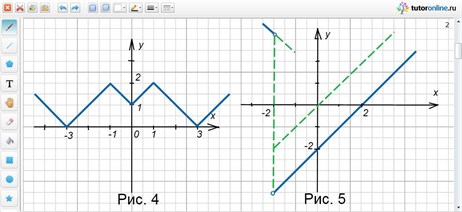
Запишем цепочку последовательных преобразований и сделаем соответствующий чертеж (рис. 4):
y = x → y = |x| → y = -|x| → y = -|x| + 1 → y = |-|x| + 1|→ y = -|-|x| + 1|→ y = -|-|x| + 1| + 2 → y = |2 –|1 – |x|||.
Рассмотрим случаи, когда преобразования симметрии и параллельного переноса не являются основным приемом при построении графиков.
Пример 5.
Построить график функции вида y = (x2 – 4)/√(x + 2)2.
Решение.
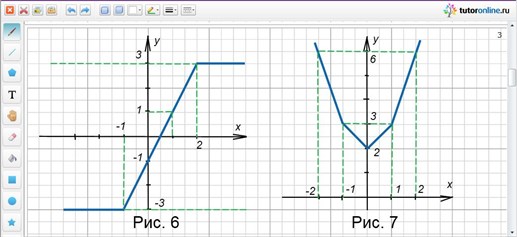
Прежде чем строить график, преобразуем формулу, которой задана функция, и получим другое аналитическое задание функции (рис. 5).
y = (x2 – 4)/√(x + 2)2 = (x– 2)(x + 2)/|x + 2|.
Раскроем в знаменателе модуль:
При x > -2, y = x – 2, а при x < -2, y = -(x – 2).
Область определения D(y) = (-∞; -2)ᴗ(-2; +∞).
Область значений E(y) = (-4; +∞).
Точки, в которых график пересекает с оси координат: (0; -2) и (2; 0).
Функция убывает при всех x из интервала (-∞; -2), возрастает при x от -2 до +∞.
Здесь нам пришлось раскрывать знак модуля и строить график функции для каждого случая.
Пример 6.
Рассмотрим функцию y = |x + 1| – |x – 2|.
Решение.
Раскрывая знак модуля, необходимо рассмотреть всевозможную комбинацию знаков подмодульных выражений.
Возможны четыре случая:
{x + 1 – x + 2 = 3, при x ≥ -1 и x ≥ 2;
{-x – 1 + x – 2 = -3, при x < -1 и x < 2;
{x + 1 + x – 2 = 2x — 1, при x ≥ -1 и x < 2;
{-x – 1 – x + 2 = -2x + 1, при x < -1 и x ≥ 2 – пустое множество.
Тогда исходная функция будет иметь вид:
{3, при x ≥ 2;
y = {-3, при x < -1;
{2x – 1, при -1 ≤ x < 2.
Получили кусочно-заданную функцию, график которой изображен на рисунке 6.
3. Алгоритм построения графиков функций вида
y = a1|x – x1| + a2|x – x2| + … + an|x – xn| + ax + b.
В предыдущем примере было достаточно легко раскрыть знаки модуля. Если же сумм модулей больше, то рассмотреть всевозможные комбинации знаков подмодульных выражений проблематично. Как же в этом случае построить график функции?
Заметим, что графиком является ломаная, с вершинами в точках, имеющих абсциссы -1 и 2. При x = -1 и x = 2 подмодульные выражения равны нулю. Практическим путем мы приблизились к правилу построения таких графиков:
Графиком функции вида y = a1|x – x1| + a2|x – x2| + … + an|x – xn| + ax + b является ломаная с бесконечными крайними звеньями. Чтобы построить такую ломаную, достаточно знать все ее вершины (абсциссы вершин есть нули подмодульных выражений) и по одной контрольной точке на левом и правом бесконечных звеньях.
Задача.
Построить график функции y = |x| + |x – 1| + |x + 1| и найти ее наименьшее значение.
Решение:
Нули подмодульных выражений: 0; -1; 1. Вершины ломаной (0; 2); (-1; 3); (1; 3). Контрольная точка справа (2; 6), слева (-2; 6). Строим график (рис. 7). min f(x) = 2.
Молодец! Раз ты дочитал это до конца, вероятно, ты все отлично усвоил. Но если вдруг что-то еще непонятно — попробуй онлайн-занятие с репетитором (подробности тут + 🎁).
Остались вопросы? Не знаете, как построить график функции с модулем?
Чтобы получить помощь репетитора – зарегистрируйтесь.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 62 1–20 | 21–40 | 41–60 | 61–62
Добавить в вариант
Найдите все значения a, при каждом из которых уравнение
имеет ровно два различных корня.
Источник: ЕГЭ по математике. Основная волна 07.06.2021. Урал, Задания 18 ЕГЭ–2021
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 310. (Часть C)
Найдите все значения a, при каждом из которых уравнение
имеет ровно два различных корня.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Санкт-Петербург, Москва, другие города. Вариант 359 (C часть), Задания 18 ЕГЭ–2021
Дано уравнение
а) Решите уравнение.
б) Найдите его корни, принадлежащие отрезку
Источник: А. Ларин: Тренировочный вариант № 165.
Найдите все корни уравнения sin(2x) = 1, удовлетворяющие неравенству
Источник: А. Ларин: Тренировочный вариант № 130.
Найти все значения параметра а при каждом из которых уравнение имеет ровно два решения.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Разные задачи, Задания 18 ЕГЭ–2021
Решите уравнение
Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Сибирь. Вариант 302., Задания 18 (С6) ЕГЭ 2013
Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 402.
Найдите все значения a, при каждом из которых уравнение
имеет единственный корень.
Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Найдите все значения параметра a, при каждом из которых уравнение
имеет единственное решение. Найдите это решение для каждого значения a.
Найти все значения a, при каждом из которых уравнение
имеет единственный корень.
Источник: ЕГЭ по математике 23.04.2013. Досрочная волна. Запад. Вариант 1.
Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 402., Задания 18 (С6) ЕГЭ 2013
Известно, что значение параметра а таково, что система уравнений
имеет единственное решение. Найдите это значение параметра a и решите систему при найденном значении параметра.
Источник: ЕГЭ по математике 2021 года. Досрочная волна., Задания 18 ЕГЭ–2021
Источник/автор: Некрасов В. Б., Гущин Д. Д. «Просвещение», 2010; Гущин Д. Д. «Учительская газета», 2013; ЕГЭ по математике − 2021
Найдите все значения a, при каждом из которых уравнение либо имеет единственное решение, либо не имеет решений.
Найдите все значения при каждом из которых уравнение
либо имеет единственное решение, либо не имеет решений.
Найдите все значения параметра при каждом из которых уравнение
имеет единственное решение.
Найдите это решение для каждого значения
Найдите все значения параметра a, при каждом из которых уравнение
имеет единственное решение. Найдите это решение для каждого значения a.
Всего: 62 1–20 | 21–40 | 41–60 | 61–62
Распространенными примерами с модулями является уравнение типа модуль в модуле.
Двойной модуль можно записать в виде формулы
||a*x-b|-c|=k*x+m.
Если k=0
то такое уравнение с модулем легче решать графическим методом. Классическое раскрытия модулей в таких ситуациях громоздкое и не дает желаемого эффекта (экономии времени) на контрольных и тестах. Графический метод позволяет за короткое время выполнить построение модульных функций и найти количество корней уравнения.
Алгоритм построения двойного, тройного модуля достаточно прост и из приведенных ниже примеров понравится многим. Для закрепления методики внизу приведены примеры для самостоятельного вычисления.
Пример 1.
Решить уравнение модуль в модуле ||x-3|-5|=3.
Решение:
Решим уравнение с модулями классическим методом и графически. Найдем ноль внутреннего модуля
x-3=0 x=3.
В точке x=3
уравнения с модулем разделяется на 2
. Кроме того, ноль внутреннего модуля является точкой симметрии графика модулей и если правая сторона уравнения равна постоянной, то корни лежат на одинаковом расстоянии от этой точки. То есть можно решить одно уравнение из двух, а остальные корней вычислить из этого условия.
Раскроем внутренний модуль для x>3
|x-3-5|=3; |x-8|=3
.
Полученное уравнение при раскрытии модуля делится на 2
Под модульная функция >0
x-8=3; x=3+8=11;
и для значений -(x-8)=3; x=8-3=5.
Оба корня уравнения удовлетворяют условию x>3,
то есть являются решениями.
Учитывая записано выше правило симметрии решений уравнения с модулями, можно не искать корни уравнения для x|-(x-3)-5|=3; |-x-2|=3
,
а вычислить их.
Значение симметрично относительно x=3
для x=11
равно
x=3-(11-3)=6-11=-5.
По той же формуле находим второе решение
x=3-(5-3)=6-5=1.
Заданное уравнение модуля в модуле имеет 4 решения
x=-5; x=1; x=5; x=11.
Теперь найдем решения уравнения с модулями графическим методом
. С внутреннего модуля |x-3|
следует что график стандартной модуль функции является смещен по оси Ох
вправо на 3
.
Дальше — отнять 5 означает что график необходимо опустить на 5 клеток по оси Oy
. Чтобы получить модуль полученной функции симметрично отражаем все что находится ниже оси Ox
.
И напоследок выполняем построение прямой y=3
, параллельной оси Ox
. Лучше всего для вычислений уравнений с модулями графически использовать тетрадь в клеточку, поскольку в ней удобно строить графики.
Окончательный вид графика модулей имеет вид
Точки пересечения модуль функции и прямой y=3
и является искомыми решениями x=-5;x=1; x=5;x=11
.
Преимущество графического метода над раскрытием модулей
для простых уравнений очевидно. Однако графически неудобно искать корни когда правая сторона имеет вид k*x+m
, то есть является прямой наклоненной к оси абсцисс под углом.
Здесь таких уравнений рассматривать не будем.
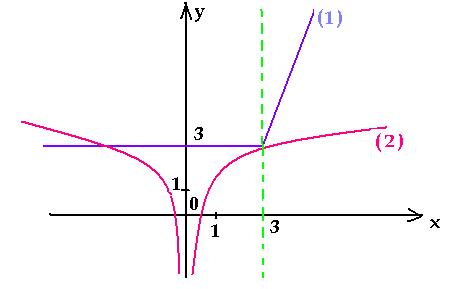
Пример 2.
Сколько корней имеет уравнение ||2x-3|-2|=2?
Решение:
Правая сторона равна постоянной, поэтому скорее найти решение можно графическим методом. Внутренний модуль обращается в нуль
|2x-3|=0 x=3/2=1,5
в точке x=1,5.
Значит в эту точку смещаем график функции y=|2x|.
Для того, чтобы его построить подставьте несколько точек и проведите через них прямые. От полученной функции вычитаем 2 то есть график опускаем на двойку вниз и, чтобы получить модуль переносим отрицательные значения (y
Видим, что заданное уравнение имеет три решения.
Пример 3.
При каком значении параметра a уравнение с модулем |||x+1|-2|-5|=a
имеет 5
решений?
Решение
: Имеем уравнение с тремя вложенными модулями. Найдем ответ с графического анализа. Начнем, как всегда, из внутреннего модуля. Он обращается в нуль
|x+1|=0 x=-1
в точке x=-1
.
Строим график модуль функции в этой точке
Повторно выполним смещение графика модуль функции вниз на 5
и симметрично переносим отрицательные значения функции. В результате получим левую сторону уравнения с модулями
y=|||x+1|-2|-5|
.
Параметр а соответствует значению параллельной прямой, которая должна пересечь график модуль функции в 5 точках. Сначала проводим такую прямую, далее ищем точку пересечения ее с осью Oy.
Это прямая y=3
, то есть искомый параметр равен a=3
.
Методом раскрытия модулей данную задачу можно было решать целый урок, если не больше. Здесь все свелось к нескольким графикам.
Ответ:
a=3
.
Пример 4.
Сколько решений имеет уравнение |||3x-3|-2|-7|=x+5 ?
Решение:
Раскроем внутренний модуль уравнения
|3x-3|=0 x=3/3=1.
Строим график функции y=|3x-3|.
Для этого на одну клетки изменения x
от найденной точки добавляем 3
клетки по y. Выполняйте построение корней уравнения в тетради в клеточку, а я расскажу как это можно сделать в среде Maple.
Restart;with(plots):
Приравниваем к нулю все переменные и подключаем модуль для работы с графикой.
> plot(abs(3*x-3),x=-2..4):
Далее опускаем график на 2
клетки вниз и симметрично оси Ox
переносим отрицательные значения (y Получим график двух внутренних модулей Полученный график опускаем на двойку и симметрично отражаем. получим график
y=||3x-3|-2|.
В математическом пакете мейпл
это равносильно записи еще одного модуля
> plot(abs(abs(3*x-3)-2),x=-2..4):
Повторно смещаем график вниз на семь единиц и симметрично переносим. Получим график функции
y=|||3x-3|-2|-7|
В Мэйпл это равносильно следующей ленте кода
> plot(abs(abs(abs(3*x-3)-2)-7),x=-5..7):
Строим прямую y=x+5
по двум точкам. Первая — пересечение прямой с осью абсцисс
Урок 5. Преобразования графиков с модулями (факультативное занятие)
09.07.2015
8999
0
Цель:
освоить основные навыки преобразования графиков с модулями.
I. Сообщение темы и цели урока
II
. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
f
(х), построить график функции у =
f
(-х) + 2?
2.
Постройте график функции:
Вариант 2
1. Как, зная график функции у =
f
(х), построить график функции у = —
f
(х) — 1?
2.
Постройте график функции:
III. Изучение нового материала
Из материала предыдущего урока видно, что способы преобразования графиков чрезвычайно полезны при их построении. Поэтому рассмотрим также основные способы преобразования графиков, содержащих модули. Эти способы являются универсальными и пригодны для любых функций. Для простоты построения будем рассматривать кусочно-линейную функцию
f
(х) с областью определения
D
(f
), график которой представлен на рисунке. Рассмотрим три стандартных преобразования графиков с модулями.
1) Построение графика функции у = |
f
(x
)|
f
/(x
), если Дх)>0,
По определению модуля получим:
Это означает, что для построения графика функции у = |
f
(x
)| надо сохранить часть графика функции у =
f
(x
), для которой у ≥ 0. Ту часть графика функции у =
f
(х), для которой у
2) Построение графика функции у =
f
(|
x
|)
Г/О), если Дх)>0,
Раскроем модуль и получим:
Поэтому для построения графика функции у =
f
(|
x
|) надо сохранить часть графика функции у =
f
(х), для которой х ≥ 0. Кроме того, эту часть надо симметрично отразить влево относительно оси ординат.
3) Построение графика уравнения |у| =
f
(x
)
По определению модуля имеем, что при
f
(х) ≥ 0 надо построить графики двух функций: у =
f
(х) и у = —
f
(х). Это означает, что для построения графика уравнения |у| =
f
(х) надо сохранить часть графика функции у =
f
(х), для которой у ≥ 0. Кроме того, эту часть надо симметрично отразить вниз относительно оси абсцисс.
Заметим, что зависимость |у| =
f
(х) не задает функцию, т. е. при х
∈
(-2,6; 1,4) каждому значению х соответствуют два значения у. Поэтому на рисунке представлен именно график уравнения |у| =
f
(х).
Используем рассмотренные способы преобразования графиков с модулями для построения графиков более сложных функций и уравнений.
Пример 1
Построим график функции
Выделим в этой функции целую часть
Такой график получается при смещении графика функции у = -1/
x
на 2 единицы вправо и на 1 единицу вниз. Графиком данной функции является гипербола.
Пример 2
Построим график функции
В соответствии со способом 1 сохраним часть графика из примера 1, для которой у ≥ 0. Ту часть графика, для которой у
Пример 3
Построим график функции
Используя способ 2, сохраним часть графика из примера 1, для которой х ≥ 0. Эту сохраненную часть, кроме того, зеркально отразим влево относительно оси ординат. Получим график функции, симметричный относительно оси ординат.
Пример 4
Построим график уравнения
В соответствии со способом 3 сохраним часть графика из примера 1, для которой у ≥ 0. Кроме того, эту сохраненную часть симметрично отразим вниз относительно оси абсцисс. Получим график данного уравнения.
Разумеется, рассмотренные способы преобразования графиков можно использовать и совместно.
Пример 5
Построим график функции
Используем график функции
построенный в примере 3. Чтобы построить данный график, сохраним те части графика 3, для которых у ≥ 0. Те части графика 3, для которых у
В тех случаях, когда модули входят в зависимость иным образом (чем в способах 1-3), необходимо эти модули раскрыть.
Пример 6
Построим график функции
Выражения х — 1 и
x
+ 2, входящие под знаки модулей, меняют свои знаки в точках х = 1 и
x
= -2 соответственно. Отметим эти точки на координатной прямой. Они разбивают ее на три интервала. Используя определения модуля, раскроем модули в каждом промежутке.
Получим:
1. При
2. При
3. При
Построим графики этих функций, учитывая интервалы для переменной х, в которых раскрывались знаки модуля. Получим ломаную прямую.
Достаточно часто при построении графиков уравнений с модулями для их раскрытия используют координатную плоскость. Поясним это следующим примером.
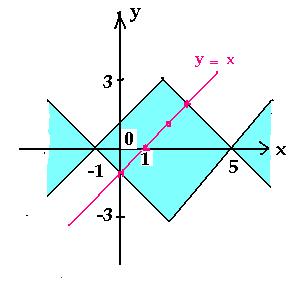
Пример 7
Построим график уравнения
Выражение у — х меняет свой знак на прямой у = х. Построим эту прямую — биссектрису первого и третьего координатных углов. Эта прямая разбивает точки плоскости на две области: 1 — точки, расположенные над прямой у – х; 2 — точки, расположенные под этой прямой. Раскроем модуль в таких областях. В области 1 возьмем, например, контрольную точку (0; 5). Видим, что для этой точки выражение у — х > 0. Раскрывая модуль, получим: у — х + у + х = 4 или
y
= 2. Строим такую прямую в пределах первой области. Очевидно, в области 2 выражение у — х
3. Постройте график дробно-линейной функции и уравнения:
4. Постройте график функции, уравнения, неравенства:
VIII. Подведение итогов урока
Введение……………………………………………………………. 3
I. График квадратичной функции, содержащей переменную
под знаком абсолютной величины
1.1. Основные определения и свойства………………………… 4
1.2. Построение графика квадратичной функции, содержащей
переменную под знаком модуля…………………………… 5
II. Построение графика квадратичной функции, содержащей
переменную под знаком модуля, в программе
Microsoft Excel…………………………………………………. 12
Заключение…………………………………………………. …. 15
Список использованной литературы………………………….. 16
Введение
Мне приходилось делить своё время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно.
А. Эйнштейн.
Когда в «стандартные» уравнения прямых, парабол, гипербол включают знак модуля, их графики становятся необычными и даже красивыми. Чтобы научиться строить такие графики, надо владеть приемами построения базовых фигур, а также твердо знать и понимать определение модуля числа. В школьном курсе математики графики с модулем рассматриваются недостаточно углубленно, именно поэтому мне захотелось расширить свои знания по данной теме, провести собственные исследования.
Цель работы – рассмотреть построение графика квадратичной функции, содержащей переменную под знаком модуля.
Объект исследования: график квадратичной функции.
Предмет исследования: изменения графика квадратичной функции в зависимости от расположения знака абсолютной величины.
Задачи:
1) Изучить литературу о свойствах абсолютной величины и квадратичной функции.
2) Исследовать изменения графика квадратичной функции в зависимости от расположения знака абсолютной величины.
3) Научиться стоить графики уравнений, используя различные программы для построения графиков, в том числе Microsoft Excel.
Методы исследования:
1) теоретический (логическая ступень познания);
2) эмпирический (исследование, эксперимент);
3) моделирование.
Практическая значимость моей работы заключается:
1) в использовании приобретенных знаний по данной теме, а также углубление их и применение к другим функциям и уравнениям;
2)в использовании навыков исследовательской работы в дальнейшей учебной деятельности.
I. График квадратичной функции, содержащей переменную под знаком абсолютной величины
1.1. Основные определения и свойства.
Функция – одно из важнейших математических понятий. Функцией называют такую зависимость переменной y от переменной x, при которой каждому значению переменной x соответствует единственное значение переменной у.
Способы задания функции:
1) аналитический способ (функция задается с помощью математической формулы);
2) табличный способ (функция задается с помощью таблицы);
3) описательный способ (функция задается словесным описанием);
4) графический способ (функция задается с помощью графика).
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значению аргумента, а ординаты – соответствующим значениям функции.
Функция, определяемая формулой у=ах2+вх+с, где х и у переменные, а параметры а, в и с – любые действительные числа, причём а 0, называется квадратичной.
График функции у=ах2+вх+с есть парабола; осью симметрии параболы у=ах2+вх+с является прямая, при а>0 «ветви» параболы направлены вверх, при аЧтобы построить график квадратичной функции, нужно:
1) найти координаты вершины параболы и отметить её в координатной плоскости;
2) построить ещё несколько точек, принадлежащих параболе;
3) соединить отмеченные точки плавной линией.
Координаты вершины параболы определяются по формулам:
, .
Абсолютной величиной положительного числа называется само положительное число, абсолютной величиной отрицательного числа называется противоположное ему положительное число. Абсолютная величина нуля принимается равной нулю, т.е.
.
Свойства:
1) Абсолютная величина суммы чисел не больше суммы абсолютных величин её слагаемых, т.е.
|а+в| |а|+|в|
2) Абсолютная величина разности двух чисел не меньше разности абсолютных величин этих чисел, т.е.
|а-в| |а|-|в| или |а-в| |в|-|а|
3) Абсолютная величина произведения равна произведению абсолютных величин сомножителей, т.е.
|а в|=|а| |в|
4) Абсолютная величина частного равна частному от деления абсолютных величин делимого и делителя, т.е.
5) Абсолютная величина степени с целым положительным показателем равна той же степени абсолютной величины основания, т.е.
|аn|=|a|n.
1.2. Построение графика квадратичной функции, содержащей переменную под знаком модуля.
…Математические сведения могут применяться умело и с пользой только в том случае, если они усвоены творчески, так, что учащийся видит сам, как можно было бы прийти к ним самостоятельно.
А.Н. Колмогоров.
Для построения графиков функций, содержащих знак модуля, как и при решении уравнений, сначала находят корни выражений, стоящих под знаком модуля. В результате ось Ох разбивается на промежутки. Убираем знаки модуля, беря каждое выражение в каждом промежутке с определённым знаком, которые находим методом интервалов.
В каждом промежутке получается функция без знака модуля. Строим график каждой функции в каждом промежутке.
В простейшем случае, когда только одно выражение стоит под знаком модуля и нет других слагаемых без знака модуля, можно построить график функции, опустив знак модуля, и затем часть графика, расположенную в области отрицательных значений y, отобразить относительно оси Ох.
Покажем на примерах некоторые приемы построения графиков функций с модулями.
Пример 1.
Сначала построим параболу у= х2– 6х +5. Чтобы получить из неё график функции у = |х2 — 6х + 5|, нужно каждую точку параболы с отрицательной ординатой заменить точкой с той же абсциссой, но с противоположной (положительной) ординатой. Иными словами, часть параболы, расположенную ниже оси Ох, нужно заменить линией, ей симметричной относительно оси Ох (Рис.1).
Пример 2.
Рассмотрим график функции у = |х|2– 6х +5.
Т. к. |х| возводится в квадрат, то независимо от знака числа х после возведения в квадрат он будет положительным. Отсюда следует, то график функции у =|х|2 — 6х +5 будет идентичен графику функции у = х2 — 6х +5, т.е. графику функции, не содержащей знака абсолютной величины (Рис.2).
Рис.2
Пример 3.
Рассмотрим график функции у = х2 – 6|х| +5.
Воспользовавшись определением модуля числа, заменим формулу
у = х2 – 6|х| +5
Теперь мы имеем дело с хорошо знакомым нам кусочным заданием зависимости. Строить график будем так:
1) построим параболу у = х2 — 6х +5 и обведём ту её часть, которая соответствует неотрицательным значениям х, т.е. часть, расположенную правее оси Оу.
2) в той же координатной плоскости построим параболу у = х2 +6х +5 и обведём ту её часть, которая соответствует отрицательным значениям х, т.е. часть, расположенную левее оси Оу. Обведённые части парабол вместе образуют график функции у = х2 — 6|х| +5 (Рис.3).
Пример 4.
Рассмотрим график функции у = |х|2 — 6|х|+5.
Т.к. график уравнения у = |х|2 – 6х +5 такой же, как и график функции без знака модуля (рассмотрено в примере 2) то следует, что график функции у = |х|2 – 6|х| +5 идентичен графику функции у = х2 – 6|х| +5, рассмотренному в примере 3 (Рис.3).
Пример 5.
Для этого построим график функции у = х2 — 6х. Чтобы получить из неё график функции у = |х2 — 6х|, нужно каждую точку параболы с отрицательной ординатой заменить точкой с той же абсциссой, но с противоположной (положительной) ординатой. Иными словами, часть параболы, расположенную ниже оси х, нужно заменить линией ей симметричной относительно оси х. Т.к. нам нужно построить график функции у = |х2 — 6х| +5, то график рассмотренной нами функции у = |х2 — 6х| нужно просто поднять по оси у на 5 единиц вверх (Рис.4).
Пример 6.
Построим график функции у = х2 — |6х+5|. Для этого воспользуемся хорошо нам известной кусочной функцией. Найдём нули функции
у = 6х +5
6х + 5 = 0 при.
Рассмотрим два случая:
1)Если, то уравнение примет вид у = х2 – 6х -5. Построим эту параболу и обведём ту её часть, где.
2)Если, то уравнение принимает вид у = х2+ 6х +5. Постоим эту параболу и обведём ту её часть, которая расположена левее точки с координатами (Рис.5).
Пример 7
.
Для этого мы построим график функции у =х2- 6|х| +5. Построение этого графика мы проводили в примере 3. Т. к. наша функция полностью находится под знаком модуля, то для того, чтобы построить график функции у = |х2 – 6|х| +5|, нужно каждую точку графика функции у = х2 – 6|х|+5 с отрицательной ординатой заменить точкой с той же абсциссой, но с противоположной (положительной) ординатой, т.е. часть параболы, расположенную ниже оси Ох, нужно заменить линией ей симметричной относительно оси Ох (Рис.6).
Рис.6
Пример 8.
Рассмотрим построение графиков вида = f (x).
Учитывая, что в формуле = f (x), f (x) , и на основании определения модуля =
Перепишем формулу = f (x) в виде у= f (x), где f (x) .
Исходя из этого, сформулируем правило-алгоритм.
Для построения графиков вида = f (x) достаточно построить график функции у = f (x) для тех х из области определения, при которых f (x) , и отразить полученную часть графика симметрично относительно оси абсцисс.
Таким образом, график зависимости = f (x) состоит из графиков двух функций: у = f (x) и у = — f (x).
Построим график функции.
Дальнейшее вставление рисунков и формул технически невозможно
Рис.7
Пример 9.
Рассмотрим построение графиков вида
Осуществляя уже известные преобразования графиков, выполним построение сначала графика y = │f (x)│, а затем уже и множества точек, координаты которых удовлетворяют условию
Алгоритм построения:
1) Строим график функции.
2) Часть графика симметрично отображаем относительно оси Ох.
3) Полученный график симметрично отображаем относительно оси Ох (Рис.8).
Рис.8
Выводы:
1.График функции y = │f (x)│ можно получить из графика y = f (x), оставив на месте ту его часть, где f (x) , и симметрично отразив относительно оси Ох другую его часть, где f (x) 2.График функции y = f (│x│) совпадает с графиком функции y = f (x) на множестве неотрицательных значений аргумента и симметричен ему относительно оси Оу на множестве отрицательных значений аргумента.
3. График функции = f (x) можно получить, построив график функции у = f (x) для тех х из области определения, при которых f (x) , и отразив полученную часть графика симметрично относительно оси абсцисс.
4. График функции можно получить, построив график функции
у = f (x) и симметрично отобразив относительно оси Ох часть графика. Полученный график симметрично отображаем относительно оси Ох.
II. Построение графика квадратичной функции, содержащей переменную под знаком модуля, в программе Microsoft Excel.
Пример 1.
Построим график функции у = |х2 – 6х +5|.
Пример 2.
Построим график функции у = х2 – 6|х| +5.
Пример 3.
Построим график функции у = |х2 – 6х| +5.
Пример 4.
Построим график функции у = х2 — |6х+5|.
Пример 5.
Построим график функции у = |х2 – 6|х| +5|.
Пример 6.
Построим график функции.
Пример 7.
Построим график функции.
Заключение
Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью.
Л. Н. Толстой.
Считаем, что в данной исследовательской работе цель достигнута, так как были решены все поставленные задачи.
Нами рассмотрено построение графика квадратичной функции, содержащей переменную под знаком модуля, и исследованы изменения графика квадратичной функции в зависимости от расположения знака абсолютной величины. Были освоены приёмы построения графиков функций вида: y = f (│x│), y = │f (x)│, y = │f (│x │)│,
Для написания данной исследовательской работы
1) была изучена литература о свойствах абсолютной величины и квадратичной функции;
2) исследованы и проанализированы изменения при построении графика квадратичной функции, в которой знак модуля содержат различные переменные;
3) построены графики уравнений с использованием программ для построения графиков Graph Master v 1.1, Microsoft Excel и другие;
При написании работы мы пользовались учебной литературой, Интернет-ресурсами, работали в таких программах, как Microsoft Word, Paint, Редактор формул, Microsoft Excel.
Тема исследований оказалась очень многогранной, требующей совершенно новых умений и навыков как на этапе исследований, так и при написании и оформлении работы.
Данный практический опыт работы с программами для построения графиков, для записи математических формул, а также полученные навыки исследовательской деятельности будут использованы нами в дальнейшей учебной деятельности, в том числе при изучении других функций и уравнений с модулем, при построении графиков этих функций.
Список использованной литературы
1.Математика. Алгебра. Функции. Анализ данных. 9 кл.: М.: Учеб. для общеобразоват. учреждений / Г. В. Дорофеев, С. Б. Суворова, Е. А. Бунимович, Л. В. Кузнецова, С. С. Минаева; Под ред. Г. В. Дорофеева. – 5-е изд., стереотип. – М.: Дрофа, 2004. – 352 с.: ил.
2. Курс высшей математики для техникумов. И. Ф. Суворов, Москва — 1967.
3. Математика. Алгебра и элементарные функции. М. И. Абрамович, М. Т. Стародубцев.
4. А.Г. Мордкович Книга для учителя. Беседы с учителями. Москва – «Оникс 21 век», «Мир и образование», 2005 г.
5.Элективный курс. Знакомьтесь: модуль! Алгебра. 8-9 классы./ Сост. Баукова Т.Т.-Волгоград: ИТД «Корифей».- 96 с.
Интернет – ресурсы
http://festival.1september.ru/articles/504401/
http://www.uztest.ru/abstracts/?idabstract=18
http://dic.academic.ru/dic.nsf/enc3p/45426
http://www.zaitseva-irina.ru/html/f1128423553.html
http://www.sorobr1.ru/index.php?option=com_content&task=view&id=8&Itemid=41
http://mschool.kubsu.ru/cdo/shabitur/kniga/sprav/function/kvfunc/kvfunct.htm
http://tvsh2004.narod.ru/alg02.html
http://info.territory.ru/univer/qvadro_func.htm
http://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%B8%D1%87%D0%BD%D0%B0%D1%8F_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F
Пошаговое построение графиков.
«Навешивание» модулей на прямые, параболы, гиперболы.
Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.
Для понимания друг друга введу немного «обзываний» системы координат:
Для начала построим график прямой y = 2x − 1.
Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую. Поэтому берем любые две точки А = (0; −1) и B = (1; 1) и проводим единственную прямую.
А если теперь добавить модуль? y = |2x − 1|.
Модуль — это всегда положительное значение
, получается, что «y» должен быть всегда положительным.
Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю
(как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).
Красота! А как же будет выглядеить график, если надеть модуль только на «х»: y = 2|x| − 1?
Одна строчка рассуждений и рисуем:
Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.
Суть построения точно такая же, только здесь отражаем относительно оси «y»
.
Смертельный номер:
y = |2|x| − 1|.
Для начала построим y = |2x − 1|, отразив относительно оси «x». В положительной части
он будет такой же, как y =|2|x| − 1|.
А после этого отражаем относительно оси «y», то, что мы получили справа:
Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках.
Разберем по винтикам параболу y
=
x²
+
x
−
2.
Точки пересечения с осью «x» получим с помощью дискриминанта: x₁
=
1 и
x
₂
=
-2.
Можно найти вершину у параболы и взять пару точек для точного построения.
А как будет выглядеть график: y
=
|x²|
+
x
−
2?
Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.
При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:
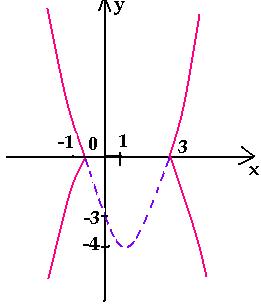
Следующий смертельный номер: |y|
=
x²
+
x
−
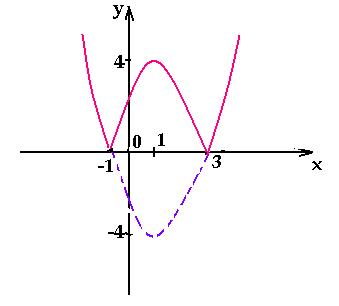
2, подумай хорошенько, а еще лучше попробуй нарисовать сам.
При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!
Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.
А настоящие профи могут разобраться, почему же данные графики выглядят так:
Легкий и средний уровень позади, и настала пора выжать концетрацию на максимум
, потому что дальше тебя ждут гиперболы, которые частенько встречаются во второй части ЕГЭ и ОГЭ.
y
=
1/x
— простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:
А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:
А что будет, если мы добавим в знаменателе «
−1»?
График сдвинется вправо на единицу.
А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!

а если добавить отдельно «−1» y = (1/x) − 1? Вниз на единицу!
Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.
Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.
Можно придумывать массу вариантов, но общий принцип остается для любого графика.
Принципы повторим в выводах в конце статьи.
Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определнию:
И построить график, разбив его на кусочно-заданные функции.
Например для прямой:
Для параболы с одним модулем будет два кусочно заданных графика:
C двумя модулями кусочно заданных графиков будет четыре:

Выводы:
- Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
- Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
- Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль
. - Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:
- Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
- Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
- Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.
- Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.
Пошаговое построение графиков.
«Навешивание» модулей на прямые, параболы, гиперболы.
Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.
Для понимания друг друга введу немного «обзываний» системы координат:
Для начала построим график прямой y = 2x − 1.
Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую.
Возьмем значение X = 0 и Х = 1 и подставим в выражение y = 2x − 1, тогда соответственно Y = − 1 и Y = 1
Через данные две точки А = (0; −1) и B = (1; 1) проводим единственную прямую:
А если теперь добавить модуль y = |2x − 1|.
Модуль — это всегда положительное значение
, получается, что «y» должен быть всегда положительным.
Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю
(как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).

Красота! А как же будет выглядеть график, если надеть модуль только на «х»: y = 2|x| − 1?
Одна строчка рассуждений и рисуем:
Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.
Здесь отражаем относительно оси «y»
. Такая же галочка, только теперь через другую ось.
Смертельный номер:
y = |2|x| − 1|.
Черную прямую y = 2x − 1 отражаем относительно оси Х, получим y = |2x − 1|. Но мы выяснили, что модуль на х влияет только на левую часть.
В правой части: y = |2x − 1| и y = |2|x| − 1| идентичны!
А после этого отражаем относительно оси «y» то, что мы получили справа налево:
Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках, значит делаем по аналогии.
Разберем по винтикам параболу y
=
x²
+
x
−
2.
Точки пересечения с осью «x» получим с помощью дискриминанта: x₁
=
1 и
x
₂
=
-2.
Можно найти вершину у параболы и взять пару точек для точного построения.
А как будет выглядеть график: y
=
|x²|
+
x
−
2?
Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.
При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:
Следующий смертельный номер: |y|
=
x²
+
x
−
2, подумай хорошенько, а еще лучше попробуй нарисовать сам.
При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!
Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.
А теперь сразу комбо:
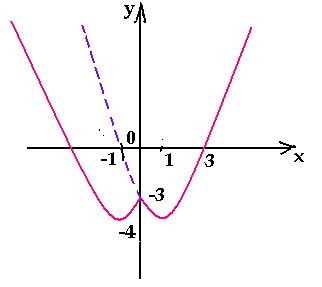
Cиний: похож на y = x² + |x| − 2, только поднят вверх. Строим график в правой части, а затем отражаем через ось Y влево.
Оранжевый: строим в правой части и отражаем относительно оси Х. Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет «шире», расходится в бока он быстрее остальных.
Зеленый: Так же начинаем с правой части и отражаем относительно оси оси Y. Получается график y = |x² + x − 2|, но еще есть −2, поэтому опустим график на 2 вниз. Теперь параболы как бы отражается относительно Y = − 2.
Легкий и средний уровень позади, и настала пора выжать концентрацию на максимум
, потому что дальше тебя ждут гиперболы, которые частенько встречаются во второй части ЕГЭ и ОГЭ.
y
=
1/x
— простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:
А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:
А что будет, если мы добавим в знаменателе «
−1»?
График сдвинется вправо на единицу.
А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!

а если добавить отдельно «−1» y = (1/x) − 1? Вниз на единицу!
Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.
Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.
Можно придумывать массу вариантов, но общий принцип остается для любого графика.
Принципы повторим в выводах в конце статьи.
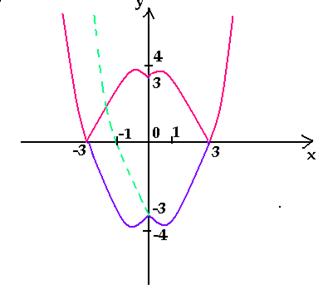
Фиолетовый: Вычитаем из дроби −1 и сдвигаем график вниз на единицу. Ставим модуль − отражаем все, что снизу вверх.
Оранжевый: Ставим +1 в знаменателе и график смещается влево на единицу. Вычитаем из дроби −1 и сдвигаем график вниз на единицу. А после этого ставим модуль − отражаем все, что снизу вверх.
Зеленый: Сначала получим фиолетовый график. После этого ставим «−» и отражаем график по горизонтали. Сгибаем лист по оси Х и переводим его вниз. Остается добавить +1, это значит, что его нужно поднять вверх на единицу.
Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определению:
И построить график, разбив его на кусочно-заданные функции.
Например для прямой:
Для параболы с одним модулем будет два кусочно-заданных графика:
C двумя модулями кусочно-заданных графиков будет четыре:

Выводы:
- Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
- Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
- Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль
. - Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:
- Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
- Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
- Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.
- Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.
Знак модуля, пожалуй, одно из самых интересных явлений в математике. В связи с этим у многих школьников возникает вопрос, как строить графики функций, содержащих модуль. Давайте подробно разберем этот вопрос.
1. Построение графиков функций, содержащих модуль
Пример 1.
Построить график функции y = x 2 – 8|x| + 12.
Решение.
Определим четность функции. Значение для y(-x) совпадает со значением для y(x), поэтому данная функция четная. Тогда ее график симметричен относительно оси Oy. Строим график функции y = x 2 – 8x + 12 для x ≥ 0 и симметрично отображаем график относительно Oy для отрицательных x (рис. 1).
Пример 2.
Следующий график вида y = |x 2 – 8x + 12|.
– Какова область значений предложенной функции? (y ≥ 0).
– Как расположен график? (Над осью абсцисс или касаясь ее).
Это значит, что график функции получают следующим образом: строят график функции y = x 2 – 8x + 12, оставляют часть графика, которая лежит над осью Ox, без изменений, а часть графика, которая лежит под осью абсцисс, симметрично отображают относительно оси Ox (рис. 2).
Пример 3.
Для построения графика функции y = |x 2 – 8|x| + 12| проводят комбинацию преобразований:
y = x 2 – 8x + 12 → y = x 2 – 8|x| + 12 → y = |x 2 – 8|x| + 12|.
Ответ: рисунок 3.
Рассмотренные преобразования справедливы для всех видов функций. Составим таблицу:
2. Построение графиков функций, содержащих в формуле «вложенные модули»
Мы уже познакомились с примерами квадратичной функции, содержащей модуль, а так же с общими правилами построения графиков функций вида y = f(|x|), y = |f(x)| и y = |f(|x|)|. Эти преобразования помогут нам при рассмотрении следующего примера.
Пример 4.
Рассмотрим функцию вида y = |2 – |1 – |x|||. Выражение, задающее функцию, содержит «вложенные модули».
Решение.
Воспользуемся методом геометрических преобразований.
Запишем цепочку последовательных преобразований и сделаем соответствующий чертеж (рис. 4):
y = x → y = |x| → y = -|x| → y = -|x| + 1 → y = |-|x| + 1|→ y = -|-|x| + 1|→ y = -|-|x| + 1| + 2 → y = |2 –|1 – |x|||.
Рассмотрим случаи, когда преобразования симметрии и параллельного переноса не являются основным приемом при построении графиков.
Пример 5.
Построить график функции вида y = (x 2 – 4)/√(x + 2) 2 .
Решение.
Прежде чем строить график, преобразуем формулу, которой задана функция, и получим другое аналитическое задание функции (рис. 5).
y = (x 2 – 4)/√(x + 2) 2 = (x– 2)(x + 2)/|x + 2|.
Раскроем в знаменателе модуль:
При x > -2, y = x – 2, а при x
Область определения D(y) = (-∞; -2)ᴗ(-2; +∞).
Область значений E(y) = (-4; +∞).
Точки, в которых график пересекает с оси координат: (0; -2) и (2; 0).
Функция убывает при всех x из интервала (-∞; -2), возрастает при x от -2 до +∞.
Здесь нам пришлось раскрывать знак модуля и строить график функции для каждого случая.
Пример 6.
Рассмотрим функцию y = |x + 1| – |x – 2|.
Решение.
Раскрывая знак модуля, необходимо рассмотреть всевозможную комбинацию знаков подмодульных выражений.
Возможны четыре случая:
{x + 1 – x + 2 = 3, при x ≥ -1 и x ≥ 2;
{-x – 1 + x – 2 = -3, при x
{x + 1 + x – 2 = 2x — 1, при x ≥ -1 и x
{-x – 1 – x + 2 = -2x + 1, при x
Тогда исходная функция будет иметь вид:
{3, при x ≥ 2;
y = {-3, при x
{2x – 1, при -1 ≤ x
Получили кусочно-заданную функцию, график которой изображен на рисунке 6.
3. Алгоритм построения графиков функций вида
y = a 1 |x – x 1 | + a 2 |x – x 2 | + … + a n |x – x n | + ax + b.
В предыдущем примере было достаточно легко раскрыть знаки модуля. Если же сумм модулей больше, то рассмотреть всевозможные комбинации знаков подмодульных выражений проблематично. Как же в этом случае построить график функции?
Заметим, что графиком является ломаная, с вершинами в точках, имеющих абсциссы -1 и 2. При x = -1 и x = 2 подмодульные выражения равны нулю. Практическим путем мы приблизились к правилу построения таких графиков:
Графиком функции вида y = a 1 |x – x 1 | + a 2 |x – x 2 | + … + a n |x – x n | + ax + b является ломаная с бесконечными крайними звеньями. Чтобы построить такую ломаную, достаточно знать все ее вершины (абсциссы вершин есть нули подмодульных выражений) и по одной контрольной точке на левом и правом бесконечных звеньях.
Задача.
Построить график функции y = |x| + |x – 1| + |x + 1| и найти ее наименьшее значение.
Решение:
Нули подмодульных выражений: 0; -1; 1. Вершины ломаной (0; 2); (-1; 3); (1; 3). Контрольная точка справа (2; 6), слева (-2; 6). Строим график (рис. 7). min f(x) = 2.
Остались вопросы? Не знаете, как построить график функции с модулем?
Чтобы получить помощь репетитора – .
blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
,
Конкурс «Презентация к уроку»
Презентация к уроку
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель урока:
- повторить построение графиков функций
содержащих знак модуля; - познакомиться с новым методом построения
графика линейно-кусочной функции; - закрепить новый метод при решении задач.
Оборудование:
- мультимедиа проектор,
- плакаты.
Ход урока
Актуализация знаний
На экране слайд 1 из презентации.
Что является графиком функции y=|x| ? (слайд 2).
(совокупность биссектрис 1 и 2 координатных
углов)
Найдите соответствие между функциями и
графиками, объясните ваш выбор (слайд 3).
Рисунок 1
Расскажите алгоритм построения графиков
функций вида y=|f(x)| на примере функции y=|x 2 -2x-3|
(слайд 4)
Ученик: чтобы построить график данной функции
нужно
Построить параболу y=x 2 -2x-3
Рисунок 2
Рисунок 3
Расскажите алгоритм построения графиков
функций вида y=f(|x|) на примере функции y=x 2 -2|x|-3
(слайд 6).
Построить параболу.
Часть графика при х 0
сохраняется и отображается симметрии
относительно оси ОУ (слайд 7)
Рисунок 4
Расскажите алгоритм построения графиков
функций вида y=|f(|x|)| на примере функции y=|x 2 -2|x|-3|
(слайд 8).
Ученик: Чтобы построить график данной функции
нужно:
Нужно построить параболу у=x 2 -2x-3
Строим у= x 2 -2|x|-3, часть графика сохраняем
и симметрично отображаем относительно ОУ
Часть над ОХ сохраняем, а нижнюю часть
симметрично отображаем относительно ОХ (слайд 9)
Рисунок 5
Следующее задание выполняем письменно в
тетрадях.
1. Построить график линейно-кусочной
функции у=|х+2|+|х-1|-|х-3|
Ученик на доске с комментарием:
Находим нули подмодульных выражений х 1 =-2,
х 2 =1, х 3 =3
Разбиваем ось на промежутки
Для каждого промежутка запишем функцию
при х
при -2 х
при 1 х
при х 3, у = х+4
Строим график линейно-кусочной функции.
Мы с вами построили график функции используя
определение модуля (слайд 10).
Рисунок 6
Предлагаю вашему вниманию “метод вершин”,
который позволяет строить график
линейно-кусочной функции (слайд 11). Алгоритм
построения дети записывают в тетрадь.
Метод вершин
Алгоритм:
- Найдем нули каждого подмодульного выражения
- Составим таблицу, в которой кроме нулей запишем
по одному значению аргумента слева и справа - Нанесем точки на координатную плоскость и
соединим последовательно
2. Разберем этот метод на той же функции
у=|х+2|+|х-1|-|х-3|
Учитель на доске, дети в тетрадях.
Метод вершин:
Найдем нули каждого подмодульного выражения;
Составим таблицу, в которой кроме нулей
запишем по одному значению аргумента слева и
справа
Нанесем точки на координатную плоскость и
соединим последовательно.
Графиком линейно-кусочной функции является
ломанная с бесконечными крайними звеньями (слайд
12) .
Рисунок 7
Каким же методом график получается быстрее и
легче?
3. Чтобы закрепить данный метод предлагаю
выполнить следующее задание:
При каких значения х функция у=|х-2|-|х+1|
принимает наибольшее значение.
Следуем алгоритму; ученик на доске.
у=|х-2|-|х+1|
х 1 =2, х 2 =-1
у(3)=1-4=3, соединяем последовательно точки.
4. Дополнительное задание
При каких значениях а уравнение ||4+x|-|x-2||=a имеет
два корня.
5. Домашняя работа
а) При каких значениях Х функция у =|2x+3|+3|x-1|-|x+2|
принимает наименьшее значение.
б) Построить график функции y=||x-1|-2|-3| .
Модуль — одна из тех вещей, о которых вроде-бы все слышали, но в действительности никто нормально не понимает. Поэтому сегодня будет большой урок, посвящённый решению уравнений с модулями.
Сразу скажу: урок будет несложный. И вообще модули — вообще тема относительно несложная. «Да конечно, несложная! У меня от неё мозг разрывается!» — скажут многие ученики, но все эти разрывы мозга происходят из-за того, что у большинства людей в голове не знания, а какая-то хрень. И цель этого урока — превратить хрень в знания.:)
Немного теории
Итак, поехали. Начнём с самого важного: что такое модуль? Напомню, что модуль числа — это просто то же самое число, но взятое без знака «минус». Т.е., например, $left| -5 right|=5$. Или $left| -129,5 right|=129,5$.
Вот так всё просто? Да, просто. А чему тогда равен модуль положительного числа? Тут ещё проще: модуль положительного числа равен самому этому числу: $left| 5 right|=5$; $left| 129,5 right|=129,5$ и т.д.
Получается любопытная вещь: разные числа могут иметь один тот же модуль. Например: $left| -5 right|=left| 5 right|=5$; $left| -129,5 right|=left| 129,5 right|=129,5$. Нетрудно заметить, что это за числа, у которых модули одинаковые: эти числа противоположны. Таким образом, отметим для себя, что модули противоположных чисел равны:
[left| -a right|=left| a right|]
Ещё один важный факт: модуль никогда не бывает отрицательным
. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.
Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:
Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.
Таким образом, если рассмотреть функцию $y=left| x right|$ и попробовать нарисовать её график, то получится вот такая «галка»:
График модуля и пример решения уравнения
Из этой картинки сразу видно, что $left| -m right|=left| m right|$, а график модуля никогда не опускается ниже оси абсцисс. Но это ещё не всё: красной линией отмечена прямая $y=a$, которая при положительных $a$ даёт нам сразу два корня: ${{x}_{1}}$ и ${{x}_{2}}$, но об этом мы поговорим позже.:)
Помимо чисто алгебраического определения, есть геометрическое. Допустим, есть две точки на числовой прямой: ${{x}_{1}}$ и ${{x}_{2}}$. В этом случае выражение $left| {{x}_{1}}-{{x}_{2}} right|$ — это просто расстояние между указанными точками. Или, если угодно, длина отрезка, соединяющего эти точки:
Модуль — это расстояние между точками на числовой прямой
Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)
Основная формула
Ну хорошо, с определением разобрались. Но легче-то от этого не стало. Как решать уравнения, содержащие этот самый модуль?
Спокойствие, только спокойствие. Начнём с самых простых вещей. Рассмотрим что-нибудь типа такого:
[left| x right|=3]
Итак, модуль$x$ равен 3. Чему может быть равен $x$? Ну, судя по определению, нас вполне устроит $x=3$. Действительно:
[left| 3 right|=3]
А есть ли другие числа? Кэп как бы намекает, что есть. Например, $x=-3$ — для него тоже $left| -3 right|=3$, т.е. требуемое равенство выполняется.
Так может, если поискать, подумать, мы найдём ещё числа? А вот обломитесь: больше чисел нет. Уравнение $left| x right|=3$ имеет лишь два корня: $x=3$ и $x=-3$.
Теперь немного усложним задачу. Пусть вместо переменной $x$ под знаком модуля тусуется функция $fleft(x right)$, а справа вместо тройки поставим произвольное число $a$. Получим уравнение:
[left| fleft(x right) right|=a]
Ну и как такое решать? Напомню: $fleft(x right)$ — произвольная функция, $a$ — любое число. Т.е. вообще любое! Например:
[left| 2x+1 right|=5]
[left| 10x-5 right|=-65]
Обратим внимание на второе уравнение. Про него сразу можно сказать: корней у него нет. Почему? Всё правильно: потому что в нём требуется, чтобы модуль был равен отрицательному числу, чего никогда не бывает, поскольку мы уже знаем, что модуль — число всегда положительное или в крайнем случае ноль.
А вот с первым уравнением всё веселее. Тут два варианта: либо под знаком модуля стоит положительное выражение, и тогда$left| 2x+1 right|=2x+1$, либо это выражение всё-таки отрицательное, и тогда $left| 2x+1 right|=-left(2x+1 right)=-2x-1$. В первом случае наше уравнение перепишется так:
[left| 2x+1 right|=5Rightarrow 2x+1=5]
И внезапно получается, что подмодульное выражение $2x+1$ действительно положительно — оно равно числу 5. Т.е. мы можем спокойно решать это уравнение — полученный корень будет кусочком ответа:
Особо недоверчивые могут попробовать подставить найденный корень в исходное уравнение и убедиться, что действительно под модулем будет положительное число.
Теперь разберём случай отрицательного подмодульного выражения:
[left{ begin{align}& left| 2x+1 right|=5 & 2x+1 lt 0 end{align} right.Rightarrow -2x-1=5Rightarrow 2x+1=-5]
Опа! Снова всё чётко: мы предположили, что $2x+1 lt 0$, и в результате получили, что $2x+1=-5$ — действительно, это выражение меньше нуля. Решаем полученное уравнение, при этом уже точно зная, что найденный корень нас устроит:
Итого мы вновь получили два ответа: $x=2$ и $x=3$. Да, объём вычислений оказался малость побольше, чем в совсем уж простом уравнении $left| x right|=3$, но принципиально ничего не изменилось. Так может, существует какой-то универсальный алгоритм?
Да, такой алгоритм существует. И сейчас мы его разберём.
Избавление от знака модуля
Пусть нам дано уравнение $left| fleft(x right) right|=a$, причём $age 0$ (иначе, как мы уже знаем, корней нет). Тогда можно избавиться от знака модуля по следующему правилу:
[left| fleft(x right) right|=aRightarrow fleft(x right)=pm a]
Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого
[left| 5x+4 right|=10Rightarrow 5x+4=pm 10]
Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:
[begin{align}& 5x+4=10Rightarrow 5x=6Rightarrow x=frac{6}{5}=1,2; & 5x+4=-10Rightarrow 5x=-14Rightarrow x=-frac{14}{5}=-2,8. end{align}]
Вот и всё! Получили два корня: $x=1,2$ и $x=-2,8$. Всё решение заняло буквально две строчки.
Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:
[left| 7-5x right|=13]
Опять раскрываем модуль с плюсом и минусом:
[begin{align}& 7-5x=13Rightarrow -5x=6Rightarrow x=-frac{6}{5}=-1,2; & 7-5x=-13Rightarrow -5x=-20Rightarrow x=4. end{align}]
Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.
Случай переменной правой части
А теперь рассмотрим вот такое уравнение:
[left| 3x-2 right|=2x]
Это уравнение принципиально отличается от всех предыдущих. Чем? А тем, что справа от знака равенства стоит выражение $2x$ — и мы не можем заранее знать, положительное оно или отрицательное.
Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней
— мы уже знаем, что модуль не может быть равен отрицательному числу.
А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».
Таким образом, сформулируем правило для произвольных функций $fleft(x right)$ и $gleft(x right)$ :
[left| fleft(x right) right|=gleft(x right)Rightarrow left{ begin{align}& fleft(x right)=pm gleft(x right), & gleft(x right)ge 0. end{align} right.]
Применительно к нашему уравнению получим:
[left| 3x-2 right|=2xRightarrow left{ begin{align}& 3x-2=pm 2x, & 2xge 0. end{align} right.]
Ну, с требованием $2xge 0$ мы как-нибудь справимся. В конце концов, можно тупо подставить корни, которые мы получим из первого уравнения, и проверить: выполняется неравенство или нет.
Поэтому решим-ка само уравнение:
[begin{align}& 3x-2=2Rightarrow 3x=4Rightarrow x=frac{4}{3}; & 3x-2=-2Rightarrow 3x=0Rightarrow x=0. end{align}]
Ну и какой их этих двух корней удовлетворяет требованию $2xge 0$? Да оба! Поэтому в ответ пойдут два числа: $x={4}/{3};$ и $x=0$. Вот и всё решение.:)
Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}]
Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:
[left| fleft(x right) right|=gleft(x right)]
И решается оно точно так же:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}Rightarrow left{ begin{align}& {{x}^{3}}-3{{x}^{2}}+x=pm left(x-{{x}^{3}} right), & x-{{x}^{3}}ge 0. end{align} right.]
С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:
[{{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}]
Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}; & 2{{x}^{3}}-3{{x}^{2}}=0; end{align}]
Выносим общий множитель ${{x}^{2}}$ за скобку и получаем очень простое уравнение:
[{{x}^{2}}left(2x-3 right)=0Rightarrow left[ begin{align}& {{x}^{2}}=0 & 2x-3=0 end{align} right.]
[{{x}_{1}}=0;quad {{x}_{2}}=frac{3}{2}=1,5.]
Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.
Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=-left(x-{{x}^{3}} right); & {{x}^{3}}-3{{x}^{2}}+x=-x+{{x}^{3}}; & -3{{x}^{2}}+2x=0; & xleft(-3x+2 right)=0. end{align}]
Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:
[left[ begin{align}& x=0 & -3x+2=0 end{align} right.]
Ну вот мы получили три корня: $x=0$, $x=1,5$ и $x={2}/{3};$. Ну и что из этого набора пойдёт в окончательный ответ? Для этого вспомним, что у нас есть дополнительное ограничение в виде неравенства:
Как учесть это требование? Да просто подставим найденные корни и проверим: выполняется неравенство при этих $x$ или нет. Имеем:
[begin{align}& x=0Rightarrow x-{{x}^{3}}=0-0=0ge 0; & x=1,5Rightarrow x-{{x}^{3}}=1,5-{{1,5}^{3}} lt 0; & x=frac{2}{3}Rightarrow x-{{x}^{3}}=frac{2}{3}-frac{8}{27}=frac{10}{27}ge 0; end{align}]
Таким образом, корень $x=1,5$ нас не устраивает. И в ответ пойдут лишь два корня:
[{{x}_{1}}=0;quad {{x}_{2}}=frac{2}{3}.]
Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.
Уравнения с двумя модулями
До сих пор мы изучали лишь самые простые уравнения — там был один модуль и что-то ещё. Это «что-то ещё» мы отправляли в другую часть неравенства, подальше от модуля, чтобы в итоге всё свелось к уравнению вида $left| fleft(x right) right|=gleft(x right)$ или даже более простому $left| fleft(x right) right|=a$.
Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:
[left| fleft(x right) right|=left| gleft(x right) right|]
Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.
Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:
[left| fleft(x right) right|=left| gleft(x right) right|Rightarrow fleft(x right)=pm gleft(x right)]
Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.
Давайте попробуем решать вот такую задачу:
[left| 2x+3 right|=left| 2x-7 right|]
Элементарно, Ватсон! Раскрываем модули:
[left| 2x+3 right|=left| 2x-7 right|Rightarrow 2x+3=pm left(2x-7 right)]
Рассмотрим отдельно каждый случай:
[begin{align}& 2x+3=2x-7Rightarrow 3=-7Rightarrow emptyset ; & 2x+3=-left(2x-7 right)Rightarrow 2x+3=-2x+7. end{align}]
В первом уравнении корней нет. Потому что когда это $3=-7$? При каких значениях $x$? «Какой ещё нафиг $x$? Ты обкурился? Там вообще нет $x$» — скажете вы. И будете правы. Мы получили равенство, не зависящее от переменной $x$, и при этом само равенство — неверное. Потому и нет корней.:)
Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:
Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)
В итоге окончательный ответ: $x=1$.
Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|]
Опять у нас уравнение вида $left| fleft(x right) right|=left| gleft(x right) right|$. Поэтому сразу переписываем его, раскрывая знак модуля:
[{{x}^{2}}-3x+2=pm left(x-1 right)]
Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:
Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми.
Но ведь ничто не мешает нам переписать исходное уравнение следующим образом:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|Rightarrow left| {{x}^{2}}-3x+2 right|=left| x-1 right|]
Что произошло? Да ничего особенного: просто поменяли левую и правую часть местами. Мелочь, которая в итоге немного упростит нам жизнь.:)
В общем, решаем это уравнение, рассматривая варианты с плюсом и с минусом:
[begin{align}& {{x}^{2}}-3x+2=x-1Rightarrow {{x}^{2}}-4x+3=0; & {{x}^{2}}-3x+2=-left(x-1 right)Rightarrow {{x}^{2}}-2x+1=0. end{align}]
Первое уравнение имеет корни $x=3$ и $x=1$. Второе вообще является точным квадратом:
[{{x}^{2}}-2x+1={{left(x-1 right)}^{2}}]
Поэтому у него единственный корень: $x=1$. Но этот корень мы уже получали ранее. Таким образом, в итоговый ответ пойдут лишь два числа:
[{{x}_{1}}=3;quad {{x}_{2}}=1.]
Миссия выполнена! Можно взять с полки и скушать пирожок. Там их 2, ваш средний.:)
Важное замечание
. Наличие одинаковых корней при разных вариантах раскрытия модуля означает, что исходные многочлены раскладываются на множители, и среди этих множителей обязательно будет общий. Действительно:[begin{align}& left| x-1 right|=left| {{x}^{2}}-3x+2 right|; & left| x-1 right|=left| left(x-1 right)left(x-2 right) right|. end{align}]
Одно из свойств модуля: $left| acdot b right|=left| a right|cdot left| b right|$ (т.е. модуль произведения равен произведению модулей), поэтому исходное уравнение можно переписать так:
[left| x-1 right|=left| x-1 right|cdot left| x-2 right|]
Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:
[begin{align}& left| x-1 right|=left| x-1 right|cdot left| x-2 right|; & left| x-1 right|-left| x-1 right|cdot left| x-2 right|=0; & left| x-1 right|cdot left(1-left| x-2 right| right)=0. end{align}]
Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:
[left[ begin{align}& left| x-1 right|=0, & left| x-2 right|=1. end{align} right.]
Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)
Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)
Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.
Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.
Итак, уравнение:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0]
Нет, это не опечатка: между модулями именно плюс. И нам нужно найти, при каких $x$ сумма двух модулей равна нулю.:)
В чём вообще проблема? А проблема в том, что каждый модуль — число положительное, либо в крайнем случае ноль. А что будет, если сложить два положительных числа? Очевидно, снова положительное число:
[begin{align}& 5+7=12 gt 0; & 0,004+0,0001=0,0041 gt 0; & 5+0=5 gt 0. end{align}]
Последняя строчка может натолкнуть на мысль: единственный случай, когда сумма модулей равна нулю — это если каждый модуль будет равен нулю:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0Rightarrow left{ begin{align}& left| x-{{x}^{3}} right|=0, & left| {{x}^{2}}+x-2 right|=0. end{align} right.]
А когда модуль равен нулю? Только в одном случае — когда подмодульное выражение равно нулю:
[{{x}^{2}}+x-2=0Rightarrow left(x+2 right)left(x-1 right)=0Rightarrow left[ begin{align}& x=-2 & x=1 end{align} right.]
Таким образом, у нас есть три точки, в которых обнуляется первый модуль: 0, 1 и −1; а также две точки, в которых обнуляется второй модуль: −2 и 1. Однако нам нужно, чтобы оба модуля обнулялись одновременно, поэтому среди найденных чисел нужно выбрать те, которые входят в оба набора. Очевидно, такое число лишь одно: $x=1$ — это и будет окончательным ответом.
Метод расщепления
Что ж, мы уже рассмотрели кучу задач и изучили множество приёмов. Думаете, на этом всё? А вот и нет! Сейчас мы рассмотрим заключительный приём — и одновременно самый важный. Речь пойдёт о расщеплении уравнений с модулем. О чём вообще пойдёт речь? Давайте вернёмся немного назад и рассмотрим какое-нибудь простое уравнение. Например, это:
[left| 3x-5 right|=5-3x]
В принципе, мы уже знаем, как решать такое уравнение, потому что это стандартная конструкция вида $left| fleft(x right) right|=gleft(x right)$. Но попробуем взглянуть на это уравнение немного под другим углом. Точнее, рассмотрим выражение, стоящее под знаком модуля. Напомню, что модуль любого числа может быть равен самому числу, а может быть противоположен этому числу:
[left| a right|=left{ begin{align}& a,quad age 0, & -a,quad a lt 0. end{align} right.]
Собственно, в этой неоднозначности и состоит вся проблема: поскольку число под модулем меняется (оно зависит от переменной), нам неясно — положительное оно или отрицательное.
Но что если изначально потребовать, чтобы это число было положительным? Например, потребуем, чтобы $3x-5 gt 0$ — в этом случае мы гарантированно получим положительное число под знаком модуля, и от этого самого модуля можно полностью избавиться:
Таким образом, наше уравнение превратится в линейное, которое легко решается:
Правда, все эти размышления имеют смысл только при условии $3x-5 gt 0$ — мы сами ввели это требование, дабы однозначно раскрыть модуль. Поэтому давайте подставим найденный $x=frac{5}{3}$ в это условие и проверим:
Получается, что при указанном значении $x$ наше требование не выполняется, т.к. выражение оказалось равно нулю, а нам нужно, чтобы оно было строго больше нуля. Печалька.:(
Но ничего страшного! Ведь есть ещё вариант $3x-5 lt 0$. Более того: есть ещё и случай $3x-5=0$ — это тоже нужно рассмотреть, иначе решение будет неполным. Итак, рассмотрим случай $3x-5 lt 0$:
Очевидно, что в модуль раскроется со знаком «минус». Но тогда возникает странная ситуация: и слева, и справа в исходном уравнении будет торчать одно и то же выражение:
Интересно, при каких таких $x$ выражение $5-3x$ будет равно выражению $5-3x$? От таких уравнений даже Капитан очевидность подавился бы слюной, но мы-то знаем: это уравнение является тождеством, т.е. оно верно при любых значениях переменной!
А это значит, что нас устроят любые $x$. Вместе с тем у нас есть ограничение:
Другими словами, ответом будет не какое-то отдельное число, а целый интервал:
Наконец, осталось рассмотреть ещё один случай: $3x-5=0$. Тут всё просто: под модулем будет ноль, а модуль нуля тоже равен нулю (это прямо следует из определения):
Но тогда исходное уравнение $left| 3x-5 right|=5-3x$ перепишется следующим образом:
Этот корень мы уже получали выше, когда рассматривали случай $3x-5 gt 0$. Более того, это корень является решением уравнения $3x-5=0$ — это ограничение, которое мы сами же и ввели, чтобы обнулить модуль.:)
Таким образом, помимо интервала нас устроит ещё и число, лежащее на самом конце этого интервала:
Объединение корней в уравнениях с модулем
Итого окончательный ответ: $xin left(-infty ;frac{5}{3} right]$. Не очень-то привычно видеть такую хрень в ответе к довольно простому (по сути — линейному) уравнению с модулем, правда? Что ж, привыкайте: в том и состоит сложность модуля, что ответы в таких уравнениях могут оказаться совершенно непредсказуемыми.
Куда важнее другое: мы только что разобрали универсальный алгоритм решения уравнения с модуляем! И состоит этот алгоритм из следующих шагов:
- Приравнять каждый модуль, имеющийся в уравнении, к нулю. Получим несколько уравнений;
- Решить все эти уравнения и отметить корни на числовой прямой. В результате прямая разобьётся на несколько интервалов, на каждом из которых все модули однозначно раскрываются;
- Решить исходное уравнение для каждого интервала и объединить полученные ответы.
Вот и всё! Остаётся лишь один вопрос: куда девать сами корни, полученные на 1-м шаге? Допустим, у нас получилось два корня: $x=1$ и $x=5$. Они разобьют числовую прямую на 3 куска:
Разбиение числовой оси на интервалы с помощью точек
Ну и какие тут интервалы? Понятно, что их три:
- Самый левый: $x lt 1$ — сама единица в интервал не входит;
- Центральный: $1le x lt 5$ — вот тут единица в интервал входит, однако не входит пятёрка;
- Самый правый: $xge 5$ — пятёрка входит только сюда!
Я думаю, вы уже поняли закономерность. Каждый интервал включает в себя левый конец и не включает правый.
На первый взгляд, такая запись может показаться неудобной, нелогичной и вообще какой-то бредовой. Но поверьте: после небольшой тренировки вы обнаружите, что именно такой подход наиболее надёжен и при этом не мешает однозначно раскрывать модули. Лучше уж использовать такую схему, чем каждый раз думать: отдавать левый/правый конец в текущий интервал или «перекидывать» его в следующий.
На этом урок заканчивается. Скачивайте задачи для самостоятельного решения, тренируйтесь, сравнивайте с ответами — и увидимся в следующем уроке, который будет посвящён неравенствам с модулями.:)
Эрднигоряева Марина
Данная работа является результатом изучения темы на факультативе в 8 классе. Здесь показываются геометрические преобразования графиков и их применение к построению графиков с модулями. Вводится понятие модуля и его свойства. Показано как строить графики с модулями различными способами: с помощью преобразований и на основе понятия модуля.Тема проекта является одной из трудных в курсе математики, относится к вопросам, рассматриваемых на факультативах,изучается в классах с улгубленным изучением математики. Тем не меннн такие задания даются во второй части ГИА, в ЕГЭ. Данная работа поможет понять как строить графики с модулями не только линейных, но и других функций(квадратичных, обратно- пропорциональных и др.) Работа поможет при подготовке к ГИА и ЕГЭ.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Графики линейной функции с модулями Работа Эрднигоряевой Марины, ученицы 8 класса МКОУ «Камышовская ООШ» Руководитель Горяева Зоя Эрднигоряевна, учитель математики МКОУ « Камышовская ООШ» с. Камышово, 2013г.
Цель проекта: Ответить на вопрос как строить графики линейных функций с модулями. Задачи проекта: Изучить литературу по данному вопросу. Изучить геометрические преобразования графиков и их применение к построению графиков с модулями. Изучить понятие модуля и его свойства. Научиться строить графики с модулями различными способами.
Прямая пропорциональность Прямой пропорциональностью называется функция, которую можно задать формулой вида y=kx , где x –независимая переменная, k -не равное нулю число.
Построим график функции y = x x 0 2 y 0 2
Геометрическое преобразование графиков Правило №1 График функции y = f (x)+ k – линейная функция — получается параллельным переносом графика функции y = f (x) на + k единиц вверх по оси О y при k> 0 или на |- k| единиц вниз по оси О y при k
Построим графики y=x+3 y=x-2
Правило № 2 График функции y=kf(x) получается растягиванием графика функции y = f (x) вдоль оси О y в a раз при a>1 и сжатием вдоль оси О y в a раз при 0Слайд 9
Построим график y=x y= 2 x
Правило № 3 График функции y =- f (x) получается симметричным отображением графика y = f (x) относительно оси О x
Правило № 4 График функции y=f(- x) получается симметричным отображением графика функции y = f (x) относительно оси О y
Правило № 5 График функции y=f(x+c) получается параллельным переносом графика функции y=f(x) вдоль оси О x вправо, если c 0 .
Построим графики y=f(x) y=f(x+2)
Определение модуля Модуль неотрицательного числа а равен самому числу а; модуль отрицательного числа а равен противоположному ему положительному числу -а. Или, |а|=а, если а ≥0 |а|=-а, если а
Графики линейных функций с модулями строятся: с использованием геометрических преобразований с помощью раскрытия определения модуля.
Правило № 6 График функции y=|f(x)| получается следующим образом: часть графика y=f(x) , лежащая над осью О x , сохраняется; часть, лежащая под осью О x , отображается симметрично, относительно оси О x .
Построить график функции y=-2| x-3|+4 Строим y ₁=| x | Строим y₂= |x — 3 | → параллельный перенос на +3 единицы вдоль оси Ох (сдвиг вправо) Строим y ₃ =+2|x-3| → растягиваем вдоль оси О y в 2 раза = 2 y₂ Строим у ₄ =-2|x-3| → симметрия относительно оси абсцисс = — y₃ Строим y₅ =-2|x-3|+4 → параллельный перенос на +4 единицы вдоль оси О y (сдвиг вверх) = y ₄ +4
График функции y =-2|x-3|+4
График функции у= 3|х|+2 y₁=|x| y₂=3|x|= 3 y₁ → растяжение в 3 раза y₃=3|x| +2= y₄+2 → сдвиг вверх на 2 единицы
Правило № 7 График функции y=f(| x |) получается из графика функции y=f(x) следующим образом: При x > 0 график функции сохраняется, и эта же часть графика симметрично отображается относительно оси О y
Построить график функции y = || x-1 | -2 |
У₁= |х| у₂=|х-1| у₃= у₂-2 у₄= |у₃| У=||х-1|-2|
Алгоритм построения графика функции y=│f(│x│)│ построить график функции y=f(│x│) . далее оставить без изменений все части построенного графика, которые лежат выше оси x . части, расположенные ниже оси x , отобразить симметрично относительно этой оси.
У=|2|х|-3| Построение: а) у= 2х-3 для х >0, б) у=-2х-3 для х Слайд 26
Правило № 8 График зависимости | y|=f(x) получается из графика функции y=f(x) если все точки, для которых f(x) > 0 сохраняются и они же симметрично переносятся относительно оси абсцисс.
Построить множество точек на плоскости, декартовы координаты которых х и у удовлетворяют уравнению |у|=||х-1|-1|.
| y|=||x-1| -1| строим два графика 1) у=||х-1|-1| и 2) у =-|| х-1|-1| y₁=|x| y₂=| x-1 | → сдвиг по оси Ох вправо на 1 единицу y₃ = | x -1 |- 1= → сдвиг на 1 единицу вниз y ₄ = || x-1|- 1| → симметрия точек графика для которых y₃ 0 относительно О x
График уравнения |y|=||x-1|-1| получаем следующим образом: 1)строим график функции y=f(x) и о с тавляем без изменений ту его часть, где y≥0 2) с помощью симметрии относительно оси Оx построим другую часть графика, соответствующую y
Построить график функции y =|x | − | 2 − x | . Решение. Здесь знак модуля входит в два различных слагаемых и его нужно снимать. 1) Найдём корни подмодульных выражений: х=0, 2-х=0, х=2 2) Установим знаки на интервалах:
График функции
Вывод Тема проекта является одной из трудных в курсе математики, относится к вопросам, рассматриваемых на факультативах, изучается в классах по углубленному изучению курса математики. Тем не менее такие задания даются во второй части ГИА. Данная работа поможет понять как строить графики с модулями не только линейных функций, но и других функций(квадратичных, обратно пропорциональных и др.). Работа поможет при подготовке к ГИА и ЕГЭ и позволит получить высокие баллы по математике.
Литература Виленкин Н.Я. , Жохов В.И.. Математика”. Учебник 6 класс Москва. Издательство “ Мнемозина”, 2010г Виленкин Н.Я., Виленкин Л.Н., Сурвилло Г.С. и др. Алгебра. 8 класс: учебн. Пособие для учащихся и классов с углубленным изучением математики. – Москва. Просвещение, 2009 г Гайдуков И.И. “Абсолютная величина”. Москва. Просвещение, 1968. Гурский И.П. “Функции и построение графиков”. Москва. Просвещение, 1968. Ящина Н.В. Приёмы построения графиков, содержащих модули. Ж/л «Математика в школе»,№3,1994г Детская энциклопедия. Москва. «Педагогика», 1990. Дынкин Е.Б., Молчанова С.А. Математические задачи. М., «Наука», 1993. Петраков И.С. Математические кружки в 8-10 классах. М., «Просвещение», 1987 . Галицкий М.Л. и др. Сборник задач по алгебре для 8-9 классов: Учебное пособие для учащихся и классов с углубленным изучением математики. – 12-е изд. – М.: Просвещение, 2006. – 301 с. Макрычев Ю.Н., Миндюк Н.Г. Алгебра: Дополнительные главы к школьному учебнику 9 кл.: Учебное пособие для учащихся школы и классов с углубленным изучением математики / Под редакцией Г.В.Дорофеева. – М.: Просвещение, 1997. – 224 с. Садыкина Н. Построение графиков и зависимостей, содержащих знак модуля /Математика. — №33. – 2004. – с.19-21 .. Кострикина Н.П “ Задачи повышенной трудности в курсе алгебры для 7-9 классов ”… Москва.: Просвещение, 2008г.
Эрднигоряева Марина
Данная работа является результатом изучения темы на факультативе в 8 классе. Здесь показываются геометрические преобразования графиков и их применение к построению графиков с модулями. Вводится понятие модуля и его свойства. Показано как строить графики с модулями различными способами: с помощью преобразований и на основе понятия модуля.Тема проекта является одной из трудных в курсе математики, относится к вопросам, рассматриваемых на факультативах,изучается в классах с улгубленным изучением математики. Тем не меннн такие задания даются во второй части ГИА, в ЕГЭ. Данная работа поможет понять как строить графики с модулями не только линейных, но и других функций(квадратичных, обратно- пропорциональных и др.) Работа поможет при подготовке к ГИА и ЕГЭ.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Графики линейной функции с модулями Работа Эрднигоряевой Марины, ученицы 8 класса МКОУ «Камышовская ООШ» Руководитель Горяева Зоя Эрднигоряевна, учитель математики МКОУ « Камышовская ООШ» с. Камышово, 2013г.
Цель проекта: Ответить на вопрос как строить графики линейных функций с модулями. Задачи проекта: Изучить литературу по данному вопросу. Изучить геометрические преобразования графиков и их применение к построению графиков с модулями. Изучить понятие модуля и его свойства. Научиться строить графики с модулями различными способами.
Прямая пропорциональность Прямой пропорциональностью называется функция, которую можно задать формулой вида y=kx , где x –независимая переменная, k -не равное нулю число.
Построим график функции y = x x 0 2 y 0 2
Геометрическое преобразование графиков Правило №1 График функции y = f (x)+ k – линейная функция — получается параллельным переносом графика функции y = f (x) на + k единиц вверх по оси О y при k> 0 или на |- k| единиц вниз по оси О y при k
Построим графики y=x+3 y=x-2
Правило № 2 График функции y=kf(x) получается растягиванием графика функции y = f (x) вдоль оси О y в a раз при a>1 и сжатием вдоль оси О y в a раз при 0Слайд 9
Построим график y=x y= 2 x
Правило № 3 График функции y =- f (x) получается симметричным отображением графика y = f (x) относительно оси О x
Правило № 4 График функции y=f(- x) получается симметричным отображением графика функции y = f (x) относительно оси О y
Правило № 5 График функции y=f(x+c) получается параллельным переносом графика функции y=f(x) вдоль оси О x вправо, если c 0 .
Построим графики y=f(x) y=f(x+2)
Определение модуля Модуль неотрицательного числа а равен самому числу а; модуль отрицательного числа а равен противоположному ему положительному числу -а. Или, |а|=а, если а ≥0 |а|=-а, если а
Графики линейных функций с модулями строятся: с использованием геометрических преобразований с помощью раскрытия определения модуля.
Правило № 6 График функции y=|f(x)| получается следующим образом: часть графика y=f(x) , лежащая над осью О x , сохраняется; часть, лежащая под осью О x , отображается симметрично, относительно оси О x .
Построить график функции y=-2| x-3|+4 Строим y ₁=| x | Строим y₂= |x — 3 | → параллельный перенос на +3 единицы вдоль оси Ох (сдвиг вправо) Строим y ₃ =+2|x-3| → растягиваем вдоль оси О y в 2 раза = 2 y₂ Строим у ₄ =-2|x-3| → симметрия относительно оси абсцисс = — y₃ Строим y₅ =-2|x-3|+4 → параллельный перенос на +4 единицы вдоль оси О y (сдвиг вверх) = y ₄ +4
График функции y =-2|x-3|+4
График функции у= 3|х|+2 y₁=|x| y₂=3|x|= 3 y₁ → растяжение в 3 раза y₃=3|x| +2= y₄+2 → сдвиг вверх на 2 единицы
Правило № 7 График функции y=f(| x |) получается из графика функции y=f(x) следующим образом: При x > 0 график функции сохраняется, и эта же часть графика симметрично отображается относительно оси О y
Построить график функции y = || x-1 | -2 |
У₁= |х| у₂=|х-1| у₃= у₂-2 у₄= |у₃| У=||х-1|-2|
Алгоритм построения графика функции y=│f(│x│)│ построить график функции y=f(│x│) . далее оставить без изменений все части построенного графика, которые лежат выше оси x . части, расположенные ниже оси x , отобразить симметрично относительно этой оси.
У=|2|х|-3| Построение: а) у= 2х-3 для х >0, б) у=-2х-3 для х Слайд 26
Правило № 8 График зависимости | y|=f(x) получается из графика функции y=f(x) если все точки, для которых f(x) > 0 сохраняются и они же симметрично переносятся относительно оси абсцисс.
Построить множество точек на плоскости, декартовы координаты которых х и у удовлетворяют уравнению |у|=||х-1|-1|.
| y|=||x-1| -1| строим два графика 1) у=||х-1|-1| и 2) у =-|| х-1|-1| y₁=|x| y₂=| x-1 | → сдвиг по оси Ох вправо на 1 единицу y₃ = | x -1 |- 1= → сдвиг на 1 единицу вниз y ₄ = || x-1|- 1| → симметрия точек графика для которых y₃ 0 относительно О x
График уравнения |y|=||x-1|-1| получаем следующим образом: 1)строим график функции y=f(x) и о с тавляем без изменений ту его часть, где y≥0 2) с помощью симметрии относительно оси Оx построим другую часть графика, соответствующую y
Построить график функции y =|x | − | 2 − x | . Решение. Здесь знак модуля входит в два различных слагаемых и его нужно снимать. 1) Найдём корни подмодульных выражений: х=0, 2-х=0, х=2 2) Установим знаки на интервалах:
График функции
Вывод Тема проекта является одной из трудных в курсе математики, относится к вопросам, рассматриваемых на факультативах, изучается в классах по углубленному изучению курса математики. Тем не менее такие задания даются во второй части ГИА. Данная работа поможет понять как строить графики с модулями не только линейных функций, но и других функций(квадратичных, обратно пропорциональных и др.). Работа поможет при подготовке к ГИА и ЕГЭ и позволит получить высокие баллы по математике.
Литература Виленкин Н.Я. , Жохов В.И.. Математика”. Учебник 6 класс Москва. Издательство “ Мнемозина”, 2010г Виленкин Н.Я., Виленкин Л.Н., Сурвилло Г.С. и др. Алгебра. 8 класс: учебн. Пособие для учащихся и классов с углубленным изучением математики. – Москва. Просвещение, 2009 г Гайдуков И.И. “Абсолютная величина”. Москва. Просвещение, 1968. Гурский И.П. “Функции и построение графиков”. Москва. Просвещение, 1968. Ящина Н.В. Приёмы построения графиков, содержащих модули. Ж/л «Математика в школе»,№3,1994г Детская энциклопедия. Москва. «Педагогика», 1990. Дынкин Е.Б., Молчанова С.А. Математические задачи. М., «Наука», 1993. Петраков И.С. Математические кружки в 8-10 классах. М., «Просвещение», 1987 . Галицкий М.Л. и др. Сборник задач по алгебре для 8-9 классов: Учебное пособие для учащихся и классов с углубленным изучением математики. – 12-е изд. – М.: Просвещение, 2006. – 301 с. Макрычев Ю.Н., Миндюк Н.Г. Алгебра: Дополнительные главы к школьному учебнику 9 кл.: Учебное пособие для учащихся школы и классов с углубленным изучением математики / Под редакцией Г.В.Дорофеева. – М.: Просвещение, 1997. – 224 с. Садыкина Н. Построение графиков и зависимостей, содержащих знак модуля /Математика. — №33. – 2004. – с.19-21 .. Кострикина Н.П “ Задачи повышенной трудности в курсе алгебры для 7-9 классов ”… Москва.: Просвещение, 2008г.
Урок 5. Преобразования графиков с модулями (факультативное занятие)
09.07.2015
8998
0
Цель:
освоить основные навыки преобразования графиков с модулями.
I. Сообщение темы и цели урока
II
. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
f
(х), построить график функции у =
f
(-х) + 2?
2.
Постройте график функции:
Вариант 2
1. Как, зная график функции у =
f
(х), построить график функции у = —
f
(х) — 1?
2.
Постройте график функции:
III. Изучение нового материала
Из материала предыдущего урока видно, что способы преобразования графиков чрезвычайно полезны при их построении. Поэтому рассмотрим также основные способы преобразования графиков, содержащих модули. Эти способы являются универсальными и пригодны для любых функций. Для простоты построения будем рассматривать кусочно-линейную функцию
f
(х) с областью определения
D
(f
), график которой представлен на рисунке. Рассмотрим три стандартных преобразования графиков с модулями.
1) Построение графика функции у = |
f
(x
)|
f
/(x
), если Дх)>0,
По определению модуля получим:
Это означает, что для построения графика функции у = |
f
(x
)| надо сохранить часть графика функции у =
f
(x
), для которой у ≥ 0. Ту часть графика функции у =
f
(х), для которой у
2) Построение графика функции у =
f
(|
x
|)
Г/О), если Дх)>0,
Раскроем модуль и получим:
Поэтому для построения графика функции у =
f
(|
x
|) надо сохранить часть графика функции у =
f
(х), для которой х ≥ 0. Кроме того, эту часть надо симметрично отразить влево относительно оси ординат.
3) Построение графика уравнения |у| =
f
(x
)
По определению модуля имеем, что при
f
(х) ≥ 0 надо построить графики двух функций: у =
f
(х) и у = —
f
(х). Это означает, что для построения графика уравнения |у| =
f
(х) надо сохранить часть графика функции у =
f
(х), для которой у ≥ 0. Кроме того, эту часть надо симметрично отразить вниз относительно оси абсцисс.
Заметим, что зависимость |у| =
f
(х) не задает функцию, т. е. при х
∈
(-2,6; 1,4) каждому значению х соответствуют два значения у. Поэтому на рисунке представлен именно график уравнения |у| =
f
(х).
Используем рассмотренные способы преобразования графиков с модулями для построения графиков более сложных функций и уравнений.
Пример 1
Построим график функции
Выделим в этой функции целую часть
Такой график получается при смещении графика функции у = -1/
x
на 2 единицы вправо и на 1 единицу вниз. Графиком данной функции является гипербола.
Пример 2
Построим график функции
В соответствии со способом 1 сохраним часть графика из примера 1, для которой у ≥ 0. Ту часть графика, для которой у
Пример 3
Построим график функции
Используя способ 2, сохраним часть графика из примера 1, для которой х ≥ 0. Эту сохраненную часть, кроме того, зеркально отразим влево относительно оси ординат. Получим график функции, симметричный относительно оси ординат.
Пример 4
Построим график уравнения
В соответствии со способом 3 сохраним часть графика из примера 1, для которой у ≥ 0. Кроме того, эту сохраненную часть симметрично отразим вниз относительно оси абсцисс. Получим график данного уравнения.
Разумеется, рассмотренные способы преобразования графиков можно использовать и совместно.
Пример 5
Построим график функции
Используем график функции
построенный в примере 3. Чтобы построить данный график, сохраним те части графика 3, для которых у ≥ 0. Те части графика 3, для которых у
В тех случаях, когда модули входят в зависимость иным образом (чем в способах 1-3), необходимо эти модули раскрыть.
Пример 6
Построим график функции
Выражения х — 1 и
x
+ 2, входящие под знаки модулей, меняют свои знаки в точках х = 1 и
x
= -2 соответственно. Отметим эти точки на координатной прямой. Они разбивают ее на три интервала. Используя определения модуля, раскроем модули в каждом промежутке.
Получим:
1. При
2. При
3. При
Построим графики этих функций, учитывая интервалы для переменной х, в которых раскрывались знаки модуля. Получим ломаную прямую.
Достаточно часто при построении графиков уравнений с модулями для их раскрытия используют координатную плоскость. Поясним это следующим примером.
Пример 7
Построим график уравнения
Выражение у — х меняет свой знак на прямой у = х. Построим эту прямую — биссектрису первого и третьего координатных углов. Эта прямая разбивает точки плоскости на две области: 1 — точки, расположенные над прямой у – х; 2 — точки, расположенные под этой прямой. Раскроем модуль в таких областях. В области 1 возьмем, например, контрольную точку (0; 5). Видим, что для этой точки выражение у — х > 0. Раскрывая модуль, получим: у — х + у + х = 4 или
y
= 2. Строим такую прямую в пределах первой области. Очевидно, в области 2 выражение у — х
3. Постройте график дробно-линейной функции и уравнения:
4. Постройте график функции, уравнения, неравенства:
VIII. Подведение итогов урока
Знак модуля, пожалуй, одно из самых интересных явлений в математике. В связи с этим у многих школьников возникает вопрос, как строить графики функций, содержащих модуль. Давайте подробно разберем этот вопрос.
1. Построение графиков функций, содержащих модуль
Пример 1.
Построить график функции y = x 2 – 8|x| + 12.
Решение.
Определим четность функции. Значение для y(-x) совпадает со значением для y(x), поэтому данная функция четная. Тогда ее график симметричен относительно оси Oy. Строим график функции y = x 2 – 8x + 12 для x ≥ 0 и симметрично отображаем график относительно Oy для отрицательных x (рис. 1).
Пример 2.
Следующий график вида y = |x 2 – 8x + 12|.
– Какова область значений предложенной функции? (y ≥ 0).
– Как расположен график? (Над осью абсцисс или касаясь ее).
Это значит, что график функции получают следующим образом: строят график функции y = x 2 – 8x + 12, оставляют часть графика, которая лежит над осью Ox, без изменений, а часть графика, которая лежит под осью абсцисс, симметрично отображают относительно оси Ox (рис. 2).
Пример 3.
Для построения графика функции y = |x 2 – 8|x| + 12| проводят комбинацию преобразований:
y = x 2 – 8x + 12 → y = x 2 – 8|x| + 12 → y = |x 2 – 8|x| + 12|.
Ответ: рисунок 3.
Рассмотренные преобразования справедливы для всех видов функций. Составим таблицу:
2. Построение графиков функций, содержащих в формуле «вложенные модули»
Мы уже познакомились с примерами квадратичной функции, содержащей модуль, а так же с общими правилами построения графиков функций вида y = f(|x|), y = |f(x)| и y = |f(|x|)|. Эти преобразования помогут нам при рассмотрении следующего примера.
Пример 4.
Рассмотрим функцию вида y = |2 – |1 – |x|||. Выражение, задающее функцию, содержит «вложенные модули».
Решение.
Воспользуемся методом геометрических преобразований.
Запишем цепочку последовательных преобразований и сделаем соответствующий чертеж (рис. 4):
y = x → y = |x| → y = -|x| → y = -|x| + 1 → y = |-|x| + 1|→ y = -|-|x| + 1|→ y = -|-|x| + 1| + 2 → y = |2 –|1 – |x|||.
Рассмотрим случаи, когда преобразования симметрии и параллельного переноса не являются основным приемом при построении графиков.
Пример 5.
Построить график функции вида y = (x 2 – 4)/√(x + 2) 2 .
Решение.
Прежде чем строить график, преобразуем формулу, которой задана функция, и получим другое аналитическое задание функции (рис. 5).
y = (x 2 – 4)/√(x + 2) 2 = (x– 2)(x + 2)/|x + 2|.
Раскроем в знаменателе модуль:
При x > -2, y = x – 2, а при x
Область определения D(y) = (-∞; -2)ᴗ(-2; +∞).
Область значений E(y) = (-4; +∞).
Точки, в которых график пересекает с оси координат: (0; -2) и (2; 0).
Функция убывает при всех x из интервала (-∞; -2), возрастает при x от -2 до +∞.
Здесь нам пришлось раскрывать знак модуля и строить график функции для каждого случая.
Пример 6.
Рассмотрим функцию y = |x + 1| – |x – 2|.
Решение.
Раскрывая знак модуля, необходимо рассмотреть всевозможную комбинацию знаков подмодульных выражений.
Возможны четыре случая:
{x + 1 – x + 2 = 3, при x ≥ -1 и x ≥ 2;
{-x – 1 + x – 2 = -3, при x
{x + 1 + x – 2 = 2x — 1, при x ≥ -1 и x
{-x – 1 – x + 2 = -2x + 1, при x
Тогда исходная функция будет иметь вид:
{3, при x ≥ 2;
y = {-3, при x
{2x – 1, при -1 ≤ x
Получили кусочно-заданную функцию, график которой изображен на рисунке 6.
3. Алгоритм построения графиков функций вида
y = a 1 |x – x 1 | + a 2 |x – x 2 | + … + a n |x – x n | + ax + b.
В предыдущем примере было достаточно легко раскрыть знаки модуля. Если же сумм модулей больше, то рассмотреть всевозможные комбинации знаков подмодульных выражений проблематично. Как же в этом случае построить график функции?
Заметим, что графиком является ломаная, с вершинами в точках, имеющих абсциссы -1 и 2. При x = -1 и x = 2 подмодульные выражения равны нулю. Практическим путем мы приблизились к правилу построения таких графиков:
Графиком функции вида y = a 1 |x – x 1 | + a 2 |x – x 2 | + … + a n |x – x n | + ax + b является ломаная с бесконечными крайними звеньями. Чтобы построить такую ломаную, достаточно знать все ее вершины (абсциссы вершин есть нули подмодульных выражений) и по одной контрольной точке на левом и правом бесконечных звеньях.
Задача.
Построить график функции y = |x| + |x – 1| + |x + 1| и найти ее наименьшее значение.
Решение:
Нули подмодульных выражений: 0; -1; 1. Вершины ломаной (0; 2); (-1; 3); (1; 3). Контрольная точка справа (2; 6), слева (-2; 6). Строим график (рис. 7). min f(x) = 2.
Остались вопросы? Не знаете, как построить график функции с модулем?
Чтобы получить помощь репетитора – .
blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Знак модуля, пожалуй, одно из самых интересных явлений в математике. В связи с этим у многих школьников возникает вопрос, как строить графики функций, содержащих модуль. Давайте подробно разберем этот вопрос.
1. Построение графиков функций, содержащих модуль
Пример 1.
Построить график функции y = x 2 – 8|x| + 12.
Решение.
Определим четность функции. Значение для y(-x) совпадает со значением для y(x), поэтому данная функция четная. Тогда ее график симметричен относительно оси Oy. Строим график функции y = x 2 – 8x + 12 для x ≥ 0 и симметрично отображаем график относительно Oy для отрицательных x (рис. 1).
Пример 2.
Следующий график вида y = |x 2 – 8x + 12|.
– Какова область значений предложенной функции? (y ≥ 0).
– Как расположен график? (Над осью абсцисс или касаясь ее).
Это значит, что график функции получают следующим образом: строят график функции y = x 2 – 8x + 12, оставляют часть графика, которая лежит над осью Ox, без изменений, а часть графика, которая лежит под осью абсцисс, симметрично отображают относительно оси Ox (рис. 2).
Пример 3.
Для построения графика функции y = |x 2 – 8|x| + 12| проводят комбинацию преобразований:
y = x 2 – 8x + 12 → y = x 2 – 8|x| + 12 → y = |x 2 – 8|x| + 12|.
Ответ: рисунок 3.
Рассмотренные преобразования справедливы для всех видов функций. Составим таблицу:
2. Построение графиков функций, содержащих в формуле «вложенные модули»
Мы уже познакомились с примерами квадратичной функции, содержащей модуль, а так же с общими правилами построения графиков функций вида y = f(|x|), y = |f(x)| и y = |f(|x|)|. Эти преобразования помогут нам при рассмотрении следующего примера.
Пример 4.
Рассмотрим функцию вида y = |2 – |1 – |x|||. Выражение, задающее функцию, содержит «вложенные модули».
Решение.
Воспользуемся методом геометрических преобразований.
Запишем цепочку последовательных преобразований и сделаем соответствующий чертеж (рис. 4):
y = x → y = |x| → y = -|x| → y = -|x| + 1 → y = |-|x| + 1|→ y = -|-|x| + 1|→ y = -|-|x| + 1| + 2 → y = |2 –|1 – |x|||.
Рассмотрим случаи, когда преобразования симметрии и параллельного переноса не являются основным приемом при построении графиков.
Пример 5.
Построить график функции вида y = (x 2 – 4)/√(x + 2) 2 .
Решение.
Прежде чем строить график, преобразуем формулу, которой задана функция, и получим другое аналитическое задание функции (рис. 5).
y = (x 2 – 4)/√(x + 2) 2 = (x– 2)(x + 2)/|x + 2|.
Раскроем в знаменателе модуль:
При x > -2, y = x – 2, а при x
Область определения D(y) = (-∞; -2)ᴗ(-2; +∞).
Область значений E(y) = (-4; +∞).
Точки, в которых график пересекает с оси координат: (0; -2) и (2; 0).
Функция убывает при всех x из интервала (-∞; -2), возрастает при x от -2 до +∞.
Здесь нам пришлось раскрывать знак модуля и строить график функции для каждого случая.
Пример 6.
Рассмотрим функцию y = |x + 1| – |x – 2|.
Решение.
Раскрывая знак модуля, необходимо рассмотреть всевозможную комбинацию знаков подмодульных выражений.
Возможны четыре случая:
{x + 1 – x + 2 = 3, при x ≥ -1 и x ≥ 2;
{-x – 1 + x – 2 = -3, при x
{x + 1 + x – 2 = 2x — 1, при x ≥ -1 и x
{-x – 1 – x + 2 = -2x + 1, при x
Тогда исходная функция будет иметь вид:
{3, при x ≥ 2;
y = {-3, при x
{2x – 1, при -1 ≤ x
Получили кусочно-заданную функцию, график которой изображен на рисунке 6.
3. Алгоритм построения графиков функций вида
y = a 1 |x – x 1 | + a 2 |x – x 2 | + … + a n |x – x n | + ax + b.
В предыдущем примере было достаточно легко раскрыть знаки модуля. Если же сумм модулей больше, то рассмотреть всевозможные комбинации знаков подмодульных выражений проблематично. Как же в этом случае построить график функции?
Заметим, что графиком является ломаная, с вершинами в точках, имеющих абсциссы -1 и 2. При x = -1 и x = 2 подмодульные выражения равны нулю. Практическим путем мы приблизились к правилу построения таких графиков:
Графиком функции вида y = a 1 |x – x 1 | + a 2 |x – x 2 | + … + a n |x – x n | + ax + b является ломаная с бесконечными крайними звеньями. Чтобы построить такую ломаную, достаточно знать все ее вершины (абсциссы вершин есть нули подмодульных выражений) и по одной контрольной точке на левом и правом бесконечных звеньях.
Задача.
Построить график функции y = |x| + |x – 1| + |x + 1| и найти ее наименьшее значение.
Решение:
Нули подмодульных выражений: 0; -1; 1. Вершины ломаной (0; 2); (-1; 3); (1; 3). Контрольная точка справа (2; 6), слева (-2; 6). Строим график (рис. 7). min f(x) = 2.
Остались вопросы? Не знаете, как построить график функции с модулем?
Чтобы получить помощь репетитора – зарегистрируйтесь .
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Пошаговое построение графиков.
«Навешивание» модулей на прямые, параболы, гиперболы.
Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.
Для понимания друг друга введу немного «обзываний» системы координат:
Для начала построим график прямой y = 2x − 1.
Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую. Поэтому берем любые две точки А = (0; −1) и B = (1; 1) и проводим единственную прямую.
А если теперь добавить модуль? y = |2x − 1|.
Модуль — это всегда положительное значение
, получается, что «y» должен быть всегда положительным.
Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю
(как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).
Красота! А как же будет выглядеить график, если надеть модуль только на «х»: y = 2|x| − 1?
Одна строчка рассуждений и рисуем:
Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.
Суть построения точно такая же, только здесь отражаем относительно оси «y»
.
Смертельный номер:
y = |2|x| − 1|.
Для начала построим y = |2x − 1|, отразив относительно оси «x». В положительной части
он будет такой же, как y =|2|x| − 1|.
А после этого отражаем относительно оси «y», то, что мы получили справа:
Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках.
Разберем по винтикам параболу y
=
x²
+
x
−
2.
Точки пересечения с осью «x» получим с помощью дискриминанта: x₁
=
1 и
x
₂
=
-2.
Можно найти вершину у параболы и взять пару точек для точного построения.
А как будет выглядеть график: y
=
|x²|
+
x
−
2?
Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.
При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:
Следующий смертельный номер: |y|
=
x²
+
x
−
2, подумай хорошенько, а еще лучше попробуй нарисовать сам.
При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!
Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.
А настоящие профи могут разобраться, почему же данные графики выглядят так:
Легкий и средний уровень позади, и настала пора выжать концетрацию на максимум
, потому что дальше тебя ждут гиперболы, которые частенько встречаются во второй части ЕГЭ и ОГЭ.
y
=
1/x
— простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:
А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:
А что будет, если мы добавим в знаменателе «
−1»?
График сдвинется вправо на единицу.
А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!

а если добавить отдельно «−1» y = (1/x) − 1? Вниз на единицу!
Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.
Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.
Можно придумывать массу вариантов, но общий принцип остается для любого графика.
Принципы повторим в выводах в конце статьи.
Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определнию:
И построить график, разбив его на кусочно-заданные функции.
Например для прямой:
Для параболы с одним модулем будет два кусочно заданных графика:
C двумя модулями кусочно заданных графиков будет четыре:

Выводы:
- Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
- Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
- Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль
. - Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:
- Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
- Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
- Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.
- Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.
В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №10 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.
Как формулируется задание 10 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.
Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.
Вот необходимая теория для решения задания №10 ЕГЭ.
Что такое функция
Чтение графика функции
Четные и нечетные функции
Периодическая функция
Обратная функция
5 типов элементарных функций и их графики
Преобразование графиков функций
Построение графиков функций
Да, теоретического материала здесь много. Но он необходим — и для решения задания 10 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.
Рекомендации:
Запоминай, как выглядят графики основных элементарных функций. Замечай особенности графиков, чтобы не перепутать параболу с синусоидой : -)
Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?
Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.
Задание 10 в формате ЕГЭ-2021
Линейная функция
Необходимая теория
1. На рисунке изображён график функции . Найдите значение
, при котором
Решение:
Найдем, чему равны k и b. График функции проходит через точки (3; 4) и (-1; -3). Подставив по очереди координаты этих точек в уравнение прямой y = kx + b, получим систему:
Вычтем из первого уравнения второе:
Уравнение прямой имеет вид:
Найдем, при каком значение функции равно -13,5.
Ответ: -7.
2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Решение:
Запишем формулы функций.
Одна из них проходит через точку (0; 1) и ее угловой коэффициент равен -1. Это линейная функция
Другая проходит через точки (-1; -1) и (-2; 4). Подставим по очереди координаты этих точек в формулу линейной функции
Вычтем из первого уравнения второе.
тогда
Прямая задается формулой:
Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:
Ответ: -1,75.
3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Решение:
Прямая, расположенная на рисунке ниже, задается формулой так как ее угловой коэффициент равен 1 и она проходит через точку (-3; -2).
Для прямой, расположенной выше, угловой коэффициент равен
Эта прямая проходит через точку (-2; 4), поэтому:
эта прямая задается формулой
Для точки пересечения прямых:
Ответ: -12.
Квадратичная функция. Необходимая теория
4. На рисунке изображен график функции Найдите b.
Решение:
На рисунке — квадратичная парабола полученная из графика функции
сдвигом на 1 вправо, то есть
Получим:
Ответ: -2.
5. На рисунке изображен график функции . Найдите с.
Решение:
На рисунке изображена парабола, ветви которой направлены вверх, значит, коэффициент при положительный. График сдвинут относительно графика функции
на 1 единицу вправо вдоль оси Ох. Формула функции имеет вид
.
Значит, с = 1.
Ответ: 1
6. На рисунке изображён график функции Найдите
Решение:
График функции проходит через точки с координатами (1; 1) и (-2; -2). Подставляя координаты этих точек в формулу функции, получим:
отсюда
Формула функции имеет вид:
Ответ: 31.
7. На рисунке изображены графики функций и
которые пересекаются в точках А и В. Найдите абсциссу точки В.
Решение:
Найдем a, b и c в формуле функции . График этой функции пересекает ось ординат в точке (0; -3), поэтому
График функции проходит через точки (-1; -3) и (2; 3). Подставим по очереди координаты этих точек в формулу функции:
отсюда
Найдем абсциссу точки B. Для точек A и B:
(это абсцисса точки A) или
(это абсцисса точки B).
Ответ: 6.
Степенные функции. Необходимая теория
8. На рисунке изображены графики функций и
, которые пересекаются в точках А и В. Найдите абсциссу точки В.
Решение:
График функции проходит через точку (2; 1); значит,
График функции проходит через точки (2; 1) и (1; -4),
— угловой коэффициент прямой; (находим как тангенс угла наклона прямой и положительному направлению оси X); тогда
Для точек A и B имеем:
Отсюда (абсцисса точки A) или
(абсцисса точки B).
Ответ: -0,2.
9. На рисунке изображён график функции . Найдите f (6,76).
Решение:
Функция задана формулой:
Ее график проходит через точку (4; 5); значит,
Тогда
Ответ: 6,5.
10. На рисунке изображен график функции . Найдите
.
Решение:
График функции на рисунке симметричен графику функции относительно оси Y. Он проходит через точку (-1; 1). Значит, формула изображенной на рисунке функции:
, а = — 1. Тогда
= 5.
Ответ: 5.
Показательная функция. Необходимая теория
11. На рисунке изображён график функции Найдите
Решение:
График функции проходит через точки (-3; 1) и (1; 4). Подставив по очереди координаты этих точек в формулу функции получим:
Поделим второе уравнение на первое:
Подставим во второе уравнение:
Ответ: 0,25.
12. На рисунке изображен график функции . Найдите
Решение:
График функции проходит через точку
Это значит, что
формула функции имеет вид:
.
Ответ: 2.
Логарифмическая функция. Необходимая теория
13. На рисунке изображён график функции Найдите
Решение:
График функции проходит через точки (-3; 1) и (-1; 2). Подставим по очереди эти точки в формулу функции.
Отсюда:
Вычтем из второго уравнения первое:
или
— не подходит, так как
(как основание логарифма).
Тогда
Ответ: 4.
14. На рисунке изображен график функции .
Найдите f(0,2).
Решение:
График логарифмической функции на рисунке проходит через точки и
. Подставив по очереди координаты этих точек в формулу функции, получим систему уравнений:
Формула функции:
Найдем :
Ответ: -7.
Тригонометрические функции. Необходимая теория
15. На рисунке изображён график функции Найдите
Решение:
График функции сдвинут на 1,5 вверх;
Значит,
Амплитуда
(наибольшее отклонение от среднего значения).
Это график функции Он получен из графика функции
растяжением в 2 раза по вертикали и сдвигом вверх на
.
Ответ:
16. На рисунке изображён график функции
Найдите .
Решение:
На рисунке — график функции Так как
График функции проходит через точку A Подставим
и координаты точки А в формулу функции.
Так как получим:
Ответ: 2.
17. На рисунке изображен график периодической функции у = f(x). Найдите значение выражения
Решение:
Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если то
Пользуясь периодичностью функции , период которой T = 4, получим:
Ответ: 5.
Друзья, мы надеемся, что на уроках математики в школе вы решаете такие задачи. Для углубленного изучения темы «Функции и графики» (задание 10 ЕГЭ по математике), а также задач с параметрами и других тем ЕГЭ — рекомендуем Онлайн-курс для подготовки к ЕГЭ на 100 баллов.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 10 ЕГЭ по математике. Графики функций» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Определение модуля
Алгебрагическое определение: | x |
=
Геометрическое определение: модулем
числа называется расстояние от точки,
изображающей это число, до начала отсчета.
Понятие модуля впервые вводится в 6 классе, в 7
классе рассматривается линейная функция и ее
график и уже можно показывать построение
несложных графиков функций, содержащих модуль.
Далее, по мере изучения различных функций, их
свойств, каждую такую тему можно заканчивать
рассмотрением более сложных графиков, в том
числе с модулем. В этой статье рассматриваются
основные приемы построения графиков таких
функций.
I. На алгебрагическом определении основан метод
«раскрытия модуля на промежутках».
Например: | x + 2 | = | x + 2 | =
метод можно применять при построении графиков
функций, содержащих один или более модулей.
Например, построим график функции у = | x + 2 | –
2x + 1 , предварительно упростив ее.
у = у
=
Если модулей несколько, то каждый из них
раскрываем на промежутках относительно точек,
обращающих каждый из них в нуль. Например,
построим график функции у = | 3 – x | – x
+ | x + 2 | + 1.
1. Если х < – 2, то у = 3 – х – х
– (х + 2) + 1, у = – 3х + 2.
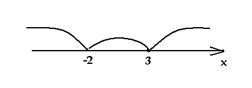
< х < 3, то у = 3 – х – х + х
+ 2 + 1, у = – х + 6.
3. Если х > 3, то у = – (3 – х) – х
+ х + 2 + 1, у = х.
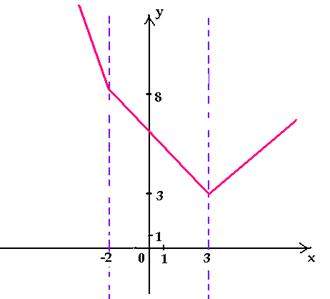
записываем как кусочно-заданную:
у =
Подобно тому, как числовая прямая точками – 2 и 3
разбивается на промежутки, координатная
плоскость прямыми х = – 2 и х = 3
разбивается на части («полосы»), в каждой из
которых строим свой график. Заметим, что данная
функция непрерывна, поэтому на «границах» части
графика должны соединяться.
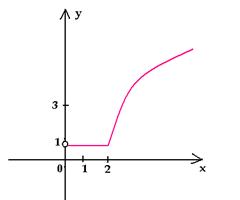
метод можно применять к функциям разных видов.
Например, построим график функции у = | log2
x – 1 | – log0,5 x.
Заметим, что х > 0.
1. Пусть log2x – 1 > 0, log2x >
1, x > 2, тогда у = log2 x – 1 +
log2 x; y = 2 log2 x – 1.
2. Пусть log2 x – 1 < 0, 0 < x < 2,
тогда у = – log2 x + 1 + log2 x; y
= 1.
Запишем функцию как кусочно-заданную:
у =
III. Рассмотрим некоторые частные случаи
функций, содержащих модуль.
1) у = | f(x) |.
По определению модуля имеем: | f(x) | =
Таким образом , для того, чтобы построить график
такой функции, необходимо взять часть графика,
лежащую не ниже оси абсцисс, а часть графика,
лежащую ниже этой оси отобразить относительно
нее в верхнюю полуплоскость. (Заметим, что «–»,
стоящий перед функцией означает симметричное
отображение графика относительно оси абсцисс).
Например, построим график функции у = | x2
– 2х – 3 |.
Построим сначала график функции у = х2
– 2х – 3. Графиком этой функции является
парабола, ветви которой направлены вверх.
Координаты ее вершины: х = 1, у = – 4. Точки
пересечения параболы с осями координат: (0; – 3); (–
1; 0); (3; 0). Далее выполняем отображение части
графика, лежащей в нижней полуплоскости,
относительно оси абсцисс.
2) у = f(| x |). Используем определение модуля: f(|
x |) =
Чтобы построить график такой функции строим
график функции у = f(x) и берем ту его
часть, где х > 0 (в правой полуплоскости).
Затем эту часть симметрично отображаем в левую
полуплоскость, где х < 0. (Заметим, что
построение графика функции f(– x) и
состоит в отображении части графика, лежащей в
правой полуплоскости в левую относительно оси
ординат).
Например, построим график функции у = х2
– 2| х | – 3. Сначала строим график функции у
= х2 – 2х – 3, далее выполняем
указанные преобразования.
3) Построим график функции y = | f(| x
|)|, например, y = | x2 – 2| х | – 3 |,
выполним последовательно преобразования,
рассмотренные в пунктах 2 и 1.
4. Рассмотрим зависимость | y | = f(x).
Ее нельзя назвать функцией, так как не
выполняется условие: каждому значению х должно
соответствовать единственное значение у.
Рассмотрим построение графика такой
зависимости (можно говорить «графика
уравнения»). Используем определение модуля: у
= f(x), если у > 0, – у = f(x),
y = – f(x), если у < 0
Получаем, чтобы построить такой график, сначала
строим график функции у = f(x) и
берем ту его часть, которая лежит в верхней
полуплоскости, где у > 0; чтобы
построить график в нижней полуплоскости (где у
< 0), нужно построенную часть отобразить
симметрично относительно оси абсцисс (знак «–»
перед функцией и означает такое отображение)
Например, построим график уравнения | y | = x2
– 2х – 3
Заметим, что графики, не относящиеся к
рассмотренным частным случаям, следует строить «
раскрывая модули на промежутках».
| x |
1 |
0 |
– 1 |
|
y |
0 |
|
|
IV. Приведем некоторые примеры
1. Построим график уравнения | y | = arccos| x
|.
2. Графическим способом можно решать и
неравенства с двумя переменными. Например,
решением неравенства | y | < arccos| x |
являются координаты точек закрашенной части
плоскости, включая границы.
Решим еще одно задание, предлагавшееся на ЕГЭ:
найти все целочисленные решения неравенства | y
| < | | x – 2 | – 3 | (х0; у0),
для которых х0 = у0. Построим
сначала график уравнения | y | = | | x – 2 | –
3 |. Решением данного неравенства будут являться
координаты точек закрашенной части плоскости,
включая границы.
Пары чисел (х0; у0),
являющиеся решениями неравенства, для которых y0
= x0, являются координатами точек,
лежащих на прямой у = х. Выберем точки с
целыми координатами: (0; – 1); (1; 0); (2; 1); (3; 2), они и
будут являться решениями данной задачи.
3. Определить, сколько корней имеет уравнение | 3
– x | + log3| x | = 2 – x.
Запишем уравнение в виде | 3 – x | + x = log3|
x | + 2. В одной системе координат построим
графики функций y = | 3 – x | = x (1) и y
= log3| x | = 2 (2). Функцию (1) запишем как
кусочно-заданную, раскрывая модуль на
промежутках:
y =
График функции (2) построим, выполняя
отображение графика y = log3x + 2
относительно оси ординат ( один из рассмотренных
частных случаев ).
Графики имеют две общие точки, следовательно,
данное уравнение имеет два корня.
V. Для повторения материала, его закрепления
предлагаем выполнить следующие задания.
1. Постройте графики функций и уравнений: y =
| y | =
; y = | | 2 – x
| – 4 |; y = | x2 – 4 | x | + 3 |; y = + 1.
2. Решите графически уравнения c одной и двумя
переменными: | 3 – x | – 3 = 2| x | – x2;
| y | = 2| x | – x2; = | x – 2,5 | –1,5.
3. Решите графически неравенства с двумя
переменными: | y | > x24x + 3;
| x | + | y | < 3.
4. Решите графически систему уравнений:
5. Найдите все значения а, при каждом из которых
уравнение | x + a | + | | x – 3 | – 4 | = 1
имеет ровно два корня.