Как решать графики функций егэ профиль парабола - Помощь в подготовке к экзаменам и поступлению

Каталог заданий.
Параболы

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 10 № 509253

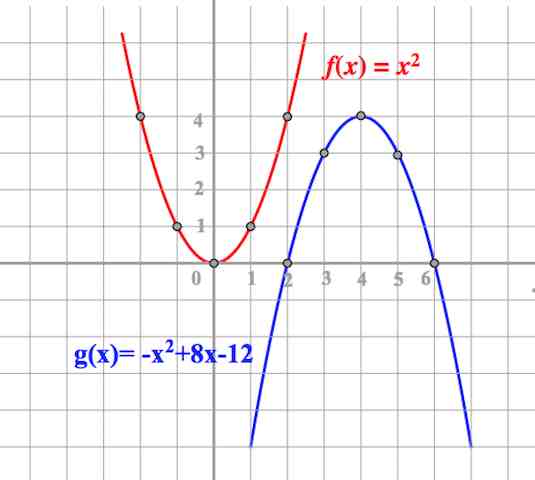
На рисунке изображены графики функций и которые пересекаются в точках A и B. Найдите абсциссу точки B.

Аналоги к заданию № 509253: 509254 509255 509259 509262 509263 509264 509268 509256 509257 509258 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

Сообщить об ошибке · Помощь

Тип 10 № 562060

На рисунке изображён график функции вида где числа a, b и c  — целые. Найдите значение

Аналоги к заданию № 562153: 562060 562154 562155 562156 562157 562158 562159 562160 562161 562162 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

Сообщить об ошибке · Помощь

Тип 10 № 562061

На рисунке изображён график функции вида где числа a, b и c  — целые. Найдите значение дискриминанта уравнения

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

1 комментарий · Сообщить об ошибке · Помощь

Тип 10 № 562153

На рисунке изображён график функции вида где числа a, b и c  — целые. Найдите значение

Аналоги к заданию № 562153: 562060 562154 562155 562156 562157 562158 562159 562160 562161 562162 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

Сообщить об ошибке · Помощь

Тип 10 № 562154

На рисунке изображён график функции вида где числа a, b и c  — целые. Найдите значение

Аналоги к заданию № 562153: 562060 562154 562155 562156 562157 562158 562159 562160 562161 562162 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

В ЕГЭ 2022 года добавили новую задачу на графики функций. Для решения этой задачи нужно сначала определить формулу функции, а затем вычислить ответ на вопрос задачи. И если вычисление ответа по известной формуле обычно не составляет труда, то вот определение самой формулы часто ставит школьников в тупик. Поэтому мы разберем три разных подхода к этому вопросу.

Замечание. Про то как определяется формула у прямой и параболы я написала в этой и этой статьях. Поэтому здесь в примерах я буду использовать другие функции – дробные, иррациональные, показательные и логарифмические, но все три описанных здесь способа работают и для линейных, и для квадратичных функций в том числе.

1 способ – находим формулу по точкам

Этот способ подходит вообще для любой девятой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений.

Давайте разберем алгоритм на примере конкретной 9-ой задачи ЕГЭ:

Алгоритм:

1. Находим 2 точки с целыми координатами. Обычно они выделены жирно, но если это не так, то не проблема найти их самому.
Пример:

2. Подставляем эти координаты в «полуфабрикат» функции. Вместо (f(x))– координату игрек, вместо (x) – икс. Получается система.

3. Решаем эту систему и получаем готовую формулу.

4. Готово, функция найдена, можно переходить ко второму этапу – вычислению (f(-8)). Если вы вдруг не знаете, что это значит – в конце статьи я рассматриваю этот момент более подробно.

Давайте посмотрим метод еще раз на примере с логарифмической функцией.
Пример:

2 способ – преобразование графиков функций

Этот способ сильно быстрее первого, но требует больше знаний. Для использования преобразований функций нужно знать, как выглядят функции без изменения и как преобразования их меняют. Наиболее удобно использовать этот способ для иррациональной функции ((y=sqrt{x}) ) и функции обратной пропорциональности ((y=frac{1}{x})).

Вот как выглядит применение этого способа:

Для использования этого способа надо знать, как выглядят изначальные функции:

И понимать, как меняются функции от преобразований:

Часто даже по «полуфабрикату» функции понятно, какие преобразования сделали с функцией:

Пример:

3 способ – гибридный

Идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти. С другой стороны, независимо от оснований любая показательная функция должна проходить через точку ((0;1)), а любая логарифмическая — через точку ((1;0)).

По смещению этих точек легко понять, как именно двигали функцию, но только если ее не растягивали, а лишь перемещали вверх-вниз, влево-вправо (как обычно и бывает в задачах на ЕГЭ).

Основание же лучше находить уже следующим действием, используя подстановку координат точки в «полуфабрикат» функции.

Как отвечать на вопросы в задаче, когда уже определили функцию

— Если просят найти (f)(любое число), то нужно это число подставить в готовую функцию вместо икса.
Пример:

— Если просят найти «при каком значении x значение функции равно *любому числу*», то надо решить уравнение, в одной части которого будет функция, а в другой — то самое число. Аналогично надо поступить, если просят «найти корень уравнения (f(x)=) *любое число*».
Пример:

— Если просят найти абсциссу точки пересечения – надо приравнять 2 функции и решить получившееся уравнение. Корень уравнения и будет искомой абсциссой. Аналогично надо делать в задачах, где даны две точки пересечения (A)(*любое число*;*другое число*) и (B(x_0;y_0)) и просят найти (x_0).
Пример:

— Если просят найти ординату точки пересечения – надо приравнять 2 функции, найти иксы и подставить подходящий икс в любую функцию. Точно также решаем если просят найти (y_0) точки пересечения двух функций.
Пример:

— Иногда просят найти просто какой-либо из коэффициентов функции. Тогда надо просто восстановить функцию и записать в ответ то, о чем спросили:
Пример:

Источник

Функция вида , где называется квадратичной функцией.

График квадратичной функции – парабола.

Рассмотрим случаи:

I СЛУЧАЙ, КЛАССИЧЕСКАЯ ПАРАБОЛА

, то есть , ,

Для построения заполняем таблицу, подставляя значения x в формулу:

Отмечаем точки (0;0); (1;1); (-1;1) и т.д. на координатной плоскости (чем с меньшим шагом мы берем значения х ( в данном случае шаг 1 ), и чем больше берем значений х, тем плавнее будет кривая), получаем параболу:

Нетрудно заметить, что если мы возьмем случай , , , то есть , то мы получим параболу, симметричную относительно оси (ох). Убедиться в этом несложно, заполнив аналогичную таблицу:

II СЛУЧАЙ, «a» ОТЛИЧНО ОТ ЕДИНИЦЫ

Что же будет, если мы будем брать , , ? Как изменится поведение параболы? При парабола изменит форму, она “похудеет” по сравнению с параболой (не верите – заполните соответствующую таблицу – и убедитесь сами):

На первой картинке (см. выше) хорошо видно, что точки из таблицы для параболы (1;1), (-1;1) трансформировались в точки (1;4), (1;-4), то есть при тех же значениях ордината каждой точки умножилась на 4. Это произойдет со всеми ключевыми точками исходной таблицы. Аналогично рассуждаем в случаях картинок 2 и 3.

А при парабола «станет шире» параболы :

Давайте подитожим:

III СЛУЧАЙ, ПОЯВЛЯЕТСЯ «С»

Теперь давайте введем в игру (то есть рассматриваем случай, когда ), будем рассматривать параболы вида . Нетрудно догадаться (вы всегда можете обратиться к таблице), что будет происходить смещение параболы вдоль оси вверх или вниз в зависимости от знака :

IV СЛУЧАЙ, ПОЯВЛЯЕТСЯ «b»

Когда же парабола “оторвется” от оси и будет, наконец, “гулять” по всей координатной плоскости? Когда перестанет быть равным .

Здесь для построения параболы нам понадобится формула для вычисления вершины: $x_o=frac{-b}{2a}$ , .

Так вот в этой точке (как в точке (0;0) новой системы координат) мы будем строить параболу , что уже нам по силам. Если имеем дело со случаем , то от вершины откладываем один единичный отрезок вправо, один вверх, – полученная точка – наша (аналогично шаг влево, шаг вверх – наша точка); если имеем дело с , например, то от вершины откладываем один единичный отрезок вправо, два – вверх и т.д.

Например, вершина параболы :

$x_o=frac{4}{2}=2$ , . Теперь главное уяснить, что в этой вершине мы будем строить параболу по шаблону параболы , ведь в нашем случае.

При построении параболы после нахождения координат вершины очень удобно учитывать следующие моменты:

1) парабола обязательно пройдет через точку . Действительно, подставив в формулу x=0, получим, что . То есть ордината точки пересечения параболы с осью (оу), это . В нашем примере (выше), парабола пересекает ось ординат в точке , так как .

2) осью симметрии параболы является прямая $x=frac{-b}{2a}$ , поэтому все точки параболы будут симметричны относительно нее. В нашем примере, мы сразу берем точку (0; -2) и строим ей симметричную относительно оси симметрии параболы, получим точку (4; -2), через которую будет проходить парабола.

3) Приравнивая к , мы узнаем точки пересечения параболы с осью (ох). Для этого решаем уравнение . В зависимости от дискриминанта, будем получать одну (, $x=-frac{b}{2a}$ ), две (, $x_{1,2}=frac{-bpmsqrt{b^2-4ac}}{2a}$ ) или нИсколько () точек пересечения с осью (ох). В предыдущем примере у нас корень из дискриминанта – не целое число, при построении нам особо нет смысла находить корни, но мы видим четко, что две точки пересечения с осью (ох) у нас будут (так как ), хотя, в общем, это видно и без дискриминанта.

Итак, давайте выработаем

Алгоритм для построения параболы, если она задана в виде

1) определяем направление ветвей ( а>0 – вверх, a<0 – вниз)

2) находим координаты вершины параболы по формуле $x_o=frac{-b}{2a}$ , .

3) находим точку пересечения параболы с осью (оу) по свободному члену , строим точку, симметричную данной относительно оси симметрии параболы (надо заметить, бывает, что эту точку невыгодно отмечать, например, потому, что значение велико… пропускаем этот пункт…)

4) В найденной точке – вершине параболы (как в точке (0;0) новой системы координат) строим параболу . Если , то парабола становится у’же по сравнению с , если , то парабола расширяется по сравнению с

5) Находим точки пересечения параболы с осью (оу) (если они еще сами “не всплыли”), решая уравнение

Пример 1

Пример 2

Замечание 1. Если же парабола изначально нам задана в виде , где – некоторые числа (например, ), то построить ее будет еще легче, потому что нам уже заданы координаты вершины . Почему?

Возьмем квадратный трехчлен и выделим в нем полный квадрат: $ax^2+bx+c=a(x^2+frac{b}{a}x+frac{c}{a})=a((x^2+2frac{b}{2a}x+frac{b^2}{4a^2})-frac{b^2}{4a^2}+frac{c}{a})=a(x+frac{b}{2a})^2-frac{b^2}{4a}+c.$ Посмотрите, вот мы и получили, что $m=frac{-b}{2a}$ , $n=-frac{b^2}{4a}+c=y(frac{-b}{2a})$ . Мы с вами ранее называли вершину параболы , то есть теперь , .

Например, $y=-frac{1}{3}{(x+2)}^2+6$ . Отмечаем на плоскости вершину параболы , понимаем, что ветви направлены вниз, парабола расширена (относительно ). То есть выполняем пункты 1; 3; 4; 5 из алгоритма построения параболы (см. выше).

Замечание 2. Если парабола задана в виде, подобном этому (то есть представлен в виде произведения двух линейных множителей), то нам сразу видны точки пересечения параболы с осью (ох). В данном случае – (0;0) и (4;0). В остальном же действуем согласно алгоритму, раскрыв скобки.

Источник

В 2022 задание 9 по математике профильного уровня изменилось — появился новый формат, проверяющий знание свойств параболы. Номер вызывает вопросы у учеников, но на деле решается просто. В статье разберем правила выполнения задания 9 ЕГЭ по математике.

Способы решения номера

9 задание по математике профильного уровня 2022 получится решить четырьмя методами.

Первый вариант

Начнем с простого способа, не требующего глубокого понимания темы. Условие выглядит следующим образом:

Присмотревшись к картинке задания 9 по профильной математике, видим: график содержит целочисленные точки. Отметим их на изображении (экзамен разрешает использовать текст КИМа). Решение требует минимум три точки:

Видим: в точке «-4» ордината равна «-3». Запишем уравнение, подставив значения значения абсциссы и ординаты:

16a — 4b + c = -3

Аналогичным образом записываем выражение, используя две остальные точки:

9a — 3b + c = -2

4a — 2b + c = 1

Получаем систему трех уравнений с тремя неизвестными. Решить достаточно легко. Простейший вариант: вычесть последнюю строчку из первых двух, избавившись от коэффициента “c”. После первое уравнение сокращаем на «2», вычитаем из него второе. Находим: a = 1. Подставляем далее, получаем:

b = 8;

c = 13.

Имея коэффициенты, переписываем уравнение, подставляем значение абсциссы:

f(x) = x² + 8x + 13

f(-12) = 144 — 96 + 13 = 61

Второй вариант

Мы решили 9 задание по математике профилю наиболее простым способом. Однако вычисления получится сократить. Построим локальную систему координат около вершины параболы:

Видим особенность параболы: в точке «1» ордината равна 1, в точке «2» — 4. Представленный график отражает классическое выражение: y = x², сдвинутое в системе координат. Известно: преобразования не меняют старший коэффициент. Делаем вывод, “a” равно “1”. Теперь найдем “b”. Используем выражение вершины параболы: x₀ = -b / 2a. По рисунку видно: x₀ = -4. Поставляя это число, найденное значение “a”, находим: b = 8. Дальнейшее решение требует одного уравнения из первого способа. Теперь выполнить номер проще.

Третий вариант

9 задание по математике профильного уровня реально упростить еще сильнее. Изучим способ образования данной параболы. Она получилась путем смещения исходной на “4” налево и на “3” вниз. Запишем уравнения. Изначальный пример:

y = x²

Сдвиг влево записывается:

y = (x + 4)²

Сдвиг вниз:

y = (x + 4)² — 3

Получаем готовое уравнение, достаточно подставить “-12”. Ответ аналогичный: 61.

Четвертый вариант

Рассмотрим последний способ выполнения задания 9 по профильной математике 2022, требующий логического мышления. Снова изучим локальную систему координат:

Сравнивая с изначальной, получим: абсцисса «-12» из условия представляет собой значение «-8» локальной системы. Это связано со сдвигом. Ордината соответственно равна “64”. Не забываем: парабола сдвинута также на три пункта вниз. Получается, итоговое значение будет на 3 меньше найденного. Ответ снова 61!

В статье мы разобрали способы решения нового 9 задания из ЕГЭ по математике. Хотите изучить принципы выполнения остальных номеров? Записывайтесь на курсы «Уникум» Российского университета дружбы народов. Обучение проходит под руководством опытных преподавателей, форматы — очный, дистанционный. Для закрепления материала существует учебный портал Unikum.

Содержание данной статьи носит ознакомительный характер. При подготовке к сдаче ЕГЭ пользуйтесь дополнительными источниками информации!

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ Профиль №10. Парабола

ЕГЭ Профиль №10. Параболаadmin2023-01-10T14:17:50+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №10. Парабола

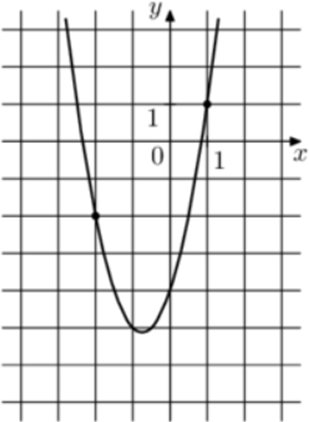
Задача 1. На рисунке изображён график функции (fleft( x right) = 2{x^2} + b,x + c.) Найдите (fleft( { — 5} right).) Ответ ОТВЕТ: 31.
Решение Парабола проходит через точки (left( {1;1} right)) и (left( { — 2; — 2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = 2 + b + c,,,,}\{ — 2 = 8 — 2b + c}end{array}} right.) Вычтем из первого уравнения второе: (3 = — 6 + 3b,,,,,,, Leftrightarrow ,,,,,,,b = 3.) Тогда: (1 = 2 + 3 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 4.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 3x — 4) и (fleft( { — 5} right) = 2 cdot {left( { — 5} right)^2} + 3 cdot left( { — 5} right) — 4 = 31.) Ответ: 31.
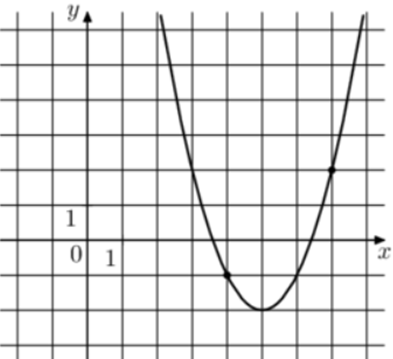
Задача 2. На рисунке изображён график функции (fleft( x right) = {x^2} + b,x + c.) Найдите (fleft( { — 1} right).) Ответ ОТВЕТ: 34.
Решение 1 Способ Парабола проходит через точки (left( {4; — 1} right)) и (left( {6; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 16 + 4b + c,,,,}\{ — 1 = 36 + 6b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: (0 = — 20 — 2b,,,,,,, Leftrightarrow ,,,,,,,b = — 10.) Тогда: ( — 1 = 16 — 40 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = 23.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = {x^2} — 10x + 23) и (fleft( { — 1} right) = {left( { — 1} right)^2} — 10 cdot left( { — 1} right) + 23 = 34.) Ответ: 34. 2 Способ Заметим, что графиком является парабола (fleft( x right) = {x^2}), вершина которой находится в точке (left( {5; — 2} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = {left( {x — 5} right)^2} — 2) и (fleft( { — 1} right) = {left( { — 1 — 5} right)^2} — 2 = 34.) Ответ: 34.
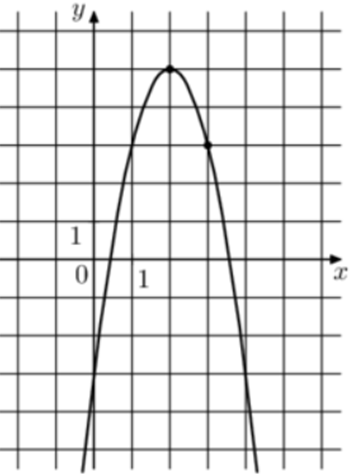
Задача 3. На рисунке изображён график функции (fleft( x right) = — 2{x^2} + b,x + c.) Найдите (fleft( 6 right).) Ответ ОТВЕТ: — 27.
Решение 1 Способ Парабола проходит через точки (left( {1;3} right)) и (left( {3;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{3 = — 2 + b + c,,,,,,,,}\{3 = — 18 + 3b + c,,,}end{array}} right.)Вычтем из первого уравнения второе: (0 = 16 — 2b,,,,,,, Leftrightarrow ,,,,,,,b = 8.)Тогда: (3 = — 2 + 8 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 3.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} + 8x — 3) и (fleft( 6 right) = — 2 cdot {6^2} + 8 cdot 6 — 3 = — 27.) Ответ: – 27. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — 2{x^2}), вершина которой находится в точке (left( {2;5} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — 2{left( {x — 2} right)^2} + 5) и (fleft( 6 right) = — 2 cdot {left( {6 — 2} right)^2} + 5 = — 27.) Ответ: – 27.
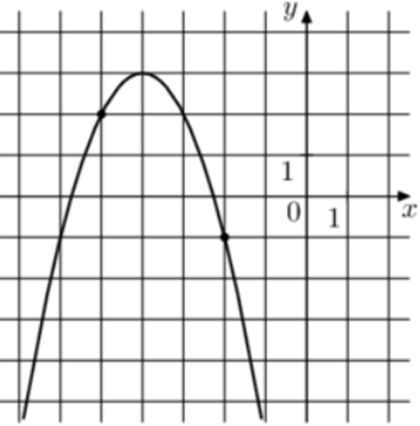
Задача 4. На рисунке изображён график функции (fleft( x right) = — {x^2} + b,x + c.) Найдите (fleft( { — 8} right).) Ответ ОТВЕТ: — 13.
Решение 1 Способ Парабола проходит через точки (left( { — 3;2} right)) и (left( { — 5;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{2 = — 9 — 3b + c,,,,,,,,}\{2 = — 25 — 5b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: (0 = 16 + 2b,,,,,,, Leftrightarrow ,,,,,,,b = — 8.) Тогда: (2 = — 9 + 24 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 13.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — {x^2} — 8x — 13) и (fleft( { — 8} right) = — {left( { — 8} right)^2} + 8 cdot left( { — 8} right) — 13 = — 13.) Ответ: – 13. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — {x^2}), вершина которой находится в точке (left( { — 4;3} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — {left( {x + 4} right)^2} + 3) и (fleft( { — 8} right) = — {left( { — 8 + 4} right)^2} + 3 = — 13.) Ответ: – 13.
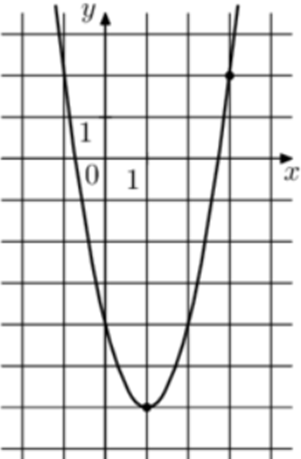
Задача 5. На рисунке изображён график функции (fleft( x right) = a,{x^2} — 4,x + c.) Найдите (fleft( { — 3} right).) Ответ ОТВЕТ: 26.
Решение 1 Способ Парабола проходит через точки (left( {1; — 6} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 6 = a — 4 + c,,,,,,,,}\{2 = 9a — 12 + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 8 = — 8a + 8,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: ( — 6 = 2 — 4 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 4.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} — 4x — 4) и (fleft( { — 3} right) = 2 cdot {left( { — 3} right)^2} — 4 cdot left( { — 3} right) — 4 = 26.) Ответ: 26. 2 Способ Заметим, что графиком является парабола (fleft( x right) = 2{x^2}), вершина которой находится в точке (left( {1; — 6} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = 2{left( {x — 1} right)^2} — 6) и (fleft( { — 3} right) = 2 cdot {left( { — 3 — 1} right)^2} — 6 = 26.) Ответ: 26.
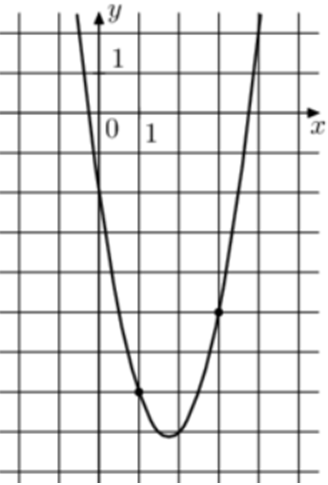
Задача 6. На рисунке изображён график функции (fleft( x right) = a,{x^2} — 7,x + c.) Найдите (fleft( 7 right).) Ответ ОТВЕТ: 47.
Решение Парабола проходит через точки (left( {1; — 7} right)) и (left( {3; — 5} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 7 = a — 7 + c,,,,,,,,}\{ — 5 = 9a — 21 + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = — 8a + 14,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: ( — 7 = 2 — 7 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 2.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} — 7x — 2) и (fleft( 7 right) = 2 cdot {7^2} — 7 cdot 7 — 2 = 47.) Ответ: 47.
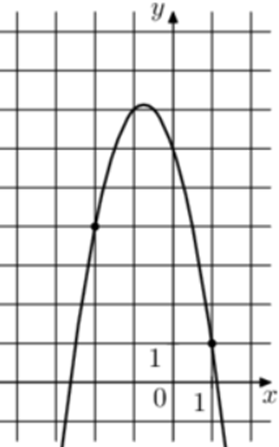
Задача 7. На рисунке изображён график функции (fleft( x right) = a,{x^2} — 3,x + c.) Найдите (fleft( { — 4} right).) Ответ ОТВЕТ: — 14.
Решение Парабола проходит через точки (left( {1;1} right)) и (left( { — 2;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = a — 3 + c,,,,,,,,}\{4 = 4a + 6 + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 3a — 9,,,,,,, Leftrightarrow ,,,,,,,a = — 2.) Тогда: (1 = — 2 — 3 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = 6.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} — 3x + 6) и (fleft( { — 4} right) = — 2 cdot {left( { — 4} right)^2} — 3 cdot left( { — 4} right) + 6 = — 14.) Ответ: – 14.
Задача 8. На рисунке изображён график функции (fleft( x right) = a,{x^2} + 10,x + c.) Найдите (fleft( { — 1} right).) Ответ ОТВЕТ: — 33.
Решение 1 Способ Парабола проходит через точки (left( {3; — 1} right)) и (left( {4;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = 9a + 30 + c}\{2 = 16a + 40 + c}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 7a — 10,,,,,,, Leftrightarrow ,,,,,,,a = — 1.) Тогда: ( — 1 = — 9 + 30 + c,,,,,,,, Leftrightarrow ,,,,,,,,c = — 22.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — {x^2} + 10x — 22) и (fleft( { — 1} right) = — {left( { — 1} right)^2} + 10 cdot left( { — 1} right) — 22 = — 33.) Ответ: – 33. 2 способ Заметим, что графиком является парабола (fleft( x right) = — {x^2}), вершина которой находится в точке (left( {5;3} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — {left( {x — 5} right)^2} + 3) и (fleft( { — 1} right) = — {left( { — 1 — 5} right)^2} + 3 = — 33.) Ответ: – 33.
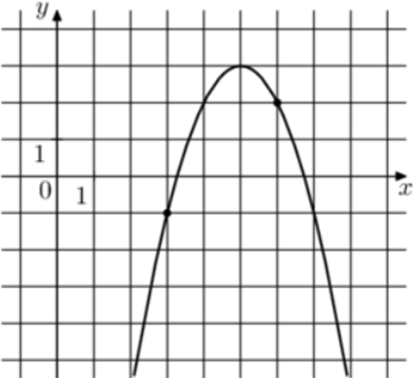
Задача 9. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x — 6.) Найдите (fleft( { — 6} right).) Ответ ОТВЕТ: 48.
Решение Парабола проходит через точки (left( {1; — 1} right)) и (left( { — 2; — 4} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 1 = a + b — 6,,,,,,,,,,,,,,,,,,,,,}\{ — 4 = 4a — 2b — 6left\| {:left( { — 2} right)} right.,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{{20}{c}}{ — 1 = a + b — 6}\{2 = — 2a + b + 3}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = 3a — 9,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: ( — 1 = 2 + b — 6,,,,,,,, Leftrightarrow ,,,,,,,,b = 3.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 3x — 6) и (fleft( { — 6} right) = 2 cdot {left( { — 6} right)^2} + 3 cdot left( { — 6} right) — 6 = 48.) Ответ: 48.
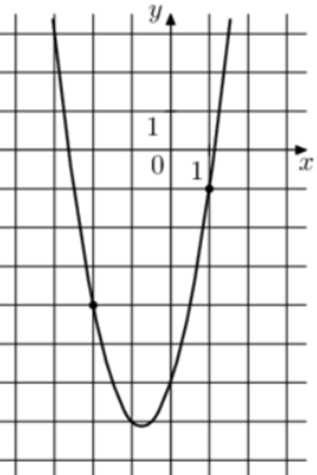
Задача 10. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x — 4.) Найдите (fleft( { — 4} right).) Ответ ОТВЕТ: 16.
Решение Парабола проходит через точки (left( {1;1} right)) и (left( { — 2; — 2} right)). Следовательно: (left{ {begin{array}{{20}{c}}{1 = a + b — 4,,,,,,,,,,,,,,,,,,,,,,,,,}\{-2 = 4a — 2b — 4left\| {:left( { — 2} right)} right.,,,}end{array},,,,, Leftrightarrow ,,,,,,,,,left{ {begin{array}{{20}{c}}{1 = a + b — 4,,,,,,,}\{1 = — 2a + b + 2}end{array}} right.} right.) Вычтем из первого уравнения второе: (0 = 3a — 6,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: (1 = 2 + b — 4,,,,,,,, Leftrightarrow ,,,,,,,,b = 3.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 3x — 4) и (fleft( { — 4} right) = 2 cdot {left( { — 4} right)^2} + 3 cdot left( { — 4} right) — 4 = 16.) Ответ: 16.
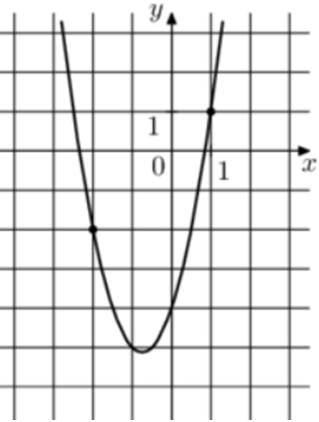
Задача 11. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + 2.) Найдите (fleft( { — 3} right).) Ответ ОТВЕТ: — 37.
Решение Парабола проходит через точки (left( {1;7} right)) и (left( {3;5} right)). Следовательно: (left{ {begin{array}{{20}{c}}{7 = a + b + 2,,,,,,,,}\{5 = 9a + 3b + 2,,,,}end{array},,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{{20}{c}}{5 = a + b,,,,,,,,,,,,}\{3 = 9a + 3bleft\| {:3} right.}end{array}} right.} right.,,,,,,,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{*{20}{c}}{5 = a + b}\{1 = 3a + b}end{array}} right.,,,,,,,,,) Вычтем из первого уравнения второе: (4 = — 2a,,,,,,, Leftrightarrow ,,,,,,,a = — 2.) Тогда: (5 = — 2 + b,,,,,,,, Leftrightarrow ,,,,,,,,b = 7.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} + 7x + 2) и (fleft( { — 3} right) = — 2 cdot {left( { — 3} right)^2} + 7 cdot left( { — 3} right) + 2 = — 37.) Ответ: – 37.
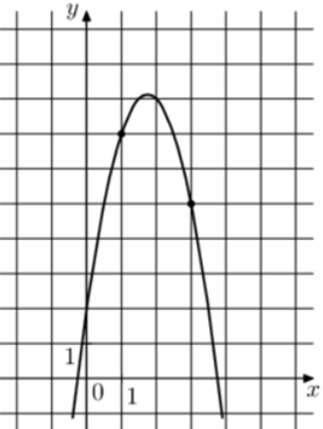
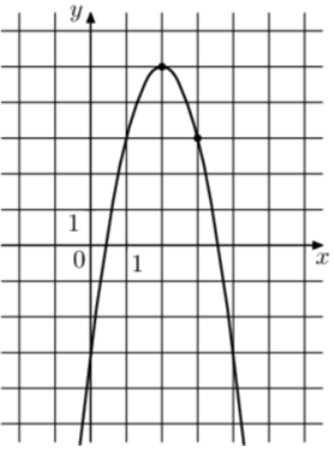
Задача 12. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x — 3.) Найдите (fleft( 8 right).) Ответ ОТВЕТ: — 67.
Решение 1 Способ Парабола проходит через точки (left( {1;3} right)) и (left( {3;3} right)). Следовательно: (left{ {begin{array}{{20}{c}}{3 = a + b — 3,,,,,,,,,,,,,,,,,,}\{3 = 9a + 3b — 3left\| {:3} right.,,,,,}end{array},,,, Leftrightarrow ,,,,,,,,left{ {begin{array}{{20}{c}}{3 = a + b — 3}\{1 = 3a + b — 1}end{array}} right.} right.) Вычтем из первого уравнения второе: (2 = — 2a — 2,,,,,,, Leftrightarrow ,,,,,,,a = — 2.) Тогда: (3 = — 2 + b — 3,,,,,,,, Leftrightarrow ,,,,,,,,b = 8.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} + 8x — 3) и (fleft( 8 right) = — 2 cdot {8^2} + 8 cdot 8 — 3 = — 67.) Ответ: – 67. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — 2{x^2}), вершина которой находится в точке (left( {2;5} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — 2{left( {x — 2} right)^2} + 5) и (fleft( 8 right) = — 2 cdot {left( {8 — 2} right)^2} + 5 = — 67.) Ответ: – 67.
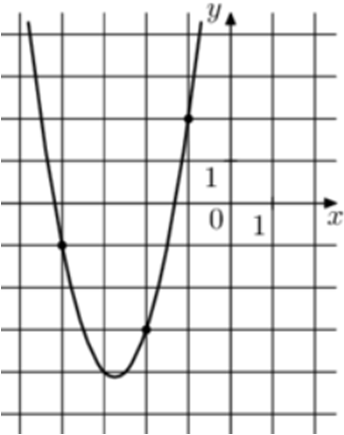
Задача 13. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + c.) Найдите (fleft( { — 7} right).) Ответ ОТВЕТ: 32.
Решение Парабола проходит через точки (left( { — 1;2} right)), (left( { — 2; — 3} right)) и (left( { — 4; — 1} right)). Следовательно: (left{ {begin{array}{{20}{c}}{2 = a — b + c,,,,,,,,,}\{ — 3 = 4a — 2b + c}\{ — 1 = 16a — 4b + c}end{array}} right.) Вычтем из первого уравнения второе: (5 = — 3a + b.) Вычтем из первого уравнения третье: (3 = — 15a + 3bleft\| {:3,,,,,,,,,, Leftrightarrow ,,,,,,,,,,1 = — 5a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{{20}{c}}{5 = — 3a + b}\{1 = — 5a + b}end{array}} right.) Вычтем из первого уравнения второе: (4 = 2a,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Тогда: (5 = — 3 cdot 2 + b,,,,,, Leftrightarrow ,,,,,,b = 11) и (2 = 2 — 11 + c,,,,, Leftrightarrow ,,,,,c = 11.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 11x + 11) и (fleft( { — 7} right) = 2 cdot {left( { — 7} right)^2} + 11 cdot left( { — 7} right) + 11 = 32.) Ответ: 32.
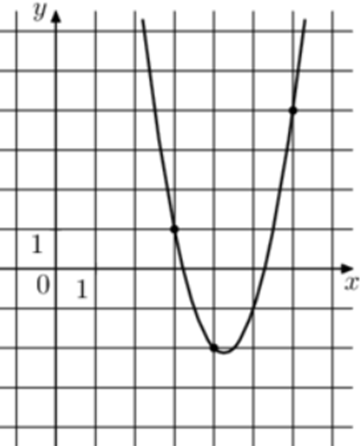
Задача 14. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + c.) Найдите (fleft( {10} right).) Ответ ОТВЕТ: 64.
Решение Парабола проходит через точки (left( {3;1} right)), (left( {4; — 2} right)) и (left( {6;4} right)). Следовательно: (left{ {begin{array}{{20}{c}}{1 = 9a + 3b + c,,,,,,,,,}\{ — 2 = 16a + 4b + c}\{4 = 36a + 6b + c}end{array}} right.) Вычтем из первого уравнения второе: (3 = — 7a — b) Вычтем из первого уравнения третье: ( — 3 = — 27a — 3bleft\| {:left( { — 3} right),,,,,,,,, Leftrightarrow ,,,,,,,,,1 = 9a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{{20}{c}}{3 = — 7a — b}\{1 = 9a + b}end{array}} right.) Прибавим к первому уравнению второе: (4 = 2a,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Тогда: (3 = — 7 cdot 2 — b,,,,,,, Leftrightarrow ,,,,,,,b = — 17) и (1 = 9 cdot 2 + 3 cdot left( { — 17} right) + c,,,,,,, Leftrightarrow ,,,,,,,c = 34.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} — 17x + 34) и (fleft( {10} right) = 2 cdot {10^2} — 17 cdot 10 + 34 = 64.) Ответ: 64.
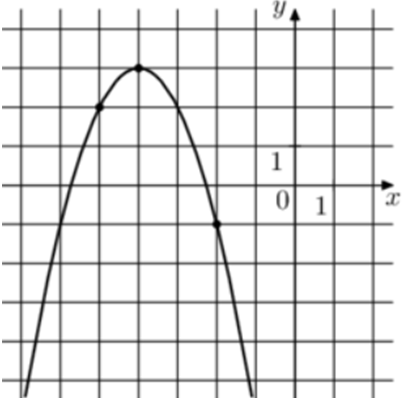
Задача 15. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + c.) Найдите (fleft( 2 right).) Ответ ОТВЕТ: — 33.
Решение 1 Способ Парабола проходит через точки (left( { — 2; — 1} right)), (left( { — 5;2} right)) и (left( { — 6; — 1} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 1 = 4a — 2b + c,,,,,,,,,}\{2 = 25a — 5b + c,,,,,,,}\{ — 1 = 36a — 6b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 21a + 3bleft\| {:3,,,,,,,,, Leftrightarrow ,,,,,,,, — 1 = — 7a + b} right..) Вычтем из первого уравнения третье: (0 = — 32a + 4bleft\| {:4,,,,,,,,,, Leftrightarrow ,,,,,,,,,,0 = — 8a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{{20}{c}}{ — 1 = — 7a + b}\{0 = — 8a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = a,,,,,,, Leftrightarrow ,,,,,,,,a = — 1.) Тогда: ( — 1 = — 7 cdot left( { — 1} right) + b,,,,,, Leftrightarrow ,,,,,,b = — и ( — 1 = 4 cdot left( { — 1} right) — 2 cdot left( { — 8} right) + c,,,,,, Leftrightarrow ,,,,,,c = — 13.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — {x^2} — 8x — 13) и (fleft( 2 right) = -{2^2} — 8 cdot 2 — 13 = — 33.) Ответ: – 33. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — {x^2}) вершина которой находится в точке (left( { — 4;3} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — {left( {x + 4} right)^2} + 3) и (fleft( 2 right) = — {left( {2 + 4} right)^2} + 3 = — 33.) Ответ: – 33.
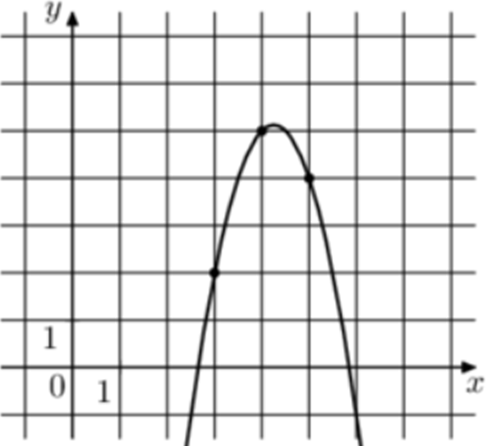
Задача 16. На рисунке изображён график функции (fleft( x right) = a,{x^2} + b,x + c.) Найдите (fleft( { — 1} right).) Ответ ОТВЕТ: — 50.
Решение Парабола проходит через точки (left( {3;2} right)), (left( {4;5} right)) и (left( {5;4} right)). Следовательно: (left{ {begin{array}{{20}{c}}{2 = 9a + 3b + c,,,,,,,,,}\{5 = 16a + 4b + c,,,,,,}\{4 = 25a + 5b + c,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 7a — b.) Вычтем из первого уравнения третье: ( — 2 = — 16a — 2bleft\| {:2,,,,,,,,, Leftrightarrow ,,,,,,,, — ,1 = — 8a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{{20}{c}}{ — 3 = — 7a — b}\{ — 1 = — 8a — b}end{array}} right.) Прибавим к первому уравнению второе: ( — 2 = a,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Тогда: ( — 3 = — 7 cdot left( { — 2} right) — b,,,,,,, Leftrightarrow ,,,,,,,b = 17) и (2 = 9 cdot left( { — 2} right) + 3 cdot 17 + c,,,,,, Leftrightarrow ,,,,,,c = — 31.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} + 17x — 31) и (fleft( { — 1} right) = — 2 cdot {left( { — 1} right)^2} + 17 cdot left( { — 1} right) — 31 = — 50.) Ответ: – 50.

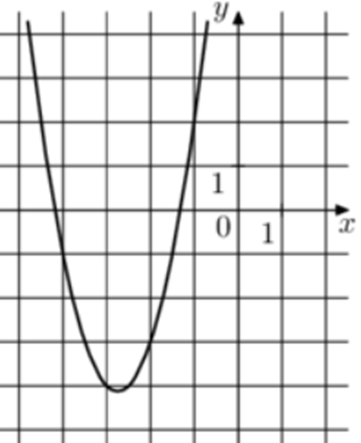
Задача 17. На рисунке изображены графики функций (fleft( x right) = a,{x^2} + b,x + c,) где a, b и c – целые. Найдите (fleft( 2 right).) Ответ ОТВЕТ: 41.
Решение Парабола проходит через точки (left( { — 2; — 3} right)), (left( { — 3; — 4} right)) и (left( { — 4; — 1} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 3 = 4a — 2b + c,,,,,,,,,}\{ — 4 = 9a — 3b + c,,,,,,,,}\{ — 1 = 16a — 4b + c,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: (1 = — 5a + b.) Вычтем из первого уравнения третье: ( — 2 = — 12a + 2bleft\| {:2,,,,,,,,, Leftrightarrow ,,,,,,,, — ,1 = — 6a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{{20}{c}}{1 = — 5a + b}\{ — 1 = — 6a + b}end{array}} right.) Прибавим к первому уравнению второе: (2 = a,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Тогда: (1 = — 5 cdot 2 + b,,,,,,,, Leftrightarrow ,,,,,,,,b = 11) и ( — 3 = 4 cdot 2 — 2 cdot 11 + c,,,,,,, Leftrightarrow ,,,,,,,c = 11.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = 2{x^2} + 11x + 11) и (fleft( 2 right) = 2 cdot {2^2} + 11 cdot 2 + 11 = 41.) Ответ: 41.
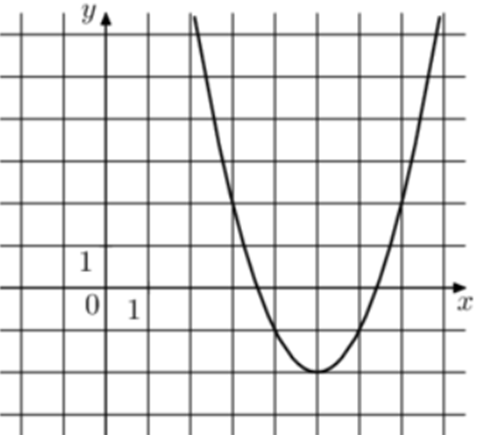
Задача 18. На рисунке изображены графики функций (fleft( x right) = a,{x^2} + b,x + c,) где a, b и c – целые. Найдите (fleft( { — 1} right).) Ответ ОТВЕТ: 34.
Решение 1 Способ Парабола проходит через точки (left( {3;2} right)), (left( {4; — 1} right)) и (left( {5; — 2} right)). Следовательно: (left{ {begin{array}{{20}{c}}{2 = 9a + 3b + c,,,,,,,,,}\{ — 1 = 16a + 4b + c,,,,,,,}\{ — 2 = 25a + 5b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: (3 = -7a — b.) Вычтем из первого уравнения третье: (4 = — 16a — 2bleft\| {:2,,,,,,,,, Leftrightarrow ,,,,,,,,,2 = — 8a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{{20}{c}}{3 = — 7a — b}\{2 = — 8a — b}end{array}} right.) Вычтем из первого уравнения второе: (1 = a,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Тогда: (3 = — 7 — b,,,,,,, Leftrightarrow ,,,,,,,b = — 10) и (2 = 9 cdot 1 + 3 cdot left( { — 10} right) + c,,,,,, Leftrightarrow ,,,,,,c = 23.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = {x^2} — 10x + 23) и (fleft( { — 1} right) = {left( { — 1} right)^2} — 10 cdot left( { — 1} right) + 23 = 34.) Ответ: 34. 2 Способ Заметим, что графиком является парабола (fleft( x right) = {x^2}), вершина которой находится в точке (left( {5; — 2} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = {left( {x — 5} right)^2} — 2) и (fleft( { — 1} right) = {left( { — 1 — 5} right)^2} — 2 = 34.) Ответ: 34.
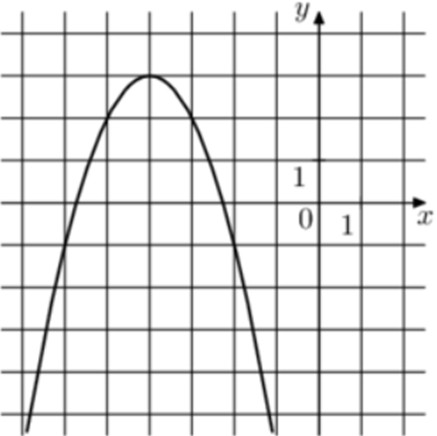
Задача 19. На рисунке изображены графики функций (fleft( x right) = a,{x^2} + b,x + c,) где a, b и c – целые. Найдите (fleft( { — 8} right).) Ответ ОТВЕТ: — 13.
Решение 1 Способ Парабола проходит через точки (left( { — 2; — 1} right)), (left( { — 3;2} right)) и (left( { — 4;3} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 1 = 4a — 2b + c,,,,,,,,,}\{2 = 9a — 3b + c,,,,,,,}\{3 = 16a — 4b + c,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 5a + b.) Вычтем из первого уравнения третье: ( — 4 = — 12a + 2bleft\| {:2,,,,,,,, Leftrightarrow ,,,,,,,, — 2 = — 6a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{{20}{c}}{ — 3 = — 5a + b}\{ — 2 = — 6a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = a,,,,,,, Leftrightarrow ,,,,,,,,a = — 1.) Тогда: ( — 3 = — 5 cdot left( { — 1} right) + b,,,,,,, Leftrightarrow ,,,,,,,b = — и ( — 1 = 4 cdot left( { — 1} right) — 2 cdot left( { — 8} right) + c,,,,,, Leftrightarrow ,,,,,,c = — 13.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — {x^2} — 8x — 13) и (fleft( { — 8} right) = — {left( { — 8} right)^2} — 8 cdot left( { — 8} right) — 13 = — 13.) Ответ: – 13. 2 Способ Заметим, что графиком является парабола (fleft( x right) = — {x^2}), вершина которой находится в точке (left( { — 4;3} right)). Следовательно, ее уравнение будет иметь вид: (fleft( x right) = — {left( {x + 4} right)^2} + 3) и (fleft( { — 8} right) = — {left( { — 8 + 4} right)^2} + 3 = — 13.) Ответ: – 13.
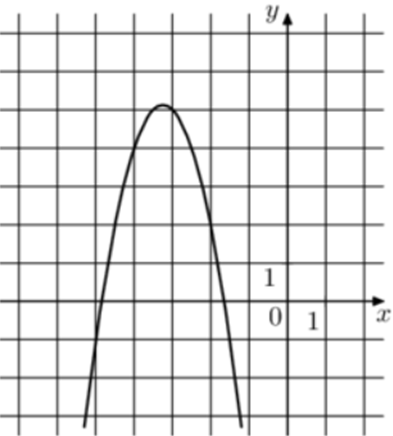
Задача 20. На рисунке изображены графики функций (fleft( x right) = a,{x^2} + b,x + c,) где a, b и c – целые. Найдите (fleft( { — 6} right).) Ответ ОТВЕТ: — 10.
Решение Парабола проходит через точки (left( { — 2;2} right)), (left( { — 3;5} right)) и (left( { — 4;4} right)). Следовательно: (left{ {begin{array}{{20}{c}}{2 = 4a — 2b + c,,,,,,,,,}\{5 = 9a — 3b + c,,,,,,,,}\{4 = 16a — 4b + c,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 3 = — 5a + b.) Вычтем из первого уравнения третье: ( — 2 = — 12a + 2bleft\| {:2,,,,,,,,, Leftrightarrow ,,,,,,,, — 1 = — 6a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{{20}{c}}{ — 3 = — 5a + b}\{ — 1 = — 6a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = a,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Тогда: ( — 3 = — 5 cdot left( { — 2} right) + b,,,,,,, Leftrightarrow ,,,,,,b = — 13) и (2 = 4 cdot left( { — 2} right) — 2 cdot left( { — 13} right) + c,,,,,,, Leftrightarrow ,,,,,,,c = — 16.) Следовательно, уравнение параболы имеет вид: (fleft( x right) = — 2{x^2} — 13x — 16) и (fleft( { — 6} right) = — 2 cdot {left( { — 6} right)^2} — 13 cdot left( { — 6} right) — 16 = — 10.) Ответ: – 10.
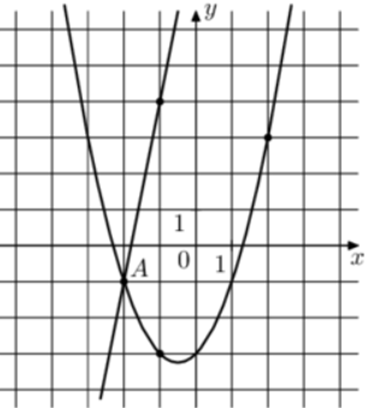
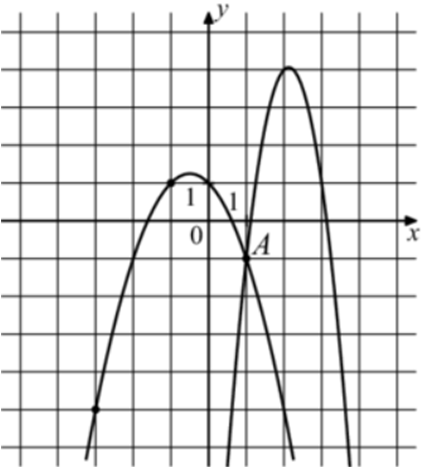
Задача 21. На рисунке изображены графики функций (fleft( x right) = 5x + 9) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B. Ответ ОТВЕТ: 6.
Решение Парабола проходит через точки (left( { — 2; — 1} right)), (left( { — 1; — 3} right)) и (left( {1; — 1} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 1 = 4a — 2b + c,,,,,,,,,}\{ — 3 = a — b + c,,,,,,,,,,,,,,,}\{ — 1 = a + b + c,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: (2 = 3a — b.) Вычтем из первого уравнения третье: (0 = 3a — 3bleft\| {:3,,,,,,,,,, Leftrightarrow ,,,,,,,,,,0 = a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{{20}{c}}{2 = 3a — b}\{0 = a — b,,,}end{array}} right.) Вычтем из первого уравнения второе: (2 = 2a,,,,, Leftrightarrow ,,,,a = 1.) Тогда: (0 = 1 — b,,,,,,,, Leftrightarrow ,,,,,,,,b = 1) и ( — 1 = 4 cdot 1 — 2 cdot 1 + c,,,,,,, Leftrightarrow ,,,,,,,c = — 3.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = {x^2} + x — 3.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = 5x + 9) и параболы (gleft( x right) = {x^2} + x — 3) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = {x^2} + x — 3}\{y = 5x + 9,,,,,,,}end{array}} right.,,,,,, Leftrightarrow ,,,,,{x^2} + x — 3 = 5x + 9,,,,,, Leftrightarrow ,,,,,,{x^2} — 4x — 12 = 0,,,,, Leftrightarrow ,,,,,{x_1} = — 2,,,,{x_2} = 4.) Значение (x = — 2) является абсциссой точки А. Следовательно, абсцисса точки В равна 4. Ответ: 4.
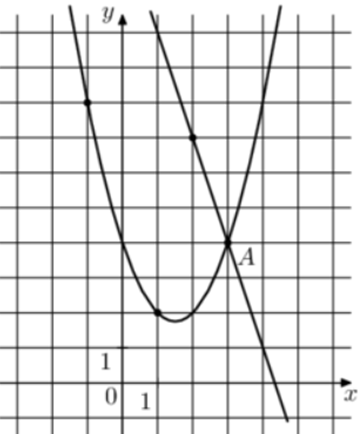
Задача 22. На рисунке изображены графики функций (fleft( x right) = — 3x + 13) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B. Ответ ОТВЕТ: — 3.
Решение Парабола проходит через точки (left( {1;2} right)), (left( {2;2} right)) и (left( {3;4} right)). Следовательно: (left{ {begin{array}{{20}{c}}{2 = a + b + c,,,,,,,,,,,,,,,,,,,,,}\{2 = 4a + 2b + c,,,,,,,,,,,,,,,}\{4 = 9a + 3b + c,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: (0 = — 3a — b.) Вычтем из первого уравнения третье: ( — 2 = — 8a — 2bleft\| {:2,,,,,,,, Leftrightarrow ,,,,,,,, — 1 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{{20}{c}}{0 = — 3a — b}\{ — 1 = — 4a — b,,,}end{array}} right.) Вычтем из первого уравнения второе: (1 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Тогда: (0 = — 3 cdot 1 — b,,,,,,,, Leftrightarrow ,,,,,,,,b = — 3) и (2 = 1 — 3 + c,,,,,,, Leftrightarrow ,,,,,,,c = 4.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = {x^2} — 3x + 4.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 3x + 13) и параболы (gleft( x right) = {x^2} — 3x + 4) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = {x^2} — 3x + 4}\{y = — 3x + 13,,,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,{x^2} — 3x + 4 = — 3x + 13,,,,,,, Leftrightarrow ,,,,,,,{x^2} = 9,,,,,,, Leftrightarrow ,,,,,{x_1} = 3,,,,{x_2} = — 3.) Значение (x = 3) является абсциссой точки А. Следовательно, абсцисса точки В равна – 3. Ответ: – 3.
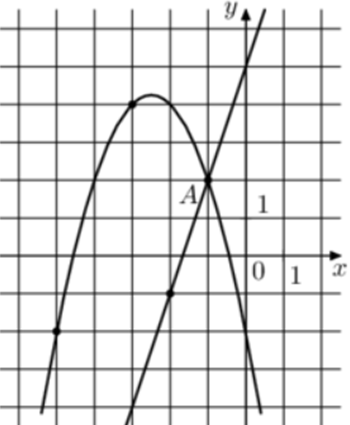
Задача 23. На рисунке изображены графики функций (fleft( x right) = 3x + 5) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B. Ответ ОТВЕТ: — 7.
Решение Парабола проходит через точки (left( { — 1;2} right)), (left( { — 2;4} right)) и (left( { — 4;2} right)). Следовательно: (left{ {begin{array}{{20}{c}}{2 = a — b + c,,,,,,,,,,,,,,,,,,,,,}\{4 = 4a — 2b + c,,,,,,,,,,,,,,,}\{2 = 16a — 4b + c,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = — 3a + b.) Вычтем из первого уравнения третье: (0 = — 15a + 3bleft\| {:3,,,,,,,, Leftrightarrow ,,,,,,,0 = — 5a + b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{{20}{c}}{ — 2 = — 3a + b}\{0 = — 5a + b,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = 2a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 1.) Тогда: ( — 2 = — 3 cdot left( { — 1} right) + b,,,,,,,, Leftrightarrow ,,,,,,,,b = — 5) и (2 = — 1 + 5 + c,,,,,,, Leftrightarrow ,,,,,,,c = — 2.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = — {x^2} — 5x — 2.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = 3x + 5) и параболы (gleft( x right) = — {x^2} — 5x — 2) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — {x^2} — 5x — 2}\{y = 3x + 5,,,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,, — {x^2} — 5x — 2 = 3x + 5,,,,,, Leftrightarrow ,,,,,{x^2} + 8x + 7 = 0,,,,,, Leftrightarrow ,,,,,{x_1} = — 1,,,,{x_2} = — 7.) Значение (x = — 1) является абсциссой точки А. Следовательно, абсцисса точки В равна – 7. Ответ: – 7.
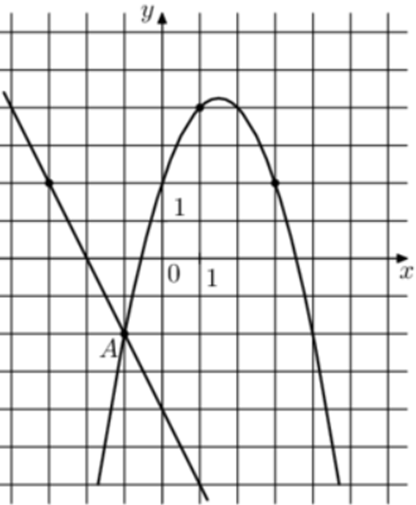
Задача 24. На рисунке изображены графики функций (fleft( x right) = — 2x — 4) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B. Ответ ОТВЕТ: 6.
Решение Парабола проходит через точки (left( { — 1; — 2} right)), (left( {1;4} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 2 = a — b + c,,,,,,,,,,,,,,,,,,,,,}\{4 = a + b + c,,,,,,,,,,,,,,,,,,,,,,}\{2 = 9a + 3b + c,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 6 = — 2b,,,,,,, Leftrightarrow ,,,,,,b = 3.) Вычтем из первого уравнения третье: ( — 4 = — 8a — 4bleft\| {:left( { — 2} right),,,,,,,,, Leftrightarrow ,,,,,,,,2 = 4a + 2b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{{20}{c}}{b = 3,,,,,,,,,,,,,,,,}\{2 = 4a + 2b,,,}end{array},,,,, Leftrightarrow ,,,,,,2 = 4a + 2 cdot 3,,,,,,,, Leftrightarrow ,,,,,,,,,a = — 1} right..) Тогда: ( — 2 = — 1 — 3 + c,,,,,,, Leftrightarrow ,,,,,,,,c = 2.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = — {x^2} + 3x + 2.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 2x — 4) и параболы (gleft( x right) = — {x^2} + 3x + 2) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — {x^2} + 3x + 2}\{y = — 2x — 4,,,,,,,,,,,}end{array}} right.,,,,, Leftrightarrow ,,,,, — ,{x^2} + 3x + 2 = — 2x — 4,,,,,, Leftrightarrow ,,,,,{x^2} — 5x — 6 = 0,,,,, Leftrightarrow ,,,,,{x_1} = — 1,,,,{x_2} = 6.) Значение (x = — 1) является абсциссой точки А. Следовательно, абсцисса точки В равна 6. Ответ: 6.
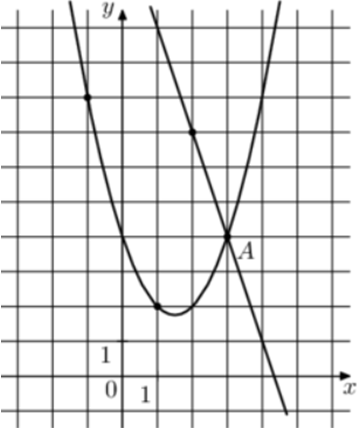
Задача 25. На рисунке изображены графики функций (fleft( x right) = — 3x + 13) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B. Ответ ОТВЕТ: 22.
Решение Парабола проходит через точки (left( {1;2} right)), (left( {2;2} right)) и (left( {3;4} right)). Следовательно: (left{ {begin{array}{{20}{c}}{2 = a + b + c,,,,,,,,,,,,,,,,,,,,,,,,,,,,}\{2 = 4a + 2b + c,,,,,,,,,,,,,,,,,,,,,,}\{4 = 9a + 3b + c,,,,,,,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: (0 = — 3a — b.) Вычтем из первого уравнения третье: ( — 2 = — 8a — 2bleft\| {:2,,,,,,,, Leftrightarrow ,,,,,,, — 1 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{{20}{c}}{0 = — 3a — b}\{ — 1 = — 4a — b}end{array}} right.) Вычтем из первого уравнения второе: (1 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Тогда: (0 = — 3 cdot 1 — b,,,,,,,, Leftrightarrow ,,,,,,,,b = — 3) и (2 = 1 — 3 + c,,,,,,, Leftrightarrow ,,,,,,,c = 4.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = {x^2} — 3x + 4.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 3x + 13) и параболы (gleft( x right) = {x^2} — 3x + 4) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = {x^2} — 3x + 4}\{y = — 3x + 13,,,,}end{array}} right.,,, Leftrightarrow ,,,{x^2} — 3x + 4 = 13 — 3x,,, Leftrightarrow ,,,{x^2} = 9,,,, Leftrightarrow ,,,{x_1} = 3,,,,{x_2} = — 3,,, Leftrightarrow ,,,{y_1} = 4,,,{y_2} = 22.) Следовательно, (Aleft( {3;4} right)) и (Bleft( { — 3;22} right)). Таким образом, ордината точки В равна 22. Ответ: 22.
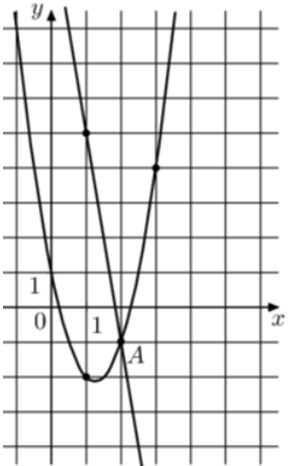
Задача 26. На рисунке изображены графики функций (fleft( x right) = — 6x + 11) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B. Ответ ОТВЕТ: 26.
Решение Парабола проходит через точки (left( {1; — 2} right)), (left( {2; — 1} right)) и (left( {3;4} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 2 = a + b + c}\{ — 1 = 4a + 2b + c}\{4 = 9a + 3b + c}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = — 3a — b.) Вычтем из первого уравнения третье: ( — 6 = — 8a — 2bleft\| {:2,,,,,,,, Leftrightarrow ,,,,,,,, — 3 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{{20}{c}}{ — 1 = — 3a — b}\{ — 3 = — 4a — b}end{array}} right.) Вычтем из первого уравнения второе: (2 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Тогда: ( — 1 = — 3 cdot 2 — b,,,,,,,, Leftrightarrow ,,,,,,,,b = — 5) и ( — 2 = 2 — 5 + c,,,,,,, Leftrightarrow ,,,,,,,c = 1.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = 2{x^2} — 5x + 1.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 6x + 11) и параболы (gleft( x right) = 2{x^2} — 5x + 1) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 2{x^2} — 5x + 1}\{y = — 6x + 11,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,2{x^2} — 5x + 1 = — 6x + 11,,,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} + x — 10 = 0,,,,,,,,, Leftrightarrow ,,,,,) ( Leftrightarrow ,,,,,,,,{x_1} = 2,,,,,,{x_2} = — frac{5}{2},,,,,,,,, Leftrightarrow ,,,,,,,{y_1} = — 1,,,,,{y_2} = 26.) Следовательно, (Aleft( {2; — 1} right)) и (Bleft( { — frac{5}{2};26} right)). Таким образом, ордината точки В равна 26. Ответ: 26.
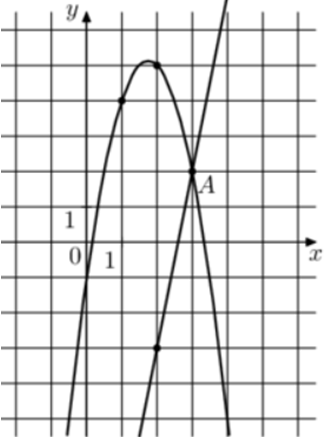
Задача 27. На рисунке изображены графики функций (fleft( x right) = 5x — 13) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B. Ответ ОТВЕТ: — 23.
Решение Парабола проходит через точки (left( {1;4} right)), (left( {2;5} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{{20}{c}}{4 = a + b + c,,,,,,,,,,,,,,,,,,,,,,,,,,,,}\{5 = 4a + 2b + c,,,,,,,,,,,,,,,,,,,,,,}\{2 = 9a + 3b + c,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = — 3a — b.) Вычтем из первого уравнения третье: (2 = — 8a — 2bleft\| {:2,,,,,,, Leftrightarrow ,,,,,,1 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{{20}{c}}{ — 1 = — 3a — b}\{1 = — 4a — b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Тогда: ( — 1 = — 3 cdot left( { — 2} right) — b,,,,,,,, Leftrightarrow ,,,,,,,,b = 7) и (4 = — 2 + 7 + c,,,,,,, Leftrightarrow ,,,,,,,c = — 1.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = — 2{x^2} + 7x — 1.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = 5x — 13) и параболы (gleft( x right) = — 2{x^2} + 7x — 1) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — 2{x^2} + 7x — 1}\{y = 5x — 13,,,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,, — 2{x^2} + 7x — 1 = 5x — 13,,,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} — 2x — 12 = 0,,,,,,,,, Leftrightarrow ,,,,,) ( Leftrightarrow ,,,,,,,,{x_1} = 3,,,,,,{x_2} = — 2,,,,,,,,, Leftrightarrow ,,,,,,,{y_1} = 2,,,,,{y_2} = — 23.) Следовательно, (Aleft( {3;2} right)) и (Bleft( { — 2; — 23} right)). Таким образом, ордината точки В равна – 23. Ответ: – 23.
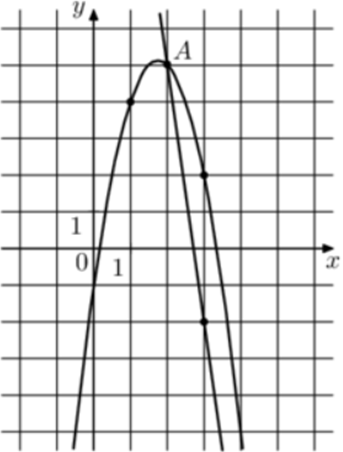
Задача 28. На рисунке изображены графики функций (fleft( x right) = — 7x + 19) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B. Ответ ОТВЕТ: — 16.
Решение Парабола проходит через точки (left( {1;4} right)), (left( {2;5} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{{20}{c}}{4 = a + b + c,,,,,,,,,,,,,,,,,,,,,,,,,,,,}\{5 = 4a + 2b + c,,,,,,,,,,,,,,,,,,,,,,}\{2 = 9a + 3b + c,,,,,,,,,,,,,,,,,,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 1 = — 3a — b.) Вычтем из первого уравнения третье: (2 = — 8a — 2bleft\| {:2,,,,,,,, Leftrightarrow ,,,,,,,,1 = — 4a — b} right..) Таким образом, получим систему уравнений: (left{ {begin{array}{{20}{c}}{ — 1 = — 3a — b}\{1 = — 4a — b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Тогда: ( — 1 = — 3 cdot left( { — 2} right) — b,,,,,,,, Leftrightarrow ,,,,,,,,b = 7) и (4 = — 2 + 7 + c,,,,,,, Leftrightarrow ,,,,,,,c = — 1.) Следовательно, уравнение параболы имеет вид: (gleft( x right) = — 2{x^2} + 7x — 1.) Чтобы найти координаты точек пересечения прямой (fleft( x right) = — 7x + 19) и параболы (gleft( x right) = — 2{x^2} + 7x — 1) необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — 2{x^2} + 7x — 1}\{y = — 7x + 19,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,, — 2{x^2} + 7x — 1 = — 7x + 19,,,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} — 14x + 20 = 0,,,,,,,,, Leftrightarrow ,,,,,) ( Leftrightarrow ,,,,,,,,{x_1} = 2,,,,,,{x_2} = 5,,,,,,,, Leftrightarrow ,,,,,,,{y_1} = 5,,,,,{y_2} = — 16.) Следовательно, (Aleft( {2;5} right)) и (Bleft( {5; — 16} right)). Таким образом, ордината точки В равна – 16. Ответ: – 16.
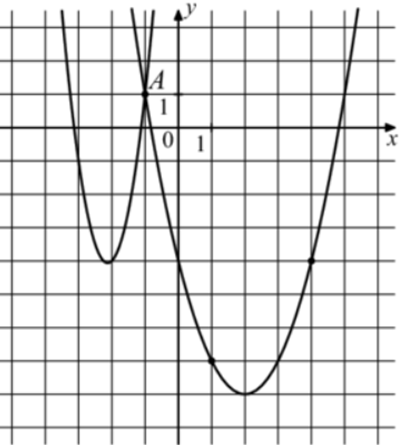
Задача 29. На рисунке изображены графики функций (fleft( x right) = 4{x^2} + 17x + 14) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B. Ответ ОТВЕТ: — 6.
Решение График функции (fleft( x right) = 4{x^2} + 17x + 14) пересекает ось ординат в точке (left( {0;14} right)). Значит, график (y = fleft( x right)) изображён слева, а график (gleft( x right) = a{x^2} + bx + c) справа. Заметим, что графиком функции (y = gleft( x right)) является парабола (gleft( x right) = {x^2}), вершина которой находится в точке (left( {2; — 8} right)). Следовательно, ее уравнение будет иметь вид: (gleft( x right) = {left( {x — 2} right)^2} — 8 = {x^2} — 4x — 4.) Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 4{x^2} + 17x + 14}\{y = {x^2} — 4x — 4,,,,,,,,,}end{array}} right.,,,,,,,,, Leftrightarrow ,,,,,,4{x^2} + 17x + 14 = {x^2} — 4x — 4,,,,,,, Leftrightarrow ,,,,,,,3{x^2} + 21x + 18 = 0left\| {:3,,,,, Leftrightarrow } right.) ( Leftrightarrow ,,,,,,,{x^2} + 7x + 6 = 0,,,,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = — 1,,,,{x_2} = — 6.) Значение (x = — 1) является абсциссой точки А. Следовательно, абсцисса точки В равна – 6. Ответ: – 6.
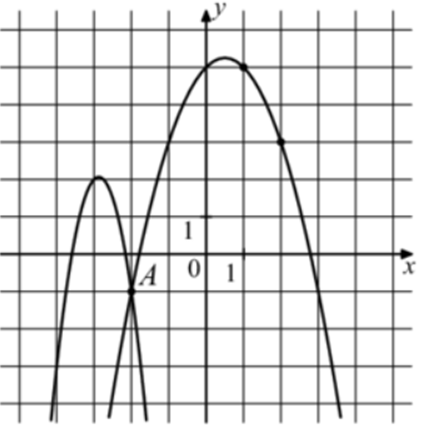
Задача 30. На рисунке изображены графики функций (fleft( x right) = — 4{x^2} — 23x — 31) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите абсциссу точки B. Ответ ОТВЕТ: — 6.
Решение График функции (fleft( x right) = — 4{x^2} — 23x — 31) пересекает ось ординат в точке (left( {0; — 31} right)). Значит график функции (y = fleft( x right)) изображен слева, а график (gleft( x right) = a{x^2} + bx + c) справа, который проходит через точки (left( { — 2; — 1} right)), (left( {1;5} right)) и (left( {2;3} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 1 = 4a — 2b + c}\{5 = a + b + c,,,,,,}\{3 = 4a + 2b + c}end{array}} right.) Вычтем из первого уравнения второе: ( — 6 = 3a — 3b.) Вычтем из первого уравнения третье: ( — 4 = — 4b,,,,,, Leftrightarrow ,,,,,b = 1.) Тогда: ( — 6 = 3a — 3,,,,,, Leftrightarrow ,,,,,,a = — 1) и ( — 1 = — 4 — 2 + c,,,,,, Leftrightarrow ,,,,,,,c = 5.) Следовательно: (gleft( x right) = — {x^2} + x + 5.) Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений: (left{ {begin{array}{{20}{c}}{y = — 4{x^2} — 23x — 31}\{y = — {x^2} + x + 5,,,,,,,,,,,}end{array}} right.,,,,, Leftrightarrow ,,,,, — 4{x^2} — 23x — 31 = — {x^2} + x + 5,,,,, Leftrightarrow ,,,,,3{x^2} + 24x + 36 = 0left\| {:3,,,, Leftrightarrow ,} right.) ( Leftrightarrow ,,,,,,{x^2} + 8x + 12 = 0,,,,,,,, Leftrightarrow ,,,,,,{x_1} = — 2,,,,,,{x_2} = — 6.) Значение (x = — 2) является абсциссой точки А. Следовательно, абсцисса точки В равна – 6. Ответ: – 6.
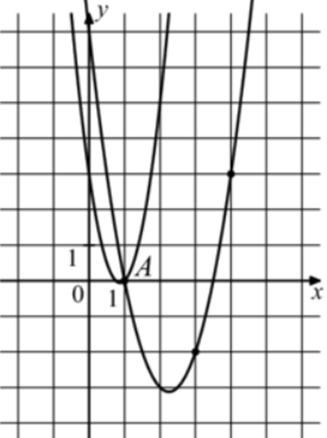
Задача 31. На рисунке изображены графики функций (fleft( x right) = 4{x^2} — 7x + 3) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B. Ответ ОТВЕТ: 33.
Решение График функции (fleft( x right) = 4{x^2} — 7x + 3) пересекает ось ординат в точке (left( {0;3} right)). Значит график функции (y = fleft( x right)) изображен слева, а график (gleft( x right) = a{x^2} + bx + c) справа, который проходит через точки (left( {1;0} right)), (left( {3; — 2} right)) и (left( {4;3} right)). Следовательно: (left{ {begin{array}{{20}{c}}{0 = a + b + c,,,,,,,,}\{ — 2 = 9a + 3b + c}\{3 = 16a + 4b + c}end{array}} right.) Вычтем из первого уравнения второе: (2 = — 8a — 2bleft\| {: 2,,,,,,, Leftrightarrow ,,,,,,,,1 = — 4a — b.} right.) Вычтем из первого уравнения третье: ( — 3 = — 15a — 3bleft\| {:3} right.,,,,,, Leftrightarrow ,,,,, — 1 = — 5a — b.) Таким образом, получим систему уравнений: (left{ {begin{array}{{20}{c}}{1 = — 4a — b}\{ — 1 = — 5a — b}end{array}} right.) Вычтем из первого уравнения второе: (2 = a,,,,,,, Leftrightarrow ,,,,,,,a = 2.) Тогда: (1 = — 4 cdot 2 — b,,,,,, Leftrightarrow ,,,,,,b = — 9) и (0 = 2 — 9 + c,,,,,,, Leftrightarrow ,,,,,,,c = 7.) Следовательно: (gleft( x right) = 2{x^2} — 9x + 7.) Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 4{x^2} — 7x + 3}\{y = 2{x^2} — 9x + 7}end{array},,,,,,, Leftrightarrow ,,,,,,4{x^2} — 7x + 3 = 2{x^2} — 9x + 7,,,,,,, Leftrightarrow ,,,,,,,2{x^2} + 2x — 4 = 0left\| {:2,,,,, Leftrightarrow } right.} right.) ( Leftrightarrow ,,,,,,,{x^2} + x — 2 = 0,,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = — 2,,,,,,,,,,,,,,{y_1} = 0,,,,{y_2} = 33.) Следовательно, (Aleft( {1;0} right)) и (Bleft( { — 2;33} right)). Таким образом, ордината точки В равна 33. Ответ: 33.
Задача 32. На рисунке изображены графики функций (fleft( x right) = — 4{x^2} + 17x — 14) и (gleft( x right) = a,{x^2} + b,x + c,) которые пересекаются в точках A и B. Найдите ординату точки B. Ответ ОТВЕТ: — 29.
Решение График функции (fleft( x right) = — 4{x^2} + 17x — 14) пересекает ось ординат в точке (left( {0; — 14} right)). Значит график функции (y = fleft( x right)) изображен справа, а график (gleft( x right) = a{x^2} + bx + c) слева, который проходит через точки (left( {1; — 1} right)), (left( { — 1;1} right)) и (left( { — 3; — 5} right)). Следовательно: (left{ {begin{array}{{20}{c}}{ — 1 = a + b + c,,,,,,}\{1 = a — b + c,,,,,,,,}\{ — 5 = 9a — 3b + c}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = 2b,,,,,,, Leftrightarrow ,,,,,,,b = — 1.) Вычтем из первого уравнения третье: (4 = — 8a + 4b,,,,, Leftrightarrow ,,,,,4 = — 8a — 4,,,,,, Leftrightarrow ,,,,,,a = — 1.) Тогда: ( — 1 = — 1 — 1 + c,,,,,, Leftrightarrow ,,,,,,,c = 1.) Следовательно: (gleft( x right) = — {x^2} — x + 1.) Чтобы найти координаты точек пересечения парабол необходимо решить систему уравнений: (left{ {begin{array}{{20}{c}}{y = — 4{x^2} + 17x — 14}\{y = — {x^2} — x + 1,,,,,,,,,,,,,}end{array}} right.,,,,,, Leftrightarrow ,,,,, — 4{x^2} + 17x — 14 = — {x^2} — x + 1,,,,,, Leftrightarrow ,,,,,3{x^2} — 18x + 15 = 0left\| {:3,,,,, Leftrightarrow } right.) ( Leftrightarrow ,,,,,,,{x^2} — 6x + 5 = 0,,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = 5,,,,,,,,,{y_1} = — 1,,,,{y_2} = — 29.) Следовательно, (Aleft( {1; — 1} right)) и (Bleft( {5; — 29} right)). Таким образом, ордината точки В равна – 29. Ответ: – 29.

Источник

Скачать материал

Сейчас обучается 54 человека из 30 регионов

Сейчас обучается 32 человека из 22 регионов

Сейчас обучается 47 человек из 27 регионов

Описание презентации по отдельным слайдам:

1 слайд

Добрый день, уважаемые коллеги! Приятно видеть вас в этой аудитории, и очень надеюсь, что сегодня у нас с вами получится интересное и полезное мероприятие.
2 слайд

Мастер-класс
учителя математики
МОУ «СОШ№ 14»
Рискуловой Тотайхан Оразалиевны
по теме:
«Анализ графиков (новое 9 задание). Подготовка к профильному ЕГЭ по математике»
а Эдельбай
Благодарненский район
3 слайд

«Расскажи мне и я забуду. Покажи мне и я пойму. Позволь мне сделать самому, и я научусь»

Конфуций
Конфуций-древнекитайский проповедник,
писатель, философ.
4 слайд

Сложно подготовить обучающихся к сдаче экзамена. Это большой труд. Но не надо бояться. Если вы хорошо знаете, объясняете, любите свой предмет и своих учеников, вы обязательно сможете подготовить их к ЕГЭ по математике.
Важный принцип — это логичность. В шутливой манере он говорит: «нормальные герои всегда идут в обход». Нужно учиться использовать наличный запас знаний, применяя различные «хитрости» и «правдоподобные рассуждения» для ответа наиболее простым и понятным способом.
Главная заповедь учителя – заметить даже самое маленькое продвижение ученика вперёд и поддержать его успех.
5 слайд

Цель мастер-класса:
показать приемы решения нового 9 задания по теме «Анализ графиков»
развивать логическое мышление, память, познавательный интерес
7 слайд

1 9 задание
На рисунке изображены графики двух линейных функций. Найдите ординату точек пересечения.
1
2
Решение
Уравнение прямой у=kx+b. Первая прямая проходит
через точки (-4;1) и (-2;4), k= 𝟑 𝟐 .
Найдем b,подставив координаты одной из точек в уравнение
1=1,5·(-4)+ b, b=7.
у=1,5х+7-уравнение1 прямой.
2) Вторая прямая проходит через точки (-1;0) и (2;3), k= 𝟑 𝟑 =𝟏.
Найдем b,подставив координаты одной из точек в уравнение
0=1·(-1)+ b, b=1.Тогда у=х+1-уравнение2 прямой.
3)Решим систему уравнений у=𝟏,𝟓𝒙+𝟕, 𝒚=𝒙+𝟏 Вычтем из 1 уравнения 2 уравнение , получим 0=0,5х+6.Отсюда х=-12.Тогда у=-11.
Ответ:-11
8 слайд

9 задание
На рисунке изображен график функции f(x)= 𝒂 x²+bx+c,где числа a,b и c-целые. Найдите значение f(-12).
Решение.
f(x)= 𝒂(x-m)²+n,где m, n-координаты вершины параболы.
m= -4,n= -3, 𝒂 =1.
f(x)=(x-(-4))²+(-3),
f(x)=(x+4)²-3,
f(-12)=(-12+4)²-3,
f(-12)=61.
Ответ:61
2
9 слайд

9 задание
На рисунке изображен график функции f(x)= 𝒙 𝟐 𝒂 +bx+c, где числа 𝒂 ,b и c-целые. Найдите значение f(4).
Решение.
f(x)= 𝟏 𝒂 (x-m)²+n,где (m, n)-координаты вершины параболы.
По графику m= -2,n= 11, 𝒂 = -2. (Введем новую систему координат через вершину параболы, тогда график
функции f(x)= 𝒙 𝟐 𝒂 проходит через точку (2;-2).
Подставив в формулу f(x)= 𝒙 𝟐 𝒂 ,найдем а)
f(x)= — 𝟏 𝟐 (x+2)²+11= — 𝟏 𝟐 x²-2x+9,значит, 𝒂 = — 2, b=-2, c=9.
Тогда f(4)= — (𝟒+𝟐)² 𝟐 +11= — 18+11= — 7.
Ответ:- 7

3
10 слайд

9 задание. На рисунке изображен график функции f(x)= 𝒂 x²+bx+c. Найдите f(-1).
Решение.
Из рисунка видно, что график проходит через (3;2);(4;5);(5;4)
9а+3b+c= 2, 16a+4b+c=𝟓, 25a+5b+c=4.
Вычтем из 2 уравнения 1-е,
получим7a+b=𝟑
Вычтем из 3уравнения 2-е,
получим 9a+b=-𝟏
Решив систему уравнений 7a+b=𝟑, 9a+b=−1;
находим 𝒂=-2 ,b=17.
Тогда f(x)=- 2 x²+17x+c и f(3)=2, найдем ,что с=-31.
f(x)=- 2 x²+17x-31,
f(-1)=-2-17-31=-50
Ответ:-50
4
11 слайд

9 задание. На рисунке изображен график функции f(x)=ах²+bx+c,где числа 𝒂 ,b и c-целые. Найдите абсциссу вершины параболы.
Решение.
Абсцисса вершины параболы найдем по формуле х 𝟎 = — 𝒃 𝟐𝒂
Из рисунка видно, что f(-3)=-2; f(-2)=1; f(-1)=6.Тогда
9а−3b+c= −2, 4a−2b+c=1, a−b+c=6 ;
вычтем из 1 уравнения 2-е, получим5a-b=-𝟑
вычтем из 2 уравнения 3-е,получим 3a-b=-𝟓.
Решив систему уравнений 5a−b=−𝟑, 3a−b=−𝟓; находим 𝒂=1 ,b=8.
Абсцисса вершины параболы х 𝟎 = — 𝒃 𝟐𝒂 =-4.
Ответ:-4

6
12 слайд

7
9 задание. На рисунке изображены графики функций f(x)=5х+9 и g(x)= ах²+bx+c, которые пересекаются в точках А и В. Найдите абсциссу точки B

Решение. По графику с=-3.График функции g(x) проходит через точки (-2;-1);(-1;-3);(2;3).
Подставим координаты точки (-1;-3), получим
-3=а- b-3.Отсюда а=b.
g(x)= ах²+аx-3.
Подставим координаты точки (2;3), получим, что а=1.
g(x)= х²+x-3.
Чтобы найти абсциссу точки ,нужно решить уравнение х²+x-3=5х+9,
х²-4x-12=0.
По теореме Виета х 𝟏 ·х 𝟐 =-12, х 𝟏 + х 𝟐 =4
По графику х 𝟏 =-2, тогда х 𝟐 =6.
Ответ:6
13 слайд

Решение.
f(x)= 𝒂(x-m)²+n,где m, n-координаты вершины параболы.
m=-3,n=3, 𝒂 =1.
f(x)=(x-(-3))²+3
f(x)=(x+3)²+3,
f(x)=х²+6х+12, так как f(x)=0.
то х²+6х+12=0
D=6²-4·1·12= -12.
Ответ:-12
Решите 9 задание
На рисунке изображен график функции f(x)= 𝒂x²+bx+c,где числа 𝒂 ,b и c-целые. Найдите значение дискриминанта уравнения f(x)=0.
8
14 слайд

Решение.
|bx+c|=0 в точке излома. Значит, bx+c=0 при х=2.

Ответ:2
9

9 задание
На рисунке изображен график функции вида 𝒇 𝒙 = 𝒂 x+|bx+c|+d, где числа 𝒂,b, c и d-целые.
Найдите корень уравнения bx+c=0
15 слайд

9 задание.
На рисунке изображён график функции вида f(x)=ax + |bx + c| +d, где числа a, b, c и d — целые. Найдите корень уравнения ax + d=0.

Решение.
|bx + c|=0 в точке излома при х=1,
Если х<1,то f(x)=ax -bx — c +d=(а-b)х+ d-с, где (а-b)-угловой коэффициент, (d-с)-ордината точки пересечения прямой с осью Ох.
По графику а-b=-4; d-с=5.
Если х>1,то f(x)=ax +bx + c +d=(а+b)х+с+ d, где а+b-угловой коэффициент, по графику а+b=2.
Продолжив прямую до пересечения с осью Оу, получим , что с+ d =-1.

Решив эти системы а−b=−4 а+b=𝟐 и с+ d =−1 d−с=5 , получим,что
a=-1;b=3;c=-3;d=2. Подставив найденные значения в уравнение ax +d=0 , получим -x + 2=0,
х=2.
Ответ:2

10
5
-1
16 слайд

11 На рисунке изображен график функции вида f(x)= 𝒂 cos(bπx+c)+d, где числа 𝒂,b, c и d-целые. Найдите 𝒇 𝟏𝟎𝟎 𝟑 .
Решение.
По графику 𝒇 𝒎𝒂𝒙 =𝟏,𝒇 𝒎𝒊𝒏 =-3
d= 𝒇 𝒎𝒂𝒙 + 𝒇 𝒎𝒊𝒏 𝟐 = 𝟏−𝟑 𝟐 = -1. |a|= 𝒇 𝒎𝒂𝒙 − 𝒇 𝒎𝒊𝒏 𝟐 = 𝟏+𝟑 𝟐 =2.
По графику 𝒂 =2, c=0, T=2
T= 𝟐𝝅 𝒃𝝅 = 𝟐 𝒃 , то есть 𝟐 𝒃 =2, отсюда b=1
f(x)=2cosπx-1,
f 𝟏𝟎𝟎 𝟑 =f 𝟗𝟔 𝟑 + 𝟒 𝟑 =𝒇 𝟑𝟐+ 𝟒 𝟑 =f 𝟒 𝟑 ,
f 𝟒 𝟑 =2cosπ· 𝟒 𝟑 -1 = 2cos 𝟒 𝟑 π-1 = 2cos π+ π 𝟑 -1= -2cos π 𝟑 −1= -2.
Ответ:-2

Т=2
17 слайд

9 задание. На рисунке изображен график функции f(x)=k х. Найдите f(2,56)
Решение.
График этой функции проходит через точку (4;-3).Подставив координаты этой точки, получим
-3=k 𝟒 ,
2k=-3,
k =-1,5.
f(2,56)=-1,5 𝟐,𝟓𝟔 =−1,5·1,6=−2,4.

Ответ:-2,4

12
18 слайд

9 задание. На рисунке изображен график функции f(x)= 𝒌 𝒙 +a. Найдите f (0,25)

Решение. График функции имеет горизонтальную асимптоту y=-2, значит, а=-2.
(График функции f(x)= 𝒌 𝒙 +a получается сдвигом графика функции f(x)= 𝒌 𝒙 вдоль оси Оу на величину |а| вверх, если а>0 и вниз если a<0)
По графику а= -2 и проходит через точку (3;-3).
-3= 𝒌 𝟑 -2 отсюда k=-3.Значит,
f(x)= −𝟑 𝒙 -2,
f(0,25)= −𝟑 𝟎,𝟐𝟓 -2= -14.
Ответ:- 14

13
19 слайд

14
9 задание. На рисунке изображен график функции f(x)= 𝒌 𝒙+а . Найдите f −𝟒 𝟐 𝟑 .
Решение.
График функции имеет вертикальную асимптоту x=2, значит, а= — 2.
(График функции f(x)= 𝒌 𝒙+а получается сдвигом графика функции f(x)= 𝒌 𝒙 вдоль оси Ох на величину |а| влево, если а>0 и вправо если a<0).
По графику а= -2 и проходит через точку (-3;-1).
-1= 𝒌 −𝟑−𝟐 , отсюда k=5.Значит,
f(x)= 𝟓 𝒙−𝟐 ,
f −𝟒 𝟐 𝟑 = 𝟓 −𝟒 𝟐 𝟑 −𝟐 =5: −𝟔 𝟐 𝟑 =-0,75.
Ответ:-0,75
20 слайд

9 задание. На рисунке изображён график функции вида f(x)= 𝒂 𝒙+𝒃 +c, где числа a, b и c — целые. Найдите f(13).
Решение.
График функции имеет горизонтальную асимптоту y=2, значит, c=2.
График функции имеет вертикальную асимптоту x=3, значит, b= — 3.
По графику f(2)=1, тогда 𝒂 𝟐−𝟑 +2=1, отсюда a=1.
Таким образом, f(x)= 𝟏 х−𝟑 +2
Найдём f(13)= 𝟏 𝟏𝟑−𝟑 +2=2,1.
f(13)=2,1.
Ответ:2,1
15
21 слайд

9 задание. На рисунке изображен график функции f(x)= 𝒌𝒙+𝒂 𝒙+𝒃 . Найдите k
Решение.
Преобразуем данную функцию
f(x)= 𝒌𝒙+𝒂 𝒙+𝒃 = 𝒌𝒙+𝒌𝒃−𝒌𝒃+𝒂 𝒙+𝒃 = 𝒌(𝒙+𝒃)−𝒌𝒃+𝒂 𝒙+𝒃 =𝒌+ 𝒂−𝒌𝒃 𝒙+𝒃 .
Или

f(x)=𝒌+ 𝒂−𝒌𝒃 𝒙+𝒃

График функции имеет горизонтальную асимптоту y=2,
значит, k=2.
Ответ:2

16
22 слайд

9 задание. На рисунке изображен график функции f(x)= 𝒌𝒙+𝒂 𝒙+𝒃 . Найдите a
Решение.
Преобразуем данную функцию
f(x)= 𝒌𝒙+𝒂 𝒙+𝒃 = 𝒌𝒙+𝒌𝒃−𝒌𝒃+𝒂 𝒙+𝒃 = 𝒌(𝒙+𝒃)−𝒌𝒃+𝒂 𝒙+𝒃 =𝒌+ 𝒂−𝒌𝒃 𝒙+𝒃 .
Или
График функции имеет горизонтальную асимптоту y=2, значит, k=2.
График функции имеет вертикальную асимптоту x=3, значит, b= — 3.
По графику f(5)=3, тогда 3= 𝟐·𝟓+𝒂 𝟏−𝟑 , отсюда а=-4.
Ответ:-4
17
f(x)=𝒌+ 𝒂−𝒌𝒃 𝒙+𝒃
23 слайд

18
9 задание. На рисунке изображен график функции f(x)=b+ 𝒍𝒐𝒈 𝒂 x.Найдите значение х при котором f(x)=2.
Решение.
График функции f(x)= b+ 𝒍𝒐𝒈 𝒂 x получается сдвигом графика функции f(x)= 𝒍𝒐𝒈 𝒂 x. вдоль оси Оу на величину
|b| вверх, если b >0 и вниз если b <0.
По графику b = -2 и проходит через точку (3;-1).
-1= -2+ 𝒍𝒐𝒈 𝒂 𝟑, отсюда а=3.Значит,
f(x)= -2 +𝒍𝒐𝒈 𝟑 x, найдем х при котором f(x)=2.
2=-2 +𝒍𝒐𝒈 𝟑 x,
𝒍𝒐𝒈 𝟑 x=4, значит, х=81.
Ответ:81
24 слайд

19
9 задание. На рисунке изображен график функции f(x)= 𝒂 𝒙+𝒃 .Найдите значение х при котором f(-5).
Решение.
График функции f(x)= 𝒂 𝒙+𝒃 получается сдвигом графика функции f(x)= 𝒂 𝒙 вдоль оси Ох на величину |b| влево, если b>0 и вправо если b<0.
По графику b= —1 и проходит через точку (3;2).
𝟐= 𝒂 𝟐 отсюда а = 𝟐 .Значит,
f(-5)= 𝟐 −𝟓−𝟏 = 𝟏 𝟐 𝟔 = 𝟏 𝟖 =𝟎,𝟏𝟐𝟓
Ответ:0,125
25 слайд

9 задание. На рисунке изображён график функции вида f(x)= 𝒂 cos(bπx+c)+d, где числа 𝒂,b, c и d-целые. Найдите 𝒇 − 𝟖 𝟑 .
Решение.
По графику 𝒇 𝒎𝒂𝒙 =𝟏,𝒇 𝒎𝒊𝒏 =-3
d= 𝒇 𝒎𝒂𝒙 + 𝒇 𝒎𝒊𝒏 𝟐 = 𝟏−𝟑 𝟐 = -1. |a|= 𝒇 𝒎𝒂𝒙 − 𝒇 𝒎𝒊𝒏 𝟐 = 𝟏+𝟑 𝟐 =2.
По графику 𝒂 =-2, c=0, T=2
T= 𝟐𝝅 𝒃𝝅 = 𝟐 𝒃 , то есть 𝟐 𝒃 =2, отсюда b=1
f(x)=-2cosπx-1,
f − 𝟖 𝟑 =f 𝟖 𝟑 =f 𝟔 𝟑 + 𝟐 𝟑 =𝒇 𝟐+ 𝟐 𝟑 =f 𝟐 𝟑 ,
f 𝟐 𝟑 =-2cosπ· 𝟐 𝟑 -1 = -2cos 𝟐 𝟑 π-1 = -2cos π− π 𝟑 -1= 2cos π 𝟑 −1= 0.
Ответ:0
20
26 слайд

1.ПРОЕКТ. Демонстрационный вариант
контрольных измерительных материалов
единого государственного экзамена 2022 года
по МАТЕМАТИКЕ. Профильный уровень. ФИПИ

2.Статград. Новое ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.

3.Образовательный портал «СДАМ ГИА» Математика профильного уровня.
27 слайд

Хорошие результаты ЕГЭ и ОГЭ по математике позволяют выпускникам школы успешно решить свои жизненные планы.
29 слайд

Мастер-класс был актуальным, полезным, интересным
Ничего нового на мастер- классе я для себя не узнал
Нарисуйте пятиугольгик или треугольник
32 слайд

Спасибо вам за то, что вы есть…

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 153 824 материала в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

20.10.2021
442
9

20.10.2021
1803
21

20.10.2021
262
3

20.10.2021
303
1

20.10.2021
266
4

Вам будут интересны эти курсы:

Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

Источник

Слайд 1

«ЗАДАНИЕ № 9 В ЕГЭ 2022 ПРОФИЛЬНОГО УРОВНЯ» Зялалова З.А учитель математики МБОУ ВСОШ №4

Слайд 2

Задание №9 . «Анализ графиков» Прямая Парабола Гипербола Логарифмическая и показательная функции Иррациональные функции Тригонометрические функции

Слайд 3

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1

Слайд 4

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:

Слайд 5

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:

Слайд 6

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:

Слайд 7

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:

Слайд 8

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:

Слайд 9

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:

Слайд 10

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение:

Слайд 11

На рисунке изображён график функции f(x)= kx + b . Найдите f( 12 ) . Задача №1 Решение: Ответ: 4.

Слайд 12

По графику функции f(x)= kx + b найдите х, при котором f( х ) = − 13,5. Задача №2

Слайд 13