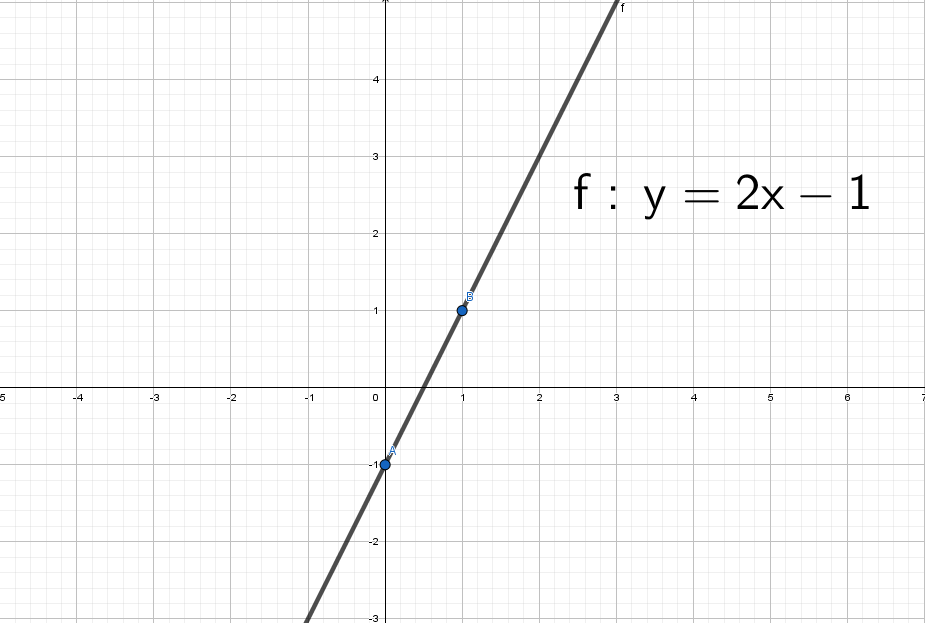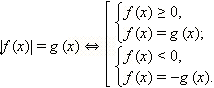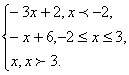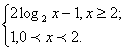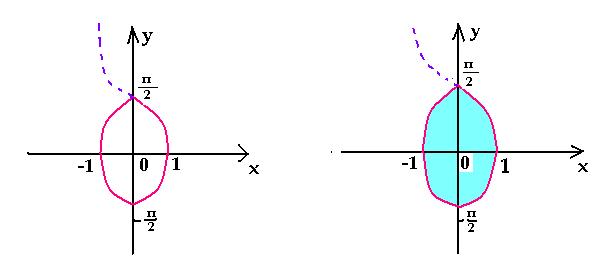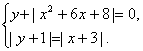Пошаговое построение графиков.
«Навешивание» модулей на прямые, параболы, гиперболы.
Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.
Для понимания друг друга введу немного «обзываний» системы координат:
Для начала построим график прямой y = 2x − 1.
Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую.
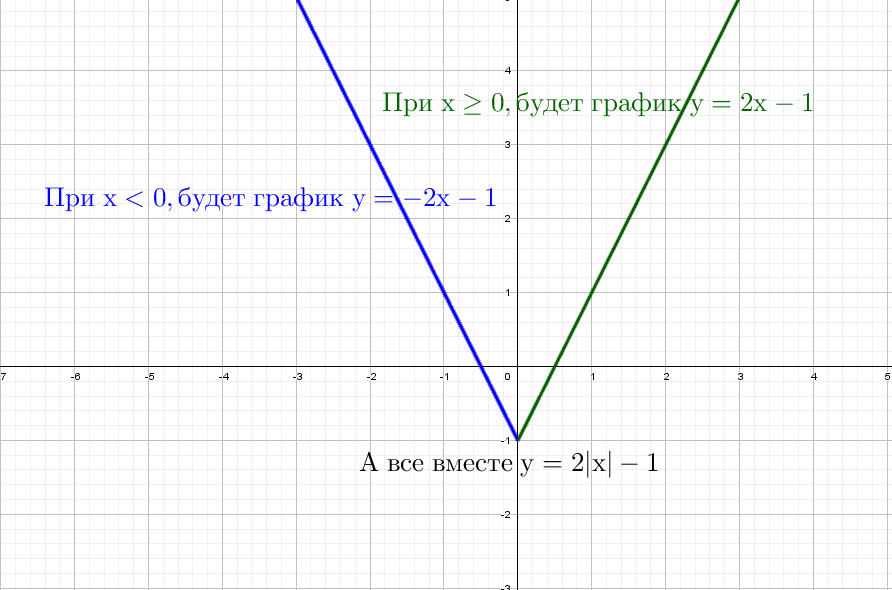
Возьмем значение X = 0 и Х = 1 и подставим в выражение y = 2x − 1, тогда соответственно Y = − 1 и Y = 1
Через данные две точки А = (0; −1) и B = (1; 1) проводим единственную прямую:
А если теперь добавить модуль y = |2x − 1|.
Модуль — это всегда положительное значение, получается, что «y» должен быть всегда положительным.
Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю (как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).
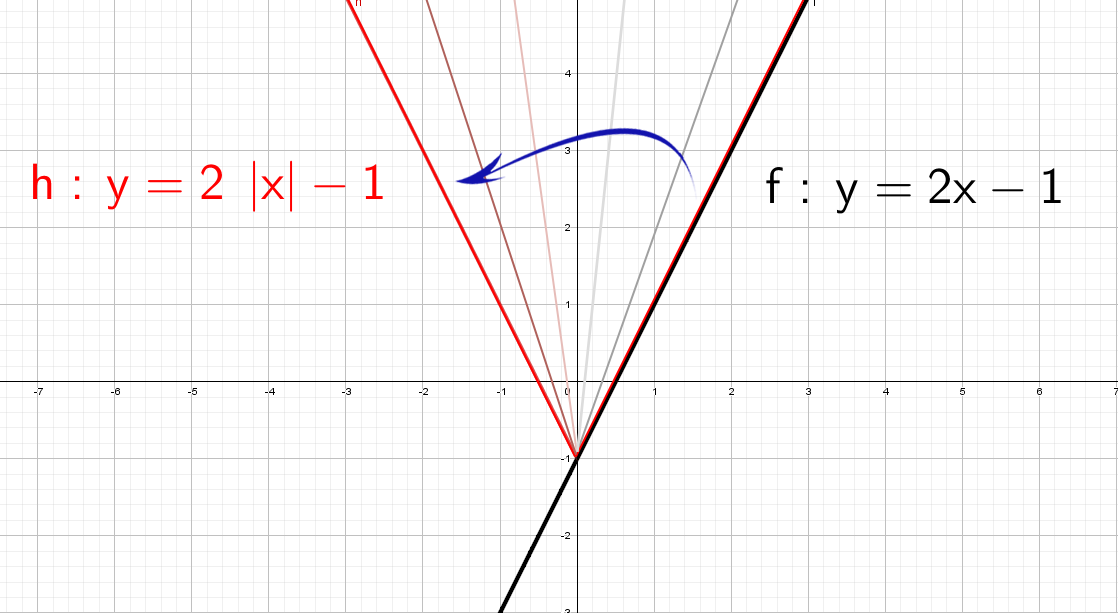
Красота! А как же будет выглядеть график, если надеть модуль только на «х»: y = 2|x| − 1?
Одна строчка рассуждений и рисуем:
Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.
Здесь отражаем относительно оси «y». Такая же галочка, только теперь через другую ось.
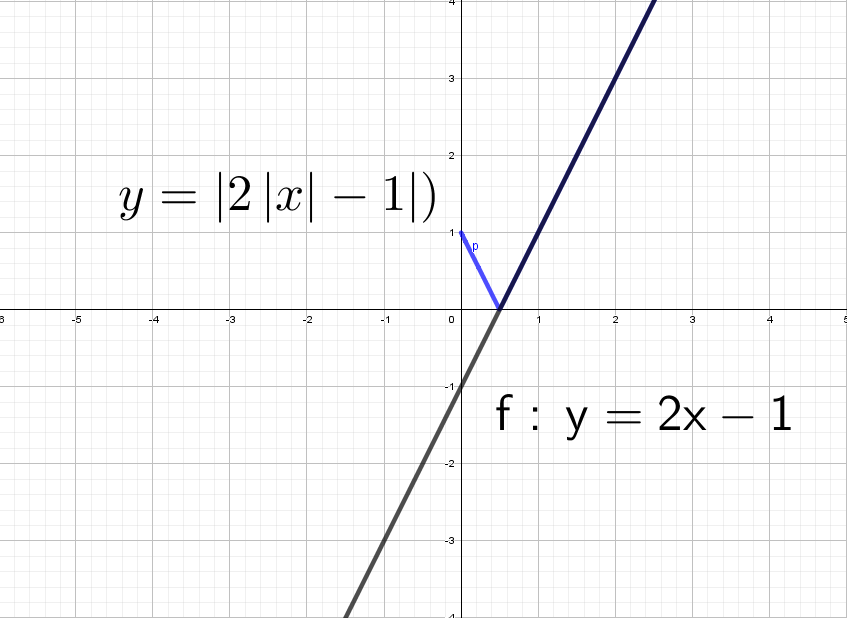
Смертельный номер: y = |2|x| − 1|.
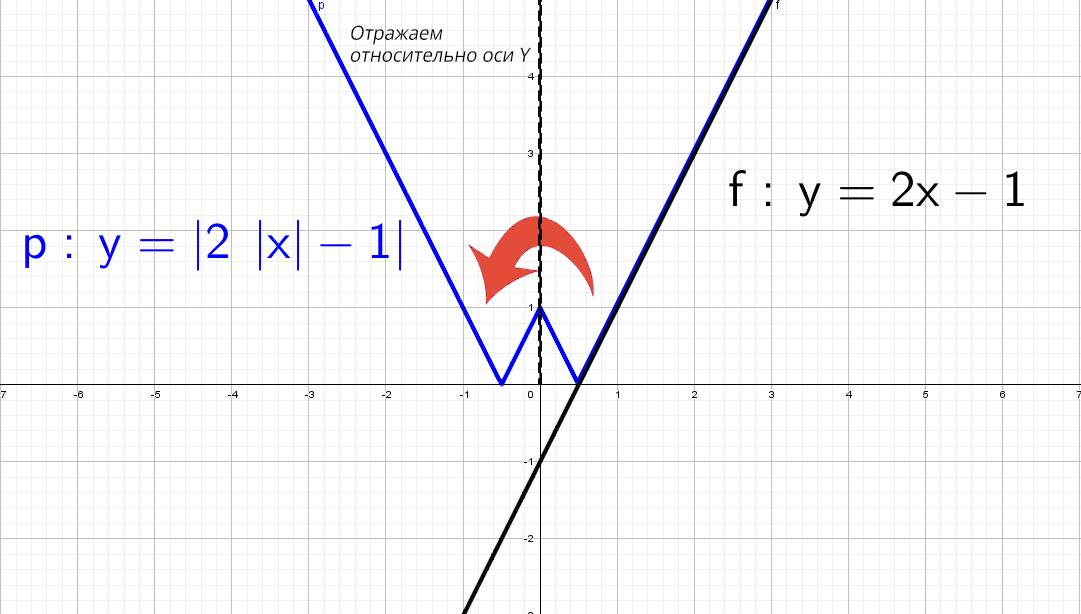
Черную прямую y = 2x − 1 отражаем относительно оси Х, получим y = |2x − 1|. Но мы выяснили, что модуль на х влияет только на левую часть.
В правой части: y = |2x − 1| и y = |2|x| − 1| идентичны!
А после этого отражаем относительно оси «y» то, что мы получили справа налево:
Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках, значит делаем по аналогии.
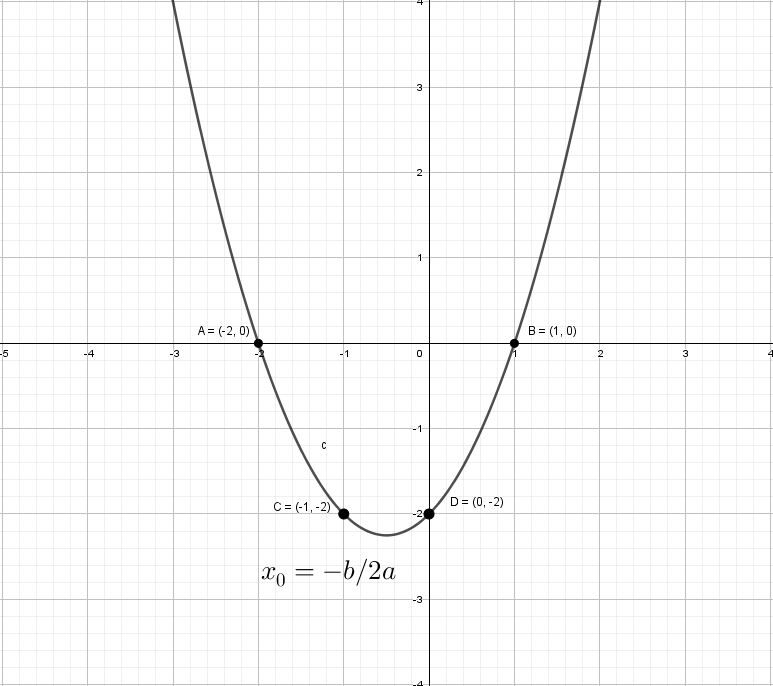
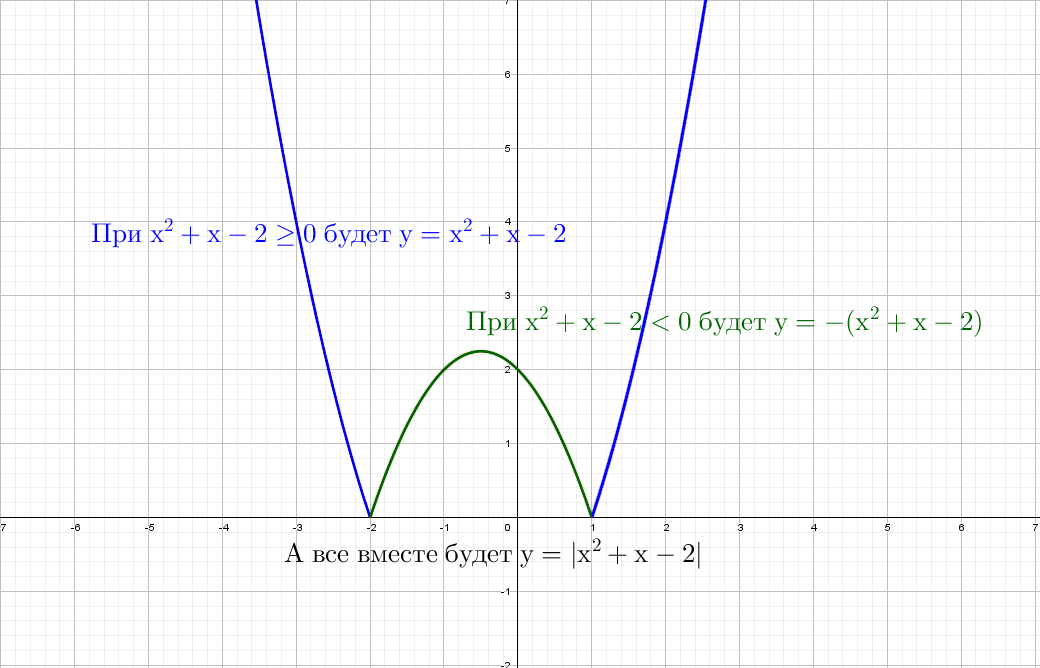
Разберем по винтикам параболу y = x² + x − 2. Точки пересечения с осью «x» получим с помощью дискриминанта: x₁ = 1 и x₂ = -2.
Можно найти вершину у параболы и взять пару точек для точного построения.
А как будет выглядеть график: y = |x²| + x − 2? Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.
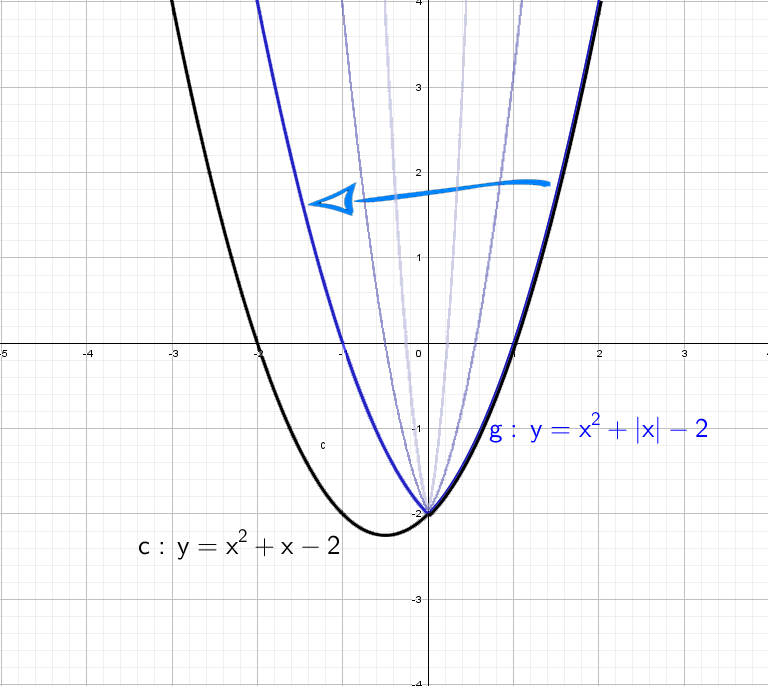
При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:
А дальше что мелочиться: рассмотри сразу остальные графики с модулем!
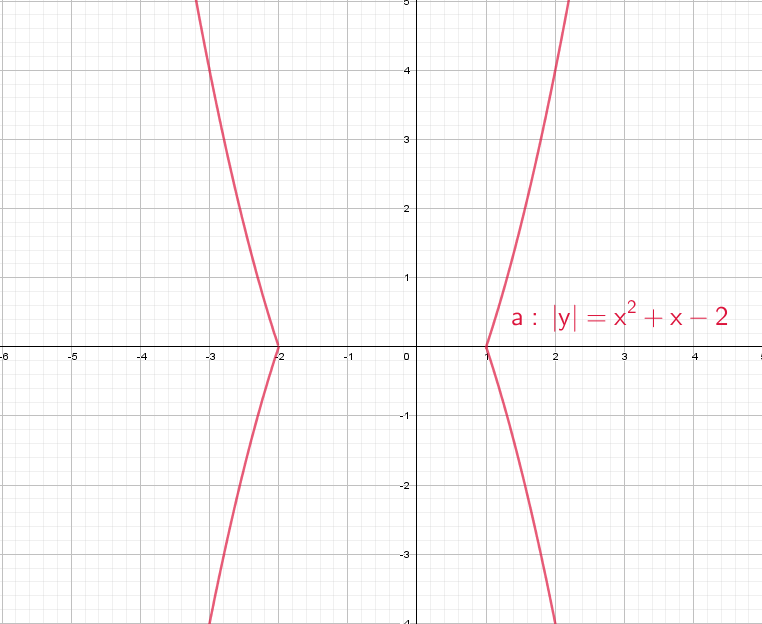
Следующий смертельный номер: |y| = x² + x − 2, подумай хорошенько, а еще лучше попробуй нарисовать сам.
При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!
Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.
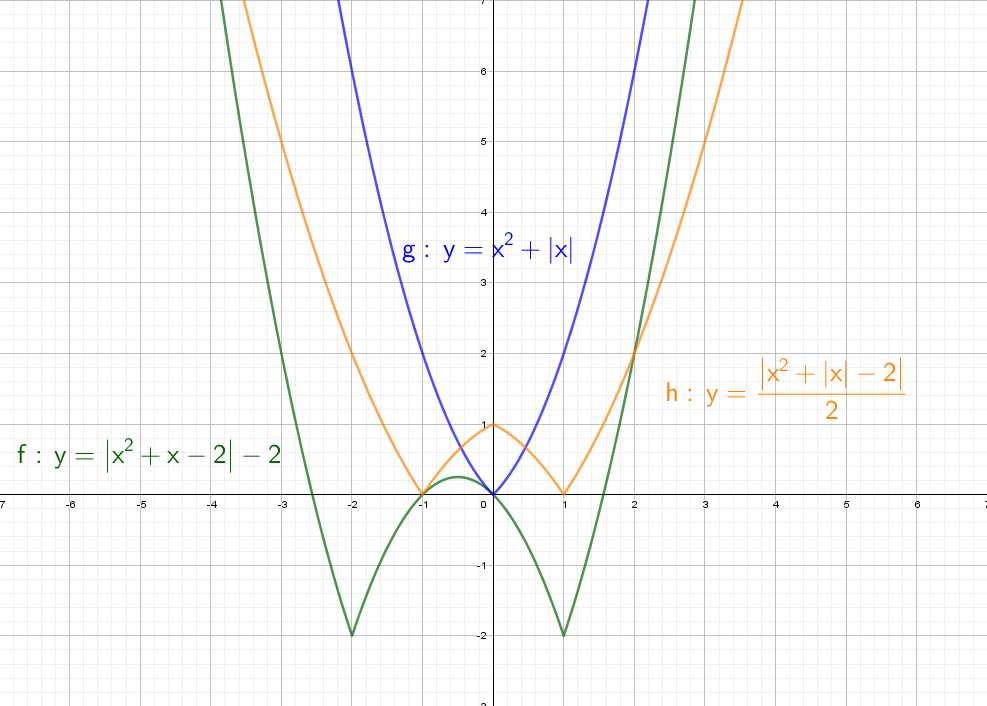
А теперь сразу комбо:
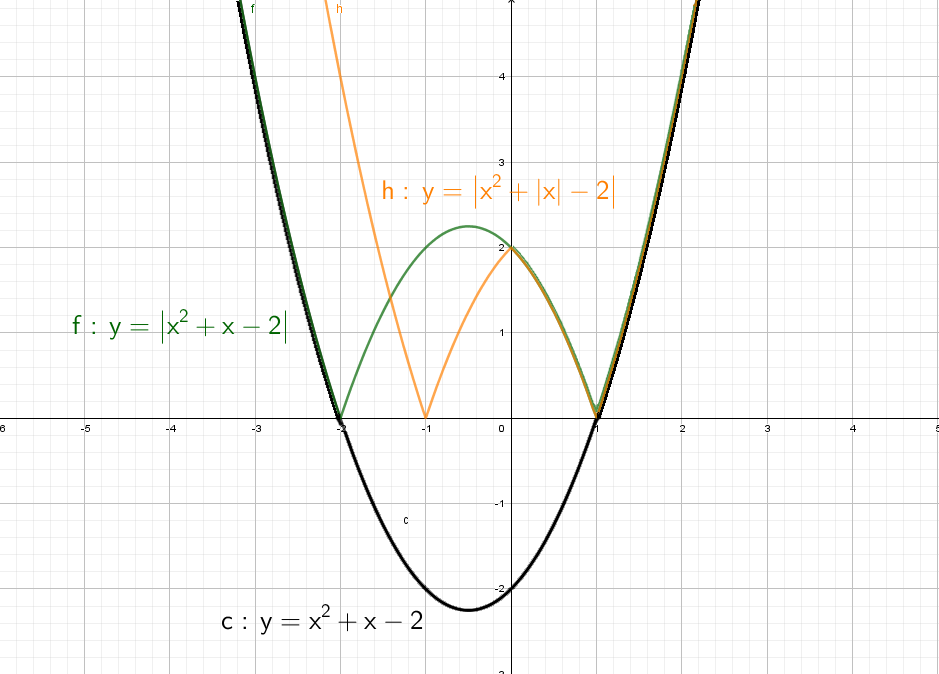
Cиний: похож на y = x² + |x| − 2, только поднят вверх. Строим график в правой части, а затем отражаем через ось Y влево.
Оранжевый: строим в правой части и отражаем относительно оси Х. Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет «шире», расходится в бока он быстрее остальных.
Зеленый: Так же начинаем с правой части и отражаем относительно оси оси Y. Получается график y = |x² + x − 2|, но еще есть −2, поэтому опустим график на 2 вниз. Теперь параболы как бы отражается относительно Y = − 2.
Легкий и средний уровень позади, и настала пора выжать концентрацию на максимум, потому что дальше тебя ждут гиперболы, которые частенько встречаются во второй части ЕГЭ и ОГЭ.
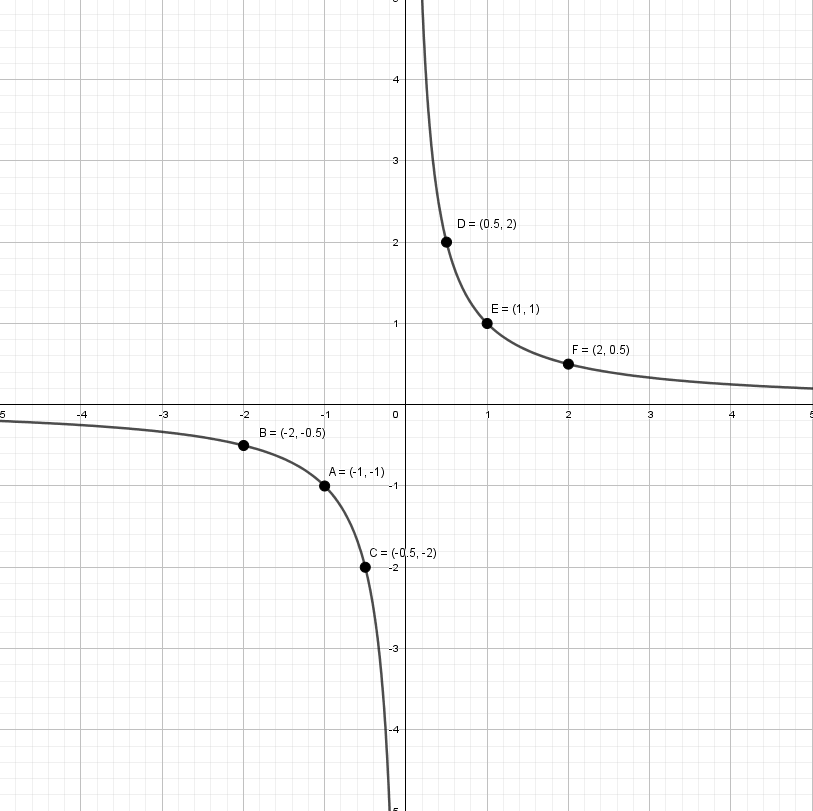
y = 1/x — простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:
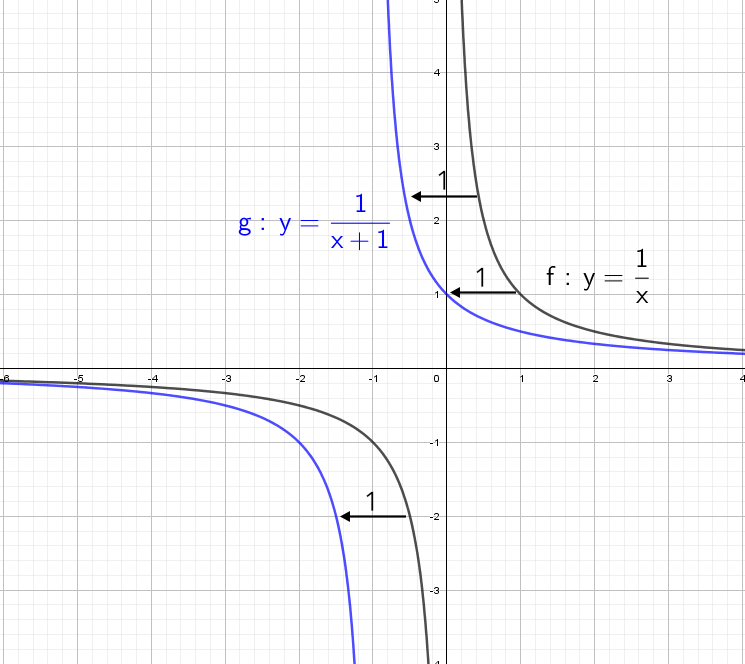
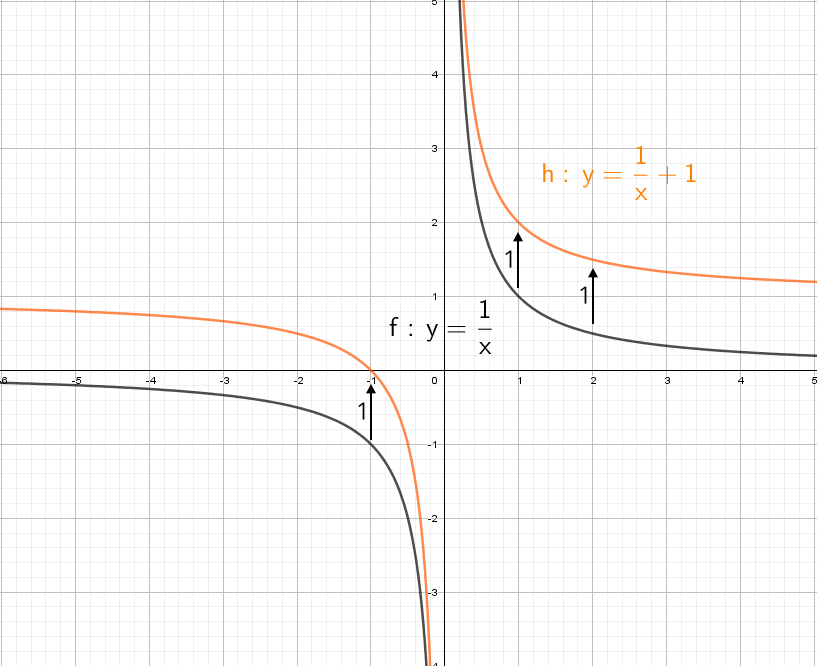
А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:
А что будет, если мы добавим в знаменателе «−1»? График сдвинется вправо на единицу.
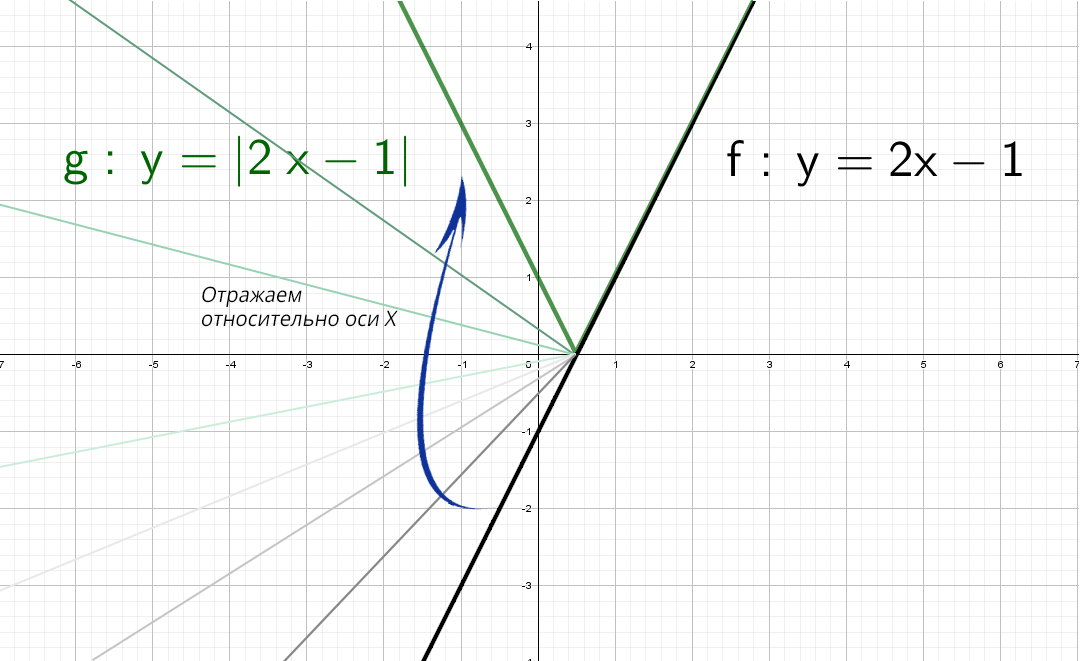
А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!
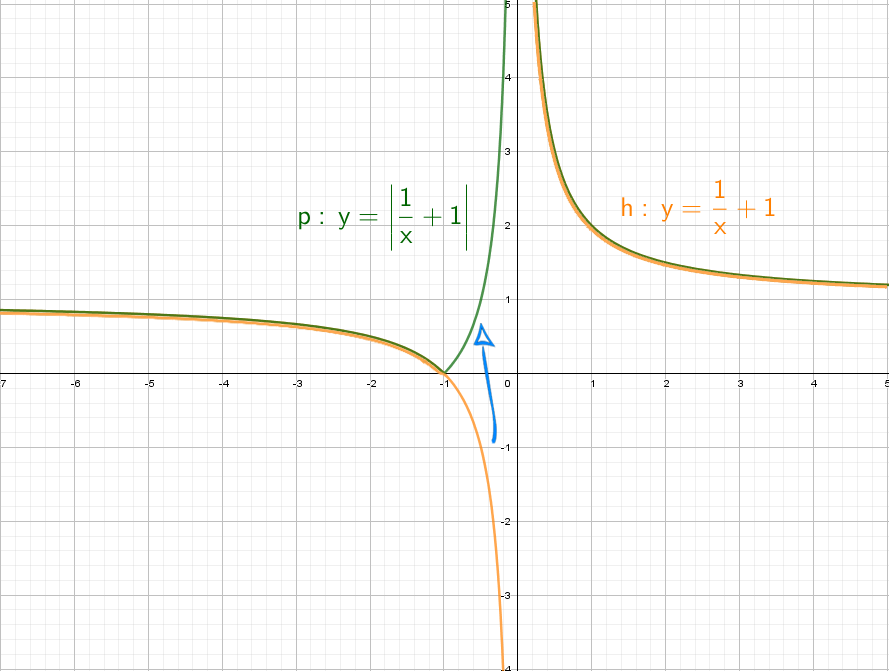
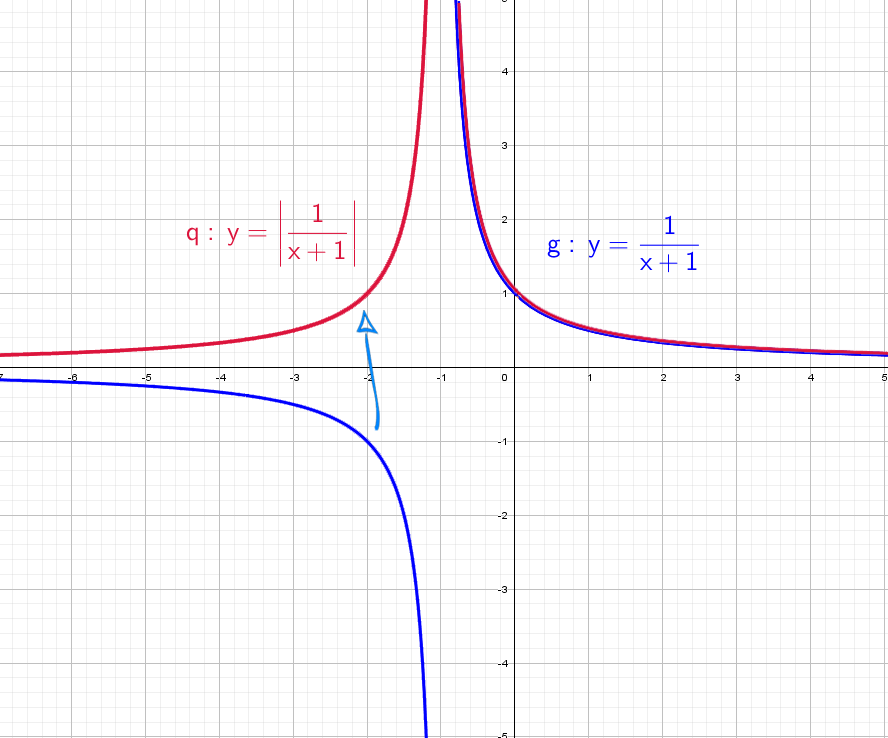
Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.
Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.
Можно придумывать массу вариантов, но общий принцип остается для любого графика. Принципы повторим в выводах в конце статьи.
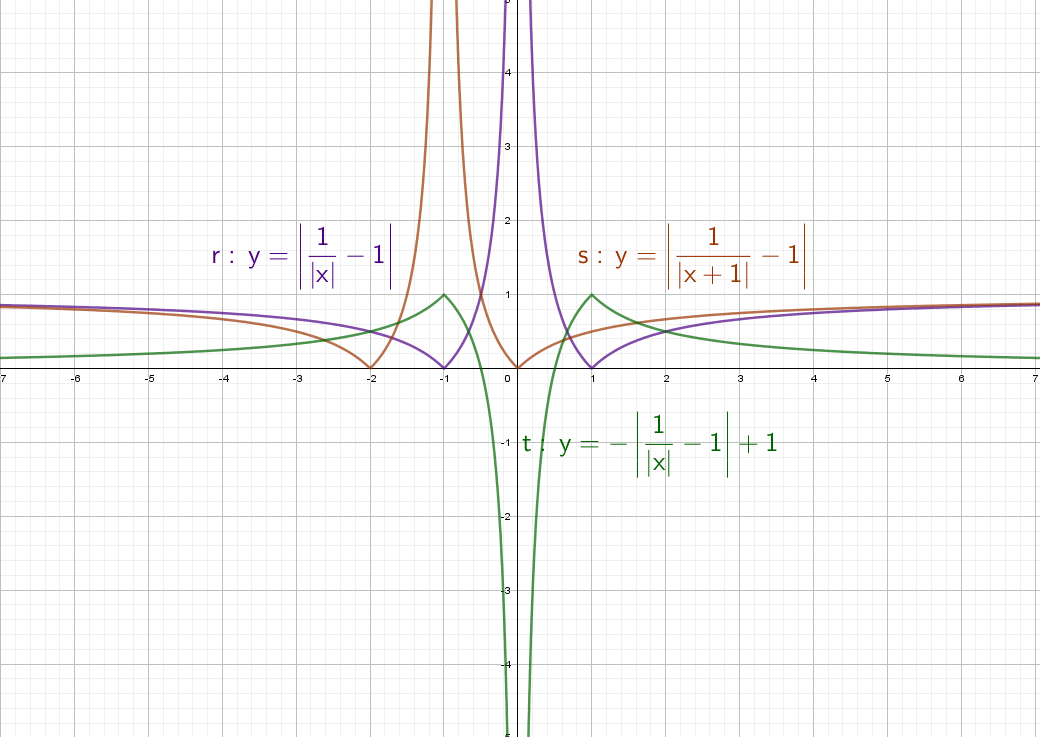
Фиолетовый: Вычитаем из дроби −1 и сдвигаем график вниз на единицу. Ставим модуль − отражаем все, что снизу вверх.
Оранжевый: Ставим +1 в знаменателе и график смещается влево на единицу. Вычитаем из дроби −1 и сдвигаем график вниз на единицу. А после этого ставим модуль − отражаем все, что снизу вверх.
Зеленый: Сначала получим фиолетовый график. После этого ставим «−» и отражаем график по горизонтали. Сгибаем лист по оси Х и переводим его вниз. Остается добавить +1, это значит, что его нужно поднять вверх на единицу.
Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определению:
И построить график, разбив его на кусочно-заданные функции.
Например для прямой:
Для параболы с одним модулем будет два кусочно-заданных графика:
C двумя модулями кусочно-заданных графиков будет четыре:
Выводы:
- Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
- Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
- Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль.
- Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:
- Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
- Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
- Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.
- Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.
Будь в курсе новых статеек, видео и легкого математического юмора.
Тема 10.
Задачи на свойства графиков функций
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
задачи на свойства графиков функций
10.01График линейной функции (прямая)
10.02График квадратичной функции (парабола)
10.03График корня
10.04График обратной пропорциональности (гипербола)
10.05График показательной функции (экспонента)
10.06График логарифмической функции
10.07График модуля
10.08Графики синуса и косинуса
10.09Комбинации нескольких графиков
Решаем задачи
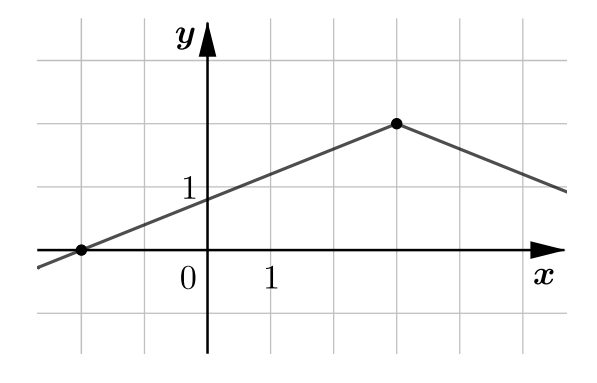
На рисунке изображена часть графика функции Найдите
Показать ответ и решение
Решим задачу методом подстановки. График функции проходит через точки
и
. Если график функции
проходит через какую-то точку, то ее координаты обращают уравнение функции в верное равенство, значит, мы имеем
систему:
Теперь мы восстановили функию , она имеет вид
На рисунке изображен график функции
Найдите
Показать ответ и решение
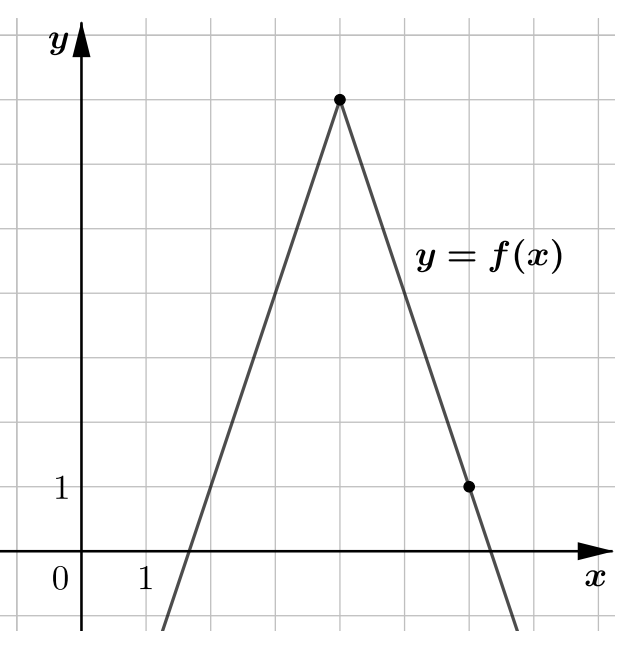
На рисунке видно, что вершина «уголка» модуля имеет координаты Также по картинке видно, что ветви уголка
направлены вниз, значит, функция имеет вид
При этом По картинке видно, что в точке
значение функции равно 0. Для того, чтобы попасть в точку
из вершины с координатами
нужно сместиться на 5 влево и на 2 вниз. Тогда понятно, что перед нами график
функции вершину которого сместили из точки
в точку
Значит, теперь мы полностью восстановили
нашу функцию, она имеет вид
Тогда окончательно имеем:
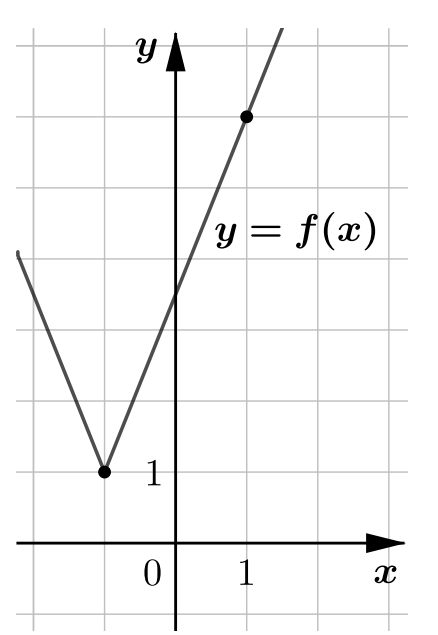
На рисунке изображен график функции
Найдите
Показать ответ и решение
На рисунке изображен «уголок модуля» — график функции
Коэффициент отвечает за угол наклона прямых, содержащих ветви графика. Он равен тангенсу угла наклона правой
ветви.
Коэффициент отвечает за сдвиг вершины уголка по оси
он равен координате вершины уголка модуля по оси
абсцисс.
Коэффициент отвечает за сдвиг вершины уголка по оси
он равен координате вершины уголка модуля по оси
ординат.
На рисунке видно, что правая ветвь графика проходит через точки и
Если прямая проходит через точки
и
то тангенс угла ее наклона равен
Вершина уголка модуля находится в точке значит,
и
Тогда
На рисунке изображен график функции
Найдите
Показать ответ и решение
На рисунке изображен «уголок модуля» — график функции
Коэффициент отвечает за угол наклона прямых, содержащих ветви графика. Он равен тангенсу угла наклона правой
ветви.
Коэффициент отвечает за сдвиг вершины уголка по оси
он равен координате вершины уголка модуля по оси
абсцисс.
Коэффициент отвечает за сдвиг вершины уголка по оси
он равен координате вершины уголка модуля по оси
ординат.
На рисунке видно, что правая ветвь графика проходит через точки и
Если прямая проходит через точки
и
то тангенс угла ее наклона равен
Вершина уголка модуля находится в точке значит,
и
Тогда
На рисунке изображен график функции
Найдите .
Показать ответ и решение
На рисунке изображен «уголок модуля» — график функции
Коэффициент отвечает за угол наклона прямых, содержащих ветви графика. Он равен тангенсу угла наклона правой
ветви.
Коэффициент отвечает за сдвиг вершины уголка по оси
, он равен координате вершины уголка модуля по оси абсцисс.
Коэффициент отвечает за сдвиг вершины уголка по оси
, он равен координате вершины уголка модуля по оси
ординат.
На рисунке видно, что правая ветвь графика проходит через точки и
. Если прямая проходит через точки
и
, то тангенс угла ее наклона равен
Вершина уголка модуля находится в точке , значит,
и
.
Тогда
На рисунке изображен график функции Найдите
Показать ответ и решение
На рисунке изображен «уголок модуля» — график функции
Коэффициент отвечает за угол наклона прямых, содержащих ветви графика. Он равен тангенсу угла наклона правой
ветви.
Коэффициент отвечает за сдвиг вершины уголка по оси
, он равен координате вершины уголка модуля по оси абсцисс.
Коэффициент отвечает за сдвиг вершины уголка по оси
, он равен координате вершины уголка модуля по оси
ординат.
На рисунке видно, что правая ветвь графика проходит через точки и
. Если прямая проходит через точки
и
, то тангенс угла ее наклона равен
Вершина уголка модуля находится в точке , значит,
и
.
Тогда
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 62 1–20 | 21–40 | 41–60 | 61–62
Добавить в вариант
Найдите все значения a, при каждом из которых уравнение
имеет ровно два различных корня.
Источник: ЕГЭ по математике. Основная волна 07.06.2021. Урал, Задания 18 ЕГЭ–2021
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 310. (Часть C)
Найдите все значения a, при каждом из которых уравнение
имеет ровно два различных корня.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Санкт-Петербург, Москва, другие города. Вариант 359 (C часть), Задания 18 ЕГЭ–2021
Дано уравнение
а) Решите уравнение.
б) Найдите его корни, принадлежащие отрезку
Источник: А. Ларин: Тренировочный вариант № 165.
Найдите все корни уравнения sin(2x) = 1, удовлетворяющие неравенству
Источник: А. Ларин: Тренировочный вариант № 130.
Найти все значения параметра а при каждом из которых уравнение имеет ровно два решения.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Разные задачи, Задания 18 ЕГЭ–2021
Решите уравнение
Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Сибирь. Вариант 302., Задания 18 (С6) ЕГЭ 2013
Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 402.
Найдите все значения a, при каждом из которых уравнение
имеет единственный корень.
Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Найдите все значения параметра a, при каждом из которых уравнение
имеет единственное решение. Найдите это решение для каждого значения a.
Найти все значения a, при каждом из которых уравнение
имеет единственный корень.
Источник: ЕГЭ по математике 23.04.2013. Досрочная волна. Запад. Вариант 1.
Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 402., Задания 18 (С6) ЕГЭ 2013
Известно, что значение параметра а таково, что система уравнений
имеет единственное решение. Найдите это значение параметра a и решите систему при найденном значении параметра.
Источник: ЕГЭ по математике 2021 года. Досрочная волна., Задания 18 ЕГЭ–2021
Источник/автор: Некрасов В. Б., Гущин Д. Д. «Просвещение», 2010; Гущин Д. Д. «Учительская газета», 2013; ЕГЭ по математике − 2021
Найдите все значения a, при каждом из которых уравнение либо имеет единственное решение, либо не имеет решений.
Найдите все значения при каждом из которых уравнение
либо имеет единственное решение, либо не имеет решений.
Найдите все значения параметра при каждом из которых уравнение
имеет единственное решение.
Найдите это решение для каждого значения
Найдите все значения параметра a, при каждом из которых уравнение
имеет единственное решение. Найдите это решение для каждого значения a.
Всего: 62 1–20 | 21–40 | 41–60 | 61–62
Знак модуля, пожалуй, одно из самых интересных явлений в математике. В связи с этим у многих школьников возникает вопрос, как строить графики функций, содержащих модуль. Давайте подробно разберем этот вопрос.
1. Построение графиков функций, содержащих модуль
Пример 1.
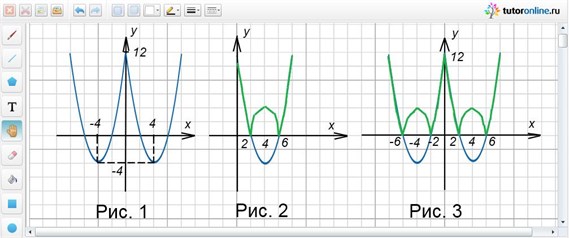
Построить график функции y = x2 – 8|x| + 12.
Решение.
Определим четность функции. Значение для y(-x) совпадает со значением для y(x), поэтому данная функция четная. Тогда ее график симметричен относительно оси Oy. Строим график функции y = x2 – 8x + 12 для x ≥ 0 и симметрично отображаем график относительно Oy для отрицательных x (рис. 1).
Пример 2.
Следующий график вида y = |x2 – 8x + 12|.
– Какова область значений предложенной функции? (y ≥ 0).
– Как расположен график? (Над осью абсцисс или касаясь ее).
Это значит, что график функции получают следующим образом: строят график функции y = x2 – 8x + 12, оставляют часть графика, которая лежит над осью Ox, без изменений, а часть графика, которая лежит под осью абсцисс, симметрично отображают относительно оси Ox (рис. 2).
Пример 3.
Для построения графика функции y = |x2 – 8|x| + 12| проводят комбинацию преобразований:
y = x2 – 8x + 12 → y = x2 – 8|x| + 12 → y = |x2 – 8|x| + 12|.
Ответ: рисунок 3.
Рассмотренные преобразования справедливы для всех видов функций. Составим таблицу:
|
Функция |
Преобразование |
|
f(|x|) |
1) Для x ≥ 0, y = f(x) 2) Для x < 0 – преобразование симметрии относительно Oy графика y = f(x), для x ≥ 0 симметричные части графика из правой полуплоскости в левую |
|
|f(x)| |
1) Для f(x) ≥ 0, |f(x)| = f(x) 2) Для f(x) < 0, |f(x)| = -f(x) Симметричное отображение части графика из нижней полуплоскости в верхнюю относительно Ox |
|
|f(|x|)| |
f(x) → f(|x|) → |f(|x|)|. |
2. Построение графиков функций, содержащих в формуле «вложенные модули»
Мы уже познакомились с примерами квадратичной функции, содержащей модуль, а так же с общими правилами построения графиков функций вида y = f(|x|), y = |f(x)| и y = |f(|x|)|. Эти преобразования помогут нам при рассмотрении следующего примера.
СЛОЖНА-А-А 🙀 Ты же знаешь, что если не разобраться в теме сейчас, то потом придется исправлять оценки. Беги на бесплатное онлайн-занятие с репетитором (подробности тут + 🎁).
Пример 4.
Рассмотрим функцию вида y = |2 – |1 – |x|||. Выражение, задающее функцию, содержит «вложенные модули».
Решение.
Воспользуемся методом геометрических преобразований.
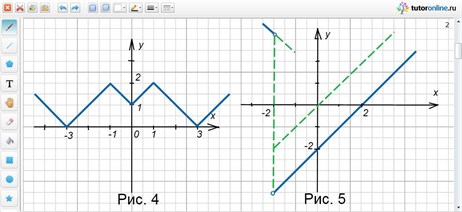
Запишем цепочку последовательных преобразований и сделаем соответствующий чертеж (рис. 4):
y = x → y = |x| → y = -|x| → y = -|x| + 1 → y = |-|x| + 1|→ y = -|-|x| + 1|→ y = -|-|x| + 1| + 2 → y = |2 –|1 – |x|||.
Рассмотрим случаи, когда преобразования симметрии и параллельного переноса не являются основным приемом при построении графиков.
Пример 5.
Построить график функции вида y = (x2 – 4)/√(x + 2)2.
Решение.
Прежде чем строить график, преобразуем формулу, которой задана функция, и получим другое аналитическое задание функции (рис. 5).
y = (x2 – 4)/√(x + 2)2 = (x– 2)(x + 2)/|x + 2|.
Раскроем в знаменателе модуль:
При x > -2, y = x – 2, а при x < -2, y = -(x – 2).
Область определения D(y) = (-∞; -2)ᴗ(-2; +∞).
Область значений E(y) = (-4; +∞).
Точки, в которых график пересекает с оси координат: (0; -2) и (2; 0).
Функция убывает при всех x из интервала (-∞; -2), возрастает при x от -2 до +∞.
Здесь нам пришлось раскрывать знак модуля и строить график функции для каждого случая.
Пример 6.
Рассмотрим функцию y = |x + 1| – |x – 2|.
Решение.
Раскрывая знак модуля, необходимо рассмотреть всевозможную комбинацию знаков подмодульных выражений.
Возможны четыре случая:
{x + 1 – x + 2 = 3, при x ≥ -1 и x ≥ 2;
{-x – 1 + x – 2 = -3, при x < -1 и x < 2;
{x + 1 + x – 2 = 2x — 1, при x ≥ -1 и x < 2;
{-x – 1 – x + 2 = -2x + 1, при x < -1 и x ≥ 2 – пустое множество.
Тогда исходная функция будет иметь вид:
{3, при x ≥ 2;
y = {-3, при x < -1;
{2x – 1, при -1 ≤ x < 2.
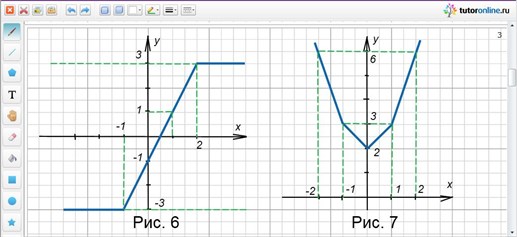
Получили кусочно-заданную функцию, график которой изображен на рисунке 6.
3. Алгоритм построения графиков функций вида
y = a1|x – x1| + a2|x – x2| + … + an|x – xn| + ax + b.
В предыдущем примере было достаточно легко раскрыть знаки модуля. Если же сумм модулей больше, то рассмотреть всевозможные комбинации знаков подмодульных выражений проблематично. Как же в этом случае построить график функции?
Заметим, что графиком является ломаная, с вершинами в точках, имеющих абсциссы -1 и 2. При x = -1 и x = 2 подмодульные выражения равны нулю. Практическим путем мы приблизились к правилу построения таких графиков:
Графиком функции вида y = a1|x – x1| + a2|x – x2| + … + an|x – xn| + ax + b является ломаная с бесконечными крайними звеньями. Чтобы построить такую ломаную, достаточно знать все ее вершины (абсциссы вершин есть нули подмодульных выражений) и по одной контрольной точке на левом и правом бесконечных звеньях.
Задача.
Построить график функции y = |x| + |x – 1| + |x + 1| и найти ее наименьшее значение.
Решение:
Нули подмодульных выражений: 0; -1; 1. Вершины ломаной (0; 2); (-1; 3); (1; 3). Контрольная точка справа (2; 6), слева (-2; 6). Строим график (рис. 7). min f(x) = 2.
Молодец! Раз ты дочитал это до конца, вероятно, ты все отлично усвоил. Но если вдруг что-то еще непонятно — попробуй онлайн-занятие с репетитором (подробности тут + 🎁).
Остались вопросы? Не знаете, как построить график функции с модулем?
Чтобы получить помощь репетитора – зарегистрируйтесь.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Определение модуля
Алгебрагическое определение: | x |
=
Геометрическое определение: модулем
числа называется расстояние от точки,
изображающей это число, до начала отсчета.
Понятие модуля впервые вводится в 6 классе, в 7
классе рассматривается линейная функция и ее
график и уже можно показывать построение
несложных графиков функций, содержащих модуль.
Далее, по мере изучения различных функций, их
свойств, каждую такую тему можно заканчивать
рассмотрением более сложных графиков, в том
числе с модулем. В этой статье рассматриваются
основные приемы построения графиков таких
функций.
I. На алгебрагическом определении основан метод
«раскрытия модуля на промежутках».
Например: | x + 2 | = | x + 2 | =
метод можно применять при построении графиков
функций, содержащих один или более модулей.
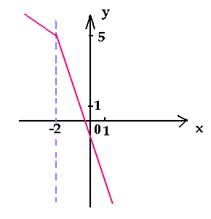
Например, построим график функции у = | x + 2 | –
2x + 1 , предварительно упростив ее.
у = у
=
Если модулей несколько, то каждый из них
раскрываем на промежутках относительно точек,
обращающих каждый из них в нуль. Например,
построим график функции у = | 3 – x | – x
+ | x + 2 | + 1.
1. Если х < – 2, то у = 3 – х – х
– (х + 2) + 1, у = – 3х + 2.
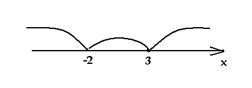
< х < 3, то у = 3 – х – х + х
+ 2 + 1, у = – х + 6.
3. Если х > 3, то у = – (3 – х) – х
+ х + 2 + 1, у = х.
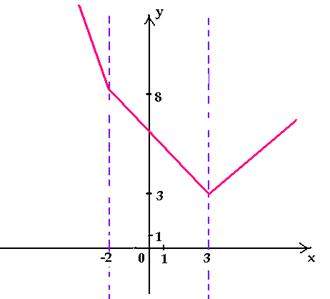
записываем как кусочно-заданную:
у =
Подобно тому, как числовая прямая точками – 2 и 3
разбивается на промежутки, координатная
плоскость прямыми х = – 2 и х = 3
разбивается на части («полосы»), в каждой из
которых строим свой график. Заметим, что данная
функция непрерывна, поэтому на «границах» части
графика должны соединяться.
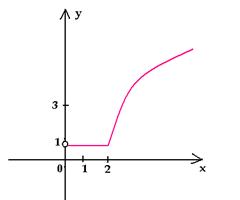
метод можно применять к функциям разных видов.
Например, построим график функции у = | log2
x – 1 | – log0,5 x.
Заметим, что х > 0.
1. Пусть log2x – 1 > 0, log2x >
1, x > 2, тогда у = log2 x – 1 +
log2 x; y = 2 log2 x – 1.
2. Пусть log2 x – 1 < 0, 0 < x < 2,
тогда у = – log2 x + 1 + log2 x; y
= 1.
Запишем функцию как кусочно-заданную:
у =
III. Рассмотрим некоторые частные случаи
функций, содержащих модуль.
1) у = | f(x) |.
По определению модуля имеем: | f(x) | =
Таким образом , для того, чтобы построить график
такой функции, необходимо взять часть графика,
лежащую не ниже оси абсцисс, а часть графика,
лежащую ниже этой оси отобразить относительно
нее в верхнюю полуплоскость. (Заметим, что «–»,
стоящий перед функцией означает симметричное
отображение графика относительно оси абсцисс).
Например, построим график функции у = | x2
– 2х – 3 |.
Построим сначала график функции у = х2
– 2х – 3. Графиком этой функции является
парабола, ветви которой направлены вверх.
Координаты ее вершины: х = 1, у = – 4. Точки
пересечения параболы с осями координат: (0; – 3); (–
1; 0); (3; 0). Далее выполняем отображение части
графика, лежащей в нижней полуплоскости,
относительно оси абсцисс.
2) у = f(| x |). Используем определение модуля: f(|
x |) =
Чтобы построить график такой функции строим
график функции у = f(x) и берем ту его
часть, где х > 0 (в правой полуплоскости).
Затем эту часть симметрично отображаем в левую
полуплоскость, где х < 0. (Заметим, что
построение графика функции f(– x) и
состоит в отображении части графика, лежащей в
правой полуплоскости в левую относительно оси
ординат).
Например, построим график функции у = х2
– 2| х | – 3. Сначала строим график функции у
= х2 – 2х – 3, далее выполняем
указанные преобразования.
3) Построим график функции y = | f(| x
|)|, например, y = | x2 – 2| х | – 3 |,
выполним последовательно преобразования,
рассмотренные в пунктах 2 и 1.
4. Рассмотрим зависимость | y | = f(x).
Ее нельзя назвать функцией, так как не
выполняется условие: каждому значению х должно
соответствовать единственное значение у.
Рассмотрим построение графика такой
зависимости (можно говорить «графика
уравнения»). Используем определение модуля: у
= f(x), если у > 0, – у = f(x),
y = – f(x), если у < 0
Получаем, чтобы построить такой график, сначала
строим график функции у = f(x) и
берем ту его часть, которая лежит в верхней
полуплоскости, где у > 0; чтобы
построить график в нижней полуплоскости (где у
< 0), нужно построенную часть отобразить
симметрично относительно оси абсцисс (знак «–»
перед функцией и означает такое отображение)
Например, построим график уравнения | y | = x2
– 2х – 3
Заметим, что графики, не относящиеся к
рассмотренным частным случаям, следует строить «
раскрывая модули на промежутках».
| x |
1 |
0 |
– 1 |
|
y |
0 |
|
|
IV. Приведем некоторые примеры
1. Построим график уравнения | y | = arccos| x
|.
2. Графическим способом можно решать и
неравенства с двумя переменными. Например,
решением неравенства | y | < arccos| x |
являются координаты точек закрашенной части
плоскости, включая границы.
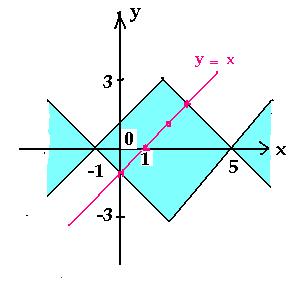
Решим еще одно задание, предлагавшееся на ЕГЭ:
найти все целочисленные решения неравенства | y
| < | | x – 2 | – 3 | (х0; у0),
для которых х0 = у0. Построим
сначала график уравнения | y | = | | x – 2 | –
3 |. Решением данного неравенства будут являться
координаты точек закрашенной части плоскости,
включая границы.
Пары чисел (х0; у0),
являющиеся решениями неравенства, для которых y0
= x0, являются координатами точек,
лежащих на прямой у = х. Выберем точки с
целыми координатами: (0; – 1); (1; 0); (2; 1); (3; 2), они и
будут являться решениями данной задачи.
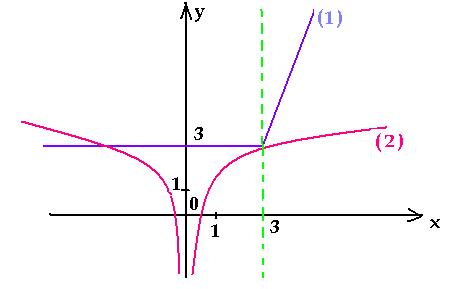
3. Определить, сколько корней имеет уравнение | 3
– x | + log3| x | = 2 – x.
Запишем уравнение в виде | 3 – x | + x = log3|
x | + 2. В одной системе координат построим
графики функций y = | 3 – x | = x (1) и y
= log3| x | = 2 (2). Функцию (1) запишем как
кусочно-заданную, раскрывая модуль на
промежутках:
y =
График функции (2) построим, выполняя
отображение графика y = log3x + 2
относительно оси ординат ( один из рассмотренных
частных случаев ).
Графики имеют две общие точки, следовательно,
данное уравнение имеет два корня.
V. Для повторения материала, его закрепления
предлагаем выполнить следующие задания.
1. Постройте графики функций и уравнений: y =
| y | =
; y = | | 2 – x
| – 4 |; y = | x2 – 4 | x | + 3 |; y = + 1.
2. Решите графически уравнения c одной и двумя
переменными: | 3 – x | – 3 = 2| x | – x2;
| y | = 2| x | – x2; = | x – 2,5 | –1,5.
3. Решите графически неравенства с двумя
переменными: | y | > x24x + 3;
| x | + | y | < 3.
4. Решите графически систему уравнений:
5. Найдите все значения а, при каждом из которых
уравнение | x + a | + | | x – 3 | – 4 | = 1
имеет ровно два корня.
Построение графиков с модулем
путём преобразований
Модуль аргумента и модуль функции
Если Вы попали на эту страницу из поисковика, миновав предыдущие разделы темы «Графики функций и их преобразования», то рекомендую сначала повторить графики основных элементарных функций и общие правила преобразования графиков функций.
В контексте построения графиков это означает использование преобразования симметрии относительно осей координат.
Пример 1.
В этом примере оба графика получены из графика функции y = x − 3.
Первый — преобразованием Гf(x) → Гf(|x|) , второй — преобразованием Гf(x) → Г|f(x)| .
Пример 2.
В этом примере оба графика получены из графика функции y = x 2 − 2x − 3.
Первый — преобразованием Гf(x) → Гf(|x|) , второй — преобразованием Гf(x) → Г|f(x)| .
Один из способов быстро и точно построить исходную параболу по характерным точкам показан в видео на канале Mathematichka.
III При построении из графика функции y = f(x) более сложных графиков, например, вида y = k·f (a|x| + b) + c или y = k·|f (ax + b)| + c тщательно соблюдайте последовательность преобразований.
Ниже показаны примеры графиков различных функций, содержащих модуль, которые получены из графика функции (y=sqrt.) y = √|x| __ .
| 1. (y=sqrt) √x _ —> | 2. (y=sqrt<|x|>) √|x| __ —> | 3. (y=sqrt<|x-1|>) y = √|x − 1| _____ | 4. (y=sqrt<|x|-1>) y = √|x| − 1 _____ | 5. (y=|sqrt-1|.) y = | √x − 1 _ | |
IV Равенство вида |y| = f (x) по определению не является функцией, так как допускает неоднозначность при вычислении значения y. Однако линию на координатной плоскости оно задает, и эту линию тоже можно построить, исходя из графика функции y = f(x) .
Для этого нужно:
- Построить график функции y = f(x) .
- Исключить его часть, расположенную ниже оси абсцисс, поскольку указанное равенство возможно только для положительных значений f(x).
- Построить нижнюю часть линии (при отрицательных y) симметричным отображением относительно оси Ox.
Эти кривые также получены из графика функции (y=sqrt). y = √x _ .
| 6. (|y|=sqrt) | 7. (|y|=|sqrt-1|) | 8. (|y|=sqrt<|x|>.) |
Пример 3.
Задан график функции y = x 2 .
Построить кривые, удовлетворяющие уравнению, |y| = x 2 − 2|x| − 5 .
Заметим, что x 2 = |x| 2 (значение четной степени, как и значение модуля, всегда неотрицательно). Поэтому, выделяя полный квадрат, преобразуем функцию к виду |y| = (|x| − 1) 2 − 6 и строим её график последовательными преобразованиями.
Строим график функции f(x) = (x − 1) 2 − 6 переносом на 1 вправо вдоль оси Ox, а затем переносом вниз на 6 единиц вдоль оси Oy.
Строим график функции f(|x|) = (|x| − 1) 2 − 6 с использованием преобразования симметрии относительно оси Oy.
Строим линии, удовлетворяющие уравнению |y| = (|x| − 1) 2 − 6 с использованием преобразования симметрии относительно оси Ox.
| 1.y = x 2 | 2.y = (x − 1) 2 | 3.y = (x − 1) 2 − 6 | 4.y = (|x| − 1) 2 − 6 |
| 5.y = (|x| − 1) 2 − 6, y ≥ 0 | 6.|y| = (|x| − 1) 2 − 6 |
Следующий график постройте самостоятельно, чтобы убедиться, что вы правильно поняли материал.
Пример 4.
Задан график функции y = x 2 .
Построить график функции y = |x 2 − 2x − 5| .
Сумма модулей
Если формула функции включает сумму или разность несколько модулей, то следует разбить координатную плоскость на участки и построить каждую ветвь графика отдельно. Границы участков определяются приравниванием каждого модуля к нулю и решением соответствующего уравнения. Подробный пример такого подхода можно увидеть в задаче 1 на странице, посвященной решению уравнений с параметрами.
Однако, если подмодульные выражения простые и содержат элементарные функции, графики которых вам хорошо известны, то можно получить результат прямым сложением ординат этих графиков в характерных точках.
Пример 5.
Построить график функции y = |x + 2| + |x − 1| .
Эти два модуля содержат только линейные функции, графиками которых являются прямые линии. В результате сложения должна получиться ломаная линия, состоящая из трёх звеньев. (2 модуля, следовательно 2 уравнения, каждое из которых имеет одно решение, следовательно 2 границы, которыми плоскость разбита на 3 участка.) Трёхзвенную ломаную можно построить по 4-ём точкам.
На одних осях независимо друг от друга строим графики функций y = |x + 2| и y = |x − 1| , используя сдвиг и отражение. Складываем ординаты в точках излома x = −2 и x = 1 и в двух удобных точках на крайних участках, например, при x = −3 и x = 3 . На приведенном рисунке красным цветом представлен результирующий график, полученный по этим 4-ём точкам: (−3;5 ), (−2;3 ), (1; 3), (3;7).
Теперь проверьте себя.
Пример 6.
Построить график функции y = |x + 2| + |x − 1| − |x| .
Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.
Есть вопросы? пожелания? замечания?
Обращайтесь — mathematichka@yandex.ru
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте ссылки.
Графики прямой, параболы, гиперболы, с модулем
Пошаговое построение графиков.
«Навешивание» модулей на прямые, параболы, гиперболы.
Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.
Для понимания друг друга введу немного «обзываний» системы координат:
Для начала построим график прямой y = 2x − 1.
Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую.
Возьмем значение X = 0 и Х = 1 и подставим в выражение y = 2x − 1, тогда соответственно Y = − 1 и Y = 1
Через данные две точки А = (0; −1) и B = (1; 1) проводим единственную прямую:
А если теперь добавить модуль y = |2x − 1|.
Модуль — это всегда положительное значение , получается, что «y» должен быть всегда положительным.
Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю (как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).

Красота! А как же будет выглядеть график, если надеть модуль только на «х»: y = 2|x| − 1?
Одна строчка рассуждений и рисуем:
Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.
Здесь отражаем относительно оси «y» . Такая же галочка, только теперь через другую ось.
Смертельный номер: y = |2|x| − 1|.
Черную прямую y = 2x − 1 отражаем относительно оси Х, получим y = |2x − 1|. Но мы выяснили, что модуль на х влияет только на левую часть.
В правой части: y = |2x − 1| и y = |2|x| − 1| идентичны!
А после этого отражаем относительно оси «y» то, что мы получили справа налево:
Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках, значит делаем по аналогии.
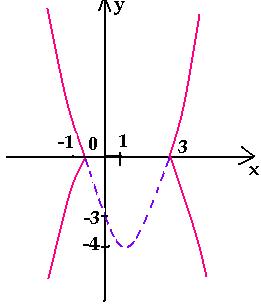
Разберем по винтикам параболу y = x² + x − 2. Точки пересечения с осью «x» получим с помощью дискриминанта: x ₁ = 1 и x ₂ = -2.
Можно найти вершину у параболы и взять пару точек для точного построения.
А как будет выглядеть график: y = |x²| + x − 2? Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.
При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:
А дальше что мелочиться: рассмотри сразу остальные графики с модулем!
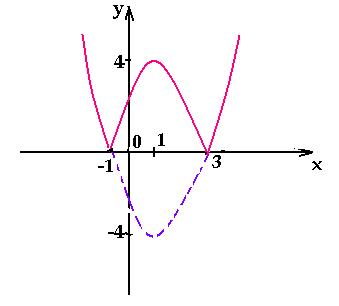
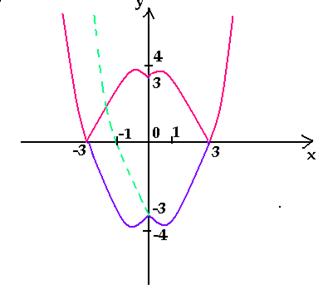
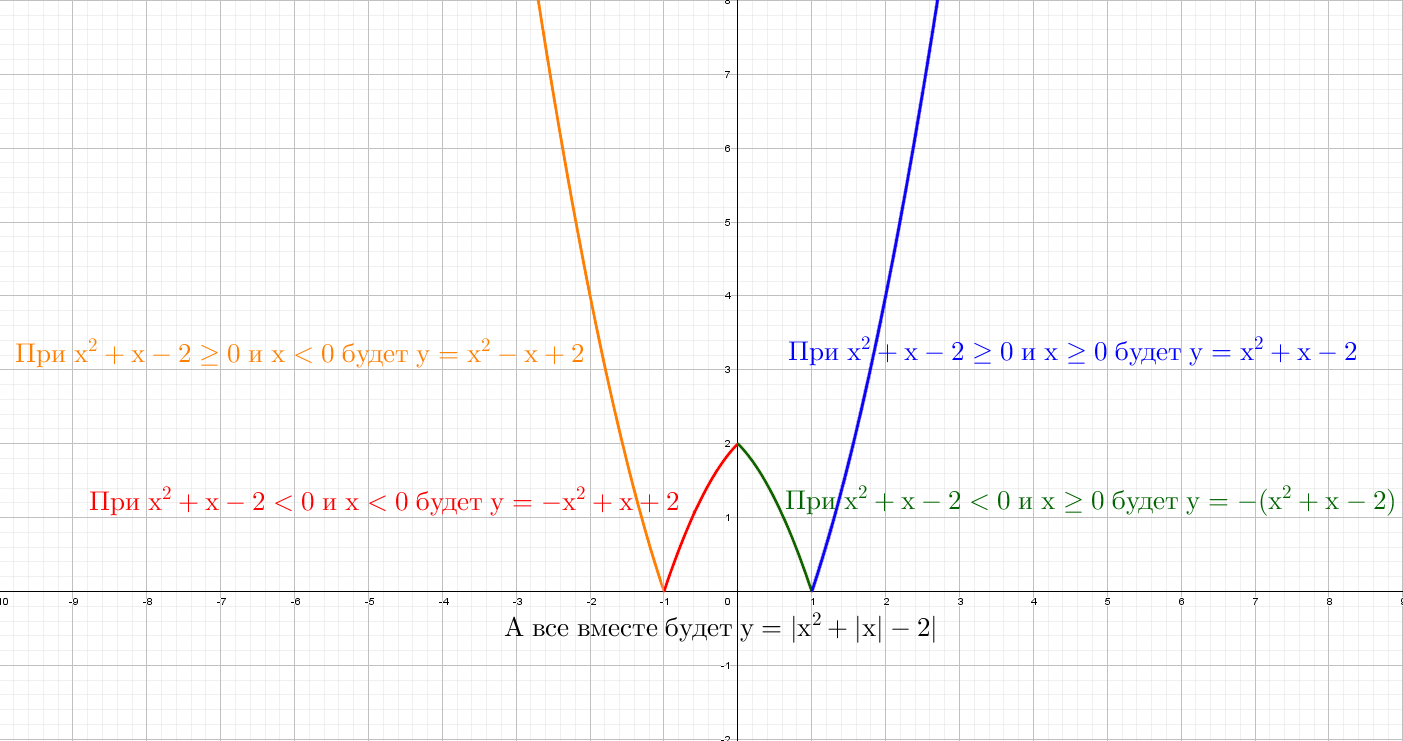
Следующий смертельный номер: |y| = x² + x − 2, подумай хорошенько, а еще лучше попробуй нарисовать сам.
При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!
Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.
А теперь сразу комбо:
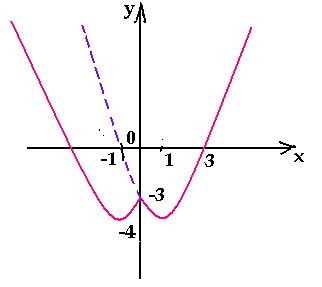
Cиний: похож на y = x² + |x| − 2, только поднят вверх. Строим график в правой части, а затем отражаем через ось Y влево.
Оранжевый: строим в правой части и отражаем относительно оси Х. Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет «шире», расходится в бока он быстрее остальных.
Зеленый: Так же начинаем с правой части и отражаем относительно оси оси Y. Получается график y = |x² + x − 2|, но еще есть −2, поэтому опустим график на 2 вниз. Теперь параболы как бы отражается относительно Y = − 2.
Легкий и средний уровень позади, и настала пора выжать концентрацию на максимум , потому что дальше тебя ждут гиперболы, которые частенько встречаются во второй части ЕГЭ и ОГЭ.
y = 1/x — простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:
А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:
А что будет, если мы добавим в знаменателе « − 1»? График сдвинется вправо на единицу.
А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!

Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.
Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.
Можно придумывать массу вариантов, но общий принцип остается для любого графика. Принципы повторим в выводах в конце статьи.
Фиолетовый: Вычитаем из дроби −1 и сдвигаем график вниз на единицу. Ставим модуль − отражаем все, что снизу вверх.
Оранжевый: Ставим +1 в знаменателе и график смещается влево на единицу. Вычитаем из дроби −1 и сдвигаем график вниз на единицу. А после этого ставим модуль − отражаем все, что снизу вверх.
Зеленый: Сначала получим фиолетовый график. После этого ставим «−» и отражаем график по горизонтали. Сгибаем лист по оси Х и переводим его вниз. Остается добавить +1, это значит, что его нужно поднять вверх на единицу.
Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определению:
И построить график, разбив его на кусочно-заданные функции.
Например для прямой:
Для параболы с одним модулем будет два кусочно-заданных графика:
C двумя модулями кусочно-заданных графиков будет четыре:

- Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
- Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
- Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль .
- Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:
- Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
- Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
- Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.
- Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.
Уравнения графиков функций с модулями
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
Администратор, решение задач
Роман
Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym
Решение задач
Андрей
facebook:
dniprovets25
источники:
http://ik-study.ru/ege_math/grafiki_s_moduliem
http://yukhym.com/ru/matematika/uravneniya-s-modulyami-graficheskij-metod.html