Как решать графы по информатике егэ - Помощь в подготовке к экзаменам и поступлению

На уроке рассматривается решение 13 задания ЕГЭ по информатике

Содержание:

Объяснение заданий 13 ЕГЭ по информатике
- Графы. Поиск количества путей
Решение заданий 13 ЕГЭ по информатике

13-е задание: «Информационные модели»

Уровень сложности

— повышенный,

Требуется использование специализированного программного обеспечения

— нет,

Максимальный балл

— 1,

Примерное время выполнения

— 3 минуты.

Проверяемые элементы содержания: Умение представлять и считывать данные в разных типах информационных моделей (схемы, карты, таблицы, графики и формулы)

До ЕГЭ 2021 года — это было задание № 15 и № _ ЕГЭ

Типичные ошибки и рекомендации по их предотвращению:

«Игнорирование указаний в условии задания, что путь должен включать (или не включать) заданные промежуточные вершины»

ФГБНУ «Федеральный институт педагогических измерений»

Графы. Поиск количества путей

Если в город R из города A можно добраться только из городов X, Y и Z, то количество различных путей из города A в город R равно сумме числа различных путей проезда из A в X, из A в Y и из A в Z, то есть:

N_R = N_X + N_Y + N_Z

где N_R — это количество путей из вершины A в вершину R
Число путей не бесконечно, исключением является только граф, в котором есть циклы – замкнутые пути.
Часто задачи с графами целесообразней решать с конца.

Решение заданий 13 ЕГЭ по информатике

Плейлист видеоразборов задания на YouTube:

Задание демонстрационного варианта 2022 года ФИПИ

13_1:

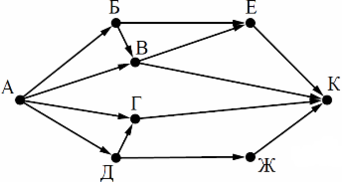
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.

Сколько существует различных путей, ведущих из города А в город М и проходящих через город Г?

✍ Решение:

Удалим ребра, которые проходят «мимо» вершины Г или до которых от пункта А можно дойти, минуя вершину Г:

1_1

Вершина В удалена, т.к. возможны только следующие траектории движения через этот пункт (которые НЕ проходят через пункт Г):
1. А — Б — В — И — М
2. А — Б — В — Е — И — М
3. А — Б — В — Е — М
4. А — Б — В — Е — К — М
Теперь посчитаем результаты по оставшимся вершинам:

М = И + Е + К 
-----
 И = Е 
   Е = Г + Ж 
    Г = Б + А + Д = 1 + 1 + 1 = 3 
    Ж = Г = 3
 К = Е + Ж

Теперь возвращаемся, подставляя найденные значения: ↑
   Е = Г + Ж = 3 + 3 = 6 
    Ж = Г = 3
 И = Е = 6 (получили из последующих шагов)
 К = Е + Ж = 6 + 3 = 9       
М = И + Е + К = 6 + 6 + 9 = 21

Результат: 21

Видео ЕГЭ по информатике (аналитическое решение):

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

13_2:

Сколько существует различных путей, ведущих из города А в город М и не проходящих через город Г?

✍ Решение:

Удалим ребра, которые проходят через вершину Г:

Теперь посчитаем результаты по оставшимся вершинам:

М = И + Е + К
-----
И = В + Е
  В = 1
  Е = В + Ж
     Ж = 1

Теперь возвращаемся, подставляя найденные значения: ↑
  Е = В + Ж = 1 + 1 = 2
И = В + Е = 1 + 2 = 3 
К = Е = 2 
М = И + Е + К = 3 + 2 + 2 = 7

Результат: 7

Подробное решение данного 13 задания в видеоуроке:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

13 задание. Демоверсия ЕГЭ 2018 информатика:

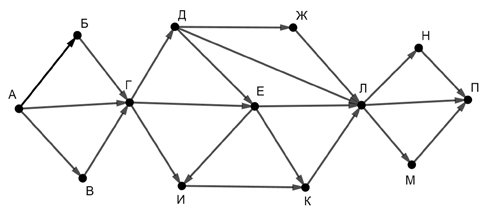
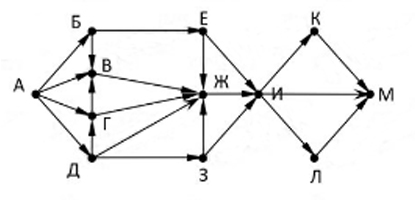
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.

Сколько существует различных путей из города А в город М, проходящих через город Ж?

✍ Решение:

Результат: 20

Подробное решение 13 задания демоверсии ЕГЭ 2018 года смотрите на видео:

📹 YouTube здесь
📹 Видеорешение на RuTube здесь

13_4:

На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Какова длина самого длинного пути из города А в город М?
Длиной пути считать количество дорог, составляющих этот путь.

✍ Решение:

Источник

Поиск путей в
графе

Разбор заданий № 15 ЕГЭ (11 кл)

Проверяемые элементы содержания: Умение представлять и считывать данные в разных типах информационных
моделей (схемы, карты, таблицы, графики и формулы). (повышенный уровень, время – 3
мин)

Что
нужно знать:

Теория
графов^{^[1]} — раздел дискретной
математики, изучающий свойства графов.

Граф представляется как
множество вершин (узлов), соединённых рёбрами.

Теория графов находит применение, например, в
геоинформационных системах

(ГИС). Существующие или вновь проектируемые
дома, сооружения, кварталы и т. п.

рассматриваются как вершины, а соединяющие
их дороги, инженерные сети, линии

электропередачи и т. п. — как рёбра.
Применение различных вычислений,

производимых на таком графе, позволяет, например,
найти кратчайший объездной

путь или ближайший
продуктовый магазин, спланировать оптимальный маршрут.

Графы^{^[2]} используют во всех отраслях нашей
жизни. Знание основ теории графов

необходимо в управлении
производством, бизнесе, при построении путей

транспортировки и
доставки, решении задач.

Графы используют в связи с развитием теории вероятности,
математической логики

и информационных
технологий.

Граф³
— множество V вершин и
набор Е неупорядоченных
и упорядоченных пар

вершин; обозначается граф через G(V, Е). Неупорядоченная
пара вершин называется

ребром, упорядоченная пара — дугой.
Граф, содержащий только рёбра,
называется

неориентированным;
граф, содержащий только дуги,— ориентированным.
Пара

вершин может соединяться двумя или более
рёбрами (дугами одного направления),

такие рёбра (дуги) называются кратными.
Дуга (или ребро) может начинаться и

кончаться в одной и той же вершине, такая
дуга (ребро) называются петлей. Вершины,

соединённые ребром или дугой, называются смежными.
Рёбра, имеющие общую

вершину, также называются смежными. Ребро
(дуга) и любая из его двух вершин

называется инцидентными. Говорят, что ребро
(u, v) соединяет
вершины u и v, а
дуга

(u, v)
начинается в вершине u и
кончается в вершине v.

Маршрут на графике — это последовательность ребер 𝑎₁,𝑎₂,…,𝑎_𝑛
, в которой конец

одного ребра служит
началом другого.

Информационные
ресурсы:

1.
Теория: Способы представления графов,

2.
Задания для тренировки: https://inf-ege.sdamgia.ru/test?a=catlistwstat

a.
Графы, содержащие
более или менее десяти вершин просмотреть

b.
Графы, содержащие
десять вершин просмотреть

3.
Онлайн-тесты Константина Полякова для подготовки к ЕГЭ: http://kpolyakov.spb.ru/school/egetest/b15.htm

Задание № 15 (ДЕМО
ФИПИ ЕГЭ-2020)

На рисунке представлена схема дорог, связывающих города А,
Б, В, Г, Д, Е, Ж, З,

И, К, Л, М. По каждой
дороге можно двигаться только в одном направлении,

указанном стрелкой. Сколько существует различных
путей из
города А в город М,

проходящих через
город Ж?

Решение:

1. Из
заданного графа исключим дуги, которые, при составлении маршрута из города А в город М,
позволяют обойти город Ж:

2. Посчитаем
последовательно количество путей до каждого из городов:

a. Начало
маршрута А = 1;

b. последовательно
будем рассматривать соседние (связанные) вершины и подсчитывать количество
проходящих через них путей:

Д = А = 1; Г =А + Д = 2; В = А
+ Г = 3; Б = А + В = 4; Е = Б
= 4;

З = Д + Г + В = 6; Ж = З + В + Б + Е = 17; И
= Ж =17; К = И =17; Л = И
= 17; М = Л + И + К = 51.

c. Подсчет
количества путей можно отобразить на графе:

Ответ: 51.

Задание № 15 (ДЕМО
ФИПИ ЕГЭ-2019)

На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З,
И, К, Л, М. По каждой дороге можно двигаться только в одном направлении,
указанном стрелкой. Сколько существует различных путей из города А в город М,
проходящих через город Л?

Решение:

1. Из
заданного графа исключим дуги, которые, при составлении маршрута из города А в город М,
позволяют обойти город Л:

2. Посчитаем
последовательно количество путей до каждого из городов и отобразим это на
графе:

Ответ: 28.

Задание № 15 (ДЕМО
ФИПИ ЕГЭ-2018)

На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З,
И, К, Л, М. По каждой дороге можно двигаться только в одном направлении,
указанном стрелкой. Сколько существует различных путей из города А в город М,
проходящих через город Ж?

Решение:

2. Посчитаем
последовательно количество путей до каждого из городов и отобразим это на
графе:

Ответ: 20.

Разбор заданий № 1. СтатГрад. Подготовка к ЕГЭ 2019^{^[3]}

Вариант №1

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, К, Л, М, Н, П, Р,
Т. По каждой дороге можно двигаться только в одном направлении, указанном
стрелкой.
Сколько существует различных путей *из города А в город Т*?

Решение:

Посчитаем последовательно количество
путей до каждого из городов: 1. Начало маршрута А
= 1;

2. последовательно
будем рассматривать соседние (связанные) вершины и подсчитывать количество
проходящих через них путей:

Д = А = 1; Г =А + Д = 2; Б = А
= 1; В = А + Б = 2; Е = А
+ Б + В + Г + Д = 7; Л =
Е = 7; К = Е = 7; М = К + Е + Л = 21; Н
= К + Л + М = 35; П = М = 35; Р = М + П = 70; Т = П
+ Р = 105.

3. Подсчет
количества путей можно отобразить на графе:

Ответ: 105.

Вариант №2

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, К, Л, М, Н, П, Р,
Т. По каждой дороге можно двигаться только в одном направлении, указанном
стрелкой.
Сколько существует различных путей *из города А в город Т*?

Решение:

Посчитаем последовательно количество путей до каждого
из городов: 1. Начало маршрута А
= 1;

Д = А = 1; Б = А = 1; Г =А + Б = 2; В = А + Б = 2; Е = А
+ Б + В + Г + Д = 7; К =
Е = 7; Л = Е = 7; М = Е + К + Л = 21; Н
= К + М + Л = 35; П = Н =
35; Р = Н = 35; Т = П
+ Р = 70.

3. Подсчет
количества путей можно отобразить на графе:

Ответ: 70.

Вариант №3

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, К, Л, М, Н, П, Р,
С, Т. По каждой дороге можно двигаться только в одном направлении, указанном
стрелкой. Сколько существует различных путей из города А в город Т, проходящих
*через город Л*?

Решение:

1. Из
заданного графа исключим дуги, которые, при составлении маршрута из города А в город Т,
позволяют обойти город Л:

4. Рассматривая
соседние (связанные) вершины, посчитаем последовательно количество путей до
каждого из городов, результат отобразим на графе (А = 1):

Ответ: 64.

Вариант №4

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, К, Л, М, Н, П, Р,
С, Т. По каждой дороге можно двигаться только в одном направлении, указанном
стрелкой. Сколько существует различных путей из города А в город Т, проходящих
*через город Н*?

Решение:

1. Из
заданного графа исключим дуги, которые, при составлении маршрута из города А в город Т,
позволяют обойти город Н:

2. Рассматривая соседние (связанные) вершины,
посчитаем последовательно количество путей до каждого из городов, результат
отобразим на графе (А = 1):

Ответ: 32.

Вариант №5

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, К, Л, М, Н, П, Р,
С, Т. По каждой дороге можно двигаться только в одном направлении, указанном
стрелкой. Сколько существует различных путей из города А в город Т, проходящих
*через город Е*?

Решение:

1. Из
заданного графа исключим дуги, которые, при составлении маршрута из города А в город Т,
позволяют обойти город Е:

Ответ: 63.

Вариант №6

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, К, Л, М, Н, П, Р,
С, Т. По каждой дороге можно двигаться только в одном направлении, указанном
стрелкой. Сколько существует различных путей из города А в город Т, проходящих
*через город В*?

Решение:

1. Из
заданного графа исключим дуги, которые, при составлении маршрута из города А в город Т,
позволяют обойти город В:

Ответ: 42.

Разбор заданий № 18. ЕГЭ 2020. Ушаков Д.М. 10 тренировочных
вариантов^{^[4]}

Вариант 1

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей *из города А в город К*?

Решение:

Рассмотрим
соседние (связанные) вершины и последовательно посчитаем количество путей до
каждого из городов, результат отобразим на графе (причем, А = 1):

Ответ: 30. Вариант 2

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей *из города А в город К*?

Решение:

Ответ: 41.

Вариант 3

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей *из города А в город К*?

Решение:

Ответ: 25

Вариант 4

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей *из города А в город К*?

Решение:

Ответ: 32

Вариант 5

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей *из города А в город К*?

Решение:

Ответ: 24

Вариант 6

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей *из города А в город К*?

Решение:

Ответ: 12

Вариант 7

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей *из города А в город К*?

Решение:

Ответ: 18

Вариант 8

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей *из города А в город К*?

Решение:

Ответ: 30

Вариант 9

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей *из города А в город К*?

Решение:

Ответ: 19

Вариант 10

На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город К, проходящих через город
Е?

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Простейшие задачи на графы

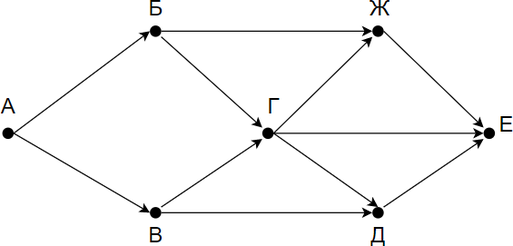
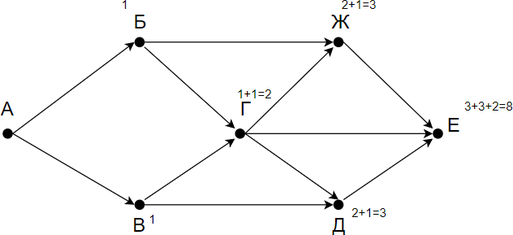
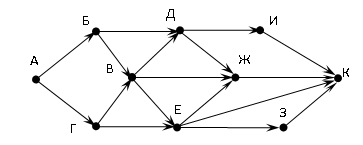
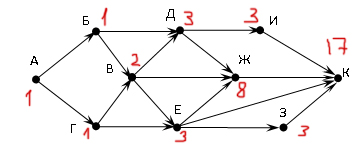
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Е?

Заметим, что количество путей в город Е является суммой путей в города Ж, Г и Д. Количество путей в город Ж — сумма путей в города Г и Б. Таким образом получаем:

Г = Б + В

Д = Г + В

Ж = Б + Г

Е = Ж + Г + Д

Заметим, что в пункты Б и В можно попасть единственным способом — из города А. Отметим на рисунке индексами сверху каждого пункта количество путей, с помощью которых в него можно попасть и посчитаем итоговое.

Ответ: 8

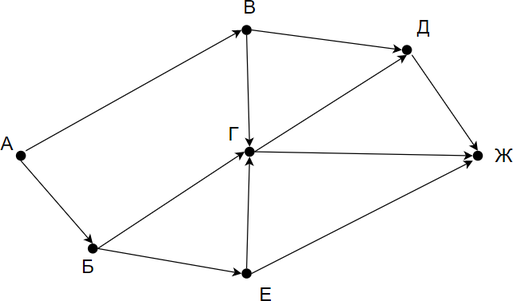
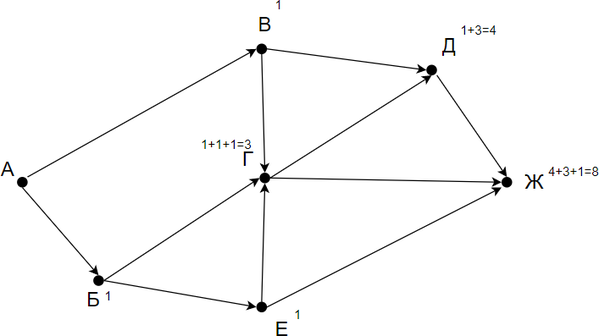
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?

Заметим, что количество путей в город Ж является суммой путей в города Д, Г и Е. Количество путей в город Г — сумма путей в город В, Б и Е. Таким образом получаем:

Г = Б + В + Е

Д = В + Г

Ж = Д + Г + Е

Заметим, что в пункты Б, В и Е можно попасть единственным способом — из города А. Отметим на рисунке индексами сверху каждого пункта количество путей, с помощью которых в него можно попасть и посчитаем итоговое.

Ответ: 8

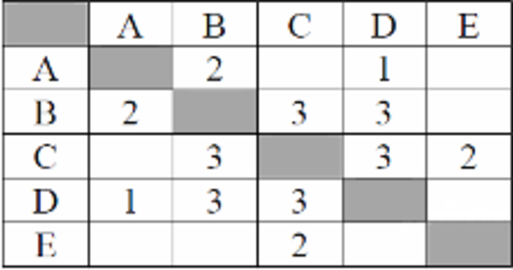
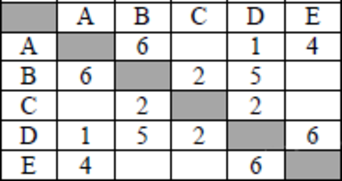
Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:

Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.

Найдём все варианты маршрутов из A в E и выберем самый короткий.

Из пункта A можно попасть в пункты B, D.

Из пункта B можно попасть в пункты C, D.

Из пункта C можно попасть в пункты D, E.

A—B—C—E: длина маршрута 7 км.

A—D—B—C—E: длина маршрута 9 км.

A—D—C—E: длина маршрута 6 км.

Самый короткий путь: A—D—C—E. Длина маршрута 6 км.

Ответ: 6

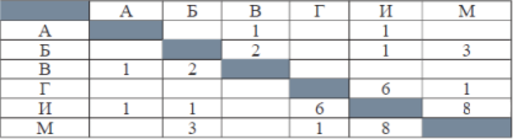
Геральт спешит выручить Цири из плена Кагыра. В таблице указана протяжённость дорог между пунктами, через которые он может пройти. Укажите длину самого короткого участка кратчайшего пути от Геральта до Цири (от точки И до точки М). Передвигаться можно только по дорогам, указанным в таблице:

Найдём все варианты маршрутов из И в М и выберем самый короткий.

Из пункта И можно попасть в пункты А, Б, Г, М.

Из пункта Г можно попасть в пункты И, М.

Из пункта В можно попасть в пункты А, Б.

Из пункта Б можно попасть в пункты В, И, М.

И—А—В—Б—М: длина маршрута 7 км.

И—Б—М: длина маршрута 4 км.

И—Г—М: длина маршрута 7 км.

И—М: длина маршрута 8 км.

Самый короткий путь: И—Б—М. Длина маршрута 4 км. Самый короткий участок этого пути равен 1 км.

Ответ: 1

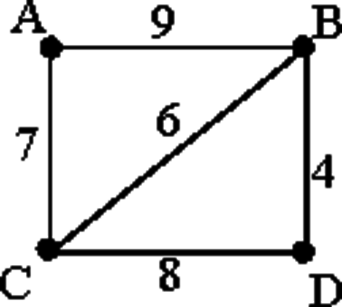
На схеме нарисованы дороги между четырьмя населёнными пунктами A, B, C, D и указаны протяжённости данных дорог.

Определите, какие два пункта наиболее удалены друг от друга (при условии, что передвигаться можно только по указанным на схеме дорогам). В ответе укажите кратчайшее расстояние между этими пунктами.

Заметим, что наиболее удалены друг от друга пункты A и D. Найдём все варианты маршрутов из A в D и выберем самый короткий.

A—B—D: длина маршрута 13 км.

A—C—D: длина маршрута 15 км.

A—B—C—D: длина маршрута 23 км.

A—C—B—D: длина маршрута 17 км.

Заметим, что кратчайшее расстояние между пунктами A и D равняется 13.

Ответ: 13

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?

Начнем считать количество путей с конца маршрута — с города К. Пусть NX — количество различных путей из города А в город X, N — общее число путей.

В К можно приехать из Е, В, Г или Ж, поэтому N = NК = NЕ + NВ + N Г + NЖ (*).

Аналогично:

NЕ = NБ + NВ = 1 + 2 = 3;

NЖ = NД = 1;

NВ = NА + NБ = 1 + 1 = 2;

NГ = NА + NД = 1 + 1 = 2;

NД = NА = 1;

NБ = NА = 1.

Подставим в формулу (*): N = 3 + 2 + 2 + 1 = 8.

Ответ: 8

Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.

Определите длину кратчайшего пути между пунктами B и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.

Проанализируем некоторые возможные маршруты.

Маршрут B—D—E, длина 11 км.

Маршрут B—C—D—E, длина 10 км.

Маршрут B—С—D—A—E, длина 9 км.

Любые другие маршруты будут длиннее маршрута B—С—D—A—E. Самый короткий путь: B—С—D—A—E. Длина маршрута 9 км.

Ответ: 9

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Сегодня разберём одно из самых лёгких заданий из ЕГЭ по информатике — задание 13. Вы с похожим типом задач могли встретится на экзамене в 9 классе по информатике.

Приступим к практическим тренировкам решения 13 задания ЕГЭ по информатике 2022.

Задача (Стандартная)

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?

Решение:

Нужно подсчитать количество путей от начальной точки А до конечной точки К.

Будем использовать специальную технику для решения 13 задания из ЕГЭ по информатике 2022

Техника:

Ставим 1 (единицу) возле начальной точки A. Далее, просматриваем ближайшие точки и анализируем, сколько входит стрелок в эти точки. В точку Б «перетекает» 1 из точки А. В точку Г тоже входит одна стрелка из точки А. Значит, тоже в эту точку «перетекает» 1 из А.

В точку В входят две стрелки. Значит, в точку В «втекает» сумма двух точек, из которых выходят эти стрелки! Получается 1 + 1 = 2.

И продолжаем в том же духе.

Число в конечной точке показывает правильный ответ!

Ответ: 17

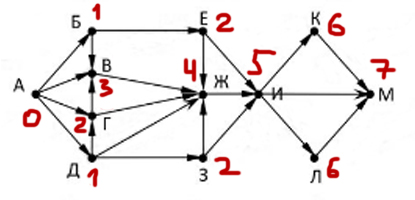
Задача (Демонстрационный вариант ЕГЭ по информатике, 2020)

На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е,
Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном
направлении, указанном стрелкой.
Сколько существует различных путей из города А в город М, проходящих
через город Ж?

Решение:

Отличие этой задачи от предыдущей заключается в том, что пути, которые будем засчитывать, обязательно должны проходить через пункт Ж. Чтобы выполнить это условие, зачеркнём стрелку из пункта Е в пункт И. Так же зачеркнём стрелку из пункта З в пункт И. По этим стрелкам ходить нельзя, т.к. если мы по ним пойдём, не будет пройден пункт Ж.

Основная техника же решения будет такой же, как и в прошлой задаче.

Ответ: 51

Продолжаем отработку 13 задания ЕГЭ по информатике 2022

Задача (Избегаемая вершина)

На рисунке – схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И, К, Л, М, Н, П

Сколько существует различных путей из пункта А в пункт П, не проходящих через пункт Е?

Решение:

Такая же задача, как и предыдущие две, только здесь, при построении путей, мы не должны проходить через точку E.

Зачеркнём те дороги, которые поведут наши пути через пункт E.

Далее, применим старый метод, который использовали ранее.

Получается ответ 27.

Ответ: 27

Рассмотрим задачу, которая была на реальном экзамене по информатике в этом году.

Задача (ЕГЭ по информатике, 2020, Москва)

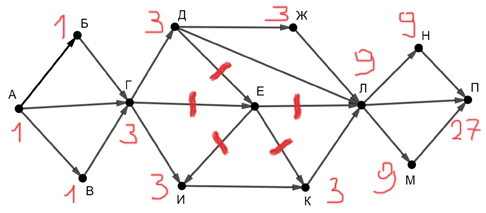
На рисунке — схема дорог, связывающих города А, Б, В, Г, Е, Ж, К, Л, М. По каждой дороге можно двигаться в одном направлении, указанном стрелкой. Какая наибольшая длина пути из А в М ?

Решение:

В этой задаче отличается вопрос от привычного нахождения количества путей. Здесь нужно найти наибольшую длину пути из начального пункта в конечный.

Возле начальной точки ставим число 0.

Смотрим сколько входит в узел стрелок. Выбираем стрелку, которая идёт из узла с наибольшим числом. При переходе по стрелочке добавляем 1.

Число, которое получится возле конечной точки и будет ответом. В этой задачке стрелок получилось 7, это и будет ответ.

Ответ: 7

Источник

Графы. Поиск количества путей

Решение заданий 13 ЕГЭ по информатике

За​да​ние № 15 (​ДЕМО ФИПИ ЕГЭ-2020​)

За​да​ние № 15 (​ДЕМО ФИПИ ЕГЭ-2019​)

За​да​ние № 15 (​ДЕМО ФИПИ ЕГЭ-2018​)

Разбор заданий № 1. ​СтатГрад. Подготовка к ЕГЭ 2019[3]

Разбор заданий № 18. ​ЕГЭ 2020. Ушаков Д.М. 10 тренировочных вариантов[4]

Простейшие задачи на графы

Задание № 15 (ДЕМО
ФИПИ ЕГЭ-2020)

Задание № 15 (ДЕМО
ФИПИ ЕГЭ-2019)

Задание № 15 (ДЕМО
ФИПИ ЕГЭ-2018)

Разбор заданий № 1. СтатГрад. Подготовка к ЕГЭ 2019^{^[3]}

Разбор заданий № 18. ЕГЭ 2020. Ушаков Д.М. 10 тренировочных
вариантов^{^[4]}