15
Сен 2022
Категория: 10 Графики функций
2022-09-15
2022-09-15
Задача 1. На рисунке изображён график функции вида где числа a, b, c и d — целые. Найдите корень уравнения
Решение: + показать
Задача 2. На рисунке изображён график функции вида где числа a, b, c и d — целые. Найдите корень уравнения
Решение: + показать
Задача 3. На рисунке изображён график функции вида где числа a, b, c и d — целые. Найдите корень уравнения
Решение: + показать
Задача 4. На рисунке изображён график функции вида где числа a, b, c и d — целые. Найдите корень уравнения
Решение: + показать

Пройти тест
Автор: egeMax |
Нет комментариев
Скачать материал

Скачать материал


- Сейчас обучается 54 человека из 30 регионов


- Сейчас обучается 32 человека из 22 регионов


- Сейчас обучается 47 человек из 27 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Графики функций
Кусочно-линейная функция
(Задание 9 ЕГЭ 2022) -
2 слайд
На рисунке изображён график функции где числа a, b, c и d — целые. Найдите корень уравнения
1
3
y1 = k1xk1 = y/x= 3/1 = 3,
-2
— 5
y2 = k2xk2 = y/x= 3/-3 = -1,
-3
3
m1 = -5
y1 = 3 x — 5
m2 = 3
y2 = — x +3 -
3 слайд
Если bx + c ≥ 0, то f(x) = ax +bx + c + d,
f(x) = (a + b) x + (c + d)
Если bx + c ≤ 0, то f(x) = ax — bx — c + d,
f(x) = (a — b) x + (-c + d)
y1 = 3 x — 5
a + b = 3
c + d = -5
y2 = — x +3
a – b = — 1
-c + d = 3
a + b = 3,
a – b = — 1
c + d = -5,
-c + d = 3
a = (3 -1) : 2, a = 1 d = (-5 + 3) : 2, d = — 1
ax +d = 0, x -1 = 0, x = 1 Ответ: 1 -
4 слайд
План решения
Составить уравнения прямых
y1 = k1x + m1 и y2 = k2x + m22. Hайти а = (k1 + k2) : 2 и d = (m1 + m2 ) : 2
(как среднее арифметическое для «а» – угловых коэффициентов прямых,
для «d» — свободных членов)3. Cоставить уравнение ax + d = n и решить его
-
5 слайд
Уравнение прямой, проходящей через две точки
Пусть в плоскости заданы две точки М(х1; у1) и К(х2;у2), тогда уравнение прямой, проходящей через эти точки, имеет вид:Если какой-либо из знаменателей равен нулю, следует приравнять к нулю соответствующий числитель
-
6 слайд
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите корень уравнения
А
В
С
а)Составим уравнение прямой АВ
А(4;4), В(3;1)Получим: у = 3х — 8
-
7 слайд
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите корень уравнения
А
В
С
а)Составим уравнение прямой АВ
А(4;4), В(3;1)Получим: у = 3х — 8
б) Составим уравнение прямой СВ
В(3;1), С(2;0) -
8 слайд
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите корень уравнения
А
В
С
а)Составим уравнение прямой АВ
А(4;4), В(3;1)Получим: у = 3х — 8
б) Составим уравнение прямой СВ
В(3;1), С(2;0)
Получим : у = х-2 -
9 слайд
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите корень уравнения
А
В
С
а)Составим уравнение прямой АВ
А(4;4), В(3;1)Получим: у = 3х — 8
б) Составим уравнение прямой СВ
В(3;1), С(2;0)
Получим : у = х-2
2) Найдем а и d.
а = (k1 + k2) : 2 -
10 слайд
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите корень уравнения
А
В
С
а)Составим уравнение прямой АВ
А(4;4), В(3;1)Получим: у = 3х — 8
б) Составим уравнение прямой СВ
В(3;1), С(2;0)
Получим : у = х-2
2) Найдем а и d.
а = (k1 + k2) : 2
а =(3 + 1) : 2, а = 2 . -
11 слайд
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите корень уравнения
А
В
С
а)Составим уравнение прямой АВ
А(4;4), В(3;1)Получим: у = 3х — 8
б) Составим уравнение прямой СВ
В(3;1), С(2;0)
Получим : у = х-2
2) Найдем а и d.
а = (k1 + k2) : 2
а =(3 + 1) : 2, а = 2 .
d = (m1 + m2 ) : 2 -
12 слайд
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите корень уравнения
А
В
С
а)Составим уравнение прямой АВ
А(4;4), В(3;1)Получим: у = 3х — 8
б) Составим уравнение прямой СВ
В(3;1), С(2;0)
Получим : у = х-2
2) Найдем а и d.
а = (k1 + k2) : 2
а =(3 + 1) : 2, а = 2 .
d = (m1 + m2 ) : 2
d = (-8 + (-2)):2 = -5, d =-5 -
13 слайд
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите корень уравнения
А
В
С
а)Составим уравнение прямой АВ
А(4;4), В(3;1)Получим: у = 3х — 8
б) Составим уравнение прямой СВ
В(3;1), С(2;0)
Получим : у = х-2
2) Найдем а и d.
а = (k1 + k2) : 2
а =(3 + 1) : 2, а = 2 .
d = (m1 + m2 ) : 2
d = (-8 + (-2)):2 = -5, d =-5
Найдем корень уравнения: 2х -5 = 0, х = 2,5 Ответ: 2,5 -
14 слайд
Задание 9 (ЕГЭ). На рисунке изображён график функции вида где числа a, b, c и d — целые. Найдите корень уравнения
А
В
С -
15 слайд
Задание 9(ЕГЭ). На рисунке изображён график функции вида где числа a, b, c и d — целые. Найдите корень уравнения
А
В
С
РешениеУравнение прямой АВ : у = -5х +8
Уравнение прямой ВС: у = -х
а = (-5-1):2, а = -3
d = (8+0):2 = 4, d= 4
Уравнение: -3х + 4 = 10. Откуда х = -2
Ответ: -2
-
16 слайд
Задание 9 (ЕГЭ). На рисунке изображён график функции вида где числа a, b, c и d — целые. Найдите корень уравнения
А
В
С
РешениеУравнение прямой АВ : у = -5х +8
Уравнение прямой ВС: у = -х
Откуда b = -2
Решая, получим с = 4
Уравнение: -2х + 4 = 0. Откуда х = 2
Ответ: 2a + b = -5,
a – b = — 1
a + b = -5,
— a + b = 1,
c + d = 8,
-c + d = 0
c + d = 8,
c — d = 0,
! Обратите внимание: 2 – абсцисса точки излома -
17 слайд
Презентацию подготовила учитель математики МАОУ Стародубской средней общеобразовательной школы №3
Г Стародуба Брянской области Коваленко И.А.
В презентации использованы материалы сайта «Решу ЕГЭ» http://reshuege.ru/test?id=1598285
Краткое описание документа:
Презентация по алгебре «Графики функций. Кусочно — линейная функция» может быть использована при подготовке к ЕГЭ (задание 9). Рассматриваются способы решения задания, связанные с кусочно — линейной функцией
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 153 824 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (углублённый уровень)», Муравин Г.К., Муравина О.В.
Тема
4. Квадратичная и дробно-линейная функции. Преобразование графиков
Больше материалов по этой теме
Другие материалы
- 19.11.2021
- 1169
- 21





- 19.11.2021
- 312
- 23

- 19.11.2021
- 159
- 0
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Подростковый возраст — важнейшая фаза становления личности»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
-
Курс повышения квалификации «Основы управления проектами в условиях реализации ФГОС»
-
Курс повышения квалификации «История и философия науки в условиях реализации ФГОС ВО»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС медицинских направлений подготовки»
-
Курс повышения квалификации «Экономика: инструменты контроллинга»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
-
Курс профессиональной переподготовки «Метрология, стандартизация и сертификация»
Графики функций
Щёлкать мышкой не надо. Презентация с голосовым сопровождением и будет перелистываться сама
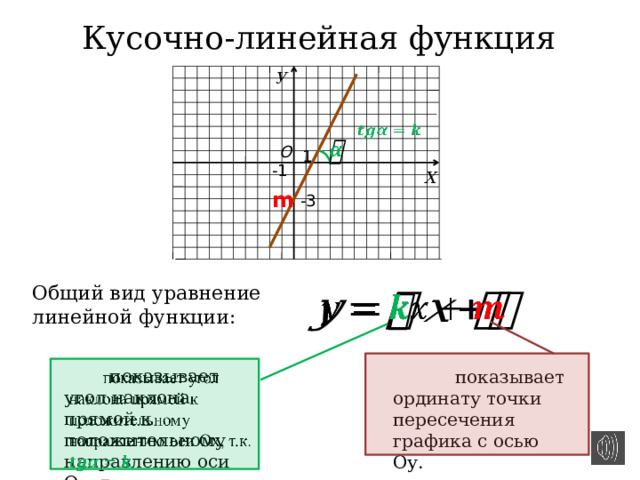
Кусочно-линейная функция
У
О
1
-1
X
m
-3
Общий вид уравнение линейной функции:
показывает угол наклона прямой к положительному направлению оси Ох, т.к.
показывает ординату точки пересечения графика с осью Оу.
2
=
=
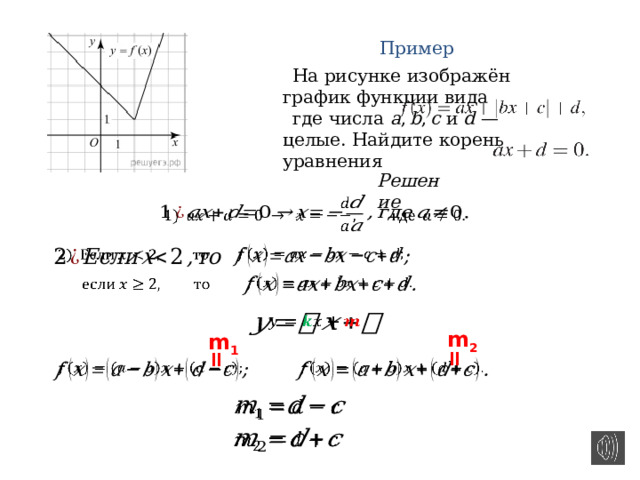
Пример
На рисунке изображён график функции вида
где числа a , b , c и d — целые. Найдите корень уравнения
Решение
m 2
m 1
У
+
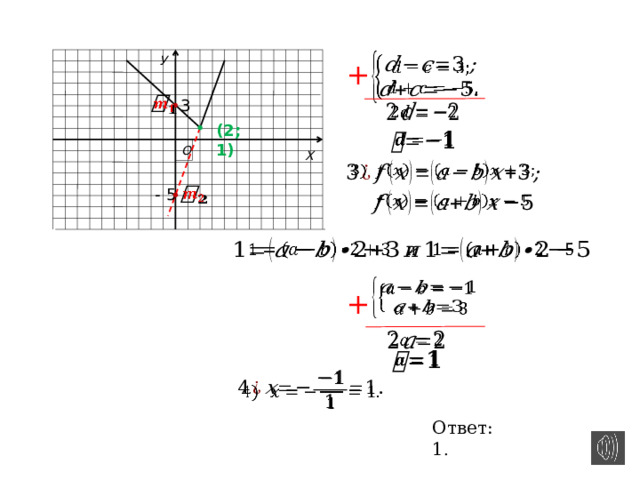
3
(2;1)
О
Х
— 5
+
Ответ: 1 .
4
У
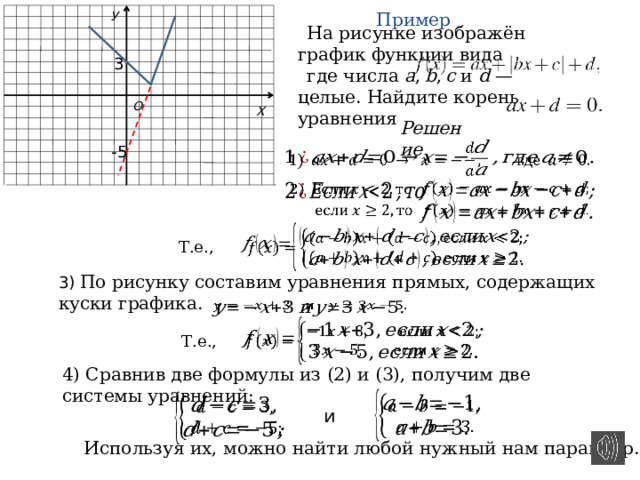
Пример
На рисунке изображён график функции вида
где числа a , b , c и d — целые. Найдите корень уравнения
3
О
Х
Решение
-5
Т.е.,
3) По рисунку составим уравнения прямых, содержащих куски графика.
Т.е.,
4) Сравнив две формулы из (2) и (3), получим две системы уравнений:
и
Используя их, можно найти любой нужный нам параметр.
5
08.11.2021

В ЕГЭ-2022 (профиль) появилось задание 9 с графиками функций в виде угла, заданных формулой с модулем. Давайте разберёмся, как проще объяснить учащимся способ решения таких задач.
Замечание. Для самоконтроля подставим координаты цветных точек в уравнение f (x) = x + |2x – 4| – 1. Каждый раз получится верное числовое равенство. Решения описаны подробно с целью обучения. В ответе требуется указать только корень уравнения.
Источник. ЕГЭ–2021, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. (sdamgia.ru)
Каталог заданий
Задания 10. Графики функций. Кусочно-линейная функция
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 10 № 563824
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите корень уравнения
Аналоги к заданию № 564186: 563824 564184 564189 564190 Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.1 Линейная функция, её график
Решение
·
·
Сообщить об ошибке · Помощь
2
Тип 10 № 564160
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите корень уравнения
Аналоги к заданию № 564160: 564185 564187 Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.1 Линейная функция, её график
Решение
·
·
Сообщить об ошибке · Помощь
3
Тип 10 № 564184
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите корень уравнения
Аналоги к заданию № 564186: 563824 564184 564189 564190 Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.1 Линейная функция, её график
Решение
·
·
Сообщить об ошибке · Помощь
4
Тип 10 № 564185
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите корень уравнения
Аналоги к заданию № 564160: 564185 564187 Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.1 Линейная функция, её график
Решение
·
·
Сообщить об ошибке · Помощь
5
Тип 10 № 564186
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите корень уравнения
Аналоги к заданию № 564186: 563824 564184 564189 564190 Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.1 Линейная функция, её график
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
23. Исследование функций и их графиков
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Кусочно-заданные функции
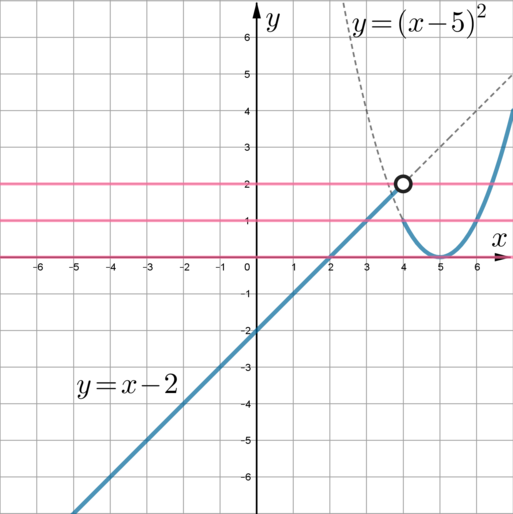
Постройте график функции [y=begin{cases} x^2-10x+25 quad text{при } xgeqslant 4,\
x-2qquad text{при }x<4. end{cases}]
Определите, при каких значениях (n) прямая (y=n) имеет с графиком ровно две общие точки.
Рассмотрим (y=x^2-10x+25). По формуле квадрата разности данную формулу можно преобразовать в (y=(x-5)^2). Следовательно, график этой функции получается из параболы (y=x^2), сдвинутой на 5 единиц вправо. Изобразим график этой функции для (xgeqslant 4).
Графиком (y=x-2) является прямая; он получается сдвигом прямой (y=x) на 2 единицы вниз. Изобразим эту прямую для (x<4). Получим:
(заметим, что так как (y=x-2) определена при (x<4), то точка ((4;2)) на этой прямой будет выколотой)
Прямая (y=n) – горизонтальная прямая. Она будет иметь с графиком данной функции 2 точки пересечения, если (n=0) (1 точка с прямой, другая – в вершине параболы) и (nin(1;2)) ((n=1) не включается, потому что тогда имеем 3 точки пересечения: одна с прямой и две другие с параболой; (n=2) не включается, так как на прямой точка ((4;2)) выколота).
Ответ: n = 0, n ∈ (1; 2)
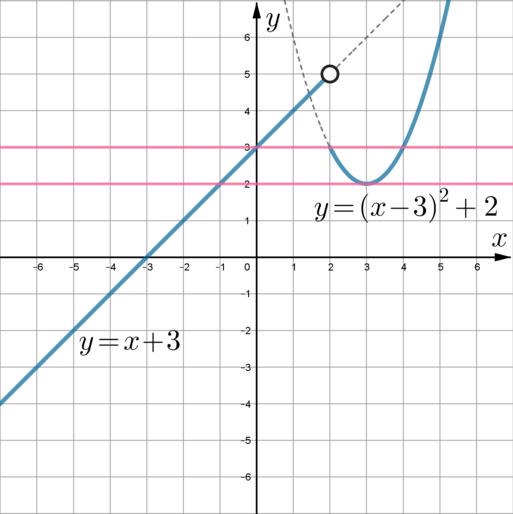
Постройте график функции [y=begin{cases} x^2-6x+11 quad text{при } xgeqslant 2,\
x+3qquad text{при }x<2. end{cases}]
Определите, при каких значениях (n) прямая (y=n) имеет с графиком три общие точки.
Рассмотрим (y=x^2-6x+11). Можно выделить полный квадрат: (x^2-6x+11=x^2-6x+9+2=(x-3)^2+2). Следовательно, графиком этой функции является парабола, причем она получается сдвигом параболы (y=x^2) на 3 единицы вправо и на 2 единицы вверх. Изобразим эту параболу для (xgeqslant 2).
Графиком (y=x+3) является прямая; он получается сдвигом прямой (y=x) на 3 единицы вверх. Изобразим эту прямую для (x<2). Получим:
(заметим, что так как (y=x+3) определена при (x<2), то точка ((2;5)) на этой прямой будет выколотой)
Прямая (y=n) – горизонтальная прямая. Она будет иметь с графиком данной функции 3 точки пересечения, если (nin(2;3]) ((n=2) не включается, потому что тогда имеем 2 точки пересечения: одна с прямой и одна в вершине параболы; (n=3) включается, так как тогда имеем 1 точку пересечения с прямой и 2 с параболой).
Ответ: n ∈ (2; 3]
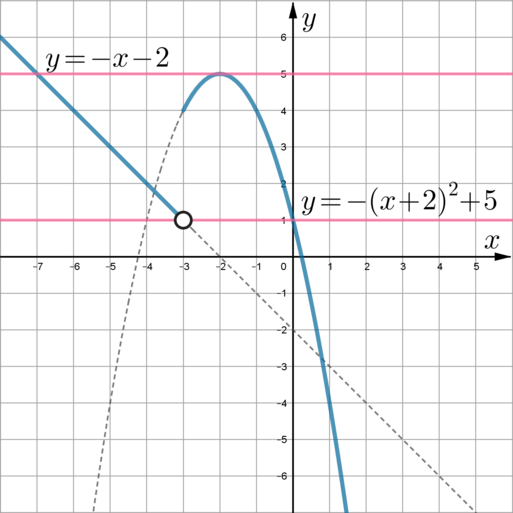
Постройте график функции [y=begin{cases} -x^2-4x+1 quad text{при } xgeqslant -3,\
-x-2qquad text{при }x<-3. end{cases}]
Определите, при каких значениях (n) прямая (y=n) имеет с графиком ровно одну общую точку.
Рассмотрим (y=-x^2-4x+1). Можно выделить полный квадрат: (-x^2-4x+1=-(x^2+4x+4-4)+1=-(x+2)^2+5). Следовательно, графиком этой функции является парабола, причем она получается сдвигом параболы (y=-x^2) на 2 единицы влево и на 5 единиц вверх. Изобразим эту параболу для (xgeqslant -3).
Графиком (y=-x-2) является прямая; он получается сдвигом прямой (y=-x) на 2 единицы вниз. Изобразим эту прямую для (x<-3). Получим:
(заметим, что так как (y=-x-2) определена при (x<-3), то точка ((-3; 1)) на этой прямой будет выколотой)
Прямая (y=n) – горизонтальная прямая. Она будет иметь с графиком данной функции одну общую точку, если (n>5) ((y=5) имеет с графиком 2 общие точки, а вот все прямые выше этой имеют с графиком одну общую точку, лежащую на прямой) и если (nleqslant 1) (тогда будет единственная общая точка, лежащая на параболе, причем (n=1) включается, так как точка ((-3;1)) на прямой выколота).
Ответ: n ∈ ( − ∞; 1]∪(5 + ∞)
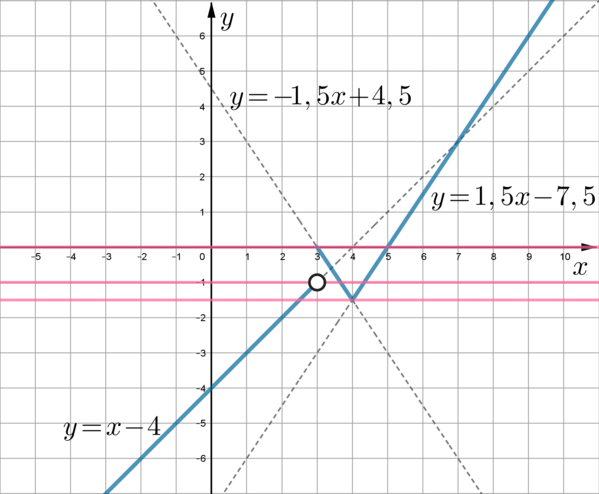
Постройте график функции [y=begin{cases} x-4 quad text{при } x<3,\
-1,5x+4,5qquad text{при }3leqslant xleqslant 4,\
1,5x-7,5 quad text{при } x>4. end{cases}]
Определите, при каких значениях (n) прямая (y=n) имеет с графиком ровно две общие точки.
Все функции являются линейными, то есть их графиками являются прямые. Получим:
(заметим, что так как (y=x-4) определена при (x<3), то точка ((3;-1)) на этой прямой будет выколота; точка ((4;-1,5)) выколота на прямой (y=1,5x-7,5), но закрашена на прямой (y=-1,5x+4,5), следовательно, в итоге она будет закрашенной)
Прямая (y=n) – горизонтальная прямая. Она будет иметь с графиком две общие точки, если:
1) ее вид будет (y=-1,5);
2) (nin [-1;0]). Тогда будут две точки пересечения, одна на отрезке прямой (y=-1,5x+4,5), другая на луче прямой (y=1,5x-7,5).
Ответ: n = −1, 5; n ∈ [ − 1; 0]
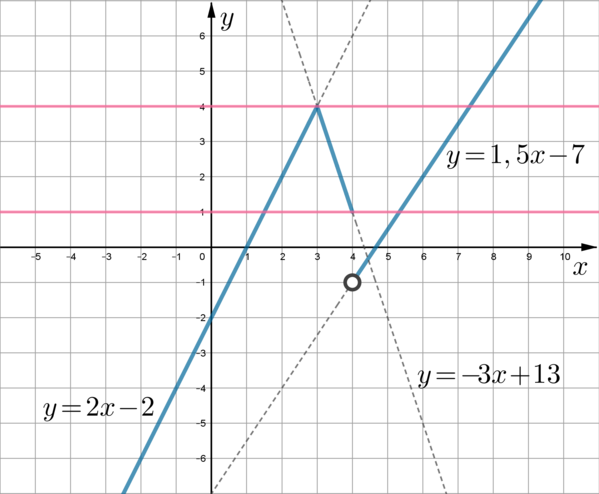
Постройте график функции [y=begin{cases} 2x-2 quad text{при } x<3,\
-3x+13qquad text{при }3leqslant xleqslant 4,\
1,5x-7 quad text{при } x>4. end{cases}]
Определите, при каких значениях (n) прямая (y=n) имеет с графиком ровно три общие точки.
Все функции являются линейными, то есть их графиками являются прямые. Получим:
(заметим, что так как (y=1,5x-7) определена при (x>4), то точка ((4;-1)) на этой прямой будет выколота; точка ((3;4)) выколота на прямой (y=2x-2), но закрашена на прямой (y=-3x+13), следовательно, в итоге она будет закрашенной)
Прямая (y=n) – горизонтальная прямая. Она будет иметь с графиком три общие точки, если (nin [1;4)).
Ответ: n ∈ [1; 4)
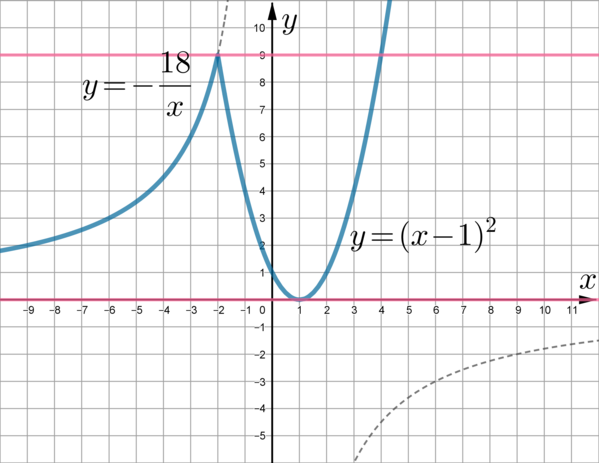
Постройте график функции [y=begin{cases} x^2-2x+1 quad text{при } xgeqslant -2,\[2ex]
-dfrac{18}x quad text{при } x<-2. end{cases}]
Определите, при каких значениях (n) прямая (y=n) имеет с графиком одну или две общие точки.
Рассмотрим (y=x^2-2x+1=(x-1)^2). Графиком этой функции является парабола, которая получается путем сдвига параболы (y=x^2) на 1 единицу вправо. Графиком (y=-frac{18}x) является гипербола, находящаяся во 2 и 4 четвертях. Получим:
(так как графики (y=(x-1)^2) и (y=-frac{18}x) пересекаются при (x=-2), то точка ((-2;9)) будет закрашенной)
(y=n) – горизонтальная прямая. Она будет иметь одну общую точку с графиком кусочно-заданной функции, если (n=0) (эта общая точка будет совпадать с вершиной параболы, на гиперболе общих точек не будет, так как (y=0) – горизонтальная асимптота данной гиперболы). А также если (ngeqslant 9), причем при (n=9) будет две общие точки, при (n>9) одна общая точка.
Ответ: n = 0, n ≥ 9

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ