Уравнения с модулем
-
Слева модуль, справа число
-
Слева модуль, справа выражение, зависящее от переменной
-
Квадратные уравнения с заменой
-
Модуль равен модулю
-
Два или несколько модулей
-
Модуль в модуле
Эта статья посвящена приёмам решения уравнений, содержащих переменную под знаком модуля.
Если на экзамене вам попадётся уравнение с модулем, его можно решить, вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда, занять это может часа полтора драгоценного экзаменационного времени.
Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.
Прежде всего вспомним определение модуля.
Если число x неотрицательное, то модуль x равен самому числу x.
А для отрицательного числа x модуль равен противоположному ему положительному числу -x.
Рассмотрим различные типы уравнений с модулем.
Начнем с простых заданий.
к оглавлению ▴
Слева модуль, справа число
Это самый простой случай. Нам поможет геометрический смысл модуля.
Модуль числа — это расстояние от нуля до данного числа. Очевидно, расстояние не может быть отрицательным. Оно или положительно, или равно нулю. Например, . Другими словами, расстояние от точки -2 до нуля равно 2. Этим мы пользуемся при решении уравнений.
1. Решим уравнение:
Решение:
На числовой прямой есть ровно две точки, расстояние от которых до нуля равно двум. Это точки 2 и -2. Значит, у уравнения есть два решения:
и
.
Ответ: -2; 2.
2. Решите уравнение:
Решение:
Ответ:
3. Решите уравнение:
Решение:
Мы получили совокупность двух квадратных уравнений. А затем решили отдельно каждое из них.
Вот что мы делали, решая квадратные уравнения:
— применили теорему Виета и нашли корни.
корней нет.
Ответ:
4. Решим уравнение:
Решение:
Задача похожа на предыдущую.
Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение равносильно совокупности двух простых:
или
Второе уравнение не имеет корней. Решения первого: x = 0 и x = 5.
Ответ: 0; 5.
к оглавлению ▴
Слева модуль, справа выражение, зависящее от переменной
Здесь приходится раскрывать модуль по определению. . . или соображать!
5.
Решение:
Уравнение распадается на два случая, в зависимости от знака выражения под модулем.
Другими словами, оно равносильно совокупности двух систем:

Решение первой системы: . У второй системы решений нет.
Ответ: 1.
6.
Решение:
Первый случай: x ≥ 3. Снимаем модуль:
Число , будучи отрицательным, не удовлетворяет условию x ≥ 3 и потому не является корнем исходного уравнения.
Выясним, удовлетворяет ли данному условию число . Для этого составим разность и определим её знак:
Значит, больше трёх и потому является корнем исходного уравнения.
Второй случай: x < 3. Снимаем модуль:
Число . больше, чем
, и потому не удовлетворяет условию x < 3. Проверим
:
Значит, . является корнем исходного уравнения.
Ответ:
7. Решите уравнение: = x.
Если уравнение имеет несколько корней, в ответе запишите меньший корень
Решение:
ОДЗ уравнения: x≠3. Так как в левой части уравнения — неотрицательная величина, должно также выполняться условие Возведем обе части уравнения в квадрат
= x
(разность квадратов),
Так как — это посторонний корень. Уравнение имеет два корня:
или
Меньший корень: 1.
Ответ: 1.
8.
Решение:
Снимать модуль по определению? Страшно даже подумать об этом, ведь дискриминант — не полный квадрат.
Давайте воспользуемся следующим правилом:
Уравнение вида равносильно совокупности двух систем:

То же самое, но немного по-другому:
Иными словами, мы решаем два уравнения, A = B и A = −B, а потом отбираем корни, удовлетворяющие условию
Приступаем. Сначала решаем первое уравнение:
Затем решаем второе уравнение:
Теперь в каждом случае проверяем знак правой части:
Подходят только и
.
Ответ:
Еще одно уравнение того же типа.
9. Решите уравнение: .
Это уравнение вида Вспомним, что оно равносильно системе:
Получим:
Решим отдельно каждое уравнение совокупности.
по теореме Виета.
Система примет вид:
Сравним и
Для сравнения мы будем использовать вот такой символ:
.
Умножим обе части этого неравенства на 2: .
Прибавим 5 к обеим частям выражения: Обе части выражения неотрицательны, поэтому возведем их в квадрат и сравним квадраты. Очевидно, 17
9. Это значит, что
и
Остальные корни, очевидно, меньше, чем -1.
Ответ: .
к оглавлению ▴
Квадратные уравнения с заменой 
Замена переменной — универсальный способ решения всевозможных уравнений. И этот способ помогает нам решать квадратные уравнения, содержащие переменную под знаком модуля.
10. Решим уравнение:
Решение:
Поскольку , удобно сделать замену |x| = t. Получаем:

Ответ: ±1.
к оглавлению ▴
Модуль равен модулю
Речь идёт об уравнениях вида Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:
Как мы получили это равенство? Покажем на примере задачи.
11. Решите уравнение:
Решение:
Возведем обе части в квадрат, поскольку они неотрицательны.
Перенесем все в левую часть и воспользуемся формулой разности квадратов:
Ответ:
12. Решим уравнение: .
Решение:
Уравнение равносильно следующей совокупности:
Решим каждое из уравнений совокупности и запишем ответ.
1)
— корни первого квадратного уравнения.
2)
— корни второго квадратного уравнения.
В ответ запишем все 4 корня.
Ответ:
к оглавлению ▴
Два или несколько модулей
13. Решим уравнение:
Решение:
Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.
Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении).
Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.
Случай 1: x ≥ 3. Все модули снимаются с «плюсом»:
Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.
Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается с «минусом»:
Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.
Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются с «минусом»:
Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.
Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:
Ничего нового. Мы и так знаем, что x = 1 является решением.
Ответ: [1; 2] ∪ {5}.
к оглавлению ▴
Модуль в модуле
14. Решим уравнение:
Решение:
Начинаем с раскрытия внутреннего модуля.
1) x ≤ 3. Получаем:
Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.
1.1) Получаем в этом случае:
Это значение x не годится, так как не принадлежит рассматриваемому промежутку.
1.2) . Тогда:
Это значение x также не годится.
Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.
2) x ≥ 3. Имеем:
Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается с «плюсом»:
Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.
Ответ: 4.
Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.
Часто в решении уравнений и неравенств с модулем используется график функции Он строится согласно определению модуля:
.
Для получаем участок графика y = x.
Для получаем участок графика y = −x. Вот этот график:
15. Решите уравнение:
Решение:
Сделаем замену переменной:
Тогда
Получим:
Мы помним, что
Решим уравнение графически. В левой части — график функции
Построим этот график. Сначала изобразим графики функций (точка минимума (3; 0)) и
(точка минимума ( -3; 0)). Можно сказать, что график функции
сдвинут относительно графика
на 3 единицы вправо, а график
— на 3 единицы влево.
И построим график суммы функций и
В точке с абсциссой 3 значение одного из слагаемых равно 0, другое слагаемое равно 6, сумма равна 6.
В точке с абсциссой -3 аналогично.
При х = 0 оба слагаемых равны 3, сумма равна 6.
Легко доказать, что сумма двух линейных функций есть линейная функция.
Поэтому при — получим горизонтальный участок. При x
3 получим луч с угловым коэффициентом, равным 2, а при x
— 3 — луч с угловым коэффициентом, равным — 2.
Решения нашего уравнения — все принадлежащие отрезку от
до
значит,
Ответ:
Мы рассмотрели все основные типы уравнений с модулями.
Читайте также о том, как решать неравенства с модулем.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Уравнения с модулем» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Решение неравенств с модулем
4 февраля 2018
- Домашняя работа
- Ответы и решения
Сегодня, друзья, не будет никаких соплей и сантиментов. Вместо них я без лишних вопросов отправлю вас в бой с одним из самых грозных противников в курсе алгебры 8—9 класса.
Да, вы всё правильно поняли: речь идёт о неравенствах с модулем. Мы рассмотрим четыре основных приёма, с помощью которых вы научитесь решать порядка 90% таких задач. А что с остальными 10%? Что ж, о них мы поговорим в отдельном уроке.:)
Однако перед тем, как разбирать какие-то там приёмы, хотелось бы напомнить два факта, которые уже необходимо знать. Иначе вы рискуете вообще не понять материал сегодняшнего урока.
Что уже нужно знать
Капитан Очевидность как бы намекает, что для решения неравенств с модулем необходимо знать две вещи:
- Как решаются неравенства;
- Что такое модуль.
Начнём со второго пункта.
Определение модуля
Тут всё просто. Есть два определения: алгебраическое и графическое. Для начала — алгебраическое:
Определение. Модуль числа $x$ — это либо само это число, если оно неотрицательно, либо число, ему противоположное, если исходный $x$ — всё-таки отрицателен.
Записывается это так:
[left| x right|=left{ begin{align} & x, xge 0, \ & -x, x lt 0. \end{align} right.]
Говоря простым языком, модуль — это «число без минуса». И именно в этой двойственности (где-то с исходным числом ничего не надо делать, а где-то придётся убрать какой-то там минус) и заключается вся сложность для начинающих учеников.
Есть ещё геометрическое определение. Его тоже полезно знать, но обращаться к нему мы будем лишь в сложных и каких-то специальных случаях, где геометрический подход удобнее алгебраического (спойлер: не сегодня).
Определение. Пусть на числовой прямой отмечена точка $a$. Тогда модулем $left| x-a right|$ называется расстояние от точки $x$ до точки $a$ на этой прямой.
Если начертить картинку, то получится что-то типа этого:
Так или иначе, из определения модуля сразу следует его ключевое свойство: модуль числа всегда является величиной неотрицательной. Этот факт будет красной нитью идти через всё наше сегодняшнее повествование.
Решение неравенств. Метод интервалов
Теперь разберёмся с неравенствами. Их существует великое множество, но наша задача сейчас — уметь решать хотя бы самые простые из них. Те, которые сводятся к линейным неравенствам, а также к методу интервалов.
На эту тему у меня есть два больших урока (между прочем, очень, ОЧЕНЬ полезных — рекомендую изучить):
- Метод интервалов для неравенств (особенно посмотрите видео);
- Дробно-рациональные неравенства — весьма объёмный урок, но после него у вас вообще не останется каких-либо вопросов.
Если вы всё это знаете, если фраза «перейдём от неравенства к уравнению» не вызывает у вас смутное желание убиться об стену, то вы готовы: добро пожаловать в ад к основной теме урока.:)
1. Неравенства вида «Модуль меньше функции»
Это одна из самых часто встречающихся задач с модулями. Требуется решить неравенство вида:
[left| f right| lt g]
В роли функций $f$ и $g$ может выступать что угодно, но обычно это многочлены. Примеры таких неравенств:
[begin{align} & left| 2x+3 right| lt x+7; \ & left| {{x}^{2}}+2x-3 right|+3left( x+1 right) lt 0; \ & left| {{x}^{2}}-2left| x right|-3 right| lt 2. \end{align}]
Все они решаются буквально в одну строчку по схеме:
[left| f right| lt gRightarrow -g lt f lt gquad left( Rightarrow left{ begin{align} & f lt g, \ & f gt -g \end{align} right. right)]
Нетрудно заметить, что избавляемся от модуля, но взамен получаем двойное неравенство (или, что тоже самое, систему из двух неравенств). Зато этот переход учитывает абсолютно все возможные проблемы: если число под модулем положительно, метод работает; если отрицательно — всё равно работает; и даже при самой неадекватной функции на месте $f$ или $g$ метод всё равно сработает.
Естественно, возникает вопрос: а проще нельзя? К сожалению, нельзя. В этом вся фишка модуля.
Впрочем, хватит философствовать. Давайте решим парочку задач:
Задача. Решите неравенство:
[left| 2x+3 right| lt x+7]
Решение. Итак, перед нами классическое неравенство вида «модуль меньше» — даже преобразовывать нечего. Работаем по алгоритму:
[begin{align} & left| f right| lt gRightarrow -g lt f lt g; \ & left| 2x+3 right| lt x+7Rightarrow -left( x+7 right) lt 2x+3 lt x+7 \end{align}]
Не торопитесь раскрывать скобки, перед которыми стоит «минус»: вполне возможно, что из-за спешки вы допустите обидную ошибку.
[-x-7 lt 2x+3 lt x+7]
Поскольку дальше нужно решить каждое неравенство отдельно, пора переходить к системе (можно было сделать это и раньше, но тогда решение получится чуть более громоздким):
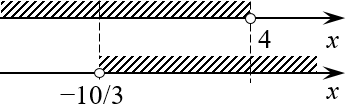
[left{ begin{align} & -x-7 lt 2x+3 \ & 2x+3 lt x+7 \ end{align} right.]
[left{ begin{align} & -3x lt 10 \ & x lt 4 \ end{align} right.]
[left{ begin{align} & x gt -frac{10}{3} \ & x lt 4 \ end{align} right.]
Задача свелась к двум элементарным неравенствам. Отметим их решения на параллельных числовых прямых:
Пересечение множеств Пересечением этих множеств и будет ответ.
Ответ: $xin left( -frac{10}{3};4 right)$
Задача. Решите неравенство:
[left| {{x}^{2}}+2x-3 right|+3left( x+1 right) lt 0]
Решение. Это задание уже чуть посложнее. Для начала уединим модуль, перенеся второе слагаемое вправо:
[left| {{x}^{2}}+2x-3 right| lt -3left( x+1 right)]
Очевидно, перед нами вновь неравенство вида «модуль меньше», поэтому избавляемся от модуля по уже известному алгоритму:
[-left( -3left( x+1 right) right) lt {{x}^{2}}+2x-3 lt -3left( x+1 right)]
Вот сейчас внимание: кто-то скажет, что я немного извращенец со всеми этими скобками. Но ещё раз напомню, что наша ключевая цель — грамотно решить неравенство и получить ответ. Позже, когда вы в совершенстве освоите всё, о чём рассказано в этом уроке, можете сами извращаться как хотите: раскрывать скобки, вносить минусы и т.д.
А мы для начала просто избавимся от двойного минуса слева:
[-left( -3left( x+1 right) right)=left( -1 right)cdot left( -3 right)cdot left( x+1 right)=3left( x+1 right)]
Теперь раскроем все скобки в двойном неравенстве:
[3x+3 lt {{x}^{2}}+2x-3 lt -3x-3]
Переходим к двойному неравенству. В этот раз выкладки будут посерьёзнее:
[left{ begin{align} & {{x}^{2}}+2x-3 lt -3x-3 \ & 3x+3 lt {{x}^{2}}+2x-3 \ end{align} right.]
[left{ begin{align} & {{x}^{2}}+5x lt 0 \ & {{x}^{2}}-x-6 gt 0 \ end{align} right.]
Оба неравенства являются квадратными и решаются методом интервалов (потому и говорю: если не знаете, что это такое, лучше пока не браться за модули). Переходим к уравнению в первом неравенстве:
[begin{align} & {{x}^{2}}+5x=0; \ & xleft( x+5 right)=0; \ & {{x}_{1}}=0;{{x}_{2}}=-5. \end{align}]
Как видим, на выходе получилось неполное квадратное уравнение, которое решается элементарно. Теперь разберёмся со вторым неравенством системы. Там придётся применить теорему Виета:
[begin{align} & {{x}^{2}}-x-6=0; \ & left( x-3 right)left( x+2 right)=0; \& {{x}_{1}}=3;{{x}_{2}}=-2. \end{align}]
Отмечаем полученные числа на двух параллельных прямых (отдельная для первого неравенства и отдельная для второго):
Опять же, поскольку мы решаем систему неравенств, нас интересует пересечение заштрихованных множеств: $xin left( -5;-2 right)$. Это и есть ответ. Ответ: $xin left( -5;-2 right)$
Думаю, после этих примеров схема решения предельно ясна:
- Уединить модуль, перенеся все другие слагаемые в противоположную часть неравенства. Таким образом мы получим неравенство вида $left| f right| lt g$.
- Решить это неравенство, избавившись от модуля по описанной выше схеме. В какой-то момент потребуется перейти от двойного неравенства к системе из двух самостоятельных выражений, каждое из которых уже можно решать отдельно.
- Наконец, останется лишь пересечь решения этих двух самостоятельных выражений — и всё, мы получим окончательный ответ.
Аналогичный алгоритм существует и для неравенств следующего типа, когда модуль больше функции. Однако там есть парочка серьёзных «но». Об этих «но» мы сейчас и поговорим.
2. Неравенства вида «Модуль больше функции»
Выглядят они так:
[left| f right| gt g]
Похоже на предыдущее? Похоже. И тем не менее решаются такие задачи совсем по-другому. Формально схема следующая:
[left| f right| gt gRightarrow left[ begin{align} & f gt g, \ & f lt -g \end{align} right.]
Другими словами, мы рассматриваем два случая:
- Сначала просто игнорируем модуль — решаем обычное неравенство;
- Затем по сути раскрываем модуль со знаком «минус», а затем умножаем обе части неравенства на −1, меня при этом знак.
При этом варианты объединены квадратной скобкой, т.е. перед нами совокупность двух требований.
Обратите внимание ещё раз: перед нами не система, а совокупность, поэтому в ответе множества объединяются, а не пересекаются. Это принципиальное отличие от предыдущего пункта!
Вообще, с объединениями и пересечениями у многих учеников сплошная путаница, поэтому давайте разберёмся в этом вопросе раз и навсегда:
- «∪» — это знак объединения. По сути, это стилизованная буква «U», которая пришла к нам из английского языка и является аббревиатурой от «Union», т.е. «Объединения».
- «∩» — это знак пересечения. Эта хрень ниоткуда не пришла, а просто возникла как противопоставление к «∪».
Чтобы ещё проще было запомнить, просто пририсуйте к этим знакам ножки, чтобы получились бокалы (вот только не надо сейчас обвинять меня в пропаганде наркомании и алкоголизма: если вы всерьёз изучаете этот урок, то вы уже наркоман):
В переводе на русский это означает следующее: объединение (совокупность) включает в себя элементы из обоих множеств, поэтому никак не меньше каждого из них; а вот пересечение (система) включает в себя лишь те элементы, которые одновременно находятся и в первом множестве, и во втором. Поэтому пересечение множеств никогда не бывает больше множеств-исходников.
Так стало понятнее? Вот и отлично. Переходим к практике.
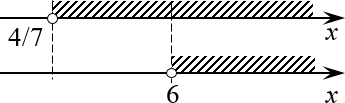
Задача. Решите неравенство:
[left| 3x+1 right| gt 5-4x]
Решение. Действуем по схеме:
[left| 3x+1 right| gt 5-4xRightarrow left[ begin{align} & 3x+1 gt 5-4x \ & 3x+1 lt -left( 5-4x right) \end{align} right.]
Решаем каждое неравенство совокупности:
[left[ begin{align} & 3x+4x gt 5-1 \ & 3x-4x lt -5-1 \ end{align} right.]
[left[ begin{align} & 7x gt 4 \ & -x lt -6 \ end{align} right.]
[left[ begin{align} & x gt 4/7 \ & x gt 6 \ end{align} right.]
Отмечаем каждое полученное множество на числовой прямой, а затем объединяем их:
Объединение множеств Совершенно очевидно, что ответом будет $xin left( frac{4}{7};+infty right)$
Ответ: $xin left( frac{4}{7};+infty right)$
Задача. Решите неравенство:
[left| {{x}^{2}}+2x-3 right| gt x]
Решение. Ну что? Да ничего — всё то же самое. Переходим от неравенства с модулем к совокупности двух неравенств:
[left| {{x}^{2}}+2x-3 right| gt xRightarrow left[ begin{align} & {{x}^{2}}+2x-3 gt x \ & {{x}^{2}}+2x-3 lt -x \end{align} right.]
Решаем каждое неравенство. К сожалению, корни там будут не оч:
[begin{align} & {{x}^{2}}+2x-3 gt x; \ & {{x}^{2}}+x-3 gt 0; \ & D=1+12=13; \ & x=frac{-1pm sqrt{13}}{2}. \end{align}]
Во втором неравенстве тоже немного дичи:
[begin{align} & {{x}^{2}}+2x-3 lt -x; \ & {{x}^{2}}+3x-3 lt 0; \ & D=9+12=21; \ & x=frac{-3pm sqrt{21}}{2}. \end{align}]
Теперь нужно отметить эти числа на двух осях — по одной оси для каждого неравенства. Однако отмечать точки нужно в правильном порядке: чем больше число, тем дальше сдвигам точку вправо.
И вот тут нас ждёт подстава. Если с числами $frac{-3-sqrt{21}}{2} lt frac{-1-sqrt{13}}{2}$ всё ясно (слагаемые в числителе первой дроби меньше слагаемых в числителе второй, поэтому сумма тоже меньше), с числами $frac{-3-sqrt{13}}{2} lt frac{-1+sqrt{21}}{2}$ тоже не возникнет затруднений (положительное число заведомо больше отрицательного), то вот с последней парочкой всё не так однозначно. Что больше: $frac{-3+sqrt{21}}{2}$ или $frac{-1+sqrt{13}}{2}$? От ответа на этот вопрос будет зависеть расстановка точек на числовых прямых и, собственно, ответ.
Поэтому давайте сравнивать:
[begin{matrix} frac{-1+sqrt{13}}{2}vee frac{-3+sqrt{21}}{2} \ -1+sqrt{13}vee -3+sqrt{21} \ 2+sqrt{13}vee sqrt{21} \end{matrix}]
Мы уединили корень, получили неотрицательные числа с обеих сторон неравенства, поэтому вправе возвести обе стороны в квадрат:
[begin{matrix} {{left( 2+sqrt{13} right)}^{2}}vee {{left( sqrt{21} right)}^{2}} \ 4+4sqrt{13}+13vee 21 \ 4sqrt{13}vee 3 \end{matrix}]
Думаю, тут и ежу понятно, что $4sqrt{13} gt 3$, поэтому $frac{-1+sqrt{13}}{2} gt frac{-3+sqrt{21}}{2}$, окончательно точки на осях будут расставлены вот так:
Случай некрасивых корней Напомню, мы решаем совокупность, поэтому в ответ пойдёт объединение, а не пересечение заштрихованных множеств.
Ответ: $xin left( -infty ;frac{-3+sqrt{21}}{2} right)bigcup left( frac{-1+sqrt{13}}{2};+infty right)$
Как видите, наша схема прекрасно работает как для простых задач, так и для весьма жёстких. Единственное «слабое место» в таком подходе — нужно грамотно сравнивать иррациональные числа (и поверьте: это не только корни). Но вопросам сравнения будет посвящён отдельный (и очень серьёзный урок). А мы идём дальше.
3. Неравенства с неотрицательными «хвостами»
Вот мы и добрались до самого интересного. Это неравенства вида:
[left| f right| gt left| g right|]
Вообще говоря, алгоритм, о котором мы сейчас поговорим, верен н только для модуля. Он работает во всех неравенствах, где слева и справа стоят гарантированно неотрицательные выражения:
[f gt g,quad fge 0,gge 0]
Что делать с этими задачами? Просто помните:
В неравенствах с неотрицательными «хвостами» можно возводить обе части в любую натуральную степень. Никаких дополнительных ограничений при этом не возникнет.
Прежде всего нас будет интересовать возведение в квадрат — он сжигает модули и корни:
[begin{align} & {{left( left| f right| right)}^{2}}={{f}^{2}}; \ & {{left( sqrt{f} right)}^{2}}=f. \end{align}]
Вот только не надо путать это с извлечением корня из квадрата:
[sqrt{{{f}^{2}}}=left| f right|ne f]
Бесчисленное множество ошибок было допущено в тот момент, когда ученик забывал ставить модуль! Но это совсем другая история (это как бы иррациональные уравнения), поэтому не будем сейчас в это углубляться. Давайте лучше решим парочку задач:
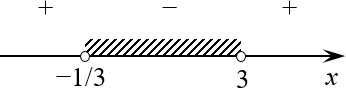
Задача. Решите неравенство:
[left| x+2 right|ge left| 1-2x right|]
Решение. Сразу заметим две вещи:
- Это нестрогое неравенство. Точки на числовой прямой будут выколоты.
- Обе стороны неравенства заведомо неотрицательны (это свойство модуля: $left| fleft( x right) right|ge 0$).
Следовательно, можем возвести обе части неравенства в квадрат, чтобы избавиться от модуля и решать задачу обычным методом интервалов:
[begin{align} & {{left( left| x+2 right| right)}^{2}}ge {{left( left| 1-2x right| right)}^{2}}; \ & {{left( x+2 right)}^{2}}ge {{left( 2x-1 right)}^{2}}. \end{align}]
На последнем шаге я слегка схитрил: поменял последовательность слагаемых, воспользовавшись чётностью модуля (по сути, умножил выражение $1-2x$ на −1).
Дальше можно перенести всё вправо и расписать разность квадратов. Только аккуратно:
[begin{align} & {{left( 2x-1 right)}^{2}}-{{left( x+2 right)}^{2}}le 0; \ & left( left( 2x-1 right)-left( x+2 right) right)cdot left( left( 2x-1 right)+left( x+2 right) right)le 0; \ & left( 2x-1-x-2 right)cdot left( 2x-1+x+2 right)le 0; \ & left( x-3 right)cdot left( 3x+1 right)le 0. \end{align}]
Решаем методом интервалов. Переходим от неравенства к уравнению:
[begin{align} & left( x-3 right)left( 3x+1 right)=0; \ & {{x}_{1}}=3;{{x}_{2}}=-frac{1}{3}. \end{align}]
Отмечаем найденные корни на числовой прямой. Ещё раз: все точки закрашены, поскольку исходное неравенство — нестрогое!
Избавление от знака модуля Напомню для особо упоротых: знаки мы берём из последнего неравенства, которое было записано перед переходом к уравнению. И закрашиваем области, требуемые в том же неравенстве. В нашем случае это $left( x-3 right)left( 3x+1 right)le 0$.
Ну вот и всё. Задача решена.
Ответ: $xin left[ -frac{1}{3};3 right]$.
Задача. Решите неравенство:
[left| {{x}^{2}}+x+1 right|le left| {{x}^{2}}+3x+4 right|]
Решение. Делаем всё то же самое. Я не буду комментировать — просто посмотрите на последовательность действий.
Возводим в квадрат:
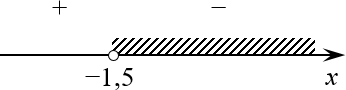
[begin{align} & {{left( left| {{x}^{2}}+x+1 right| right)}^{2}}le {{left( left| {{x}^{2}}+3x+4 right| right)}^{2}}; \ & {{left( {{x}^{2}}+x+1 right)}^{2}}le {{left( {{x}^{2}}+3x+4 right)}^{2}}; \ & {{left( {{x}^{2}}+x+1 right)}^{2}}-{{left( {{x}^{2}}+3x+4 right)}^{2}}le 0; \ & left( {{x}^{2}}+x+1-{{x}^{2}}-3x-4 right)times \ & times left( {{x}^{2}}+x+1+{{x}^{2}}+3x+4 right)le 0; \ & left( -2x-3 right)left( 2{{x}^{2}}+4x+5 right)le 0. \end{align}]
Метод интервалов:
[begin{align} & left( -2x-3 right)left( 2{{x}^{2}}+4x+5 right)=0 \ & -2x-3=0Rightarrow x=-1,5; \ & 2{{x}^{2}}+4x+5=0Rightarrow D=16-40 lt 0Rightarrow varnothing . \end{align}]
Всего один корень на числовой прямой:
Ответ — целый интервал Ответ: $xin left[ -1,5;+infty right)$.
Небольшое замечание насчёт последней задачи. Как точно подметил один мой ученик, оба подмодульных выражения в данном неравенстве заведомо положительны, поэтому знак модуля можно без ущерба для здоровья опустить.
Но это уже совсем другой уровень размышлений и другой подход — его условно можно назвать методом следствий. О нём — в отдельном уроке. А сейчас перейдём к финальной части сегодняшнего урока и рассмотрим универсальный алгоритм, который работает всегда. Даже тогда, когда все предыдущие подходы оказались бессильны.:)
4. Метод перебора вариантов
А что, если все эти приёмы не помогут? Если неравенство не сводится неотрицательным хвостам, если уединить модуль не получается, если вообще боль-печаль-тоска?
Тогда на сцену выходит «тяжёлая артиллерия» всей математики — метод перебора. Применительно к неравенствам с модулем выглядит он так:
- Выписать все подмодульные выражения и приравнять их к нулю;
- Решить полученные уравнения и отметить найденные корни на одной числовой прямой;
- Прямая разобьётся на несколько участков, внутри которого каждый модуль имеет фиксированный знак и потому однозначно раскрывается;
- Решить неравенство на каждом таком участке (можно отдельно рассмотреть корни-границы, полученные в пункте 2 — для надёжности). Результаты объединить — это и будет ответ.:)
Ну как? Слабо? Легко! Только долго. Посмотрим на практике:
Задача. Решите неравенство:
[left| x+2 right| lt left| x-1 right|+x-frac{3}{2}]
Решение. Эта хрень не сводится к неравенствам вида $left| f right| lt g$, $left| f right| gt g$ или $left| f right| lt left| g right|$, поэтому действуем напролом.
Выписываем подмодульные выражения, приравниваем их к нулю и находим корни:
[begin{align} & x+2=0Rightarrow x=-2; \ & x-1=0Rightarrow x=1. \end{align}]
Итого у нас два корня, которые разбивают числовую прямую на три участка, внутри которых каждый модуль раскрывается однозначно:
Разбиение числовой прямой нулями подмодульных функций Рассмотрим каждый участок отдельно.
1. Пусть $x lt -2$. Тогда оба подмодульных выражения отрицательны, и исходное неравенство перепишется так:
[begin{align} & -left( x+2 right) lt -left( x-1 right)+x-1,5 \ & -x-2 lt -x+1+x-1,5 \ & x gt 1,5 \end{align}]
Получили довольно простое ограничение. Пересечём его с исходным предположением, что $x lt -2$:
[left{ begin{align} & x lt -2 \ & x gt 1,5 \end{align} right.Rightarrow xin varnothing ]
Очевидно, что переменная $x$ не может одновременно быть меньше −2, но больше 1,5. Решений на этом участке нет.
1.1. Отдельно рассмотрим пограничный случай: $x=-2$. Просто подставим это число в исходное неравенство и проверим: выполняется ли оно?
[begin{align} & {{left. left| x+2 right| lt left| x-1 right|+x-1,5 right|}_{x=-2}} \ & 0 lt left| -3 right|-2-1,5; \ & 0 lt 3-3,5; \ & 0 lt -0,5Rightarrow varnothing . \end{align}]
Очевидно, что цепочка вычислений привела нас к неверному неравенству. Следовательно, исходное неравенство тоже неверно, и $x=-2$ не входит в ответ.
2. Пусть теперь $-2 lt x lt 1$. Левый модуль уже раскроется с «плюсом», но правый — всё ещё с «минусом». Имеем:
[begin{align} & x+2 lt -left( x-1 right)+x-1,5 \ & x+2 lt -x+1+x-1,5 \& x lt -2,5 \end{align}]
Снова пересекаем с исходным требованием:
[left{ begin{align} & x lt -2,5 \ & -2 lt x lt 1 \end{align} right.Rightarrow xin varnothing ]
И снова пустое множество решений, поскольку нет таких чисел, которые одновременно меньше −2,5, но больше −2.
2.1. И вновь частный случай: $x=1$. Подставляем в исходное неравенство:
[begin{align} & {{left. left| x+2 right| lt left| x-1 right|+x-1,5 right|}_{x=1}} \ & left| 3 right| lt left| 0 right|+1-1,5; \ & 3 lt -0,5; \ & 3 lt -0,5Rightarrow varnothing . \end{align}]
Аналогично предыдущему «частному случаю», число $x=1$ явно не входит в ответ.
3. Последний кусок прямой: $x gt 1$. Тут все модули раскрываются со знаком «плюс»:
[begin{align} & x+2 lt x-1+x-1,5 \ & x+2 lt x-1+x-1,5 \ & x gt 4,5 \end{align}]
И вновь пересекаем найденное множество с исходным ограничением:
[left{ begin{align} & x gt 4,5 \ & x gt 1 \end{align} right.Rightarrow xin left( 4,5;+infty right)]
Ну наконец-то! Мы нашли интервал, который и будет ответом.
Ответ: $xin left( 4,5;+infty right)$
Напоследок — одно замечание, которое, возможно, убережёт вас от глупых ошибок при решении реальных задач:
Решения неравенств с модулями обычно представляют собой сплошные множества на числовой прямой — интервалы и отрезки. Гораздо реже встречаются изолированные точки. И ещё реже случается так, что границ решения (конец отрезка) совпадает с границей рассматриваемого диапазона.
Следовательно, если границы (те самые «частные случаи») не входят в ответ, то почти наверняка не войдут в ответ и области слева-справа от этих границ. И напротив: граница вошла в ответ — значит, и какие-то области вокруг неё тоже будут ответами.
Помните об этом, когда проверяете свои решения.
Смотрите также:
- Неравенства с модулем: графическое решение
- Уравнения, содержащие несколько модулей, вложенных друг в друга: как их решать?
- Решение ЕГЭ-2011: вариант 1, часть B
- Сводный тест по задачам B15 (1 вариант)
- Учимся расщеплять ответы в тригонометрических уравнениях
- Задача C1: тригонометрия и показательная функция — 1 вариант
Поиск
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 146 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Решите неравенство:
Источник: А. Ларин. Тренировочный вариант № 292.
Решите систему неравенств
Источник: А. Ларин: Тренировочный вариант № 57.
Найдите все значения a, при каждом из которых наименьшее значение функции
меньше −2.
Источник: ЕГЭ по математике 29.03.2019. Досрочная волна. Вариант 3 (только часть С)., Задания 18 (С6) ЕГЭ 2019
Решите неравенство
Источник: А. Ларин. Тренировочный вариант № 353.
Решите неравенство:
Источник: А. Ларин. Тренировочный вариант № 297.
Решите систему неравенств
Решите неравенство
Источник: А. Ларин. Тренировочный вариант № 345.
Решите неравенство
Решите неравенство:
Решите неравенство
Источник: А. Ларин: Тренировочный вариант № 170.
Решите неравенство:
Источник: А. Ларин. Тренировочный вариант № 293.
Решите неравенство:
Источник: А. Ларин. Тренировочный вариант № 396.
Решите неравенство:
Решите неравенство:
Источник: А. Ларин. Тренировочный вариант № 389.
Решите неравенство:
Решите систему неравенств
Источник: А. Ларин: Тренировочный вариант № 18.
Решите систему неравенств:
Источник: А. Ларин: Тренировочный вариант № 54.
Решите систему неравенств
Источник: А. Ларин: Тренировочный вариант № 3.
Решите неравенство
Решите систему неравенств
Всего: 146 1–20 | 21–40 | 41–60 | 61–80 …
ЗАДАНИЕ 15 ЕГЭ. НЕРАВЕНСТВА С МОДУЛЕМ.
Модулем (абсолютной величиной) называется функция, которая каждому числу 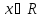
То есть, другими словами, модуль х – это расстояние от 0 (начало координат) до точки х. Т.к. расстояние – величина неотрицательная, то модуль х не может быть отрицательным: 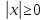
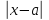
Свойства модуля:
Геометрический смысл модуля:
Рассмотрим на примерах.
-
. Решениями такого неравенства являются все числа, которые удалены от начала координат на расстояние, меньшее 8.
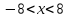
-
. Решением такого неравенства являются все числа, которые удалены от точки 5 на расстояние, не больше 3.
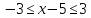
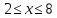
-
. Решением этого неравенства являются все числа, которые удалены от начала координат на расстояние, не меньшее 2.
-
. Решением этого неравенства являются все числа, которые удалены от точки
на расстояние, большее 5.
-
. Данное неравенство решений не имеет, т.к. расстояние не может быть отрицательным. Аналогично,
решений не имеет.
-
. Это неравенство имеет единственное решение
.
-
. Данное неравенство имеет бесконечно много решений, т.к. расстояние от точки х до нуля всегда больше отрицательного числа.
.
Виды неравенств, содержащих модуль:
-
Неравенство содержит некоторое выражение
под модулем и число вне модуля:
, где а – некоторое число.
Например, .
-
Неравенство, содержит выражение с переменной под знаком модуля и вне его:
.
Например, .
-
Неравенство, которое содержит несколько модулей:
Например, .
-
Неравенства вида , где
Например, .
-
Неравенства, решаемые заменой переменной.
Например, .
Способы решения неравенств, содержащих модуль:
-
Решение неравенств с помощью геометрического свойства модуля.
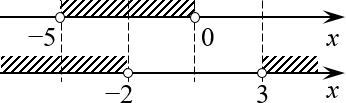
Пример 1.
Решением исходного неравенства будут все значения х, которые удовлетворяют хотя бы одному неравенству из совокупности и каждому неравенству из системы.
Ответ: .
Пример 2.
Решением исходного неравенства будут все значения х, которые удовлетворяют и совокупности, и двойному неравенству.
Ответ:
-
Решение неравенств, используя определение модуля.
Пример.
Воспользуемся определением модуля:
Ответ:
-
Решение неравенств методом возведения в квадрат.
Пример 1.
Левая и правая части данного неравенства являются положительными выражениями, поэтому их можно возвести в квадрат:
Так как 2 – чётный показатель степени, то по свойству 6 получаем:
Применяем формулу разности квадратов:
Значит,
Ответ:
Пример 2.
Применяем формулу разности квадратов:
Умножаем обе части неравенства на 400 (каждую скобку на 20):
Ответ:
-
Метод перебора вариантов (метод интервалов).
Так как этот метод достаточно сложный, приведём алгоритм его применения.
-
Выписать все подмодульные выражения, приравнять их к нулю и решить уравнения.
-
Найденные корни отметить на одной числовой прямой и на каждом получившемся участке определить знаки каждого подмодульного выражения.
-
Раскрыть модули согласно знакам на каждом участке и решить получившиеся неравенства.
-
Результаты объединить.
Пример.
Решим согласно алгоритму.
-
Раскроем модули на каждом участке.
Учитывая, условие , получаем:
Учитывая условие ,
Учитывая условие ,
-
Объединяя решения всех трёх неравенств, получим решение исходного неравенства:
Ответ:
-
Решение неравенств методом замены переменной.
Пример 1.
Сделаем замену переменной: . Тогда, согласно свойству 6
и неравенство примет вид:
Значит, . Возвращаемся в замену:
Ответ:
Пример 2.
Сделаем замену переменной: . Тогда неравенство принимает вид:
Значит, . Возвращаемся в замену переменной:
Ответ:
-
Графический способ решения неравенств.
Пример.
Решим это неравенство графически. Справа у нас линейная функция, графиком является прямая, проходящая через точки . Слева под знаком модуля квадратичная функция, графиком является парабола с вершиной в точке
, ветви направлены вверх. Т.к. квадратичная функция стоит под знаком модуля, то её отрицательная часть (там, где у отрицателен) отображается относительно оси Ох. Строим графики.
Графики пересекаются в точках А и В. Для того, чтобы выполнялось исходное неравенство, необходимо, чтобы прямая располагалась выше параболы. Это заштрихованный участок. Ему соответствует . Сами точки пересечения не включаются в промежуток, т.к. исходное неравенство строгое.
Ответ:
Приведённые ниже задания взяты из базы данных ЕГЭ.
-
Решить неравенство:
Решение. Упростим неравенство:
ОДЗ:
Левая и правая части полученного неравенства имеют одинаковые знаменатели, причём положительные при всех х из области допустимых значений.
Умножая обе части неравенства на знаменатель (он положителен!!!), получаем неравенство:
Воспользуемся первым способом решения неравенств, содержащих модуль (с помощью геометрического свойства модуля).
Учитывая ОДЗ, получаем:
Ответ:
-
Решить неравенство:
Решение.
Упростим неравенство:
Это неравенство удобно решать методом замены переменной:
. Тогда, учитывая 6 свойство модуля,
. Значит, неравенство принимает вид:
Отмечаем на числовой прямой нули левой части неравенства:
Значит, . Возвращаемся в замену переменной, т.е. вместо
ставим
. Получаем двойное неравенство, которое решаем в виде системы неравенств:
Ответ:
-
Решить неравенство:
Решение.
Упростим неравенство:
Воспользуемся методом перебора вариантов (методом интервалов):
-
Приравняем к нулю подмодульные выражения и найдём корни:
-
Отметим корни на числовой прямой и определим знаки подмодульных выражений на получившихся промежутках:
-
Раскроем модули на каждом промежутке.
Учитывая условие, что , получаем:
Учитывая условие, что , получаем:
Учитывая условие, что , получаем:
-
Объединяем решения всех трёх вариантов:
Ответ:
-
Решить неравенство:
Решение.
Воспользуемся первым способом решения неравенств, содержащих модуль (с помощью геометрического свойства модуля):
Ответ:
-
Решить неравенство:
Решение.
Преобразуем неравенство:
Воспользуемся методом замены переменной:
. Тогда неравенство примет вид:
Значит, . Учитывая условие
, сделанное при замене переменной, делаем вывод, что данное неравенство имеет решения только при
. Вернёмся к замене переменной:
Это уравнение имеет корни только в двух случаях:
Ответ:
-
Решить неравенство:
Решение.
Воспользуемся методом перебора вариантов. Так как под модулем у нас только х, то вариантов всего два:
|
1. |
2. |
||
|
|
|
||
|
|
|
||
Объединяя решения обоих случаев, получаем решение исходного неравенства:
Ответ:
-
Решить неравенство:
Решение.
Воспользуемся методом замены переменной:
. Тогда неравенство принимает вид:
Значит, учитывая условие , сделанное при замене переменной, получаем:
Вернёмся в замену переменной:
Значит, решение исходной системы имеет вид:
Ответ:
Задания для самостоятельного решения.
Решить неравенства:
Ответы на задания для самостоятельного решения.
8
Уравнения с модулем
Эта статья посвящена приёмам решения различных уравнений и неравенств, содержащих
переменную под знаком модуля.
Если на экзамене вам попадётся уравнение или неравенство с модулем, его можно решить,
вообще не зная никаких специальных методов и пользуясь только определением модуля. Правда,
занять это может часа полтора драгоценного экзаменационного времени.
Поэтому мы и хотим рассказать вам о приёмах, упрощающих решение таких задач.
Прежде всего вспомним, что
Рассмотрим различные типы уравнений с модулем. (К неравенствам перейдём позже.)
Слева модуль, справа число
Это самый простой случай. Решим уравнение
Есть только два числа, модули которых равны четырём. Это 4 и −4. Следовательно, уравнение
равносильно совокупности двух простых:
Второе уравнение не имеет решений. Решения первого: x = 0 и x = 5.
Переменная как под модулем, так и вне модуля
Здесь приходится раскрывать модуль по определению. . . или соображать!
Уравнение распадается на два случая, в зависимости от знака выражения под модулем.
Другими словами, оно равносильно совокупности двух систем:
Решение первой системы: . У второй системы решений нет.
Ответ: 1.
Первый случай: x ≥ 3. Снимаем модуль:
Число , будучи отрицательным, не удовлетворяет условию x ≥ 3 и потому не является корнем исходного уравнения.
Выясним, удовлетворяет ли данному условию число . Для этого составим разность и определим её знак:
Значит, больше трёх и потому является корнем исходного уравнения
Стало быть, годятся лишь и .
Ответ:
Квадратные уравнения с заменой |x| = t
Поскольку , удобно сделать замену |x| = t. Получаем:
Модуль равен модулю
Речь идёт об уравнениях вида |A| = |B|. Это — подарок судьбы. Никаких раскрытий модуля по определению! Всё просто:
Например, рассмотрим уравнение: . Оно равносильно следующей совокупности:
Остаётся решить каждое из уравнений совокупности и записать ответ.
Два или несколько модулей
Не будем возиться с каждым модулем по отдельности и раскрывать его по определению — слишком много получится вариантов. Существует более рациональный способ — метод интервалов.
Выражения под модулями обращаются в нуль в точках x = 1, x = 2 и x = 3. Эти точки делят числовую прямую на четыре промежутка (интервала). Отметим на числовой прямой эти точки и расставим знаки для каждого из выражений под модулями на полученных интервалах. (Порядок следования знаков совпадает с порядком следования соответствующих модулей в уравнении.)
Таким образом, нам нужно рассмотреть четыре случая — когда x находится в каждом из интервалов.
Случай 1: x ≥ 3. Все модули снимаются «с плюсом»:
Полученное значение x = 5 удовлетворяет условию x ≥ 3 и потому является корнем исходного уравнения.
Случай 2: 2 ≤ x ≤ 3. Последний модуль теперь снимается «с минусом»:
Полученное значение x также годится — оно принадлежит рассматриваемому промежутку.
Случай 3: 1 ≤ x ≤ 2. Второй и третий модули снимаются «с минусом»:
Мы получили верное числовое равенство при любом x из рассматриваемого промежутка [1; 2] служат решениями данного уравнения.
Случай 4: x ≤ 1 ≤ 1. Второй и третий модули снимаются «с минусом»:
Ничего нового. Мы и так знаем, что x = 1 является решением.
Модуль в модуле
Начинаем с раскрытия внутреннего модуля.
1) x ≤ 3. Получаем:
Выражение под модулем обращается в нуль при . Данная точка принадлежит рассматриваемому
промежутку. Поэтому приходится разбирать два подслучая.
1.1) Получаем в этом случае:
Это значение x не годится, так как не принадлежит рассматриваемому промежутку.
1.2) . Тогда:
Это значение x также не годится.
Итак, при x ≤ 3 решений нет. Переходим ко второму случаю.
Здесь нам повезло: выражение x + 2 положительно в рассматриваемом промежутке! Поэтому никаких подслучаев уже не будет: модуль снимается «с плюсом»:
Это значение x находится в рассматриваемом промежутке и потому является корнем исходного уравнения.
Так решаются все задачи данного типа — раскрываем вложенные модули по очереди, начиная с внутреннего.
Читайте также о том, как решать неравенства с модулем.
Уравнения_с_модулями
материал для подготовки к егэ (гиа) по алгебре (10 класс) на тему
Элективный курс по математике для учащихся 10-11 классов
Скачать:
| Вложение | Размер |
|---|---|
| 20295_uravneniya_s_modulyami.rar | 306.42 КБ |
Предварительный просмотр:
Занятие 1. Алгебраические уравнения с модулем.
Чтобы решить уравнение, содержащее переменную под знаком модуля, следует освободиться от знака модуля, воспользовавшись его определением:
При решении таких уравнений обычно поступают следующим образом:
- находят те значения переменной, при которых выражения, стоящие под знаком модуля, обращаются в нуль;
- область допустимых значений переменной разбивается на промежутки, на каждом из которых выражения, стоящие под знаком модуля, сохраняют знак;
- на каждом из найденных промежутков решается уравнение без знака модуля.
Совокупность решений на указанных промежутках составляет решение исходного уравнения.
Пример 1 . Решите уравнение: .
Найдем те значения переменной, при которых выражение, стоящее под знаком модуля, обращаются в нуль: х – 2 = 0, х = 2.
— +
Рассмотрим решение уравнения на промежутках: х (2; ).
1. Если х , то 2 – х = 5; — х = 3; х = — 3; — 3
2. Если : х (2; ), то х – 2 = 5; х = 7; 7 (2; ).
Пример 2 . Решите уравнение: = х + 2.
В левой части уравнения стоит неотрицательное число, следовательно
х + 2 0., т.е. х — 2. Раскроем модуль с учетом, что х — 2, получим:
х + 2 = х +2, решением уравнения является любое число х .
Пример 3. Решите уравнение: .
Найдем те значения переменной, при которых выражения, стоящие
под знаком модуля, обращаются в нуль: 2х + 1+ 0; х = — 0,5; х – 4 =0; х = 4.
— — + — + +
Рассмотрим решение уравнения на промежутках: х (4;+ ).
1. Если х , то -2х – 1 = — х + 4; -х = 5; х = — 5;
2. Если х , то 2х + 1 = — х +4; 3х = 3; х = 1.
3. Если х (4; + ), то 2х + 1 = х – 4; х = — 5;
Пример 4. Решите уравнение: 0,6 = х 2 + 0,27.
Найдем то значения переменной, при котором выражение, стоящее под знаком модуля, обращаются в нуль: х – 0,3 = 0; х = 0,3.
— +
0,3 х
0,6(0,3 – х) = х 2 + 0,27;
0,18 – 0,6х = х 2 + 0,27;
х 2 + 0,6х + 0,09 = 0;
2. Если х (0,3; + ), то
0,6(х — 0,3) = х 2 + 0,27;
0,6 х – 0,18 = х 2 + 0,27;
х 2 – 0,6х + 0,45 = 0;
D = 0,36 – 1,8 = — 1,44, т.к. D
Пример 5 . Решите уравнение: х 2 + 4 — 7х + 11 = 0.
Найдем то значения переменной, при котором выражение, стоящее под знаком модуля, обращаются в нуль: х – 3 = 0; х = 3.
— +
3 х
х 2 – 4(х – 3) – 7х + 11 = 0;
х 2 – 4х + 12 – 7х + 11 = 0;
х 2 – 11х + 23 = 0;
х 2 + 4х — 12 – 7х + 11 = 0;
1. = -2. Ответ: пустое множество;
2. = 5. Ответ: — 7; 3.
3. = 11. Ответ: — 4; 7.
4. = х. Ответ: пустое множество.
5. = 5 – 4х. Ответ: 1.
8. . Ответ: — 3,5; 3,5.
9. = + 2. Ответ: — 7; — 1.
.
По теме: методические разработки, презентации и конспекты
Методические рекомендации по теме: «Решение уравнений с модулем в курсе математики 7-8 класса»
Методические рекомендации по теме: «Решение уравнений с модулем в курсе математики 7-8 класса». В работе представлены способы решения уравнений с модулем. Даны карточки заданий: с применением классифи.
презентация уравнения с модулем
Данная презентация предназначена для использования на уроках алгеьбры и начал анализа в старшей школе при обобщении темы «Уравнения с модулем и способы их решения». Также презентацию можно использоват.
Решение дробно — рациональных уравнений с модулем.
Данная презентация разработана для подготовки учащихся 10 классса к КДР, может быть полезна для подготовки учащихся 11 класса к ЕГЭ.
Урок — семинар в 11 классе «Решение показательных и логарифмических уравнений с модулем»
Данный урок — семинар рекомендуется для работы в профильном классе, а также материал этого занятия можно использовать на факультативном занятии. Здесь предложен конспект урока, презентация, разадаточн.
Презентация к уроку»Графики уравнений с модулями»
Методическая разработка для повышения наглядности и качества усвоения материала по теме:»Графики уравнений с модулями».Основная цель-познакомить учащихся с основными приёмами построения графиков уравн.
Презентация «Уравнения с модулем»
Урок обобщения и систематизации знаний по теме: «Решение уравнений с модулем».
Решение уравнений, содержащих модуль.
Конспект урока для элективного занятия в 9 классе.
Уравнения с модулем
Что такое уравнение с модулем
Модуль числа — абсолютная величина, демонстрирующая удаленность точки от начала координат.
В том случае, когда число является отрицательным, его модуль соответствует числу, ему противоположному. Для неотрицательного числа модуль равен этому числу.
| x | = x , x ≥ 0 — x , x 0
Уравнения с модулем являются такими уравнениями, в составе которых имеется переменная, заключенная в знак модуля.
Самое простое уравнение с модулем |f(x)|=a является равносильным совокупности
Здесь a>0. При а отрицательном у такого уравнения отсутствует решение.
Уравнения с модулем могут быть предложены в качестве самостоятельного задания. Кроме того, подобные выражения нередко образуются в процессе решения других видов уравнений, к примеру, квадратных или иррациональных.
Разберем подробное решение квадратного уравнения:
Заметим, что справа имеется квадрат числа 4:
На первый взгляд, нужно избавиться от квадратов, чтобы получить линейное уравнение. С другой стороны, существует правило:
Вычисления следует продолжить с учетом записанной формулы. Тогда получим уравнение с модулем:
x 2 = 4 2 ⇔ x 2 = 4 2 ⇔ x = 4
Рассмотрим для тренировки пример, когда уравнения с модулем появляются при решении иррациональных уравнений. Например, дано уравнение:
2 x — 1 2 = 9 x 2 + 12 x + 4
Согласно стандартному алгоритму действий, в этом случае потребуется выполнить действия:
- перенос слагаемых;
- приведение подобных;
- решение квадратного уравнения, например, с помощью дискриминанта.
Второй вариант решения предусматривает использование формулы сокращенного умножения квадрат суммы:
9 x 2 + 12 x + 4 = 3 x + 2 2
Преобразуем сложное уравнение:
2 x — 1 2 = 3 x + 2 2
На первый взгляд, можно избавиться от квадратов и решить линейное уравнение. Однако:
В результате получим:
2 x — 1 2 = 3 x + 2 2 ⇔ 2 x — 1 = 3 x + 2 .
При решении уравнений, которые содержат модуль, необходимо помнить свойства модуля:
- Модуль числа является неотрицательным числом: x ≥ 0 , x = 0 ⇔ x = 0 .
- Противоположные числа равны друг другу по модулю: — x = x .
- Произведение пары или более чисел по модулю равно произведению модулей этих чисел: x · y = x · y .
- Частное пары чисел по модулю равно частному модулей этих чисел: x y = x y , y ≠ 0 .
- Сумма чисел по модулю в любом случае меньше или равна сумме модулей данных чисел: x + y ≤ x + y .
- Постоянный множитель, который больше нуля, допустимо вынести за знак модуля: c x = c · x при c > 0 .
- Квадрат какого-то числа по модулю равен квадрату данного числа: x 2 = x 2 .
Пример 3
Руководствуясь перечисленными свойствами модуля, рассмотрим решение уравнения:
Заметим, что x равен x при x больше либо равно нулю. Значение –x возможно, когда x является отрицательным числом. Таким образом:
x = 7 ⇔ x = 7 , п р и x ≥ 0 — x = 7 , п р и x 0 ⇔ x = 7 x = — 7
Рассмотрим несколько иное уравнение:
В этом случае логика такая же, как в предыдущем примере:
x = — 7 ⇔ x = — 7 , при x ≥ 0 — x = — 7 , при x 0 ⇔ x = — 7 x ≥ 0 ⇒ р е ш е н и я н е т x = 7 x 0 ⇒ р е ш е н и я н е т
Способы решения уравнений с модулями для 10 и 11 классов
Существует три основных вида уравнений с модулем, которые предусматривают определенные подходы к решению:
- Уравнения x = a . x = a ⇔ x = a , п р и x ≥ 0 — x = a , п р и x 0 ⇔ x = a x = — a .
- Уравнения вида x = y . x = y ⇔ y ≥ 0 x = y x = — y
Примеры решения задач с объяснением
Уравнения, которые содержат модуль и имеют вид |x| = |a|, решают с помощью определения модуля.
Рассмотрим в качестве примера:
Определим x . Когда x ≥ 0 , значение равно х . Если x – х . Таким образом:
x = 5 ⇔ x = 5 при x ≥ 0 — x = 5 при x 0 ⇔ x = 5 x = — 5 .
Получим, что решением уравнения являются -5; 5.
Рассмотрим следующее задание, в рамках которого необходимо решить уравнение:
Воспользуемся стандартным алгоритмом:
x = — 3 ⇔ x = — 3 при x ≥ 0 — x = — 3 при x 0 ⇔ x = — 3 x ≥ 0 ⇒ решений нет x = 3 x 0 ⇒ решений нет
Согласно первому свойству модуля:
x ≥ 0 , то есть модуль в любом случае не является отрицательным числом.
Можно обобщить рассмотренные действия и записать правило для решения уравнений, которые имеют вид x = a . Данное правило можно использовать в работе:
x = a ⇒ a ≥ 0 x = a x = — a .
Используя данное правило, решим уравнение:
По сравнению с предыдущим примером, здесь под знаком модуля записано иное выражение. Однако суть решения от этого не меняется. Зная правило, выполним замену:
x — 5 = 3 ⇔ 3 ≥ 0 x — 5 = 3 x — 5 = — 3 ⇒ x = 8 x = 2
Решим следующее уравнение:
Воспользуемся правилом и получим:
3 x — 5 = 3 ⇔ 3 ≥ 0 3 x — 5 = 3 3 x — 5 = — 3 ⇒ x = 8 3 x = 2 3
Далее рассмотрим решение уравнений, которые записаны в виде | x | = | y | .
При раскрытии модулей, согласно определению, возникнет необходимость во множестве проверок. Например, потребуется определить, какое число является положительным, а какое будет отрицательным. Полученную в результате систему в дальнейшем необходимо упростить.
Второй вариант решения подразумевает изначально краткую запись вычислений. Вспомним, что по свойству модуля:
Применим это свойство к нашему примеру и исключим знаки модулей из уравнения:
x = y ⇔ x 2 = y 2 ⇔ x 2 = y 2 ⇔ x 2 — y 2 = 0 ⇔
⇔ x — y x + y = 0 ⇔ x = y x = — y .
Рассмотрим еще несколько примеров.
Воспользуемся рассмотренным правилом применения свойства модуля, получим:
x + 1 = 2 x — 1 ⇔ x + 1 = 2 x — 1 x + 1 = — 2 x — 1 ⇔ x = 2 x = 0 .
Решение выполняем по аналогии с предыдущими заданиями:
2 x — 9 = 3 — x ⇔ 2 x — 9 = 3 — x 2 x — 9 = x — 3 ⇔ 3 x = 12 x = 6 ⇔ x = 4 x = 6 .
Разберем на примере, как решать уравнения вида | x | = y .
Заметим, что справа записана переменная, которая может быть положительным или отрицательным числом. Исходя из того, что модуль не может быть отрицательным числом, убедимся в том, что эта переменная также не является отрицательным числом:
x = y ⇔ y ≥ 0 x = y x = — y
Воспользуемся стандартным алгоритмом:
x + 1 = 1 — 2 x ⇔ 1 — 2 x ≥ 0 x + 1 = 1 — 2 x x + 1 = 2 x — 1 ⇔ x ≤ 1 2 x = 0 x = 2 ⇔ x = 0 .
Заметим, что без проверки на положительность части уравнения, которая записана с правой стороны, существуют риски появления посторонних корней в решении. К примеру, проверим x=2 путем подстановки в начальное уравнение x + 1 = 1 — 2 x :
2 + 1 = 1 — 2 · 2 ⇔ 3 = — 3 не является верным.
При решении уравнений с модулем также применяют метод интервалов. Данный способ следует применять в тех случаях, когда уравнение содержит более двух модулей.
Рассмотрим пример такого выражения:
x + 3 — 2 x — 1 = 1
Первый модуль имеет вид:
Согласно определению модуля, при раскрытии знака выражение под ним сохраняется без изменений, если:
После раскрытия знака модуля получим противоположный знак, когда:
x + 3 = x + 3 , если x + 3 ≥ 0 — x — 3 , если x + 3 0 .
По аналогии выполним преобразования второго модуля:
2 x — 1 = 2 x — 1 , если 2 x — 1 ≥ 0 1 — 2 x , если 2 x — 1 0 .
Сложность заключается в том, что требуется проанализировать много вариантов, то есть по два варианта для каждого из модулей. Всего получится четыре уравнения. А в том случае, когда модулей три, потребуется рассмотреть восемь уравнений. Возникает необходимость в сокращении числа вариантов.
Заметим, что в нашем примере не предусмотрено одновременное выполнение всех условий:
Данные условия противоречивы относительно друг друга. В связи с этим, нецелесообразно раскрывать второй модуль со знаком плюс, когда первый модуль раскрыт со знаком минус. В результате получилось избавиться от одного уравнения.
Обобщая эту информацию, можно записать алгоритм действий. В первую очередь следует вычислить корни выражений, заключенных под знаком модуля. В результате получаются такие х , при которых выражения принимают нулевые значения:
x + 3 = 0 ⇒ x = — 3 2 x — 1 = 0 ⇒ x = 1 2
С помощью стандартного способа интервалов можно отметить на координатной прямой корни выражений, которые находятся под модулями, и расставить знаки. Далее для каждого из полученных интервалов нужно составить и решить уравнение.
В этом случае оба модуля раскрываются со знаком минус:
— x + 3 + 2 x — 1 = 1 ⇔ — x — 3 + 2 x — 1 = 1 ⇔ x = 5 > — 3 является сторонним корнем.
В данном выражении первый модуль раскроется со знаком плюс, а второй — со знаком минус:
x + 3 + 2 x — 1 = 1 ⇔ x + 3 + 2 x — 1 = 1 ⇔ x = — 1 3 полученный корень соответствует своему интервалу.
Теперь для обоих модулей будет записан знак плюс:
x + 3 — 2 x — 1 = 1 ⇔ x + 3 — 2 x + 1 = 1 ⇔ x = 3 данный корень также подходит для решения.
Выполним проверку корней. В первом случае корень посторонний:
x = 5 : 5 + 3 — 2 · 5 — 1 = 8 — 9 = — 1 ≠ 1
Второй корень является решением:
x = — 1 3 : — 1 3 + 3 — 2 · — 1 3 — 1 = 8 3 — 5 3 = 1 .
Третий корень также является решением:
x = 3 : 3 + 3 — 2 · 3 — 1 = 6 — 5 = 1 .
Таким образом, запишем ответ: — 1 3 ; 3 .
Существует ряд уравнений, в которых модуль расположен под знаком модуля. К примеру:
В этом случае следует раскрывать модули поочередно. Проанализируем два варианта решения.
Первое решение подразумевает вычисления для уравнения, которое имеет вид:
f x = a ⇔ f x = a f x = — a
Здесь f x является подмодульным выражением. Применительно к нашей задаче, это:
x — 5 = 3 ⇔ x — 5 = 3 x — 5 = — 3 ⇔ x = 8 x = 2
Получена пара простейших уравнений аналогичного вида, то есть:
x = 8 x = — 8 x = 2 x = — 2
Данные четыре числа являются решениями. Проверить это можно путем подстановки ответов в исходное уравнение.
Второй вариант решения является универсальным и позволяет справиться с нестандартными задачами.
Раскроем сначала внутренние модули:
Начальное уравнение будет записано, как пара уравнений:
x ≥ 0 x — 5 = 3 x 0 — x — 5 = 3
Задачи для самостоятельного решения
Найти корни уравнения:
Здесь нужно возвести в квадрат все части выражения, сохраняя знак плюса справа. Тогда получится система:
Найдем корни квадратного уравнения:
3 x 2 — 18 x + 24 = 0
В процессе потребуется сократить уравнение на 3:
D = ( — 6 ) 2 — 4 · 1 · 8 = 36 — 32 = 4
Заметим, что D>0. В таком случае у уравнения есть пара решений, которые можно определить так:
x 1 , 2 = — b ± D 2 a ⇒ x 1 , 2 = 6 ± 4 2 · 1 ⇒ x 1 , 2 = 6 ± 2 2 ⇒ x 1 = 4 , x 2 = 2
Заметим, что оба корня больше единицы. Это соответствует условию. В результате начальное уравнение обладает двумя решениями:
x 1 = 4 и x 2 = 2
Ответ: x 1 = 4 , x 2 = 2
Найти корни уравнения:
Здесь требуется возвести в квадрат обе части уравнения:
( 3 x — 1 ) 2 = ( x + 5 ) 2
9 x 2 — 6 x + 1 = x 2 + 10 x + 25
8 x 2 — 16 x — 24 = 0
Заметим, что получившееся равенство можно сократить на число 8:
Используя теорему Виета, определим корни уравнения. Предположим, что x 1 и x 2 являются в данном случае решениями, тогда:
x 1 + x 2 = 2 , а x 1 · x 2 = — 3 ⇒ x 1 = 3 и x 2 = — 1 . .
Ответ: x 1 = 3 , x 2 = — 1
Нужно решить уравнение:
| x + 1 | + | x — 5 | = 20
Воспользуемся методом интервалов. Определим х , при которых модули принимают нулевые значения:
x + 1 = 0 ⇒ x = — 1 ; x — 5 = 0 ⇒ x = 5
С помощью данных точек координатная прямая будет поделена на три интервала:
Далее необходимо решить уравнение в каждом случае:
Корень соответствует определенному ранее промежутку.
Этот промежуток не имеет корней.
Этот корень соответствует определенному ранее интервалу.
Ответ: x 1 = — 8 , x 2 = 12
3 x + 1 = 1 — 2 x ⇔ 3 x + 3 = 1 — 2 x 3 x + 3 = 2 x — 1 ⇔ 5 x = — 2 x = — 4 ⇔ x = — 2 5 x = — 4 .
Ответ: x = — 2 5 , x = — 4
Найти корни уравнения:
2 x — 9 = 3 — x ⇔ 3 — x ≥ 0 2 x — 9 = 3 — x 2 x — 9 = x — 3
x ≤ 3 3 x = 12 x = 6 ⇔ x ≤ 3 x = 4 x = 6 ⇔ x ∈ ∅ .
Найти корни уравнения:
— 2 x + 4 = 3 — 4 x ⇔ 2 x + 8 = 4 x — 3 ⇔ ;
4 x — 3 ≥ 0 2 x + 8 = 4 x — 3 2 x + 8 = 3 — 4 x ⇔ x ≥ 3 4 x = 11 2 x = — 5 6 ⇔ x = 11 2 .
Найти корни уравнения:
2 x 2 — 15 = x ⇔ x ≥ 0 2 x 2 — x — 15 = 0 1 2 x 2 + x — 15 = 0 2
Найдем корни квадратных уравнений:
Заметим, что они обладают идентичным дискриминантом:
D = 1 + 4 · 2 · 15 = 121 = 11 2 .
1 : x 1 , 2 = 1 ± 11 4 ⇔ x = 3 x = — 5 2
2 : x 1 , 2 = — 1 ± 11 4 ⇔ x = — 3 x = 5 2
Таким образом, начальное уравнение можно записать в виде системы:
2 x 2 — 15 = x ⇔ x ≥ 0 x = 3 x = — 5 2 x = — 3 x = 5 2 ⇔ x = 3 x = 5 2
Найти корни уравнения:
x + 2 — 3 x — 1 + 4 — x = 3
x + 2 — 3 x — 1 + 4 — x = 3 x + 2 = 0 ⇒ x = — 2 3 x — 1 = 0 ⇒ x = 1 3 4 — x = 0 ⇒ x = 4
— x + 2 + 3 x — 1 + 4 — x = 3
x = 2 > — 2 ⇒ — этот корень является посторонним.
x + 2 + 3 x — 1 + 4 — x = 3 ⇔
3 x = — 2 ⇔ x = — 2 3 ∈ — 2 ; 1 3 этот корень удовлетворяет условиям.
x + 2 — 3 x — 1 + 4 — x = 3 ⇔ — 3 x = — 4 ⇔ x = 4 3 ∈ 1 3 ; 4 этот корень удовлетворяет условиям.
x + 2 — 3 x — 1 — 4 — x = 3 ⇔ x = 4 ⇔ x = — 4 4 — корень посторонний
Ответ: — 2 3 ; 4 3 .
Найти корни уравнения:
3 x — 5 + 3 + 2 x = 2 x + 1
3 x — 5 + 3 + 2 x = 2 x + 1 ⇔ 3 x — 5 + 3 + 2 x — 2 x + 1 = 0 .
3 x — 5 = 0 ⇒ x = 5 3 3 + 2 x = 0 ⇒ x = — 3 2 x + 1 = 0 ⇒ x = — 1
— 3 x — 5 — 3 + 2 x + 2 x + 1 = 0 ⇔
— 3 x = — 4 ⇔ x = 4 3 > — 3 2 ⇒ — корень является посторонним
— 3 x — 5 + 3 + 2 x + 2 x + 1 = 0 ⇔
x = — 10 — 1 ⇒ — корень является посторонним
— 3 x — 5 + 3 + 2 x — 2 x + 1 = 0 ⇔
— 3 x = — 6 ⇔ x = 2 > 5 3 ⇒ — корень является посторонним
3 x — 5 + 3 + 2 x — 2 x + 1 = 0 ⇔
3 x = 4 ⇔ x = 4 3 5 3 ⇒ — корень является посторонним
В результате на рассмотренных интервалах графика координатной прямой отсутствуют корни. В таком случае уравнение не имеет решений.
источники:
http://nsportal.ru/shkola/algebra/library/2015/04/20/uravneniya-s-modulyami
http://wika.tutoronline.ru/algebra/class/9/uravneniya-s-modulem




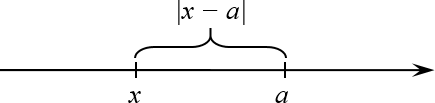

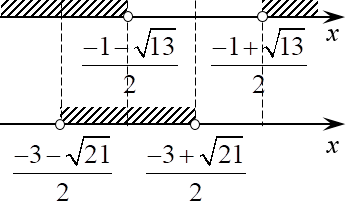
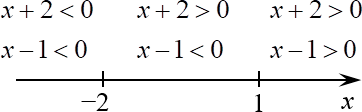
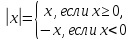
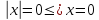
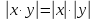
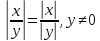
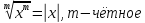
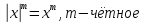
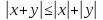
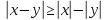
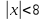 . Решениями такого неравенства являются все числа, которые удалены от начала координат на расстояние, меньшее 8.
. Решениями такого неравенства являются все числа, которые удалены от начала координат на расстояние, меньшее 8.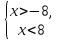
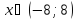
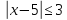 . Решением такого неравенства являются все числа, которые удалены от точки 5 на расстояние, не больше 3.
. Решением такого неравенства являются все числа, которые удалены от точки 5 на расстояние, не больше 3. 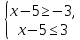
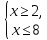
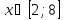
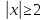 . Решением этого неравенства являются все числа, которые удалены от начала координат на расстояние, не меньшее 2.
. Решением этого неравенства являются все числа, которые удалены от начала координат на расстояние, не меньшее 2.



