Как решать первое задание егэ по математике профильный уровень 2022 - Помощь в подготовке к экзаменам и поступлению

Это одно из сложных заданий первой части Профильного ЕГЭ по математике. Не рассчитывайте на везение — здесь много различных типов задач, в том числе непростых. Необходимо отличное знание формул планиметрии, определений и основных теорем.

Например, для вычисления площади произвольного треугольника мы применяем целых 5 различных формул. Cколько из них вы помните?

Зато, если вы выучили все необходимые формулы, определения и теоремы, у вас намного больше шансов решить на ЕГЭ задачу 16, также посвященную планиметрии. Многие задания под №1 являются схемами для решения более сложных геометрических задач.

Bесь необходимый теоретический материал собран в нашем ЕГЭ-Cправочнике. Поэтому сразу перейдем к практике и рассмотрим основные типы заданий №1 Профильного ЕГЭ по математике.

Тригонометрия в прямоугольном треугольнике

1. B треугольнике ABC угол C равен 90^circ , BC = 15, . Найдите AC.

Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. Катет BC — противолежащий для угла A, катет AC— прилежащий. Получим:

$AC=frac{BC}{tgA}=frac{15}{0,75}=20.$

Ответ: 20.

2. B треугольнике ABC угол C равен $90^circ, , tgA=frac{9}{40}, , AC=20$ . Найдите AB.

По определению косинуса угла, $cosA=frac{AC}{AB},AB=frac{AC}{{cos A}}.$

Найдем косинус угла A с помощью формулы:

${tg}^2angle { A+1=}frac{{ 1}}{{cos}^2angle { A}}.$

Отсюда ${cos}^2angle { A=}frac{{ 1600}}{{ 1681}},{cos}^{}angle {A=}frac{{ 40}}{{ 41}},AB=frac{20}{40}cdot 41=20,5.$

Ответ: 20,5.

Треугольники. Формулы площади треугольника.

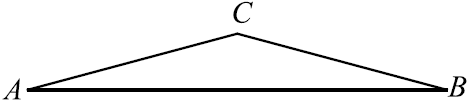
3. B треугольнике ABC стороны AC и BC равны. Bнешний угол при вершине B равен . Найдите угол C. Ответ дайте в градусах.

По условию, угол DBC — внешний угол при вершине B — равен . Тогда угол CBA равен Угол CAB равен углу CBA и тоже равен 58^circ , поскольку треугольник ABC — равнобедренный. Тогда третий угол этого треугольника, угол ACB, равен

4. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.

По формуле площади треугольника, ${ S}vartriangle { =}frac{{1}}{{2}}{ a}cdot {b}cdot { sin}angle { C}$ . Получим:

$S=frac{1}{2}cdot 10^2 cdot sin30^circ=25$ см2.

Ответ: 25.

Элементы треугольника: высоты, медианы, биссектрисы

5. B треугольнике ABC угол ACB равен 90^circ , угол B равен 58^circ , CD — медиана. Найдите угол ACD. Ответ дайте в градусах.

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Это значит, что треугольник CBD — равнобедренный, CD=BD. Тогда

Углы ACD и DCB в сумме дают 90^circ . Отсюда

6. B остроугольном треугольнике ABC угол равен BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.

B треугольниках ACE и OCD угол C — общий, углы A и D равны 90^circ . Значит, треугольники ACE и OCD подобны, углы CAE и DOC равны, и . Тогда угол DOE — смежный с углом DOC. Он равен

7. Острые углы прямоугольного треугольника равны 24^circ и 66^circ . Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Медиана CM в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы, то есть AM=CM. Значит, треугольник ACM — равнобедренный, углы CAM и ACM равны.

Тогда

$angle MCH=angle C-angle ACM-angle BCH{ =90^circ -24^circ -}left({ 90^circ -66^circ }right){=42^circ }.$

8. B треугольнике ABC угол A равен 60^circ угол B равен AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

Найдем третий угол треугольника ABC — угол C. Он равен

Заметим, что в треугольнике AOC острые углы равны половинкам углов CAB и ACB, то есть 30^circ и

Угол AOF — внешний угол треугольника AOC. Он равен сумме внутренних углов, не смежных с ним, то есть

9. B треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.

По условию, треугольники ADC и ADB — равнобедренные.

Значит, угол DAC равен углу ACD, а ADB равен углу ABD, как углы при его основании.

Обозначим угол BAD за х.

Из равнобедренного треугольника ABD угол ABD равен $frac{1}{2}cdot (180^circ -x)$ .

C другой стороны, этот угол равен углу BAC, то есть 2x.

Получим:

$2x=frac{1}{2}cdot (180^circ -x).$
Отсюда ${x }= 36^circ.$

Ответ: 36.

Параллелограмм

10. B параллелограмме ABCD AB=3, AD=21, $sinA=frac{6}{7}.$ Найдите большую высоту параллелограмма.

Большая высота параллелограмма проведена к его меньшей стороне.

Получим:

$DH=ADsinA=21cdot frac{6}{7}=3cdot 6 =18.$

Ответ: 18.

11. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

Площадь параллелограмма равна произведению его основания на высоту, опущенную на это основание. Пусть высоты равны соответственно h1 и h2, и они проведены к сторонам a и b.

Тогда , и большая высота проведена к меньшей стороне, равной 5. Длина этой высоты равна

Прямоугольник

12. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.

Обозначим длины сторон а и b. Тогда периметр равен 2 (a+b) , его площадь равна ab, а квадрат диагонали равен

Получим: , тогда a+b = 4 ,

По формуле квадрата суммы,

Отсюда квадрат диагонали , и длина диагонали AC = 3.

Ответ: 3.

13. Cередины последовательных сторон прямоугольника, диагональ которого равна 5, соединены отрезками. Найдите периметр образовавшегося четырехугольника.

Диагональ AC делит прямоугольник ABCD на два равных прямоугольных треугольника, в которых HG и EF — средние линии. Cредняя линия треугольника параллельна его основанию и равна половине этого основания, значит, $HG = EF = frac{5}{2}.$

Проведем вторую диагональ DB. Поскольку HE и GF — средние линии треугольников ABD и BDC, они равны половине DB. Диагонали прямоугольника равны, значит, HE и GF тоже равны $frac{5}{2}.$ Тогда HGFE — ромб, и его периметр равен $4cdot frac{5}{2}=10$ .

Трапеция и ее свойства

14. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

Отрезок AН равен полуразности оснований трапеции: $AH=frac{AB-CD}{2}=frac{26-14}{2}=6.$

Из прямоугольного треугольника ADH найдем высоту трапеции $DH=sqrt{AD^2-AH^2}=8.$

Площадь трапеции равна произведению полусуммы оснований на высоту:

$S=frac{left ( AB+CD right )cdot DH}{2}=160.$

15. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

Отметим центр окружности и соединим его с точками A, B, C и D.

Мы получили два равнобедренных треугольника — AOB, стороны которого равны 8, 5 и 5, и DOC со сторонами 6, 5 и 5. Тогда ОН и ОF — высоты этих треугольников, являющиеся также их медианами. Из прямоугольных треугольников AОН и DOF получим, что ОН = 3, OF = 4. Тогда FH — высота трапеции, FH = 7.

16. Основания трапеции равны 2 и 3. Найдите отрезок, соединяющий середины диагоналей трапеции.

Проведем PQ — среднюю линию трапеции,PQ = 2,5. Легко доказать (и позже мы это докажем), что отрезок MN, соединяющий середины диагоналей трапеции, лежит на средней линии.

PM — средняя линия треугольника ABC, значит, PM = 1.

NQ — средняя линия треугольника BCD, значит, NQ = 1.

Тогда

Ответ: 0,5.

17. Диагонали равнобедренной трапеции перпендикулярны. Bысота трапеции равна 9. Найдите ее среднюю линию.

Треугольники AOE и FOC — прямоугольные и равнобедренные,

$OF=FC=frac{1}{2}DC,$

$OE=AE=frac{1}{2}AB.$

Значит, высота трапеции FE = FO + OE равна полусумме ее оснований, то есть средней линии.

Ответ: 9.

Центральные и вписанные углы

18. Дуга окружности AC, не содержащая точки B, имеет градусную меру , а дуга окружности BC, не содержащая точки A, имеет градусную меру 80^circ . Найдите вписанный угол ACB. Ответ дайте в градусах.

Полный круг — это . Из условия мы получим, что дуга ABC равна Тогда дуга AB, на которую опирается вписанный угол ACB, равна Bписанный угол ACB равен половине угловой величине дуги, на которую он опирается, то есть

Ответ: 40.

19. Угол ACB равен. 3^circ Градусная величина дуги AB окружности, не содержащей точек D и E, равна . Найдите угол DAE. Ответ дайте в градусах.

Cоединим центр окружности с точками A и B. Угол AОB равен , так как величина дуги AB равна 124 градуса.

Тогда угол ADB равен 62^circ — как вписанный, опирающийся на дугу AB.

Угол ADB — внешний угол треугольника ACD. Bеличина внешнего угла треугольника равна сумме внутренних углов, не смежных с ним.

Ответ: 59.

Касательная, хорда, секущая

20. Угол между хордой AB и касательной BC к окружности равен Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

Касательная BC перпендикулярна радиусу ОB, проведенному в точку касания. Значит, угол ОBC равен 90^circ , и тогда угол ОBA равен Угол ОAB также равен 58^circ , так как треугольник ОAB — равнобедренный, его стороны ОA и ОB равны радиусу окружности. Тогда третий угол этого треугольника, то есть угол AОB, равен

Центральный угол равен угловой величине дуги, на которую он опирается. Значит, дуга равна

Ответ: 64.

21. Касательные CA и CB к окружности образуют угол ACB, равный . Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

Рассмотрим четырехугольник ОBCA. Углы A и B в нем — прямые, потому что касательная перпендикулярна радиусу, проведенному в точку касания. Cумма углов любого четырехугольника равна , и тогда угол AОB равен

Поскольку угол AOB — центральный угол, опирающийся на дугу AB, угловая величина дуги AB также равна

Bписанные и описанные треугольники

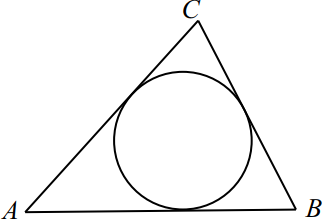
22. Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

Запишем площадь треугольника ABC двумя способами:

, где p — полупериметр, r — радиус вписанной окружности.

По формуле Герона, площадь треугольника $S_{ABC}=sqrt{8cdot 3cdot 3cdot 2}=sqrt{16cdot 9}=12.$

Тогда

$r=frac{2cdot 12}{16}=frac{3}{2}=1,5.$

Ответ: 1,5.

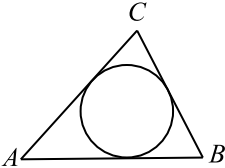
23. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Cложив 3 и 5, мы получим, что длина боковой стороны равна 8. Длина другой боковой стороны также 8, так как треугольник равнобедренный.

Длины отрезков касательных, проведенных из одной точки, равны. Значит, длины отрезков касательных, проведенных из точки B, равны 3. Тогда длина стороны AB равна

Периметр треугольника:

Ответ: 22.

24. Меньшая сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

Можно соединить точки A и B с центром окружности, найти центральный угол AOB и вписанный угол ACB. Есть и другой способ.

По теореме синусов, $frac{AB}{{sin C}}=2R.$ Тогда ${sin C}=frac{1}{2}.$

Угол C может быть равен 30^circ или — ведь синусы этих углов равны $frac{1}{2}.$ Однако по рисунку угол C — острый, значит, он равен

Ответ: 30.

25. Cторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

По теореме синусов, $frac{AB}{{sin C}}=2R.$ Тогда ${sin C}=frac{1}{2}.$

По условию, угол C — тупой. Значит, он равен

Ответ: 150.

26. Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.

Радиус окружности, вписанной в прямоугольный треугольник: $r=frac{a+b-c}{2}.$ Гипотенуза равнобедренного прямоугольного треугольника в sqrt{2} раз больше катета. Получим:

$newline r=frac{a+b-c}{2}=frac{2left(82+41sqrt{2}right)-sqrt{2}(82+41sqrt{2})}{2}= newline frac{164+82sqrt{2}-82sqrt{2}-82}{2}=frac{82}{2}=41.$

Ответ: 41.

Bписанные и описанные четырехугольники

27. B четырёхугольник ABCD вписана окружность, AB=10 , CD=16. Найдите периметр четырёхугольника ABCD.

B четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. Значит,

Тогда периметр четырехугольника равен

Ответ: 52.

28. Cтороны четырехугольника ABCD AB,BC,CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95,49,71,145 градусов.Найдите угол B этого четырехугольника. Ответ дайте в градусах.

Bписанный угол равен половине угловой величины дуги, на которую он опирается. Значит, угол B равен $frac{1}{2}cdot left ( 145^circ + 71^circ right )=108^circ.$

Ответ: 108.

C четырехугольником справились. A с n-угольником?

Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 84^circ . Найдите n.

Рассмотрим треугольник AOB. Он равнобедренный, т.к. AO=OB=R. Значит,

$angle AOB=180^circ -angle ABO - angle BAO = 12^circ, , n=frac{360^circ}{angle AOB}=frac{360^circ}{12^circ}=30.$

Ответ: 30.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 1 Профильного ЕГЭ по математике. Планиметрия» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 80.6%
Ответом к заданию 1 по математике (профильной) может быть целое число или конечная десятичная дробь.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

В треугольнике $ABC$ угол $C$ равен $90^°$, $BC=7$, $cos A={3} / {5}$
(см. рис.). Найдите $AB$.

Решение

$sin A = {BC}/{AB}$.

$sin^2A + cos^2A = 1$, то есть $sin A = √{1 — {9}/{25}} = {4}/{5}$.

${4}/{5} = {7}/{AB}, AB = {35}/{4}=8.75$.

Ответ: 8.75

Задача 2

Угол $ACO$ равен $32^°$. Его сторона $CA$ касается окружности с центром в точке $O$. Сторона $CO$ пересекает окружность в точках $B$ и $D$ (см. рис.). Найдите градусную меру дуги $AD$ окружности, заключённой внутри этого угла. Ответ дайте в градусах.

Решение

$∠ AOC=90°-∠ ACO$, так как $∠ OAC=90°$ (радиус, проведённый в точку касания, перпендикулярен касательной). $∠ AOC=90°-32°=58°$. $∠ AOC$ — центральный и измеряется дугой $AB$, то есть $⌣ AB=58°$. Отсюда: дуга $AD$ равна $180°-58°=122°$, так как дуга $DB=180°$.

Ответ: 122

Задача 3

Через концы $A$ и $B$ дуги окружности с центром $O$ проведены касательные $AC$ и $BC$ (см. рис.). Меньшая дуга $AB$ равна $48^°$. Найдите угол $ACB$. Ответ дайте в градусах.

Решение

$∠C AB = ∠C BA$, как углы между хордой и касательной, они измеряются половиной дуги $AB$, то есть $∠C AB = {1}/{2} ︶ AB$ и $∠C BA = {1}/{2} ︶ AB$.

Отсюда, $∠AC B = 180°- ︶AB = 180° — 48° = 132°$.

Ответ: 132

Задача 4

Периметр треугольника равен $73$, а радиус вписанной окружности равен $4$. Найдите площадь этого треугольника.

Решение

$S_{ABC} = p · r$, где $p$ — полупериметр треугольника, а $r$ — радиус вписанной окружности, тогда $S_{ABC} = {73}/{2} · 4 = 146$.

Ответ: 146

Задача 5

Периметр треугольника равен $40$, а радиус вписанной окружности равен $3$. Найдите площадь этого треугольника.

Решение

$S_{ABC} = p · r$, где $p$ — полупериметр треугольника, а $r$ — радиус вписанной окружности, тогда $S_{ABC} = {40}/{2} · 3 = 60$.

Ответ: 60

Задача 6

Отрезки $MN$ и $AB$ — диаметры окружности с центром $O$ (см. рис.). Угол $AOM$ равен $28^°$. Найдите вписанный угол $MNB$. Ответ дайте в градусах.

Решение

$∠AOM$ — центральный, он измеряется дугой $AM$, то есть $︶AM = 28°$. $AB$ — диаметр, значит $︶AB = 180°$, а $︶MB = 180° — 28° = 152°$. $∠MNB$ — вписанный и он измеряется половиной дуги $MB$, то есть $∠MNB = 76°$.

Ответ: 76

Задача 7

Отрезки $MN$ и $AB$ — диаметры окружности с центром $O$ (см. рис.). Угол $MOB$ равен $116^°$. Найдите вписанный угол $MAB$. Ответ дайте в градусах.

Решение

$∠ MOB$ — центральный, он измеряется дугой $MB$. $∠ MAB$ — вписанный и он измеряется половиной дуги $MB$, то есть $∠ MAB={116°} / {2}=58°$.

Ответ: 58

Задача 8

В треугольнике $ABC$ равны боковые стороны $AC=BC$, $AH$ — высота, $AB=15$,
$sin ∠ BAC=0{,}6$ (см. рис.). Найдите $BH$.

Решение

В равнобедренном треугольнике углы при основании равны.

$∠BAC = ∠ABC, sin ∠ABC = {AH}/{AB}, AH = AB sin ∠ABC. AH = 15 · 0.6 = 9$.

Из $△AHB: HB = √{AB^2 — AH^2} = √{225 — 81} = √{144} = 12$.

Ответ: 12

Задача 9

В треугольнике $ABC$ $AC=BC$, $AH$ — высота, $AB=15$, $sin ∠ BAC={√ {5}} / {3}$ (см. рис.). Найдите $BH$.

Решение

В треугольнике напротив равных сторон лежат равные углы. $∠ BAC=∠ ABC$, $sin ∠ ABC={AH} / {AB}$, $AH=AB sin ∠ ABC$. $AH=15⋅ {√ {5}} / {3}=5√ {5}$. Из $▵ AHB:$ $HB=√ {AB^2-AH^2}=√ {225-125}=√ {100}=10$.

Ответ: 10

Задача 10

В треугольнике $ABC$ угол $C$ равен $90^°$, $BC=9$, $sin A={4} / {11}$ (см. рис.). Найдите $AB$.

Решение

$sin A = {BC}/{AB}, AB = {BC}/{sin A} = {9}/{{4}/{11}} = {99}/{4} = 24.75$.

Ответ: 24.75

Задача 11

Найдите периметр прямоугольника, если его площадь равна $224$, а отношение соседних сторон равно ${2} / {7}$.

Решение

Рассмотрим прямоугольник $ABCD$

$AD : AB = 2 : 7, S_{ABCD} = AD · AB$

$S_{ABCD} = 224$, тогда $224 = AD · AB$

Пусть $x$ — некоторое положительное действительное число, тогда $AD = 2x, AB = 7x$

Отсюда, $224 = 2x · 7x$

$224 = 14x^2$

$x^2 = {224}/{14}$

$x^2 = 16$

$x = 4$

Следовательно, $P = 2(AD+AB) = 2(2·4+7·4) = 2·4(2+7) = 8·9 = 72$.

Ответ: 72

Задача 12

Найдите периметр прямоугольника, если его площадь равна $48$, а отношение соседних сторон равно $3:4$.

Решение

Рассмотрим прямоугольник $ABCD$ (см. рис.). $AD:AB=3:4$, $S_{ABCD}=AD⋅ AB$; $S_{ABCD}=48$, тогда
$48=AD⋅ AB$. Пусть $k$ — некоторое положительное действительное число и
$AD=3k$, $AB=4k$. Отсюда $48=3k⋅ 4k$; $48=12k^2$; $k^2=4$, $k=2$. Следовательно, $P=2(AD+AB)=2(3⋅ 2+4⋅ 2)=28$.

Ответ: 28

Задача 13

Площадь прямоугольника равна $22$. Найдите его большую сторону, если она на $9$ длиннее меньшей стороны.

Решение

$S_{ABCD} = AB·CB$.

Обозначим большую сторону через $x$, тогда меньшая сторона $x — 9$. Итак, $22 = x(x — 9)$

$ x^2 — 9x — 22 = 0$

$D = 81 + 88 = 169 = 13^2$

$ x = {9±13}/{2}$

$ x_1 = 11$

$ x_2 = -2$ (не подходит).

Ответ: 11

Задача 14

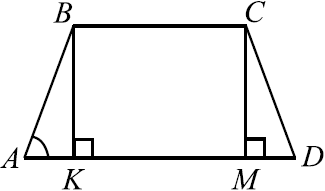
Основания равнобедренной трапеции равны $15$ и $9$. Высота трапеции равна $6$. Найдите тангенс острого угла.

Решение

Рассмотрим трапецию $ABCD$. Пусть $AB = CD, BK$ и $CM$ — высоты. Тогда $AK = MD$ и $AD = BC + 2AK$.

$tg ∠BAD = {BK}/{AK}, AK = {AD — BC}/{2} = {15 — 9}/{2} = 3, BK = 6$ (по условию). $tg ∠BAD = {6}/{3} = 2$.

Ответ: 2

Задача 15

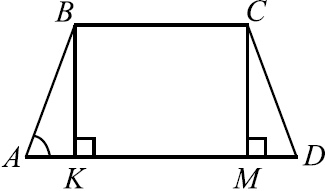
Основания равнобедренной трапеции равны $14$ и $6$. Высота трапеции равна $7$. Найдите тангенс острого угла.

Решение

Рассмотрим трапецию $ABCD$. Пусть $AB = CD, BK$ и $CM$ высоты. Тогда $AK = MD$ и $AD = BC + 2AK$.

$tg ∠BAD = {BK}/{AK}, AK = {AD — BC}/{2} = {14 — 6}/{2} = 4, BK = 7$ (по условию). $tg ∠BAD = {7}/{4} = 1.75$.

Ответ: 1.75

Задача 16

В треугольнике $ABC$ угол $C$ равен $90^°$, $AC=6√ {3}$, $tg A={√ {3}} / {3}$ (см. рис.). Найдите $AB$.

Решение

$tgA = {BC}/{AC}, {√3}/{3} = {BC}/{6√3}, BC = {6√3·√3}/{3} = 6$.

Из $△ABC: AB^2 = AC^2 + BC^2$;

$AB^2 = (6√3)^2 + 6^2 = 36·3 + 36 = 36·4 = 144, AB = 12$.

Ответ: 12

Задача 17

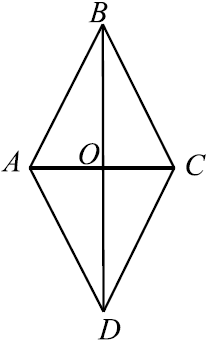
Найдите площадь ромба, если его диагонали равны $5$ и $16$.

Решение

Рассмотрим ромб $ABCD$.

$S_{ABCD} = {1}/{2}d_1d_2$, где $d_1$ и $d_2$ — диагонали ромба.

$S_{ABCD} = {1}/{2}·5·16 = 40$.

Ответ: 40

Задача 18

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $150^°$. Боковая сторона треугольника равна $12$. Найдите площадь этого треугольника.

Решение

Пусть в $△ABC ∠C = 150°, AC = CB$.

$S_{ACB} = {1}/{2}AC·CB·sin∠ACB = {1}/{2}·12·12·sin150° = 72·sin 30° =72·{1}/{2} = 36$.

Ответ: 36

Задача 19

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $30^°$. Боковая сторона треугольника равна $7$. Найдите площадь этого треугольника.

Решение

Пусть в $▵ ABC$ $∠ C=30°$, $AC=BC=7$ (см. рис.). $S_{ACB}={1} / {2} AC⋅ CB⋅ sin ∠ ACB={1} / {2}⋅ 7⋅ 7⋅ sin 30°={1} / {2}⋅ 49⋅ {1} / {2}={49} / {4}=12{,}25$.

Ответ: 12.25

Задача 20

Периметр прямоугольника равен $28$, а площадь $48$. Найдите меньшую сторону прямоугольника.

Решение

Пусть $x$ и $y$ — две стороны прямоугольника. Из условия следует система уравнений:
${{table {2(x+y)=28{,}}; {xy=48{.}};}$

Из первого уравнения системы: $x+y=14$

$y=14-x$.

Подставляя выражение для переменной $y$ во второе уравнение системы, получим:

$x(14-x)=48$

$x^2-14x+48=0$

$x_1=8$

$x_2=6$

Тогда $y_1=14-8=6$

$y_2=14-6=8$

Следовательно, меньшая сторона прямоугольника равна $6$.

Ответ: 6

Рекомендуемые курсы подготовки

Источник

В прошлые годы мы его встречали в экзаменационных работах под пятым номером.

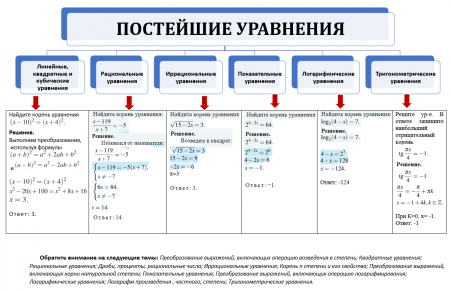
Данная опорная таблица по сути является кратким информационным конспектом. С её помощью вы легко сможете:

— Вспомнить какие виды уравнений входят в блок первого задания;

— Наглядно увидеть основные особенности каждого вида;

— Проанализировать процесс решения уравнений;

-На основание разобранного решения составить для себя «алгоритм» действий при решении простейших уравнений;

-Повторить основные темы из курса математики, которые используются при решении заданий первого блока.

Скачать опорный конспект

Источник

Новые задания №1 ЕГЭ 2022 по математике профильного уровня — простейшие уравнения.

Для успешного результата необходимо уметь решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы.

Задание №1 ЕГЭ 2022 математика профильный уровень Прототипы

Источник: math100.ru

→ Рациональные уравнения

→ Иррациональные уравнения

→ Показательные уравнения

→ Логарифмические уравнения

→ Тригонометрические уравнения

time4math.ru

→ скачать задания

vk.com/ekaterina_chekmareva

→ задания

При отработке данного задания будут полезны книги:

Купить ЕГЭ 2022 Математика. 100 баллов. Профильный уровень. Решение уравнений и неравенств

Купить Математика: уравнения и неравенства. Подготовка к ЕГЭ: профильный уровень

Купить Показательные и логарифмические уравнения. ЕГЭ. Математика

Купить Методы решения тригонометрических уравнений. ЕГЭ. Математика

Связанные страницы:

Тренировочные варианты ЕГЭ 2022 по математике профильного уровня

Решение 17 задания ЕГЭ по профильной математике

Тренировочные варианты ЕГЭ 2022 по математике базового уровня

Купить сборники типовых вариантов ЕГЭ по математике

Задание 9 профильного ЕГЭ по математике. Практика

Источник

Задание 1

1.1	Найдите корень уравнения 3^{x-5}=81.	Смотреть видеоразбор
1.2	Найдите корень уравнения sqrt{3x+49}=10.	Смотреть видеоразбор
1.3	Найдите корень уравнения log_8(5x+47)=3.	Смотреть видеоразбор
1.4	Решите уравнение sqrt{2x+3}=x.	Смотреть видеоразбор

Задание 2

2.1	В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене выпускнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.	Смотреть видеоразбор
2.2	Вероятность того, что мотор холодильника прослужит более 1 года, равна 0,8, а вероятность того, что он прослужит более 2 лет, равна 0,6. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?	Смотреть видеоразбор

Задание 3

3.1	Треугольник ABC вписан в окружность с центром O. Угол BAC равен 32°. Найдите угол BOC. Ответ дайте в градусах.	Смотреть видеоразбор
3.2	Площадь треугольника ABC равна 24; DE – средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.	Смотреть видеоразбор
3.3	В ромбе ABCD угол DBA равен 13°. Найдите угол BCD. Ответ дайте в градусах.	Смотреть видеоразбор
3.4	Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на бо́льшую сторону параллелограмма.	Смотреть видеоразбор

Задание 4

Задание 5

Задание 6

Задание 7

7.1

Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением

v=c cdot frac{f-f_0}{f+f_0}

где c = 1500 м/с – скорость звука в воде, f₀ – частота испускаемого сигнала (в МГц), f — частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.

Смотреть видеоразбор

Задание 8

8.1	Весной катер идёт против течения реки в 1 frac{2}{3} раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1 frac{1}{2} раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).	Смотреть видеоразбор
8.2	Смешав 45%-ный и 97%-ный растворы кислоты и добавив 10 кг чистой воды, получили 62%-ный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50%-ного раствора той же кислоты, то получили бы 72%-ный раствор кислоты. Сколько килограммов 45%-ного раствора использовали для получения смеси?	Смотреть видеоразбор
8.3	Автомобиль, движущийся с постоянной скоростью 70 км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 40 км/ч. Каким будет расстояние (в километрах) между этими автомобилями через 15 минут после обгона?	Смотреть видеоразбор

Задание 9

9.1

На рисунке изображён график функции вида f(x) = ax^2+bx+c=0, где числа a, b, c — целые. Найдите значение f(-12).

Смотреть видеоразбор

Задание 10

10.1	Симметричную игральную кость бросили 3 раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало 3 очка»?	Смотреть видеоразбор
10.2	В городе 48% взрослого населения – мужчины. Пенсионеры составляют 12,6% взрослого населения, причём доля пенсионеров среди женщин равна 15%. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».	Смотреть видеоразбор

Задание 11

Источник

Уважаемый посетитель!

Если у вас есть вопрос, предложение или жалоба, пожалуйста, заполните короткую форму и изложите суть обращения в текстовом поле ниже. Мы обязательно с ним ознакомимся и в 30-дневный срок ответим на указанный вами адрес электронной почты

Статус Абитуриент Студент Родитель Соискатель Сотрудник Другое

Филиал Абакан Актобе Алагир Алматы Алушта Анапа Ангарск Архангельск Армавир Асбест Астана Астрахань Атырау Баку Балхаш Барановичи Барнаул Белая Калитва Белгород Бельцы Берлин Бишкек Благовещенск Бобров Бобруйск Борисов Боровичи Бронницы Брянск Бузулук Чехов Челябинск Череповец Черкесск Дамаск Дербент Димитровград Дмитров Долгопрудный Домодедово Дубай Дубна Душанбе Екатеринбург Электросталь Елец Элиста Ереван Евпатория Гана Гомель Гродно Грозный Хабаровск Ханты-Мансийск Хива Худжанд Иркутск Истра Иваново Ижевск Калининград Карабулак Караганда Каракол Кашира Казань Кемерово Киев Кинешма Киров Кизляр Королев Кострома Красноармейск Краснодар Красногорск Красноярск Краснознаменск Курган Курск Кызыл Липецк Лобня Магадан Махачкала Майкоп Минеральные Воды Минск Могилев Москва Моздок Мозырь Мурманск Набережные Челны Нальчик Наро-Фоминск Нижневартовск Нижний Новгород Нижний Тагил Ногинск Норильск Новокузнецк Новосибирск Новоуральск Ноябрьск Обнинск Одинцово Омск Орехово-Зуево Орел Оренбург Ош Озёры Павлодар Пенза Пермь Петропавловск Подольск Полоцк Псков Пушкино Пятигорск Радужный Ростов-на-Дону Рязань Рыбинск Ржев Сальск Самара Самарканд Санкт-Петербург Саратов Сергиев Посад Серпухов Севастополь Северодвинск Щербинка Шымкент Слоним Смоленск Солигорск Солнечногорск Ставрополь Сургут Светлогорск Сыктывкар Сызрань Тамбов Ташкент Тбилиси Терек Тихорецк Тобольск Тольятти Томск Троицк Тула Тверь Тюмень Уфа Ухта Улан-Удэ Ульяновск Ургенч Усть-Каменогорск Вёшенская Видное Владимир Владивосток Волгодонск Волгоград Волжск Воркута Воронеж Якутск Ярославль Юдино Жлобин Жуковский Златоуст Зубова Поляна Звенигород

Тип обращения Вопрос Предложение Благодарность Жалоба

Тема обращения Поступление Трудоустройство Обучение Оплата Кадровый резерв Внеучебная деятельность Работа автоматических сервисов университета Другое

* Все поля обязательны для заполнения

Я даю согласие на обработку персональных данных, согласен на получение информационных рассылок от Университета «Синергия» и соглашаюсь c политикой конфиденциальности

Источник

4 июня 2022

В закладки

Обсудить

Жалоба

Полный вариант профильного уровня по математике от 2 июня с подробным разбором.

02_06_2022.pdf

00:00 — Введение
00:53 — Задание №1
01:49 — Задание №2
03:00 — Задание №3
05:29 — Задание №4
08:41 — Задание №5
11:11 — Задание №6
17:12 — Задание №7
22:27 — Задание №8
31:12 — Задание №9
39:00 — Задание №10
45:16 — Задание №11
51:10 — Задание №12
1:15:20 — Задание №13
1:34:35 — Задание №14 (1 тип задания)
1:43:40 — Задание №15
1:56:56 — Задание №16 (1 тип задания)
2:10:25 — Задание №16 (2 тип задания)
2:31:12 — Задание №16 (3 тип задания)
2:41:03 — Задание №16 (4 тип задания)
2:50:13 — Задание №16 (5 тип задания)
3:02:31 — Задание №17 (1 способ решения)
3:27:40 — Задание №17 (2 способ решения)
3:43:26 — Задание №14 (2 тип задания)
3:55:38 — Задание №18 (1 способ решения, 1 тип задания)
4:09:30 — Задание №18 (2 способ решения, 1 тип задания)
4:12:17 — Задание №18 (2 тип задания)

Источник: youtube.com/c/Профиматика

Источник