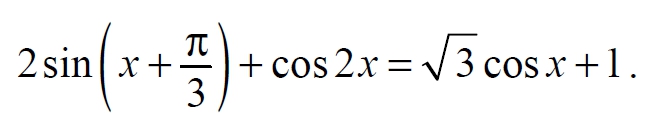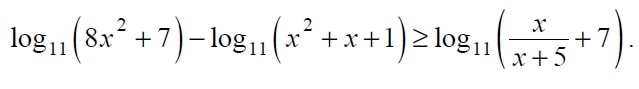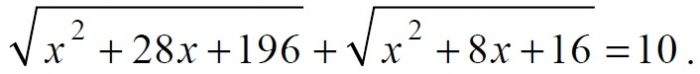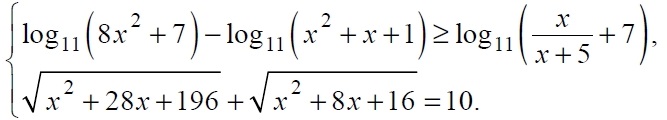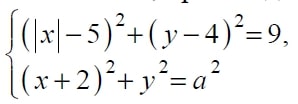Задания первой части (1-11) профильного ЕГЭ по математике в новом формате 2022.
Все задачи для тестов взяты из открытого банка с сайта mathege.ru. Подборка группы vk.com/egeatom/
Предыдущие варианты:
4ege.ru/tr…
4ege.ru/tr…
В задании №5 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.
Вот список тем, которые стоит повторить:
Квадратные уравнения
Арифметический квадратный корень
Корни и степени
Показательная функция
Показательные уравнения
Логарифмическая функция
Логарифмические уравнения
Тригонометрический круг
Формулы приведения
Формулы тригонометрии
Простейшие тригонометрические уравнения 1
Уравнения, сводящиеся к квадратным
1. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.
С левой частью уравнения все понятно. Дробь умножается на
А в правой части — смешанное число
Его целая часть равна 19, а дробная часть равна
Запишем это число в виде неправильной дроби:
Получим:
или
Выбираем меньший корень.
Ответ: -6,5.
2. Решите уравнение
Возведем в квадрат левую часть уравнения. Получим:
Ответ: -6.
Дробно-рациональные уравнения
3. Найдите корень уравнения
Перенесем единицу в левую часть уравнения. Представим 1 как и приведем дроби к общему знаменателю:
Ответ: -2.
Это довольно простой тип уравнений. Главное — внимательность.
Иррациональные уравнения
Так называются уравнения, содержащие знак корня — квадратного, кубического или n-ной степени.
4. Решите уравнение:
Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.
Значит, .
Возведём обе части уравнения в квадрат:
Решим пропорцию:
Условие при этом выполняется.
Ответ: 87.
5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.
Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:
.
Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

Мы получили, что . Это единственный корень уравнения.
Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:
Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни:
или
Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.
Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.
Ответ: 8.
6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Запишем решение как цепочку равносильных переходов:

Ответ: 9.
Показательные уравнения
При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.
7. Решите уравнение
Вспомним, что Уравнение приобретает вид:
Функция
монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
откуда
Ответ: 4.
8. Решите уравнение
Представим как
Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.
Ответ: 7,5.
9. Решите уравнение
Представим в виде степени с основанием 3 и воспользуемся тем, что
Ответ: 12,5.
Логарифмические уравнения
Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.
И конечно, помним про область допустимых значений логарифма:
Логарифмы определены только для положительных чисел.
Основание логарифма должно быть положительно и не равно единице.
10. Решите уравнение:
Область допустимых значений: . Значит,
Представим 2 в правой части уравнения как , чтобы слева и справа в уравнении были логарифмы по основанию 5.
Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом
Ответ: 21.
11. Решите уравнение:
Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

Ответ: -4.
12. Решите уравнение:
Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:
Записываем решение как цепочку равносильных переходов.
.
Ответ: 19.
13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.
Получим систему:
Первое уравнение мы получили просто из определения логарифма.
Квадратное уравнение имеет два корня: и
Очевидно, корень является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения:
Ответ: 12.
Тригонометрические уравнения (Часть 1 ЕГЭ по математике)
Тригонометрические уравнения? В первой части вариантов ЕГЭ? — Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.
14. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.
Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.
Сделаем замену Получим:
Получаем решения: Вернемся к переменной x.
Поделим обе части уравнения на
и умножим на 4.
Первой серии принадлежат решения
Вторая серия включает решения
Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это
Ответ: -2.
15. Решите уравнение: В ответе напишите наименьший положительный корень.
Решение:
Сделаем замену Получим:
Решения этого уравнения:
Вернемся к переменной х:
Умножим обе части уравнения на 4 и разделим на
.
Выпишем несколько решений уравнения и выберем наименьший положительный корень:
Наименьший положительный корень
Ответ: 2.
Мы разобрали основные типы уравнений, встречающихся в задании №5 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №5. Простейшие уравнения. Профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
Решение ПРОЕКТа (перспективная модель) ЕГЭ 2022 по математике (профильный уровень). Демоверсия ФИПИ для 11 класса. Комплексные числа.
Задание 1.
Найдите корень уравнения 3x–5 = 81
ИЛИ
Найдите корень уравнения
ИЛИ
Найдите корень уравнения log8 (5x + 47) = 3
ИЛИ
Решите уравнение . Если корней окажется несколько, то в ответ запишите наименьший из них.
Задание 2.
В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
ИЛИ
Вероятность того, что мотор холодильника прослужит более 1 года, равна 0,8, а вероятность того, что он прослужит более 2 лет, равна 0,6. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?
Задание 3.
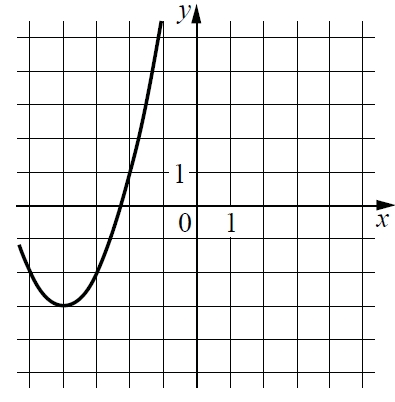
На рисунке изображён график функции вида f(x) = ax2 + bx + c, где числа a, b и c – целые. Найдите значение f(−12).
Задание 4.
Треугольник ABC вписан в окружность с центром О. Угол ВАС равен 32°. Найдите угол ВОС. Ответ дайте в градусах.
ИЛИ
Площадь треугольника ABC равна 24, DE — средняя линия, параллельная стороне АВ. Найдите площадь треугольника CDE.
ИЛИ
В ромбе ABCD угол DBA равен 13°. Найдите угол BCD. Ответ дайте в градусах.
ИЛИ
Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на большую сторону параллелограмма.
Задание 5.
Найдите sin2α, ecли cosα = 0,6 и π < a < 2π.
ИЛИ
Найдите значение выражения 16·log74√7
ИЛИ
Найдите значение выражения 41/5·169/10
Задание 6.
В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде? Ответ дайте в сантиметрах.
ИЛИ
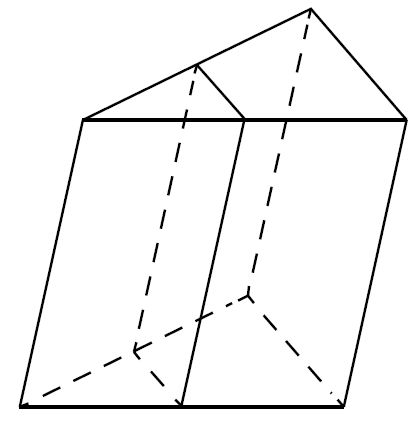
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.
ИЛИ
Через точку, лежащую на высоте прямого кругового конуса и делящую её в отношении 1:2, считая от вершины конуса, проведена плоскость, параллельная его основанию и делящая конус на две части. Каков объём той части конуса, которая примыкает к его основанию, если объём всего конуса равен 54?
Задание 7.
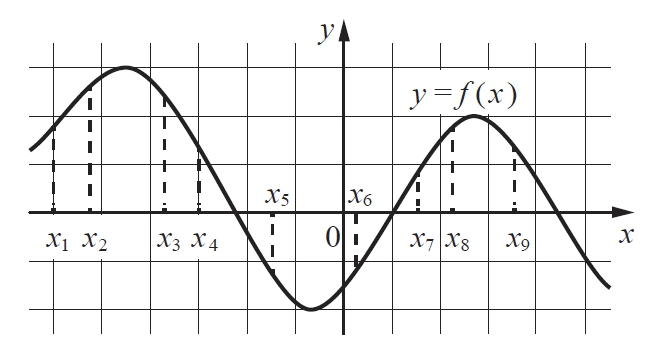
На рисунке изображён график дифференцируемой функции у = f(x). На оси абсцисс отмечены девять точек: x1, x2, … x9.
Найдите все отмеченные точки, в которых производная функции f(x) отрицательна. В ответе укажите количество этих точек.
ИЛИ
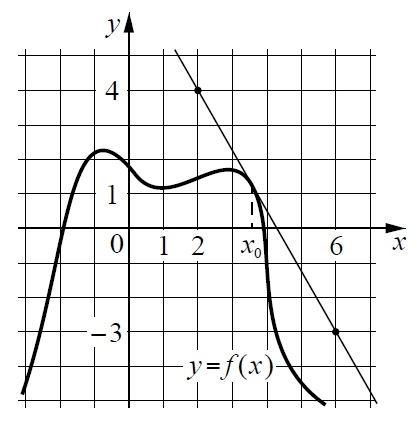
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
ИЛИ
На рисунке изображён график y = f ‘(x) – производной функции f (x), определённой на интервале (−9;12) . В какой точке отрезка [−8;11] функция f (x) принимает f (x) наибольшее значение?
Задание 8.
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением
где с = 1500 м/с — скорость звука в воде, f0 – частота испускаемого сигнала (в МГц), f – частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.
Задание 9.
Весной катер идёт против течения реки в 1 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1
раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
ИЛИ
Смешав 45-процентный и 97-процентный растворы кислоты и добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси?
ИЛИ
Автомобиль, движущийся с постоянной скоростью 70 км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 40 км/ч. Каким будет расстояние (в километрах) между этими автомобилями через 15 минут после обгона?
Задание 10.
Симметричную игральную кость бросили три раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало три очка»?
ИЛИ
В городе 48% взрослого населения мужчины. Пенсионеры составляют 12,6% взрослого населения, причем доля пенсионеров среди женщин равна 15%. Для проведения исследования социологи случайным образом выбрали взрослого мужчину, проживающего в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».
Задание 11.
Про комплексное число z известно, что |z − 4 − 7i| = |z + 4 − i|. Найдите наименьшее значение |z|.
Задание 12.
Найдите наименьшее значение функции
y = 9x – 9ln(x + 11) + 7
на отрезке [–10,5 ; 0].
ИЛИ
Найдите точку максимума функции y = (x + 
ИЛИ
Найдите точку минимума функции
Задание 13.
Решите уравнение
Задание 15.
а) Решите неравенство
ИЛИ
б) Решите уравнение
ИЛИ
в) Решите систему
Задание 16.
15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
Найдите наибольшее значение r , при котором общая сумма выплат будет меньше 1,2 млн рублей.
Задание 18.
Найдите все положительные значения a, при каждом из которых система
имеет единственное решение.
Источник варианта: fipi.ru
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 4
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
В прошлые годы мы его встречали в экзаменационных работах под пятым номером.
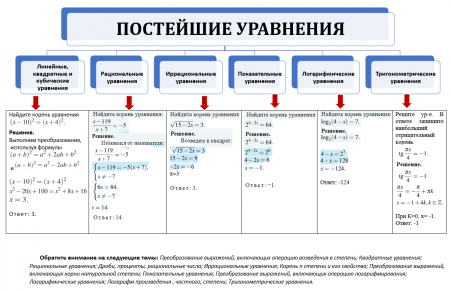
Данная опорная таблица по сути является кратким информационным конспектом. С её помощью вы легко сможете:
— Вспомнить какие виды уравнений входят в блок первого задания;
— Наглядно увидеть основные особенности каждого вида;
— Проанализировать процесс решения уравнений;
-На основание разобранного решения составить для себя «алгоритм» действий при решении простейших уравнений;
-Повторить основные темы из курса математики, которые используются при решении заданий первого блока.
Скачать опорный конспект
Задание 1
| 1.1 | Найдите корень уравнения 3^{x-5}=81. | Смотреть видеоразбор |
| 1.2 | Найдите корень уравнения sqrt{3x+49}=10. | Смотреть видеоразбор |
| 1.3 | Найдите корень уравнения log_8(5x+47)=3. | Смотреть видеоразбор |
| 1.4 | Решите уравнение sqrt{2x+3}=x. | Смотреть видеоразбор |
Задание 2
| 2.1 | В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене выпускнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах. | Смотреть видеоразбор |
| 2.2 | Вероятность того, что мотор холодильника прослужит более 1 года, равна 0,8, а вероятность того, что он прослужит более 2 лет, равна 0,6. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет? | Смотреть видеоразбор |
Задание 3
| 3.1 | Треугольник ABC вписан в окружность с центром O. Угол BAC равен 32°. Найдите угол BOC. Ответ дайте в градусах. | Смотреть видеоразбор |
| 3.2 | Площадь треугольника ABC равна 24; DE – средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE. | Смотреть видеоразбор |
| 3.3 | В ромбе ABCD угол DBA равен 13°. Найдите угол BCD. Ответ дайте в градусах. | Смотреть видеоразбор |
| 3.4 | Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на бо́льшую сторону параллелограмма. | Смотреть видеоразбор |
Задание 4
Задание 5
Задание 6
Задание 7
| 7.1 | Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением
v=c cdot frac{f-f_0}{f+f_0}
, где c = 1500 м/с – скорость звука в воде, f0 – частота испускаемого сигнала (в МГц), f — частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с. |
Смотреть видеоразбор |
Задание 8
| 8.1 | Весной катер идёт против течения реки в 1 frac{2}{3} раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1 frac{1}{2} раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч). | Смотреть видеоразбор |
| 8.2 | Смешав 45%-ный и 97%-ный растворы кислоты и добавив 10 кг чистой воды, получили 62%-ный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50%-ного раствора той же кислоты, то получили бы 72%-ный раствор кислоты. Сколько килограммов 45%-ного раствора использовали для получения смеси? | Смотреть видеоразбор |
| 8.3 | Автомобиль, движущийся с постоянной скоростью 70 км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 40 км/ч. Каким будет расстояние (в километрах) между этими автомобилями через 15 минут после обгона? | Смотреть видеоразбор |
Задание 9
| 9.1 | На рисунке изображён график функции вида f(x) = ax^2+bx+c=0, где числа a, b, c — целые. Найдите значение f(-12). |
Смотреть видеоразбор |
Задание 10
| 10.1 | Симметричную игральную кость бросили 3 раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало 3 очка»? | Смотреть видеоразбор |
| 10.2 | В городе 48% взрослого населения – мужчины. Пенсионеры составляют 12,6% взрослого населения, причём доля пенсионеров среди женщин равна 15%. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером». | Смотреть видеоразбор |
Задание 11
За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 80.6%
Ответом к заданию 1 по математике (профильной) может быть целое число или конечная десятичная дробь.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
В треугольнике $ABC$ угол $C$ равен $90^°$, $BC=7$, $cos A={3} / {5}$
(см. рис.). Найдите $AB$.
Решение
$sin A = {BC}/{AB}$.
$sin^2A + cos^2A = 1$, то есть $sin A = √{1 — {9}/{25}} = {4}/{5}$.
${4}/{5} = {7}/{AB}, AB = {35}/{4}=8.75$.
Ответ: 8.75
Задача 2
Угол $ACO$ равен $32^°$. Его сторона $CA$ касается окружности с центром в точке $O$. Сторона $CO$ пересекает окружность в точках $B$ и $D$ (см. рис.). Найдите градусную меру дуги $AD$ окружности, заключённой внутри этого угла. Ответ дайте в градусах.
Решение
$∠ AOC=90°-∠ ACO$, так как $∠ OAC=90°$ (радиус, проведённый в точку касания, перпендикулярен касательной). $∠ AOC=90°-32°=58°$. $∠ AOC$ — центральный и измеряется дугой $AB$, то есть $⌣ AB=58°$. Отсюда: дуга $AD$ равна $180°-58°=122°$, так как дуга $DB=180°$.
Ответ: 122
Задача 3
Через концы $A$ и $B$ дуги окружности с центром $O$ проведены касательные $AC$ и $BC$ (см. рис.). Меньшая дуга $AB$ равна $48^°$. Найдите угол $ACB$. Ответ дайте в градусах.
Решение
$∠C AB = ∠C BA$, как углы между хордой и касательной, они измеряются половиной дуги $AB$, то есть $∠C AB = {1}/{2} ︶ AB$ и $∠C BA = {1}/{2} ︶ AB$.
Отсюда, $∠AC B = 180°- ︶AB = 180° — 48° = 132°$.
Ответ: 132
Задача 4
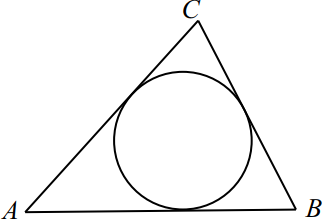
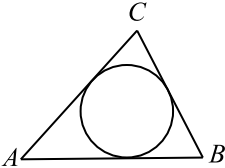
Периметр треугольника равен $73$, а радиус вписанной окружности равен $4$. Найдите площадь этого треугольника.
Решение
$S_{ABC} = p · r$, где $p$ — полупериметр треугольника, а $r$ — радиус вписанной окружности, тогда $S_{ABC} = {73}/{2} · 4 = 146$.
Ответ: 146
Задача 5
Периметр треугольника равен $40$, а радиус вписанной окружности равен $3$. Найдите площадь этого треугольника.
Решение
$S_{ABC} = p · r$, где $p$ — полупериметр треугольника, а $r$ — радиус вписанной окружности, тогда $S_{ABC} = {40}/{2} · 3 = 60$.
Ответ: 60
Задача 6
Отрезки $MN$ и $AB$ — диаметры окружности с центром $O$ (см. рис.). Угол $AOM$ равен $28^°$. Найдите вписанный угол $MNB$. Ответ дайте в градусах.
Решение
$∠AOM$ — центральный, он измеряется дугой $AM$, то есть $︶AM = 28°$. $AB$ — диаметр, значит $︶AB = 180°$, а $︶MB = 180° — 28° = 152°$. $∠MNB$ — вписанный и он измеряется половиной дуги $MB$, то есть $∠MNB = 76°$.
Ответ: 76
Задача 7
Отрезки $MN$ и $AB$ — диаметры окружности с центром $O$ (см. рис.). Угол $MOB$ равен $116^°$. Найдите вписанный угол $MAB$. Ответ дайте в градусах.
Решение
$∠ MOB$ — центральный, он измеряется дугой $MB$. $∠ MAB$ — вписанный и он измеряется половиной дуги $MB$, то есть $∠ MAB={116°} / {2}=58°$.
Ответ: 58
Задача 8
В треугольнике $ABC$ равны боковые стороны $AC=BC$, $AH$ — высота, $AB=15$,
$sin ∠ BAC=0{,}6$ (см. рис.). Найдите $BH$.
Решение
В равнобедренном треугольнике углы при основании равны.
$∠BAC = ∠ABC, sin ∠ABC = {AH}/{AB}, AH = AB sin ∠ABC. AH = 15 · 0.6 = 9$.
Из $△AHB: HB = √{AB^2 — AH^2} = √{225 — 81} = √{144} = 12$.
Ответ: 12
Задача 9
В треугольнике $ABC$ $AC=BC$, $AH$ — высота, $AB=15$, $sin ∠ BAC={√ {5}} / {3}$ (см. рис.). Найдите $BH$.
Решение
В треугольнике напротив равных сторон лежат равные углы. $∠ BAC=∠ ABC$, $sin ∠ ABC={AH} / {AB}$, $AH=AB sin ∠ ABC$. $AH=15⋅ {√ {5}} / {3}=5√ {5}$. Из $▵ AHB:$ $HB=√ {AB^2-AH^2}=√ {225-125}=√ {100}=10$.
Ответ: 10
Задача 10
В треугольнике $ABC$ угол $C$ равен $90^°$, $BC=9$, $sin A={4} / {11}$ (см. рис.). Найдите $AB$.
Решение
$sin A = {BC}/{AB}, AB = {BC}/{sin A} = {9}/{{4}/{11}} = {99}/{4} = 24.75$.
Ответ: 24.75
Задача 11
Найдите периметр прямоугольника, если его площадь равна $224$, а отношение соседних сторон равно ${2} / {7}$.
Решение
Рассмотрим прямоугольник $ABCD$
$AD : AB = 2 : 7, S_{ABCD} = AD · AB$
$S_{ABCD} = 224$, тогда $224 = AD · AB$
Пусть $x$ — некоторое положительное действительное число, тогда $AD = 2x, AB = 7x$
Отсюда, $224 = 2x · 7x$
$224 = 14x^2$
$x^2 = {224}/{14}$
$x^2 = 16$
$x = 4$
Следовательно, $P = 2(AD+AB) = 2(2·4+7·4) = 2·4(2+7) = 8·9 = 72$.
Ответ: 72
Задача 12
Найдите периметр прямоугольника, если его площадь равна $48$, а отношение соседних сторон равно $3:4$.
Решение
Рассмотрим прямоугольник $ABCD$ (см. рис.). $AD:AB=3:4$, $S_{ABCD}=AD⋅ AB$; $S_{ABCD}=48$, тогда
$48=AD⋅ AB$. Пусть $k$ — некоторое положительное действительное число и
$AD=3k$, $AB=4k$. Отсюда $48=3k⋅ 4k$; $48=12k^2$; $k^2=4$, $k=2$. Следовательно, $P=2(AD+AB)=2(3⋅ 2+4⋅ 2)=28$.
Ответ: 28
Задача 13
Площадь прямоугольника равна $22$. Найдите его большую сторону, если она на $9$ длиннее меньшей стороны.
Решение
$S_{ABCD} = AB·CB$.
Обозначим большую сторону через $x$, тогда меньшая сторона $x — 9$. Итак, $22 = x(x — 9)$
$ x^2 — 9x — 22 = 0$
$D = 81 + 88 = 169 = 13^2$
$ x = {9±13}/{2}$
$ x_1 = 11$
$ x_2 = -2$ (не подходит).
Ответ: 11
Задача 14
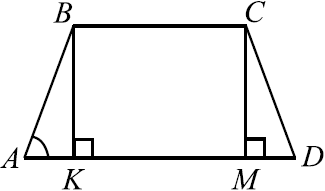
Основания равнобедренной трапеции равны $15$ и $9$. Высота трапеции равна $6$. Найдите тангенс острого угла.
Решение
Рассмотрим трапецию $ABCD$. Пусть $AB = CD, BK$ и $CM$ — высоты. Тогда $AK = MD$ и $AD = BC + 2AK$.
$tg ∠BAD = {BK}/{AK}, AK = {AD — BC}/{2} = {15 — 9}/{2} = 3, BK = 6$ (по условию). $tg ∠BAD = {6}/{3} = 2$.
Ответ: 2
Задача 15
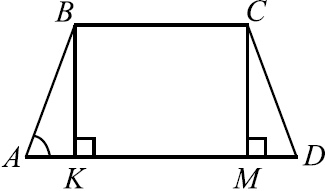
Основания равнобедренной трапеции равны $14$ и $6$. Высота трапеции равна $7$. Найдите тангенс острого угла.
Решение
Рассмотрим трапецию $ABCD$. Пусть $AB = CD, BK$ и $CM$ высоты. Тогда $AK = MD$ и $AD = BC + 2AK$.
$tg ∠BAD = {BK}/{AK}, AK = {AD — BC}/{2} = {14 — 6}/{2} = 4, BK = 7$ (по условию). $tg ∠BAD = {7}/{4} = 1.75$.
Ответ: 1.75
Задача 16
В треугольнике $ABC$ угол $C$ равен $90^°$, $AC=6√ {3}$, $tg A={√ {3}} / {3}$ (см. рис.). Найдите $AB$.
Решение
$tgA = {BC}/{AC}, {√3}/{3} = {BC}/{6√3}, BC = {6√3·√3}/{3} = 6$.
Из $△ABC: AB^2 = AC^2 + BC^2$;
$AB^2 = (6√3)^2 + 6^2 = 36·3 + 36 = 36·4 = 144, AB = 12$.
Ответ: 12
Задача 17
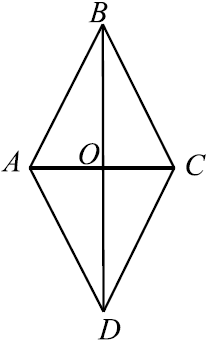
Найдите площадь ромба, если его диагонали равны $5$ и $16$.
Решение
Рассмотрим ромб $ABCD$.
$S_{ABCD} = {1}/{2}d_1d_2$, где $d_1$ и $d_2$ — диагонали ромба.
$S_{ABCD} = {1}/{2}·5·16 = 40$.
Ответ: 40
Задача 18
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $150^°$. Боковая сторона треугольника равна $12$. Найдите площадь этого треугольника.
Решение
Пусть в $△ABC ∠C = 150°, AC = CB$.
$S_{ACB} = {1}/{2}AC·CB·sin∠ACB = {1}/{2}·12·12·sin150° = 72·sin 30° =72·{1}/{2} = 36$.
Ответ: 36
Задача 19
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $30^°$. Боковая сторона треугольника равна $7$. Найдите площадь этого треугольника.
Решение
Пусть в $▵ ABC$ $∠ C=30°$, $AC=BC=7$ (см. рис.). $S_{ACB}={1} / {2} AC⋅ CB⋅ sin ∠ ACB={1} / {2}⋅ 7⋅ 7⋅ sin 30°={1} / {2}⋅ 49⋅ {1} / {2}={49} / {4}=12{,}25$.
Ответ: 12.25
Задача 20
Периметр прямоугольника равен $28$, а площадь $48$. Найдите меньшую сторону прямоугольника.
Решение
Пусть $x$ и $y$ — две стороны прямоугольника. Из условия следует система уравнений:
${{table {2(x+y)=28{,}}; {xy=48{.}};}$
Из первого уравнения системы: $x+y=14$
$y=14-x$.
Подставляя выражение для переменной $y$ во второе уравнение системы, получим:
$x(14-x)=48$
$x^2-14x+48=0$
$x_1=8$
$x_2=6$
Тогда $y_1=14-8=6$
$y_2=14-6=8$
Следовательно, меньшая сторона прямоугольника равна $6$.
Ответ: 6
Рекомендуемые курсы подготовки
Новые задания №1 ЕГЭ 2022 по математике профильного уровня — простейшие уравнения.
Для успешного результата необходимо уметь решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы.
Задание №1 ЕГЭ 2022 математика профильный уровень Прототипы
| Источник: math100.ru | → Рациональные уравнения
→ Иррациональные уравнения → Показательные уравнения → Логарифмические уравнения → Тригонометрические уравнения |
| time4math.ru | → скачать задания |
| vk.com/ekaterina_chekmareva | → задания |
При отработке данного задания будут полезны книги:
Купить ЕГЭ 2022 Математика. 100 баллов. Профильный уровень. Решение уравнений и неравенств
Купить Математика: уравнения и неравенства. Подготовка к ЕГЭ: профильный уровень
Купить Показательные и логарифмические уравнения. ЕГЭ. Математика
Купить Методы решения тригонометрических уравнений. ЕГЭ. Математика
Связанные страницы:
Тренировочные варианты ЕГЭ 2022 по математике профильного уровня
Решение 17 задания ЕГЭ по профильной математике
Тренировочные варианты ЕГЭ 2022 по математике базового уровня
Купить сборники типовых вариантов ЕГЭ по математике
Задание 9 профильного ЕГЭ по математике. Практика