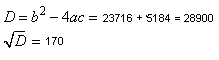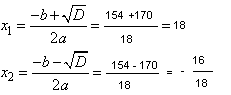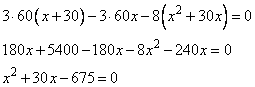Задание 9 Профильного ЕГЭ по математике – это несколько типов текстовых задач. Условия и «сюжеты» задач могут быть разными. При этом в каждой из них нужно построить математическую модель, то есть обозначить какие-либо величины за переменные, составить уравнение и решить его. И еще есть неочевидные секреты их решения. О них – в конце статьи.
Вот основные типы текстовых задач, которые могут вам встретиться на ЕГЭ под номером 9. Переходите по ссылкам, читайте краткую теорию и разбирайте вместе с нами решения задач!
1. Задачи на движение




Формула работает и в этом случае. Здесь
– расстояние,
– скорость,
– время.
А секрет задач на движение по окружности: тот, кто обгоняет, проезжает на 1 круг больше, если это первый обгон. И на n кругов больше, если обогнал другого в -ный раз.
6. Задачи на нахождение средней скорости
По определению, средняя скорость получается, если всё расстояние поделить на всё время. В общем случае она не равна среднему арифметическому скоростей, а находится по следующей формуле:
.
7. Задачи на движение протяженных тел, встречное движение и обгон
Да, это те самые задачи, где поезд проходит через туннель. Или проезжает мимо платформы. И нам нужно учитывать длину поезда.
Есть еще задачи на встречное движение или обгон. Например, два поезда движутся навстречу друг другу (конечно, по параллельным путям), или один поезд обгоняет другой. Такие задачи удобно решать в движущейся системе отсчета.
Но и это не все. Есть еще задачи ЕГЭ на арифметическую и геометрическую прогрессии.

Арифметическая прогрессия в задачах ЕГЭ по математике
9. Задачи на геометрическую прогрессии
Геометрическая прогрессия в задачах ЕГЭ по математике
И еще мы обещали секреты решения текстовых задач на движение и работу. Читайте и применяйте!
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 9. Текстовые задачи u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Текстовые задачи»
Открытый банк заданий по теме текстовые задачи. Задания B11 из ЕГЭ по математике (профильный уровень)
Задание №1106
Условие
Наташе надо изготовить 300 бумажных журавликов. Ежедневно она делает на одно и то же количество журавликов больше по сравнению с предыдущим днём. В первый день Наташа сделала 6 журавликов. Сколько журавликов было сделано в последний день, если на всю работу потребовалось 15 дней?
Показать решение
Решение
Из условия следует, что количество бумажных «журавликов» ежедневно увеличивалось на одно и тоже число. Количество ежедневно сделанных бумажных «журавликов» образует арифметическую прогрессию, при этом первый член прогрессии равен 6. По формуле суммы первых членов арифметической прогрессии имеем
a_1+a_2+a_3+…+a_{15}= frac{a_1+a_{15}}{2}cdot15= 300,
6+a_{15}=40,
a_{15}=40-6=34.
Наташа в последний день изготовила 34 бумажных «журавлика»
Ответ
34
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1105
Условие
Два велосипедиста одновременно отправились из деревни A в деревню B, расстояние между которыми 21 км. Скорость первого велосипедиста была на 3 км/ч больше скорости второго велосипедиста. Найдите скорость второго велосипедиста, если он приехал в деревню B на 10 мин позже первого. Ответ дайте в км/ч.
Показать решение
Решение
Обозначим скорость второго велосипедиста через x км/ч. Тогда скорость первого (x+3) км/ч, а время первого велосипедиста на прохождение всего пути frac{21}{x+3}ч, время второго велосипедиста, затраченное на прохождение всего пути frac{21}{x}ч. Разница во времени равна 10 мин = frac16часа.
Составим и решим уравнение: frac{21}{x}-frac{21}{x+3}=frac16,
6(21(x+3)-21x)=x(x+3),
x^2+3x-378=0,
x_1=18, x_2=-21.
Отрицательная скорость не удовлетворяет условию задачи. Скорость второго велосипедиста равна 18 км/ч.
Ответ
18
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1104
Условие
Коле надо посадить 350 кустов роз. Ежедневно он сажает на одно и то же количество кустов больше по сравнению с предыдущим днём. В первый день он посадил 8 кустов роз. Сколько кустов было посажено в последний день, если на всю работу потребовалось 20 дней?
Показать решение
Решение
Из условия следует, что количество посаженных кустов роз ежедневно увеличивалось на одно и тоже число. Количество ежедневно посаженных роз образует арифметическую прогрессию, при этом первый член равен 8. По формуле суммы первых членов арифметической прогрессии получаем a_1+a_2+a_3+…+a_{20}= frac{a_1+a_{20}}{2}cdot20= 350,
8+a_{20}=35,
a_{20}=35-8=27.
Коля в последний день посадил 27 кустов роз.
Ответ
27
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1103
Условие
Обе трубы наполняют бассейн за 6 часов, а первая труба — за 10 часов. За сколько часов наполнит бассейн вторая труба?
Показать решение
Решение
Объём бассейна примем за 1. Тогда за 1 час две трубы заполнят frac16часть бассейна, первая труба за 1 час заполнит frac{1}{10}часть бассейна. Значит, вторая труба за 1 час заполнит frac16-frac{1}{10}=frac{1}{15}часть бассейна. Весь бассейн вторая труба заполнит за 1 : frac{1}{15}=frac{15}{1}=15часов.
Ответ
15
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1102
Условие
Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если ёмкость объёмом 420 литров она заполняет на 15 минут дольше, чем вторая труба заполняет ёмкость объёмом 280 литров?
Показать решение
Решение
Пусть первая труба пропускает x литров воды в минуту. Тогда вторая труба пропускает за одну минуту x + 2 литра. Первая труба заполняет ёмкость объёмом 420 литров за время frac{420}{x} мин, а вторая труба заполняет ёмкость объёмом 280 литров за frac{280}{x+2} мин, что различается на 15 минут.
Составим и решим уравнение:
frac{420}{x}-frac{280}{x+2}=15,
frac{84}{x}-frac{56}{x+2}=3,
84(x+2)-56x=3x(x+2),
28x+168=3x^2+6x,
3x^2-22x-168=0,
x_1=12, x_2=-frac{14}{3}.
Отрицательное значение не удовлетворяет условию. Первая труба пропускает 12 литров воды в минуту.
Ответ
12
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1101
Условие
Моторная лодка прошла против течения реки 160 км и вернулась в пункт отправления, затратив на обратный путь на 8 часов меньше времени. Известно, что в неподвижной воде лодка движется со скоростью 15 км/ч. Найдите скорость течения реки. Ответ дайте в км/ч.
Показать решение
Решение
Обозначим скорость течения реки через x км/ч. Тогда скорость лодки по течению реки (15 + x) км/ч, скорость лодки против течения реки (15 — x) км/ч. Время, затраченное лодкой на путь по течению реки frac{160}{15+x} ч, время, затраченное на путь против течения реки — frac{160}{15-x} ч.
Составим и решим уравнение:
frac{160}{15-x}-frac{160}{15+x}=8,
frac{20}{15-x}-frac{20}{15+x}=1,
20(15+x-15+x)= (15-x)(15+x),
20cdot2x=225-x^2,
40x=225-x^2,
x^2+40x-225=0,
x_1=5, x_2=-45.
Скорость течения положительна, она равна 5 км/ч.
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1100
Условие
Два мотоциклиста выехали одновременно из города A в город B, расстояние между которыми 171 км. За один час первый мотоциклист проезжает расстояние на 40 км больше второго мотоциклиста. Найдите скорость второго мотоциклиста, если он приехал в пункт В на 2,5 часа позже первого. Ответ дайте в км/ч.
Показать решение
Решение
Обозначим скорость второго мотоциклиста через x км/ч, тогда по условию скорость первого мотоциклиста (x + 40) км/ч. Время, затраченное на прохождение всего пути первым мотоциклистом, равно frac{171}{x+40} ч. Время, затраченное на прохождение всего пути вторым мотоциклистом, равно frac{171}{x} ч.
Составим и решим уравнение:
frac{171}{x}-frac{171}{x+40}=2,5,
171(x + 40) — 171x = 2,5x(x + 40),
171x+171cdot40-171x = 2,5x^2 + 100x,
2,5x^2+100x-171cdot40 =0,
x^2+40x-171cdot16=0,
x_1 = 36, x_2 = -76.
Отрицательная скорость не удовлетворяет условию. Скорость второго мотоциклиста
36 км/ч.
Ответ
36
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1099
Условие
Елена сделала вклад в банк в размере 5500 рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Спустя год Наталья положила такую же сумму в этот же банк и на тех же условиях. Ещё через год Елена и Наталья одновременно закрыли вклады и забрали деньги. В результате Елена получила на 739,2 рубля больше, чем получила Наталья. Найдите, какой процент годовых начислял банк по вкладам?
Показать решение
Решение
Пусть процент годовых будет x, тогда через год вклад Елены составил:
5500 + 0, 01x cdot 5500 = 5500(1 + 0,01x) рублей, а ещё через год — 5500(1 + 0,01x)^2 рублей. Вклад Натальи лежал в банке только год, потому он равен 5500(1 + 0,01x) рублей. А разность между получившимися вкладами Елены и Натальи составила 739,2 рубля.
Составим и решим уравнение:
5500(1+ 0,01x)^2-5500(1+0,01x)= 739,2,
(1+0,01x)^2-(1+0,01x)=0,1344,
x^2+100x-1344=0,
x_1=-112,enspace x_2=12.
Банк начислял 12% годовых.
Ответ
12
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1098
Условие
Предприниматель Петров получил в 2005 году прибыль в размере 12,000 рублей. Каждый следующий год его прибыль увеличивалась на 110% по сравнению с предыдущим годом. Сколько рублей заработал Петров за 2008 год?
Показать решение
Решение
В 2005 году прибыль составляла 12,000 рублей, каждый следующий год она увеличивалась на 110%, то есть становилась 210% = 2,1 от предыдущего года. Через три года она будет равна 12,000 cdot 2,1^3 = 111,132 рубля.
Ответ
111132
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1097
Условие
Имеется два сплава. Первый сплав содержит 12% железа, второй — 28% железа. Масса второго сплава больше массы первого на 2 кг. Из этих двух сплавов изготовили третий сплав с содержанием железа 21%. Найдите массу третьего сплава. Ответ дайте в килограммах.
Показать решение
Решение
Обозначим массу первого сплава через x кг. Тогда масса второго сплава (x + 2) кг. Содержание железа в первом сплаве равно 0,12x кг, во втором сплаве — 0,28(x + 2) кг. Третий сплав имеет массу x + x + 2 = 2x + 2 (кг), и в нём содержание железа равно 2(x + 1) cdot 0,21 = 0,42(x + 1) кг.
Составим и решим уравнение:
0,12x+ 0,28(x + 2) = 0,42(x+1),
6x + 14(x + 2) = 21(x + 1),
x = 7.
Третий сплав имеет массу 2 cdot 7 + 2 = 16 (кг).
Ответ
16
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
Пример:
Первый рабочий изготавливает $200$ деталей за время, которое второй рабочий потратит на изготовление $180$ таких же деталей. Найдите производительность первого рабочего, если он изготавливает в минуту на $2$ детали больше, чем второй?
Решение:
Пусть $х$ деталей/мин — производительность второго рабочего, тогда $(х+2)$ деталей/мин — производительность первого рабочего.
Создаем стандартную таблицу и столбец «Производительность»(р) заполняем данными с неизвестными.
| $A$(работа) | $p$(производительность) | $t$(время) | |
| Первый рабочий | $(x+2)$ | ||
| Второй рабочий | $x$ |
Так как первый рабочий изготовил $200$ деталей — это его выполненная работа, у второго рабочего работа равна $180$ деталей.
| $A$(работа) | $p$(производительность) | $t$(время) | |
| Первый рабочий | $200$ | $(x+2)$ | |
| Второй рабочий | $180$ | $x$ |
Третий столбец заполняем по формуле $t={A}/{p}$.
| $A$(работа) | $p$(производительность) | $t$(время) | |
| Первый рабочий | $200$ | $(x+2)$ | ${200}/{(x+2)}$ |
| Второй рабочий | $180$ | $x$ | ${180}/{x}$ |
Именно содержимое третьего столбца будем использовать для составления уравнения к задаче. По условию задачи время на выполнение работы рабочие затратили одинаковое. Поэтому содержимое третьего столбца приравняем друг к другу.
${200}/{(x+2)}={180}/{x}$
Решим полученное уравнение по свойству пропорции: произведение крайних членов пропорции равно произведению средних членов пропорции.
$180(х+2)=200х$
Разделим обе части уравнения на $20$
$9(х+2)=10х$
Раскроем скобки и приведем подобные слагаемые
$9х+18=10х$
$х=18$ (деталей в минуту)- производительность второго рабочего.
$(х+2)=18+2=20$ (деталей в минуту)- производительность первого рабочего.
Ответ: $20$
Задачи на совместную работу
Задачи на совместную работу отличаются от обычных, представленных выше, тем, что в них работа выполняется одновременно (совместно) несколькими рабочими (трубами и т.д.).
При совместной работе задачи решаются через производительность.
Производительность при совместной работе равна сумме производительности каждого из рабочих.
$р_{совместная}=р_1+р_2…+р_n$
Пример:
В помощь садовому насосу, перекачивающему $6$ литров воды за $4$ минуты, подключили второй насос, перекачивающий тот же объём воды за $2$ минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать $27$ литров воды?
Решение:
Найдем производительность первого насоса. Работа (А) первого насоса – $6$ литров, время работы $t=4$ минуты.
$р_1={A}/{t}={6}/{4}={3}/{2}$ (литров/минуту)
Найдем производительность второго насоса. Второй насос выполняет тот же объем работы, т.е перекачивает $6$ литров воды. Время работы второго насоса $t=2$ минуты.
$р_2={A}/{t}={6}/{2}=3$(литров/минуту)
Найдем совместную производительность
$р_{совместная}=р_1+р_2={3}/{2}+3={3+6}/{2}={9}/{2}$ (литров/минуту)
Чтобы найти время, за которое оба насоса перекачивают $27$ литров воды, надо всю работу, т.е. $27$ литров разделить на совместную производительность
$t={A}/{p}={27}/{{9}/{2}}={27·2}/{9}=6$ минут.
Ответ: $6$
Процент – это сотая доля числа.
Процент обозначается символом $%$.
- Чтобы найти процент от числа, надо заданное число разделить на 100 и умножить на величину процента. $%$ от $а={а·%}/{100}$.
- Чтобы найти число по его указанному проценту, нужно заданное число разделить на заданную величину процента, а результат умножить на $100$.
Задачи на скидки:
Скидка — это понижение цены товара или услуги. Чаще всего скидку указывают в процентах.
Чтобы найти цену товара с учетом скидки необходимо:
- Из $100%$ отнять процент скидки.
- Найти полученный процент от полной стоимости товара.
Пример:
Зимняя куртка стоит $4500$ рублей. Сезонная скидка составляет $20%$. Сколько надо заплатить за куртку с учетом скидки.
Решение:
Найдем, сколько процентов будет стоить куртка, после скидки: $100%-20%=80%$
Посчитаем, сколько составляет 80% от 4500 рублей. Чтобы найти процент от числа, надо заданное число разделить на $100$ и умножить на величину процента.
${4500·80}/{100}=3600$ рублей- это цена куртки, после скидки.
Ответ: $3600$
Слайд 1
Алгебра Часть 1 Задачи на сплавы Преподаватель высшей категории Анисимова Оксана Михайловна ВИФК Кадетский корпус (спортивная школа)
Слайд 2
?? всего концентрация Масса вещества Было 5 14 % Добавили 5 — — стало 5+5=10 ? 0,7 Решение задач «задание 11» №1 Ответ: 7 В сосуд, содержащий 5 литров 14-процентного водного раствора некоторого вещества, добавили 5 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Слайд 3
?? всего концентрация Масса вещества I x 15% 0,15x II x 17% 0,17x I+II 2x ? 0,15x + 0,17x = 0,32x Решение задач «задание 11» № 2 Ответ: 16 Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Слайд 4
?? всего концентрация Масса вещества I 4 20% 0,2·4=0,8 II 6 35% 0,35·6=2,1 I+II 4+6=10 ? 0,8 + 2,1 = 2,9 Решение задач «задание 11» № 3 Ответ: 29 Смешали 4 литра 20-процентного водного раствора некоторого вещества с 6 литрами 35- процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Слайд 5
?? всего концентрация Масса вещества I II I+II Решение задач «задание 11» № 4 .1 Ответ: 90 Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго? ?? всего концентрация Масса вещества I x 10% 0,1x II y 35% 0,35y I+II 150 30% 0,3·150=45 0,1x+0,35y=45
Слайд 6
?? всего концентрация Масса вещества I II I+II Решение задач «задание 11» № 4 .2 Ответ: 18 Имеется два сплава. Первый содержит 20% никеля, второй — 45% никеля. Из этих двух сплавов получили третий сплав массой 90 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была больше массы второго? ?? всего концентрация Масса вещества I x 2 0% 0, 2 x II y 4 5% 0, 4 5y I+II 90 30% 0,3· 90 = 27 0, 2 x+0, 4 5y=27
Слайд 7
Первый год Второй год I II I+II Решение задач «задание 11» № 5 Ответ: 110 Численность волков в двух заповедниках составляла 210 особей. Через год обнаружили, что в первом заповеднике численность волков возросла на 10%, а во втором — на 30%. В результате общая численность волков в двух заповедниках составила 251.Сколько волков было в первом из заповедников первоначально? ?? Первый год Второй год I x x+0,1x II y y+0,3y I+II 210 251
Слайд 8
?? всего Процентное содержание Масса вещества I II I+II Решение задач «задание 11» № 6 .1 Ответ: 27 Имеется два сплава. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах. ?? всего Процентное содержание Масса вещества I x 5% 0,05x II x+9 14% 0,14(x+9) I+II 2x+9 11% 0,11(2x+9)= 0,05x+0,14(x+9)
Слайд 9
?? всего Процентное содержание Масса вещества I II I+II Решение задач «задание 11» №6.2 Ответ: 9 Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третье го сплава. Ответ дайте в килограммах. ?? всего Процентное содержание Масса вещества I x 10 % 0,1x II x+ 3 40 % 0,4(x+3) I+II 2x+3 30 % 0,3(2x+3)= 0,1x+0,4(x+3)
Слайд 10
Решение задач «задание 11» №7.1 Смешав 6-процентный и 74-процентный растворы кислоты и добавив 10 кг чистой воды, получили 19-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50- процентного раствора той же кислоты, то получили бы 24-процентный раствор кислоты. Сколько килограммов 6-процентного раствора использовали для получения смеси? ?? всего Процент Масса вещества I x 6% 0,06x II y 74% 0,74y Добавили 1 раз 10 — — Получили 1 раз x+y+10 19% 0.19(x+y+10)= =0,06x+0,74y Добавили 2раз 10 50% 0,5·10=5 Получили 2 раз x+y+10 24% 0. 24 (x+y+10)= =0,06x+0,74y +5
Слайд 11
Решение задач «задание 11» №7.1 ?? всего Процент Масса вещества I x 6% 0,06x II y 74% 0,74y Добавили 1 раз 10 — — Получили 1 раз x+y+10 19% 0.19(x+y+10)= =0,06x+0,74y Добавили 2раз 10 50% 0,5·10=5 Получили 2 раз x+y+10 24% 0. 24 (x+y+10)= =0,06x+0,74y +5
Слайд 12
Решение задач «задание 11» №7.1 Ответ: 70
Слайд 13
Самостоятельно Сборник «4000 задач» № 1586 , № 1590 № 1587 , № 11 вариант1 №11 вариант2
Слайд 14
Алгебра Урок №11 Часть 2 Задачи на совместную работу Преподаватель высшей категории Анисимова Оксана Михайловна ВИФК Кадетский корпус (спортивная школа)
Слайд 15
Объем работы Производительность (скорость) время I II Решение задач «задание 11» №1 .1 Ответ: 6 Объем работы Производительность (скорость) время I 20 x+4 II 60 x
Слайд 16
На изготовление 16 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 40 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает второй рабочий? Объем работы Производительность (скорость) время I II Решение задач «задание 11» №1 .2 Ответ: 5 Объем работы Производительность (скорость) время I 16 x+3 II 40 x
Слайд 17
Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 1 минуту дольше, чем вторая труба? Объем работы Производительность (скорость) время I II Решение задач «задание 11» №1 .3 Ответ: 10 Объем работы Производительность (скорость) время I 110 x II 110 x+1
Слайд 18
Решение задач «задание 11» № 2.1 Ответ: 16 Объем работы Производительность (скорость) время I 12y·10 12y 10 24yx 12y+12y X II 21y·10 21y 10 9yx 21y-12y=9y X !!!
Слайд 19
Решение задач «задание 11» № 2.2 Ответ: 16 Объем работы Производительность (скорость) время I 16y·7=112y 16y 7 24yx 16y+8y=24y X II 25y·7=175y 25y 7 17yx 25y-8y=17y X !!! Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 16 рабочих, а во второй — 25 рабочих. Через 7 дней после начала работы в первую бригаду перешли 8 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.
Слайд 20
Самостоятельно Сборник «4000 задач» № 1639 №1652 № 1622
Слайд 21
Интернет ссылки
Текстовые задачи
В задании №11 ЕГЭ по математике профильного уровня требуется решить текстовую задачу. Как правило задача сводится к составлению двух уравнений с двумя неизвестными, которые необходимо выразить, подставить, вычислить и получить ответ! Приступим к разбору, так как какой-либо теории тут нет.
Разбор типовых вариантов заданий №11 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
[su_note note_color=”#defae6″]
Весной катер идёт против течения реки в 1 2/3 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 3/2 раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
[/su_note]
Алгоритм решения:
- Обозначаем неизвестные скорости переменными х и у.
- Составляем систему уравнений, исходя из условия.
- Выражаем х из одного уравнения системы через переменную у.
- Найденное выражение подставляем в другое уравнение системы и решаем получившееся уравнение.
- Записываем ответ.
Решение:
1. Пусть скорость катера равна х км/ч, а скорость течения весной у км/ч. Тогда y–1 (км/ч) – скорость течения летом.
Скорость катера по течению весной равна х+у км/ч, а против течения х – у км/ч. Летом соответственно скорости по течению и против равны: х+(у – 1) и х – (у – 1) км/ч.
2. По условию катер идет весной по течению со скоростью, которая составляет 5/3 от скорости против течения. Имеем: х+у=(5/3)(х – у).
Летом эти скорости разнятся в 3/2раза. То есть: х+(у – 1)=(3/2)(х – (у – 1).
Составим систему уравнений:
3. Выразим x через y из первого уравнения:
(5/3)(x–y)=(x+y),
(5/3)x – (5/3)y = x + y,
–(5/3)y – y = x – (5/3)x,
–(8/3)y = –(2/3)x,
8y = 2x,
4y = x,
х=4у.
4. Подставляем полученное значение в другое равенство
(3/2)(4y–(y–1)) = 4y+(y–1).
Отсюда
(3/2)(4y–y+1) = 4y+y–1,
(3/2)(3y+1) = 5y–,
(9/2)y + 3/2 = 5y–1,
(9/2)y – 5y = –1 – 3/2,
(9/2)y – (10/2)y = –1 – 3/2,
–(1/2)y = –5/2,
(1/2)y = 5/2,
y = 5.
Следовательно, скорость течения весной равна 5 км/ч.
Ответ: 5.
Второй вариант задания
[su_note note_color=”#defae6″]
Расстояние между пристанями А и В равно 77 км. Из А в В по течению реки отправился плот, а через 1 час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 40 км. Найдите скорость моторной лодки в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.
[/su_note]
Алгоритм решения:
- Обозначаем неизвестную скорость переменной х.
- Составляем уравнение для решения задачи, учитывая условие.
- Решаем получившееся уравнение.
- Делаем вывод.
- Записываем ответ.
Решение:
1. Пусть скорость лодки равна х км/ч. Тогда ее скорость по течению равна х+4 км/ч, а против течения х – 4 км/ч.
2. Пока лодка шла из точки A к точке B и обратно, плот по течению реки проплыл 40 км. Скорость течения равна 4 км/ч, можно установить, сколько времени двигался плот: 40:4=10 ч. Лодка отправилась в путь на 1 ч позже: 10 – 1= 9 ч. Расстояние в 77 км в направлении течения моторная лодка проплыла за ч, а против течения за
ч. Время, которое лодка была в движении туда и обратно равно 9 ч. Получаем уравнение:
Упрощаем полученное уравнение, и находим из него х:
77(х – 4)+77(х + 4)=9(х + 4)(х – 4)
77х – 77∙4 + 77х + 77∙4 = 9 (х2 – 16)
154х – 9х2 + 9∙16
– 9х2+ 154х + 144 = 0
9х2 – 154х – 144=0
Решаем квадратное уравнение через дискриминант, получаем:
Скорость не может быть отрицательной, тогда второй корень не удовлетворяет условию. Получаем, что скорость моторной лодки равнялась 18 км/ч.
Ответ: 18.
Третий вариант задания (из Ященко, №31)
[su_note note_color=”#defae6″]
Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 30 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 2 часа 40 минут позже автомобилиста. Ответ дайте в километрах в час.
[/su_note]
Алгоритм решения:
- Вводим переменную х.
- Составляем уравнение, исходя из условия.
- Решаем получившееся уравнение.
- Делаем вывод.
- Записываем ответ.
Решение:
1. Обозначим через х скорость движения велосипедиста.
2. Скорость автомобилиста на 30 км/ч выше, следовательно, она равна х+30. Автомобиль 60 км проезжает за часов, а велосипедист за
часов. По условию велосипедист прибыл на 2 часа 40 минут (8/3 часа) позже в назначенный пункт, чем автомобилист.
Получаем уравнение
3. Решаем полученное уравнение. Для этого преобразуем его:
Решаем квадратное уравнение, получаем два корня
Скорость не может быть отрицательной, значит, второй корень уравнения не удовлетворяет условию. Значит, велосипедист двигался со скоростью 15 км/ч.
Ответ: 15.
Даниил Романович | Просмотров: 8k