Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
2
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Центр. Вариант 1.
3
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: РЕШУ ЕГЭ — Предэкзаменационная работа 2014 по математике.
4
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Урал. Вариант 203., Задания 13 (С1) ЕГЭ 2013
5
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: Задания 13 (С1) ЕГЭ 2017, ЕГЭ 28.04.2014 по математике. Досрочная волна. Вариант 1., Задания 13 (С1) ЕГЭ 2014
Пройти тестирование по этим заданиям
Уравнения, часть С
Теория к заданию 13 из ЕГЭ по математике (профильной)
Уравнения, часть $С$
Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.
Схема решения сложных уравнений:
- Перед решением уравнения надо для него записать область допустимых значений (ОДЗ).
- Решить уравнение.
- Выбрать из полученных корней уравнения то, которые удовлетворяют ОДЗ.
ОДЗ различных выражений (под выражением будем понимать буквенно — числовую запись):
1. Выражение, стоящее в знаменателе, не должно равняться нулю.
2. Подкоренное выражение, должно быть не отрицательным.
3. Подкоренное выражение, стоящее в знаменателе, должно быть положительным.
4. У логарифма: подлогарифмическое выражение должно быть положительным; основание должно быть положительным; основание не может равняться единице.
Логарифмические уравнения
Для решения логарифмических уравнений необходимо знать свойства логарифмов: все свойства логарифмов мы будем рассматривать для $a > 0, a≠ 1, b> 0, c> 0, m$ – любое действительное число.
1. Для любых действительных чисел $m$ и $n$ справедливы равенства:
2. Логарифм произведения равен сумме логарифмов по тому же основанию от каждого множителя.
3. Логарифм частного равен разности логарифмов от числителя и знаменателя по тему же основанию
4. При умножении двух логарифмов можно поменять местами их основания
6. Формула перехода к новому основанию
7. В частности, если необходимо поменять местами основание и подлогарифмическое выражение
Можно выделить несколько основных видов логарифмических уравнений:
Представим обе части уравнения в виде логарифма по основанию $2$
Если логарифмы по одинаковому основанию равны, то подлогарифмические выражения тоже равны.
Т.к. основания одинаковые, то приравниваем подлогарифмические выражения
Перенесем все слагаемые в левую часть уравнения и приводим подобные слагаемые
Проверим найденные корни по условиям $table< x^2-3x-5>0; 7-2x>0;$
При подстановке во второе неравенство корень $х=4$ не удовлетворяет условию, следовательно, он посторонний корень
- Метод замены переменной.
В данном методе надо:
Решите уравнение $log_<2>√x+2log_<√x>2-3=0$
1. Запишем ОДЗ уравнения:
$table< х>0,text»так как стоит под знаком корня и логарифма»; √х≠1→х≠1;$
2. Сделаем логарифмы по основанию $2$, для этого воспользуемся во втором слагаемом правилом перехода к новому основанию:
3. Далее сделаем замену переменной $log_<2>√x=t$
4. Получим дробно — рациональное уравнение относительно переменной t
Приведем все слагаемые к общему знаменателю $t$.
Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
5. Решим полученное квадратное уравнение по теореме Виета:
6. Вернемся в п.3, сделаем обратную замену и получим два простых логарифмических уравнения:
Прологарифмируем правые части уравнений
Приравняем подлогарифмические выражения
Чтобы избавиться от корня, возведем обе части уравнения в квадрат
7. Подставим корни логарифмического уравнения в п.1 и проверим условие ОДЗ.
Первый корень удовлетворяет ОДЗ.
$<table 16 >0; 16≠1;$ Второй корень тоже удовлетворяет ОДЗ.
- Уравнения вида $log_x+log_x+c=0$. Такие уравнения решаются способом введения новой переменной и переходом к обычному квадратному уравнению. После того, как корни уравнения будут найдены, надо отобрать их с учетом ОДЗ.
Дробно рациональные уравнения
- Если дробь равна нулю, то числитель равен нулю, а знаменатель не равен нулю.
- Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно-рациональным.
Чтобы решить дробно рациональное уравнение, необходимо:
- Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ)
- Найти общий знаменатель дробей, входящих в уравнение;
- Умножить обе части уравнения на общий знаменатель;
- Решить получившееся целое уравнение;
- Исключить из его корней те, которые не удовлетворяют условию ОДЗ.
- Если в уравнении участвуют две дроби и числители их равные выражения, то знаменатели можно приравнять друг к другу и решить полученное уравнение, не обращая внимание на числители. НО учитывая ОДЗ всего первоначального уравнения.
Показательные уравнения
Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.
При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются
3. При возведении степени в степень основание остается прежним, а показатели перемножаются
4. При возведении в степень произведения в эту степень возводится каждый множитель
5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель
6. При возведении любого основания в нулевой показатель степени результат равен единице
7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби
8. Радикал (корень) можно представить в виде степени с дробным показателем
Виды показательных уравнений:
1. Простые показательные уравнения:
а) Вида $a^=a^$, где $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием ($а >0, a≠1$) равны только тогда, когда равны их показатели.
b) Уравнение вида $a^=b, b>0$
Для решения таких уравнений надо обе части прологарифмировать по основанию $a$, получается
2. Метод уравнивания оснований.
3. Метод разложения на множители и замены переменной.
- Для данного метода во всем уравнении по свойству степеней надо преобразовать степени к одному виду $a^$.
- Сделать замену переменной $a^=t, t > 0$.
- Получаем рациональное уравнение, которое необходимо решить путем разложения на множители выражения.
- Делаем обратные замену с учетом того, что $t > 0$. Получаем простейшее показательное уравнение $a^=t$, решаем его и результат записываем в ответ.
По свойству степеней преобразуем выражение так, чтобы получилась степень 2^x.
Сделаем замену переменной $2^x=t; t>0$
Получаем кубическое уравнение вида
Умножим все уравнение на $2$, чтобы избавиться от знаменателей
Разложим левую часть уравнения методом группировки
Вынесем из первой скобки общий множитель $2$, из второй $7t$
Дополнительно в первой скобке видим формулу разность кубов
Далее скобку $(t-1)$ как общий множитель вынесем вперед
Произведение равно нулю, когда хотя бы один из множителей равен нулю
Решим первое уравнение
Решим второе уравнение через дискриминант
Получили три корня, далее делаем обратную замену и получаем три простых показательных уравнения
4. Метод преобразования в квадратное уравнение
- Имеем уравнение вида $А·a^<2f(x)>+В·a^+С=0$, где $А, В$ и $С$ — коэффициенты.
- Делаем замену $a^=t, t > 0$.
- Получается квадратное уравнение вида $A·t^2+B·t+С=0$. Решаем полученное уравнение.
- Делаем обратную замену с учетом того, что $t > 0$. Получаем простейшее показательное уравнение $a^=t$, решаем его и результат записываем в ответ.
Способы разложения на множители:
- Вынесение общего множителя за скобки.
Чтобы разложить многочлен на множители путем вынесения за скобки общего множителя надо:
- Определить общий множитель.
- Разделить на него данный многочлен.
- Записать произведение общего множителя и полученного частного (заключив это частное в скобки).
Разложить на множители многочлен: $10a^<3>b-8a^<2>b^2+2a$.
Общий множитель у данного многочлена $2а$, так как на $2$ и на «а» делятся все члены. Далее найдем частное от деления исходного многочлена на «2а», получаем:
Это и есть конечный результат разложения на множители.
Применение формул сокращенного умножения
1. Квадрат суммы раскладывается на квадрат первого числа плюс удвоенное произведение первого числа на второе число и плюс квадрат второго числа.
2. Квадрат разности раскладывается на квадрат первого числа минус удвоенное произведение первого числа на второе и плюс квадрат второго числа.
3. Разность квадратов раскладывается на произведение разности чисел и их сумму.
4. Куб суммы равен кубу первого числа плюс утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа плюс куб второго числа.
5. Куб разности равен кубу первого числа минус утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа и минус куб второго числа.
6. Сумма кубов равна произведению суммы чисел на неполный квадрат разности.
7. Разность кубов равна произведению разности чисел на неполный квадрат суммы.
Метод группировки
Методом группировки удобно пользоваться, когда на множители необходимо разложить многочлен с четным количеством слагаемых. В данном способе необходимо собрать слагаемые по группам и вынести из каждой группы общий множитель за скобку. У нескольких групп после вынесения в скобках должны получиться одинаковые выражения, далее эту скобку как общий множитель выносим вперед и умножаем на скобку полученного частного.
Разложить многочлен на множители $2a^3-a^2+4a-2$
Для разложения данного многочлена применим метод группировки слагаемых, для этого сгруппируем первые два и последние два слагаемых, при этом важно правильно поставить знак перед второй группировкой, мы поставим знак + и поэтому в скобках запишем слагаемые со своими знаками.
Далее из каждой группы вынесем общий множитель
После вынесения общих множителей получили пару одинаковых скобок. Теперь данную скобку выносим как общий множитель.
Произведение данных скобок — это конечный результат разложения на множители.
С помощью формулы квадратного трехчлена.
Если имеется квадратный трехчлен вида $ax^2+bx+c$, то его можно разложить по формуле
$ax^2+bx+c=a(x-x_1)(x-x_2)$, где $x_1$ и $x_2$ — корни квадратного трехчлена
Уравнения смешанного типа егэ математика
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а) Решим уравнение
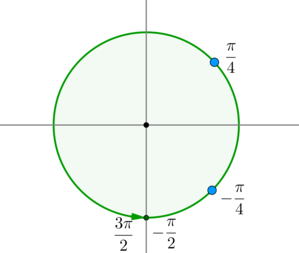
б) С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа:
Ответ: а) б)
Это синус вначале нужно писать
Нет. Нужно внимательно читать решение задачи, и следить за смыслом, а не бездумно механически действовать по заученным формулам.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а) Преобразуем исходное уравнение:
б) С помощью числовой окружности отберем корни, принадлежащие отрезку Получим числа:
Ответ : а) б)
если же tgx=1,то там рассматриваются два корня: x=п/4+2пn x=5п/4+2пn
и как раз через эти два корня я нашла корни,принадлежащие промежутку,но почему в ответе под а у вас одно решение?
эти две точки можно объединить, что у нас и сделано
почему при решении было выполнено деление на 3^cos(x), ведь тогда теряется корень 3^cos(x)=0?
такого корня нет, поэтому он не теряется
Извиняюсь, что задаю вопрос не совсем по теме, но когда вообще МОЖНО делить на неизвестное, а когда нельзя? Я не одну статью прочитал на эту тему, но все понять не могу. Одни говорят, что можно, но при этом происходит потеря корней, а другие говорят — что можно и делают это, третьи говорят, что будет потеря корней, но это МОЖНО делать.
Короче говоря. как мне кажется, это самая не разобранная тема. О ней вообще нет инфы в должном обьеме. Пожалуйста, обьсните в кратце, когда МОЖНО, а когда НЕЛЬЗЯ.
p.s. я понял, что МОЖНО, вроде как, когда не происходит изменение ОДЗ, но опять же, а когда оно проиходит?
Думаю, мне не одному этот вопрос требуется.
Подробный ответ ЗДЕСЬ невозможен. Лучше задать его, нажав ссылку «Помощь по заданию».
Если кратко, то правило простое: НЕЛЬЗЯ делить на нуль. На положительные и отрицательные числа делить можно, соблюдая правила.
Число положительно при любом значении
, поэтому на него можно делить.
В уравнении , если Вы поделите на
, то потеряете корень
. Поэтому делить на
нельзя.
Выход может быть таким: рассмотрите два случая
1. , тогда
верное равенство. Значит
− корень.
2. , тогда
и на него можно поделить. Получим
.
Ответ:
А вот уравнение можно делить на
. Потому что по ОДЗ
, а значит на ОДЗ
Репетитор по математике
Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».
Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]
Стоимость занятий
Набор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат.
Видеокурсы подготовки к ЕГЭ-2021
Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.
Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.
Группа Вконтакте
В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.
Преимущества
Педагогический стаж
Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.
Собственная методика
За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.
Гарантированный результат
За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.
Индивидуальная работа
Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.
источники:
http://ege.sdamgia.ru/test?theme=201
http://mathlesson.ru/node/8031
ЕГЭ Профиль №12. Уравнения смешанного типа, содержащие тригонометрические функции
Задание 907
Дано уравнение $$sqrt{1-sin ^{2}x}=sin x$$.
a) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку $$left [frac{5pi}{2};4pi right ]$$
Ответ: А) $$frac{pi}{4}+2pi n;frac{3pi}{4}+2pi m,n,min Z$$ Б) $$frac{11pi}{4}$$
Скрыть
$$ sqrt{1-sin ^{2}x}=sin x Leftrightarrow left{begin{matrix}sqrt{1-sin ^{2}x}geq 0\ sin xgeq 0\ 1-sin ^{2}x=sin ^{2} xend{matrix}right.$$ $$Leftrightarrow left{begin{matrix} 1-sin ^{2}xgeq 0\ sin xgeq 0\ 1-sin ^{2}x=sin ^{2} xend{matrix}right.$$ $$Leftrightarrow left{begin{matrix}sin ^2 xleq 1\ sin xgeq 0\ 1=2sin ^{2} xend{matrix}right.$$ $$Leftrightarrow left{begin{matrix}sin ^{2}xleq 1\ sin xgeq 0\ sin x = pm frac{sqrt{2}}{2}end{matrix}right.$$ $$Leftrightarrow sin x = frac{sqrt{2}}{2}$$ $$Leftrightarrow left{begin{matrix} x=frac{pi}{4}+2pi n , nin Z\ x=frac{3pi}{4}+2pi n nin Zend{matrix}right.$$
Задание 3248
Дано уравнение $$log_{2}sin xcdotlog_{sin x}cos^{2}x=-1$$ .
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку
Ответ: а) $$frac{pi}{4}+2pi n$$; $$frac{3pi}{4}+2pi n$$; б) $$frac{17pi}{4}$$; $$frac{19pi}{4}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$log_{2}sin xcdotlog_{sin x}cos^{2}x=-1$$ $$left{begin{matrix}sin x>0\cos^{2}x>0\sin xneq1end{matrix}right.$$ $$left{begin{matrix}xin(2pi n;pi+2pi n)\xneqfrac{pi}{2}+pi nend{matrix}right.$$ $$frac{1}{log_{sin x}2}cdotlog_{sin x}cos^{2}x=-1$$ $$frac{log_{sin x}cos^{2}x}{log_{sin x}2}=-1$$ $$log_{2}cos^{2}x=-1$$ $$cos^{2}x=frac{1}{2}$$ $$left{begin{matrix}cos x=frac{sqrt{2}}{2}\cos x=-frac{sqrt{2}}{2}end{matrix}right.$$ $$left{begin{matrix}x=pmfrac{pi}{4}+2pi n\x=pmfrac{3pi}{4}+2pi nend{matrix}right.$$ $$nin Z$$ С учетом ОДЗ: $$x_{1}=frac{pi}{4}+2pi n$$ $$x_{2}=frac{3pi}{4}+2pi n$$ б) $$4pi+frac{pi}{4}=frac{17pi}{4}$$ $$5pi-frac{pi}{4}=frac{19pi}{4}$$
Задание 4068
а)Решите уравнение $$5^{2sin 2x}=(frac{1}{25})^{cos (frac{3pi}{2}+x)}$$
б)Найдите все корни этого уравнения, принадлежащие отрезку $$[frac{3pi}{2};3pi]$$
Ответ:
Задание 4082
Решите систему уравнений
$$left{begin{matrix} 16^{cos x}-10*4^{cos x}+16=0\ sqrt{y}+2cos x=0 end{matrix}right.$$
Ответ:
Задание 4083
Решите систему уравнений
$$left{begin{matrix} y^{2}=x\ sin y^{2}=cos x end{matrix}right.$$
Ответ:
Задание 4084
Решите систему уравнений
$$left{begin{matrix} 2cos 2x +3sin x = 1\ y^{2}cos x + ycos x + frac{sqrt{15}}{2}=0 end{matrix}right.$$
Ответ:
Задание 4085
Решите уравнение $$(sin x — frac{sqrt{3}}{2})sqrt{3x^{2}-7x+4}=0$$
Ответ:
Задание 4086
а) Решите уравнение $$ (frac{4}{9})^{cos x}+2*(frac{2}{3})^{cos x}-3=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[frac{5pi}{2};4pi]$$
Ответ:
Задание 4087
а) Решите уравнение $$12^{sin x}=4^{sin x}*3^{-sqrt{3}cos x}$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[frac{5pi}{2};4pi]$$
Ответ:
Задание 4088
а) Решите уравнение $$(25^{cos x})^{sin x}=5^{cos x}$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-frac{5pi}{2};-pi]$$
Ответ:
Задание 4089
а) Решите уравнение $$4^{sin x} + 4^{-sin x}=frac{5}{2}$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[frac{5pi}{2};4pi]$$
Ответ:
Задание 4090
а) Решите уравнение $$(frac{2}{5})^{cos x} + (frac{5}{2})^{cos x}=2$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[2pi;frac{7pi}{2}]$$
Ответ:
Задание 4091
а) Решите уравнение $$5^{2sin 2x}=(frac{1}{25})^{cos (frac{3pi}{2}+x)}$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[frac{3pi}{2};3pi]$$
Ответ:
Задание 4116
а) Решите уравнение $$log_2 (cos x + sin 2x +8) =3$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[frac{3pi}{2};3pi]$$
Ответ:
Задание 4117
а) Решите уравнение $$2log_{2} ^{2} (2cos x) — 9log_{2} (2cos x) +4 =0$$
б) Найдите корни этого уравнения, принадлежащие отрезку $$[-2pi;-frac{pi}{2}]$$
Ответ:
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Смешанные уравнения
Задание
1
#3039
Уровень задания: Равен ЕГЭ
Решите уравнение [{large{log_3left(9^{sin x}+9right)=sin
x-log_{frac13}left(28-2cdot 3^{sin x}right)}}]
Заметим, что (sin x=log_3 3^{sin x}). Сделаем замену (3^{sin
x}=t, t>0). Тогда уравнение примет вид: [log_3(t^2+9)=log_3t+log_3(28-2t)] ОДЗ уравнения: [begin{cases} t^2+9>0\
t>0\ 28-2t>0 end{cases} quadLeftrightarrowquad 0<t<14] Решим уравнение на ОДЗ. [log_3(t^2+9)=log_3(t(28-2t)) quadRightarrowquad 3t^2-28t+9=0] Корнями данного уравнения являются (t_1=9) и (t_2=frac13). Оба корня подходят по ОДЗ.
Сделаем обратную замену:
(3^{sin x}=9 quadLeftrightarrowquad sin x=2). Данное уравнение не имеет решений.
(3^{sin x}=dfrac13 quadLeftrightarrowquad sin x=-1
quadLeftrightarrowquad x=-dfrac{pi}2+2pi n, ninmathbb{Z}).
Ответ:
(-dfrac{pi}2+2pi n, ninmathbb{Z})
Задание
2
#3137
Уровень задания: Сложнее ЕГЭ
1) Решите уравнение [6+log_2(4cos x)cdot
log_2(16sin^2x)=log_2(64cos^3x)+log_2(256sin^4x)]
2) Найдите все его корни, принадлежащие промежутку (left[-dfrac{pi}2;dfrac{3pi}2right].)
1) Выпишем ОДЗ: [begin{cases}
cos x>0\
sin^2x>0\
cos^3x>0\
sin^4x>0 end{cases} quadLeftrightarrowquad
begin{cases}
cos x>0\
sin xne 0 end{cases}] Решим на ОДЗ. Сделаем замену: (t=log_2(4cos x), quad z=log_2(16sin^2x)), тогда уравнение примет вид: [6+tcdot z=3t+2z quadLeftrightarrowquad (tz-3t)-(2z-6)=0
quadLeftrightarrowquad (t-2)(z-3)=0] Следовательно, решением являются [left[ begin{gathered} begin{aligned}
&log_2(4cos x)=2\
&log_2(16sin^2x)=3
end{aligned} end{gathered} right.
quadRightarrowquad left[ begin{gathered} begin{aligned}
&cos x=1\[2ex]
&sin^2x=dfrac12
end{aligned} end{gathered} right.
quadRightarrowquad left[ begin{gathered} begin{aligned}
&x=2pi n, ninmathbb{Z}\[2ex]
&x=dfrac{pi}4+2pi k, kinmathbb{Z}\[2ex]
&x=-dfrac{pi}4+2pi k, kinmathbb{Z}\[2ex]
&x=dfrac{3pi}4+2pi k, kinmathbb{Z}\[2ex]
&x=-dfrac{3pi}4+2pi k, kinmathbb{Z}
end{aligned} end{gathered} right.]
Так как по ОДЗ (cos x>0) и (sin xne 0), то подходят лишь [x=pmdfrac{pi}4+2pi k, kinmathbb{Z}]
2) По окружности видно, что в указанный отрезок входят только (-dfrac{pi}4) и (dfrac{pi}4).
Ответ:
1) (pmdfrac{pi}4+2pi k, kinmathbb{Z})
2) (-dfrac{pi}4; dfrac{pi}4)
Задание
3
#3257
Уровень задания: Сложнее ЕГЭ
а) Решите уравнение [log_{sqrt2}{left(log_{sin
x+1}{left(2-cos^2x+2sin xright)^{cos 4x}}right)}=2]
б) Найдите все корни уравнения, принадлежащие промежутку ([-2pi;0]).
а)
1) Запишем ОДЗ левой части:
(begin{cases} sin x+1>0\ sin x+1ne 1\
2-cos^2x+2sin x>0 end{cases} quad Rightarrow quad
begin{cases}
sin xne -1\
sin xne 0\
2-(1-sin^2x)+2sin x>0 end{cases} quad Rightarrow)
(Rightarrow quad
begin{cases}
sin xne -1\
sin xne 0\
(sin x+1)^2>0 end{cases} quad Rightarrow quad begin{cases}
sin xne -1\
sin xne 0 end{cases})
2) Решим само уравнение на ОДЗ. Рассмотрим внутренний логарифм. Из ОДЗ мы уже поняли, что (2-cos^2x+2sin x=(sin x+1)^2). Таким образом:
[log_{sin x+1}{left(left(sin x+1right)^2right)^{cos 4x}}=
log_{sin x+1}{left(sin x+1right)^{2cos 4x}}=2cos 4x]
Таким образом, уравнение приобретает вид:
(log_{sqrt2}{2cos 4x}=2 quad Rightarrow quad 2cos
4x=(sqrt2)^2quad Rightarrow quad cos 4x=1quad Rightarrow )
(Rightarrow quad 4x=2pi n, ninmathbb{Z} quad Rightarrow quad
x=dfrac{pi}2n, ninmathbb{Z})
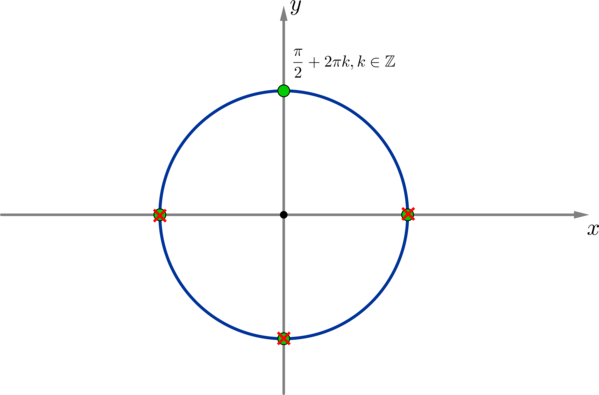
3) Пересечем данное решение с ОДЗ (в данном случае это удобно сделать по окружности):
Таким образом, нам подходит всего одна точка на окружности, в которую попадают углы вида: [x=dfrac{pi}2+2pi k,
kinmathbb{Z}]
б) Отберем корни:
[-2pileqslant dfrac{pi}2+2pi kleqslant 0 quad Rightarrow quad
-dfrac54leqslant kleqslant -dfrac14]
Таким образом, единственное целое (k), подходящее в неравенство, это (k=-1). При таком (k) получаем корень (x=-dfrac{3pi}2).
Ответ:
а) (dfrac{pi}2+2pi k, kinmathbb{Z})
б) (-dfrac{3pi}2)
Задание
4
#3138
Уровень задания: Сложнее ЕГЭ
Решите уравнение [{large{5^{x^2}+5^{2-x^2}=5left(1+sindfrac{pi}2xright)}}]
Преобразуем уравнение, разделив обе части равенства на (5): [5^{x^2-1}+5^{1-x^2} = 1+sin dfrac{pi}2x quad Leftrightarrowquad
5^{x^2-1}+dfrac1{5^{x^2-1}} = 1+sin dfrac{pi}2x] Заметим, что левая часть представляет собой сумму двух взаимно обратных чисел: (t+frac1t), причем положительных. Как известно, сумма двух положительных взаимно обратных чисел не превосходит (2), следовательно, [5^{x^2-1}+dfrac1{5^{x^2-1}}geqslant 2] Заметим, что (sin dfrac{pi}2xleqslant 1) при всех (x), следовательно, правая часть [1+sin dfrac{pi}2xleqslant 2] Таким образом, равенство может достигаться тогда и только тогда, когда обе части равенства равны (2): [begin{cases}
5^{x^2-1}+dfrac1{5^{x^2-1}}=2\[2ex]
1+sin dfrac{pi}2x=2 end{cases}]
Сумма взаимно обратных чисел равна (2) тогда и только тогда, когда каждое из них равно (1), следовательно: [begin{cases}
5^{x^2-1}=1\[2ex]
sin dfrac{pi}2x=1
end{cases} quadLeftrightarrowquad
begin{cases}
x^2-1=0\[2ex]
dfrac{pi}2x=dfrac{pi}2+2pi n, ninmathbb{Z}
end{cases} quadLeftrightarrowquad begin{cases}
x=pm 1\[2ex]
x=1+4 n, ninmathbb{Z}
end{cases} quadLeftrightarrowquad x=1.]
Ответ: 1
Задание
5
#1912
Уровень задания: Сложнее ЕГЭ
а) Решите уравнение [cos (x^2+x)+cos
left(x+dfrac{2pi}3right)+cos left(x+dfrac{4pi}3right)=0]
б) Найдите все корни, принадлежащие отрезку ([0;2]).
а) Применим формулу суммы косинусов (cosalpha+cos
beta=2cosdfrac{alpha+beta}2cosdfrac{alpha-beta}2):
[cos(x^2+x)+2cos(pi+x)cosleft(-dfrac{pi}3right)=0 quad Leftrightarrow
quad cos(x^2+x)+2cdot(-cos x)cdot dfrac12=0 quad
Leftrightarrow]
[Leftrightarrow quad cos(x^2+x)-cos x=0 quad Leftrightarrow quad
-2sin dfrac{x^2+2x}2sin dfrac{x^2}2=0 quad Leftrightarrow]
[Leftrightarrow quad
left[ begin{gathered} begin{aligned}
&sin dfrac{x^2+2x}2=0\[3pt]
&sin dfrac{x^2}2=0
end{aligned} end{gathered} right. quad Leftrightarrow quad
left[ begin{gathered} begin{aligned}
&x^2+2x-2pi n, ninmathbb{Z}\
&x^2=2pi k, kinmathbb{Z}
end{aligned} end{gathered} right.]
Первое уравнение совокупности является квадратным и имеет решения, когда
(D=4(1+2pi
n)geqslant 0 Rightarrow n=0;1;2;dots)
Тогда (x=-1pm sqrt{1+2pi n}, n=0;1;2;dots)
Второе уравнение имеет решения, когда (2pi kgeqslant 0 Rightarrow
k=0;1;2;dots)
Тогда (x=pmsqrt{2pi k}, k=0;1;2;dots)
Эти две серии корней пересекаются по решению (x=0) (при (n=k=0)), поэтому из одной серии необходимо убрать это решение, например, из второй. Тогда (x=pm sqrt{2pi k}, k=1;2;dots)
б) Рассмотрим первую серию корней: (x_1=-1-sqrt{1+2pi n_1},
n_1=0;1;2;dots)
Заметим, что в этой серии все (x) будут отрицательными, т.к. (-sqrt{A}leqslant 0 Rightarrow -sqrt{A}-1leqslant -1).
Значит, нет корней из отрезка ([0;2]).
Рассмотрим вторую серию корней: (x_2=-1+sqrt{1+2pi n_2},
n_2=0;1;2;dots)
при (n_2=0) (x_2=-1+sqrt1=0) – подходит;
при (n_2=1) (x_2=-1+sqrt{1+2pi}sim 1,dots) — подходит;
при (n_2=2) (x_2=-1+sqrt{1+4pi}>2) — уже не подходит.
Далее при возрастании (n_2) будет увеличиваться и (x_2).
Аналогично рассуждая в третьей и четвертой сериях, получим, что в них нет корней из промежутка ([0;2]).
Ответ:
а) (-1pm sqrt{1+2pi n}; pmsqrt{2pi k};
ninmathbb{N}cup{0}, kinmathbb{N})
б) (0;-1+sqrt{1+2pi})
Задание
6
#1673
Уровень задания: Сложнее ЕГЭ
a) Решите уравнение
[begin{aligned}
(mathrm{tg}^2,(2x) + mathrm{ctg}^2,(2x) — 2)cdot mathrm{arcsin}, (x^2) = 0.
end{aligned}]
б) Найдите все его корни, принадлежащие промежутку ([-pi; 0]).
ОДЗ: [sin 2x neq 0,quad cos 2x neq 0,quad -1 leq x^2 leq 1] (так как (mathrm{tg}, (2x)) не теряет смысл при (cos (2x) neq 0), (mathrm{ctg}, (2x)) не теряет смысл при (sin (2x) neq 0), (mathrm{arcsin}, (x^2)) не теряет смысл при (-1 leq x^2 leq 1)). Решим на ОДЗ:
а) Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысла.
Рассмотрим сначала уравнение [mathrm{arcsin}, (x^2) = 0.] По определению (mathrm{arcsin}, (x^2)) – это угол в радианах, лежащий на (left[-dfrac{pi}{2}; dfrac{pi}{2}right]), синус которого равен (x^2). [mathrm{arcsin}, (x^2) = 0qquadRightarrowqquad sin (0) = x^2qquadRightarrowqquad x^2 = 0qquadRightarrowqquad x = 0.] Однако, (x = 0) не подходит по ОДЗ, следовательно (x = 0) – не является корнем исходного уравнения.
Рассмотрим теперь [mathrm{tg}^2,(2x) + mathrm{ctg}^2, (2x) — 2 = 0] заметим, что на ОДЗ (mathrm{tg}, (2x)cdotmathrm{ctg}, (2x) = 1), тогда (mathrm{ctg}, (2x) = dfrac{1}{mathrm{tg}, (2x)}).
Сделаем замену (mathrm{tg}, (2x) = t), тогда рассматриваемое уравнение примет вид
[begin{aligned}
t^2 + dfrac{1}{t^2} — 2 = 0,
end{aligned}]
причём на ОДЗ (0 neq mathrm{tg},(2x) = t), тогда можно домножить последнее уравнение на (t^2): (t^4 + 1 — 2t^2 = 0quadLeftrightarrowquad t^4 + 1 — 2t^2 = (t^2 — 1)^2quadLeftrightarrow)
(Leftrightarrow quad (t^2 — 1)^2 = 0quadLeftrightarrowquad t^2 — 1 = 0quadLeftrightarrowquad t = pm 1.)
Так как (t = mathrm{tg},(2x)), то (mathrm{tg},(2x) = pm 1), откуда находим (2x = pm dfrac{pi}{4} + pi k), тогда (x = pm dfrac{pi}{8} + dfrac{pi k}{2}), где (kinmathbb{Z}). Однако, на ОДЗ (-1 leq x^2 leq 1), то есть (-1 leq x leq 1):
[-1 leq dfrac{pi}{8} + dfrac{pi k}{2} leq 1qquadLeftrightarrowqquad -dfrac{8}{pi} leq 1 + 4 k leq dfrac{8}{pi},] но (kinmathbb{Z}), тогда по ОДЗ среди таких корней подходит только корень при (k = 0): (x = dfrac{pi}{8}).
[-1 leq -dfrac{pi}{8} + dfrac{pi k}{2} leq 1qquadLeftrightarrowqquad -dfrac{8}{pi} leq -1 + 4 k leq dfrac{8}{pi},] но (kinmathbb{Z}), тогда по ОДЗ среди таких корней подходит только корень при (k = 0): (x = -dfrac{pi}{8}).
б) Среди корней (pm dfrac{pi}{8}) на отрезок ([-pi; 0]) попадает только (-dfrac{pi}{8}).
Ответ:
а) (dfrac{pi}{8}), (-dfrac{pi}{8}).
б) (-dfrac{pi}{8}).
Задание
7
#3254
Уровень задания: Сложнее ЕГЭ
Найдите сумму корней уравнения
[x+1=2log_2{(2^x+1)}-2log_4{(2016-2^{-x})}]
ОДЗ уравнения: (2016-2^{-x}>0).
Преобразуем уравнение на ОДЗ:
[log_2{2^{x+1}}=log_2{dfrac{(2^x+1)^2}{2016-2^{-x}}} quad Rightarrow quad
2^{x+1}=dfrac{(2^x+1)^2}{2016-2^{-x}}]
Сделаем замену: (2^x=t>0). Тогда уравнение примет вид:
[2t=dfrac{(t+1)^2}{2016-frac 1t} quad Rightarrow quad
2tcdot left(2016-frac1tright)=t^2+2t+1 quad (text{т.к. }
2016-frac1t>0 text{ по ОДЗ})]
Уравнение сведется к квадратному: [t^2-4030t+3=0]
которое имеет два корня: (t_1, t_2), причем оба положительны (т.к. их произведение равно (3), то есть положительно, и сумма равна (4030), то есть тоже положительна). Проверим, подходят ли оба эти корня по ОДЗ. Для начала преобразуем ОДЗ: [2016-frac1t>0 quad Rightarrow quad 2016t-1>0 quad Rightarrow
quad t>dfrac 1{2016}]
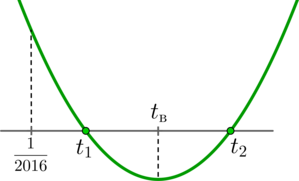
Заметим, что абсцисса вершины параболы (y=t^2-4030t+3) — это (t_{text{в}}=dfrac{4030}2=2015>frac1{2016}).
Следовательно, если выполнено (y(frac1{2016})>0), то это будет значить, что оба корня находятся правее (frac1{2016}):
Проверкой убеждаемся, что действительно (y(frac1{2016})>0). Значит, оба корня (t_1) и (t_2) подходят по ОДЗ.
Заметим, что (t_1cdot t_2=2^{x_1}cdot 2^{x_2}=2^{x_1+x_2}). Следовательно, (x_1+x_2=log_2{(t_1cdot t_2)}=log_2{3}).
Ответ:
(log_23)

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Открытое
занятие кружка в 11 классе по теме «Подготовка к ЕГЭ. Решение уравнений
смешанного типа»
Цель: успешная
подготовка к государственной итоговой аттестации
Задачи:
Образовательные: выработать
у обучающихся прочные навыки в умении решать показательные, логарифмические,
тригонометрические и смешанные уравнения ЕГЭ. Углубить знания по теме.
Развивающие:
развивать у обучающихся умение анализировать, синтезировать, сравнивать,
обобщать, развивать внимание, навыки самоконтроля, вычислительные навыки.
Воспитательные:
вырабатывать самостоятельность при работе на занятии, прививать трудолюбие,
аккуратность при выполнении вычислений, прививать интерес к математике.
Задачи занятия:
1. Повторить
основные типы уравнений, наиболее типичные приемы и методы их решения
2. Систематизировать
знания по данной теме
3. Отработать
навыки применения знаний при решении заданий типа ЕГЭ (№ 13)
Тип занятия:
закрепление и систематизация знаний и умений по теме. Подготовка к ЕГЭ.
Формы:
·
Коллективная
·
Индивидуальная
·
Фронтальная
Методы:
·
Словесный
·
Наглядный
·
Практический
·
Беседа
Оборудование: тетрадь
для консультаций, компьютер, проектор, экран, презентация
Ход
занятия
1. Организационный
момент
Вступительное
слово: Здравствуйте, ребята. Настраиваемся на занятие, а оно необычное,
открытое и проходит в рамках районного методического объединения учителей
математики. Эпиграфом к занятию будут такие слова: (слайд 2)
Результат учения
равен произведению способности на старательность. Если старательность равна
нулю, то и все произведение равно нулю. А способности есть у каждого.
И сегодня мы
продолжим отрабатывать умения и навыки, которые вы должны будете
продемонстрировать, решая задание № 13 экзаменационной работы профильного
уровня.
2. Систематизация
и повторение пройденного материала
Вспомнить:
·
Какие уравнения вы знаете?
·
Какие из них мы решали на прошлом занятии
(показательные, логарифмические, тригонометрические)
3. Формулирование
темы и задач занятия
Вызвать к доске по очереди 3-х
обучающихся: устно
— Рассказать, какие уравнения называются
показательными? Как решать такие уравнения (методы, приемы)?
— Рассказать, какие уравнения называются
логарифмическими? Методы и приемы решения логарифмических уравнений.
— Рассказать, какие уравнения называются
тригонометрическими? Методы и приемы решения тригонометрических уравнений.
Одновременно у доски 3 человека:
— Поворот точки вокруг начала координат
— Свойства логарифмов
— Тригонометрические: основное
тригонометрическое тождество, формулы сложения, двойного и половинного угла,
формулы приведения, сумма и разность синусов и косинусов).
4. Работа
устно (базовые, слайд 3)
5. Работа
письменно (слайд 4)
В экзаменационных работах
вам предлагается не просто решить уравнение (задание № 13 а)), но и указать
корни этого уравнения на определенном отрезке. Предлагаю найти корни последнего
уравнения на отрезке [-. Определить корни можно
несколькими способами:
— отбор корней по
тригонометрической окружности (улитка), наиболее наглядный, простой.
— отбор корней по
грфику
— Отбор корней
неравенством
— Отбор корней по
значениям n
Решение уравнений
(слайд 5)
6. Оценивание
выполнения задания
Задание № 13
проверяет умение решать уравнения. Примерное время выполнения задания
обучающимися 13-20 минут и оценивается в 2 балла (слайд 6)
7. Самостоятельное
решение уравнения с последующей проверкой
8. Дома
Используя
различные источники сети интернет, найти аналогичные задания, решить их и
оформить на листе А4. Подготовиться к защите. Задания не должны совпадать.
9. Рефлексия.
Вернуться к эпиграфу и сформулировать свои выводы:
— Сегодня на уроке я
узнал(а)…
— Было интересно…
— Было трудно…
— Меня удивило…
— Урок дал мне для жизни…
10. Итог.
Закончить занятие мне бы хотелось словами
Пьера Лапласа: «То, что мы не знаем – ограниченно, а то чего мы не знаем –
бесконечно». Поэтому обогащайтесь знаниями, чаще находитесь в этой
бесконечности. Спасибо за работу.
Примеры:
(sin2x+3x=3)
(15^{cosx} =3^{cosx}cdot5^{sinx})
(log_2{x}=3+x)
Решение смешанного уравнения
Каждое такое уравнение решается очень индивидуально. Общего метода решения – нет. В некоторых уравнениях нужно умело использовать формулы. В других помогут графики функций.
Пример. Решить уравнение (log_2x=-x+1).
Решение:
Здесь никакие преобразования не помогут найти корень. Это отличительный признак уравнений, решающихся графически.
Представим левую и правую части уравнения как функции: (f(x)=log_2x) и (g(x)=-x+1). Уравнения требует, чтоб они были равны – значит, графики этих функций должны пересекаться, а точка пересечения и будет корнем уравнения.
Построим графики функций и найдем точки пересечений.

Единственная точка пересечения — ((1;0)). Значит, корнем уравнения будет значение (x=1). Проверим это подстановкой:
(log_21=-1+0)
(0=0)
Сошлось.
Ответ: (1).
Конечно, некоторые из вас сразу нашли этот корень простым подбором, но это не будет полноценным решением. Почему? Потому что вы не можете быть уверены, что других корней нет, а график функций снимает этот вопрос — он четко показывает: корень здесь только один.
Пример(задание из ЕГЭ). Решите уравнение (15^{cosx} =3^{cosx} cdot 5^{sinx}).
Решение:
|
(15^{cosx} =3^{cosx}cdot 5^{sinx} ) |
Это показательно—тригонометрическое уравнение. |
|
|
(3^{cosx} cdot 5^{cosx} = 3^{cosx} cdot 5^{sinx}) |
Перенесем выражение из правой части в левую. |
|
|
(3^{cosx} cdot 5^{cosx} — 3^{cosx} cdot 5^{sinx}=0) |
Вынесем за скобки (3^{cosx}). |
|
|
(3^{cosx}(5^{cosx} -5^{sinx})=0) |
Решаем методом расщепления. |
|
|
(3^{cosx} =0) или (5^{cosx} -5^{sinx} =0) |
В какую степень надо возвести тройку, чтоб она стала нулем? Ни в какую, положительное число в любой степени останется положительным числом. Поэтому у первого уравнения нет решения. |
|
|
нет корней (5^{cosx}=5^{sinx}) |
Имеем показательное уравнение. Решаем его как обычно — «убираем» основания степеней. |
|
|
(cosx=sinx) |
Делим уравнение на (sinx). Это можно сделать т.к. (sinx=0) не будет решением уравнения. Значит синус икс – не ноль, и поэтому на него можно делить. |
|
|
(сtg x=1) |
Решаем базовое тригонометрическое уравнение. |
|
|
( x=)(frac{π}{4})(+πk), (k∈Z). |
Ответ: ( x=)(frac{π}{4})(+πk), (k∈Z).
Скачать статью