Как решать второе задание егэ по математике профильный уровень

Задание 2 Профильного ЕГЭ по математике – это основы стереометрии. Это задачи на вычисление объемов и площадей поверхности многогранников и тел вращения.

Ничего сложного здесь нет. Все эти задачи доступны даже десятикласснику. И даже гуманитарию.

Как решать задания по стереометрии из первой части Профильного ЕГЭ?

Повторим формулы для вычисления объемов и площадей поверхности многогранников (призмы, пирамиды… ) и тел вращения (цилиндра, конуса и шара)

Проверим себя – умеем ли мы рисовать чертежи?

Посмотрим, как решаются простые задачи по стереометрии и задачи с секретами.

Запоминаем один из главных лайфхаков решения задач по стереометрии:

Отношение объемов подобных тел  равно кубу коэффициента подобия.

Если все линейные размеры объемного тела увеличить в k раз, то его площадь увеличится в k^2 раз, а объем в k^3 раз.

S_2=k^2 cdot S_1

V_2=k^3 cdot V_1

И решаем задачи. У нас все получится!

1. Во сколько раз увеличится площадь поверхности и объем куба, если его ребро увеличить в два раза?

Отношение площадей поверхности подобных тел равно квадрату коэффициента подобия, а отношение объемов – кубу коэффициента подобия. При увеличении ребра в 2 раза площадь поверхности увеличится в 4 раза, а объем – в 8 раз.

2. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.

Плоскость, параллельная основанию, отсекает от конуса меньший конус, все линейные размеры которого в 3 раза меньше, чем у большого. Поэтому площадь сечения в 9 раз меньше площади основания. Она равна 2.

3. Объем пирамиды равен 10. Через середину высоты параллельно основанию пирамиды проведено сечение, которое является основанием меньшей пирамиды с той же вершиной. Найдите объем меньшей пирамиды.

 

Меньшая пирамида подобна большой, коэффициент подобия k=frac{1}{2}. Отношение объемов  подобных тел равно кубу коэффициента подобия. Поэтому объем меньшей пирамиды в 8 раз меньше объема исходной пирамиды. Он равен  frac{10}{8}=1,25.

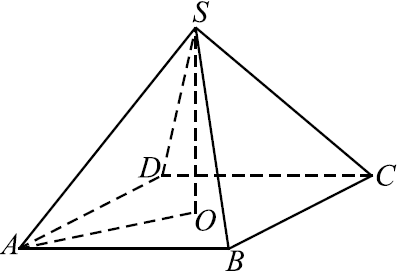
4. Объём правильной четырёхугольной пирамиды SABCD равен 116. Точка E — середина ребра SB. Найдите объём треугольной пирамиды EABC.

Площадь основания пирамиды ЕАВС в 2 раза меньше, чем у пирамиды ABCDS. Высота пирамиды ЕАВС равна половине высоты пирамиды ABCDS. Значит, объем пирамиды ЕАВС в 4 раза меньше объема пирамиды ABCDS. Он равен frac{116}{4}=29.

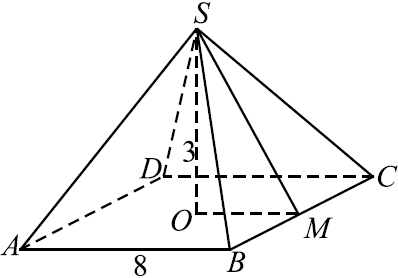
5. В правильной четырехугольной пирамиде SABCD точка E – середина ребра AB, боковое ребро SC равно 4, длина отрезка SE равна sqrt{10}.  Найти объем пирамиды SABCD .

Найдем сторону основания пирамиды. По теореме Пифагора, для треугольника  SAE получаем, что AE=sqrt{6}. Соответственно, сторона основания пирамиды равна 2sqrt{6}. Если обозначить центр основания за H, то высоту пирамиды  найдем по теореме Пифагора, для треугольника SHE – она равна 2.

Применяя формулу для объема пирамиды V=frac{1}{3}S_{ABCD}cdot h, получаем ответ: 16.

Многие задания №2 Профильного ЕГЭ по математике можно считать подготовительными – для того, чтобы научиться решать задачу 14 из второй части ЕГЭ.

Для решения некоторых из них стоит выучить основные определения и теоремы стереометрии. В общем, то, что входит в программу по стереометрии.

6. Стороны основания треугольной пирамиды равны 15, 16 и 17. Боковые ребра наклонены к плоскости основания под углами 45°. Найдите объем пирамиды.

Пусть точка О – проекция точки S на плоскость основания пирамиды. Прямоугольные треугольники АОS, ВОS, СОS равны (по общему катету ОS и острому углу). Значит, АО = ВО = СО. Точка О, равноудаленная от вершин основания, – это центр окружности, описанной вокруг треугольника АВС. Тогда АО = ВО = СО = OS = R, где R – радиус этой окружности.

Радиус описанной окружности найдем по формуле

R=frac{abc}{4S}.

Площадь triangle ABC найдем по формуле Герона:

S_{triangle ABC}=sqrt{p(p-a)(p-b)(p-c)}, где p=frac{15+16+17}{2}=24  – полупериметр.

S_{triangle ABC}= sqrt{24cdot 9cdot 8cdot 7}=sqrt{3cdot 8cdot 3cdot 3cdot 8cdot 7}=24sqrt{21};

R=frac{15cdot 16cdot 17}{4cdot 24sqrt{21}}=frac{5cdot 17}{2sqrt{21}};

V=frac{1}{3}S_{triangle ABC}cdot OS=frac{1}{3}cdot 24sqrt{21}cdot frac{5cdot 17}{2cdot sqrt{21}}=4cdot5cdot17=340.

Заметим, что если боковые ребра пирамиды наклонены к плоскости основания под одинаковым углом, то вершина проецируется в центр основания.

7. В правильной треугольной призме ABCA_1B_1C_1, все ребра которой равны 3, найдите угол между прямыми AA_1 и  BC_1. Ответ дайте в градусах.

Угол между скрещивающимися прямыми равен углу между параллельными им прямыми, лежащими в одной плоскости. Поскольку CC_1 и AA_1 параллельны, найдем угол между CC_1 и BC_1. Он равен 45 градусов, так как грань   –  квадрат.

Ответ: 45.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Профильный ЕГЭ по математике. Задание №2. Стереометрия» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

ЕГЭ по математике Профиль. Задание 2: Уметь строить и исследовать простейшие математические модели. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

ЕГЭ Профиль. Задание № 2.

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 2 проверяет умение использовать элементы теории вероятностей при решении прикладных задач. Для его выполнения понадобится производить действия с дробями и совершать простые вычисления. Задание представляет собой текстовую задачу, которая решается с помощью базовых арифметических операций. В ответе необходимо указать целое или дробное число, записанное в виде конечной десятичной дроби.

План выполнения:

  1. Внимательно прочитайте задачу.
  2. Выявите число всех элементарных событий и число благоприятствующих событий, не пропустив ни одного из всех возможных исходов и не включая ни одного лишнего.
  3. При решении задачи на классическое определение вероятности установите, зависимы (совместны) или независимы (несовместны) элементарные события.
  4. Выполните на черновике необходимые вычисления.
  5. Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

Задачи на классическое
определение вероятности

ЕГЭ по математике Профиль. Задание 2

Задача № 2 (1). В коробке лежит 40 шаров: 20 чёрных, 4 жёлтых и 16 зелёных. Наугад из коробки достают один шар. Найдите вероятность того, что этот шар будет жёлтым.

Решение:
ЕГЭ по математике Профиль. Задание 2

Ответ: 0,1.

Задача № 2 (2). Участников шахматного турнира разбивают на пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шахматистов, среди которых 11 спортсменов из России, в том числе Пётр Орлов. Найдите вероятность того, что Пётр Орлов будет играть с шахматистом из России.

Решение:
ЕГЭ по математике Профиль. Задание 2

Ответ: 0,4.

Задача № 2 (3). У Дениса в копилке лежит 6 рублёвых, 3 двухрублёвых, 2 пятирублёвых и 4 десятирублёвых монеты. Денис наугад достал из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 60 рублей.

Решение:
ЕГЭ по математике Профиль. Задание 2

Ответ: 0,4.

Задачи на использование теорем
о вероятностях событий

ЕГЭ по математике Профиль. Задание 2

Задача № 2 (4). Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,2. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

Решение:
ЕГЭ по математике Профиль. Задание 2

Ответ: 0,96.

Задача № 2 (5). При проверке на вирусное заболевание делают анализ крови. Если анализ выявляет вирус, то результат является положительным. У больных анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на заболевание, действительно больны. Найдите вероятность того, что результат анализа у пациента будет положительным. Ответ округлите до сотых.

Решение:
ЕГЭ по математике Профиль. Задание 2

Ответ: 0,05.

Задача № 2 (6). На экзамене по истории ученик отвечает на один вопрос из списка. Вероятность того, что это вопрос по теме «Крепостное право», равна 0,2. Вероятность того, что это вопрос по теме «Февральская революция», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене ученику достанется вопрос по одной из этих двух тем.

Решение:
ЕГЭ по математике Профиль. Задание 2

Ответ: 0,35.

Тренировочные задания с самопроверкой

№ 2.1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Ответ округлите до сотых.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 2

№ 2.2. В некотором городе на 6000 появившихся на свет младенцев приходится 3360 девочек. Найдите частоту рождения мальчиков в этом городе.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 2

№ 2.3. Вероятность того, что на тесте по математике ученица Настя верно решит не менее 12 задач, равна 0,84. Вероятность того, что Настя решит больше 11 задач, равна 0,96. Найдите вероятность того, что Настя решит ровно 12 задач.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 2

№ 2.4. Склад освещается двумя фонарями с лампами. Вероятность перегорания лампы одного фонаря в течение одного месяца равна 0,4. Найдите вероятность того, что в течение месяца хотя бы одна лампа не перегорит.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 2

№ 2.5. Вероятность того, что батарейка бракованная, равна 0,05. Покупатель в магазине выбирает случайную упаковку, в которой две такие батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 2

Вы смотрели: ЕГЭ по математике Профиль. Задание 2: Уметь строить и исследовать простейшие математические модели. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».


Просмотров:
17 330

Источник

Второе задание профильного ЕГЭ по математике проверяет умение учащихся работать с графической информацией.
 
Тип задания: с кратким ответом
Уровень сложности: базовый
Количество баллов: 1
Примерное время на выполнение: 2 минуты

Задание 2 ЕГЭ математика

Экзаменующемуся предстоит извлечь информацию из графика функции или диаграммы, и затем обработать её в соответствии с условием задачи. В большинстве случаев даже задание в несколько действий можно выполнить устно.

Для успешного выполнения задания необходимо усвоить следующие понятия:
— функция;
— ось абсцисс;
— ось ординат;
— возрастание и убывание функции;
— график функции;
— область определения функции;
— область значения функции;
— максимум и минимум функции;
— наибольшее и наименьшее значение функции на отрезке;
— столбчатая диаграмма;
— круговая диаграмма.

Необходимые умения:
— определять цену деления;
— определять значение функции по заданному аргументу;
— определять аргумент по известному значению функции;
— выделять на графике функции указанный отрезок;
— определять по графику наибольшее и наименьшее значение функции на отрезке;
— находить на графике максимумы и минимумы, определять соответствующие им аргументы и значения функции;
— находить промежутки возрастания и убывания функции.

Пример №1

ЕГЭ по математике 2 задание профильный уровень рисунок 1

На графике дана зависимость высоты тела над поверхностью земли от времени. По оси абсцисс отложено время в минутах, по оси ординат – высота в метрах. Определите высоту, на которой находилось тело через 7 минут после начала движения.

Решение:

1) На горизонтальной оси находим точку, соответствующую 7-ми минутам.

ЕГЭ по математике 2 задание профильный уровень рисунок 2

2) От найденной точки вверх проводим вертикальную прямую. Находим точку пересечения прямой с графиком.

ЕГЭ по математике 2 задание профильный уровень рисунок 3

3) Проводим горизонтальную прямую к оси ординат.

4) Находим точку пересечения прямой с осью ординат.

ЕГЭ по математике 2 задание профильный уровень рисунок 4

5) Полученная точка находится посередине между отметками 15м и 20м. Найдем ее значение (15+20):2=17,5

Ответ: 17,5.

Пример №2

ЕГЭ по математике 2 задание профильный уровень рисунок 5

С 18 по 20 апреля проводилось измерение температуры воздуха. Результаты измерений представлены в виде графика. Какого максимального значения достигала температура воздуха 19 апреля?

Решение:

1) На горизонтальной оси выделяем отрезок, соответствующий 19-му апреля.

ЕГЭ по математике 2 задание профильный уровень рисунок 6

2) Находим на этом участке самую высокую точку графика.

3) Проводим из этой точки горизонтальную прямую до оси ординат и получаем искомую температуру.

ЕГЭ по математике 2 задание профильный уровень рисунок 7

Ответ: 14.

Пример №3

ЕГЭ по математике 2 задание профильный уровень рисунок 8

В помещении имеется кондиционер с датчиком температуры воздуха. Зависимость температуры воздуха в помещении с кондиционером от времени показана на графике. Температура указана в градусах Цельсия. Кондиционер включается, когда температура воздуха превышает максимально допустимое значение, и выключается, когда воздух охлаждается до необходимой температуры.  Определите по графику, сколько минут был отключен кондиционер.

Решение:

1) Когда кондиционер отключен, температура воздуха повышается. График возрастает.

2) Находим на графике возрастающий участок.

ЕГЭ по математике 2 задание профильный уровень рисунок 9

3) Из крайних точек этого отрезка проводим вертикальные прямые на горизонтальную ось и находим моменты включения (6 минут) и выключения (9 минут) кондиционера.

ЕГЭ по математике 2 задание профильный уровень рисунок 10

4) Находим время работы кондиционера: 9-6=3 минуты.

Ответ: 3.

Пример №4

ЕГЭ по математике 2 задание профильный уровень рисунок 11

Крутящий момент двигателя зависит от числа оборотов. На графике по горизонтальной оси отложено число оборотов в минуту. По вертикальной – крутящий момент в Н*м. Какое минимальное число оборотов должен совершать двигатель, чтобы его крутящий момент составил 90Н*м?

Решение:

В этой задаче полезно определить цену деления по обеим осям. Для этого берем наименьшее отмеченное число и делим его на число делений до этого числа.

По оси абсцисс получаем 1000/4=250.
По оси ординат 20/2=10.

1) На оси ординат находим точку, соответствующую 90 Н*м. Это значение на оси не отмечено. Оно находится на одно деление выше точки 80.

ЕГЭ по математике 2 задание профильный уровень рисунок 12

2) От найденной точки проводим горизонтальную линию.

3) Линия пересекает график в двух точках.

ЕГЭ по математике 2 задание профильный уровень рисунок 13

4) Т.к. по условию задачи нужно определить наименьшее число оборотов, то выбираем левую точку.

5) Опускаем от нее вертикальную линию на ось ординат, находим точку пересечения.

ЕГЭ по математике 2 задание профильный уровень рисунок 14

6) Найденная точка расположена на три деления правее отметки 1000. Найдем ее значение, пользуясь известной ценой деления. 1000+3*250=1750.

Ответ: 1750.

Пример №5

ЕГЭ по математике 2 задание профильный уровень рисунок 15

С 5 по 18 апреля измерялось суточное количество осадков. Результаты измерения указаны точками на графике. По горизонтальной оси отложены даты, по вертикальной – количество осадков в мм. Для удобства чтения графика точки соединены отрезками. Сколько дней с 5 по 18 апреля суточное количество осадков составляло менее 3мм?

Решение:

Для решения данной задачи надо уметь различать понятия «более» и «не менее». Разница в том, учитывается или нет пограничное значение. «Более 3мм» – это 4, 5, и так далее. Т.е. дни, когда выпадало 3мм осадков, не считаем, потому что нас интересуют числа больше 3. «Не менее 3 мм» – считать начинаем от 3, т.к. в этом случае оно соответствует условию.

1) На вертикальной оси находим точку, обозначенную числом 3.

2) Проводим горизонтальную прямую.

ЕГЭ по математике 2 задание профильный уровень рисунок 16

3) Считаем точки, расположенные на прямой и выше её.

ЕГЭ по математике 2 задание профильный уровень рисунок 17

Ответ: 8.

Пример №6

ЕГЭ по математике 2 задание профильный уровень рисунок 18

В течение 2016 года в населенном пункте проводилось измерение температуры воздуха. На диаграмме указана среднемесячная температура воздуха в градусах Цельсия.  Сколько месяцев в 2016 году среднемесячная температура в населенном пункте была выше 15 градусов?

Решение:

1) Число, соответствующее 15 градусам на вертикальной оси не отмечено.
Выясним, какому количеству делений соответствует 1 градус.
Определим цену деления 4/2=2. Т.е. одно деление соответствует двум градусам, значит, одному градусу соответствует половина деления. Точка, соответствующая 15 градусам находится на половину деления ниже 16.

2) От найденной точки проводим горизонтальную линию.

ЕГЭ по математике 2 задание профильный уровень рисунок 19

3) Определяем, сколько столбиков диаграммы оказались выше линии.

ЕГЭ по математике 2 задание профильный уровень рисунок 20

Ответ: 3.

Практика показывает, что большинство ошибок во втором задании вызвано попытками решить его устно. При подготовке такие задания действительно легко решаются. Но от волнения взгляд экзаменующегося легко перескакивает с одной строчки на другую. Задание расположено в самом начале билета, поэтому многие учащиеся не успевают успокоиться к моменту его решения. Поэтому все необходимые вспомогательные линии и точки нужно рисовать прямо на графиках в бланке заданий. На это не уйдет много времени, а вероятность ошибки снизится в несколько раз.

Читайте также разбор 1 задания по математике профильного уровня.

Источник

За это задание ты можешь получить 1 балл. На решение дается около 5 минут. Уровень сложности: базовый.
Средний процент выполнения: 66.7%
Ответом к заданию 2 по математике (профильной) может быть целое число или конечная десятичная дробь.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

Из единичного куба вырезана правильная четырёхугольная призма со стороной основания $0{,}7$ и боковым ребром $1$. Найдите площадь поверхности получившейся фигуры (cм. рис.).

Решение

Поверхность оставшейся части куба состоит из боковой поверхности куба, площадь которой равна 4·1·1=4, боковой поверхности призмы, площадь которой равна 4·0,7·1=2.8, и двух равных фигур (см. заштрихованную фигуру на рисунке), площадь каждой из которых равна 1·1 — 0,7·0,7 = 0.51. Таким образом, площадь поверхности оставшейся части куба равна 4 + 2.8 + 2 · 0.51 = 7.82.

Ответ: 7.82

Задача 2

Если каждое ребро куба увеличить на $1$ (см. рис.), то площадь его поверхности увеличится на $42$. Найдите ребро куба.

Решение

Пусть ребро куба равно $x$. Площадь поверхности куба равна $6x^2$. Если ребро куба увеличить на $1$, то оно станет равным $(x + 1)$, а площадь поверхности $6(x + 1)^2$. Так как площадь поверхности при этом увеличится на $42$, то $6(x + 1)^2 — 6x^2 = 42$, откуда $12x + 6 = 42, 12x = 36, x = 3$.

Ответ: 3

Задача 3

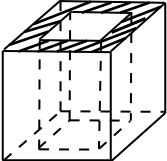
Куб вписан в шар радиуса $2√ 3$. Найдите объём куба.

Решение

Так как диагональ куба, вписанного в шар, равна диаметру шара, то $√3a = 2R$, где $a$ — ребро куба, $R = 2√3$ — радиус шара. Тогда $a√3 = 4√3, a = 4$. Объём куба равен $a^3 = 64$.

Ответ: 64

Задача 4

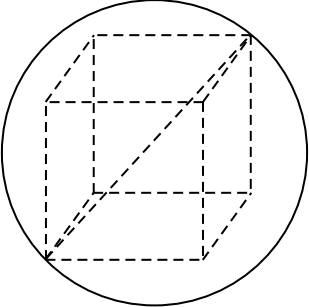
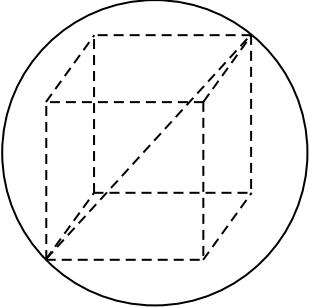
Куб вписан в шар радиуса $1{,}5√ 3$. Найдите объём куба.

Решение

Так как диагональ куба, вписанного в шар, равна диаметру шара, то $√3a = 2R$, где $a$ — ребро куба, $R = 1.5√3$ — радиус шара. Тогда $√3a = 3√3, a = 3$. Объём куба равен $a^3 = 27$.

Ответ: 27

Задача 5

Объём куба равен $64$ (см. рис.). Найдите площадь его поверхности.

Решение

Пусть ребро куба равно $x$. По условию объём куба равен $64$, тогда $x^3=64$, откуда $x=4$. Площадь грани куба равна $x^2=16$. Площадь поверхности куба равна $6x^2=6⋅16=96$.

Ответ: 96

Задача 6

Длина окружности основания цилиндра равна $6$. Площадь боковой поверхности равна $21$. Найдите высоту цилиндра.

Решение

Площадь боковой поверхности цилиндра вычисляется по формуле $S_{бок} = 2πRH$, где $R$ — радиус основания, $H$ — высота цилиндра. По условию $2πR = 6, S_{бок} = 21$, тогда $H = 21 : 6 = 3.5$.

Ответ: 3.5

Задача 7

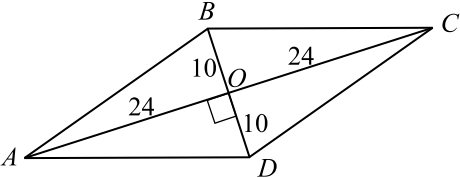
В основании прямой призмы лежит ромб с диагоналями, равными $20$ и $48$ (см. рис.). Площадь её поверхности равна $1272$. Найдите боковое ребро этой призмы.

Решение

Так как диагонали ромба перпендикулярны и точкой пересечения делятся пополам, то сторону ромба найдём из прямоугольного треугольника $AOD$ по теореме Пифагора.

$AD = √{AO^2 + OD^2} = √{24^2 + 10^2} = 26$.

Площадь ромба $S_{осн} = {1}/{2}d_1 · d_2$, где $d_1$ и $d_2$ — диагонали ромба. $S_{осн} = {1}/{2} · 48 · 20 = 480$. Пусть боковое ребро призмы равно $x$. Площадь поверхности призмы равна $S = S_{бок} + 2S_{осн} = 1272$, откуда $S_{бок} = 1272 — 960 = 312$. Так как $S_{бок} = 4 · 26 · x$, то $104x = 312$, откуда $x = 3$.

Ответ: 3

Задача 8

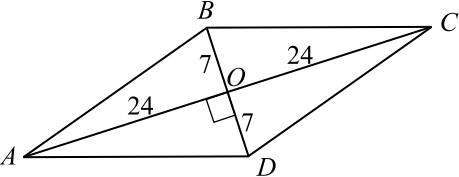
В основании прямой призмы лежит ромб с диагоналями, равными $14$ и $48$ (см. рис.). Площадь её поверхности равна $1232$. Найдите боковое ребро этой призмы.

Решение

Так как диагонали ромба перпендикулярны и точкой пересечения делятся пополам, то сторону ромба найдём из прямоугольного треугольника $AOD$ по теореме Пифагора.

$AD = √{AO^2 + OD^2} = √{24^2 + 7^2} = 25$.

Площадь ромба $S_{осн} = {1}/{2}d_1 · d_2$, где $d_1$ и $d_2$ — диагонали ромба. $S_{осн} = {1}/{2} · 48 · 14 = 336$. Пусть боковое ребро призмы равно $x$. Площадь поверхности призмы равна $S = S_{бок} + 2S_{осн} = 1232$, откуда $S_{бок} = 1232 — 672 = 560$. Так как $S_{бок} = 4 · 25 · x$, то $100x = 560$, откуда $x = 5.6$.

Ответ: 5.6

Задача 9

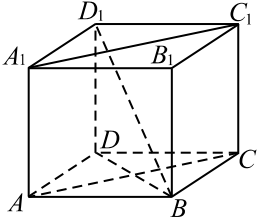
В правильной четырёхугольной призме $ABCDA_1B_1 C_1 D_1$ ребро $AA_1$ равно $24$, а диагональ $BD_1$ равна $26$ (см. рис.). Найдите площадь сечения призмы плоскостью, проходящей через точки $A$, $A_1$ и $C$.

Решение

Сечением призмы плоскостью, проходящей через точки $A, A_1$ и $C$, является прямоугольник $AA_1C_1C$, площадь которого равна $S = AA_1 · AC$. Выразим катет $BD$ из прямоугольного треугольника $BDD_1 : BD = √{BD_1^2 — DD_1^2} = √{26^2 — 24^2} = √{(26 — 24)(26 + 24)} = 10$. Так как $BD = AC$, то $S = 24 · 10 = 240$.

Ответ: 240

Задача 10

Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен $7$.

Решение

$V_{цилиндра}=S_{осн}⋅ H$, $V_{конуса}={1} / {3} S_{осн}⋅ H$. По условию конус
и цилиндр имеют общее основание и общую высоту, значит,
$V_{цилиндра}=3V_{конуса}=21$.

Ответ: 21

Задача 11

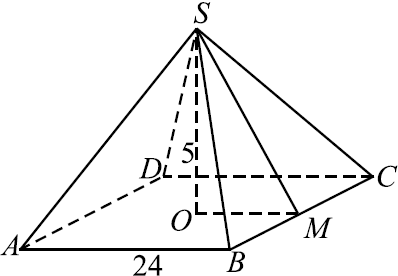
Найдите площадь поверхности правильной четырёхугольной пирамиды, стороны основания которой равны $24$ и высота равна $5$ (см. рис.).

Решение

Площадь $S$ поверхности правильной четырёхугольной пирамиды $SABCD$ равна сумме площади основания $S_{осн}$ и площади боковой поверхности $S_{бок}: S = S_{осн} + S_{бок} = AB^2 + 4S_{SBC}. SM$ — апофема.

$S_{осн} = AB^2 = 576, SM$ найдём по теореме Пифагора как гипотенузу прямоугольного треугольника $SOM: SM = √{SO^2 + OM^2} = √{SO^2 + ({1}/{2}AB)^2} = √{5^2 + 12^2} = 13$.

$S_{бок} = 4S_{SBC} = 4·{1}/{2}·24·13 = 4·156=624. $

$S = 576 + 624 = 1200$.

Ответ: 1200

Задача 12

Найдите площадь поверхности правильной четырёхугольной пирамиды, стороны основания которой равны $8$ и высота равна $3$ (см. рис.).

Решение

Площадь $S$ поверхности правильной четырёхугольной пирамиды $SABCD$ равна сумме площади основания $S_{осн}$ и площади боковой поверхности $S_{осн} + S_{бок} = AB^2 + 4S_{SBC}$

$SM$ — апофема.

$S_{осн} = AB^2 = 64$

$SM$ найдём по теореме Пифагора как гипотенузу прямоугольного треугольника $SOM: SM = √{SO^2 + OM^2} = √{SO^2 + ({1}/{2}AB)^2} = √{3^2 + 4^2} = 5$.

$S_{бок} = 4S_{SBC} = 4·{1}/{2}·8·5 = 80$

$S_{осн} + S_{бок} = 64 + 80 = 144$

Ответ: 144

Задача 13

В правильной четырёхугольной пирамиде высота равна $3$, объём равен $32$ (cм. рис.). Найдите боковое ребро этой пирамиды.

Решение

Объём пирамиды вычисляется по формуле $V = {1}/{3}·S_{осн}·H$, где $H = 3$ — высота пирамиды. Площадь основания равна $S_{осн} = 3{V}/{H} = {3·32}/{3} = 32$, откуда длина стороны квадрата, лежащего в основании пирамиды, равна $√{32} = 4√2$. Диагональ квадрата $AC = 8$.

Боковое ребро $SA$ найдём как гипотенузу прямоугольного треугольника $AOS$, где $SO$ — высота пирамиды. $AS = √{SO^2 + OA^2} = √{SO^2 + ({1}/{2}AC)^2} = √{3^2 + 4^2} = 5$.

Ответ: 5

Задача 14

В правильной четырёхугольной пирамиде высота равна $9$, объём равен $864$ (cм. рис.). Найдите боковое ребро этой пирамиды.

Решение

Объём пирамиды вычисляется по формуле $V = {1}/{3}·S_{осн}·H$, где $H = 9$ — высота пирамиды. Площадь основания равна $S_{осн} = 3{V}/{H} = {3·864}/{9} = 288$, откуда длина стороны квадрата, лежащего в основании пирамиды, равна $√{288} = 12√2$. Диагональ квадрата $AC = 24$.

Боковое ребро $SA$ найдём как гипотенузу прямоугольного треугольника $AOS$, где $SO$ — высота пирамиды. $AS = √{SO^2 + OA^2} = √{SO^2 + ({1}/{2}AC)^2} = √{9^2 + 12^2} = 15$.

Ответ: 15

Задача 15

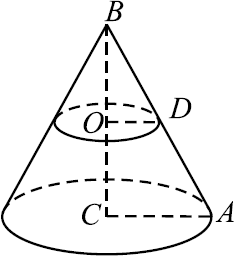
Площадь основания конуса равна $27$. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной $2$ и $4$, считая от вершины (см. рис.). Найдите площадь сечения конуса этой плоскостью.

Решение

Пусть $CA = R$ — радиус основания конуса, сечение конуса плоскостью, параллельной плоскости основания конуса — круг, радиус которого $OD = r$.

$OD ‖ AC$, следовательно, $△ABC ∼ △DBO$ по первому признаку подобия ($∠ACB = ∠DOB = 90°, ∠ABC$ — общий). По условию $BO = 2, OC = 4$, значит, $BC = 6$, откуда ${BO}/{BC} = {OD}/{AC} = {1}/{3}, {πr^2}/{πR^2} = {1}/{9}$. Значит, площадь сечения конуса плоскостью, параллельной плоскости основания конуса, в $9$ раз меньше плоскости основания конуса, то есть равна $27 : 9 = 3$.

Ответ: 3

Задача 16

Если каждое ребро куба увеличить на 3, то его площадь поверхности увеличится на 126. Найдите ребро куба.

Решение

$S_1=6а^2$
$ S_2=6(a+3)^2$
$ 6(a+3)^2-6а^2=126$
$ 6(а^2+6а+9)-6а^2=126$
$ 6а^2+36а+54-6а^2=126$
$ 36а=126-54$
$ 36а=72$
$ а=2$.

Ответ: 2

Рекомендуемые курсы подготовки

Источник

Практика по заданию №2 ЕГЭ 2022 по математике профильного уровня — классическое определение вероятности.

Для выполнения задания №2 необходимо умение решать простейшие задачи по теории вероятностей.

Практика

Примеры заданий:

1. В чемпионате по гимнастике участвуют 56 спортсменок: 27 из Норвегии, 15 из Дании, остальные из Швеции. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Швеции.

2. Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 46 спортсменов, среди которых 28 спортсменов из России, в том числе Дмитрий Тоснин. Найдите вероятность того, что в первом туре Дмитрий Тоснин будет играть с каким либо спортсменом из России.

3. Научная конференция проводится в 4 дня. Всего запланировано 80 докладов – первые два дня по 12 докладов, остальные распределены поровну между третьим и четвёртым днями. На конференции планируется доклад профессора М. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?

4. Фабрика выпускает сумки. В среднем на 150 качественных сумок приходится 14 сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

5. В сборнике билетов по химии всего 15 билетов, в 6 из них встречается вопрос по теме «Кислоты». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Кислоты».

Связанные страницы:

Источник

Работа с графиками и диаграммами

Второе задание в ЕГЭ профильного уровня по математике направлено на анализ диаграмм и вычисления каких-либо значений. В начале нам необходимо найти нужную информацию, а затем правильно её обработать. Данные манипуляции мы проделывали неоднократно и в ОГЭ, и в ЕГЭ базового уровня. 🙂

Разбор типовых вариантов заданий №2 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

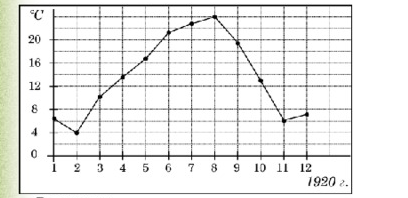
[su_note note_color=”#defae6″]

На рисунке точками показана средняя температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указаны номера месяцев, по вертикали – температура в градусах Цельсия. Для наглядности точки соединены линией. Сколько месяцев средняя температура была больше 18 градусов Цельсия?

[/su_note]

Алгоритм решения:
  1. Находим на рисунке отметку для температуры 18 градусов.
  2. Отмечаем точки, которые лежат выше 18-ти градусов.
  3. Подсчитываем, сколько их.
  4. Записываем ответ.
Решение:

1. 18 градусов располагается посередине между 16 и 20 градусами. Они отмечены на рисунке.

2. Отметим точки, которые расположены выше. Это месяцы под номером 6,7,8,9.

3. Получилось 4 точки. Значит, температура выше 18-ти градусов была 4 месяца.

Ответ: 4.

Второй вариант задания (из Ященко, №2)

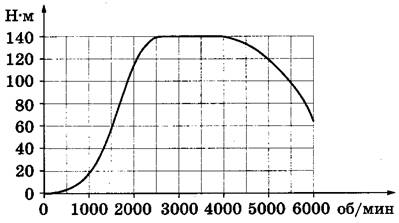
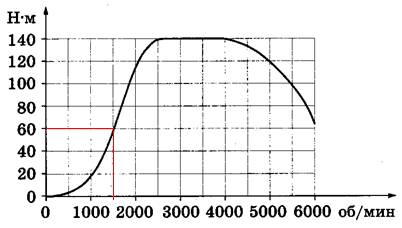
[su_note note_color=”#defae6″]

На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Н∙м. Какое число оборотов в минуту должен совершать двигатель, чтобы крутящий момент был не менее 60 Н∙м?

[/su_note]

Алгоритм решения:
  1. Рассматриваем график.
  2. Отыскиваем по оси ОУ заданное значение.
  3. Ищем соответствующее число оборотов по ОХ.
  4. Записываем ответ.
Решение:

1. На координатной плоскости по оси ОУ отложены значения крутящего момента, а на оси ОХ число оборотов двигателя.

2. Находим по ОУ требуемое значение крутящего момента: 60 Н∙м.

3. Проводим через 60 горизонтальную линию до пересечения ее с кривой. Из точки пересечения опускаем перпендикуляр на ось ОХ и находим число оборотов, которое соответствует данному значению крутящего момента. Оно равно 1500 об/мин (см. линии красного цвета на рисунке внизу).

Значит, искомое число оборотов 1500.

Ответ: 1500.

Третий вариант задания (из Ященко, №7)

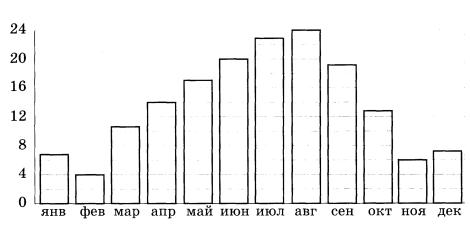
[su_note note_color=”#defae6″]

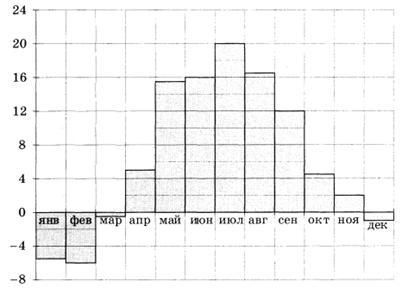
На диаграмме показана среднемесячная температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по приведённой диаграмме разность между наибольшей и наименьшей среднемесячными температурами. Ответ дайте в градусах Цельсия.

[/su_note]

Алгоритм решения:
  1. Анализируем столбчатую диаграмму.
  2. Среди столбиков находим самый высокий
  3. Находим самый низкий столбик.
  4. Определяем разность полученных значений..
  5. Записываем ответ.
Решение:

1. Столбчатая диаграмма составлена за год. Наибольшая температура будет там, где столбик самый высокий, а при самая маленькая там, где низенький столбик.

2. Рассмотрев рисунок, видим, что самый высоких столбик на диаграмме соответствует августу. Температура была в этом месяце 240С.

3. находим самый низкий столбик. Он соответствует температуре +40С.

4. Значит, в Сочи максимальная температура была средняя температуру в августе, +240С. Минимальная температура воздуха была в феврале и соответствовала отметке 40С.

5. Разность между максимальной и минимальной температурами равна 240–40 =200.

Ответ: 20º.

Четвертый вариант задания (из Ященко, №15)

[su_note note_color=”#defae6″]

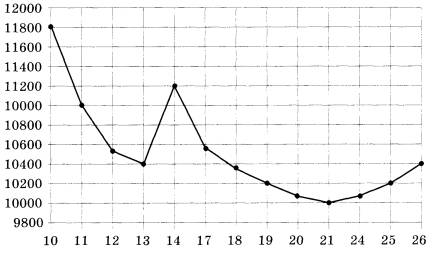
На рисунке жирными точками показана цена никеля на момент закрытия биржевых торгов во все рабочие дни с 10 по 26 ноября 2008 года. По горизонтали указываются числа месяца, по вертикали — цена тонны никеля в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку разность между наибольшей и наименьшей ценой никеля на момент закрытия торгов в указанный период (в долларах США за тонну).

[/su_note]

Алгоритм решения:
  1. Изучаем график.
  2. Находим на оси ОУ точку, расположенную выше всех остальных.
  3. Находим точку ниже всех остальных.
  4. Находим искомую разность..
  5. Делаем выводы.
  6. Записываем ответ.
Решение:

1. На оси OY наивысшая точка соответствует значению 11800 долларов десятого ноября.

2. Самая низкая точка находится не уровне 10000 долларов.

3. Устанавливаем, какова разница между показателями цен:

11800-10000=1800.

4. Значит, разница между наименьшей и наибольшей ценами равна 1800 долларов.

Ответ: 1800.

Пятый вариант задания (из Ященко, №19)

[su_note note_color=”#defae6″]

На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько месяцев в 2003 году средняя температура была отрицательной.

[/su_note]

Алгоритм решения:
  1. Рассматриваем диаграмму.
  2. Устанавливаем в каких месяцах была отрицательная средняя температура и подсчитываем количество месяцев.
  3. Записываем ответ.
Решение:

1. На диаграмме есть столбики, уходящие вверх. А есть опускающиеся вниз. Те, которые опускаются вверх, указывают на отрицательные значения среднемесячной температуры.

2. Таких месяцев с отрицательной температурой всего четыре: в январе, феврале, марте и декабре.

Значит, отрицательные показаний температуры были 4 месяца за год.

Ответ: 4.

Даниил Романович | Просмотров: 5.7k

Источник

Итоговый экзамен по математике сдают все. Те, кто поступает на гуманитарные специальности (филология, юриспруденция, международные отношения) выбирают базовый уровень — вопросы в нем легче, а оценки «3» достаточно для получения аттестата. Профильный уровень сдают будущие экономисты, инженеры и программисты — на этих специальностях без знания математики не обойтись, ее обязательно изучают на первых курсах. Но это непростой предмет. Даже в профильных математических классах не всегда дают достаточно знаний. Если ваша цель — поступление в топовый вуз на техническую специальность, без курсов подготовки к ЕГЭ не обойтись. Это касается не только профильного уровня, но и ЕГЭ по математике базового. «Задание 2, как решать?» — часто спрашивают школьники, сдающие этот экзамен. В этой статье мы проведем разбор задания 2 из ЕГЭ по математике профильного и базового уровня. 

Теория

В задании 2 ЕГЭ по профильной математике теория достаточно простая. Это номер базового уровня сложности, он приносит 1 балл. Выпускникам дается график (иногда — диаграмма), нужно проанализировать его в соответствии с условием. Определение аргумента функции, поиск максимального и минимального значения — навыки, которые нужны для этого задания ЕГЭ. 2 часть математики профильного уровня тоже содержит номера с графиками, поэтому эта теория пригодится и там. То, что нужно знать для решения задания 2 ЕГЭ по математике профильного уровня: 

  • теория 2 задания егэ по математикефункция и ее график;
  • оси абсцисс и ординат;
  • промежутки возрастания и убывания функции;
  • области определения и значения функции;
  • максимум и минимум функции;
  • наибольшее и наименьшее значения на промежутке;
  • диаграммы;
  • цена деления на графике. 

Перечисленные понятия нужны для сдачи любого уровня ЕГЭ. Но задание 2 по базовой математике проверяет другие навыки. В нем выпускник должен произвести вычисления со степенями. Этот номер тоже считается легким, однако для его выполнения нужно знать куда больше теории. Формулы для ЕГЭ по базовой математике, к заданию 2:

  • определение степени — an = a • a • a … • a, где n — натуральное число. a называют основанием степени, n — показателем. 
  • a0 = 1.
  • a1 = a.
  • a-n = 1 / an.
  • anm=man.
  • an • am = an+m.
  • an • bn = (a • b)n.
  • an / am = an-m.
  • an / bn = (a / b)n.

Разбор задания 2

Решение задания 2 по математике ЕГЭ мы начнем с профильного уровня. 

Задача. Замеры температуры проводились в течение 3 дней. Какой была минимальная температура 18 апреля? 

Решение. Подобное задание 2 на ЕГЭ по математике профильного уровня кажется очень простым, однако в нем легко ошибиться. Обратим внимание на два момента: «18 апреля» и «минимальная». Для начала отсекаем колонки, относящиеся к 19 и 20 апреля — про них ничего не спрашивают. После этого ищем самую низкую точку и находим ее ординату. 

Ответ: 6.

Задача. В помещении стоит кондиционер с датчиком температуры. Когда она достигает определенного максимального значения, кондиционер включается. Когда комната остужается до необходимой температуры, кондиционер автоматически выключается. На графике показана зависимость температуры от времени. Укажите, сколько минут кондиционер был выключен.

Решение. В этом номере важно умение логически рассуждать. Когда кондиционер отключен, температура увеличивается. На графике это показывается ростом функции вверх. Чтобы определить, сколько минут кондиционер был выключен, нужно найти область возрастания функции. Это промежуток между числами 6 и 9 на оси абсцисс. Теперь мы ищем время: 9 — 6 = 3.

Ответ: 3.

За выполнение такого простого номера можно получить 1 балл на экзамене по математике. Разбор задания 2 ЕГЭ мы продолжим базовым уровнем. Здесь встречаются несколько типов вопросов: степенные выражения с одинаковыми и разными основаниями, поиск частного, произведения и суммы. Чтобы посмотреть все существующие виды заданий, зайдите на «Решу ЕГЭ» по базовой математике. Задание 2 там представлено более чем 40 вариантами. А в рамках этой статьи мы разберем несколько примеров задания 2 из ЕГЭ по математике базового уровня. 

егэ по математике базаНайти значение выражения

Задача. 4 • 72 + 6 • 72.

Решение. У слагаемых есть общий множитель, который мы можем вынести за скобку. После этого считаем выражение в скобке, потом возводим число в степень и перемножаем: (4 + 6) • 72 = 10 • 72 = 10 • 49 = 490.

Ответ: 490.

Найти значение выражения (разные основания)

Задача. 80,76 • 640,12.

Решение. Нужно привести степени к одинаковому основанию, представив 64 как 82. После этого их можно перемножить: 80,76 • 640,12 = 80,76 • (8)2*0,12 = 80,76+0,24 = 81 = 8.

Ответ: 8.

Найти значение выражения (одинаковые основания)

Задача. 26 • 2-2 / 22.

Решение. В данном примере расчеты можно провести сразу же. Умножение степеней с одинаковым основанием заменяем на сложение показателей, деление — на их вычитание: 26 + (-2) — 2 = 26 — 4 = 22 = 4.

Ответ: 4. 

задача частное от деления математикаНайти частное от деления

Задача. 1,6 • 102 : 4 • 10-2.

Решение. У степеней одинаковое основание, поэтому мы можем поделить их, найдя разность показателей. После этого мы делим числа без степеней и выполняем умножение: 1,6 : 4 • 102 — (-2) = 1,6 : 4 • 104 = 1,6 : 4 • 10000 = 0,4 • 10000 = 4000.

Ответ: 4000.

Найти произведение

Задача. 4 • 105 • 2,3 • 10-7.

Решение: Степени имеют одинаковые основания, поэтому мы можем умножить их, сложив показатели. После этого результат умножаем на остальные числа: 4 • 2,3 • 105 + (-7) = 4 • 2,3 • 10-2 = 4 • 2,3 • 0,01 = 9,2 • 0,01 = 0,092. 

Ответ: 0,092.

Найти сумму

Задача. 9,4 • 102 + 2,1 • 103.

Решение. Мы возводим числа в степень, затем выполняем умножение и сложение: 9,4 • 100 + 2,1 • 1000 = 940 + 2100 = 3040.

Ответ: 3040. 

Теперь вы знаете чуть больше теории для ЕГЭ по математике. Задание 2 из профильного уровня достаточно легкое (хотя без практики тут тоже не обойтись), а вот в базе придется рассуждать и выполнять вычисления. Но и его можно выполнить без труда, если должным образом подготовиться к ЕГЭ. Однако, лучший результат всегда дают занятия с опытными преподавателями, знающими специфику экзамена. Если нанимать репетитора для вас дорого, обратите внимание на курсы. Там разбирают не только задание 2 ЕГЭ по математике, но и многие другие номера, в том числе вторую часть. Грамотная подготовка — ключ к хорошим баллам, а значит, и месту на бюджете. 

Источник

Понравилась статья? Поделить с друзьями:
  • Как решать второе задание егэ по информатике 2022
  • Как решать второе задание егэ по географии
  • Как решать второе задание егэ по биологии 2023
  • Как решать второе задание егэ информатика 2023
  • Как решать все задания егэ по математике профильный уровень