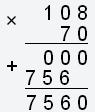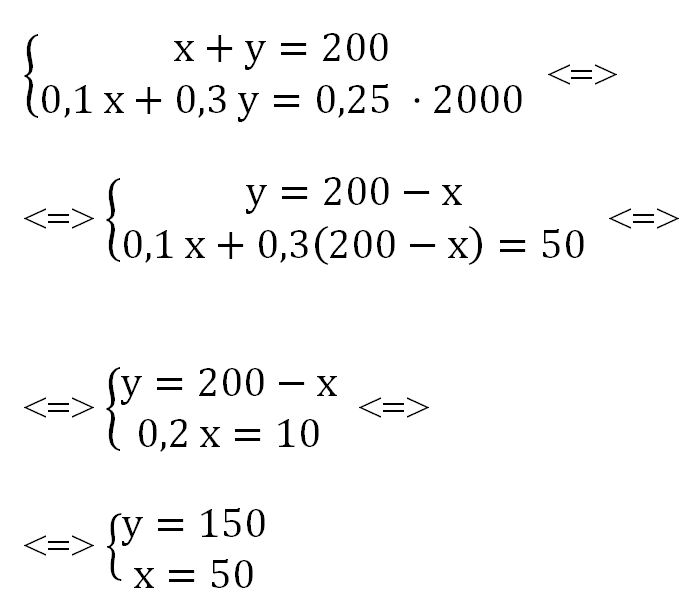Как решать задачи на проценты 11 класс егэ базовый уровень

---

Задачи на проценты

---

[su_box title=”Описание задания” style=”soft” box_color=”#c1e8cc” title_color=”#0c0a0a”]

В задании №3 ЕГЭ по математике нам предстоит решить простую задачу на проценты или часть от целого. Данные задачи в большинстве случаев интуитивно понятны, так как взяты из реальных жизненных ситуаций, тем не менее необходимо быть внимательным при их выполнении.

Тематика заданий: часть от целого, доли, проценты

Бал: 1 из 20

Сложность задания: ♦♦◊

Примерное время выполнения: 3 мин.

[/su_box]

---

Разбор типовых вариантов заданий №3 ЕГЭ по математике базового уровня

---

Вариант 3МБ1

[su_note note_color=”#defae6″]

Банк начисляет на срочный вклад 8% годовых. Вкладчик положил на счёт 7000 рублей. Сколько рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?

[/su_note]

Алгоритм выполнения:

• Вариант 1.

1. Сложить 100% и процент годовых.
2. Найти 1% от суммы, для этого сумму разделить на 100.
3. Умножить стоимость 1% на искомое количество процентов.

• Вариант 2.

1. Сложить 100% и процент годовых.
2. Полученные проценты перевести в десятичную дробь (разделить на сто).
3. Найти процент от числа (число умножить на полученную десятичную дробь).

Решение:

• Вариант 1.

Вклад 8 % годовых означает, что начальная сумма 7000 рублей через год увеличится на 8%, то есть составит 100+8=108% от исходной суммы.

Способ нахождения процента от числа №1. Для того, чтобы найти процент от числа нужно данное число разделить на 100(узнать сколько составляет 1 %), а затем умножить на искомое количество процентов.

Вычислим 108% от 7000, получим:

1. 7000 : 100 = 70(рублей) – составит 1 %.
2. 70 · 108 = 7560(рублей) – составит вклад через год.

• Вариант 2.

Вклад 8 % годовых означает, что начальная сумма 7000 рублей через год увеличится на 8%, то есть составит 100+8=108% от исходной суммы.

Способ нахождения процента от числа №2. Для того, чтобы найти процент от числа, нужно перевести искомый процент в десятичную дробь(разделить на сто), затем умножит число на полученную десятичную дробь.

108% = 108 : 100 = 1,08

7000 · 1,08 или

.

Выполнив умножение столбиком, имеем:

Ответ: 7560.

---

Вариант 3МБ2

[su_note note_color=”#defae6″]

Банк начисляет на срочный вклад 7 % годовых. Вкладчик положил на счёт 3000 рублей. Сколько рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?

[/su_note]

Алгоритм выполнения:

• Вариант 1.

1. Сложить 100% и процент годовых.
2. Найти 1% от суммы, для этого сумму разделить на 100.
3. Умножить стоимость 1% на искомое количество процентов.

• Вариант 2.

1. Сложить 100% и процент годовых.
2. Полученные проценты перевести в десятичную дробь (разделить на сто).
3. Найти процент от числа (число умножить на полученную десятичную дробь).

Решение:

• Вариант 1.

Вклад 7 % годовых означает, что начальная сумма 3000 рублей через год увеличится на 7%, то есть составит 100+7=107% от исходной суммы.

Способ нахождения процента от числа №1. Для того, чтобы найти процент от числа нужно данное число разделить на 100(узнать сколько составляет 1 %), а затем умножить на искомое количество процентов.

Вычислим 107% от 3000, получим:

1. 3000 : 100 = 30(рублей) – составит 1 %.
2. 30 · 107 = 3210(рублей) – составит вклад через год.

• Вариант 2.

Вклад 7 % годовых означает, что начальная сумма 3000 рублей через год увеличится на 7%, то есть составит 100+7=107% от исходной суммы.

Способ нахождения процента от числа №2. Для того, чтобы найти процент от числа, нужно перевести искомый процент в десятичную дробь (разделить на сто), затем умножит число на полученную десятичную дробь.

107% = 107 : 100 = 1,07

3000 · 1,07 или

Ответ: 3210.

---

Вариант 3МБ3

[su_note note_color=”#defae6″]

В сентябре 1 кг слив стоил 40 рублей, в октябре сливы подорожали на 40%, а в ноябре ещё на 15%. Сколько рублей стоил 1 кг слив после подорожания в ноябре?

[/su_note]

Алгоритм выполнения:

1. Найти сколько составляет один процент от начальной стоимости.
2. Сложить 100% и на сколько процентов произошло подорожание впервые.
3. Умножить стоимость одного процента на полученное количество процентов.
4. Найти стоимость 1% от новой стоимости.
5. Сложить 100 % и количество процентов, на которое подорожал товар во второй раз.
6. Умножить стоимость одного процента на полученное количество процентов.

Решение с пояснениями:

Найдем сколько составляет один процент от начальной стоимости:

40 : 100 = 0,4 (рублей) – составляет 1 % от начальной стоимости.

Сложим 100% и на сколько процентов произошло подорожание впервые.

100 + 40 = 140 (%) – составила стоимость от начальной цены после первого подорожания.

Умножим стоимость одного процента на полученное количество процентов.

140 · 0,4 = 56 (рублей) – стали стоить сливы в октябре.

Найдем стоимость 1% от новой стоимости.

56 : 100 = 0,56 (рубля) – 1% от новой стоимости.

Сложим 100 % и количество процентов, на которое подорожал товар во второй раз.

100 + 15 = 115 (%) – составила стоимость в ноябре от цены в октябре.

Умножим стоимость одного процента на полученное количество процентов.

115 · 0,56 = 64,4 (рубля) – конечная стоимость.

Решение в общем виде:

Подорожание на 40% означает увеличение стоимости на 140%, то есть, 40 рублей становятся равными

 рублей.

Затем, в ноябре стоимость слив увеличилась еще на 15%, что составило

 рублей.

Замечание: обратите внимание, что в данной задаче нельзя просто складывать проценты 40+15=55% и вычислять 155% от 40 рублей! Это будет приводить к неверным решениям.

Ответ: 64,4.

---

Вариант 3МБ4

[su_note note_color=”#defae6″]

В сентябре 1 кг винограда стоил 90 рублей, в октябре виноград подорожал на 20 %, а в ноябре ещё на 25 %. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?

[/su_note]

Алгоритм выполнения:

1. Найти сколько составляет один процент от начальной стоимости.
2. Сложить 100% и на сколько процентов произошло подорожание впервые.
3. Умножить стоимость одного процента на полученное количество процентов.
4. Найти стоимость 1% от новой стоимости.
5. Сложить 100 % и количество процентов, на которое подорожал товар во второй раз.
6. Умножить стоимость одного процента на полученное количество процентов.

Подробный разбор:

Найдем сколько составляет один процент от начальной стоимости:

90 : 100 = 0,9 (рублей) – составляет 1 % от начальной стоимости.

Сложим 100% и на сколько процентов произошло подорожание впервые.

100 + 20 = 120 (%) – составила стоимость от начальной цены после первого подорожания.

Умножим стоимость одного процента на полученное количество процентов.

120 · 0,9 = 108 (рублей) – стали стоить сливы в октябре.

Найдем стоимость 1% от новой стоимости.

108 : 100 = 1,08 (рубля) – 1% от новой стоимости.

Сложим 100 % и количество процентов, на которое подорожал товар во второй раз.

100 + 25 = 125 (%) – составила стоимость в ноябре от цены в октябре.

Умножим стоимость одного процента на полученное количество процентов.

125 · 1,08 = 135 (рублей) – конечная стоимость.

Решение в общем виде:

Подорожание на 20% означает увеличение стоимости на 120%, то есть, для 90 рублей имеем:

 рублей.

Затем, в ноябре стоимость слив увеличилась еще на 25%, что составило

 рублей.

Замечание: обратите внимание, что в данной задаче нельзя просто складывать проценты 20+25=45% и вычислять 145% от 90 рублей! Это будет приводить к неверным решениям.

Ответ: 135.

---

Вариант 3МБ5

[su_note note_color=”#defae6″]

Ивану Кузьмичу начислена заработная плата 20000 рублей. Из этой суммы вычитается налог на доход физических лиц в размере 13 %. Сколько рублей он получит после уплаты подоходного налога?

[/su_note]

Алгоритм выполнения:

• Вариант 1.

1. Вычесть из 100% налог в процентах.
2. Найти 1% от начальной суммы, для этого сумму разделить на 100.
3. Умножить стоимость 1% на искомое количество процентов.

• Вариант 2.

1. Вычесть из 100% налог в процентах.
2. Полученные проценты перевести в десятичную дробь (разделить на сто).
3. Найти процент от числа (число умножить на полученную десятичную дробь).

Решение:

• Вариант 1.

Вычтем из 100% налог в процентах.

100 – 13 = 87 (%) – получит Иван Кузьмич после вычета налога.

Найдем 1 % от начальной суммы.

20000 : 100 = 200 (рублей) – составит 1%.

Найдем 87% от 20000.

87 · 200 = 17400 (рублей) – получит Иван Кузьмич.

• Вариант 2.

Вычтем из 100% налог в процентах. 100 – 13 = 87 (%)

Полученные проценты переведем в десятичную дробь (разделить на сто). 87 : 100 = 0,87

Найдем процент от числа (число умножить на полученную десятичную дробь).

20000 · 0,87 = 17400 (рублей)

Ответ: 17400 рублей получит Иван Кузьмич.

---

Вариант 3МБ6

[su_note note_color=”#defae6″]

ЕГЭ по физике сдавали 25 выпускников школы, что составляет треть от общего числа выпускников. Сколько выпускников этой школы не сдавали экзамен по физике?

[/su_note]

Решение:

Нам известно, что количество учеников, сдававших ЕГЭ по физике равно 25, и это составляет 1/3 от общего числа выпускников. Значит 25 – это 1/3, тогда общее число учеников:

25 • 3 = 75

Количество учеников, не сдававших ЕГЭ по физике, равно:

75 – 25 = 50

Ответ: 50

---

Вариант 3МБ7

[su_note note_color=”#defae6″]

Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена стоимость футболки?

[/su_note]

Алгоритм выполнения

1. От 800 отнимаем 680. Узнаем, сколько рублей составило снижение.
2. Делим результат вычитания на 800. Это даст нам долю, которую составляет скидка от первоначальной стоимости.
3. Полученное число умножаем на 100. Получаем снижение в процентах.

Решение:

800 – 680 = 120 (руб.) – составляет снижение

120 : 800 = 0,15 – доля скидки

0,15 ·100 = 15 %

Ответ: 15

---

Вариант 3МБ8

[su_note note_color=”#defae6″]

В магазине вся мебель продается в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 5% от стоимости купленной мебели. Шкаф стоит 3500 рублей (наверное, это было очень давно – прим. ред. 🙂 ) Во сколько рублей обойдется покупка этого шкафа вместе со сборкой?

[/su_note]

Алгоритм выполнения

1. Определяем, сколько составляет 5% от стоимости мебели. Для этого 3500 делит на 100 и умножаем на 5.
2. К 3500 прибавляем полученное число.

Решение:

3500 : 100 · 5 = 175 (руб.) – стоимость сборки мебели

3500 + 175 = 3675 (руб.) стоит мебель со сборкой

Ответ: 3675

---

Вариант 3МБ9

[su_note note_color=”#defae6″]

Товар на распродаже уценили на 40%, при этом он стал стоить 840 рублей. Сколько рублей стоит товар до распродажи?

[/su_note]

Алгоритм выполнения

1. От 100 % вычитаем 40%, чтобы найти, сколько процентов составляет уцененная стоимость. Получим 60 %.
2. Воспользуемся правилом нахождения целого по его части. Для этого 840 разделим на 60 и умножим на 100.

Решение:

100 – 40 = 60 % – составляет цена товара после его уценки.

840 : 60 · 100 = 1400 (руб.)

1400

---

Вариант 3МБ10

[su_note note_color=”#defae6″]

Магазин делает пенсионерам скидку. Батон хлеба стоит в магазине 15 рублей, а пенсионер заплатил за него 14 рублей 40 копеек (грандиозная скидка – прим. ред. 😉 ) Сколько процентов составила скидка для пенсионера?

[/su_note]

Алгоритм выполнения

1. От 15 руб. отнимаем 14 руб.40 коп. Так найдем сумму скидки. Выразим эту сумму в рублях.
2. Полученное число разделим на 15 и умножим на 100 %.

Решение:

15 руб. – 14 руб.40 коп. = 60 коп. = 0,6 руб.

0,6 : 15 ·100 % = 4 %.

Ответ: 4

---

Вариант 3МБ11

[su_note note_color=”#defae6″]

Число хвойных деревьев в парке относится к числу лиственных как 93:7. Других деревьев в парке нет. Сколько процентов деревьев в парке составляют лиственные?

[/su_note]

Алгоритм выполнения

1. Суммируем 93 и 7, чтобы найти общее кол-во деревьев в парке.
2. Кол-во лиственных деревьев (7) делим на общее кол-во деревьев и умножаем на 100 %.

Решение:

93 + 7 = 100 (шт.) – деревьев всего в парке.

7 : 100 ·100 = 7 %

Ответ: 7

---

Вариант 3МБ12

[su_note note_color=”#defae6″]

Городской бюджет составляет 48 млн. рублей, а расходы на одну из его статей составили 40%. Сколько миллионов рублей потрачены на эту статью бюджета?

[/su_note]

Алгоритм выполнения

Нужно применить правило нахождения части от целого по ее проценту. Для этого целое делится на 100 и умножается на кол-во процентов.

Решение:

48 : 100 · 40 = 19,2 (млн.руб.)

Ответ: 19,2

---

Вариант 3МБ13

[su_note note_color=”#defae6″]

Поступивший в продажу в феврале мобильный телефон стоил 1800 рублей. В июне он стал стоить 1530 рублей. На сколько процентов снизилась цена мобильного телефона в период с февраля по июнь?

[/su_note]

Алгоритм выполнения

1. Из 1800 вычитаем 1530. Определяем, сколько рублей составила скидка.
2. Полученное число делим на первоначальную цену и умножаем на 100 %.

Решение:

1800 – 1530 = 270 (руб.) – скидка

270 : 1800 · 100 = 15 %

Ответ: 15

---

Вариант 3МБ14

[su_note note_color=”#defae6″]

В период распродажи магазин снижал цены дважды: в первый раз на 10%, во второй – на 25%. Сколько рублей стал стоить чайник после второго снижения цен, если до начала распродажи он стоил 1600 рублей?

[/su_note]

Алгоритм выполнения

1. Определяем, сколько (в руб.) составляет 10 % от стоимости чайника. Для этого 1600 делим на 100 и умножаем на 10.
2. От первоначальной стоимости отнимаем сумму скидки, составляющей 10 %.
3. Полученную цену со скидкой делим на 100 и умножаем на 25. Так найдем величину скидки (в руб.) после второго снижения цены.
4. От числа, полученного в п.2 отнимаем число, полученное в п.3.

Решение:

1600 : 100 · 10 = 160 (руб.) – составляет скидка в 10 %

1600 – 160 = 1440 (руб.) – стал стоить чайник после понижения цены на 10 %

1440 : 100 · 25 = 360 (руб.) составляет скидка в 25 %

1440 – 360 = 1080 (руб.)

Ответ: 1080

---

Вариант 3МБ15

[su_note note_color=”#defae6″]

Магазин детских товаров закупает погремушки по оптовой цене 110 рублей за одну штуку и продает с наценкой 30%. Сколько рублей будут стоить 4 такие погремушки, купленные в этом магазине?

[/su_note]

Алгоритм выполнения

1. Определяем, сколько рублей составляет наценка в 30 %. Для этого закупочную стоимость делим на 100 и умножаем на 30.
2. К закупочной стоимости прибавляет сумму наценки.
3. Полученное число умножаем на 4.

Решение:

110 : 100 · 30 = 33 (руб.) – равна наценка

110 + 33 = 143 (руб.) – стоит погремушка в магазине

143 · 4 = 572 (руб.) – стоят 4 погремушки

Ответ: 572

---

Вариант 3МБ16

[su_note note_color=”#defae6″]

Число больных гриппом в школе уменьшилось за месяц в два раза. На сколько процентов уменьшилось число больных гриппом?

[/su_note]

Алгоритм выполнения

1. Обозначим число больных через х. Тогда кол-во больных через месяц станет равным х/2.
2. х/2 делим на х и умножаем на 100 %. Так найдем кол-во процентов, которое составит число больных через месяц по отношению к первоначальному их кол-ву. В процессе вычисления х сократится.

Решение:

х / 2 : х · 100 % = х / 2· 1 / х· 100 % =1 / 2 · 100 % = 0,5 · 100 % = 50 %

Ответ: 50

Даниил Романович | Просмотров: 14.5k

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Чтобы найти процент от числа, надо заданное число разделить на $100$ и умножить на величину процента.

$n%$ от $а={а⋅n}/{100}$

Чтобы найти число по его указанному проценту, нужно заданное число разделить на заданную величину процента, а результат умножить на $100$.

Задачи на скидки

Скидка — это снижение цены товара или услуги. Чаще всего скидку указывают в процентах.

Чтобы найти цену товара с учетом скидки необходимо:

1. Из $100%$ вычесть процент скидки.
2. Найти полученный процент от полной стоимости товара.

Задачи на вклады, кредиты, наценки

Чтобы найти сумму денег с учетом годовой ставки, необходимо:

1. К $100%$ прибавить годовой процент вклада.
2. Найти полученный процент от изначального количества денег.

В некоторых задачах на проценты удобно использовать пропорцию, например:

                  Д
Е П А Р Т А М Е Н Т     О Б Р А З О В А Н И Я     г. М О С К В Ы

Юго
– Западное окружное управление образования Государственное бюджетное
образовательное учреждение города Москвы

 средняя общеобразовательная школа № 1101

Ул. Академика Варги, 34                                                              8(495)339-77-39

КУРСОВАЯ РАБОТА

по теме: «Решение задач на проценты»

Учитель:
Федорова С.В. 

2018
– 2019 уч. год

План работы

1.     Основные
задачи на проценты, тренировочные задачи …………………………… 2

2.     Задачи
на смеси и сплавы

I.        
к смеси или сплаву добавляют вещество
…………………………………………….. 4

II.     
две смеси (сплава) смешали в одну (один сплав)
……………………………….. 7

III.  
разборка задач
………………………………………………………………………………..
12

3.    
Задачи с последовательным повышением (понижением) процента,
разбор- ка задач
………………………………………………………………………………………………..
14

4.     Задачи
на высушивание ягод, грибов, винограда ………………………………….
18

5.     Интересные
задачи «из жизни торговли»
……………………………………………… 20

6.     Литература…
……………………………………………………………………………………….24

1. Основные
задачи на проценты, тренировочные задачи.

I.         Нахождение процента от
числа. Найти p% от числа а

правило	пропорция
Чтобы найти процент от числа, надо это число умножить на десятичную дробь, соответствую- щую проценту, т.е. p  a 100	a −100% b(?) − p% b =  p  a 100

Примеры:

✓  8%
от 6 кг.

8

8% =                                   = 0,08, т.е. 0,08 6 = 0,48кг. 100

✓  0,4%
от 0,25 с.        

                         0,4                      

     0,4% =
= 0,004 , т.е. 0,004  0,25 = 0,001с.

100

✓  20%
от 15,25

15,25 −
100%               15,25 
20

                                              b =   = 3,05

        b(?) − 20%                      100

 Примечание: хорошо, если ученики понимают, что 5%
от числа а это

   ⁵   
a = ¹  a = a : 20 ; 10%
от а это ¹ 
a = a :10
 и т.д.

      100
       20                                       10

✓ 12% от а  

     a −
100%              a 12

                                      b = = 0,12a

     b(?)
−12%              100

✓  75%
от 80%

      (процент)    (число)

3

0,75 80
= 80 = 60%

4

Подборка задач:

Что больше: а) 15% от 17 или 17%
от 15; б) 1,2% от 48 или 12% от 480;

в) 147% от 621 или 125% от 549;
г) 72% от 150 или 70% от 152; д) 80% от а или 40% от 2а; е) 36% от 2,5b или
1,5% от 80b?

             II.      Нахождение числа по его
проценту.

Найти число, если p%
от него равно b

правило	пропорция
Чтобы найти число по его проценту, надо часть числа разделить на десятичную дробь, соответ- p ствующую проценту, т.е. a = b :   100	a(?) −100% b − p% a = 100 b p

Примеры:

✓  От
какой величины 7% составляют 7 руб.

7 : 0,07 = 700 : 7 =100 р.

✓ 
12% от ? составляют 36 экземпляров 36 : 0,12 = 3600 :12 = 300 экз.

1

✓ 
25% от ? составляют 10г. (или  от ? равно 10 г.) 4

     a −
100%         a
= 10 100 = 40 г.

10 −
25%                          25

✓  300%
от ? равны b ?

     a(?) −100%
             b 100
  b  

 a = =  . b − 300% 300 3

Подборка задач:

Сравнить величины, если:

а) 40% первой составляют 300
руб., а 30% второй составляют 400 руб.;

б) 150% первой составляют 120
руб., а 120% второй составляют 90 руб.;

в) 50% первой составляют 0,5а
руб., а 20% второй составляют 0,2а руб.;

г) 12,5% первой составляют b
руб., а 30% второй составляют 3b руб.?

             III.
    Нахождение процентного отношения двух чисел.

правило	пропорция
Чтобы узнать, сколько процентов одно число составляет от второго, надо первое число разде- лить на второе и результат умножить на 100.	a   −100% b   − p (?)% b p% = 100 a

Примеры: сколько процентов составляют

✓  16с
от 50с?

16

 100
= 32%

50

✓  15
г от 1 кг?

15

                                                100 =
1,5%

1000

✓  1,2
от 0,15?  

     0,15 −
100%         p%
= ^{1,2 100} ₌
800%

                                               1,2
− p%       0,15

✓  2а
от 8а?

8a −100% 2a 100 
p% =
 = 25% . 2a
− p%  8a

Подборка задач:

№1. В каком случае процентное
отношение больше:

а) 8 отличников из 40 учащихся
или 9 отличников из 50 учащихся;

б) 6 разбитых
лампочек из 20 или 7 разбитых лампочек из 30? № 2. Какое изменение более
значительно:

а) подорожание с 400 руб. до 500
руб. или с 500 руб. до 600 руб.;

б) похудание со 100 кг до 90 кг
или с 50 кг до 40 кг?

2. Задачи на смеси
и сплавы.

             I.       К смеси или сплаву
добавляют вещество.

В этих задачах нужно:

1)       
отделить вещество в смеси (сплаве) по массе от всей смеси
(сплава), поль- зуясь правилом I или пропорцией.

2)       
понимать, что при добавлении вещества оно прибавляется, по массе,
ко всей смеси (сплаву) и к конкретному веществу

вода + вода

соль
+ соль золото + золото Пример: К 40% раствору серной кислоты добавили 50 г
чистой серной ки- слоты, после чего концентрация раствора стала равна 60%.
Найти первона- чальный вес раствора.

Пусть х (г) – первоначальный вес
раствора, тогда, если кислота составляет 40%, то ее масса 0,4х (г).

Составляем пропорцию:

x +
50 − 100%

                                               ;                          

0,4x +
50 − 60% 

Получаем:                                        

                   100(0,4x + 50) = 60(x + 50)    / :10

10(0,4x +
50) = 6(x + 50)

4x +
500 = 6x + 300

2x =
200 x =
100

Ответ: 100 г.

Пример: К раствору, содержащему 30
г соли, добавили 400 г воды, после че- го концентрация соли уменьшилась на 10%.
Найти первоначальную концен- трацию соли в растворе.

Пусть х (г) – вес первоначального раствора, тогда
процентное содержание

 соли
в нем: 30 100 = 3000 .

                                        x
              x

По условию задачи составляем пропорцию:

^{x + 400 − 100%}   p% =
3000  (измененный процент соли в
новом рас-

      30 −
p%                              x +
400

творе).

По условию задачи процентное содержание соли в растворе
уменьшилось на

10%. Составим и решим уравнение:

3000  3000

      −                                                                = 10 / :10

           x      x + 400

          300  300
        

      −            =

x   x + 400 x = 200

200 (г) – вес первоначального раствора, процентное
содержание соли в нем

      3000    3000            

                    =         = 15%

           x
       200

Ответ: 15%

Пример: В 5 кг сплава олова и цинка содержится 80% цинка.
Сколько кг оло- ва надо добавить к сплаву, чтобы процентное содержание цинка
стало вдвое

меньше?

 

0,8 5 = 4,0 (кг) – чистый цинк

2) Пусть
х кг олова добавили к сплаву, тогда

5 +
x − 100%

4 −
80% : 2 = 40%

Получаем уравнение:

40(5 +
x) = 100  4 5 + x = 10 x = 5

Ответ: 5 кг олова Подборка задач:

№ 1. Имеется кусок сплава меди с
оловом общей массой 24 кг, содержащий 45% меди. Сколько чистого олова надо
прибавить к этому куску сплава, чтобы полученный новый сплав содержал 40 %
меди? Ответ: 3

№ 2. Сплав меди с цинком,
содержащий 5 кг цинка, сплавили с 15 кг цинка. В результате содержание меди в
сплаве понизилось по сравнению с первона- чальным на 30%. Какова была
первоначальная масса сплава, если известно, что она была меньше 20 кг? Ответ:
10

№ 3. Сплав золота с серебром,
содержащий 80 г золота, сплавили со 100 г чистого золота. В результате
содержание золота в сплаве повысилось по сравнению с первоначальным на 20%.
Сколько серебра в сплаве? Ответ: 120 № 4. Если к раствору кислоты добавить 50 г
воды, то его концентрация станет равной 15%. Если же к первоначальному раствору
добавить 50 г ки- слоты, то его концентрация станет равной 40%. Найти
первоначальную концентрацию раствора. Ответ: 16

             II.      Две смеси (сплава) смешали
в одну (один сплав).

В этих задачах нужно:

1)  Отделить вещество от
всей смеси (сплава)

2)  Когда
получается смесь, то массы исходный растворов (сплавов) склады- ваются.

медь + медь

соль + соль золото
+ золото

Пример: Имеется два сплава меди и свинца. Один сплав содержит
15% меди, а другой – 65% меди. Сколько нужно взять каждого сплава, чтобы
получить 200 г сплава, содержащего 30% меди?

Эту задачу можно решать с одной переменной, но удобнее
ввести две.

Пусть х (г) – вес первого сплава, а у (г) –
вес второго сплава.

Отделим медь от каждого сплава. В первом 15% от х – 0,15х
(чистая медь), во втором 65% от у – 0,65у (чистая медь).

При сплавлении первого и второго сплавов получаем: x
+ y − 100%

 30(x + y) =100(0,15x + 0,65y) 0,15x
+ 0,65y − 30%

Составим и решим систему:

    x +
y = 200                 x + y = 200    x = 140

     
                                ; 
                   ; 

30x
+ 30 y = 15x + 65y 15x − 35y = 0  y = 60

Ответ: 140 г и 60 г.

Пример: Имеется два разных сплава меди,
процент содержания меди в пер- вом сплаве на 40% меньше, чем во втором. Когда
оба сплава сплавили вме- сте, то новый сплав стал содержать 36% меди. Известно,
что в первом сплаве было 6 кг меди, а во втором вдвое больше. Каково процентное
содержание меди в обоих сплавах?

+ =

Пусть х (кг) – вес первого сплава, а у (кг)
– вес второго сплава.

                            6           600

p%(I ) =   100 =      x x

                               12           1200

p%(II ) =        100 =  y       y

По условию задачи процент содержания меди
в первом сплаве на 40% мень- ше, чем во втором, тогда:

1200 − 600 = 40 / : 20 y        x

      60    30       

              −     = 2

        y      x

Пропорция, соответствующая сумме двух
сплавов, выглядит следующим об- разом:

x + y −
100%



     6
+12 − 36%          

x +
y = 18 100 ;

36

x + y =
50

Составим и решим систему уравнений:

     60
   30       

                         −     =
2



      
y      x

^x + y = 50

Эту задачу можно решать, составив другую
модель, приняв за х и у процент- ное содержание меди в каждом из
сплавов. Тогда

1   _сплав: m1 −100%     _
m1 ₌
600 6 − x%
  x

                            m2  −100%
             1200

2   сплав:  m 2=   12 −
y%       y

600  + 1200  −
100%

1 + 2 сплав:        x         y                     

6 +12
− 36%

      600    1200   18 100 

                 +         =             ;

          x         y          36

600 + 1200 = 50 / : 50; x       y

      12    24       

             +     = 1

        x      y

Составим и решим систему:

  y − x = 40  x  = 20

     12  +
24  ₌
1; y ₌ 60

    
x    y        

Эта модель удобнее тем, что полученные величины являются
ответом к задаче.

Ответ: 20% и 60%.

Пример: В какой пропорции нужно смешать
10% и 35% растворы аммиачной селитры, чтобы приготовить 15%-ный раствор?

Пусть х (г) – весь первый раствор, у (г) –
весь второй раствор. Найти х : у.

                                                                                                 x
+ y − 100%              _

0,1x
+ 0,35y − 15%

15(x
+ y) = 100( 0,1x
+ 0,35)

15x
+ 15 y = 10x + 35 y

5x = 20 y

x                     
4 y x = 4 y  =      = 4 :1

y                     
y

Ответ: 4 : 1.

Пример: Если два раствора кислоты смешать
в отношении 1 : 4, то получится раствор, содержащий 38% кислоты. Если же эти
растворы смешать в отно- шении 4 : 1, то получится раствор, содержащий 32%
кислоты. Найти про- центное содержание кислоты во втором растворе.

Проиллюстрируем первое предложение условия задачи:

         Каждый из
растворов имеет свою концентрацию p₁ и p₂.

Тогда                      p1  

Первой кислоты по массе p₁% от х,
т.е.   x ; 100      p2

Второй кислоты по массе p₂%
от 4х, т.е. ^{ 4x .} 100 x + 4x − 100%

Составляем
пропорцию для нового раствора:       p₁ x +
4 p₂ x
− 38%

                                                         100
   100

Получаем первое
уравнение системы: p¹                       4
p₂   /:
x  0

   5x 
38 = 100x(
    ₊
)

                                         100
   100

190 =
p₁ + 4 p₂

Проиллюстрируем второе предложение условия задачи:

 

Процентное
содержание растворов осталось p₁ и p₂.

p1

Первой кислоты по массе p₁%
от 4у, т.е.          ^{ 4 y ;} 100            p2  

Второй кислоты по массе p₂% от у,
т.е.            y .

100 

4                
y + y −
100%  Составляем
пропорцию для нового раствора: 100p₁   
4 y + 100p_{2 } 
y ₋
32%

Получаем второе уравнение системы:

                                         p¹                               p²

5                
y  32 =
100(        
4 y +         
y)

                                      100
        100

160 y = p₁  4 y + p₂  y / : y  0

160 =
4 p₁ + p₂

Составим и решим систему уравнений:

 
p₁  + 4 p₂  = 190 ; _
 p₁ = 30

4
p1   + p2 = 160 
p2 = 40

Ответ: 40%

             III.    Разборка задач

Пример: Сплавляя два одинаковых по весу
слитка, состоящих только из зо- лота и серебра, с разным содержанием золота,
получили сплав, в котором со- держится 3 кг золота. Если бы второй слиток был в
два раза тяжелее, то в сплаве содержалось бы 11 кг серебра. Известно, что
процентное содержание золота в первом слитке было на 20% больше, чем во втором.
Сколько кило- граммов серебра содержится в полученном сплаве?

Проиллюстрируем первое предложение задачи:

Отделим золото от каж- дого
из сплавов.

                                                                                   p
+ 20

Масса чистого золота в первом куске —    ^{ x (кг)} 100            p         

Масса чистого золота во втором куске —         ^{ x} (кг).

100

По условию задачи в новом сплаве
содержится 3 кг чистого золота, получаем уравнение:

      p +
20        p

    
x +                          x =
3;

  x100
p +  20 ₊  100p  _
= 3;

         
                 


100     100  p
+ 10

 x = 3 (*) 50

Находясь в условиях второго предложения
«Если бы…», получаем следую- щую математическую модель:

Масса чистого золота в первом куске — p ⁺
20  2x (кг)
100    p         

Масса чистого золота во втором куске —         ^{ x} (кг).

100

По условию задачи новый сплав содержал бы
11 кг чистого серебра. Его вес получим, вычитая из веса всего сплава вес
чистого золота:

3x − p ^{+ 20}  2x −
 ^p   x = 11

                   100            100

     x 300 − 2 p − 40 − p  ₌ 11

      ^          100          ^
 

    160 − 3 p            

 x = 11 (**) 100

Разделим уравнение (**) на (*), понимая, что x  0.

     160 −
3 p     

   100 ^{ x}₌
11;   p + 10  x 3

              50        

160 −
3 p  50           11

     =       ;

            100      p + 10    3

     160 − 3 p    11

=  ;

480 −
9 p = 22 p
+ 220;

13 p = 260; p = 20

Таким образом, получаем, что в первом
сплаве чистого золота 40 %, а во вто- ром – 20%.

Читаем внимательно
вопрос задачи: «Сколько кг серебра содержится в по- лученном сплаве?». Делаем
вывод, что в первом сплаве чистого серебра 60%, а во втором – 80%. Т.е.

В первом сплаве чистого серебра по массе
– 0,6х (кг), во втором – 0,8х (кг), в новом сплаве – 1,4х (кг).

Нам известно, что в новом сплаве содержится 3 кг чистого
золота, поэтому

0,4x +
0,2x = 3
0,6x = 3 x
= 5

Тогда 1,4x =1,4  5 = 7(кг) Ответ: 7 кг.

Подборка задач:

№1. Смешали 30%-ный раствор
соляной кислоты с 10%-ным и получили 600 г 15%-го раствора. Сколько граммов
10%-го раствора было взято? Ответ: 450

№2. Два сосуда с раствором щелочи
разных концентраций (по объему) содержат вме- сте 20 л раствора. Первый сосуд
содержит 4 л щелочи, а второй – 6 л. Сколько процен- тов щелочи содержит первый
сосуд, если второй содержит щелочи на 40% меньше пер- вого? Ответ: 80

№3. Имеется два раствора кислоты.
Первый раствор состоит из 1056 г кислоты и 44 г воды, а второй – из 756 г
кислоты и 1344 г воды. Из этих растворов нужно получить 1500 г нового раствора,
содержание кислоты в котором 40%. Сколько граммов первого раствора нужно для
этого взять? Ответ: 100

№4. Имеется два достаточно
больших слитка сплава золота с медью. Первый слиток содержит 92% золота, а
второй – 80% золота. Из этих слитков надо получить 600 г сплава, содержание
золота в котором 85%. Определите массу куска, который для этого необходимо
взять от первого слитка. Ответ: 250

3. Задачи
с последовательным понижением, повышением процента. Основная ошибка,
которую допускают учащиеся при решении задач этого типа, это сложение и
вычитание процентов, которое категорически нельзя допускать, т.к. проценты
берутся от разных величин.

Пример: В двух магазинах были одинаковые
цены. В одном магазине их сначала пони- зили на 15%, а потом повысили на 10%, а
в другом – сначала повысили на 10%, а потом понизили на 15%. Как изменились
цены в этих магазинах по сравнению с первоначаль- ной? В каком из них выгоднее
покупать товар?

1   магазин:

Эту запись можно прочесть как 93,5% от х
(0,935 – десятичная дробь, соот- ветствующая проценту), т.е. по сравнению с
первоначальной ценой в этом магазине она понизилась на 6,5%.

2   магазин:

                                                             ,
т.е. 93,5% от х. Как мы видим, цены в магазинах не стали разными, но так
бывает не всегда! Пример: Цена первого товара поднялась на 40%, а потом еще на
25%. Цена второго товара поднялась на 30%, после чего оказалось, что цена
первого то- вара на 40% выше второго. На сколько процентов первоначальная цена
пер- вого товара была больше цены второго товара?

1   товар:

                                                                       
, т.е.

175% от х.

2   товар:

После чего оказалось, что цена первого товара на 40% выше
цены второго. Внимание! С какой величиной происходит сравнение (второй товар),
ту цену и принимаем за 100%, т.е.

             

Эту запись читаем: х составляет 104% от у, т.е.
104% — 100%= 4% — на столь- ко процентов первоначальная цена первого товара
была больше первона- чальной цены второго товара.

Ответ: на 4%

 Замечание: если бы вопрос звучал
«На сколько процентов цена второго това- ра была ниже цены первого товара?», то
ответ не был бы, конечно, 4%, т.к. сравнение производится с ценой первого
товара, поэтому p% ₌ (x − y) 100 x

      x − 100%                       (1,04 y)
100

                                                p% =                      

      (x
− y) − p%                        1,04
y

                                                                          4
y      400      11     

                                                       p%
=         _{=
       =}
3    %

                                                                     1,04
y    104      13

Пример: Цена первого товара на 10% больше
цены второго товара. На второй товар цена вначале поднялась на 21%, а потом еще
раз поднялась на 25%. На сколько процентов требуется поднять цену первого
товара, чтобы цены обо- их товаров стали одинаковыми?

1 товар: 1,1х, т.к. цена первого товара на 10%
больше цены второго.

1 товар: х – 100%

Покажем изменение цены второго товара:

                  +21% om x                                                                      +25%om 1,21x

x⎯1⎯00%⎯+21%⎯=12⎯1%=1⎯,21→1,21x⎯1⎯00%⎯+25%⎯=12⎯5%=1⎯,25→1,251,21x =1,5125x,  
т.е.   151,25% от х.

По условию задачи нужно поднять цену
первого товара, чтобы цены стали одинаковыми, т.е.

1,1x −
100%         p%
= 1,25 1,21x 100 = 125 1,1 = 137,5%

1,5125x
− p%                                1,1x

Значит,
137,5% −100% = 37,5%

Ответ: на 37,5%

Пример: Товар стоил 4000 руб. После двух
последовательных повышений цены он стал стоить 4830 руб. Какова была цены
товара после первого по- вышения, если процент повышения во второй раз был на
10% больше, чем в первый раз?

  4000   _100%+
  +
p %                  ^100
+ p  4000 = (100 + p)  40^ + p %₁₀₀+10_%%+ _p om_%(100+₁₀+_% p = )40

                 ⎯⎯⎯p %⎯=(10⎯0+ p )⎯:100→ ^ 100                                                                                                                                          _^
 ⎯⎯⎯(11⎯0+ p )⎯:100 ⎯⎯→

_

^{110 + p}  (100 + p)  40 = 4830^

     
100                                  

Составим и решим уравнение:

(110 +
p)(100 + p)
 2  / 5  ₌
4830

                              5                               2

(110 +
p)(100 + p)
= 12075

После раскрытия скобок и упрощения получаем:

p² +
210 p −1075
= 0 p = 5

По условию задачи нужно узнать цену
товара после первого повышения це- ны, т.е. (100 +
p)  40 =105 40 = 4200

Ответ: 4200 руб.

Подборка задач:

№1. Как изменилась величина, если
она:

а) сначала увеличилась на 20%, а
потом увеличилась на 25%;

б) сначала увеличилась на 20%, а
потом уменьшилась на 25%;

в) сначала уменьшилась на 20%, а
потом уменьшилась на 25%;

г) сначала уменьшилась на 20%, а
потом увеличилась на 25%? №2. Как изменилась температура воздуха, если она:

а) сначала увеличилась на 25%, а
потом уменьшилась на 40%;

б) сначала уменьшилась на 60%, а
потом увеличилась на 80%;

в) сначала увеличилась на 5%, а
потом на 20%;

г) сначала уменьшилась на 10%, а
потом на 30%?

№ 3. В двух магазинах цены были
одинаковые. В одном магазине их сначала понизили на 40%, а потом повысили на
40%, а в другом – сначала повысили на 50%, но зато потом понизили на 50%. Как
изменились цены в этих мага- зинах по сравнению с первоначальной?

№ 4. а) Одну сторону
прямоугольника увеличили на 20%, а другую – на 25%. На сколько процентов
увеличилась площадь прямоугольника?

б) Одну сторону прямоугольника
увеличили на 60%, а другую уменьшили на 60%. Как изменилась площадь
прямоугольника и на сколько процентов?

в) Длина прямоугольника в 3 раза
больше ширины. Длину уменьшили на 20%, а ширину уменьшили на 40%. На сколько
процентов уменьшился периметр прямоугольника?

г) Ширина прямоугольника в 4 раза
меньше длины. Длину увеличили на 10%, а ширину уменьшили на 20%. Как и на
сколько процентов изменился периметр прямоугольника?

№ 5. После двух последовательных
повышений размер пенсии был увеличен на 56%. На сколько процентов повысили
пенсию в первый раз, если второе повышение было в полтора раза больше первого
(в процентном отношении)? Ответ: 20

№ 6. За два года количество
безработных в регионе снизилось на 60%. На сколько процентов снизилась
безработица за первый год, если во второй год снижение было в два с половиной
раза больше, чем в предыдущем (в про- центном отношении)? Ответ: 20

№ 7. Расценки на грузоперевозки
по железной дороге увеличивались за год дважды: на 20% в первый раз, и на 10% —
во второй. Определите, на сколько процентов возрастут расходы почтовой фирмы на
железнодорожный транспорт, если объем перевозимой ею по железной дороге почты
вырос на 30%. Ответ: 71,6

4. Задачи на
высушивание ягод, грибов, винограда

Этот класс задач учащиеся решают очень
плохо, хотя они решаются доволь- но просто. Главное, представлять себе, что
виноград, ягоды, грибы состоят из:

Клеточное вещество остается
неизменимым как в свежем, так и в засушенном виде.

Пример: Свежие грибы содержат 90% воды, а
сухие 12% воды. Сколько ки- лограммов сухих грибов получится из 33 килограмм
свежих?

По условию имеем 33 кг свежих грибов,
отделим от них клеточное вещество, т.е. 0,1 33 = 3,3 кг.

Переходим к сухим грибам, помним, что те же 3,3 кг клеточного
вещества остается в них от свежих грибов. а (кг) – 100 %        3,3100

                                                       a =                  a = 3,75

3,3 (кг) – 88 %                        ⁸⁸

Ответ: 3,75 кг.

Пример: Из 10 кг свежих фруктов получают
3,5 сушеных фруктов, содержа- щих 20% воды. Каково процентное содержание воды в
свежих фруктах?

Отделим в сухих фруктах клеточное вещество от влаги:

80% от 3,5 кг – это              
(кг), это масса клеточного вещества содер- жится и в свежих фруктах.

Сразу получим процентное содержание влаги:

Ответ: 72%

 Примечание: задачи об обогащении
руды имеют тот же смысл, только вместо клеточного вещества думаем о чистой
руде, вместо воды представляем при- меси.

Пример: Руда содержит 40% примесей, а
выплавленный из нее металл со- держит 4% примесей. Сколько тонн руды необходимо
взять, чтобы выпла- вить из нее 15 тонн металла?

Отделим чистую руду от примесей в
15 тоннах металла:               (т) Сколько же чистой руды содержится в руде с
40% примесей. Составим про- порцию:

       
                                   (т)

Ответ: 24 тонны.

Подборка задач:

№1. Свежие грибы содержат по массе 90% воды, а сухие –
20%. Сколько надо собрать свежих грибов, чтобы из них получить 4,5 кг сухих
грибов? Ответ:36 кг.

№2. Собрали 100 кг грибов.
Оказалось, что их влажность 99%. Когда их подсушили, то влажность снизилась до
98%. Какой стала масса этих гри- бов после того, как их подсушили? Ответ: 50
кг.

№3. Собрали 42 кг свежих грибов,
содержащих по массе 95% воды. Когда их подсушили, они стали весить 3 кг. Каков
процент содержания воды по массе в сухих грибах? Ответ: 30 кг.

№4. Только что добытый каменный
уголь содержит 2% воды, а после двух- недельного пребывания на воздухе он
содержит 20% воды. На сколько кг увеличилась масса добытой тонны угля после
того, как уголь две недели по- лежал на воздухе? Ответ:225 кг.

5. Интересные задачи из «жизни
торговли»

Очень интересные задачи, для решения
которых нужно понимать некоторые ключевые моменты:

•      Когда
продают что-либо, то основным показателем являются, цена, ко- личество,
стоимость;

•      Когда
получают прибыль от продажи партии товара, то она складыва- ется из тех же
показателей, что и выше, только цена является разницей между закупочной ценой и
ценой с наценкой (реализации);

•      Нужно
очень внимательно читать условие задачи, оформлять которое проще в виде
таблицы;

•     
Не бояться вводить более двух переменных.

Пример: Ювелирное изделие состоит из серебра и золота. В
начале года се- ребро дорожает на 5%, а золото – на 20% по сравнению с
предыдущим го- дом, в результате чего стоимость ювелирного изделия
увеличивается на 15%. Какую часть ювелирного изделия составляет золото, если в
предыдущем году 1 г золота стоил в 18 раз дороже 1 г серебра? (ответ дать в
виде десятичной дроби)

		Цена за 1 г	Кол-во в г	Стоимость
До подорожания	Золото	18х	m	18xm
Серебро	х	n	xn
После подорожания	Золото		m	21,6xm
Серебро	1,05x	n	1,05xn

Составим пропорцию:

Получаем уравнение:

                                                      
(по условию задачи)

      
Золото составляет   часть всего изделия, значит   

Ответ: 0,1

Пример: Салон модной одежды выставил на
продажу новую коллекцию, сде- лав наценку 140% от закупочной цены. После
продажи 0,85 все коллекции салон распродал оставшуюся часть с одинаковой
скидкой от продажной цены (в процентном отношении) на все элементы коллекции.
Сколько процентов составила эта скидка, если прибыль салона от продажи всей
коллекции со- ставила 113% от закупочной цены?

Внимание! Наценка 140% от закупочной цены означает, что                          от
закупочной цены, т.е. 2,4х – цена продажи в салоне. Прибыль салона
составила 113% от закупочной цены. Это значит, что

                  
Составим таблицу:

	Закупочная цена	Цена с наценкой	Количество	Стоимость
покупка	х	—	а	ха
продажа	х	2,4х	0,85а
х	*	0,15a

 *Скидка
в p% от цены 2,4х вычисляется:           

Составим пропорцию:

  (2xa
,4−   0,85100xa%
+  2,4  0,15xa^1− p ) ₋
213%

                                                                              

                                                                        100  

Получаем, что

                                           p  

213 = 2,485 + 151 − 100 



     213 ₌               15 p _


                2,485 + 15 −     

                                       100 

213 = 240 − 24 ^{15 p}

1000

     24 15 p        

= 27

 

p = 75

Ответ: 75%

Пример: Магазин получил партию товара и
продал 30% этого товара с при- былью 20%, а 50% оставшегося товара – с прибылью
40%. Какую прибыль получил магазин от реализации товара, оставшегося после двух
распродаж, если общая прибыль от продажи всей партии товара составила 27%.

	цена	количество	стоимость
партия	x	a	xa
1 продажа	1,2x	0,3a	0,36xa
2 продажа	1,4x	0,5(a − 0,3a) = 0,35a	1,4x  0,35a = 0,49xa
остаток	x 1 + p  * 100                    	a − 0,3a − 0,35a = 0,35a p	0,35xa 1+ p   100  p             

* повышение цены х (руб) на p%, т.е. x +         x = ^x1+     ^

                                                                                                                                                   

                                                                                                                   100
           100  

По условию задачи прибыль составила 27%, т.е. 100% + 27% =127%.

Составим и решим пропорцию:

  0xa
,85−xa
100 +
%0,35 xa^1+
p _
− 127%

                                                      

                                                100  

Получаем, что

       85 +  ₊  p ^_ = 127

35_1   
100  

35 p

 = 127 −120 100

      35 p                   7 100                                         Ответ:
20%

       = 7  p =                 p = 20%

      100                         35

Подборка задач:

№ 1.
Антикварный магазин, купив портсигар и статуэтку, продал их, полу- чив 40%
прибыли. Во сколько раз портсигар обошелся дороже магазина, чем статуэтка, если
на портсигаре было получено 35% прибыли, а на статуэт- ке – 60%? Ответ: 4

№ 2. Кондитерская фабрика
производит 20 видов шоколада. В новом году 5 из этих видов будут производить на
10% больше, а другие 7 видов – на 20% больше. На сколько процентов увеличится
выпуск шоколада на фабрике, если в старом году все виды шоколада производились
в одинаковом количестве?

Ответ: 9,5

№ 3. Молокозавод планирует
увеличить выпуск продукции на 10%. На сколь- ко процентов увеличится чистая
прибыль завода, если отпускная цена на его продукцию возросла на 15%, а ее
себестоимость для завода, которая до этого составляла ¾ отпускной цены,
увеличилась на 20%. Ответ: 10 № 4. В результате расширения компании сотовой
связи и одновременного снижения тарифов на 50% ежемесячный объем продаж ее
услуг вырос в 3 раза. Через сколько месяцев дополнительная прибыль, получаемая
компани- ей, компенсирует затраты на расширение, если они составили половину
прежнего годового дохода компании? Ответ: 12

Литература:

1.     Дорофеев
Г.В., Петерсон Л.Г., Математика. 6 класс. Часть 1. – М.: «Ба- ласс», «Ювента»,
2004. – 112 с.: ил.

2.     П.А.
Андриянов, В.И. Ермаков, Сборник задач по математике. Для подготовительных
курсов. Издание пятое, — М.: Издательство «Менед- жер», 2005. – 160 с.

3.     Лысенков,
Сборник задач для подготовки к ЕГЭ, — М.: издательство «Легион», — 2013.

Предлагаем разобрать три задачи, приведенные ниже. Это задание №11 из ЕГЭ прошлых лет, рекомендованные как тренировочные.

Задача № 1

Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 20 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?

Решение

Согласно условию получается, что виноград содержит 10% питательного вещества, а изюм — 95%.

Представим проценты в долях от «1»:

10% = 0,1

95% = 0,95

Поэтому 20 кг изюма содержат питательного вещества:

20 · 0,95 = 19 кг

Таким образом, для получения 20 килограммов изюма требуется винограда:

= 190 кг

Ответ: 190.

Нужна помощь в подготовке к эказмену? Смотрите курсы подготовки к ЕГЭ по математике в Санкт-Петербурге!

---

Задача № 2

Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

Решение

Пусть масса первого сплава «х» кг, а масса второго – «у» кг.

Представим проценты в долях от «1»:

10% = 0,1

30% = 0,3

25% = 0,25

Тогда массовое содержание никеля в первом и втором сплавах получится:

«0,1· х»  и  «0,3 · у» соответственно.

Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:

Получаем, что:

у – х = 150 – 50 = 100

Первый сплав легче второго на 100 килограммов.

Ответ: 100.

---

Задача № 3

Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Решение

Пусть масса первого сплава «х» кг,

масса второго сплава – «х + 3» кг,

масса третьего сплава – «2х + 3» кг.

Первый сплав содержит 10% меди, второй – 40% меди, третий сплав – 30% меди.

Представим проценты в долях от «1»:

10% = 0,1

40% = 0,4

30% = 0,3

Тогда можем записать:

0,1·х + 0,4·(х + 3) = 0,3·(2х + 3) <=>

<=> 0,5 ·х + 1,2 = 0,6 ·х + 0,9 <=>

<=> х = 3     и    2·х + 3 = 9

Таким образом, масса третьего сплава равна 9 кг.

Ответ: 9.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Вариант 1 3. Простейшие текстовые задачи (Проценты, округление)

1. Еже­ме­сяч­ная плата за те­ле­фон со­став­ля­ет 300 руб­лей в месяц. В сле­ду­ю­щем году она уве­ли­чит­ся на 6%. Сколь­ко руб­лей будет со­став­лять еже­ме­сяч­ная плата за те­ле­фон в сле­ду­ю­щем году?

2. Налог на до­хо­ды со­став­ля­ет 13 % от за­ра­бот­ной платы. После удер­жа­ния на­ло­га на до­хо­ды Мария Кон­стан­ти­нов­на по­лу­чи­ла 12 180 руб­лей. Сколь­ко руб­лей со­став­ля­ет за­ра­бот­ная плата Марии Кон­стан­ти­нов­ны?

3. При опла­те услуг через пла­теж­ный тер­ми­нал взи­ма­ет­ся ко­мис­сия 5%. Тер­ми­нал при­ни­ма­ет суммы крат­ные 10 руб­лям. Аня хочет по­ло­жить на счет сво­е­го мо­биль­но­го те­ле­фо­на не мень­ше 300 руб­лей. Какую ми­ни­маль­ную сумму она долж­на по­ло­жить в при­ем­ное устрой­ство дан­но­го тер­ми­на­ла?

4. Цена на элек­три­че­ский чай­ник была по­вы­ше­на на 25 % и со­ста­ви­ла 2625 руб­лей. Сколь­ко руб­лей стоил чай­ник до по­вы­ше­ния цены?

5. В на­ча­ле года число або­нен­тов те­ле­фон­ной ком­па­нии «Юг» со­став­ля­ло 600 тыс. че­ло­век, а в конце года их стало 630 тыс. че­ло­век. На сколь­ко про­цен­тов уве­ли­чи­лось за год число або­нен­тов этой ком­па­нии?

6. Налог на до­хо­ды со­став­ля­ет 13% от за­ра­бот­ной платы. За­ра­бот­ная плата Ивана Кузь­ми­ча равна 22 500 руб­лей. Какую сумму он по­лу­чит после упла­ты на­ло­гов? Ответ дайте в руб­лях.

7. Налог на до­хо­ды в Рос­сии со­став­ля­ет 13% от за­ра­бот­ной платы. За­ра­бот­ная плата Ивана Кузь­ми­ча равна 20 000 руб­лей. Сколь­ко руб­лей он по­лу­чит после упла­ты на­ло­га на до­хо­ды?

8. Роз­нич­ная цена учеб­ни­ка 180 руб­лей, она на 20% выше опто­вой цены. Какое наи­боль­шее число таких учеб­ни­ков можно ку­пить по опто­вой цене на 10 000 руб­лей?

9. Цена на элек­три­че­ский чай­ник была по­вы­ше­на на 20% и со­ста­ви­ла 2400 руб­лей. Сколь­ко руб­лей стоил чай­ник до по­вы­ше­ния цены?

10. В на­ча­ле года число або­нен­тов те­ле­фон­ной ком­па­нии «Север» со­став­ля­ло 600 тыс. че­ло­век, а в конце года их стало 660 тыс. че­ло­век. На сколь­ко про­цен­тов уве­ли­чи­лось за год число або­нен­тов этой ком­па­нии?

Вариант 2 3. Простейшие текстовые задачи (Проценты, округление)

1.Тет­радь стоит 10 руб­лей. Какое наи­боль­шее число таких тет­ра­дей можно будет ку­пить на 650 руб­лей после по­ни­же­ния цены на 20%?

2. Еже­ме­сяч­ная плата за те­ле­фон со­став­ля­ет 300 руб­лей в месяц. В сле­ду­ю­щем году она уве­ли­чит­ся на 6%. Сколь­ко руб­лей будет со­став­лять еже­ме­сяч­ная плата за те­ле­фон в сле­ду­ю­щем году?

3. Число по­се­ти­те­лей сайта уве­ли­чи­лось за месяц впя­те­ро. На сколь­ко про­цен­тов уве­ли­чи­лось число по­се­ти­те­лей сайта за этот месяц?

4. Тет­радь стоит 24 рубля. Сколь­ко руб­лей за­пла­тит по­ку­па­тель за 60 тет­ра­дей, если при по­куп­ке боль­ше 50 тет­ра­дей ма­га­зин де­ла­ет скид­ку 10% от сто­и­мо­сти всей по­куп­ки?

5. Фут­бол­ка сто­и­ла 800 руб­лей. После сни­же­ния цены она стала сто­ить 680 руб­лей. На сколь­ко про­цен­тов была сни­же­на цена на фут­бол­ку?

6. В на­ча­ле года число або­нен­тов те­ле­фон­ной ком­па­нии «Запад» со­став­ля­ло 700 тыс. че­ло­век, а в конце года их стало 840 тыс. че­ло­век. На сколь­ко про­цен­тов уве­ли­чи­лось за год число або­нен­тов этой ком­па­нии?

7.Же­лез­но­до­рож­ный билет для взрос­ло­го стоит 290 руб­лей. Сто­и­мость би­ле­та для школь­ни­ка со­став­ля­ет 50% от сто­и­мо­сти би­ле­та для взрос­ло­го. Груп­па со­сто­ит из 16 школь­ни­ков и 3 взрос­лых. Сколь­ко руб­лей стоят би­ле­ты на всю груп­пу?

8. В на­ча­ле года число або­нен­тов те­ле­фон­ной ком­па­нии «Во­сток» со­став­ля­ло 800 тыс. че­ло­век, а в конце года их стало 880 тыс. че­ло­век. На сколь­ко про­цен­тов уве­ли­чи­лось за год число або­нен­тов этой ком­па­нии?

9. Ивану Кузь­ми­чу на­чис­ле­на за­ра­бот­ная плата 20 000 руб­лей. Из этой суммы вы­чи­та­ет­ся налог на до­хо­ды фи­зи­че­ских лиц в раз­ме­ре 13%. Сколь­ко руб­лей он по­лу­чит после упла­ты по­до­ход­но­го на­ло­га?

10. Роз­нич­ная цена учеб­ни­ка 180 руб­лей, она на 20% выше опто­вой цены. Какое наи­боль­шее число таких учеб­ни­ков можно ку­пить по опто­вой цене на 7900 руб­лей?

Вариант 3 3. Простейшие текстовые задачи (Проценты, округление)

1. Ма­га­зин за­ку­па­ет цве­точ­ные горш­ки по опто­вой цене 120 руб­лей за штуку и про­да­ет с на­цен­кой 20%. Какое наи­боль­шее число таких горш­ков можно ку­пить в этом ма­га­зи­не на 1000 руб­лей?

2. Толь­ко 94% из 27 500 вы­пуск­ни­ков го­ро­да пра­виль­но ре­ши­ли за­да­чу B1. Сколь­ко че­ло­век пра­виль­но ре­ши­ли за­да­чу В1?

3. В сен­тяб­ре 1 кг огур­цов стоил 50 руб­лей, в ок­тяб­ре огур­цы по­до­ро­жа­ли на 20%, а в но­яб­ре еще на 20%. Сколь­ко руб­лей стоил 1 кг огур­цов после по­до­ро­жа­ния в но­яб­ре?

4. Цена на элек­три­че­ский чай­ник была по­вы­ше­на на 11 % и со­ста­ви­ла 2109 руб­лей. Сколь­ко руб­лей стоил чай­ник до по­вы­ше­ния цены?

5. Тет­радь стоит 10 руб­лей. Какое наи­боль­шее число таких тет­ра­дей можно будет ку­пить на 650 руб­лей после по­ни­же­ния цены на 20%?

6. Среди 40 000 жи­те­лей го­ро­да 60% не ин­те­ре­су­ет­ся фут­бо­лом. Среди фут­боль­ных бо­лель­щи­ков 80% смот­ре­ло по те­ле­ви­зо­ру финал Лиги чем­пи­о­нов. Сколь­ко жи­те­лей го­ро­да смот­ре­ло этот матч по те­ле­ви­зо­ру?

7. Фла­кон шам­пу­ня стоит 170 руб­лей. Какое наи­боль­шее число фла­ко­нов можно ку­пить на 1100 руб­лей во время рас­про­да­жи, когда скид­ка со­став­ля­ет 35%?

8. При опла­те услуг через пла­теж­ный тер­ми­нал взи­ма­ет­ся ко­мис­сия 8%. Тер­ми­нал при­ни­ма­ет суммы, крат­ные 10 руб­лям. Аня хочет по­ло­жить на счет сво­е­го мо­биль­но­го те­ле­фо­на не мень­ше 500 руб­лей. Какую ми­ни­маль­ную сумму она долж­на по­ло­жить в при­ем­ное устрой­ство дан­но­го тер­ми­на­ла?

9. Кли­ент взял в банке кре­дит 12000 руб­лей на год под 13% го­до­вых. Он дол­жен по­га­шать кре­дит, внося в банк еже­ме­сяч­но оди­на­ко­вую сумму денег, с тем чтобы через год вы­пла­тить всю сумму, взя­тую в кре­дит, вме­сте с про­цен­та­ми. Сколь­ко руб­лей он дол­жен вно­сить в банк еже­ме­сяч­но?

10. Товар на рас­про­да­же уце­ни­ли на 30%, при этом он стал сто­ить 350 руб­лей. Сколь­ко руб­лей стоил товар до рас­про­да­жи?

Вариант 4 3. Простейшие текстовые задачи (Проценты, округление)

1. Рост Джона 6 футов 1 дюйм. Вы­ра­зи­те рост Джона в сан­ти­мет­рах, если в 1 футе 12 дюй­мов, а в 1 дюйме 2,54 см. Ре­зуль­тат округ­ли­те до це­ло­го числа сан­ти­мет­ров.

2. При опла­те услуг через пла­теж­ный тер­ми­нал взи­ма­ет­ся ко­мис­сия 5%. Тер­ми­нал при­ни­ма­ет суммы крат­ные 10 руб­лям. Аня хочет по­ло­жить на счет сво­е­го мо­биль­но­го те­ле­фо­на не мень­ше 300 руб­лей. Какую ми­ни­маль­ную сумму она долж­на по­ло­жить в при­ем­ное устрой­ство дан­но­го тер­ми­на­ла?

3. Пло­щадь зе­мель фер­мер­ско­го хо­зяй­ства, отведённых под по­сад­ку сель­ско­хо­зяй­ствен­ных куль­тур, со­став­ля­ет 63 га и рас­пре­де­ле­на между зер­но­вы­ми и бах­че­вы­ми куль­ту­ра­ми в от­но­ше­нии 4:5 со­от­вет­ствен­но. Сколь­ко гек­та­ров за­ни­ма­ют бах­че­вые куль­ту­ры?

4. Фла­кон шам­пу­ня стоит 160 руб­лей. Какое наи­боль­шее число фла­ко­нов можно ку­пить на 1000 руб­лей во время рас­про­да­жи, когда скид­ка со­став­ля­ет 25% ?

5.В сен­тяб­ре 1 кг огур­цов стоил 50 руб­лей, в ок­тяб­ре огур­цы по­до­ро­жа­ли на 20%, а в но­яб­ре еще на 20%. Сколь­ко руб­лей стоил 1 кг огур­цов после по­до­ро­жа­ния в но­яб­ре?

6. Число по­се­ти­те­лей сайта уве­ли­чи­лось за месяц вчет­ве­ро. На сколь­ко про­цен­тов уве­ли­чи­лось число по­се­ти­те­лей сайта за этот месяц?

7.В го­ро­де N живет 1 500 000 жи­те­лей. Среди них 20% детей и под­рост­ков. Среди взрос­лых 35% не ра­бо­та­ет (пен­си­о­не­ры, сту­ден­ты, до­мо­хо­зяй­ки и т. п.). Сколь­ко взрос­лых жи­те­лей ра­бо­та­ет?

8. 14 вы­пуск­ни­ков школы со­би­ра­ют­ся учить­ся в тех­ни­че­ских вузах. Они со­став­ля­ют 28% от числа всех вы­пуск­ни­ков. Сколь­ко в школе вы­пуск­ни­ков?

9. Налог на до­хо­ды со­став­ля­ет 13% от за­ра­бот­ной платы. После удер­жа­ния на­ло­га на до­хо­ды Мария Кон­стан­ти­нов­на по­лу­чи­ла 13 050 руб­лей. Сколь­ко руб­лей со­став­ля­ет за­ра­бот­ная плата Марии Кон­стан­ти­нов­ны?

10. Еже­ме­сяч­ная плата за те­ле­фон со­став­ля­ет 240 руб­лей в месяц. В сле­ду­ю­щем года она уве­ли­чит­ся на 5%. Сколь­ко руб­лей будет со­став­лять еже­ме­сяч­ная плата за те­ле­фон в сле­ду­ю­щем году?

Вариант 5 3. Простейшие текстовые задачи (Проценты, округление)

1. В городе N живет 500000 жителей. Среди них 20% детей и подростков. Среди взрослых 25% не работает (пенсионеры, студенты, домохозяйки и т.п.). Сколько взрослых жителей работает?

2. При оплате услуг через платежный терминал взимается комиссия 5%. Терминал принимает суммы кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала?

3. Только 90% из 30000 вы­пуск­ни­ков го­ро­да пра­виль­но ре­ши­ли за­да­чу № 1. Сколь­ко вы­пуск­ни­ков из этого го­ро­да не­пра­виль­но ре­ши­ли за­да­чу № 1?

4. Ежемесячная плата за телефон составляет 250 рублей в месяц. В следующем году она увеличится на 4%. Сколько рублей будет составлять ежемесячная плата за телефон в следующем году?

5. Только 90% из 6000 выпускников города правильно решили задачу №2. Сколько выпускников из этого города правильно решили задачу №2?

6. Тетрадь стоит 7 рублей. Сколько рублей заплатит покупатель за 90 тетрадей, если при покупке больше 50 тетрадей магазин делает скидку 20% от стоимости всей покупки?

7. Тетрадь стоит 40 рублей. Какое наибольшее число таких тетрадей можно будет купить на 950 рублей после понижения цены на 25%?

8. Товар на распродаже уценили на 45%, при этом он стал стоить 110 рублей. Сколько рублей стоил товар до распродажи?

9. Налог на до­хо­ды со­став­ля­ет 13% от за­ра­бот­ной платы. За­ра­бот­ная плата Ивана Кузь­ми­ча равна 22 500 рублей. Какую сумму он по­лу­чит после упла­ты налогов? Ответ дайте в рублях.

10. В на­ча­ле года число або­нен­тов те­ле­фон­ной ком­па­нии «Юг» со­став­ля­ло 300 тыс. человек, а в конце года их стало 345 тыс. человек. На сколь­ко про­цен­тов уве­ли­чи­лось за год число або­нен­тов этой компании?

Вариант 6 3. Простейшие текстовые задачи (Проценты, округление)

1. В городе N живет 500000 жителей. Среди них 20% детей и подростков. Среди взрослых 25% не работает (пенсионеры, студенты, домохозяйки и т.п.). Сколько взрослых жителей работает?

2. Только 90% из 6000 выпускников города правильно решили задачу №2. Сколько выпускников из этого города правильно решили задачу №2?

3. В го­ро­де 180 000 жителей, при­чем 30% из них ― пенсионеры. Сколь­ко жи­те­лей этого го­ро­да не яв­ля­ют­ся пенсионерами?

4. При оплате услуг через платежный терминал взимается комиссия 5%. Терминал принимает суммы кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала?

5. Площадь зе­мель фер­мер­ско­го хозяйства, отведённых под по­сад­ку сель­ско­хо­зяй­ствен­ных культур, со­став­ля­ет 42 га и рас­пре­де­ле­на между зер­но­вы­ми и тех­ни­че­ски­ми куль­ту­ра­ми в от­но­ше­нии 3 : 4. Сколь­ко гек­та­ров за­ни­ма­ют тех­ни­че­ские культуры?

6. В ма­га­зи­не вся ме­бель продаётся в разо­бран­ном виде. По­ку­па­тель может за­ка­зать сбор­ку ме­бе­ли на дому, сто­и­мость ко­то­рой со­став­ля­ет 10 % от сто­и­мо­сти куп­лен­ной мебели. Шкаф стоит 3100 рублей. Во сколь­ко руб­лей обойдётся по­куп­ка этого шкафа вме­сте со сборкой?

7. Товар на распродаже уценили на 40%, при этом он стал стоить 810 рублей. Сколько рублей стоил товар до распродажи?

8. Налог на до­хо­ды со­став­ля­ет 13% от за­ра­бот­ной платы. За­ра­бот­ная плата Ивана Кузь­ми­ча равна 31 500 рублей. Какую сумму он по­лу­чит после упла­ты налогов? Ответ дайте в рублях.

9. Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена цена на футболку?

10. Городской бюд­жет составляет 82 млн рублей, а рас­хо­ды на одну из его ста­тей составили 15%. Сколь­ко миллионов руб­лей потрачено на эту ста­тью бюджета?

Вариант 7 3. Простейшие текстовые задачи (Проценты, округление)

1. Цена на электрический чайник была повышена на 25 % и составила 2625 рублей. Сколько рублей стоил чайник до повышения цены?

2. 70 выпускников школы собираются учиться в технических вузах. Они составляют 40% от числа выпускников. Сколько в школе выпускников?

3. Пачка сливочного масла стоит 66 рублей. Пенсионерам магазин делает скидку 5%. Сколько рублей заплатит пенсионер за пачку масла?

4. Число больных гриппом в школе уменьшилось за месяц в два раза. На сколько процентов уменьшилось число больных гриппом?

5. Только 70 % из 3000 выпускников города правильно решили задачу № 6. Сколько выпускников из этого города правильно решили задачу № 6?

6. В вы­бо­рах участ­во­ва­ли два кандидата. Го­ло­са из­би­ра­те­лей рас­пре­де­ли­лись между ними в от­но­ше­нии 3:2. Сколь­ко про­цен­тов го­ло­сов по­лу­чил проигравший?

7. Держатели дис­конт­ной карты книж­но­го ма­га­зи­на по­лу­ча­ют при по­куп­ке скид­ку 3%. Книга стоит 300 рублей. Сколь­ко руб­лей за­пла­тит дер­жа­тель дис­конт­ной карты за эту книгу?

8. Налог на до­хо­ды составляет 13 % от за­ра­бот­ной платы. После удер­жа­ния налога на до­хо­ды Мария Кон­стан­ти­нов­на получила 17 400 рублей. Сколь­ко рублей со­став­ля­ет заработная плата Марии Константиновны?

9. В школе 171 ученик изучал французский язык, что составляет 36% от числа всех учеников. Сколько учеников учится в школе?

10. В городе N живет 500000 жителей. Среди них 20% детей и подростков. Среди взрослых 25% не работает (пенсионеры, студенты, домохозяйки и т.п.). Сколько взрослых жителей работает?

Вариант 8 3. Простейшие текстовые задачи (Проценты, округление)

1. В ма­га­зи­не вся ме­бель продаётся в разо­бран­ном виде. По­ку­па­тель может за­ка­зать сбор­ку ме­бе­ли на дому, сто­и­мость ко­то­рой со­став­ля­ет 15 % от сто­и­мо­сти куп­лен­ной мебели. Шкаф стоит 3000 рублей. Во сколь­ко руб­лей обойдётся по­куп­ка этого шкафа вме­сте со сборкой?

2. Розничная цена учебника 180 рублей, она на 20% выше оптовой цены. Какое наибольшее число таких учебников можно купить по оптовой цене на 7900 рублей?

3. В вы­бо­рах участ­во­ва­ли два кандидата. Го­ло­са из­би­ра­те­лей рас­пре­де­ли­лись между ними в от­но­ше­нии 3:2. Сколь­ко про­цен­тов го­ло­сов по­лу­чил проигравший?

4. Клиент взял в банке кре­дит 12000 рублей на год под 13% годовых. Он дол­жен погашать кредит, внося в банк еже­ме­сяч­но одинаковую сумму денег, с тем чтобы через год вы­пла­тить всю сумму, взя­тую в кредит, вме­сте с процентами. Сколь­ко рублей он дол­жен вносить в банк ежемесячно?

5. Налог на до­хо­ды составляет 13 % от за­ра­бот­ной платы. После удер­жа­ния налога на до­хо­ды Мария Кон­стан­ти­нов­на получила 17 400 рублей. Сколь­ко рублей со­став­ля­ет заработная плата Марии Константиновны?

6. Ивану Кузь­ми­чу на­чис­ле­на за­ра­бот­ная плата 20 000 рублей. Из этой суммы вы­чи­та­ет­ся налог на до­хо­ды фи­зи­че­ских лиц в раз­ме­ре 13%. Сколь­ко руб­лей он по­лу­чит после упла­ты по­до­ход­но­го налога?

7. При опла­те услуг через пла­теж­ный тер­ми­нал взи­ма­ет­ся ко­мис­сия 8%. Тер­ми­нал при­ни­ма­ет суммы, крат­ные 10 рублям. Аня хочет по­ло­жить на счет сво­е­го мо­биль­но­го те­ле­фо­на не мень­ше 500 рублей. Какую ми­ни­маль­ную сумму она долж­на по­ло­жить в при­ем­ное устрой­ство дан­но­го терминала?

8. Магазин закупает цветочные горшки по оптовой цене 100 рублей за штуку и продает с наценкой 30%. Какое наибольшее число таких горшков можно купить в этом магазине на 1200 рублей?

9. Число хвойных деревьев в парке относится к числу лиственных как 9:16. Других деревьев в парке нет. Сколько процентов деревьев в парке составляют лиственные?

10. Шариковая ручка стоит 30 рублей. Какое наибольшее число таких ручек можно будет купить на 300 рублей после повышения цены на 25%?

Вариант 9 3. Простейшие текстовые задачи (Проценты, округление)

1. Товар на рас­про­да­же уце­ни­ли на 20%, при этом он стал сто­ить 940 р. Сколь­ко руб­лей стоил товар до распродажи?

2. Студент получил свой первый гонорар в размере 700 рублей за выполненный перевод. Он решил на все полученные деньги купить букет тюльпанов для своей учительницы английского языка. Какое наибольшее количество тюльпанов сможет купить студент, если удержанный у него налог на доходы составляет 13% гонорара, тюльпаны стоят 60 рублей за штуку и букет должен состоять из нечетного числа цветов?

3. Студент получил свой первый гонорар в размере 800 рублей за выполненный перевод. Он решил на все полученные деньги купить букет роз для своей учительницы английского языка. Какое наибольшее количество роз сможет купить студент, если удержанный у него налог на доходы составляет 13% гонорара, розы стоят 100 рублей за штуку и букет должен состоять из нечетного числа цветов?

4. Городской бюд­жет составляет 82 млн рублей, а рас­хо­ды на одну из его ста­тей составили 15%. Сколь­ко миллионов руб­лей потрачено на эту ста­тью бюджета?

5. Площадь земель фермерского хозяйства, отведённых под посадку сельскохозяйственных культур, составляет 42 гектара и распределена между зерновыми и техническими культурами в отношении 3 : 4 соответственно. Сколько гектаров занимают технические культуры?

6. Призёрами городской олимпиады по математике стали 25 учащихся, что составило 5% от числа участников. Сколько человек участвовало в олимпиаде?

7. В сентябре 1 кг винограда стоил 90 рублей, в октябре виноград подорожал на 20%, а в ноябре ещё на 25%. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?

8. Футболка сто­и­ла 500 рублей. После сни­же­ния цены она стала сто­ить 390 рублей. На сколь­ко про­цен­тов была сни­же­на цена на футболку?

9. В начале учебного года в школе было 600 учащихся, а к концу года их стало 630. На сколько процентов увеличилось за учебный год число учащихся?

10. Клиент взял в банке кредит 60 000 рублей на год под 17% годовых. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?

Вариант 10 3. Простейшие текстовые задачи (Проценты, округление)

1. Призёрами городской олимпиады по математике стали 99 учеников, что составило 9% от числа участников. Сколько человек участвовало в олимпиаде?

2. Держатели дисконтной карты книжного магазина получают при покупке скидку 5%. Книга стоит 200 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?

3. Только 80 % из 2500 выпускников города правильно решили задачу № 1. Сколько выпускников из этого города правильно решили задачу № 1?

4. В начале учебного года в школе было 600 учащихся, а к концу года их стало 630. На сколько процентов увеличилось за учебный год число учащихся?

5. Налог на до­хо­ды со­став­ля­ет 13% от за­ра­бот­ной платы. После удер­жа­ния на­ло­га на до­хо­ды Мария Кон­стан­ти­нов­на по­лу­чи­ла 6960 рублей. Сколь­ко руб­лей со­став­ля­ет за­ра­бот­ная плата Марии Константиновны?

6. В школе фран­цуз­ский язык изу­ча­ют 99 учащихся, что со­став­ля­ет 33 % от числа всех уча­щих­ся школы. Сколь­ко уча­щих­ся в школе?

7. Товар на рас­про­да­же уце­ни­ли на 30%, при этом он стал сто­ить 350 рублей. Сколь­ко руб­лей стоил товар до распродажи?

8. При опла­те услуг через пла­теж­ный тер­ми­нал взи­ма­ет­ся ко­мис­сия 8%. Тер­ми­нал при­ни­ма­ет суммы, крат­ные 10 рублям. Аня хочет по­ло­жить на счет сво­е­го мо­биль­но­го те­ле­фо­на не мень­ше 500 рублей. Какую ми­ни­маль­ную сумму она долж­на по­ло­жить в при­ем­ное устрой­ство дан­но­го терминала?

9. На пост пред­се­да­те­ля школь­но­го со­ве­та пре­тен­до­ва­ли два кандидата. В го­ло­со­ва­нии при­ня­ли уча­стие 189 человек. Го­ло­са между кан­ди­да­та­ми рас­пре­де­ли­лись в от­но­ше­нии 2:7. Сколь­ко го­ло­сов по­лу­чил победитель?

10. В выборах участвовали два кандидата. Голоса избирателей распределились между ними в отношении 3:2. Сколько процентов голосов получил проигравший?

3. Простейшие текстовые задачи (Проценты, округление)
Вариант 1 318 14000 320 2100 5 19575 17400 66 2000 10	Вариант 2 81 318  400 1296 15  20 3190  10 17400 52	Вариант 3 6 25850 72 1900 81 12800 9 550 1130 500	Вариант 4 185 320 35 8 72 300 780000 50 15000 252	Вариант 5 300000 320 3000 260 5400 504 31 200 19575 15
Вариант 6 300000 5400 126000 320 24 3410 1350 27405 15 12,3	Вариант7 2100 175 62,7 50 2100 40 291 20000 475 10.300000	Вариант 8 3450 52 40 1130 20000 17400 550 9 64 8	Вариант 9 1175 9 5 12,3 24 500 135 22 5 5850	Вариант 10 1100 190 2000 5 8000 300 500 550 147 40