Как решать задачи с часами егэ математика - Помощь в подготовке к экзаменам и поступлению

Часы со стрелками показывают 4 часа 45 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

Часы со стрелками показывают 6 часов 35 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Часы со стрелками показывают 1 час 35 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

Часы со стрелками показывают 11 часов 20 минут. Через сколько минут минутная стрелка в первый раз поравняется с часовой?

Часы со стрелками показывают 6 часов 45 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Часы со стрелками показывают 2 часа ровно. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 8 часов 20 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Часы со стрелками показывают 2 часа 5 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 1 час 55 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 8 часов ровно. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Часы со стрелками показывают 2 часа 25 минут. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

Часы со стрелками показывают 3 часа 10 минут. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

Часы со стрелками показывают 3 часа 25 минут. Через сколько минут минутная стрелка в восьмой раз поравняется с часовой?

Часы со стрелками показывают 4 часа 5 минут. Через сколько минут минутная стрелка в восьмой раз поравняется с часовой?

Часы со стрелками показывают 7 часов 5 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Часы со стрелками показывают 5 часов 45 минут. Через сколько минут минутная стрелка в шестой раз поравняется с часовой?

Часы со стрелками показывают 8 часов 50 минут. Через сколько минут минутная стрелка в третий раз поравняется с часовой?

Часы со стрелками показывают 1 час 25 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 11 часов 55 минут. Через сколько минут минутная стрелка в первый раз поравняется с часовой?

Часы со стрелками показывают 1 час 30 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 1 час 40 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 4 часа 40 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

Часы со стрелками показывают 4 часа 35 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

Часы со стрелками показывают 7 часов 20 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Часы со стрелками показывают 9 часов 15 минут. Через сколько минут минутная стрелка в третий раз поравняется с часовой?

Часы со стрелками показывают 3 часа 30 минут. Через сколько минут минутная стрелка в восьмой раз поравняется с часовой?

Часы со стрелками показывают 2 часа 40 минут. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

Часы со стрелками показывают 2 часа 50 минут. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

Часы со стрелками показывают 9 часов 45 минут. Через сколько минут минутная стрелка в третий раз поравняется с часовой?

Часы со стрелками показывают 7 часов 40 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Часы со стрелками показывают 6 часов 10 минут. Через сколько минут минутная стрелка в шестой раз поравняется с часовой?

Часы со стрелками показывают 4 часа 25 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

Часы со стрелками показывают 10 часов ровно. Через сколько минут минутная стрелка в второй раз поравняется с часовой?

Часы со стрелками показывают 9 часов 30 минут. Через сколько минут минутная стрелка в третий раз поравняется с часовой?

Часы со стрелками показывают 8 часов 35 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Часы со стрелками показывают 10 часов 20 минут. Через сколько минут минутная стрелка в второй раз поравняется с часовой?

Часы со стрелками показывают 4 часа 15 минут. Через сколько минут минутная стрелка в восьмой раз поравняется с часовой?

Часы со стрелками показывают 5 часов 25 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

Часы со стрелками показывают 7 часов 15 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Часы со стрелками показывают 5 часов 5 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

Часы со стрелками показывают 5 часов 30 минут. Через сколько минут минутная стрелка в шестой раз поравняется с часовой?

Часы со стрелками показывают 6 часов ровно. Через сколько минут минутная стрелка в шестой раз поравняется с часовой?

Часы со стрелками показывают 8 часов 5 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Часы со стрелками показывают 10 часов 15 минут. Через сколько минут минутная стрелка в второй раз поравняется с часовой?

Часы со стрелками показывают 6 часов 55 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Часы со стрелками показывают 1 час ровно. Через сколько минут минутная стрелка в одиннадцатый раз поравняется с часовой?

Часы со стрелками показывают 6 часов 15 минут. Через сколько минут минутная стрелка в шестой раз поравняется с часовой?

Часы со стрелками показывают 1 час 45 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 10 часов 25 минут. Через сколько минут минутная стрелка в второй раз поравняется с часовой?

Часы со стрелками показывают 6 часов 5 минут. Через сколько минут минутная стрелка в шестой раз поравняется с часовой?

Часы со стрелками показывают 4 часа 10 минут. Через сколько минут минутная стрелка в восьмой раз поравняется с часовой?

Часы со стрелками показывают 8 часов 15 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Часы со стрелками показывают 11 часов 30 минут. Через сколько минут минутная стрелка в первый раз поравняется с часовой?

Часы со стрелками показывают 2 часа 10 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Часы со стрелками показывают 8 часов 30 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Часы со стрелками показывают 7 часов 25 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Часы со стрелками показывают 6 часов 30 минут. Через сколько минут минутная стрелка в шестой раз поравняется с часовой?

Часы со стрелками показывают 2 часа 55 минут. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

Часы со стрелками показывают 5 часов 10 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

Часы со стрелками показывают 5 часов 35 минут. Через сколько минут минутная стрелка в шестой раз поравняется с часовой?

Часы со стрелками показывают 11 часов 50 минут. Через сколько минут минутная стрелка в первый раз поравняется с часовой?

Часы со стрелками показывают 2 часа 35 минут. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

Часы со стрелками показывают 7 часов 50 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Часы со стрелками показывают 6 часов 40 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Часы со стрелками показывают 5 часов ровно. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

Источник

18
Апр 2012

08 Задание (2022)ТЕКСТОВЫЕ ЗАДАЧИ

Задача про стрелки часов. Задание 11

1. Задание 11 (№ 99600)

Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Эта задача ничуть не сложнее, чем задача на движение по кругу. У нас по кругу движутся часовая и минутная стрелки. Минутная стрелка за час проходит полный круг, то есть 360°. Значит, ее скорость равна 360° в час. Часовая стрелка за час проходит угол 30° ( это угол между двумя соседними числами на циферблате). Значит, ее скорость 30° в час.

В 8 часов 00 минут расстояние между стрелками составляет 240°:

360°t-30°t=240°

t=240°/330°=8/11

То есть через 8/11 часа стрелки первый раз встретятся.

Теперь до следующей встречи минутная стрелка пройдет на 360° больше, чем часовая. Пусть это произойдет через х часов.

Получим уравнение:

360°х-30°х=360°. Отсюда х=12/11. И так еще два раза.

Получаем, что минутная стрелка в четвертый раз поравняется с часовой через 8/11+12/11+12/11+12/11= 4 часа= 240 мин.

Ответ: 240 мин.

2. Задание 11 (№ 114773). Часы со стрелками показывают 1 час 35 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

В этой задаче скорость движения стрелок будем выражать в градусах/минуту.

Скорость минутной стрелки равна 360˚/60=6˚ в минуту.

Скорость часовой стрелки равна 30˚/60=0,5˚ в минуту.

В 0 часов положение часовой и минутной стрелок совпадало. 1 час 35 минут — это 95 минут. За это время минутная стрелка прошла 95х6=570˚=360˚+210˚, а часовая прошла 95×0,5˚=47,5˚. И у нас такая картинка:

Первый раз стрелки встретятся через время t_1 , когда часовая стрелка повернется на $0,5{t_1}^{circ}$ , а минутная на 150˚+47,5˚ больше. Получаем уравнение для t_1 :

$150^{circ}+47,5^{circ}+0,5{t_1}=6t_1$

Отсюда $t_1={395^{circ}}/{11}$

Следующий раз стрелки встретятся, когда минутная пройдет на круг больше часовой: $6t_2-0,5t_2=360^{circ}$

$t_2={360^{circ}}/{5,5}={720^{circ}}/{11}$

И так 9 раз.

Минутная стрелка в десятый раз поравняется с часовой через $t_1+9t_2={395^{circ}}/{11}+9{720^{circ}}/{11}={6875^{circ}}/{11}=625$ минут

Ответ: 625

И.В. Фельдман, репетитор по математике.

Для вас другие записи этой рубрики:

Текстовая задача. ДВИ МГУ 2016
Видеолекция «Решение текстовых задач на движение по кругу и воде»
Задача про вклады. Задание В14 (2014) (Диагностическая работа 24 сентября)
Задача на проценты. Пакеты акций. Задание 19
Видеолекция «Решение текстовых задач на работу и прогрессии»
Видеолекция «Решение текстовых задач на движение по прямой»

Источник

17 января 2011

Самая первая, но не всегда самая простая задача ЕГЭ. Основная тема — это применение навыков счета в повседневной жизни. Алгебра и ничего кроме алгебры. Задачи B1 всегда относятся к одной из трех категорий:

Расчет времени по часам,
Задачи на проценты,
Поиск максимально или минимально возможного значения.

Зачем вообще нужны эти категории? Дело в том, что для каждой из них существует быстрый, универсальный, а главное простой способ решения. Чуть позже мы обязательно рассмотрим эти способы, а пока главное — научиться выделять категории.

Задача. Магазин открывается в 10 часов утра, а закрывается в 10 часов вечера. Обеденный перерыв длится с 15 до 16 часов. Сколько часов в день открыт магазин?

Очевидно, перед нами задача на расчет времени по часам.

Задача. Сырок стоит 5 рублей 80 копеек. Какое наибольшее число сырков можно купить на 60 рублей?

Это задача третьей категории (поиск максимального значения).

Задача. Стоимость покупки с учетом 7-процентной скидки по дисконтной карте составила 3720 рублей. Сколько рублей пришлось бы заплатить за покупку при отсутствии дисконтной карты?

Это задача на проценты — вторая категория.

Бывают сложные задачи, где присутствуют сразу две категории. Например, задачи на проценты с дальнейшим поиском максимально или минимально возможного значения. Такие задачи разбиваются на два независимых шага, каждый из которых решается отдельно.

Расчет времени по часам

В первую очередь переводим все время в 24-часовой формат, если это еще не сделано в самой задаче. Для этого достаточно добавить 12 часов ко всем значениям, которые даны после полудня.

Затем чертим «cтрелу времени». Это обычная координатная ось. Ее длину и единичный отрезок подбираем так, чтобы поместилось 24 деления. Это будут 24 часа — достаточно, чтобы решить любую задачу этой категории.

Задача. Перевести в 24-формат время: 8:30 утра, 10 часов вечера, 1 час дня, 17:30

8:30 утра — это просто 8:30. Ничего не изменилось, т.к. время указано до полудня.
10 часов вечера — это 10 + 12 = 22:00.
1 час дня — это 1 + 12 = 13:00.
17:30 — так и остается 17:30, т.к. время уже в 24-часовом формате.

Задача. Поезд «Санкт-Петербург — Нижний Новгород» отправляется в 17:30, а прибывает в 8:30 на следующее утро. Сколько часов поезд находится в пути?

Начертим стрелу времени и отметим часы, начиная с 17:00:

Далее считаем число целых отрезков. Еще один целый отрезок получится, если объединить две половинки в начале и конце стрелы. Итого, поезд находится в пути 14 + 1 = 15 часов.

Задачи на проценты

Как правило, в таких задачах обыгрывается реальная жизненная ситуация. В них обязательно описывается величина, которая затем увеличивается или уменьшается на несколько процентов. При этом требуется найти либо конечное значение величины, либо начальное. Изредка встречаются задачи, где указано начальное и конечное значение, а требуется найти проценты.

Как решать такие задачи? Пусть x_{начальное} — исходное значение рассматриваемой величины, x_{конечное} — конечное значение, k — изменение в процентах. Тогда справедлива формула:

Перед переменной k ставится знак «плюс», если величина возрастает, либо «минус» — если убывает. Все задачи на проценты составлены так, что в этой формуле неизвестна лишь одна величина — ее и требуется найти, решив линейное уравнение.

Задача. До снижения цен книга стоила 800 рублей, а после снижения стала стоить 680 рублей. На сколько процентов была снижена цена книги?

Очевидно, x_{начальное} = 800, x_{конечное} = 680. По условию, цена книги снижается, поэтому имеем:

Задача. После повышения цен на 16% килограмм рыбы стал стоить 696 рублей. Сколько рублей стоила рыба до повышения цены?

По условию, цена рыбы повышается, причем x_{конечное} = 696, k = 16. Подставляем в формулу:

Задача. Фирма закупает у поставщика мобильные телефоны по 9000 рублей, а продает с наценкой 40%. Сколько придется заплатить конечному покупателю?

Начальная цена x_{начальное} = 9000, она повышается, причем k = 40. Получаем:

Поиск максимально или минимально возможного значения

Такие задачи встречаются очень часто, и они всегда связаны с округлением числа в большую или меньшую сторону. Не имеет значения, о чем идет речь в задаче, главное помнить следующее правило.

Чтобы найти максимально возможное значение, числа округляются в меньшую сторону. Для нахождения минимально возможного значения, наоборот, округляем в большую сторону.

Многие, кто впервые слышат это правило, удивленно спрашивают: «И это все?» Да, все. Достаточно определить, что именно требуется найти — и решение станет очевидным. В задаче B1 нет и не может быть сложных математических выкладок.

Задача. Из летнего лагеря уезжают 208 детей и 23 надзирателя. В автобусах 44 посадочных места. Какое наименьшее количество автобусов нужно вызвать, чтобы отвезти всех домой?

Из фразы «какое наименьшее количество» следует, что мы ищем минимально возможное значение, т.е. округлять будем в большую сторону. Всего нужно 208 + 23 = 231 посадочных мест, т.е. 231 : 44 = 5,25 автобусов. Округляем в большую сторону — получаем 6 автобусов.

Задача. В супермаркете проходит рекламная акция: покупая две шоколадки, покупатель получает третью шоколадку в подарок. Шоколадка стоит 32 рубля. Какое наибольшее число шоколадок можно получить за 250 рублей?

Очевидно, требуется найти наибольшее значение, т.е. округляем все числа в меньшую сторону.

Для начала выясним, сколько шоколадок можно купить на 250 рублей без учета рекламной акции: 250 : 32 = 7,8125. Округляем в меньшую сторону — получаем 7 шоколадок.

Теперь выясним, сколько шоколадок можно получить дополнительно. Т.к. за каждые две шоколадки получаем одну в подарок, всего будет 7 : 2 = 3,5, т.е. 3 шоколадки.

Наконец, находим общее число шоколадок: 7 + 3 = 10.

Задача. Бумага продается в пачках по 500 листов. За неделю в офисе расходуется 1400 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 4 недели?

По условию, требуется найти наименьшее значение, поэтому округляем в большую сторону.

Выясним, сколько листов бумаги расходуется за 4 недели: 1400 · 4 = 5600. В каждой пачке 500 листов, т.е. потребуется 5600 : 500 = 11,2 пачки. Округляем в большую сторону — получаем 12.

Комбинированные и нестандартные задачи

Бывает, в одной задаче объединены сразу две категории. Кроме того, в задачу могут вводиться дополнительные условия. Такие задачи вызывают наибольшие трудности.

Для решения сначала надо разбить условие на две части — каждая из своей категории. А затем решить эти части как отдельные задачи. Как правило, результаты первой части станут исходными данными для второй.

Задача. Ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 300 рублей после повышения цены на 20%?

Сначала найдем цену новой ручки (задача на проценты), а затем найдем количество ручек (поиск максимального значения).

По условию, цена ручки повышается, причем x_{начальное} = 40, k = 20. Находим x_{конечное}:

Итак, теперь ручка стоит 48 рублей. Тогда, имея 300 рублей, мы можем купить 300 : 48 = 6,25 ручек. Т.к. требуется найти наибольшее значение, округляем в меньшую сторону и поiлучаем 6 ручек.

Задача. Хозяин овощной лавки купил на оптовом рынке 100 кг помидоров и заплатил 4000 рублей. А затем начал продавать их по 100 рублей за килограмм. При этом оказалось, что 15% помидоров испортились, поэтому хозяин не смог их продать. Какую прибыль он получил?

Это задача на проценты с дополнительным требованием. Важно понимать, что прибыль — это разность между доходами и расходами.

Сначала найдем, сколько килограмм помидоров было продано. Очевидно, x_{начальное} = 100, k = 15, при этом величина уменьшается. Имеем:

По условию, цена продажи составила 100 рублей за 1 кг, поэтому доход составил 85 · 100 = 8500 рублей. С учетом расходов, хозяин получил прибыль 8500 − 4000 = 4500 рублей.

Смотрите также:

Решение задач B1: № 1—16
Решение задач B1: №17—32
Введение системы координат
Площадь круга
C2: расстояние между двумя прямыми
ЕГЭ-2014 по математике и открытый банк задач

Источник

ЕГЭ. Задача про часы

Движение по окружности

№ 1 . Часы со стрелками показывают 8 часов ровно. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

x д

Часовая

1 д/ч

равны

) д

Минутн.

12 д/ч

Составим и решим уравнение

Ответ: 240 .

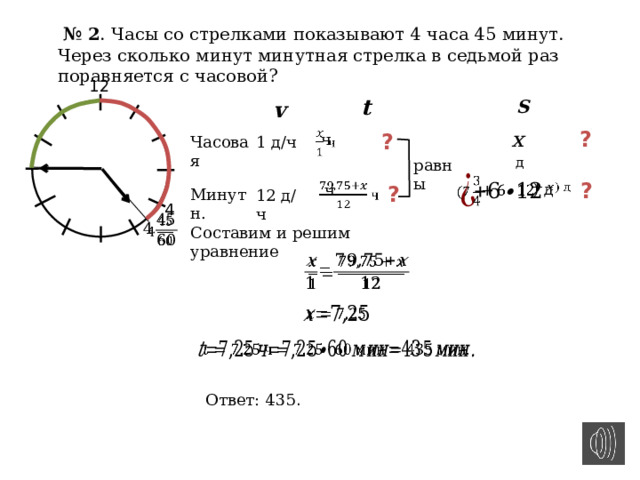
№ 2 . Часы со стрелками показывают 4 часа 45 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

x д

Часовая

1 д/ч

равны

) д

Минутн.

12 д/ч

Составим и решим уравнение

Ответ: 435 .

Задачи для самостоятельного решения

1. Часы со стрелками показывают 6 часов 35 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

2. Часы со стрелками показывают 1 час 35 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

3. Часы со стрелками показывают 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

4. Часы со стрелками показывают 11 часов 20 минут. Через сколько минут минутная стрелка в первый раз поравняется с часовой?

5. Часы со стрелками показывают 6 часов 45 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

6. Часы со стрелками показывают 2 часа ровно. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

7. Часы со стрелками показывают 8 часов 20 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

8. Часы со стрелками показывают 2 часа 5 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

9. Часы со стрелками показывают 1 час 55 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

10. Часы со стрелками показывают 8 часов ровно. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Жми звёздочку, чтобы посмотреть ответ

Ответы:

№ /п

Ответ

325

625

540

315

600

220

605

240

Жми звёздочку, чтобы вернуться к задачам

Источник

Разбираем задачи В13. Речь пойдёт о задачах про стрелки часов. Это тоже движение по кругу. И принципы решения те же самые.

Вот пример простейшей задачи:

1. Часы со стрелками показывают 11 часов 20 минут. Через сколько минут минутная стрелка в первый раз поравняется с часовой?

Ответ очевиден, через 40 минут, когда будет ровно двенадцать. Даже если сразу не смогли понять, то нарисовав циферблат (сделав эскиз) на листке, вы без труда определите ответ.

Ответ: 40

2. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Это, пожалуй, самая сложная задача из вариантов ЕГЭ про циферблат. Но…
Эта задача ничуть не сложнее, чем задача на движение по кругу. У нас по кругу движутся часовая и минутная стрелки. Минутная стрелка за час проходит полный круг, то есть 360°. Значит, ее скорость равна 360° в час. Часовая стрелка за час проходит угол 30° ( это угол между двумя соседними числами на циферблате). Значит, ее скорость 30° в час.

В 8 часов 00 минут расстояние между

стрелками составляет 240°:

Пусть минутная стрелка в первый раз встретится с часовой через t часов. За это время минутная стрелка пройдет 360°t, а часовая 30°t, причем минутная пройдет на 240° больше, чем часовая. Получим уравнение:

360°t-30°t=240°

t=240°/330°=8/11

То есть через 8/11 часа стрелки первый раз встретятся.

Теперь до следующей встречи минутная стрелка пройдет на 360° больше, чем часовая. Пусть это произойдет через х часов.

Получим уравнение:

360°х-30°х=360°. Отсюда х=12/11. И так еще два раза.

Получаем, что минутная стрелка в четвертый раз поравняется с часовой через 8/11+12/11+12/11+12/11= 4 часа= 240 мин.

Ответ: 240 мин.

Конечно, есть простое решение — взять часы со стрелками и убедиться, что в четвертый раз стрелки поравняются через 4 часа, ровно в 12.00.
А как быть, если у вас электронные часы и вы не можете решить задачу экспериментально?

За один час минутная стрелка проходит один круг, а часовая 1/12 часть круга. Пусть их скорости равны 1 (круг в час) и 1/12 (круга в час). Старт — в 8.00. Найдем время, за которое минутная стрелка в первый раз догонит часовую.

Минутная стрелка пройдет на 2/3 круга больше, поэтому уравнение будет таким:

(1 — 1/12)x = 2/3

Решив его, получим, что x = 8./11 часа. Итак, в первый раз стрелки поравняются через 8/11 часа. Пусть во второй раз они поравняются через время z. Минутная стрелка пройдет расстояние 1 * z, а часовая 1/12 z, причем минутная стрелка пройдет на один круг больше. Запишем уравнение:

Решив его, получим, что z = 12/11 часа. Итак, через 12/11 часа стрелки поравняются во второй раз, еще через 12/11 часа — в третий, и еще через 12/11 часа — в четвертый.

Значит, если старт был в 8.00, то в четвертый раз стрелки поравняются через

Ответ полностью согласуется с «экспериментальным» решением!

Ответ: 240

Вы убедились, что запутаться очень легко?

СОВЕТЫ БЫВАЛОГО:

На ЕГЭ с такой задачей можно легко запутаться, вычислить неверно или просто потерять много времени на решение.

Вы можете решить данную задачу за одну минуту. Как? Просто!

Возьмите с собой на ЕГЭ механические часы со стрелками… Догадались?

Если вам попадёт такая задача, то берёте часы, ставите исходное время оговоренное в условии (например, 8.00) и прокручиваете заданное число раз. А затем смотрите: сколько «отмотали» минут от исходного времени. Вот и всё.

3. Часы со стрелками показывают 1 час 35 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

В этой задаче скорость движения стрелок будем выражать в градусах/минуту.

Скорость минутной стрелки равна 360˚/60=6˚ в минуту.

Скорость часовой стрелки равна 30˚/60=0,5˚ в минуту. В 0 часов положение часовой и минутной стрелок совпадало. 1 час 35 минут — это 95 минут. За это время минутная стрелка прошла 95х6=570˚=360˚+210˚, а часовая прошла 95×0,5˚=47,5˚.

Первый раз стрелки встретятся через время t1, когда часовая стрелка повернется на 0,5t1, а минутная на 150˚+47,5˚ больше. Получаем уравнение для t1:

Отсюда

Следующий раз стрелки встретятся, когда минутная пройдет на круг больше часовой:

И так 9 раз.

Минутная стрелка в десятый раз поравняется с часовой через 625 минут

Ответ: 625

Источник

28 января 2022

В закладки

Обсудить

Жалоба

Движение по окружности.

m8dvi.pptx
m8dvi.pdf

10. Часы со стрелками показывают 8 часов ровно. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Ответы

1) 325
2) 625
3) 540
4) 40
5) 315
6) 600
7) 220
2
9) 605
10) 240

Автор: Бабошкина Любовь Юрьевна.

Источник

В этой публикации рассмотрим задачу: в условии говорится о движении стрелок часов. Это задача на движение. Рассмотрим разные подходы к решению, будет и такой, при применении которого такие задания будете решать не более чем за одну минуту. Приступим! Алгебраический подход к решению:

zadacha

99600. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

За один час минутная стрелка проходит один круг, то есть скорость хода стрелки будет ОДИН круг в час. Часовая за час проходит 1/12 круга, то есть её скорость будет 1/12 круга в час. Обозначим время которое идут стрелки переменной «t».

Тогда до встречи стрелки пройдут:

*В данном случае у нас роль расстояния играет круг циферблата .

Отставание минутной от часовой составляло 8 часов – это 2/3 круга. То есть получается, что разность между пройденными «расстояниями» составляет 2/3.

*Если вам удобнее занести данные в таблицу, то:

Можем записать:

Итак, в первый раз стрелки пересекутся через 8/11 часа.

Пусть во второй раз они пересекутся через время z. Минутная стрелка пройдет расстояние 1∙z, а часовая (1/12)∙z, причем минутная стрелка пройдет на один круг больше. Запишем уравнение:

Значит через 12/11 часа стрелки пересекутся во второй раз, еще через 12/11 часа — в третий, и еще через 12/11 часа — в четвертый.

Значит если старт был в 8.00, то в четвертый раз стрелки пересекутся через:

Ответ: 240

*Если развита интуиция и логическое мышление, то ответ в данной задаче можно дать сразу по прочтении условия. Смотрите: первый раз стрелки пересекутся в девятом часу, второй раз в десятом, третий в одиннадцатом, а четвёртый ровно в двенадцать, то есть через 4 часа (240 минут).

zadacha

Ещё задача. Часы со стрелками показывают 4 часа 45 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой?

Отставание минутной от часовой составляло 7 часов 45 минут, то есть 7 плюс ¾ часа. Переведём в часть круга. Воспользуемся пропорцией:

По аналогии с предыдущей задачей:

Итак, в первый раз стрелки пересекутся через 31/44 часа.

Пусть во второй раз они пересекутся через время z, тогда:

Значит через 12/11 часа стрелки пересекутся во второй раз, еще через 12/11 часа — в третий и так далее … Значит если старт был в 4:45, то в седьмой раз стрелки пересекутся через:

В минутах это 7∙60+15=435.

Ответ: 435.

Небольшой итог! При решении необходимо:

— определить отставание минутной стрелки от часовой в частях круга,

— далее вычислить через какое время стрелки пересекутся в первый раз,

— затем определить время пересечения стрелок во второй и последующие разы (его можно просто запомнить 12/11 часа – это время через которое стрелки встречаются «от пресечения до пересечения»),

— далее вычислить общее время.

Но! Теперь СПЕЦ-совет для решения такой задачи на самом экзамене. Ведь не секрет, что время имеет большую ценность и разбрасываться им на экзамене просто преступно ))).

Способ второй (простая логика)! Решаем за минуту!

Давайте разберём предыдущую задачу. Время 4 часа 45 минут.

Первый раз стрелки пересекутся между пятью и шестью часами, то есть в шестом часу, второй в седьмом часу, третий раз в восьмом, четвёртый в девятом, пятый в десятом, шестой в одиннадцатом, седьмой в 12 часов.

То есть времени пройдёт 7 часов 15 минут, 7∙60+15=435.

Таким образом, просто загибая пальцы на руке вы решаете задачу за одну минуту без лишних вычислений.

Теперь ряд задач на часы со стрелками для отработки.

zadacha

На часах 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?

Время 3 часа. Первый раз стрелки пересекутся в четвёртом часу, второй в пятом часу, третий раз в шестом, четвёртый в седьмом, пятый в восьмом, шестой в девятом, седьмой в десятом, восьмой в одиннадцатом, девятый в 12 часов.

То есть пройдёт 9 часов, 9∙60=540 минут.

zadacha

Время 11 часов 40 минут. Через сколько минут минутная стрелка в первый раз поравняется с часовой?

Первый раз стрелки пересекутся 12 часов, то есть через 20 минут.

zadacha

Время 6 часов 45 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

Первый раз стрелки пересекутся в восьмом часу, второй в девятом, третий раз в десятом, четвёртый в одиннадцатом в 12 часов.

То есть времени пройдёт от 6:45 до 12 пройдёт 5 часов 15 минут, 5∙60+15=315 минут.

zadacha

Время 6 часов 35 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

То есть времени пройдёт от 6:35 до 12 пройдёт 5 часов 25 минут, 5∙60+25=325 минут.

zadacha

Время 2 часа ровно. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Первый раз стрелки пересекутся в третьем часу, …. , десятый в 12 часов.

То есть времени пройдёт 10 часов, 10∙60=600 минут.

zadacha

Время 8 часов 20 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Первый раз стрелки пересекутся в девятом часу, второй в десятом, третий раз в одиннадцатом, четвёртый в 12 часов.

То есть времени от 8:20 до 12 пройдёт 3 часов 40 минут, 3∙60+40=220 минут.

zadacha

Время 2 часа 5 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

Первый раз стрелки пересекутся в третьем часу, …. , десятый в 12 часов.

То есть пройдёт 9 часов 55 минут, 9∙60+55=595 минут.

Ответ: 595

Как видите, такие задачи можно решать устно. Заметили что все они составлены таким образом, что последнее пересечение стрелок попадает на 12:00? Иначе в ответе нельзя получить целое число или конечную десятичную дробь (это требование и условие для задач экзамена). Только через следующие 12 часов (это ещё плюс 11 пересечений).

На этом всё!

С уважением, Александр.

*Делитесь информацией в социальных сетях

Источник