1
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 82 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
2
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 16 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
3
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 14 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
4
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 36 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
5
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 6 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
6
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 12 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
7
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 40 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
8
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 62 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
9
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 52 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
10
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 56 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
11
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 76 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
12
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 44 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
13
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 72 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
14
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 86 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
15
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 96 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
16
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 2 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
17
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 90 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
18
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 92 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
19
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 32 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
20
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 22 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
21
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 20 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
22
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 68 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
23
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 100 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
24
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 18 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
25
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 88 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
26
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 94 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
27
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 24 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
28
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 12 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
29
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 12 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
В текстовых задачах на ЕГЭ по математике профильного уровня встречаются задачи про виноград и изюм(и похожие на них). Изучив данную статью вы научитесь решать задачи такого типа: “Изюм получается в процессе сушки винограда. Виноград содержит ( n% ) влаги, а изюм ( p% ).Сколько килограммов винограда требуется для получения ( k ) килограммов изюма?”. В данных задачах ( p, n, k ) — это произвольные числа. Такие задачи относятся к разделу “задачи на концентрацию, смеси и сплавы”.
Чем характерны задачи на ЕГЭ по математике:
- Из одного объекта получается другой путем высушивания. Например:
- Сушеных грибы получаются из спелых
- Из абрикосов получают урюк
- Сухари – из хлеба
- Из вишни получают сушеную вишню и т.п.
- Известно процентное содержание влаги обоих объектов (например, в винограде содержится 85% ваги, в изюме 7% влаги)
- Известна масса одного из объектов. Либо масса того, что получится в итоге, либо масса того, из чего получим второй объект.
Смысл решения текстовых задач на смеси
Рассмотри классическую текстовую задачу про виноград и изюм на ЕГЭ по математике. Изюм получается из винограда в процессе сушки. Содержание винограда, как и изюма, состоит из какого-то количества влаги (жидкости, воды) и сухого вещества (косточки, кожура и т.п.). В процессе сушки испаряется вода, значит уменьшается масса влаги, а что остается постоянным всегда? Правильно, сухое вещество. На него процесс выпаривания или сушки не оказывает влияния. Поэтому, мы можем выяснить массу сухого вещества в винограде, затем массу сухого вещества в изюме и приравнять их.
Как вычислить массу сухого вещества?
В текстовых задачах про изюм и виноград мы можем выясним, сколько сухого вещества в объекте. Например, в винограде содержится 95% влаги, отсюда мы запросто вычисляем сколько составляет процентное содержание сухого вещества: 100-95=5%. Далее, по задаче, например, известно, что дано 21 кг винограда, тогда масса сухого вещества в этом винограде: ( 21cdotdfrac{5}{100} ) кг. Если нам неизвестно, сколько килограммов, то обозначаем массу за ( x ) и получим: ( xcdotdfrac{5}{100} ) .
Алгоритм решения текстовых задач на смеси и концентрацию
- Выяснить процентное содержание сухого вещества в обоих объектах
- Вычислить массу сухого вещества в обоих ответах
- Приравнять массы сухого вещества (тем самым, мы составили уравнение)
- Записать ответ
Видео-урок
Чтобы лучше понять, как решать текстовые задачи про виноград и изюм (то есть задачи на концентрацию и смеси) на ЕГЭ по математике профильного уровня, рекомендую посмотреть видео урок. Перед просмотром Вы можете самостоятельно решить следующие текстовые задачи, а затем проверить свое решение с помощью видео-урока:
- Виноград содержит 91% влаги, а изюм – 7%. Сколько килограммов винограда требуется для получения 21 килограммов изюма, если известно, что изюм получается в процессе сушки винограда?
- Спелые грибы содержат 80% влаги, а сушеные грибы – 20%. Сколько килограммов сушеных грибов получится из 25 килограммов спелых грибов?
Нестандартная задача на смеси и сплавы: изюм и виноград
9 июля 2013
- Скачать тест
- Ответы к тесту
В каждой задаче должна быть изюминка, и в B14 она тоже есть. Сегодня мы рассмотрим задачу про виноград и изюм. Формально это обычная задача на смеси и сплавы, но многие ученики, даже разобравшиеся с этой темой, все равно не понимают, как решать данную задачу.
В этом коротком видео мы пошагово разберем решение задачи про изюм и виноград. Это довольно сложная задача B14 из ЕГЭ по математике, поэтому дальше идут три задачи для самостоятельного решения. Попробуйте потренироваться на них — и задачи на смеси и сплавы вам будут нестрашны.:)
Смотрите также:
- Сложная задача B14: работа трех исполнителей
- Семья из трех человек (нестандартная задача)
- Тест к уроку «Десятичные дроби» (1 вариант)
- Как решать задачи про смеси и сплавы
- Формула простого процента: неизвестно конечное значение
- Задача B14: сложные проценты
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 54 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
Источники: fipi, os.fipi, Досрочная волна (Резерв) 2018, Основная волна 2013.
Решение:
Обозначим за х массу винограда. Количество сухого вещества в изюме 0,95·54, а в винограде 0,1·х.
Составим уравнение:
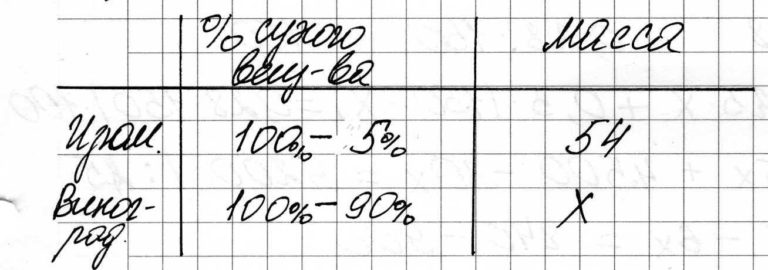
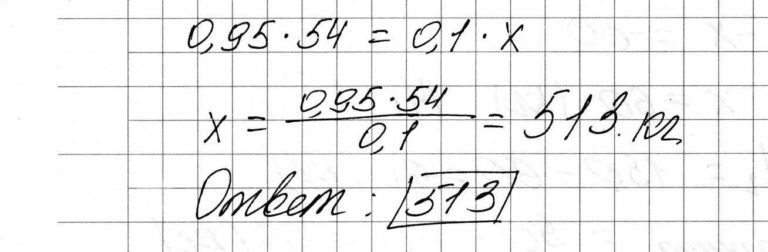
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
1
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 82 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
2
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 16 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
3
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 14 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
4
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 36 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
5
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 6 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
6
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 12 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
7
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 40 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
8
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 62 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
9
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 52 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
10
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 56 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
11
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 76 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
12
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 44 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
13
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 72 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
14
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 86 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
15
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 96 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
16
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 2 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
17
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 90 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
18
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 92 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
19
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 32 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
20
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 22 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
21
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 20 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
22
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 68 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
23
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 100 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
24
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 18 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
25
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 88 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
26
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 94 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
27
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 24 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
28
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 12 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
29
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 12 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
ЗАДАЧИ НА СУШЕНЫЕ ФРУКТЫ.
23.3-7.Свежие фрукты содержат 86% воды, а высушенные — 23%. Сколько сухих фруктов получится из 341 кг свежих фруктов?
Решение. При решении подобных задач следует определить ту величину, которая не меняется при высыхании (уменьшении влажности). Неизменной в данных процессах остается масса сухого вещества, т. е. продукта, в котором полностью отсутствует вода.
Если 341 кг фруктов имеют влажность 86 %, то жидкость составляет 341 × 0,86 = 293,26 кг, а сухое вещество имеет массу 341- 293,26 = 47,74 кг.
Масса сухого вещества не меняется при высыхании, поэтому в сухих фруктах, содержащих 23 % воды, сухое вещество составляет 77 %. Следовательно,
47,74кг——77%
Х кг – 100 %
откуда Х= 47,74∙100/ 77 = 62кг.
Ответ: из 341 кг свежих фруктов получится 62 кг сухих.
55.3-В7—Свежие фрукты содержат 78% воды, а высушенные — 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
РЕШЕНИЕ: Если 78 кг фруктов имеют влажность 78 %, то жидкость составляет 78 × 0,78 = 60,84 кг, а сухое вещество имеет массу 78 – 60,84 = 17,16кг.
Масса сухого вещества не меняется при высыхании, поэтому в сухих фруктах, содержащих 22 % воды, сухое вещество составляет 78 %.
Следовательно, 17,16кг——78%
Х кг – 100 % откуда Х= 17,16∙100: 78 = 22кг. Ответ: из 78 кг свежих фруктов получится 22 кг сухих.
66.3-9 Свежие фрукты содержат 79% воды, а высушенные — 16%. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов?
РЕШЕНИЕ:
х кг = свежих фруктов 100%-79%=21% — сухого вещества в свежих фруктах 100%-16%=84% — сухого вещества в сухих фруктах
Уравнение: 0,21х=72*0,84 х=288 х=288(кг) — надо взять свежих фруктов
87.3-12. Свежие фрукты содержат 89% воды, а высушенные — 23%. Сколько требуется свежих фруктов для приготовления 84 кг высушенных фруктов?
РЕШЕНИЕ: х кг = свежих фруктов 100%-89%=11% — сухого вещества в свежих фруктах 100%-23%=77% — сухого вещества в сухих фруктах Уравнение: 0,11х=84*0,77 х=588 х=588(кг) — надо взять свежих фруктов
215.3.42. Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько сухих фруктов получится из 288 кг свежих фруктов?
РЕШЕНИЕ: При решении подобных задач следует определить ту величину, которая не меняется при высыхании (уменьшении влажности). Неизменной в данных процессах остается масса сухого вещества, т. е. продукта, в котором полностью отсутствует вода. Если 288 кг фруктов имеют влажность 80 %, то жидкость составляет 288 × 0,8 = 230,4кг, а сухое вещество имеет массу 288 — 230,4 = 57,6 кг. Масса сухого вещества не меняется при высыхании, поэтому в сухих фруктах, содержащих 28 % воды, сухое вещество составляет 74 %. Следовательно, 57,6——74%
Х кг – 100 % откуда Х= 57,6∙100 74 = 7кг. Ответ: из 20 кг свежих фруктов получится 7 кг сухих.
216.Задача 5.Свежие фрукты содержат 72 % воды, а сухие – 20 % воды. Сколько сухих фруктов получится из 20 кг свежих?
Решение. При решении подобных задач следует определить ту величину, которая не меняется при высыхании (уменьшении влажности). Неизменной в данных процессах остается масса сухого вещества, т. е. продукта, в котором полностью отсутствует вода. Если 20 кг фруктов имеют влажность 72 %, то жидкость составляет 20 × 0,72 = 14,4 кг, а сухое вещество имеет массу 20 – 14,4 = 5,6 кг. Масса сухого вещества не меняется при высыхании, поэтому в сухих фруктах, содержащих 20 % воды, сухое вещество составляет 80 %. Следовательно, 5,6 кг являются 0,8 частью от общей массы сухих фруктов, а вся масса равняется 5,6 0,8 = 7кг.Можно было получить результат, составив пропорцию 5,6 кг- 80 %
Х кг – 100 % откуда Х= 5,6∙100 80 = 7кг. Ответ: из 20 кг свежих фруктов получится 7 кг сухих.
433.3.80( 1). Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько требуется свежих фруктов для приготовления 80 кг высушенных фруктов?
РЕШЕНИЕ: х кг = свежих фруктов 100%-80%=20% — сухого вещества в свежих фруктах 100%-28%=72% — сухого вещества в сухих фруктах Уравнение: 0,2х=0,72*80 0,2х=57,6 х=57,6:0,2 х=288(кг) — надо взять свежих фруктов
ІІ способ: 100%-80%=20% — сухого вещества в свежих фруктах 100%-28%=72% — сухого вещества в сухих фруктах 80кг-100% ?кг — 72% 80*72:100=288/5(кг) — сухого вещества в сухих фруктах, что составляет 20% в свежих 288/5 кг — 20% ?кг — 100% 288/5*100:20=288(кг)
434.3.80(2 ). Свежие фрукты содержат 78% воды, а высушенные — 22%. Сколько требуется свежих фруктов для приготовления 22 кг высушенных фруктов?
РЕШЕНИЕ: х кг = свежих фруктов 100%-78%=22% — сухого вещества в свежих фруктах 100%-22%=78% — сухого вещества в сухих фруктах Уравнение: 0,22х=22*0,78 х=78 х=78(кг) — надо взять свежих фруктов
435 3.80(3 ). Свежие фрукты содержат 75% воды, а высушенные — 25%. Сколько требуется свежих фруктов для приготовления 45 кг высушенных фруктов?
РЕШЕНИЕ: х кг = свежих фруктов 100%-75%=25% — сухого вещества в свежих фруктах 100%-25%=75% — сухого вещества в сухих фруктах Уравнение: 0,25х=45*0,75 х=135 х=135(кг) — надо взять свежих фруктов
436.3.80(4 ). Свежие фрукты содержат 79% воды, а высушенные — 16%. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов?
РЕШЕНИЕ: х кг = свежих фруктов 100%-79%=21% — сухого вещества в свежих фруктах 100%-16%=84% — сухого вещества в сухих фруктах Уравнение: 0,21х=72*0,84 х=288 х=288(кг) — надо взять свежих фруктов
437.3.80(5 ). Свежие фрукты содержат 89% воды, а высушенные — 23%. Сколько требуется свежих фруктов для приготовления 23 кг высушенных фруктов?
РЕШЕНИЕ: х кг = свежих фруктов 100%-79%=21% — сухого вещества в свежих фруктах 100%-16%=84% — сухого вещества в сухих фруктах Уравнение: 0,21х=72*0,84 х=288 х=288(кг) — надо взять свежих фруктов
438.3.80(6 ). Свежие фрукты содержат 95% воды, а высушенные — 22%. Сколько требуется свежих фруктов для приготовления 55 кг высушенных фруктов?
РЕШЕНИЕ: х кг = свежих фруктов 100%-95%=5% — сухого вещества в свежих фруктах 100%-22%=78% — сухого вещества в сухих фруктах Уравнение: 0,05х=55*0,78 х=858 х=858(кг) — надо взять свежих фруктов
439. 3.80(7 ). Свежие фрукты содержат 93% воды, а высушенные — 16%. Сколько требуется свежих фруктов для приготовления 21 кг высушенных фруктов? ОТВЕТ:259
440.3.80(8 ). Свежие фрукты содержат 88% воды, а высушенные — 30%. Сколько требуется свежих фруктов для приготовления 6 кг высушенных фруктов? ОТВЕТ:35
441.3.80( 9). Свежие фрукты содержат 88% воды, а высушенные — 30%. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов? ОТВЕТ:420
442.3.80( 10). Свежие фрукты содержат 84% воды, а высушенные — 16%. Сколько требуется свежих фруктов для приготовления 44 кг высушенных фруктов? ОТВЕТ:231
443.3.80(11 ). Свежие фрукты содержат 86% воды, а высушенные — 30%. Сколько требуется свежих фруктов для приготовления 94 кг высушенных фруктов? ОТВЕТ:470
444.3.80(12 ). Свежие фрукты содержат 72% воды, а высушенные — 26%. Сколько требуется свежих фруктов для приготовления 84 кг высушенных фруктов? ОТВЕТ:222
445.3.80(13 ). Свежие фрукты содержат 84% воды, а высушенные — 17%. Сколько требуется свежих фруктов для приготовления 16 кг высушенных фруктов? ОТВЕТ:83
446. 3.80(14 ). Свежие фрукты содержат 86% воды, а высушенные — 23%. Сколько требуется свежих фруктов для приготовления 72 кг высушенных фруктов? ОТВЕТ:396
447.3.80( 15). Свежие фрукты содержат 89% воды, а высушенные — 23%. Сколько требуется свежих фруктов для приготовления 84 кг высушенных фруктов? ОТВЕТ:588
448.3.80(16 ). Свежие фрукты содержат 81% воды, а высушенные — 16%. Сколько требуется свежих фруктов для приготовления 95 кг высушенных фруктов? ОТВЕТ:420
449.3.80( 17). Свежие фрукты содержат 91% воды, а высушенные — 19%. Сколько требуется свежих фруктов для приготовления 84 кг высушенных фруктов? ОТВЕТ:756
450. 3.80(18 ). Свежие фрукты содержат 85% воды, а высушенные — 16%. Сколько требуется свежих фруктов для приготовления 75 кг высушенных фруктов? ОТВЕТ:420
451.3.80( 19). Свежие фрукты содержат 90% воды, а высушенные — 24%. Сколько требуется свежих фруктов для приготовления 90 кг высушенных фруктов? ОТВЕТ:684
452. 3.80(20 ). Свежие фрукты содержат 86% воды, а высушенные — 23%. Сколько требуется свежих фруктов для приготовления 62 кг высушенных фруктов? ОТВЕТ:341
525.Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 54 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
РЕШЕНИЕ: Пусть Х кг. взяли винограда. Виноград содержит 90% воды, а сухого вещества 10%, изюм содержит 5% воды, а сухого 95%, тогда сухого в изюме 54∙ 0,95, а в винограде 0,1 ∙ Х, отсюда уравнение 54∙ 0,95 =0,1∙ Х, Х = 513. ОТВЕТ: 513
526. Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 42 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
РЕШЕНИЕ: Пусть Х кг. взяли винограда. Виноград содержит 90% воды, а сухого вещества 10%, изюм содержит 5% воды, а сухого 95%, тогда сухого в изюме 42∙ 0,95, а в винограде 0,1 ∙ Х, отсюда уравнение 42∙ 0,95 =0,1∙ Х, Х = 399. ОТВЕТ: 399
527. Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 58 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
РЕШЕНИЕ: Пусть Х кг. взяли винограда. Виноград содержит 90% воды, а сухого вещества 10%, изюм содержит 5% воды, а сухого 95%, тогда сухого в изюме 58∙ 0,95, а в винограде 0,1 ∙ Х, отсюда уравнение 58∙ 0,95 =0,1∙ Х, Х = 399. ОТВЕТ: 399
541.10.B 14 № 99574. Виноград содержит 90% влаги, а изюм — 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма? Решение В винограде-ВОДЫ-90%, СУХОГО-10%. Пусть Х кг нужно взять винограда, а сухого в нем 0,1Х. В изюме – воды 5%, сухого-95%. Изюма нужно получить 20 кг, а сухого в нем будет 0,95∙ 20 Отсюда уравнение 0,1Х.= 0,95∙ 20, Х=190. Ответ: 19
Предварительный просмотр:
Задачи на движение с учётом длины объектов.
В задачах на движение протяжных тел требуется определить длину одного из них, или учесть его длину при нахождении компонент движения. Можно выделить основные виды таких задач. Это – определение длины поезда проезжающего
- мимо точечного объекта – стрелочник, семафор, придорожный столб;
- мимо длинного объекта – платформа, мост, туннель, лесополоса;
- мимо идущего пешехода ( навстречу или в том же направлении);
- мимо движущегося длинного объекта – поезд, баржа.
Лучше всего решать такие задачи с помощью схем, где длинный объект изображается вектором (стрелкой). И полезно помнить, что все точки длинного объекта (поезда) движутся с одинаковой скоростью – со скоростью поезда. Поэтому достаточно для себя выбрать одну из них ( например, крайнюю правую – «нос» объекта) и решать задачу, как задачу на движение именно этой точки.
Рассмотрим на конкретных задачах.
- Поезд, двигаясь равномерно со скоростью 84 км/ч, проезжает мимо семафора за 24 секунды. Найти длину поезда в метрах.
«Мимо семафора за 24 сек» — это время от момента, когда со столбом поравнялся «нос» поезда, до момента, когда со столбом поравнялся «хвост» поезда. За это время «нос» поезда успеет «уехать» на расстояние, равное длине поезда.
Таким образом, «Мимо семафора за 24сек» — это значит, что за 24сек поезд проходит расстояние, равное своей длине.
S = V ∙ t = lпоезда
Ответ: 560 метров
Вывод: Время движения мимо неподвижной точки – это время, за которое длинный объект проходит расстояние, равное своей длине.
- Поезд проезжает мост со скоростью 90 км/ч за 42 секунды. Какова длина поезда, если длина моста 634 метров?
«Проезжает мост за 42 сек» – это время от момента, когда на мост въезжает «нос» поезда, до момента, когда с моста съезжает «хвост» поезда. За это время «нос» поезда успеет «уехать» на расстояние, равное.
Таким образом, «Проезжает мост за 42 сек» – это значит, что за 42 сек поезд проходит расстояние, равное сумме длин моста и поезда.
S = V ∙ t = l моста + lпоезда
l моста + lпоезда = 90 км/ч ∙ 42 сек = 1050 м; lпоезда = 416 м
Ответ: длина поезда 416 метров
Вывод: Если длинный объект движется мимо неподвижного длинного объекта, то он проходит расстояние равное сумме длин обоих объектов
- Какова длина поезда, успевающего проехать мимо идущего навстречу ему вдоль путей пешехода за 6 секунд, если скорость пешехода 4,2 км/ч, а скорость поезда 108 км/ч?
«Проехать мимо идущего навстречу пешехода за 6 секунд» — это время от момента, когда с пешеходом поравнялся «нос» поезда, до момента, когда с пешеходом поравнялся «хвост» поезда, то есть
от и до .
Это равносильно задаче на встречное движение пешехода и хвоста. Между пешеходом и «хвостом» поезда расстояние, равное длине поезда, через 6 секунд хвост и пешеход встретятся. Каково расстояние между ними, если их скорости известны.
Тогда (Vпоезда + Vпешехода)∙ t = Sобщее = lпоезда;
или lпоезда = Sобщее = Sпоезда + S пешехода
lпоезда = ( 108км/ч + 4,2 км/ч) ∙ 6 сек = 187 м
Ответ: длина поезда 187 м
Вывод: Если длинный объект движется мимо идущего навстречу пешехода, то длина поезда равна сумме расстояний, пройденным пешеходом и поездом вместе.
- Какова длина поезда, успевающего проехать мимо идущего вдоль путей в том же направлении пешехода за 30 секунд, если скорость пешехода 5,4 км/ч, а скорость поезда 123 км/ч?
«проехать мимо идущего в том же направлении пешехода за30 секунд» — это время от момента, когда с пешеходом поравнялся «нос» поезда, до момента, когда с пешеходом поравнялся «хвост» поезда, то есть это время
от и до .
Это равносильно задаче на движение в одном направлении пешехода и хвоста. «Хвост» поезда начал догонять пешехода, когда расстояние между ними было равно длине поезда, и через 30 секунд догнал пешехода. Каким было расстояние между ними, если их скорости известны.
Тогда (Vпоезда – Vпешехода)∙ t = Sобщее = lпоезда;
или lпоезда = Sобщее = Sпоезда – S пешехода
lпоезда = ( 123 км/ч – 5,4 км/ч) ∙ 30 сек = 980 м
Ответ: длина поезда 980 м
Вывод: Если длинный объект движется мимо идущего в том же направлении пешехода, то длина поезда равна разности расстояний, пройденным поездом и пешеходом.
- Две сороконожки проползали мимо друг друга 12 секунд. Скорость старшей из них 54 см/мин, а скорость младшей из них 61 см/мин. Какова длина младшей, если старшая к своим годам достигла 12 см.
«Проползали мимо друг друга 48 секунд» — это время между моментом, когда совместятся их носы, до момента, когда совместятся их хвосты. Другими словами, перед нами задача на встречное движение хвостов при исходном расстоянии, равном сумме длин сороконожек.
Тогда (V1 + V2)∙ t = Sобщее = l1 + l2
l1 + l2 = (54см/мин + 69 см/мин) ∙ 48 сек = 23 см; l2 = 11см
Ответ: длина младшей сороконожки 11 см.
- Старый удав и резвый уж ползли к водопою. При этом уж, имея скорость 46 см/с, прополз мимо удава, длиной 8 метров, за 24 секунды. Какова длина ужа, если скорость удава 11 см/сек.
«Прополз мимо удава за 24 секунды» — это время от момента, когда нос ужа поравнялся с хвостом удава, до момента, когда хвост ужа поравнялся с носом удава, то есть это время за которое хвост ужа догонит нос удава, если расстояние между ними равно сумме их длин.
Тогда (Vужа – Vудава)∙ t = Sобщее = l ужа + l удава ;
l ужа + l удава = (46 см/с – 11 см/с) ∙24 = 840 см; l ужа = 840 см – 8м = 40см
Ответ: длина ужа 40 см.
Возможны другие задачи, в которых сочетаются разные ситуации шести основных случаев, или иначе расставлены данные задачи и вопрос задач.
- Электричка проходит мимо столба за 8 секунд. За какое время (в секундах) пройдут мимо друг друга пассажирский поезд и электричка, если скорость пассажирского поезда равна скорости электрички, а длина пассажирского поезда в полтора раза больше длины электрички?
Решение: 1). Пусть длина электрички а метров, тогда длина поезда 1,5а метра.
2). «Мимо столба за 8 сек» — это время от момента, когда со столбом поравнялся нос электрички, до момента, когда со столбом поравнялся хвост электрички, за это время нос электрички успел «уехать» на расстояние, равное длине электрички.
Таким образом, «Мимо столба за 8 сек» — это значит, что за 8 сек электричка проходит расстояние, равное своей длине.
Тогда скорость электричкики (а/8) м/с, такая же скорость и у поезда.
3).»Пройдут мимо друг друга пассажирский поезд и электричка» — это время от момента, когда объекты «коснутся » носами, до момента, когда объекты «коснутся » хвостами. Перефразируем эту часть задачи:
Хвост электрички и хвост поезда начали двигаться навстречу друг другу, когда между ними было расстояние, равное сумме длин электрички и поезда. Через сколько секунд они встретятся, если их скорости равны и равны а/8?
Надо общее расстояние (а+1.5а) разделить на общую скорость (а/8+а/8), т.е. (2.5а)/(а/4)=20
Ответ: за 20 сек
- Подъезжая к станции скорый поезд снизил скорость в момент, когда между кабиной машиниста и началом платформы было 320 метров, и через снова набрал её, когда между его хвостом и концом платформы стало 230 метров. С какой скоростью шёл скорый мимо платформы, если его длина 210 метров, а длина платформы 400 метров?
Решение:
Vпоезда ∙t = Sпоезда = (320+400+230+210)м; Vпоезда =1160 м : 12 мин. = 5,8 км/ч
9. Поезд длиной 240 метров мимо смотрителя прошёл за 12 секунд. Какова длина железнодорожного моста ( в км ), если на его прохождение поезд потратил 1 мин. ( Ответ: 0.96 км )
10. Найти скорость и длину поезда, зная, что он проходит мимо светофора за 7 секунд, и тратит 25 секунд на прохождение с той же скоростью вдоль платформы длиной 378 метров. ( Ответ: 75,6 км/ч и 147 м )
11. Два поезда длиной 490 м и 210 м равномерно движутся навстречу друг другу по параллельным путям. Машинист одного из них заметил встречный состав на расстоянии 700 м; после этого через 28 секунд поезда встретились. Найти скорость каждого из них ( в км/ч ), если один из них проезжает мимо светофора на 35 с дольше другого. ( Ответ: 36 км/ч и 54 км/ч )
12. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 160 метров, второй — длиной 140 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 300 метров. Через 9 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 900 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
13. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 140 метров, второй — длиной 60 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 800 метров. Через 15 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 1000 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
14. Поезд, двигаясь равномерно со скоростью 183 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 3 км/ч, за 13 секунд. Найдите длину поезда в метрах.
15. Три свечи имеют одинаковую длину, но разную толщину. Первая свеча была зажжена на 1 час раньше двух других, зажженных одновременно. В некоторый момент горения первая и третья свечи стали одной длины, а через 2 часа после этого одинаковой длины стали первая и вторая свечи. За сколько часов сгорает первая свеча, если вторая сгорает за 12 часов, а третья – за 8 часов? ( Ответ: 16 часов )

