Как решать задачи с масками егэ информатика - Помощь в подготовке к экзаменам и поступлению

Сегодня научимся решать 12 задание из ЕГЭ по информатике 2022.

В основном 12 задание решается шаблонно с помощью Питона, но есть и задачи, в которых нужен особый подход.

Перейдём к классической задачке из ЕГЭ по информатике 2022.

Задача (Классическая)

Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов.

1. заменить (v, w)

2. нашлось (v)

Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.
Дана программа для исполнителя Редактор:

НАЧАЛО
ПОКА нашлось (2222) ИЛИ нашлось (666)
  ЕСЛИ нашлось (2222)
    ТО заменить (2222, 6)
    ИНАЧЕ заменить (666, 2)
  КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ

Какая строка получится в результате применения приведённой выше программы к строке, состоящей из 239 идущих подряд цифр 6? В ответе запишите полученную строку.

Решение:

Решим задачу с помощью программы на Python’е.

s = '6'*239

while ('2222' in s) or ('666' in s):
    if '2222' in s:
        s = s.replace('2222', '6', 1)
    else:
        s = s.replace('666', '2', 1)

print(s)

Здесь в начале формируется строка, состоящая из 239 шестёрок. Потом эта строка подаётся в программу. Программу переводим с русского языка на язык Питон.

Третий параметр в функции replace обозначает, что замену нужно производить один раз. Это в точности соответствует предложенной функции заменить.

Ответ получается 2266.

Ответ: 2266

В следующей типовой задаче из ЕГЭ по информатике 2022 нужно сообразить один момент.

Задача (Нужно сообразить)

Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.

1. заменить (v, w)
2. нашлось (v)

Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w, вторая проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Дана программа для исполнителя Редактор:

НАЧАЛО
  ПОКА нашлось (21) ИЛИ нашлось (31) ИЛИ нашлось (23)
    ЕСЛИ нашлось (21)
      ТО заменить (21, 12)
    КОНЕЦ ЕСЛИ
    ЕСЛИ нашлось (31)
      ТО заменить (31, 13)
    КОНЕЦ ЕСЛИ
    ЕСЛИ нашлось (23)
      ТО заменить (23, 32)
    КОНЕЦ ЕСЛИ
  КОНЕЦ ПОКА
КОНЕЦ

На вход приведённой ниже программе поступает строка, содержащая 50 цифр 1, 50 цифр 2 и 50 цифр 3, расположенных в произвольном порядке. Запишите без разделителей символы, которые имеют порядковые номера 10, 90 и 130 в получившейся строке.

Решение:

Здесь сказали, что начальный порядок цифр в строке неизвестен. А просят написать конкретные данные на выходе. Отсюда делаем вывод, что любой порядок в начале приводит к одному и тому же результату.

В строке заведём цифры по порядку: в начале единицы, потом двойки, потом тройки.

s = '1'*50 + '2'*50 + '3'*50

while ('21' in s) or ('31' in s) or ('23' in s):
    if '21' in s:
        s = s.replace('21', '12', 1)
    if '31' in s:
        s = s.replace('31', '13', 1)
    if '23' in s:
        s = s.replace('23', '32', 1)

print(s[9] + s[89] + s[129])

Чтобы обратится к конкретному символу в строке, используем конструкцию s[позиция символа]. Но нумерация начинается с нуля.

В ответе запишем 132.

Ответ: 132

В следующей примерной задаче из ЕГЭ по информатике 2022 опять используем Питон.

Задача (Снова программируем)

1. заменить (v, w)

2. нашлось (v)

НАЧАЛО
ПОКА нашлось (111)
  заменить (111, 22)
  заменить (222, 11)
КОНЕЦ ПОКА
КОНЕЦ

Известно, что исходная строка содержала более 70 единиц и не содержала других цифр. Укажите минимально возможную длину исходной строки, при которой в результате работы этой программы получится строка, содержащая максимально возможное количество единиц.

Решение:

Здесь мы попробуем с помощью программы формировать строчки с разной длиной и смотреть, какое количество единиц получится на выходе.

for i in range(71, 1000):
    s = '1'*i
    while '111' in s:
        s = s.replace('111', '22', 1)
        s = s.replace('222', '11', 1)

    print(i, s.count('1'))

Посмотрев результаты, понимаем, что максимальное количество единиц в окончательной строке равно 4. А минимальное количество единиц в изначальной строке, чтобы получилось в итоге 4 единицы, равно 73.

Ответ: 73

Ещё один частый гость в тренировочных вариантах из ЕГЭ по информатике 2022.

Задача (Сумма цифр + непонятный символ)

1. заменить (v, w)
2. нашлось (v)

НАЧАЛО
  ПОКА нашлось (>1) ИЛИ нашлось (>2) ИЛИ нашлось (>3)
    ЕСЛИ нашлось (>1)
      ТО заменить (>1, 22>)
    КОНЕЦ ЕСЛИ
    ЕСЛИ нашлось (>2)
      ТО заменить (>2, 2>1)
    КОНЕЦ ЕСЛИ
    ЕСЛИ нашлось (>3)
      ТО заменить (>3, 1>2)
    КОНЕЦ ЕСЛИ
  КОНЕЦ ПОКА
КОНЕЦ

На вход приведённой ниже программе поступает строка, начинающаяся с символа «>», а затем содержащая 28 цифр 1, 18 цифр 2 и 35 цифр 3, расположенных в произвольном порядке. Определите сумму числовых значений цифр строки, получившейся в результате выполнения программы. Так, например, если результат работы программы представлял бы собой строку, состоящую из 50 цифр 4, то верным ответом было бы число 200.

Решение:

Здесь снова результат будет одним и тем же независимо от того, как будут расположены числа в начале.

s = '>' + '1'*28 + '2'*18 + '3'*35

while ('>1' in s) or ('>2' in s) or ('>3' in s):
    if '>1' in s:
        s = s.replace('>1', '22>', 1)
    if '>2' in s:
        s = s.replace('>2', '2>1', 1)
    if '>3' in s:
        s = s.replace('>3', '1>2', 1)

# Находим сумму цифр в строке
sm=0
for i in range(0, len(s)):
    if s[i]!='>':
        sm = sm + int(s[i])
        
print(sm)

Чтобы найти сумму цифр, мы пробегаем по всей строке с помощью цикла range. Если символ не равен «>», то превращаем его в число с помощью функции int() и суммируем в переменную sm.

Получается 465.

Ответ: 465

Задача (Трудно запрограммировать)

1. заменить (v, w)
2. нашлось (v)

НАЧАЛО
  ПОКА нашлось (11)
    ЕСЛИ нашлось(112)
      ТО заменить (112, 5)
      ИНАЧЕ заменить (11, 3)
  КОНЕЦ ПОКА
КОНЕЦ

Исходная строка содержит 23 единицы и 5 двоек, других цифр нет, точный порядок расположения цифр неизвестен. Какую наибольшую сумму цифр может иметь строка, которая получится после выполнения программы?

Решение:

Здесь не важно, по какой ветке будет идти программа, прирост в сумме цифр будет всегда равен 1. Поэтому можно расположить в начале только 1, а затем все двойки в исходной строке.

Одиннадцать раз символы ’11’ превратятся в ‘3’. Тогда 11 * 3 = 33. Останутся цифры ‘122222’. Их сумма равна 11.

В ответе получается 33 + 11 = 44.

Ответ: 44

Задача (Крепкий орешек)

1. заменить (v, w)
2. нашлось (v)

НАЧАЛО
  ПОКА нашлось (01) или нашлось (02)
    заменить (01, 2202)
    заменить (02, 10)
  КОНЕЦ ПОКА
КОНЕЦ

Известно, что начальная строка начиналась с нуля, а далее содержала только единицы и двойки. После выполнения данной программы получилась строка, содержащая 40 единиц и 64 двойки. Сколько двоек было в исходной строке ?

Решение:

Посмотрим, во что превращается 1:

01 -> 2202 -> 2210

Посмотрим, во что превращается 2:

02 -> 10

Т.е. в окончательном результате двойки могли возникнуть только из 1. Двоек получается в два раза больше, чем было изначально единиц.

Получается, что изначальное количество единиц равно 64 / 2 = 32. Эти 32 единицы так же принесли 32 единицы. Всего 40 единиц стало. Значит, ещё 8 единиц получилось в результате преобразования 02 -> 10. Т.е. двоек будет 8.

Теперь попробуем решить задачу с помощью программы. Здесь неизвестно количество единиц и двоек. Поэтому придётся создавать вложенные циклы. Предположим, что количество единиц и двоек меньше 100, чтобы программа отработала за адекватное время.

for i in range(1, 100):
    for j in range(1, 100):
        
        s = '0' + '1'*i + '2'*j

        while ('01' in s) or ('02' in s):
            s = s.replace('01', '2202', 1)
            s = s.replace('02', '10', 1)

        if s.count('1')==40 and s.count('2')==64:
            print(j)

Получается количество двоек равно восьми.

Ответ: 8

Решим задачу про Робота, которая в последнее время редко встречается на экзамене по информатике.

Задача (Робот)

Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости, состоит из 8 команд. Четыре команды — это команды-приказы:

При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх , вниз , влево , вправо .

Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:

сверху свободно

снизу свободно

слева свободно

справа свободно

Цикл
   ПОКА условие
       последовательность команд
   КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
    ТО команда1
    ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно)

В конструкциях ПОКА и ЕСЛИ условие может содержать команды проверки, а также слова И, ИЛИ, НЕ, обозначающие логические операции.

Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены, то он разрушится и программа прервётся.

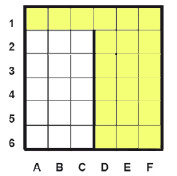
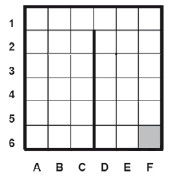
Сколько клеток лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?

НАЧАЛО
  ПОКА снизу свободно ИЛИ справа свободно
    ПОКА справа свободно
        вправо
    КОНЕЦ ПОКА
    ЕСЛИ снизу свободнo
        ТО вниз
    КОНЕЦ ЕСЛИ
  КОНЕЦ ПОКА
КОНЕЦ

ЕГЭ по информатике 2021 - задание 12 (Лабиринт, где живёт Робот)

Решение:

Проанализируем внимательно программу для Робота.

В программе есть главный цикл, внутри цикла проверяется сначала возможность двигаться вправо. Если есть такая возможность, робот будет двигаться до упора с помощью ещё одного цикла. Потом после того как больше нет возможности двигаться вправо, с помощью основного цикла и записанного условия будет перемещаться вниз, пока есть такая возможность.

Если нет возможности двигаться ни вправо, ни вниз, то Робот завершает программу.

Поняв этот алгоритм не сложно отметить те клетки, стартовав с которых, Робот остановится на клетке F6.

Ещё раз, Робот до упору будет двигаться вправо, потом до упору вниз, насколько это возможно. Вот алгоритм в двух словах.

Важно в этих задачах простыми словами сформулировать алгоритм, чтобы можно было проверять целые блоки лабиринта.

Количество клеток, удовлетворяющие условию будет 21.

Ответ: 21

12 Задание из ЕГЭ по информатике 2021 выглядит обычно объёмным, но на деле описываются обычные конструкции (Циклы и условия), которые есть в большинстве языках программирования.

Задача (Чертёжник)

Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнить команду сместиться на(a, b), где a, b — целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b).

Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на(2, -3) переместит Чертёжника в точку (6, -1).

Цикл

ПОВТОРИ число РАЗ

последовательность команд

КОНЕЦ ПОВТОРИ

означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).

Чертёжнику был дан для исполнения следующий алгоритм (число повторений и величины смещения в первой из повторяемых команд неизвестны):

НАЧАЛО
сместиться на(8, -60)
  ПОВТОРИ ... РАЗ
    сместиться на(..., ...)
    сместиться на(4, -6)
  КОНЕЦ ПОВТОРИ
сместиться на(-35, -3)
КОНЕЦ

В результате выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшие число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ» ?

Решение:

Эта задача похоже на задачу Кузнечик, которую рассматривали в 5 задании.

Напишем для переменной x уравнение.

8 + n * x + n * 4 — 35 = 0

Всё выражение приравниваем к нулю, т.к. Чертёжник возвращается в исходную точку, т.е. как ни ходил Чертёжник, он никуда в итоге не сдвинулся.

n — положительное целое число, количество повторений.

x — целое число, смещение по координате x.

n * x + n * 4 = 27

n * ( x + 4 ) = 27

Нужно подобрать x и n, чтобы равенство было верным.

Число n может быть 27, 9, 3, 1. Нам нужно выбрать число n, как можно больше.

Проверим число 27! Тогда выражение x + 4 = 1 => x = -3. Теперь нужно проверить это число для координаты y.

-60 + n * y — n * 6 — 3 = 0

27 * y — 27 * 6 = 63

27 * ( y — 6 ) = 63

Видим, что нельзя подобрать такое целое число для 27, чтобы при умножении получалось 63.

Проверим число 9! Тогда выражение x + 4 = 3 => x = -1. Теперь нужно проверить это число для координаты y.

-60 + n * y — n * 6 — 3 = 0

9 * y — 9 * 6 = 63

9 * ( y — 6 ) = 63

Видим, что можно подобрать такое целое число для 9, чтобы при умножении получалось 63. Это число 7. Значит, y — 6 = 7 => y = 13

Мы подобрали все нужные числа и нашли наибольшее число n=9.

Ответ: 9

Некоторые формулировки задач были взяты с сайтов:

https://kpolyakov.spb.ru/
https://inf-ege.sdamgia.ru/

Счастливых экзаменов по информатике!

почему 5-ую задачу сложно запрограммировать? тут ведь тоже произвольный порядок
я пробовал в программе ставить сначала единицы, а потом двойки и наоборот — сначала двойки а потом единицы
печатаю s и суммирую цифры
получается везде 44

Если бы сама программа была немного другая, то могло и не получится. Т.е. тут нужно самостоятельно провести анализ, при каком расположении цифр сумма будет максимальной.

Обожаю ваш сайт! Спасибо за пояснение усложненных задач.

Источник

Всего: 145 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая  — к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес,  — в виде четырёх байтов, причём каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого разряда  — нули. Адрес сети получается в результате применения поразрядной конъюнкции к заданным IP-адресу узла и маске.

Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.

Для узла с IP-адресом 119.83.208.27 адрес сети равен 119.83.192.0. Каково наименьшее возможное количество единиц в разрядах маски?

Источник: Демонстрационная версия ЕГЭ—2017 по информатике.

Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.

Для узла с IP-адресом 57.179.208.27 адрес сети равен 57.179.192.0. Каково наибольшее возможное количество единиц в разрядах маски?

Источник: Демонстрационная версия ЕГЭ—2018 по информатике.

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая  — к адресу самого узла в этой сети. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого места  — нули. Обычно маска записывается по тем же правилам, что и IP-адрес,  — в виде четырёх байтов, причём каждый байт записывается в виде десятичного числа. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске.

Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.

Узлы с IP-адресами 140.37.235.224 и 140.37.235.192 находятся в одной сети. Определите последний байт маски сети. Количество возможных единиц в маске этой сети должно быть наибольшим.

Источник: ЕГЭ — 2019. Досрочная волна. Вариант 1.

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая  — к адресу самого узла в этой сети. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого места  — нули. Обычно маска записывается по тем же правилам, что и IP-адрес,  — в виде четырёх байтов, причём каждый байт записывается в виде десятичного числа. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске.

Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.

Для узла с IP-адресом 113.191.169.34 адрес сети равен 113.191.160.0. Каково наименьшее возможное количество единиц в разрядах маски?

Источник: ЕГЭ по информатике 13.06.2019. Основная волна, Центр. Вариант Имаева-Зубовой — «Котолис».

Для узла с IP-адресом 153.82.140.123 адрес сети равен 153.82.136.0. Определите третий слева октет маски подсети. Ответ запишите в виде десятичного числа.

Источник: ЕГЭ — 2018. Досрочная волна. Вариант 1., ЕГЭ — 2018. Досрочная волна. Вариант 2.

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая  — к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес  — в виде четырёх байтов, причём каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого разряда  — нули. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске.

Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.

Для узла с IP-адресом 111.81.88.27 адрес сети равен 111.81.80.0. Чему равен третий слева байт маски? Ответ запишите в виде десятичного числа.

Источник: ЕГЭ — 2018. Досрочная волна. Вариант 2., ЕГЭ — 2018. Досрочная волна. Вариант 1.

Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.

Для узла с IP-адресом 117.191.37.84 адрес сети равен 117.191.37.80. Чему равно наименьшее возможное значение последнего (самого правого) байта маски? Ответ запишите в виде десятичного числа.

Источник: Демонстрационная версия ЕГЭ—2019 по информатике.

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая – к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес, – в виде четырёх байтов, причём каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого разряда  — нули. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске.

Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.

Для узла с IP-адресом 111.81.176.27 адрес сети равен 111.81.160.0. Чему равен третий слева байт маски? Ответ запишите в виде десятичного числа.

Источник: ЕГЭ — 2019. Досрочная волна. Вариант 2.

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая  — к адресу самого узла в этой сети. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого места  — нули. Обычно маска записывается по тем же правилам, что и IP-адрес,  — в виде четырёх байтов, причём каждый байт записывается в виде десятичного числа. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске.

Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.

Для узла с IP-адресом 15.51.208.15 адрес сети равен 15.51.192.0. Чему равно наибольшее возможное значение третьего слева байта маски?

Источник: ЕГЭ по информатике 13.06.2019. Основная волна. Юг-Центр.

Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.

Для узла с IP-адресом 111.81.27.224 адрес сети равен 111.81.27.192. Чему равен последний (самый правый) байт маски? Ответ запишите в виде десятичного числа.

Источник: Демонстрационная версия ЕГЭ−2020 по информатике

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая  — к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске.

По заданным IP-адресу узла и маске определите адрес сети.

IP –адрес узла: 224.9.195.133

Маска: 255.255.192.0

При записи ответа выберите из приведенных в таблице чисел четыре элемента IP-адреса и запишите в нужном порядке соответствующие им буквы, без использования точек.

A	B	C	D	E	F	G	H
0	9	16	128	133	192	195	224

Пример. Пусть искомый IP-адрес 192.168.128.0, и дана таблица

A	B	C	D	E	F	G	H
128	168	255	8	127	0	17	192

В этом случае правильный ответ будет записан в виде: HBAF

В терминологии сетей TCP/IP маской сети называется 32-разрядная двоичная (то есть состоящая из нулей и единиц) последовательность. Маска определяет, какая часть IP-адреса узла сети относится к адресу сети, а какая  — к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске. По заданным IP-адресу узла и маске определите адрес сети.

IP-адрес узла: 217.8.244.3

Маска: 255.255.252.0

При записи ответа выберите из приведённых в таблице чисел четыре элемента IP-адреса сети и запишите в нужном порядке соответствующие им буквы без использования точек.

A	B	C	D	E	F	G	H
0	3	8	217	224	244	252	255

Пример. Пусть искомый IP-адрес: 192.168.128.0, и дана таблица:

A	B	C	D	E	F	G	H
128	168	255	8	127	0	17	192

В этом случае правильный ответ будет записан в виде: HBAF.

Источник: Демонстрационная версия ЕГЭ—2015 по информатике.

IP-адрес узла: 249.17.100.96

Маска: 255.255.224.0

A	B	C	D	E	F	G	H
0	17	54	96	100	224	249	255

Пусть искомый IP-адрес 192.168.128.0, и дана таблица

A	B	C	D	E	F	G	H
128	168	255	8	127	0	17	192

В этом случае правильный ответ будет записан в виде: HBAF.

IP-адрес узла: 111.32.96.96

Маска: 255.255.192.0

A	B	C	D	E	F	G	H
0	32	64	96	100	111	192	255

Пусть искомый IP-адрес 192.168.128.0, и дана таблица

A	B	C	D	E	F	G	H
128	168	255	8	127	0	17	192

В этом случае правильный ответ будет записан в виде: HBAF.

В терминологии сетей TCP/IP маской сети называется 32-разрядная двоичная (то есть состоящая из нулей и единиц) последовательность. Маска определяет, какая часть IP-адреса узла сети относится к адресу сети, а какая – к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске. По заданным IP-адресу узла и маске определите адрес сети.

IP-адрес узла: 199.145.130.81

Маска: 255.255.128.0

A	B	C	D	E	F	G	H
0	81	113	128	130	145	199	225

Пример.

Пусть искомый IP-адрес: 192.168.128.0, и дана таблица

A	B	C	D	E	F	G	H
128	168	255	8	127	0	17	192

В этом случае правильный ответ будет записан в виде: HBAF

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая – к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес. Адрес сети получается в результате применения поразрядной конъюнкции к заданным IP-адресу узла и маске. По заданным IP-адресу узла и маске определите адрес сети.

IP-адрес: 240.144.182.134 Маска: 255.255.248.0

A	B	C	D	E	F	G	H
0	134	144	176	182	240	248	6

Пример. Пусть искомый адрес сети 192.168.128.0 и дана таблица

A	B	C	D	E	F	G	H
128	168	255	8	127	0	17	192

В этом случае правильный ответ будет HBAF.

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая – к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес. Адрес сети получается в результате применения поразрядной конъюнкции к заданным IP-адресу узла и маске. По заданным IP-адресу узла и маске определите адрес сети.

IP-адрес узла: 32.130.201.117

Маска: 255.255.240.0

A	B	C	D	E	F	G	H
240	201	192	130	117	32	9	0

Пример. Пусть искомый адрес сети 192.168.128.0 и дана таблица

A	B	C	D	E	F	G	H
128	168	255	8	127	0	17	192

В этом случае правильный ответ будет HBAF.

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая – к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске. По заданным IP-адресу узла и маске определите адрес сети.

IP-адрес узла: 217.19.128.131

Маска: 255.255.192.0

При записи ответа выберите из приведённых в таблице чисел четыре элемента IP-адреса сети и запишите в нужном порядке соответствующие им буквы, без использования точек.

A	B	C	D	E	F	G	H
0	16	19	64	128	131	192	217

Пример.

Пусть искомый IP-адрес: 192.168.128.0, и дана таблица

A	B	C	D	E	F	G	H
128	168	255	8	127	0	17	192

В этом случае правильный ответ будет записан в виде: HBAF

Источник: Демонстрационная версия ЕГЭ—2013 по информатике.

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая — к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес. Адрес сети получается в результате применения поразрядной конъюнкции к заданным IP-адресу узла и маске.

По заданным IP-адресу узла и маске определите адрес сети. IP-адрес узла: 234.95.131.37 Маска: 255.255.192.0 При записи ответа выберите из приведённых в таблице чисел четыре элемента IP-адреса и запишите в нужном порядке соответствующие им буквы без использования точек.

При записи ответа выберите из приведенных в таблице чисел 4 фрагмента четыре элемента IP-адреса и запишите в нужном порядке соответствующие им буквы без точек.

A	B	C	D	E	F	G	H
0	19	95	110	128	192	208	234

Пример. Пусть искомый адрес сети 192.168.128.0 и дана таблица

A	B	C	D	E	F	G	H
128	168	255	8	127	0	17	192

В этом случае правильный ответ будет HBAF.

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая — к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес. Адрес сети получается в результате применения поразрядной конъюнкции к заданным IP-адресу узла и маске.

По заданным IP-адресу узла и маске определите адрес сети.

IP-адрес узла: 237.195.158.37

Маска: 255.255.192.0

При записи ответа выберите из приведённых в таблице чисел четыре элемента IP-адреса и запишите в нужном порядке соответствующие им буквы без использования точек.

A	B	C	D	E	F	G	H
0	192	128	195	224	237	248	255

Пример. Пусть искомый адрес сети 192.168.128.0 и дана таблица

A	B	C	D	E	F	G	H
128	168	255	8	127	0	17	192

В этом случае правильный ответ будет HBAF.

Всего: 145 1–20 | 21–40 | 41–60 | 61–80 …

Источник

Задание 12. Сетевые адреса: Демонстрационный вариант ЕГЭ по информатике 2018; государственный выпускной экзамен 2018; тренировочные варианты ЕГЭ по информатике, тематические тестовые задания и задачи из тренажера по информатике 2018

12 задание. Демоверсия ЕГЭ 2018 информатика:

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая – к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес, – в виде четырёх байтов, причём каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого разряда – нули.
Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске.

Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.

Для узла с IP-адресом 57.179.208.27 адрес сети равен 57.179.192.0. Каково наибольшее возможное количество единиц в разрядах маски?

📹 Видеоразбор

✍ Показать решение:

Поскольку адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске, то получим:

 255.255.?.?    -> маска
&
 57.179.208.27  -> IP-адрес
=
 57.179.192.0   -> адрес сети

Так как первые два байта слева в IP-адресе узла и адресе сети совпадают, значит, в маске для получения такого результата при поразрядной конъюнкции в двоичной системе должны быть все единицы. Т.е.:

11111111₂ = 255₁₀

Для того, чтобы найти оставшиеся два байта маски, необходимо перевести соответствующие байты в IP-адресе и адресе сети в 2-ю систему счисления. Сделаем это:

208₁₀ = 11010000₂
192₁₀ = 11000000₂

Теперь посмотрим, какая может быть маска для данного байта. Пронумеруем биты маски справа налево:

 _{7  6 5  4 3  2  1  0}
 1 1 1 0 0 0 0 0   -> маска
&
 1 1 0 1 0 0 0 0
=
 1 1 0 0 0 0 0 0

Для 5-го бита получаем: ? & 0 = 0 -> в маске может находиться как единица, так и 0. Но так как по заданию у нас спрашивается наибольшее возможное количество единиц, то, значит, необходимо сказать, что в маске данный бит равен 1.
Для 4-го бита получаем: ? & 1 = 0 -> в маске может находиться только 0.
Так как в маске сначала идут единицы, а затем все нули, то после этого нуля в 4-м бите все остальные будут нули. И 4-й слева байт маски будет равен 0₁₀.
Получим маску: 11111111.11111111.11100000.00000000.
Посчитаем количество единиц в маске:

8 + 8 + 3 = 19

Результат: 19

Решение 12 задания ЕГЭ по информатике, вариант 1 (ФИПИ, «ЕГЭ информатика и ИКТ, типовые экзаменационные варианты 2018», С.С. Крылов, Т.Е. Чуркина):

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая – к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес, – в виде четырёх байтов, причём каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого разряда – нули.
Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске.

Например, если IP-адрес узла равен 211.132.255.41, а маска равна 255.255.201.0, то адрес сети равен 211.132.201.0.

Для узла с IP-адресом 200.230.100.23 адрес сети равен 200.230.0.0. Чему равно наименьшее возможное значение второго слева байта маски? Ответ запишите в виде десятичного числа.

✍ Показать решение:

Рассмотрим получение адреса сети из IP-адреса узла с учетом, что маска сети не известна:

 ? . ? . ? . ?  -> маска сети
200.230.100.23  -> IP-адрес 
200.230.0  .0   -> адрес сети

Нас интересует второй слева байт маски (выделенный). Ему соответствует 230 и в IP-адресе и в адресе сети. Поскольку необходимо выполнение операции поразрядной конъюнкции, то переведем число 230 в 2-ю систему счисления:

230|0
115|1
 57|1
 28|0
 14|0
  7|1
  3|1
  1

230₁₀ = 11100110₂

Теперь проанализируем, чему могут равняться биты маски, чтобы при поразрядной конъюнкции получилось бы необходимое число:

? ? ? ? ? ? ? ?   _&
1 1 1 0 0 1 1 0   ₌
1 1 1 0 0 1 1 0

Учтем, что, во-первых, необходимо получить наименьшее значение, и, во-вторых, в маске после бита равного нулю, единиц уже быть не должно. Тогда имеем:

1 1 1 1 1 1 1 0   _&
1 1 1 0 0 1 1 0   ₌
1 1 1 0 0 1 1 0

Четвертый слева бит маски (выделен) не может быть нулем, т.к. остальные справа биты тоже должны быть нулями; в таком случаем конъюнкция с единицей вернет 0, а в нашем случае справа есть единицы. То же самое замечание касается пятого слева бита маски.
Переведем получившееся число в десятичную систему счисления:

11111110₂ = 128 + 64 + 32 + 16 + 8 + 4 + 2 = 254₁₀

Результат: 254

12 задание ЕГЭ по информатике, вариант 10 (ФИПИ, «ЕГЭ информатика и ИКТ, типовые экзаменационные варианты 2018», С.С. Крылов, Т.Е. Чуркина):

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая – к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес, – в виде четырёх байтов, причём каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого разряда – нули.
Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске.

По заданным IP-адресу узла и маске определите третий слева байт адреса сети. IP-адрес узла: 155.102.133.70. Маска: 255.255.240.0. Ответ запишите в виде десятичного числа.

📹 Видеоразбор

ЕГЭ по информатике -> ЕГЭ 2018 -> ЕГЭ 2018 — 12

Источник

ЕГЭ информатика 25 задание разбор, теория, как решать.

Создание программы для обработки целочисленной информации, (В) — 2 балла

Е25.21 соответствующие маске 1?2139*4, делящиеся на 2023 без остатка

Назовём маской числа последовательность цифр, в которой также могут встречаться следующие символы: – символ «?» означает ровно одну произвольную цифру; – символ «*» означает любую последовательность цифр произвольной длины; в том числе «*» может задавать и пустую последовательность. Например, маске 123*4?5 соответствуют числа 123405 и 12300405. Среди натуральных чисел, не превышающих 1010, найдите все числа, …

Е25.20 M(k) нельзя представить в виде произведения трёх различных натуральных чисел

Пусть M(k) = 9 000 000 + k, где k – натуральное число. Найдите пять наименьших значений k, при которых M(k) нельзя представить в виде произведения трёх различных натуральных чисел, не равных 1. В ответе запишите найденные значения k в порядке возрастания. чно. Открытый вариант ИНФОРМАТИКА КИМ ЕГЭ 2022 — задание №25

Е25.19 найдите все числа, соответствующие маске 12345?7?8, делящиеся на число 23 без остатка.

Назовём маской числа последовательность цифр, в которой также могут встречаться следующие символы: – символ «?» означает ровно одну произвольную цифру; – символ «*» означает любую последовательность цифр произвольной длины; в том числе «*» может задаватьи пустую последовательность. Например, маске 123*4?5 соответствуют числа 123405 и 12300405. Среди натуральных чисел, не превышающих 109, найдите все числа, соответствующие …

Е25.18 Пусть М — сумма минимального и максимального натуральных делителей целого числа

Пусть М — сумма минимального и максимального натуральных делителей целого числа, не считая единицы и самого числа. Если таких делителей у числа нет, то значение М считается равным нулю. Напишите программу, которая перебирает целые числа, большие 220 000, в порядке возрастания и ищет среди них такие, для которых значение М оканчивается на 4. Выведите первые …

Е25.17 Пусть M(N) – пятый по величине делитель натурального числа N без учёта самого числа и единицы

Пусть M(N) – пятый по величине делитель натурального числа N без учёта самого числа и единицы. Например, M(1000) = 100. Если у числа N меньше 5 различных делителей, не считая единицы и самого числа, считаем, что M(N) = 0. Найдите 5 наименьших натуральных чисел, превышающих 460 000 000, для которых M(N) > 0. В ответе …

Е25.16 10 простых чисел наиболее приближенные к числу 10000000

Напишите программу, которая находит 10 простых чисел наиболее приближенные к числу 10000000 (10 миллионов). Причем 5 найденных чисел должны быть меньше заданного числа, остальные 5 чисел-больше. Найденные числа расположите в порядке возрастания. В качестве ответа выведите пары чисел — расстояние от найденного числа до 10000000 и само число. Например, для числа 50 ответ должен быть …

Е25.15 Пусть M (N) – сумма двух наибольших различных натуральных делителей

Пусть M (N) – сумма двух наибольших различных натуральных делителей натурального числа N, не считая самого числа. Если у числа N меньше двух таких делителей, то M (N) считается равным 0. Найдите 5 наименьших натуральных чисел, превышающих 12 000 000, для которых 0 < M (N) < 10 000. В ответе запишите найденные значения M …

Е25.14 Найдите все натуральные числа, N, принадлежащие отрезку [200 000 000; 400 000 000]

Найдите все натуральные числа, N, принадлежащие отрезку [200 000 000; 400 000 000], которые можно представить в виде N = 2m · 3n, где m – чётное число, n – нечётное число. В ответе запишите все найденные числа в порядке возрастания. Ответы: СтатГрад Вариант ИН2010501 26.04.2021– задание №25

Е25.13 Найдите 5 наименьших натуральных чисел, превышающих 200 000 000,

Пусть M (N) – произведение 5 наименьших различных натуральных делителей натурального числа N, не считая единицы. Если у числа N меньше 5 таких делителей, то M (N) считается равным нулю. Найдите 5 наименьших натуральных чисел, превышающих 200 000 000, для которых 0 < M (N) < N. В ответе запишите найденные значения M (N) в …

Е25.12 Пусть M – сумма минимального и максимального натуральных делителей целого числа

Пусть M – сумма минимального и максимального натуральных делителей целого числа, не считая единицы и самого числа. Если таких делителей у числа нет, то значение M считается равным нулю. Напишите программу, которая перебирает целые числа, бо́льшие 700 000, в порядке возрастания и ищет среди них такие, для которых значение M оканчивается на 8. Выведите первые …

Источник

I решение егэ по информатике

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Международный конкурс по экологии «Экология России»

Доступно для всех учеников 1-11 классов и дошкольников

Типовое задание № 2

(базовый уровень, время – 3 мин)

Тема: Анализ таблиц истинности логических выражений.

Умение строить таблицы истинности и логические схемы.

1.5.1. Высказывания, логические операции, кванторы, истинность высказывания

1.1.6. Умение строить модели объектов, систем и процессов в виде таблицы истинности для логического высказывания

К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической логике ( Ù, Ú,), неудобны, интуитивно непонятны и никак не проявляют аналогии с обычной алгеброй. Автор, к своему стыду, до сих пор иногда путает Ù и Ú. Поэтому на его уроках операция «НЕ» обозначается чертой сверху, «И» – знаком умножения (поскольку это все же логическое умножение), а «ИЛИ» – знаком «+» (логическое сложение). В разных учебниках используют разные обозначения. К счастью, в начале задания ЕГЭ приводится расшифровка закорючек ( Ù, Ú,), что еще раз подчеркивает проблему.

Что нужно знать :

Условные обозначения логических операций

A, не A (отрицание, инверсия)

A Ù B, A и B (логическое умножение, конъюнкция)

A Ú B, A или B (логическое сложение, дизъюнкция)

A → B импликация (следование)

A º B эквивалентность (равносильность)

Операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:

A → B = A Ú B или в других обозначениях A → B =

Иногда для упрощения выражений полезны формулы де Моргана:

(A Ù B) = A Ú B

(A Ú B) = A Ù B

Если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», «импликация», и самая последняя – «эквивалентность»

Таблица истинности выражения определяет его значения при всех возможных комбинациях исходных данных

Если известна только часть таблицы истинности, соответствующее логическое выражение однозначно определить нельзя, поскольку частичной таблице могут соответствовать несколько разных логических выражений (не совпадающих для других вариантов входных данных);

Количество разных логических функций, удовлетворяющих неполной таблице истинности, равно, где – число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 23=8 строчек, если заданы только 6 из них, то можно найти 28-6=22=4 разных логических функции, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)

Логическая сумма A + B + C + … равна 0 (выражение ложно) тогда и только тогда, когда все слагаемые одновременно равны нулю, а в остальных случаях равна 1 (выражение истинно)

Логическое произведение A · B · C · … равно 1 (выражение истинно) тогда и только тогда, когда все сомножители одновременно равны единице, а в остальных случаях равно 0 (выражение ложно)

Логическое следование (импликация) А→В равна 0 тогда и только тогда, когда A (посылка) истинна, а B (следствие) ложно

Эквивалентность А º B равна 1 тогда и только тогда, когда оба значения одновременно равны 0 или одновременно равны 1

Решение задач второго типа в MS Excel

1. Составить таблицу входных значения, перечисляя все комбинации переменных в порядке возрастания двоичного кода. Для этого подсчитать n число переменных в исходном выражении, выписать наборы входных переменных. Количество наборов входных переменных 2 n.

2. Для каждой строки находим логическое решение. Для этого:

· Подсчитать общее число логических операций в выражении;

· Установить последовательность выполнения логических операций с учетом скобок и приоритетов.

3. Выполнить поиск значения функции, отсортировать данное значение по искомой части (1 или 0).

A Ù B, A и B (логическое умножение, конъюнкция)

(A Ù B) = A Ú B

Базовый уровень, время 3 мин.

Infourok. ru

31.07.2017 2:01:32

2017-07-31 02:01:32

Источники:

Https://infourok. ru/reshenie-vtorogo-zadaniya-ege-po-informatike-s-pomoshyu-ms-excel-6049901.html

Информатика ЕГЭ 12 задание разбор и объяснение » /> » /> .keyword { color: red; } I решение егэ по информатике

Старое Информатика ЕГЭ 12 задание разбор

Адрес документа в Интернете (с английского — URL — Uniform Resource Locator) состоит из следующих частей:

Http

Ftp

Https

://

Каталоги на сервере разделяются прямым слэшем «/»

имя протокола сетевой службы – определяет тип сервера HTTP (протокол передачи гипертекста); разделитель в виде символа двоеточия и двух символов Slash; полное доменное имя сервера; путь поиска web-документа на компьютере; имя web-сервера; домен верхнего уровня «org»; имя национального домена «ru»; каталог main на компьютере; каталог news в каталоге main; конечная цель поиска – файл main_news. html.

Сетевые адреса

Физический адрес или MAC-адрес – уникальный адрес, «вшитый» на производстве — 48-битный код сетевой карты (в 16-ричной системе):

IP-адрес – адрес компьютера (32-битное число), состоящий из: номер сети + номер компьютера в сети (адрес узла):

Маска подсети:

необходима для определения того, какие компьютеры находятся в той же подсети; маска в двоичном коде всегда имеет структуру: сначала все единицы, затем все нули:

Та часть IP-адреса, которая соответствует битам маски равным единице, относится к адресу сети, а часть, соответствующая битам маски равным нулю – это числовой адрес компьютера

Расчет номера сети по IP-адресу и маске сети

В маске подсети Старшие биты, отведенные в IP-адресе компьютера Для номера сети, Имеют значение 1 (255); Младшие биты, отведенные в IP-адресе компьютера для Адреса компьютера в подсети, имеют значение 0.

Порядковый номер компьютера в сети

Число компьютеров в сети

Количество компьютеров сети определяется по маске: младшие биты маски — нули — отведены в IP-адресе компьютера под адрес компьютера в подсети.

1_11

Если маска:

То число компьютеров в сети:

Из них 2 специальных: адрес сети и широковещательный адрес

Решение заданий 12 ЕГЭ по информатике

Ip-адрес и доменное имя сайта: правила построения

На месте преступления были обнаружены четыре обрывка бумаги. Следствие установило, что на них записаны фрагменты одного IP-адреса. Криминалисты обозначили эти фрагменты буквами А, Б, В и Г. Восстановите IP-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем IP-адресу.

255

Ответ: ВГАБ

На сервере School. edu находится файл Rating. net, доступ к которому осуществляется по протоколу Http. Фрагменты адреса данного файла закодированы буквами А, Ь, с… g (см. таблицу). Запишите последовательность этих букв, которая кодирует адрес указанного файла в Интернете.

A	.edu
B	School
C	.net
D	/
E	Rating
F	Http
G	://

Ответ:Fgbadec

Определение адреса сети по IP-адресу и маске сети

В терминологии сетей TCP/IP маской сети называют двоичное число, которое показывает, какая часть IP-адреса узла сети относится к адресу сети, а какая – к адресу узла в этой сети. Адрес сети получается в результате применения поразрядной конъюнкции к заданному адресу узла и его маске.

По заданным IP-адресу узла сети и маске Определите адрес сети:

При записи ответа выберите из приведенных в таблице чисел четыре элемента IP-адреса и запишите в нужном порядке соответствующие им буквы без точек.

A	B	C	D	E	F	G	H
0	145	255	137	128	240	88	92

✍ Решение:

145.92

137

240

BHEA

Результат: BHEA

Предлагаем посмотреть подробный видеоразбор:

Определение маски сети

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая — к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес, — в виде четырех байтов, причем каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого разряда — нули. Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске.

Например, если IP-адрес узла равен 211.132.255.41, а маска равна 255.255.201.0, то адрес сети равен 211.132.201.0

Для узла с IP-адресом 200.15.70.23 адрес сети равен 200.15.64.0. Чему равно Наименьшее возможное значение третьего слева байта маски? Ответ запишите в виде десятичного числа.

✍ Решение:

192

Результат: 192

Пошаговое решение данного 12 задания ЕГЭ по информатике доступно в видеоуроке:

В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится к адресу сети, а какая – к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IP-адрес, – в виде четырёх байтов, причём каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого разряда – нули.
Адрес сети получается в результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске.

Например, если IP-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.

Для узла с IP-адресом 57.179.208.27 адрес сети равен 57.179.192.0. Каково Наибольшее возможное количество Единиц в разрядах маски?

✍ Решение:

? & 0 = 0

Наибольшее

? & 1 = 0

11111111.11111111.11100000.00000000

Результат: 19

Подробное решение 12 задания демоверсии ЕГЭ 2018 года смотрите на видео:

Два узла, находящиеся в разных подсетях, имеют IP-адреса 132.46.175.26 и 132.46.170.130. В масках обеих подсетей Одинаковое количество единиц. Укажите Наименьшее возможное Количество единиц в масках этих подсетей.

В маске подсети сначала следуют единичные биты, которые соответствуют адресу подсети в IP-адресе компьютера. Так как адреса подсети двух компьютеров из условия задачи разные, но при этом количество единиц в их масках совпадает, то необходимо определить в IP-адресах компьютеров первый слева бит, который у них будет различен. Этот бит будет относиться к адресу подсети, а остальные биты, идущие справа от него, могут относиться уже к адресу компьютера. Таким образом, найдем первый слева различный бит: Получаем, что в маске подсети все биты, включая тот, что соответствует выделенным, будут равны единице. Отобразим это, переводя в двоичную систему счисления только интересующий нас байт. Выделим ту часть адресов, которая соответствует наименьшему возможному адресу подсети (соответственно, наименьшему количеству единиц в маске): 255 для маски — это 8 единиц. Посчитаем общее количество единиц в маске (она одинакова для обеих компьютеров):

Ответ: 22

Количество различных значений маски

Для узла с IP-адресом 93.138.161.94 адрес сети равен 93.138.160.0. Для скольких Различных значений маски это возможно?

✍ Решение:

Результат: 5

Определение номера компьютера

Если маска подсети 255.255.255.128 и IP-адрес компьютера в сети 122.191.12.189, то номер компьютера в сети равен _____.

✍ Решение:

128

189

Результат: 61

Подробное решение данного задания смотрите на видео:

Количество адресов компьютеров

В терминологии сетей TCP/IP маской подсети называется 32-разрядное двоичное число, определяющее, какие именно разряды IP-адреса компьютера являются общими для всей подсети — в этих разрядах маски стоит 1. Обычно маски записываются в виде четверки десятичных чисел — по тем же правилам, что и IP-адреса.

Для некоторой подсети используется маска 255.255.255.192. Сколько различных Адресов компьютеров теоретически допускает эта маска, если два адреса (адрес сети и широковещательный) не используют?

Порядковый номер компьютера в сети

1_11

Если маска:

То число компьютеров в сети:

Из них 2 специальных: адрес сети и широковещательный адрес

Таким образом, найдем первый слева различный бит.

Labs-org. ru

11.10.2018 5:56:05

2018-10-11 05:56:05

Источники:

Https://labs-org. ru/ege-12_/

Теория и решение 15 задания егэ по информатике » /> » /> .keyword { color: red; } I решение егэ по информатике

Решение 15 задания ЕГЭ по информатике про основные законы Алгебры Логики

15-е задание: «Основные законы алгебры логики»
Уровень сложности — повышенный,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 5 минут.

Проверяемые элементы содержания: Знание основных понятий и законов математической логики

«Важно понимать, что выражение должно быть тождественно истинно, т. е. истинно при любых допустимых значениях переменных x и у, а не только при некоторых наборах значений»

Элементы математической логики

Для решения 15 задания, потребуется знание таблиц истинности.

Для выполнения задания рекомендуется повторить следующие темы:

(A ∧ B) ∨ C = (A ∨ C) ∧ (B ∨ C)
(A ∨ B) ∧ С = (A ∧ С) ∨ (B ∧ С)
И наоборот:
(A ∨ B) ∧ (A ∨ C) = A ∨ (B ∧ C)
(A ∧ B) ∨ (A ∧ C) = A ∧ (B ∨ C)

A ∨ A ∧ B = A
A ∧ (A ∨ B) = A
A ∨ A ∧ B = A ∨ B
A ∨ A ∧ B = A ∨ B
A ∧ (A ∨ B) = A ∧ B
A ∧ (A ∨ B) = A ∧ B

выражения в скобках, операции «НЕ», операции «И», операции «ИЛИ», операции «импликация» операции «эквиваленция»

A → B → C → D = ((A → B) → C) → D

Математическая логика и теория множеств

Пересечение

Логическому умножению

Объединение

Сложению

Пересечением

Пример:

Пример разности множеств:

Для большей определенности стоит рассмотреть тему круги Эйлера

Задания с отрезками и ДЕЛ

Для решения заданий необходимо знать рассмотренную тему о множествах.

Для упрощения решений можно пользоваться следующими законами.

1. Если в задании формула тождественно истинна (равна 1), и
2. после упрощения A Без отрицания
То используется закон:

Где B — известная часть выражения.

1. Если в задании формула тождественно истинна (равна 1), и
2. после упрощения A С отрицанием
То используется закон:

Где B — известная часть выражения.

1. Если в задании формула тождественно ложна (равна 0), и
2. после упрощения A Без отрицания
То используется закон:

Где B — известная часть выражения.

1. Если в задании формула тождественно ложна (равна 0), и
2. после упрощения A С отрицанием
То используется закон:

Задания с поразрядной конъюнкцией

В задании 15 ЕГЭ встречаются задачи, связанные с поразрядной конъюнкцией.
Например:

Означает поразрядную конъюнкцию (логическое «И») между двоичными значениями двух чисел — 5 и 26. Выполняется так:

Задания, связанные с поразрядной конъюнкцией, решаются несколькими способами. Рассмотрим один из них.

Обозначим: Для решения методом, предложенным А. В. Здвижковой, пригодится использование следующих свойств:

Условие Zk → Zm истинно для любых натуральных значений X тогда и только тогда, когда Все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.

На деле, это означает, что если имеем: то сначала введем замену: а затем, используя свойство 3, определим истинность высказывания Z29 → Z5: таким образом, получили:

Так, например, если в задании имеем: то сначала введем замену и, используя свойство 4, получим:

Решение заданий 15 ЕГЭ по информатике

Плейлист видеоразборов задания на YouTube:

Задания с множествами

Элементами множества А являются натуральные числа. Известно, что выражение

Истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение Суммы элементов множества A .

Введем обозначения: Выполним преобразования: Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть ( А ) была непременно истинной, необходимо, чтобы известная часть была ложна: То есть получаем: Таким образом имеем пересечение (умножение) двух множеств Q и P. То есть необходимо выбрать элементы, которые встречаются в обоих множествах одновременно: Сумма элементов:

Ответ: 12

📹 Видеорешение на RuTube здесь

Элементами множества А являются натуральные числа. Известно, что выражение

Истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение Суммы элементов множества A .

Ответ: 18

Элементами множеств А, P, Q являются натуральные числа, причём P = , Q = . Известно, что выражение

Истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наибольшее возможное Количество элементов в множестве A .

Введем обозначения: Выполним преобразования: Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть ( А ) была непременно истинной, необходимо, чтобы известная часть была ложна: То есть получаем: Таким образом имеем разность двух множеств Q и P. То есть это новое множество, элементы которого принадлежат P, но не принадлежат Q : Количество элементов = 7

Ответ: 7

Элементами множества А являются натуральные числа. Известно, что выражение

Истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите Наименьшее возможное количество элементов множества A.

Введем обозначения: Выполним преобразования: Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть ( А ) была непременно истинной, необходимо, чтобы известная часть была ложна: То есть получаем: Таким образом имеем пересечение двух множеств Q и P : Количество элементов = 1

Ответ: 1

Задания с отрезками на числовой прямой

Отрезки на числовой прямой:

На числовой прямой даны два отрезка: P=[44,48] и Q=[23,35].

Укажите Наибольшую возможную длину отрезка А, для которого формула

Тождественно Ложна, то есть принимает значение 0 при любом значении переменной X.

✍ Решение:

X ϵ

Результат: 4
✎ Решение 2 (программирование):
Внимание! этот способ подходит НЕ для всех заданий с отрезками!
Python:

PascalABC. net:

С подробным Аналитическим решением задания 15 ЕГЭ по информатике можно ознакомиться по видео:

📹 Видеорешение на RuTube здесь

Отрезки на числовой прямой:

15_9: Разбор 15 (18) задания ЕГЭ по информатике, вариант 5 (ФИПИ, «ЕГЭ информатика и ИКТ, типовые экзаменационные варианты 2018», С. С. Крылов, Т. Е. Чуркина):

На числовой прямой даны два отрезка: P = [10,20] и Q = [30,40].

Укажите Наибольшую возможную длину отрезка A, для которого формула

Тождественно Истинна, то есть принимает значение 1 при любом значении переменной X.

✍ Решение:

Упростим выражение, введя обозначения: Запишем формулу с новыми обозначениями, учитывая, что по условию она должна быть тождественно истинной: Избавимся от импликации: Используем закон Де Моргана для последующего преобразования: А — наше неизвестное, а выделенную часть формулы можно найти. Необходимо, чтобы А = 1. Значит, предположим, что А = 0, тогда P ∧ Q = 1 (если P ∧ Q = 0, то А может равняться и 0 и 1, так как имеет место операция логического сложения ∨) Значит, имеем P ∧ Q = 1. Кроме того, в данном случае имеет место операция конъюнкция, которую проще вычислить, если выражение равно 1 (так как для конъюнкции существует один единственный случай истинности: 1 & 1 = 1). Таким образом имеем утверждения: Т. е. A истинно (=1) на промежутке пересечения отрезков P и Q. Отобразим отрезки на числовой прямой, чтобы найти искомое значение:

Результат: 10

Отрезки на числовой прямой:

15_10: Вариант 6: ФИПИ, «ЕГЭ информатика и ИКТ, типовые экзаменационные варианты 2018», С. С. Крылов, Т. Е. Чуркина:

На числовой прямой даны два отрезка: P = [3, 20] и Q = [6, 12].

Укажите наибольшую возможную длину отрезка A, для которого формула

Тождественно Истинна, то есть принимает значение 1 при любом значении переменной X.

✍ Решение:

Упростим выражение, введя обозначения: Запишем формулу с новыми обозначениями, учитывая, что по условию она должна быть тождественно истинной: Избавимся от импликации:

Далее возможно 2 способа решения.

✎ 2 способ:
После того, как мы избавились от импликации, имеем:

Результат: 8

С решением задания 15 вы также можете ознакомиться, посмотрев видео (аналитическое решение):

📹 Видеорешение на RuTube здесь

Отрезки на числовой прямой:

15_11: Вариант 7: ФИПИ, «ЕГЭ информатика и ИКТ, типовые экзаменационные варианты 2018», С. С. Крылов, Т. Е. Чуркина:

На числовой прямой даны два отрезка: P = [11, 21] и Q = [15, 40].

Укажите Наибольшую возможную длину отрезка A, для которого формула

Тождественно Истинна, то есть принимает значение 1 при любом значении переменной X.

✍ Решение:

P = 1 и Q = 0

P = 0 и Q = 1

Результат: 19

Задания с ДЕЛ

Поиск наибольшего А, известная часть Дел ∨ Дел = 1

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого Наибольшего натурального числа А формула

Тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной Х)?

✍ Решение:

Истинно

Далее можно решать задание либо с помощью кругов Эйлера, либо с помощью логических рассуждений.

Решение с помощью логических рассуждений:

Решение с помощью кругов Эйлера:

Результат: 8

✎ Решение 2 (программирование):
Python:

For A in range(1,500): OK = 1 for x in range(1,1000): OK *= ((x % 40 == 0) or (x % 64 == 0))<=(x % a== 0) if ok: print( a )

PascalABC. net:

Begin for var A := 1 to 500 do begin var ok := 1; for var x := 1 to 1000 do begin if (((x mod 40 = 0) or (x mod 64 = 0))

Результат: 8

Поиск наименьшего А, известная часть Дел ∧ Дел = 1

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого Наименьшего натурального числа А формула

Тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной Х)?

✍ Решение:

Избавимся от импликации:

✎ Решение 2 (программирование). Язык Python, Pascal:

Из общего выражения:

For A in range(1,50): OK = 1 for x in range(1,1000): OK *= (x % A == 0)

Begin for var A := 1 to 50 do begin var ok := 1; for var x := 1 to 1000 do begin if (x mod A = 0) 0)or (x mod 42 = 0)) = false then begin ok := 0; break; end; end; if (ok = 1) then begin print(A); break; end end; end.

OK — переменная-индикатор: если находится такое А при котором, диапазон всех значений x, подставленных в выражение, возвращает истинное значение выражения, то ОК остается равным 1, т. к. используется операция умножения (до цикла ОК необходимо присвоить единице).
Следует иметь в виду, что в программировании вместо операции импликация ( -> ) можно использовать нестрогое неравенство: . Т. к. таблица истинности для операции импликация соответствует операции

Результат: 3

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого Наименьшего натурального числа А формула

Тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной Х)?

✍ Решение:

✎ Решение 2 (программирование). Язык Python:

Из общего выражения:

For A in range(1,500): OK = 1 for x in range(1,1000): OK *= ((x % 19 != 0) or (x % 15 != 0))

Результат: 285

Задания с поразрядной конъюнкцией

Обозначим через M & n поразрядную конъюнкцию неотрицательных целых чисел M и N. Так, например, 12&6 = 11002&01102 = 01002 = 4

Для какого наименьшего неотрицательного целого числа A формула

Тождественно Ложна (то есть принимает значение 0 при любом неотрицательном значении переменной X)?

✍ Решение:

Стоит заметить, что для такого типа задач, нет универсального единственного решения. Поэтому на видео, расположенном ниже, представлено два варианта решения.
✎ Способ 1:
Рассмотрим один из вариантов решения:

Ответ: 3

Используем метод А. В. Здвижковой.

Произвести замену (x & K = 0) на Zk Выполнить преобразования по свойству импликации и закону Де Моргана. Стремиться прийти к выражению с конъюнкциями без отрицаний типа: Zk * Zm. Все выражения типа Zk * Zm преобразовать по свойству
Zk * Zm = Zk or m. Путем преобразований прийти к импликации: Zk → Zm.

Условие Zk → Zm истинно для любых натуральных значений x тогда и только тогда, когда все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.

Результат: 3

Детальный Разбор данного задания 15 ЕГЭ по информатике предлагаем посмотреть на видео:

Вариант решения №1 (универсальный, теоретический):

📹 Видеорешение на RuTube здесь

Вариант решения №2 (не универсальный, но простой):

Обозначим через M & N поразрядную конъюнкцию неотрицательных целых чисел M и N. Так, например, 12&6 = 11002&01102 = 01002 = 4

Для какого наибольшего неотрицательного целого числа A формула

Тождественно Истинна (то есть принимает значение 1 при любом неотрицательном значении переменной X)?

✍ Решение:

Результат: 38

Подробное Решение данного задания 15 ЕГЭ по информатике предлагаем посмотреть в видео уроке:
Способ 1:

📹 Видеорешение на RuTube здесь
Способ 2:

📹 Видеорешение на RuTube здесь

Поразрядная конъюнкция:

Определите Наименьшее натуральное число А из интервала [43, 55], такое, что выражение

Тождественно ложно (то есть принимает значение 0 при любом натуральном значении переменной Х)?

✍ Решение:

Кратко изложенное решение *:

Результат: 48

Определите Набольшее натуральное число A, такое что выражение

Тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной Х)?

✍ Решение:

По правилу импликации

3-й

Результат: 8

Задания на поиск наибольшего или наименьшего числа А

Поиск наибольшего или наименьшего числа А:

Для какого наибольшего целого числа А формула

Тождественно Истинна, то есть принимает значение 1 при любых целых неотрицательных X и Y?

Важно: Поскольку используется метод полного перебора, то возможна ситуация, когда транслятор будет работать слишком медленно. Но работоспособность представленного алгоритма проверена на онлайн компиляторах.

Begin for var A := 200 downto -100 do begin var OK := 1; for var x := 0 to 100 do for var y := 0 to 100 do if ((x

For A in range(200,-100,-1): OK = 1 for x in range(0,100): for y in range(0,100): OK *= ((x<=9) <= (x*x<=a)) and((y*y<=a) <= (y<=9)) if ok: print(a) break

✎ Способ 2 (теоретическое решение):

Условно разделим исходное выражение на части:

(импликация 0 → 0 = 1)

Результат: 99

Подробное решение 15 (18) задания демоверсии ЕГЭ 2018 года смотрите на видео (аналитическое решение):

📹 Видеорешение на RuTube здесь

Поиск наибольшего или наименьшего числа А:

Укажите Наименьшее значение А, при котором выражение

Истинно для любых целых положительных значений X и Y.

✍ Решение:

Begin for var A := -100 to 200 do begin var OK := 1; for var x := 1 to 100 do for var y := 1 to 100 do if ((y+3*x20)or(y>40)) = false then begin OK := 0; break; end; if OK = 1 then begin print(A); break end; end; end.

For A in range(-100,200): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (y+3*x 20) or (y > 40) if OK: print(A) break

✎ Способ 2 (теоретическое решение):

X = 20

Y = 40

Результат: 101

Подробное решение досрочного ЕГЭ 2018 года смотрите на видео (аналитическое решение):

📹 Видеорешение на RuTube здесь

Поиск наибольшего или наименьшего числа А:

Для какого наибольшего целого неотрицательного числа А выражение

✎ Решение 2 (программное):
Python:

For A in range(200,0,-1): OK = 1 for x in range(0,100): for y in range(0,100): OK *= (48!=y+2*x) or(A

Результат: 15

Видео решения 15 (18) задания демоверсии ЕГЭ 2019 (аналитическое решение):

📹 Видеорешение на RuTube здесь

Поиск наибольшего или наименьшего числа А:

15_19. Разбор 15 (18) задания ЕГЭ вариант № 3, 2019 Информатика и ИКТ Типовые экзаменационные варианты (10 вариантов), С. С. Крылов, Т. Е. Чуркина:

Для какого наименьшего целого числа А формула

✎ Решение 2 (программное):
Python:

For A in range(-100,100): OK = 1 for x in range(0,100): for y in range(0,100): OK *= (y+5*x<=34)<=((y-x >4)or(y<=a)) if ok: print( a ) break

Begin for var A := -100 to 100 do begin var OK := true; for var x := 0 to 100 do begin for var y := 0 to 100 do begin OK := (y + 5 * x 4) or (y

Результат: 9

Поиск наибольшего или наименьшего числа А:

Укажите Наименьшее целое значение А при котором выражение

(2y + 5x 100) ∨ (3x – 2y > 70)

Истинно для любых целых положительных значений X и Y.

For A in range(-200,200): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (2*y + 5*x < a) or (2*x + 4*y >100) or (3*x — 2*y > 70) if OK: print( A ) break

Begin for var A := -200 to 200 do begin var OK := true; for var x := 1 to 100 do begin for var y := 1 to 100 do begin OK := (2*y + 5*x < a) or (2*x + 4*y >100) or (3*x — 2*y > 70); if OK = false then break; end; if OK = false then break; end; if OK then begin print(A); break; end; end; end.

Результат: 171

Видео разбора задания смотрите на видео (аналитическое решение):

📹 Видеорешение на RuTube здесь

Поиск наибольшего или наименьшего числа А:

Укажите Наибольшее целое значение А при котором выражение

(3y – x > A) ∨ (2x + 3y ✎ Решение 1 (теоретическое):

✎ Решение (программное):
Python:

For A in range(200,-200,-1): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (3*y-x>A) or (2*x+3*y

Решение заданий 15 ЕГЭ по информатике

Плейлист видеоразборов задания на YouTube:

Элементами множества А являются натуральные числа. Известно, что выражение

Истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение Суммы элементов множества A .

Ответ: 12

📹 Видеорешение на RuTube здесь

Элементами множества А являются натуральные числа. Известно, что выражение

Истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наименьшее возможное значение Суммы элементов множества A .

Ответ: 18

Элементами множеств А, P, Q являются натуральные числа, причём P = , Q = . Известно, что выражение

Истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите наибольшее возможное Количество элементов в множестве A .

Введем обозначения: Выполним преобразования: Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть ( А ) была непременно истинной, необходимо, чтобы известная часть была ложна: То есть получаем: Таким образом имеем разность двух множеств Q и P. То есть это новое множество, элементы которого принадлежат P, но не принадлежат Q : Количество элементов = 7

Ответ: 7

Элементами множества А являются натуральные числа. Известно, что выражение

Истинно (т. е. принимает значение 1) при любом значении переменной х.

Определите Наименьшее возможное количество элементов множества A.

Введем обозначения: Выполним преобразования: Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть ( А ) была непременно истинной, необходимо, чтобы известная часть была ложна: То есть получаем: Таким образом имеем пересечение двух множеств Q и P : Количество элементов = 1

Ответ: 1

Пример:

Сумма элементов.

Labs-org. ru

29.12.2017 0:42:23

2017-12-29 00:42:23

Источники:

Https://labs-org. ru/ege-15/

Источник