Всего: 42 1–20 | 21–40 | 41–42
Добавить в вариант
Два насоса перекачивают нефть из двух резервуаров в танкер. Сначала I‐й насос перекачал всю нефть из первого резервуара, затем нефть из второго резервуара была перекачана вместе I‐м и II‐м насосами. После того, как была перекачана всей нефти, оказалось, что время, необходимое для завершения работы, в
раза меньше времени, за которое мог бы перекачать всю нефть один I‐й насос. Кроме того, известно, что если бы из второго резервуара нефть перекачивал только II‐й насос, то ему для этого потребовалось бы вдвое больше времени, нежели I‐ому насосу для перекачки всей нефти из обоих резервуаров. Определите, во сколько раз производительность I‐го насоса больше производительности II‐го.
Источник: А. Ларин: Тренировочный вариант № 195.
Первый и второй насосы наполняют бассейн за 9 минут, второй и третий — за 14 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
Первый и второй насосы наполняют бассейн за 9 минут, второй и третий — за 12 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
Первый и второй насосы наполняют бассейн за 10 минут, второй и третий — за 15 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
Первый и второй насосы, работая вместе, наполняют бассейн за 90 минут, второй и третий, работая вместе, — за 140 минут, а первый и третий, работая вместе, — за 180 минут. За сколько минут заполнят бассейн все три насоса, работая вместе?
Первый и второй насосы, работая вместе, наполняют бассейн за 80 минут, второй и третий, работая вместе, — за 90 минут, а первый и третий, работая вместе, — за 240 минут. За сколько минут заполнят бассейн все три насоса, работая вместе?
Первый насос наполняет бак за 20 минут, второй — за 30 минут, а третий — за 1 час. За сколько минут наполнят бак три насоса, работая одновременно?
Химический комбинат получил заказ на изготовление этилового спирта, соляной кислоты и дистиллированной воды. Для готовой продукции потребовалась 21 железнодорожная цистерна. При перекачивании были использованы три специализированных насоса: сначала первый насос наполнил четыре цистерны этиловым спиртом, затем второй насос наполнил шестнадцать цистерн соляной кислотой и в завершение третий насос наполнил одну цистерну дистиллированной водой. Найдите минимально возможное время, затраченное на перекачивание всех продукции, если известно, что суммарная производительность всех насосов равна семи цистернам в сутки.
Источник: А. Ларин. Тренировочный вариант № 307. (Часть C)
Первый и второй насосы наполняют бассейн за 10 минут, второй и третий — за 15 минут, а первый и третий — за 24 минуты. За сколько минут три эти насоса заполнят бассейн, работая вместе?
Раздел: Арифметика
В среднем из 2000 садовых насосов, поступивших в продажу, 2 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Источник: ЕГЭ по математике 23.04.2013. Досрочная волна. Восток. Вариант 1.
Для заполнения бассейна используют 2 насоса. Известно, что если включить первый на 1 ч, а затем только второй на 4 ч, бассейн будет заполнен не меньше чем на четверть и не более чем на 40%. Если включить первый на 3 ч, затем только второй на 2 ч, бассейн будет наполнен не меньше чем на 30% и не больше чем на половину. На сколько процентов максимально может наполнить бассейн один первый насос за 1 час?
Источник: А. Ларин. Тренировочный вариант № 303. (Часть C)
Первый садовый насос перекачивает 5 литров воды за 2 минуты, второй насос перекачивает тот же объём воды за 3 минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 25 литров воды?
В помощь садовому насосу, перекачивающему 9 литров воды за 1 минуту, подключили второй насос, перекачивающий тот же объем воды за 2 минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 54 литра воды?
При производстве в среднем на каждые 2982 исправных насоса приходится 18 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
В среднем из 1400 садовых насосов, поступивших в продажу, 7 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
В среднем из 500 садовых насосов, поступивших в продажу, 4 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
В среднем из 2000 садовых насосов, поступивших в продажу, 20 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
В среднем из 2000 садовых насосов, поступивших в продажу, 14 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
При производстве в среднем на каждые 1683 исправных насоса приходится 17 неисправных. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
В среднем из 1500 садовых насосов, поступивших в продажу, 9 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Всего: 42 1–20 | 21–40 | 41–42
Первый и второй насосы наполняют бассейн за 9 минут, второй и третий – за 12 минут, а первый и третий – за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
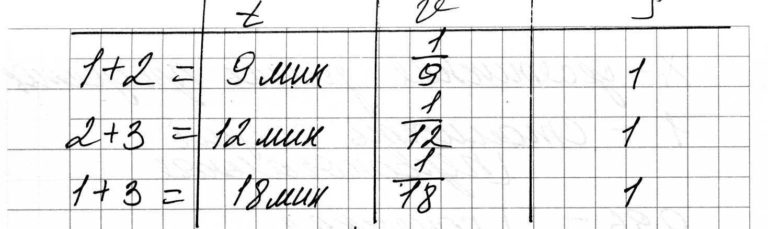
Сложим скорости насосов и поделим на два, так как каждый насос будет повторятся дважды.
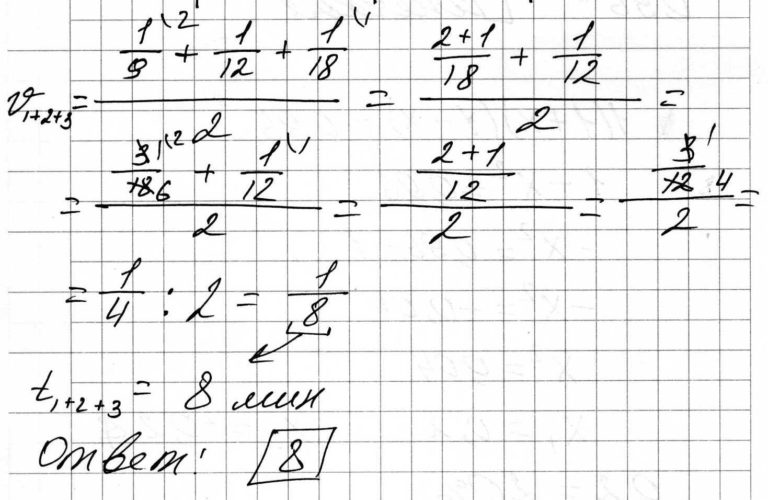
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4 / 5. Количество оценок: 22
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
6 февраля 2014
Это последнее видео из серии уроков, посвященных задачам B14 из ЕГЭ по математике. И сегодня мы детально разберем довольно сложную задачу на производительность труда, которая сводится к трем уравнениям с тремя неизвестными. Будьте внимательны: в этой задаче важно буквально каждое слово!
Задача B14. Первый и второй насосы, работая вместе, наполняют бассейн за 9 часов. Второй и третий насосы, работая вместе, наполняют этот же бассейн за 18 часов, а первый и третий насосы — за 12 часов. За сколько минут наполнят бассейн три насоса, работая одновременно?
Основные ошибки при решении этой задачи:
- Ученики не понимают, что нас интересует лишь суммарная производительность всех трех насосов. В результате начинают считать каждый насос (переменные x, y и z), что очень часто приводит к арифметическим ошибкам — ведь числа получаются довольно некрасивыми.
- Даже если ученик сосчитает все правильно, ответ зачастую все равно оказывается неправильным, потому что от нас требуется найти время в минутах. А в процессе решения мы получаем не минуты, а часы.
Вот и все, что нужно знать для решения задач B14 на производительность труда. Теперь, посмотрев эти уроки и самостоятельно потренировавшись, вы решите любую (абсолютно любую!) задачу B14 в настоящем ЕГЭ по математике. Желаю вам успехов на экзамене, а мы идем дальше — к задачам B15.:)
Смотрите также:
- Изюм и виноград (смеси и сплавы)
- Семья из трех человек (нестандартная задача)
- Умножение и деление десятичных дробей
- Так сокращать дроби нельзя!
- Вебинар по задачам 18: модуль и окружности
- Случай четырехугольной пирамиды
Сложная задача B14: работа трех исполнителей
Это последнее видео из серии уроков, посвященных задачам B14 из ЕГЭ по математике. И сегодня мы детально разберем довольно сложную задачу на производительность труда, которая сводится к трем уравнениям с тремя неизвестными. Будьте внимательны: в этой задаче важно буквально каждое слово!
Задача B14. Первый и второй насосы, работая вместе, наполняют бассейн за 9 часов. Второй и третий насосы, работая вместе, наполняют этот же бассейн за 18 часов, а первый и третий насосы — за 12 часов. За сколько минут наполнят бассейн три насоса, работая одновременно?
Основные ошибки при решении этой задачи:
- Ученики не понимают, что нас интересует лишь суммарная производительность всех трех насосов. В результате начинают считать каждый насос (переменные x, y и z), что очень часто приводит к арифметическим ошибкам — ведь числа получаются довольно некрасивыми.
- Даже если ученик сосчитает все правильно, ответ зачастую все равно оказывается неправильным, потому что от нас требуется найти время в минутах. А в процессе решения мы получаем не минуты, а часы.
Вот и все, что нужно знать для решения задач B14 на производительность труда. Теперь, посмотрев эти уроки и самостоятельно потренировавшись, вы решите любую (абсолютно любую!) задачу B14 в настоящем ЕГЭ по математике. Желаю вам успехов на экзамене, а мы идем дальше — к задачам B15.:)
Источник статьи: http://www.berdov.com/ege/text_problem/tri-nasosa/
Как решать задачи с насосами егэ
Первый и второй насосы наполняют бассейн за 9 минут, второй и третий — за 14 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
Наименьшее общее кратное чисел 9, 14 и 18 равно 126. За 126 минут первый и второй, второй и третий, первый и третий насосы (каждый учтен дважды) заполнят 14 + 9 + 7 = 30 бассейнов. Следовательно, работая одновременно, первый, второй и третий насосы заполняют 15 бассейнов за 126 минут, а значит, 1 бассейн за 8,4 минуты.
За одну минуту первый и второй насосы заполнят 1/9 бассейна, второй и третий — 1/14 бассейна, а первый и третий — 1/18 бассейна. Работая вместе, за одну минуту два первых, два вторых и два третьих насоса заполнят
бассейна.
Тем самым, они могли бы заполнить бассейн за 21/5 минуты или за 4,2 минуты. Поскольку каждый из насосов был учтен два раза, в реальности первый, второй и третий насосы, работая вместе, могут заполнить бассейн за 8,4 минуты.
Приведем алгебраическое решение Тимура Алиева.
Пусть x — производительность первого насоса, y — производительность второго насоса, z — производительность третьего насоса. Тогда
Сложив уравнения, получим
Тогда при совместной работе всех трех насосов время заполнения бассейна составит минуты.
Источник статьи: http://math-ege.sdamgia.ru/problem?id=323852
Как решать задачи с насосами егэ
Первый и второй насосы наполняют бассейн за 9 минут, второй и третий — за 14 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
Наименьшее общее кратное чисел 9, 14 и 18 равно 126. За 126 минут первый и второй, второй и третий, первый и третий насосы (каждый учтен дважды) заполнят 14 + 9 + 7 = 30 бассейнов. Следовательно, работая одновременно, первый, второй и третий насосы заполняют 15 бассейнов за 126 минут, а значит, 1 бассейн за 8,4 минуты.
За одну минуту первый и второй насосы заполнят 1/9 бассейна, второй и третий — 1/14 бассейна, а первый и третий — 1/18 бассейна. Работая вместе, за одну минуту два первых, два вторых и два третьих насоса заполнят
бассейна.
Тем самым, они могли бы заполнить бассейн за 21/5 минуты или за 4,2 минуты. Поскольку каждый из насосов был учтен два раза, в реальности первый, второй и третий насосы, работая вместе, могут заполнить бассейн за 8,4 минуты.
Приведем алгебраическое решение Тимура Алиева.
Пусть x — производительность первого насоса, y — производительность второго насоса, z — производительность третьего насоса. Тогда
Сложив уравнения, получим
Тогда при совместной работе всех трех насосов время заполнения бассейна составит минуты.
Источник статьи: http://ege.sdamgia.ru/problem?id=323852
Как решать задачи с насосами егэ
Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей за час изготавливает второй рабочий, если известно, что первый за час изготавливает на 1 деталь больше?
Обозначим — число деталей, которые изготавливает за час второй рабочий. Тогда первый рабочий за час изготавливает
деталь. На изготовление 110 деталей первый рабочий тратит на 1 час меньше, чем второй рабочий, отсюда имеем:
Таким образом, второй рабочий изготавливает 10 деталей в час.
Если первый рабочий тратит на час меньше, то не должно ли быть (110/n+1) — 1?
Объясните, пожалуйста, никак не сообразить
Большее время равно увеличеному на час меньшему.
так как у второго время выполнения больше идет,то чтобы уравнять время выполнения,надо к первой работе прибавить 1 час
Заказ на 156 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей за час изготавливает первый рабочий, если известно, что он за час изготавливает на 1 деталь больше второго?
Обозначим — число деталей, которые изготавливает за час первый рабочий, тогда второй рабочий за час изготавливает
деталь,
На изготовление 156 деталей первый рабочий тратит на 1 час меньше, чем второй рабочий, отсюда имеем:
Таким образом, первый рабочий изготавливает 13 деталей в час.
если брать за n число деталей второго рабочего ,а первого n+1 то получим в конце уравнение n^2+n-156=0 где корнями будут числа 12 и -13 следовательно ответ 12. Но по данному решению ответ 13 не понимаю объясните кто-нибудь.
Таким образом вы найдёте число деталей, которые изготавливает в час второй рабочий. Первый рабочий изготавливает на одну деталь в час больше, следовательно, ответ — 13.
На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?
Обозначим – число деталей, которые изготавливает за час первый рабочий, тогда второй рабочий за час изготавливает
деталей,
На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей, отсюда имеем:
Таким образом, первый рабочий делает 25 деталей в час
На изготовление 99 деталей первый рабочий тратит на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей. Известно, что первый рабочий за час делает на 1 деталь больше, чем второй. Сколько деталей в час делает второй рабочий?
Обозначим — число деталей, которые изготавливает за час второй рабочий. Тогда первый рабочий за час изготавливает
деталь. На изготовление 99 деталей первый рабочий тратит на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей, отсюда имеем:
Таким образом, второй рабочий делает 10 деталей в час.
Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй – за три дня?
Обозначим и
— объёмы работ, которые выполняют за день первый и второй рабочий, соответственно, полный объём работ примем за 1. Тогда по условию задачи
и
Решим полученную систему:
Тем самым, первый рабочий за день выполняет одну двадцатую всей работы, значит, работая отдельно, он справится с ней за 20 дней.
Приведем арифметическое решение.
Пусть первый рабочий, работая один, выполняет в день некоторую часть работы; назовем ее нормой. Тогда второй выполняет две трети нормы, а вместе рабочие выполняют пять третьих нормы. За 12 дней рабочие выполнят всю работу или норм. Следовательно, первый рабочий один может выполнить всю работу за 20 дней.
Приведем арифметическое решение Павла Юкляева.
Первый рабочий работает в 1,5 раза быстрее второго. Тогда, работая вместе, рабочие будут работать в 2,5 раза быстрее, чем один второй рабочий. Следовательно, один второй рабочий потратил бы на выполнение заказа 12 · 2,5 = 30 дней, тогда один первый рабочий потратил бы 30 : 1,5 = 20 дней.
Источник статьи: http://ege.sdamgia.ru/test?theme=87
Решение задач на движение, работу, трубы и насосы. Задача из ЕГЭ №11, ОГЭ №22.
На сколько показывает практика, многие ребята избегают решения задач. Это происходит по разным причинам. В основном, это кажется сложным. Безусловно, есть такие задачи, но сегодня не о них.
Есть такой универсальный метод, который подходит для решения более простых задач на движение, насосов, работу. Этот способ хорош, когда речь идет о двух составляющих в задачах. Например: движение «туда-обратно», два автомобиля, два насоса, принтера итд. Такие задачи даются на ОГЭ №22 и ЕГЭ №11.
Строго говоря, методов и способ имеется множество, и, каждый пользуется тем, который ему ближе и понятнее. Покажу свой, для тех, кто вабще не берется решать такие задачи. Это табличный метод. Здесь достаточно внести в таблицу данные задачи и составить уравнение.
Возьмем для наглядности самую простую:
Нарисуем табличку и заполним ее, исходя из условия:
Чем хорош этот способ, так это тем, что особенно думать здесь не нужно. Всегда имеется три колонки, в одной из которых будет стоять конкретное число, в данном случае 208 — расстояние, во вторую вносится икс, а в третьей записывается выражение, которое составляется из двух заполненных, согласно формуле движения.
Именно из этих двух, полученных выражений и составляется уравнение. Чтобы его составить в задаче всегда имеется дополнительное условие. В данном случае это то, что лодка затратила на обратный путь на 5ч меньше.
Здесь у многих начинаются головняки. Куда прибавить или отнять эту пятерку? Да не надо ее никуда прибавлять/отнимать. Задачи такого типа называются «на разницу» . Дешевле-дороже, быстрее-медленнее, короче-длиннее на столько-то.
Само слово, которое обозначает величину «больше/меньше» не важнО. Как только вы видите, что в задаче написано «на столько-то», сразу нужно понимать, что уравнение составляется со знаком минус.
То есть, из большего выражения вычитаем меньшее, равно «разница».
Поясню: в данной задаче мы получили два выражения: 208/(х+5) и 208/(х-5). Из таблицы понятно, что это время, t. Если лодка движется против течения, то на один и тот же путь, она затратит больше времени, чем по течению. Логично?
Следовательно, выражение 208/(х-5) — большее, 208/(х+5) — меньшее, а 5ч — разница.
Вот и уравнение: 208/(х-5) — 208/(х+5) = 5. Приводить его решение я не буду, это отдельная тема. Давайте возьмем другую задачу:
Источник статьи: http://zen.yandex.ru/media/id/5d15af75fea5d300afaf8fd5/reshenie-zadach-na-dvijenie-rabotu-truby-i-nasosy-zadacha-iz-ege-11-oge-22-60c5a8ef123d127494acf13f
ЕГЭ Профиль №9. Задачи на работу
Скачать файл в формате pdf.
ЕГЭ Профиль №9. Задачи на работу
| Задача 1. Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?
Пусть x дет/ч делает второй рабочий, тогда (x + 1) дет/ч делает первый рабочий.
Первый рабочий на изготовление 110 деталей тратит на 1 час меньше. Следовательно: (frac{{110}}{x} — frac{{110}}{{x + 1}} = 1,,,, Leftrightarrow ,,,,frac{{110left( {x + 1} right) — 110x}}{{xleft( {x + 1} right)}} = 1,,,, Leftrightarrow ,,,,frac{{110}}{{xleft( {x + 1} right)}} = 1,,,, Leftrightarrow ,,,,,xleft( {x + 1} right) = 110,,,, Leftrightarrow ) ( Leftrightarrow ,,,,{x^2} + x — 110 = 0,;,,,,,,,,,D = 1 + 4 cdot 110 = 441;) ({x_1} = frac{{ — 1 + 21}}{2} = 10;,,,,{x_2} = frac{{ — 1 — 21}}{2} = — 11.) Так как (x > 0), то второй рабочий делает 10 деталей в час. Ответ: 10. |
||||||||||||
| Задача 2. На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?
Пусть x дет/ч делает первый рабочий, тогда (x — 3) дет/ч делает второй рабочий.
Первый рабочий тратит на 6 часов меньше. Следовательно: (frac{{550}}{{x — 3}} — frac{{475}}{x} = 6,,,, Leftrightarrow ,,,,frac{{550x — 475left( {x — 3} right)}}{{xleft( {x — 3} right)}} = 6,,,, Leftrightarrow ,,,,frac{{550x — 475x + 475 cdot 3}}{{xleft( {x — 3} right)}} = 6,,,, Leftrightarrow ,,,,) (6xleft( {x — 3} right) = 75x + 475 cdot 3,,left| {,:,} right.3,,,, Leftrightarrow ,,,,2{x^2} — 6x = 25x + 475,,,, Leftrightarrow ,,,,2{x^2} — 31x — 475 = 0;) (D = 961 + 8 cdot 475 = 4761;,,,,,,,,sqrt D = 69;) ({x_1} = frac{{31 + 69}}{4} = 25;,,,,{x_2} = frac{{31 — 69}}{4} = — frac{{19}}{2}.) Так как (x > 3), то первый рабочий делает 25 деталей за час. Ответ: 25. |
||||||||||||
| Задача 3. Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй — за три дня?
Пусть первый рабочий, работая отдельно, выполнил работу за х дней. Так как второй рабочий за 3 дня выполняет такую часть работы, которую первый за 2 дня, то он выполнит всю работу за (frac{3}{2}x) дней. Пусть объём равен А:
Работая вместе, то есть с общей производительностью (frac{A}{x} + frac{{2A}}{{3x}}), рабочие выполняют всю работу (А) за 12 дней. Следовательно: (left( {frac{A}{x} + frac{{2A}}{{3x}}} right) cdot 12 = A,,,, Leftrightarrow ,,,,frac{{3A + 2A}}{{3x}} cdot 12 = A,,,, Leftrightarrow ,,,,frac{{5A cdot 4}}{x} = A,,,left| {:A} right.,,,,,, Leftrightarrow ,,,,,,,frac{{20}}{x} = 1,,,, Leftrightarrow ,,,,x = 20.) Таким образом, первый рабочий, работая отдельно, выполнит работу за 20 дней. Ответ: 20. |
||||||||||||
| Задача 4. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 1 минуту дольше, чем вторая труба?
Пусть первая труба пропускает x литров в минуту, тогда вторая пропускает (x + 1) литр в минуту.
Первая труба тратит на 1 мин больше чем вторая. Следовательно: (frac{{110}}{x} — frac{{110}}{{x + 1}} = 1,,,, Leftrightarrow ,,,,frac{{110left( {x + 1} right) — 110x}}{{xleft( {x + 1} right)}} = 1,,,, Leftrightarrow ,,,,frac{{110}}{{xleft( {x + 1} right)}} = 1,,,, Leftrightarrow ,,,,,xleft( {x + 1} right) = 110,,,, Leftrightarrow ) ( Leftrightarrow ,,,,{x^2} + x — 110 = 0,,,,,,,,,,D = 1 + 4 cdot 110 = 441;) ({x_1} = frac{{ — 1 + 21}}{2} = 10;,,,,{x_2} = frac{{ — 1 — 21}}{2} = — 11.) Так как (x > 0), то первая труба пропускает 10 литров в минуту. Ответ: 10. |
||||||||||||
| Задача 5. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 2 минуты дольше, чем вторая труба заполняет резервуар объемом 99 литров?
Пусть первая труба пропускает x литров в минуту, тогда вторая пропускает (x + 1) литр в минуту.
Первая труба тратит на 2 минуты больше чем вторая. Следовательно: (frac{{110}}{x} — frac{{99}}{{x + 1}} = 2,,,, Leftrightarrow ,,,,frac{{110left( {x + 1} right) — 99x}}{{xleft( {x + 1} right)}} = 2,,,, Leftrightarrow ,,,,frac{{110x + 110 — 99x}}{{xleft( {x + 1} right)}} = 2,,,, Leftrightarrow ,,,,,) ( Leftrightarrow ,,,,2xleft( {x + 1} right) = 11x + 110,,,, Leftrightarrow ,,,,2{x^2} + 2x = 11x + 110,,,,, Leftrightarrow ,,,,2{x^2} — 9x — 110 = 0) (D = 81 + 8 cdot 110 = 961;,,,,,,,{x_1} = frac{{9 + 31}}{4}, = 10;,,,,,{x_2} = frac{{9 — 31}}{4} = — frac{{11}}{2}.) Так как (x > 0), то первая труба пропускает 10 литров в минуту. Ответ: 10. |
||||||||||||
| Задача 6. Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 375 литров она заполняет на 10 минут быстрее, чем первая труба заполняет резервуар объемом 500 литров?
Пусть вторая труба пропускает x литров в минуту, тогда первая пропускает (x — 5) литров в минуту.
Первая труба тратит на 10 минут больше чем вторая. Следовательно: (frac{{500}}{{x — 5}} — frac{{375}}{x} = 10,,,, Leftrightarrow ,,,,frac{{500x — 375left( {x — 5} right)}}{{xleft( {x — 5} right)}} = 10,,,, Leftrightarrow ,,,,frac{{500x — 375x + 375 cdot 5}}{{xleft( {x — 5} right)}} = 10,,,, Leftrightarrow ) ( Leftrightarrow ,,,,,10xleft( {x — 5} right) = 125x + 375 cdot 5,,left| {,:} right.,5,,,, Leftrightarrow ,,,,2{x^2} — 10x = 25x + 375,,,, Leftrightarrow ,,,,2{x^2} — 35x — 375 = 0;) (D = {35^2} + 8 cdot 375 = {5^2} cdot {7^2} + 8 cdot {5^2} cdot 15 = {5^2}left( {49 + 120} right) = {5^2} cdot 169;,,,,,,,,,,sqrt D = 5 cdot 13 = 65;) ({x_1} = frac{{35 + 65}}{4}, = 25;,,,,,{x_2} = frac{{35 — 65}}{4} = — frac{{15}}{2}.) Так как (x > 0), то вторая труба пропускает 25 литров в минуту. Ответ: 25. |
||||||||||||
| Задача 7. Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?
После 3 часов работы первому на выполнение заказа осталось работать ещё 12 часов, но так как к нему присоединился второй рабочий, и они стали работать вместе, то им на завершение заказа потребуется 6 часов. Следовательно, заказ будет выполнен за 3 + 6 = 9 часов. Ответ: 9. |
||||||||||||
| Задача 8. Один мастер может выполнить заказ за 12 часов, а другой — за 6 часов. За сколько часов выполнят заказ оба мастера, работая вместе?
Первый мастер за 1 час выполняет (frac{1}{{12}}) часть работы, а второй (frac{1}{6}). Следовательно, работая вместе, два мастера выполняют (frac{1}{{12}} + frac{1}{6} = frac{1}{4}) часть работы. Поэтому всю работу мастера выполнят за 4 часа. Ответ: 4. Замечание: Выведем формулу для совместной работы двух рабочих. Пусть первый рабочий может выполнить работу А за время ({t_1}), а второй за время ({t_2}). Тогда производительность первого рабочего ({W_1} = frac{A}{{{t_1}}}), второго ({W_2} = frac{A}{{{t_2}}}). Следовательно, при совместной работе их общая производительность будет равна: (frac{A}{{{t_1}}} + frac{A}{{{t_2}}}). Пусть ({t_{совм}}) — время за которое будет выполнена работа А при совместной работе. Тогда (frac{A}{{{t_{совм}}}}) будет общая производительность двух рабочих, которая равна (frac{A}{{{t_1}}} + frac{A}{{{t_2}}}), то есть: (frac{A}{{{t_1}}} + frac{A}{{{t_2}}} = frac{A}{{{t_{совм}}}}). Сократив на А, получим: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}). Если работа выполняется тремя субъектами за время ({t_1}), ({t_2}) и ({t_3}) соответственно, то время совместного выполнения того же объёма работы равно: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{{t_{совм}}}}). Так как первый рабочий выполняет заказ за 12 часов, а второй за 6 часов, то ({t_1} = 12), ({t_2} = 6). Тогда: (frac{1}{{12}} + frac{1}{6} = frac{1}{{{t_{совм}}}},,,,,, Leftrightarrow ,,,,,frac{1}{4} = frac{1}{{{t_{совм}}}},,,,,, Leftrightarrow ,,,,,,{t_{совм}} = 4). |
||||||||||||
| Задача 9. Первый насос наполняет бак за 20 минут, второй — за 30 минут, а третий — за 1 час. За сколько минут наполнят бак три насоса, работая одновременно?
Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). В данном случае ({t_1} = 20) минут, ({t_2} = 30) минут, ({t_3} = 1) час = 60 минут: (frac{1}{{20}} + frac{1}{{30}} + frac{1}{{60}} = frac{1}{{{t_{совм}}}},,,,, Leftrightarrow ,,,,,frac{{3 + 2 + 1}}{{60}} = frac{1}{{{t_{совм}}}},,,,,, Leftrightarrow ,,,,,frac{6}{{60}} = frac{1}{{{t_{совм}}}},,,,, Leftrightarrow ,,,,,,{t_{совм}} = 10). Ответ: 10. |
| Задача 10. Игорь и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь — за 18 часов. За сколько часов мальчики покрасят забор, работая втроем?
Пусть Игорь, Паша и Володя каждый покрасят забор за время ({t_1}), ({t_2}) и ({t_3})соответственно. Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Тогда получим систему уравнений: (left{ {begin{array}{*{20}{c}} {frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{9};} \ {frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{12}};} \ {frac{1}{{{t_1}}} + frac{1}{{{t_3}}} = frac{1}{{18.}}} end{array}} right.) Прибавим к первому уравнению второе и третье: (frac{2}{{{t_1}}} + frac{2}{{{t_2}}} + frac{2}{{{t_3}}} = frac{1}{9} + frac{1}{{12}} + frac{1}{{18}},,,,, Leftrightarrow ,,,,,frac{2}{{{t_1}}} + frac{2}{{{t_2}}} + frac{2}{{{t_3}}} = frac{1}{4},left| {,:2,,,,, Leftrightarrow } right.,,,,,frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{8}.) Так как спрашивают, за сколько часов мальчики покрасят забор, работая втроем, то: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{{t_{совм}}}}). Следовательно: (frac{1}{{{t_{совм}}}} = frac{1}{8},,,,, Leftrightarrow ,,,,,,{t_{совм}} = 8.) Ответ: 8. |
||||||||||||
| Задача 11. Даша и Маша пропалывают грядку за 12 минут, а одна Маша — за 20 минут. За сколько минут пропалывает грядку одна Даша?
Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Пусть ({t_1} = 20) минут время, за которое Маша пропалывает грядку, а ({t_2}) – время за которое Даша. При этом ({t_{совм}} = 12) минут. (frac{1}{{20}} + frac{1}{{{t_2}}} = frac{1}{{12}},,,,, Leftrightarrow ,,,,,frac{1}{{{t_2}}} = frac{1}{{12}} — frac{1}{{20}},,,,, Leftrightarrow ,,,,frac{1}{{{t_2}}} = frac{1}{{30}},,,,,, Leftrightarrow ,,,,,{t_2} = 30) минут. Ответ: 30. |
||||||||||||
| Задача 12. Две трубы наполняют бассейн за 3 часа 36 минут, а одна первая труба наполняет бассейн за 6 часов. За сколько часов наполняет бассейн одна вторая труба?
Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Пусть ({t_1} = 6) часов время, за которое первая труба наполняет бассейн, а ({t_2}) – время второй трубы. При этом ({t_{совм}} = 3) часа 36 минут = (3frac{{36}}{{60}}) часа = (frac{{18}}{5}) часа. (frac{1}{6} + frac{1}{{{t_2}}} = frac{5}{{18}},,,, Leftrightarrow ,,,,frac{1}{{{t_2}}} = frac{5}{{18}} — frac{1}{6},,,,, Leftrightarrow ,,,,frac{1}{{{t_2}}} = frac{1}{9},,,,, Leftrightarrow ,,,,{t_2} = 9) часов. Ответ: 9. |
||||||||||||
| Задача 13. Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Пусть x – минут время, за которое вторая труба наполняет резервуар, а x + 6 минут время первой трубы. При этом ({t_{совм}} = 4) минуты: (frac{1}{{x + 6}} + frac{1}{x} = frac{1}{4},,,,, Leftrightarrow ,,,,,,frac{{x + x + 6}}{{xleft( {x + 6} right)}} = frac{1}{4},,,,, Leftrightarrow ,,,,{x^2} + 6x = 4left( {2x + 6} right),,,, Leftrightarrow ,,,,,{x^2} — 2x — 24 = 0;) (D = 4 + 4 cdot 24 = 100;,,,,,,{x_1} = frac{{2 + 10}}{2} = 6;,,,,,{x_2} = frac{{2 — 10}}{2} = — 4.) Так как (x > 0), то вторая труба наполнит резервуар за 6 минут. Ответ: 6. |
||||||||||||
| Задача 14. В помощь садовому насосу, перекачивающему 5 литров воды за 2 минуты, подключили второй насос, перекачивающий тот же объем воды за 3 минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 25 литров воды?
Первый нанос перекачивает (frac{5}{2}) л/мин, а второй (frac{5}{3}) л/мин. Тогда вместе они перекачивают (frac{5}{2} + frac{5}{3} = frac{{25}}{6}) л/мин. Следовательно, 25 литров они перекачают за (25:frac{{25}}{6} = 6) минут. Ответ: 6. |
||||||||||||
| Задача 15. Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 8 вопросов текста, а Ваня — на 9. Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Вани на 20 минут. Сколько вопросов содержит тест?
Пусть тест содержит х вопросов.
Так как Петя закончил свой тест на 20 минут ((frac{1}{3}) часа) позже Вани, то: (frac{x}{8} — frac{x}{9} = frac{1}{3},,,, Leftrightarrow ,,,,frac{x}{{72}} = frac{1}{3},,,,, Leftrightarrow ,,,,x = 24.) Следовательно, тест содержит 24 вопроса. Ответ: 24. |
||||||||||||
| Задача 16. Плиточник должен уложить 175 м2 плитки. Если он будет укладывать на 10 м2 в день больше, чем запланировал, то закончит работу на 2 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?
Пусть плиточник планирует укладывать х м2 плитки в день.
Следовательно: (frac{{175}}{x} — frac{{175}}{{x + 10}} = 2,,,, Leftrightarrow ,,,,frac{{175left( {x + 10} right) — 175x}}{{xleft( {x + 10} right)}} = 2,,,, Leftrightarrow ,,,,frac{{175 cdot 10}}{{xleft( {x + 10} right)}} = 2,,,, Leftrightarrow ) ( Leftrightarrow ,,,,2xleft( {x + 10} right) = 175 cdot 10,,left| {,:} right.2,,,, Leftrightarrow ,,,,{x^2} + 10x — 875 = 0) (D = 100 + 4 cdot 875 = 3600;,,,,,{x_1} = frac{{ — 10 + 60}}{2} = 25;,,,,,{x_2} = frac{{ — 10 — 60}}{2} = — 35.) Так как (x > 0), то плиточник планировал укладывать 25 м2 плитки в день. Ответ: 25. |
||||||||||||
| Задача 17. Первый и второй насосы наполняют бассейн за 9 минут, второй и третий — за 14 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
Пусть первый, второй и третий насосы заполняют бассейн за время ({t_1}), ({t_2}) и ({t_3}) соответственно. Воспользуемся формулой: (frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{{{t_{совм}}}}) (смотри замечание к задаче 8). Тогда получим систему уравнений: ()(left{ {begin{array}{*{20}{c}} {frac{1}{{{t_1}}} + frac{1}{{{t_2}}} = frac{1}{9};} \ {frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{1}{{14}};} \ {frac{1}{{{t_1}}} + frac{1}{{{t_3}}} = frac{1}{{18.}}} end{array}} right.) Прибавим к первому уравнению второе и третье: (frac{2}{{{t_1}}} + frac{2}{{{t_2}}} + frac{2}{{{t_3}}} = frac{1}{9} + frac{1}{{14}} + frac{1}{{18}},,,,, Leftrightarrow ,,,,,frac{2}{{{t_1}}} + frac{2}{{{t_2}}} + frac{2}{{{t_3}}} = frac{5}{{21}},left| {,:2,,,,, Leftrightarrow } right.,,,,,,frac{1}{{{t_1}}} + frac{1}{{{t_2}}} + frac{1}{{{t_3}}} = frac{5}{{42}}.) Так как спрашивается, за сколько минут три насоса заполнят бассейн, работая вместе, то: (frac{1}{{{t_{совм}}}} = frac{5}{{42}},,,,, Leftrightarrow ,,,,,,{t_{совм}} = 8,4) минуты. Ответ: 8,4. |
||||||||||||
| Задача 18. Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали строить два одинаковых дома. В первой бригаде было 16 рабочих, а во второй — 25 рабочих. Через 7 дней после начала работы в первую бригаду перешли 8 рабочих из второй бригады, в результате чего оба дома были построены одновременно. Сколько дней потребовалось бригадам, чтобы закончить работу в новом составе?
Количество рабочих будем считать производительностью. Пусть в новом составе рабочие доделывали дома t дней. В сумме до и после перехода рабочих каждая из бригад выполнила всю работу. Тогда: (16 cdot 7 + 24 cdot t = 25 cdot 7 + 17t,,,, Leftrightarrow ,,,,7t = 25 cdot 7 — 16 cdot 7,,,, Leftrightarrow ,,,,t = 9.) Следовательно, рабочим понадобилось 9 дней, чтобы закончить работу в новом составе. Ответ: 9. |
Задача про три насоса — второй способ
Первый и второй насосы наполняют бассейн за 35 минут, второй и третий насосы – за 40 минут, первый и третий – за 56 минут. За сколько минут наполнят бассейн три насоса, работая вместе?
Решим эту задачу другим способом.
Так как первый и второй насосы наполняют бассейн на 35 мин, то за 1 мин они наполнят 1/35 часть бассейна.
Второй и третий насосы за 1 мин наполнят 1/40 часть бассейна.
Первый и третий — 1/56 часть бассейна.
Сложим эти три дроби.
Так как каждый насос был сосчитан два раза, то получается, что 6 насосов за 1 мин наполнят 114 часть бассейна.
Тогда весь бассейн 6 насосов заполнят за 14 мин.
Следовательно, три насоса заполнят бассейн за 28 минут.
Смотрите видеоурок с подробным решением задачи.
Интересная статья? Поделитесь ею пожалуйста с другими:
Примем объем работы за единицу. Пусть x — количество дней, за которое необходимо выполнить всю работу Виктору; за y дней работу выполнит Алексей, Андрей выполнит всю работу за z дней; тогда frac{1}{x} — производительность Виктора, frac{1}{y} — производительность Алексея, frac{1}{z} — производительность Андрея.
По первому условию Виктор и Алексей сделают всю работу за 8 дней, значит, их общая производительность frac18. Составим уравнение frac{1}{x}+frac{1}{y}=frac18.
По второму условию Виктор и Андрей сделают всю работу за 8 дней. Значит, их общая производительность frac18. Составим уравнение frac{1}{x}+frac{1}{z}=frac18.
По третьему условию Андрей и Алексей выполнят всю работу за 12 дней. Значит, их общая производительность frac{1}{12}. Составим уравнение frac{1}{y}+frac{1}{z}=frac{1}{12}.
Получим систему уравнений:
begin{cases} frac{1}{x}+frac{1}{y}=frac18,\ frac{1}{x}+frac{1}{z}=frac18,\ frac{1}{y}+frac{1}{z}=frac{1}{12}; end{cases}
2left( frac{1}{x}+frac{1}{y}+frac{1}{z} right )=frac18+frac18+frac{1}{12},
2left( frac{1}{x}+frac{1}{y}+frac{1}{z} right )=frac13,
frac{1}{x}+frac{1}{y}+frac{1}{z}=frac16,
1:frac16=6 (дней).
Итак, всю работу Виктор, Алексей и Андрей сделают за 6 дней.