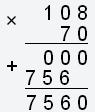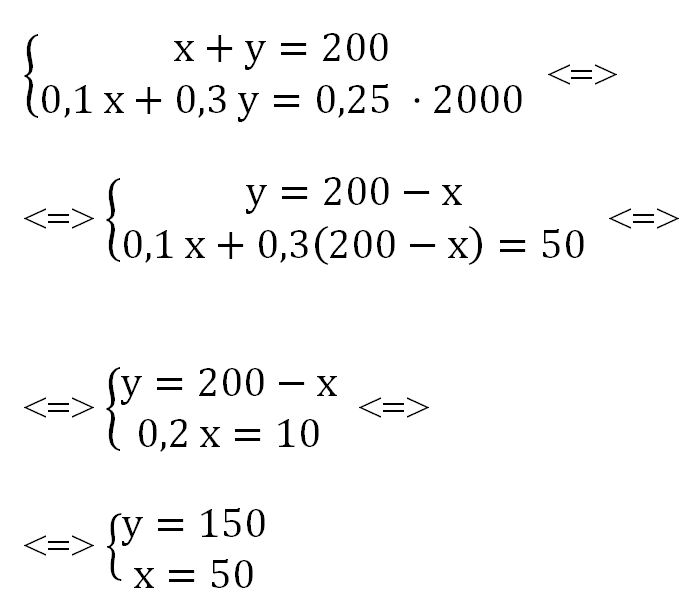Как решать задачи с процентами егэ базовый уровень

---

Задачи на проценты

---

[su_box title=”Описание задания” style=”soft” box_color=”#c1e8cc” title_color=”#0c0a0a”]

В задании №3 ЕГЭ по математике нам предстоит решить простую задачу на проценты или часть от целого. Данные задачи в большинстве случаев интуитивно понятны, так как взяты из реальных жизненных ситуаций, тем не менее необходимо быть внимательным при их выполнении.

Тематика заданий: часть от целого, доли, проценты

Бал: 1 из 20

Сложность задания: ♦♦◊

Примерное время выполнения: 3 мин.

[/su_box]

---

Разбор типовых вариантов заданий №3 ЕГЭ по математике базового уровня

---

Вариант 3МБ1

[su_note note_color=”#defae6″]

Банк начисляет на срочный вклад 8% годовых. Вкладчик положил на счёт 7000 рублей. Сколько рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?

[/su_note]

Алгоритм выполнения:

• Вариант 1.

1. Сложить 100% и процент годовых.
2. Найти 1% от суммы, для этого сумму разделить на 100.
3. Умножить стоимость 1% на искомое количество процентов.

• Вариант 2.

1. Сложить 100% и процент годовых.
2. Полученные проценты перевести в десятичную дробь (разделить на сто).
3. Найти процент от числа (число умножить на полученную десятичную дробь).

Решение:

• Вариант 1.

Вклад 8 % годовых означает, что начальная сумма 7000 рублей через год увеличится на 8%, то есть составит 100+8=108% от исходной суммы.

Способ нахождения процента от числа №1. Для того, чтобы найти процент от числа нужно данное число разделить на 100(узнать сколько составляет 1 %), а затем умножить на искомое количество процентов.

Вычислим 108% от 7000, получим:

1. 7000 : 100 = 70(рублей) – составит 1 %.
2. 70 · 108 = 7560(рублей) – составит вклад через год.

• Вариант 2.

Вклад 8 % годовых означает, что начальная сумма 7000 рублей через год увеличится на 8%, то есть составит 100+8=108% от исходной суммы.

Способ нахождения процента от числа №2. Для того, чтобы найти процент от числа, нужно перевести искомый процент в десятичную дробь(разделить на сто), затем умножит число на полученную десятичную дробь.

108% = 108 : 100 = 1,08

7000 · 1,08 или

.

Выполнив умножение столбиком, имеем:

Ответ: 7560.

---

Вариант 3МБ2

[su_note note_color=”#defae6″]

Банк начисляет на срочный вклад 7 % годовых. Вкладчик положил на счёт 3000 рублей. Сколько рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?

[/su_note]

Алгоритм выполнения:

• Вариант 1.

1. Сложить 100% и процент годовых.
2. Найти 1% от суммы, для этого сумму разделить на 100.
3. Умножить стоимость 1% на искомое количество процентов.

• Вариант 2.

1. Сложить 100% и процент годовых.
2. Полученные проценты перевести в десятичную дробь (разделить на сто).
3. Найти процент от числа (число умножить на полученную десятичную дробь).

Решение:

• Вариант 1.

Вклад 7 % годовых означает, что начальная сумма 3000 рублей через год увеличится на 7%, то есть составит 100+7=107% от исходной суммы.

Способ нахождения процента от числа №1. Для того, чтобы найти процент от числа нужно данное число разделить на 100(узнать сколько составляет 1 %), а затем умножить на искомое количество процентов.

Вычислим 107% от 3000, получим:

1. 3000 : 100 = 30(рублей) – составит 1 %.
2. 30 · 107 = 3210(рублей) – составит вклад через год.

• Вариант 2.

Вклад 7 % годовых означает, что начальная сумма 3000 рублей через год увеличится на 7%, то есть составит 100+7=107% от исходной суммы.

Способ нахождения процента от числа №2. Для того, чтобы найти процент от числа, нужно перевести искомый процент в десятичную дробь (разделить на сто), затем умножит число на полученную десятичную дробь.

107% = 107 : 100 = 1,07

3000 · 1,07 или

Ответ: 3210.

---

Вариант 3МБ3

[su_note note_color=”#defae6″]

В сентябре 1 кг слив стоил 40 рублей, в октябре сливы подорожали на 40%, а в ноябре ещё на 15%. Сколько рублей стоил 1 кг слив после подорожания в ноябре?

[/su_note]

Алгоритм выполнения:

1. Найти сколько составляет один процент от начальной стоимости.
2. Сложить 100% и на сколько процентов произошло подорожание впервые.
3. Умножить стоимость одного процента на полученное количество процентов.
4. Найти стоимость 1% от новой стоимости.
5. Сложить 100 % и количество процентов, на которое подорожал товар во второй раз.
6. Умножить стоимость одного процента на полученное количество процентов.

Решение с пояснениями:

Найдем сколько составляет один процент от начальной стоимости:

40 : 100 = 0,4 (рублей) – составляет 1 % от начальной стоимости.

Сложим 100% и на сколько процентов произошло подорожание впервые.

100 + 40 = 140 (%) – составила стоимость от начальной цены после первого подорожания.

Умножим стоимость одного процента на полученное количество процентов.

140 · 0,4 = 56 (рублей) – стали стоить сливы в октябре.

Найдем стоимость 1% от новой стоимости.

56 : 100 = 0,56 (рубля) – 1% от новой стоимости.

Сложим 100 % и количество процентов, на которое подорожал товар во второй раз.

100 + 15 = 115 (%) – составила стоимость в ноябре от цены в октябре.

Умножим стоимость одного процента на полученное количество процентов.

115 · 0,56 = 64,4 (рубля) – конечная стоимость.

Решение в общем виде:

Подорожание на 40% означает увеличение стоимости на 140%, то есть, 40 рублей становятся равными

 рублей.

Затем, в ноябре стоимость слив увеличилась еще на 15%, что составило

 рублей.

Замечание: обратите внимание, что в данной задаче нельзя просто складывать проценты 40+15=55% и вычислять 155% от 40 рублей! Это будет приводить к неверным решениям.

Ответ: 64,4.

---

Вариант 3МБ4

[su_note note_color=”#defae6″]

В сентябре 1 кг винограда стоил 90 рублей, в октябре виноград подорожал на 20 %, а в ноябре ещё на 25 %. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?

[/su_note]

Алгоритм выполнения:

1. Найти сколько составляет один процент от начальной стоимости.
2. Сложить 100% и на сколько процентов произошло подорожание впервые.
3. Умножить стоимость одного процента на полученное количество процентов.
4. Найти стоимость 1% от новой стоимости.
5. Сложить 100 % и количество процентов, на которое подорожал товар во второй раз.
6. Умножить стоимость одного процента на полученное количество процентов.

Подробный разбор:

Найдем сколько составляет один процент от начальной стоимости:

90 : 100 = 0,9 (рублей) – составляет 1 % от начальной стоимости.

Сложим 100% и на сколько процентов произошло подорожание впервые.

100 + 20 = 120 (%) – составила стоимость от начальной цены после первого подорожания.

Умножим стоимость одного процента на полученное количество процентов.

120 · 0,9 = 108 (рублей) – стали стоить сливы в октябре.

Найдем стоимость 1% от новой стоимости.

108 : 100 = 1,08 (рубля) – 1% от новой стоимости.

Сложим 100 % и количество процентов, на которое подорожал товар во второй раз.

100 + 25 = 125 (%) – составила стоимость в ноябре от цены в октябре.

Умножим стоимость одного процента на полученное количество процентов.

125 · 1,08 = 135 (рублей) – конечная стоимость.

Решение в общем виде:

Подорожание на 20% означает увеличение стоимости на 120%, то есть, для 90 рублей имеем:

 рублей.

Затем, в ноябре стоимость слив увеличилась еще на 25%, что составило

 рублей.

Замечание: обратите внимание, что в данной задаче нельзя просто складывать проценты 20+25=45% и вычислять 145% от 90 рублей! Это будет приводить к неверным решениям.

Ответ: 135.

---

Вариант 3МБ5

[su_note note_color=”#defae6″]

Ивану Кузьмичу начислена заработная плата 20000 рублей. Из этой суммы вычитается налог на доход физических лиц в размере 13 %. Сколько рублей он получит после уплаты подоходного налога?

[/su_note]

Алгоритм выполнения:

• Вариант 1.

1. Вычесть из 100% налог в процентах.
2. Найти 1% от начальной суммы, для этого сумму разделить на 100.
3. Умножить стоимость 1% на искомое количество процентов.

• Вариант 2.

1. Вычесть из 100% налог в процентах.
2. Полученные проценты перевести в десятичную дробь (разделить на сто).
3. Найти процент от числа (число умножить на полученную десятичную дробь).

Решение:

• Вариант 1.

Вычтем из 100% налог в процентах.

100 – 13 = 87 (%) – получит Иван Кузьмич после вычета налога.

Найдем 1 % от начальной суммы.

20000 : 100 = 200 (рублей) – составит 1%.

Найдем 87% от 20000.

87 · 200 = 17400 (рублей) – получит Иван Кузьмич.

• Вариант 2.

Вычтем из 100% налог в процентах. 100 – 13 = 87 (%)

Полученные проценты переведем в десятичную дробь (разделить на сто). 87 : 100 = 0,87

Найдем процент от числа (число умножить на полученную десятичную дробь).

20000 · 0,87 = 17400 (рублей)

Ответ: 17400 рублей получит Иван Кузьмич.

---

Вариант 3МБ6

[su_note note_color=”#defae6″]

ЕГЭ по физике сдавали 25 выпускников школы, что составляет треть от общего числа выпускников. Сколько выпускников этой школы не сдавали экзамен по физике?

[/su_note]

Решение:

Нам известно, что количество учеников, сдававших ЕГЭ по физике равно 25, и это составляет 1/3 от общего числа выпускников. Значит 25 – это 1/3, тогда общее число учеников:

25 • 3 = 75

Количество учеников, не сдававших ЕГЭ по физике, равно:

75 – 25 = 50

Ответ: 50

---

Вариант 3МБ7

[su_note note_color=”#defae6″]

Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена стоимость футболки?

[/su_note]

Алгоритм выполнения

1. От 800 отнимаем 680. Узнаем, сколько рублей составило снижение.
2. Делим результат вычитания на 800. Это даст нам долю, которую составляет скидка от первоначальной стоимости.
3. Полученное число умножаем на 100. Получаем снижение в процентах.

Решение:

800 – 680 = 120 (руб.) – составляет снижение

120 : 800 = 0,15 – доля скидки

0,15 ·100 = 15 %

Ответ: 15

---

Вариант 3МБ8

[su_note note_color=”#defae6″]

В магазине вся мебель продается в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 5% от стоимости купленной мебели. Шкаф стоит 3500 рублей (наверное, это было очень давно – прим. ред. 🙂 ) Во сколько рублей обойдется покупка этого шкафа вместе со сборкой?

[/su_note]

Алгоритм выполнения

1. Определяем, сколько составляет 5% от стоимости мебели. Для этого 3500 делит на 100 и умножаем на 5.
2. К 3500 прибавляем полученное число.

Решение:

3500 : 100 · 5 = 175 (руб.) – стоимость сборки мебели

3500 + 175 = 3675 (руб.) стоит мебель со сборкой

Ответ: 3675

---

Вариант 3МБ9

[su_note note_color=”#defae6″]

Товар на распродаже уценили на 40%, при этом он стал стоить 840 рублей. Сколько рублей стоит товар до распродажи?

[/su_note]

Алгоритм выполнения

1. От 100 % вычитаем 40%, чтобы найти, сколько процентов составляет уцененная стоимость. Получим 60 %.
2. Воспользуемся правилом нахождения целого по его части. Для этого 840 разделим на 60 и умножим на 100.

Решение:

100 – 40 = 60 % – составляет цена товара после его уценки.

840 : 60 · 100 = 1400 (руб.)

1400

---

Вариант 3МБ10

[su_note note_color=”#defae6″]

Магазин делает пенсионерам скидку. Батон хлеба стоит в магазине 15 рублей, а пенсионер заплатил за него 14 рублей 40 копеек (грандиозная скидка – прим. ред. 😉 ) Сколько процентов составила скидка для пенсионера?

[/su_note]

Алгоритм выполнения

1. От 15 руб. отнимаем 14 руб.40 коп. Так найдем сумму скидки. Выразим эту сумму в рублях.
2. Полученное число разделим на 15 и умножим на 100 %.

Решение:

15 руб. – 14 руб.40 коп. = 60 коп. = 0,6 руб.

0,6 : 15 ·100 % = 4 %.

Ответ: 4

---

Вариант 3МБ11

[su_note note_color=”#defae6″]

Число хвойных деревьев в парке относится к числу лиственных как 93:7. Других деревьев в парке нет. Сколько процентов деревьев в парке составляют лиственные?

[/su_note]

Алгоритм выполнения

1. Суммируем 93 и 7, чтобы найти общее кол-во деревьев в парке.
2. Кол-во лиственных деревьев (7) делим на общее кол-во деревьев и умножаем на 100 %.

Решение:

93 + 7 = 100 (шт.) – деревьев всего в парке.

7 : 100 ·100 = 7 %

Ответ: 7

---

Вариант 3МБ12

[su_note note_color=”#defae6″]

Городской бюджет составляет 48 млн. рублей, а расходы на одну из его статей составили 40%. Сколько миллионов рублей потрачены на эту статью бюджета?

[/su_note]

Алгоритм выполнения

Нужно применить правило нахождения части от целого по ее проценту. Для этого целое делится на 100 и умножается на кол-во процентов.

Решение:

48 : 100 · 40 = 19,2 (млн.руб.)

Ответ: 19,2

---

Вариант 3МБ13

[su_note note_color=”#defae6″]

Поступивший в продажу в феврале мобильный телефон стоил 1800 рублей. В июне он стал стоить 1530 рублей. На сколько процентов снизилась цена мобильного телефона в период с февраля по июнь?

[/su_note]

Алгоритм выполнения

1. Из 1800 вычитаем 1530. Определяем, сколько рублей составила скидка.
2. Полученное число делим на первоначальную цену и умножаем на 100 %.

Решение:

1800 – 1530 = 270 (руб.) – скидка

270 : 1800 · 100 = 15 %

Ответ: 15

---

Вариант 3МБ14

[su_note note_color=”#defae6″]

В период распродажи магазин снижал цены дважды: в первый раз на 10%, во второй – на 25%. Сколько рублей стал стоить чайник после второго снижения цен, если до начала распродажи он стоил 1600 рублей?

[/su_note]

Алгоритм выполнения

1. Определяем, сколько (в руб.) составляет 10 % от стоимости чайника. Для этого 1600 делим на 100 и умножаем на 10.
2. От первоначальной стоимости отнимаем сумму скидки, составляющей 10 %.
3. Полученную цену со скидкой делим на 100 и умножаем на 25. Так найдем величину скидки (в руб.) после второго снижения цены.
4. От числа, полученного в п.2 отнимаем число, полученное в п.3.

Решение:

1600 : 100 · 10 = 160 (руб.) – составляет скидка в 10 %

1600 – 160 = 1440 (руб.) – стал стоить чайник после понижения цены на 10 %

1440 : 100 · 25 = 360 (руб.) составляет скидка в 25 %

1440 – 360 = 1080 (руб.)

Ответ: 1080

---

Вариант 3МБ15

[su_note note_color=”#defae6″]

Магазин детских товаров закупает погремушки по оптовой цене 110 рублей за одну штуку и продает с наценкой 30%. Сколько рублей будут стоить 4 такие погремушки, купленные в этом магазине?

[/su_note]

Алгоритм выполнения

1. Определяем, сколько рублей составляет наценка в 30 %. Для этого закупочную стоимость делим на 100 и умножаем на 30.
2. К закупочной стоимости прибавляет сумму наценки.
3. Полученное число умножаем на 4.

Решение:

110 : 100 · 30 = 33 (руб.) – равна наценка

110 + 33 = 143 (руб.) – стоит погремушка в магазине

143 · 4 = 572 (руб.) – стоят 4 погремушки

Ответ: 572

---

Вариант 3МБ16

[su_note note_color=”#defae6″]

Число больных гриппом в школе уменьшилось за месяц в два раза. На сколько процентов уменьшилось число больных гриппом?

[/su_note]

Алгоритм выполнения

1. Обозначим число больных через х. Тогда кол-во больных через месяц станет равным х/2.
2. х/2 делим на х и умножаем на 100 %. Так найдем кол-во процентов, которое составит число больных через месяц по отношению к первоначальному их кол-ву. В процессе вычисления х сократится.

Решение:

х / 2 : х · 100 % = х / 2· 1 / х· 100 % =1 / 2 · 100 % = 0,5 · 100 % = 50 %

Ответ: 50

Даниил Романович | Просмотров: 14.5k

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Задачи на проценты из вариантов ЕГЭ по математике

Смотри также видео «Текстовые задачи на ЕГЭ по математике».
Текстовая задача — это не только задача на движение и работу. Есть еще задания на проценты, на растворы, сплавы и смеси, на движение по окружности и нахождение средней скорости. О них мы и расскажем.

Начнем с задач на проценты. Если эта тема сложна для тебя — посмотри материал простейшие текстовые задачи. В частности, в нем мы сформулировали важное правило: за  мы принимаем ту величину, с которой сравниваем.

Мы также вывели полезные формулы:

если величину увеличить на процентов, получим
если величину уменьшить на процентов, получим
если величину увеличить на процентов, а затем уменьшить на , получим

если величину дважды увеличить на процентов, получим
если величину дважды уменьшить на процентов, получим

Воспользуемся ими для решения задач.

---

. В  году в городском квартале проживало  человек. В  году в результате строительства новых домов число жителей выросло на , а в  году — на  по сравнению с  годом. Сколько человек стало проживать в квартале в  году?

По условию, в  году число жителей выросло на , то есть стало равно  человек.

А в  году число жителей выросло на , теперь уже по сравнению с  годом. Получаем, что в  году в квартале стало проживать  жителей.

Следующая задача предлагалась на пробном ЕГЭ по математике в декабре  года. Она проста, но справились с ней немногие.

---

. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на  дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?

На первый взгляд кажется, что в условии ошибка и цена акций вообще не должна измениться. Ведь они подорожали и подешевели на одно и то же число процентов! Но не будем спешить. Пусть при открытии торгов в понедельник акции стоили  рублей. К вечеру понедельника они подорожали на  и стали стоить . Теперь уже эта величина принимается за , и к вечеру вторника акции подешевели на  по сравнению этой величиной. Соберем данные в таблицу:

По условию, акции в итоге подешевели на 

Получаем, что

Поделим обе части уравнения на (ведь он не равен нулю) и применим в левой части формулу сокращенного умножения:

По смыслу задачи, величина положительна.
Получаем, что .

---

. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за  рублей, через два года был продан за  рублей.

Эта задача тоже решается по одной из формул, приведенных в начале статьи. Холодильник стоил  рублей. Его цена два раза уменьшилась на , и теперь она равна:

---

. Четыре рубашки дешевле куртки на . На сколько процентов пять рубашек дороже куртки?

Пусть стоимость рубашки равна , стоимость куртки . Как всегда, принимаем за сто процентов ту величину, с которой сравниваем, то есть цену куртки. Тогда стоимость четырех рубашек составляет  от цены куртки, то есть .

Стоимость одной рубашки — в  раза меньше:

А стоимость пяти рубашек:

Получили, что пять рубашек на  дороже куртки.

Ответ: .

---

. Семья состоит из мужа, жены и их дочери-студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на . Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на  Сколько процентов от общего дохода семьи составляет зарплата жены?

Нарисуем таблицу. Ситуации, о которых говорится в задаче («если бы зарплата мужа увеличилась, если бы стипендия дочки уменьшилась…») назовем «ситуация » и «ситуация ».

	муж	жена	дочь	Общий доход
В реальности
Ситуация
Ситуация

Осталось записать систему уравнений:

Но что же мы видим? Два уравнения и три неизвестных! Мы не сможем найти , и по отдельности. Правда, нам это и не нужно. Лучше возьмем первое уравнение и из обеих его частей вычтем сумму .

Получим:

Это значит, что зарплата мужа составляет  от общего дохода семьи.

Во втором уравнении мы тоже вычтем из обеих частей выражение , упростим и получим, что

Значит, стипендия дочки составляет  от общего дохода семьи. Тогда зарплата жены составляет  общего дохода.

Ответ:

Чтобы найти процент от числа, надо заданное число разделить на $100$ и умножить на величину процента.

$n%$ от $а={а⋅n}/{100}$

Чтобы найти число по его указанному проценту, нужно заданное число разделить на заданную величину процента, а результат умножить на $100$.

Задачи на скидки

Скидка — это снижение цены товара или услуги. Чаще всего скидку указывают в процентах.

Чтобы найти цену товара с учетом скидки необходимо:

1. Из $100%$ вычесть процент скидки.
2. Найти полученный процент от полной стоимости товара.

Задачи на вклады, кредиты, наценки

Чтобы найти сумму денег с учетом годовой ставки, необходимо:

1. К $100%$ прибавить годовой процент вклада.
2. Найти полученный процент от изначального количества денег.

В некоторых задачах на проценты удобно использовать пропорцию, например:

Предлагаем разобрать три задачи, приведенные ниже. Это задание №11 из ЕГЭ прошлых лет, рекомендованные как тренировочные.

Задача № 1

Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 20 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?

Решение

Согласно условию получается, что виноград содержит 10% питательного вещества, а изюм — 95%.

Представим проценты в долях от «1»:

10% = 0,1

95% = 0,95

Поэтому 20 кг изюма содержат питательного вещества:

20 · 0,95 = 19 кг

Таким образом, для получения 20 килограммов изюма требуется винограда:

= 190 кг

Ответ: 190.

Нужна помощь в подготовке к эказмену? Смотрите курсы подготовки к ЕГЭ по математике в Санкт-Петербурге!

---

Задача № 2

Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

Решение

Пусть масса первого сплава «х» кг, а масса второго – «у» кг.

Представим проценты в долях от «1»:

10% = 0,1

30% = 0,3

25% = 0,25

Тогда массовое содержание никеля в первом и втором сплавах получится:

«0,1· х»  и  «0,3 · у» соответственно.

Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:

Получаем, что:

у – х = 150 – 50 = 100

Первый сплав легче второго на 100 килограммов.

Ответ: 100.

---

Задача № 3

Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Решение

Пусть масса первого сплава «х» кг,

масса второго сплава – «х + 3» кг,

масса третьего сплава – «2х + 3» кг.

Первый сплав содержит 10% меди, второй – 40% меди, третий сплав – 30% меди.

Представим проценты в долях от «1»:

10% = 0,1

40% = 0,4

30% = 0,3

Тогда можем записать:

0,1·х + 0,4·(х + 3) = 0,3·(2х + 3) <=>

<=> 0,5 ·х + 1,2 = 0,6 ·х + 0,9 <=>

<=> х = 3     и    2·х + 3 = 9

Таким образом, масса третьего сплава равна 9 кг.

Ответ: 9.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Обычно базовую математику выбирают ребята, у которых есть план: надо как можно скорее разделаться с бесполезным для поступления предметом и сосредоточиться на своем наборе вступительных. Из этой статьи вы узнаете, как сдать базовую математику максимально быстро и просто.

В этом материале мы сделаем акцент на простых номерах, которые принесут вам балл почти задаром! Они обозначены пометкой «Обязательно делать» — таких заданий 10. Как раз с запасом на ошибки, ведь минимум для сдачи базовой математики — 7 баллов.

Для тех, кто хочет получить выше тройки — это 12 баллов и выше, — мы дали рекомендации по еще 3 задачам. В сумме получается 13 номеров. Решите их все, и твердая четверка у вас в кармане.

Какие задания решать, чтобы сдать базовую математику

Задание 1: обязательно делать

Проверяется ваше умение разделить случаи, когда требуется округлить величину в большую сторону, а когда — в меньшую.

Если вы ходите в магазин с наличными, то сталкиваетесь с подобными задачами каждый день. Разделим 100 рублей на стоимость одной упаковки йогурта. Не забывайте приводить все величины к одной размерности:

100 : 14,6 = 6, 849…

Так сколько баночек йогурта вам продадут? На 7 штук денег не хватает, значит, округлить полученную величину надо до целого в меньшую сторону. Математическое правило округление в этой задаче не поможет.

Ответ: 6.

Если одна пачка рассчитана на 6 рулонов, то на 63 рулона:

63 : 6 = 10,5. 

Но полпачки вам не продаст. Включаем логику: возьмем меньше — не хватит еще половины пачки на три последних рулона. Значит, округлить надо в большую сторону, взять клей с небольшим запасом. Математическое правило округления снова игнорируем.

Ответ: 11.

Задание 2: обязательно делать

Это задача на здравый смысл. Нужно соотнести величины с их возможными значениями.

Вряд ли грузовой автомобиль может весить как 3 шоколадки (300 г), а взрослый человек — 8 т.

Давайте вместе подберем значения.

• Взрослый человек обычно весит от 50 до 100 кг — что из этого подходит? Конечно, 65 кг.
• Грузовой автомобиль достаточно большой и тяжелый, скорее всего, он весит несколько тонн. Нам подходит 8 т.
• Книга обычно не такая большая и весит до 1 кг. Из оставшегося подойдет 300 г.
• А пуговка совсем маленькая. Значит, берем самый легкий вес — 5 г.

Ответ:

Главное — внимательно перенести ответы в бланк: 3142.

Задание 3: обязательно делать

Задание на работу с графиком, диаграммой или таблицей. Вооружайтесь карандашом, читайте условие с предельной внимательностью и безжалостно отмечайте нужные по условию значения на изображении в КИМ. Вы и представить не можете, сколько выпускников теряет тут баллы по невнимательности.

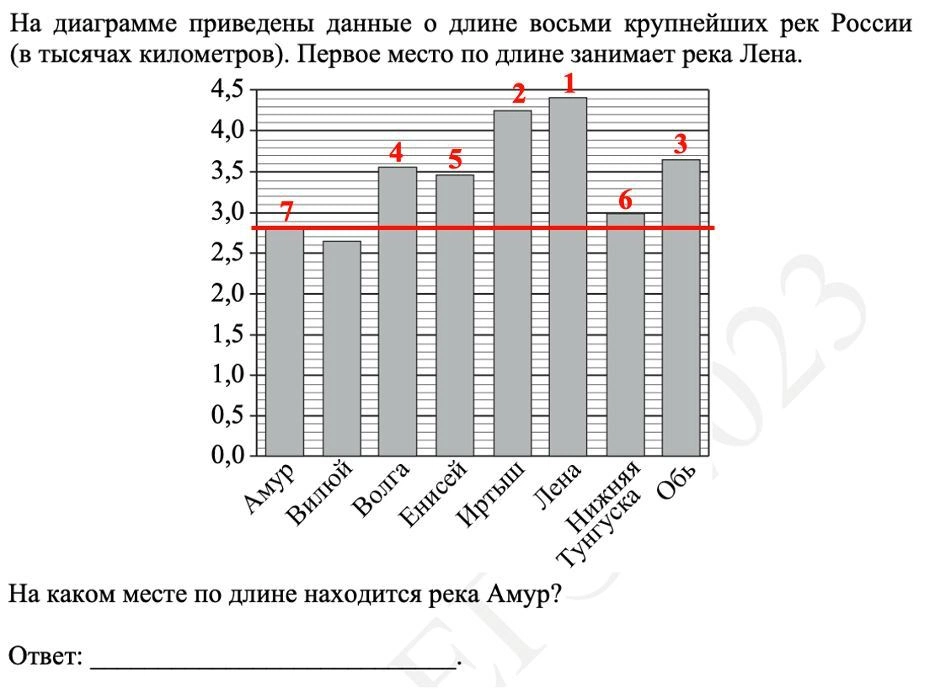
Мы ярко отметили уровень, соответствующий Амуру, в итоге посчитать все более длинные реки стало проще простого. У вас на экзамене будет так же наглядно!

Ответ: 7.

Задание 4: обязательно делать

Задание проверяет навык работы с формулами. Алгоритм решения напоминает решение задачек на уроке по физике:

• Выписываем формулу из условия.
• Определяем, что нужно найти: единственную букву, значение которой не дано.
• Выражаем искомую величину.
• Подставляем значения из условия в формулу.
• Ищем неизвестное.

Самое трудное тут — правильно выразить искомую величину. Для этого повторяем порядок выполнения арифметических операций, свойства умножения, тренируемся перекидывать через равно множители и слагаемые.

И да, в базе эта задача проста настолько, что даже перекидывать ничего не придется. Нужная величина уже будет слева от равно.

Задание 5: обязательно делать

Простая задача на определение вероятности, которая поможет вам точно сдать базовую математику.

Решаем с помощью формулы:

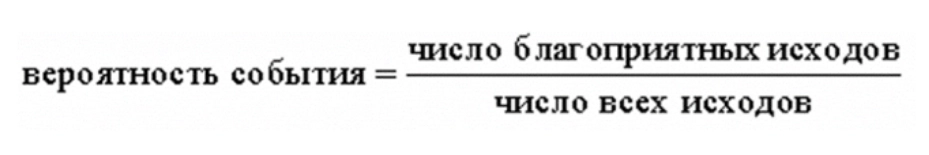
Внимательно читайте вопрос: спрашивают вероятность купить исправную лампочку. Если из ста 3 неисправны, значит, остальные в порядке и подойдет любая из оставшихся 97. Это и есть наши благоприятные исходы из формулы.

97 : 100 = 0,97.

Ответ: 0,97.

Будьте внимательны: иногда в задаче есть указание к округлению. Значит, ответ у вас выйдет некрасивый, в виде бесконечной десятичной дроби, которую вы округлите до нужного разряда.

Еще один подвох: формулировка с предлогом «на». К примеру, «На 100 лампочек 3 неисправны. Найдите вероятность купить неисправную». Подходящие исходы тут даны явно: 3 неисправные лампочки. А вот число всех исходов спрятано, и найти его будет нужно сложением исправных и неисправных лампочек: 100 + 3 = 103.

Задание 6: обязательно делать

Задание проверяет навык чтения информации из таблицы и подбора подходящего по условию варианта.

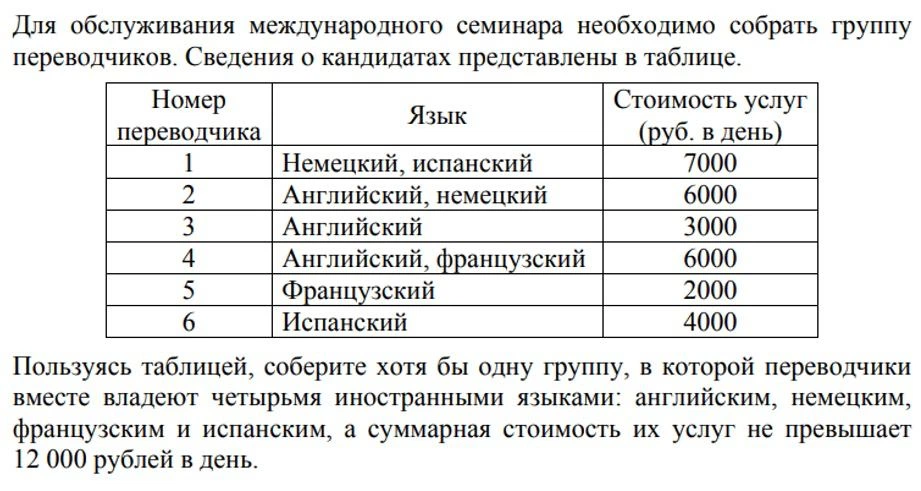
Например, вы нашли вариант позвать первого, третьего и пятого переводчиков. Получите весь набор языков как раз за 12 тысяч. Но обратите внимание, что это решение далеко не единственное.

Ответ: 135.

Задание 7

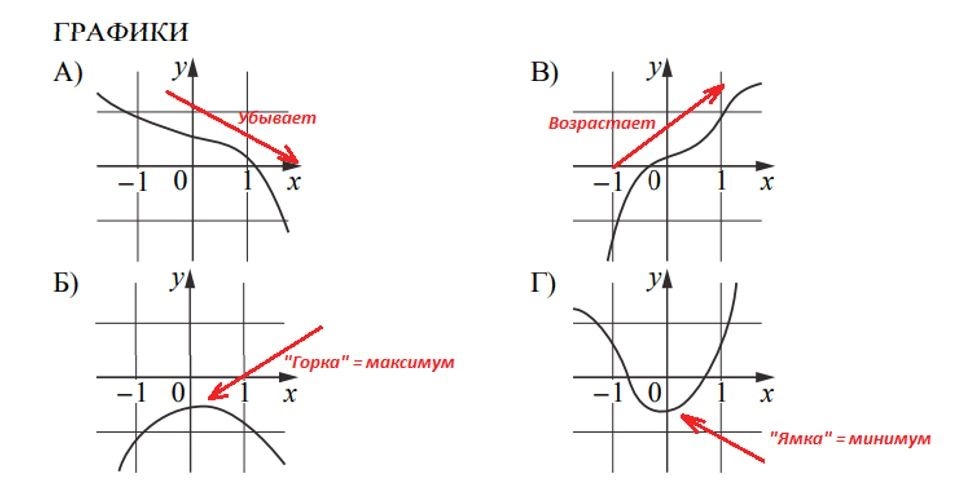
Мы не выделяем это задание в обязательные, так как для его выполнения понадобится навык анализа поведения функции по графику. Но, как его решать, сейчас коротко расскажем.

Запомним: точка максимума будет на «горке», точка минимума — в «ямке». Функция убывает, если идет вниз слева направо. Возрастает, если идет вверх слева направо.

Если не повезет, то придется вспомнить азы теории по производной.

Здесь все дело в касательных. Нужно внимательно к ним присмотреться. Если касательная к графику возрастает, то значение производной будет положительное, если убывает — отрицательное. Производная будет тем больше по величине (модулю), чем быстрее возрастает или убывает касательная.

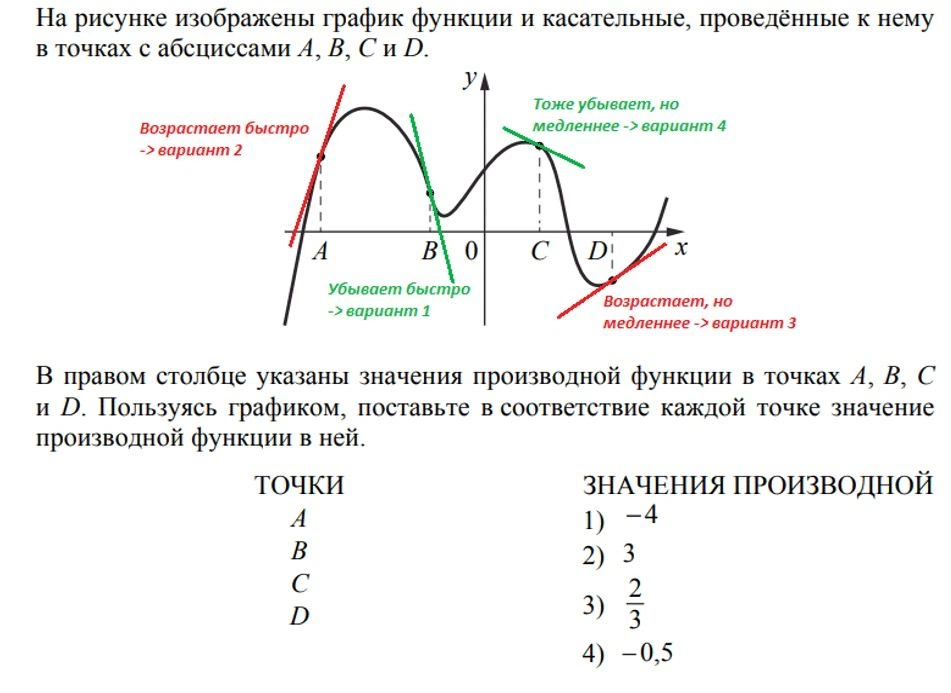
Ответ: 2143.

Задание 8: обязательно делать

Задача проверяет умение делать логичные выводы из утверждения. Иногда попадаются совсем простые задания, к таким даже дополнительно готовиться не надо.

Все, что от вас требуется, — схематично изобразить на черновике ясень, рябину и осину, указать известную разницу в высоте и внимательно сопоставить картинку с утверждениями.

Важно: не додумывайте дополнительные условия, не указанные в тексте задачи. Учитесь читать строго то, что написано.

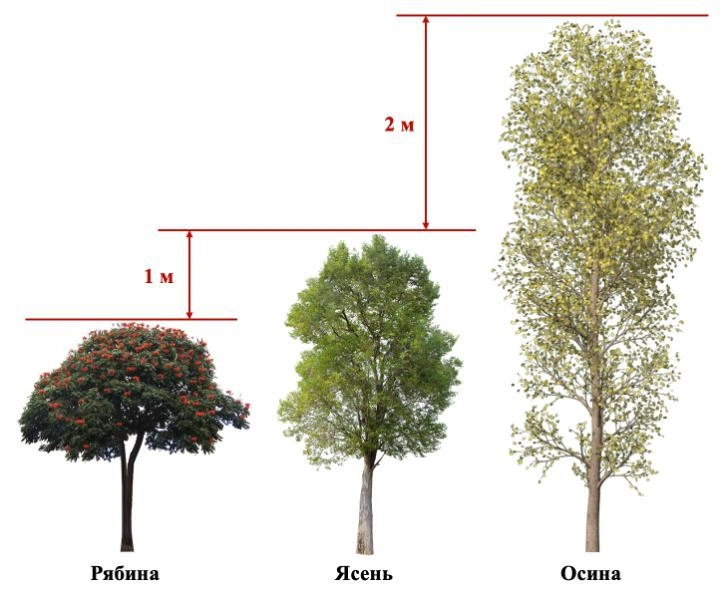
Исходя из рисунка выше получаем, что верны только утверждения 1 и 4.

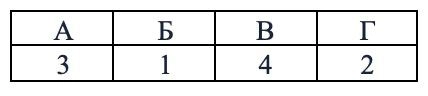
Ответ: 14.

А бывают случаи, когда с визуализацией задачки придется постараться.

Тут иллюстрация не так очевидна, но нам помогут круги Эйлера. Этот инструмент позволяет наглядно изобразить множество объектов. В данном случае — школьников. Давайте прикинем, как ребята могут распределиться по кружкам.

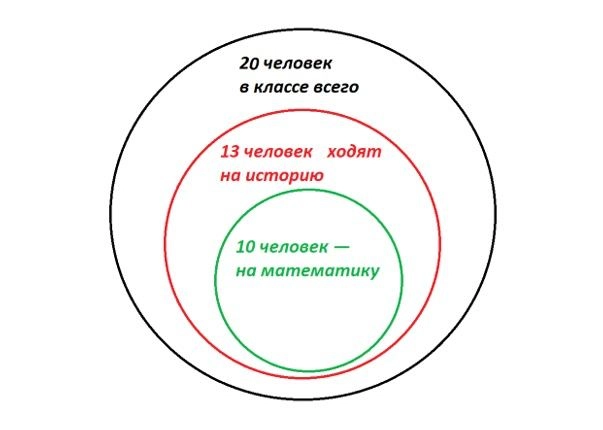
Например, так. Тут из 20 человек на кружки в итоге ходят 13. Причем 10 из них очень активны и выбрали сразу два предмета. Трое ограничились только историей.

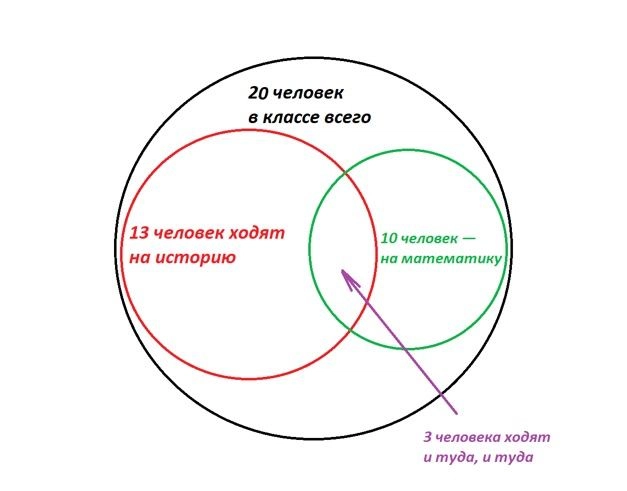
Или вот так. Если ребята задались целью по максимуму не пересекаться на дополнительных занятиях, то… У них не получится, и как минимум трое запишутся сразу на оба факультатива.

Конечно, возможны еще промежуточные варианты, но мы нарисовали два крайних. Теперь попробуем ответить на вопросы.

1. Смотрим на первую картинку. Даже если все ребята будут очень стараться посетить оба кружка, они ограничены условиями задачи и максимум на оба попадут 10 человек из 20. Нет.
2. Тут надо рассмотреть другую крайность, которую мы изобразили на второй картинке. Как бы ребята ни старались не встречаться на кружках, хотя бы трое попадут на оба сразу. Да.
3. Уж точно неверно. На обеих наших картинках есть ребята, которые ходят на историю, но не ходят на математику. Нет.
4. Смотрим на первую картинку. Оба кружка могут посещать максимум 10 человек. 

Ответ: 24.

Так что для решения иногда мало логики — понадобится еще немного воображения. Потренируйтесь, и ваши шансы получить балл увеличатся.

Задание 14: обязательно делать

Задание проверяет базовые навыки счета, которым учат в 5–6-м классах. Чтобы получить балл и сдать базовую математику, надо:

• уметь выполнять арифметические действия с обыкновенными и десятичными дробями;
• правильно расставлять порядок действий;
• быть предельно внимательными.

Уделите пару вечеров отработке алгоритмов сложения, вычитания, умножения и деления обыкновенных и десятичных дробей, и это задание у вас в кармане.

Задание 15

Составители экзамена проверяют ваш навык работы с процентами и единицами отношения. Такие задачи бывают четырех типов.

Тип 1. Найти часть от числа

Часть может быть выражена в процентах или сразу в виде дроби. Например, придется искать треть от чего-то.

Рассмотрим на примере реальной задачи из экзамена:

Прочувствуйте специфику задачи: нам известно целое — вся зарплата до вычета налога. А работать мы будем с кусочком — 13 процентами. Сколько это в рублях, нам еще предстоит узнать.

Чтобы ответить на вопрос задачи, нужно сделать три шага:

1. Перевести процент в десятичную дробь.

Для этого всегда надо количество процентов поделить на 100.

13 : 100 = 0,13.

2. Найти, сколько это от зарплаты в рублях.

Запоминаем главное правило для этого типа задач: чтобы найти дробь от числа, надо число умножить на эту дробь.

12 500 ∙ 0,13 = 1 625 (руб.) — налог, который удержат с зарплаты Ивана Кузьмича.

3. Ответить на вопрос задачи.

У нас просили зарплату после вычета налога, а не сам налог.

12 500 – 1625 = 10 875 (руб.).

Ответ: 10 875.

Будьте внимательны: многие совершают ошибку именно на последнем шаге!

Тип 2. Найти число по его части

Прочувствуйте разницу с прошлой задачей: тут 124 — и есть 25%, то есть одна и та же величина выражена в процентах и в абсолютных величинах, в данном случае — в учениках. Просят узнать целое — 100%.

1. Переводим процент в десятичную дробь:

25 : 100 = 0,25.

2. Находим, сколько учеников всего.

Правило для этого типа задач: чтобы найти целое, надо часть разделить на дробь.

124 : 0,25 = 496 (уч.) — всего.

Ответ: 496.

Тип 3. Найти, сколько процентов часть составляет от целого

Особенность подобных заданий: не дано процентов, есть только абсолютные величины. В данном случае — стоимость футболки в рублях.

1. Находим, какую долю новая цена составляет от первоначальной.

Запоминаем правило: чтобы найти, какую долю часть составляет от целого, надо часть разделить на целое.

680 : 800 = 0,85.

2. Переводим долю в процент.

В прошлых задачах мы уже дважды выполнили обратное действие. В этот раз сделаем наоборот: умножим полученную дробь на 100.

0,85 ∙ 100 = 85% — столько процентов новая цена составляет от старой.

3. Отвечаем на вопрос задачи.

Нас спросили, на сколько процентов цена снизилась, что стала 85% от первоначальной. Конечно, изначально она была 100%. Итого:

100 – 85 = 15%.

Ответ: 15%.

Тип 4. Задачи на соотношение

Если перефразировать условие, то за первого кандидата проголосовали 3 части избирателей, а за второго — 2 части. Особенность этих частей в том, что они одинаковые по величине.

Если одна будет состоять из 10 человек, то за первого кандидата будет 30, а за второго — 20.

1. Считаем общее количество частей:

3 + 2 = 5.

2. Узнаем, сколько голосов составляет одна такая часть.

Тут речь о процентах проголосовавших. Сколько всего проголосовало? Конечно, 100%! Значит, каждая из пяти частей «весит»

100 : 5 = 20%.

3. Отвечаем на вопрос задачи.

За проигравшего проголосовало меньше частей избирателей. В нашем случае 2.

20 ∙ 2 = 40%.

Ответ: 40%.

Решение этих задач удобнее всего оформить табличкой:

1 часть = 100% : 5 = 20%.

Если рассчитываете решать текстовую задачу, включите здравый смысл. Ответ всегда можно проверить на адекватность благодаря обычной логике. 

Задание 16: обязательно делать

Задание на решение выражения. На самом деле оно проверяет знание теории, так как в этом задании вам могут встретиться:

• выражения со степенями,
• иррациональные выражения,
• логарифмические выражения,
• тригонометрические выражения.

Ваша задача, соответственно, — знать:

• свойства степеней

• свойства корней

• свойства логарифмов

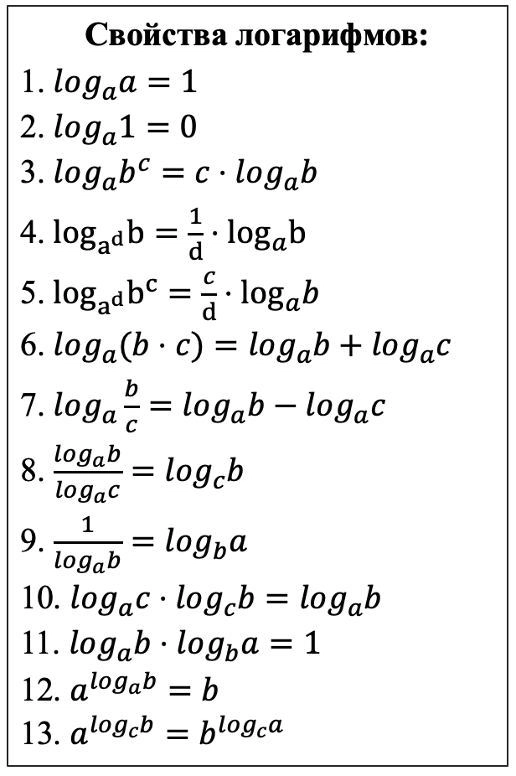
• формулы тригонометрии

Вы можете подробно ознакомиться с ними и научиться выводить в этой статье.

Обратите внимание: нужная теория будет в справочных материалах на экзамене, но это не поможет, если вы не научитесь применять ее для решения заданий. Практика обязательна!

Задание 17: обязательно делать

В номере с уравнениями вам не встретятся тригонометрические. Зато вы точно увидите там:

• линейные уравнения

Раскрываем скобки, если они есть, слагаемые с х переносим в одну сторону от равно, без х — в другую. Приводим подобные и решаем простейшее уравнение.

• квадратные уравнения

Бывают полные и неполные, всего надо повторить три алгоритма решения! А формула дискриминанта еще и в справочных материалах есть.

• иррациональные уравнения

Это те, что с корнем. Чтобы избавиться от корня, возводим обе части уравнения в квадрат и решаем получившееся уравнение. Есть нюансы с областью допустимых значений: подставьте полученные корни в исходное уравнение и проверьте, выполняется ли равенство. Если нет, то подставленное значение решением не будет.

• показательные уравнения

Ваша задача — с помощью формул свойств степеней привести уравнение к виду, когда слева и справа от равно в основании степени будет одно и то же число. После приравниваем показатели и решаем. Вот так:

Ответ: 7.

• логарифмические уравнения

С помощью формул свойств логарифмов приводим уравнение к виду, когда слева и справа от равно будет логарифм с одинаковым основанием. После приравниваем выражения под логарифмом и решаем.

Ответ: 67.

Прелесть уравнений в том, что ответ всегда можно проверить подстановкой вместо x в уравнение. Не забывайте проверять, ведь это возможность убедиться на 100%, что вы не упустите заветный балл.

Задание 19

Если хотите сдать базовую математику и решить номер 19, надо ознакомиться со свойствами целых чисел и признаками делимости. Иногда решение можно найти даже подбором! Попробуйте — времени на базовом ЕГЭ вам точно хватит.

Для начала нужно запомнить все признаки делимости.

А теперь посмотрим на типичное задание 19.

Тут помогут признаки делимости. Отдельного признака для 12 нет, потому нам надо разложить его на множители, признаки делимости для которых есть. 

• На 3: сумма всех цифр делится на 3.
• На 4: число, образованное последними двумя цифрами, делится на 4.

Начнем с признака для 4. Пока что наше число заканчивается на 13 и на 4 не делится. Попробуем вычеркнуть последнюю цифру, и число будет заканчиваться на 61. Тоже не подходит. Вычеркнем еще одну: теперь на конце 76… Вот оно! От изначального числа осталось 751576, две цифры уже вычеркнули, осталось убрать одну.

Теперь проверим признак для 3: 7 + 5 + 1 + 5 + 7 + 6 = 31. Какое ближайшее число разделится на 3? Конечно, 30. Если мы вычеркнем единичку, все сойдется.

Ответ: 75576.

Другой вариант задания:

А задание такого типа можно попытаться подобрать, расположений не слишком много. Мы все же постараемся порассуждать, чтобы уменьшить количество возможных вариантов.

Чтобы число делилось на 10, оно должно заканчиваться на 0. Например, это получится, если сложить 7 + □7 + □□6. Уже немного легче. Остальное просто подберем. Под условие задачи подойдет 7 + 27 + 356 = 390.

Ответ: 390.

Какие задания мы не разобрали и почему

Теперь вы знаете, как сдать базовую математику, решив всего семь заданий. Но некоторые номера базового ЕГЭ включают слишком большое разнообразие прототипов, и методы их решения не ограничиваются парой простых алгоритмов.

Например, в эту группу относятся все задания по геометрии: с 9 по 13. Чтобы решать геометрию, мало знать основные фигуры и формулы. Необходим навык, который вырабатывается только практикой. Однако у нас есть статья про окружность — в ней вы найдете много полезной информации.

Задание 18 обычно, хотя и не всегда, содержит неравенство.

Это объемный блок теории, которую тоже необходимо подкреплять практикой. Но, может, вам повезет и попадется задачка на расположение значений на числовой прямой.

Тут достаточно примерно прикинуть значения и аккуратно внести ответы в бланк. Ясно, что 7/3  больше 2, но меньше 3. Корень из 26 равен 5 с копейками, а степень –1 из 3/5 сделает 5/3, или чуть больше 1,5. Подобные задания надо пытаться делать обязательно!

Задание 20. С этим заданием ученики знакомы еще с 9-го класса, так как оно было под номером 21 на ОГЭ. Это текстовая задача:

• на производительность,
• движение (по прямой, воде, окружности),
• сплавы и смеси,
• проценты (пиджаки, рубашки, брюки; бюджет семьи; акции, которые растут и падают),
• прогрессии.

В задании 21 на ОГЭ не было прогрессий, но они были в первой части на ОГЭ, так что ничего нового.

Задание 21. Здесь попадаются разные типы неочевидных задач на логику — чем-то они даже похожи на олимпиадные. Решение каждой нужно рассматривать отдельно и подробно. Если хотите прочитать о том, какие задачи бывают в 21-м номере, пишите в комментариях, и Maximum поделится своими методами решения!

Не знаете, какой вуз выбрать? Воспользуйтесь бесплатной консультацией в нашем центре. Что это такое? Все просто: вы расскажете о себе и о своих интересах. А специалист посоветует, на какие специальности обратить внимание, в какой вуз поступать, какие ЕГЭ сдавать. Так вы сэкономите время на подготовку и сможете выбрать образование, которое точно окажется для вас интересным и полезным!

Вариант № 1

 1. Флакон
шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000
рублей во время распродажи, когда скидка составляет 25% ?

2. Тетрадь 
стоит  40  рублей.  Какое  наибольшее  число  таких  тетрадей

можно будет купить на 750 рублей после
понижения цены на 10%?

3. Оптовая цена
учебника 170 рублей. Розничная цена на 20% выше оптовой. Какое наибольшее число
таких учебников можно купить по розничной цене на 7000 рублей?

4. Цена на
электрический чайник была повышена на 16% и составила

3480 рублей. Сколько рублей стоил чайник до
повышения цены?

5.  Магазин
закупает цветочные горшки по оптовой цене 120 рублей за

штуку и продает с наценкой 20%. Какое
наибольшее число таких горшков можно купить в этом магазине на 1000 рублей?

6. Налог на доходы
составляет 13% от заработной платы.  Заработная

плата Ивана Кузьмича равна 12 500 рублей.
Сколько рублей он получит после вычета налога на доходы?

7. Розничная
цена учебника 180 рублей, она на 20% выше оптовой цены. Какое наибольшее число
таких учебников можно купить по оптовой цене на 10 000 рублей?

8. В школе 124
ученика изучают французский язык, что составляет 25%

от числа всех учеников. Сколько учеников
учится в школе?

9. В школе 800
учеников, из них 30% — ученики начальной школы.

Среди учеников средней и старшей школы 20%
изучают немецкий язык. Сколько учеников в школе изучают немецкий язык, если в
начальной школе немецкий язык не изучается?

Вариант № 2

1. Шариковая 
ручка  стоит  40  рублей.  Какое  наибольшее  число  таких

ручек можно будет купить на 900 рублей
после повышения цены на 10%?

2.В городе N
живет 200 000 жителей. Среди них 15% детей и подростков.  Среди взрослых
жителей 45% не работает (пенсионеры, студенты, домохозяйки и т. п.). Сколько
взрослых жителей работает?

3.  Железнодорожный
билет для взрослого стоит 720 рублей. Стоимость

билета для школьника составляет 50% от
стоимости билета для взрослого. Группа состоит из 15 школьников и 2 взрослых.
Сколько рублей стоят билеты на всю группу?

4. Футболка
стоила 800 рублей. После снижения цены она стала стоить

680 рублей. На сколько процентов была
снижена цена на футболку?

5. Клиент взял
в банке кредит 12 000 рублей на год под 16%. Он должен

погашать кредит, внося в банк ежемесячно
одинаковую сумму денег, с тем чтобы через год выплатить всю сумму, взятую в
кредит, вместе с процентами. Сколько рублей он должен вносить в банк
ежемесячно?

6. Налог на
доходы составляет 13% от заработной платы. После удержа‐

ния налога на доходы Мария Константиновна
получила 9570 рублей. Сколько рублей составляет заработная плата Марии
Константиновны?

7. 27
выпускников школы собираются учиться в технических вузах. Они

составляют 30% от числа выпускников.
Сколько в школе выпускников?

8. Пачка
сливочного масла стоит 60 рублей. Пенсионерам магазин делает скидку 5%. Сколько
рублей заплатит пенсионер за пачку масла?

9. Среди 40 000
жителей города 60% не интересуется футболом. Среди

футбольных болельщиков 80% смотрело по
телевизору финал Лиги чемпионов. Сколько жителей города смотрело этот матч по
телевизору?