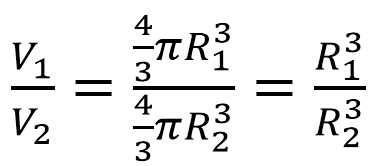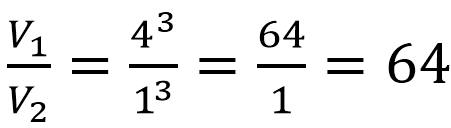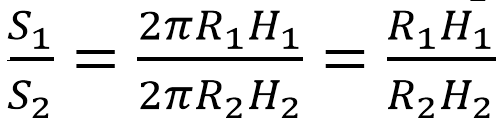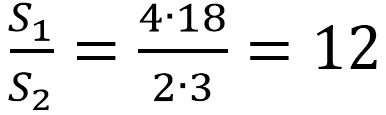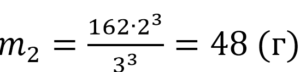Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
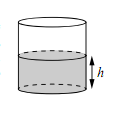
В цилиндрический сосуд налили 2000 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см3.
2
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в
раза больше первого? Ответ дайте в сантиметрах.
3
Объем первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
4
Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на
5
В цилиндрический сосуд налили 6 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,5 раза. Найдите объём детали. Ответ выразите в куб. см.
Пройти тестирование по этим заданиям
10
Сен 2013
Категория: 02 Стереометрия
02. Цилиндр.
2013-09-10
2022-09-11
Задача 1. Радиус основания цилиндра равен высота равна
Найдите площадь боковой поверхности цилиндра, деленную на
.
Решение: + показать
Задача 2. Площадь боковой поверхности цилиндра равна а диаметр основания равен
Найдите высоту цилиндра.
Решение: + показать
Задача 3. Длина окружности основания цилиндра равна высота равна
Найдите площадь боковой поверхности цилиндра.
Решение: + показать
Задача 4. Площадь осевого сечения цилиндра равна Найдите площадь боковой поверхности цилиндра, деленную на
.
Решение: + показать
Задача 5. Объём первого цилиндра равен 48 м У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра (в м
).
Решение: + показать
Задача 6. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
Решение: + показать
Задача 7. В цилиндрический сосуд налили см
воды. Уровень воды при этом достигает высоты
см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на
см. Чему равен объем детали? Ответ выразите в см
Решение: + показать
Задача 8. В цилиндрический сосуд налили см
воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в
раза. Найдите объем детали.
Ответ выразите в см
Решение: + показать
Задача 9. В цилиндрическом сосуде уровень жидкости достигает см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в
раза больше первого? Ответ выразите в сантиметрах.
Решение: + показать
Задача 10. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 11. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 12. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 13. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Вы можете пройти тест “Цилиндр”
Автор: egeMax |
комментария 3
Печать страницы
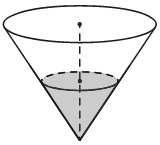
Формулировка задачи: В сосуде, имеющем форму конуса, уровень жидкости достигает K/L высоты. Объём сосуда N мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13 (Задачи по стереометрии).
Рассмотрим, как решаются подобные задачи на примерах и выведем общий способ решения.
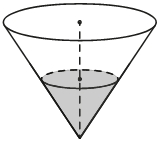
Пример задачи 1:
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём сосуда 1600 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах.
Решение:
Судя по картинке, есть 2 конуса: большой и малый, полностью заполненный водой. Данные конусы подобны с коэффициентом подобия, равным 1/2, так как большой конус заполнен водой ровно наполовину.
Поскольку в задаче дан объем большего конуса и по нему нужно получить объем меньшего, а объемы любых двух подобных объемных фигур относятся как куб коэффициента подобия, можно составить следующее соотношение:
Vмал.кон. / Vбол.кон. = (1/2)3
Выразим из этого соотношения объем малого конуса и вычислим его:
Vмал.кон. = Vбол.кон. ⋅ (1/2)3 = 1600 / 8 = 200 мл
Ответ: 200
Пример задачи 2:
В сосуде, имеющий форму конуса, уровень жидкости достигает 6/7 высоты. Объем сосуда 3430 мл. Чему равен объём налитой жидкости? Ответ дайте в миллиметрах.
Решение:
В задаче присутствуют 2 подобных конуса. Поскольку высота меньшего конуса составляет 6/7 высоты большего, это число является коэффициентом подобия. Объемы любых двух подобных объемных фигур относятся как куб коэффициента подобия, поэтому можно составить следующее соотношение:
Vмал.кон. / Vбол.кон. = (6/7)3
Выразим из этого соотношения объем малого конуса и вычислим его:
Vмал.кон. = Vбол.кон. ⋅ (6/7)3 = 3430 ⋅ 216 / 343 = 2160 мл
Ответ: 2160
В общем виде решение данной задачи по стереометрии выглядит следующим образом:
ОБЪЕМ ЖИДКОСТИ = N ⋅ (K/L)3
где N – объем сосуда, K/L – часть высоты, которую занимает уровень жидкости.
Остается лишь подставить конкретные значения и подсчитать результат.
Наглядная стереометрия
В 13 задании ЕГЭ базового уровня мы будем иметь дело с задачами по стереометрии, но не абстрактными, а наглядными примерами. Это могут быть задачи на уровень жидкости в сосудах, которую я разобрал ниже, или же задачи на модификации фигуры – например, у которой отрезали вершины. Нужно быть готовым к решению простых задач по стереометрии – они обычно сводятся сразу к задачам на плоскости, необходимо только правильно посмотреть на чертеж.
Разбор типовых вариантов заданий №13 ЕГЭ по математике базового уровня
Вариант 13МБ1
[su_note note_color=”#defae6″]
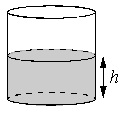
Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у данного? Ответ дайте в сантиметрах.
[/su_note]
Алгоритм выполнения:
- Записать формулу объема цилиндра.
- Подставить значения для цилиндра с жидкостью в первом и во втором случае.
- Объем жидкости не изменялся, следовательно, можно приравнять объемы.
- Полученное уравнение решить относительно второй высоты h2.
- Подставить данные и вычислить искомую величину.
Решение:
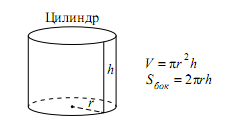
Запишем формулу объема цилиндра.
Если вы забыли формулу объема цилиндра, то напомню, как ее можно легко вывести. Объем простых фигур, таких как куб и цилиндр, можно вычислить умножив площадь основания на высоту. Площадь основания в случае с цилиндром равна площади окружности, которую, вы, наверняка помните: π • r2.
Следовательно, объем цилиндра равен π • r2 • h
Подставим значения для цилиндра с жидкостью в первом и во втором случае.
V1 = π r1 2 h1
V2 = π r2 2 h2
Объем жидкости не изменялся, следовательно, можно приравнять объемы.
V1 = V2
Левые части равны, значит можно приравнять и правые.
π r1 2 h1 = π r2 2 h2
Полученное уравнение решим относительно второй высоты h2.
h2 – неизвестный множитель. Чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.
h2 =( π r1 2 h1)/ π r2 2
По условию площадь основания стала в 4 раза больше, то есть r2 = 4 r1 .
Подставим r2 = 4 r1 в выражение для h1.
Получим: h2 =( π r1 2 h1)/ π (4 r1) 2
Полученную дробь сократим на π, получим h2 =( r1 2 h1)/ 16 r1 2
Полученную дробь сократим на r1, получим h2 = h1/ 16.
Подставим известные данные: h2 = 80/ 16 = 5 см.
Ответ: 5.
Вариант 13МБ2
[su_note note_color=”#defae6″]
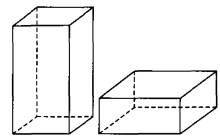
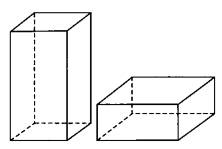
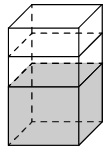
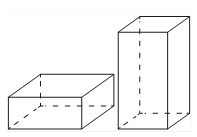
Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в четыре с половиной раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?
[/su_note]
Алгоритм выполнения:
- Записать формулу, для вычисления объема правильной четырехугольной призмы.
- Записать в общем виде формулу для нахождения объема в первом и втором случае.
- Найти отношение объемов.
- Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы.
- Сократить получившуюся дробь.
Решение:
Запишем формулу, для вычисления объема правильной четырехугольной призмы.
V = a · b · c
Запишем в общем виде формулу для нахождения объема в первом и втором случае.
V1 = a1 · b1 · c1
V2 = a2 · b2 · c2
Найдем отношение объемов.
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2)
Преобразуем полученное выражение с учетом соотношения измерений первой и второй призмы.
По условию c1 = 4,5 c2 (первая коробка в четыре с половиной раза выше второй),
b2 = 3 b1 (вторая коробка втрое шире первой).
Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a2 = 3 a1
Подставим эти выражения в формулу отношения объемов:
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2) = (a1 · b1 · 4,5c2)/ ( 3a1 · 3b1 · c2) = (a1 · b1 · 4,5c2)/ ( 9a1 · b1 · c2)
Сократим получившуюся дробь на a1 · b1 · c2. Получим:
V1 / V2 = (a1 · b1 · 4,5c2)/ ( 9a1 · b1 · c2) = 4,5/9 = ½.
Объем первой коробочки в 2 раза меньше объема второй.
Ответ: 2.
Вариант 13МБ3
[su_note note_color=”#defae6″]
Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в полтора раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?
[/su_note]
Алгоритм выполнения:
- Записать формулу, для вычисления объема правильной четырехугольной призмы.
- Записать в общем виде формулу для нахождения объема в первом и втором случае.
- Найти отношение объемов.
- Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы.
- Сократить получившуюся дробь.
Решение:
Запишем формулу, для вычисления объема правильной четырехугольной призмы.
V = a · b · c
Запишем в общем виде формулу для нахождения объема в первом и втором случае.
V1 = a1 · b1 · c1
V2 = a2 · b2 · c2
Найдем отношение объемов.
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2)
Преобразуем полученное выражение с учетом соотношения измерений первой и второй призмы.
По условию c1 = 1,5 c2 (первая коробка в полтора раза выше второй), b2 = 3 b1 (вторая коробка втрое шире первой).
Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a2 = 3 a1
Подставим эти выражения в формулу отношения объемов:
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2) = (a1 · b1 · 1,5c2)/ ( 3a1 · 3b1 · c2) = (a1 · b1 · 1,5c2)/ ( 9a1 · b1 · c2)
Сократим получившуюся дробь на a1 · b1 · c2. Получим:
V1 / V2 = (a1 · b1 · 1,5c2)/ ( 9a1 · b1 · c2) = 1,5/9 = 15/(10 · 9) = 3/(2 · 9) = 1/ (2 · 3) = 1/6.
Объем первой коробочки в 6 раза меньше объема второй.
Ответ: 6.
Вариант 13МБ4
[su_note note_color=”#defae6″]
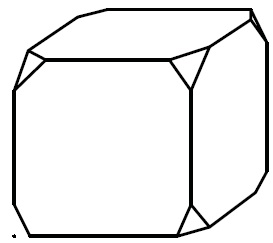
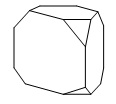
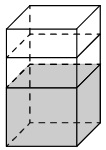
От деревянного кубика отпилили все его вершины (см. рис.). Сколько граней у получившегося многогранника (невидимые ребра на рисунке не изображены)?
[/su_note]
Сначала вспомним сколько всего граней и вершин у куба: шесть граней и восемь вершин. Теперь на месте каждой вершины образуется новая грань после отпила, значит у модифицированного в задании куба шесть родных граней и восемь новых (после отпила). Итого получаем: 6 + 8 = 14 граней.
Ответ: 14.
Если бы нас спросили, а сколько вершин у нового “куба”. Очевидно, если вместо одной становится три, а их всего восемь, то получаем: 8 • 3 = 24
Вариант 13МБ5
[su_note note_color=”#defae6″]
Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго – 6 и 4. Во сколько раз объем второго цилиндра больше объема первого?
[/su_note]
Алгоритм выполнения
- Записываем ф-лу для вычисления объема цилиндра.
- Вводим обозначения для радиуса основания и высоты 1-го цилиндра. Выражаем подобным образом аналогичные параметры 2-го цилиндра.
- Формируем формулы для объема 1-го и 2-го цилиндров.
- Вычисляем отношение объемов.
Решение:
Объем цилиндра равен: V=πR2H. Обозначим радиус основания 1-го цилиндра через R1, а его высоту – через Н1. Соответственно, радиус основания 2-го цилиндра обозначим через R2, а высоту – через Н2.
Отсюда получим: V1=πR12H1, V2=πR22H2.
Запишем искомое отношение объемов:
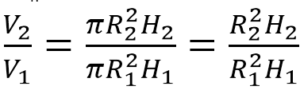
Подставляем в полученное отношение числовые данные:
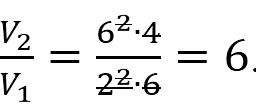
Вывод: объем 2-го цилиндра больше объема 1-го в 6 раз.
Вариант 13МБ6
[su_note note_color=”#defae6″]
В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке поднялся в 1,4 раза. Найдите объем детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
[/su_note]
Алгоритм выполнения
- Вводим обозначения для объема до погружения детали и после. Пусть это будет соответственно V1 и V2.
- Фиксируем значение для V1. Выражаем V2 через V1. Находим значение V2.
- Переводим результат, полученный в литрах, в куб.см.
Решение:
Объем бака до погружения V1=5 (л). Т.к. после погружения детали объем стал равным V2. Согласно условию, увеличение составило 1,4 раза, поэтому V2=1,4V1.
Отсюда получаем: V2=1,4·5=7 (л).
Т.о., разница объемов, которая и составляет объем детали, равна:
V2–V1=7–5=2 (л).
2 л=2·1000=2000 (куб.см).
Вариант 13МБ7
[su_note note_color=”#defae6″]
Вода в сосуде цилиндрической формы находится на уровне h=80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у первого? Ответ дайте в сантиметрах.
[/su_note]
Алгоритм выполнения
- Записываем ф-лу для расчета объема цилиндра.
- На основании этой формулы записываем 2 уравнения – для вычисления объема воды в 1-м и 2-м сосудах. Для этого используем в формуле соответствующие индексы 1 и 2.
- Поскольку воду просто переливают их одного сосуда в другой, то ее объем не изменяется. Поэтому приравниваем полученные уравнения. Из полученного единственного уравнения находим уровень воды во 2-м сосуде, выраженный высотой h2.
Решение:
Объем цилиндра равен: V=Sоснh=πR2h.
Объем воды в 1-м сосуде: V1=πR12h1.
Объем во 2-м сосуде: V2=πR22h2.
Приравниваем V1 и V2: πR12h1=πR22h2.
Сокращаем на π, выражаем h2:
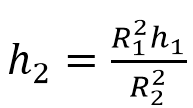
По условию R2=2R1. Отсюда:
.
Вариант 13МБ8
[su_note note_color=”#defae6″]
От деревянной правильной треугольной призмы отпилили все ее вершины (см. рис.). Сколько вершин у получившегося многогранника (невидимые ребра на рисунке не изображены)?
[/su_note]
Алгоритм выполнения
- Определяем количество вершин у треугольной призмы.
- Анализируем изменения, которые произойдут при отпиливании всех вершин. Подсчитываем кол-во вершин у нового многогранника.
Решение:
Вершины призмы формируют вершины оснований (верхнего и нижнего). Поскольку основаниями правильной треугольной призмы являются правильные треугольники, то вершин у такой призмы 3·2=6 штук.
Спилив вершины призмы, получим вместо них небольшие (по сравнению с размерами самой призмы) треугольники. Это отображено и на рисунке. То есть вместо каждой вершины образуется 3 новых. Следовательно, их кол-во станет равным: 6·3=18.
Вариант 13МБ9
[su_note note_color=”#defae6″]
Даны две коробки, имеющие форму правильной четырехугольной призмы, стоящей на основании. Первая коробка в четыре с половиной раза ниже второй, а вторая второе уже первой. Во сколько раз объем первой коробки больше объема второй?
[/su_note]
Алгоритм выполнения
- Вводим обозначения для линейных параметров коробок и их объемов.
- Определяем зависимость линейных параметров согласно условию.
- Записываем формулу для вычисления объема призмы.
- Адаптируем эту формулу для объемов коробок.
- Находим отношение объемов.
Решение:
Т.к. форма коробок – правильная призма, то в их основании лежат квадраты. Поэтому можем обозначить длину и ширину каждой коробки одинаково. Пусть для первой коробки это а1, а для второй а2. Высоты коробок обозначим соответственно h1 и h2. Объемы – V1 и V2.
Согласно условию, h2=4,5h1, а1=3а2.
Объем призмы равен: V=Sоснh. Т.к. в основании коробок лежит квадрат, то Sосн=а2. Отсюда: V=a2h.
Для 1-й коробки имеем: V1=a12h1. Для 2-й коробки: V2=a22h2.
Тогда получаем отношение:
Ответ: 2
Вариант 13МБ10
[su_note note_color=”#defae6″]
В сосуде, имеющем форму конуса, уровень жидкости достигает ½ высоты. Объем сосуда 1600 мл. Чему равен объем налитой жидкости? Ответ дайте в миллилитрах.
[/su_note]
Алгоритм выполнения
- Доказываем, что данные в условии конусы подобны.
- Определяем коэффициент подобия.
- Используя свойство для объемов подобных тел, находим объем жидкости.
Решение:
Если рассматривать сечение конуса по двум его противоположно расположенным образующим (осевое сечение), то видим, что полученные таким способом треугольники большого конуса и малого (образованного жидкостью) подобны. Это следует из равенства их углов. Т.е. имеем: у конусов подобны высоты и радиусы основания. Отсюда делаем вывод: т.к. линейные параметры конусов подобны, то и конусы подобны.
По условию высота малого конуса (жидкости) составляет ½ высоты конуса. Значит, коэффициент подобия малого и большого конусов равен ½.
Применяем св-во подобия тел, которое заключается в том, их объемы относятся как коэффициет подобия в кубе. Обозначим объем большого конуса V1, малого – V2. Получим:
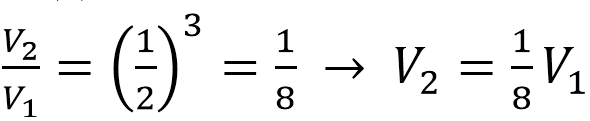
Поскольку по условию V1=1600 мл, то V2=1600/8=200 мл.
Вариант 13МБ11
[su_note note_color=”#defae6″]
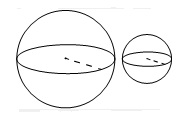
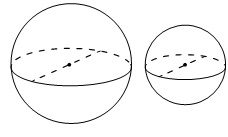
Даны два шара с радиусами 4 и 1. Во сколько раз объем большего шара больше объема меньшего?
[/su_note]
Алгоритм выполнения
- Записываем формулу для вычисления объема шара.
- Адаптируем формулу для каждого из шаров. Для этого используем индексы 1 и 2.
- Записываем отношение объемов, вычисляем его, подставив числовые данные из условия.
Решение:
Объем шара вычисляется по ф-ле: .
Отсюда объем 1-го (большего) шара равен 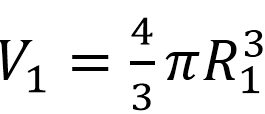
.
Составим отношение объемов:
Подставляем в полученную формулу числовые данные из условия:
Вывод: объем большего шара в 64 раза больше.
Вариант 13МБ12
[su_note note_color=”#defae6″]
Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 4 и 18, а второго – 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
[/su_note]
Алгоритм выполнения
- Записываем формулу для определения площади бок.поверхности цилиндра.
- Переписываем ее дважды с использованием соответствующих индексов – для 1-го (большего) и 2-го (меньшего) цилиндров.
- Находим отношение площадей. Вычисляем отношения, используя числовые данные из условия.
Решение:
Площадь бок.поверхности цилиндра вычисляется так: S=2πRH.
Для 1-го цилиндра имеем: S1=2πR1H1. Для 2-го цилиндра: S2=2πR2H2.
Составим отношение этих площадей:
Найдем числовое значение полученного отношения:
Вывод: площадь боковой поверхности 1-го цилиндра больше в 12 раз.
Вариант 13МБ13
[su_note note_color=”#defae6″]
Однородный шар диаметром 3 см весит 162 грамма. Сколько граммов весит шар диаметром 2 см, изготовленный из того же материала?
[/su_note]
Алгоритм выполнения
- Записываем формулу для определения массы большего шаров через плотность и объем.
- Объем в этой формуле расписываем через ф-лу объема шара (через его радиус).
- Записываем ф-лу для массы меньшего шара, расписываем объем через радиус (по аналогии с пп.1 и 2).
- Поскольку оба шара изготовлены из одного и того же материала, то найденное значение для плотности можем использовать в ф-ле для массы меньшего шара. Вычисляем искомую массу.
Решение:
Масса большего (1-го) шара равна: m1=ρV1. Объем этого шара составляет V1=(4/3)πR13. Отсюда получаем: m1=(4/3)πρR13. Из этого уравнения выразим плотность: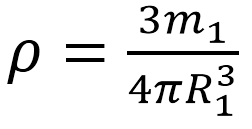
Масса меньшего (2-го) шара равна: m2=ρV2. Объем шара: V2=(4/3)πR23. В ур-ние для m2 подставим выражения для ρ и V2. Получаем:
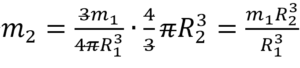
Вариант 13МБ14
[su_note note_color=”#defae6″]
В бак, имеющий форму правильной четырехугольной призмы со стороной основания, равной 40 см, налита жидкость. Чтобы измерить объем детали сложной формы, ее полностью погружают в эту жидкость. Найдите объем детали, если после ее погружения уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах.
[/su_note]
Алгоритм выполнения
- Определяем часть призмы, соответствующую объему погруженной детали.
- Вычисляем объем детали на основании формулы для определения объема прямой призмы с квадратом в основании.
Решение:
Погруженная в жидкость деталь занимает объем, соответствующий столбу жидкости, высота которого равна 10 см, т.е. разнице, возникшей между начальной высотой жидкости и конечной (после погружения). Это означает, что деталь имеет объем, равный части жидкости, занимающей объем 40х40х10 (см).
Найдем этот объем:
V=40·40·10=16000 (см3).
Даниил Романович | Просмотров: 19.1k
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Цилиндр»
Открытый банк заданий по теме цилиндр. Задания B8 из ЕГЭ по математике (профильный уровень)
Производная и первообразная функции
Задание №1075
Тип задания: 8
Тема:
Цилиндр
Условие
В цилиндрическом сосуде уровень жидкости достигает 20 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в два раза больше диаметра первого? Ответ выразите в сантиметрах.
Показать решение
Решение
Пусть R — радиус основания первого сосуда, тогда 2R — радиус основания второго сосуда. По условию объём жидкости V в первом и втором сосуде один и тот же. Обо-значим через H — уровень, на который поднялась жидкость во втором сосуде. Тогда
V=pi R^2 cdot 20, и V=pi (2R)^2H = 4pi R^2H. Отсюда pi R^2 cdot 20 = 4pi R^2H, 20 = 4H, H =5
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №911
Тип задания: 8
Тема:
Цилиндр
Условие
В цилиндрический сосуд налили 2000 см3 воды. Уровень жидкости оказался равным 15 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объём детали? Ответ выразите в см3.
Показать решение
Решение
Пусть R — радиус основания цилиндра, а h — уровень воды, налитой в сосуд. Тогда объём налитой воды равен объёму цилиндра с радиусом основания R и высотой h. Vводы = Sосн. · h = pi R^2cdot h. Согласно условию выполняется равенство 2000=pi R^2cdot15. Отсюда, pi R^2=frac{2000}{15}=frac{400}{3}.
Пусть H — уровень воды в сосуде после погружения в него детали. Тогда суммарный объем воды и детали равен объему цилиндра с радиусом основания R и высотой H. По условию H=h+9=15+9=24. Значит, Vводы + детали = pi R^2cdot H=frac{400}{3}cdot24=3200. Следовательно, Vдетали = Vводы + детали − Vводы = 3200-2000=1200.
Ответ
1200
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №315
Тип задания: 8
Тема:
Цилиндр
Условие
Найдите высоту цилиндра, если радиус его основания равен 8, а площадь боковой поверхности 96pi.
Показать решение
Решение
S=2pi rh,
96pi=2picdot8h,
h=frac{96pi}{16pi}=6.
Ответ
6
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №72
Тип задания: 8
Тема:
Цилиндр
Условие
В сосуд цилиндрический формы налили 500 куб. см воды. Определите объем детали полностью погруженной в воду, если после погружения уровень жидкости увеличился в 1,2 раза. Выразите ответ в куб. см.
Показать решение
Решение
Обозначим за V1 изначальный объем жидкости в цилиндре. После погружения детали, объем жидкости увеличился в 1,2 раза, значит конечный объем жидкости равен V2 = 1,2·V1. Объем детали равен разности объемов до и после погружения, значит V = V_2-V_1=1,2cdot 500-500=100 куб. см.
Ответ
100
Задание №71
Тип задания: 8
Тема:
Цилиндр
Условие
Уровень жидкости в первом сосуде цилиндрической формы достигает 63 см. Диаметр второго сосуда, такой же формы, больше диаметра первого в 3 раза. Определите уровень жидкости, если ее перелить из первого сосуда во второй. Ответ укажите в сантиметрах.
Показать решение
Решение
Формула вычисления объема первого цилиндра имеет вид:
V_1=pi cdot R_1^2 cdot h_1=pileft ( frac{d_1}{2} right )^2h_1, где:
d1 – диаметр цилиндра;
h1 – высота цилиндра.
Так как диаметр второго сосуда в 3 раза больше диаметра первого, то его объем равен: V_2=pileft ( frac{3d_1}{2} right )^2h_2
При переливе жидкости ее исходный объем не изменяется, т.е.: V1 = V2, а значит справедливо равенство: pileft(frac{d_1}{2}right)^2h_1=pileft(frac{3d_1}{2}right)^2h_2
Подставим значения из условия, упростим выражение и найдем искомую высоту жидкости второго сосуда h2:
pi enspacefrac{d_1^{2}}{4}enspace 63=pi enspacefrac{9d_1^{2}}{4}enspace h_2
frac{63}{4}=frac{9}{4}h_2
h_2=frac{63}{9}=7
Ответ
7
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
Среди задач ЕГЭ по физике некоторую трудность при всей своей простоте представляют задачи на влажность. По всей видимости существует некоторое недопонимание сути проблемы. Попробуем разобраться.
В воздухе всегда находится некоторое количество воды в газообразном виде, в виде пара. Это происходит потому, что над поверхностью любой жидкости происходит испарение и конденсация жидкости. В открытом сосуде процесс испарения может преобладать над процессом конденсации. Испаряться вода может до тех пор, пока не наступит динамическое равновесие между испарением и конденсацией молекул воды.
Относительная влажность — это отношение плотности пара в воздухе к плотности насыщенного пара.
Но если вспомнить, что плотность газа пропорциональна давлению газа, то получим формулу определения влажности:
,
где р — парциальное давление, р0 — давление насыщенного пара.
Давление насыщенного пара величина постоянная для заданной температуры. Она меняется только с изменением температуры: увеличивается с увеличением температуры и уменьшается с уменьшением температуры.
Задача 1: Относительная влажность воздуха в закрытом сосуде 30 %. Какой станет относительная влажность, если объём сосуда при неизменной температуре уменьшить в 2 раза? (Ответ дать в процентах.)
Решение: Относительная влажность определяется отношением парциального давления пара к давлению насыщенного пара
Даление насыщенного пара зависит от температуры, а она — не менялась, следовательно р0 не меняется. Объем сосуда уменьшили вдвое при неизменных условиях, следовательно, парциальное давление увеличилось тоже в 2 раза.
Ответ: 60%
Задача 2: Относительная влажность воздуха в закрытом сосуде 40 %. Какой станет относительная влажность, если объём сосуда при неизменной температуре уменьшить в 3 раза? (Ответ дать в процентах.)
Решение: Условия задач №1 и №2 отличаются только цифрами, поэтому все выше сказанное относится и к этой задаче. Но больше, чем р0, парциальное давление пара в сосуде быть не может. Следовательно, в сосуде будет насыщенный пар и вода.
Ответ: 100%
Задача 3: В закрытом цилиндре с перегородкой посередине с одной стороны находится сухой воздух, с другой — влажный, относительная влажность которого составляет 50%. Какая влажность установится в цилиндре, если убрать перегородку.
Решение: Парциальное давление пара за перегородкой , учитывая, что φ =, будет равно р = 0,5р0 Если перегородку открыть, то при неизменной температуре объем увеличится в 2 раза. Следовательно давление уменьшится в 2 раза и будет р = 0,25р0. Следовательно, влажность будет φ = 25%.
Ответ: 25%
Задача 4: В вертикальном цилиндрическом сосуде под поршнем находится воздух, водяной пар и капли воды на стенках сосуда. Поршень начинают медленно поднимать, увеличивая объём сосуда. В середине процесса подъёма поршня капли воды в сосуде исчезают, температура пара остается неизменной в течение всего процесса подъёма поршня. Затем сосуд с паром нагревают при неизменном положении поршня. Как будет меняться при этих процессах влажность воздуха в сосуде? Ответ поясните, указав какие физические явления и закономерности вы использовали для объяснения.
Решение: 1. Пар в сосуде был насыщенным, так как в сосуде помимо воздуха были капли воды.
2.Поршень поднимают, и до тех пор, пока вода не исчезнет, влажность 100%. Но с этого момента объем больше не увеличивают.
3. Сосуд с паром нагревают, следовательно влажность уменьшается, так как с увеличением температуры увеличивается давление насыщенного пара рнп, а парциальное давление не меняется, т.к. не меняется количество пара в воздухе.
Ответ: будет уменьшаться
Подробнее смотреть здесь→
11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на растворы, смеси и сплавы
(blacktriangleright) Концентрация вещества в растворе (сплаве) – это процент содержания этого вещества в растворе (сплаве): [text{концентрация вещества}=dfrac{text{масса вещества}}{text{масса раствора}}cdot 100%]
(blacktriangleright) Заметим, что в задачах из данной подтемы зачастую удобно составлять уравнения относительно кислоты или активного вещества.
Задание
1
#846
Уровень задания: Равен ЕГЭ
Сергей смешал раствор, содержащий (20%) кислоты и раствор, содержащий (40%) той же кислоты. В итоге у него получился раствор, содержащий (32,5%) кислоты, причём объём полученного раствора (4) литра. Сколько литров раствора, содержащего (20%) кислоты, использовал Сергей при смешивании?
Пусть (x) литров раствора, содержащего (20%) кислоты использовал Сергей при смешивании, тогда
(4 — x) литров раствора, содержащего (40%) кислоты использовал Сергей при смешивании,
(dfrac{20}{100}x) – объём кислоты в растворе, содержащем (20%) кислоты, (dfrac{40}{100}(4 — x)) – объём кислоты в растворе, содержащем (40%) кислоты.
Так как в итоге кислоты оказалось (dfrac{32,5}{100} cdot 4 = 1,3) литра, то:
[dfrac{20}{100}x + dfrac{40}{100}(4 — x) = 1,3,] откуда находим (x = 1,5).
Ответ: 1,5
Задание
2
#844
Уровень задания: Равен ЕГЭ
Один газ в сосуде А содержал (21%) кислорода, второй газ в сосуде В содержал (5%) кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит (14,6%) кислорода. Найдите массу третьего газа. Ответ дайте в граммах.
Пусть (x) грамм – масса второго газа, тогда
(x + 300) грамм – масса первого газа,
(dfrac{21}{100}(x + 300)) грамм – масса кислорода в первом газе,
(dfrac{5}{100}x) грамм – масса кислорода во втором газе,
тогда масса кислорода в третьем газе составляет (dfrac{14,6}{100}(2x + 300)) грамм.
Так как третий газ возник в результате смешивания первого и второго, то:
[dfrac{21}{100}(x + 300) + dfrac{5}{100}x = dfrac{14,6}{100}(2x + 300),] откуда находим (x = 600). Таким образом, масса третьего газа равна (600 + 600 + 300 = 1500) грамм.
Ответ: 1500
Задание
3
#843
Уровень задания: Равен ЕГЭ
Иван случайно смешал молоко жирностью (2,5%) и молоко жирностью (6%). В итоге у него получилось 5 литров молока жирностью (4,6%). Сколько литров молока жирностью (2,5%) было у Ивана до смешивания?
Пусть (x) литров молока жирностью (2,5%) было у Ивана, тогда
(5 — x) литров молока жирностью (6%) было у Ивана,
(dfrac{2,5}{100}x) – объём жира в молоке жирностью (2,5%), (dfrac{6}{100}(5 — x)) – объём жира в молоке жирностью (6%).
Так как в итоге жира оказалось (dfrac{4,6}{100} cdot 5 = 0,23) литра, то:
(dfrac{2,5}{100}x + dfrac{6}{100}(5 — x) = 0,23), откуда находим (x = 2).
Ответ: 2
Задание
4
#841
Уровень задания: Равен ЕГЭ
В сосуде А содержится 3 литра 17-процентного водного раствора вещества Х. Из сосуда В в сосуд А перелили 7 литров 19-процентного водного раствора вещества Х. Сколько процентов составляет концентрация полученного в сосуде А раствора?
Концентрация в процентах – это отношение объёма вещества к объёму смеси, умноженное на 100(%). До переливания в сосуде А было (3 cdot 0,17 = 0,51) литра вещества Х, в сосуде В было (7 cdot 0,19 = 1,33) литра вещества Х.
После переливания объём вещества Х в сосуде А стал (0,51 + 1,33 = 1,84) литра, а объём всего раствора (3 + 7 = 10) литров. Тогда концентрация в процентах составила [dfrac{1,84}{10} cdot 100% = 18,4%.]
Ответ: 18,4
Задание
5
#2133
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (5)-процентного раствора кислоты, чем объём (10)-процентного раствора той же кислоты, чтобы при смешивании получить (7)-процентный раствор?
Пусть объём (5)-процентного раствора кислоты равен (x) литров, а объём (10)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,05x + 0,1y = 0,07(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = dfrac{3}{2} = 1,5,,] таким образом, ответ: (1,5).
Ответ: 1,5
Задание
6
#2134
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (20)-процентного раствора кислоты, чем объём (14)-процентного раствора той же кислоты, чтобы при смешивании получить (18)-процентный раствор?
Пусть объём (20)-процентного раствора кислоты равен (x) литров, а объём (14)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,2x + 0,14y = 0,18(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = 2,,] таким образом, ответ: (2).
Ответ: 2
Задание
7
#2629
Уровень задания: Равен ЕГЭ
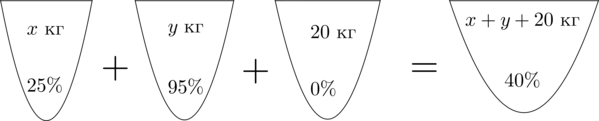
Смешав (25)-процентный и (95)-процентный растворы кислоты и добавив (20) кг чистой воды, получили (40)-процентный раствор кислоты. Если бы вместо (20) кг воды добавили (20) кг (30)-процентного раствора той же кислоты, то получили бы (50)-процентный раствор кислоты. Сколько килограммов (25)-процентного раствора использовали для получения смеси?
Заметим, что вода – это раствор, не содержащий кислоту, то есть содержащий (0%) кислоты.
Пусть (x) кг – масса раствора с (25)-процентным содержанием кислоты, (y) кг – масса раствора с (95)-процентным содержанием кислоты. Составим схему, описывающую получение (40)-процентного раствора:
Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит (x) кг, а в нем (25%) кислоты, то в килограммах в нем (dfrac{25}{100}cdot x) кислоты.
Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{0}{100}cdot 20=dfrac{40}{100}cdot (x+y+20)]
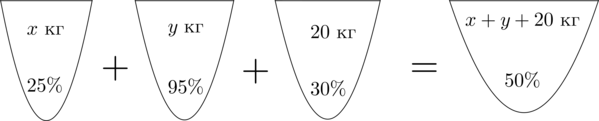
Аналогично составим схему, описывающую получение (50)-процентного раствора:
Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{30}{100}cdot 20=dfrac{50}{100}cdot (x+y+20)]
Таким образом, решив систему из полученных двух уравнений, найдем (x). Для этого можно умножить оба уравнения на (100), чтобы сделать их проще на вид:
[begin{cases}
25x+95y+0=40(x+y+20)\
25x+95y+30cdot 20=50(x+y+20)
end{cases}]
Вычтем из второго уравнения первое и получим новую систему:
[begin{aligned} &begin{cases}
25x+95y=40(x+y+20)\
30cdot 20=10(x+y+20)
end{cases} quad Rightarrow quad begin{cases}
5x+19y=8(x+y+20)\
y=40-x end{cases} quad Rightarrow \[2ex] Rightarrow quad
&begin{cases}
3x-11(40-x)+160=0\
y=40-x end{cases} quad Rightarrow quad begin{cases}
x=20\y=20end{cases} end{aligned}]
Таким образом, раствора с (25%) кислоты было (20) кг.
Ответ: 20

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ