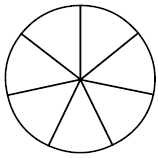
Сколько спиц в колесе?
В контрольно-измерительных материалах для подготовки к ОГЭ часто встречаются в модуле
«Геометрия» простые задачи об углах между соседними спицами в колесах. При их решении важно помнить, что все углы между спицами равны, количество углов равно количеству спиц и в полной окружности 360 градусов.
Задача 1. Колесо имеет 15 спиц. Углы между соседними спицами равны. Найдите
величину угла (в градусах), который образуют две соседние спицы.
Решение. 360:15=24 градуса.
Ответ 24.
Задача 2. Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 18 градусам?
Решение. 360:18=20 спиц.
Ответ 20.
Задачи для самостоятельного решения.
- Колесо имеет 30 спиц. Углы между соседними спицами равны. Найдите
величину угла (в градусах), который образуют две соседние спицы. - Колесо имеет 12 спиц. Углы между соседними спицами равны. Найдите
величину угла (в градусах), который образуют две соседние спицы. - Колесо имеет 10 спиц. Углы между соседними спицами равны. Найдите
величину угла (в градусах), который образуют две соседние спицы. - Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 12 градусам?
- Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 15 градусам?
- Сколько спиц в колесе, в котором угол между любыми соседними спицами равен 30 градусам?
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Подобные треугольники
Два треугольника называются подобными, если углы одного треугольника соответственно равны углам другого треугольника, а стороны одного треугольника соответственно пропорциональны сторонам другого треугольника.
Подобие треугольников обозначается значком «∼». Запишем подобие двух треугольников:
△ A B C ∼ △ A 1 B 1 C 1
Соответственные стороны двух подобных треугольников – это стороны, которые лежат напротив равных углов.
Пары равных углов:
∠ A и ∠ A 1
∠ B и ∠ B 1
∠ C и ∠ C 1
Пары соответственных сторон:
B C и B 1 C 1
A C и A 1 C 1
A B и A 1 B 1
Представьте себе, что на смартфоне или планшете вы открыли изображение треугольника. Вы захотели получше его рассмотреть и увеличили изображение. Сам треугольник увеличился, но его пропорции сохранились (он не сплюснулся, не вытянулся, просто стал больше). Вот такие два треугольника: исходный и увеличенный будут подобными. Масштаб увеличенной картинки изменился в k. Это число k будет являться коэффициентом подобия этих треугольников.
Коэффициент подобия k это число, равное отношению соответственных сторон подобных треугольников.
k = A 1 B 1 A B = A 1 C 1 A C = B 1 C 1 B C
- Если стороны большего треугольника относить к сторонам меньшего треугольника, то коэффициент подобия k > 1.
- Если стороны меньшего треугольника относить к сторонам большего треугольника, то коэффициент подобия k < 1.
Отношение периметров подобных треугольников равно коэффициенту подобия.
P △ A 1 B 1 C 1 P △ A B C = k
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
S △ A 1 B 1 C 1 S △ A B C = k 2
Признаки подобия треугольников
Первый признак подобия треугольников (по двум углам)
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
∠ A = ∠ A 1 ∠ B = ∠ B 1 | ⇒ △ A B C ∼ △ A 1 B 1 C 1
Второй признак подобия треугольников (по двум сторонам и углу между ними)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
∠ A = ∠ A 1 A 1 B 1 A B = A 1 C 1 A C = k | ⇒ △ A B C ∼ △ A 1 B 1 C 1
Третий признак подобия треугольников (по трём сторонам)
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
A 1 B 1 A B = A 1 C 1 A C = B 1 C 1 B C = k ⇒ △ A B C ∼ △ A 1 B 1 C 1
Задачи про часы и стрелки
В задании 17 ОГЭ встречаются задачи, в которых необходимо найти угол между часовой и минутной стрелкой. Давайте разберёмся, как их решать.
Часовой циферблат – это окружность.
Градусная мера всей окружности равна 360 ° .
Стрелки – стороны центральных углов.
На окружности 60 маленьких делений и 12 больших.
Каждое маленькое деление отсекает от окружности дугу, градусная мера которой равна 360 ° 60 = 6 ° .
Каждое большое деление отсекает от окружности дугу, градусная мера которой равна 360 ° 12 = 30 ° .
Можно рассуждать, что одна большая дуга содержит пять маленьких, то есть её градусная мера равна 6 ° ⋅ 5 = 30 ° .
Задачи про колесо со спицами
В задании 17 ОГЭ встречаются задачи, в которых дано колесо со спицами и требуется определить либо угол между соседними спицами (если дано количество спиц), либо количество спиц (если дан угол между соседними спицами). Будем разбираться, как такие задачи решать.
Пусть у нас есть колесо, в котором n спиц. Тогда эти спицы образуют n равных центральных углов α .
Формула, которая связывает количество спиц и угол между двумя соседними:
α ⋅ n = 360 °
Задачи на лестницу и ступеньки
В задаче данного типа дана лестница, состоящая из n ступенек. Каждая ступенька характеризуется своей высотой (вертикальный отрезок) и длиной (горизонтальный отрезок). Сама лестница характеризуется своей длиной (отрезок AC), высотой (отрезок BC) и отрезком AB.
Высота всей лестницы – количество ступенек, умноженное на высоту одной ступеньки. Длина всей лестницы – количество ступенек, умноженное на длину одной ступеньки. Для нахождения длины лестницы необходимо применить теорему Пифагора.
Задачи на нахождение длин и площадей
Теоретический и практический материал по нахождению площадей треугольников и четырехугольников можно найти в уроках 3 и 4 модуля геометрия.
Перейти по ссылкам:
- Площадь треугольника
- Площадь равностороннего треугольника
- Площадь прямоугольного треугольника
- Площадь параллелограмма
- Площадь ромба
- Площадь прямоугольника
- Площадь квадрата
- Площадь трапеции
Вашему вниманию предлагается видео-лекция, конспект этой видео-лекции и тестирование по всем типам задач, предусмотренных авторами-составителями контрольно-измерительных материалов (КИМов) ЕГЭ 2020 в рамках задачи №8 базового уровня.
Задача №8 — это задача на определение площади, периметра и основных геометрических характеристик плоских геометрических фигур (треугольника, параллелограмма, ромба, трапеции, круга), вычисление длин отрезков в декартовой системе координат, применение теоремы Пифагора, признаков подобия треугольников и пропорций. Тестирование сформировано преимущественно на основе задач этого типа, предлагаемых авторами ЕГЭ на экзаменах прошлых лет, а также на основе открытого банка задач. Для успешной подготовки к решению задачи №8 рекомендуется сначала внимательно просмотреть видео-лекцию (или изучить составленный по ней конспект), после чего переходить к тестированию.
Ваш прогноз на ЕГЭ: из 20 баллов.
Статистика
Теорема Пифагора, средние линии, окружность и круг
Видео-урок
Домашняя работа по теме «Теорема Пифагора, средние линии, окружность и круг»
Тестирование по теме «Теорема Пифагора, средние линии, окружность и круг»
Тестирование
Периметр, площадь, пропорции
Видео-урок
Домашняя работа по теме «Периметр, площадь, пропорции»
Тестирование по теме «Периметр, площадь, пропорции»
Тестирование
© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены
На рисунке показано, как выглядит колесо с 7 спицами. Сколько будет спиц в колесе, если угол между соседними спицами в нём будет равен 20°?
Источник: fipi
Решение:
На рисунке видим, что у колеса 7 спиц и оно поделено ими тоже на 7 углов.
Всё колесо образует угол, равный 360°. Если каждый угол равен 20°, то таких углов будет:
360°/20° = 18 штук
Значит и 18 спиц.
Ответ: 18.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 5
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Главная страница » Пример №53 из задания 10
Пример №53 из задания 10
Колесо имеет 25 спиц. Углы между соседними спицами равны. Найдите величину угла (в градусах), который образуют две соседние спицы.
Решение
Две соседние спицы – это один сектор. Весь круг равен (360 circ), а углы между спицами равны (по условию), то величина угла, которую образуют две соседние спицы равна (360div25=14,4circ).
Ответ: (14,4).
Источник: ЕГЭ 2023 Математика. Базовый уровень. Типовые экзаменационные варианты. 30 вариантов (вариант 
Определите усилия, действующие в спицах велосипедного колеса, и напряжения, возникающие в ободе при приложении к оси колеса силы Р (рис. 68).
Грунт, на который опирается колесо, можно считать жестким. Число спиц п велико настолько, что позволяет рассматривать спицы не как отдельные стержни, а как непрерывную среду.
Провести числовой расчет при следующих данных: Р = 40 кг; радиус колеса R = 31 см; момент инерции сечения обода J = 0,3 см4 , число спиц п = 36; диаметр спиц d = 2 мм. Материал обода и спиц—сталь, Е = 2 ·106 кг/см2.
Если спицы рассматривать как непрерывную упругую среду, то для любой точки обода сила, действующая со стороны спиц, будет пропорциональна радиальному смещению соответствующей точки обода w. Таким образом, мы сталкиваемся здесь с задачей о расчете кольца с упругим основанием.
На единицу длины обода приходится спиц. Со стороны каждой спицы на обод действует сила
,где l — длина спицы (l ≈ R), F—площадь поперечного сечения спицы.
На единицу длины обода, таким образом, действует сила 

Теперь составим дифференциальное уравнение упругой линии кольца. За независимую переменную выберем угол φ, отсчитываемый от вершины кольца (рис. 266).
Из кольца выделим элементарный участок длины R dφ и в произведенных сечениях приложим внутренние силы N, Q и М. Со стороны спиц на этот участок будет действовать сила kwRdφ. Составим уравнения равновесия для этого элементарного участка. Проектируем все силы на радиальную ось. Тогда получим
Условие равенства нулю суммы проекций всех сил на ось, касательную к дуге круга, дает
Приравниваем нулю сумму моментов сил относительно точки О
и исключаем из этих уравнений Q и N.Тогда имеем

Изменение кривизны 
но, как известно,
Так как при положительном перемещении w, направленном от центра круга, кривизна кольца уменьшается, в правой части этого выражения стоит знак минус. Изменение кривизны в этом выражении состоит из двух величин. Первое слагаемое соответствует изменению кривизны за счет простого расширения кольца. Второе слагаемое


Теперь после подстановки М дифференциальное уравнение принимает следующий окончательный вид:
где

Решением этого уравнения будет
где

Так как кольцо деформируется симметрично относительно вертикальной оси, функция w должна быть четной функцией, т. е. при перемене знака при φ с плюса на минус должна оставаться неизменной. Поэтому произвольные постоянные С3 и С4, стоящие при нечетных функциях, полагаем равными нулю. Остальные постоянные определяются из следующих условий:
Последнее условие означает, что при нагружении колеса верхняя и нижняя точки остаются на одной вертикали. Действительно, если рассмотреть элемент обода колеса до и после деформации (рис. 267),
то нетрудно установить, что условие его нерастяжимости напишется в виде
где v — перемещение по касательной к дуге контура, или
Так как смещение по касательной в точках φ = 0 и φ = π отсутствует, то отсюда и вытекает условие в).
При С3 = С4 = 0 выражения для изгибающего момента
и поперечной силы
принимают вид
Теперь, раскрывая граничные условия а), б) и в), получаем:
Решаем эти уравнения:
Окончательно выражения для w и М принимают вид:
где для сокращения обозначено:
Усилие, приходящееся на одну спицу, будет, очевидно, равно

Проведем числовой подсчет. Из выражений (1) и (2), полагая модули упругости спиц и обода равными, получаем:
Далее, согласно (3) вычисляем:
Теперь находим:
Согласно (6) имеем:
Выражения (5) и (7) могут быть переписаны в виде
Отсюда видно, что при небольших значениях φ второе и третье слагаемые в скобках будут весьма малы, и М и Рc практически не меняются. На основании этих выражений строим эпюры изгибающего момента М и усилий в спицах Рc (рис. 268).
При силе Р = 40 кг получаем: Mmax= 88 кг см; наибольшее усилие на спицу Рс max = 11.2 кг. Понятно, что в полученном результате не учитывается предварительное натяжение спиц, которое задается им при сборке. Естественно, это предварительное натяжение должно превышать по абсолютной величине Рс mах.
Рассмотренная задача впервые решена Н. Е. Жуковским.