На уроке рассматривается разбор 15 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи
Содержание:
- Объяснение задания 15 ЕГЭ по информатике
- Элементы математической логики
- Математическая логика и теория множеств
- Задания с отрезками и ДЕЛ
- Задания с поразрядной конъюнкцией
- Решение заданий 15 ЕГЭ по информатике
- Задания с множествами
- Задания с отрезками на числовой прямой
- Задания с ДЕЛ
- Задания с поразрядной конъюнкцией
- Задания на поиск наибольшего или наименьшего числа А
15-е задание: «Основные законы алгебры логики»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 5 минут.
Проверяемые элементы содержания: Знание основных понятий и законов математической логики
До ЕГЭ 2021 года — это было задание № 18 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Важно понимать, что выражение должно быть тождественно истинно, т.е. истинно при любых допустимых значениях переменных x и у, а не только при некоторых наборах значений»
ФГБНУ «Федеральный институт педагогических измерений»
Элементы математической логики
-
Для решения 15 задания, потребуется знание таблиц истинности.
- операцию импликация можно преобразовать в операции ИЛИ и НЕ:
- операцию эквивалентность можно преобразовать:
- операцию XOR (сложение по модулю 2) можно преобразовать так:
- кроме того, могут пригодиться базовые аксиомы и формулы:
- Порядок выполнения логических операций:
- выражения в скобках,
- операции «НЕ»,
- операции «И»,
- операции «ИЛИ»,
- операции «импликация»
- операции «эквиваленция»
- последовательность из операций импликации выполняется слева направо (при этом соблюдается принцип «операции с одинаковым приоритетом выполняются слева направо»):
Для выполнения задания рекомендуется повторить следующие темы:
Преобразование логических операций:
A → B = ¬ A ∨ B
или
A → B = A + B
A ↔ B = A ⊕ B = A ∧ B ∨ A ∧ B
или
A ↔ B = A ⊕ B = A · B + A · B
A ⊕ B = (¬A ∧ B) ∨ (A ∧ ¬B)
или
A ⊕ B = (A · B) + (A · B)
Законы алгебры логики:
| Закон двойного отрицания: |
¬¬ A = A |
| Закон исключения третьего: |
A ∧ ¬ A = 0 или A · A = 0 |
| Закон повторения (идемпотентности): |
A ∧ A = A или A · A = A |
| Законы исключения логических констант: |
A ∧ 0 = 0 |
| Переместительный (коммутативный) закон: |
A ∧ B = B ∧ A |
| Сочетательный (ассоциативный) закон: |
(A ∧ B) ∧ C = A ∧ (B ∧ C) |
| Распределительный (дистрибутивный) закон: |
(A ∧ B) ∨ C = (A ∨ C) ∧ (B ∨ C) |
| Закон общей инверсии (Законы де Моргана): |
¬ (A ∧ B) = ¬ A ∨ ¬ B |
| Закон исключения (склеивания): |
(A ∧ B) ∨(¬A ∧ B) = B |
| Упрощать выражения можно с помощью формул: | |
| Закон поглощения: |
A ∨ A ∧ B = A |
A → B → C → D = ((A → B) → C) → D
Математическая логика и теория множеств
- пересечение множеств соответствует логическому умножению, а объединение – логическому сложению;
- пересечением двух множеств называется новое множество, состоящее из элементов, принадлежащих одновременно обеим множествам:
- объединением двух множеств называется новое множество, состоящее из элементов, принадлежащих отдельно каждому из множеств (без повторений);
- пустое множество
∅– это множество, в котором не содержится ни одного элемента; пустому множеству в теории множеств соответствует0; - универсальное множество
U(на кругах Эйлера обозначается в виде прямоугольника) – это множество, содержащее все возможные элементы определенного типа (например, все вещественные числа): - универсальное множество соответствует логической единице: для любого множества целых чисел
Xсправедливы равенства: - разностью двух множеств
AиBназывается новое множество, элементы которого принадлежатA, но не принадлежатB: - дополнение множества
X– это разность между универсальным множествомUи множествомX(например, для целых чисел¬ X– все целые числа, не входящие вX) - пусть требуется выбрать множество
Aтак, чтобы выполнялось равенствоA ∨ X = I; в этом случае множествоAдолжно включать дополнение¬ X, то естьA ≥¬ X(или A ⊇¬ X), то естьAmin = ¬ X - пусть требуется выбрать множество
Aтак, чтобы выполнялось равенство¬ A ∨ X = I, в этом случае множество¬ Aдолжно включать дополнение¬ X, то есть¬ A ⊇ ¬ X; отсюдаA ⊆ X, то естьAmax = X
Пример:
Пример:
X ∨ U = U и X ∧ U = X
Пример разности множеств:
Для большей определенности стоит рассмотреть тему круги Эйлера
Задания с отрезками и ДЕЛ
Для решения заданий необходимо знать рассмотренную тему о множествах.
Для упрощения решений можно пользоваться следующими законами.
1. Если в задании формула тождественно истинна (равна 1), и
2. после упрощения A без отрицания
то используется закон:
Amin = ¬B
где B — известная часть выражения.
1. Если в задании формула тождественно истинна (равна 1), и
2. после упрощения A с отрицанием
то используется закон:
Amax = B
где B — известная часть выражения.
1. Если в задании формула тождественно ложна (равна 0), и
2. после упрощения A без отрицания
то используется закон:
Amax = ¬B
где B — известная часть выражения.
1. Если в задании формула тождественно ложна (равна 0), и
2. после упрощения A с отрицанием
то используется закон:
Amin = B
где B — известная часть выражения.
Задания с поразрядной конъюнкцией
В задании 15 ЕГЭ встречаются задачи, связанные с поразрядной конъюнкцией.
Например:
5 & 26
означает поразрядную конъюнкцию (логическое «И») между двоичными значениями двух чисел — 5 и 26. Выполняется так:
5 = 1012 26 = 110102 0 = 000002
Задания, связанные с поразрядной конъюнкцией, решаются несколькими способами. Рассмотрим один из них.
- Обозначим:
(x & K = 0) как Zk
Zk * Zm = Zk or m
(X & 5 = 0) ∧ (X & 26 = 0)
Z5 ∧ Z26
Z5 ∧ Z26 = Z26 or 5 помним, что дизъюнкция - это операция логическое "ИЛИ" (сложение) 5 = 1012 26 = 110102 31 = 111112
Z5 ∧ Z26 = Z31
Zk + Zm = Zk and m
(X & 28 = 0) ∨ (X & 22 = 0)
Z28 ∨ Z22
Z28 ∨ Z22 = Z28 and 22
помним, что конъюнкция - это операция логическое "И" (умножение)
28 = 111002
22 = 101102
101002 = 2010
Z28 ∨ Z22 = Z20
Условие Zk → Zm истинно для любых натуральных значений x тогда и только тогда, когда все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.
- На деле, это означает, что если имеем:
X & 29 = 0 → X & 5 = 0 Истинно или Ложно?
Z29 → Z5
Z29 → Z5 = 1 (истине), тогда, когда: 29 = 111012 5 = 1012 единичные биты двоичного числа 5 входят в единичные биты двоичного числа 29 (совпадают с ними)
Z29 → Z5 = 1 (истинно)
(x & 125 = 5) то же самое, что и
Z120 * ¬Z4 * ¬Z1 = 1 (истине)
- Так, например, если в задании имеем:
X & 130 = 3
X & 130 = 3 то же самое, что и Z127 * ¬Z2 * ¬Z1 т.е. 3 = 2 + 1 : 2 = 10 1 = 01 3 = 11
Решение заданий 15 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Задания с множествами
Множества:
15_16:
Элементами множества А являются натуральные числа. Известно, что выражение
((x ∈ {1, 3, 5, 7, 9, 11}) → ¬(x ∈ {3, 6, 9, 12})) ∨ (x ∈ A)
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наименьшее возможное значение суммы элементов множества A.
✍ Решение:
- Введем обозначения:
P ≡ (x ∈ {1, 3, 5, 7, 9, 11}) ;
Q ≡ (x ∈ {3, 6, 9, 12}) ;
A ≡ (x ∈ A).
(P → ¬Q) ∨ A = 1 Избавимся от импликации: ¬P ∨ ¬Q ∨ A = 1
А) была непременно истинной, необходимо, чтобы известная часть была ложна:¬P ∨ ¬Q ∨ А = 1 0 1
¬P ∨ ¬Q = 0, или ¬P = 0 отсюда P = 1 ¬Q = 0 отсюда Q = 1
Q и P. То есть необходимо выбрать элементы, которые встречаются в обоих множествах одновременно:A = {3,9}
3 + 9 = 12
Ответ: 12
Аналитическое решение:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Множества:
15_17:
Элементами множества А являются натуральные числа. Известно, что выражение
(x ∈ {2, 4, 6, 8, 10, 12}) → (((x ∈ {3, 6, 9, 12, 15}) ∧ ¬(x ∈ A)) →
→ ¬(x ∈ {2, 4, 6, 8, 10, 12}))
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наименьшее возможное значение суммы элементов множества A.
Типовые задания для тренировки
✍ Решение:
- Введем обозначения:
P≡(x ∈ {2, 4, 6, 8, 10, 12}) ;
Q ≡ (x ∈ {3, 6, 9, 12, 15}) ;
A ≡ (x ∈ A).
P → ((Q ∧ ¬A) → ¬P) = P → (¬(Q ∧ ¬А) ∨ ¬P) = ¬P ∨ (¬(Q ∧ ¬А) ∨ ¬P) = ¬P ∨ ¬Q ∨ А.
А) была непременно истинной, необходимо, чтобы известная часть была ложна:¬P ∨ ¬Q ∨ А = 1 0 1
¬P ∨ ¬Q = 0, или ¬P = 0 отсюда P = 1 ¬Q = 0 отсюда Q = 1
Q и P. То есть необходимо выбрать элементы, которые встречаются в обоих множествах одновременно:A = {6,12}
6 + 12 = 18
Ответ: 18
Множества:
15_18: Закон распределения
Элементами множеств А, P, Q являются натуральные числа, причём P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}. Известно, что выражение
( (x ∈ A) → (x ∈ P) ) ∧ ( (x ∈ Q) → ¬(x ∈ A) )
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наибольшее возможное количество элементов в множестве A.
Типовые задания для тренировки
✍ Решение:
- Введем обозначения:
P ≡ (x ∈ P); Q ≡ (x ∈ Q); A ≡ (x ∈ A).
Избавимся от импликации: (¬A ∨ P) ∧ (¬Q ∨ ¬A) = 1 Применим распределительный закон (но можно вывести самостоятельно): ¬A ∨ (P ∧ ¬Q) = 1
А) была непременно истинной, необходимо, чтобы известная часть была ложна:¬A ∨ (P ∧ ¬Q) = 1 0 1
P ∧ ¬Q = 1, или P = 1 и ¬Q = 1 отсюда Q = 0
Q и P. То есть это новое множество, элементы которого принадлежат P, но не принадлежат Q:A = {2, 4, 8, 10, 14, 16, 20}
Ответ: 7
Множества:
15_20:
Элементами множества А являются натуральные числа. Известно, что выражение
¬(x ∈ A) →¬(x ∈ {1, 3, 7}) ∨ (¬(x ∈ {1, 2, 4, 5, 6}) ∧ (x ∈ {1, 3, 7}))
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наименьшее возможное количество элементов множества A.
✍ Решение:
- Введем обозначения:
P ≡ (x ∈ {1, 3, 7});
Q ≡ (x ∈ {1, 2, 4, 5, 6});
A ≡ (x ∈ A).
Избавимся от импликации: A ∨ ¬P ∨ (¬Q ∧ P) = 1 Применим закон поглощения (но можно вывести самостоятельно): A ∨ ¬P ∨ ¬Q = 1
А) была непременно истинной, необходимо, чтобы известная часть была ложна:A ∨ ¬P ∨ ¬Q = 1 1 0
¬P ∨ ¬Q = 0, или P = 1 и Q = 1
Q и P:A = {1}
Ответ: 1
Задания с отрезками на числовой прямой
Отрезки на числовой прямой:
15_3:
На числовой прямой даны два отрезка: P=[44,48] и Q=[23,35].
Укажите наибольшую возможную длину отрезка А, для которого формула
((x ϵ P) → (x ϵ Q)) ∧ (x ϵ A)
тождественно ложна, то есть принимает значение 0 при любом значении переменной x.
✍ Решение:
- Упростим формулу, избавившись от ‘x ϵ‘:
(P → Q) ∧ A
правило импликации: a → b = ¬a ∨ b
(¬P ∨ Q) ∧ A
(¬P ∨ Q) ∧ A = 0
(¬P ∨ Q) ∧ A 0 ∧ 0 = 0 0 ∧ 1 = 0 1 ∧ 0 = 0 1 ∧ 1 = 1
1. (¬P ∨ Q) = 1 ∨ 0 = 1 - на данном отрезке А должно равняться 0
2. (¬P ∨ Q) = 1 ∨ 1 = 1 - на данном отрезке А должно равняться 0
3. (¬P ∨ Q) = 1 ∨ 0 = 1 - на данном отрезке А должно равняться 0
4. (¬P ∨ Q) = 0 ∨ 0 = 0 - на данном отрезке А может! равняться 1
5. (¬P ∨ Q) = 1 ∨ 0 = 1 - на данном отрезке А должно равняться 0
48 - 44 = 4
Результат: 4
✎ Решение 2 (программирование):
Внимание! этот способ подходит НЕ для всех заданий с отрезками!
Python:
1 2 3 4 5 6 7 8 9 |
def f(a1,a2,x): return((44<=x<=48)<=(23<=x<=35))and(a1<=x<=a2) maxim = 0 for a1 in range (1,200): for a2 in range (a1+1,200): if all(f(a1,a2,x)==0 for x in range (1,200)):# если все ложны if a2-a1>maxim: maxim=a2-a1 print(a1,a2, a2-a1) # сами точки отрезка и длина |
Вывод:
44 45 1
44 46 2
44 47 3
44 48 4
PascalABC.net:
Вывод:
С подробным аналитическим решением задания 15 ЕГЭ по информатике можно ознакомиться по видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Отрезки на числовой прямой:
15_9:
На числовой прямой даны два отрезка: P = [10,20] и Q = [30,40].
Укажите наибольшую возможную длину отрезка A, для которого формула
((x ∈ P) → (x ∈ Q)) → ¬(x ∈ A)
тождественно истинна, то есть принимает значение 1 при любом значении переменной x.
Типовые задания для тренировки
✍ Решение:
- Упростим выражение, введя обозначения:
A: x ∈ A P: x ∈ P Q: x ∈ Q
(P → Q) → ¬A = 1
(P → Q) → ¬A = 1 => ¬(P → Q) ∨ ¬A = 1 => ¬(¬P ∨ Q) ∨ ¬A = 1
¬(¬P ∨ Q) ∨ ¬A = 1 =>
P ∧ ¬Q ∨ ¬A = 1
А = 1 P = 1 ¬Q = 1 или Q = 0
Результат: 10
Отрезки на числовой прямой:
15_10:
На числовой прямой даны два отрезка: P = [3, 20] и Q = [6, 12].
Укажите наибольшую возможную длину отрезка A, для которого формула
((x ∈ P) ~ (x ∈ Q)) → ¬(x ∈ A)
тождественно истинна, то есть принимает значение 1 при любом значении переменной x.
✍ Решение:
- Упростим выражение, введя обозначения:
A: x ∈ A P: x ∈ P Q: x ∈ Q
(P ~ Q) → ¬A = 1
(P ~ Q) → ¬A = 1 => ¬(P ~ Q) ∨ ¬A = 1
Далее возможно 2 способа решения.
✎ 1 способ:
(a ~ b) = a * b + ¬a * ¬b
¬(P ~ Q) = ¬((P ∧ Q) ∨ (¬P ∧ ¬Q)) = = ¬(P ∧ Q) ∧ ¬(¬P ∧ ¬Q)
¬(P ∧ Q) ∧ ¬(¬P ∧ ¬Q) = = ¬(P ∧ Q) ∧ (P ∨ Q)
¬(P ∧ Q) ∧ (P ∨ Q) ∨ ¬A = 1
¬(P ∧ Q) ∧ (P ∨ Q) = 1 А = 1
✎ 2 способ:
После того, как мы избавились от импликации, имеем:
¬(P ~ Q) ∨ ¬A = 1
Результат: 8
С решением задания 15 вы также можете ознакомиться, посмотрев видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Отрезки на числовой прямой:
15_11:
На числовой прямой даны два отрезка: P = [11, 21] и Q = [15, 40].
Укажите наибольшую возможную длину отрезка A, для которого формула
(x ∈ A) → ¬((x ∈ P) ~ (x ∈ Q))
тождественно истинна, то есть принимает значение 1 при любом значении переменной x.
Типовые задания для тренировки
✍ Решение:
- Упростим выражение, введя обозначения:
A: x ∈ A P: x ∈ P Q: x ∈ Q
A → ¬(P ~ Q) = 1
A → ¬(P ~ Q) = 1 =>
¬A ∨ ¬(P ~ Q) = 1
Результат: 19
Задания с ДЕЛ
Поиск наибольшего А, известная часть Дел ∨ Дел = 1
15_7:
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наибольшего натурального числа А формула
(ДЕЛ(x, 40) ∨ ДЕЛ(x, 64)) → ДЕЛ(x, A)
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Типовые задания для тренировки
✍ Решение:
- Введем обозначения:
A = ДЕЛ(x,A); D40 = ДЕЛ(x, 40); D64 = ДЕЛ(x, 64)
(D40 ∨ D64) → A = 1
¬(D40 ∨ D64) ∨ A = 1 или (¬D40 ∧ ¬D64) ∨ A = 1
(¬D40 ∧ ¬D64) ∨ A = 1 1 2
Т.е. (¬D40 ∧ ¬D64) должно быть = 0. Это нам ничего не дает, т.к. конъюнкция ложна в трех случаях (1*0, 0*1 и 0*0), т.е. D40 и D64 могут быть равны как 0, так и 1 (исключение составляет лишь вариант, когда оба D истинны, тогда логическое умножение 1 * 1 ≠ 0).
¬D40 ∧ ¬D64 = 0 или ¬(¬D40 ∧ ¬D64) = 1 Преобразуем по закону Де Моргана и получим: D40 ∨ D64 = 1
Далее можно решать задание либо с помощью кругов Эйлера, либо с помощью логических рассуждений.
Решение с помощью логических рассуждений:
x, которые делятся на А и при этом делятся на 40 ИЛИ делятся на 64:x/A :x/40 ∨x/64
x = 40, 64, 80, 120, 128, 160, 192, 200, ...
A, начиная с самого наименьшего (единицы), на которые делятся все x без исключения:А = 1, 2, 4, 8
А равно 8.НОД (40,64) = 8
40,64 (64 - 40 = 24)
40,24 (40 - 24 = 16)
24,16 (24 - 16 = 8)
16,8 (16 - 8 = 8)
8,8
Решение с помощью кругов Эйлера:
64 / 40 = 1 (24 остаток) 40 / 24 = 1 (16 остаток) 24 / 16 = 1 (8 остаток) 16 / 8 = 2 (0 остаток) - НОД = 8 +++ 40 / 8 = 5 64 / 8 = 8
Результат: 8
✎ Решение 2 (программирование):
Python:
1 2 3 4 5 6 |
for A in range(1,500): OK = 1 for x in range(1,1000): OK *= ((x % 40 == 0) or (x % 64 == 0))<=(x % A== 0) if OK: print( A ) |
Вывод:
1
2
4
8
PascalABC.net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
begin for var A := 1 to 500 do begin var ok := 1; for var x := 1 to 1000 do begin if (((x mod 40 = 0) or (x mod 64 = 0)) <= (x mod A = 0)) = false then begin ok := 0; break; end; end; if (ok = 1) then print(A) end; end. |
Вывод:
1
2
4
8
Результат: 8
Поиск наименьшего А, известная часть Дел ∧ ¬Дел = 1
15_5:
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наименьшего натурального числа А формула
ДЕЛ(x, A) → (¬ДЕЛ(x, 28) ∨ ДЕЛ(x, 42))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Типовые задания для тренировки
✍ Решение:
Имеем:
ДЕЛ(x, A) → (¬ДЕЛ(x, 28) ∨ ДЕЛ(x, 42)) = 1
A = ДЕЛ(x,A); D28 = ДЕЛ(x, 28); D42 = ДЕЛ(x, 42)
A → (¬D28 ∨ D42) = 1
Избавимся от импликации:
¬A ∨ (¬D28 ∨ D42) = 1
¬A ∨ (¬D28 ∨ D42) = 1 1 2
(¬D28 ∨ D42) = 0 один случай: когда ¬D28 = 0 и D42 = 0
x/¬A :x/28 ∧x/¬42
x, которые НЕ делятся на А и при этом делятся на 28 И НЕ делятся на 42:x = 28, 56,84, 112, 140,168, 196, 224, ...
A, начиная с самого наименьшего (единицы), на которые НЕ делятся все x без исключения:А = 1, 2, 3
А равно 3.✎ Решение 2 (программирование). Язык Python, Pascal:
-
Из общего выражения:
ДЕЛ(x, A) → (¬ДЕЛ(x, 28) ∨ ДЕЛ(x, 42)) = 1
А, необходимо рассмотреть диапазон натуральных значений x. Если выражение будет истинным для диапазона всех рассматриваемых х, то такое А необходимо вывести на экран.А (ограничим их числом 50, т.к. необходимо найти наименьшее А), будем запускать внутренний цикл, перебирающий значения х (х ограничим числом 1000, будем рассматривать данный диапазон, как «любое натуральное значение переменной х»).Python:
for A in range(1,50): OK = 1 for x in range(1,1000): OK *= (x % A == 0) <= ((x % 28 != 0) or (x % 42== 0)) if OK: print( A ) break
PascalABC.net:
begin for var A := 1 to 50 do begin var ok := 1; for var x := 1 to 1000 do begin if (x mod A = 0) <= ((x mod 28 <> 0)or (x mod 42 = 0)) = false then begin ok := 0; break; end; end; if (ok = 1) then begin print(A); break; end end; end.
OK — переменная-индикатор: если находится такое А при котором, диапазон всех значений x, подставленных в выражение, возвращает истинное значение выражения, то ОК остается равным 1, т.к. используется операция умножения (до цикла ОК необходимо присвоить единице).
Следует иметь в виду, что в программировании вместо операции импликация (->) можно использовать нестрогое неравенство: <=. Т.к. таблица истинности для операции импликация соответствует операции <=:
a b F(a<=b) 0 0 1 0 1 1 1 0 0 1 1 1
А, т.к. используется оператор break для выхода из цикла после первого найденного значения:3
Результат: 3
15_6:
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наименьшего натурального числа А формула
(¬ДЕЛ(x, 19) ∨ ¬ДЕЛ(x, 15)) → ¬ДЕЛ(x, A)
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
✍ Решение:
- Введем обозначения:
A = ДЕЛ(x,A); D19 = ДЕЛ(x, 19); D15 = ДЕЛ(x, 15)
(¬D19 ∨ ¬D15) → ¬A = 1
D19 ∧ D15 ∨ ¬A = 1
¬A ∨ D19 ∧ D15 = 1 1 2
¬A ∨ D19 ∧ D15 = 1 0 ∨ 1 = 1
¬A = 0 при D19 ∧ D15 = 1 или A = 1 при D19 = 1 и D15 = 1
A = 1 D19 = 1 D15 = 1
19 * 2 = 38 (38 не делится на 15) 19 * 3 = 57 (57 не делится на 15) 19 * 4 = 76 (76 не делится на 15) 19 * 5 = 95 (95 не делится на 15) ... 19 * 10 = 190 (190 не делится на 15) 19 * 15 = 285 (285 делится на 15)
✎ Решение 2 (программирование). Язык Python:
-
Из общего выражения:
(¬ДЕЛ(x, 19) ∨ ¬ДЕЛ(x, 15)) → ¬ДЕЛ(x, A) = 1
А, необходимо рассмотреть диапазон натуральных значений x. Если выражение будет истинным для диапазона всех рассматриваемых х, то такое А необходимо вывести на экран.А (ограничим их числом 500, т.к. необходимо найти наименьшее А), будем запускать внутренний цикл, перебирающий значения х (х ограничим числом 1000, будем рассматривать данный диапазон, как «любое натуральное значение переменной х»).for A in range(1,500): OK = 1 for x in range(1,1000): OK *= ((x % 19 != 0) or (x % 15 != 0))<= (x % A!= 0) if OK: print( A )
OK — переменная-индикатор: если находится такое А при котором, диапазон всех значений x, подставленных в выражение, возвращает истинное значение выражения, то ОК остается равным 1, т.к. используется операция умножения (до цикла ОК необходимо присвоить единице).
Следует иметь в виду, что в программировании вместо операции импликация (->) можно использовать нестрогое неравенство: <=. Т.к. таблица истинности для операции импликация соответствует операции <=:
a b F(a<=b) 0 0 1 0 1 1 1 0 0 1 1 1
А:285
Результат: 285
Задания с поразрядной конъюнкцией
Поразрядная конъюнкция:
15_1:
Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 12&6 = 11002&01102 = 01002 = 4
Для какого наименьшего неотрицательного целого числа A формула
(X & A = 0) ∧ ¬(X & 35 ≠ 0 → X & 52 ≠ 0)
тождественно ложна (то есть принимает значение 0 при любом неотрицательном значении переменной X)?
✍ Решение:
Стоит заметить, что для такого типа задач, нет универсального единственного решения. Поэтому на видео, расположенном ниже, представлено два варианта решения.
✎ Способ 1:
Рассмотрим один из вариантов решения:
- Удалим из формулы X&, чтобы сократить ее запись:
(A = 0) ∧ ¬(35 ≠ 0 → 52 ≠ 0)
(A = 0) ∧ ¬(35 ≠ 0 → 52 ≠ 0)
(A = 0) ∧ ¬(35 ≠ 0 → 52 ≠ 0) 1 2
правило импликации: a → b = ¬a ∨ b
(A = 0) ∧ ¬(35 = 0 ∨ 52 ≠ 0)
т.к. в результате получается отрицание того, что 35 ≠ 0,
то убираем знак "не равно": было 35 ≠ 0, стало 35 = 0
закон де Моргана: ¬ (A ∨ B) = ¬ A ∧ ¬ B
A = 0 ∧ 35 ≠ 0 ∧ 52 = 0 = 0
0 ∧ 0 = 0 0 ∧ 1 = 0 1 ∧ 0 = 0 1 ∧ 1 = 1
(A = 0) ∧ 35 ≠ 0 ∧ 52 = 0 = 0 0 ∧ 1 = 0
35 ≠ 0 ∧ 52 = 0 = истинно (=1) если: 35 ≠ 0 = истинно (=1) и 52 = 0 = истинно (=1) так как стоит логическое умножение ∧ - смотрим выше таблицу истинности для конъюнкции
35 ≠ 0 = 1 (истина) и 52 = 0 = 1 (истина) и A = 0 = 0 (ложь)
35: 100011 (≠ 0) 52: 110100 (= 0)
| 52 | 1 | 1 | 0 | 1 | 0 | 0 |
|---|---|---|---|---|---|---|
| X | 0 | 0 | ? | 0 | ? | ? |
| 35 | 1 | 0 | 0 | 0 | 1 | 1 |
|---|---|---|---|---|---|---|
| X | 1 | ? | ? | ? | 1 | 1 |
0 0 ? 0 ? ? &
1 ? ? ? 1 1
0 0 ? 0 1 1
| X | 0 | 0 | ? | 0 | 1 | 1 |
|---|---|---|---|---|---|---|
| A | 0 | 0 | 0 | 0 | 1 | 1 |
0000112 = 310
Ответ: 3
✎ Способ 2*:
-
Используем метод А.В. Здвижковой.
- Выполним последовательно следующие пункты:
- Произвести замену (x & K = 0) на Zk
- Выполнить преобразования по свойству импликации и закону Де Моргана.
- Стремиться прийти к выражению с конъюнкциями без отрицаний типа: Zk * Zm.
- Все выражения типа Zk * Zm преобразовать по свойству
Zk * Zm = Zk or m. - Путем преобразований прийти к импликации: Zk → Zm.
- Согласно первому пункту производим замену:
A ∧ ¬(¬Z35 → ¬Z52) = 0
¬(A ∧ ¬(¬Z35 → ¬Z52)) = 1
¬A ∨ (¬Z35 → ¬Z52) = 1
¬A ∨ (Z35 ∨ ¬Z52) = 1
¬A ∨ ¬Z52 ∨ Z35 = 1
¬(A ∧ Z52) ∨ Z35 = 1
(A ∧ Z52) → Z35 = 1
ZA ∨ 52 → Z35 = 1
Условие Zk → Zm истинно для любых натуральных значений x тогда и только тогда, когда все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.
A = ??0?11 52 = 110100 A or 52 = 110111 35 = 100011
Аmin = 112 = 310
Результат: 3
Детальный разбор данного задания 15 ЕГЭ по информатике предлагаем посмотреть на видео:
Вариант решения №1 (универсальный, теоретический):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Вариант решения №2 (не универсальный, но простой):
📹 YouTube здесь
Поразрядная конъюнкция:
15_2:
Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 12&6 = 11002&01102 = 01002 = 4
Для какого наибольшего неотрицательного целого числа A формула
X & A ≠ 0 → (X & 36 = 0 → X & 6 ≠ 0)
тождественно истинна (то есть принимает значение 1 при любом неотрицательном значении переменной X)?
✍ Решение:
-
✎ Способ 1:
- Произведем замену:
z36 = (x&36 = 0), z6 = (x&6 = 0), A = (x&A = 0)
¬A → (z36 → ¬ z6)
¬A → (z36 → ¬ z6) = A + ¬z36 + ¬z6
A + ¬z36 + ¬z6 = A + ¬(z36 * z6)
A + ¬(z36 * z6) = ¬(z36 * z6) + A = (z36 * z6) → A
z36 * z6 = z36 or 6
1001002 -> 36 1102 -> 6 100100 110 1001102 -> 36 or 6 = 3810
z38 → A
A = 1001102 = 3810
✎ Способ 2:
x&A ≠ 0 → (x&36 = 0 → x&6 ≠ 0) = 1
A = (x&A = 0); P = (x&36 = 0); Q = (x&6 = 0);
¬A → (P → ¬Q) = 1
A ∨ (¬P ∨ ¬Q) = 1
¬P ∨ ¬Q нам необходимо подобрать такой вариант (равный 0 или 1), при котором единственно возможным значением A была бы единица (1). A ∨ (¬P ∨ ¬Q) = 1;
или
1 ∨ (0) = 1
¬P ∨ ¬Q = 0 Отсюда имеем: ¬P = 0 и ¬Q = 0 (дизъюнкция равна 0 в единственном случае, когда все операнды равны 0)
Q = 1 и P = 1
100100 : 36 000110 : 6 0**0** : маска P (x&36 = 0) ***00* : маска Q (x&6 = 0)
0**0** : маска P (x&36 = 0) ***00* : маска Q (x&6 = 0) 0**00* : общая маска x *00**0 : маска для A (x&A = 0) т.е. в тех битах А, где может получиться единица (звездочки в обеих масках),
мы поставили нули.
100110 = 3810
Результат: 38
Подробное решение данного задания 15 ЕГЭ по информатике предлагаем посмотреть в видео уроке:
Способ 1:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Способ 2:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Поразрядная конъюнкция:
15_8:
Определите наименьшее натуральное число А из интервала [43, 55], такое, что выражение
((x & 17 ≠ 0) → ((x & A ≠ 0) → (x & 58 ≠ 0))) → → ((x & 8 = 0) ∧ (x & A ≠ 0) ∧ (x & 58 = 0))
тождественно ложно (то есть принимает значение 0 при любом натуральном значении переменной х)?
Типовые задания для тренировки
✍ Решение:
-
Кратко изложенное решение *:
- Введем обозначения:
(¬Z17 → (¬A → ¬Z58)) → (z8 ∧ ¬A ∧ Z58) = 0
¬(((¬Z17 → (¬A → ¬Z58)) → (z8 ∧ ¬A ∧ Z58)) = 1
Z8 ∧ Z58 = Z8 or 58 :
8 = 1000 or
58 = 111010
111010 = 58
Z8 ∧ Z58 = Z58
¬(¬(Z17 ∨ A ∨ ¬Z58) ∨ (¬A ∧ Z58)) = 1
(Z17 ∨ A ∨ ¬Z58) ∧ ¬(¬A ∧ Z58)) = 1
(Z17 ∨ A ∨ ¬Z58) ∧ (A ∨ ¬Z58) = 1
A ∨ ¬Z58 = 1
¬Z58 ∨ A => Z58 → A = 1
43 = 101011 - не подходит! 58 = 111010 44 = 101100 - не подходит! 58 = 111010 45 = 101101 - не подходит! 58 = 111010 46 = 101110 - не подходит! 58 = 111010 47 = 101111 - не подходит! 58 = 111010 48 = 110000 - подходит! 58 = 111010
Результат: 48
Поразрядная конъюнкция:
15_15:
Определите набольшее натуральное число A, такое что выражение
((x & 26 = 0) ∨ (x & 13 = 0)) → ((x & 78 ≠ 0) → (x & A = 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной х)?
Типовые задания для тренировки:
✍ Решение:
- Для упрощения восприятия введем обозначения:
z26 = (x & 26 = 0) z13 = (x & 13 = 0) z78 = (x & 78 = 0) A = (x & A = 0)
(z26 ∨ z13) → (¬z78 → A) = 1
(z26 ∨ z13) → (z78 ∨ A) = 1
26 : 11010 единичные биты: 4, 3, 1 13 : 1101 единичные биты: 3, 2, 0 ∧ =------------------------ 01000 = 810
z8 → (z78 ∨ A) z78: не влияет на решение, так как операция дизъюнкция истинна тогда, когда хотя бы один операнд истинен z8 → A : ????
Наибольшее А = 1000 = 810
Результат: 8
Задания на поиск наибольшего или наименьшего числа А
Поиск наибольшего или наименьшего числа А:
15_4: 15 задание. Демоверсия ЕГЭ 2018 информатика:
Для какого наибольшего целого числа А формула
тождественно истинна, то есть принимает значение 1 при любых целых неотрицательных x и y?
✍ Решение:
✎ Способ 1 (программный):
Важно: Поскольку используется метод полного перебора, то возможна ситуация, когда транслятор будет работать слишком медленно. Но работоспособность представленного алгоритма проверена на онлайн компиляторах.
Pascalabc.net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
begin for var A := 200 downto -100 do begin var OK := 1; for var x := 0 to 100 do for var y := 0 to 100 do if ((x <= 9) <= (x * x <= A)) and ((y * y <= A) <= (y <= 9)) = false then begin OK := 0; break; end; if OK = 1 then begin print(A); break end; end; end. |
| Бейсик: |
Python:
for A in range(200,-100,-1): OK = 1 for x in range(0,100): for y in range(0,100): OK *= ((x<=9) <= (x*x<=A)) and((y*y<=A) <= (y<=9)) if OK: print(A) break |
| С++: |
✎ Способ 2 (теоретическое решение):
- Условно разделим исходное выражение на части:
- Главное действие (внешняя операция) в исходном выражении — это конъюнкция. Конъюнкция истинна, когда все операнды истинны. Т.е. в задаче обе части
1и2должны быть истинными (т.к. по условию общая формула должна быть истинной).
-
Рассмотрим часть
- если в
1.1имеем x > 9, то часть1будет истинна независимо от А. Значит, значение числа А влияет на решение только при выполнении условия: - теперь, для того чтобы в части
1, выражение было истинным, надо чтобы часть1.2была истинной: - таким образом, получаем:
1:
x<=9
(импликация 0 → 0 = 1, 0 → 1 = 1)
x*x <= A
(импликация 1 → 1 = 1)
x <= 9 x2 <= A при любых x
возьмем максимальное натуральное: x=9, тогда A>=81
Рассмотрим часть 2:
2.2 истинно (т.е. y <= 9), то часть 2 будет истинна независимо от А. Значит, значение числа А влияет на решение только при выполнении условия:y > 9
2 выражение было истинным, надо чтобы часть 2.1 была ложной:y * y > A
(импликация 0 → 0 = 1)
y > 9 y2 > A при любых y
возьмем наименьшее возможное по условию натуральное: y = 10, тогда A < 100
Результат: 99
Подробное решение 15 задания демоверсии ЕГЭ 2018 года смотрите на видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Поиск наибольшего или наименьшего числа А:
✍ Решение:
✎ Способ 1 (программный):
Важно: Поскольку используется метод полного перебора, то возможна ситуация, когда транслятор будет работать слишком медленно. Но работоспособность представленного алгоритма проверена на онлайн компиляторах.
Pascalabc.net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
begin for var A := -100 to 200 do begin var OK := 1; for var x := 1 to 100 do for var y := 1 to 100 do if ((y+3*x<A) or (x >20)or(y>40)) = false then begin OK := 0; break; end; if OK = 1 then begin print(A); break end; end; end. |
| Бейсик: |
Python:
for A in range(-100,200): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (y+3*x<A) or (x > 20) or (y > 40) if OK: print(A) break |
| С++: |
✎ Способ 2 (теоретическое решение):
- Определим основные части выражения, выделив отдельно неизвестную часть — с А, и, так сказать, известную часть, то есть остальную.
1 2 (y+3x < A) ∨ (x > 20) ∨ (y > 40)
(y+3x < A) ∨ (x > 20) ∨ (y > 40) 1 или 0? 1 = 1 Не подходит!
1. (y+3x < A) = 1 2. (x > 20) ∨ (y > 40) = 0
x <= 20 y <= 40
А > 3x + y A > 3*20 + 40 A > 100
Результат: 101
Подробное решение досрочного ЕГЭ 2018 года смотрите на видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Поиск наибольшего или наименьшего числа А:
15_0:Разбор 15 задания. Демоверсия егэ по информатике 2019:
Для какого наибольшего целого неотрицательного числа А выражение
(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y)
тождественно истинно, т.е. принимает значение 1 при любых целых неотрицательных x и y?
✍ Решение:
✎ Решение 1 (теоретическое):
- Разделим общее выражение на две части. Выделим неизвестную часть красным:
(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y)
(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y) = 1
0 1
y + 2x = 48 : при x = 0, y = 48 при y = 0, 2x = 48 => x = 24
x + 2x = 48 => 3x = 48 x = 16
✎ Решение 2 (программное):
Python:
1 2 3 4 5 6 7 8 |
for A in range(200,0,-1): OK = 1 for x in range(0,100): for y in range(0,100): OK *= (48!=y+2*x) or(A<x)or (A<y) if OK: print(A) break |
Результат: 15
Видео решения 15 задания демоверсии ЕГЭ 2019 (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Поиск наибольшего или наименьшего числа А:
15_19:
Для какого наименьшего целого числа А формула
(y + 5x <= 34) → ((y — x > 4) ∨ (y <= A))
тождественно истинна, т.е. принимает значение 1 при любых целых неотрицательных x и y?
✍ Решение:
- Общая идея такова:
необходимо упростить формулу так, чтобы последняя операция (внешняя) выполнялась со скобкой, в которой находится искомое A. После чего разделить формулу на две части, в одной из которых находится искомое. - Избавимся от импликации, это даст нам возможность опустить общие скобки во второй части формулы:
¬(y + 5x <= 34) ∨ (y - x > 4) ∨ (y <= A)
¬(y + 5x <= 34) ∨ (y - x > 4) ∨ (y <= A) = 1 1 часть 2 часть
¬(y + 5x <= 34) ∨ (y - x > 4) ∨ (y <= A) = 1 1 часть = 0 2 часть = 1
y + 5x > 34 = 0, значит: 1. y + 5x <= 34 y - x > 4 = 0, значит: 2. y - x <= 4
y <= A или A >= y
34 - 5x = 4 + x 30 = 6x x = 5 Найдем y: y = 4 + 5 = 9
y = 9:
A >= 9 => наименьшее A = 9
✎ Решение 2 (программное):
Python:
1 2 3 4 5 6 7 8 |
for A in range(-100,100): OK = 1 for x in range(0,100): for y in range(0,100): OK *= (y+5*x<=34)<=((y-x >4)or(y<=A)) if OK: print( A ) break |
PascalABC.NET:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
begin for var A := -100 to 100 do begin var OK := true; for var x := 0 to 100 do begin for var y := 0 to 100 do begin OK := (y + 5 * x <= 34) <= ((y - x > 4) or (y <= A)); if OK = false then break; end; if OK = false then break; end; if OK then begin print(A); break; end; end; end. |
Результат: 9
Поиск наибольшего или наименьшего числа А:
15_13:
Укажите наименьшее целое значение А при котором выражение
(2y + 5x < A) ∨ (2x + 4y > 100) ∨ (3x – 2y > 70)
истинно для любых целых положительных значений x и y.
Типовые задания для тренировки
✍ Решение:
-
✎ Решение (программное):
Python:
1 2 3 4 5 6 7 8 |
for A in range(-200,200): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (2*y + 5*x < A) or (2*x + 4*y > 100) or (3*x - 2*y > 70) if OK: print( A ) break |
PascalABC.NET:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
begin for var A := -200 to 200 do begin var OK := true; for var x := 1 to 100 do begin for var y := 1 to 100 do begin OK := (2*y + 5*x < A) or (2*x + 4*y > 100) or (3*x - 2*y > 70); if OK = false then break; end; if OK = false then break; end; if OK then begin print(A); break; end; end; end. |
Результат: 171
Видео разбора задания смотрите на видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Поиск наибольшего или наименьшего числа А:
15_14:
Укажите наибольшее целое значение А при котором выражение
(3y – x > A) ∨ (2x + 3y < 30) ∨ (2y – x < –31)
истинно для любых целых положительных значений x и y.
Типовые задания для тренировки
✍ Решение:
-
✎ Решение 1 (теоретическое):
- Разделим выражение на две части: часть с неизвестным = 1, часть известная = 0:
(3y – x > A) ∨ (2x + 3y < 30) ∨ (2y – x < –31) = 1
(1) (2x + 3y) >= 30, y >= (30 - 2x) / 3 x = (30 - 3y) /2
(2) (2y – x >=–31) y >= (x - 31) / 2 x = 2y + 31
(1) x | y 0 | 10 15| 0
(2) x | y 0 | -15 ( целые) 30|0
A<3y-x:A < 3y – x, то будем перемещать А снизу вверх. Наибольшее значение А будет достигнуто в указанной точке пересечения с прямой (2).если y = 1, то x = 2*1 + 31 = 33
А < 3y - x A < 3-33, A < -30, A=-31
✎ Решение (программное):
Python:
1 2 3 4 5 6 7 8 |
for A in range(200,-200,-1): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (3*y-x>A) or (2*x+3*y<30) or (2*y-x<-31) if OK: print(A) break |
Результат: -31
* В некоторых задачах использован метод, предложенный А.В. Здвижковой
Привет! Сегодня посмотрим задачи на отрезки из 15 задания ЕГЭ по информатике.
Решим с помощью шаблона на Python и помощью рассуждений. Повторите основные логические операции в этой статье.
Покажу Вам уникальный и понятный способ для борьбы с задачами на отрезки из 15 задания ЕГЭ по информатике.
Приступим к тренировочным задачам на отрезки.
Задача (Fight)
На числовой прямой даны два отрезка B=[10; 15] и С=[20; 27]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение
¬(((x ∈ B) ∨ (x ∈ C)) ⟶ (x ∈ A))
ложно (т.е. принимает значение 0) при любом значении переменной x.
Решение:
Решение с помощью шаблона на языке Python.
Приведу собственную разработку, как можно решить задачи на отрезки из 15 задания ЕГЭ по информатике с помощью шаблона на языке Python (Питон).
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x = i/2 if not( (F(10, 15, x) or F(20, 27, x)) ) or F(a, b, x): k=k+1 if k==199: mn=min(mn, b-a) print(mn)
Здесь заводим функцию F(a, b, x). Она принимает три параметра: начало отрезка a, конец отрезка b и точку x. Если точка x лежит в отрезке [a;b], то функция вернёт True, иначе False.
Затем делаем два вложенных цикла. Это поиск отрезка A. Переменная a — это начало отрезка A. Переменная b — это конец отрезка A. Для каждой точки a пробуем различные точки b, которые находится правее, чем точка a. Мы начинаем проходить переменной b со значения a, потому что в некоторых задачах длина искомого отрезка A может быть равна нулю.
Для каждого отрезка-кандидата заводим счётчик k. Прокручиваем переменную i в диапазоне от 1 до 199 включительно. А x будет крутится от 0.5 до 99.5 с шагом 0.5, тем самым имитируя фразу при любых значениях x.
Внутри «цикла i» проверяем логическое выражение. Если выражение удовлетворяет условию задачи, то прибавляем к счётчику k единицу для данного отрезка A=[a; b].
При составлении логического выражения может помочь табличка.
| Логическая операция | Представление в Питоне |
| Отрицание ¬ | not() |
| Логическое умножение ∧ | and |
| Логическое сложение ∨ | or |
| Следование A ⟶ B | not(A) or B |
| Равносильность ≡ | == |
После окончания «цикла i» проверяем счёт k. Если логическое выражение сработало при всех значениях x, то в счётчике будет число 199. Это количество итераций в «цикле i». Если такое выполняется, то нам подходит этот отрезок A.
Среди всех отрезков A, которые удовлетворяют условию задачи, выбираем с наименьшей длиной с помощью функции min.
Примечание: У нас всегда получается отрезок A c квадратными скобками на концах A=[a, b]. Даже, если в задачке должен быть отрезок с выколотыми точками, то на длину это никак не влияет, если мы ищем минимальный отрезок, поэтому всё равно будет получатся правильный ответ. Если же мы ищем наибольшую длину, нужно получать всегда отрезок A=(a,b) c выколотыми точками. Об этот речь пойдёт ниже.
Получается 17.
Решение с помощью рассуждений.
Видим, что ко всему выражению применяется логическое отрицание. Мы можем убрать это отрицание, но тогда нужно будет сделать, чтобы выражение было истинным, а не ложным.
В подобных задачах идём от обратного. Нам нужно найти, когда выражение будет истинным, но мы исследуем случай, когда выражение будет стремится ко лжи.
Найдём, при каких значениях x левое выражение будет выдавать 1.
Здесь заштрихованы те иксы, которые приводят к тому, что левое выражение выдаёт 1. Это опасные x. Они «приближают» всё выражение к нулю.
Наша задача этого не допустить. У нас есть только один инструмент: подобрать такой отрезок A, чтобы правое выражение при опасных иксах выдавало 1. Тогда мы получим желаемый результат.
Т.е. при опасных иксах правое выражение должно выдавать 1. Чтобы покрыть все иксы приходится брать отрезок A=[10, 27].
В ответе напишем длину отрезка A: 27 — 10 = 17. Здесь достаточно из наибольшей точки отнять наименьшую.
Ответ: 17
Задача (Раунд 2)
На числовой прямой даны два отрезка: B = [14; 20] и С = [15; 27]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение
¬(x ∈ A) ⟶ ((x ∈ B) ≡ (x ∈ C))
истинно (т.е. принимает значение 1) при любом значении переменной x.
Решение:
Решение с помощью шаблона на языке Python.
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x=i/2 if F(a, b, x) or (F(14, 20, x) == F(15, 27, x)): k=k+1 if k==199: mn=min(mn, b-a) print(mn)
Получается ответ 13.
Решение с помощью рассуждений.
«Главной скрипкой» логического выражение является следование. Именно эта операция соединяет большие блоки логического выражения.
Нас будет интересовать тот случай, когда логическое выражение, наоборот, будет стремится к 0. Тогда правое логическое подвыражение должно равняться 0, а с помощью левого подвыражения, где находится отрезок A, мы будем исправлять ситуацию.
Заштрихуем те значения x, при которых правое подвыражение даёт ноль. Равносильность даёт ноль, когда два выражения имеют разные значения. Т.е. если x находится в одном отрезке, то в другом отрезке его не должно быть.
В подобных задачах можно не обращать внимание на закрашенные и выколотые точки на концах отрезков, потому что в дальнейшем нужно найти длину отрезка A, а длина от этого не зависит. Поэтому пишем и рисуем отрезки с некоторым приближением до одной точки.
Получаются два отрезка [14; 15) и (20; 27]. Это и есть «опасные» значения x. При этих значениях выражение уже «наполовину» ложно. Но с помощью A мы не дадим превратится ему в 0 при любых иксах.
Если левое подвыражение будет равно 1 при опасных значениях икс, то как раз получится то, что нам не нужно. Поэтому при опасных значениях иск, в левом выражении должен быть ноль.
Т.к. там стоит отрицание, убрав его, можно сказать, что в левом подвыражении должна стоять 1 при опасных значениях икс.
Чтобы покрыть все два отрезка опасных значений, выбираем A=[14; 27]. Нас просили найти минимальный отрезок A. Меньше не можем взять, т.к. тогда не все заштрихованные иксы будут закрыты.
Длина получается 27 — 14 = 13.
Ответ: 13
Задача (Отрезок максимальной длины)
На числовой прямой даны два отрезка: P = [43; 49] и Q = [44; 53]. Укажите наибольшую возможную длину такого отрезка A, что формула
((x ∈ A) → (x ∈ P)) ∨ (x ∈ Q)
тождественно истинна, то есть принимает значение 1 при любых x.
Решение:
Решение с помощью шаблона на языке Python.
def F(a, b, x): if a <= x <= b: return True else: return False def F2(a, b, x): if a < x < b: return True else: return False mx=0 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x=i/2 if (not(F2(a, b, x)) or F(43, 49, x)) or F(44, 53, x): k=k+1 if k==199: mx=max(mx, b-a) print(mx)
Ответ получается 10. Здесь ищем максимальный отрезок A. При поиске отрезка максимальной длины, нужно создать функцию F2, и её применять к отрезку A, чтобы получался всегда отрезок с выколотыми точками A=(a, b).
Решение с помощью рассуждений.
Главная скрипка — это логическое или. Эта логическая операция соединяет два больших выражения.
Идём от обратного. Исследуем, когда выражение будет стремится к 0.
Логическое или выдаёт ноль, когда оба выражения равны нулю.
В начале лучше разобраться с тем выражением, где нет отрезка A. Это правое подвыражение. Там должен получаться ноль. Заштрихуем те иксы, которые выдают в правом подвыражении ноль.
В левом выражение стоит следование. Эта операция равна нулю, когда из 1 следует 0. С помощью отрезка A мы будем спасать ситуацию. Заштрихуем, когда икс НЕ принадлежит P. Добавим это действие к предыдущей штриховке.
Таким образом, мы получили опасные иксы. Это все иксы, кроме отрезка [43; 53].
Именно при этих иксах выражение (x ∈ A) не должно выдавать 1. Выбираем отрезок A=[43; 53].
Мы могли бы взять отрезок и меньше, например [44; 49], но нас просили взять наибольший отрезок.
Длина равна 53 — 43 = 10.
Ответ: 10
Задача (Крепкий орешек)
На числовой прямой даны три интервала: P=[10,15], Q=[5,20] и R=(15,25]. Определите наименьшую возможную длину отрезка A, при выборе которого выражение
((x ∉ A) → (x ∈ P)) ≡ ((x ∈ Q) → (x ∈ R))
будет ложно при любых x.
Решение:
Решение с помощью шаблона на языке Python.
def F(a, b, x): if a <= x <= b: return True else: return False def F2(a, b, x): if a < x <= b: return True else: return False mn=10**9 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x = i / 2 if not( (F(a, b, x) or F(10, 15, x)) == (not(F(5, 20, x)) or F2(15, 25, x)) ): k=k+1 if k==199: mn=min(mn, b-a) print(mn)
Здесь заводим ещё одну функцию F2 для отрезка R с выколотой левой точкой. Ответ получается 5.
Решение с помощью рассуждений.
Нужна ложь, но мы рассмотрим, когда равносильность выдаёт 1.
1) Рассмотрим первый случай 1 ≡ 1.
Рассмотрим левое выражение. Узнаём, когда оно выдаёт ноль, а потом сделаем инверсию, чтобы не рассматривать 3 случая.
Получается, что в отрезке Q иксы должны находится, а в R нет.
Сделаем инверсию.
Получается интервал x ∈ (-∞ 5) U (15; ∞). Это те иксы, при которых в правом выражении будет 1.
Рассмотрим, когда левое выражение выдаёт 1.
a) 0 → 0
Учитывая вышеописанный интервал, понимаем, что иксы и так не лежат в отрезке P. Чтобы спаси ситуацию, нужно, чтобы выражение (x ∉ A) выдавало 1, при x ∈ (-∞ 5) U (15; ∞). Тогда левое выражение будет выдавать 0, а правое 1.
Следовательно, можем выбрать любой отрезок A в интервале [5; 15].
б) 0 → 1
При x ∈ (-∞ 5) U (15; ∞) выражение (x ∈ P) никогда не выдаст 1. Значит, в этом варианте 1 ≡ 1 никогда не будет.
в) 1 → 1
Аналогично невозможна и эта ситуация.
Перейдём ко второму случаю.
2) Рассмотрим случай 0 ≡ 0.
Когда правое выражение выдаёт ноль, мы уже смотрели. Это отрезок [5; 15].
Изучим те значения x, при которых левое выражение тоже будет выдавать 0 на отрезке [5; 15].
Тогда опасные иксы будут выглядеть следующим образом:
Т.е. это интервал [5; 15], но без отрезка P. Именно при x ∈ [5; 10) мы должны получать 0 в выражении (x ∉ A), чтобы спасти ситуацию. Получается A=[5;10). Меньше взять отрезок не можем, иначе не все опасные иксы будут покрыты.
Этот отрезок хорошо соотносится с первым вариантом 1) 1 ≡ 1.
Ответ получается 10 — 5 = 5.
Ответ: 5
Задача (Вперёд к победе!)
На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите
наименьшую возможную длину такого отрезка A, для которого логическое
выражение.
(x ∈ D) → ((¬(x ∈ C) ∧ ¬(x ∈ A)) → ¬(x ∈ D))
истинно (т.е. принимает значение 1) при любом значении переменной х.
Решение:
Решение с помощью шаблона на языке Python.
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 100): for b in range(a, 100): k=0 for i in range(1, 200): x = i / 2 if not(F(17, 58, x)) or (not((not(F(29, 80, x)) and not(F(a, b, x)))) or not(F(17, 58, x))): k=k+1 if k==199: mn=min(mn, b-a) print(mn)
Решение с помощью рассуждений.
«Главной скрипкой» данного логического выражения является следование, потому что эта операция соединяет различные логические блоки.
Нам нельзя допустить, чтобы первое выражение принимало 1, а второе 0, одновременно.
Рассмотрим при каких значениях x реализуется этот страшный вариант.
Видно, что, если левое выражение (x ∈ D) равно 1, то ¬(x ∈ D) в правой части автоматически выдаёт 0.
Чтобы умножение в правой части давало 1, необходимо, чтобы выражение ¬(x ∈ C) было истинным.
Тогда опасные значения — это отрезок D без отрезка C. Т.е., чтобы иксы были в отрезке D, но не были в отрезке С одновременно.
Опасные значения получаются [17; 29]. Чтобы опасный сценарий нейтрализовать, выражение ¬(x ∈ A) должно принимать значение 0. Тогда (x ∈ A) должно выдавать 1. Чтобы это происходило всегда при опасных значениях, принимаем A=[17, 29]. Длина получается 12.
Ответ: 12
Теория и практика решения задания 15 ЕГЭ по информатике
Мнемоническое правило
Соционика – это информационная психология
Один из ее главных принципов – дополнение до целого ( дополнение противоположностью )
Решающая формула
В алгебре логики есть формула дополнения до целого:
А ¬А = 1
В некоторых задачах мы будем использовать вместо этой формулы умножение противоположностей:
А ¬А = 0
Типы задания 15
- Задания на отрезки
- Задания на множества
- Задания на поразрядную конъюнкцию
- Задания на условие делимости
- Задания на функции
Задания на отрезки
( № 376 ) На числовой прямой даны два отрезка: P=[4,15] и Q=[12,20]. Укажите наименьшую возможную длину такого отрезка A, что формула ((x ∈ P) ∧ (x ∈ Q)) → (x ∈ A)
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
Источник — сайт Полякова К.Ю.
Решающая формула
Для выбора решающей формулы важно внимательно прочитать требование задачи.
В нашей задаче в требовании сказано:
принимает значение 1 при любом значении переменной х.
Выбор решающей формулы очевиден:
А ¬А = 1
Решение задачи на отрезки
Разделим решение задачи на этапы:
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на отрезки
- Легенда – это удобные нам условные обозначения, которые мы будем использовать при решении.
Введем следующие обозначения:
P = x P
Q = x Q
A = x A
Решение задачи на отрезки
2) Формализация условия – перепишем формулу из условия задачи в соответствие с легендой.
Было:
((x ∈ P) ∧ (x ∈ Q)) → (x ∈ A) = 1
Стало:
(P ∧ Q) → A = 1
Решение задачи на отрезки
3) Решение логического уравнения – вначале это, возможно, самый сложный этап в решении задачи. Но позже, при накоплении опыта, он уже не будет казаться таким уж сложным
Рассмотрим решение логического уравнения по шагам.
Решение задачи на отрезки
3.1. Представим логическое следование в базовых логических операциях по формуле: А → В = ¬А В :
(P ∧ Q) → A = 1
¬ (P ∧ Q) A = 1
Решение задачи на отрезки
3.2. Сведем получившееся выражение к решающей формуле: А ¬А = 1 (в алгебре логики справедлив закон коммутативности, т.е. А ¬А = ¬А А) :
¬(P ∧ Q) A = 1, отсюда
¬А = ¬(P ∧ Q)
Ответом в логическом уравнении будет:
А = P ∧ Q.
Решение задачи на отрезки
4) Интерпретация полученного результата .
Наш ответ: А = P ∧ Q .
В алгебре логики это выражение означает пересечение объемов двух логических объектов. По условию нашей задачи – это пересечение отрезков P и Q .
Решение задачи на отрезки
Пересечение отрезков P и Q можно визуализировать: P=[4,15] и Q=[12,20].
15
12
20
4
По условию нашей задачи, нам нужна минимальная длина отрезка А . Находим ее: 15 – 12 = 3 .
Ответ: 3 .
Ответ на сайте Полякова К.Ю.: 3
Задания на отрезки
(№ 360) На числовой прямой даны три отрезка: P=[10,25], Q=[15,30] и R=[25,40]. Какова максимальная длина отрезка A, при котором формула ((x ∈ Q) → (x ∉ R) ) ∧ (x ∈ A) ∧ (x ∉ P)
тождественно ложна, то есть принимает значение 0 при любом значении переменной х?
Источник — сайт Полякова К.Ю.
Решающая формула
Для выбора решающей формулы важно внимательно прочитать требование задачи.
В нашей задаче в требовании сказано:
принимает значение 0 при любом значении переменной х.
Выбор решающей формулы очевиден:
А ¬А = 0
Решение задачи на отрезки
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на отрезки
- Легенда
R = x R
Q = x Q
A = x A
P = x P
Решение задачи на отрезки
2) Формализация условия
Было:
((x ∈ Q) → (x ∉ R) ) ∧ (x ∈ A) ∧ (x ∉ P) = 0
Стало:
( Q → ¬R ) ∧ A ∧ ¬ P = 0
Решение задачи на отрезки
3) Решение логического уравнения
( Q → ¬R ) ∧ A ∧ ¬ P = 0
3.1. Представим логическое следование в базовых логических операциях по формуле: А → В = ¬А В , и переставим множители согласно закону коммутативности умножения:
A ∧ (¬ Q ¬R ) ∧ ¬ P = 0
Решение задачи на отрезки
3) Решение логического уравнения
A ∧ ( ¬ Q ¬R ) ∧ ¬ P = 0
3.2. Сведем получившееся выражение к решающей формуле: А ¬А = 0 и найдем, чему равно ¬А :
¬А = (¬ Q ¬R ) ∧ ¬ P
Решение задачи на отрезки
3) Решение логического уравнения
¬А = (¬ Q ¬R ) ∧ ¬ P
3.3. Упростим выражение для ¬А по закону де Моргана ¬А ¬В=¬(А В) :
¬А = ¬ (Q R ) ∧ ¬ P,
и по другому закону де Моргана ¬А ¬В =¬(А В ) :
¬А = ¬ (Q R P)
Решение задачи на отрезки
3) Решение логического уравнения
¬А = ¬ (Q R P)
3.4. Очевидно, что
А = Q R P
Решение задачи на отрезки
4) Интерпретация полученного результата
А = Q R P
Отрезок А – это пересечение отрезков Q и R и его объединение с отрезком Р .
Решение задачи на отрезки
Пересечение отрезков R и Q можно визуализировать: Q=[15,30] и R=[25,40].
30
25
40
15
Отрезок P=[10,25] нанесем на наш чертеж и объединим с пересечением:
25
30
15
40
10
Решение задачи на отрезки
А = Q R P
40
25
30
10
15
По условию нашей задачи, нам нужна максимальная длина отрезка А . Находим ее: 30 – 10 = 20 .
Ответ: 20 .
Ответ на сайте Полякова К.Ю.: 20
27
2. Задания на множества
(№ 386) Элементами множеств А, P, Q являются натуральные числа, причём P={1,2,3,4,5,6}, Q={3,5,15}. Известно, что выражение (x ∉ A) → ((x ∉ P) ∧ (x ∈ Q)) ∨ (x ∉ Q)
истинно (т.е. принимает значение 1 при любом значении переменной х. Определите наименьшее возможное количество элементов в множестве A.
Источник — сайт Полякова К.Ю.
Решение задачи на множества
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на множества
- Легенда
A = x ∈ A
P = x ∈ P
Q = x ∈ Q
Решение задачи на множества
2) Формализация условия
Было:
(x ∉ A) → ((x ∉ P) ∧ (x ∈ Q)) ∨ (x ∉ Q) = 1
Стало:
¬ A → (¬P ∧ Q) ¬ Q = 1
Решение задачи на множества
3) Решение логического уравнения
¬ A → (¬P ∧ Q) ¬ Q = 1
3.1. Представим логическое следование в базовых логических операциях и сгруппируем:
A ((¬P ∧ Q) ¬ Q) = 1
Решение задачи на множества
A (( ¬P ∧ Q) ¬Q) = 1
3.2. Сведем получившееся выражение к решающей формуле:
А ¬А = 1
и найдем, чему равно ¬А :
¬А = (¬P ∧ Q) ¬Q
Решение задачи на множества
¬А = (¬P ∧ Q) ¬Q
3.3. Упростим выражение для ¬А, раскрыв скобки по закону дистрибутивности сложения:
¬А = ( ¬P ¬Q) (Q ¬Q)
Q ¬Q = 1
¬А = ( ¬P ¬Q)
Решение задачи на множества
¬А = ( ¬P ¬Q)
По закону де Моргана:
¬А = ¬(P Q)
3.4. Очевидно, что
А = P Q
Решение задачи на множества
А = P Q
4) Интерпретация полученного результата
Искомое множество А представляет собой пересечение множеств P и Q.
Решение задачи на множества
Искомое множество А есть пересечение множеств
P = 1, 2, 3 , 4, 5 , 6 и Q = { 3 , 5 ,15}, таким образом A = { 3 , 5 }
и содержит только 2 элемента.
Ответ: 2
Ответ на сайте Полякова: 2
2. Задания на множества
(№ 368) Элементами множеств А, P, Q являются натуральные числа, причём P={2,4,6,8,10,12} и Q={4,8,12,116}. Известно, что выражение (x ∈ P) → (((x ∈ Q) ∧ (x ∉ A)) → (x ∉ P))
истинно (т. е. принимает значение 1 ) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.
Источник — сайт Полякова К.Ю.
Решение задачи на множества
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на множества
- Легенда
A = x ∈ A
P = x ∈ P
Q = x ∈ Q
Решение задачи на множества
2) Формализация условия
Было:
(x ∈ P)→(((x ∈ Q) ∧ (x ∉ A))→(x ∉ P)) = 1
Стало:
P → ((Q ∧ ¬ A) → ¬ P) = 1
Решение задачи на множества
3) Решение логического уравнения
P → ((Q ∧ ¬ A) → ¬ P) = 1
3.1. Представим первое логическое следование (в скобках) в базовых логических операциях :
P → ( ¬ (Q ∧ ¬ A) ¬ P) = 1
Решение задачи на множества
P → ( ¬ (Q ∧ ¬ A) ¬ P) = 1
Представим второе логическое следование в базовых логических операциях, применим закон де Моргана и перегруппируем:
¬ P ( ¬ (Q ∧ ¬ A) ¬ P) = 1
¬ P ¬ Q A ¬ P = 1
Решение задачи на множества
A ( ¬ P ¬ Q ¬ P) = 1
3.2. Сведем получившееся выражение к решающей формуле:
А ¬А = 1
и найдем, чему равно ¬А :
¬А = ( ¬ P ¬ Q ¬ P)
Решение задачи на множества
¬А = ¬ P ¬ Q ¬ P
3.3. Упростим выражение для ¬А по формуле А А = А :
¬А = ¬ P ¬ Q
Далее, по закону де Моргана получаем:
¬А = ¬( P Q)
Решение задачи на множества
¬А = ¬(P Q)
3.4. Очевидно, что
А = P Q
4) Интерпретация полученного результата
Искомое множество А представляет собой пересечение множеств P и Q.
Решение задачи на множества
Искомое множество А есть пересечение множеств
P = 2, 4 , 6, 8 , 10, 12 и
Q = { 4 , 8 , 12 , 16}, таким образом
A = { 4 , 8 , 12 }
и содержит только 3 элемента, сумма которых 4+8+12=24 .
Ответ: 24
Ответ на сайте Полякова: 24
3. Задания на поразрядную конъюнкцию
(№ 379) Обозначим через m & n пораз-рядную конъюнкцию неотрицательных целых чисел m и n . Так, например, 14 & 5 = 1110 2 & 0101 2 = 0100 2 = 4. Для какого наименьшего неотрицательного целого числа А формула (x & 29 ≠ 0) → ((x & 12 = 0) → (x & А ≠ 0))
тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?
Решение задачи на поразрядную конъюнкцию
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на поразрядную конъюнкцию
- Легенда
Легенда для задач на поразрядную конъюнкцию отличается от всех остальных случаев:
B = (x & 29 ≠ 0)
C = (x & 12 ≠ 0)
A = (x & А ≠ 0)
Решение задачи на поразрядную конъюнкцию
Мы принимаем за истинное высказывание поразрядную конъюнкцию, отличную от нуля, иначе поразрядная конъюнкция теряет свой логический смысл, т.к. всегда можно представить Х всеми нулями.
Решение задачи на поразрядную конъюнкцию
2) Формализация условия
Было:
(x & 29 ≠ 0)→((x & 12 = 0)→(x & А ≠ 0))=1
Стало:
В → ( ¬С → А) = 1
Решение задачи на поразрядную конъюнкцию
3) Решение логического уравнения
В → ( ¬С → А) = 1
В → (С А) = 1
(¬В С) А = 1
¬А = ¬В С
¬А = ¬(В ¬ С)
Очевидно, что
А = В ¬ С
Решение задачи на поразрядную конъюнкцию
4) Интерпретация полученного результата
Искомое двоичное значение поразрядной конъюнкции А – это двоичное значение поразрядной конъюнкции значения В и инверсии двоичного значения С .
Решение задачи на поразрядную конъюнкцию
B = (x & 29 ≠ 0)
В или 29 = 11101 2
C = (x & 12 ≠ 0)
12 = 1100 2
¬С или инверсия 12 = 0011 2
Решение задачи на поразрядную конъюнкцию
В или 29 = 11101 2
¬С или инверсия 12 = 0011 2
А = В ¬ С
х 11101 2
0011 2
10001 2
А = 1 0001 2 = 17
Ответ на сайте Полякова: 17
27
3. Задания на поразрядную конъюнкцию
(№ 375) Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответ-ствующими битами двоичной записи). Определите наименьшее натуральное число A, такое что выражение (X & 49 ≠ 0) → ((X & 33 = 0) → (X & A ≠ 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?
Решение задачи на поразрядную конъюнкцию
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи на поразрядную конъюнкцию
- Легенда
Легенда для задач на поразрядную конъюнкцию отличается от всех остальных случаев:
B = (x & 49 ≠ 0)
C = (x & 33 ≠ 0)
A = (x & А ≠ 0)
Решение задачи на поразрядную конъюнкцию
2) Формализация условия
Было:
(X & 49 ≠ 0) → ((X & 33 = 0) → (X & A ≠ 0))=1
Стало:
В → ( ¬С → А) = 1
Решение задачи на поразрядную конъюнкцию
3) Решение логического уравнения
В → ( ¬С → А) = 1
В → (С А) = 1
(¬В С) А = 1
¬А = (¬В С)
Очевидно:
А = В ¬С
Решение задачи на поразрядную конъюнкцию
4) Интерпретация полученного результата
Искомое двоичное значение поразрядной конъюнкции А – это двоичное значение поразрядной конъюнкции значения В и инверсии двоичного значения С .
Решение задачи на поразрядную конъюнкцию
B = (x & 49 ≠ 0)
В или 49 = 110001 2
C = (x & 33 ≠ 0)
33 = 100001 2
¬С или инверсия 33 = 011110 2
Решение задачи на поразрядную конъюнкцию
В или 49 = 110001 2
¬С или инверсия 33 = 011110 2
А = В ¬ С
х 110001 2
011110 2
010000 2
А = 1 0000 2 = 16
Ответ на сайте Полякова: 16
27
4. Задания на условие делимости
(№ 372) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула ¬ДЕЛ(x,А) → (¬ДЕЛ(x,21) ∧ ¬ДЕЛ(x,35))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Источник — сайт Полякова К.Ю.
Решение задачи
на условие делимости
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи
на условие делимости
- Легенда
Легенда простая: А = ДЕЛ(x,А)
21 = ДЕЛ(х,21)
35 = ДЕЛ(x,35)
Решение задачи
на условие делимости
2) Формализация условия
Было:
¬ДЕЛ(x,А) → (¬ДЕЛ(x,21) ∧ ¬ДЕЛ(x,35))
тождественно истинна (то есть принимает значение 1)
Стало:
¬А → (¬21 ∧ ¬35) = 1
Решение задачи
на условие делимости
3) Решение логического уравнения
¬А → (¬21 ∧ ¬35) = 1
А (¬21 ∧ ¬35) = 1
¬А = ¬21 ∧ ¬35
Очевидно, что
А = 21 35
Решение задачи
на условие делимости
4) Интерпретация полученного результата
А = 21 35
В данной задаче это самый сложный этап решения. Нужно понять, что же представляет из себя число А – НОК или НОД или …
Решение задачи
на условие делимости
4) Интерпретация полученного результата
А = 21 35
Итак, наше число А таково, что Х делится на него без остатка, тогда и только тогда, когда Х делится без остатка на 21 или на 35. В этом случае ищем
А = НОД (21, 35) = 7
Ответ на сайте Полякова: 7
4. Задания на условие делимости
(№ 370) Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула ¬ДЕЛ(x,А) → ((ДЕЛ(x,6) → ¬ДЕЛ(x,4))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Источник — сайт Полякова К.Ю.
Решение задачи
на условие делимости
- Легенда
- Формализация условия
- Решение логического уравнения
- Интерпретация полученного результата
Решение задачи
на условие делимости
- Легенда
А = ДЕЛ(x,А)
6 = ДЕЛ(x,6)
4 = ДЕЛ(x,4)
Решение задачи
на условие делимости
2) Формализация условия
Было:
¬ДЕЛ(x,А) → ((ДЕЛ(x,6) → ¬ДЕЛ(x,4))
тождественно истинна (то есть принимает значение 1
Стало:
¬А → (6 → ¬4) = 1
Решение задачи
на условие делимости
3) Решение логического уравнения
¬А → (6 → ¬4) = 1
¬А → (¬ 6 ¬4) = 1
А (¬ 6 ¬4) = 1
¬А = ¬ 6 ¬4
Очевидно:
А = 6 4
Решение задачи
на условие делимости
4) Интерпретация полученного результата
А = 6 4
Итак, А таково, что Х делится на него без остатка тогда и только тогда, когда Х делится без остатка и на 6, и на 4. Т.е. А = НОК(6, 4) = 12
Ответ на сайте Полякова: 12

5. Задания на функции
Укажите наибольшее целое значение А, при котором выражение
( y + 2 x 99) ∨ ( y A ) ∨ ( x A )
истинно для любых целых положительных значений x и y .

Решение задачи
на функции
1) первое выражение не зависит от выбора A :
( y + 2 x 99)
2) таким образом, нам нужно выбрать значение A так, чтобы условие ( y A ) or ( x A ) выполнялось при всех x и y , для которых ложно ( y + 2 x 99) , то есть истинно ( y + 2 x = 99) или y = –2 x + 99
Решение задачи
на функции
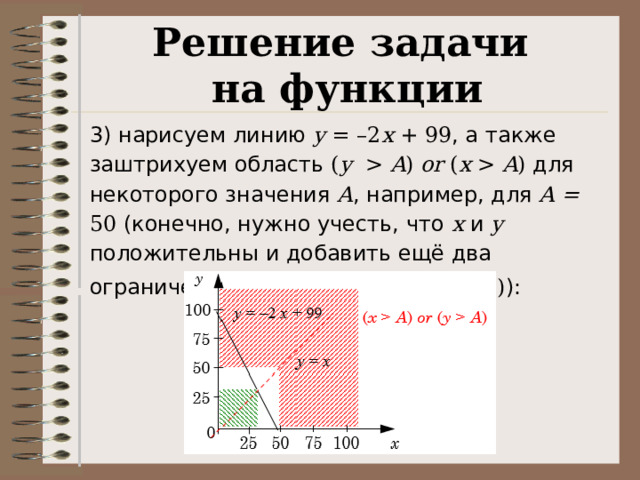
3) нарисуем линию y = –2 x + 99 , а также заштрихуем область ( y A ) or ( x A ) для некоторого значения A , например, для A = 50 (конечно, нужно учесть, что x и y положительны и добавить ещё два ограничения: ( x 0) and ( y 0) ):
Решение задачи
на функции
4) по условию задачи нужно, чтобы все точки отрезка прямой y = –2 x + 99 в первой четверти плоскости оказались в заштрихованной зоне
5) поэтому все точки образовавшегося белого квадрата, в том числе и его вершина ( A, A ) , должны находиться строго под этим отрезком; такой квадрат, соответствующий максимальному значению A , выделен на рисунке зелёной штриховкой
Решение задачи
на функции
6) находим координаты вершины зелёного квадрата: находим точку пересечения прямых y = –2 x + 99 и y = x ; эта задача сводится к линейному уравнению x = –2 x + 99 решение которого – x = 33
7) значение A должно быть меньше этого x , поэтому максимальное значение A = 32
Ответ: 32

5. Задания на функции
Укажите наименьшее целое значение А, при котором выражение
( y + 3 x A ) ∨ (2 y +x 50) ∨ (4 y – x
истинно для любых целых положительных значений x и y .

Решение задачи
на функции
1) второе и третье выражения не зависят от выбора A : (2 y +x 50) or (4 y – x
2) таким образом, нам нужно выбрать значение A так, чтобы условие ( y + 3 x A ) выполнялось при всех x и y , для которых ложно (2 y +x 50) or (4 y – x y +x 50) and (4 y – x 40)
3) последние два условия можно переписать в виде
( y – x /2 + 25) and ( y x /4 + 10)
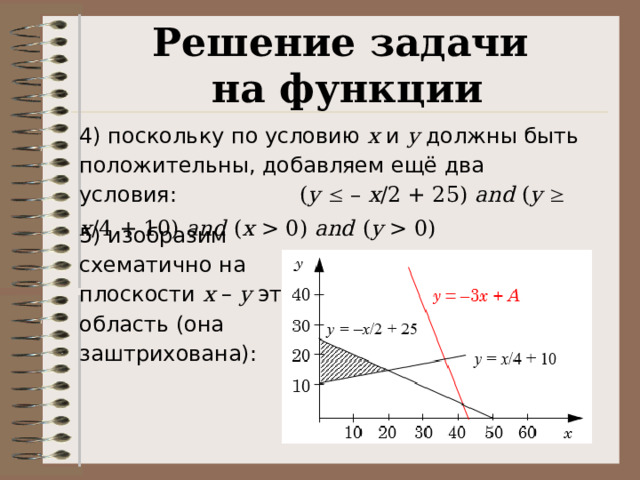
Решение задачи
на функции
4) поскольку по условию x и y должны быть положительны, добавляем ещё два условия: ( y – x /2 + 25) and ( y x /4 + 10) and ( x 0) and ( y 0)
5) изобразим схематично на плоскости x – y эту область (она заштрихована):
Решение задачи
на функции
6) для всех точек этой области должно выполняться условие y + 3 x A , равносильное условию y x +A
7) это значит, что вся область должна лежать ниже линии y = – 3 x +A ; одна такая подходящая линия показана на рисунке сверху
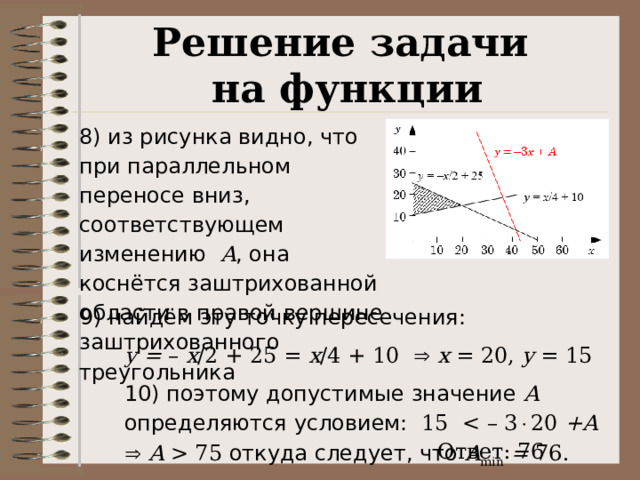
Решение задачи
на функции

9) найдём эту точку пересечения:
y = – x /2 + 25 = x /4 + 10 x = 20, y = 15
10) поэтому допустимые значение A определяются условием: 15 +A A 75 откуда следует, что A min = 76.
Ответ: 76
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
На числовой прямой даны два отрезка: P = [2, 10] и Q = [6, 14]. Выберите такой отрезок A, что формула
( (x ∈ А) → (x ∈ P) ) ∨ (x ∈ Q)
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
1) [0, 3]
2) [3, 11]
3) [11, 15]
4) [15, 17]
2
На числовой прямой даны три отрезка: P = [10, 40], Q = [5, 15] и R = [35, 50]. Выберите такой отрезок A, что формула
( (x ∈ А) → (x ∈ P) ) ∨ ((x ∈ Q)→ (x ∈ R))
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
1) [9, 20)
2) [3, 12]
3) [3, 7]
4) [120, 130]
3
На числовой прямой даны два отрезка: P = [5, 15] и Q = [10,20]. Выберите такой отрезок A, что формула
(x ∈ P) ∧ (x ∉ Q) ∧ (x ∈ A)
тождественно ложна, то есть принимает значение 0 при любом значении переменной х.
1) [0, 7]
2) [8, 15]
3) [15, 20]
4) [7, 20]
4
На числовой прямой даны три отрезка: P = [10,15], Q = [10,20] и R=[5,15]. Выберите такой интервал A, что формулы
(x ∈ A) → (x ∈ P) и (x ∈ Q) → (x ∈ R)
тождественно равны, то есть принимают равные значения при любом значении переменной х (за исключением, возможно, конечного числа точек).
1) [5, 12]
2) [10, 17]
3) [12, 20]
4) [15, 25]
5
На числовой прямой даны два отрезка: Р = [30, 45] и Q = [40, 55]. Выберите такой отрезок А, что обе приведённые ниже формулы истинны при любом значении переменной х:
( ¬(x ∈ A) → (¬(x ∈ P)) )
((x ∈ Q)→ (x ∈ A))
1) [25, 50]
2) [25, 65]
3) [35, 50]
4) [35, 85]
Пройти тестирование по этим заданиям
Характеристика задания
1. Тип ответа: числовой ответ.
2. Структура содержания задания: дано логическое выражение.
3. Уровень сложности задания: повышенный.
4. Примерное время выполнения: (3) минуты.
5. Количество баллов: (1).
6. Требуется специальное программное обеспечение: необязательно.
7. Задание проверяет знание основных понятий и законов математической логики.
Пример задания (демоверсия (2022))
Рис. (1). Пример задания
Вспомнить основные логические операции можно тут.
Вспомнить законы алгебры логики можно тут.
Для решения введём обозначения:
A−x∈A,D−x∈D,C−x∈C,
для упрощения выражения воспользуемся формулой
A→B=¬A∨B
:
.
Воспользуемся законом общей инверсии, повторения и двойного отрицания:
.
По условию задачи выражение
¬D∨C∨A
должно быть истинно при любом (x). Представим полученное решение на числовой прямой:
Рис. (2). Графическое решение
Из рисунка видно, что отрезок (A) должен перекрыть незакрашенную область на числовой оси, которая не входит в область
¬D∨C
.
Наименьший возможный отрезок в этом случае — [(17), (29)], его длина — (12).
Ответ: (12).
Источники:
Рис. 1. Пример задания. © ЯКласс.
Рис. 2. Графическое решение. © ЯКласс.


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой

Была в сети 24.11.2022 11:28
Подлесных Елена Викторовна
учитель информатики и физики
37 лет
1 447
27 953
30.03.2022 20:49
Решение задач с отрезками с помощью программирования на языке Python
Просмотр содержимого документа
«Решение задач c отрезками на Python»
Решение задач ЕГЭ №15 (отрезки) способом программирования на Python (Для составления решений использовались задачи с сайта К.Полякова https://kpolyakov.spb.ru/school/ege.htm)
№4876

№4972

№4973

№4974

№4962

№4545

№4874

№4563

Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Скачать материал
Выберите документ из архива для просмотра:
задания для мастер-класса ЕГЭ15.docx
Решение задания ЕГЭ 15.pptx
Выбранный для просмотра документ задания для мастер-класса ЕГЭ15.docx
Скачать материал


- Сейчас обучается 84 человека из 29 регионов


- Сейчас обучается 33 человека из 18 регионов


- Сейчас обучается 118 человек из 41 региона


Выбранный для просмотра документ Решение задания ЕГЭ 15.pptx

Скачать материал
Описание презентации по отдельным слайдам:
-
1 слайд
Решение задания ЕГЭ 15
«руками» и программой
Учитель МАОУ гимназия №40
им. Ю.А. Гагарина
Медведькова Н.А.
Калининград, 2022г. -
2 слайд
Таблица истинности логических операций
– таблица НЕ;– таблица И;– таблица ИЛИ;
– импликационная таблица; – таблица эквиваленции. -
3 слайд
Порядок выполнения логических операций
– в первую очередь выполняется отрицание ;
– во вторую очередь – конъюнкция ;
– затем – дизъюнкция ;
– потом импликация ;
– и, наконец, низший приоритет имеет эквиваленция
. -
-
5 слайд
Основные формулы преобразования
-
6 слайд
Упростить выражения
Задание 1
Упростить логическую формулу : ((A B) (B C))ОТВЕТЗадание 2
Упростить логическую формулу: (x y) (x y) xОТВЕТЗадание 3
Выразить эквиваленцию p q через отрицание, конъюнкцию, дизъюнкцию и раскрыть скобкиОТВЕТ -
7 слайд
ЕГЭ 15 сегодня
В ЕГЭ15 на сегодняшний день всего 5 типов задач:
задачи с отрезками, задачи с множествами, задачи на делимость, на конъюнкцию и задачи на графики«Руками» очень удобно решаются задачи с отрезками, задачи с множествами, решаются задачи на делимость, на конъюнкцию.
Программой удобно решать задачи на графики
-
8 слайд
Алгоритм решения ЕГЭ15 «руками»
Обозначить логические высказывания.
Упростить логическое выражение до импликации (A B) и «читаемого» вида.
«Прочитать» логическое выражение.
Найти ответ на задание. -
9 слайд
Задачи ЕГЭ 15
Элементами множества А являются натуральные числа. Известно, что выражение
¬(x {2, 4, 8, 12, 16}) ¬(x {3, 6, 7, 15}) ¬(x {3, 6, 7, 15}) (x A)
истинно (т. е. принимает значение 1) при любом значении переменной х.Определите наименьшее возможное количество элементов множества A.
Ответ: 4 -
10 слайд
Задачи ЕГЭ 15
Элементами множеств А, P, Q являются натуральные числа,
причём P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20},
Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}.
Известно, что выражение
( (x P) → (x A) ) (¬(x A) → ¬(x Q) )
истинно (т. е. принимает значение 1) при любом значении переменной х.Определите наименьшее возможное количество элементов в множестве A.
Ответ: 3 -
11 слайд
Задачи ЕГЭ 15
На числовой прямой даны два отрезка: P = [12, 24] и Q = [18 ,30].
Отрезок A таков, что формула (x A) → ((x P) → (x Q))
истинна при любом значении переменной x.Какое наименьшее количество точек, соответствующих нечётным целым числам, может содержать отрезок A?
Ответ: 3 -
12 слайд
Алгоритм решения ЕГЭ15 «руками»
Обозначить логические высказывания.
Упростить логическое выражение до импликации (A B) и «читаемого» вида.
«Прочитать» логическое выражение.
Найти ответ на задание. -
13 слайд
«Читаем» логические выражения
-
14 слайд
Задачи ЕГЭ15
Введём выражение mn, обозначающее поразрядную конъюнкцию m и n (логическое «И» между соответствующими битами двоичной записи). Определите наименьшее натуральное число A, такое что выражение
(X 107 = 0) → ((X 55 ≠ 0) → (X A ≠ 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)? -
15 слайд
Программа
#(X & 107 = 0) → ((X & 55 ≠ 0) → (X & A ≠ 0))def f(x,a):
return (x&107==0) <= ((x&55!=0) <= (x&a!=0))
for a in range(1,1000):
if all(f(x,a)==1 for x in range(1,10000)):
print(a); break
#Ответ: 20 -
16 слайд
Задачи ЕГЭ 15
Введём выражение m n, обозначающее поразрядную конъюнкцию m и n (логическое «И» между соответствующими битами двоичной записи). Определите наибольшее натуральное число A, такое что выражение
(( (X 13 ≠ 0) ∨ (X A ≠ 0)) → (X 13 ≠0)) ∨ ((X A ≠ 0) ∧ (X 39 = 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?
Ответ: 8 -
17 слайд
Программа
# (( (X 13 ≠ 0) ∨ (X A ≠ 0)) → (X 13 ≠0)) ∨ ((X A ≠ 0) ∧ (X 39 = 0))def f(x,a):
return (((x 13!=0) or (x a!=0)) <= (x 13!=0)) or ((x a!=0) and (x 39==0))
for a in range(1000):
if all(f(x,a)==1 for x in range(10000)):
print(a)
#Ответ: 13 -
18 слайд
Задачи ЕГЭ 15
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на m». Для какого наименьшего натурального числа А формула
(ДЕЛ(x, 15) ∧ ¬ДЕЛ(x, 21)) → (¬ДЕЛ(x, A) ∨ ¬ДЕЛ(x, 15))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)? -
19 слайд
Программа
#(ДЕЛ(x, 15) ∧ ¬ДЕЛ(x, 21)) → (¬ДЕЛ(x, A) ∨ ¬ДЕЛ(x, 15))def f(x,a):
return ((x%15==0) and (x%21!=0)) <= ((x%a!=0) or (x%15!=0))
for a in range(1,100):
if all(f(x,a)==1 for x in range(1,1000)):
print(a);break
#Ответ: 7 -
20 слайд
Задачи ЕГЭ 15
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа A формула
ДЕЛ(A, 7) ∧ (ДЕЛ(240, x) → (¬ДЕЛ(A, x) → ¬ДЕЛ(780, x)))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)? -
21 слайд
Программа
#ДЕЛ(A, 7) ∧ (ДЕЛ(240, x) → (¬ДЕЛ(A, x) → ¬ДЕЛ(780, x)))def f(x,a):
return (a%7==0) and ((240%x==0) <= ((a%x!=0)<=(780%x!=0)))
for a in range(1,1000):
if all(f(x,a)==1 for x in range(1,10000)):
print(a);break
#Ответ: 420 -
22 слайд
Задачи ЕГЭ 15
Найдите максимальное значение параметра А, при котором выражение
(2х + у ≠ 70) ∨ (x < y) ∨ (A < x)
истинно (т.е. принимает значение 1) при любых неотрицательных значениях x и у. -
23 слайд
Программа
#(2х + у ≠ 70) ∨ (x < y) ∨ (A < x)
for a in range(1,200):
fl=True
for x in range(0,100):
for y in range(0,100):
if ((2*x+y!=70) or (x<y) or (a<x))==0:
fl=False
break
if fl:
print(a)
#Ответ: 23 -
-
25 слайд
Программа
#(x > 39) ∨ (y > 26) ∨ (2x + 4y < A)for a in range(1,500):
fl=True
for x in range(0,100):
for y in range(0,100):
if ((x>39) or (y>26) or (2*x+4*y<a))==0:
fl=False
break
if fl: print(a)#Ответ: 183
-
26 слайд
Какие у Вас есть вопросы?
Рада нашей встрече!
Благодарю за внимание!
-
27 слайд
Ответ: B A C
((A B) (B C)) == (A + B) (B + C) == (A + B) (B * C) ==
== (A + B) + (B * C) == (A * B) + (B * C) == (A * B) * (B * C) ==
== (A + B) * (B + C) == (A +B) * (B + C) == A * B + B + A * C + B * C ==
== B * (A + 1 + C) + A *C == B * 1 + A *C == B + A * C == B A C
НАЗАД -
28 слайд
Ответ: ( p q) (p q)
p q ==
== ( p q) (p q) ==
== (p q) (q p) ==
== (( p q) q) (( p q) p) ==
== ( q p) 0 0 (p q) ==
== ( q p) (p q) ==
== p q q p
НАЗАД -
29 слайд
Ответ: x y
( x y) (x y) x ==
== ( x y) ( x y) x ==
== (x y) x ( x y)==
== (x y) (x x) (x y)==
== (x y) 0 (x y) ==
== x y x y ==
== x y y x == x y
НАЗАД
Краткое описание документа:
В архиве находится презентация к уроку, задания (документ Word) для закрепления изученного материала, программы на PYTHON’e. Время проведения 2 академических часа
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 153 824 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы






- 30.12.2022
- 23
- 1
- 30.12.2022
- 26
- 2
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс повышения квалификации «Организация работы по формированию медиаграмотности и повышению уровня информационных компетенций всех участников образовательного процесса»
-
Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»
-
Курс профессиональной переподготовки «Информационные технологии в профессиональной деятельности: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
-
Курс повышения квалификации «Введение в программирование на языке С (СИ)»
-
Курс профессиональной переподготовки «Управление в сфере информационных технологий в образовательной организации»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс повышения квалификации «Специфика преподавания дисциплины «Информационные технологии» в условиях реализации ФГОС СПО по ТОП-50»
























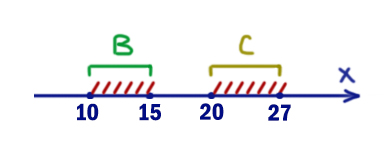
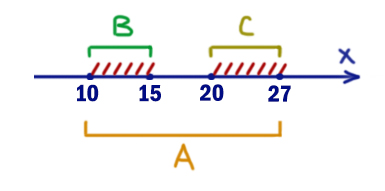

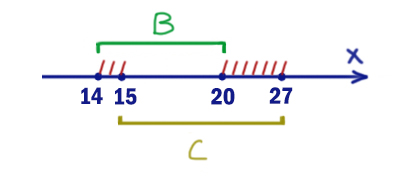
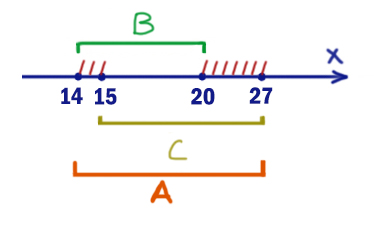

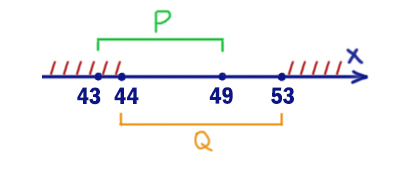
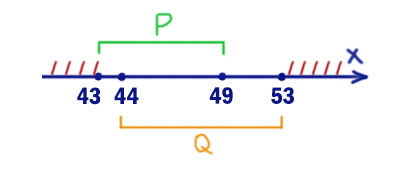
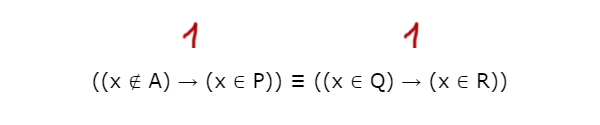
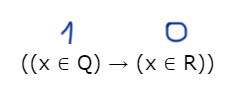
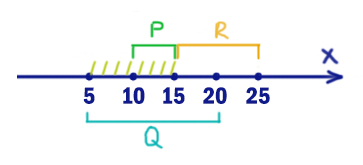
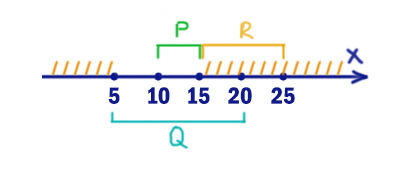
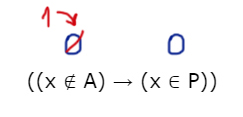
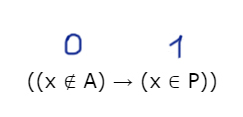
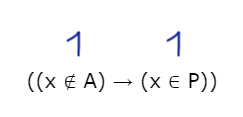
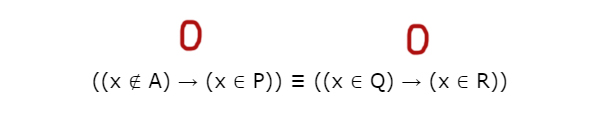
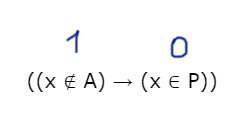
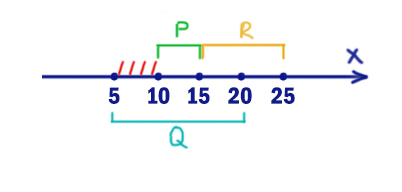
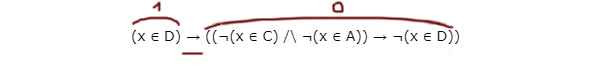
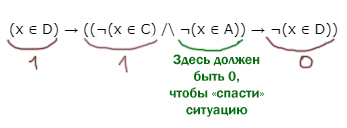
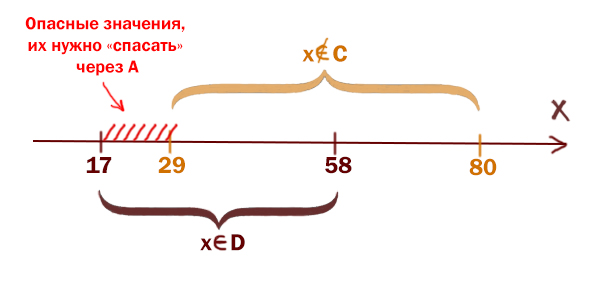


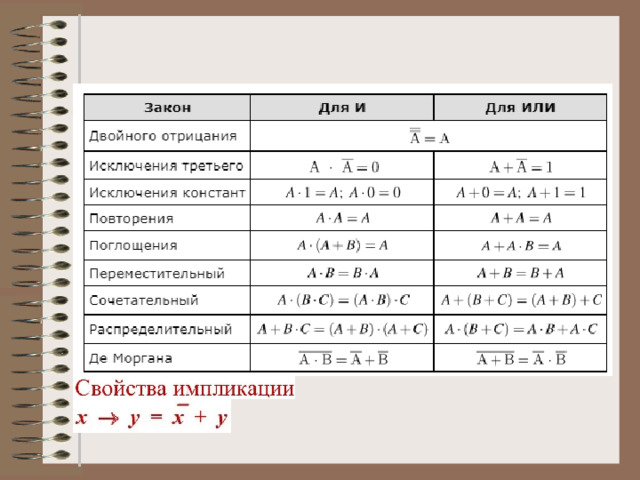


![Задания на отрезки ( № 376 ) На числовой прямой даны два отрезка: P=[4,15] и Q=[12,20]. Укажите наименьшую возможную длину такого отрезка A, что формула ((x ∈ P) ∧ (x ∈ Q)) → (x ∈ A) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Источник - сайт Полякова К.Ю.](https://fsd.videouroki.net/html/2023/01/26/v_63d249777a998/img5.jpg)








![Решение задачи на отрезки Пересечение отрезков P и Q можно визуализировать: P=[4,15] и Q=[12,20]. 15 12 20 4 По условию нашей задачи, нам нужна минимальная длина отрезка А . Находим ее: 15 – 12 = 3 . Ответ: 3 . Ответ на сайте Полякова К.Ю.: 3](https://fsd.videouroki.net/html/2023/01/26/v_63d249777a998/img14.jpg)
![Задания на отрезки (№ 360) На числовой прямой даны три отрезка: P=[10,25], Q=[15,30] и R=[25,40]. Какова максимальная длина отрезка A, при котором формула ((x ∈ Q) → (x ∉ R) ) ∧ (x ∈ A) ∧ (x ∉ P) тождественно ложна, то есть принимает значение 0 при любом значении переменной х? Источник - сайт Полякова К.Ю.](https://fsd.videouroki.net/html/2023/01/26/v_63d249777a998/img15.jpg)









![Решение задачи на отрезки Пересечение отрезков R и Q можно визуализировать: Q=[15,30] и R=[25,40]. 30 25 40 15 Отрезок P=[10,25] нанесем на наш чертеж и объединим с пересечением: 25 30 15 40 10](https://fsd.videouroki.net/html/2023/01/26/v_63d249777a998/img25.jpg)



















































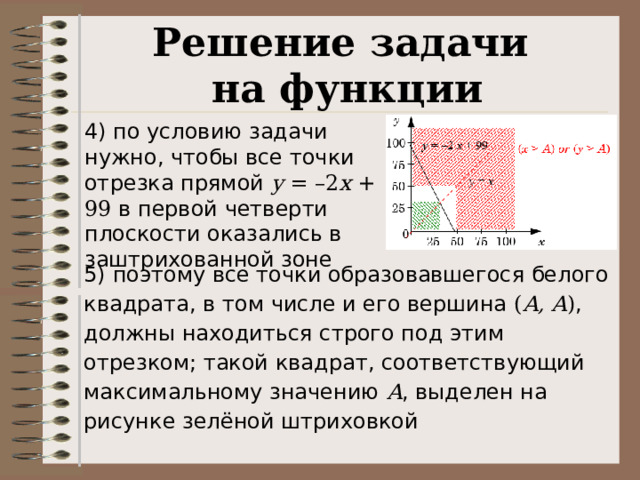
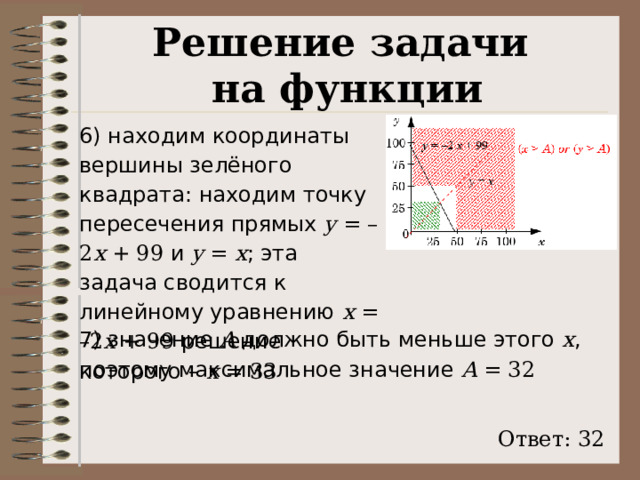
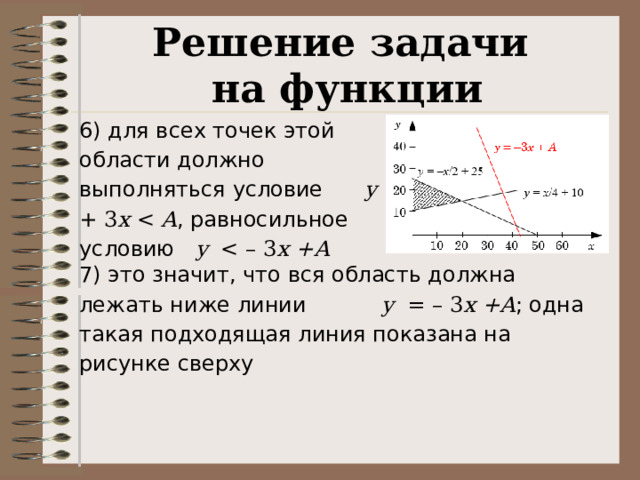












![Задачи ЕГЭ 15На числовой прямой даны два отрезка: P = [12, 24] и Q = [1... Задачи ЕГЭ 15На числовой прямой даны два отрезка: P = [12, 24] и Q = [1...](https://documents.infourok.ru/b55b67f2-d42e-462e-9ce7-d965dfbc5461/1/slide_11.jpg)


















