Как решать задания с графиками егэ математика профиль - Помощь в подготовке к экзаменам и поступлению

В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №10 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.

Как формулируется задание 10 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.

Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.

Вот необходимая теория для решения задания №10 ЕГЭ.

Что такое функция

Чтение графика функции

Четные и нечетные функции

Периодическая функция

Обратная функция

5 типов элементарных функций и их графики

Преобразование графиков функций

Построение графиков функций

Да, теоретического материала здесь много. Но он необходим — и для решения задания 10 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.

Рекомендации:

Запоминай, как выглядят графики основных элементарных функций. Замечай особенности графиков, чтобы не перепутать параболу с синусоидой : -)

Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?

Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.

Задание 10 в формате ЕГЭ-2021

Линейная функция

Необходимая теория

1. На рисунке изображён график функции . Найдите значение , при котором

Решение:

Найдем, чему равны k и b. График функции проходит через точки (3; 4) и (-1; -3). Подставив по очереди координаты этих точек в уравнение прямой y = kx + b, получим систему:

$left{ begin{array}{c}3k+b=4 \-k+b=-3 end{array}right..$

Вычтем из первого уравнения второе:

$left{ begin{array}{c}4k=7 \-k+b=-3 end{array};right. left{ begin{array}{c}k=frac{7}{4} \b=-frac{5}{4} end{array}right. .$

Уравнение прямой имеет вид:

$displaystyle y=frac{7}{4}x-frac{5}{4}.$

Найдем, при каком значение функции равно -13,5.

$displaystyle frac{7}{4}x-frac{5}{4}=-13,5;$

7x=-49;

x=-7.

Ответ: -7.

2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Запишем формулы функций.

Одна из них проходит через точку (0; 1) и ее угловой коэффициент равен -1. Это линейная функция y=-x+1.

Другая проходит через точки (-1; -1) и (-2; 4). Подставим по очереди координаты этих точек в формулу линейной функции y=kx+b.

$left{ begin{array}{c}-k+b=-1 \-2k+b=4 end{array}right. .$

Вычтем из первого уравнения второе.

k=-5; тогда b=-6.

Прямая задается формулой:

Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:

$left{ begin{array}{c}y=-x+1 \y=-5x-6 end{array} ;right. begin{array}{c}-x+1=-5x-6 ; \x=-frac{7}{4}=-1,75. end{array}$

Ответ: -1,75.

3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Прямая, расположенная на рисунке ниже, задается формулой y=x+1, так как ее угловой коэффициент равен 1 и она проходит через точку (-3; -2).

Для прямой, расположенной выше, угловой коэффициент равен $displaystyle frac{3}{2}=1,5.$

Эта прямая проходит через точку (-2; 4), поэтому: b=7, эта прямая задается формулой

Для точки пересечения прямых:

x=-12.

Ответ: -12.

Квадратичная функция. Необходимая теория

4. На рисунке изображен график функции Найдите b.

Решение:

На рисунке — квадратичная парабола $y={left(x-aright)}^2,$ полученная из графика функции y=x^2 сдвигом на 1 вправо, то есть a=1.

Получим: $fleft(xright)={left(x-1right)}^2=x^2-2x+1;$

b=-2.

Ответ: -2.

5. На рисунке изображен график функции $y={left(x-cright)}^2$ . Найдите с.

Решение:

На рисунке изображена парабола, ветви которой направлены вверх, значит, коэффициент при x^2 положительный. График сдвинут относительно графика функции y=x^2 на 1 единицу вправо вдоль оси Ох. Формула функции имеет вид $y={left(x-1right)}^2$ .

Значит, с = 1.

Ответ: 1

6. На рисунке изображён график функции Найдите

Решение:

График функции проходит через точки с координатами (1; 1) и (-2; -2). Подставляя координаты этих точек в формулу функции, получим:

$left{ begin{array}{c}2+b+c=1 \2cdot 4-2b+c=-2 end{array}right. .$

$left{ begin{array}{c}b+c=-1 \-2b+c=-10 end{array};right.$ отсюда b=3, c=-4.

Формула функции имеет вид:

Ответ: 31.

7. На рисунке изображены графики функций и которые пересекаются в точках А и В. Найдите абсциссу точки В.

Решение:

Найдем a, b и c в формуле функции . График этой функции пересекает ось ординат в точке (0; -3), поэтому c=-3.

График функции g(x) проходит через точки (-1; -3) и (2; 3). Подставим по очереди координаты этих точек в формулу функции:

$left{ begin{array}{c}a-b-3=-3 \4a+2b-3=3 end{array};right.$ отсюда a=b=1;

Найдем абсциссу точки B. Для точек A и B:

x=-2 (это абсцисса точки A) или x=6 (это абсцисса точки B).

Ответ: 6.

Степенные функции. Необходимая теория

8. На рисунке изображены графики функций $displaystyle fleft(xright)=frac{k}{x}$ и , которые пересекаются в точках А и В. Найдите абсциссу точки В.

Решение:

График функции $displaystyle y=frac{k}{x}$ проходит через точку (2; 1); значит, $displaystyle frac{k}{2}=1;$

$displaystyle k=2, ; fleft(xright)=frac{2}{x}.$

График функции проходит через точки (2; 1) и (1; -4), a=5 — угловой коэффициент прямой; (находим как тангенс угла наклона прямой и положительному направлению оси X); тогда b=-9.

Для точек A и B имеем:

$displaystyle frac{2}{x}=5x-9;$

Отсюда x=2 (абсцисса точки A) или x=-0,2 (абсцисса точки B).

Ответ: -0,2.

9. На рисунке изображён график функции . Найдите f (6,76).

Решение:

Функция задана формулой:

Ее график проходит через точку (4; 5); значит, k=2,5;

Тогда

Ответ: 6,5.

10. На рисунке изображен график функции . Найдите .

Решение:

График функции на рисунке симметричен графику функции относительно оси Y. Он проходит через точку (-1; 1). Значит, формула изображенной на рисунке функции: , а = — 1. Тогда = 5.

Ответ: 5.

Показательная функция. Необходимая теория

11. На рисунке изображён график функции $fleft(xright)=a^{x+b}.$ Найдите

Решение:

График функции проходит через точки (-3; 1) и (1; 4). Подставив по очереди координаты этих точек в формулу функции $fleft(xright)=a^{x+b},$ получим:

$left{ begin{array}{c}a^{-3+b}=1 \a^{1+b}=4 end{array}.right.$

Поделим второе уравнение на первое:

$a^{1+b+3-b}=4; ; a^4=4;; a=sqrt{2}.$

Подставим во второе уравнение:

$displaystyle {sqrt{2}}^{1+b}=4;; 2^{frac{1+b}{2}}=2^2;; 1+b=4;; b=3.$

$displaystyle fleft(xright)={left(sqrt{2}right)}^{x+3};; fleft(-7right)={left(sqrt{2}right)}^{-7+3}={left(sqrt{2}right)}^{-4}=frac{1}{4}=0,25.$

Ответ: 0,25.

12. На рисунке изображен график функции . Найдите

Решение:

График функции проходит через точку Это значит, что

a=2, формула функции имеет вид: .

Ответ: 2.

Логарифмическая функция. Необходимая теория

13. На рисунке изображён график функции $fleft(xright)={{log}_a left(x+bright)}.$ Найдите

Решение:

График функции $y={{log}_a left(x+bright) }$ проходит через точки (-3; 1) и (-1; 2). Подставим по очереди эти точки в формулу функции.

$left{ begin{array}{c}{{log}_a left(-3+bright)=1 } \{{log}_a left(-1+bright) }=2 end{array}.right.$

Отсюда: $left{ begin{array}{c}b-3=a \b-1=a^2 end{array}.right.$

Вычтем из второго уравнения первое:

a=2 или a=-1 — не подходит, так как (как основание логарифма).

Тогда $fleft(xright)={{log}_2 left(x+5right) };$

$fleft(11right)={{log}_2 16=4.}$

Ответ: 4.

14. На рисунке изображен график функции $fleft(xright)=a{{log}_5 x }-c$ .

Найдите f(0,2).

Решение:

График логарифмической функции на рисунке проходит через точки и . Подставив по очереди координаты этих точек в формулу функции, получим систему уравнений:

$left{ begin{array}{c}a{{log}_5 1 }-c=-2 \a{{log}_5 5 }-c=3 end{array};right.$

$left{ begin{array}{c}-c=-2 \a-c=3 end{array};right.$

$left{ begin{array}{c}c=2 \a=5 end{array}.right.$

Формула функции: $fleft(xright)=5{{log}_5 x }-2.$

Найдем $displaystyle fleft(0,2right)=fleft(frac{1}{5}right)$ :

$displaystyle 5cdot {{log}_5 frac{1}{5} }-2=-5-2=-7.$

Ответ: -7.

Тригонометрические функции. Необходимая теория

15. На рисунке изображён график функции Найдите

Решение:

График функции сдвинут на 1,5 вверх; Значит, b=1,5. Амплитуда a=2 (наибольшее отклонение от среднего значения).

Это график функции Он получен из графика функции растяжением в 2 раза по вертикали и сдвигом вверх на 1,5 .

Ответ: b=1,5.

16. На рисунке изображён график функции

Найдите .

Решение:

На рисунке — график функции Так как b=-1,5.

График функции проходит через точку A $displaystyle (frac{pi}{4}; ; frac{1}{2}).$ Подставим и координаты точки А в формулу функции.

$displaystyle a tg frac{pi}{4}-1,5=frac{1}{2}.$

Так как $displaystyle tg frac{pi}{4}=1,$ получим: a = 2.

Ответ: 2.

17. На рисунке изображен график периодической функции у = f(x). Найдите значение выражения

Решение:

Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если то

Пользуясь периодичностью функции , период которой T = 4, получим:

Ответ: 5.

Друзья, мы надеемся, что на уроках математики в школе вы решаете такие задачи. Для углубленного изучения темы «Функции и графики» (задание 10 ЕГЭ по математике), а также задач с параметрами и других тем ЕГЭ — рекомендуем Онлайн-курс для подготовки к ЕГЭ на 100 баллов.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 10 ЕГЭ по математике. Графики функций» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

В ЕГЭ 2022 года добавили новую задачу на графики функций. Для решения этой задачи нужно сначала определить формулу функции, а затем вычислить ответ на вопрос задачи. И если вычисление ответа по известной формуле обычно не составляет труда, то вот определение самой формулы часто ставит школьников в тупик. Поэтому мы разберем три разных подхода к этому вопросу.

Замечание. Про то как определяется формула у прямой и параболы я написала в этой и этой статьях. Поэтому здесь в примерах я буду использовать другие функции – дробные, иррациональные, показательные и логарифмические, но все три описанных здесь способа работают и для линейных, и для квадратичных функций в том числе.

1 способ – находим формулу по точкам

Этот способ подходит вообще для любой девятой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений.

Давайте разберем алгоритм на примере конкретной 9-ой задачи ЕГЭ:

Алгоритм:

1. Находим 2 точки с целыми координатами. Обычно они выделены жирно, но если это не так, то не проблема найти их самому.
Пример:

2. Подставляем эти координаты в «полуфабрикат» функции. Вместо (f(x))– координату игрек, вместо (x) – икс. Получается система.

3. Решаем эту систему и получаем готовую формулу.

4. Готово, функция найдена, можно переходить ко второму этапу – вычислению (f(-8)). Если вы вдруг не знаете, что это значит – в конце статьи я рассматриваю этот момент более подробно.

Давайте посмотрим метод еще раз на примере с логарифмической функцией.
Пример:

2 способ – преобразование графиков функций

Этот способ сильно быстрее первого, но требует больше знаний. Для использования преобразований функций нужно знать, как выглядят функции без изменения и как преобразования их меняют. Наиболее удобно использовать этот способ для иррациональной функции ((y=sqrt{x}) ) и функции обратной пропорциональности ((y=frac{1}{x})).

Вот как выглядит применение этого способа:

Для использования этого способа надо знать, как выглядят изначальные функции:

И понимать, как меняются функции от преобразований:

Часто даже по «полуфабрикату» функции понятно, какие преобразования сделали с функцией:

Пример:

3 способ – гибридный

Идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти. С другой стороны, независимо от оснований любая показательная функция должна проходить через точку ((0;1)), а любая логарифмическая — через точку ((1;0)).

По смещению этих точек легко понять, как именно двигали функцию, но только если ее не растягивали, а лишь перемещали вверх-вниз, влево-вправо (как обычно и бывает в задачах на ЕГЭ).

Основание же лучше находить уже следующим действием, используя подстановку координат точки в «полуфабрикат» функции.

Как отвечать на вопросы в задаче, когда уже определили функцию

— Если просят найти (f)(любое число), то нужно это число подставить в готовую функцию вместо икса.
Пример:

— Если просят найти «при каком значении x значение функции равно *любому числу*», то надо решить уравнение, в одной части которого будет функция, а в другой — то самое число. Аналогично надо поступить, если просят «найти корень уравнения (f(x)=) *любое число*».
Пример:

— Если просят найти абсциссу точки пересечения – надо приравнять 2 функции и решить получившееся уравнение. Корень уравнения и будет искомой абсциссой. Аналогично надо делать в задачах, где даны две точки пересечения (A)(*любое число*;*другое число*) и (B(x_0;y_0)) и просят найти (x_0).
Пример:

— Если просят найти ординату точки пересечения – надо приравнять 2 функции, найти иксы и подставить подходящий икс в любую функцию. Точно также решаем если просят найти (y_0) точки пересечения двух функций.
Пример:

— Иногда просят найти просто какой-либо из коэффициентов функции. Тогда надо просто восстановить функцию и записать в ответ то, о чем спросили:
Пример:

Источник

Графики функций.

Задание 10 ЕГЭ по
математике (профильный уровень)

Как формулируется задание 10 ЕГЭ по математике? По графику функции, который
дается в условии, вам нужно определить неизвестные параметры в ее формуле.
Возможно — найти значение функции в некоторой точке или координаты точки
пересечения графиков функций.

Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами
обладают графики элементарных функций. Надо уметь читать графики, то есть
получать из них необходимую информацию. Например, определять формулу функции по
ее графику.

Рекомендации:

Запоминай, как
выглядят графики основных элементарных функций.

Замечай
особенности графиков, чтобы не перепутать параболу с синусоидой : -)

Проверь себя:
какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по
горизонтали или по вертикали, растянуть, перевернуть?

Разбирая решения
задач, обращай внимание на то, как мы ищем точки пересечения графиков или
неизвестные переменные в формуле функции. Такие элементы оформления встречаются
также в задачах с параметрами.

Важный
принцип — это логичность. В шутливой манере он говорит: «нормальные герои
всегда идут в обход». Нужно учиться использовать наличный запас знаний,
применяя различные «хитрости» и «правдоподобные
рассуждения» для ответа наиболее простым и понятным способом.

Источник

Каталог заданий.
Параболы

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 10 № 509253

На рисунке изображены графики функций и которые пересекаются в точках A и B. Найдите абсциссу точки B.

Аналоги к заданию № 509253: 509254 509255 509259 509262 509263 509264 509268 509256 509257 509258 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

Сообщить об ошибке · Помощь

Тип 10 № 562060

На рисунке изображён график функции вида где числа a, b и c  — целые. Найдите значение

Аналоги к заданию № 562153: 562060 562154 562155 562156 562157 562158 562159 562160 562161 562162 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

Сообщить об ошибке · Помощь

Тип 10 № 562061

На рисунке изображён график функции вида где числа a, b и c  — целые. Найдите значение дискриминанта уравнения

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

1 комментарий · Сообщить об ошибке · Помощь

Тип 10 № 562153

На рисунке изображён график функции вида где числа a, b и c  — целые. Найдите значение

Аналоги к заданию № 562153: 562060 562154 562155 562156 562157 562158 562159 562160 562161 562162 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

Сообщить об ошибке · Помощь

Тип 10 № 562154

На рисунке изображён график функции вида где числа a, b и c  — целые. Найдите значение

Аналоги к заданию № 562153: 562060 562154 562155 562156 562157 562158 562159 562160 562161 562162 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график

Решение

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

: ЕГЭ по математике профиль

Вебинар на тему: «Задание 9 в профильном ЕГЭ по математике 2022 года. Графики функций».

Лектор: Кулабухов Сергей Юрьевич

Графики функций на ЕГЭ 2022 года. Задание №9

→ презентация решение задач №9

→ практика по заданию №9 профильного ЕГЭ по математике 2022

Связанные страницы:

Источник

: ЕГЭ по математике профиль

Новые задания №9 ЕГЭ 2022 по профильной математике — графики функций.

Для успешного результата необходимо уметь выполнять действия с функциями.

Задание №9 ЕГЭ 2022 математика профильный уровень Прототипы

Из кодификатора 2022 года для выполнения 9 задания нужно изучить основные элементарные функции, их свойства и графики:

3.3.1 Линейная функция, её график

3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график

3.3.3 Квадратичная функция, её график

3.3.4 Степенная функция с натуральным показателем, её график

3.3.5 Тригонометрические функции, их графики

3.3.6 Показательная функция, её график

3.3.7 Логарифмическая функция, её график

Уметь выполнять действия с функциями: определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций:

При отработке данного задания будут полезны книги:

Купить ЕГЭ. Математика. Графики функций, уравнения и неравенства, содержащие переменную под знаком модуля

Купить Задачи с параметрами. Применение свойств функций, преобразование неравенств

Связанные страницы:

MATHM
>>
ЕГЭ
>>
ЕГЭ профиль

Задача 9

ЗАДАЧА 9
сортировка
по темам

СПИСОК ТЕМ

Тема 1: График параболы
Тема 2: График гиперболы и корня
Тема 3: График модуля
Тема 4: Графики тригонометрических функций
Тема 5: График показательной функции и логарифма
Тема 6: Пересечение графиков

Задачи разделены на темы. Задачи из любой темы вполне реально встретить на настоящем экзамене ЕГЭ. Внутри каждой темы задачи
мы постарались расположить по возрастанию сложности.

Тема 1: График параболы.

посмотреть ответ

посмотреть решение

видеоурок 1 по графику параболы

yotube

видеоурок 2 по графику параболы

yotube

посмотреть ответ

посмотреть решение 1

посмотреть решение 2

видеоурок 1 по графику параболы

yotube

видеоурок 2 по графику параболы

yotube

посмотреть ответ

посмотреть решение 1

посмотреть решение 2

видеоурок 1 по графику параболы

yotube

видеоурок 2 по графику параболы

yotube

посмотреть ответ

посмотреть решение 1

посмотреть решение 2

видеоурок 1 по графику параболы

yotube

видеоурок 2 по графику параболы

yotube

посмотреть ответ

посмотреть решение 1

посмотреть решение 2

видеоурок 1 по графику параболы

yotube

видеоурок 2 по графику параболы

yotube

посмотреть ответ

посмотреть решение

видеоурок 1 по графику параболы

yotube

видеоурок 2 по графику параболы

yotube

посмотреть ответ

посмотреть решение 1

посмотреть решение 2

видеоурок 1 по графику параболы

yotube

видеоурок 2 по графику параболы

yotube

посмотреть ответ

посмотреть решение

видеоурок 1 по графику параболы

yotube

видеоурок 2 по графику параболы

yotube

посмотреть ответ

посмотреть решение 1

посмотреть решение 2

видеоурок 1 по графику параболы

yotube

видеоурок 2 по графику параболы

yotube

посмотреть ответ

посмотреть решение

видеоурок 1 по графику параболы

yotube

видеоурок 2 по графику параболы

yotube

посмотреть ответ

посмотреть решение 1

посмотреть решение 2

видеоурок 1 по графику параболы

yotube

видеоурок 2 по графику параболы

yotube

посмотреть ответ

посмотреть решение 1

посмотреть решение 2

видеоурок 1 по графику параболы

yotube

видеоурок 2 по графику параболы

yotube

Тема 2: График гиперболы и корня.

посмотреть ответ

посмотреть решение

видеоурок по графику гиперболы

yotube

посмотреть ответ

посмотреть решение

видеоурок по графику гиперболы

yotube

посмотреть ответ

посмотреть решение

видеоурок по графику гиперболы

yotube

посмотреть ответ

посмотреть решение

видеоурок по графику гиперболы

yotube

посмотреть ответ

посмотреть решение

видеоурок по графику корня

yotube

посмотреть ответ

посмотреть решение

видеоурок по графику корня

yotube

посмотреть ответ

посмотреть решение

видеоурок по графику корня

yotube

посмотреть ответ

посмотреть решение

видеоурок по графику корня

yotube

посмотреть ответ

посмотреть решение

видеоурок по графику корня

yotube

посмотреть ответ

посмотреть решение

видеоурок по графику корня

yotube

Тема 3: График модуля.

посмотреть ответ

посмотреть решение

видеоурок по графику модуля

yotube

посмотреть ответ

посмотреть решение

видеоурок по графику модуля

yotube

посмотреть ответ

посмотреть решение

видеоурок по графику модуля

yotube

посмотреть ответ

посмотреть решение

видеоурок по графику модуля

yotube

Тема 4: Графики тригонометрических функций.

посмотреть ответ

посмотреть решение

видеоурок 1 по графикам тригонометрических функций

yotube

видеоурок 2 по графикам тригонометрических функций

yotube

посмотреть ответ

посмотреть решение

видеоурок 1 по графикам тригонометрических функций

yotube

видеоурок 2 по графикам тригонометрических функций

yotube

посмотреть ответ

посмотреть решение

видеоурок 1 по графикам тригонометрических функций

yotube

видеоурок 2 по графикам тригонометрических функций

yotube

посмотреть ответ

посмотреть решение

видеоурок 1 по графикам тригонометрических функций

yotube

видеоурок 2 по графикам тригонометрических функций

yotube

посмотреть ответ

посмотреть решение

видеоурок 1 по графикам тригонометрических функций

yotube

видеоурок 2 по графикам тригонометрических функций

yotube

посмотреть ответ

посмотреть решение

видеоурок 1 по графикам тригонометрических функций

yotube

видеоурок 2 по графикам тригонометрических функций

yotube

Тема 5: График показательной функции и логарифма.

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

Тема 6: Пересечение графиков.

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

посмотреть ответ

посмотреть решение

Решение заданий варианта досрочного периода ЕГЭ 2022 от 28 марта 2022 по математике (профильный уровень). Досрочник КИМ. Досрочная волна 2022. Полный разбор. ГДЗ профиль решебник для 11 класса. Ответы с решением.

Все материалы получены из открытых источников и публикуются после окончания экзамена в ознакомительных целях.

Задание 1.
Найдите корень уравнения log₂(7 – x) = 5.

Задание 2.
В чемпионате по гимнастике участвуют 4 спортсменки из Аргентины, 7 из Бразилии, 5 из Германии и 4 из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Бразилии.

ИЛИ

В чемпионате по гимнастике участвуют 70 спортсменок: 25 из США, 17 из Мексики, остальные из Канады. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Канады.

Задание 3.
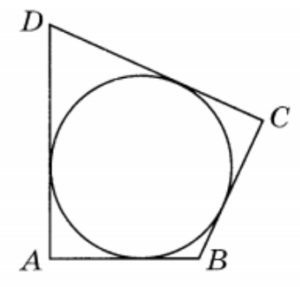
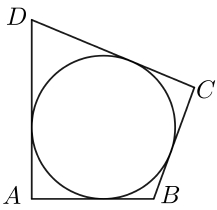
В четырёхугольник ABCD вписана окружность, AB = 8, BC = 5 и CD = 27. Найдите четвёртую сторону четырёхугольника.

ИЛИ

В четырехугольник ABCD, периметр которого равен 56, вписана окружность. Найдите AB, если CD = 13.

Задание 4.
Найдите значение выражения 4^{frac{1}{5}}cdot 16^{frac{9}{10}}

ИЛИ

Найдите значение выражения frac{5^{3,7}cdot 6^{4,7}}{30^{2,7}}

Задание 5.
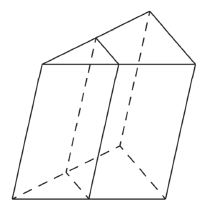
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.

ИЛИ

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 37. Найдите площадь боковой поверхности исходной призмы.

Задание 6.
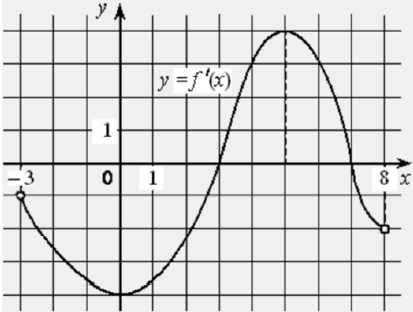
На рисунке изображён график функции y = f ′(x) − производной функции f(x), определённой на интервале (−3; 8). Найдите точку максимума функции f(x).

ИЛИ

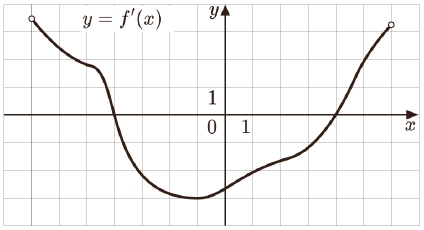
На рисунке изображён график y = f ′(x) – производной функции f(x), определённой на интервале (−7; 6). Найдите точку минимума функции f(x).

Задание 7.
При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу со скоростями u и v (в м/с) соответственно, частота звукового сигнала f (в Гц), регистрируемого приёмником, вычисляется по формуле: , где f₀ = 170 Гц – частота исходного сигнала, c – скорость распространения сигнала в среде (в м/с), а u = 2 м/с и v = 17 м/с – скорости приёмника и источника относительно среды. При какой скорости c (в м/с) распространения сигнала в среде частота сигнала в приёмнике f будет равна 180 Гц? Ответ дайте в м/с.

ИЛИ

В розетку электросети подключены приборы, общее сопротивление которых составляет R₁ = 90 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление R₂ этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R₁ Ом и R₂ Ом их общее сопротивление дается формулой R_общ = (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в Омах.

Задание 8.
Имеется два сплава. Первый содержит 50% никеля, второй – 15% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

ИЛИ

Имеется два сплава. Первый сплав содержит 5 % меди, второй – 14 % меди. Масса второго сплава больше массы первого на 5 кг. Из этих двух сплавов получили третий сплав, содержащий 12 % меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Задание 9.
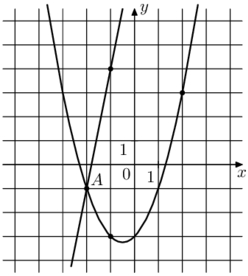
На рисунке изображён график функции f(x) = 5x + 9 и g(x) = ax² + bx + c, которые пересекаются в точках А и В. Найдите абсциссу точки В.

ИЛИ

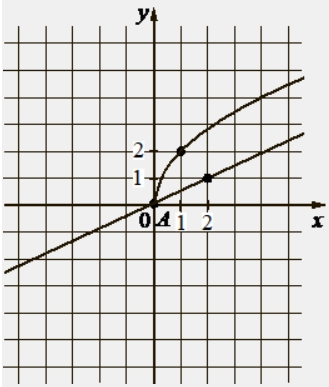
На рисунке изображены графики функций видов f(x) = a√x и g(x) = kx, пересекающиеся в точках A и B. Найдите абсциссу точки B.

Задание 10.
Помещение освещается тремя лампами. Вероятность перегорания каждой лампы в течение года равна 0,3. Лампы перегорают независимо друг от друга. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

ИЛИ

Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.

Задание 11.
Найдите точку минимума функции y = x√x – 5x + 4.

Задание 12.
а) Решите уравнение 4^{sin x} + 4^{sin(x + π)} = frac{5}{2}.
б) Найдите все корни этого уравнения, принадлежащие отрезку [frac{5pi}{2};4pi].

Задание 13.
Вне плоскости правильного треугольника ABC взята точка D так, что cos∠DAB = cos∠DAC = 0, 2.
а) Докажите, что прямые AD и BC перпендикулярны.
б) Найдите расстояние между прямыми AD и BC, если известно, что AB = 2.

Задание 14.
Решите неравенство frac{log_{2}^{}(32x)-1}{log_{2}^{2}x-log_{2}^{}x^{5}}ge -1

Задание 15.
15-го декабря планируется взять кредит размером 600 тыс. рублей в банке на 26 месяцев. Условия возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца с 1-го по 25-й долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца;
– к 15-му числу 26-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 25-го месяца, если общая сумма выплат после полного погашения кредита составит 691 тысяч рублей?

Задание 16.
В треугольник ABC вписана окружность, которая касается AB в точке P. Точка М середина стороны AB.
а) Докажите, что MP=frac{|BC-AC|}{2}.
б) Найдите углы треугольника ABC, если известно, что отрезок MP равен половине радиуса окружности вписанной в треугольник ABC, BC > AC, отрезки MC и MA равны.

Задание 17.
Найдите всe значения параметра a, при каждом их которых система

begin{cases} frac{xy^{2}-2xy-4y+8}{sqrt{4-y}}=0, y=ax. end{cases}

имеет ровно 3 различных решения.

Задание 18.
Каждое из четырех последовательных натуральных чисел поделили на его первую цифру и сложили все полученные числа, а полученную сумму обозначили за S.
а) Может ли S = 41frac{11}{24}?
б) Может ли S = 569frac{29}{72}?
в) Какое наибольшее целое значение может принимать S, если известно, что 4 исходных числа не меньше 400 и не больше 999?

Источники заданий варианта: школа Пифагора, Профиматика, беседы vk.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.7 / 5. Количество оценок: 12

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.

Лучшие репетиторы для сдачи ЕГЭ

Открытый банк заданий по теме графики. Задания B2 из ЕГЭ по математике (профильный уровень)

Ответ

2000

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1037

Тип задания: 2
Тема:
Графики

Условие

Мощность отопителя в автомобиле регулируется дополнительным сопротивлением, которое можно менять, поворачивая рукоятку в салоне машины. При уменьшении сопротивления, увеличивается сила тока в электрической цепи электродвигателя, что приводит к ускорению вращения мотора отопителя. На графике показана зависимость силы тока от сопротивления в цепи. На оси абсцисс отложено сопротивление (в омах), а на оси ординат — сила тока в амперах. Рукоятку отопителя повернули таким образом, что ток в цепи снизился с 8 до 4 ампер. По графику определите, на сколько омов при этом увеличилось сопротивление?

Показать решение

Решение

Используя рисунок, определим на оси ординат промежуток от 8 до 4 ампер (ток в цепи электродвигателя уменьшается), ему соответствует промежуток на оси абсцисс от 1 до 2,5 Ом, то есть сопротивление в цепи увеличилось на 1,5 Ома.

Ответ

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Лучшие репетиторы для сдачи ЕГЭ

Источник

💡 Если Вы — учитель математики, то Вы можете создавать готовые карточки для учеников с индивидуальными заданиями и с ответами для отработки заданий на графики функций. Данные задачи доступны в Конструкторе бесплатно.

3. На рисунке изображён график функции y=3x^2+bx+c . Найдите f(6) . [Ответ: 10]	Смотреть видеоразбор похожего >>
4. На рисунке изображён график функции y=ax^2+12x+c . Найдите f(7) . [Ответ: -74]	Смотреть видеоразбор похожего >>
5. На рисунке изображён график функции y=ax^2+bx+12 . Найдите f(-7) . [Ответ: 19]	Смотреть видеоразбор похожего >>
6. На рисунке изображён график функции y=ax^2+bx+c . Найдите f(1) . [Ответ: 49]	Смотреть видеоразбор похожего >>
7. На рисунке изображён график функции y=ax^2+bx+c , где числа a , b и c — целые. Найдите f(-5) . [Ответ: -29]	Смотреть видеоразбор похожего >>
8. На рисунке изображён график функции f(x)=frac{k}{x}+a . Найдите f(0.1) . [Ответ: -17]	Смотреть видеоразбор похожего >>
9. На рисунке изображён график функции f(x)=frac{k}{x}+a . Найдите, при каком значении x значение функции равно -4.4 . [Ответ: -12.5]	Смотреть видеоразбор похожего >>
10. На рисунке изображён график функции f(x)=frac{k}{x+a} . Найдите f(-3.5) . [Ответ: 6]	Смотреть видеоразбор похожего >>
11. На рисунке изображён график функции f(x)=frac{k}{x+a} . Найдите значение x , при котором f(x) = 10 . [Ответ: 0.6]	Смотреть видеоразбор похожего >>
12. На рисунке изображён график функции f(x)=frac{kx+a}{x+b} . Найдите k . [Ответ: 1]	Смотреть видеоразбор похожего >>
13. На рисунке изображён график функции f(x)=frac{kx+a}{x+b} . Найдите a . [Ответ: 2]	Смотреть видеоразбор похожего >>
14. На рисунке изображён график функции f(x)=b+log_ax . Найдите f(frac{1}{9}) . [Ответ: 3]	Смотреть видеоразбор похожего >>
15. На рисунке изображён график функции f(x)=b+log_ax . Найдите значение x , при котором f(x)=-11 . [Ответ: 64]	Смотреть видеоразбор похожего >>
16. На рисунке изображён график функции f(x)=log_a(x+b) . Найдите f(26) . [Ответ: -2]	Смотреть видеоразбор похожего >>
17. На рисунке изображён график функции f(x)=log_a(x+b) . Найдите значение x , при котором f(x)=4 . [Ответ: 82]	Смотреть видеоразбор похожего >>
18. На рисунке изображён график функции f(x) = a^x+b . Найдите f(-2) . [Ответ: 22]	Смотреть видеоразбор похожего >>
19. На рисунке изображён график функции f(x) = a^x+b . Найдите значение x , при котором f(x) = 77 . [Ответ: -4]	Смотреть видеоразбор похожего >>
20. На рисунке изображён график функции f(x) = a^{x+b} . Найдите f(4) . [Ответ: 9]	Смотреть видеоразбор похожего >>
21. На рисунке изображён график функции f(x) = a^{x+b} . Найдите значение x , при котором f(x) = 64 . [Ответ: 8]	Смотреть видеоразбор похожего >>
22. На рисунке изображён график функции f(x) = ksqrt{x} . Найдите f(8.41) . [Ответ: 8.7]	Смотреть видеоразбор похожего >>
23. На рисунке изображён график функции f(x) = ksqrt{x} . Найдите значение x , при котором f(x)=-6.75 . [Ответ: 7.29]	Смотреть видеоразбор похожего >>
24. На рисунке изображены графики функций f(x)=-4x+22 и g(x)=ax^2+bx+c , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: 9]	Смотреть видеоразбор похожего >>
25. На рисунке изображены графики функций f(x)=-6x-28 и g(x)=ax^2+bx+c , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: 38]	Смотреть видеоразбор похожего >>
26. На рисунке изображены графики функций f(x)=frac{k}{x} и g(x)=ax+b , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: 0.2]	Смотреть видеоразбор похожего >>
27. На рисунке изображены графики функций f(x)=frac{k}{x} и g(x)=ax+b , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: 20]	Смотреть видеоразбор похожего >>
28. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков. [Ответ: -2.08]	Смотреть видеоразбор похожего >>
29. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков. [Ответ: -2.4]	Смотреть видеоразбор похожего >>
30. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков. [Ответ: -11.3]	Смотреть видеоразбор похожего >>
31. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков. [Ответ: 6.8]	Смотреть видеоразбор похожего >>
32. На рисунке изображены графики функций f(x) = 2x^2+16x+30 и g(x) = ax^2+bx+c , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: -9]	Смотреть видеоразбор похожего >>
33. На рисунке изображены графики функций f(x) = -2x^2-3x+1 и g(x) = ax^2+bx+c , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: -13]	Смотреть видеоразбор похожего >>
34. На рисунке изображены графики функций f(x)=asqrt{x} и g(x)=kx+b , которые пересекаются в точке A. Найдите абсциссу точки A. [Ответ: 3.24]	Смотреть видеоразбор похожего >>
35. На рисунке изображены графики функций f(x)=asqrt{x} и g(x)=kx+b , которые пересекаются в точке A. Найдите ординату точки A. [Ответ: 9]	Смотреть видеоразбор похожего >>
36. На рисунке изображён график функции f(x) = asin{x}+b . Найдите a . [Ответ: 2]	Смотреть видеоразбор похожего >>
37. На рисунке изображён график функции f(x) = asin{x}+b . Найдите b . [Ответ: 1,5]	Смотреть видеоразбор похожего >>
38. На рисунке изображён график функции f(x) = acos{x}+b . Найдите a . [Ответ: 1,5]	Смотреть видеоразбор похожего >>
39. На рисунке изображён график функции f(x) = acos{x}+b . Найдите b . [Ответ: −1]	Смотреть видеоразбор похожего >>
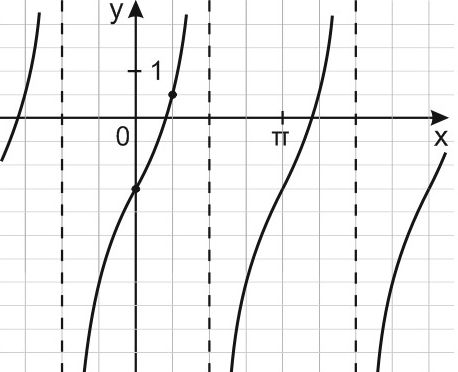
40. На рисунке изображён график функции f(x) = a;tg{x}+b . Найдите a . [Ответ: 2]	Смотреть видеоразбор похожего >>
41. На рисунке изображён график функции f(x) = a;tg{x}+b . Найдите b . [Ответ: −1,5]	Смотреть видеоразбор похожего >>

Источник