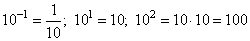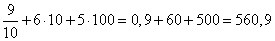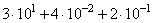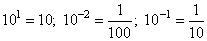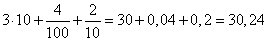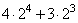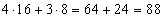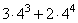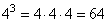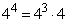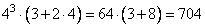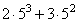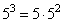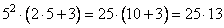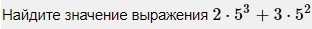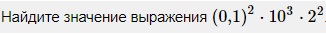Операции со степенями
[su_box title=”Описание задания” style=”soft” box_color=”#c1e8cc” title_color=”#0c0a0a”]
Во задании №2 ЕГЭ по математике необходимо продемонстрировать знания работы со степенными выражениями.
Тематика заданий: операции со степенями
Бал: 1 из 20
Сложность задания: ♦◊◊
Примерное время выполнения: 3 мин.
[/su_box]
Теория к заданию №2
Правила обращения со степенями можно представить следующим образом:
Кроме этого, следует напомнить об операциях с дробями:
Теперь можно перейти к разбору типовых вариантов! 🙂
Разбор типовых вариантов заданий №2 ЕГЭ по математике базового уровня
Во всех заданиях, аналогично первому заданию, нам необходимо найти значение выражения.
Вариант 2МБ1
Алгоритм выполнения:
- Представить число с отрицательным показателем в виде правильной дроби.
- Выполнить первое умножение.
- Представить степени чисел в виде простых чисел, заменив степени их умножением.
- Выполнить умножение.
- Выполнить сложение.
Решение:
Чтобы представить отрицательную степень числа в виде обыкновенной дроби, необходимо 1 разделить на это число, но уже в положительной степени.
То есть: 10-1 = 1/101 = 1/10
Выполним первое умножение, то есть умножение целого числа на правильную дробь. Для этого числитель дроби умножим на целое число, а знаменатель оставим без изменения.
9 · 1/10 = (9 · 1)/10 = 9/10
Первая степень числа всегда есть само число.
101 = 10
Вторая степень числа – это число умноженное само на себя.
102 = 10 · 10 = 100
Вычислим значение выражения, учитывая, что
получим:
Ответ: 560,9
Вариант 2МБ2
Алгоритм выполнения:
- Представить первую степень числа в виде целого числа.
- Представить отрицательные степени чисел в виде правильных дробей.
- Выполнить умножение целых чисел.
- Выполнить умножение целых чисел на правильные дроби.
- Выполнить сложение.
Решение:
Первая степень числа всегда есть само число. (101 = 10)
Чтобы представить отрицательную степень числа в виде обыкновенной дроби, необходимо 1 разделить на это число, но уже в положительной степени.
То есть:
10-1 = 1/101 = 1/10
10-2 = 1/102 = 1/(10 · 10) = 1/100
Выполним умножение целых чисел.
3 · 101 = 3 · 10 = 30
Выполним умножение целых чисел на правильные дроби.
4 · 10-2 = 4 · 1/100 = (4 ·1)/100 = 4/100
2 · 10-1 = 2 · 1/10 = (2 · 1)/10 = 2/10
Вычислим значение выражения, учитывая, что
получим:
Ответ: 30,24
Вариант 2МБ3
Алгоритм выполнения:
- Представить степени чисел в виде умножения и вычислить значение степеней чисел.
- Выполнить умножение.
- Выполнить сложение.
Решение:
Представим степени чисел в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
24 = 2 · 2 · 2 · 2 = 16
23 = 2 · 2 · 2 = 8
Выполним умножение:
4 · 24 = 4 · 16 = 64
3 · 23 = 3 · 8 = 24
Вычислим значение выражения:
Ответ: 88
Вариант 2МБ4
Алгоритм выполнения:
- Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
- Вынести общий множитель за скобку.
- Выполнить действие в скобках.
- Представить степень числа в виде умножения и вычислить значение степени числа.
- Выполнить умножение.
Решение:
Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
44 = 4 · 43
Вынесем общий множитель за скобку
3 · 43 + 2 · 44 = 43 · (3 + 2 · 4)
Выполним действие в скобках.
(3 + 2 · 4) = (3 + 
Представим степень числа в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
43 = 4 · 4 · 4 = 64
Вычислим значение выражения, учитывая, что
получим:
Ответ: 704
Вариант 2МБ5
Алгоритм выполнения:
- Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
- Вынести общий множитель за скобку.
- Выполнить действие в скобках.
- Представить степень числа в виде умножения и вычислить значение степени числа.
- Выполнить умножение.
Решение:
Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
53 = 5 · 52
Вынесем общий множитель за скобку
2 · 53 + 3 · 52 = 52 · (2 · 5 + 3)
Выполним действие в скобках.
(2 · 5 + 3) = (10 + 3) = 13
Представим степень числа в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
52 = 5 · 5 = 25
Вычислим значение выражения, учитывая, что
, а
получим:
Выполняем умножение в столбик, имеем:
Ответ: 325
Вариант 2МБ6
Решение:
В данном задании удобней привести значения к более привычному виду, а именно записать числа в числителе и знаменателе в стандартном виде:
После этого можно выполнить деление 24 на 6, в результате получим 4.
Десять в четвертой степени при делении на десять в третьей степени даст десять в первой, или просто десять, поэтому мы получим:
4 • 10 = 40
Ответ: 40
Вариант 2МБ6
Решение:
В данном случае мы должны заметить, что число 6 в знаменателе раскладывается на множители 2 и 3 в степени 5:
После этого можно выполнить сокращения степеней у двойки: 6-5=1, у тройки: 8-5=3.
Теперь возводим 3 в куб и умножаем на 2, получая 54.
Ответ: 54
Вариант 2МБ6
Алгоритм выполнения
- Применяем к числителю св-во степеней (ах)у=аху. Получаем 3–6.
- Применяем к дроби св-во степеней ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
(3–3)2 /3–8 = 3–6 /3–8= 3–6–(–8)) = 3–6+8 = 32 = 9
Ответ: 9
Вариант 2МБ7
Алгоритм выполнения
- Используем для степени в числителе (149) св-во (аb)х=ax·bx. 14 разложим на произведение 2 и 7. Получим произведение степеней с основаниями 2 и 7.
- Преобразуем выражение в 2 дроби, каждая из которых будет содержать степени с одинаковыми основаниями.
- Применяем к дробям св-во степеней ax/ay=ax–y.
- Находим полученное произведение.
Решение:
149 / 27·78 = (2·7)9 / 27·78 = 29·79 / 27 78 = 29–7·79–8 = 22·71 = 4·7 = 28
Ответ: 28
Вариант 2МБ8
Алгоритм выполнения
- Выносим за скобки общий множитель 52=25.
- Выполняем в скобках умножение чисел 2 и 5. Получаем 10.
- Выполняем в скобках сложение 10 и 3. Получаем 13.
- Выполняем умножение общего множителя 25 и 13.
Решение:
2·53+3·52 = 52·(2·5+3) = 25·(10+3) = 25·13 = 325
Ответ: 325
Вариант 2МБ9
Алгоритм выполнения
- Возводим в квадрат (–1). Получим 1, поскольку происходит возведение в четную степень.
- Возводим (–1) в 5-ю степень. Получим –1, т.к. происходит возведение в нечетную степень.
- Выполняем действия умножения.
- Получаем разность двух чисел. Находим ее.
Решение:
6·(–1)2+4·(–1)5 = 6·1+4·(–1) = 6+(–4) = 6–4 = 2
Ответ: 2
Вариант 2МБ10
Алгоритм выполнения
- Преобразуем множители 103 и 102 в целые числа.
- Находим произведения путем переноса десят.запятой вправо на соответствующее число знаков.
- Находим результирующую сумму.
Решение:
9,4·103+2,2·102 = 9,4·1000+2,2·100 = 9400+220 = 9620
Ответ: 9620
Вариант 2МБ11
Алгоритм выполнения
- Преобразуем 102 в целое число и выполняем умножение в числителе путем переноса деся.запятой.
- Преобразуем 10–2 в десят.дробь и выполняем умножение в знаменателе путем переноса десят.запятой влево.
- Домножаем числитель и знаменатель на 100, чтобы избавиться от десят.запятой в знаменателе.
- Находим результат путем деления числителя дроби на ее знаменатель.
Решение:
1,6·102 / 4·10–2 = 1,6·100 / 4·0,01 = 160/ 0,04 = 160·100 / 0,04·100 = 16000 / 4 = 4000
Ответ: 40000
Вариант 2МБ12
Алгоритм выполнения
- Применяем к дроби св-ва степеней ax·ay=ax+y и ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
3–10·35 / 3–7 = 3–10+5 /3–7 = 3–5 / 3–7 = 3–5–(–7)) = 3–5+7 = 32 = 9
Ответ: 9
Вариант 2МБ13
Алгоритм выполнения
- Представляем выражение в знаменателе как степень с основанием 8. Далее применяем св-во степеней (ах)у=аху, получаем 812.
- Применяем к дроби св-во степеней ax/ay=ax–y.
Решение:
813 /646 =813 / (82)6 =813 /812 = 813–12 = 81 = 8
Ответ: 8
Вариант 2МБ14
Алгоритм выполнения
- Преобразуем степени в числителе дроби и в делителе (число 92) так, чтобы получились степени с основанием 3.
- Используем св-во степеней (ах)у=аху для преобразованных степеней.
- Используем св-во степеней ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
274 /36 : 92 =(33)4 / 36 : (32)2 = 312/36 : 34 = 312–6–4 = 32 = 9
Ответ: 9
Вариант 2МБ15
Алгоритм выполнения
- Возводим каждый из множителей в соответствующую степень. Получим соответственно: 0,01, 1000, 4.
- Перемножаем 0,01 и 1000 путем переноса десят.запятой вправо на 3 знака. Получим 10.
- Умножаем 10 на 4.
Решение:
(0,1)2·103·22 = 0,01·1000·4 = 10·4 = 40
Ответ: 40
Даниил Романович | Просмотров: 18.6k
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика базового уровня
Математика базового уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Действия со степенями
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 16 № 26738
Найдите значение выражения
Аналоги к заданию № 26738: 71883 26753 61695 61697 61699 61701 61703 61705 61707 61709 … Все
Раздел кодификатора ФИПИ: Действия со степенями
Решение
·
·
Сообщить об ошибке · Помощь
2
Тип 16 № 62113
Найдите значение выражения
Аналоги к заданию № 62113: 26919 62061 62063 62065 62067 62069 62071 62073 62075 62077 … Все
Раздел кодификатора ФИПИ: Действия со степенями
Решение
·
·
Сообщить об ошибке · Помощь
3
Тип 16 № 62429
Найдите значение выражения
Аналоги к заданию № 62429: 62433 26925 62387 62389 62391 62393 62395 62397 62399 62401 … Все
Раздел кодификатора ФИПИ: Действия со степенями
Решение
·
·
Сообщить об ошибке · Помощь
4
Тип 16 № 508383
Найдите значение выражения
Аналоги к заданию № 508383: 506365 509587 515693 515713 520550 520570 520590 520610 Все
Источник: Пробный экзамен Санкт-Петербург 2014. Вариант 1.
Раздел кодификатора ФИПИ: Действия со степенями
Решение
·
·
Сообщить об ошибке · Помощь
5
Тип 16 № 508403
Найдите значение выражения
Аналоги к заданию № 508403: 509727 512579 512599 512620 512640 512710 512730 512750 512770 514401 … Все
Источник: Пробный экзамен Санкт-Петербург 2014. Вариант 2.
Раздел кодификатора ФИПИ: Действия со степенями
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Найдите значения выражений
| 1 | 2cdot8^2+3cdot8^2 | Смотреть видеоразбор >> |
| 2 | frac{1,6cdot10^2}{4cdot10^{-2}} | Смотреть видеоразбор >> |
| 3 | frac{6^{-3}cdot6^7}{6^2} | Смотреть видеоразбор >> |
| 4 | frac{(4^{-4})^2}{4^{-10}} | Смотреть видеоразбор >> |
| 5 | frac{4^3}{2^5} | Смотреть видеоразбор >> |
| 6 | frac{2^4cdot6^6}{12^5} | Смотреть видеоразбор >> |
| 7 | 6cdot(-1)^2+4cdot(-1)^5 | Смотреть видеоразбор >> |
| 8 | (5cdot10^5 )cdot(1,7cdot10^{-3}) | Смотреть видеоразбор >> |
| 9 | frac{3^{-10}cdot3^5}{3^{-7}} | Смотреть видеоразбор >> |
| 10 | frac{3^{-13}}{(3^5)^{-3}} | Смотреть видеоразбор >> |
| 11 | frac{3^{10}}{27^3} | Смотреть видеоразбор >> |
| 12 | frac{4^{12}cdot2^7}{8^{10}} | Смотреть видеоразбор >> |
| 13 | 9cdot10^3+5cdot10^2+3cdot10^1 | Смотреть видеоразбор >> |
| 14 | (5,7cdot10^3):(1,9cdot10^{-2}) | Смотреть видеоразбор >> |
| 15 | frac{2^{-8}cdot2^8}{2^{-3}} | Смотреть видеоразбор >> |
| 16 | frac{5^{-2}cdot5^7}{5^3} | Смотреть видеоразбор >> |
| 17 | frac{9^{10}cdot3^2}{27^7} | Смотреть видеоразбор >> |
| 18 | 9,4cdot10^3+2,2cdot10^2 | Смотреть видеоразбор >> |
| 19 | (0,1)^2cdot10^3cdot2^2 | Смотреть видеоразбор >> |
| 20 | frac{2^5}{2^3cdot2^{-1}} | Смотреть видеоразбор >> |
| 21 | frac{4^{-2}cdot4^3}{4^{-1}} | Смотреть видеоразбор >> |
| 22 | frac{8^3}{2^4}:2^2 | Смотреть видеоразбор >> |
| 23 | 38cdot10-1,3cdot10^2 | Смотреть видеоразбор >> |
| 24 | frac{(0,1)^2}{10^{-3}}cdot10^2 | Смотреть видеоразбор >> |
| 25 | frac{2^7}{2^5cdot2} | Смотреть видеоразбор >> |
| 26 | frac{2^6cdot2^{-2}}{2^2} | Смотреть видеоразбор >> |
| 27 | frac{3^5cdot4^6}{12^5} | Смотреть видеоразбор >> |
Во задании №2 ЕГЭ по математике необходимо продемонстрировать знания работы со степенными выражениями.
Тематика заданий: операции со степенями
Бал: 1 из 20
Сложность задания: ♦◊◊
Примерное время выполнения: 3 мин.
Теория к заданию №2
Правила обращения со степенями можно представить следующим образом:
Кроме этого, следует напомнить об операциях с дробями:
Теперь можно перейти к разбору типовых вариантов!
Разбор типовых вариантов заданий №2 ЕГЭ по математике базового уровня
Во всех заданиях, аналогично первому заданию, нам необходимо найти значение выражения.
Вариант 2МБ1
 Алгоритм выполнения:
Алгоритм выполнения:
- Представить число с отрицательным показателем в виде правильной дроби.
- Выполнить первое умножение.
- Представить степени чисел в виде простых чисел, заменив степени их умножением.
- Выполнить умножение.
- Выполнить сложение.
Решение:
Чтобы представить отрицательную степень числа в виде обыкновенной дроби, необходимо 1 разделить на это число, но уже в положительной степени.
То есть: 10-1 = 1/101 = 1/10
Выполним первое умножение, то есть умножение целого числа на правильную дробь. Для этого числитель дроби умножим на целое число, а знаменатель оставим без изменения.
9 · 1/10 = (9 · 1)/10 = 9/10
Первая степень числа всегда есть само число.
101 = 10
Вторая степень числа – это число умноженное само на себя.
102 = 10 · 10 = 100
Вычислим значение выражения, учитывая, что
получим:
Ответ: 560,9
Вариант 2МБ2
Алгоритм выполнения:
- Представить первую степень числа в виде целого числа.
- Представить отрицательные степени чисел в виде правильных дробей.
- Выполнить умножение целых чисел.
- Выполнить умножение целых чисел на правильные дроби.
- Выполнить сложение.
Решение:
Первая степень числа всегда есть само число. (101 = 10)
Чтобы представить отрицательную степень числа в виде обыкновенной дроби, необходимо 1 разделить на это число, но уже в положительной степени.
То есть:
10-1 = 1/101 = 1/10
10-2 = 1/102 = 1/(10 · 10) = 1/100
Выполним умножение целых чисел.
3 · 101 = 3 · 10 = 30
Выполним умножение целых чисел на правильные дроби.
4 · 10-2 = 4 · 1/100 = (4 ·1)/100 = 4/100
2 · 10-1 = 2 · 1/10 = (2 · 1)/10 = 2/10
Вычислим значение выражения, учитывая, что
получим:
Ответ: 30,24
Вариант 2МБ3
Алгоритм выполнения:
- Представить степени чисел в виде умножения и вычислить значение степеней чисел.
- Выполнить умножение.
- Выполнить сложение.
Решение:
Представим степени чисел в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
24 = 2 · 2 · 2 · 2 = 16
23 = 2 · 2 · 2 = 8
Выполним умножение:
4 · 24 = 4 · 16 = 64
3 · 23 = 3 · 8 = 24
Вычислим значение выражения:
Ответ: 88
Вариант 2МБ4
Алгоритм выполнения:
- Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
- Вынести общий множитель за скобку.
- Выполнить действие в скобках.
- Представить степень числа в виде умножения и вычислить значение степени числа.
- Выполнить умножение.
Решение:
Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
44 = 4 · 43
Вынесем общий множитель за скобку
3 · 43 + 2 · 44 = 43 · (3 + 2 · 4)
Выполним действие в скобках.
(3 + 2 · 4) = (3 + 
Представим степень числа в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
43 = 4 · 4 · 4 = 64
Вычислим значение выражения, учитывая, что
получим:
Ответ: 704
Вариант 2МБ5
Алгоритм выполнения:
- Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
- Вынести общий множитель за скобку.
- Выполнить действие в скобках.
- Представить степень числа в виде умножения и вычислить значение степени числа.
- Выполнить умножение.
Решение:
Представим степень числа таким образом, чтобы можно было вынести за скобку общий множитель.
53 = 5 · 52
Вынесем общий множитель за скобку
2 · 53 + 3 · 52 = 52 · (2 · 5 + 3)
Выполним действие в скобках.
(2 · 5 + 3) = (10 + 3) = 13
Представим степень числа в виде умножения. Для того чтобы представить степень числа в виде умножения, нужно это число умножить само на себя столько раз сколько содержится в показателе степени.
52 = 5 · 5 = 25
Вычислим значение выражения, учитывая, что
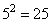
получим:
Выполняем умножение в столбик, имеем:
Ответ: 325
Вариант 2МБ6
Решение:
В данном задании удобней привести значения к более привычному виду, а именно записать числа в числителе и знаменателе в стандартном виде:
После этого можно выполнить деление 24 на 6, в результате получим 4.
Десять в четвертой степени при делении на десять в третьей степени даст десять в первой, или просто десять, поэтому мы получим:
4 • 10 = 40
Ответ: 40
Вариант 2МБ6
Решение:
В данном случае мы должны заметить, что число 6 в знаменателе раскладывается на множители 2 и 3 в степени 5:
После этого можно выполнить сокращения степеней у двойки: 6-5=1, у тройки: 8-5=3.
Теперь возводим 3 в куб и умножаем на 2, получая 54.
Ответ: 54
Вариант 2МБ6
Алгоритм выполнения
- Применяем к числителю св-во степеней (ах)у=аху. Получаем 3–6.
- Применяем к дроби св-во степеней ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
(3–3)2 /3–8 = 3–6 /3–8= 3–6–(–8)) = 3–6+8 = 32 = 9
Ответ: 9
Вариант 2МБ7
Алгоритм выполнения
- Используем для степени в числителе (149) св-во (аb)х=ax·bx. 14 разложим на произведение 2 и 7. Получим произведение степеней с основаниями 2 и 7.
- Преобразуем выражение в 2 дроби, каждая из которых будет содержать степени с одинаковыми основаниями.
- Применяем к дробям св-во степеней ax/ay=ax–y.
- Находим полученное произведение.
Решение:
149 / 27·78 = (2·7)9 / 27·78 = 29·79 / 27 78 = 29–7·79–8 = 22·71 = 4·7 = 28
Ответ: 28
Вариант 2МБ8
Алгоритм выполнения
- Выносим за скобки общий множитель 52=25.
- Выполняем в скобках умножение чисел 2 и 5. Получаем 10.
- Выполняем в скобках сложение 10 и 3. Получаем 13.
- Выполняем умножение общего множителя 25 и 13.
Решение:
2·53+3·52 = 52·(2·5+3) = 25·(10+3) = 25·13 = 325
Ответ: 325
Вариант 2МБ9
Алгоритм выполнения
- Возводим в квадрат (–1). Получим 1, поскольку происходит возведение в четную степень.
- Возводим (–1) в 5-ю степень. Получим –1, т.к. происходит возведение в нечетную степень.
- Выполняем действия умножения.
- Получаем разность двух чисел. Находим ее.
Решение:
6·(–1)2+4·(–1)5 = 6·1+4·(–1) = 6+(–4) = 6–4 = 2
Ответ: 2
Вариант 2МБ10
Алгоритм выполнения
- Преобразуем множители 103 и 102 в целые числа.
- Находим произведения путем переноса десят.запятой вправо на соответствующее число знаков.
- Находим результирующую сумму.
Решение:
9,4·103+2,2·102 = 9,4·1000+2,2·100 = 9400+220 = 9620
Ответ: 9620
Вариант 2МБ11
Алгоритм выполнения
- Преобразуем 102 в целое число и выполняем умножение в числителе путем переноса деся.запятой.
- Преобразуем 10–2 в десят.дробь и выполняем умножение в знаменателе путем переноса десят.запятой влево.
- Домножаем числитель и знаменатель на 100, чтобы избавиться от десят.запятой в знаменателе.
- Находим результат путем деления числителя дроби на ее знаменатель.
Решение:
1,6·102 / 4·10–2 = 1,6·100 / 4·0,01 = 160/ 0,04 = 160·100 / 0,04·100 = 16000 / 4 = 4000
Ответ: 40000
Вариант 2МБ12
Алгоритм выполнения
- Применяем к дроби св-ва степеней ax·ay=ax+y и ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
3–10·35 / 3–7 = 3–10+5 /3–7 = 3–5 / 3–7 = 3–5–(–7)) = 3–5+7 = 32 = 9
Ответ: 9
Вариант 2МБ13
Алгоритм выполнения
- Представляем выражение в знаменателе как степень с основанием 8. Далее применяем св-во степеней (ах)у=аху, получаем 812.
- Применяем к дроби св-во степеней ax/ay=ax–y.
Решение:
813 /646 =813 / (82)6 =813 /812 = 813–12 = 81 = 8
Ответ: 8
Вариант 2МБ14
Алгоритм выполнения
- Преобразуем степени в числителе дроби и в делителе (число 92) так, чтобы получились степени с основанием 3.
- Используем св-во степеней (ах)у=аху для преобразованных степеней.
- Используем св-во степеней ax/ay=ax–y.
- Возводим 3 в полученную степень.
Решение:
274 /36 : 92 =(33)4 / 36 : (32)2 = 312/36 : 34 = 312–6–4 = 32 = 9
Ответ: 9
Вариант 2МБ15
Алгоритм выполнения
- Возводим каждый из множителей в соответствующую степень. Получим соответственно: 0,01, 1000, 4.
- Перемножаем 0,01 и 1000 путем переноса десят.запятой вправо на 3 знака. Получим 10.
- Умножаем 10 на 4.
Решение:
(0,1)2·103·22 = 0,01·1000·4 = 10·4 = 40
Ответ: 40
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Выражения со степенями»
Открытый банк заданий по теме выражения со степенями. Задания B9 из ЕГЭ по математике (профильный уровень)
Геометрические фигуры в пространстве: нахождение длины, площади, объема
Задание №921
Тип задания: 9
Тема:
Выражения со степенями
Условие
Найдите значение выражения 19a^{10}a^{14}:(5a^{12})^2.
Показать решение
Решение
Выполним преобразования:
19a^{10}a^{14}:(5a^{12})^2= 19a^{10+14}:(5^2a^{12cdot2})= frac{19a^{24}}{25a^{24}}= 0,76.
Ответ
0,76
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №919
Тип задания: 9
Тема:
Выражения со степенями
Условие
Найдите значение выражения 3^{0,74}cdot9^{0,13}.
Показать решение
Решение
Выполним преобразования:
3^{0,74}cdot(3^2)^{0,13}= 3^{0,74}cdot3^{0,26}= 3^{0,74+0,26}= 3^1= 3
Ответ
3
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №157
Тип задания: 9
Тема:
Выражения со степенями
Условие
Найдите значение выражения frac{g(x+5)}{g(x+3)}, если g(x)=3^x.
Показать решение
Решение
Чтобы решить эту задачу, необходимо представить числитель и знаменатель дроби в явном виде. Для этого возведем 3 в степень равную аргументу функции. Получим:
frac{g(x+5)}{g(x+3)}=frac{3^{x+5}}{3^{x+3}}= 3^{x+5-x-3}=3^2=9
Ответ
9
Задание №156
Тип задания: 9
Тема:
Выражения со степенями
Условие
Найдите значение выражения xcdot2^{-6x+3}cdot8^{2x} при x = 5.
Показать решение
Решение
Выполним преобразования:
xcdot2^{-6x+3}cdot8^{2x}= xcdot2^{-6x+3}cdotleft (2^3 right )^{2x}= xcdot2^{-6x+3}cdot2^{6x}= xcdot2^{-6x+3+6x}= xcdot2^3=8x
Подставим значение x = 5 из условия:
8x = 8cdot5=40
Ответ
40
Задание №132
Тип задания: 9
Тема:
Выражения со степенями
Условие
Найдите значение выражения 0,6^{tfrac{3}{11}}cdot5^{tfrac{10}{11}}cdot45^{tfrac{4}{11}}.
Показать решение
Решение
Выполним преобразования:
0,6^{tfrac{3}{11}}cdot5^{tfrac{10}{11}}cdot45^{tfrac{4}{11}}= left (frac35 right )^{tfrac{3}{11}}cdot5^{tfrac{10}{11}}cdot(5cdot9)^{tfrac{4}{11}}= 3^{tfrac{3}{11}}cdot5^{-tfrac{3}{11}}cdot5^{tfrac{10}{11}}cdot5^{tfrac{4}{11}}cdotleft (3^2 right )^{tfrac{4}{11}}= 3^{tfrac{3}{11}+tfrac{8}{11}}cdot5^{-tfrac{3}{11}+tfrac{10}{11}+tfrac{4}{11}}= 3cdot5=15.
Ответ
15
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928



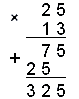
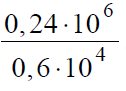
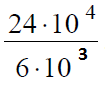
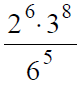
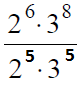
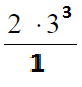








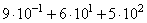 Алгоритм выполнения:
Алгоритм выполнения: