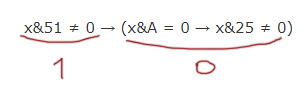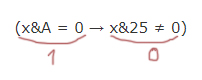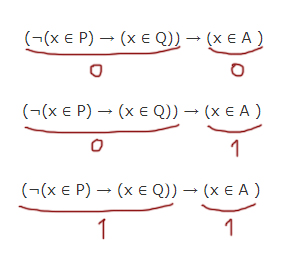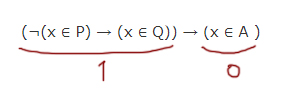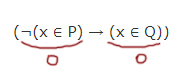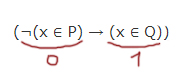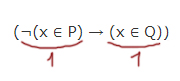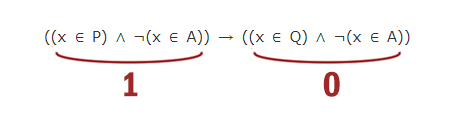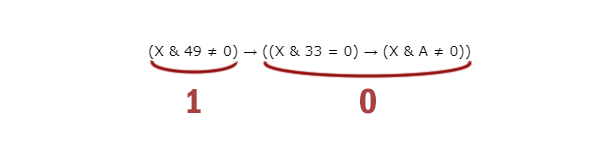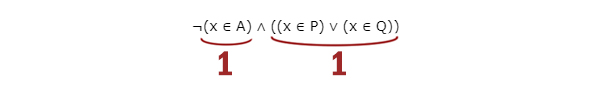На уроке рассматривается разбор 15 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи
Содержание:
- Объяснение задания 15 ЕГЭ по информатике
- Элементы математической логики
- Математическая логика и теория множеств
- Задания с отрезками и ДЕЛ
- Задания с поразрядной конъюнкцией
- Решение заданий 15 ЕГЭ по информатике
- Задания с множествами
- Задания с отрезками на числовой прямой
- Задания с ДЕЛ
- Задания с поразрядной конъюнкцией
- Задания на поиск наибольшего или наименьшего числа А
15-е задание: «Основные законы алгебры логики»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 5 минут.
Проверяемые элементы содержания: Знание основных понятий и законов математической логики
До ЕГЭ 2021 года — это было задание № 18 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Важно понимать, что выражение должно быть тождественно истинно, т.е. истинно при любых допустимых значениях переменных x и у, а не только при некоторых наборах значений»
ФГБНУ «Федеральный институт педагогических измерений»
Элементы математической логики
-
Для решения 15 задания, потребуется знание таблиц истинности.
- операцию импликация можно преобразовать в операции ИЛИ и НЕ:
- операцию эквивалентность можно преобразовать:
- операцию XOR (сложение по модулю 2) можно преобразовать так:
- кроме того, могут пригодиться базовые аксиомы и формулы:
- Порядок выполнения логических операций:
- выражения в скобках,
- операции «НЕ»,
- операции «И»,
- операции «ИЛИ»,
- операции «импликация»
- операции «эквиваленция»
- последовательность из операций импликации выполняется слева направо (при этом соблюдается принцип «операции с одинаковым приоритетом выполняются слева направо»):
Для выполнения задания рекомендуется повторить следующие темы:
Преобразование логических операций:
A → B = ¬ A ∨ B
или
A → B = A + B
A ↔ B = A ⊕ B = A ∧ B ∨ A ∧ B
или
A ↔ B = A ⊕ B = A · B + A · B
A ⊕ B = (¬A ∧ B) ∨ (A ∧ ¬B)
или
A ⊕ B = (A · B) + (A · B)
Законы алгебры логики:
| Закон двойного отрицания: |
¬¬ A = A |
| Закон исключения третьего: |
A ∧ ¬ A = 0 или A · A = 0 |
| Закон повторения (идемпотентности): |
A ∧ A = A или A · A = A |
| Законы исключения логических констант: |
A ∧ 0 = 0 |
| Переместительный (коммутативный) закон: |
A ∧ B = B ∧ A |
| Сочетательный (ассоциативный) закон: |
(A ∧ B) ∧ C = A ∧ (B ∧ C) |
| Распределительный (дистрибутивный) закон: |
(A ∧ B) ∨ C = (A ∨ C) ∧ (B ∨ C) |
| Закон общей инверсии (Законы де Моргана): |
¬ (A ∧ B) = ¬ A ∨ ¬ B |
| Закон исключения (склеивания): |
(A ∧ B) ∨(¬A ∧ B) = B |
| Упрощать выражения можно с помощью формул: | |
| Закон поглощения: |
A ∨ A ∧ B = A |
A → B → C → D = ((A → B) → C) → D
Математическая логика и теория множеств
- пересечение множеств соответствует логическому умножению, а объединение – логическому сложению;
- пересечением двух множеств называется новое множество, состоящее из элементов, принадлежащих одновременно обеим множествам:
- объединением двух множеств называется новое множество, состоящее из элементов, принадлежащих отдельно каждому из множеств (без повторений);
- пустое множество
∅– это множество, в котором не содержится ни одного элемента; пустому множеству в теории множеств соответствует0; - универсальное множество
U(на кругах Эйлера обозначается в виде прямоугольника) – это множество, содержащее все возможные элементы определенного типа (например, все вещественные числа): - универсальное множество соответствует логической единице: для любого множества целых чисел
Xсправедливы равенства: - разностью двух множеств
AиBназывается новое множество, элементы которого принадлежатA, но не принадлежатB: - дополнение множества
X– это разность между универсальным множествомUи множествомX(например, для целых чисел¬ X– все целые числа, не входящие вX) - пусть требуется выбрать множество
Aтак, чтобы выполнялось равенствоA ∨ X = I; в этом случае множествоAдолжно включать дополнение¬ X, то естьA ≥¬ X(или A ⊇¬ X), то естьAmin = ¬ X - пусть требуется выбрать множество
Aтак, чтобы выполнялось равенство¬ A ∨ X = I, в этом случае множество¬ Aдолжно включать дополнение¬ X, то есть¬ A ⊇ ¬ X; отсюдаA ⊆ X, то естьAmax = X
Пример:
Пример:
X ∨ U = U и X ∧ U = X
Пример разности множеств:
Для большей определенности стоит рассмотреть тему круги Эйлера
Задания с отрезками и ДЕЛ
Для решения заданий необходимо знать рассмотренную тему о множествах.
Для упрощения решений можно пользоваться следующими законами.
1. Если в задании формула тождественно истинна (равна 1), и
2. после упрощения A без отрицания
то используется закон:
Amin = ¬B
где B — известная часть выражения.
1. Если в задании формула тождественно истинна (равна 1), и
2. после упрощения A с отрицанием
то используется закон:
Amax = B
где B — известная часть выражения.
1. Если в задании формула тождественно ложна (равна 0), и
2. после упрощения A без отрицания
то используется закон:
Amax = ¬B
где B — известная часть выражения.
1. Если в задании формула тождественно ложна (равна 0), и
2. после упрощения A с отрицанием
то используется закон:
Amin = B
где B — известная часть выражения.
Задания с поразрядной конъюнкцией
В задании 15 ЕГЭ встречаются задачи, связанные с поразрядной конъюнкцией.
Например:
5 & 26
означает поразрядную конъюнкцию (логическое «И») между двоичными значениями двух чисел — 5 и 26. Выполняется так:
5 = 1012 26 = 110102 0 = 000002
Задания, связанные с поразрядной конъюнкцией, решаются несколькими способами. Рассмотрим один из них.
- Обозначим:
(x & K = 0) как Zk
Zk * Zm = Zk or m
(X & 5 = 0) ∧ (X & 26 = 0)
Z5 ∧ Z26
Z5 ∧ Z26 = Z26 or 5 помним, что дизъюнкция - это операция логическое "ИЛИ" (сложение) 5 = 1012 26 = 110102 31 = 111112
Z5 ∧ Z26 = Z31
Zk + Zm = Zk and m
(X & 28 = 0) ∨ (X & 22 = 0)
Z28 ∨ Z22
Z28 ∨ Z22 = Z28 and 22
помним, что конъюнкция - это операция логическое "И" (умножение)
28 = 111002
22 = 101102
101002 = 2010
Z28 ∨ Z22 = Z20
Условие Zk → Zm истинно для любых натуральных значений x тогда и только тогда, когда все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.
- На деле, это означает, что если имеем:
X & 29 = 0 → X & 5 = 0 Истинно или Ложно?
Z29 → Z5
Z29 → Z5 = 1 (истине), тогда, когда: 29 = 111012 5 = 1012 единичные биты двоичного числа 5 входят в единичные биты двоичного числа 29 (совпадают с ними)
Z29 → Z5 = 1 (истинно)
(x & 125 = 5) то же самое, что и
Z120 * ¬Z4 * ¬Z1 = 1 (истине)
- Так, например, если в задании имеем:
X & 130 = 3
X & 130 = 3 то же самое, что и Z127 * ¬Z2 * ¬Z1 т.е. 3 = 2 + 1 : 2 = 10 1 = 01 3 = 11
Решение заданий 15 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Задания с множествами
Множества:
15_16:
Элементами множества А являются натуральные числа. Известно, что выражение
((x ∈ {1, 3, 5, 7, 9, 11}) → ¬(x ∈ {3, 6, 9, 12})) ∨ (x ∈ A)
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наименьшее возможное значение суммы элементов множества A.
✍ Решение:
- Введем обозначения:
P ≡ (x ∈ {1, 3, 5, 7, 9, 11}) ;
Q ≡ (x ∈ {3, 6, 9, 12}) ;
A ≡ (x ∈ A).
(P → ¬Q) ∨ A = 1 Избавимся от импликации: ¬P ∨ ¬Q ∨ A = 1
А) была непременно истинной, необходимо, чтобы известная часть была ложна:¬P ∨ ¬Q ∨ А = 1 0 1
¬P ∨ ¬Q = 0, или ¬P = 0 отсюда P = 1 ¬Q = 0 отсюда Q = 1
Q и P. То есть необходимо выбрать элементы, которые встречаются в обоих множествах одновременно:A = {3,9}
3 + 9 = 12
Ответ: 12
Аналитическое решение:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Множества:
15_17:
Элементами множества А являются натуральные числа. Известно, что выражение
(x ∈ {2, 4, 6, 8, 10, 12}) → (((x ∈ {3, 6, 9, 12, 15}) ∧ ¬(x ∈ A)) →
→ ¬(x ∈ {2, 4, 6, 8, 10, 12}))
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наименьшее возможное значение суммы элементов множества A.
Типовые задания для тренировки
✍ Решение:
- Введем обозначения:
P≡(x ∈ {2, 4, 6, 8, 10, 12}) ;
Q ≡ (x ∈ {3, 6, 9, 12, 15}) ;
A ≡ (x ∈ A).
P → ((Q ∧ ¬A) → ¬P) = P → (¬(Q ∧ ¬А) ∨ ¬P) = ¬P ∨ (¬(Q ∧ ¬А) ∨ ¬P) = ¬P ∨ ¬Q ∨ А.
А) была непременно истинной, необходимо, чтобы известная часть была ложна:¬P ∨ ¬Q ∨ А = 1 0 1
¬P ∨ ¬Q = 0, или ¬P = 0 отсюда P = 1 ¬Q = 0 отсюда Q = 1
Q и P. То есть необходимо выбрать элементы, которые встречаются в обоих множествах одновременно:A = {6,12}
6 + 12 = 18
Ответ: 18
Множества:
15_18: Закон распределения
Элементами множеств А, P, Q являются натуральные числа, причём P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}. Известно, что выражение
( (x ∈ A) → (x ∈ P) ) ∧ ( (x ∈ Q) → ¬(x ∈ A) )
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наибольшее возможное количество элементов в множестве A.
Типовые задания для тренировки
✍ Решение:
- Введем обозначения:
P ≡ (x ∈ P); Q ≡ (x ∈ Q); A ≡ (x ∈ A).
Избавимся от импликации: (¬A ∨ P) ∧ (¬Q ∨ ¬A) = 1 Применим распределительный закон (но можно вывести самостоятельно): ¬A ∨ (P ∧ ¬Q) = 1
А) была непременно истинной, необходимо, чтобы известная часть была ложна:¬A ∨ (P ∧ ¬Q) = 1 0 1
P ∧ ¬Q = 1, или P = 1 и ¬Q = 1 отсюда Q = 0
Q и P. То есть это новое множество, элементы которого принадлежат P, но не принадлежат Q:A = {2, 4, 8, 10, 14, 16, 20}
Ответ: 7
Множества:
15_20:
Элементами множества А являются натуральные числа. Известно, что выражение
¬(x ∈ A) →¬(x ∈ {1, 3, 7}) ∨ (¬(x ∈ {1, 2, 4, 5, 6}) ∧ (x ∈ {1, 3, 7}))
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наименьшее возможное количество элементов множества A.
✍ Решение:
- Введем обозначения:
P ≡ (x ∈ {1, 3, 7});
Q ≡ (x ∈ {1, 2, 4, 5, 6});
A ≡ (x ∈ A).
Избавимся от импликации: A ∨ ¬P ∨ (¬Q ∧ P) = 1 Применим закон поглощения (но можно вывести самостоятельно): A ∨ ¬P ∨ ¬Q = 1
А) была непременно истинной, необходимо, чтобы известная часть была ложна:A ∨ ¬P ∨ ¬Q = 1 1 0
¬P ∨ ¬Q = 0, или P = 1 и Q = 1
Q и P:A = {1}
Ответ: 1
Задания с отрезками на числовой прямой
Отрезки на числовой прямой:
15_3:
На числовой прямой даны два отрезка: P=[44,48] и Q=[23,35].
Укажите наибольшую возможную длину отрезка А, для которого формула
((x ϵ P) → (x ϵ Q)) ∧ (x ϵ A)
тождественно ложна, то есть принимает значение 0 при любом значении переменной x.
✍ Решение:
- Упростим формулу, избавившись от ‘x ϵ‘:
(P → Q) ∧ A
правило импликации: a → b = ¬a ∨ b
(¬P ∨ Q) ∧ A
(¬P ∨ Q) ∧ A = 0
(¬P ∨ Q) ∧ A 0 ∧ 0 = 0 0 ∧ 1 = 0 1 ∧ 0 = 0 1 ∧ 1 = 1
1. (¬P ∨ Q) = 1 ∨ 0 = 1 - на данном отрезке А должно равняться 0
2. (¬P ∨ Q) = 1 ∨ 1 = 1 - на данном отрезке А должно равняться 0
3. (¬P ∨ Q) = 1 ∨ 0 = 1 - на данном отрезке А должно равняться 0
4. (¬P ∨ Q) = 0 ∨ 0 = 0 - на данном отрезке А может! равняться 1
5. (¬P ∨ Q) = 1 ∨ 0 = 1 - на данном отрезке А должно равняться 0
48 - 44 = 4
Результат: 4
✎ Решение 2 (программирование):
Внимание! этот способ подходит НЕ для всех заданий с отрезками!
Python:
1 2 3 4 5 6 7 8 9 |
def f(a1,a2,x): return((44<=x<=48)<=(23<=x<=35))and(a1<=x<=a2) maxim = 0 for a1 in range (1,200): for a2 in range (a1+1,200): if all(f(a1,a2,x)==0 for x in range (1,200)):# если все ложны if a2-a1>maxim: maxim=a2-a1 print(a1,a2, a2-a1) # сами точки отрезка и длина |
Вывод:
44 45 1
44 46 2
44 47 3
44 48 4
PascalABC.net:
Вывод:
С подробным аналитическим решением задания 15 ЕГЭ по информатике можно ознакомиться по видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Отрезки на числовой прямой:
15_9:
На числовой прямой даны два отрезка: P = [10,20] и Q = [30,40].
Укажите наибольшую возможную длину отрезка A, для которого формула
((x ∈ P) → (x ∈ Q)) → ¬(x ∈ A)
тождественно истинна, то есть принимает значение 1 при любом значении переменной x.
Типовые задания для тренировки
✍ Решение:
- Упростим выражение, введя обозначения:
A: x ∈ A P: x ∈ P Q: x ∈ Q
(P → Q) → ¬A = 1
(P → Q) → ¬A = 1 => ¬(P → Q) ∨ ¬A = 1 => ¬(¬P ∨ Q) ∨ ¬A = 1
¬(¬P ∨ Q) ∨ ¬A = 1 =>
P ∧ ¬Q ∨ ¬A = 1
А = 1 P = 1 ¬Q = 1 или Q = 0
Результат: 10
Отрезки на числовой прямой:
15_10:
На числовой прямой даны два отрезка: P = [3, 20] и Q = [6, 12].
Укажите наибольшую возможную длину отрезка A, для которого формула
((x ∈ P) ~ (x ∈ Q)) → ¬(x ∈ A)
тождественно истинна, то есть принимает значение 1 при любом значении переменной x.
✍ Решение:
- Упростим выражение, введя обозначения:
A: x ∈ A P: x ∈ P Q: x ∈ Q
(P ~ Q) → ¬A = 1
(P ~ Q) → ¬A = 1 => ¬(P ~ Q) ∨ ¬A = 1
Далее возможно 2 способа решения.
✎ 1 способ:
(a ~ b) = a * b + ¬a * ¬b
¬(P ~ Q) = ¬((P ∧ Q) ∨ (¬P ∧ ¬Q)) = = ¬(P ∧ Q) ∧ ¬(¬P ∧ ¬Q)
¬(P ∧ Q) ∧ ¬(¬P ∧ ¬Q) = = ¬(P ∧ Q) ∧ (P ∨ Q)
¬(P ∧ Q) ∧ (P ∨ Q) ∨ ¬A = 1
¬(P ∧ Q) ∧ (P ∨ Q) = 1 А = 1
✎ 2 способ:
После того, как мы избавились от импликации, имеем:
¬(P ~ Q) ∨ ¬A = 1
Результат: 8
С решением задания 15 вы также можете ознакомиться, посмотрев видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Отрезки на числовой прямой:
15_11:
На числовой прямой даны два отрезка: P = [11, 21] и Q = [15, 40].
Укажите наибольшую возможную длину отрезка A, для которого формула
(x ∈ A) → ¬((x ∈ P) ~ (x ∈ Q))
тождественно истинна, то есть принимает значение 1 при любом значении переменной x.
Типовые задания для тренировки
✍ Решение:
- Упростим выражение, введя обозначения:
A: x ∈ A P: x ∈ P Q: x ∈ Q
A → ¬(P ~ Q) = 1
A → ¬(P ~ Q) = 1 =>
¬A ∨ ¬(P ~ Q) = 1
Результат: 19
Задания с ДЕЛ
Поиск наибольшего А, известная часть Дел ∨ Дел = 1
15_7:
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наибольшего натурального числа А формула
(ДЕЛ(x, 40) ∨ ДЕЛ(x, 64)) → ДЕЛ(x, A)
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Типовые задания для тренировки
✍ Решение:
- Введем обозначения:
A = ДЕЛ(x,A); D40 = ДЕЛ(x, 40); D64 = ДЕЛ(x, 64)
(D40 ∨ D64) → A = 1
¬(D40 ∨ D64) ∨ A = 1 или (¬D40 ∧ ¬D64) ∨ A = 1
(¬D40 ∧ ¬D64) ∨ A = 1 1 2
Т.е. (¬D40 ∧ ¬D64) должно быть = 0. Это нам ничего не дает, т.к. конъюнкция ложна в трех случаях (1*0, 0*1 и 0*0), т.е. D40 и D64 могут быть равны как 0, так и 1 (исключение составляет лишь вариант, когда оба D истинны, тогда логическое умножение 1 * 1 ≠ 0).
¬D40 ∧ ¬D64 = 0 или ¬(¬D40 ∧ ¬D64) = 1 Преобразуем по закону Де Моргана и получим: D40 ∨ D64 = 1
Далее можно решать задание либо с помощью кругов Эйлера, либо с помощью логических рассуждений.
Решение с помощью логических рассуждений:
x, которые делятся на А и при этом делятся на 40 ИЛИ делятся на 64:x/A :x/40 ∨x/64
x = 40, 64, 80, 120, 128, 160, 192, 200, ...
A, начиная с самого наименьшего (единицы), на которые делятся все x без исключения:А = 1, 2, 4, 8
А равно 8.НОД (40,64) = 8
40,64 (64 - 40 = 24)
40,24 (40 - 24 = 16)
24,16 (24 - 16 = 8)
16,8 (16 - 8 = 8)
8,8
Решение с помощью кругов Эйлера:
64 / 40 = 1 (24 остаток) 40 / 24 = 1 (16 остаток) 24 / 16 = 1 (8 остаток) 16 / 8 = 2 (0 остаток) - НОД = 8 +++ 40 / 8 = 5 64 / 8 = 8
Результат: 8
✎ Решение 2 (программирование):
Python:
1 2 3 4 5 6 |
for A in range(1,500): OK = 1 for x in range(1,1000): OK *= ((x % 40 == 0) or (x % 64 == 0))<=(x % A== 0) if OK: print( A ) |
Вывод:
1
2
4
8
PascalABC.net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
begin for var A := 1 to 500 do begin var ok := 1; for var x := 1 to 1000 do begin if (((x mod 40 = 0) or (x mod 64 = 0)) <= (x mod A = 0)) = false then begin ok := 0; break; end; end; if (ok = 1) then print(A) end; end. |
Вывод:
1
2
4
8
Результат: 8
Поиск наименьшего А, известная часть Дел ∧ ¬Дел = 1
15_5:
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наименьшего натурального числа А формула
ДЕЛ(x, A) → (¬ДЕЛ(x, 28) ∨ ДЕЛ(x, 42))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Типовые задания для тренировки
✍ Решение:
Имеем:
ДЕЛ(x, A) → (¬ДЕЛ(x, 28) ∨ ДЕЛ(x, 42)) = 1
A = ДЕЛ(x,A); D28 = ДЕЛ(x, 28); D42 = ДЕЛ(x, 42)
A → (¬D28 ∨ D42) = 1
Избавимся от импликации:
¬A ∨ (¬D28 ∨ D42) = 1
¬A ∨ (¬D28 ∨ D42) = 1 1 2
(¬D28 ∨ D42) = 0 один случай: когда ¬D28 = 0 и D42 = 0
x/¬A :x/28 ∧x/¬42
x, которые НЕ делятся на А и при этом делятся на 28 И НЕ делятся на 42:x = 28, 56,84, 112, 140,168, 196, 224, ...
A, начиная с самого наименьшего (единицы), на которые НЕ делятся все x без исключения:А = 1, 2, 3
А равно 3.✎ Решение 2 (программирование). Язык Python, Pascal:
-
Из общего выражения:
ДЕЛ(x, A) → (¬ДЕЛ(x, 28) ∨ ДЕЛ(x, 42)) = 1
А, необходимо рассмотреть диапазон натуральных значений x. Если выражение будет истинным для диапазона всех рассматриваемых х, то такое А необходимо вывести на экран.А (ограничим их числом 50, т.к. необходимо найти наименьшее А), будем запускать внутренний цикл, перебирающий значения х (х ограничим числом 1000, будем рассматривать данный диапазон, как «любое натуральное значение переменной х»).Python:
for A in range(1,50): OK = 1 for x in range(1,1000): OK *= (x % A == 0) <= ((x % 28 != 0) or (x % 42== 0)) if OK: print( A ) break
PascalABC.net:
begin for var A := 1 to 50 do begin var ok := 1; for var x := 1 to 1000 do begin if (x mod A = 0) <= ((x mod 28 <> 0)or (x mod 42 = 0)) = false then begin ok := 0; break; end; end; if (ok = 1) then begin print(A); break; end end; end.
OK — переменная-индикатор: если находится такое А при котором, диапазон всех значений x, подставленных в выражение, возвращает истинное значение выражения, то ОК остается равным 1, т.к. используется операция умножения (до цикла ОК необходимо присвоить единице).
Следует иметь в виду, что в программировании вместо операции импликация (->) можно использовать нестрогое неравенство: <=. Т.к. таблица истинности для операции импликация соответствует операции <=:
a b F(a<=b) 0 0 1 0 1 1 1 0 0 1 1 1
А, т.к. используется оператор break для выхода из цикла после первого найденного значения:3
Результат: 3
15_6:
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наименьшего натурального числа А формула
(¬ДЕЛ(x, 19) ∨ ¬ДЕЛ(x, 15)) → ¬ДЕЛ(x, A)
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
✍ Решение:
- Введем обозначения:
A = ДЕЛ(x,A); D19 = ДЕЛ(x, 19); D15 = ДЕЛ(x, 15)
(¬D19 ∨ ¬D15) → ¬A = 1
D19 ∧ D15 ∨ ¬A = 1
¬A ∨ D19 ∧ D15 = 1 1 2
¬A ∨ D19 ∧ D15 = 1 0 ∨ 1 = 1
¬A = 0 при D19 ∧ D15 = 1 или A = 1 при D19 = 1 и D15 = 1
A = 1 D19 = 1 D15 = 1
19 * 2 = 38 (38 не делится на 15) 19 * 3 = 57 (57 не делится на 15) 19 * 4 = 76 (76 не делится на 15) 19 * 5 = 95 (95 не делится на 15) ... 19 * 10 = 190 (190 не делится на 15) 19 * 15 = 285 (285 делится на 15)
✎ Решение 2 (программирование). Язык Python:
-
Из общего выражения:
(¬ДЕЛ(x, 19) ∨ ¬ДЕЛ(x, 15)) → ¬ДЕЛ(x, A) = 1
А, необходимо рассмотреть диапазон натуральных значений x. Если выражение будет истинным для диапазона всех рассматриваемых х, то такое А необходимо вывести на экран.А (ограничим их числом 500, т.к. необходимо найти наименьшее А), будем запускать внутренний цикл, перебирающий значения х (х ограничим числом 1000, будем рассматривать данный диапазон, как «любое натуральное значение переменной х»).for A in range(1,500): OK = 1 for x in range(1,1000): OK *= ((x % 19 != 0) or (x % 15 != 0))<= (x % A!= 0) if OK: print( A )
OK — переменная-индикатор: если находится такое А при котором, диапазон всех значений x, подставленных в выражение, возвращает истинное значение выражения, то ОК остается равным 1, т.к. используется операция умножения (до цикла ОК необходимо присвоить единице).
Следует иметь в виду, что в программировании вместо операции импликация (->) можно использовать нестрогое неравенство: <=. Т.к. таблица истинности для операции импликация соответствует операции <=:
a b F(a<=b) 0 0 1 0 1 1 1 0 0 1 1 1
А:285
Результат: 285
Задания с поразрядной конъюнкцией
Поразрядная конъюнкция:
15_1:
Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 12&6 = 11002&01102 = 01002 = 4
Для какого наименьшего неотрицательного целого числа A формула
(X & A = 0) ∧ ¬(X & 35 ≠ 0 → X & 52 ≠ 0)
тождественно ложна (то есть принимает значение 0 при любом неотрицательном значении переменной X)?
✍ Решение:
Стоит заметить, что для такого типа задач, нет универсального единственного решения. Поэтому на видео, расположенном ниже, представлено два варианта решения.
✎ Способ 1:
Рассмотрим один из вариантов решения:
- Удалим из формулы X&, чтобы сократить ее запись:
(A = 0) ∧ ¬(35 ≠ 0 → 52 ≠ 0)
(A = 0) ∧ ¬(35 ≠ 0 → 52 ≠ 0)
(A = 0) ∧ ¬(35 ≠ 0 → 52 ≠ 0) 1 2
правило импликации: a → b = ¬a ∨ b
(A = 0) ∧ ¬(35 = 0 ∨ 52 ≠ 0)
т.к. в результате получается отрицание того, что 35 ≠ 0,
то убираем знак "не равно": было 35 ≠ 0, стало 35 = 0
закон де Моргана: ¬ (A ∨ B) = ¬ A ∧ ¬ B
A = 0 ∧ 35 ≠ 0 ∧ 52 = 0 = 0
0 ∧ 0 = 0 0 ∧ 1 = 0 1 ∧ 0 = 0 1 ∧ 1 = 1
(A = 0) ∧ 35 ≠ 0 ∧ 52 = 0 = 0 0 ∧ 1 = 0
35 ≠ 0 ∧ 52 = 0 = истинно (=1) если: 35 ≠ 0 = истинно (=1) и 52 = 0 = истинно (=1) так как стоит логическое умножение ∧ - смотрим выше таблицу истинности для конъюнкции
35 ≠ 0 = 1 (истина) и 52 = 0 = 1 (истина) и A = 0 = 0 (ложь)
35: 100011 (≠ 0) 52: 110100 (= 0)
| 52 | 1 | 1 | 0 | 1 | 0 | 0 |
|---|---|---|---|---|---|---|
| X | 0 | 0 | ? | 0 | ? | ? |
| 35 | 1 | 0 | 0 | 0 | 1 | 1 |
|---|---|---|---|---|---|---|
| X | 1 | ? | ? | ? | 1 | 1 |
0 0 ? 0 ? ? &
1 ? ? ? 1 1
0 0 ? 0 1 1
| X | 0 | 0 | ? | 0 | 1 | 1 |
|---|---|---|---|---|---|---|
| A | 0 | 0 | 0 | 0 | 1 | 1 |
0000112 = 310
Ответ: 3
✎ Способ 2*:
-
Используем метод А.В. Здвижковой.
- Выполним последовательно следующие пункты:
- Произвести замену (x & K = 0) на Zk
- Выполнить преобразования по свойству импликации и закону Де Моргана.
- Стремиться прийти к выражению с конъюнкциями без отрицаний типа: Zk * Zm.
- Все выражения типа Zk * Zm преобразовать по свойству
Zk * Zm = Zk or m. - Путем преобразований прийти к импликации: Zk → Zm.
- Согласно первому пункту производим замену:
A ∧ ¬(¬Z35 → ¬Z52) = 0
¬(A ∧ ¬(¬Z35 → ¬Z52)) = 1
¬A ∨ (¬Z35 → ¬Z52) = 1
¬A ∨ (Z35 ∨ ¬Z52) = 1
¬A ∨ ¬Z52 ∨ Z35 = 1
¬(A ∧ Z52) ∨ Z35 = 1
(A ∧ Z52) → Z35 = 1
ZA ∨ 52 → Z35 = 1
Условие Zk → Zm истинно для любых натуральных значений x тогда и только тогда, когда все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.
A = ??0?11 52 = 110100 A or 52 = 110111 35 = 100011
Аmin = 112 = 310
Результат: 3
Детальный разбор данного задания 15 ЕГЭ по информатике предлагаем посмотреть на видео:
Вариант решения №1 (универсальный, теоретический):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Вариант решения №2 (не универсальный, но простой):
📹 YouTube здесь
Поразрядная конъюнкция:
15_2:
Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 12&6 = 11002&01102 = 01002 = 4
Для какого наибольшего неотрицательного целого числа A формула
X & A ≠ 0 → (X & 36 = 0 → X & 6 ≠ 0)
тождественно истинна (то есть принимает значение 1 при любом неотрицательном значении переменной X)?
✍ Решение:
-
✎ Способ 1:
- Произведем замену:
z36 = (x&36 = 0), z6 = (x&6 = 0), A = (x&A = 0)
¬A → (z36 → ¬ z6)
¬A → (z36 → ¬ z6) = A + ¬z36 + ¬z6
A + ¬z36 + ¬z6 = A + ¬(z36 * z6)
A + ¬(z36 * z6) = ¬(z36 * z6) + A = (z36 * z6) → A
z36 * z6 = z36 or 6
1001002 -> 36 1102 -> 6 100100 110 1001102 -> 36 or 6 = 3810
z38 → A
A = 1001102 = 3810
✎ Способ 2:
x&A ≠ 0 → (x&36 = 0 → x&6 ≠ 0) = 1
A = (x&A = 0); P = (x&36 = 0); Q = (x&6 = 0);
¬A → (P → ¬Q) = 1
A ∨ (¬P ∨ ¬Q) = 1
¬P ∨ ¬Q нам необходимо подобрать такой вариант (равный 0 или 1), при котором единственно возможным значением A была бы единица (1). A ∨ (¬P ∨ ¬Q) = 1;
или
1 ∨ (0) = 1
¬P ∨ ¬Q = 0 Отсюда имеем: ¬P = 0 и ¬Q = 0 (дизъюнкция равна 0 в единственном случае, когда все операнды равны 0)
Q = 1 и P = 1
100100 : 36 000110 : 6 0**0** : маска P (x&36 = 0) ***00* : маска Q (x&6 = 0)
0**0** : маска P (x&36 = 0) ***00* : маска Q (x&6 = 0) 0**00* : общая маска x *00**0 : маска для A (x&A = 0) т.е. в тех битах А, где может получиться единица (звездочки в обеих масках),
мы поставили нули.
100110 = 3810
Результат: 38
Подробное решение данного задания 15 ЕГЭ по информатике предлагаем посмотреть в видео уроке:
Способ 1:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Способ 2:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Поразрядная конъюнкция:
15_8:
Определите наименьшее натуральное число А из интервала [43, 55], такое, что выражение
((x & 17 ≠ 0) → ((x & A ≠ 0) → (x & 58 ≠ 0))) → → ((x & 8 = 0) ∧ (x & A ≠ 0) ∧ (x & 58 = 0))
тождественно ложно (то есть принимает значение 0 при любом натуральном значении переменной х)?
Типовые задания для тренировки
✍ Решение:
-
Кратко изложенное решение *:
- Введем обозначения:
(¬Z17 → (¬A → ¬Z58)) → (z8 ∧ ¬A ∧ Z58) = 0
¬(((¬Z17 → (¬A → ¬Z58)) → (z8 ∧ ¬A ∧ Z58)) = 1
Z8 ∧ Z58 = Z8 or 58 :
8 = 1000 or
58 = 111010
111010 = 58
Z8 ∧ Z58 = Z58
¬(¬(Z17 ∨ A ∨ ¬Z58) ∨ (¬A ∧ Z58)) = 1
(Z17 ∨ A ∨ ¬Z58) ∧ ¬(¬A ∧ Z58)) = 1
(Z17 ∨ A ∨ ¬Z58) ∧ (A ∨ ¬Z58) = 1
A ∨ ¬Z58 = 1
¬Z58 ∨ A => Z58 → A = 1
43 = 101011 - не подходит! 58 = 111010 44 = 101100 - не подходит! 58 = 111010 45 = 101101 - не подходит! 58 = 111010 46 = 101110 - не подходит! 58 = 111010 47 = 101111 - не подходит! 58 = 111010 48 = 110000 - подходит! 58 = 111010
Результат: 48
Поразрядная конъюнкция:
15_15:
Определите набольшее натуральное число A, такое что выражение
((x & 26 = 0) ∨ (x & 13 = 0)) → ((x & 78 ≠ 0) → (x & A = 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной х)?
Типовые задания для тренировки:
✍ Решение:
- Для упрощения восприятия введем обозначения:
z26 = (x & 26 = 0) z13 = (x & 13 = 0) z78 = (x & 78 = 0) A = (x & A = 0)
(z26 ∨ z13) → (¬z78 → A) = 1
(z26 ∨ z13) → (z78 ∨ A) = 1
26 : 11010 единичные биты: 4, 3, 1 13 : 1101 единичные биты: 3, 2, 0 ∧ =------------------------ 01000 = 810
z8 → (z78 ∨ A) z78: не влияет на решение, так как операция дизъюнкция истинна тогда, когда хотя бы один операнд истинен z8 → A : ????
Наибольшее А = 1000 = 810
Результат: 8
Задания на поиск наибольшего или наименьшего числа А
Поиск наибольшего или наименьшего числа А:
15_4: 15 задание. Демоверсия ЕГЭ 2018 информатика:
Для какого наибольшего целого числа А формула
тождественно истинна, то есть принимает значение 1 при любых целых неотрицательных x и y?
✍ Решение:
✎ Способ 1 (программный):
Важно: Поскольку используется метод полного перебора, то возможна ситуация, когда транслятор будет работать слишком медленно. Но работоспособность представленного алгоритма проверена на онлайн компиляторах.
Pascalabc.net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
begin for var A := 200 downto -100 do begin var OK := 1; for var x := 0 to 100 do for var y := 0 to 100 do if ((x <= 9) <= (x * x <= A)) and ((y * y <= A) <= (y <= 9)) = false then begin OK := 0; break; end; if OK = 1 then begin print(A); break end; end; end. |
| Бейсик: |
Python:
for A in range(200,-100,-1): OK = 1 for x in range(0,100): for y in range(0,100): OK *= ((x<=9) <= (x*x<=A)) and((y*y<=A) <= (y<=9)) if OK: print(A) break |
| С++: |
✎ Способ 2 (теоретическое решение):
- Условно разделим исходное выражение на части:
- Главное действие (внешняя операция) в исходном выражении — это конъюнкция. Конъюнкция истинна, когда все операнды истинны. Т.е. в задаче обе части
1и2должны быть истинными (т.к. по условию общая формула должна быть истинной).
-
Рассмотрим часть
- если в
1.1имеем x > 9, то часть1будет истинна независимо от А. Значит, значение числа А влияет на решение только при выполнении условия: - теперь, для того чтобы в части
1, выражение было истинным, надо чтобы часть1.2была истинной: - таким образом, получаем:
1:
x<=9
(импликация 0 → 0 = 1, 0 → 1 = 1)
x*x <= A
(импликация 1 → 1 = 1)
x <= 9 x2 <= A при любых x
возьмем максимальное натуральное: x=9, тогда A>=81
Рассмотрим часть 2:
2.2 истинно (т.е. y <= 9), то часть 2 будет истинна независимо от А. Значит, значение числа А влияет на решение только при выполнении условия:y > 9
2 выражение было истинным, надо чтобы часть 2.1 была ложной:y * y > A
(импликация 0 → 0 = 1)
y > 9 y2 > A при любых y
возьмем наименьшее возможное по условию натуральное: y = 10, тогда A < 100
Результат: 99
Подробное решение 15 задания демоверсии ЕГЭ 2018 года смотрите на видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Поиск наибольшего или наименьшего числа А:
✍ Решение:
✎ Способ 1 (программный):
Важно: Поскольку используется метод полного перебора, то возможна ситуация, когда транслятор будет работать слишком медленно. Но работоспособность представленного алгоритма проверена на онлайн компиляторах.
Pascalabc.net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
begin for var A := -100 to 200 do begin var OK := 1; for var x := 1 to 100 do for var y := 1 to 100 do if ((y+3*x<A) or (x >20)or(y>40)) = false then begin OK := 0; break; end; if OK = 1 then begin print(A); break end; end; end. |
| Бейсик: |
Python:
for A in range(-100,200): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (y+3*x<A) or (x > 20) or (y > 40) if OK: print(A) break |
| С++: |
✎ Способ 2 (теоретическое решение):
- Определим основные части выражения, выделив отдельно неизвестную часть — с А, и, так сказать, известную часть, то есть остальную.
1 2 (y+3x < A) ∨ (x > 20) ∨ (y > 40)
(y+3x < A) ∨ (x > 20) ∨ (y > 40) 1 или 0? 1 = 1 Не подходит!
1. (y+3x < A) = 1 2. (x > 20) ∨ (y > 40) = 0
x <= 20 y <= 40
А > 3x + y A > 3*20 + 40 A > 100
Результат: 101
Подробное решение досрочного ЕГЭ 2018 года смотрите на видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Поиск наибольшего или наименьшего числа А:
15_0:Разбор 15 задания. Демоверсия егэ по информатике 2019:
Для какого наибольшего целого неотрицательного числа А выражение
(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y)
тождественно истинно, т.е. принимает значение 1 при любых целых неотрицательных x и y?
✍ Решение:
✎ Решение 1 (теоретическое):
- Разделим общее выражение на две части. Выделим неизвестную часть красным:
(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y)
(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y) = 1
0 1
y + 2x = 48 : при x = 0, y = 48 при y = 0, 2x = 48 => x = 24
x + 2x = 48 => 3x = 48 x = 16
✎ Решение 2 (программное):
Python:
1 2 3 4 5 6 7 8 |
for A in range(200,0,-1): OK = 1 for x in range(0,100): for y in range(0,100): OK *= (48!=y+2*x) or(A<x)or (A<y) if OK: print(A) break |
Результат: 15
Видео решения 15 задания демоверсии ЕГЭ 2019 (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Поиск наибольшего или наименьшего числа А:
15_19:
Для какого наименьшего целого числа А формула
(y + 5x <= 34) → ((y — x > 4) ∨ (y <= A))
тождественно истинна, т.е. принимает значение 1 при любых целых неотрицательных x и y?
✍ Решение:
- Общая идея такова:
необходимо упростить формулу так, чтобы последняя операция (внешняя) выполнялась со скобкой, в которой находится искомое A. После чего разделить формулу на две части, в одной из которых находится искомое. - Избавимся от импликации, это даст нам возможность опустить общие скобки во второй части формулы:
¬(y + 5x <= 34) ∨ (y - x > 4) ∨ (y <= A)
¬(y + 5x <= 34) ∨ (y - x > 4) ∨ (y <= A) = 1 1 часть 2 часть
¬(y + 5x <= 34) ∨ (y - x > 4) ∨ (y <= A) = 1 1 часть = 0 2 часть = 1
y + 5x > 34 = 0, значит: 1. y + 5x <= 34 y - x > 4 = 0, значит: 2. y - x <= 4
y <= A или A >= y
34 - 5x = 4 + x 30 = 6x x = 5 Найдем y: y = 4 + 5 = 9
y = 9:
A >= 9 => наименьшее A = 9
✎ Решение 2 (программное):
Python:
1 2 3 4 5 6 7 8 |
for A in range(-100,100): OK = 1 for x in range(0,100): for y in range(0,100): OK *= (y+5*x<=34)<=((y-x >4)or(y<=A)) if OK: print( A ) break |
PascalABC.NET:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
begin for var A := -100 to 100 do begin var OK := true; for var x := 0 to 100 do begin for var y := 0 to 100 do begin OK := (y + 5 * x <= 34) <= ((y - x > 4) or (y <= A)); if OK = false then break; end; if OK = false then break; end; if OK then begin print(A); break; end; end; end. |
Результат: 9
Поиск наибольшего или наименьшего числа А:
15_13:
Укажите наименьшее целое значение А при котором выражение
(2y + 5x < A) ∨ (2x + 4y > 100) ∨ (3x – 2y > 70)
истинно для любых целых положительных значений x и y.
Типовые задания для тренировки
✍ Решение:
-
✎ Решение (программное):
Python:
1 2 3 4 5 6 7 8 |
for A in range(-200,200): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (2*y + 5*x < A) or (2*x + 4*y > 100) or (3*x - 2*y > 70) if OK: print( A ) break |
PascalABC.NET:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
begin for var A := -200 to 200 do begin var OK := true; for var x := 1 to 100 do begin for var y := 1 to 100 do begin OK := (2*y + 5*x < A) or (2*x + 4*y > 100) or (3*x - 2*y > 70); if OK = false then break; end; if OK = false then break; end; if OK then begin print(A); break; end; end; end. |
Результат: 171
Видео разбора задания смотрите на видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Поиск наибольшего или наименьшего числа А:
15_14:
Укажите наибольшее целое значение А при котором выражение
(3y – x > A) ∨ (2x + 3y < 30) ∨ (2y – x < –31)
истинно для любых целых положительных значений x и y.
Типовые задания для тренировки
✍ Решение:
-
✎ Решение 1 (теоретическое):
- Разделим выражение на две части: часть с неизвестным = 1, часть известная = 0:
(3y – x > A) ∨ (2x + 3y < 30) ∨ (2y – x < –31) = 1
(1) (2x + 3y) >= 30, y >= (30 - 2x) / 3 x = (30 - 3y) /2
(2) (2y – x >=–31) y >= (x - 31) / 2 x = 2y + 31
(1) x | y 0 | 10 15| 0
(2) x | y 0 | -15 ( целые) 30|0
A<3y-x:A < 3y – x, то будем перемещать А снизу вверх. Наибольшее значение А будет достигнуто в указанной точке пересечения с прямой (2).если y = 1, то x = 2*1 + 31 = 33
А < 3y - x A < 3-33, A < -30, A=-31
✎ Решение (программное):
Python:
1 2 3 4 5 6 7 8 |
for A in range(200,-200,-1): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (3*y-x>A) or (2*x+3*y<30) or (2*y-x<-31) if OK: print(A) break |
Результат: -31
* В некоторых задачах использован метод, предложенный А.В. Здвижковой
Сегодняшний урок посвящён 15 заданию из ЕГЭ по информатике 2022.
Темой этого урока связана с преобразованием логических выражений.
Теорию для преобразования логических выражений Вы можете посмотреть в этой статье. Как можно работать с логическими выражениями на питоне, можно прочитать в этой статье.
Перейдём к практике решения задач 15 задания из ЕГЭ по информатике 2022.
Задача (Неравенство, одна переменная)
Какое количество натуральных чисел удовлетворяет логическому условию:
¬(X2 ≥ 9) ∨ ¬((X < 7) ∨ (X ≥ 10)) ?
Решение:
Первый способ (с помощью питона).
k=0 for x in range(1, 1000): if not(x**2 >= 9) or not((x < 7) or (x>=10)): k = k + 1 print(k)
Здесь перебираем с помощью цикла for натуральные числа от 1 до 1000.
Если логическое выражение выдаёт истину, то мы подсчитываем такой вариант.
Программа напечатает число 5.
Второй способ (с помощью рассуждений).
Натуральные числа — это целые, положительные числа. Например: 1, 2, 3, 4, и т. д.
Преобразуем первое выражение ¬(X2 ≥ 9) = (X2 < 9). Отрицание внесли в скобки. В этом случае знак, который находится в скобках, нужно поменять на противоположный.
Важно: Если было строгое неравенство, то оно станет нестрогим, и наоборот, если было неравенство нестрогим, то оно станет строгим.
Получается, что выражение (X2 < 9) будет истинно только при двух значениях: X = 1, X = 2.
Во втором выражении ¬((X < 7) ∨ (X ≥ 10)) удобно применить формулу Де Моргана.
Формула де Моргана:
¬(A ∨ B) = ¬A ∧ ¬B
¬(A ∧ B) = ¬A ∨ ¬B
Преобразуем выражение по формуле де Моргана и внесём отрицание в скобки:
¬((X < 7) ∨ (X ≥ 10)) = ¬(X < 7) ∧ ¬(X ≥ 10) = (X ≥ 7) ∧ (X < 10)
Получилось выражение (X ≥ 7) ∧ (X < 10). Между двумя выражениями стоит логическое умножение. Значит, одновременно должны выполняться и первое неравенство, и второе. Таким образом, получается, что подходят три значение для выражения (X ≥ 7) ∧ (X < 10). Это X = 7, X = 8, X = 9.
Обратимся к самому начальному логическому условию. Там два выражения соединятся логическим сложением. Значит, мы должны объединить те случаи, когда у нас первое выражение становится истинным (X=1, X=2), и те случаи, когда второе выражение становится истинным (X = 7, X = 8, X = 9).
Получается всего 5 натуральных чисел удовлетворяют изначальному логическому условию.
Ответ: 5
Разберём ещё одну разминочную задачу для подготовки к ЕГЭ по информатике 2022.
Задача (Неравенство, две переменные)
Для какого наибольшего целого неотрицательного числа A выражение
(x ≥ A) ∨ (y ≥ A) ∨ (x * y ≤ 205)
тождественно истинно, т.е. принимает значение 1 при любых целых положительных x и y ?
Решение:
Первый способ (с помощью питона).
for A in range(0, 300): k=0 for x in range(1, 301): for y in range(1, 301): if (x >= A) or (y >= A) or (x * y <= 205): k=k+1 if k==90000: print(A)
В первом цикле перебираем значения для A. Здесь мы пытаемся подобрать ответ в диапазоне от 0 до 300. Этот диапазон меньше, чем в прошлой задаче. Потому что здесь три вложенных цикла, и если перебирать числа от 0 до 1000, то программа может работать очень долго. При необходимости можно указать другой диапазон.
Для каждого A устанавливаем счётчик k в ноль.
Затем перебираем все числа в диапазоне от 1 до 300 (включительно) для переменных x и y, тем самым имитируем фразу «для любых x и y».
Если логическое выражение сработает при каждом значении x и y, то считается, что значение A нам подходит, и в счётчике по окончанию вложенных циклов будет значение 90000 (300 * 300 = 90000).
Наибольшее число, которое напечатает программа равно 15.
Второй способ (с помощью рассуждений).
Здесь есть три выражения в скобках, которые соединены логическим сложением. При логическом сложении достаточно хотя бы одного выражения, где будет истина, чтобы всё общее выражение было истинно.
Если мы сделаем A слишком большим, к примеру A = 250, то найдутся такие x = 16, y = 16, при которых все три условия в скобках не будут выполняться, и, значит, всё общее выражение будет ложным.
Следовательно, нам нужно выбрать таким A, чтобы не было возможности подобрать x, y, при которых все три выражения ложны.
Сделаем так: пока x и y меньше A, должно «работать» третье выражение в скобках. Как только x или y сравняются с A — начинают «работать» первое или второе выражение.
До какого же максимального значения могут дойти x и y, чтобы перемножение этих двух чисел было меньше или равно 205 (x * y <= 205) ?
15 * 15 = 225
14 * 14 = 196
Получается, пока числа x и y меньше 15, «выручает» третье выражение (x * y ≤ 205), как только станут x ≥ 15 и y ≥ 15, будут «работать» первое и второе выражение.
Отсюда получаем, что максимальное число A = 15
Ответ: 15
Задача (Функция ДЕЛ)
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула
¬ДЕЛ(x, А) → (ДЕЛ(x, 6) → ¬ДЕЛ(x, 9))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?
Решение:
Первый способ (с помощью питона).
def D(n, m): if n%m==0: return True else: return False for A in range(1, 1000): k=0 for x in range(1, 1001): if D(x, A) or (not(D(x, 6)) or not(D(x, 9))): k=k+1 if k==1000: print(A)
Здесь мы формируем функцию ДЕЛ (функцию D). Если n делится на m, то функция возвращает Истину, в противном случае функция возвращает Ложь.
Далее решаем примерно так же, как и в прошлых задачах: для каждого числа A перебираем все значения x. Следование расписываем по формуле A ⟶ B = ¬A ∨ B.
Наибольшее число здесь получается равно 18.
Второй способ (с помощью рассуждений).
Рассмотрим случай, когда в левой части логического выражения будет 1, а в правой 0. В остальных случаях беспокоится не за что, потому что вся формула будет выдавать истину.
Посмотрим, когда в правой части получается ноль. Функция ДЕЛ(x, 6) должна выдавать истину. Т.е. x должен делится на 6. А функция ¬ДЕЛ(x, 9) должна выдавать ноль. Т.е. без отрицания ДЕЛ(x, 9) должна выдавать истину. Значит, x так же делится на 9.
x делится на 6 => x = 2*3*n, n ∈ N
x делится на 9 => x = 3*3*n, n ∈ N
Чтобы выполнялся случай, когда в правой части получается ноль, икс должен быть равен x = 3*3*2*n (n ∈ N). Т.е. получается, что икс должен быть кратен 18.
Т.е. получается, что когда x делится на 18, в правой части логического выражения будет получатся ноль. Чтобы спасти ситуацию, мы должны в левой части логического выражения не получать 1. Следовательно, ¬ДЕЛ(x, А) должно выдавать ноль. Значит, ДЕЛ(x, А) должно выдавать 1. Таким образом, приходим к выводу, что A должно равняться 18.
Если получится опасная ситуация, когда x кратен 18, то она будет нейтрализована, ведь в левой части будет получатся ноль.
Ответ: 18
Ещё один важный тип задач 15 задания ЕГЭ по информатике 2022
Задача (Поразрядная конъюнкция)
Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 11102 & 01012 = 4
Для какого наименьшего неотрицательного целого числа A формула
x&51 ≠ 0 → (x&A = 0 → x&25 ≠ 0)
тождественно истинна (то есть принимает значение 1 при любом неотрицательном целом значении переменной x)?
Решение:
Первый способ (с помощью питона).
for A in range(0, 1000): k=0 for x in range(0, 1000): if x&51==0 or (x&A!=0 or x&25!=0): k=k+1 if k==1000: print(A)
Здесь следование преобразовываем по формуле: A ⟶ B = ¬A ∨ B. Так же и A, и x неотрицательные числа. Поэтому мы перебираем их диапазон, начиная с нуля. Из-за этого в цикле, который перебирает переменную x, мы устанавливаем верхнюю границы равной 1000, а не 1001. Тогда тоже будет 1000 повторений в этом цикле.
Наименьшее число равно 34.
Второй способ (с помощью рассуждений).
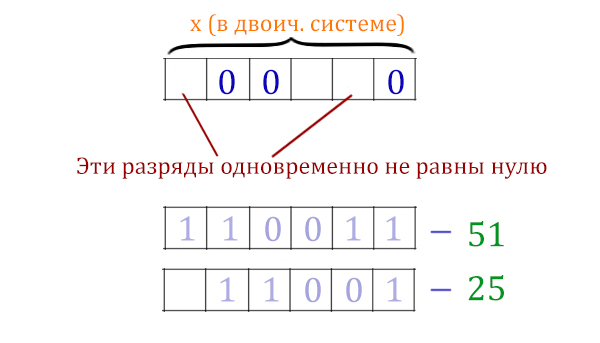
Переведём числа 51 и 25 в двоичную систему.
51 = 1100112
25 = 110012
Формула будет тождественно ложна, когда
Этого допустить нельзя!
При каком x получается в левой выражении формулы истина ? Если у икса в двоичном представлении в тех разрядах, где у числа 51 стоят 1, будет хотя бы в одном месте 1.
Рассмотрим правое выражение формулы. Ноль получается в единственном случае:
Рассмотрим выражение x&25 ≠ 0. Чтобы в этом логическом выражении получился ноль, нужно x&25 = 0. Посмотрим на двоичное представление числа 25. В тех разрядах, где стоят единицы, у икс должны быть нули (для x&25 = 0).
Сформулируем окончательное условие для x, при котором возникает опасность превращение общей формулы в ложь.
Нам нужно «поломать эту песенку» с помощью x&A = 0. Т.е. нельзя допускать, чтобы это выражение было истинно.
Получается, что A = 1000102. Это наименьшее из возможных число, при котором мы точно себя обезопасим от того, что вся формула будет ложна.
A = 1000102 в десятичной системе будет 34.
Ответ: 34
Ещё один тип задач 15 задания ЕГЭ по информатике
Задача (числовая прямая)
На числовой прямой даны отрезки P=[5, 13] и Q=[8, 19]. Укажите наименьшую возможную длину такого отрезка A, что формула (¬(x ∈ P) → (x ∈ Q)) → (x ∈ A ) верна при любых значениях x.
Решение:
Первый способ (с помощью питона).
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 200): for b in range(a, 200): k=0 for i in range(-200, 200): x = i / 2 if not((F(5, 13, x) or F(8, 19, x))) or F(a, b, x): k=k+1 if k==400: mn= min(mn, b-a) print(mn)
Получается ответ 14. Более подробно, как решать задачи на ОТРЕЗКИ из 15 задания ЕГЭ по информатике на Python, можете посмотреть в этой статье.
Второй способ (с помощью рассуждений).
Если будут такие варианты:
То нам беспокоится не о чём. Потому что формула всегда будет истинна! (см. таблицу истинности для следования →)
Нас же будет интересовать этот случай.
При таком раскладе вся формула будет ложна! Нам нужно этого не допустить при любом значении x!
Единица получается в первом подвыражении в трёх случаях:
1) Случай
Выражение ¬(x ∈ P) получается ложно, когда (x ∈ P) будет истинно! Получается при x ∈ [5, 13] выражение ¬(x ∈ P) — ложно!
Выражение (x ∈ Q) ложно, когда x ∉ [8, 19]
Какой же минимальной длины должен быть отрезок A, чтобы этот случай не проходил при любом x ? При этом случае отрезок A должен быть равен [5, 8). Тогда левое выражение пусть и может стать единицей при x ∈ [5, 8), но выражение (x ∈ A) будет также равно 1 при x ∈ [5, 8)! И схема 1 → 0 не пройдёт. Будет 1 → 1.
Для 1 случая A=[5, 
2) Случай
При каких x выражение ¬(x ∈ P) обращается в ноль, мы уже рассматривали: x ∈ [5, 13].
Второе выражение «выдаёт» 1 при x ∈ [8, 19].
Получается, что при при x ∈ [8; 13] первое выражение в скобках в главной формуле будет тождественно истинно!
С помощью отрезка A нужно это нейтрализовать путём превращения второго выражения в скобках в главной формуле в 1, пока x ∈ [8; 13]. Значит, для этого случая A = [8; 13]
3) Случай
В выражении ¬(x ∈ P) единица получается, когда в выражении (x ∈ P) получается ноль. Тогда x ∉ [5, 13]!
Чтобы во втором выражении (x ∈ Q) была единица, нужно, чтобы x ∈ [8, 19].
Получается, что 3 случай выполняется, если x ∈ (13, 19].
С помощью отрезка A нужно этому противодействовать! Нужно чтобы выражение (x ∈ A) было всегда 1 при x ∈ (13, 19]. Тогда A должно быть (13, 19].
Следовательно, для третьего случая A=(13, 19].
Нам нельзя допустить ни одного случая! Поэтому, объединив все случаи, получаем, что A=[5, 19].
Длина отрезка равна 14.
Ответ: 14
Ещё одна задача про числовую прямую из банка тренировочных заданий ЕГЭ по информатике 2021.
Задача (Числовая прямая, закрепление)
На числовой прямой даны отрезки P=[5, 13] и Q=[8, 19]. Укажите наименьшую возможную длину такого отрезка A, что формула ((x ∈ P) ∧ ¬(x ∈ A)) → ((x ∈ Q) ∧ ¬(x ∈ A)) верна при любых значениях x.
Решение:
Первый способ (с помощью питона).
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 200): for b in range(a, 200): k=0 for i in range(-200, 200): x = i / 2 if not((F(5, 13, x) and not(F(a, b, x)))) or (F(8, 19, x) and not(F(a, b, x))): k=k+1 if k==400: mn=min(mn, b-a) print(mn)
Второй способ (с помощью рассуждений).
Формула может быть ложна, когда
Во всех остальных случаях, формула всегда верна.
Чтобы выражение ((x ∈ P) ∧ ¬(x ∈ A)) было тождественно 1, выражение (x ∈ P) обязательно должно быть тождественно 1. А, значит, x ∈ [5, 13] — это опасная зона, при которой появляется возможность обратить всю формулу в ноль!
Мы можем сразу пресечь эту опасность с помощью отрезка A. Выбрать такой отрезок, чтобы он всегда «выдавал» ложь при x ∈ [5, 13]. Для этого достаточно выбрать A=[5, 13]! Но вдруг его можно сделать ещё более маленьким за счёт правой части формулы ?
Предположим, что отрезок A сделали ещё меньшим. Тогда при каком-то x (x ∈ [5, 13]) выражение ¬(x ∈ A) будет «выдавать» 1! Причём такое же выражение стоит и в правой части формулы! Там тоже будет 1 для выражения ¬(x ∈ A).
Нас же в этом случае должно выручить выражение (x ∈ Q). Если оно «выдаст» 1 в этот «сложный» момент, то мы спасены! Ведь тогда получается, что правая часть всей формулы будет «выдавать» не 0, а 1. Посмотрим при каких x из отрезка [5, 13] приходит это спасение.
Видим, что в интервале x ∈ [8, 13] нас спасает выражение (x ∈ Q).
Значит, отрезок A можно сократить до A=[5, 8).
Длина отрезка будет равна 3!
Ответ: 3
Задачи для закрепления
Задача (Неравенство, две переменные, закрепление)
Для какого наибольшего целого неотрицательного числа A выражение
(x < A) ∧ (y < A) ∧ (x * y > 603)
тождественно ложно, т.е. принимает значение 0 при любых целых положительных x и y ?
Решение:
Первый способ (с помощью питона).
for A in range(0, 300): k=0 for x in range(1, 301): for y in range(1, 301): if not( (x < A) and (y < A) and (x * y > 603) ): k=k+1 if k==90000: print(A)
Т.к. выражение должно быть ЛОЖНО, то обернём логическое выражение в функцию not(). Видим, что программа не сильно отличается от прошлой задачи. Данный шаблон подходит для большинства задач подобного типа.
Наибольшее число получается равно 25.
Второй способ (с помощью рассуждений).
В этой задаче нужно, чтобы общее выражение было ложно!
Если мы поставим отрицание над всем выражением, то можно искать такое максимальное A, при котором всё выражение тождественно истинно, а не ложно!
¬((x < A) ∧ (y < A) ∧ (x * y > 603)) = ¬(x < A) ∨ ¬(y < A) ∨ ¬(x * y > 603)
Здесь применили формулу де Моргана! Т.е. каждое подвыражение получило отрицание + соединительная логическая операция (логическое умножение) сменилась на противоположную операцию (логическое сложение).
Внесём отрицание в скобки. Получается:
(x ≥ A) ∨ (y ≥ A) ∨ (x * y ≤ 603)
Получили ситуацию, как в прошлой задаче! Напомню, что теперь нужно, чтобы общее выражение было истинно.
Найдём максимальное число, до которого могут «подняться» x и y, чтобы ещё работало третье выражение!
Обратите внимание, что x и y — симметричны. Значит, что верхняя планка для x и y будет одно и тоже число.
Поэтому вспоминаем таблицу квадратов.
25 * 25 = 625
24 * 24 = 576
Получается, что максимальное число до которого могут «дойти» x и y, чтобы «работало» третье выражение, равно 24.
Тогда, начиная с 25 для x и y, должны работать первое и второе выражение.
Получается, что максимальное число для A равно 25.
Ответ: 25
Ещё одна задачка подобного типа из тренировочных упражнений 15 задания ЕГЭ по информатике.
Задача (Неравенство, две переменные, закрепление)
Для какого наименьшего целого числа A формула
(3 * x + y < A) ∨ (x < y) ∨ (16 ≤ x)
тождественно истинна, т.е. принимает значение 1 при любых целых неотрицательных x и y ?
Решение:
Первый способ (с помощью питона).
for A in range(-300, 300): k=0 for x in range(1, 301): for y in range(1, 301): if (3*x + y < A) or (x < y) or (16 <= x): k=k+1 if k==90000: print(A)
Наименьшее число равно 61. Здесь не сказали, что A принимает неотрицательные значения, поэтому мы включили в диапазон для A числа, которые меньше нуля. Из-за этого увеличилось время выполнения программы, но ответ получим за приемлемое время.
Второй способ (с помощью рассуждений).
Чтобы вся формула была тождественно истинна, нужно, чтобы хотя бы одно выражение «выдавало» истину, т.к. выражения в формуле соединяются с помощью логического сложения!
Взглянем на третье выражение. Пока x ≥ 16, всё идёт как надо. Третье выражение будет истинно, и, значит, вся формула будет истинна.
Но если x ≤ 15, то нужно, чтобы нас «спасало» первое или второе выражение.
Рассмотрим второе выражение. Пока y > x (x ≤ 15) => y > 15, у нас всё нормально, второе выражение будет истинно, и вся формула будет истинна.
Теперь обратим внимание на первое выражение. Оно должно нас «спасать», когда третье и второе выражение «не спасло»! Это возможно, если x ≤ 15 (иначе «спасло» бы третье выражение), а так же y ≤ 15 (иначе «спасало» бы второе выражение).
Но, чтобы первое выражение было всегда истинно при x ≤ 15 и y ≤ 15, мы должны подобрать число A при максимальных x и y (x=15, y=15)! Ведь для более маленьких значений выражение (3 * x + y < A) точно будет истинно.
Получается:
3 * 15 + 15 < A
60 < A
Нужно найти наименьшее число для A, при котором A > 60. Тогда там, где не «спасли» третье и второе выражение, точно «спасёт» первое выражение. Получается A = 61.
Ответ: 61
Задача (ЕГЭ по информатике, Москва, 2020)
Для какого наибольшего целого неотрицательного числа A выражение
(x > A) ∨ (y > x) ∨ (2 * y + x < 110)
тождественно истинно, то есть принимает значение 1 при любых целых неотрицательных x и y ?
Решение:
Первый способ (с помощью питона).
for A in range(0, 300): k=0 for x in range(1, 301): for y in range(1, 301): if (x > A) or (y > x) or (2 * y + x < 110): k=k+1 if k==90000: print(A)
Максимальное число получается равно 36.
Второй способ (с помощью рассуждений).
Пока y > x, второе подвыражение всегда истинно, значит, и всё выражение истинно.
Теперь будем рассматривать случай y ≤ x.
Рассмотрим третье подвыражение. Найдём максимальные значения для x и для y, которые они одновременно могут принимать, и при которых ещё выполняется третье условие.
Т.к. мы рассматриваем случай y ≤ x, то максимальное число для y будет xmax т.е. ymax = xmax.
Тогда
2 * xmax + xmax < 110
3 * xmax < 110
36 * 3 = 108
37 * 3 = 111
xmax = ymax = 36
Если x «перевалит» за 36, и при этом y ≤ x (иначе «спасает» второе подвыражение), то должно «спасать» первое выражение.
Получается, что наибольшее значение A будет равно 36.
Ответ: 36
Следующий тип задач часто можно встретить в тренировочных вариантах ЕГЭ по информатике 2022.
Задача (С функцией ДЕЛ, закрепление)
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа A формула
ДЕЛ(120, A) ∧ ((ДЕЛ(x, 70) ∧ ДЕЛ(x, 30)) → ДЕЛ(x, A))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Решение:
Первый способ (с помощью питона).
def D(n, m): if n%m==0: return True else: return False for A in range(1, 1000): k=0 for x in range(1, 1001): if D(120, A) and (not(D(x, 70) and D(x, 30)) or D(x, A)): k=k+1 if k==1000: print(A)
Наибольшее число получается равно 30.
Второй способ (с помощью рассуждений).
Рассмотрим левую часть логического выражения. Мы видим, что число 120 должно делится на A. Значит, для A уже есть некоторое ограничение (A <= 120).
Рассмотрим правую часть выражения. Изучим, когда она превращается в ноль. Тогда
Т.е. x должен делится на 70 и одновременно x должен делится на 30.
x = 70*n = 2*5*7*n (n ∈ N)
x = 30*n = 2*5*3*n (n ∈ N)
Чтобы одновременно выполнялись два условия, икс должен быть равен x = 2*5*7*3*n (n ∈ N).
Для того, чтобы правое выражение не превращалось в ноль, x как раз должен делится на число 2*5*7*3. Тогда будет 1->1. Т.е. число A должно равняться 2*5*7*3. Но мы сказали, что A <= 120, плюс, должно являться делителем числа 120. Значит, должны снизить значение для A.
Рассмотрим значение 2*5*7 для числа A (Предыдущее число, но без тройки). Для правой части оно подходит, т.к. «при малейшей» возможности превращения правого выражения в ноль (т.е. ДЕЛ(x, 70) = True), у нас будет спасаться ситуация, т.к. ДЕЛ(x, A) так же
будет равно 1. И снова получаем 1->1. Но это значение не подходит для левой части, ведь тогда A не является делителем числа 120.
Приходится брать число 2*5*3 (без семёрки). Здесь ситуация аналогично предыдущему случаю, только теперь это число является делителем числа 120.
В ответе напишем 30.
Ответ: 30
Задача (Поразрядная конъюнкция, закрепление)
Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответствующими битами двоичной записи). Определите наименьшее натуральное число A, такое что выражение
(X & 49 ≠ 0) → ((X & 33 = 0) → (X & A ≠ 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?
Решение:
Первый способ (с помощью питона).
for A in range(1, 1000): k=0 for x in range(1, 1001): if (x&49==0) or ((x&33!=0) or (x&A!=0)): k=k+1 if k==1000: print(A)
Наименьшее число равно 16.
Второй способ (с помощью рассуждений).
Переведём числа 49 и 33 в двоичную систему.
4910 = 1100012
3310 = 1000012
Рассмотрим случай, когда функция стремится превратится в ноль.
Чтобы левое выражение выдавало истину, икс должен иметь 1 (единицу) в первом разряде или во второй разряде, или в последнем разряде (в 6-ти битном числе).
Рассмотрим правое выражение. Посмотрим, когда выражение (X & 33 = 0) выдаёт истину. Первый бит и последний бит должен быть равен нулю. Т.е получается, что в 6-ти битном числе нас интересует второй бит. Если он будет равен 1 и при этом первый бит и последний будут равны 0, то возникает опасная ситуация, которую нужно спасть.
При выше описанных условиях выражение (X & A ≠ 0) должно выдавать истину. Тогда наименьшее A равно 100002 = 162.
Ответ: 16
Задача (числовая прямая, закрепление 2)
На числовой прямой даны два отрезка: P = [20, 30] и Q = [35, 60]. Найдите наименьшую возможную длину отрезка A, при котором формула
¬(x ∈ A) ∧ ((x ∈ P) ∨ (x ∈ Q))
тождественно ложна, то есть принимает значение 0 при любых x.
Решение:
Первый способ (с помощью питона).
def F(a, b, x): if a <= x <= b: return True else: return False mn=10**9 for a in range(0, 200): for b in range(a, 200): k=0 for i in range(-200, 200): x = i / 2 if not(not(F(a, b, x)) and (F(20, 30, x) or F(35, 60, x))): k=k+1 if k==400: mn=min(mn, b-a) print(mn)
Ответ будет 40.
Второй способ (с помощью рассуждений).
Рассмотрим наоборот, когда логическое выражение выдаёт истину.
В правой части получается 1, когда x ∈ P или x ∈ Q. Именно в эти моменты выражение ¬(x ∈ A) должно спасать ситуацию и выдавать 0. Тогда без отрицания (x ∈ A) должно выдавать 1. Чтобы покрыть два отрезка, берём A=[20; 60].
Минимальная длина получается 60-20=40.
Ответ: 40
На этом всё! Увидимся в новых уроках по подготовке к ЕГЭ по информатике!
Добрый день! А как в 5 задаче (про числовую прямую) получился ответ 14?
В конце же получается, что A принадлежит [5, 19], то есть длина отрезка 15.
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 — 15 штук
Или я что-то неправильно понял?
Считается количество единиц, а не сколько целых чисел в этом отрезке.
И в самой последней задаче на закрепление, у вас, видимо, та же ошибка. Не 40, а 41 должно быть?
Как решать 15 задание с «~» тильдой на питоне?
Как например это задание:
На числовой прямой даны два отрезка: P = [7, 14] и Q = [9, 11]. Укажите наибольшую возможную длину промежутка A, для которого формула
((x ∈ P) ~ (x ∈ Q)) → ¬(x ∈ A)
Грамотное объяснение. Безумно здорово, что есть объяснения как на питон (перебором) так и чисто в математической форме, потому что в информатике оба подхода, мне кажется, равносильны. Спасибо
ЕГЭ информатика 15 задание разбор, теория, как решать.
Преобразование логических выражений, (П) — 1 балл
Е15.42 Для какого наименьшего натурального числа А формула (ДЕЛ(x, 2) → ¬ДЕЛ(x, 3)) / (x + A ≥ 100)
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула (ДЕЛ(x, 2) → ¬ДЕЛ(x, 3)) / (x + A ≥ 100) тождественно истинна (т.е. принимает значение 1) при любом натуральном значении переменной х? Ответ: Демонстрационный вариант ЕГЭ 2023 г. – задание №15
Читать далее
Е15.41 для которого формула ((x ∈ Q) ≡ (x ∈ P)) ∨ (¬(x ∈ A) → ((x ∈ P) ∧ ¬(x ∈ Q))) тождественно истинна
На числовой прямой даны два отрезка: P = [ 6; 4 5] и Q = [18; 52]. Укажите наименьшую возможную длину такого отрезка A, для которого формула ((x ∈ Q) ≡ (x ∈ P)) ∨ (¬(x ∈ A) → ((x ∈ P) ∧ ¬(x ∈ Q))) тождественно истинна (т. е. принимает значение 1 при любом …
Читать далее
Е15.40 выражение (2у + 3х ≠ 135) ∨ (у > А) ∨ (x > A) истинно
Определите наибольшее целое значение A, при котором выражение (2у + 3х ≠ 135) ∨ (у > А) ∨ (x > A) истинно для любых целых положительных значений х и у. Ответ: Апробация ЕГЭ по информатике 19 февраля 2022 – задание №15 Тренировочный экзамен по информатике и ИКТ (КЕГЭ) в компьютерной форме
Читать далее
Е15.39 формула (x ∈ Q) → (((x ∈ P) ≡ (x ∈ Q)) ∨ (¬(x ∈ P) → (x ∈ A))) тождественно истинна
На числовой прямой даны два отрезка: P = [69; 91] и Q = [77; 114]. Укажите наименьшую возможную длину такого отрезка A, для которого формула (x ∈ Q) → (((x ∈ P) ≡ (x ∈ Q)) ∨ (¬(x ∈ P) → (x ∈ A))) тождественно истинна (т. е. принимает значение 1 при любом значении переменной …
Читать далее
Е15.38 выражение ((x & 26 ≠ 0) ∨ (x & 13 ≠ 0)) → ((x & 29 = 0) → (x & A ≠ 0)) тождественно истинно
Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 11102&01012 = 01002 = 4 . Определите наименьшее натуральное число A, такое что выражение ( (x & 26 ≠ 0) ∨ (x & 13 ≠ 0)) → ((x & 29 = 0) → (x & A ≠ 0)) тождественно истинно …
Читать далее
Е15.37 формула (x ∈ Q) → (¬(x ∈ P) → ¬((x ∈ Q) ∧ ¬(x ∈ A))) тождественно истинна
На числовой прямой даны два отрезка: P = [19; 94] и Q = [4; 61]. Укажите наименьшую возможную длину такого отрезка A, для которого формула (x ∈ Q) → (¬(x ∈ P) → ¬((x ∈ Q) ∧ ¬(x ∈ A))) тождественно истинна (т. е. принимает значение 1 при любом значении переменной х). Ответ: источник: …
Читать далее
Е15.36 формула ( (x ∈ А) → (x ∈ P) ) / (x ∈ Q) тождественно истинна
На числовой прямой даны два отрезка: P = [5, 17] и Q = [13, 23]. Найдите наибольшую возможную длину отрезка A, при котором формула ( (x ∈ А) → (x ∈ P) ) / (x ∈ Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Ответ: источник: informatikaexpert.ru
Читать далее
Е15.35 ДЕЛ(A, 40) / (ДЕЛ(780, x) → (¬ДЕЛ(A, x) → ¬ДЕЛ(180, x)))
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа A формула ДЕЛ(A, 40) / (ДЕЛ(780, x) → (¬ДЕЛ(A, x) → ¬ДЕЛ(180, x))) тождественно истинна, то есть принимает значение 1 при любом натуральном x? Ответ: СтатГрад Вариант ИН2010401 17.03.2021– задание №15
Читать далее
Е15.34 формула x & 85 = 0 → (x & 54 ≠ 0 → x & А ≠ 0) тождественно истинна
Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Например, 14 & 5 = 11102 & 01012 = 01002 = 4. Для какого наименьшего неотрицательного целого числа А формула x & 85 = 0 → (x & 54 ≠ 0 → x & А ≠ 0) тождественно истинна (т. е. принимает …
Читать далее
Е15.33 формула ((x ∈ P) ∧ ¬(x ∈ A)) → ¬(x ∈ Q) тождественно истинна
На числовой прямой даны два отрезка: P = [10, 32] и Q = [18, 45]. Найдите наименьшую возможную длину отрезка A, при котором формула ((x ∈ P) ∧ ¬(x ∈ A)) → ¬(x ∈ Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Источник: informatikaexpert.ru
Читать далее
За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: повышенный.
Средний процент выполнения: 68.7%
Ответом к заданию 15 по информатике может быть цифра (число) или слово.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
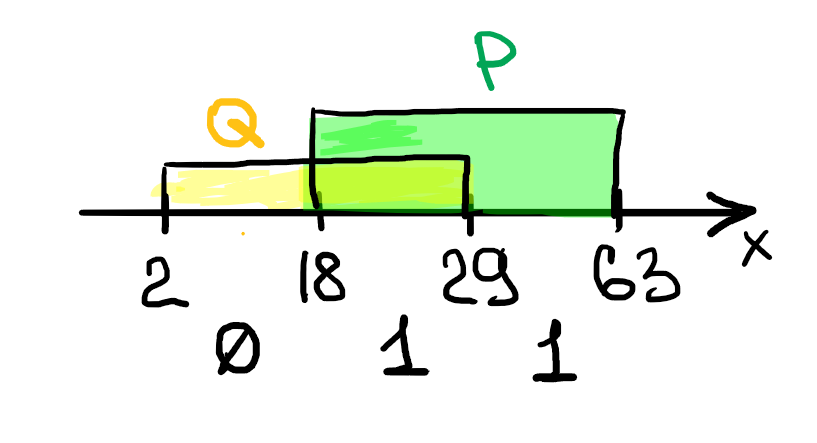
На числовой прямой даны два отрезка: P = [18, 63] и Q = [2, 29]. Укажите наименьшую возможную длину такого отрезка A, что логическое выражение
$ (¬(x ∈ A) → ((x ∈ P) ∧ (x ∈ A))) ∨ ((x ∈ Q) → (x ∈ P))$
тождественно истинно, то есть принимает значение 1 при любом значении переменной x.
Решение
1) преобразуем выражение, заменив (x∈A) на А, (x∈P) на P,(x∈Q) на Q
(¬A / P*A) / ¬Q / P
первую скобку преобразуем по формуле поглощения
A / ¬Q / P
2) Строим числовую прямую и отмечаем на ней значения известной части (¬Q / P)
3) Чтобы выражение было истинным на всей числовой оси, необходимо и достаточно, чтобы A ∈ [2, 18], поскольку на этом отрезке известная часть ложна. Длина отрезка = 16
Ответ: 16
Задача 2
Даны множества P = {5, 8, 19, 24, 42, 124}, Q = {3, 8, 12, 24, 64, 127, 211} и A. Элементами множества являются натуральные числа. Известно, что выражение
((x ∈ A) → ¬((x ∈ P) ∨ (x ∈ A))) ∨ ¬((x ∈ Q) → ¬(x ∈ P)).
истинно (т. е. принимает значение 1) при любом значении переменной x. Определите наибольшее возможное значение суммы элементов множества A.
Решение
Обозначим $P↖{∼}$: (x ∈ P); $Q↖{∼}$: (x ∈ Q); $A↖{∼}$: (x ∈ A).
Перепишем исходное выражение: ($A↖{∼}$ → ¬($P↖{∼}$ ∨ $A↖{∼}$)) ∨ ¬($Q↖{∼}$ → ¬ $P↖{∼}$).
На основании законов алгебры логики преобразуем это выражение.
($A↖{∼}$ → ¬($P↖{∼}$ ∨ $A↖{∼}$)) ∨ ¬($Q↖{∼}$ → ¬ $P↖{∼}$) ≡
≡ (¬ $A↖{∼}$ ∨ ¬($P↖{∼}$ ∨ $A↖{∼}$)) ∨ ¬(¬$Q↖{∼}$ ∨ ¬ $P↖{∼}$) ≡
≡ ¬ $A↖{∼}$ ∨ (¬ $P↖{∼}$ ∧ ¬ $A↖{∼}$) ∨ ($Q↖{∼}$ ∧ $P↖{∼}$) ≡
≡ ¬ $A↖{∼}$ ∨ ($Q↖{∼}$ ∧ $P↖{∼}$)
Возвращаясь к исходным выражениям, получим: ((x ∉ A) ∨ ((x ∈ Q)) ∧ (x ∈ P)).
Логическое выражение (x ∈ Q)) ∧ (x ∈ P) истинно на промежутке на множестве Q ∩ P = {8, 24}. Согласно условию, нужно выбрать такое множество A, что для любого целого x будет истинным выражение (x ∉ A) ∨ x ∈ {8, 24}. При этом множество A должно содержать наибольшее число элементов.
Таким множеством A является {8, 24}.Сумма элементов этого множества равна 32.
Ответ: 32
Задача 3
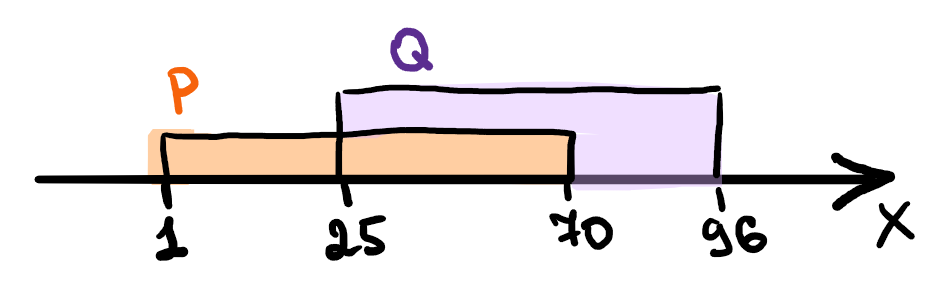
На числовой прямой даны два отрезка: P = [1, 70] и Q = [25, 96]. Укажите наибольшую возможную длину такого отрезка A, что логическое выражение
((x ∈ P) → ((x ∈ Q) ∧ (x ∈ P))) → ¬(x ∈ A)
тождественно истинно, то есть принимает значение 1 при любом значении переменной x.
Решение
Преобразуем выражение:
((x ∈ P) → ((x ∈ Q) ∧ (x ∈ P))) → ¬(x ∈ A) преобразуем импликацию
(¬(x ∈ P) / ((x ∈ Q) ∧ (x ∈ P))) → ¬(x ∈ A) применяем формулу поглощения
(¬(x ∈ P) / (x ∈ Q)) → ¬(x ∈ A) преобразуем импликацию
(x ∈ P) / ¬(x ∈ Q) / ¬(x ∈ A)
Известная часть: (x ∈ P) / ¬(x ∈ Q) истинна на отрезке от 1 до 25.
Чтобы выражение было истинно на всей числовой прямой, необходимо чтобы ¬(x ∈ A) было истинно, поэтому отрезок не должен лежать вне границ отрезка [1, 25], то есть А ∈ [1, 25] и его длина 25 — 1 = 24
Ответ: 24
Задача 4
На числовой прямой даны два отрезка: P = [2, 35] и Q = [12, 54]. Укажите наибольшую возможную длину такого отрезка A, что логическое выражение
$ ((x ∈ P) → ((x ∈ Q) ∧ (x ∈ P))) → ¬(x ∈ A)$
тождественно истинно, то есть принимает значение 1 при любом значении переменной x.
Задача 5
Для какого наименьшего целого числа A выражение
$((x^4 < A) → (x ≤ 2)) ∧ ((y < 7) → (y^2 < A))$
тождественно истинно (то есть принимает значение 1 при любых целых неотрицательных значениях переменных x и y)?
Задача 6
Для какого наибольшего целого числа A выражение
$((x ≤ 6) → (x^2 ≤ A)) ∧ ((y^3 ≤ A) → (y ≤ 3))$
тождественно истинно (то есть принимает значение 1 при любых целых неотрицательных значениях переменных x и y)?
Задача 7
Для какого наименьшего целого числа A выражение
$((x · x < A) ∨ (x ≥ 8)) ∧ ((y · y < A) → (y < 8))$
тождественно истинно (то есть принимает значение 1 при любых целых неотрицательных значениях переменных x и y)?
Задача 8
Для какого наибольшего целого неотрицательно числа A выражение
$(4 · x + 8 · y ≠ 124) ∨ (x > 3 · A − 1) ∨ (2 · y > A)$
тождественно истинно (то есть принимает значение 1 при любых целых неотрицательных значениях переменных x и y)?
Задача 9
Для какого наибольшего целого неотрицательно числа A выражение
(5 · x + 2 · y ≠ 32) ∨ (x > A − 
тождественно истинно (то есть принимает значение 1 при любых целых неотрицательных значениях переменных x и y)?
Задача 10
Для какого наименьшего целого неотрицательно числа A выражение
$(x + 2 · y ≤ A) ∨ (x > 25) ∨ (y > 12)$
тождественно истинно (то есть принимает значение 1 при любых целых неотрицательных значениях переменных x и y)?
Рекомендуемые курсы подготовки
Автор — Лада Борисовна Есакова.
Подсчет путей в ориентированном графе. ЗАДАЧА № 15.
В этой задаче требуется подсчитать количество путей, ведущих из одной вершины графа в другую. Обычно задачу решают преобразованием графа в дерево. Однако, при сложной структуре графа такое решение становится очень трудоемким. Велика вероятность ошибки.
Рассмотрим простой и эффективный способ решения.
В этой задаче мы имеем дело с ориентированным графом (графом, у которого ребра имеют направление). Т.е. ребра имеют вид стрелок. Две вершины, соединенные напрямую стрелкой, называются смежными. Вершина, из которой выходит стрелка, называется предком, а вершина, в которую входит стрелка – потомком.
Несложно понять, что количество путей, которыми можно попасть в некоторую вершину, равно сумме количеств путей предков этой вершины.
Пример:
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?
Решение:
Каждой вершине, начиная с начальной (A), поставим в соответствие индекс, равный количеству путей, которыми можно попасть в эту вершину. Для вершины A (начало пути) индекс всегда равен 1 (в начало пути можно попасть единственным образом – никуда не двигаясь). Теперь сформулируем правило: индекс вершины равен сумме индексов его предков. Исходя из этого индекс Б равен 1 (предок у Б один – вершина A).
У вершины Д предками являются А и Б, значит индекс вершины Д равен 1+1=2.
Очевидно, что мы можем посчитать индекс только тех вершин, индексы предков которых уже посчитаны. Например, мы не можем посчитать индекс Г, пока не посчитан индекс В. Двигаясь последовательно, мы рассчитаем индексы всех вершин.
Индекс вершины Ж и будет ответом задачи.
Ответ: 11
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задача №15. Графы. Поиск количества путей.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n.
Так, например, 14 & 5 = 11102 & 01012 = 01002 = 4. Для какого наименьшего неотрицательного целого числа А формула
x & 29 ≠ 0 → (x & 17 = 0 → x & А ≠ 0)
тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной x)?
2
Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 11102&01012 = 01002 = 4.
Для какого наименьшего неотрицательного целого числа А формула
x&25 ≠ 0 → (x&17 = 0 → x&А ≠ 0)
тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной х)?
3
Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14 & 5 = 11102 & 01012 = 01002 = 4. Для какого наименьшего неотрицательного целого числа А формула
x & 29 ≠ 0 → (x & 12 = 0 → x & А ≠ 0)
тождественно истинна (то есть принимает значение 1 при любом неотрицательном целом значении переменной х)?
4
Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n.
Так, например, 14&5 = 11102&01012 = 01002 = 4.
Для какого наименьшего неотрицательного целого числа А формула
тождественно истинна (то есть принимает значение 1 при любом неотрицательном целом значении переменной x)?
5
Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n.
Например, 14&5 = 11102&01012 = 01002 = 4.
Для какого наименьшего неотрицательного целого числа А формула
x&25 ≠ 0 → (x&9 = 0 → x&А ≠ 0)
тождественно истинна (то есть принимает значение 1 при любом неотрицательном целом значении переменной х)?
Пройти тестирование по этим заданиям