Задание 9 Профильного ЕГЭ по математике – это несколько типов текстовых задач. Условия и «сюжеты» задач могут быть разными. При этом в каждой из них нужно построить математическую модель, то есть обозначить какие-либо величины за переменные, составить уравнение и решить его. И еще есть неочевидные секреты их решения. О них – в конце статьи.
Вот основные типы текстовых задач, которые могут вам встретиться на ЕГЭ под номером 9. Переходите по ссылкам, читайте краткую теорию и разбирайте вместе с нами решения задач!
1. Задачи на движение




Формула работает и в этом случае. Здесь
– расстояние,
– скорость,
– время.
А секрет задач на движение по окружности: тот, кто обгоняет, проезжает на 1 круг больше, если это первый обгон. И на n кругов больше, если обогнал другого в -ный раз.
6. Задачи на нахождение средней скорости
По определению, средняя скорость получается, если всё расстояние поделить на всё время. В общем случае она не равна среднему арифметическому скоростей, а находится по следующей формуле:
.
7. Задачи на движение протяженных тел, встречное движение и обгон
Да, это те самые задачи, где поезд проходит через туннель. Или проезжает мимо платформы. И нам нужно учитывать длину поезда.
Есть еще задачи на встречное движение или обгон. Например, два поезда движутся навстречу друг другу (конечно, по параллельным путям), или один поезд обгоняет другой. Такие задачи удобно решать в движущейся системе отсчета.
Но и это не все. Есть еще задачи ЕГЭ на арифметическую и геометрическую прогрессии.

Арифметическая прогрессия в задачах ЕГЭ по математике
9. Задачи на геометрическую прогрессии
Геометрическая прогрессия в задачах ЕГЭ по математике
И еще мы обещали секреты решения текстовых задач на движение и работу. Читайте и применяйте!
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 9. Текстовые задачи u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
В 2022 задание 9 по математике профильного уровня изменилось — появился новый формат, проверяющий знание свойств параболы. Номер вызывает вопросы у учеников, но на деле решается просто. В статье разберем правила выполнения задания 9 ЕГЭ по математике.
Способы решения номера
9 задание по математике профильного уровня 2022 получится решить четырьмя методами.
Первый вариант
Начнем с простого способа, не требующего глубокого понимания темы. Условие выглядит следующим образом:
Присмотревшись к картинке задания 9 по профильной математике, видим: график содержит целочисленные точки. Отметим их на изображении (экзамен разрешает использовать текст КИМа). Решение требует минимум три точки:
Видим: в точке «-4» ордината равна «-3». Запишем уравнение, подставив значения значения абсциссы и ординаты:
16a — 4b + c = -3
Аналогичным образом записываем выражение, используя две остальные точки:
9a — 3b + c = -2
4a — 2b + c = 1
Получаем систему трех уравнений с тремя неизвестными. Решить достаточно легко. Простейший вариант: вычесть последнюю строчку из первых двух, избавившись от коэффициента “c”. После первое уравнение сокращаем на «2», вычитаем из него второе. Находим: a = 1. Подставляем далее, получаем:
b = 8;
c = 13.
Имея коэффициенты, переписываем уравнение, подставляем значение абсциссы:
f(x) = x2 + 8x + 13
f(-12) = 144 — 96 + 13 = 61
Второй вариант
Мы решили 9 задание по математике профилю наиболее простым способом. Однако вычисления получится сократить. Построим локальную систему координат около вершины параболы:
Видим особенность параболы: в точке «1» ордината равна 1, в точке «2» — 4. Представленный график отражает классическое выражение: y = x2, сдвинутое в системе координат. Известно: преобразования не меняют старший коэффициент. Делаем вывод, “a” равно “1”. Теперь найдем “b”. Используем выражение вершины параболы: x0 = -b / 2a. По рисунку видно: x0 = -4. Поставляя это число, найденное значение “a”, находим: b = 8. Дальнейшее решение требует одного уравнения из первого способа. Теперь выполнить номер проще.
Третий вариант
9 задание по математике профильного уровня реально упростить еще сильнее. Изучим способ образования данной параболы. Она получилась путем смещения исходной на “4” налево и на “3” вниз. Запишем уравнения. Изначальный пример:
y = x2
Сдвиг влево записывается:
y = (x + 4)2
Сдвиг вниз:
y = (x + 4)2 — 3
Получаем готовое уравнение, достаточно подставить “-12”. Ответ аналогичный: 61.
Четвертый вариант
Рассмотрим последний способ выполнения задания 9 по профильной математике 2022, требующий логического мышления. Снова изучим локальную систему координат:
Сравнивая с изначальной, получим: абсцисса «-12» из условия представляет собой значение «-8» локальной системы. Это связано со сдвигом. Ордината соответственно равна “64”. Не забываем: парабола сдвинута также на три пункта вниз. Получается, итоговое значение будет на 3 меньше найденного. Ответ снова 61!
В статье мы разобрали способы решения нового 9 задания из ЕГЭ по математике. Хотите изучить принципы выполнения остальных номеров? Записывайтесь на курсы «Уникум» Российского университета дружбы народов. Обучение проходит под руководством опытных преподавателей, форматы — очный, дистанционный. Для закрепления материала существует учебный портал Unikum.
Содержание данной статьи носит ознакомительный характер. При подготовке к сдаче ЕГЭ пользуйтесь дополнительными источниками информации!
В 2022 задание 9 по математике профильного уровня изменилось — появился новый формат, проверяющий знание свойств параболы. Номер вызывает вопросы у учеников, но на деле решается просто. В статье разберем правила выполнения задания 9 ЕГЭ по математике.
Способы решения номера
9 задание по математике профильного уровня 2022 получится решить четырьмя методами.
Первый вариант
Начнем с простого способа, не требующего глубокого понимания темы. Условие выглядит следующим образом:
Присмотревшись к картинке задания 9 по профильной математике, видим: график содержит целочисленные точки. Отметим их на изображении (экзамен разрешает использовать текст КИМа). Решение требует минимум три точки:
Видим: в точке «-4» ордината равна «-3». Запишем уравнение, подставив значения значения абсциссы и ординаты:
16a — 4b + c = -3
Аналогичным образом записываем выражение, используя две остальные точки:
9a — 3b + c = -2
4a — 2b + c = 1
Получаем систему трех уравнений с тремя неизвестными. Решить достаточно легко. Простейший вариант: вычесть последнюю строчку из первых двух, избавившись от коэффициента “c”. После первое уравнение сокращаем на «2», вычитаем из него второе. Находим: a = 1. Подставляем далее, получаем:
b = 8;
c = 13.
Имея коэффициенты, переписываем уравнение, подставляем значение абсциссы:
f(x) = x2 + 8x + 13
f(-12) = 144 — 96 + 13 = 61
Второй вариант
Мы решили 9 задание по математике профилю наиболее простым способом. Однако вычисления получится сократить. Построим локальную систему координат около вершины параболы:
Видим особенность параболы: в точке «1» ордината равна 1, в точке «2» — 4. Представленный график отражает классическое выражение: y = x2, сдвинутое в системе координат. Известно: преобразования не меняют старший коэффициент. Делаем вывод, “a” равно “1”. Теперь найдем “b”. Используем выражение вершины параболы: x0 = -b / 2a. По рисунку видно: x0 = -4. Поставляя это число, найденное значение “a”, находим: b = 8. Дальнейшее решение требует одного уравнения из первого способа. Теперь выполнить номер проще.
Третий вариант
9 задание по математике профильного уровня реально упростить еще сильнее. Изучим способ образования данной параболы. Она получилась путем смещения исходной на “4” налево и на “3” вниз. Запишем уравнения. Изначальный пример:
y = x2
Сдвиг влево записывается:
y = (x + 4)2
Сдвиг вниз:
y = (x + 4)2 — 3
Получаем готовое уравнение, достаточно подставить “-12”. Ответ аналогичный: 61.
Четвертый вариант
Рассмотрим последний способ выполнения задания 9 по профильной математике 2022, требующий логического мышления. Снова изучим локальную систему координат:
Сравнивая с изначальной, получим: абсцисса «-12» из условия представляет собой значение «-8» локальной системы. Это связано со сдвигом. Ордината соответственно равна “64”. Не забываем: парабола сдвинута также на три пункта вниз. Получается, итоговое значение будет на 3 меньше найденного. Ответ снова 61!
В статье мы разобрали способы решения нового 9 задания из ЕГЭ по математике. Хотите изучить принципы выполнения остальных номеров? Записывайтесь на курсы «Уникум» Российского университета дружбы народов. Обучение проходит под руководством опытных преподавателей, форматы — очный, дистанционный. Для закрепления материала существует учебный портал Unikum.
Содержание данной статьи носит ознакомительный характер. При подготовке к сдаче ЕГЭ пользуйтесь дополнительными источниками информации!
- ЕГЭ по математике профиль
Новые задания №9 ЕГЭ 2022 по профильной математике — графики функций.
Для успешного результата необходимо уметь выполнять действия с функциями.
Задание №9 ЕГЭ 2022 математика профильный уровень Прототипы
| Скачать задания | Источник |
| Новые задания 9 | ФИПИ |
| Прототипы задания №9 | vk.com/mathegeexam |
| Скачать задания | vk.com/ekaterina_chekmareva |
| → Теория → Задачи → Шпаргалка |
vk.com/abel_mat |
| Линейная функция | math100.ru |
| Парабола | |
| Гипербола | |
| Логарифмическая и показательная функции | |
| Иррациональные функции | |
| Тригонометрические функции |
Из кодификатора 2022 года для выполнения 9 задания нужно изучить основные элементарные функции, их свойства и графики:
3.3.1 Линейная функция, её график
3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график
3.3.3 Квадратичная функция, её график
3.3.4 Степенная функция с натуральным показателем, её график
3.3.5 Тригонометрические функции, их графики
3.3.6 Показательная функция, её график
3.3.7 Логарифмическая функция, её график
Уметь выполнять действия с функциями: определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций:
При отработке данного задания будут полезны книги:
Купить ЕГЭ. Математика. Графики функций, уравнения и неравенства, содержащие переменную под знаком модуля
Купить Задачи с параметрами. Применение свойств функций, преобразование неравенств
Связанные страницы:
Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи в разделе контакты
💡 Если Вы — учитель математики, то Вы можете создавать готовые карточки для учеников с индивидуальными заданиями и с ответами для отработки заданий на графики функций. Данные задачи доступны в Конструкторе бесплатно.
|
3. На рисунке изображён график функции y=3x^2+bx+c . Найдите f(6) . [Ответ: 10] |
Смотреть видеоразбор похожего >> |
|
4. На рисунке изображён график функции y=ax^2+12x+c . Найдите f(7) . [Ответ: -74] |
Смотреть видеоразбор похожего >> |
|
5. На рисунке изображён график функции y=ax^2+bx+12 . Найдите f(-7) . [Ответ: 19] |
Смотреть видеоразбор похожего >> |
|
6. На рисунке изображён график функции y=ax^2+bx+c . Найдите f(1) . [Ответ: 49] |
Смотреть видеоразбор похожего >> |
|
7. На рисунке изображён график функции y=ax^2+bx+c , где числа a , b и c — целые. Найдите f(-5) . [Ответ: -29] |
Смотреть видеоразбор похожего >> |
|
8. На рисунке изображён график функции f(x)=frac{k}{x}+a . Найдите f(0.1) . [Ответ: -17] |
Смотреть видеоразбор похожего >> |
|
9. На рисунке изображён график функции f(x)=frac{k}{x}+a . Найдите, при каком значении x значение функции равно -4.4 . [Ответ: -12.5] |
Смотреть видеоразбор похожего >> |
|
10. На рисунке изображён график функции f(x)=frac{k}{x+a} . Найдите f(-3.5) . [Ответ: 6] |
Смотреть видеоразбор похожего >> |
|
11. На рисунке изображён график функции f(x)=frac{k}{x+a} . Найдите значение x , при котором f(x) = 10 . [Ответ: 0.6] |
Смотреть видеоразбор похожего >> |
|
12. На рисунке изображён график функции f(x)=frac{kx+a}{x+b} . Найдите k . [Ответ: 1] |
Смотреть видеоразбор похожего >> |
|
13. На рисунке изображён график функции f(x)=frac{kx+a}{x+b} . Найдите a . [Ответ: 2] |
Смотреть видеоразбор похожего >> |
|
14. На рисунке изображён график функции f(x)=b+log_ax . Найдите f(frac{1}{9}) . [Ответ: 3] |
Смотреть видеоразбор похожего >> |
|
15. На рисунке изображён график функции f(x)=b+log_ax . Найдите значение x , при котором f(x)=-11 . [Ответ: 64] |
Смотреть видеоразбор похожего >> |
|
16. На рисунке изображён график функции f(x)=log_a(x+b) . Найдите f(26) . [Ответ: -2] |
Смотреть видеоразбор похожего >> |
|
17. На рисунке изображён график функции f(x)=log_a(x+b) . Найдите значение x , при котором f(x)=4 . [Ответ: 82] |
Смотреть видеоразбор похожего >> |
|
18. На рисунке изображён график функции f(x) = a^x+b . Найдите f(-2) . [Ответ: 22] |
Смотреть видеоразбор похожего >> |
|
19. На рисунке изображён график функции f(x) = a^x+b . Найдите значение x , при котором f(x) = 77 . [Ответ: -4] |
Смотреть видеоразбор похожего >> |
|
20. На рисунке изображён график функции f(x) = a^{x+b} . Найдите f(4) . [Ответ: 9] |
Смотреть видеоразбор похожего >> |
|
21. На рисунке изображён график функции f(x) = a^{x+b} . Найдите значение x , при котором f(x) = 64 . [Ответ: 8] |
Смотреть видеоразбор похожего >> |
|
22. На рисунке изображён график функции f(x) = ksqrt{x} . Найдите f(8.41) . [Ответ: 8.7] |
Смотреть видеоразбор похожего >> |
|
23. На рисунке изображён график функции f(x) = ksqrt{x} . Найдите значение x , при котором f(x)=-6.75 . [Ответ: 7.29] |
Смотреть видеоразбор похожего >> |
|
24. На рисунке изображены графики функций f(x)=-4x+22 и g(x)=ax^2+bx+c , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: 9] |
Смотреть видеоразбор похожего >> |
|
25. На рисунке изображены графики функций f(x)=-6x-28 и g(x)=ax^2+bx+c , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: 38] |
Смотреть видеоразбор похожего >> |
|
26. На рисунке изображены графики функций f(x)=frac{k}{x} и g(x)=ax+b , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: 0.2] |
Смотреть видеоразбор похожего >> |
|
27. На рисунке изображены графики функций f(x)=frac{k}{x} и g(x)=ax+b , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: 20] |
Смотреть видеоразбор похожего >> |
|
28. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков. [Ответ: -2.08] |
Смотреть видеоразбор похожего >> |
|
29. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков. [Ответ: -2.4] |
Смотреть видеоразбор похожего >> |
|
30. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков. [Ответ: -11.3] |
Смотреть видеоразбор похожего >> |
|
31. На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков. [Ответ: 6.8] |
Смотреть видеоразбор похожего >> |
|
32. На рисунке изображены графики функций f(x) = 2x^2+16x+30 и g(x) = ax^2+bx+c , которые пересекаются в точках A и B. Найдите абсциссу точки B. [Ответ: -9] |
Смотреть видеоразбор похожего >> |
|
33. На рисунке изображены графики функций f(x) = -2x^2-3x+1 и g(x) = ax^2+bx+c , которые пересекаются в точках A и B. Найдите ординату точки B. [Ответ: -13] |
Смотреть видеоразбор похожего >> |
|
34. На рисунке изображены графики функций f(x)=asqrt{x} и g(x)=kx+b , которые пересекаются в точке A. Найдите абсциссу точки A. [Ответ: 3.24] |
Смотреть видеоразбор похожего >> |
|
35. На рисунке изображены графики функций f(x)=asqrt{x} и g(x)=kx+b , которые пересекаются в точке A. Найдите ординату точки A. [Ответ: 9] |
Смотреть видеоразбор похожего >> |
|
36. На рисунке изображён график функции f(x) = asin{x}+b . Найдите a . [Ответ: 2] |
Смотреть видеоразбор похожего >> |
|
37. На рисунке изображён график функции f(x) = asin{x}+b . Найдите b . [Ответ: 1,5] |
Смотреть видеоразбор похожего >> |
|
38. На рисунке изображён график функции f(x) = acos{x}+b . Найдите a . [Ответ: 1,5] |
Смотреть видеоразбор похожего >> |
|
39. На рисунке изображён график функции f(x) = acos{x}+b . Найдите b . [Ответ: −1] |
Смотреть видеоразбор похожего >> |
|
40. На рисунке изображён график функции f(x) = a;tg{x}+b . Найдите a . [Ответ: 2] |
Смотреть видеоразбор похожего >> |
|
41. На рисунке изображён график функции f(x) = a;tg{x}+b . Найдите b . [Ответ: −1,5] |
Смотреть видеоразбор похожего >> |
Преобразования и вычисления
В задании №9 ЕГЭ по математике профильного уровня нам необходимо выполнить преобразование выражений и произвести элементарные вычисления. Чаще всего в этом разделе встречаются тригонометрические выражения, поэтому для успешного выполнения необходимо знать формулы приведения и другие тригонометрические тождества.
Разбор типовых вариантов заданий №9 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
[su_note note_color=”#defae6″]
Найдите sin2α , если cosα = 0,6 и π < α < 2π.
[/su_note]
Алгоритм решения:
- Находим значение синуса данного угла.
- Вычисляем значение sin2α.
- Записываем ответ.
Решение:
1. α лежит в третьей или четвертой четвертях, значит синус угла отрицательный. Воспользуемся осномным тригонометрическим тождеством:
2. По формуле синуса двойного угла: sin2α = 2sinαcosα = 2∙(-0,8)∙0,6 = -0,96
Ответ: -0,96.
Второй вариант задания (из Ященко, №1)
[su_note note_color=”#defae6″]
Найдите , если
.
[/su_note]
Алгоритм решения:
- Преобразуем формулу косинуса двойного угла.
- Вычисляем косинус.
- Записываем ответ.
Решение:
1. Преобразуем формулу косинуса двойного угла:
2. Вычисляем косинус искомого угла 2α, умноженный на 25, подставив данное значение косинуса угла α
Ответ: -7.
Третий вариант задания (из Ященко, №16)
[su_note note_color=”#defae6″]
Найдите значение выражения .
[/su_note]
Алгоритм решения:
- Рассматриваем выражение.
- Используем свойства тригонометрических функций для определения значений синуса и косинуса заданных углов.
- Вычисляем значение выражения.
- Записываем ответ.
Решение:
1. Выражение представляет собой произведение чисел и значений тригонометрических функций отрицательных углов.
2. Воспользуемся формулами:
3. Тогда получаем:
Ответ: -23.
Четвертый вариант задания (из Ященко)
[su_note note_color=”#defae6″]
Найдите значение выражения 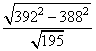
[/su_note]
Алгоритм решения:
- Анализируем выражение.
- Преобразовываем и вычисляем выражение.
- Записываем ответ.
Решение:
1. Выражение содержит два корня. Под корнем в числителе стоит разность квадратов. Для упрощения вычислений можно разность квадратов разложить на множители по формуле сокращенного умножения.
2. Преобразовываем выражение и вычисляем его значение:
Ответ: 4.
Пятый вариант задания (из Ященко)
[su_note note_color=”#defae6″]
Найдите значение выражения .
[/su_note]
Алгоритм решения:
- Анализируем выражение.
- Преобразовываем и вычисляем выражение.
- Записываем ответ.
Решение:
1. Данное выражение представляет собой произведение множителей, которые можно по формулам сокращенного умножения записать в виде разности квадратов:
2. Имеем:
Ответ: -5.
Даниил Романович | Просмотров: 10.8k
Каталог заданий.
Параболы
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 10 № 509253
На рисунке изображены графики функций
и
которые пересекаются в точках A и B. Найдите абсциссу точки B.
Аналоги к заданию № 509253: 509254 509255 509259 509262 509263 509264 509268 509256 509257 509258 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график
Решение
·
·
Сообщить об ошибке · Помощь
2
Тип 10 № 562060
На рисунке изображён график функции вида
где числа a, b и c — целые. Найдите значение
Аналоги к заданию № 562153: 562060 562154 562155 562156 562157 562158 562159 562160 562161 562162 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график
Решение
·
·
Сообщить об ошибке · Помощь
3
Тип 10 № 562061
На рисунке изображён график функции вида
где числа a, b и c — целые. Найдите значение дискриминанта уравнения
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график
Решение
·
·
1 комментарий · Сообщить об ошибке · Помощь
4
Тип 10 № 562153
На рисунке изображён график функции вида
где числа a, b и c — целые. Найдите значение
Аналоги к заданию № 562153: 562060 562154 562155 562156 562157 562158 562159 562160 562161 562162 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график
Решение
·
·
Сообщить об ошибке · Помощь
5
Тип 10 № 562154
На рисунке изображён график функции вида
где числа a, b и c — целые. Найдите значение
Аналоги к заданию № 562153: 562060 562154 562155 562156 562157 562158 562159 562160 562161 562162 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.3 Квадратичная функция, её график
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям























.png)

.png)