Как решить первое задание в егэ по математике профильный уровень

В задании №5 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.

Вот список тем, которые стоит повторить:

Квадратные уравнения

Арифметический квадратный корень

Корни и степени

Показательная функция

Показательные уравнения

Логарифмическая функция

Логарифмические уравнения

Тригонометрический круг

Формулы приведения

Формулы тригонометрии

Простейшие тригонометрические уравнения 1

Уравнения, сводящиеся к квадратным

1. Решите уравнение frac{6}{13}x^2=19frac{1}{2}. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.

С левой частью уравнения все понятно. Дробь frac{6}{13} умножается на x^2. А в правой части — смешанное число 19frac{1}{2}. Его целая часть равна 19, а дробная часть равна frac{1}{2}. Запишем это число в виде неправильной дроби:

19frac{1}{2}= frac{19cdot 2+1}{2} = frac{39}{2}.

Получим:

frac{6}{13}x^2=frac{39}{2};

x^2=frac{39cdot 13}{2cdot 6}=frac{13cdot 3cdot 13}{2cdot 6}=frac{{13}^2}{4};

x=pm frac{13}{2};

x_1=-6,5 или x_2=6,5.

Выбираем меньший корень.

Ответ: -6,5.

2. Решите уравнение left ( x-6 right )^2=-24x.

Возведем в квадрат левую часть уравнения. Получим:

left ( x-6 right )^2=-24xLeftrightarrow x^2-12x+36=-24xLeftrightarrow

Leftrightarrow x^2+12x+36=0Leftrightarrow left ( x+6 right )^2=0Leftrightarrow x=-6.

Ответ: -6.

Дробно-рациональные уравнения

3. Найдите корень уравнения

Перенесем единицу в левую часть уравнения. Представим 1 как frac{4x-5}{4x-5} и приведем дроби к общему знаменателю:

frac{5x-3}{4x-5}-frac{4x-5}{4x-5}=0;

frac{x+2}{4x-5}=0;

x= - 2.

Ответ: -2.

Это довольно простой тип уравнений. Главное — внимательность.

Иррациональные уравнения

Так называются уравнения, содержащие знак корня — квадратного, кубического или n-ной степени.

4. Решите уравнение:

sqrt{frac{6}{4{x}-54} } =frac{1}{7}.

Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.

Значит, .

Возведём обе части уравнения в квадрат:

frac{6}{4{x}-{ 54}} =frac{1}{49}.

Решим пропорцию:

4{x}-{ 54}={ 6}cdot { 49};

4{x}=348;

{ x}={ 87}.

Условие  при этом выполняется.

Ответ: 87.

5. Решите уравнение sqrt{72-x}=x. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.

Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

left{begin{matrix} 72-x=x^2\72-xgeq 0 hfill \xgeq 0 hfill end{matrix}right..

Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

sqrt{72-x}=x Leftrightarrow left{begin{matrix} 72-x=x^2\72-x geq 0 \x geq 0 end{matrix}right. Leftrightarrow

.

Мы получили, что x=8. Это единственный корень уравнения.

Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:

72-xge 0.

Возводят обе части уравнения в квадрат. Получают квадратное уравнение: x^2+x-72=0. Находят его корни: x=8 или x=-9. Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.

Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.

Ответ: 8.

6. Решите уравнение sqrt{45+4x}=x. Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Запишем решение как цепочку равносильных переходов:

.

Ответ: 9.

Показательные уравнения

При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.

7. Решите уравнение 5^{x-7}=frac{1}{125}.

Вспомним, что 125 = 5{}^{3}. Уравнение приобретает вид: 5{}^{x}{}^{-}{}^{7 }= 5{}^{-}{}^{3}. Функция y = 5^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

x - 7 = -3, откуда x = 4.

Ответ: 4.

8. Решите уравнение {left(frac{1}{49}right)}^{x-8}=7.

Представим {left(frac{1}{49}right)}^{ } как 7^{-2};

{left(7^{-2}right)}^{x-8}=7;

7^{-2x+16}=7.

Функция y = 7^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

-2x+16=1;

-2x=-15;

x=7,5.

Ответ: 7,5.

9. Решите уравнение left(frac{1}{9} right)^{{ x}-13} =3.

Представим {textstylefrac{1}{9}} в виде степени с основанием 3 и воспользуемся тем, что left({ a}^{{ m}} right)^{{ n}} ={ a}^{{ mn}}.

left(3^{-2} right)^{{ x}-{ 13}} =3;
3^{-2{ x}+{ 26}} =3^{1} ;

-2{ x}+{ 26}={ 1};

{ x}={ 12,5}.

Ответ: 12,5.

Логарифмические уравнения

Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.

И конечно, помним про область допустимых значений логарифма:

Логарифмы определены только для положительных чисел.

Основание логарифма должно быть положительно и не равно единице.

10. Решите уравнение:

{{log}_5 left(4+xright)=2 }.

Область допустимых значений: . Значит, 

Представим 2 в правой части уравнения как {{log}_5 25 }, чтобы слева и справа в уравнении были логарифмы по основанию 5.

{{log}_5 left(4+xright)={{log}_5 25 } }.

Функция y = {{log}_5 x } монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом 

4+x=25;
x=21.

Ответ: 21.

11. Решите уравнение: {{log}_8 left(x^2+xright)={{log}_8 left(x^2-4right) } }.

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

.

Ответ: -4.

12. Решите уравнение: 2^{{{log}_4 left(4x+5right) }}=9.

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

{{log}_4 b }=frac{{{log}_2 b }}{{{log}_2 4 }}=frac{{{log}_2 b }}{2}.

Записываем решение как цепочку равносильных переходов.

.

Ответ: 19.

13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

{{log}_{x-5} 49=2 }.

В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.

Получим систему:

small left{begin{matrix} left ( x-5 right )^2=49\x-50 \x-5 neq 1 end{matrix}right..

Первое уравнение мы получили просто из определения логарифма.

Квадратное уравнение имеет два корня: x=12 и x=-2.

Очевидно, корень x=-2 является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения: x=12.

Ответ: 12.

Тригонометрические уравнения (Часть 1 ЕГЭ по математике)

Тригонометрические уравнения? В первой части вариантов ЕГЭ? — Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.

14. Найдите корень уравнения: cos frac{pi (x+1)}{4}=frac{sqrt{2}}{2}. В ответе запишите наибольший отрицательный корень.

Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.

Сделаем замену frac{pi left(x+1right)}{4}=t. Получим: cos t=frac{sqrt{2}}{2}.

Получаем решения: t=pm frac{pi }{4}+2pi n, nin Z. Вернемся к переменной x.

frac{pi (x+1)}{4}=pm frac{pi }{4}+2pi n, nin Z. Поделим обе части уравнения на pi и умножим на 4.

x+1=pm 1+8n, nin Z;

left[ begin{array}{c}x=8n, nin Z \x=-2+8n end{array}right..

Первой серии принадлежат решения -8; 0; 8dots

Вторая серия включает решения -2; 6; 14dots

Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это x = -2.

Ответ: -2.

15. Решите уравнение: tg frac{pi left( x+1right)}{4}= -1. В ответе напишите наименьший положительный корень.

Решение:

Сделаем замену frac{pi left(x+1right)}{4}=t. Получим:tgt=-1. Решения этого уравнения:

t=-frac{pi }{4}+pi n, nin Z. Вернемся к переменной х:

frac{pi left(x+1right)}{4}=-frac{pi }{4}+pi n, n in Z. Умножим обе части уравнения на 4 и разделим на pi.

x+1=-1+4n;

x=-2+4n.

Выпишем несколько решений уравнения и выберем наименьший положительный корень:

x=-2 ;2; 6dots Наименьший положительный корень x = 2.

Ответ: 2.

Мы разобрали основные типы уравнений, встречающихся в задании №5 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №5. Простейшие уравнения. Профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Представлено: текстовой задачей.
Тип задания: с кратким ответом.
Уровень сложности: базовый.
Количество баллов: 1.
Примерное время на выполнение: 2 минуты.

Предполагается, что большинство выпускников, сдающих математику профильного уровня, способны выполнить первое задание устно.

Задание 1 ЕГЭ математика

Необходимые для его выполнения знания ученик должен усвоить уже к 5-6 классу. А именно:

  • арифметические действия;
  • десятичные дроби;
  • округление десятичных дробей;
  • перевод одних единиц измерения в другие;
  • проценты;
  • пропорции;
  • построение математической модели задачи;
  • интерпретация результата решения задачи;
  • учет реальных ограничений в интерпретации результата.

В основном встречаются задания пяти типов:

  • бытовые задачи (необходимо что-то посчитать: время в пути, стоимость товара, расход электроэнергии и т.д.);
  • на округление результата с избытком или недостатком с учетом реальных ограничений (например, сколько булочек можно купить на 100 рублей – округляем с недостатком, а сколько потребуется для ремонта рулонов обоев – с избытком);
  • на вычисление процентов (сколько будет стоить товар со скидкой, сколько процентов учащихся успешно сдали экзамены, и т.д.)
  • на пропорции (сколько таких же книг можно купить на другую сумму, сколько времени потребуется на преодоление другого расстояния с той же скоростью, и т.д.)
  • различные комбинации четырех предыдущих вариантов.

Труднее всего выпускники справляются с заданиями, где нужно посчитать время или перевести единицы из одних в другие. Важно помнить, что время считается не в десятичной системе (в сутках 24 часа, а в часе 60 минут). При решении первого задания иногда требуются дополнительные знания, например, понятие о часовом времени. Однако все вполне решаемо.

Примеры заданий ЕГЭ по математике

Пример №1

Полет самолета происходит на высоте 39000футов. 1 фут равен 30,5 см. Найдите высоту полета в метрах. Ответ округлите до целых.

Решение: Вместо фута подставим равную величину в сантиметрах, затем сантиметры переведем в метры
39000футов=39000*30,5см=1189500см=1189500*0,01м=1189,5м
В данной задаче округление производим по правилу математического округления.
1189,5м≈1190м

Ответ: 1190

Пример №2

Спортсмен пробежал 500м за 1 минуту 12 секунд. Найдите его среднюю скорость. Ответ дайте в километрах в час.

Решение: Сначала переведем 1 минуту 12 секунд в секунды.
1мин+12с= 60с+12с=72с
Так как среднюю скорость надо дать в км/ч, можем поступить двумя способами.
1) Сначала вычислить скорость в м/с и затем перевести в км/ч.
2) Перевести время в часы, расстояние в километры и затем вычислить скорость.

В данной задаче во втором способе вычисления оказываются проще.
500м=500*0,001км=0,5км
72с=72*(1/3600)ч=0,02ч
0,5 км/0,02ч=25км/ч

Ответ: 25

Пример № 3

Пакет молока стоит 45 рублей. В первой половине дня для пенсионеров предусмотрена скидка в размере 10%. Сколько рублей заплатит пенсионер за 2 пакета молока в 11 часов утра?

Решение: Сначала определяем, получит ли пенсионер скидку. 11 часов утра – время до обеда, значит получит. Дальше возможны три способа решения.

1 способ: Определяем стоимость пакета молока в процентах
100-10=90%
Находим стоимость пакета молока в рублях
45р*0,9=40,5р
Вычисляем стоимость двух пакетов молока
40,5р*2=81р

2 способ: Находим размер скидки на один пакет
45р*0,1=4,5р
Определяем цену 1 пакета молока со скидкой
45р-4,5р=40,5р
Вычисляем стоимость 2 пакетов
40,5р*2=81р

3 способ: Находим стоимость двух пакетов без скидки
45р*2=90р
Определяем размер скидки на два пакета молока
90р*0,1=9р
Вычисляем стоимость покупки
90р-9р=81р

Ответ: 81

Пример №4

Оптовая цена общей тетради составляет 40 рублей. Розничный магазин продает тетради с наценкой 20%. Сколько тетрадей сможет купить школьник, имея 570 рублей?

Решение: Находим наценку в рублях
40р*0,2=8р
Вычисляем розничную стоимость тетради
40р+8р=48р
Определяем количество тетрадей
570/48=11,875
По смыслу ответ округлить надо в меньшую сторону, так как на 12-ую тетрадь денег недостаточно.

Ответ: 11

Пример №5

Для участников конференции закупается чай. В каждой упаковке 100 пакетиков чая. За день расходуется 130 пакетиков. Какое количество упаковок необходимо закупить, если конференция продлится 4 дня.

Решение: Находим необходимое количество пакетиков чая
130пакетиков*4дня=520пакетиков
Находим нужное количество упаковок
520пакетиков/100пакетиков в упаковке= 5,2 упаковки/ По смыслу этого задания результат надо округлить в большую сторону, т.к. 5 упаковок не хватит.

Ответ: 6

Пример №6

Поезд Москва-Нижневартовск отправляется в 13:25 и прибывает на следующий день в 12:25 по местному времени. Сколько часов поезд находится в пути, если время в Нижневартовске на два часа опережает московское. Ответ дайте в часах

Решение:
Переводим время в Нижневартовске в московское
12ч 25мин+2ч=14ч 25мин
Вычисляем время в пути с учетом, что поезд прибывает через сутки
14ч 25мин+24ч-13ч 25мин=25ч

Ответ: 25

Первое задание обычно не вызывает затруднений. Однако в нем бывает довольно много ошибок, вызванных банальной невнимательностью. Прежде, чем записать ответ, прочитайте еще раз задачу. Что требуется найти? Убедитесь, что вы нашли именно то, что спрашивается в задаче, и после этого записывайте ответ.

Источник

Простейшие текстовые задачи

В первом задании профильного уровня ЕГЭ по математике нам необходимо решить простую текстовую задачу. На самом деле, мы уже встречались с решением текстовых задач как и в базовом уровне ЕГЭ. В этом случае подробно останавливаться я не планирую, поэтому перейдем непосредственно к рассмотрению примера. Трудностей, думаю, у Вас не возникнет. 🙂

Разбор типовых вариантов заданий №1 ЕГЭ по математике профильного уровня

Первый вариант (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

Поезд отправился из Санкт-Петербурга в 23 часа 50 минут (время московское) и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?

[/su_note]

Алгоритм решения:
  1. Сравниваем время отправления и прибытия.
  2. Находим. Сколько времени поезд шел до окончания времени первых суток.
  3. Определяем время движения.
  4. Записываем ответ.
Решение:

1. Поезд вышел в 23 часа 50 минут. До конца суток оставалось 10 минут.

2. Следующие сутки он был в пути 7 часов 50 минут.

3. Значит всего в пути он был: 7 часов 50 минут+10 минут=8 часов.

Ответ: 8 часов.

Второй вариант задания (из Ященко, №2)

[su_note note_color=”#defae6″]

Держатели дисконтной карты книжного магазина получают при покупке скидку 6%. Книга стоит 650 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?

[/su_note]

Алгоритм решения:
  1. Определяем объем скидки.
  2. Вычитаем из стоимости товара величину скидки.
  3. 3аписываем ответ.
Решение:

1. Скидка в 6% означает, что покупатель заплатит за книгу на 6% меньше стоимости книги. Найдем эту сумму: 650∙6/100=39 (рублей).

2. Вычитаем из стоимости книги величину скидки: 650-39=611.

3. Значит, за покупку покупатель заплатит 611 рублей.

Ответ: 611.

Третий вариант задания (из Ященко, №4)

[su_note note_color=”#defae6″]

Призёрами городской олимпиады по математике стали 36 учеников, что составило 20 % от числа участников. Сколько человек участвовало в олимпиаде?

[/su_note]

Алгоритм решения:
  1. Записываем проценты в виде десятичной дроби.
  2. Делим число учеников, ставших призерами, на эту дробь.
  3. Записываем ответ.
Решение:

1. Для того чтобы число записать в виде десятичной дроби необходимо число процентов разделить на 100 и убрать знак процентов. Выполняем это:

20/100=0,2

2. Делим 36 на полученную дробь: 36:0,2=180.

3. Значит, в олимпиаде участвовало 180 человек.

Ответ: 180.

Четвертый вариант задания (из Ященко, №7)

[su_note note_color=”#defae6″]

Для ремонта квартиры требуется 59 рулонов обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 8 рулонов?

[/su_note]

Алгоритм решения:
  1. Определяем, сколько раз по 8 рулонов содержит искомое их количество.
  2. Если число получилось не целое, к полученной целой части прибавляем 1.
  3. Записываем ответ.
Решение:

1. Разделим 59 на 8, чтобы определить, сколько раз по 8 содержит данное число:

http://self-edu.ru/htm/ege2016_36/files/1_1.files/image001.gif ,

Одна пачка клея рассчитана на 8 рулонов, а на все рулоны понадобится 7+1=8 пачек.

Значит, для ремонта нужно купить 8 пачек клея.

Ответ: 8.

Пятый вариант задания (из Ященко, №8)

[su_note note_color=”#defae6″]

Тетрадь стоит 13 рублей. Сколько рублей заплатит покупатель за 40 тетрадей, если при покупке больше 30 тетрадей магазин делает скидку 10% от стоимости всей покупки?

[/su_note]

Алгоритм решения:
  1. Находим, сколько стоят 40 тетрадей.
  2. Определяем объем скидки.
  3. Вычитаем полученную сумму из стоимости всех тетрадей.
  4. Записываем ответ.
Решение:

1. Найдем стоимость всех тетрадей:

http://self-edu.ru/htm/ege2016_36/files/2_1.files/image001.gif  руб.

2. Тетрадей было куплено более 30, следовательно, скидка составляла 10%. Определим объем скидки в рублях. Для этого проценты переведем в десятичную дробь и умножим стоимость всей покупки на эту дробь: 10%=10/100=0,1.

520∙0.1=52 (рубля).

3. Вычтем размер скидки из общей стоимости покупки: 520 – 52=468.

4. Значит, покупатель заплатил за тетради 468 рублей.

Ответ: 468.

Даниил Романович | Просмотров: 15.5k

Источник

Профильный уровень ЕГЭ по математике, в отличие от базового, более сложный и его должны сдавать выпускники, планирующие поступать в вузы на технические, инженерные, экономические специальности.

Задания в экзаменационной работе обычно выстроены от простого к сложному и первое задание это, как правило, самое легкое, как бы разминочное. Так и Задание 1 ЕГЭ по профильной математике – это задание базового уровня на знания элементарной математики, представляющее собой простейшую задачу на несложные арифметические действия.

• Вид задания — текстовая задача.

• Тип — с кратким ответом.

• Сложность — базовая.

• Максимальное количество получаемых баллов — 1.

• Период выполнения — 120 секунд.

Необходимые знания

1 задание егэ по математике

1-е Задание по профильной математике — это текстовая задача базового уровня сложности. Ответ должен быть дан в краткой форме в виде целого числа или конечной десятичной дроби, оценивается в 1 балл.

 Для выполнения задания необходимо знать:

  • арифметические действия;
  • простые и десятичные дроби и действия с ними;
  • проценты;
  • пропорции;
  • перевод одних единиц измерения в другие;
  • построение математической модели задачи;
  • интерпретация результата решения задачи;
  • учет реальных ограничений в интерпретации результата.

5 типов заданий

Наиболее часто встречаются задания пяти типов:

  • задачи, связанные с жизненными ситуациями (определение времени, веса, стоимости и т.д.);
  • на вычисление процентов;
  • на округление результата в большую или меньшую сторону;
  • на пропорции;
  • различные комбинации четырех предыдущих вариантов. 

Опыт подготовки к ЕГЭ прошлых лет показал, что у учащихся часто возникают трудности с решением задач на перевод из одних единиц измерения в другие (часы в сек., км в см, кг в гр. и т. п.). Следует обратить внимание на то, что часы и минуты считаются не в десятичной системе, ведь в часе – 60 минут, а в минуте – 60 секунд. Наиболее эффективным способом подготовки к профильной математике являются курсы «Уникум» РУДН по математике. Здесь вы получите разбор всех типов заданий, теорию и практику, пробные варианты ЕГЭ на протяжении всей подготовки. Преподаватель курсов, в том числе, сделает разбор 1-го задания ЕГЭ по математике профильного уровня.

Примеры

6 примеров по математике 1 заданиеПример 1

Автомобиль проехал 80 миль, в 1 миле 1609,34 метров. Сколько километров проехал автомобиль? Ответ округлить до целого значения.

Решение:

Определяем сколько км в 1 миле: 1 миля=1609,34 м:1000 м=1,60934 км

Сколько км проехал автомобиль: 80 миль*1,60934 км=128,7472 км

Округляем до целого значения по правилам математического округления: 128,7472  км

Ответ: 129

Пример 2

В магазине по акции продаются шоколадки. Обычная цена 1 шоколадки 35 рублей. По акции 3 шоколадки продаются по цене 2-х. Какое максимальное количество шоколадок может по акции приобрести покупатель, если он готов потратить на них не более 300 рублей?

Решение:

Определяем стоимость 3 шоколадок по акции: 2 шок.*35 руб.+1 шок.*0 руб.=70 руб. 

При продаже по акции 3 шоколадки являются одной товарной позицией. Определим, сколько таких товарных позиций можно купить на 300 руб.: 300 руб.:70 руб.=4,29

Округляем до целого, т.к. шоколадки продаются только по 3 шт.: 4*3 шок.= 12 шок.

Ответ: 12

Пример 3

Площадь стен в ванной составляет 23,8 м2. Сколько понадобится пластиковых панелей для отделки стен, если панель имеет размер 40 Х 120 см.

Решение:

Переведем размеры 1 панели из см в м: 40 см:100=0,4 м и 120 см:100=1,2 м

Площадь 1 панели в м2: 0,4м*1,2м=0,48 м2

В 23,8 м2 уложится: 23,8 м2:0,48 м2=49,58 шт.

Поскольку панели продаются целиком, для покрытия всей площади понадобится 50 панелей.

Ответ: 50

Пример 4

Средняя скорость полета самолета составляет 360 км/час. Определить его среднюю скорость в м/сек.

Решение:

Переводим км в метры: 360*1000 м=360 000 м

Часы в минуты: 1 час=60 мин, минуты в секунды: 60 мин=60*60сек= 3600 сек

Определяем скорость: 360 000 м:3600 сек=100 м/сек

Ответ: 100

Пример 5

Поезд отправился из Самары в Москву в 22 часа 10 минут (время московское) и прибыл в Москву в 10 часов 10 минут на следующие сутки. Сколько часов поезд находился в пути?

Решение:

В день отбытия из Самары поезд был в пути: 24 ч-22 ч 10 мин=23 ч 60 мин–22 ч 10 мин=1 ч 50 мин

В день прибытия поезд был в пути: 10 ч 10 мин

Общее время в пути: 1 ч 50 мин+10 ч 10 мин=11 ч 60 мин=12 ч

Ответ: 12

Пример 6

Олег живет в 9-этажном многоподъездном доме. На каждом этаже находится по 4 квартиры. Олег живёт в квартире №81. Укажите номер подъезда, в котором живёт Олег?

Решение:

Количество квартир в одном подъезде: 9 * 4=32

Значит квартиры распределяются по подъездам так:

1-й подъезд – с 1-й по 32-ю

2-й – с 33-й по 64-ю

3-й – с 65-й по 96-ю

Квартира №81 находится в 3-м подъезде

Ответ: 3

В Задании 1 профильной математики как правило встречаются задачи на действия с дробями в том или ином виде.

Действия с дробями

действие с дробями математика 1 заданиеДля того, чтобы получить правильный ответ на 1 задание ЕГЭ по математике, теорию нужно знать в первую очередь. Сложности у сдающих ЕГЭ возникают с дробями и задачами, где представлены дроби. Дробью называется форма представления числа. Сама дробная черта означает деление. Делимое — это числитель дроби, знаменатель — делитель. С дробями можно делать все то, что и с обычными числами: делить, умножать, складывать, вычитать.

Сложение дробей

Сложение дробей с одинаковыми знаменателями.

Пример: сложить дроби 

Числители 1-й и 2-й дроби складываются, знаменатель остается неизменным

Сложение дробей с различающимися знаменателями:

Пример: сложить дроби 

Сначала дроби нужно привести к общему знаменателю, таким знаменателем является произведение знаменателей 1-й и 2-й дроби, а числитель 1-й дроби умножается на знаменатель 2-й, числитель 2-й дроби на знаменатель 1-й. Затем числители складываются: 

Вычитание дробей проводится аналогично сложению. Просто числители не складываются, а вычитаются.

Умножение дробей

Пример: перемножить дроби: 

Просто перемножаются числители и знаменатели 

Деление дробей

Пример:  разделить 

Деление заменяем на умножение на дробь обратную дроби, на которую делим 

Как видите, задачи из Задания 1 по профильной математике легкие, на знания математики из курса младших и средних классов, что, однако не отменяет необходимость освежить в памяти эти знания и еще раз порешать эти несложные задачи. Особенно полезно решать реальные варианты заданий прошлых лет под контролем опытных преподавателей. А такую возможность и дают подготовительные курсы «Уникум» РУДН по математике.

Источник
ЕГЭ по математике профиль

Материал для отработки заданий №1 в ЕГЭ по профильной математике — теория и практика.

Задание №1 в варианте ЕГЭ по математике профильного уровня  – одно из самых легких. И тем не менее ученики часто ошибаются, решая такие задачи. Почему?

Потому что не прочитали условие или допустили арифметическую ошибку.

Внимательно читайте условие и проверяйте решение.

Задачи в разъяснениях специально подобраны так, чтобы представить все возможные типы заданий.

Автор: Алькаева Лариса Рахимовна

→ скачать конспект

→ скачать практические задания

Виды задач в задании №1:

— вычисления, простейшие уравнения и пропорции;

— задачи на округление (с недостатком, с избытком);

— задачи на проценты

Источник информации: vk.com/club169850563

Связанные страницы:

Источник

За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 80.6%
Ответом к заданию 1 по математике (профильной) может быть целое число или конечная десятичная дробь.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

В треугольнике $ABC$ угол $C$ равен $90^°$, $BC=7$, $cos A={3} / {5}$
(см. рис.). Найдите $AB$.

Решение

$sin A = {BC}/{AB}$.

$sin^2A + cos^2A = 1$, то есть $sin A = √{1 — {9}/{25}} = {4}/{5}$.

${4}/{5} = {7}/{AB}, AB = {35}/{4}=8.75$.

Ответ: 8.75

Задача 2

Угол $ACO$ равен $32^°$. Его сторона $CA$ касается окружности с центром в точке $O$. Сторона $CO$ пересекает окружность в точках $B$ и $D$ (см. рис.). Найдите градусную меру дуги $AD$ окружности, заключённой внутри этого угла. Ответ дайте в градусах.

Решение

$∠ AOC=90°-∠ ACO$, так как $∠ OAC=90°$ (радиус, проведённый в точку касания, перпендикулярен касательной). $∠ AOC=90°-32°=58°$. $∠ AOC$ — центральный и измеряется дугой $AB$, то есть $⌣ AB=58°$. Отсюда: дуга $AD$ равна $180°-58°=122°$, так как дуга $DB=180°$.

Ответ: 122

Задача 3

Через концы $A$ и $B$ дуги окружности с центром $O$ проведены касательные $AC$ и $BC$ (см. рис.). Меньшая дуга $AB$ равна $48^°$. Найдите угол $ACB$. Ответ дайте в градусах.

Решение

$∠C AB = ∠C BA$, как углы между хордой и касательной, они измеряются половиной дуги $AB$, то есть $∠C AB = {1}/{2} ︶ AB$ и $∠C BA = {1}/{2} ︶ AB$.

Отсюда, $∠AC B = 180°- ︶AB = 180° — 48° = 132°$.

Ответ: 132

Задача 4

Периметр треугольника равен $73$, а радиус вписанной окружности равен $4$. Найдите площадь этого треугольника.

Решение

$S_{ABC} = p · r$, где $p$ — полупериметр треугольника, а $r$ — радиус вписанной окружности, тогда $S_{ABC} = {73}/{2} · 4 = 146$.

Ответ: 146

Задача 5

Периметр треугольника равен $40$, а радиус вписанной окружности равен $3$. Найдите площадь этого треугольника.

Решение

$S_{ABC} = p · r$, где $p$ — полупериметр треугольника, а $r$ — радиус вписанной окружности, тогда $S_{ABC} = {40}/{2} · 3 = 60$.

Ответ: 60

Задача 6

Отрезки $MN$ и $AB$ — диаметры окружности с центром $O$ (см. рис.). Угол $AOM$ равен $28^°$. Найдите вписанный угол $MNB$. Ответ дайте в градусах.

Решение

$∠AOM$ — центральный, он измеряется дугой $AM$, то есть $︶AM = 28°$. $AB$ — диаметр, значит $︶AB = 180°$, а $︶MB = 180° — 28° = 152°$. $∠MNB$ — вписанный и он измеряется половиной дуги $MB$, то есть $∠MNB = 76°$.

Ответ: 76

Задача 7

Отрезки $MN$ и $AB$ — диаметры окружности с центром $O$ (см. рис.). Угол $MOB$ равен $116^°$. Найдите вписанный угол $MAB$. Ответ дайте в градусах.

Решение

$∠ MOB$ — центральный, он измеряется дугой $MB$. $∠ MAB$ — вписанный и он измеряется половиной дуги $MB$, то есть $∠ MAB={116°} / {2}=58°$.

Ответ: 58

Задача 8

В треугольнике $ABC$ равны боковые стороны $AC=BC$, $AH$ — высота, $AB=15$,
$sin ∠ BAC=0{,}6$ (см. рис.). Найдите $BH$.

Решение

В равнобедренном треугольнике углы при основании равны.

$∠BAC = ∠ABC, sin ∠ABC = {AH}/{AB}, AH = AB sin ∠ABC. AH = 15 · 0.6 = 9$.

Из $△AHB: HB = √{AB^2 — AH^2} = √{225 — 81} = √{144} = 12$.

Ответ: 12

Задача 9

В треугольнике $ABC$ $AC=BC$, $AH$ — высота, $AB=15$, $sin ∠ BAC={√ {5}} / {3}$ (см. рис.). Найдите $BH$.

Решение

В треугольнике напротив равных сторон лежат равные углы. $∠ BAC=∠ ABC$, $sin ∠ ABC={AH} / {AB}$, $AH=AB sin ∠ ABC$. $AH=15⋅ {√ {5}} / {3}=5√ {5}$. Из $▵ AHB:$ $HB=√ {AB^2-AH^2}=√ {225-125}=√ {100}=10$.

Ответ: 10

Задача 10

В треугольнике $ABC$ угол $C$ равен $90^°$, $BC=9$, $sin A={4} / {11}$ (см. рис.). Найдите $AB$.

Решение

$sin A = {BC}/{AB}, AB = {BC}/{sin A} = {9}/{{4}/{11}} = {99}/{4} = 24.75$.

Ответ: 24.75

Задача 11

Найдите периметр прямоугольника, если его площадь равна $224$, а отношение соседних сторон равно ${2} / {7}$.

Решение

Рассмотрим прямоугольник $ABCD$

$AD : AB = 2 : 7, S_{ABCD} = AD · AB$

$S_{ABCD} = 224$, тогда $224 = AD · AB$

Пусть $x$ — некоторое положительное действительное число, тогда $AD = 2x, AB = 7x$

Отсюда, $224 = 2x · 7x$

$224 = 14x^2$

$x^2 = {224}/{14}$

$x^2 = 16$

$x = 4$

Следовательно, $P = 2(AD+AB) = 2(2·4+7·4) = 2·4(2+7) = 8·9 = 72$.

Ответ: 72

Задача 12

Найдите периметр прямоугольника, если его площадь равна $48$, а отношение соседних сторон равно $3:4$.

Решение

Рассмотрим прямоугольник $ABCD$ (см. рис.). $AD:AB=3:4$, $S_{ABCD}=AD⋅ AB$; $S_{ABCD}=48$, тогда
$48=AD⋅ AB$. Пусть $k$ — некоторое положительное действительное число и
$AD=3k$, $AB=4k$. Отсюда $48=3k⋅ 4k$; $48=12k^2$; $k^2=4$, $k=2$. Следовательно, $P=2(AD+AB)=2(3⋅ 2+4⋅ 2)=28$.

Ответ: 28

Задача 13

Площадь прямоугольника равна $22$. Найдите его большую сторону, если она на $9$ длиннее меньшей стороны.

Решение

$S_{ABCD} = AB·CB$.

Обозначим большую сторону через $x$, тогда меньшая сторона $x — 9$. Итак, $22 = x(x — 9)$

$ x^2 — 9x — 22 = 0$

$D = 81 + 88 = 169 = 13^2$

$ x = {9±13}/{2}$

$ x_1 = 11$

$ x_2 = -2$ (не подходит).

Ответ: 11

Задача 14

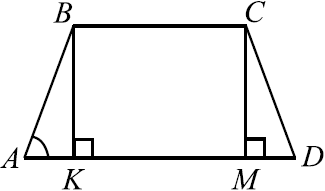
Основания равнобедренной трапеции равны $15$ и $9$. Высота трапеции равна $6$. Найдите тангенс острого угла.

Решение

Рассмотрим трапецию $ABCD$. Пусть $AB = CD, BK$ и $CM$ — высоты. Тогда $AK = MD$ и $AD = BC + 2AK$.

$tg ∠BAD = {BK}/{AK}, AK = {AD — BC}/{2} = {15 — 9}/{2} = 3, BK = 6$ (по условию). $tg ∠BAD = {6}/{3} = 2$.

Ответ: 2

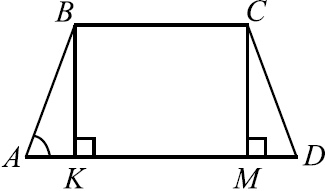
Задача 15

Основания равнобедренной трапеции равны $14$ и $6$. Высота трапеции равна $7$. Найдите тангенс острого угла.

Решение

Рассмотрим трапецию $ABCD$. Пусть $AB = CD, BK$ и $CM$ высоты. Тогда $AK = MD$ и $AD = BC + 2AK$.

$tg ∠BAD = {BK}/{AK}, AK = {AD — BC}/{2} = {14 — 6}/{2} = 4, BK = 7$ (по условию). $tg ∠BAD = {7}/{4} = 1.75$.

Ответ: 1.75

Задача 16

В треугольнике $ABC$ угол $C$ равен $90^°$, $AC=6√ {3}$, $tg A={√ {3}} / {3}$ (см. рис.). Найдите $AB$.

Решение

$tgA = {BC}/{AC}, {√3}/{3} = {BC}/{6√3}, BC = {6√3·√3}/{3} = 6$.

Из $△ABC: AB^2 = AC^2 + BC^2$;

$AB^2 = (6√3)^2 + 6^2 = 36·3 + 36 = 36·4 = 144, AB = 12$.

Ответ: 12

Задача 17

Найдите площадь ромба, если его диагонали равны $5$ и $16$.

Решение

Рассмотрим ромб $ABCD$.

$S_{ABCD} = {1}/{2}d_1d_2$, где $d_1$ и $d_2$ — диагонали ромба.

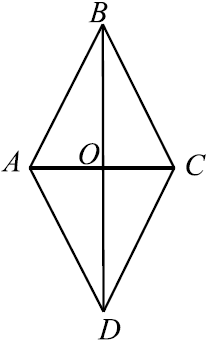
$S_{ABCD} = {1}/{2}·5·16 = 40$.

Ответ: 40

Задача 18

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $150^°$. Боковая сторона треугольника равна $12$. Найдите площадь этого треугольника.

Решение

Пусть в $△ABC ∠C = 150°, AC = CB$.

$S_{ACB} = {1}/{2}AC·CB·sin∠ACB = {1}/{2}·12·12·sin150° = 72·sin 30° =72·{1}/{2} = 36$.

Ответ: 36

Задача 19

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $30^°$. Боковая сторона треугольника равна $7$. Найдите площадь этого треугольника.

Решение

Пусть в $▵ ABC$ $∠ C=30°$, $AC=BC=7$ (см. рис.). $S_{ACB}={1} / {2} AC⋅ CB⋅ sin ∠ ACB={1} / {2}⋅ 7⋅ 7⋅ sin 30°={1} / {2}⋅ 49⋅ {1} / {2}={49} / {4}=12{,}25$.

Ответ: 12.25

Задача 20

Периметр прямоугольника равен $28$, а площадь $48$. Найдите меньшую сторону прямоугольника.

Решение

Пусть $x$ и $y$ — две стороны прямоугольника. Из условия следует система уравнений:
${{table {2(x+y)=28{,}}; {xy=48{.}};}$

Из первого уравнения системы: $x+y=14$

$y=14-x$.

Подставляя выражение для переменной $y$ во второе уравнение системы, получим:

$x(14-x)=48$

$x^2-14x+48=0$

$x_1=8$

$x_2=6$

Тогда $y_1=14-8=6$

$y_2=14-6=8$

Следовательно, меньшая сторона прямоугольника равна $6$.

Ответ: 6

Рекомендуемые курсы подготовки

Источник

Понравилась статья? Поделить с друзьями:
  • Как решить задачу с параметром егэ
  • Как решить задачу по математике по егэ
  • Как решить задачи по геометрии в егэ
  • Как решить задание 2 егэ по информатике с помощью компьютера
  • Как решить задание 18 егэ математика профиль