Как решить задачи по геометрии в егэ - Помощь в подготовке к экзаменам и поступлению

Геометрия на ЕГЭ по математике

Геометрия на профильном ЕГЭ по математике — одна из сложных тем для абитуриентов. Дело в том, что когда-то экзамен по геометрии в школе был обязательным, а сейчас — нет. В результате у большинства абитуриентов знания по геометрии близки к нулю.

Геометрия на профильном ЕГЭ — это три задачи в части 1 (сюда входит и планиметрия, и стереометрия), а также задача 14 (стереометрия) и для многих недосягаемая задача 16 (геометрия) из второй части. Как же научиться их решать?

Начнем с планиметрии. Прежде всего, выучите основные формулы геометрии.

На нашем сайте вы найдете курс геометрии с нуля — основные определения, формулы и теоремы, а также разбор множества экзаменационных задач по геометрии из части 1.

Для решения задач по геометрии из части 2 нужна более серьезная подготовка.

Первый этап — теория. Необходимый материал есть в учебнике по геометрии за 7-9 класс (автор — А. В. Погорелов или Л. С. Атанасян). Выпишите в тетрадь определения и формулировки теорем. Сделайте чертежи. Доказывать теоремы старайтесь самостоятельно.

Программа по геометрии.

1. Треугольники. Элементы треугольника. Вершины и стороны. Высоты, медианы, биссектрисы (определения).

2. Построение треугольника: практические задания.
а) Три стороны треугольника ABC равны 4,6 и сантиметров соответственно. Постройте треугольник ABC с помощью циркуля и линейки.
б) В треугольнике ABC угол равен градусов, сторона равна , равна . Постройте треугольник ABC .
в) В треугольнике ABC сторона равна , угол равен $26^{circ}$ , угол равен $58^{circ}$ . Постройте треугольник ABC .

3. Три признака равенства треугольников. Неравенство треугольника.

4. Постройте с помощью циркуля и линейки:
а) серединный перпендикуляр к отрезку;
б) биссектрису угла.

5. Углы при параллельных прямых и секущей. Вертикальные, смежные, соответственные, односторонние и накрест лежащие углы. Их определение и свойства.

6. Теорема о сумме углов треугольника.

7. Внешний угол треугольника.

8. Постройте в одном и том же треугольнике
а) Три высоты. Рассмотрите также случаи тупоугольного и прямоугольного треугольника.
б) Три биссектрисы.
в) Три медианы.

9. Равнобедренный треугольник. Определение и свойства. Высота в равнобедренном треугольнике.

10. Средняя линия треугольника и ее свойства.

11. Прямоугольный треугольник. Теорема Пифагора.

12. Определения синуса, косинуса и тангенса:
— для острого угла прямоугольного треугольника;
— для произвольного угла.

13. Четырехугольники. Сумма углов четырехугольника.

14. Параллелограмм. Определение и свойства. Площадь параллелограмма.

15. Виды параллелограммов и их свойства (ромб, прямоугольник, квадрат).

16. Трапеция. Средняя линия трапеции. Площадь трапеции.

17. Подобные треугольники. Три признака подобия треугольников.

18. Площадь треугольника. Формулы $S=frac{1}{2}ah$ и $S=frac{1}{2}absin C$ .

19. Теоремы синусов и косинусов.

20. Чему равно отношение площадей подобных фигур.

21. Свойство медианы (в каком отношении делятся медианы в точке пересечения?)

22. Свойство биссектрисы (в каком отношении биссектриса делит противоположную сторону?)

23. Окружность и круг. Длина окружности. Площадь круга. Длина дуги и площадь сектора.

24. Теорема о радиусе, проведенном в точку касания.

25. Центральный и вписанный углы. Связь между ними.

26. Теоремы о вписанных углах.

27. Теорема о пересекающихся хордах.

28. Теорема об отрезках длин касательных, проведенных из одной точки.

29. Теорема о секущей и касательной.

30. Дан треугольник ABC . Постройте:
а) окружность, вписанную в данный треугольник;
б) окружность, описанную вокруг данного треугольника.
Где находятся центры этих окружностей?

31. Еще три формулы площади треугольника (через радиус вписанной окружности, через радиус описанной окружности и формула Герона).

32. Когда можно вписать окружность в четырехугольник? Когда — описать вокруг четырехугольника?

Программа по стереометрии

Разбирая и решая задания ЕГЭ по геометрии, вы заметите очень интересную вещь. Простые задачи из части 1, разобранные на нашем сайте, часто оказываются базовыми схемами, на которых строятся сложные задачи из части 2 профильного ЕГЭ.

Решая на ЕГЭ задачи по геометрии, обращайте особое внимание на оформление. Помните совет, который дал абитуриентам автор бестселлера «Математика — абитуриенту» В. В. Ткачук. Вот он, этот ценнейший совет:

«Подробность решения должна быть такова, чтобы его мог понять человек в 10 (десять) раз глупее вас».

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Геометрия на ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Мотивация

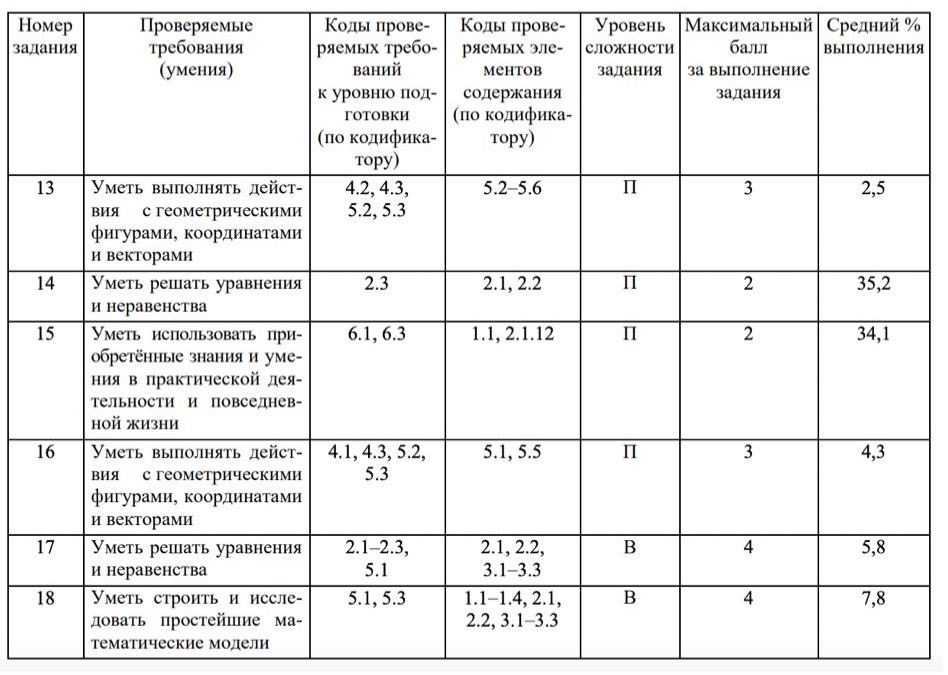
Если вы откроете список всех задач по Планиметрии №16, которые встречались на ЕГЭ по Профилю за всё время его существования, вы удивитесь тому, как сильно она усложнилась, и на сегодняшний день на этой позиции стоит достаточно содержательная геометрическая задача с действительно порой навороченными конструкциями, которые вводят в ступор, начинающих её решать школьников. Всё это еще приправлено тем, что из года в год, на фоне эволюции этой задачи, или из-за этого, процент учеников школ решающих геометрию в ЕГЭ весьма низкий:

Хуже решается только задача по Стереометрии №13. Отсюда комом накатывается мнение, что «№16 решать дано не всем», «лучше меньше баллов, зато точно решу №12», «я нарисовал треугольник, а что делать не вижу дальше» и куча других деструктивных мыслей, которые точно не помогают вам в подготовке к ЕГЭ. По факту, из моего личного опыта, задачи по Геометрии что в ЕГЭ, что в ОГЭ, очень плохо решаются в силу отсутствия какого-то четкого алгоритма действий(как это есть в параметрах, уравнениях и неравенствах, финансовой математике), которые бы точно приводили к конкретным результатам — делай раз, делай два…

Всё правда, нам нужен не просто набор теории и формул с фактами, этого недостаточно. Нам нужна практика, опыт решения задач и стараться чувствовать эту логику при решении задач. И тут я не открою странных лайфхаков, секретных методик, будистких тайн и введьминых приколов. Будем честны, нужно время, конкретная структура и понятный набор ресурсов.

В рамках этой статьи я вложу весь свой преподавательский опыт и свои знания, как человека, который не перестаёт учиться и осваивать новые знания, чтобы помочь вам забрать на экзамене баллы за одну из самых сложных задач.

Начинаем с азов

Давайте представим, что ваша задача поднять с нуля ваши знания по геометрии на приемлемый для ЕГЭ и выше уровень. Нам не обойтись без основ и фундамента, с которым вы встречались со времен 7 класса. Что делаем? Берем учебник Атанасяна, и тут у многих расширятся зрачки и волна ужаса пройдет ледяной лавиной от бровей до мизинцев. На самом деле прошу не пугаться, нам нужен какой-то подробный школьный учебник, в котором будет изложена вся структурированная теория, необходимая и та, что мы можем применять для решения задач. Если у вас есть альтернативный — без проблем, используйте его.

Схема работы следующая: открываем со второй главы и для каждого параграфа нас будут интересовать все доказанные теоремы, а вернее не просто сухой факт, а то откуда он берется и как его доказать. Сначала пробуем сами как-то к этому придти, если не получается, то смотрим на то, какое доказательство приводит автор.

Важно! Мы не сидим тупо перед книжкой, развивая геморрой, мы берем ручку и листочек, и сидим выписываем, конспектируем и пробуем доказывать все указанные теоремы. А после просматриваем задачи в конце, решать все не нужно, только те, которые вам покажутся реально сложными и с наскока не понятными как решать.

Что нам это даст? Мы учимся воспринимать конструкции, понимать логику построения доказательства в геометрии того или иного утверждения, а также мы сами того не подозревая запоминаем всю нужную информацию, которую мы будем применять позже для решения задач №16 на ЕГЭ!

Подумайте сами, математика — это про структуру, логику, и сколько вам нужно времени чтобы зазубрить строчку предложения? 5 ? 10 минут? А на сколько вас хватит держать это всё в голове? Вы забудете при первой же возможности. Нам нужна логика доказательства этого факта, благодаря которой наш мозг будет обучаться новому подходу в мышлении и все что связанно с геометрическими фактами вы запомните намного лучше, если будете реально пытаться доказать простейшие факты из учебника. А также на самом экзамене, уровень стресса которого пробивает все возможные значения, вы будете 100% уверены, что используемый вами факт при решении задачи не вымысел возбужденного воображения.

Сколько нужно на это времени? Если идти со скоростью две главы в день, то около недели.

Как закрепить полученный результат на практике?

Теперь, друг, ты — мощь и сила! Но без практики нам не обойтись поэтому все полученные навыки начинаем применять для решения конкретных задач. Тут нам поможет книга Гордина «Планиметрия».

Схема работы с ней следующая: можете кратко просмотреть задачи данные в качестве разобранных в начале каждой главы, попробовать решить самостоятельно и потом сравнить с данным решением. Далее, переходим на отработку задач первого уровня, тут прям всё решать нет большого смысла, хоть и страшно полезно, но в режиме ограниченного времени сразу смотрим на задачи второго уровня и пытаемся прорешать максимальное количество в каждом разделе. После того как разобрались со вторым уровнем стараемся решить задачи из третьего, но тут уже можно прыгать с задачи на задачу, так как местами именно в третий уровень уже включены задачи чуть сложнее ЕГЭ. И ещё: главы про симметрии, вектора, координаты и повороты можете пропускать, если чувствуете нехватку сил, времени и вдохновения.

Кабанеем

Если со всем предыдущими пунктами справились — Glückwünsch! Поздравляю! У нас как раз есть время чтобы порешать сложные задачи и разобрать другие методы для планиметрии Прасолова. Это поможет вам разобраться с самыми разнообразными методами, которые могут повстречаться вам при решении геометрических задач. Плюс, будет реально посмотреть эту книгу и книгу Ткачука при подготовке уже к ДВИ МГУ, но это совсем другая история))

Уровень: Убийца планиметрии

На этом мы выходим на финальный этап и раз наша цель именно ЕГЭ, то дальше делаем следующее:

Открываем все задачи ЕГЭ с 2014 года и планомерно их прорешиваем. Такая процедура даст нам понимание того, что такое реальные ЕГЭшные задачи, а не Статград, от которого порой хочется сбежать. Плюс нарабатывается навык решения задачи за ограниченное время и правильное оформление всего что вы нарешали.

На этом всё?

На этом этапе я всегда даю себе время на подумать, потому что хочется что-то ещё добавить и впихнуть максимальное количество пользы. Но в данном случае, я в одной статье уместил годы опыта и сотни учеников. Схема рабочая, пользуйтесь.

Всегда рад отзывам и комментариям!

С Пламенной любовью,
Никита Салливан из Умскул.

Источник

7 декабря 2017

В закладки

Обсудить

Жалоба

Основные методы решения задач по геометрии на ЕГЭ

Задания №14 и №16 повышенного уровня сложности с развёрнутым ответом.

Презентация: mr-geo.pdf

Источник

Как подготовиться к решению заданий ЕГЭ № 14 по стереометрии | 1С:Репетитор

Как показывают результаты профильного экзамена по математике, задачи по геометрии — в числе самых сложных для выпускников. Тем не менее, решить их, хотя бы частично, а значит заработать дополнительные баллы к общему результату возможно. Для этого необходимо, конечно, знать достаточно много о «поведении» геометрических фигур и уметь применять эти знания для решения задач. Здесь мы постараемся дать некоторые рекомендации, как подготовиться к решению задачи по стереометрии.

Эта задача обычно состоит из двух частей:

доказательной, в которой вас попросят доказать некоторое утверждение для заданной конфигурации геометрических тел;

вычислительной, в которой нужно найти некоторую величину, опираясь на то утверждение, которое вы доказали в первой части задачи.

За решение данной задачи на экзамене по математике в 2018 году можно получить максимум два первичных балла. Допускается решить только «доказательную» или только «вычислительную» часть задачи и заработать в этом случае один первичный балл.

Многие школьники на экзамене даже не приступают к решению задачи №14, хотя она значительно проще, например, задачи № 16 — по планиметрии.

В задачу № 14 традиционно включается лишь несколько вопросов из всех возможных для стереометрических задач:

нахождение расстояний в пространстве;

нахождение углов в пространстве;

построение сечения многогранников плоскостью;

нахождение площади этого сечения или объемов многогранников, на которые эта плоскость поделила исходный многогранник.
В соответствии с этими вопросами строится и подготовка к решению задачи.

Сначала, разумеется, нужно выучить все необходимые аксиомы и теоремы, которые понадобятся для доказательной части задачи. Помимо того, что знание аксиом и теорем поможет вам на экзамене непосредственно при решении задачи, их повторение позволит систематизировать и обобщить ваши знания по стереометрии вообще, то есть создать из этих знаний некую целостную картину.

Итак, что же нужно выучить?

Способы задания плоскости в пространстве, взаимное расположение прямых и плоскостей в пространстве.

Определения, признаки и свойства параллельных прямых и плоскостей в пространстве.

Определения, признаки и свойства перпендикулярных прямых и плоскостей в пространстве.

После того как вы повторили теорию, можно приступать к рассмотрению методов решения задач. В курсе «1C:Репетитор» представлены все необходимые материалы для подготовки: видеолекции с теорией, тренажеры с пошаговым решением задач, тесты для самопроверки, интерактивные модели, позволяющие ученикам 10-х и 11-х классов наглядно рассмотреть методы решения задач по стереометрии, в том числе на примерах задач ЕГЭ 2017 года.

Мы рекомендуем решать задачи в такой последовательности:

Углы в пространстве (между скрещивающимися прямыми, между прямой и плоскостью, между плоскостями);
Расстояния в пространстве (между двумя точками, между точкой и прямой, между точкой и плоскостью, между скрещивающимися прямыми);
Решение многогранников, то есть нахождение углов между ребрами и гранями, расстояний между ребрами, площадей поверхностей, объемов по заданным в условии задачи элементам;
Сечения многогранников — методы построения сечений (например, метод следов) и нахождения площадей сечений и объемов получившихся после построения сечения многогранников (например, использование свойств перпендикулярной проекции и метод объемов).

Для всех указанных типов задач существуют различные методы решения:

классический (основанный на определениях и признаках);

метод проекций;

метод замены точки;

метод объемов.

Эти методы нужно знать и уметь применять, так как есть задачи, которые довольно сложно решаются одним методом и гораздо проще — другим.

При решении стереометрических задач более эффективным по сравнению с классическим методом нередко оказывается векторно-координатный. Классический метод решения задач требует отличного знания аксиом и теорем стереометрии, умения применять их на практике, строить чертежи пространственных тел и сводить стереометрическую задачу к цепочке планиметрических. Классический метод, как правило, быстрее приводит к искомому результату, чем векторно-координатный, но требует определенной гибкости мышления. Векторно-координатный метод представляет собой набор готовых формул и алгоритмов, но при этом требует более длительных расчетов; тем не менее, для некоторых задач, например, для нахождения углов в пространстве, он предпочтительнее классического.

Многим абитуриентам не позволяет справиться со стереометрической задачей неразвитое пространственное воображение. В этом случае мы рекомендуем использовать для самоподготовки интерактивные тренажеры с динамическими моделями пространственных тел. Такие тренажеры есть на портале «1С:Репетитор» (для перехода к их использованию необходимо зарегистрироваться): работая с ними, вы не только сможете «выстроить» решение задачи «по шагам», но и на объемной модели увидеть все этапы построения чертежа в различных ракурсах.

С помощью таких же динамических чертежей мы рекомендуем учиться строить сечения многогранников. Кроме того, что модель автоматически проверит правильность вашего построения, вы сами сможете, рассматривая сечение с разных сторон, убедиться, верно или неверно оно построено, и если неправильно, то в чем именно ошибка. Построение сечения на бумаге, с помощью карандаша и линейки, конечно, таких возможностей не дает. Посмотрите пример построения сечения пирамиды плоскостью с использованием такой модели (Нажмите на картинку, что бы перейти к тренажеру):

Последний вопрос, на который надо обратить внимание, — это нахождение площадей сечений или объемов, получившихся после построения сечения многогранников. Здесь также существуют подходы и теоремы, которые позволяют в общем случае существенно сократить трудозатраты на поиск решения и получение ответа. В курсе «1С:Репетитор» мы знакомим вас с этими приемами.

Если вы следовали нашим советам, разобрались со всеми вопросами, которые здесь затронуты, и решили достаточное количество задач, то велика вероятность, что вы практически готовы к решению задачи по стереометрии на профильном ЕГЭ по математике в 2018 году. Дальше необходимо только поддерживать себя «в форме» до самого экзамена, то есть решать, решать и решать задачи, совершенствуя свое умение применять изученные приемы и методы в разных ситуациях. Удачи!

Регулярно тренируйтесь в решении задач

Чтобы начать заниматься на портале «1С:Репетитор», достаточно зарегистрироваться.
Вы можете:

Начать заниматься бесплатно.
Получить доступ ко всей теории и тренажерам задачи №14. Это стоит всего 990 рублей.
Купить доступ к этой задаче в составе экспресс-курса «Геометрия» и научиться решать задачи №14 и №16 на максимальный балл.

Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Включают теорию в форме текстов, слайдов и видео, задачи с решениями, интерактивные тренажеры, модели, и тесты.

Остались вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.

Здесь ключевые фразы, чтобы поисковые роботы лучше находили наши советы:
Как решать задание 14 на экзамене ЕГЭ, задачи по геометрии, решение задач, по стереометрии, методы решения задач, тренажеры, видео, КИМ ЕГЭ 2017, подготовка к ЕГЭ, профиль математика, математика профильного уровня, решение задачи по наклонной треугольной призме, грани, взаимно перпендикулярно, общее ребро, плоскости, точки, ребро равно, боковая поверхность, решение задач на сечение многогранника, перпендикулярное сечение, вычислить объем фигуры, в основании прямой треугольной призмы лежит, признаки равенства и подобия треугольников, примеры решения задач ЕГЭ по геометрии, вычисление сечения, задачи по математике профильного уровня, применение методов сечения, решение задач на площадь, задачи ЕГЭ 2017 по стереометрии, подготовка к ЕГЭ, выпускникам 11 класса, в 2018 году, поступающим в технический вуз.

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.

а)  докажите, что биссектриса угла С делит отрезок МN пополам

б)  пусть Р  — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.

Источник: ЕГЭ по математике 19.06.2014. Основная волна, резервная волна. Запад. Вариант 1

Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°.

а)  Докажите, что ∠CBE = ∠COE.

б)  Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE  =  24.

Медианы AA₁, BB₁ и CC₁ треугольника ABC пересекаются в точке M. Известно, что AC  =  3MB.

а)  Докажите, что треугольник ABC прямоугольный.

б)  Найдите сумму квадратов медиан AA₁ и CC₁, если известно, что AC = 12.

На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M  — середина стороны AB.

а)  Докажите, что

б)  Найдите расстояние от точки M до центров квадратов, если AC  =  10, BC  =  32 и ∠ACB  =  30°.

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016

На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.

а)  Докажите, что точки A, B, K и E лежат на одной окружности.

б)  Найдите радиус этой окружности, если AB = 12, CH = 5.

Пройти тестирование по этим заданиям

Источник